Iron Loss Calculation Methods for Numerical Analysis of 3D-Printed Rotating Machines: A Review
Abstract
1. Introduction

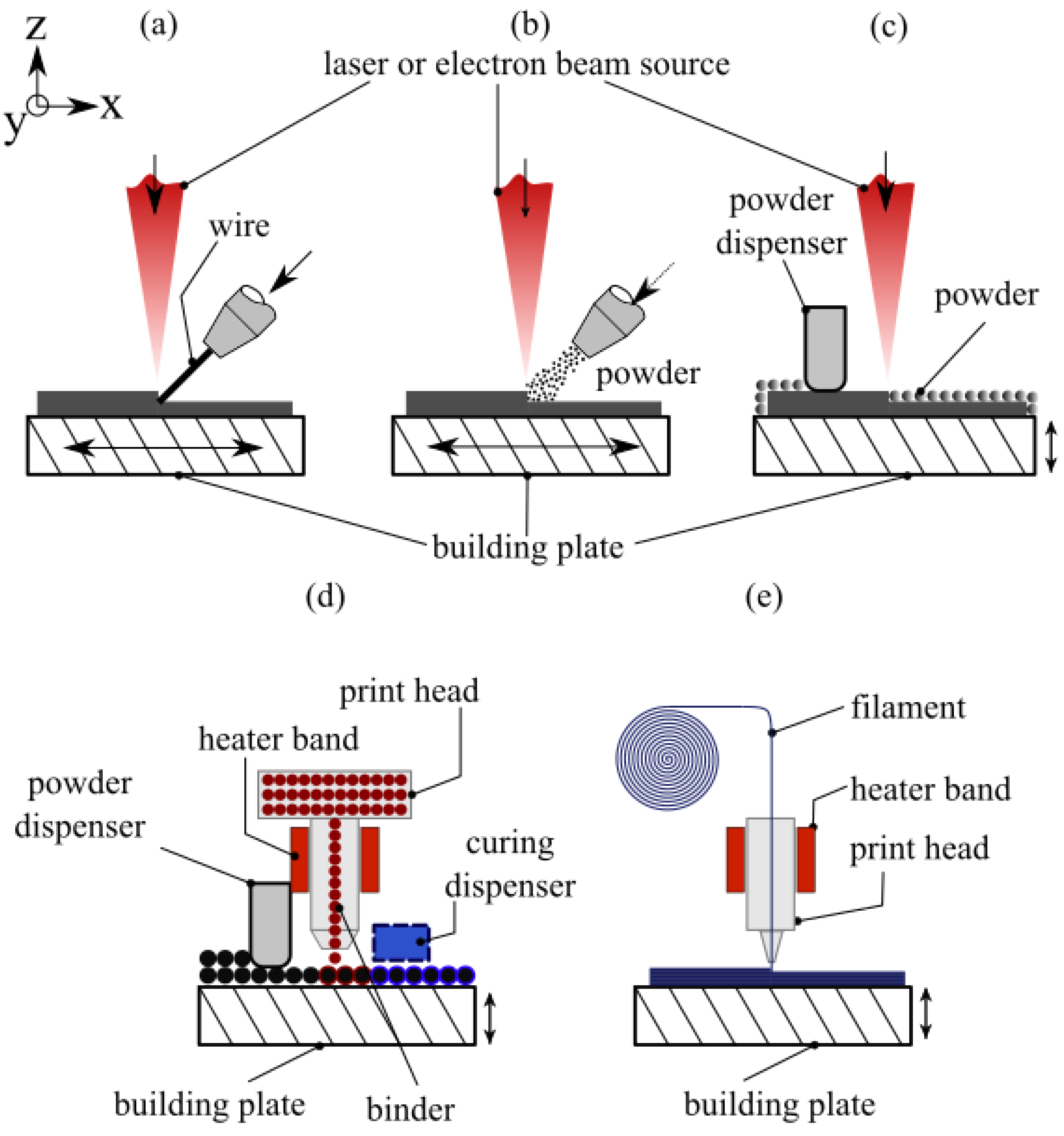
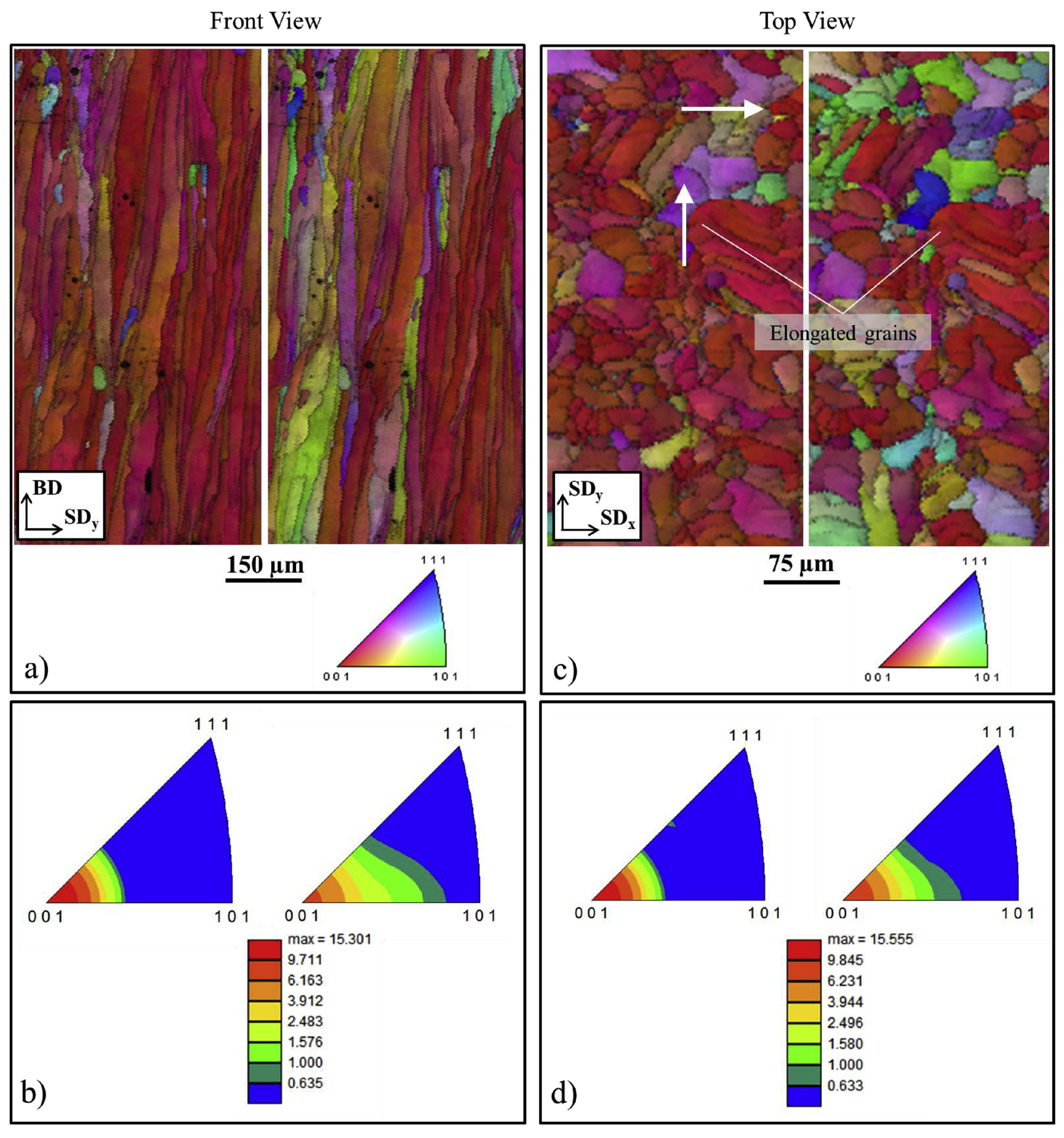
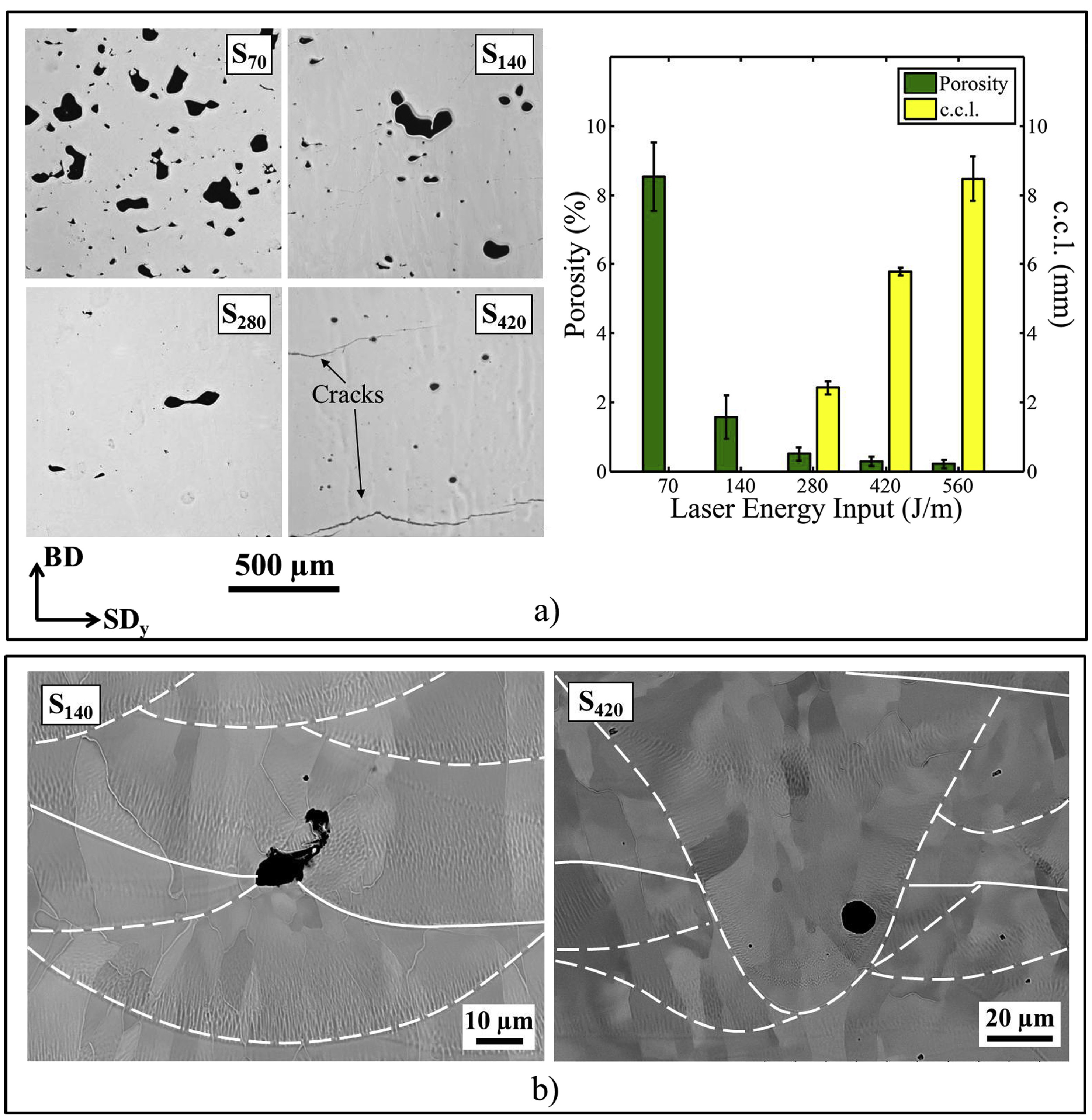
2. Advancements of 3D Printing Technology
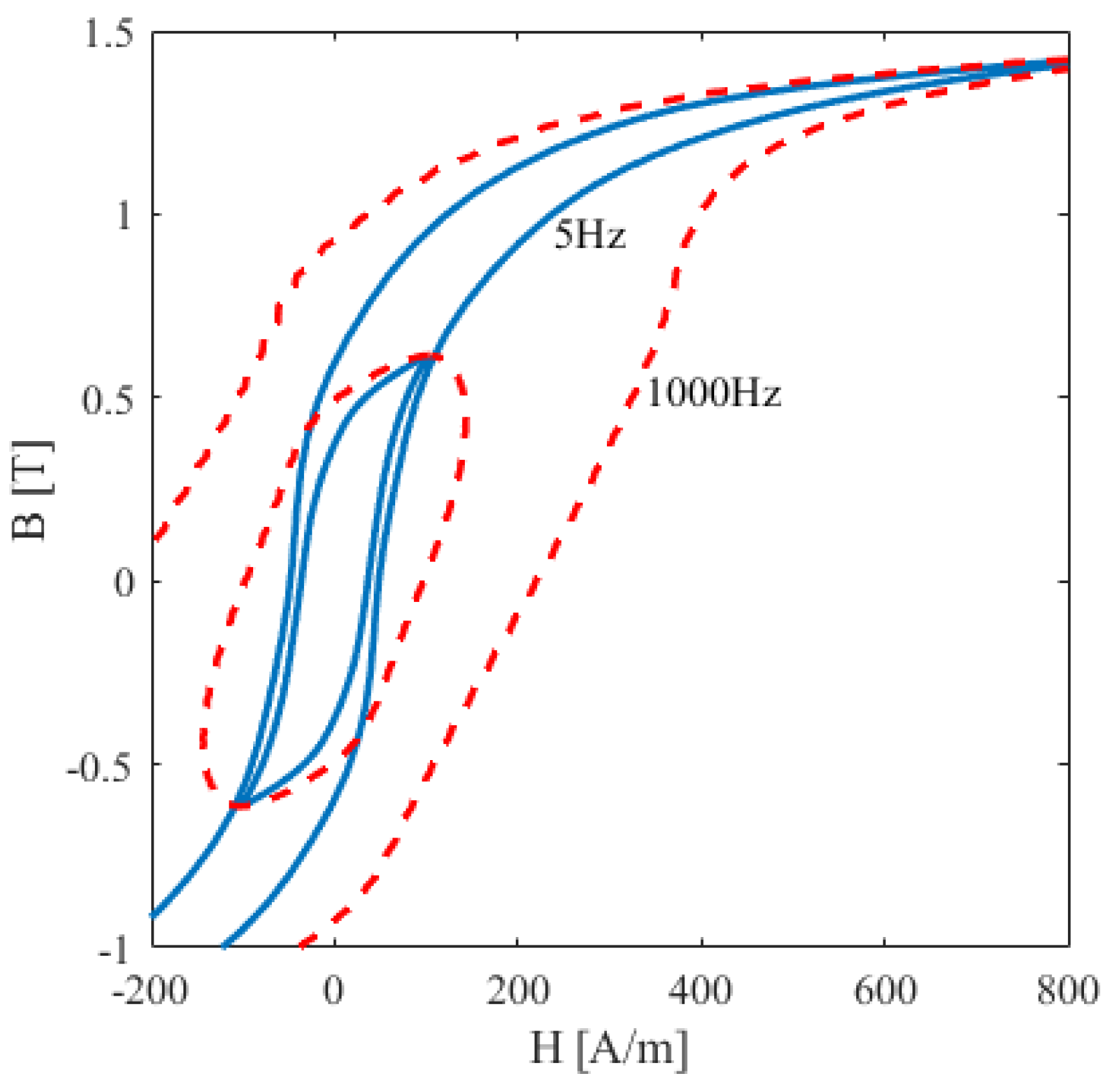
3. Measurement Methodologies for Iron Losses
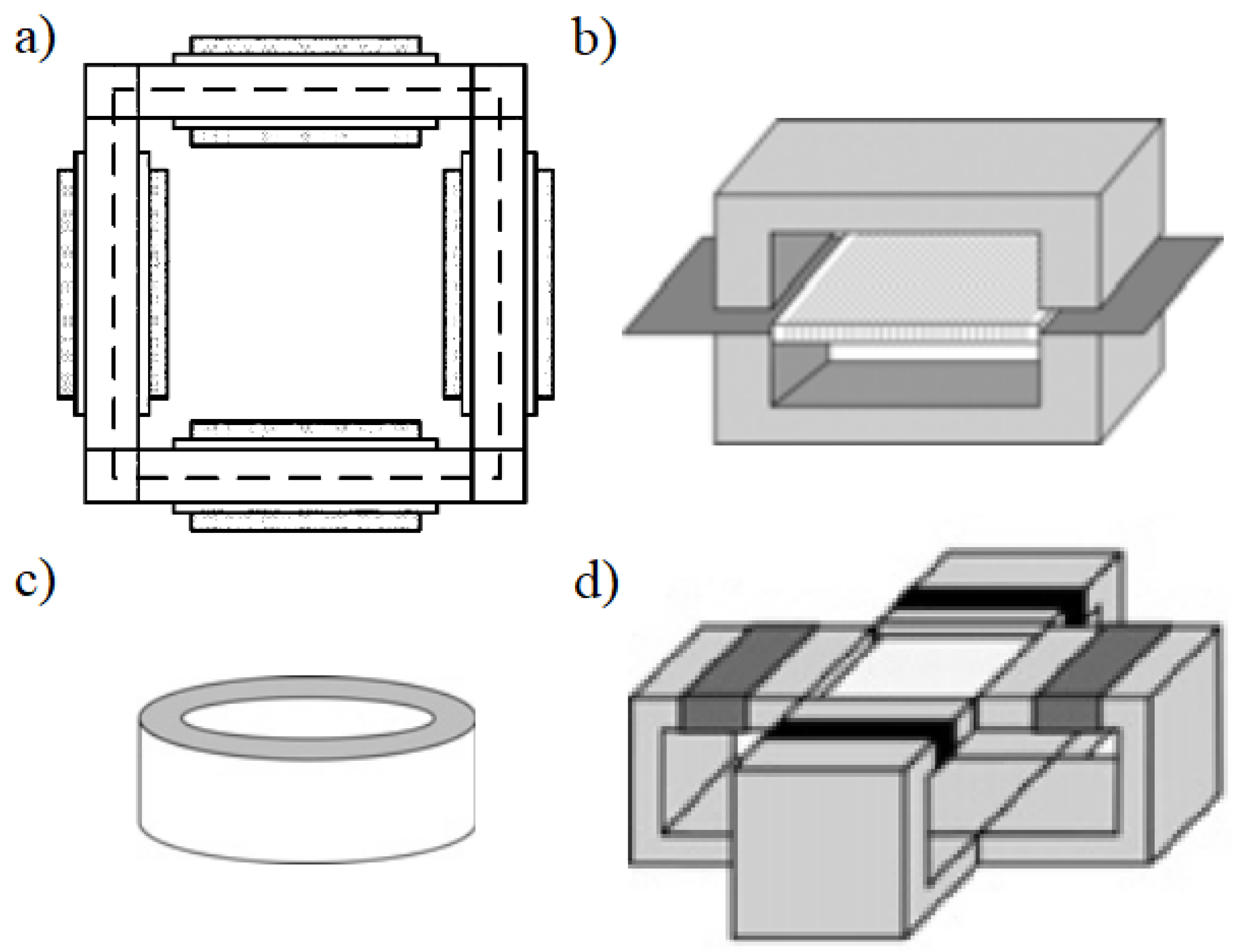
3.1. Epstein Frame
3.2. Single-Sheet Tester Measurement
3.3. Toroidal Sample Measurement
3.4. Multidimensional Measurement Methods
4. Iron Loss Modelling Approaches, an Overview
4.1. Steinmetz-Equation-Based Formulas
4.2. Separation of the Losses
Rotational Losses
4.3. Advanced Mathematical Models for the Hysteresis
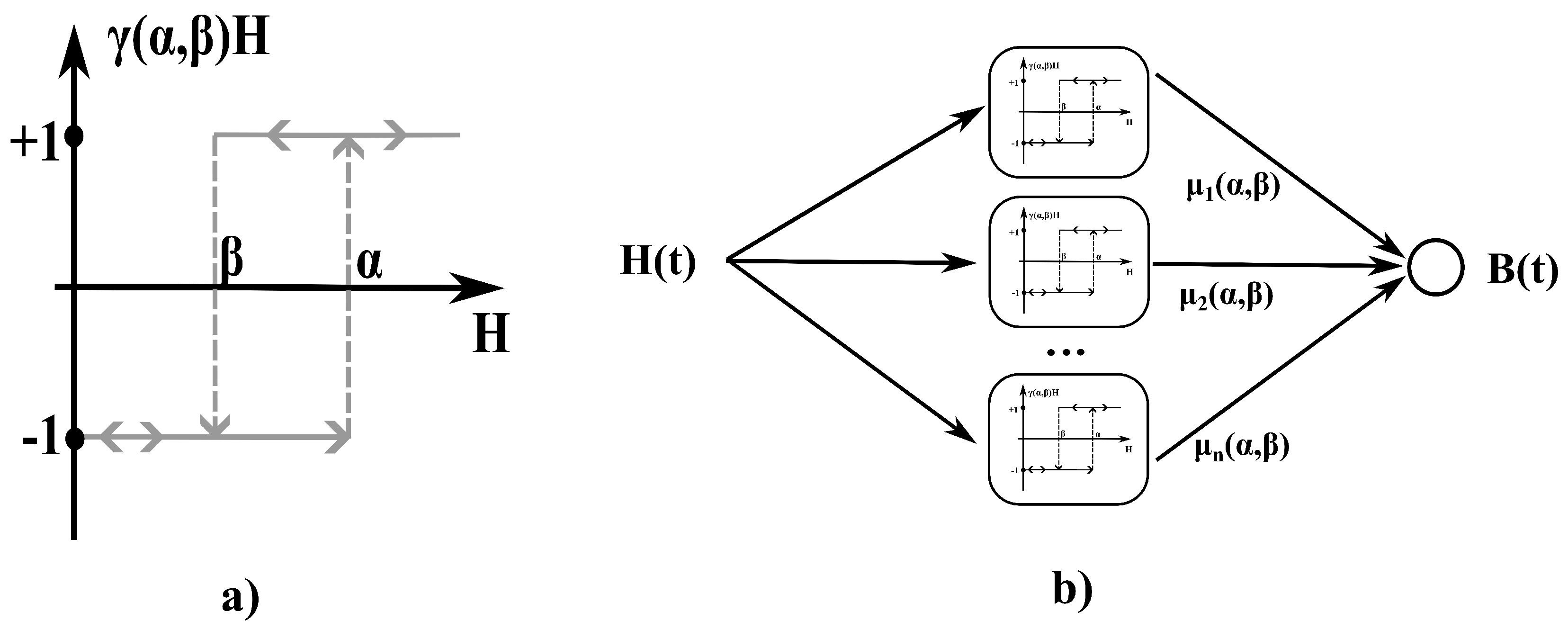
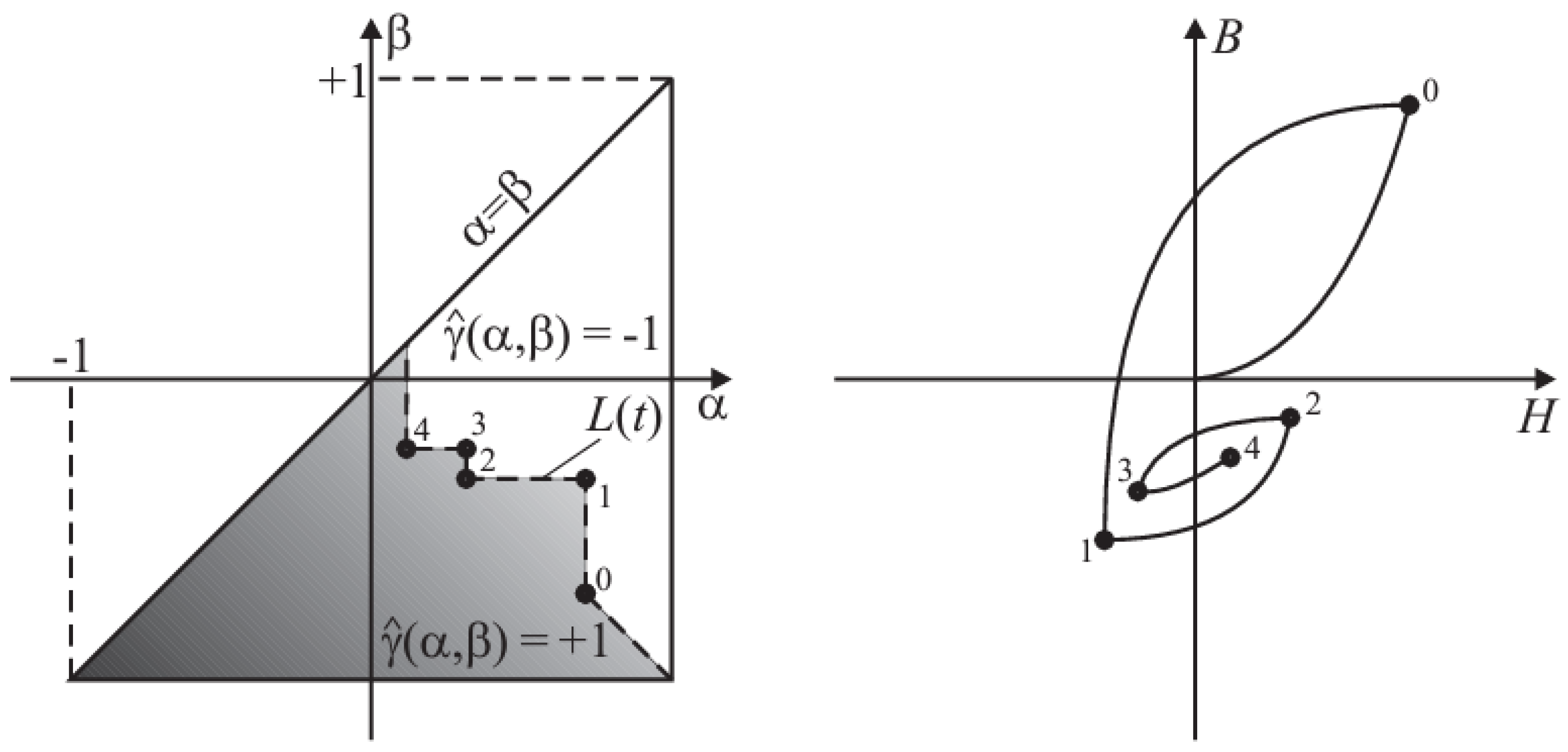
Classical Preisach-Model
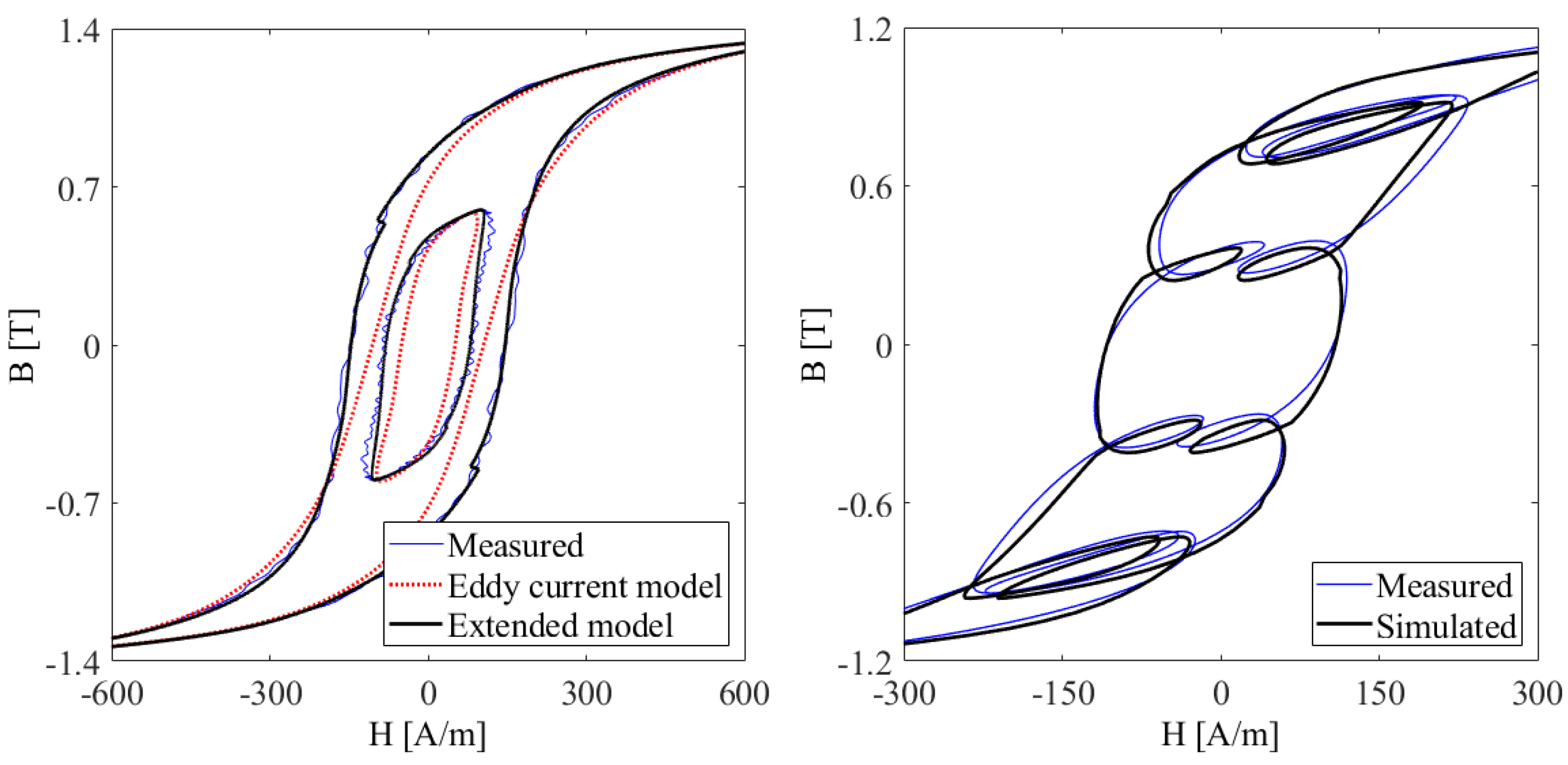
4.4. Dynamic Preisach Model
Hysteresis of a Lamination
- Solve (30) by the finite-element method (start with the value of and of the previous time instant), which gives at every node of the mesh;
- The magnetic flux density at every node can be obtained by the Preisach model with the input of ;
- The residual term is given by rearranging (27), i.e., ;
- The term is updated by (29).
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kang, N.; El Mansori, M.; Guittonneau, F.; Liao, H.; Fu, Y.; Aubry, E. Controllable mesostructure, magnetic properties of soft magnetic Fe-Ni-Si by using selective laser melting from nickel coated high silicon steel powder. Appl. Surf. Sci. 2018, 455, 736–741. [Google Scholar] [CrossRef]
- Lemke, J.; Simonelli, M.; Garibaldi, M.; Ashcroft, I.; Hague, R.; Vedani, M.; Wildman, R.; Tuck, C. Calorimetric study and microstructure analysis of the order-disorder phase transformation in silicon steel built by SLM. J. Alloys Compd. 2017, 722, 293–301. [Google Scholar] [CrossRef]
- Garibaldi, M.; Ashcroft, I.; Lemke, J.; Simonelli, M.; Hague, R. Effect of annealing on the microstructure and magnetic properties of soft magnetic Fe-Si produced via laser additive manufacturing. Scr. Mater. 2018, 142, 121–125. [Google Scholar] [CrossRef]
- Garibaldi, M.; Ashcroft, I.; Hillier, N.; Harmon, S.; Hague, R. Relationship between laser energy input, microstructures and magnetic properties of selective laser melted Fe-6.9. Mater. Charact. 2018, 143, 144–151. [Google Scholar] [CrossRef]
- Żrodowski, Ł.; Wysocki, B.; Wrblewski, R.; Krawczyska, A.; Adamczyk-Cielak, B.; Zdunek, J.; Byskun, P.; Ferenc, J.; Leonowicz, M.; wiszkowski, W. New approach to amorphization of alloys with low glass forming ability via selective laser melting. J. Alloys Compd. 2019, 771, 769–776. [Google Scholar] [CrossRef]
- Goll, D.; Schuller, D.; Martinek, G.; Kunert, T.; Schurr, J.; Sinz, C.; Schubert, T.; Bernthaler, T.; Riegel, H.; Schneider, G. Additive manufacturing of soft magnetic materials and components. Addit. Manuf. 2019, 27, 428–439. [Google Scholar] [CrossRef]
- Heer, B.; Bandyopadhyay, A. Compositionally graded magnetic-nonmagnetic bimetallic structure using laser engineered net shaping. Mater. Lett. 2018, 216, 16–19. [Google Scholar] [CrossRef]
- Ayat, S.; Simpson, N.; Dagus, B.; Rudolph, J.; Lorenz, F.; Drury, D. Design of Shaped-Profile Electrical Machine Windings for Multi-Material Additive Manufacture. In Proceedings of the 2020 International Conference on Electrical Machines (ICEM), Gothenburg, Sweden, 23–26 August 2020; Volume 1, pp. 1554–1559. [Google Scholar] [CrossRef]
- Garibaldi, M. Laser Additive Manufacturing of Soft Magnetic Cores for Rotating Electrical Machinery: Materials Development and Part Design. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2018. [Google Scholar]
- Sarap, M.; Kallaste, A.; Shams Ghahfarokhi, P.; Tiismus, H.; Vaimann, T. Utilization of additive manufacturing in the thermal design of electrical machines: A review. Machines 2022, 10, 251. [Google Scholar] [CrossRef]
- Giannotta, N.; Sala, G.; Bianchini, C.; Torreggiani, A. A Review of Additive Manufacturing of Soft Magnetic Materials in Electrical Machines. Machines 2023, 11, 702. [Google Scholar] [CrossRef]
- Ghahfarokhi, P.S.; Podgornovs, A.; Kallaste, A.; Cardoso, A.J.M.; Belahcen, A.; Vaimann, T.; Tiismus, H.; Asad, B. Opportunities and Challenges of Utilizing Additive Manufacturing Approaches in Thermal Management of Electrical Machines. IEEE Access 2021, 9, 36368–36381. [Google Scholar] [CrossRef]
- Hernandez, M.; Messagie, M.; Hegazy, O.; Marengo, L.; Winter, O.; Van Mierlo, J. Environmental impact of traction electric motors for electric vehicles applications. Int. J. Life Cycle Assess. 2017, 22, 54–65. [Google Scholar] [CrossRef]
- Horváth, C. The Current Situation of the Rare-Earth Material Usage in the Field of Electromobility. In Proceedings of the Vehicle and Automotive Engineering 4; Jármai, K., Cservenák, Á., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 493–504. [Google Scholar] [CrossRef]
- Schoppa, A.; Delarbre, P.; Holzmann, E.; Sigl, M. Magnetic properties of soft magnetic powder composites at higher frequencies in comparison with electrical steels. In Proceedings of the 2013 3rd International Electric Drives Production Conference (EDPC), Nuremberg, Germany, 29–30 October 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Landgraf, F.; Emura, M.; Teixeira, J.; de Campos, M. Effect of grain size, deformation, aging and anisotropy on hysteresis loss of electrical steels. J. Magn. Magn. Mater. 2000, 215–216, 97–99. [Google Scholar] [CrossRef]
- Naumoski, H.; Riedmller, B.; Minkow, A.; Herr, U. Investigation of the influence of different cutting procedures on the global and local magnetic properties of non-oriented electrical steel. J. Magn. Magn. Mater. 2015, 392, 126–133. [Google Scholar] [CrossRef]
- Kalsoom, U.; Nesterenko, P.N.; Paull, B. Recent developments in 3D printable composite materials. RSC Adv. 2016, 6, 60355–60371. [Google Scholar] [CrossRef]
- Pham, T.; Kwon, P.; Foster, S. Additive manufacturing and topology optimization of magnetic materials for electrical machines—A review. Energies 2021, 14, 283. [Google Scholar] [CrossRef]
- Andreiev, A.; Hoyer, K.P.; Hengsbach, F.; Haase, M.; Tasche, L.; Duschik, K.; Schaper, M. Powder bed fusion of soft-magnetic iron-based alloys with high silicon content. J. Mater. Process. Technol. 2023, 317, 117991. [Google Scholar] [CrossRef]
- Andreiev, A.; Hoyer, K.P.; Dula, D.; Hengsbach, F.; Haase, M.; Gierse, J.; Zimmer, D.; Tröster, T.; Schaper, M. Soft-magnetic behavior of laser beam melted FeSi3 alloy with graded cross-section. J. Mater. Process. Technol. 2021, 296, 117183. [Google Scholar] [CrossRef]
- Garibaldi, M.; Ashcroft, I.; Simonelli, M.; Hague, R. Metallurgy of high-silicon steel parts produced using Selective Laser Melting. Acta Mater. 2016, 110, 207–216. [Google Scholar] [CrossRef]
- Wu, W.; Li, X.; Liu, Q.; Fuh, J.Y.H.; Zheng, A.; Zhou, Y.; Ren, L.; Li, G. Additive manufacturing of bulk metallic glass: Principles, materials and prospects. Mater. Today Adv. 2022, 16, 100319. [Google Scholar] [CrossRef]
- Kocsis, B.; Hatos, I.; Varga, L.K. 3D-printed metal–insulator layered structure. J. Magn. Magn. Mater. 2022, 563, 169994. [Google Scholar] [CrossRef]
- Nam, Y.G.; Koo, B.; Chang, M.S.; Yang, S.; Yu, J.; Park, Y.H.; Jeong, J.W. Selective laser melting vitrification of amorphous soft magnetic alloys with help of double-scanning-induced compositional homogeneity. Mater. Lett. 2020, 261, 127068. [Google Scholar] [CrossRef]
- Bence, K. Fém-Szigetelő Kompozitok Előállítása Járműipari célú Felhasználáshoz. Ph.D. Thesis, Széchenyi István University, Győr, Hungary, 2023. [Google Scholar]
- M270 Steel BH Curve Data. Available online: https://doc.modelica.org/Modelica%203.2.3/Resources/helpMapleSim/Magnetic/FluxTubes/Material/HysteresisTableData/index.html (accessed on 10 August 2023).
- Bali, M. Magnetic Material Degradation Due to Different Cutting Techniques and Its Modeling for Electric Machine Design. Ph.D. Thesis, Technischen Universitat Graz, Graz, Austria, 2016. [Google Scholar]
- Tiismus, H.; Kallaste, A.; Belahcen, A.; Tarraste, M.; Vaimann, T.; Rasslkin, A.; Asad, B.; Shams Ghahfarokhi, P. AC Magnetic Loss Reduction of SLM Processed Fe-Si for Additive Manufacturing of Electrical Machines. Energies 2021, 14, 1241. [Google Scholar] [CrossRef]
- Krings, A. Iron Losses in Electrical Machines-Influence of Material Properties, Manufacturing Processes, and Inverter Operation. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2014. [Google Scholar]
- Lee, J.; Seo, J.H.; Kikuchi, N. Topology optimization of switched reluctance motors for the desired torque profile. Struct. Multidiscip. Optim. 2010, 42, 783–796. [Google Scholar] [CrossRef]
- Kim, D.H.; Sykulski, J.K.; Lowther, D.A. The implications of the use of composite materials in electromagnetic device topology and shape optimization. IEEE Trans. Magn. 2009, 45, 1154–1157. [Google Scholar] [CrossRef]
- Tiismus, H.; Kallaste, A.; Vaimann, T.; Rassõlkin, A. State of the art of additively manufactured electromagnetic materials for topology optimized electrical machines. Addit. Manuf. 2022, 55, 102778. [Google Scholar] [CrossRef]
- Koopmann, J.; Voigt, J.; Niendorf, T. Additive manufacturing of a steel–ceramic multi-material by selective laser melting. Metall. Mater. Trans. B 2019, 50, 1042–1051. [Google Scholar] [CrossRef]
- Kocsis, B.; Fekete, I.; Varga, L. Metallographic and magnetic analysis of direct laser sintered soft magnetic composites. J. Magn. Magn. Mater. 2020, 501, 166425. [Google Scholar] [CrossRef]
- Ding, C.; Liu, L.; Mei, Y.; Ngo, K.D.; Lu, G.Q. Magnetic paste as feedstock for additive manufacturing of power magnetics. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 615–618. [Google Scholar]
- Lin, P.H.; Yang, B.Y.; Tsai, M.H.; Chen, P.C.; Huang, K.F.; Lin, H.H.; Lai, C.H. Manipulating exchange bias by spin–orbit torque. Nat. Mater. 2019, 18, 335–341. [Google Scholar] [CrossRef]
- Cramer, C.L.; Nandwana, P.; Yan, J.; Evans, S.F.; Elliott, A.M.; Chinnasamy, C.; Paranthaman, M.P. Binder jet additive manufacturing method to fabricate near net shape crack-free highly dense Fe-6.5 wt.% Si soft magnets. Heliyon 2019, 5, e02804. [Google Scholar] [CrossRef]
- Kustas, A.B.; Susan, D.F.; Johnson, K.L.; Whetten, S.R.; Rodriguez, M.A.; Dagel, D.J.; Michael, J.R.; Keicher, D.M.; Argibay, N. Characterization of the Fe-Co-1.5 V soft ferromagnetic alloy processed by Laser Engineered Net Shaping (LENS). Addit. Manuf. 2018, 21, 41–52. [Google Scholar]
- Khatri, B.; Lappe, K.; Noetzel, D.; Pursche, K.; Hanemann, T. A 3D-Printable Polymer-Metal Soft-Magnetic Functional Composite—Development and Characterization. Materials 2018, 11, 189. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Ge, T.; Ngo, K.D.T.; Mei, Y.; Lu, G.Q. Ferrite Paste Cured With Ultraviolet Light for Additive Manufacturing of Magnetic Components for Power Electronics. IEEE Magn. Lett. 2018, 9, 1–5. [Google Scholar] [CrossRef]
- Kokkinis, D.; Schaffner, M.; Studart, A.R. Multimaterial magnetically assisted 3D printing of composite materials. Nat. Commun. 2015, 6, 8643. [Google Scholar] [CrossRef] [PubMed]
- Paranthaman, M.P.; Shafer, C.S.; Elliott, A.M.; Siddel, D.H.; McGuire, M.A.; Springfield, R.M.; Martin, J.; Fredette, R.; Ormerod, J. Binder Jetting: A Novel NdFeB Bonded Magnet Fabrication Process. Jom 2016, 68, 1978–1982. [Google Scholar] [CrossRef]
- Shahrubudin, N.; Lee, T.C.; Ramlan, R. An overview on 3D printing technology: Technological, materials, and applications. Procedia Manuf. 2019, 35, 1286–1296. [Google Scholar] [CrossRef]
- Szabó, L.; Fodor, D. The key role of 3D printing technologies in the further development of electrical machines. Machines 2022, 10, 330. [Google Scholar] [CrossRef]
- Kallaste, A.; Vaimann, T.; Rassãlkin, A. Additive design possibilities of electrical machines. In Proceedings of the 2018 IEEE 59th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 12–13 November 2018; pp. 1–5. [Google Scholar]
- Snoek, J. Dispersion and absorption in magnetic ferrites at frequencies above one Mc/s. Physica 1948, 14, 207–217. [Google Scholar] [CrossRef]
- Mager, A. About the influence of grain size on the coercivity. Ann. Phys. Leipzig 1952, 446, 15–16. [Google Scholar] [CrossRef]
- Hu, Y.; Cong, W. A review on laser deposition-additive manufacturing of ceramics and ceramic reinforced metal matrix composites 2018. Ceram. Int. 2018, 44, 20599–20612. [Google Scholar] [CrossRef]
- Zhang, H.; LeBlanc, S. Processing parameters for selective laser sintering or melting of oxide ceramics. Addit. Manuf.-High-Perform. Met.-Alloy.-Model. Optim. 2018, 10, 1–44. [Google Scholar]
- Nakai, Y.; Mishima, F.; Akiyama, Y.; Nishijima, S. Development of magnetic separation system for powder separation. IEEE Trans. Appl. Supercond. 2010, 20, 941–944. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.; Stucker, B.; Khorasani, M.; Gibson, I.; Rosen, D.; Stucker, B.; Khorasani, M. Materials for additive manufacturing. Addit. Manuf. Technol. 2021, 379–428. [Google Scholar]
- Sahasrabudhe, H.; Bandyopadhyay, A. Additive Manufacturing of Reactive In Situ Zr Based Ultra-High Temperature Ceramic Composites. Jom 2016, 68, 822–830. [Google Scholar] [CrossRef]
- Fan, Z.; Zhao, Y.; Tan, Q.; Mo, N.; Zhang, M.X.; Lu, M.; Huang, H. Nanostructured Al2O3-YAG-ZrO2 ternary eutectic components prepared by laser engineered net shaping. Acta Mater. 2019, 170, 24–37. [Google Scholar] [CrossRef]
- Zheng, B.; Topping, T.; Smugeresky, J.E.; Zhou, Y.; Biswas, A.; Baker, D.; Lavernia, E.J. The Influence of Ni-Coated TiC on Laser-Deposited IN625 Metal Matrix Composites. Metall. Mater. Trans. A 2010, 41, 568–573. [Google Scholar] [CrossRef]
- Shen, M.Y.; Tian, X.J.; Liu, D.; Tang, H.B.; Cheng, X. Microstructure and fracture behavior of TiC particles reinforced Inconel 625 composites prepared by laser additive manufacturing. J. Alloys Compd. 2018, 734, 188–195. [Google Scholar] [CrossRef]
- Tan, H.; Hao, D.; Al-Hamdani, K.; Zhang, F.; Xu, Z.; Clare, A.T. Direct metal deposition of TiB2/AlSi10Mg composites using satellited powders. Mater. Lett. 2018, 214, 123–126. [Google Scholar] [CrossRef]
- Cao, S.; Gu, D.; Shi, Q. Relation of microstructure, microhardness and underlying thermodynamics in molten pools of laser melting deposition processed TiC/Inconel 625 composites. J. Alloys Compd. 2017, 692, 758–769. [Google Scholar] [CrossRef]
- Farayibi, P.; Abioye, T.; Kennedy, A.; Clare, A. Development of metal matrix composites by direct energy deposition of satellited powders. J. Manuf. Process. 2019, 45, 429–437. [Google Scholar] [CrossRef]
- Huang, Y.; Wu, D.; Zhao, D.; Niu, F.; Zhang, H.; Yan, S.; Ma, G. Process optimization of melt growth alumina/aluminum titanate composites directed energy deposition: Effects of scanning speed. Addit. Manuf. 2020, 35, 101210. [Google Scholar] [CrossRef]
- Amar, A.; Li, J.; Xiang, S.; Liu, X.; Zhou, Y.; Le, G.; Wang, X.; Qu, F.; Ma, S.; Dong, W.; et al. Additive manufacturing of high-strength CrMnFeCoNi-based High Entropy Alloys with TiC addition. Intermetallics 2019, 109, 162–166. [Google Scholar] [CrossRef]
- Svetlizky, D.; Zheng, B.; Vyatskikh, A.; Das, M.; Bose, S.; Bandyopadhyay, A.; Schoenung, J.M.; Lavernia, E.J.; Eliaz, N. Laser-based directed energy deposition (DED-LB) of advanced materials. Mater. Sci. Eng. A 2022, 840, 142967. [Google Scholar] [CrossRef]
- Traxel, K.D.; Bandyopadhyay, A. Naturally architected microstructures in structural materials via additive manufacturing. Addit. Manuf. 2020, 34, 101243. [Google Scholar] [CrossRef]
- Zou, J.; Gaber, Y.; Voulazeris, G.; Li, S.; Vazquez, L.; Liu, L.F.; Yao, M.Y.; Wang, Y.J.; Holynski, M.; Bongs, K.; et al. Controlling the grain orientation during laser powder bed fusion to tailor the magnetic characteristics in a Ni-Fe based soft magnet. Acta Mater. 2018, 158, 230–238. [Google Scholar] [CrossRef]
- De Oliveira, A.R.; De Oliveira, V.F.; Teixeira, J.C.; Del Conte, E.G. Investigation of the build orientation effect on magnetic properties and Barkhausen Noise of additively manufactured maraging steel 300. Addit. Manuf. 2021, 38, 101827. [Google Scholar] [CrossRef]
- Ouyang, D.; Li, N.; Xing, W.; Zhang, J.; Liu, L. 3D printing of crack-free high strength Zr-based bulk metallic glass composite by selective laser melting. Intermetallics 2017, 90, 128–134. [Google Scholar] [CrossRef]
- Jung, H.Y.; Choi, S.J.; Prashanth, K.G.; Stoica, M.; Scudino, S.; Yi, S.; Kühn, U.; Kim, D.H.; Kim, K.B.; Eckert, J. Fabrication of Fe-based bulk metallic glass by selective laser melting: A parameter study. Mater. Des. 2015, 86, 703–708. [Google Scholar] [CrossRef]
- Shen, Y.; Li, Y.; Chen, C.; Tsai, H.L. 3D printing of large, complex metallic glass structures. Mater. Des. 2017, 117, 213–222. [Google Scholar] [CrossRef]
- Borkar, T.; Conteri, R.; Chen, X.; Ramanujan, R.; Banerjee, R. Laser additive processing of functionally-graded Fe–Si–B–Cu–Nb soft magnetic materials. Mater. Manuf. Process. 2017, 32, 1581–1587. [Google Scholar] [CrossRef]
- Gibson, M.A.; Mykulowycz, N.M.; Shim, J.; Fontana, R.; Schmitt, P.; Roberts, A.; Ketkaew, J.; Shao, L.; Chen, W.; Bordeenithikasem, P.; et al. 3D printing metals like thermoplastics: Fused filament fabrication of metallic glasses. Mater. Today 2018, 21, 697–702. [Google Scholar] [CrossRef]
- Arnold, H.; Elmen, G. Bell System Tech. J. USA Tel. Tel. 1923, 2, 101. [Google Scholar]
- Redjdal, N.; Salah, H.; Hauet, T.; Menari, H.; Chérif, S.; Gabouze, N.; Azzaz, M. Microstructural, electrical and magnetic properties of Fe35Co65 thin films grown by thermal evaporation from mechanically alloyed powders. Thin Solid Films 2014, 552, 164–169. [Google Scholar] [CrossRef][Green Version]
- Schönrath, H.; Spasova, M.; Kilian, S.; Meckenstock, R.; Witt, G.; Sehrt, J.; Farle, M. Additive manufacturing of soft magnetic permalloy from Fe and Ni powders: Control of magnetic anisotropy. J. Magn. Magn. Mater. 2019, 478, 274–278. [Google Scholar] [CrossRef]
- Ouyang, G.; Chen, X.; Liang, Y.; Macziewski, C.; Cui, J. Review of Fe-6.5 wt% Si high silicon steelA promising soft magnetic material for sub-kHz application. J. Magn. Magn. Mater.s 2019, 481, 234–250. [Google Scholar] [CrossRef]
- Plotkowski, A.; Carver, K.; List, F.; Pries, J.; Li, Z.; Rossy, A.M.; Leonard, D. Design and performance of an additively manufactured high-Si transformer core. Mater. Des. 2020, 194, 108894. [Google Scholar] [CrossRef]
- Goodall, A.D.; Chechik, L.; Mitchell, R.L.; Jewell, G.W.; Todd, I. Cracking of soft magnetic FeSi to reduce eddy current losses in stator cores. Addit. Manuf. 2023, 70, 103555. [Google Scholar] [CrossRef]
- Magnetic Materials Part 2: Methods of Measurement of the Magnetic Properties of Electrical Steel Strip and Sheet by Means of an Epstein Frame; Standard, International Electrotechnical Commission: London, UK, 2008.
- Magnetic Materials Part 4: Methods of Measurement of the Magnetic Properties of Magnetic Sheet and Strip by Means of a Single Sheet Tester; Standard, International Electrotechnical Commission: London, UK, 2010.
- Magnetic Materials Part 6: Methods of Measurement of the Magnetic Properties of Magnetically Soft Metallic and Powder Materials at Frequencies in the Range 20 Hz to 100 kHz by the Use of Ring Specimens; Standard, International Electrotechnical Commission: London, UK, 2018.
- Fiorillo, F. Measurements of magnetic materials. Metrologia 2010, 47, S114. [Google Scholar] [CrossRef]
- Selema, A.; Beretta, M.; Van Coppenolle, M.; Tiismus, H.; Kallaste, A.; Ibrahim, M.N.; Rombouts, M.; Vleugels, J.; Kestens, L.A.; Sergeant, P. Evaluation of 3D-Printed Magnetic Materials For Additively-Manufactured Electrical Machines. J. Magn. Magn. Mater. 2023, 569, 170426. [Google Scholar] [CrossRef]
- Tiismus, H.; Kallaste, A.; Belahcen, A.; Vaimann, T.; Rassõlkin, A.; Lukichev, D. Hysteresis measurements and numerical losses segregation of additively manufactured silicon steel for 3D printing electrical machines. Appl. Sci. 2020, 10, 6515. [Google Scholar] [CrossRef]
- Bramerdorfer, G.; Kitzberger, M.; Wckinger, D.; Koprivica, B.; Zurek, S. State-of-the-art and future trends in soft magnetic materials characterization with focus on electric machine design Part 1. TM-Tech. Mess. 2019, 86, 540–552. [Google Scholar] [CrossRef]
- Antonelli, E.; Cardelli, E.; Faba, A. Epstein frame: How and when it can be really representative about the magnetic behavior of laminated magnetic steels. IEEE Trans. Magn. 2005, 41, 1516–1519. [Google Scholar] [CrossRef]
- Pham, T.Q.; Mellak, C.; Suen, H.; Boehlert, C.J.; Muetze, A.; Kwon, P.; Foster, S.N. Binder Jet Printed Iron Silicon with Low Hysteresis Loss. In Proceedings of the 2019 IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019; pp. 1045–1052. [Google Scholar] [CrossRef]
- Yamamoto, T.; Ohya, Y. Single sheet tester for measuring core losses and permeabilities in a silicon steel sheet. IEEE Trans. Magn. 1974, 10, 157–159. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, J.; Yang, Q.; Lin, Z.W.; Guo, Y.; Zhang, C. Study on rotational hysteresis and core loss under three-dimensional magnetization. IEEE Trans. Magn. 2011, 47, 3520–3523. [Google Scholar] [CrossRef]
- Plotkowski, A.; Pries, J.; List, F.; Nandwana, P.; Stump, B.; Carver, K.; Dehoff, R. Influence of scan pattern and geometry on the microstructure and soft-magnetic performance of additively manufactured Fe-Si. Addit. Manuf. 2019, 29, 100781. [Google Scholar] [CrossRef]
- Serrano, D.; Li, H.; Wang, S.; Guillod, T.; Luo, M.; Bansal, V.; Jha, N.K.; Chen, Y.; Sullivan, C.R.; Chen, M. Why MagNet: Quantifying the Complexity of Modeling Power Magnetic Material Characteristics. IEEE Trans. Power Electron. 2023, 1–25. [Google Scholar] [CrossRef]
- Smith, A.; Edey, K. Influence of manufacturing processes on iron losses. In Proceedings of the Seventh International Conference on Electrical Machines and Drives, Durham, UK, 11–13 September 1995. [Google Scholar]
- Bramerdorfer, G.; Kitzberger, M.; Wöckinger, D.; Koprivica, B.; Zurek, S. State-of-the-art and future trends in soft magnetic materials characterization with focus on electric machine design–Part 2. TM-Tech. Mess. 2019, 86, 553–565. [Google Scholar] [CrossRef]
- Michaelides, A.; Simkin, J.; Kirby, P.; Riley, C. Permanent magnet (de-) magnetization and soft iron hysteresis effects: A comparison of FE analysis techniques. COMPEL- Int. J. Comput. Math. Electr. Electron. Eng. 2010, 29, 1090–1096. [Google Scholar] [CrossRef][Green Version]
- Zirka, S.; Moroz, Y.I. Hysteresis modeling based on transplantation. IEEE Trans. Magn. 1995, 31, 3509–3511. [Google Scholar] [CrossRef]
- Steinmetz, C.P. On the law of hysteresis. Trans. Am. Inst. Electr. Eng. 1892, 9, 1–64. [Google Scholar] [CrossRef]
- Venkatachalam, K.; Sullivan, C.R.; Abdallah, T.; Tacca, H. Accurate prediction of ferrite core loss with nonsinusoidal waveforms using only Steinmetz parameters. In Proceedings of the 2002 IEEE Workshop on Computers in Power Electronics, Mayaguez, PR, USA, 3–4 June 2002; pp. 36–41. [Google Scholar]
- Bilgin, B.; Liang, J.; Terzic, M.V.; Dong, J.; Rodriguez, R.; Trickett, E.; Emadi, A. Modeling and analysis of electric motors: State-of-the-art review. IEEE Trans. Transp. Electrif. 2019, 5, 602–617. [Google Scholar] [CrossRef]
- Brittain, J.E. A steinmetz contribution to the AC power revolution. Proc. IEEE 1984, 72, 196–197. [Google Scholar] [CrossRef]
- Brockmeyer, A. Experimental evaluation of the influence of DC-premagnetization on the properties of power electronic ferrites. In Proceedings of the Applied Power Electronics Conference. APEC’96, San Jose, CA, USA, 3–7 March 1996; Volume 1, pp. 454–460. [Google Scholar]
- Li, J.; Abdallah, T.; Sullivan, C.R. Improved calculation of core loss with nonsinusoidal waveforms. In Proceedings of the Conference Record of the 2001 IEEE Industry Applications Conference. 36th IAS Annual Meeting (Cat. No. 01CH37248), Chicago, IL, USA, 30 September–4 October 2001; Volume 4, pp. 2203–2210. [Google Scholar]
- Baguley, C.; Carsten, B.; Madawala, U. The effect of DC bias conditions on ferrite core losses. IEEE Trans. Magn. 2008, 44, 246–252. [Google Scholar] [CrossRef]
- Mu, M. High Frequency Magnetic Core Loss Study. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2013. [Google Scholar]
- Li, Z.; Han, W.; Xin, Z.; Liu, Q.; Chen, J.; Loh, P.C. A Review of Magnetic Core Materials, Core Loss Modeling and Measurements in High-Power High-Frequency Transformers. CPSS Trans. Power Electron. Appl. 2022, 7, 359–373. [Google Scholar] [CrossRef]
- Shen, W.; Wang, F.; Boroyevich, D.; Tipton, C.W. Loss characterization and calculation of nanocrystalline cores for high-frequency magnetics applications. IEEE Trans. Power Electron. 2008, 23, 475–484. [Google Scholar] [CrossRef]
- Van den Bossche, A.; Valchev, V.C.; Georgiev, G.B. Measurement and loss model of ferrites with non-sinusoidal waveforms. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No. 04CH37551), Aachen, Germany, 20–25 June 2004; Volume 6, pp. 4814–4818. [Google Scholar]
- Chen, K. Iron-loss simulation of laminated steels based on expanded generalized steinmetz equation. In Proceedings of the 2009 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 27–31 March 2009; pp. 1–3. [Google Scholar]
- Sullivan, C.R. High frequency core and winding loss modeling. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013; pp. 1482–1499. [Google Scholar]
- Albach, M.; Durbaum, T.; Brockmeyer, A. Calculating core losses in transformers for arbitrary magnetizing currents a comparison of different approaches. In Proceedings of the PESC Record. 27th Annual IEEE Power Electronics Specialists Conference, Baveno, Italy, 23–27 June 1996; Volume 2, pp. 1463–1468. [Google Scholar]
- Reinert, J.; Brockmeyer, A.; De Doncker, R.W. Calculation of losses in ferro-and ferrimagnetic materials based on the modified Steinmetz equation. IEEE Trans. Ind. Appl. 2001, 37, 1055–1061. [Google Scholar] [CrossRef]
- Krings, A.; Soulard, J. Overview and comparison of iron loss models for electrical machines. J. Electr. Eng. 2010, 10, 8. [Google Scholar]
- Villar, I.; Rufer, A.; Viscarret, U.; Zurkinden, F.; Etxeberria-Otadui, I. Analysis of empirical core loss evaluation methods for non-sinusoidally fed medium frequency power transformers. In Proceedings of the 2008 IEEE International Symposium on Industrial Electronics, Cambridge, UK, 30 June–2 July 2008; pp. 208–213. [Google Scholar]
- Sullivan, C.R.; Harris, J.H.; Herbert, E. Core loss predictions for general PWM waveforms from a simplified set of measured data. In Proceedings of the 2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Palm Springs, CA, USA, 21–25 February 2010; pp. 1048–1055. [Google Scholar]
- Van den Bossche, A.P.; Van de Sype, D.M.; Valchev, V.C. Ferrite loss measurement and models in half bridge and full bridge waveforms. In Proceedings of the 2005 IEEE 36th Power Electronics Specialists Conference, Dresden, Germany, 16 June 2005; pp. 1535–1539. [Google Scholar]
- Van den Bossche, A.P.; Valchev, V.C.; Van de Sype, D.M.; Vandenbossche, L.P. Ferrite losses of cores with square wave voltage and DC bias. J. Appl. Phys. 2006, 99, 08M908. [Google Scholar] [CrossRef]
- Jordan, H. Die ferromagnetischen Konstanten für schwache Wechselfelder. Elektr. Nach. Techn. 1924, 1. [Google Scholar]
- Goodenough, J.B. Summary of losses in magnetic materials. IEEE Trans. Magn. 2002, 38, 3398–3408. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Xue, S.; Chu, W.; Feng, J.; Guo, S.; Chen, Z.; Peng, J. Evaluation of iron loss models in electrical machines. IEEE Trans. Ind. Appl. 2018, 55, 1461–1472. [Google Scholar] [CrossRef]
- Kuczmann, M.; Orosz, T. Temperature-Dependent Ferromagnetic Loss Approximation of an Induction Machine Stator Core Material Based on Laboratory Test Measurements. Energies 2023, 16, 1116. [Google Scholar] [CrossRef]
- Pry, R.; Bean, C. Calculation of the energy loss in magnetic sheet materials using a domain model. J. Appl. Phys. 1958, 29, 532–533. [Google Scholar] [CrossRef]
- Bertotti, G. General properties of power losses in soft ferromagnetic materials. IEEE Trans. Magn. 1988, 24, 621–630. [Google Scholar] [CrossRef]
- Ferro, A.; Montalenti, G.; Soardo, G. Non linearity anomaly of power losses vs. frequency in various soft magnetic materials. IEEE Trans. Magn. 1975, 11, 1341–1343. [Google Scholar] [CrossRef]
- Bertotti, G.; Di Schino, G.; Milone, A.F.; Fiorillo, F. On the effect of grain size on magnetic losses of 3% non-oriented SiFe. Le J. Phys. Colloq. 1985, 46, C6-385–C6-388. [Google Scholar] [CrossRef]
- Krings, A.; Nategh, S.; Stening, A.; Grop, H.; Wallmark, O.; Soulard, J. Measurement and modeling of iron losses in electrical machines. In Proceedings of the 5th International Conference Magnetism and Metallurgy WMM’12, Ghent, Belgium, 20–22 June 2012; pp. 101–119. [Google Scholar]
- Boll, R.; GmbH, H.V. Weichmagnetische Werkstoffe: Einführung in den Magnetismus; VAC-Werkstoffe und ihre Anwendungen; Siemens-Aktien-Ges.; Publicis Corporate Publishing: Erlangen, Germany, 1990. [Google Scholar]
- Pluta, W.A. Some properties of factors of specific total loss components in electrical steel. IEEE Trans. Magn. 2010, 46, 322–325. [Google Scholar] [CrossRef]
- Dems, M.; Komeza, K.; Szulakowski, J.; Kubiak, W. Modeling of core loss for non-oriented electrical steel. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2018, 38, 1874–1884. [Google Scholar] [CrossRef]
- Cheaytani, J.; Benabou, A.; Tounzi, A.; Dessoude, M.; Chevallier, L.; Henneron, T. End-region leakage fluxes and losses analysis of cage induction motors using 3-D finite-element method. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Rodriguez-Sotelo, D.; Rodriguez-Licea, M.A.; Araujo-Vargas, I.; Prado-Olivarez, J.; Barranco-Gutiérrez, A.I.; Perez-Pinal, F.J. Power losses models for magnetic cores: A review. Micromachines 2022, 13, 418. [Google Scholar] [CrossRef]
- Durna, E. Recursive inductor core loss estimation method for arbitrary flux density waveforms. J. Power Electron. 2021, 21, 1724–1734. [Google Scholar] [CrossRef]
- Campara, E.; Solokovic, A. Iron Loss Modelling fo a Permanent Magnet Synchronous Motor. Master’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2020. [Google Scholar]
- Help, A.F. Modified Bertotti Model Identification Tool. Available online: https://2021.help.altair.com/2021.2/flux/Flux/Help/english/UserGuide/English/topics/BertottiIdentificationTool.htm (accessed on 8 August 2023).
- COMSOL. ACDC Module Documentation; COMSOL: Los Angeles, CA, USA, 1998–2018. [Google Scholar]
- Meeker, D. Finite element method magnetics. FEMM 2010, 4, 162. [Google Scholar]
- Karban, P.; Pánek, D.; Orosz, T.; Petrášová, I.; Doležel, I. FEM based robust design optimization with Agros and Ārtap. Comput. Math. Appl. 2021, 81, 618–633. [Google Scholar] [CrossRef]
- Takezawa, M.; Wada, Y.; Yamasaki, J.; Honda, T.; Kaido, C. Effect of grain size on domain structure of thin nonoriented Si-Fe electrical sheets. IEEE Trans. Magn. 2003, 39, 3208–3210. [Google Scholar] [CrossRef]
- Ionel, D.M.; Popescu, M.; McGilp, M.I.; Miller, T.; Dellinger, S.J.; Heideman, R.J. Computation of core losses in electrical machines using improved models for laminated steel. IEEE Trans. Ind. Appl. 2007, 43, 1554–1564. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A.; Lazzari, M.; Pastorelli, M. Predicting iron losses in soft magnetic materials with arbitrary voltage supply: An engineering approach. IEEE Trans. Magn. 2003, 39, 981–989. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A.; Ionel, D.M.; Popescu, M.; Staton, D.A.; Vaschetto, S. A general model to predict the iron losses in PWM inverter-fed induction motors. IEEE Trans. Ind. Appl. 2010, 46, 1882–1890. [Google Scholar] [CrossRef]
- Chen, J.; Wang, D.; Cheng, S.; Wang, Y.; Zhu, Y.; Liu, Q. Modeling of temperature effects on magnetic property of nonoriented silicon steel lamination. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Weiss, P.; Planer, V. Hysteresis in rotating fields. J. Phys. (Theor. Appl.) 1908, 4, 5–27. [Google Scholar] [CrossRef][Green Version]
- Kaplan, A. Magnetic core losses resulting from a rotating flux. J. Appl. Phys. 1961, 32, S370–S371. [Google Scholar] [CrossRef]
- Ivanyi, A. Hysteresis in rotation magnetic field. Phys. B Condens. Matter 2000, 275, 107–113. [Google Scholar] [CrossRef]
- Enokizono, M.; Suzuki, T.; Sievert, J.; Xu, J. Rotational power loss of silicon steel sheet. IEEE Trans. Magn. 1990, 26, 2562–2564. [Google Scholar] [CrossRef]
- Rens, J.; Vandenbossche, L.; Dorez, O. Iron Loss Modelling of Electrical Traction Motors for Improved Prediction of Higher Harmonic Losses. World Electr. Veh. J. 2020, 11, 24. [Google Scholar] [CrossRef]
- Zhu, J.; Zhong, J.; Ramsden, V.; Guo, Y. Power losses of soft magnetic composite materials under two-dimensional excitation. J. Appl. Phys. 1999, 85, 4403–4405. [Google Scholar] [CrossRef]
- Zhong, J.J. Measurement and Modelling of Magnetic Properties of Materials with Rotating Fluxes. Ph.D. Thesis, University of Technology Sydney, Ultimo, Australia, 2002. [Google Scholar]
- Guo, Y.; Zhu, J.; Zhong, J. Measurement and modelling of magnetic properties of soft magnetic composite material under 2D vector magnetisations. J. Magn. Magn. Mater. 2006, 302, 14–19. [Google Scholar] [CrossRef]
- Guo, Y.; Zhu, J.G.; Zhong, J.; Lu, H.; Jin, J.X. Measurement and modeling of rotational core losses of soft magnetic materials used in electrical machines: A review. IEEE Trans. Magn. 2008, 44, 279–291. [Google Scholar]
- Yan, J.; Di, C.; Bao, X.; Zhu, Q. Iron Losses Model for Induction Machines Considering the Influence of Rotational Iron Losses. IEEE Trans. Energy Convers. 2022, 38, 971–981. [Google Scholar] [CrossRef]
- Fiorillo, F.; Rietto, A. Rotational and alternating energy loss vs. magnetizing frequency in SiFe laminations. J. Magn. Magn. Mater. 1990, 83, 402–404. [Google Scholar] [CrossRef]
- Guo, Y.; Zhu, J.G.; Wu, W. Thermal analysis of soft magnetic composite motors using a hybrid model with distributed heat sources. IEEE Trans. Magn. 2005, 41, 2124–2128. [Google Scholar]
- Mre, G.; Leijon, M. Review of Play and Preisach Models for Hysteresis in Magnetic Materials. Materials 2023, 16, 2422. [Google Scholar] [CrossRef]
- Livingston, J. A review of coercivity mechanisms. J. Appl. Physics 1981, 52, 2544–2548. [Google Scholar] [CrossRef]
- Hadjipanayis, G.; Singleton, E.; Tang, Z. Magnetization reversal in ferrite magnets. J. Magn. Magn. Mater. 1989, 81, 318–322. [Google Scholar] [CrossRef]
- Hadjipanayis, G.C.; Kim, A. Domain wall pinning versus nucleation of reversed domains in R-Fe-B magnets. J. Appl. Phys. 1988, 63, 3310–3315. [Google Scholar] [CrossRef]
- de Campos, M.F.; de Castro, J.A. An overview on nucleation theories and models. J. Rare Earths 2019, 37, 1015–1022. [Google Scholar] [CrossRef]
- Bergqvist, A.; Engdahl, G. A phenomenological differential-relation-based vector hysteresis model. J. Appl. Phys. 1994, 75, 5484–5486. [Google Scholar] [CrossRef]
- Bergqvist, A. Magnetic vector hysteresis model with dry friction-like pinning. Phys. B Condens. Matter 1997, 233, 342–347. [Google Scholar] [CrossRef]
- Jiles, D.C.; Atherton, D.L. Theory of ferromagnetic hysteresis. J. Magn. Magn. Mater. 1986, 61, 48–60. [Google Scholar] [CrossRef]
- Kis, P. Jiles-Atherton Model Implementation to Edge Finite Element Method. Ph.D. Thesis, Budapest University of Technology and Economics, Budapest, Hungary, 2006. [Google Scholar]
- Iványi, A. Hysteresis Models in Electromagnetic Computation; Akadémiai Kiadó: Budapest, Hungary, 1997. [Google Scholar]
- Sarker, P.C.; Guo, Y.; Lu, H.; Zhu, J.G. Improvement on parameter identification of modified Jiles-Atherton model for iron loss calculation. J. Magn. Magn. Mater. 2022, 542, 168602. [Google Scholar] [CrossRef]
- Miklás, K. Ferromagnetic Hysteresis in Case of the Numerical Computing of Electromagnetic Fields. Ph.D. Thesis, Metropolitan Transportation Authority, New York, NY, USA, 2014. (In Hungarian). [Google Scholar]
- Kuczmann, M. Simulation of a vector hysteresis measurement system taking hysteresis into account by the vector Preisach model. Phys. B Condens. Matter 2008, 403, 433–436. [Google Scholar] [CrossRef]
- Kuczmann, M. Dynamic Preisach model identification applying FEM and measured BH curve. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2014, 33, 2043–2052. [Google Scholar] [CrossRef]
- Kuczmann, M. Dynamic Preisach hysteresis model. J. Adv. Res. Phys. 2010, 1, 011003. [Google Scholar]
- Szabó, Z.; Füzi, J. Implementation and identification of Preisach type hysteresis models with Everett Function in closed form. J. Magn. Magn. Mater. 2016, 406, 251–258. [Google Scholar] [CrossRef]
- Szabó, Z. Preisach functions leading to closed form permeability. Phys. B Condens. Matter 2006, 372, 61–67. [Google Scholar] [CrossRef]
- Fuzi, J. Analytical approximation of Preisach distribution functions. IEEE Trans. Magn. 2003, 39, 1357–1360. [Google Scholar] [CrossRef]
- Mayergoyz, I. Mathematical models of hysteresis. IEEE Trans. Magn. 1986, 22, 603–608. [Google Scholar] [CrossRef]
- Novak, M.; Eichler, J.; Kosek, M. Difficulty in identification of Preisach hysteresis model weighting function using first order reversal curves method in soft magnetic materials. Appl. Math. Comput. 2018, 319, 469–485. [Google Scholar] [CrossRef]
- Chen, L.; Yi, Q.; Ben, T.; Zhang, Z.; Wang, Y. Parameter identification of Preisach model based on velocity-controlled particle swarm optimization method. AIP Adv. 2021, 11, 015022. [Google Scholar] [CrossRef]
- Jiaqiang, E.; Qian, C.; Zhu, H.; Peng, Q.; Zuo, W.; Liu, G. Parameter-identification investigations on the hysteretic Preisach model improved by the fuzzy least square support vector machine based on adaptive variable chaos immune algorithm. J. Low Freq. Noise, Vib. Act. Control 2017, 36, 227–242. [Google Scholar] [CrossRef]
- Galinaitis, W.S.; Joseph, D.S.; Rogers, R.C. Parameter identification for Preisach models of hysteresis. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Pittsburgh, PA, USA, 9–12 September 2001; Volume 80289, pp. 1409–1417. [Google Scholar]
- Della Torre, E.; Vajda, F. Parameter identification of the complete-moving-hysteresis model using major loop data. IEEE Trans. Magn. 1994, 30, 4987–5000. [Google Scholar] [CrossRef]
- Chevalier, T.; Kedous-Lebouc, A.; Cornut, B.; Cester, C. A new dynamic hysteresis model for electrical steel sheet. Phys. B Condens. Matter 2000, 275, 197–201. [Google Scholar] [CrossRef]
- Vo, A.T.; Fassenet, M.; Préault, V.; Espanet, C.; Kedous-Lebouc, A. New formulation of Loss-Surface Model for accurate iron loss modeling at extreme flux density and flux variation: Experimental analysis and test on a high-speed PMSM. J. Magn. Magn. Mater. 2022, 563, 169935. [Google Scholar] [CrossRef]
- Dupré, L.; De Wulf, M.; Makaveev, D.; Permiakov, V.; Pulnikov, A.; Melkebeek, J. Modelling of electromagnetic losses in asynchronous machines. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2003, 22, 1051–1065. [Google Scholar] [CrossRef]
- Bottauscio, O.; Chiampi, M.; Dupré, L.; Repetto, M.; Von Rauch, M.; Melkebeek, J. Dynamic Preisach modeling of ferromagnetic laminations: A comparison of different finite-element formulations. Le J. Phys. IV 1998, 8, Pr2-647–Pr2-650. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Marketos, P.; Moses, A.J. Congruency-based hysteresis models for transient simulation. IEEE Trans. Magn. 2004, 40, 390–399. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Harrison, R.G.; Chiesa, N. Inverse hysteresis models for transient simulation. IEEE Trans. Power Deliv. 2013, 29, 552–559. [Google Scholar] [CrossRef]
- Stratton, J.A. Electromagnetic Theory; McGraw-Hill Book Company: New York, NY, USA, 1941. [Google Scholar]
- Hantila, I.F.; Grama, G. An overrelaxation method for the computation of the fixed point of a contractive mapping. Rev. Roum. Sci. Tech. Electrotech. Energetique 1974, 27, 395–398. [Google Scholar]
- Zirka, S.E.; Moroz, Y.I.; Marketos, P.; Moses, A.J. Viscosity-based magnetodynamic model of soft magnetic materials. IEEE Trans. Magn. 2006, 42, 2121–2132. [Google Scholar] [CrossRef]




| B [T] | P @ 5 Hz | P @ 50 Hz | P @ 100 Hz | P @ 200 Hz |
|---|---|---|---|---|
| 0.2 | 0.01/0.01 (0.01) | 0.08/0.093 (0.08) | 0.17/0.22 (0.21) | 0.39/0.55 (0.55) |
| 0.6 | 0.05/0.05 (0.05) | 0.54/0.616 (0.60) | 1.16/1.49 (1.52) | 2.67/3.98 (4.10) |
| 1.0 | 0.12/0.12 (0.12) | 1.30/1.50 (1.38) | 2.85/3.66 (3.74) | 6.69/9.96 (9.96) |
| 1.4 | 0.23/0.23 (0.22) | 2.53/2.85 (2.57) | 5.54/6.87 (6.78) | 13.1/18.4 (17.7) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orosz, T.; Horváth, T.; Tóth, B.; Kuczmann, M.; Kocsis, B. Iron Loss Calculation Methods for Numerical Analysis of 3D-Printed Rotating Machines: A Review. Energies 2023, 16, 6547. https://doi.org/10.3390/en16186547
Orosz T, Horváth T, Tóth B, Kuczmann M, Kocsis B. Iron Loss Calculation Methods for Numerical Analysis of 3D-Printed Rotating Machines: A Review. Energies. 2023; 16(18):6547. https://doi.org/10.3390/en16186547
Chicago/Turabian StyleOrosz, Tamás, Tamás Horváth, Balázs Tóth, Miklós Kuczmann, and Bence Kocsis. 2023. "Iron Loss Calculation Methods for Numerical Analysis of 3D-Printed Rotating Machines: A Review" Energies 16, no. 18: 6547. https://doi.org/10.3390/en16186547
APA StyleOrosz, T., Horváth, T., Tóth, B., Kuczmann, M., & Kocsis, B. (2023). Iron Loss Calculation Methods for Numerical Analysis of 3D-Printed Rotating Machines: A Review. Energies, 16(18), 6547. https://doi.org/10.3390/en16186547








