Piezoelectric Energy Harvester for Harnessing Rotational Kinetic Energy through Linear Energy Conversion

Abstract

Real-time condition monitoring of various types of machinery using sensor technology has gained significant importance in recent years. However, relying on batteries to power these sensors proves to be sub-optimal, as it necessitates regular charging or replacement. To address this, harvesting waste energy from ambient sources emerges as a more efficient alternative. Everyday applications like vehicle wheels, fans, and turbines present ambient sources of waste rotational energy. In this study, we propose a novel rotational energy harvester design that converts rotational energy into linear energy. This linear energy impacts a piezoelectric disk, generating an electric potential. Through simulations, the expected electric potential at varying frequencies was evaluated. Subsequently, experimental tests were conducted by connecting the harvester to a rectifier for AC-to-DC signal conversion and an oscilloscope for voltage measurement. A DC motor replicated the rotational motion at the frequencies from the simulation, and the power output was measured. Using the power transfer theorem, simulation and experimental power outputs were calculated, resulting in values of 188, 513, and 1293 μW and 88.89, 336, and 923 μW, respectively. These results reveal that the designed harvester is competitive with those of existing rotational energy harvester designs, demonstrating the promising potential of this novel harvester.

1. Introduction

The significance of the energy-harvesting (EH) domain is experiencing a notable upsurge owing to the escalating interest in establishing self-powered systems [1]. These self-powered systems encompass an array of innovative applications, including wireless sensors that obviate the need for periodic recharging or replacements [2], generators integrated into roadways to harness energy from moving vehicles [3], and the utilization of antennas to capture electromagnetic waves for energy retrieval [1]. The essence of EH lies in its capability to harness energy from ambient sources that would otherwise go to waste, and subsequently convert it into electrical energy for direct application use. Notably, EH can be derived from diverse sources, encompassing mechanical energies, thermal energies, and electromagnetic waves. In the domain of mechanical EH, the prevailing techniques involve piezoelectric EH, electrostatic EH, and electromagnetic EH [4].

Piezoelectric energy harvesting stands out as one of the most extensively researched techniques in the EH domain, chiefly because of its superior attributes such as heightened energy density, elevated voltages, increased capacitance, and minimal mechanical damping [5,6]. Furthermore, piezoelectric harvesters exhibit a commendable advantage in terms of their compact size and flexible form [5], rendering them highly suitable for integration into self-powered systems that demand minimal volume, prolonged lifespan, and negligible maintenance requirements [5].

Piezoelectric energy conversion has already found diverse applications, one of which is in pressure sensors, where it effectively harnesses compression force for energy utilization [7]. Many of these applications predominantly capitalize on linear mechanical energy and successfully convert it into electrical energy.

Nonetheless, in real-life scenarios, numerous ambient sources generate rotational mechanical energy, posing a unique challenge for energy harvesting. Rotational energy sources, such as vehicle tires, power plant turbines, and helicopter blades, represent prominent examples of such cases. Consequently, a growing interest has emerged in the development of energy-harvesting systems specifically designed to scavenge rotational energy. Extensive research endeavors have been dedicated to exploring and devising such systems to harness this untapped source of energy.

Khameneifar et al. [2] proposed a novel piezoelectric energy harvester that harnessed gravitational force, aided by a tip-mass. Their design involved four piezoelectric cantilever beams interconnected to a rotating hub, each fitted with a mass at its far tip. The energy harvester induced mechanical vibration energy in the flexible beam due to the gravitational force applied to the tip-mass while the hub rotated. The piezoelectric transducer, attached along the beam, converted the induced mechanical vibration energy into electricity. By utilizing mathematical analysis and experimental validation, they derived expressions for the electrical power, determined the optimum load resistance, and identified the maximum power output achievable with their 65 g tip-mass setup, resulting in 4.3 V at 85 rad/s, with a maximum power output of 30.8 μW. Guan and Liao [8] proposed a similar concept with a slight variation in design. In their setup, the tip-mass was placed inwards rather than outwards. This arrangement reduced the radius of rotation, resulting in a decreased centrifugal force. By bringing the centrifugal force closer to the gravitational force, the piezoelectric beam exhibited enhanced vibration, leading to a higher voltage generation. Their design achieved voltage outputs ranging from 5 to 37 V for frequencies of 44–84 rad/s, with generated power varying between 83.5–825 μW, depending on the rotational frequency. Machado et al. [9] proposed a specialized design optimized for low-frequency applications, utilizing gravitational force as the main driving mechanism. The system demonstrated the ability to produce relatively high voltages, ranging from 7 to 20 V, within the low-frequency range of 4.7 to 14.7 rad/s. The power output achieved by this energy harvester was measured at 102 to 845 μW, with a mechanical-to-electrical conversion of 86% to 79%, respectively. Their setup involved an electric motor with a variable speed controller. The harvested voltage output was compared to theoretical predictions, showing good agreement. The system implemented an AC-DC conversion circuit to rectify the AC generated voltage, and the rectified voltage was calculated analytically and validated with experimental results. Furthermore, the conversion efficiency for mechanical to electrical power was evaluated using an analytical model, indicating variations in efficiency with rotation frequency and electrical load resistance. Another approach was presented by Kim S et al. [10], who introduced an underwater piezoelectric energy harvester employing a propeller-based design with “hitting sticks” that rotate and impact an acrylic plate connected to a piezoelectric cantilever beam. This technique allowed for easy control of the bending length of the piezoelectric module, enabling frequency matching to maximize output power. The experimental setup operated at a water flow rate of 1.2 m/s, matching a frequency of 24.5 Hz with four hitting sticks and an 80 mm bending length. At this configuration, the system generated a high voltage of 50 V at 154 rad/s, with an impressive output power of 17 mW. Impedance matching was performed, resulting in a high voltage of 50 V at 154 rad/s with an impressive output power of 17 mW at a resistance of 10.8 kΩ. Yang et al. [11] introduced a gullwing-structured rotational-energy-harvesting strategy that applied periodic pressure to two flexible piezoelectric buckled-bridges, enabling effective electromechanical conversion. The harvester achieved a peak open-circuit voltage of 20 V at an applied rotational frequency of 49 rad/s. The energy storage and practical output power were evaluated through capacitor charging experiments, with capacitors of 100 μF and 470 μF reaching charging voltages of 14.7 V after 38 s and 154 s, respectively. The harvester provided an average electrical energy output of no less than 0.2 mJ per second. A common power management chip optimized its output, resulting in a maximum output power of 0.4 mW at the matching resistance of 30 kΩ, with a high power density of 6.54 μW mm⁻³. These findings demonstrate the potential of the gullwing-structured harvester for low-frequency rotational applications, making it a promising solution for powering wireless sensors in diverse environmental settings.

Furthermore, designs utilizing permanent magnets to induce bending in piezoelectric beams were also explored. Celik et al. [12] proposed a single-layer piezoelectric setup with two permanent magnets—one on a rotating shaft and another on the tip of the piezoelectric layer. The interaction between these magnets caused bending of the piezoelectric disk. The harvester generated 6 V at approximately 30 rad/s, with a power output of 3.6 μW. The setup for the test of the PZT layer of the proposed harvester involved a magnetic excitation unit, rectifier and storage circuit, signal generator, laser displacement sensor (LDS), and data acquisition and monitoring units. The setup allowed the examination of the vibration characteristics of the piezoelectric material under the magnetic force. The dynamics of the PZT were explored for a wide range of frequencies, and suitable excitation strength was applied to the electromagnet to minimize damping effects and enable competitive elastic forces with the field excitation. The PZT layer used in the experiments had specified capacitance and stiffness values. Measurements were conducted for various parameters, such as the amplitude and frequency of the excitation waveform, displacement of the layer tip, and input/output voltages. Na et al. [13] presented a multi-layer system employing permanent magnets. Their design consisted of six vertically connected piezoelectric films attached to a top disk stator, and below it, six magnets were mounted on a rotating disk. As the disk rotated, the bending of the piezoelectric layers generated electrical energy. The system achieved a voltage output of 22 V at 30 rad/s, producing a power output of 5.84 mW. The energy-harvesting characteristics and evaluation of the proposed wind energy harvester were conducted through various experimental measurements. The output voltage of the open circuit was measured using an oscilloscope, and the generated output power was determined using a formula considering the root-mean-square voltage and the load resistance. The deformation of the piezoelectric buckled-plate cantilever (PBC) under excitation was measured with a laser displacement meter. The wind energy harvester’s design and parameters were illustrated, and its performance was systematically assessed in a hand-made wind tunnel with controlled wind speeds. Each PBC was connected to a rectifying circuit, and their electrical output voltage and current were evaluated by connecting all six PBCs in series or parallel. The output power characteristics were measured using a digital power meter. While magnetic systems demonstrated impressive power output, a significant drawback of these designs lay in their considerable size, which could potentially present practical challenges in certain applications.

Many of the studies mentioned above aimed to convert rotational mechanical motion into vibration to leverage the traditional vibrational EH method [14]. However, vibrational EH typically necessitates matching the input vibrational frequency with the resonance frequency of the EH systems to attain maximum power generation. This constraint restricts the design flexibility of EH systems, often resulting in intricate mechanical designs, which can escalate costs and compromise reliability.

As an alternative approach, converting rotational motions into linear motion for EH offers a promising solution to circumvent the resonance frequency limitation and potentially simplify the design while efficiently harnessing rotational energy. This paper proposes an efficient EH design that achieves the harvesting of rotational energy by adeptly converting it into linear energy.

2. Materials and Methodology

2.1. Materials and Equipment

In this study, a variety of materials and equipment were employed to investigate the rotational energy harvester. The R&S HM8118 LCR bridge played a crucial role in testing different frequencies, enabling the determination of the piezoelectric disk’s minimum impedance and resonance frequency.

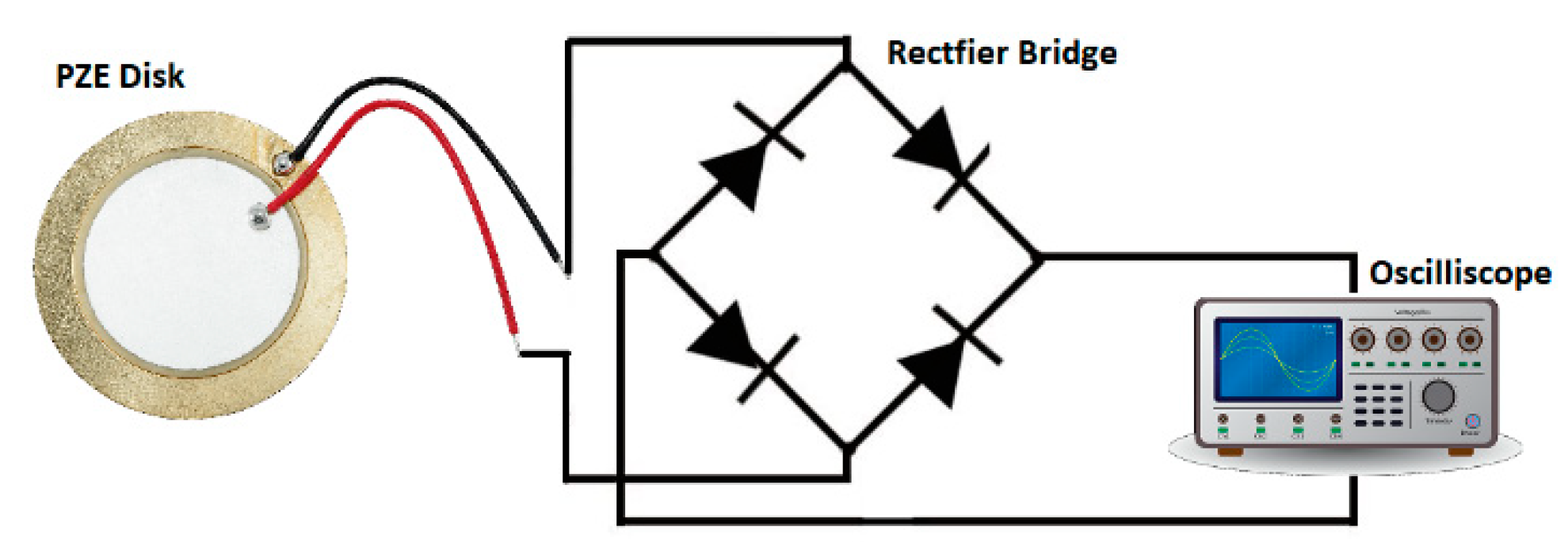
To induce rotational motion in the harvester, a DC supply was utilized, providing the necessary power to the DC motor. For precise voltage measurement, a Keysight Oscilloscope was utilized, ensuring accurate data collection from the piezoelectric disk. A rectifier (KBPC-5010) was used to convert the AC signal from the PZE disk to a DC signal.

Fabrication of the energy harvester and its components was made possible by the use of a 3D printer, offering the advantage of physical experimentation, corroborating the simulation results.

At the core of the energy harvester was the 20 mm piezoelectric disk, complemented by a 27 mm protective disk. This critical component efficiently converted mechanical energy into electrical energy during impacts, while also ensuring its safety and longevity through the protective disk.

2.2. Engineering the Rotational Energy Harvester

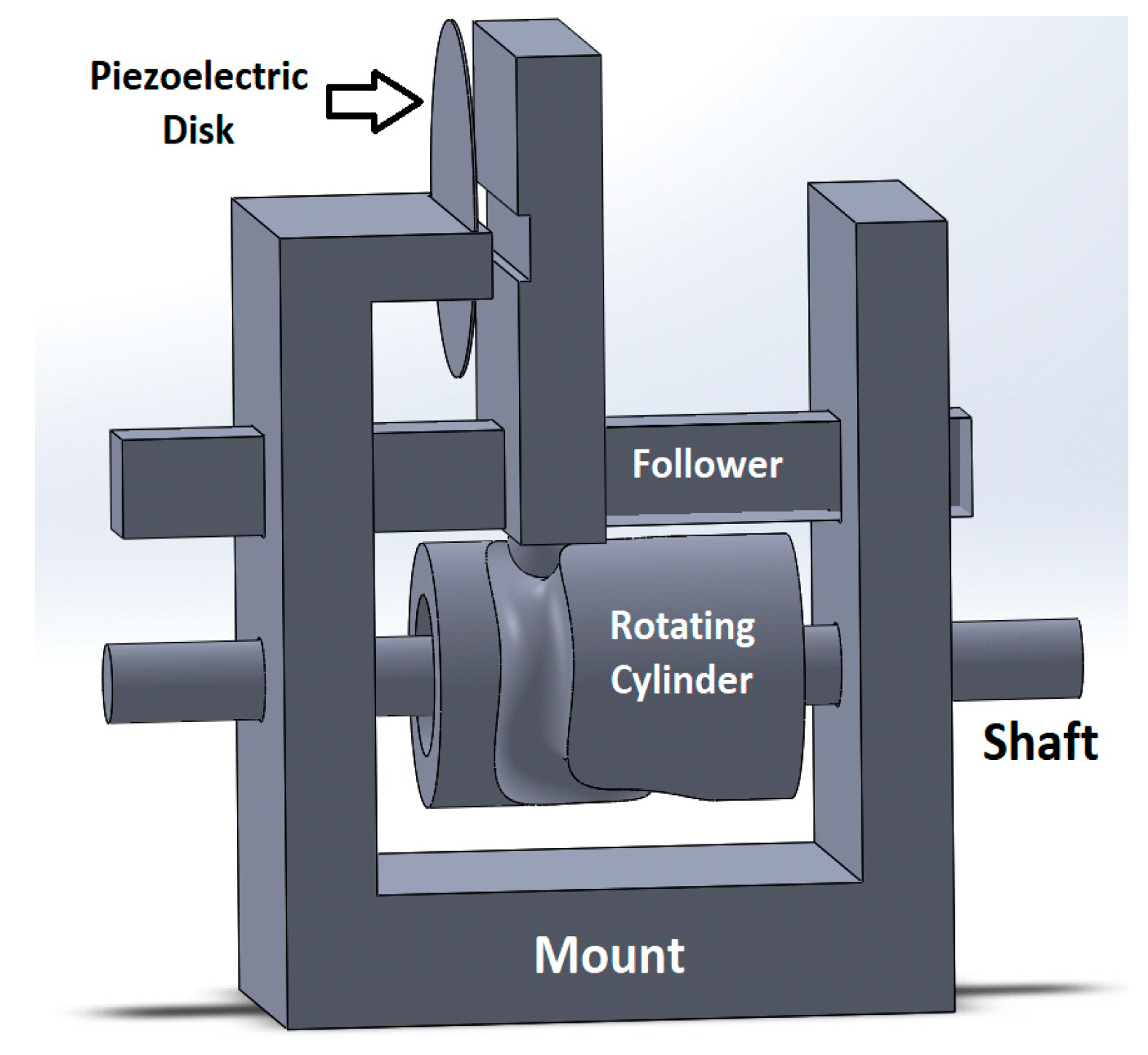
The novel design of the rotational energy harvester centers around a cylindrical component with a strategically placed groove serving as the pivotal rotating element. A follower, affixed to the cylinder through a spherical structure, plays a crucial role as the impacting element. Its primary responsibility involves striking the piezoelectric (PZE) disk, thereby inducing the necessary mechanical motion.

As the cylinder rotates, this constructed setup sets the follower in motion, causing it to move back and forth in a controlled manner, thus ensuring precise impacts on the piezoelectric disk. These impactful interactions between the follower and the PZE disk effectively translate rotational energy into linear motion, ultimately leading to the generation of valuable electrical energy.

2.2.1. Rotating Element

The cylinder features a functional design, with a diameter of 20 mm and a length of 30 mm. Along the cylinder’s surface, a groove measuring 14 mm in width is engraved, tailored to accommodate a 6 mm diameter sphere with a perfect fit.

On one face of the cylinder, a circular cut with a diameter of 2.5 mm and a length of 10 mm is implemented, intended for the insertion of a DC motor shaft. On the opposite face, a 12 mm diameter circle with a length of 15 mm is incorporated to facilitate the insertion of a 12 mm bearing and a 6 mm shaft. This arrangement ensures unrestricted rotation of the cylinder, thus optimizing the performance of the rotational energy harvester.

2.2.2. Impacting Element

The follower constitutes a solid block measuring 7 × 27 × 47 mm, designed to play a pivotal role in the energy harvester’s operation. Positioned at the bottom end of this block is a 5.6 mm diameter sphere to ensure a secure placement within the groove.

At the bottom face of the follower, a sturdy 7 × 7 × 72.9 mm square rod is incorporated to facilitate motion in only one dimension, enabling smooth and controlled back-and-forth movements of the follower within the groove. Additionally, a carefully measured 3 × 27 × 10 mm rectangular cut, situated approximately midway through the face, serves as a crucial feature to prevent the follower from unintended impacts with the mount or other elements during the harvester’s operation.

2.2.3. Support for the Rotating and Impacting Elements

To provide robust support for the rotating and impacting elements, a mount was designed in two separate parts. The first part consists of a base measuring 40 × 30 × 10 mm, securely attached to a rectangular block measuring 7.5 × 30 × 60 mm. This block features two precisely crafted cuts: a 7 × 7 mm square cut, allowing the square rod to pass through effortlessly, and a 6.4 mm diameter circular cut, providing a perfect fit for the shaft.

Two measured circular cuts, each with a diameter of 2 mm, serve as sturdy anchoring points, ensuring a secure and reliable attachment to the other side of the mount.

The second part of the mount has the same dimensions as the block of the first part, including corresponding square and circular cuts. However, this side omits the circular cut and instead integrates a 20 × 15 mm square cut, offering easy insertion of the DC motor. Additionally, a 10 × 30 × 5 mm rectangular block is firmly attached to the top face, with a 0.5 × 27 mm cut at its end, providing a secure space for the piezoelectric disk.

Like the first part, the bottom of the second part also incorporates a 2 mm diameter circular cut, ensuring a snug connection when both parts are assembled together. This comprehensive design guarantees optimal stability and support for the rotational and impacting elements of the energy harvester. Figure 1 illustrates the final conceptual design of the energy harvester. It is important to note that the PZE disk in the illustration is solely for demonstrative purposes and was not part of the final 3D-printed system.

2.3. Modeling and Simulation

Modeling and simulation were carried out using COMSOL, employing a simplified model that included the follower and a 20 mm diameter, 0.25 mm thickness piezoelectric disk. Figure 2 demonstrates the simplified model in the simulation software.

The material chosen for the disk was PZT-5H, while PLA was selected as the material for the follower. As the properties of PLA (density, Young’s modulus, and Poisson’s ratio) were not pre-loaded in COMSOL, they were acquired from Farah et al. [15].

In the simulation, the follower was positioned 6.82 mm away from the disk, and a periodic motion was introduced using a sine equation:

$$D=-0.007\sin \left(\omega t\right)$$

where D is the displacement, 0.007 represents the amplitude in meters, ω denotes the angular frequency, and t signifies the elapsed time.

During the simulation, the follower initiated motion along the negative x-axis towards the piezoelectric disk, governed by the displacement equation above.

A time-dependent study was performed. It encompassed three distinct frequencies: 50, 60, and 100 rad/s, selected to mimic common frequencies encountered in real-world applications. For instance, vehicle wheels typically exhibit rotational speeds ranging between 7 and 13.5 Hz [8], equivalent to 44–84 rad/s. The simulation was conducted with a maximum time span of 0.04 s, enabling the acquisition of voltage values resulting from a single impact event.

2.4. Fabrication and Testing of the Final Design

To fabricate the final design, 3D printing was utilized, materializing the intricate components into physical form as seen in Figure 3. The voltage values were then measured by linking the piezoelectric disk to a rectifier, and subsequently connecting the rectifier to an oscilloscope to acquire the output voltage readings. Figure 4 illustrates the experimental set-up for obtaining the voltage measurements.

Additionally, to achieve the desired rotational frequencies, the DC voltage was adjusted within the range of 2–4 V, ensuring optimal performance and accurate evaluation of the energy harvester’s capabilities.

2.5. Impedance Measurement

The internal impedance of the piezoelectric disk was measured using an LCR bridge. The LCR bridge measures the inductance (L), capacitance (C), and resistance (R) (in this case, the impedance). The bridge has 4 probes: 2 probes to measure the current, and 2 probes to measure the voltage.

The following steps were taken to measure the impedance:

(1)

The four probes were connected to the piezoelectric disk.

(2)

The frequency of the LCR bridge was varied from 2 Hz to 200 kHz in 69 steps.

(3)

The frequency with the minimum impedance was recorded. This is the resonance frequency.

(4)

The impedance, inductance, and capacitance for the minimum frequency was recorded.

(5)

The impedance, inductance, and capacitance were also recorded for the frequency one step above, and one step below.

3. Results

3.1. Simulation Results

The simulation encompassed three distinct frequencies: 50 rad/s, 60 rad/s, and 100 rad/s, with corresponding AC output signals resulting in peak voltages of 6.10 V, 10.07 V, and 15.64 V, respectively.

To convert the AC signal into a DC signal, the absolute values of the obtained voltages were taken. Figure 5 and Figure 6 graphically represent the waveforms before and after the DC conversion, providing a clear visualization of the signal transformation.

3.2. Experimental Results

Experimental results were acquired by utilizing a DC motor to induce rotation in the cylinder. The corresponding input DC voltages, currents, and the resulting rotational frequencies are provided in

Table 1. The input DC power and the corresponding frequency.

DC Voltage	DC Current	Input Power	Frequency
2 V	0.41 A	0.82 W	50 rad/s
2.5 V	0.43 A	1.075 W	65 rad/s
3.5 V	0.63 A	2.205 W	95 rad/s

.

The experimental results yielded maximum output voltages of 4.19 V, 8.15 V, and 13.5 V from the piezoelectric disk at 50 rad/s, 65 rad/s, and 95 rad/s, respectively. These values were obtained after voltage rectification. Figure 7 illustrates the experimental results obtained from the piezoelectric disk, while Figure 8 offers a comparative analysis between the simulation and experimental outcomes.

3.3. Minimum Impedance and Resonance

The impedance measurement was performed experimentally using an LCR bridge, and it revealed the resonance frequency of the PZE disk to be at 120 kHz. This is where the impedance is at its minimum value. Additionally, impedance values were recorded at 150 kHz (one step above) and 100 kHz (one step below) to further characterize the behavior.

The LCR bridge also provided values for inductance and capacitance at each of the mentioned frequencies (100, 120, and 150 kHz). By utilizing these inductance and capacitance values, the exact frequency was determined since the step increments in the LCR bridge’s input frequency were quite significant (from 100 Hz to 120 Hz to 150 Hz). This approach enables precise identification of the exact frequencies by using the below equations:

$${\omega }^2=\frac{1}{LC} and f=\frac{\omega }{2\pi }$$

The data obtained are summarized in

Table 2. LCR Data and the calculated frequency.

Impedance	Inductance	Capacitance	Exact Frequency
127.52 $\mathrm{k}\mathsf{\Omega }$	514.31 mH	4.2068 pF	108,201 Hz
49.375 $\mathrm{k}\mathsf{\Omega }$	293.77 mH	5.6993 pF	123,000 Hz
431.35 $\mathrm{k}\mathsf{\Omega }$	1.4874 H	0.78214 pF	147,558 Hz

.

Hence, the minimum impedance was found to be 49.375 kΩ at a resonant frequency of 123 kHz.

3.4. Maximum Power Harvested

To achieve maximum power, it is crucial to perform a process known as impedance matching to match the load resistance ($R_L$) with the internal impedance ($Z_I$) at the resonant frequency [16]:

$$Z_I=R_L$$

Based on experimental findings, the internal impedance was determined to be 49.375 kΩ at the resonant frequency of 123 kHz.

The maximum power ($P_{max}$) can then be obtained using the maximum power transfer theorem [3]:

$$P_{max}={\left(\frac{V}{Z_I+R_L}\right)}^2{R}_L$$

The maximum power is generated when impedance matching is achieved, and the load resistance equals the internal impedance:

$$P_{max}=\frac{V^2}{4Z_I}$$

The same formula for maximum power can also be derived using equations for internal impedance [16] and $V_{OC}$ [8]:

$$Z_I={\left(C_{pzt}{\omega }_n\right)}^{-1}$$

$$V_{OC}=\sqrt{\frac{4P}{C_{pzt}\omega }}$$

Substituting $Z_I$ into the second formula, and re-arranging for P yields:

$$P=\frac{{V_{OC}}^2}{4Z_I}$$

Therefore, for the energy harvester to attain its maximum power output, it must be connected to a load with a total resistance equal to the internal impedance (49.375 kΩ) of the PZE disk at its resonance frequency (123 kHz). The peak voltages measured by the oscilloscope, as observed in Figure 5 and Figure 6, were used for calculating the maximum power generated in the maximum power equation.

During the simulation, the energy harvester was tested at frequencies of 50, 60, and 100 rad/s. However, in the actual experimentation, due to the limitations of the DC motor, the achievable frequencies were 50, 65, and 95 rad/s. Varying the DC motor’s voltage level to obtain precise frequencies proved challenging within the given constraints.

Table 3. Simulation and Experimental Power harvested at different frequencies.

Frequency (Rad/s)	Simulation Power	Experimental Power
50 vs. 50	$188\mathsf{\mu }\mathrm{W}$	$88.89\mathsf{\mu }\mathrm{W}$
60 vs. 65 rad/s	$513\mathsf{\mu }\mathrm{W}$	$336\mathsf{\mu }\mathrm{W}$
100 vs. 95 rad/s	$1239\mathsf{\mu }\mathrm{W}$	$923\mathsf{\mu }\mathrm{W}$

presents a comparison between the values obtained from simulation and the experimental results.

3.5. Energy-Collection Effiecieny

The energy-collection efficiency of the harvester was evaluated using a DC motor to simulate rotational motion from various ambient sources. If the efficiency were assessed solely with respect to the DC motor, it would be extremely low. For instance, at 50 rad/s, the input power was 0.82 W (as per Table 1), while the experimental output power was 88.89 μW (as per Table 3). Hence:

$$Effeciency=\frac{OutputPower}{InputPower}=\frac{8.889\times {10}^{-5}}{0.82}=0.011\%$$

In practical applications, the harvester will scavenge energy from ambient sources rather than a DC motor. Therefore, the exact energy collection efficiency will vary based on the ambient source, as the rotational energy for each source (e.g., helicopter blades vs. wheels) will differ, even if they share the same rotational frequency, due to differences in moment of inertia.

It is essential to emphasize that the scavenged energy is typically waste energy not utilized efficiently. The harvester capitalizes on this waste energy, allowing the input power to be used for other applications while the harvester efficiently harnesses the otherwise wasted power for practical purposes.

4. Discussion

4.1. Discrepancy in Simulation and Experimental Results

The simulation and experimental results exhibit a clear discrepancy, with the difference ranging from 14% to 31% and the voltage difference remaining approximately 2 V for each of the three different frequencies tested. Initially, it is essential to assess whether these discrepancies fall within the expected error range. The LCR bridge provides an error of 0.05% in impedance measurement, while the oscilloscope has a 0.1% error in voltage measurement.

For the 50 rad/s case, the voltage is measured at 4.19 V, while the impedance is recorded as 49,375 Ω. Considering the given errors, the maximum power estimation is calculated as follows:

$$\begin{array}{c}V=4.19+\left(4.19V\times 0.1\%\right)=4.19419\mathrm{V}\\ Z_I=\mathrm{49,375}\mathsf{\Omega }-\left(\mathrm{49,375}\times 0.05\%\right)=\mathrm{49,350}\mathsf{\Omega }\\ P_{max}=\frac{{\left(4.19419V\right)}^2}{4\times \mathrm{49,350}\mathsf{\Omega }}=89.11\mathsf{\mu }\mathrm{W}\end{array}$$

The minimum value is determined in the same manner, with the error subtracted from the voltage and added to the impedance, resulting in a value of 88.67 μW. Both values represent an error of approximately 0.25%, indicating a substantial deviation from the observed simulation results.

The same analysis is performed for the 100 rad/s case, yielding upper- and lower-bound power estimates of 925 μW and 920.5 μW, respectively. These values also significantly deviate from the simulation results, with a maximum error of 0.27%. These calculated errors cannot justify the discrepancy between the simulation and experimental results.

Therefore, the observed discrepancies must be due to other factors. Three factors can be attributed to these discrepancies. Firstly, the simulation measures the open-circuit voltage, while the experimental results measure the rectified voltage. The conversion from AC to DC introduces signal loss, leading to a reduction in the rectified voltage compared to the open-circuit voltage.

Secondly, the simulation simplifies the model by imposing a periodic motion on the follower in the absence of the cylinder and the mount, neglecting friction between the follower and these components. In reality, friction causes energy loss and decreases the impact force, resulting in a lower generated voltage.

Thirdly, the presence of wires on the piezoelectric disk surface, necessary for electrical measurement, introduces tension force and slows down the motion of the follower during impacts, leading to a decrease in the impact force and, consequently, the generated voltage.

The most significant cause of discrepancy is the first factor, which is the AC-to-DC signal conversion, wherein the silicon rectifier used (KBPC-5010) has a maximum voltage drop of 1.1 V per element, depending on the AC peak voltage [17]. With two diodes, the maximum voltage drop reaches 2.2 V, which explains the observed deviation between the simulation and experimental results.

4.2. The Primary Source of Voltage Generation

It is crucial to identify the primary source of voltage generation. Therefore, theoretical calculations were performed to determine the impact force and, consequently, the generated voltage.

Given that the groove on the cylinder is 14 mm, and the period of the follower for 95 rad/s is 0.066 s, the follower would travel 14 mm back and forth in 0.066 s. Hence:

$$Velocity=\frac{28\mathrm{mm}}{0.066\mathrm{s}}=0.4242\mathrm{m}/\mathrm{s}$$

During the cylinder’s rotation, approximately 12.5% of the total period would be allocated to impacting the disk. This is evident in Figure 7, as the impact time peaks’ period is around 8 times less than the period between one impact and another. Therefore, the impact time is:

$$\begin{array}{c}\mathsf{\Delta }t=0.125\times 0.066\mathrm{s}=0.00825\mathrm{s}\\ a=\frac{\mathsf{\Delta }\nu }{\mathsf{\Delta }t}=51.42\mathrm{m}/{\mathrm{s}}^2\end{array}$$

To calculate the mass, it is essential to determine the impacting volume first. This can be achieved by multiplying the area of impact (the area of the disk) by the thickness of the follower. Once the impacting volume is obtained, the impacting mass can be calculated by multiplying the impacting volume with the density of the material.

$$Area=\pi {\left(10\mathrm{mm}\right)}^2=314.16{\mathrm{mm}}^2$$

The thickness of the follower is 7 mm. So:

$$Volume=2199.12\mathrm{m}{\mathrm{m}}^3$$

The density of PLA is $1.3\mathrm{g}/\mathrm{c}{\mathrm{m}}^3$ [15].

$$\begin{array}{c}mass=1.3\frac{\mathrm{g}}{\mathrm{c}{\mathrm{m}}^3}\times 0.002199\mathrm{c}{\mathrm{m}}^3=0.002859\mathrm{g}\\ =2.86\times {10}^{-6}\mathrm{k}\mathrm{g}\end{array}$$

$$\begin{array}{c}F=ma\\ =2.86\times {10}^{-6}\mathrm{k}\mathrm{g}\times 51.42\mathrm{m}/{\mathrm{s}}^2\end{array}$$

$$F=15.8\times {10}^{-5}\mathrm{N}$$

The impact force calculated is notably low, so factors like friction and wire interactions would have a minimal impact on the voltage reduction. Therefore, the primary source of voltage generation would arise from another factor, which is the bending of the disk caused by the impact.

As explained in the Section 2, the follower was allowed to move 7 mm towards the disk while being placed 6.82 mm away. This would result in the follower moving 0.18 mm (around 72% of the disk’s thickness) into the disk, leading to bending, as depicted in Figure 9. This bending effect is a crucial factor in generating the observed voltage in the harvester.

Prior research has established that the electrical output of the harvester is contingent on the rate of bending deflection [18]. It demonstrated that the electrical conversion efficiency relies on several factors, with a particular focus on the ratio of the electrochemical coupling coefficient to mechanical damping. Higher mechanical damping leads to reduced oscillations, and since mechanical damping is inversely proportional to the conversion efficiency, elevated mechanical damping results in lower electrical conversion efficiency.

The bending also explains the observed trends in the simulation results’ graphs in Figure 5. Smaller voltage peaks are evident immediately after the highest peak, which can be attributed to the oscillation of the disk. Following the impact, the disk undergoes slight back-and-forth oscillations as the follower moves away before the next impact. This oscillation is possible only if the disk had bent after the impact.

Moreover, the experimental results depicted in Figure 7 reveal inconsistent maximum voltage peaks. For instance, in the 95 rad/s results, the second peak shows the highest voltage, while the other peaks display lower voltages. This disparity can be attributed to the cylinder’s movement along the rotating shaft when the DC motor is driving the cylinder. As a result, the follower is distanced from the piezoelectric disk, making it unable to maintain a precise 0.18 mm movement into the disk consistently.

Balancing the cylinder’s proximity to the disk becomes a challenging task in practice. If the cylinder is moved too close, the follower will stop upon impact. Conversely, keeping it too far would lead to lower voltage generation due to decreased bending. Therefore, the lower voltage peaks observed in this scenario are associated with reduced bending of the disk.

4.3. The Power Harvested from the Design

The power output obtained from the rotational energy harvester varied from 188 $\mathsf{\mu }\mathrm{W}$ to 1239 $\mathsf{\mu }\mathrm{W}$ in the simulation results and 88.89 $\mathsf{\mu }\mathrm{W}$ to 923 $\mathsf{\mu }\mathrm{W}$ in the experimental results, covering frequencies ranging from 50 to 100 rad/s. To thoroughly evaluate the performance of the rotational-to-linear energy harvester, a comprehensive comparison with power outputs from other existing harvesters is crucial.

However, an inherent challenge emerges due to the diverse frequency tested among different harvesters, making a direct comparison less straightforward but still plausible with appropriate analysis. Figure 10 presents the results obtained from the designed rotational-to-linear energy harvester, compared with pertinent data sourced from the existing literature. This comparative visualization offers insights into the effectiveness and efficiency of the proposed design in relation to its counterparts, shedding light on the unique advantages and potential improvements of the harvester.

Figure 10 visually presents the power output acquired at different frequencies from various harvesters. A straightforward comparison can be made by assessing the power-to-frequency ratio for each harvester. Although a higher power-to-frequency ratio may not be a conclusive measure of superior efficiency, it can serve as a preliminary indicator for comparison.

For the sake of relevance and meaningful comparison, hybrid harvesters and the multi-layer magnetic harvester [13] were intentionally excluded from this analysis. Their exclusion is due to their bulkier nature, which can result in higher power output but sacrifices one of the main advantages of piezoelectric harvesters—compact size. The emphasis on maintaining a smaller size is a pivotal feature of piezoelectric harvesters, and by excluding these bulkier systems, the comparison offers a more pertinent and insightful evaluation of efficiency among the showcased harvesters.

Khameneifar et al. [2] and Guan and Liao [8] designed outward tip-mass and inward tip-mass gravitational harvesters, respectively. The harvester from this study demonstrated results comparable to the inward tip-mass gravitational harvester while surpassing the outward tip-mass one. Notably, both of these gravitational harvesters are larger in size and use four piezoelectric beams for power generation, posing a disadvantage in terms of complexity and bulkiness.

Machado et al. [9] also developed a gravitational harvester with a significantly higher power-to-frequency ratio compared to other harvesters in the graph. However, this specific harvester was tailored for low-frequency applications, making it challenging to deduce its performance at higher frequencies. Additionally, it incorporates various mechanical parts, such as springs, to ensure high power generation at lower frequencies, contributing to its relatively complex design.

Çelik et al. [12] introduced the single-layer magnetic harvester, which yielded a much lower power-to-frequency ratio, producing only 0.0036 mW at 30 rad/s. S. Kim et al. [10] devised an underwater propeller system with “hitting sticks,” utilizing high frequency for generating power. Although this system achieved a comparable power-to-frequency ratio to the harvester from this work (a ratio of 0.01 vs. 0.097), its application is limited to underwater scenarios.

Lastly, Yang et al. [11] created the gullwing-structured harvester, which produced higher power of 0.4 mW at a lower frequency of 45 rad/s. In comparison, the harvester from this work generated 0.08889 mW (four times less) at 50 rad/s, but nearly matched its power by generating 0.336 mW at 65 rad/s. However, the gullwing harvester employs two piezoelectric beams, adding complexity to the design compared to the single-disk configuration of the harvester from this study.

Hence, the rotational energy harvester developed in this work demonstrates comparable results to existing harvesters, showcasing its potential for further optimization and improvement. The simplicity of its design, combined with competitive power outputs, makes it a promising candidate for practical applications and opens avenues for enhancing its efficiency and performance.

4.4. Practical Applications of Rotational Piezoelectric Energy Harvesters

The rotational piezoelectric energy harvester finds versatile applications depending on the rotational speeds of the specific systems it is integrated into. For instance, in vehicles where wheels rotate at speeds of 7–13.5 Hz [8] or 44–84 rad/s, the harvester can generate an electrical power output of approximately 500 μW. This power output is more than sufficient to meet the energy demands of wireless sensors, typically requiring less than 20 μW [19].

In the context of helicopter blades, which have a limited operational lifespan, real-time condition monitoring becomes critical to prevent potential failures. Helicopter blades that theoretically last for 10,000 flight hours are typically used for only 3000 flight hours to mitigate risks associated with failure [20]. As the cost of discarding aircraft after 3000 h is substantial, the introduction of real-time sensors becomes essential for proactive monitoring and reduced costs. With helicopter blades rotating at 400 rpm [21] (approximately 42 rad/s), the rotational energy harvester can generate approximately 89 μW of power at 50 rad/s, making it well-suited to power wireless sensors installed on critical components, such as the turboprop shaft.

Furthermore, the harvester’s application extends to diesel power plants, where it can be employed in two-stroke-cycle or four-stroke-cycle diesel engines with medium-speed operations ranging from 200 to 1000 rpm [22]. Similarly, it can be integrated into car engines with engine operating speeds between 700 and 5500 rpm [23], with potential placement on the crankshaft. In these scenarios, the harvester can serve as a power source for wireless sensors or temperature sensors due to its ability to generate higher power outputs [24].

In conclusion, the rotational piezoelectric energy harvester showcases its adaptability across various rotational speed regimes, making it a viable energy-harvesting solution for diverse applications in industries such as transportation, aerospace, and power generation.

5. Conclusions

In conclusion, this study introduced a novel rotational-energy-harvesting design that explored the efficient conversion of rotational motion into linear energy, enabling the generation of electrical power through the utilization of a piezoelectric disk. The simulation and experimental results unequivocally demonstrate the effectiveness of this harvester in producing electrical energy at varying rotational frequencies, with simulation power outputs of 188 μW, 513 μW, and 1293 μW, and experimental power outputs of 88.89 μW, 336 μW, and 923 μW, respectively. These findings not only underscore the competitive performance of the harvester compared to existing rotational-energy-harvesting systems but also reveal its potential for real-world applications.

A notable advantage of this harvester lies in its mechanical simplicity, offering cost-effectiveness and reliability, making it a promising option for widespread implementation. Additionally, the harvester’s flexibility allows for future enhancements, such as the incorporation of dual piezoelectric disks on each side of the mount, which could lead to even greater power generation.

In practical applications, this rotational energy harvester presents significant promise in diverse industries. From harnessing energy from vehicle wheels to supporting wireless sensors, its versatility extends to monitoring helicopter blades to mitigate potential failures and reduce operational costs. Furthermore, its adaptability to diesel power plants and car engines at various RPM ranges opens avenues for its integration as wireless or temperature sensors.

The designed rotational piezoelectric energy harvester showcases a compelling solution for converting rotational motion into electrical energy. Its commendable performance, coupled with the potential for further optimization, positions it as a potential contributor to self-powered systems and real-time monitoring applications. As research progresses and technology advances, this innovative energy-harvesting technology could offer valuable contributions to sustainable energy practices in the future.