Study of Contact Pressure Distribution in Bolted Encapsulated Proton Exchange Membrane Fuel Cell Membrane Electrode Assembly
Abstract
:1. Introduction
2. Materials and Methods
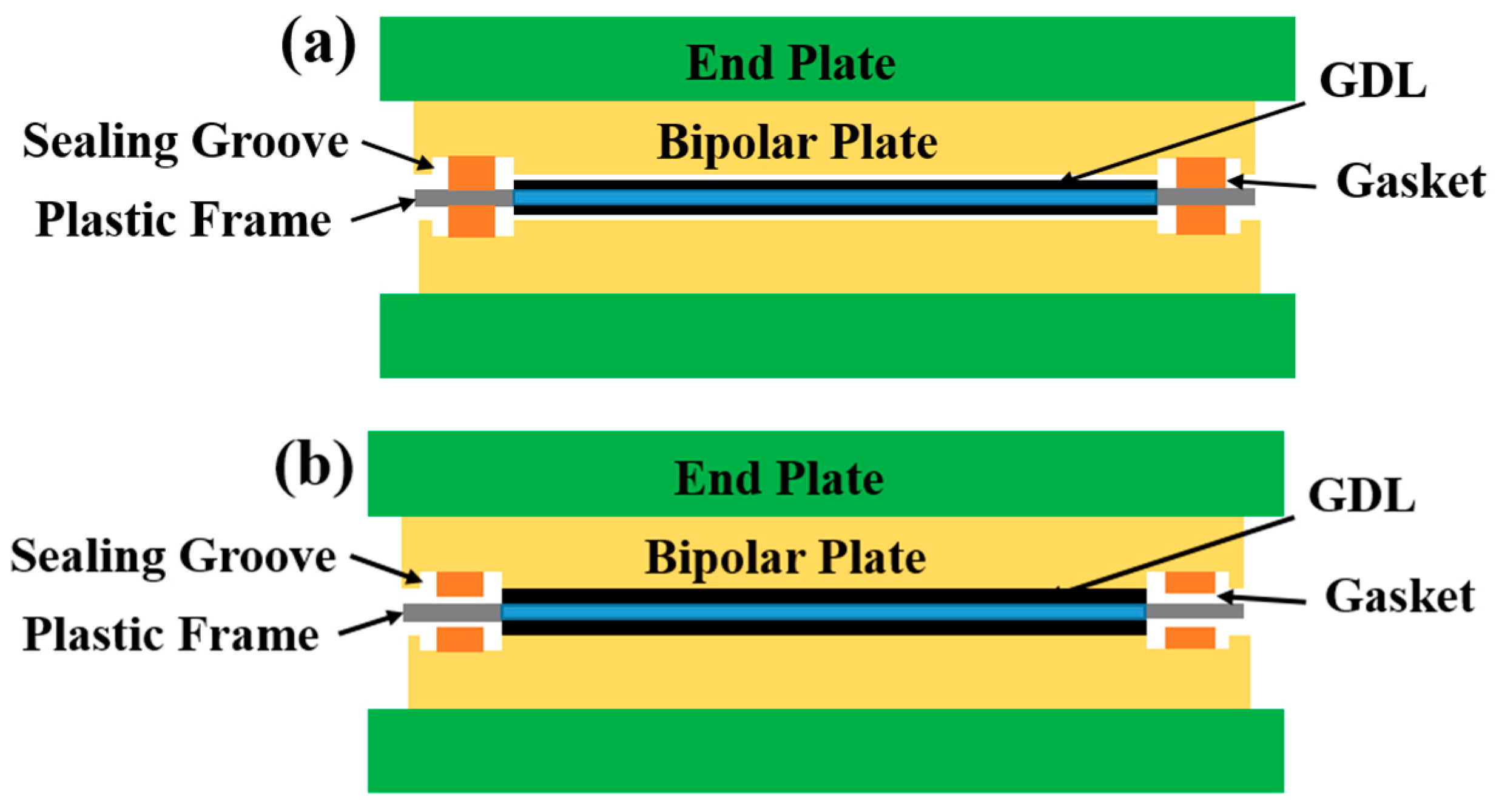
2.1. Geometry and Mesh
2.2. Boundary Conditions and Loads
2.3. Material Properties
3. Results and Discussion
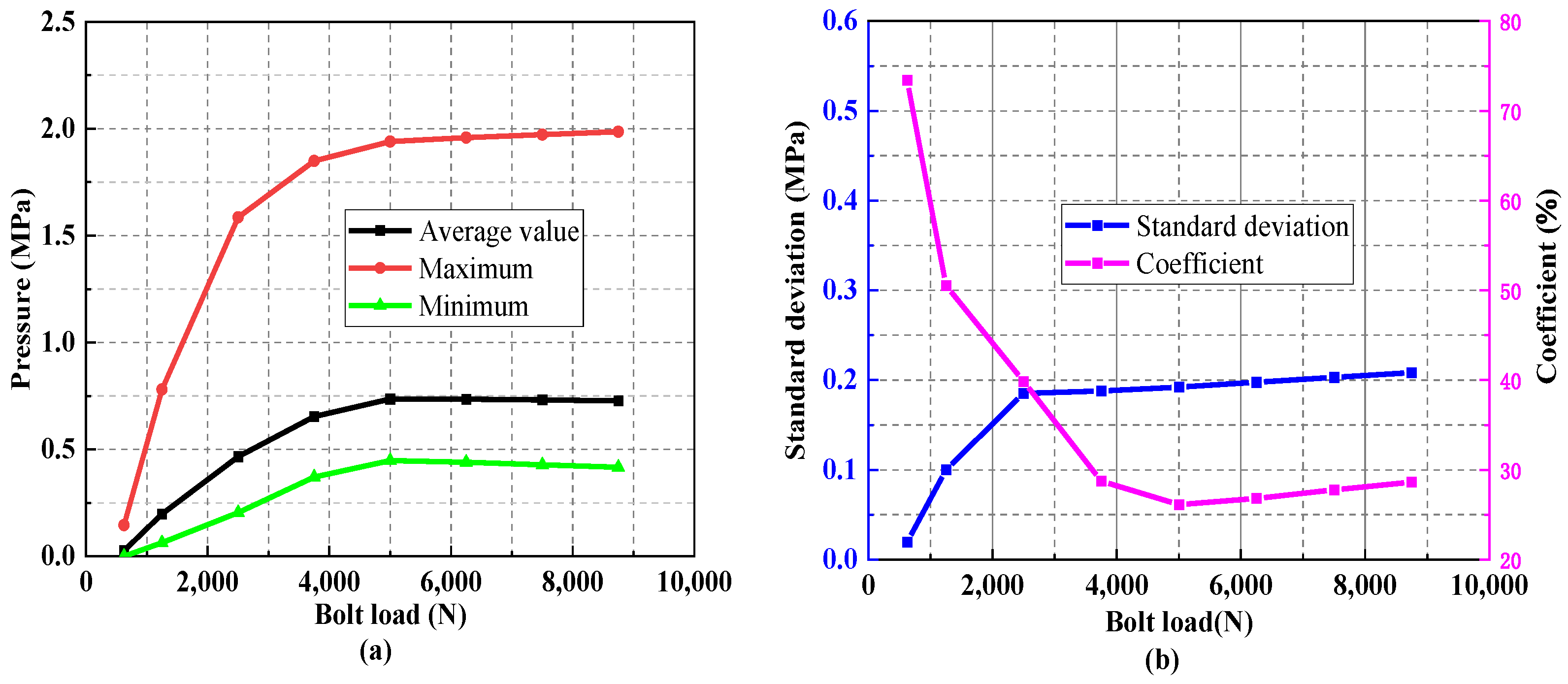
3.1. Effect of Bolt Load
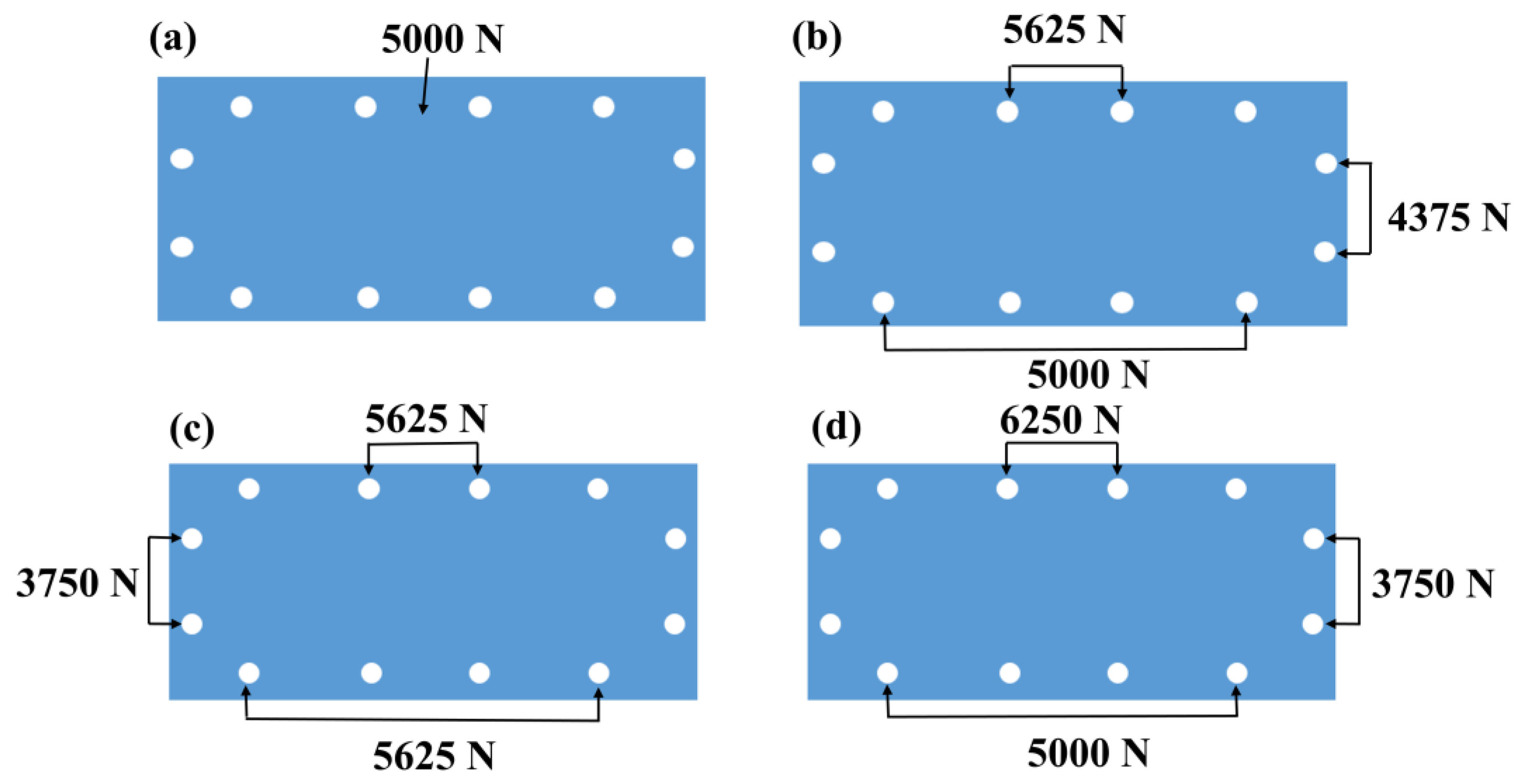
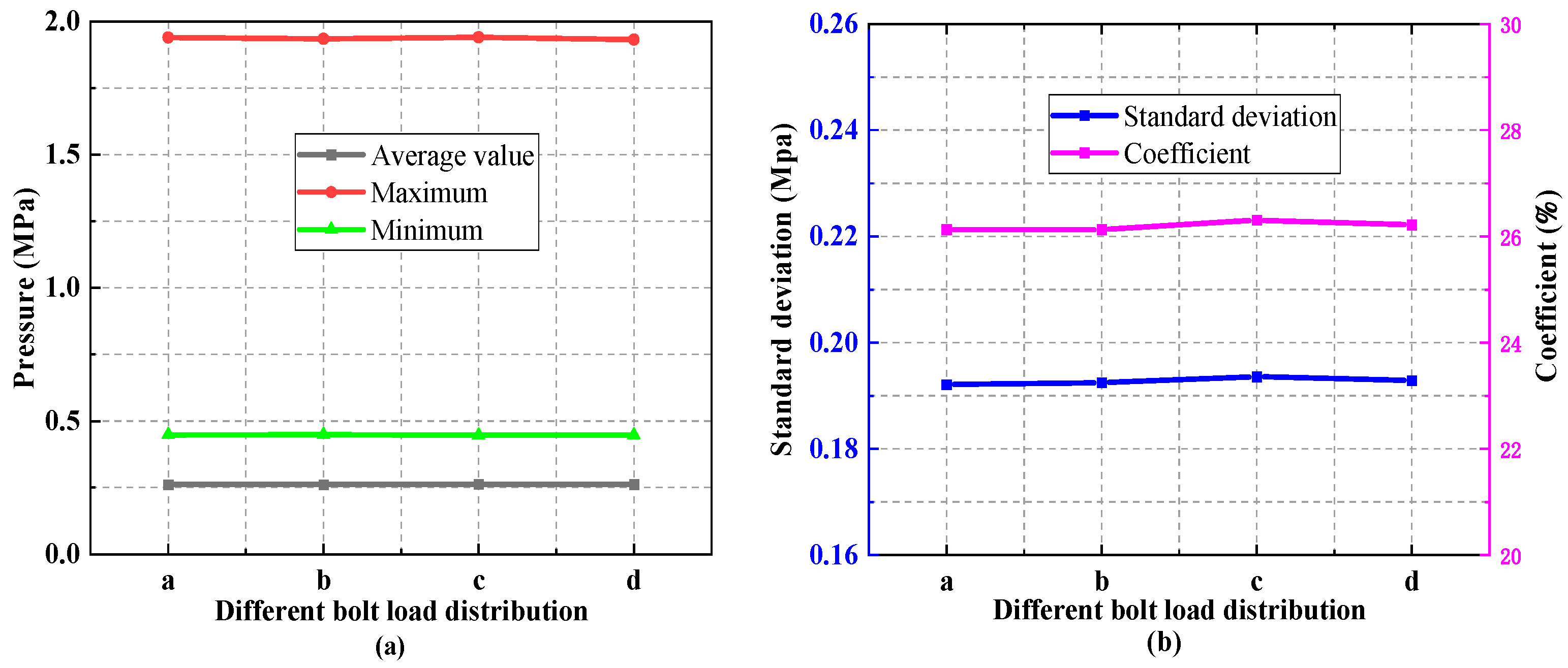
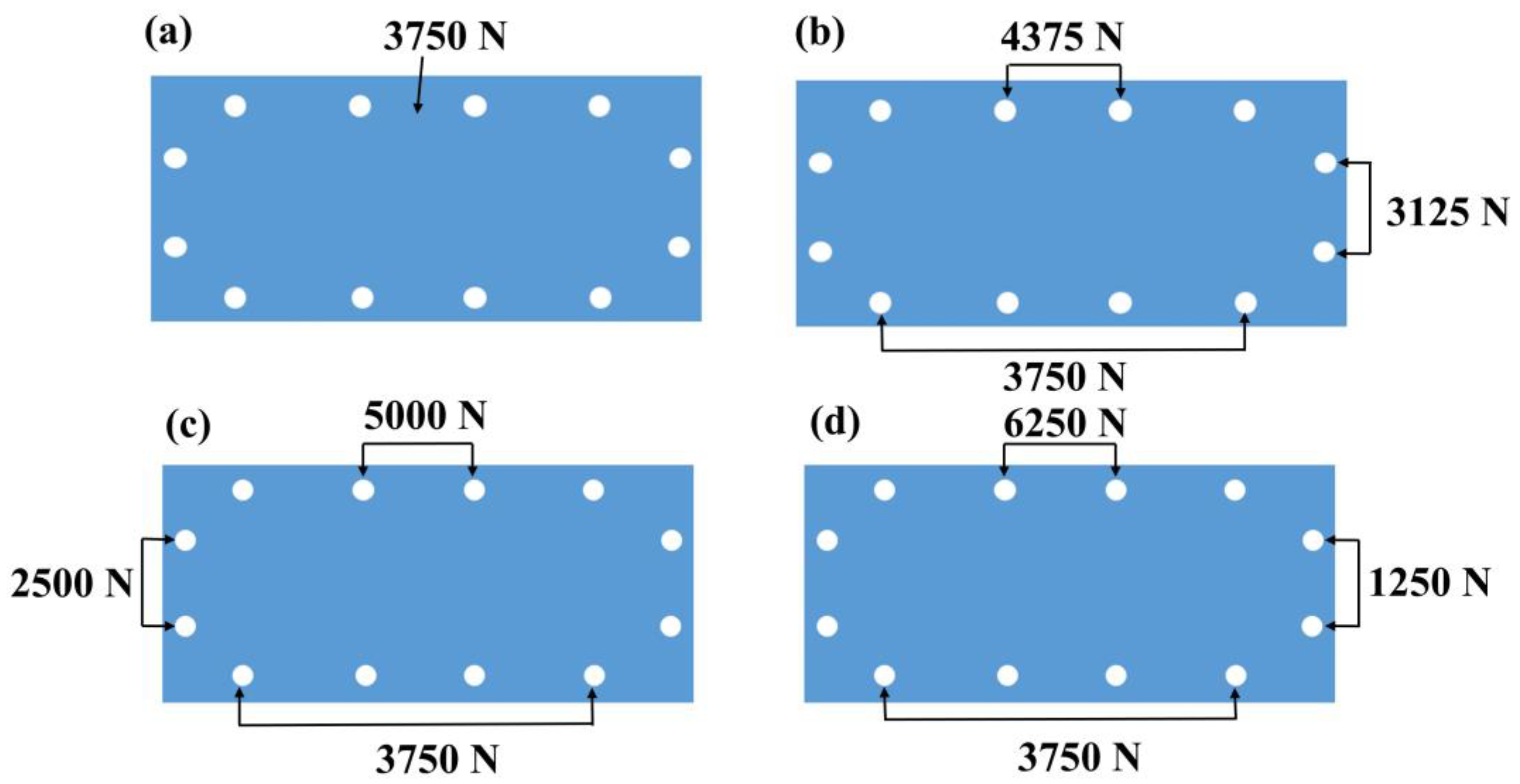
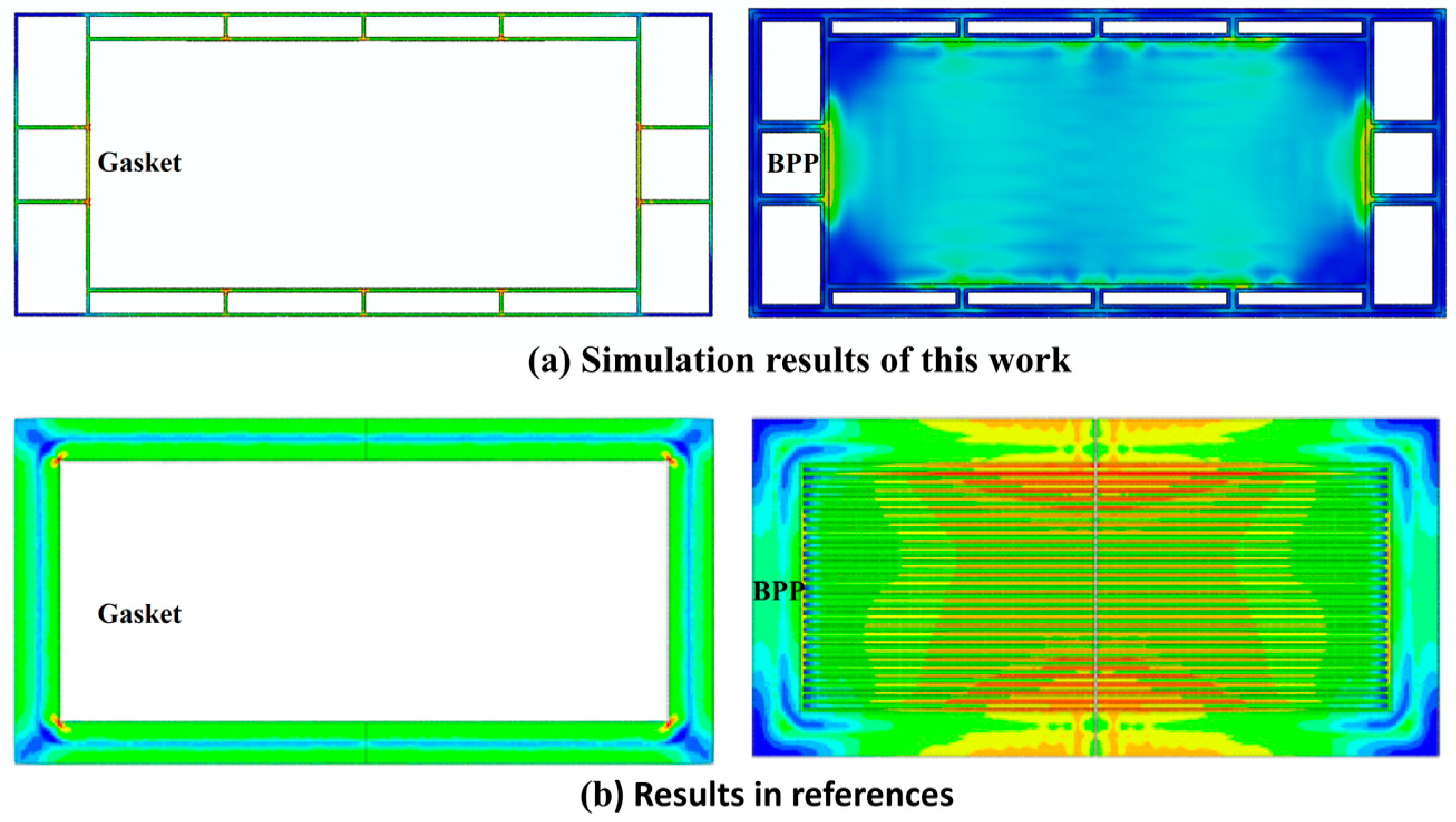
3.2. Effect of Bolt Load Distribution
3.3. Effect of Gasket Material Properties
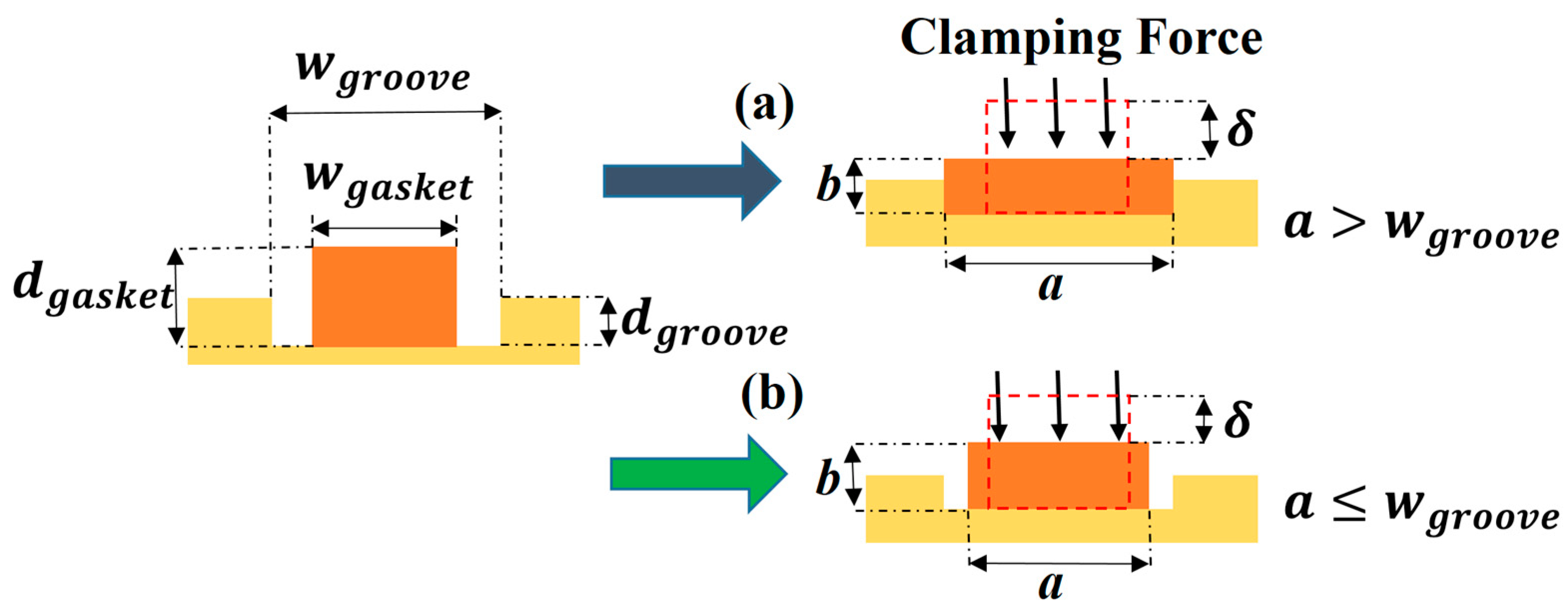
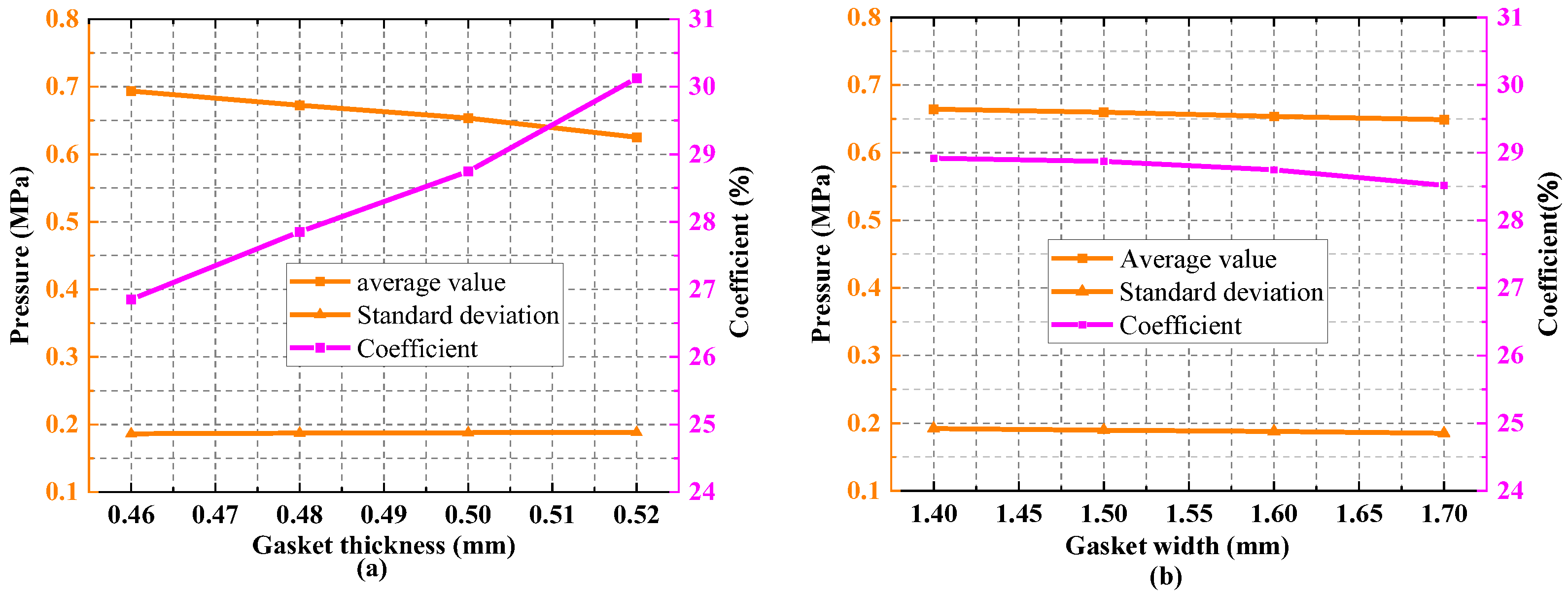
3.4. Effect of Gasket Size
- Gasket thickness (fixed width):
- 2.
- Gasket width (fixed thickness):
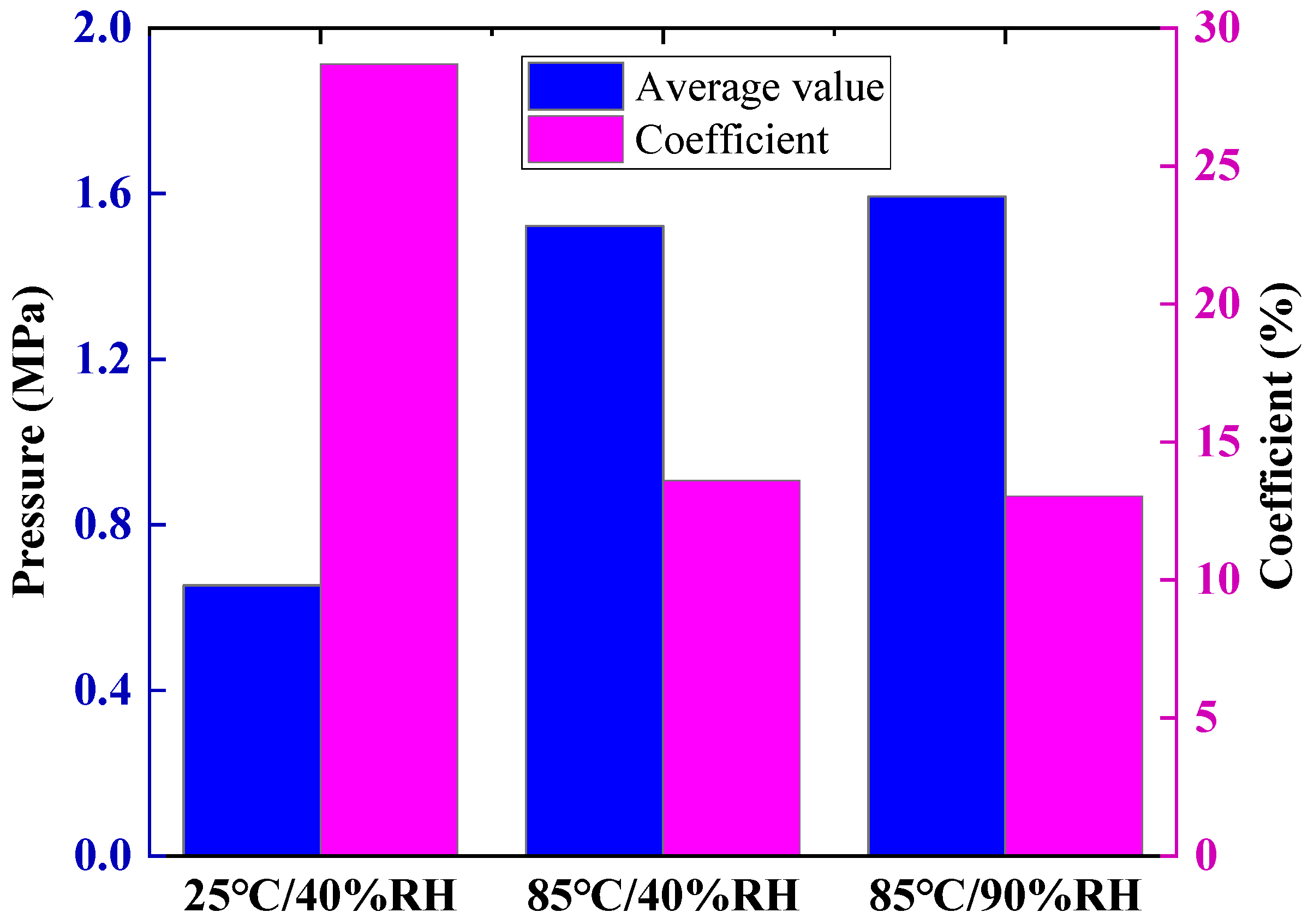
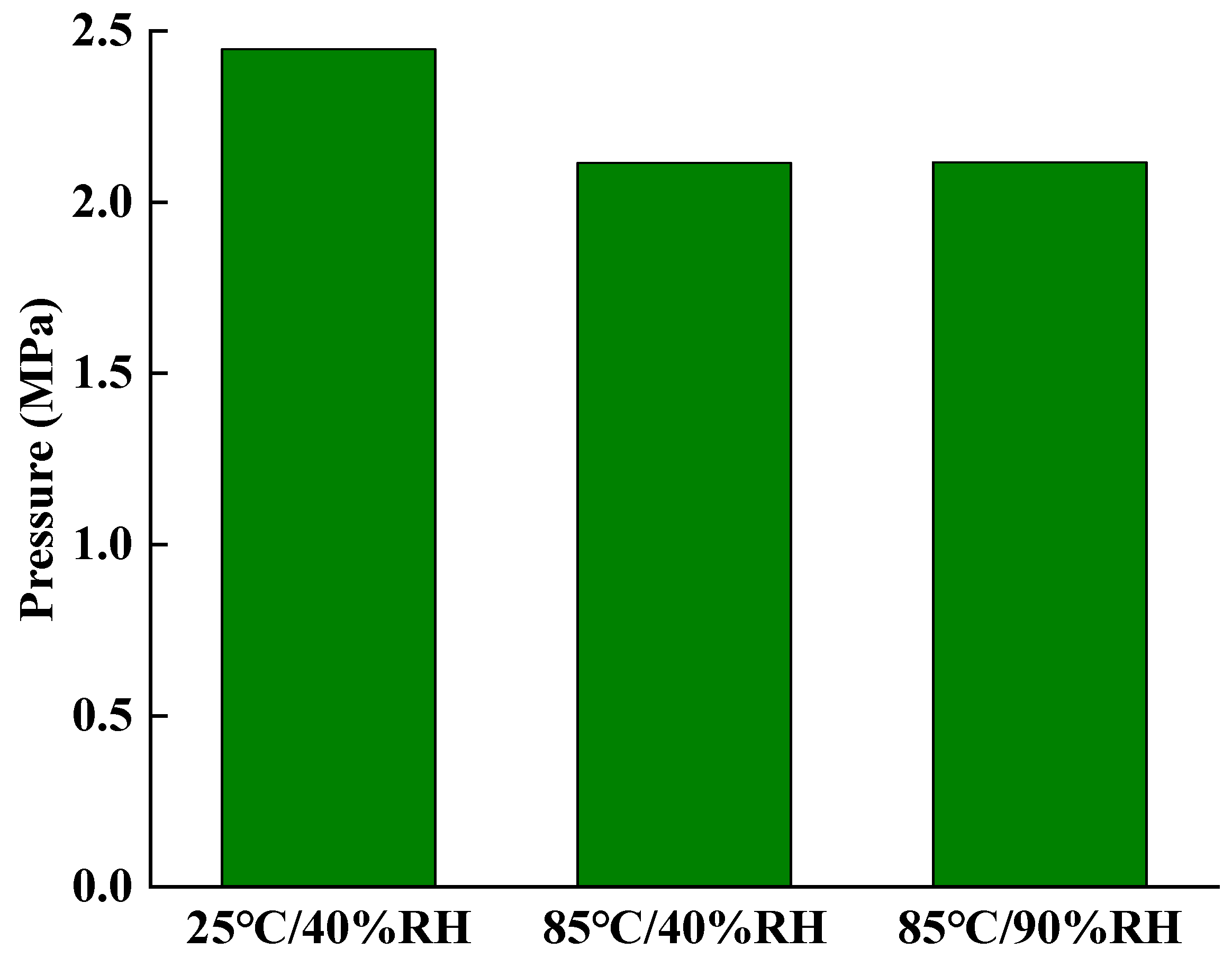
3.5. Effects of Working Operating Conditions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, C.; Cho, S.H.; Cho, S.M.; Na, Y.; Kim, S.; Kim, D.K. Review of hydrogen infrastructure: The current status and roll-out strategy. Int. J. Hydrog. Energy 2023, 48, 1701–1716. [Google Scholar] [CrossRef]
- Aminudin, M.A.; Kamarudin, S.K.; Lim, B.H.; Majilan, E.; Masdar, M.; Shaari, N. An overview: Current progress on hydrogen fuel cell vehicles. Int. J. Hydrog. Energy 2023, 48, 4371–4388. [Google Scholar] [CrossRef]
- Olabi, A.G.; Wilberforce, T.; Alanazi, A.; Vichare, P.; Sayed, E.T.; Maghrabie, H.M.; Elsaid, K.; Abdelkareem, M.A. Novel Trends in Proton Exchange Membrane Fuel Cells. Energies 2022, 15, 4949. [Google Scholar] [CrossRef]
- Wen, C.-Y.; Lin, Y.-S.; Lu, C.-H. Experimental study of clamping effects on the performances of a single proton exchange membrane fuel cell and a 10-cell stack. J. Power Sources 2009, 192, 475–485. [Google Scholar] [CrossRef]
- Mao, X.; Ying, R.; Yuan, Y.; Li, F.; Shen, B. Simulation and analysis of hydrogen leakage and explosion behaviors in various compartments on a hydrogen fuel cell ship. Int. J. Hydrog. Energy 2021, 46, 6857–6872. [Google Scholar] [CrossRef]
- Zhang, Z.; Tao, W.-Q. Effect of assembly pressure on the performance of proton exchange membrane fuel cell. Energy Storage Sav. 2023, 2, 359–369. [Google Scholar] [CrossRef]
- Martín-Alcántara, A.; González-Morán, L.; Pino, J.; Guerra, J.; Iranzo, A. Effect of the Gas Diffusion Layer Design on the Water Management and Cell Performance of a PEM Fuel Cell. Processes 2022, 10, 1395. [Google Scholar] [CrossRef]
- Asghari, S.; Shahsamandi, M.H.; Ashraf Khorasani, M.R. Design and manufacturing of end plates of a 5kW PEM fuel cell. Int. J. Hydrog. Energy 2010, 35, 9291–9297. [Google Scholar] [CrossRef]
- Lee, W.; Ho, C.-H.; Van Zee, J.W.; Murthy, M. The effects of compression and gas diffusion layers on the performance of a PEM fuel cell. J. Power Sources 1999, 84, 45–51. [Google Scholar] [CrossRef]
- Zhao, C.; Xing, S.; Liu, W.; Chen, M.; Wang, Y.; Wang, H. An experimental study on pressure distribution and performance of end-plate with different optimization parameters for air-cooled open-cathode LT-PEMFC. Int. J. Hydrog. Energy 2020, 45, 17902–17915. [Google Scholar] [CrossRef]
- Dey, T.; Deshpande, J.; Singdeo, D.; Ghosh, P.C. Study of PEM Fuel Cell End Plate Design by Structural Analysis Based on Contact Pressure. J. Energy 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Chien, C.-H.; Hu, Y.-L.; Su, T.-H.; Liu, H.-T.; Wang, C.-T.; Yang, P.-F.; Lu, Y.-X. Effects of bolt pre-loading variations on performance of GDL in a bolted PEMFC by 3-D FEM analysis. Energy 2016, 113, 1174–1187. [Google Scholar] [CrossRef]
- Carral, C.; Mélé, P. A numerical analysis of PEMFC stack assembly through a 3D finite element model. Int. J. Hydrog. Energy 2014, 39, 4516–4530. [Google Scholar] [CrossRef]
- Bates, A.; Mukherjee, S.; Hwang, S.; Lee, S.C.; Kwon, O.; Choi, G.H.; Park, S. Simulation and experimental analysis of the clamping pressure distribution in a PEM fuel cell stack. Int. J. Hydrog. Energy 2013, 38, 6481–6493. [Google Scholar] [CrossRef]
- Bograchev, D.; Gueguen, M.; Grandidier, J.-C.; Martemianov, S. Stress and plastic deformation of MEA in fuel cells. Int. J. Hydrog. Energy 2008, 180, 393–401. [Google Scholar]
- Mikkola, M.; Tingelöf, T.; Ihonen, J.K. Modelling compression pressure distribution in fuel cell stacks. J. Power Sources 2009, 193, 269–275. [Google Scholar] [CrossRef]
- Toghyani, S.; Moradi Nafchi, F.; Afshari, E.; Hasanpour, K.; Baniasadi, E.; Atyabi, S.A. Thermal and electrochemical performance analysis of a proton exchange membrane fuel cell under assembly pressure on gas diffusion layer. Int. J. Hydrog. Energy 2018, 43, 4534–4545. [Google Scholar] [CrossRef]
- Kusoglu, A.; Karlsson, A.M.; Santare, M.H.; Cleghorn, S.; Johnson, W.B. Mechanical behavior of fuel cell membranes under humidity cycles and effect of swelling anisotropy on the fatigue stresses. J. Power Sources 2007, 170, 345–358. [Google Scholar] [CrossRef]
- Tang, Y.; Santare, M.H.; Karlsson, A.M.; Cleghorn, S.; Johnson, W.B. Stresses in Proton Exchange Membranes Due to Hygro-Thermal Loading. J. Fuel Cell Sci. Technol. 2006, 3, 119–124. [Google Scholar] [CrossRef]
- Kleemann, J.; Finsterwalder, F.; Tillmetz, W. Characterisation of mechanical behaviour and coupled electrical properties of polymer electrolyte membrane fuel cell gas diffusion layers. J. Power Sources 2009, 190, 92–102. [Google Scholar] [CrossRef]
- Alizadeh, E.; Barzegari, M.M.; Momenifar, M.; Ghadimi, M.; Saadat, S. Investigation of contact pressure distribution over the active area of PEM fuel cell stack. Int. J. Hydrog. Energy 2016, 41, 3062–3071. [Google Scholar] [CrossRef]
- Liu, B.; Liu, L.F.; Wei, M.Y.; Wu, C.W. Vibration mode analysis of the proton exchange membrane fuel cell stack. J. Power Sources 2016, 331, 299–307. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, Y. Sealing performance and mechanical behavior of PEMFCs sealing system based on thermodynamic coupling. Int. J. Hydrog. Energy 2020, 45, 23480–23489. [Google Scholar] [CrossRef]
- Huang, X.; Liu, S.; Yu, X.; Liu, Y.; Zhang, Y.; Xu, G. A mechanism leakage model of metal-bipolar-plate PEMFC seal structures with stress relaxation effects. Int. J. Hydrog. Energy 2022, 47, 2594–2607. [Google Scholar] [CrossRef]
- Zhou, Y.; Lin, G.; Shih, A.; Hu, S. Assembly pressure and membrane swelling in PEM fuel cells. J. Power Sources 2009, 192, 544–551. [Google Scholar] [CrossRef]
- Tang, Y.; Karlsson, A.M.; Santare, M.H.; Gilbert, M.; Cleghorn, S.; Johnson, W.B. An experimental investigation of humidity and temperature effects on the mechanical properties of perfluorosulfonic acid membrane. Mater. Sci. Eng. A 2006, 425, 297–304. [Google Scholar] [CrossRef]
- Shinde, U.; Koorata, P.K. Numerical investigation on the sensitivity of endplate design and gas diffusion material models in quantifying localized interface and bulk electrical resistance. Int. J. Hydrog. Energy 2021, 46, 17358–17373. [Google Scholar] [CrossRef]
- Pacheco, C.; Barbosa, R.; Ordoñez, L.; Sierra, J.; Escobar, B. Design, simulation and experimental characterization of a high-power density fuel cell. Int. J. Hydrog. Energy 2021, 46, 26197–26204. [Google Scholar] [CrossRef]
- Yu, H.N.; Kim, S.S.; Suh, J.D.; Lee, D.G. Composite endplates with pre-curvature for PEMFC (polymer electrolyte membrane fuel cell). Compos. Struct. 2010, 92, 1498–1503. [Google Scholar] [CrossRef]
- Alizadeh, E.; Ghadimi, M.; Barzegari, M.M.; Saadat, S.H.M. Development of contact pressure distribution of PEM fuel cell’s MEA using novel clamping mechanism. Energy 2017, 131, 92–97. [Google Scholar] [CrossRef]
- Wang, X.; Song, Y.; Zhang, B. Experimental study on clamping pressure distribution in PEM fuel cells. J. Power Sources 2008, 179, 305–309. [Google Scholar] [CrossRef]
- Chen, Z.; Xing, Y.; Cao, J.; Yang, F.; Zhang, X. Leakage Analysis of PEMFC Sealing System Considering Temperature Cycling. Energies 2023, 16, 5475. [Google Scholar] [CrossRef]
- Xing, S.; Zhao, C.; Liu, W.; Zou, J.; Chen, M.; Wang, H. Effects of bolt torque and gasket geometric parameters on open-cathode polymer electrolyte fuel cells. Appl. Energy 2021, 303, 117632. [Google Scholar] [CrossRef]
- Uzundurukan, A.; Bilgili, M.; Devrim, Y. Examination of compression effects on PEMFC performance by numerical and experimental analyses. Int. J. Hydrog. Energy 2020, 45, 35085–35096. [Google Scholar] [CrossRef]
- Gatto, I.; Urbani, F.; Giacoppo, G.; Barbera, O.; Passalacqua, E. Influence of the bolt torque on PEFC performance with different gasket materials. Int. J. Hydrog. Energy 2011, 36, 13043–13050. [Google Scholar] [CrossRef]
- El-Kharouf, A.; Steinberger-Wilckens, R. The Effect of Clamping Pressure on Gas Diffusion Layer Performance in Polymer Electrolyte Fuel Cells. Fuel Cells 2015, 15, 802–812. [Google Scholar] [CrossRef]
- Hashimasa, Y.; Numata, T.; Moriya, K.; Watanabe, S. Study of fuel cell structure and heating method. J. Power Sources 2006, 155, 182–189. [Google Scholar] [CrossRef]
- Pharoah, J.G.; Burheim, O.S. On the temperature distribution in polymer electrolyte fuel cells. J. Power Sources 2010, 195, 5235–5245. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, Y.; Han, C.; Zhang, H. Stress response and contact behavior of PEMFC during the assembly and working condition. Int. J. Hydrog. Energy 2021, 46, 30467–30478. [Google Scholar] [CrossRef]
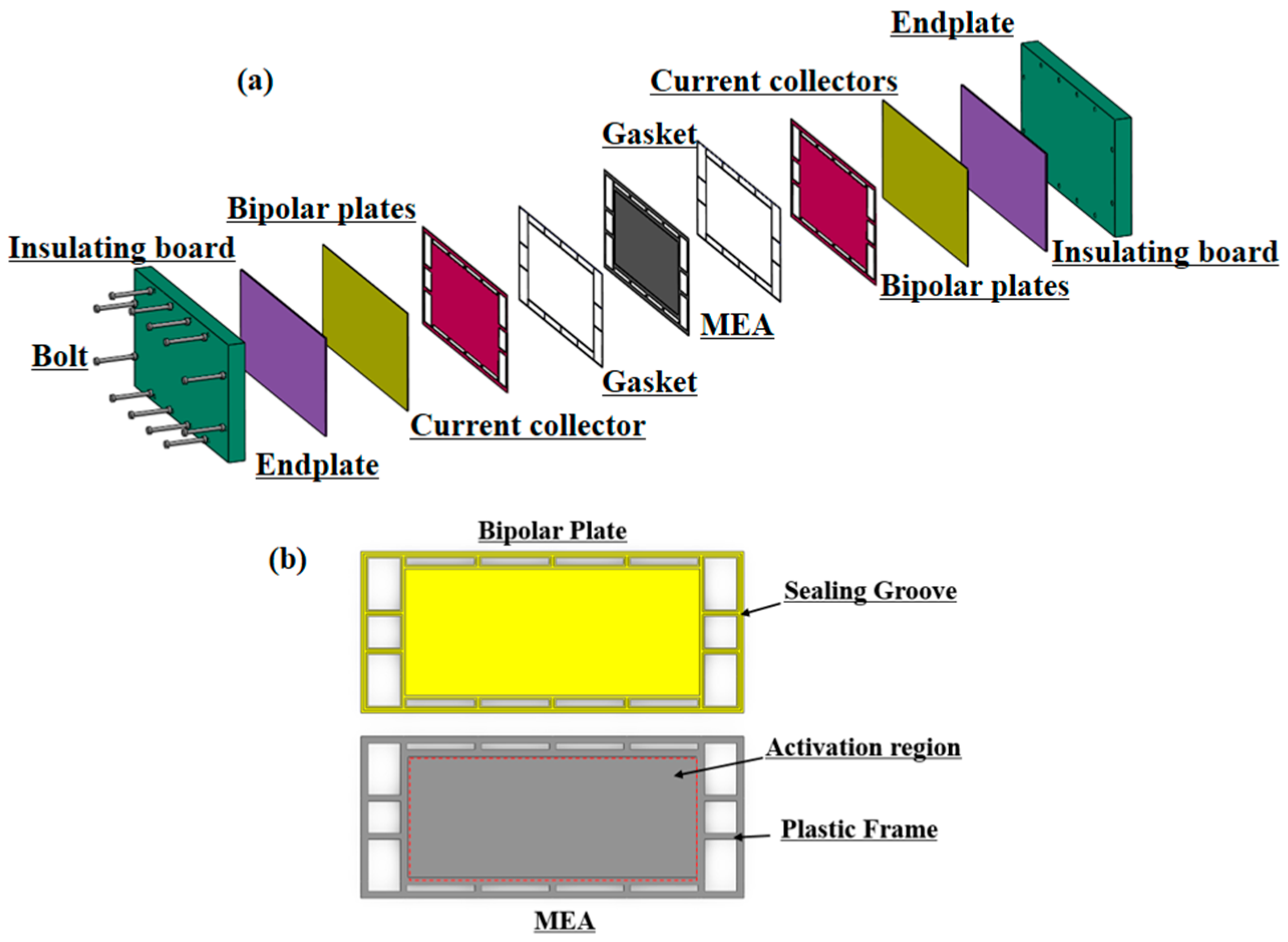
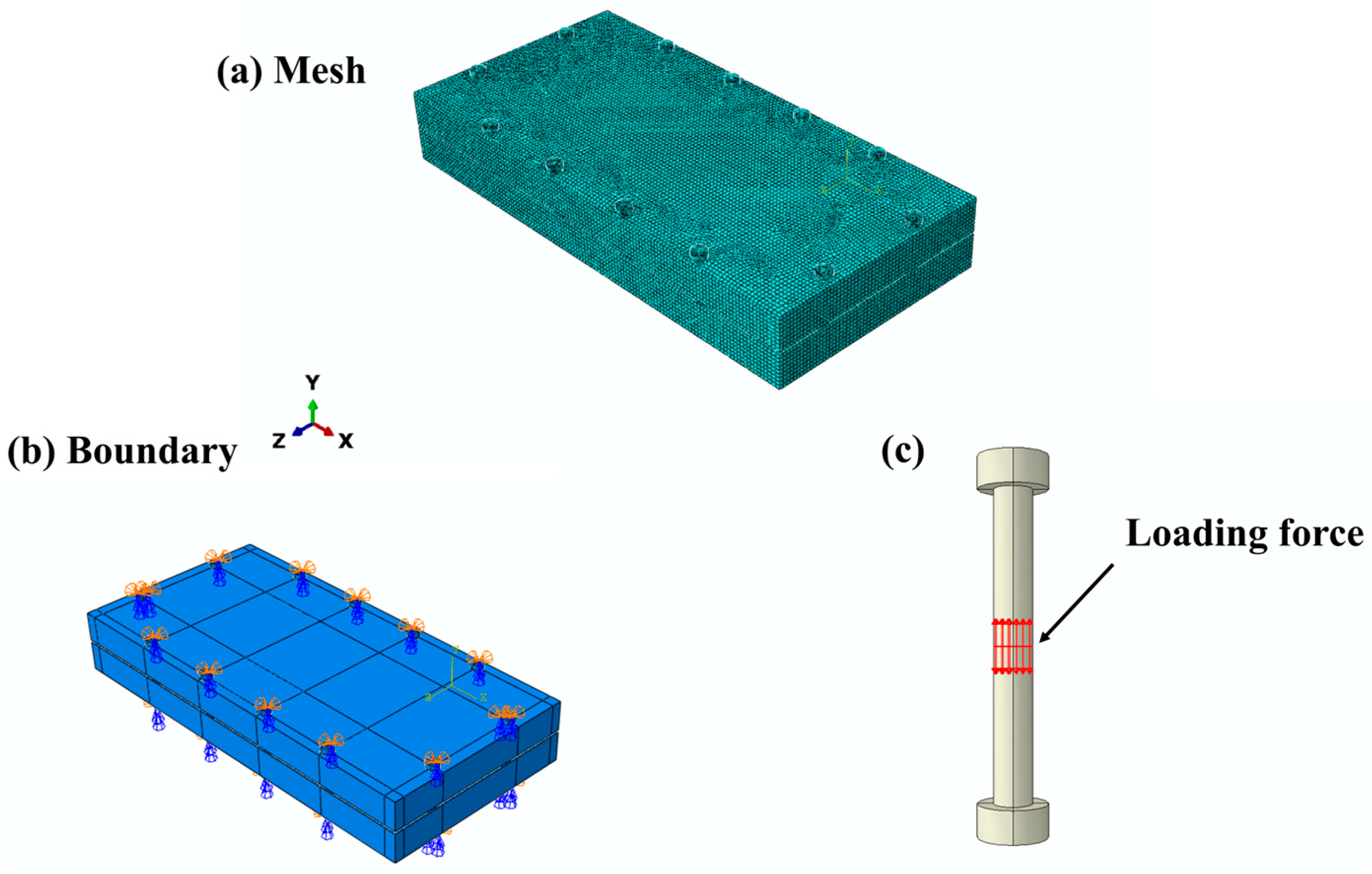






| Part | Materials | Modulus of Elasticity (Mpa) | Poisson’s Ratio (/°C) | Density (kg/m3) | Thermal Conductivity (/W·m−1·°C−1) | Coefficient of Thermal Expansion (/10−6) | Specific Thermal Capacity/(/J·kg−1·°C−1) |
|---|---|---|---|---|---|---|---|
| End plate | Alloy | 137,800 | 0.33 | 2850 | 217.7 | 22.2 | 880 |
| Bipolar Plate | Stainless steel | 210,000 | 0.30 | 7850 | 16.3 | 18 | 510 |
| Gasket | Rubber | 60 HA | 1100 | 0.25 | 77 | 1400 | |
| Frame | Polymer | 10,000 | 0.28 | 900 | 0.4 | 78 | 1200 |
| PEM | Nafion®112 | Neglected | Neglected | Neglected | Neglected | 123 | Neglected |
| GDL | Carbon cloth | 6.3 | 0.09 | 400 | 1.7 | 0.8 | 710 |
| Insulator | Nylon | 15,000 | 0.1 | 1000 | 1.4 | 137 | 1500 |
| Collector plate | Copper | 100,000 | 0.33 | 8920 | 401 | 16.6 | 390 |
| Bolts–Nuts | Stainless steel | 210,000 | 0.30 | 7850 | 16.3 | 18 | 510 |
| HA | 30 | 40 | 50 | 60 | 70 |
|---|---|---|---|---|---|
| C10 | 0.12879 | 0.18234 | 0.25618 | 0.35992 | 0.50567 |
| C01 | 0.045585 | 0.04559 | 0.06405 | 0.08998 | 0.12642 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, G.; Xing, Y.; Cao, J.; Wang, Y.; Peng, L.; Miao, X. Study of Contact Pressure Distribution in Bolted Encapsulated Proton Exchange Membrane Fuel Cell Membrane Electrode Assembly. Energies 2023, 16, 6487. https://doi.org/10.3390/en16186487
Ren G, Xing Y, Cao J, Wang Y, Peng L, Miao X. Study of Contact Pressure Distribution in Bolted Encapsulated Proton Exchange Membrane Fuel Cell Membrane Electrode Assembly. Energies. 2023; 16(18):6487. https://doi.org/10.3390/en16186487
Chicago/Turabian StyleRen, Gui, Yanfeng Xing, Juyong Cao, Ying Wang, Linfa Peng, and Xuelong Miao. 2023. "Study of Contact Pressure Distribution in Bolted Encapsulated Proton Exchange Membrane Fuel Cell Membrane Electrode Assembly" Energies 16, no. 18: 6487. https://doi.org/10.3390/en16186487
APA StyleRen, G., Xing, Y., Cao, J., Wang, Y., Peng, L., & Miao, X. (2023). Study of Contact Pressure Distribution in Bolted Encapsulated Proton Exchange Membrane Fuel Cell Membrane Electrode Assembly. Energies, 16(18), 6487. https://doi.org/10.3390/en16186487





