A Review of the CFD Method in the Modeling of Flow Forces

Abstract

Hydraulic valves are key components of fluid power systems. They control the flow rate and pressure in hydraulic lines, actuator motion, and direction. Valves that control flow rate or pressure can be divided into two main categories: spool-type valves, where control components are similar to the piston inside a sleeve with control orifices; and seat-type valves, in which a poppet inside a seat opens and closes the flow. Forces induced on valve components during oil flow are crucial to the valve’s operational capabilities. They can be calculated using a formula originating from the momentum conservation equation for a two-dimensional control volume. Increasing demands for flow rate and pressure control accuracy cause flow forces to be calculated much more accurately than when using the analytical formula. Therefore, computational fluid dynamics (CFD) simulations are the only effective tool for their calculation. This paper reviews the CFD approaches used for calculating flow forces inside hydraulic valves. It presents typical approaches used for evaluating flow forces inside hydraulic valves. The oldest and most common are conducted for a fixed position of valve components for defined flow conditions, which do not cover all components of flow forces. The dynamic flow forces can be calculated using more complex CFD models using fluid–structure interaction (FSI) techniques. This paper presents available FSI techniques for the simulation of transient flow forces, mainly for valves whose component position is determined by the forces occurring during oil flow.

1. Introduction

Hydraulic valves are substantial components of fluid power systems regardless of the intended system function. In principle, valves are used for controlling the flow rate and pressure in a hydraulic system. These capabilities enable them to be used as key components for controlling the direction and speed of actuators and pressure in the system. Hydraulic valves are a very wide family of hydraulic components which can be divided into a few groups [1]:

• Valves controlling flow directions.
• Valves controlling pressure.
• Valves controlling flow rate.
• Other valves (e.g., pressure switchers).

They can be implemented directly in hydraulic lines, as cartridges in plates, or other components such as pumps or motors. Regardless of the abovementioned classification, valves mostly use two types of control components:

• The poppet type, which is mostly used for pressure control;
• The spool type, which is used to control the flow rate or the flow direction.

Valves play an essential role in hydraulic systems, making significant contributions to system performance and functionality. Therefore, the modeling of valve operation is key to a system’s operational and functional features. The substantial forces in valve modeling are those induced during fluid flow. Historically, flow forces are evaluated using momentum theory and the control volume approach. However, this method has many limitations and is ineffective in capturing the nature of flow inside hydraulic valves. It applies to the relatively simple geometry of control components and fails in improving valve performance despite many attempts to modify the original idea. New capabilities in modeling flow forces have brought about CFD methods, which are able to simulate oil flow inside valves far more accurately. The first implementations of CFD methods focused on the modification of the analytical formula for the calculation of flow forces. Later, they expanded to the direct evaluation of flow forces in hydraulic valves. In principle, two main types of CFD implementation can be found in the evaluation of flow forces:

-

Valve control components are fixed for steady-state or transient flow and/or phase changes.

-

The position of the control components is determined by flowing fluid.

The first type is the most commonly used, while the second is still minor due to much higher computational effort. It employs fluid–structure interaction (FSI) techniques, allowing valve operation to be almost fully reflected. This paper is organized in the following way:

• Section 2, Flow forces in Hydraulic Valves, presents the theory of flow forces and the relevant implemented method. This section presents the investigated axial and radial forces induced by fluid flow for two main types of hydraulic valves, the poppet and spool types.
• Section 3, CFD Methods, presents the basic theory of CFD and the relevant turbulence models and illustrates flow force evaluation in CFD simulations. This section also introduces methods that can be used for the FSI simulation of hydraulic valves.
• Section 4, CFD Simulations of Steady-State Flow Forces is a literature review of CFD simulation of steady-state component of flow forces for hydraulic valves.
• Section 5, CFD Simulations of Transient Flow Forces. This section is an introduction to the FSI simulation of typical hydraulic valves. It presents available research on FSI simulation for hydraulic valves and the idea of using FSI techniques to simulate hydraulic valves. An idea for the implementation of the most common FSI techniques is presented: deforming mesh, immersed solid, sliding mesh, and the overset mesh. For clarity, these techniques were implemented on simplified valve types.
• Section 6, Discussion, summarizes the most common assumptions that are used for different CFD approaches for flow force simulations. It also presents the pros and cons as well as the limitations of various FSI techniques in practical applications.
• Section 7, Conclusions, presents the typical assumptions which are used in the CFD simulation of flow forces. It presents the main features of CFD simulations for steady-state and transient conditions.

2. Flow Forces in Hydraulic Valves

Oil flows inside valve chambers along the spool or poppet axis and induces axial and radial forces. The axial forces are mostly the subject of research. These forces significantly affect operational valve performance and may influence accuracy over controlled quantity (pressure or flow rate). The spool valve is mainly used for flow rate control, while the poppet type is used for pressure. Flow and pressure control valves can be operated manually or electromechanically. A spool moving inside a cylindrical chamber with orifices controls the amount of oil delivered to receivers. The poppet control surface matches the valve seat and releases pressure from the system when moving. The typical structure of hydraulic valves is presented in Figure 1.

The axial flow forces induced on the valve components during oil flow can be derived from the flow-governing equations. The mass and momentum conservation equations, well-known as Navier–Stokes equations, can describe the oil flow inside the hydraulic valve. The general form of the mass conservation equation (the continuity equation) is [2] as follows:

$$\frac{\mathsf{\partial }\tilde{\rho }}{\mathsf{\partial }t}+▽·\left(\tilde{\rho }\overrightarrow{\tilde{v}}\right)=Q_s$$

(1)

The general form of momentum conservation equation can be written as [2]:

$$\frac{\mathsf{\partial }}{\mathsf{\partial }t}\left(\tilde{\rho }\overrightarrow{\tilde{v}}\right)+▽·\left(\tilde{\rho }\overrightarrow{\tilde{v}}\overrightarrow{\tilde{v}}\right)=-▽\tilde{p}+▽\left(\overline{\overline{\tau }}\right)+\tilde{\rho }\overrightarrow{g}+\overrightarrow{S}$$

(2)

The term $\overline{\overline{\tau }}$ is a stress tensor expressed as

$$\overline{\overline{\tau }}=\mu \left[\left(▽\overrightarrow{\tilde{v}}+▽{\overrightarrow{\tilde{v}}}^T\right)-\frac{2}{3}▽\overrightarrow{\tilde{v}}I\right]$$

(3)

where $\mu$ is fluid viscosity, I is unit tensor, $\overrightarrow{g}$ is gravity, $Q_s$ is the fluid source, and $\overrightarrow{S}$ is the external momentum source.

The first works on axial flow forces in hydraulic valves were carried out by Lee et al. [3], Guillon [4], and Blackburn [5], who proposed using the control volume $CV$ and the equation of momentum conservation. The steady-state axial force $F_{ax}$ (Figure 1) in the valves can be derived from the integral form of Equation (2) for the control volume $CV$ marked as in Figure 1 with the following assumptions:

• The flow is steady and irrotational so that the flow can be treated as 2D flow;
• The oil is a homogeneous, incompressible liquid with constant properties;
• Body and shear forces are negligible;
• Valves are perfectly sealed without internal leakage;
• Elastic deformation is negligible,
• The phase changes are negligible.

Considering the control volume $CV$, the momentum conservation equation is

$$\sum {\overrightarrow{F}}_{CV}=\rho \frac{d}{dt}\underset{CV}{\int \int \int }\overrightarrow{u}dCV+\rho \underset{CS}{\int \int }\overrightarrow{u}\overrightarrow{u}dCS=0$$

(4)

where $CS$ is a surface over the control volume $CV$, and ${\overrightarrow{F}}_{CV}$ is the total force for the control volume $CV$.

On the other hand, ${\overrightarrow{F}}_{CV}$ can be presented as surface forces over $CS$:

$$\sum {\overrightarrow{F}}_{CV}=\underset{CS}{\int \int }\overline{\overline{\tau }}\overrightarrow{n}dCS$$

(5)

Finally, we have

$$\rho \underset{CS}{\int \int }\overrightarrow{u}\overrightarrow{u}dCS-\underset{CS}{\int \int }\overline{\overline{\tau }}\overrightarrow{n}dCS=0$$

(6)

Neglecting viscous forces and assuming steady-state conditions, Equation (6) has the following form:

$$\rho \left(\underset{S_2}{\int \int }{u}_2^2-\underset{S_1}{\int \int }{u}_1^2\right)=\underset{S,P}{\int \int }{\tau }_{nn}\overrightarrow{n}$$

(7)

The right-hand side of Equation (7) is a force on the spool or poppet, where ${\tau }_{nn}$ is a normal component of the stress tensor for the spool or poppet CV wall (fluid pressure). After integration, Equation (7) is

$${\overrightarrow{F}}_{S,P}=\rho Q\left(u_{2}cos\theta -u_1\right)$$

(8)

Force ${\overrightarrow{F}}_{S,P}$ acts on the $CV$ surface. Taking into account the direction, the reaction on the spool or poppet is $F_{ax}$

$$F_{ax}=\rho Q\left(u_{2}cos\theta -u_1\right)$$

(9)

For spool valves the force $F_{ax}$ always tends to close the valve. As the fluid velocity $u_1\ll u_2$, Equation (9) is

$$F_{ax}=\rho Q{u}_{2}cos\theta$$

(10)

The research of Lee et al. [3], Guillon [4], and Blackburn [5] conducted on the flow forces showed the jet angle for a spool valve with a small valve opening, presented in Figure 1a $\theta \approx {69}^{\circ }$. Thus, the steady-state force for the spool valve can be presented as follows:

$$F_{ax}=0.36\rho Q{u}_2$$

(11)

For poppet valves, the jet angle $\theta =\alpha$. According to Blackburn [5], Equation (10) is valid for the flow direction presented in Figure 1 as well as for the reverse one. The jet angle $\theta$ depends on angles $\psi$ and $\zeta$ and the flow direction. When fluid flows into the valve chamber, the jet angle $\theta$ varies with the value of radial clearance $R_c$. The relationship between the jet angle $\theta$ and radial clearance $R_c$ is shown in Figure 2. In contrast to spool valves, the direction of axial flow forces can be changed with the proper shape of the lift component [1].

The experimental tests indicate that the jet angle $\theta$ depends not only on radial clearance $R_c$ but also on the spool and sleeve rounding value. Figure 3 shows the relationship between the measurement of axial flow forces for various spool valve openings with different rounding values r and radial clearance $R_c$. Curve 4 shows theoretical axial forces for a fixed value of r = 0 mm and $R_c$ = 0 mm, while curve 1 shows forces for r = 0 mm and $R_c$ = 0.00762 mm. It can be noted that significant differences are found in the middle valve opening, while for small and full openings, they are almost negligible.

As mentioned earlier, the axial flow forces in spool valves tend to close valves. Therefore, the shape of the valve spool is often created in a way to minimize flow forces, as presented in Figure 4.

For such a case, the axial force can be calculated from the following formula [5]:

$$F_{ax}=\rho Q{u}_2\left(cos{\theta }_1-cos{\theta }_2\right)$$

(12)

Expanding the above equation for the assumption that the flow is fully turbulent with a developed velocity profile [6], the axial force is

$$F_{ax}=\varrho \frac{Q^2}{u_{2max}A}\sqrt{\frac{2\Delta p}{\varrho }}\left(cos{\theta }_1-cos{\theta }_2\right)$$

(13)

where $u_{2max}$ is the maximal influx velocity, A is the theoretical influx area, and $\Delta p$ is the pressure drop.

The most significant limitation in the practical application of Equations (11) and (13) is the estimation of the maximal fluid velocity in the vena contracta. It requires the discharge coefficient value, which has to be approximated from the existing theoretical research or determined by experiments for a real-world valve design. In addition, the research conducted by Borghi et al. [6] showed that the jet angle might deviate from the theoretical value due to the Coanda effect. These problems become even more extensive for spool valves that have additional notches on control surfaces (Figure 5) or for a sliding piston with circumferential holes (Figure 6).

Equations (10) and (12) are valid for constant ambient temperature. When the valve is exposed to temperature variations, Zhang et al. [9] proposed a formula for calculation of axial flow forces at temperature T in the following form:

$$F_{ax}^T=2C_q^T{A}^T\Delta pcos\theta$$

(14)

The jet angle can be expressed as

$$cos\theta =0.358+\frac{0.577}{1+0.642{\left(2x/R_c^T\right)}^{1.26}}$$

(15)

The discharge coefficient is related to the Reynolds number $C_q^T=f\left(Re\right)$, where Re can be expressed as

$$Re=\frac{2x_s}{u^T}\sqrt{\frac{2\Delta p}{{\rho }^T}}$$

(16)

The poppet-type valves give the impression of a simpler structure than a spool valve. Furthermore, it can be assumed that the jet angle $\theta$ equals the cone angle $\alpha$. However, the straightforward use of Equation (10) might be problematic because conical control components are very often combined with additional elements that might affect the flow forces in a significant way. Figure 7 shows a pressure relief valve with a poppet as a control element equipped with a damper and flow deflector.

Borghi et al. [6] presented experimental results for the compensated spool control valve, which showed significant differences between the calculated and measured values for specific working conditions (opening and flow rate). One of the reasons was that the analytical formula derived from the momentum conservation equation, Equation (12), might not capture all force components induced during fluid flow. These additional forces can be called dynamic flow forces. Another indicated reason is the assumption that a two-dimensional flow might not entirely reflect the nature of flow in a real valve. An attempt to evaluate the dynamic component of flow forces during oil flow inside the spool control valve was taken by Del Vescovo et al. [10]. He also employed the momentum theory approach to evaluate the unsteady component of axial flow forces, which arise from the momentum of oil captured inside the valve chamber. This force can be expressed as

$$F_{dax}=\varrho l_j\frac{dQ}{dt}$$

(17)

where $l_j$ is the distance between jets incoming to the chamber and outgoing flow.

This research shows that the transient force component ranges from few to almost 20% of static flow forces.

The radial component of flow forces is less recognized in the literature. There are two origins of radial forces. The first one is unbalanced pressure force on the land of a spool caused by the eccentricity between the lands and the corresponding bore and geometrical imperfections. This force can be expressed as [5]

$$F_r=\frac{\pi a{r}_t\Delta p}{2b}\left(1-\frac{2C+r_t}{\sqrt{{(2C+r_t)}^2-4b^2}}\right)$$

(18)

where $r_t$ is the radial taper of the spool land, C is the radial clearance at the large end of the land, b is eccentricity, and a is the radius of the land at the large end.

The second is an unbalanced pressure force due to the nonuniform oil flow through the valve chamber and control orifices. Research on radial forces was conducted by Lisowski et al. [11] and Lu et al. [12]. Lu et al. [13] formulated different formulas for the calculation of radial forces, but in principle, all of these studies define radial force as a function of jet angle, opening value, pressure, and fluid velocity.

Small dimensions and working conditions (high pressure and velocity) are unable to direct the observation of oil flow inside hydraulic valves. The only way to verify the nature of flow inside valves is to measure such quantities as the volumetric flow rate or pressure at the valve inlet and outlet. New possibilities in the field have brought about CFD (computational fluid dynamics) methods. They allow for the simulation of oil flow regardless of valve geometry complexity in various scenarios, including phase changes (cavitation), transient flow, or flow during valve component motion. This review presents an approach to CFD simulation to evaluate flow forces in hydraulic valves. The most common technique of CFD simulation for hydraulic valves is reviewed. Additionally, the approach which can be used for evaluating dynamic flow forces is presented. Those techniques are deformed mesh and fluid–structure interaction (FSI) simulations, for which possible applications for poppet and spool valves are presented.

3. CFD Methods

Equations (1) and (2) cannot be directly used to simulate the flow of oil inside hydraulic valves due to the nature of such flow, which is bounded by valve walls and might be highly turbulent. Therefore, one of the widely used approaches in computational fluid dynamics is the replacement of instantaneous variables with time-averaged values and fluctuations over those values. Thus, any flow scalar can be presented as

$$\tilde{\varphi }=\varphi +{\varphi }^{\prime }$$

(19)

where $\varphi$ is a time-averaged value and ${\varphi }^{\prime }$ is the fluctuation over this value. Replacing the instantaneous values with the above, the N-S equations are transformed to Reynolds-averaged N-S equations:

$$\frac{\mathsf{\partial }\rho }{\mathsf{\partial }t}+\frac{\mathsf{\partial }}{\mathsf{\partial }{x}_j}\left(\rho u_i\right)=0$$

(20)

$$\frac{\mathsf{\partial }}{\mathsf{\partial }t}\left(\rho u_i\right)+\frac{\mathsf{\partial }}{\mathsf{\partial }{x}_i}\left(\rho u_i{u}_j\right)=\frac{\mathsf{\partial }p}{\mathsf{\partial }{x}_i}+\frac{\mathsf{\partial }}{\mathsf{\partial }{x}_j}\left[\mu \left(\frac{\mathsf{\partial }{u}_i}{\mathsf{\partial }{x}_j}+\frac{\mathsf{\partial }{u}_j}{\mathsf{\partial }{x}_i}-\frac{2}{3}{\delta }_{ij}\frac{\mathsf{\partial }{u}_l}{\mathsf{\partial }{x}_l}\right)\right]+\frac{\mathsf{\partial }}{\mathsf{\partial }{x}_j}\left(-\rho \overline{{u_i}^{\prime }{u_j}^{\prime }}\right).$$

(21)

The term $-\rho \overline{{u_i}^{\prime }{u_j}^{\prime }}$, which is called Reynolds stress, must be modeled closely to RANS equations. One of the most common approaches is the Boussinesq approach, which defines the Reynolds stress for the gradient of the mean fluid velocity gradient.

$$-\rho \overline{{u_i}^{\prime }{u_j}^{\prime }}={\mu }_t\left(\frac{\mathsf{\partial }{u}_i}{\mathsf{\partial }{x}_j}+\frac{\mathsf{\partial }{u}_j}{\mathsf{\partial }{x}_i}\right)-\frac{2}{3}\left(\rho k+{\mu }_t\frac{\mathsf{\partial }{u}_k}{\mathsf{\partial }{x}_k}\right){\delta }_{ij}$$

(22)

where ${\delta }_{ij}$ is the Koronecker function, expressed as

$${\delta }_{ij}=\left\{\begin{array}{cc}1& i=j\\ 0& i\ne j\end{array}\right.$$

(23)

The turbulent viscosity ${\mu }_t$ can be derived from additional transport equations (a turbulence model). The oldest model and the most commonly used in the simulation of hydraulic valves is the $k-ϵ$ model, which employs two transport equations for the turbulence kinetic energy k and turbulence dissipation rate $ϵ$ [14].

$${\mu }_t=\rho C_{\mu }\frac{k^2}{\epsilon }$$

(24)

The turbulence kinetic energy is

$$\frac{\mathsf{\partial }}{\mathsf{\partial }t}\left(\rho k\right)+\frac{\mathsf{\partial }}{\mathsf{\partial }{x}_i}\left(\rho k{u}_i\right)=\frac{\mathsf{\partial }}{\mathsf{\partial }{x}_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\frac{\mathsf{\partial }k}{\mathsf{\partial }{x}_j}\right]+G_k+G_b-\rho \epsilon -Y_M+S_k$$

(25)

The turbulence dissipation rate is

$$\frac{\mathsf{\partial }}{\mathsf{\partial }t}\left(\rho \epsilon \right)+\frac{\mathsf{\partial }}{\mathsf{\partial }{x}_i}\left(\rho \epsilon u_i\right)=\frac{\mathsf{\partial }}{\mathsf{\partial }{x}_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_{\epsilon }}\right)\frac{\mathsf{\partial }\epsilon }{\mathsf{\partial }{x}_j}\right]+C_{1ϵ}\frac{\epsilon }{k}\left(G_k+C_{3\epsilon }{G}_b\right)-C_{2\epsilon }\rho \frac{{\epsilon }^2}{k}+S_{\epsilon }$$

(26)

where $C_{1ϵ}$, $C_{2ϵ}$, $C_{3ϵ}$, and $C_{\mu }$ are constants, $G_b$ is buoyancy component of turbulence kinetic energy, $Y_M$ is a term of the fluctuating dilatation in compressible turbulence to the dissipation rate, $S_k$ and $S_{\epsilon }$ are source terms, and ${\sigma }_k$ and ${\sigma }_{\epsilon }$ are Prandtl numbers for k and $\epsilon$, respectively. The standard $k-\epsilon$ model is robust and relatively effective, giving acceptable accuracy [14]. However, it is dedicated to fully turbulent flow and cannot capture the separated flow properly. Another drawback is an isotropic turbulence formulation. To overcome the drawbacks, modifications to the model were introduced. The oil flow inside valves is a combination of wall-bounded laminar flow [15,16], jet flow, and separated flow. All of these flows can exist altogether or one can be transformed into another during the valve opening. Some researchers indicate that the standard $k-\epsilon$ model or its modification ($RNG$$k-\epsilon$) [17,18,19,20] can be used to simulate flow inside hydraulic valves. The $RNG$$k-\epsilon$ model defines turbulence kinetic energy as [21]

$$\frac{\mathsf{\partial }}{\mathsf{\partial }t}\left(\rho k\right)+\frac{\mathsf{\partial }}{\mathsf{\partial }{x}_i}\left(\rho k{u}_i\right)=\frac{\mathsf{\partial }}{\mathsf{\partial }{x}_j}\left[\left({\alpha }_k{\mu }_{ef}\right)\frac{\mathsf{\partial }k}{\mathsf{\partial }{x}_j}\right]+G_k+G_b-\rho \epsilon -Y_M+S_k$$

(27)

$$G_k=-\rho \overline{{u_i}^{\prime }{u_j}^{\prime }}\frac{\mathsf{\partial }{u}_i}{\mathsf{\partial }{x}_j}$$

(28)

The turbulence dissipation rate:

$$\frac{\mathsf{\partial }}{\mathsf{\partial }t}\left(\rho \epsilon \right)+\frac{\mathsf{\partial }}{\mathsf{\partial }{x}_i}\left(\rho \epsilon u_i\right)=\frac{\mathsf{\partial }}{\mathsf{\partial }{x}_j}\left[\left({\alpha }_k{\mu }_{ef}\right)\frac{\mathsf{\partial }\epsilon }{\mathsf{\partial }{x}_j}\right]+C_{1ϵ}\frac{\epsilon }{k}\left(G_k+C_{3\epsilon }{G}_b\right)-C_{2\epsilon }\rho \frac{{\epsilon }^2}{k}-R_{\epsilon }+S_{\epsilon }$$

(29)

The effective viscosity ${\mu }_{ef}$ is

$${\mu }_{ef}=\mu \widehat{\nu }$$

(30)

$$d\left(\frac{{\rho }^{2}k}{\sqrt{\epsilon \mu }}\right)=1.72\frac{\widehat{\nu }}{\sqrt{{\widehat{\nu }}^3-1+C_{\nu }}}d\widehat{\nu }$$

(31)

where $C_{\mu }$ is different than for the standard $k-ϵ$ model.

The turbulent viscosity is modified to account for the effect of swirl or rotation in the following way:

$${\mu }_t={\mu }_{t0}f\left({\alpha }_s,\Omega ,\frac{k}{\epsilon }\right)$$

(32)

For a high Reynolds number $(\frac{{\mu }_{mol}}{{\mu }_{ef}}\ll 1)$, ${\alpha }_k={\alpha }_{\epsilon }=1.393$, and ${\alpha }_0=1$. The values ${\alpha }_k$ and ${\alpha }_s$ are the inverse effective Prandtl numbers.

Simic et al. [22] made a comparison of the standard $k-\epsilon$, $k-\omega$, and $SST$$k-\omega$ turbulence model with the experimental test of flow forces for a seat valve. The research showed that the $SST$$k-\omega$ could also be used in the calculation of flow forces of hydraulic valves. The turbulence kinetic energy, k, in the $SST$$k-\omega$ model is expressed as [23]

$$\frac{\mathsf{\partial }}{\mathsf{\partial }t}\left(\rho k\right)+\frac{\mathsf{\partial }}{\mathsf{\partial }{x}_i}\left(\rho k{u}_i\right)=\frac{\mathsf{\partial }}{\mathsf{\partial }{x}_j}\left[{\Gamma }_k\frac{\mathsf{\partial }k}{\mathsf{\partial }{x}_j}\right]+G_k-Y_k+S_k,$$

(33)

$$G_k=-\rho \overline{{u_i}^{\prime }{u_j}^{\prime }}\frac{\mathsf{\partial }{u}_i}{\mathsf{\partial }{x}_j}.$$

(34)

The specific dissipation rate $\omega$ is

$$\frac{\mathsf{\partial }}{\mathsf{\partial }t}\left(\rho \omega \right)+\frac{\mathsf{\partial }}{\mathsf{\partial }{x}_i}\left(\rho \omega u_j\right)=\frac{\mathsf{\partial }}{\mathsf{\partial }{x}_j}\left[{\Gamma }_{\omega }\frac{\mathsf{\partial }\omega }{\mathsf{\partial }{x}_j}\right]+G_{\omega }-Y_{\omega }+D_{\omega }+S_{\omega },$$

(35)

where the effective diffusivities for k and $\omega$ are as follows

$${\Gamma }_k=\mu +\frac{{\mu }_t}{{\sigma }_k},$$

(36)

$${\Gamma }_{\omega }=\mu +\frac{{\mu }_t}{{\sigma }_{\omega }}.$$

(37)

${\sigma }_k$ and ${\sigma }_{\omega }$ are the Prandtl numbers for k and $\omega$, respectively.

The turbulent viscosity is given by

$${\mu }_t=\frac{\rho k}{\omega }\frac{1}{max\left[\frac{1}{{\alpha }^{*}},\frac{S{F}_2}{{\alpha }_1\omega }\right]},$$

(38)

where S is the strain rate magnitude, and ${\alpha }^{*}$ is the low Reynolds number correction coefficient.

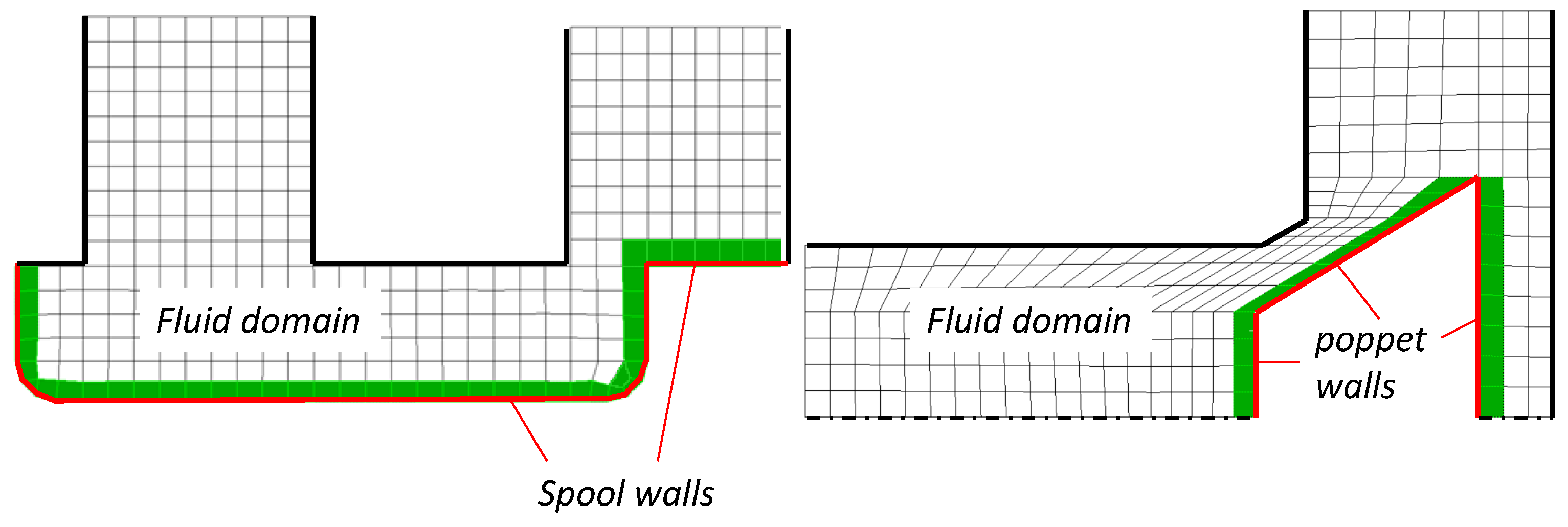
The CFD simulations remove almost all restrictions regarding valve geometry or the type of flow (axisymmetric flow) used in momentum theory for volume control, described earlier. The flow forces on the spool or poppet can be directly computed during CFD simulation. Using Equation (5), the axial flow forces are the sum of shear forces arising from fluid viscosity and normal forces induced by fluid pressure. Flow forces on valve control components are calculated as

$$F_{ax}=\sum _1^m\overline{\overline{\tau }}n$$

(39)

where m represents cells adjacent to the spool or poppet wall, as shown in Figure 8, and n is a normal vector of cell surfaces at the walls.

For the simulation of moving mesh for control volume, CV, for which the boundary is moving, the conservation equation for any flow scalar $\varphi$ is

$$\frac{d}{dt}\underset{CV}{\int \int \int }\rho \varphi dCV+\underset{CS}{\int \int }\rho (\overrightarrow{u}-{\overrightarrow{u}}_m)dCS=\underset{CS}{\int \int }\Gamma \nabla \varphi dCS+\underset{CV}{\int \int \int }{S}_{\varphi }dCV$$

(40)

where $u_m$ is the velocity of moving mesh, and $S_{\varphi }$ is a source term of $\varphi$.

The above equation is also valid for the sliding mesh technique.

The immersed solid, which is also used as one of the techniques for simulating body motion in CFD, modifies the momentum conservation equation, Equation (2), with the source term $S_i$:

$$S_i=-\alpha \beta C\left(u_i-u_{S_i}\right)$$

(41)

where C is a source momentum coefficient, $\alpha$ is the momentum scaling factor, $\beta$ is the forcing factor, $u_i$ is the fluid velocity, and $u_{S_i}$ is the forcing fluid velocity due to the motion of immersed solid.

The source term in the momentum conservation equation is

$$S_i=-\alpha \beta C\left(u_i-u_{S_i}\right)$$

(42)

where C is a source momentum coefficient, $\alpha$ is the momentum scaling factor, $\beta$ is the forcing factor, $u_i$ is the fluid velocity, and $u_{S_i}$ is forcing fluid velocity due to motion of immersed solid.

4. CFD Simulations of Steady-State Flow Forces

This section shows the application of CFD methods in the simulation of the flow forces in hydraulic valves. The research referenced here either originated or made a significant contribution to the use of CFD methods in evaluating flow forces inside hydraulic valves.

CFD simulations of hydraulic valves can generally be divided into two main categories. The first category is a simulation focused on the verification and modification of the formula for calculating flow forces or directly calculating flow forces for specific designs of hydraulic valves. These are mostly simulations for steady-state conditions, where the flow parameters are known, and the valve control component positions are fixed. The first CFD simulations on flow forces in hydraulic valves were focused on verification theory, as presented in the Introduction and Equation (10). Borghi et al. [6] used the 2D axisymmetric model to verify the jet angle and the reasons for the differences. This research shows that assumptions for momentum theory might be a good approximation only for a specific valve opening, and the Coanda effect might affect the jet angle. Yuan et al. [24] used 3D CFD simulation to investigate the viscosity effect on flow forces and its transient component on 3D models. In this research, the viscous component of the steady flow forces was proposed. Amirante et al. [25] used the dynamic mesh technique on the 3D axisymmetric model in research on unsteady flow forces in spool valves. This research showed that flow forces in the initial opening phase act in the opening direction, then change direction, reaching the maximal peak value. The peak value increased with the flow rate but was always achieved for the same opening. The situation changed for the closed center directional valve, where the peak value depends on the flow rate and pressure drop and occurs in different openings. Rundo et al. [26] used CFD simulation for the verification of the flow forces calculated with the use of momentum theory and the Bernoulli equation. The study concluded that both approaches agree with CFD simulation for divergent flow, but more significant differences occur for convergent flow with and without back pressure. Additionally, it confirmed that multiphase flow, including cavitation, is required to evaluate flow forces. Amirante et al. [27] used a slice of the 3D fluid domain to simulate oil flow inside the flow control valve, while Lisowski et al. [28], for a similar valve, used the entire 3D fluid domain model. He confirmed that the analytical formula is insufficient to calculate flow forces in hydraulic valves with complex geometry. He also determined the jet angle for different valve openings. Herakovic et al. [29] used 3D models for the simulation of fluid flow in steady-state conditions and received a good agreement with experimental data thanks to the refined grid on control components and the $SST$k-$\omega$ turbulence model. Due to the CFD advantages, one of which is undoubtedly insensitivity to geometrical complexity, CFD tools are often used in research on the influence of valve control component geometry on flow forces affecting their performance or characteristics. In [30], the authors showed that the spool notch shape significantly influences the discharge coefficient, flow forces, and jet angle. The flow forces obtained for spheroid notches were much smaller than for a triangle and U-shape. Ref. [31] shows research on the effect of the shape of the spool cavity and control surface on the flow force values. They proved that the conical shape of the cavity surface and the triangular shape of the control surface can reduce the flow force values. Amirante et al. [32] combined CFD simulation for the spool valve and optimization solver to minimize flow forces. The four design parameters were defined to find the optimal spool shape and reduce flow forces at about 15 % for the fully opened valve. At the small opening, the recorded differences between the optimized shape and the original were marginal. In [33], the authors present the investigation of a seat valve with a damping tail. The obtained results indicate that flow forces could be significantly decreased in the range of almost 85% by using a damping tail. CFD tools are often used together with lumped parameter simulation tools to simulate valve dynamics and analyze the operation of valves or entire hydraulic systems. In such cases, CFD is used to directly calculate flow forces or extract variables for the analytical formula, such as discharge coefficient, jet angle, or flow rate. In [6], the authors showed that the jest angle for small openings differs from the theoretical one and that the axisymmetric CFD model is accurate only for a specific range of valve openings. In [34], the authors concluded that lumped parameter methods and CFD could supplement each other. The first one can be used at the initial stage of the design to deliver information that could be used as a starting point for more extensive CFD simulation. Qianpeng et al. [35] used lumped parameter packages to define boundary conditions for the CFD model of a spool valve. Such implementation allowed tuning the CFD model and calculation flow forces and verifying spool clamping in specific working conditions. CFD simulation on flow forces also includes research on the influence of parameters other than valve geometry. Bigliardi et al. [36] used multiphase flow simulation to investigate the influence of oil aeration on flow forces. This simulation employed a two-phase flow with phase changes (cavitation). The study focused on phase changes during oil flow and their influence on flow forces. The difference between measured values was calculated and can be explained by neglecting the shear stress on the valve spool. One of the few studies on radial forces is presented in [37]. Hong et al. [37] simulated oil flow inside the gap between spool land and bore and with spiral grooves. One of the results was that the radial groves provide more uniform pressure distribution at the valve land, and consequently minimize the radial force. A CFD simulation on a spool valve but of a rotary type was performed by Wang et al. [38] and Okhotnikov et al. [39], aimed at the evaluation of jet angle, discharge coefficient, and flow torque. In both studies, the jet angle and flow torque in the function of valve opening were obtained.

5. CFD Simulations of Transient Flow Forces

The second category of CFD simulation is a transient simulation, where flow parameters and the position of control components may vary in time. This category includes the fluid–structure interaction (FSI) technique, where the flowing oil interacts with valve components, defining their position in the valve. A single-phase and homogeneous flow is usually used in both categories, in which the oil parameters are constant. The FSI simulations are more challenging and are not very often used in hydraulic valve simulation. The CFD simulation is either performed for a simplified axisymmetric model [10] or for spool control valves in which the spool is actuated to a specific position [40]. For the poppet valves such as those presented in Figure 6 or the flow control valve presented in Figure 7, an additional technique, fluid–structure interaction (FSI), has to be employed. In both types of valves, the position of the control components is set by the force equilibrium. A performed transient simulation for a poppet valve with a deflector with the use of deforming mesh and FSI is presented in [41]. This study includes almost all of the simulation types presented above. This simulation was conducted for a 3D model of a conical-shaped poppet to evaluate flow forces during flow with phase changes and deforming mesh. Calculating transient (dynamic) flow forces requires valve component motion, which can be realized by at least a few techniques available with almost all general-purpose CFD codes, such as Ansys Fluent, CFX, Star CCM+ or OpenFOAM. The abovementioned CFD techniques for simulating transient flow forces using FSI are presented hereafter in Figure 9, Figure 10, Figure 11 and Figure 12. They represent both types of valves schematically as the axisymmetrical models similar to those in Figure 1. The grid and structure of the CFD model for all presented models are shown in a simplified way to reflect only the idea of each FSI technique. One of the most popular techniques employs deforming mesh requiring a fluid domain, which can be stretched or expanded as the valve components move. This method was implemented in simulations presented in [40,41]. 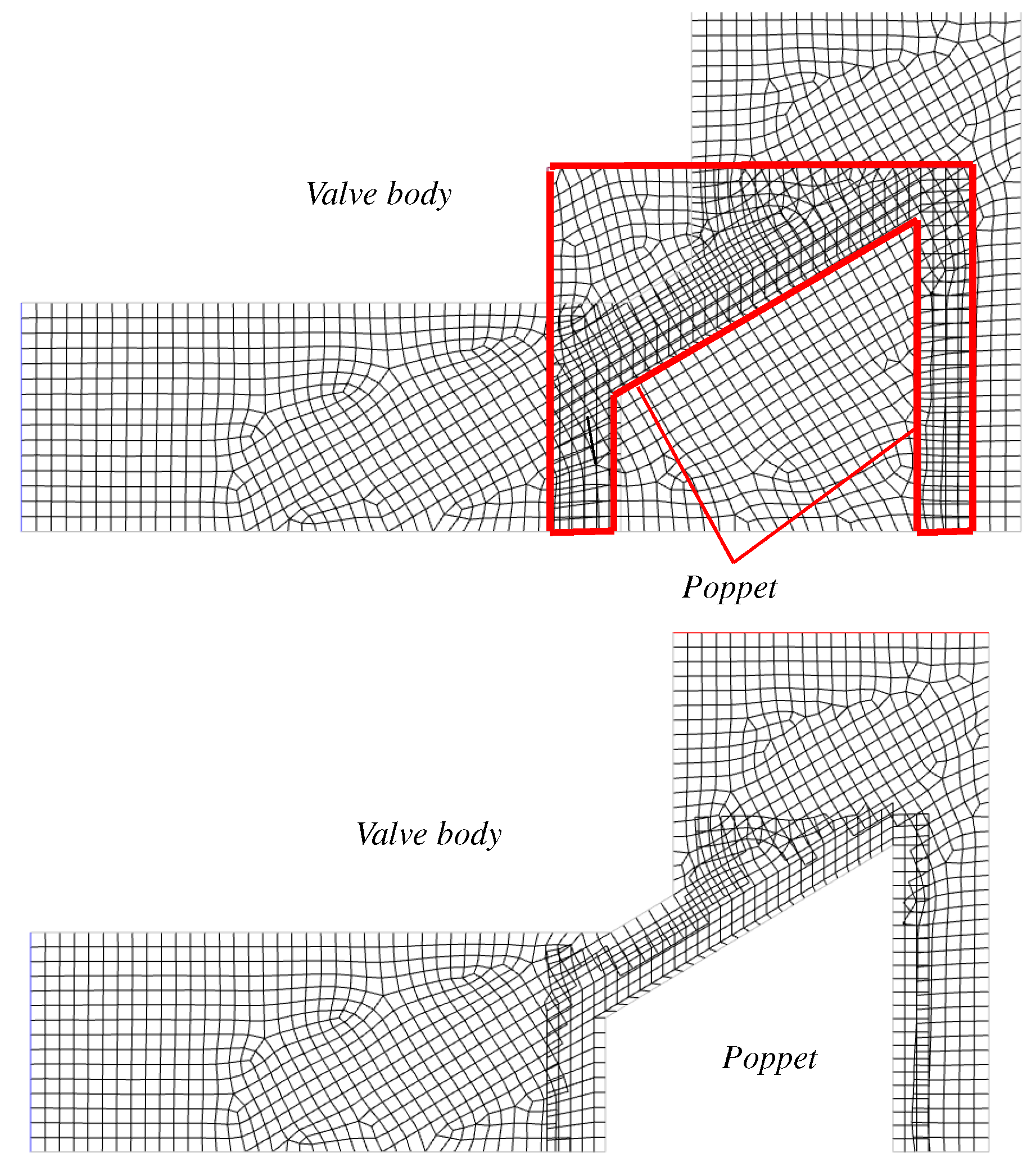The idea of this method is presented in Figure 9. The green mesh region is a mesh that deforms during control component motion. The other part of the fluid domain remains unchanged.

The motion of the valve components can be simplified as one-dimensional motion in their centers of gravity. It is a relatively simple task for valves where control elements are actuated. More challenging is the situation involving valves for which the force balance determines the position of the control element.

Another method, presented in Figure 10, was implemented in [42,43]. It is named “immersed solid”, where the fluid and solid mesh (or a boundary) overlap. The red boundary in Figure 10 indicates the walls of the spool and poppet during motion. This method uses mesh for the fluid domain (grey) and solids, which are moving control components (green and brown). The domain of oil flow is created between overlapping solid and fluid domains.

Figure 10. Immersed solid. (a) Spool valve. (b) Poppet valve. The green and brown region is a solid mesh that moves during valve motion. The top pictures show closed valves, and the bottom opened.

Figure 10. Immersed solid. (a) Spool valve. (b) Poppet valve. The green and brown region is a solid mesh that moves during valve motion. The top pictures show closed valves, and the bottom opened.

The transient simulation can also be achieved by using two fluid subdomains, which are not directly connected in computational cells but by the interface between them. It provides lossless mass transfer between subdomains. Figure 11 shows an idea of using sliding mesh for a spool valve. In principle, it consists of two or more fluid domains (green and grey) that are not connected in computational cells but can slide along the interface (blue line).

Figure 11. Sliding mesh. The blue line is the interface between two fluid subdomains. The red line indicates spool walls. The top picture shows a closed valve while the bottom is opened.

Figure 11. Sliding mesh. The blue line is the interface between two fluid subdomains. The red line indicates spool walls. The top picture shows a closed valve while the bottom is opened.

The practical implementation of the method is presented in studies [40,44], while the idea is presented in Figure 11. Both subdomains slide along the interface line, providing valve closing and opening. The youngest technology of moving mesh, known as the overset mesh, seems very promising in the simulation of the spool and poppet valves. Lv et al. [45] used the overset mesh technique for the simulation of oil flow in the two-stage flapper–nozzle pilot valve while the flapper was moving. The potential usage of this method for the flow simulation of the poppet valve is shown in Figure 12. The fluid domain is created by overlapping two independent computational meshes (subdomains), which permits the motion of one subdomain. The initial grid presented in the top picture shows an imaginary part of the fluid domain over the poppet. The process of merging both fluid domains is presented in the bottom picture. The final mesh is created using overlapped regions between both domains.

Figure 12. Overset mesh. The top picture shows an initial mesh. The bottom pictures shows mesh during simulation.

Figure 12. Overset mesh. The top picture shows an initial mesh. The bottom pictures shows mesh during simulation.

6. Discussion

The majority of presented cases use CFD simulation for calculating the steady-state axial flow forces. The radial component is neglected. Regardless of the isotropic turbulent formulation, the RNG k-epsilon turbulence model seems to be adequate to predict flow inside hydraulic valves in a proper way. The CFD simulations with a fixed component position evaluate flow forces with acceptable accuracy for valves whose control components are actuated by a solenoid or other actuator. For the valves presented in Figure 6 and Figure 7, where the control element position depends on a force equilibrium, such an approach may not be accurate enough. A fluid–structure interaction simulation seems to be an ideal antidote due to the ability to include component motion induced by fluid flow. However, such simulations are not very often used in the simulation of hydraulic valves. The main problem is perhaps not computational effort but the requirements of the CFD model. The FSI technique uses moving mesh, which can be realized in many ways. One of them is deforming mesh, which has to be prepared to predict deformation with acceptable quality. Moreover, even if such a grid is prepared, the problem of a small opening is still present. One of the problems with deforming mesh is presented in Figure 13. A very compressed grid produces a highly skewed cell with negative volume, which may require preventative measures like remeshing during simulation or evaluating the minimal opening value, which is not covered during simulation. Problems with mesh quality during deformation can be solved using the overset mesh technique. However, the grid has to be prepared to avoid holes (dummy cells) in the area of overlapping cells and for small openings. Some CFD codes have been used to solve the problem of small openings by defining the minimal distance between walls in motion [46].

The immersed body technique does not have such strict requirements regarding grid quality. However, at the interface between overlapping domains, the grid has to be fine enough to capture solid domains accurately. Furthermore, this technique does not employ wall function but only the interface between the fluid and solid domain, which implies that shear forces are not considered for immersed solids [48]. In contrast, the sliding mesh might be an ideal solution for spool valves but is almost impossible to implement for poppet valves. In practice, the implementation of only one technique might not be effective. Therefore, some researchers have used a few of them together: deforming mesh and sliding mesh [25] or deforming mesh and remeshing [41]. Another problem in valves where the force balance determines the control element position is the implementation of the control element motion. It can be realized directly using CFD code with an embedded six DOF solver or with an external solver. Flow simulation at a small opening is generally problematic, not only with regard to the simulation aspect. The nature of flow suddenly changes from wall-bounded laminar flow into free jet flow or separated flow. These are conditions under which cavitation [15] is likely to occur along with massive heat generation. However, attempts at such a complex simulation task have also been taken. Finesso et al. [41] created a CFD model of a relief valve, including component motion, mesh deformation, and phase changes. Additionally, in many practical applications, pressure pulsation in hydraulic lines is unavoidable. Valves also are subjected to mechanical vibrations, introducing another unsteady factor [49]. In general, CFD simulation with deforming mesh and component motion could be used to simulate valve operation or determine valve characteristics. However, it is far more complicated to implement than the typical combination of a steady-state CFD model and lumped parameter simulation.

7. Conclusions

The available research shows that the following assumptions are commonly used in CFD simulations of flow forces inside hydraulic valves:

• Fluid has the constant properties of hydraulic oil at normal operating temperature.
• Fluid is homogeneous, single-phase, and incompressible.
• The valve components walls are smooth. The roughness is neglected.
• The spool/poppet and bore/seat geometry are ideal, without any imperfections.
• Steady-state conditions are commonly implemented.
• Heat transfer is neglected.
• Phase changes are neglected.
• A standard k-$\epsilon$ or $RNG$ k-$\epsilon$ turbulence model is used.

CFD simulations of flow forces are conducted using two main approaches:

• Steady-state conditions and fixed positions of valve control components.
• Transient simulation using FSI simulation,

The first can be characterized by the following:

• Used for both types of valves (spool and poppet).
• Suitable for static flow forces and dynamic components arising from unsteady flow.
• Relatively simple CFD model.
• A short time of simulation.
• Suitable for experimental verification due to the fixed valve components’ positions.
• Unable to capture the full spectrum of the dynamic component of flow forces.
• Suitable for the sensitivity analysis of valve geometry on flow forces.
• Requires additional simulation tools for the determination of valve characteristics.

The second can be characterized by the following:

• Suitable for evaluating both force components: static and dynamic.
• More computationally expensive.
• The FSI technique has to be selected for a particular type of valve.
• A more complex CFD model must be adequately prepared depending on the FSI technique used.
• Indirect experimental verification.
• Capable of the direct simulation of valve performance (static and dynamic valve characteristics).
• Requires an additional solver for determining component motion.
• Problems with simulation in small valve openings, except for the sliding mesh technique implemented for spool valves.
• Suitable for the sensitivity analysis of valve geometry on flow forces.