Real-Time ITO Layer Thickness for Solar Cells Using Deep Learning and Optical Interference Phenomena
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiment Principle
2.2. Experiment Method
2.2.1. ITO Film Fabrication and Building Instrument
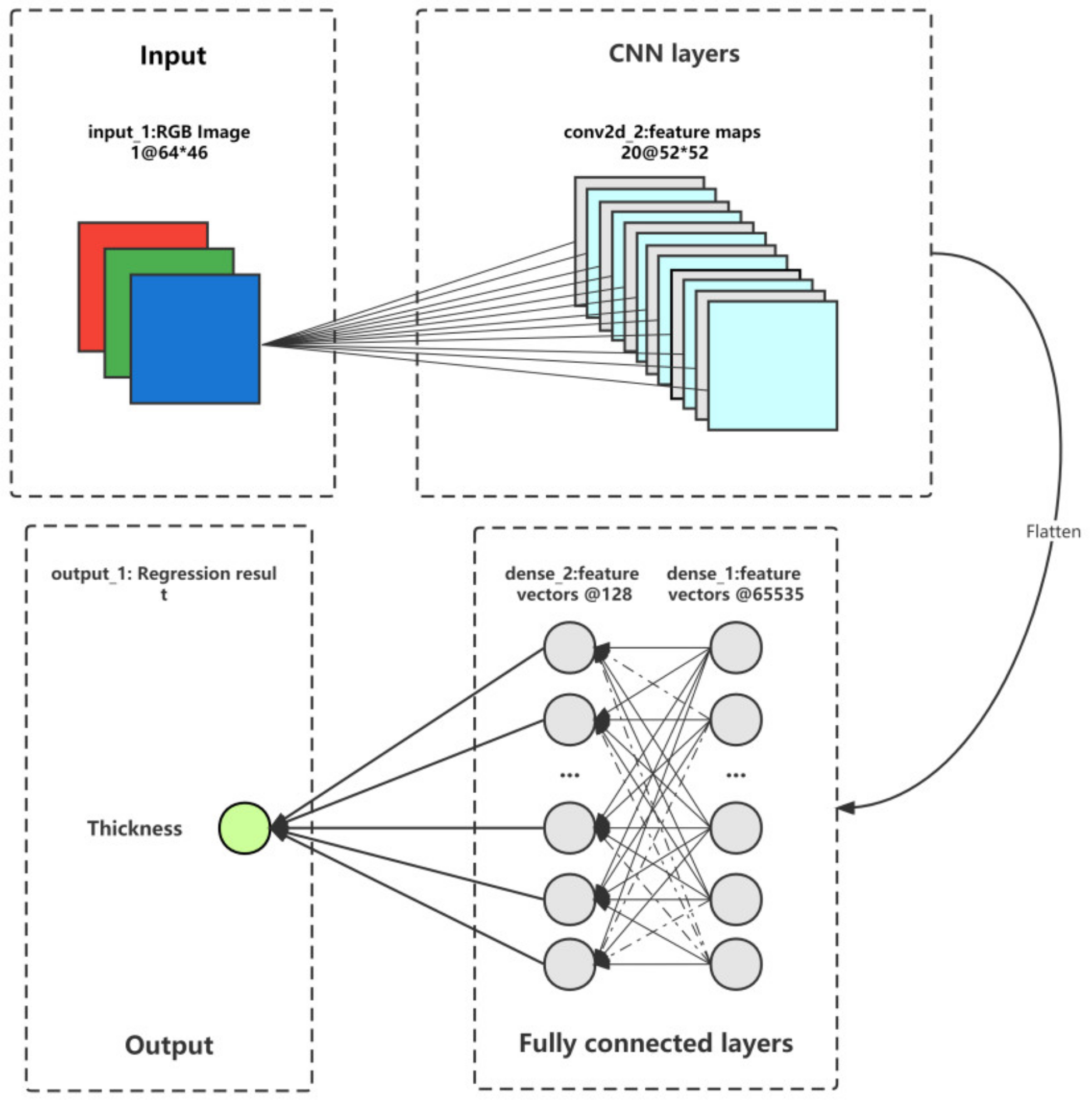
2.2.2. Overall Architecture of the Model
2.2.3. Components of the Model
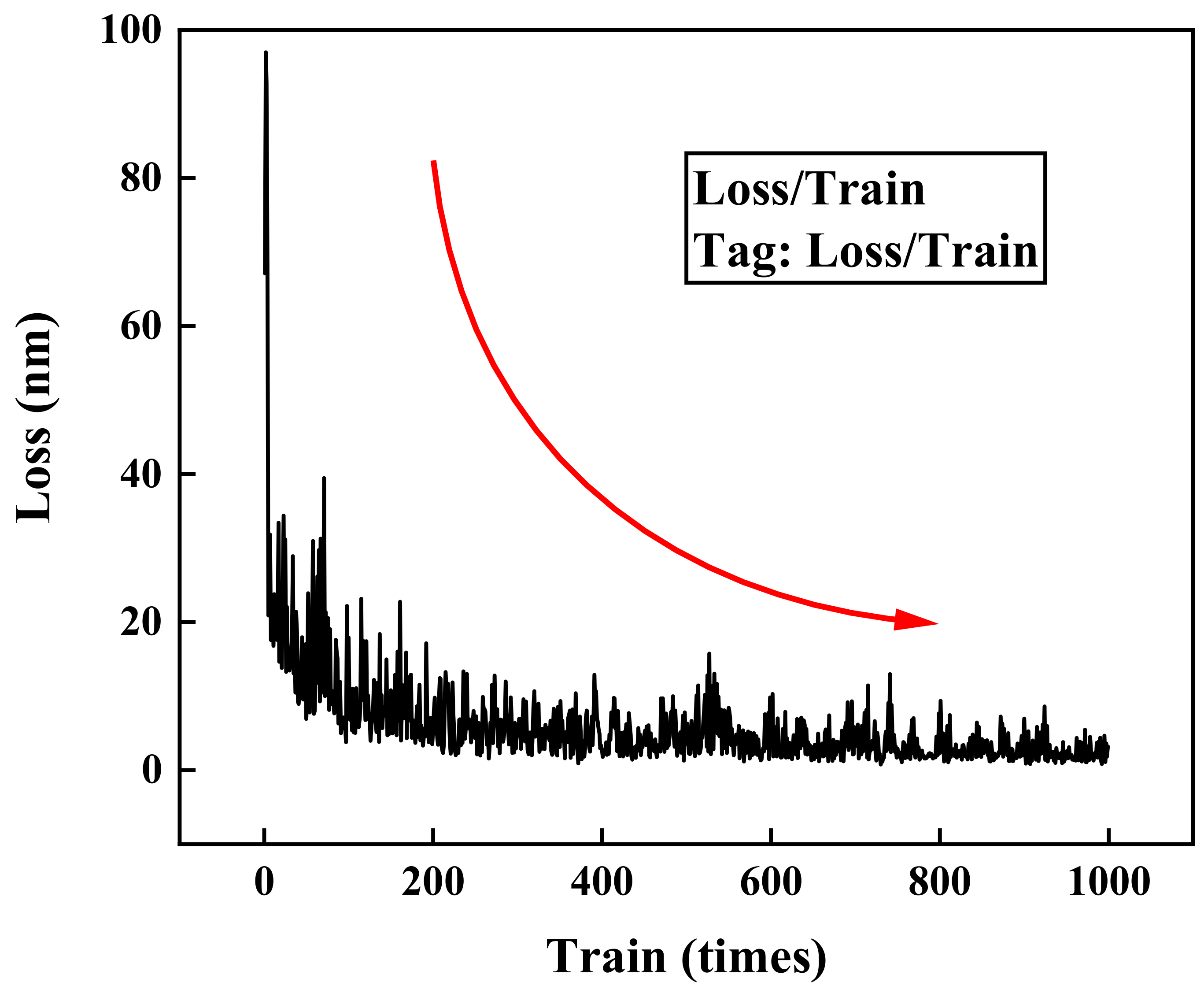
2.2.4. Training Configuration
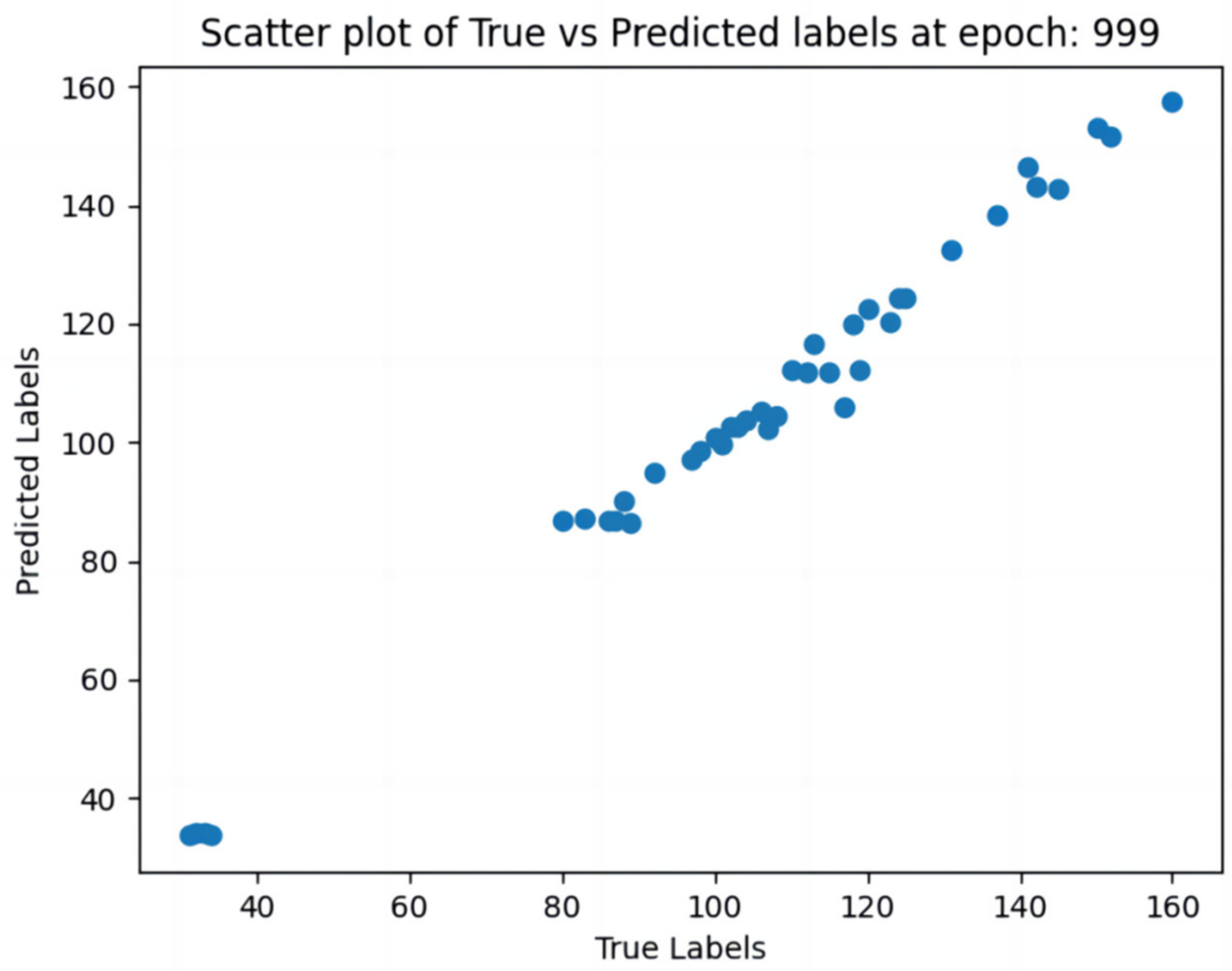
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Grätzel, M. Solar energy conversion by dye-sensitized photovoltaic cells. Inorg. Chem. 2005, 44, 6841–6851. [Google Scholar] [CrossRef]
- Bagher, A.M.; Vahid, M.M.A.; Mohsen, M. Types of solar cells and application. Am. J. Opt. Photonics 2015, 3, 94–113. [Google Scholar] [CrossRef]
- Hayat, M.B.; Ali, D.; Monyake, K.C.; Alagha, L.; Ahmed, N. Solar energy—A look into power generation, challenges, and a solar-powered future. Int. J. Energy Res. 2019, 43, 1049–1067. [Google Scholar] [CrossRef]
- Sulaman, M.; Yang, S.Y.; Zhang, Z.H.; Imran, A.; Bukhtiar, A.; Ge, Z.H.; Tang, Y.; Jiang, Y.R.; Tang, L.B.; Zou, B.S. Lead-free tin-based perovskite nanocrystals for high-performance self-driven bulk-heterojunction photodetectors. Mater. Today Phys. 2022, 27, 1100829. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, J.; Ma, X.; Gao, J.; Xu, C.; Yang, K.; Wang, Z.; Zhang, J.; Zhang, F. A critical review on semitransparent organic solar cells. Nano Energy 2020, 78, 105376. [Google Scholar] [CrossRef]
- Roy, P.; Sinha, N.K.; Tiwari, S.; Khare, A. A review on perovskite solar cells: Evolution of architecture, fabrication techniques, commercialization issues and status. Sol. Energy 2020, 198, 665–688. [Google Scholar] [CrossRef]
- Riede, M.; Spoltore, D.; Leo, K. Organic solar cells—the path to commercial success. Adv. Energy Mater. 2021, 11, 2002653. [Google Scholar] [CrossRef]
- Massiot, I.; Cattoni, A.; Collin, S. Progress and prospects for ultrathin solar cells. Nat. Energy 2020, 5, 959–972. [Google Scholar] [CrossRef]
- Andreani, L.C.; Bozzola, A.; Kowalczewski, P.; Liscidini, M.; Redorici, L. Silicon solar cells: Toward the efficiency limits. Adv. Phys. X 2019, 4, 1548305. [Google Scholar] [CrossRef]
- Le, A.H.T.; Dao, V.A.; Pham, D.P.; Kim, S.; Dutta, S.; Nguyen, C.P.T.; Lee, Y.; Kim, Y.; Yi, J. Damage to passivation contact in silicon heterojunction solar cells by ITO sputtering under various plasma excitation modes. Sol. Energy Mater. Sol. Cells 2019, 192, 36–43. [Google Scholar] [CrossRef]
- Sousa, M.G.; Da Cunha, A.F. Optimization of low temperature RF-magnetron sputtering of indium tin oxide films for solar cell applications. Appl. Surf. Sci. 2019, 484, 257–264. [Google Scholar] [CrossRef]
- Amalathas, A.P.; Alkaisi, M.M. Effects of film thickness and sputtering power on properties of ITO thin films deposited by RF magnetron sputtering without oxygen. J. Mater. Sci. Mater. Electron. 2016, 27, 11064–11071. [Google Scholar] [CrossRef]
- Pla, J.; Tamasi, M.; Rizzoli, R.; Losurdo, M.; Centurioni, E.; Summonte, C.; Rubinelli, F. Optimization of ITO layers for applications in a-Si/c-Si heterojunction solar cells. Thin Solid Film. 2003, 425, 185–192. [Google Scholar] [CrossRef]
- Huang, M.; Hameiri, Z.; Aberle, A.G.; Mueller, T. Comparative study of amorphous indium tin oxide prepared by pulsed-DC and unbalanced RF magnetron sputtering at low power and low temperature conditions for heterojunction silicon wafer solar cell applications. Vacuum 2015, 119, 68–76. [Google Scholar] [CrossRef]
- Hotovy, J.; Hüpkes, J.; Böttler, W.; Marins, E.; Spiess, L.; Kups, T.; Smirnov, V.; Hotovy, I.; Kováč, J. Sputtered ITO for application in thin-film silicon solar cells: Relationship between structural and electrical properties. Appl. Surf. Sci. 2013, 269, 81–87. [Google Scholar] [CrossRef]
- Dao, V.A.; Choi, H.; Heo, J.; Park, H.; Yoon, K.; Lee, Y.; Kim, Y.; Lakshminarayan, N.; Yi, J. rf-Magnetron sputtered ITO thin films for improved heterojunction solar cell applications. Curr. Appl. Phys. 2010, 10, S506–S509. [Google Scholar] [CrossRef]
- Muneshwar, T.P.; Varma, V.; Meshram, N.; Soni, S.; Dusane, R.O. Development of low temperature RF magnetron sputtered ITO films on flexible substrate. Sol. Energy Mater. Sol. Cells 2010, 94, 1448–1450. [Google Scholar] [CrossRef]
- Alzaid, M.; Mohamed, W.S.; El-Hagary, M.; Shaaban, E.R.; Hadia, N.M.A. Optical properties upon ZnS film thickness in ZnS/ITO/glass multilayer films by ellipsometric and spectrophotometric investigations for solar cell and optoelectronic applications. Opt. Mater. 2021, 118, 111228. [Google Scholar] [CrossRef]
- Emam-Ismail, M.; El-Hagary, M.; El-Sherif, H.M.; El-Naggar, A.M.; El-Nahass, M.M. Spectroscopic ellipsometry and morphological studies of nanocrystalline NiO and NiO/ITO thin films deposited by e-beams technique. Opt. Mater. 2021, 112, 110763. [Google Scholar] [CrossRef]
- Baldner, F.O.; Costa, P.B.; Gomes, J.F.S.; Leta, F.R. A review on computer vision applied to mechanical tests in search for better accuracy. In Advances in Visualization and Optimization Techniques for Multidisciplinary Research: Trends in Modelling and Simulations for Engineering Applications; Springer: Berlin/Heidelberg, Germany, 2020; pp. 265–281. [Google Scholar]
- Rong, D.; Xie, L.; Ying, Y. Computer vision detection of foreign objects in walnuts using deep learning. Comput. Electron. Agric. 2019, 162, 1001–1010. [Google Scholar] [CrossRef]
- DeCost, B.L.; Holm, E.A. A computer vision approach for automated analysis and classification of microstructural image data. Comput. Mater. Sci. 2015, 110, 126–133. [Google Scholar] [CrossRef]
- Holm, E.A.; Cohn, R.; Gao, N.; Matson, T.P.; Lei, B.; Yarasi, S.R. Overview: Computer vision and machine learning for microstructural characterization and analysis. Metall. Mater. Trans. A 2020, 51, 5985–5999. [Google Scholar] [CrossRef]
- Sethian, J.A. Level Set Methods and Fast Marching Methods: Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- DeCost, B.L.; Holm, E.A. Characterizing powder materials using keypoint-based computer vision methods. Comput. Mater. Sci. 2017, 126, 438–445. [Google Scholar] [CrossRef]
- Wang, S.Y.; Zhang, P.Z.; Zhou, S.Y.; Wei, D.B.; Ding, F.; Li, F.K. A computer vision based machine learning approach for fatigue crack initiation sites recognition. Comput. Mater. Sci. 2020, 171, 109259. [Google Scholar] [CrossRef]
- Cifuentes-Alcobendas, G.; Domínguez-Rodrigo, M. More than meets the eye: Use of computer vision algorithms to identify stone tool material through the analysis of cut mark micro-morphology. Archaeol. Anthropol. Sci. 2021, 13, 167. [Google Scholar] [CrossRef]
- Karthikeyan, S.; Subbarayan, M.R.; Beemaraj, R.K.; Sivakandhan, C. Computer vision-based surface roughness measurement using artificial neural network. Mater. Today Proc. 2022, 60, 1325–1328. [Google Scholar]
- Yang, Y.; Qiu, T.; Kong, F.; Fan, J.; Ou, H.; Xu, Q.; Chu, P.K. Interference effects on indium tin oxide enhanced Raman scattering. J. Appl. Phys. 2012, 111, 33110. [Google Scholar] [CrossRef]
- Granlund, T.; Pettersson, L.A.A.; Anderson, M.R.; Inganäs, O. Interference phenomenon determines the color in an organic light emitting diode. J. Appl. Phys. 1997, 81, 8097–8104. [Google Scholar] [CrossRef]
- Halliday, D.; Resnick, R.; Walker, J. Fundamentals of Physics; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Ni, Z.; Mou, S.; Zhou, T.; Cheng, Z. Broader color gamut of color-modulating optical coating display based on indium tin oxide and phase change materials. Appl. Opt. 2018, 57, 3385–3389. [Google Scholar] [CrossRef]
- Lyu, Y.; Mou, S.; Ni, Z.; Bai, Y.; Sun, Y.; Cheng, Z. Multi-color modulation of solid-state display based on thermally induced color changes of indium tin oxide and phase changing materials. Opt. Express 2017, 25, 1405–1412. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Hariharan, P. Optical Interferometry, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. [Google Scholar]
- Yamashita, R.; Nishio, M.; Do, R.G.; Togashi, K. Convolutional neural networks: An overview and application in radiology. Insights Imaging 2018, 9, 611–629. [Google Scholar] [CrossRef] [PubMed]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), IEEE, Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar]
- O’Shea, K.; Nash, R. An introduction to convolutional neural networks. arXiv 2015, arXiv:1511.08458. [Google Scholar]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Bayar, B.; Stamm, M.C. A deep learning approach to universal image manipulation detection using a new convolutional layer. In Proceedings of the 4th ACM Workshop on Information Hiding and Multimedia Security, Vigo, Spain, 20–22 June 2016; pp. 5–10. [Google Scholar]
- Cordonnier, J.B.; Loukas, A.; Jaggi, M. On the relationship between self-attention and convolutional layers. arXiv 2019, arXiv:1911.03584. [Google Scholar]
- Giusti, A.; Cireşan, D.C.; Masci, J.; Gambardella, L.M.; Schmidhuber, J. Fast image scanning with deep max-pooling convolutional neural networks. In Proceedings of the 2013 IEEE International Conference on Image Processing, IEEE, Melbourne, VIC, Australia, 15–18 September 2013; pp. 4034–4038. [Google Scholar]
- Graham, B. Fractional max-pooling. arXiv 2014, arXiv:1412.6071. [Google Scholar]
- Nagi, J.; Ducatelle, F.; Di Caro, G.A.; Cireşan, D.; Meier, U.; Giusti, A.; Nagi, F.; Schmidhuber, J.; Gambardella, L.M. Max-pooling convolutional neural networks for vision-based hand gesture recognition. In Proceedings of the 2011 IEEE International Conference on Signal and Image Processing Applications (ICSIPA), Kuala Lumpur, Malaysia, 16–18 November 2011; pp. 342–347. [Google Scholar]
- Basha SH, S.; Dubey, S.R.; Pulabaigari, V.; Mukherjee, S. Impact of fully connected layers on performance of convolutional neural networks for image classification. Neurocomputing 2020, 378, 112–119. [Google Scholar] [CrossRef]
- Ding, X.; Xia, C.; Zhang, X.; Chu, X.; Han, J.; Ding, G. Repmlp: Re-parameterizing convolutions into fully-connected layers for image recognition. arXiv 2021, arXiv:2105.01883. [Google Scholar]
- Zhang, C.L.; Luo, J.H.; Wei, X.S.; Wu, J. In defense of fully connected layers in visual representation transfer. In Advances in Multimedia Information Processing, Proceedings of the PCM 2017: 18th Pacific-Rim Conference on Multimedia, Harbin, China, 28–29 September 2017; Revised Selected Papers, Part II 18; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 807–817. [Google Scholar]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)–Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, X.; Wang, B.; Khokhar, M.Q.; Zahid, M.A.; Pham, D.P.; Yi, J. Real-Time ITO Layer Thickness for Solar Cells Using Deep Learning and Optical Interference Phenomena. Energies 2023, 16, 6049. https://doi.org/10.3390/en16166049
Fan X, Wang B, Khokhar MQ, Zahid MA, Pham DP, Yi J. Real-Time ITO Layer Thickness for Solar Cells Using Deep Learning and Optical Interference Phenomena. Energies. 2023; 16(16):6049. https://doi.org/10.3390/en16166049
Chicago/Turabian StyleFan, Xinyi, Bojun Wang, Muhammad Quddamah Khokhar, Muhammad Aleem Zahid, Duy Phong Pham, and Junsin Yi. 2023. "Real-Time ITO Layer Thickness for Solar Cells Using Deep Learning and Optical Interference Phenomena" Energies 16, no. 16: 6049. https://doi.org/10.3390/en16166049
APA StyleFan, X., Wang, B., Khokhar, M. Q., Zahid, M. A., Pham, D. P., & Yi, J. (2023). Real-Time ITO Layer Thickness for Solar Cells Using Deep Learning and Optical Interference Phenomena. Energies, 16(16), 6049. https://doi.org/10.3390/en16166049






