Optimal Voltage Control Method for a Step Voltage Regulator Considering the Under-Load Tap Changer in a Distribution System Interconnected with a Renewable Energy Source
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Contribution
2. Voltage Control Strategy for the SVR
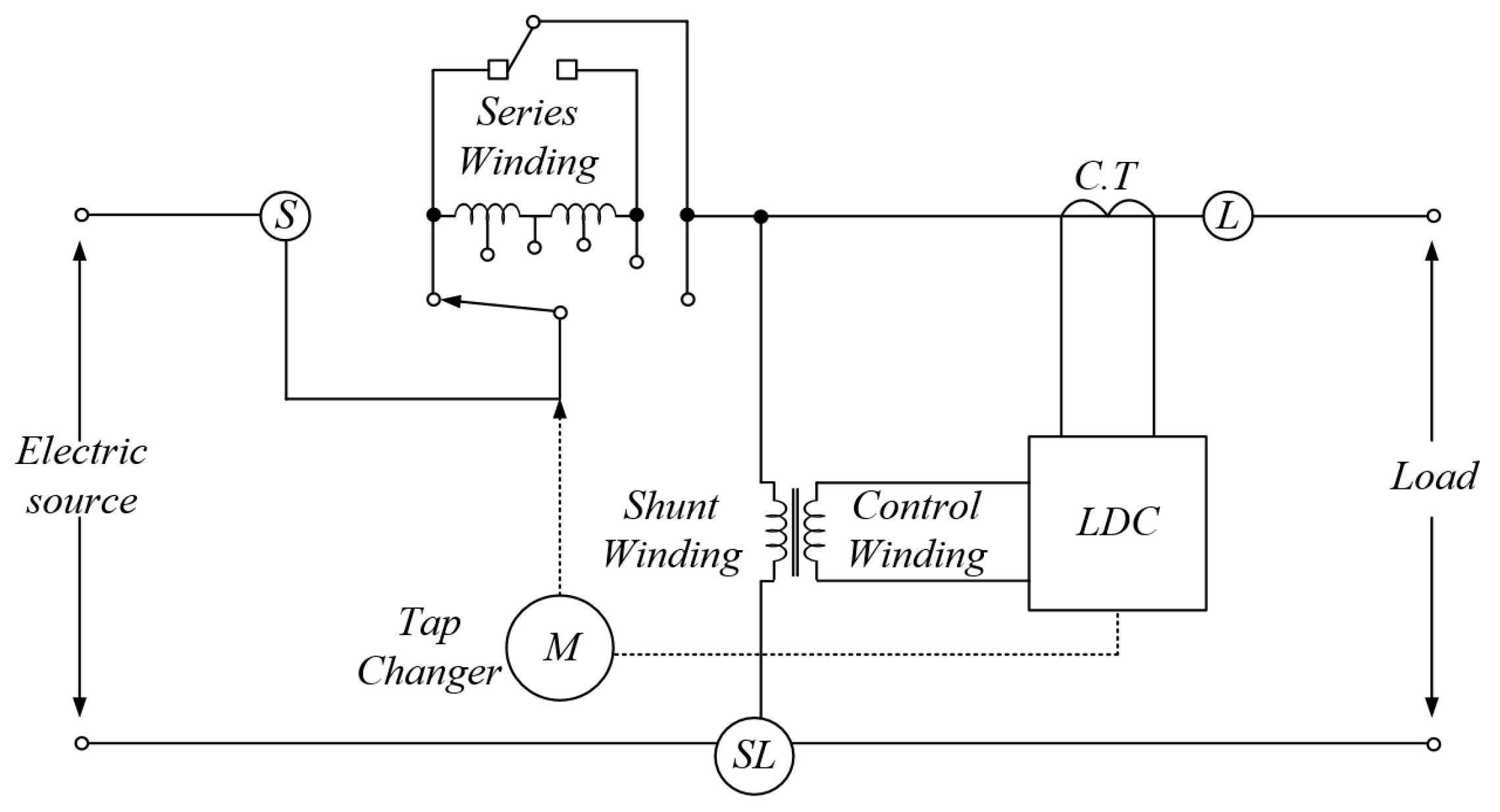
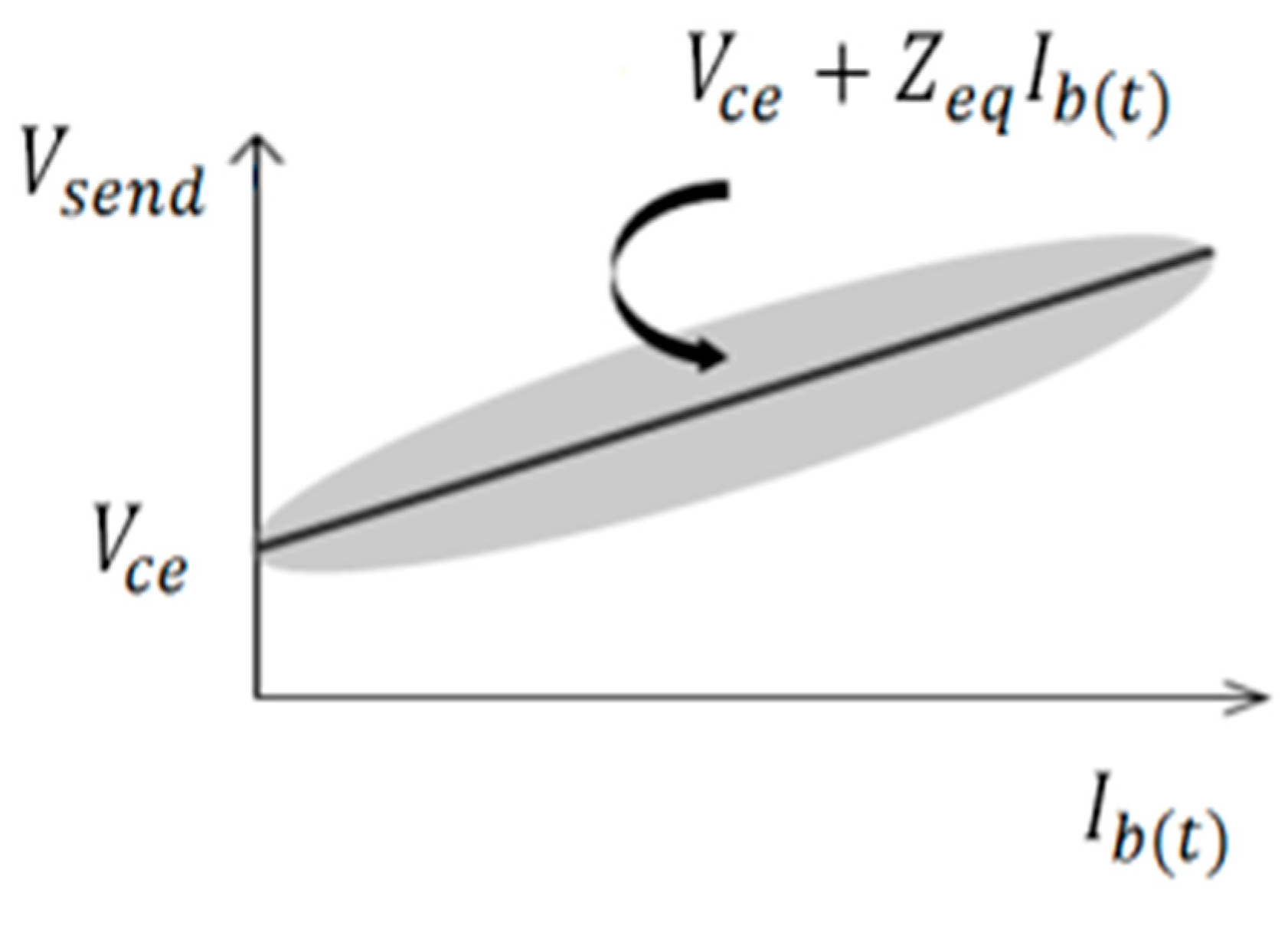
2.1. Optimal Sending Voltage via the LDC Method
2.2. Voltage Control Method for the SVR
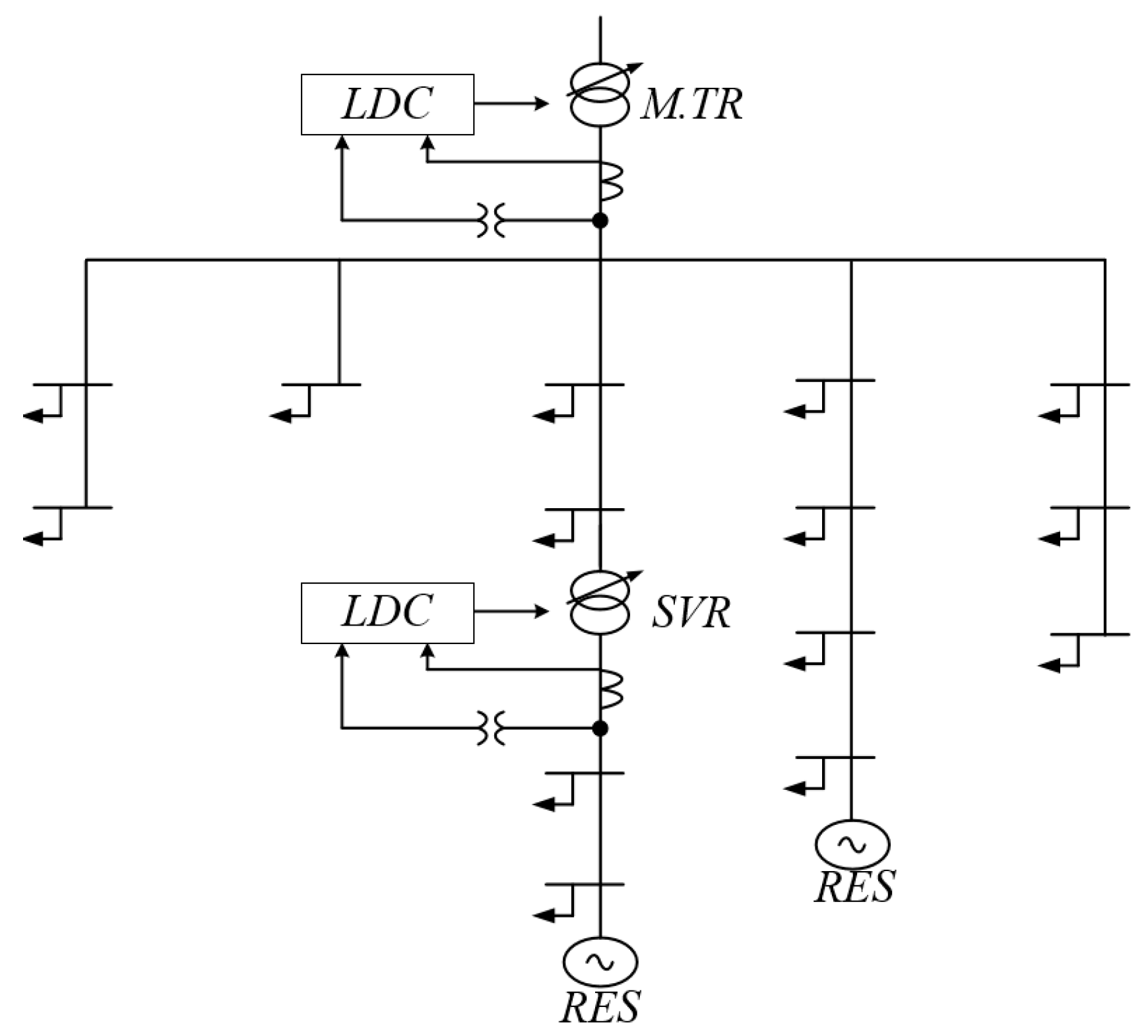
3. Voltage Control Strategy for the SVR Considering the ULTC
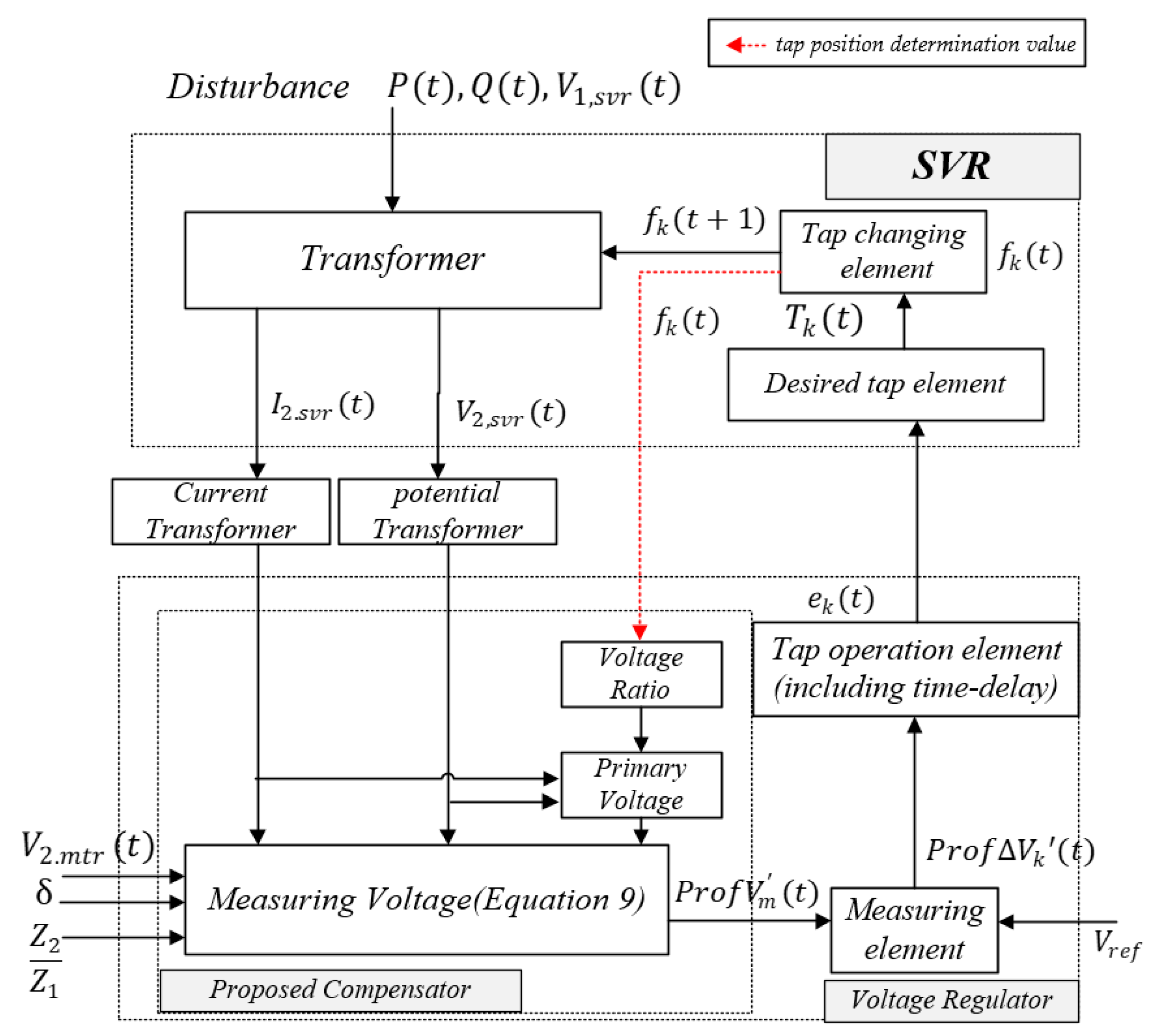
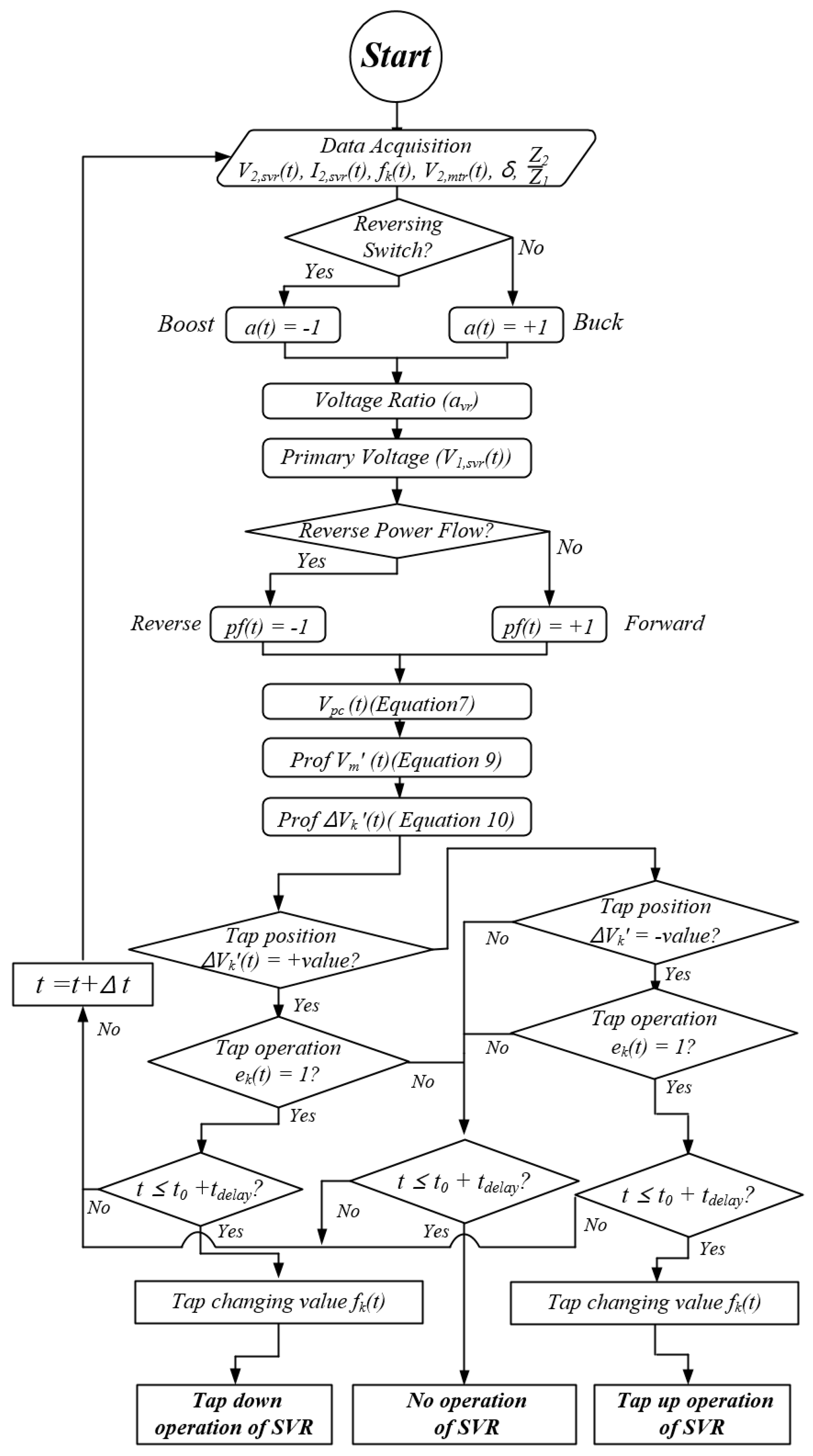
3.1. Voltage Control Method for the SVR Considering the ULTC
3.2. Tap Operation Method for the SVR
4. Case Studies
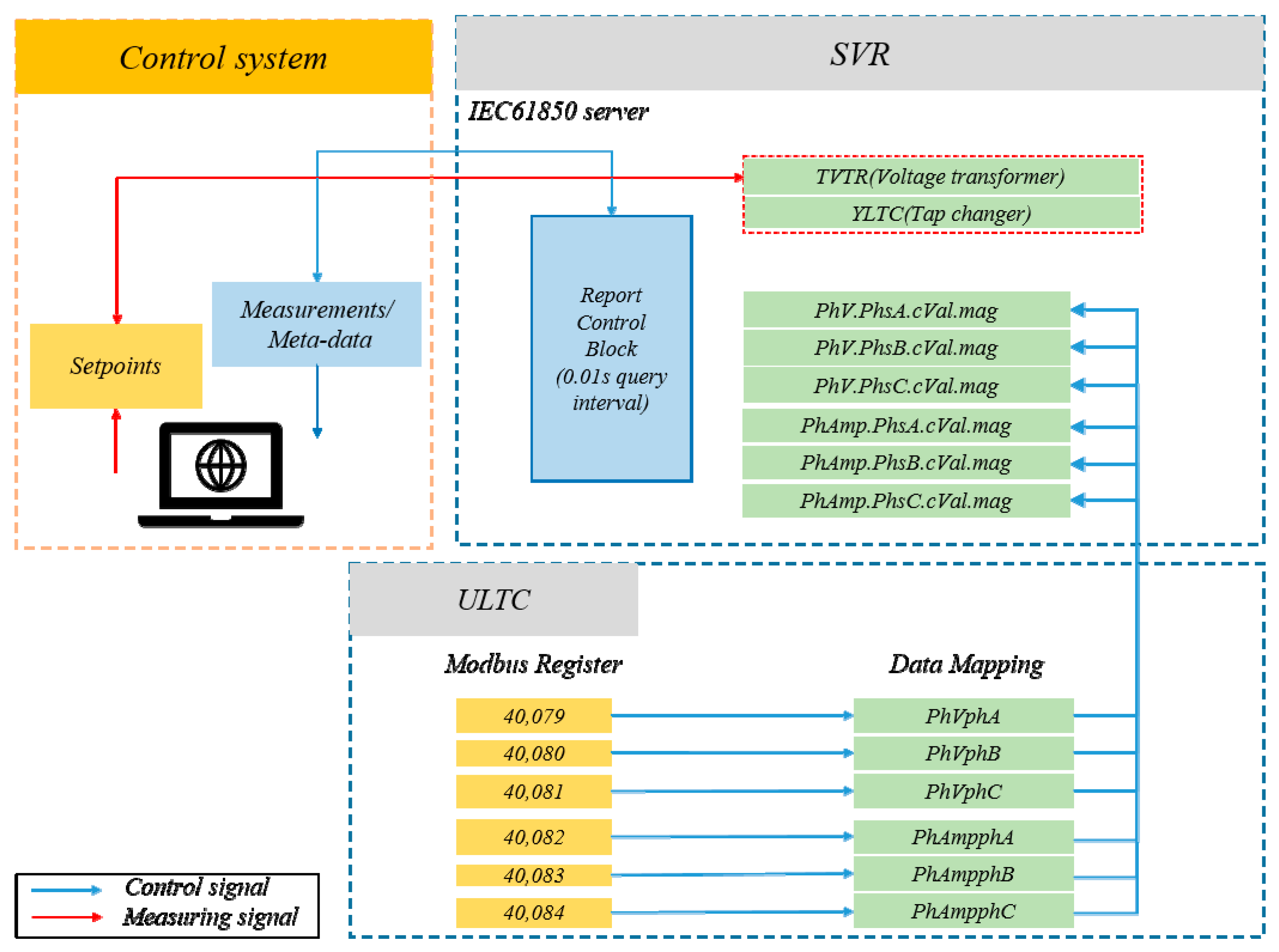
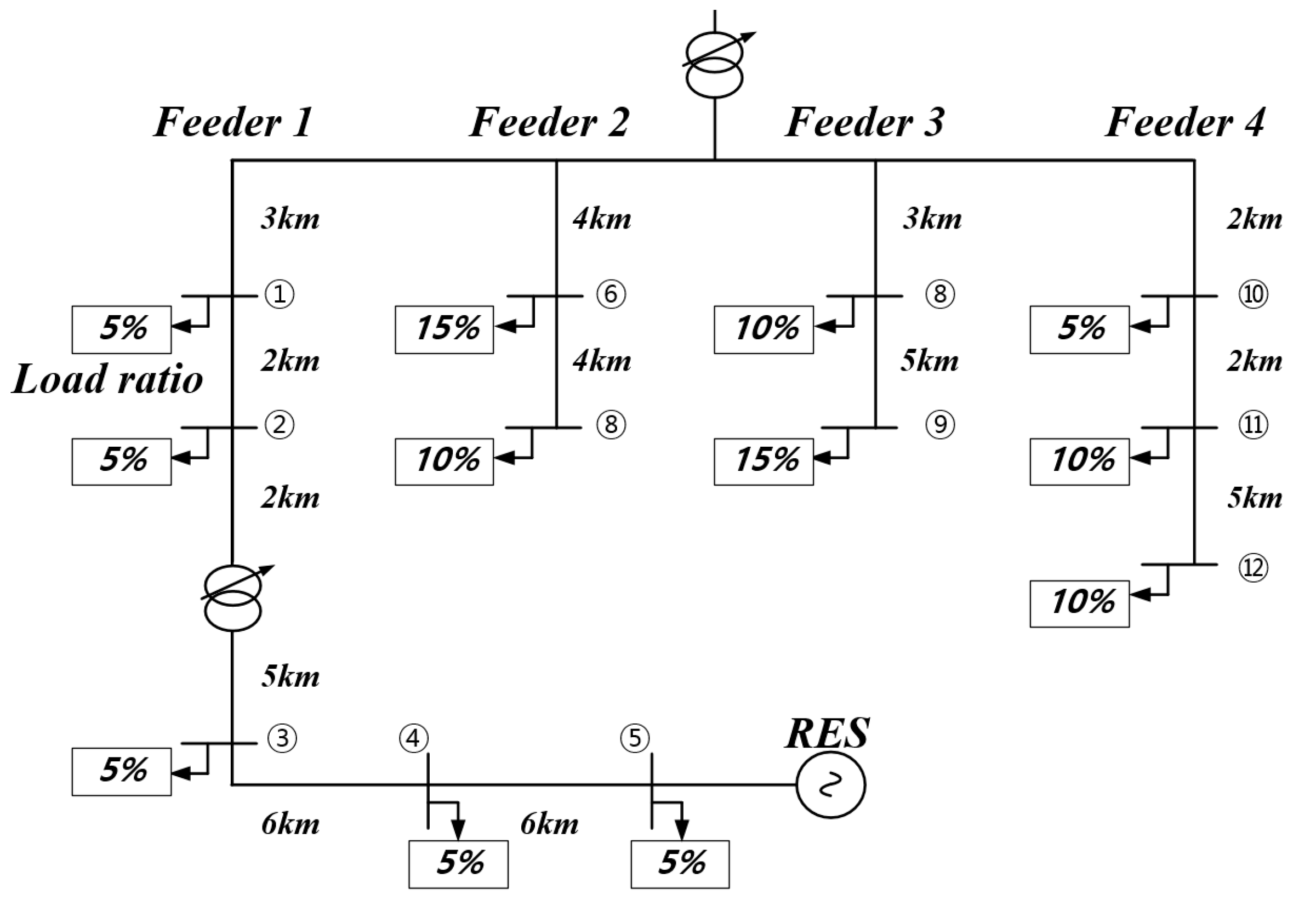
4.1. Simulation Conditions
- ①
- Case 1 (without the SVR method): Operation of the ULTC by the fixed sending (22.9 kV) voltage without the SVR.
- ②
- Case 2 (fixed (SVR) method): Operation of the ULTC by the LDC and SVR by the fixed (22.9 kV) sending voltage output voltage.
- ③
- Case 3 (LDC (SVR) method): Individual operation of the ULTC by the LDC method and SVR by the LDC method
- ④
- Case 4 (proposed (SVR) method): Coordinated operation of the SVR by the proposed control method considering operation of the ULTC by the LDC method
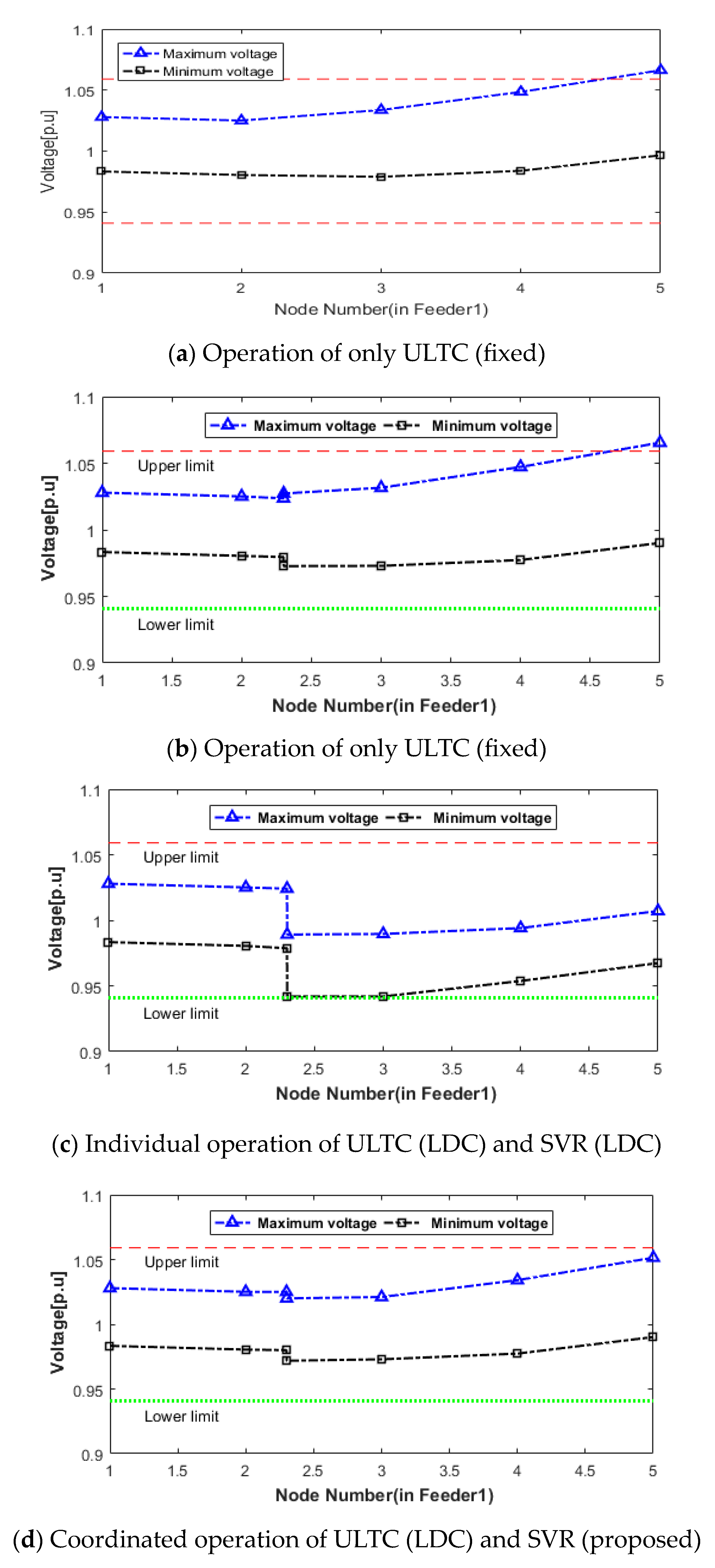
4.2. Simulation Results
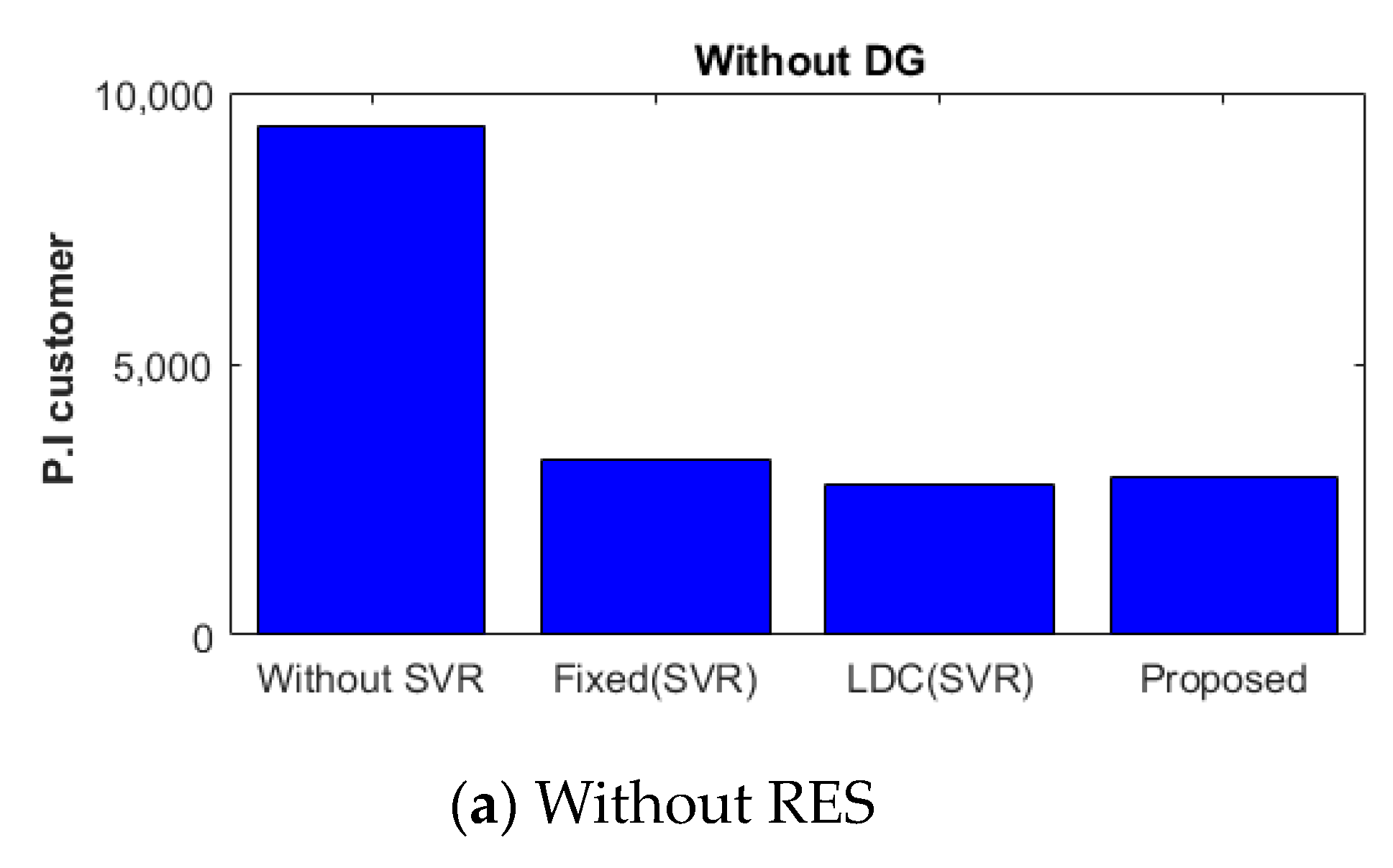
4.2.1. Voltage Characteristic without an RES
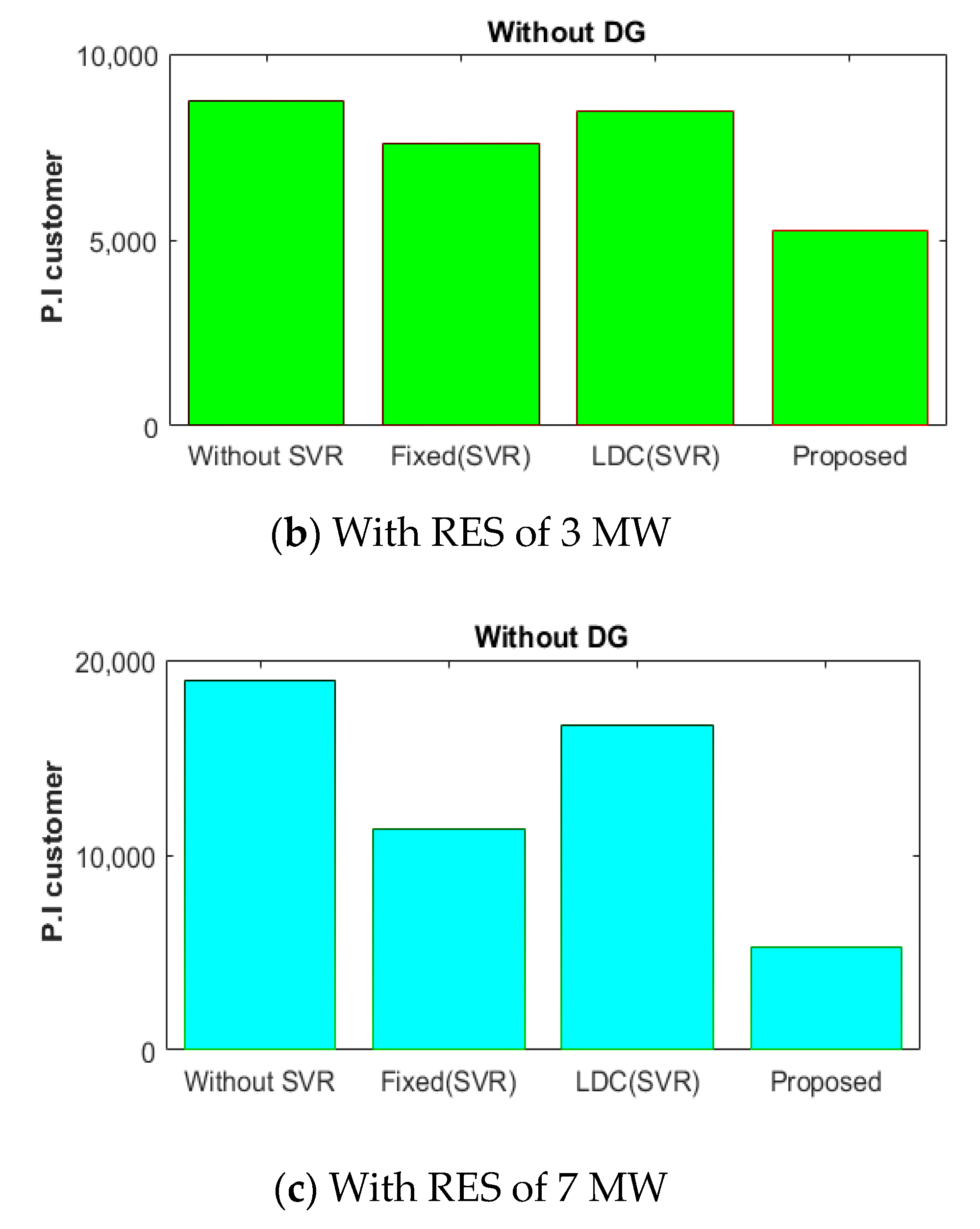
4.2.2. Voltage Characteristics with an RES of 3 MW
4.2.3. Voltage Characteristics with an RES of 7 MW
4.3. Performance Verification
5. Conclusions
- (1)
- In order to overcome the limitations of existing voltage control methods for the SVR, this paper proposes a novel voltage control method for the SVR which is adapted to the optimal compensation rate, recalculation value of the measured voltage with the characteristics of the power flow and the output voltage of the ULTC via LDC operation.
- (2)
- This paper points out the threshold of the exiting voltage control method when an RES is introduced into the distribution system and the proposed voltage control method to overcome such problems. Additionally, the performance of the proposed method is validated by comparing it with case studies of existing methods. Based on the simulation, this paper verified that the proposed voltage control method is a useful tool for operating the SVR by receiving additional voltage control characteristics of the ULTC, which is the control for the output voltage of the MTR.
- (3)
- From the simulation results of the proposed control method for the SVR by considering the control method of the ULTC, it was clear that the customer voltage could be sustained under reasonable conditions. Meanwhile, the coordinated operation between the SVR and ULTC could solve the over- and under voltage. Therefore, it is confirmed that the proposed method can make the customer voltage of the distribution feeder with the RES keep better voltage conditions.
- (4)
- Moreover, from the simulation results of the performance index, it is clear that the proposed control method can improve the voltage distribution even if the introduction of the RES is significantly increased compared to the existing methods.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nara, K.; Ishizu, S.; Mishima, Y. Voltage control availability of distributed generators in power distribution system. In Proceedings of the 2005 IEEE Russia Power Tech, St. Petersburg, Russia, 27–30 June 2005; pp. 1–6. [Google Scholar]
- Nzimako, O.; Wierckx, R. Modeling and Simulation of a Grid-Integrated Photovoltaic System Using a Real-Time Digital Simulator. IEEE Trans. Ind. Appl. 2016, 53, 1326–1336. [Google Scholar] [CrossRef]
- Khazaei, J.; Piyasinghe, L.; Miao, Z. Real-time digital simulation modeling of single-phase PV in RT-LAB. In Proceedings of the PES General Meeting|Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar]
- Caldon, R.; Coppo, M.; Turri, R. Distributed voltage control strategy for LV networks with inverter-interfaced generators. Electr. Power Syst. Res. 2014, 107, 85–92. [Google Scholar] [CrossRef]
- Meersman, B.; Renders, B.; Degroote, L.; Vandoorn, T.; Vandevelde, L. Three-phase inverter-connected DG-units and voltage unbalance. Electr. Power Syst. Res. 2011, 81, 899–906. [Google Scholar] [CrossRef]
- Einfalt, A.; Kupzog, F.; Brunner, H.; Lugmaier, A. Control strategies for smart Low voltage grids—The project DG DemoNet—Smart LV grid. In Proceedings of the Integration of Renewables into the Distribution Grid, CIRED 2012 Workshop, Lisbon, Portugal, 29–30 May 2012; pp. 1–4. [Google Scholar]
- Kechroud, A.; Ribeiro, P.F.; Kling, W.L. Distributed generation support for voltage regulation: An adaptive approach. Electr. Power Syst. Res. 2014, 107, 213–220. [Google Scholar] [CrossRef]
- Watanabe, K.; Aoki, U.H.; Sekizaki, S. Determination Method of Optimal Sending Voltage for Voltage Regulation by LRT Control in Distribution System with a Large amount of PVs. In Proceedings of the International Conference on Electrical Engineering, Denpasar, Indonesia, 1–11 July 2012; pp. 20–25. [Google Scholar]
- Lee, E.M.; Kim, M.Y.; Rho, D.S.; Sohn, S.W.; Kim, J.E.; Park, C.H. A Study on the Optimal Introduction of Step Voltage Regulator(SVR) in Distribution Feeders. Trans. KIEE 2004, 53A, 610–618. [Google Scholar]
- Kersting, W.H. Distribution Feeder Voltage Regulation Control. IEEE Trans. Ind. Appl. 2010, 46, 620–626. [Google Scholar] [CrossRef]
- Calovic, M.S. Modeling and Analysis of Under Load Tap Changing Transformer Control Systems. IEEE Trans. Power Appar. Syst. 1984, PAS-103, 1909–1915. [Google Scholar] [CrossRef]
- Choi, J.H.; Kim, J.C. Advanced Voltage Regulation Method at the Power Distribution Systems Interconneted with Dispersed Stroage and Generation Systems. IEEE Trans. Power Deliv. 2000, 15, 691–696. [Google Scholar] [CrossRef]
- Kojovic, L.A. Modern techniques to study voltage regulator-DG interactions in distribution systems. In Proceedings of the 2008 IEEE/PES Transmission and Distribution Conference and Exposition, Chicago, IL, USA, 21–24 April 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–6. [Google Scholar]
- Kojovic, L.A. Coordination of distributed generation and step voltage regulator operations for improved distribution system voltage regulation. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006. [Google Scholar]
- Sugimoto, J.; Yokoyama, R.; Fujita, G.; Fukuyama, Y. Cooperative Allocation of SVR and SVC for Voltage Fluctuation in Case of Connecting Distributed Generators. IEEJ Trans. Power Energy 2006, 126, 1191–1198. [Google Scholar] [CrossRef]
- Kim, J.-B.; Lee, M.G.; Lee, J.H.; Ryu, J.C.; Choi, T.S.; Park, M.S.; Kim, J.E. Control Method of Step Voltage Regulator on Distribution Lines with Distributed Generation. Energies 2022, 15, 9579. [Google Scholar] [CrossRef]
- MKim, Y.; Rho, D.S.; Oh, Y.T.; An, J.Y.; Kim, J.E.; Kim, E.S. A Study on the Optimal Voltage Regulation in Distribution Systems with Dispersed Generation Systems. Trans. KIEE 2005, 54A, 251–258. [Google Scholar]
- Kim, B.; Rho, D.S. Optimal voltage regulation method for distribution systems with distributed generation systems using the artificial neural networks. J. Electr. Electron. Eng. 2013, 8, 712–718. [Google Scholar] [CrossRef]






| Contents | |
|---|---|
| Characteristics of Previous Papers | Characteristics of Present Paper |
|
|
| Feeder Number | Section Number | Impedance | Length (km) | Power Factor | Load (MW) Ratio | RES, SVR Location | |
|---|---|---|---|---|---|---|---|
| R (Ω/km) | X (Ω/km) | ||||||
| 1 | 1 | 0.182 | 0.391 | 3 | 0.9 | 0.5 MVA (5%) | - |
| 1 | 2 | 0.182 | 0.391 | 2 | 0.9 | 0.5 MVA (5%) | - |
| 1 | 3 | 0.182 | 0.391 | 7 | 0.9 | 0.5 MVA (5%) | SVR |
| 1 | 4 | 0.182 | 0.391 | 6 | 0.9 | 0.5 MVA (5%) | - |
| 1 | 5 | 0.182 | 0.391 | 6 | 0.9 | 0.5 MVA (5%) | RES |
| 2 | 6 | 0.182 | 0.391 | 4 | 0.9 | 1.5 MVA (15%) | - |
| 2 | 7 | 0.182 | 0.391 | 4 | 0.9 | 1 MVA (10%) | - |
| 3 | 8 | 0.182 | 0.391 | 3 | 0.9 | 1 MVA (10%) | - |
| 3 | 9 | 0.182 | 0.391 | 5 | 0.9 | 1.5 MVA (15%) | - |
| 4 | 10 | 0.182 | 0.391 | 2 | 0.9 | 0.5 MVA (5%) | - |
| 4 | 10 | 0.182 | 0.391 | 2 | 0.9 | 1 MVA (10%) | - |
| 4 | 11 | 0.182 | 0.391 | 5 | 0.9 | 1 MVA (10%) | - |
| Classification | Contents | Value |
|---|---|---|
| Main Transformer | Bank capacity | 45/60 [MVA] |
| Nominal voltage | 22.9 [kV] | |
| % impedance of MTR | 0.0042 + j0.15 [p.u] | |
| Rated capacity | 45/60 [MVA] | |
| Number of taps | 17 taps | |
| Range of voltage control | ±10 [%] | |
| db (dead band) | 0.0125 [p.u] | |
| Equivalent impedance | 0.074 + j0.035 [p.u] | |
| Load center voltage | 0.97 [p.u] | |
| SVR | Rated capacity () | 9000 [kVA] |
| Total number of tabs | 32 taps | |
| Range of voltage control | ±10 [%] | |
| db (dead band) | 0.00625 [p.u] | |
| Equivalent impedance | 0.088 + j0.043 [p.u] | |
| Load center voltage | 0.97 [p.u] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.-o.; Kim, D.-J.; Kim, C.-S.; Kim, B. Optimal Voltage Control Method for a Step Voltage Regulator Considering the Under-Load Tap Changer in a Distribution System Interconnected with a Renewable Energy Source. Energies 2023, 16, 6039. https://doi.org/10.3390/en16166039
Lee H-o, Kim D-J, Kim C-S, Kim B. Optimal Voltage Control Method for a Step Voltage Regulator Considering the Under-Load Tap Changer in a Distribution System Interconnected with a Renewable Energy Source. Energies. 2023; 16(16):6039. https://doi.org/10.3390/en16166039
Chicago/Turabian StyleLee, Hyun-ok, Dae-Jin Kim, Chun-Sung Kim, and Byungki Kim. 2023. "Optimal Voltage Control Method for a Step Voltage Regulator Considering the Under-Load Tap Changer in a Distribution System Interconnected with a Renewable Energy Source" Energies 16, no. 16: 6039. https://doi.org/10.3390/en16166039
APA StyleLee, H.-o., Kim, D.-J., Kim, C.-S., & Kim, B. (2023). Optimal Voltage Control Method for a Step Voltage Regulator Considering the Under-Load Tap Changer in a Distribution System Interconnected with a Renewable Energy Source. Energies, 16(16), 6039. https://doi.org/10.3390/en16166039







