Energy Management of Microgrids with a Smart Charging Strategy for Electric Vehicles Using an Improved RUN Optimizer
Abstract
:1. Introduction
- The stochastic energy management of an MG is solved with implementation of a smart charging strategy for EVs.
- An improved version of the RUN optimizer based on FDB and Weibull flight distribution is proposed for solving the energy management problem.
- Energy management of the MG is solved at a deterministic level for cost reduction using the proposed optimizer; the obtained results are compared to other optimization algorithms.
- Energy management of the MG is solved by considering the uncertainties of the EVs, load and output power of the WTs.
2. Problem Formulation
2.1. Objective Function
2.2. Constraints
- (a)
- Equality Constraints
- (b)
- Inequality Constraints
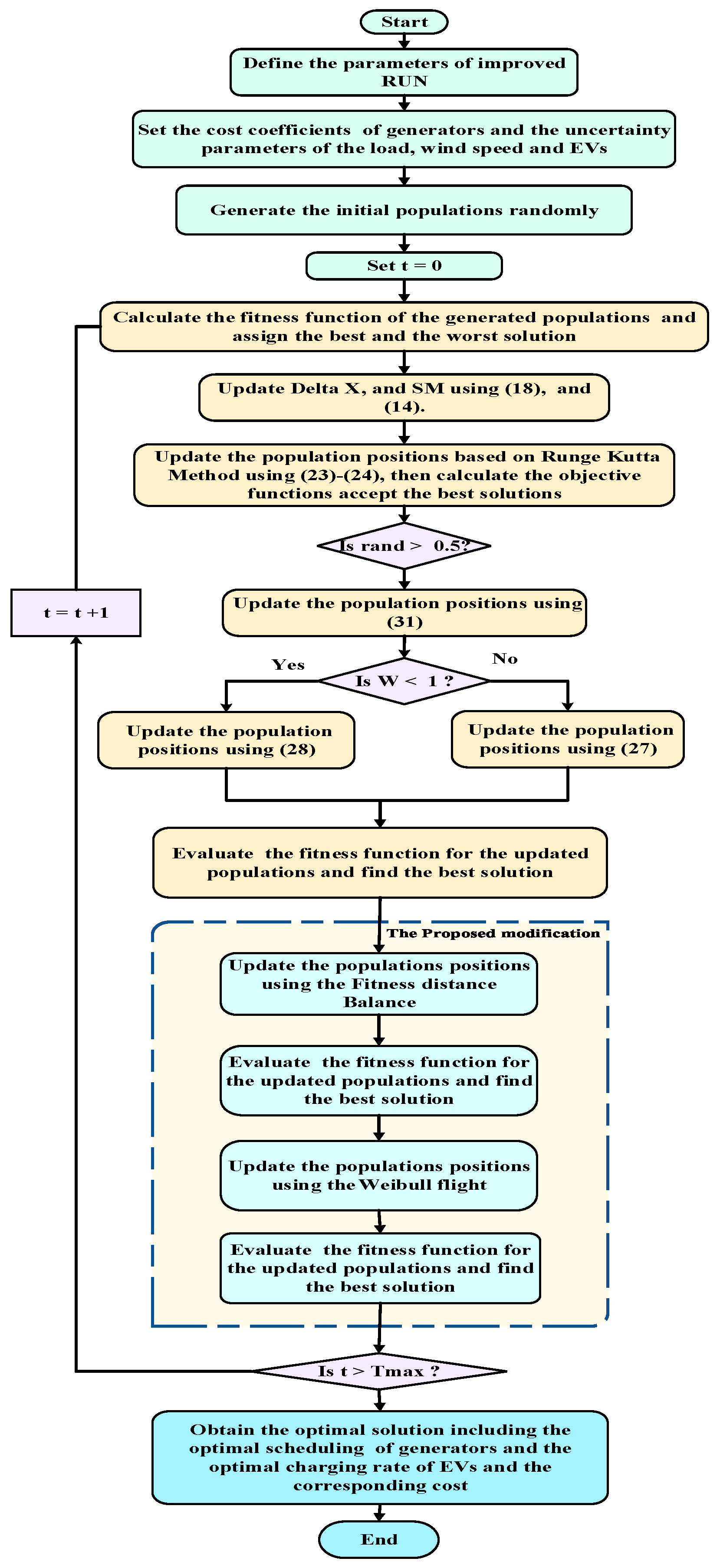
3. RUNge Kutta Optimizer (RUN)
- Step 1: Initialization
- Step 2: Root of the search mechanism
- Step 3: Updating the solution
- Step 4: EQS updating
| Algorithm 1. The pseudocode of the EQS |
| Update the value of using (29). Find the using (31). if if Update using (27). else Update using (28). end end if if Update using (32). end end |
4. The improved RUNge Kutta Optimizer (IRUN)
4.1. Weibull Flight Distribution
4.2. The Fitness–Distance Balance (FDB)
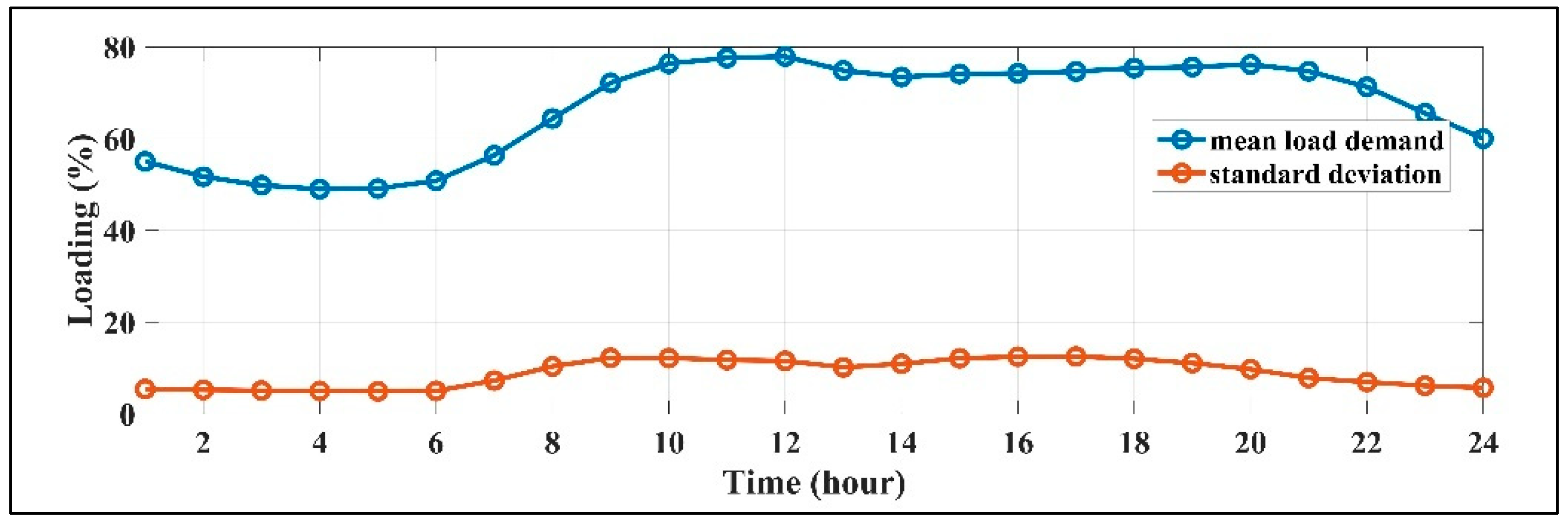
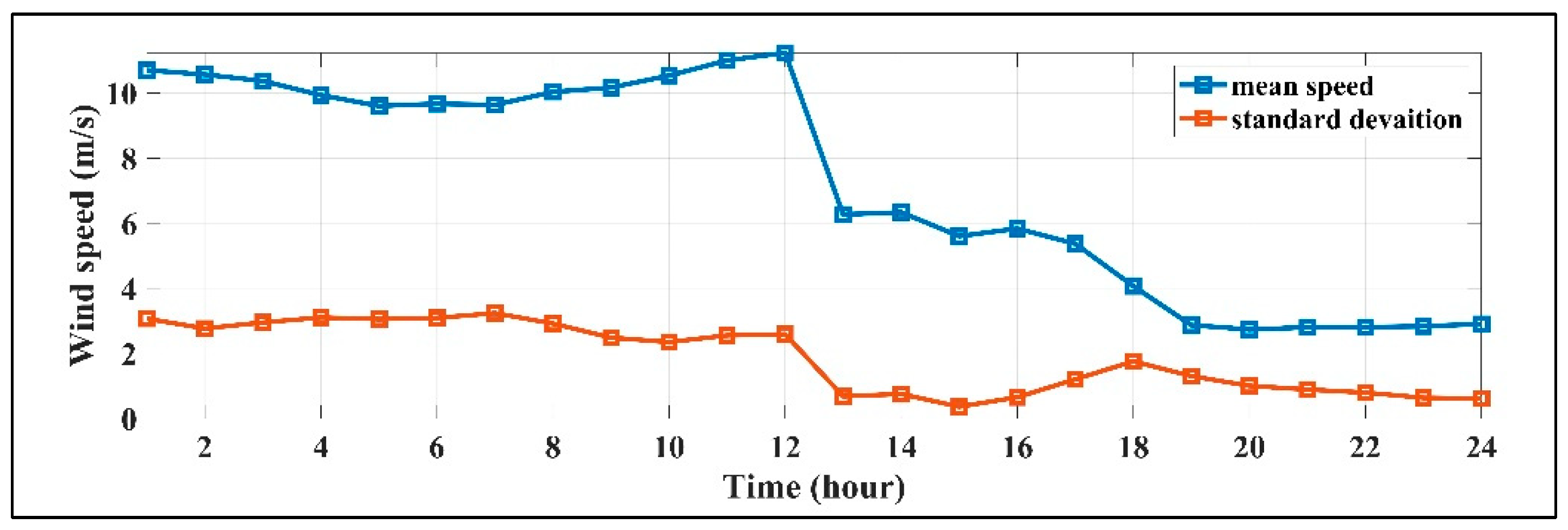
5. Uncertainty Representation
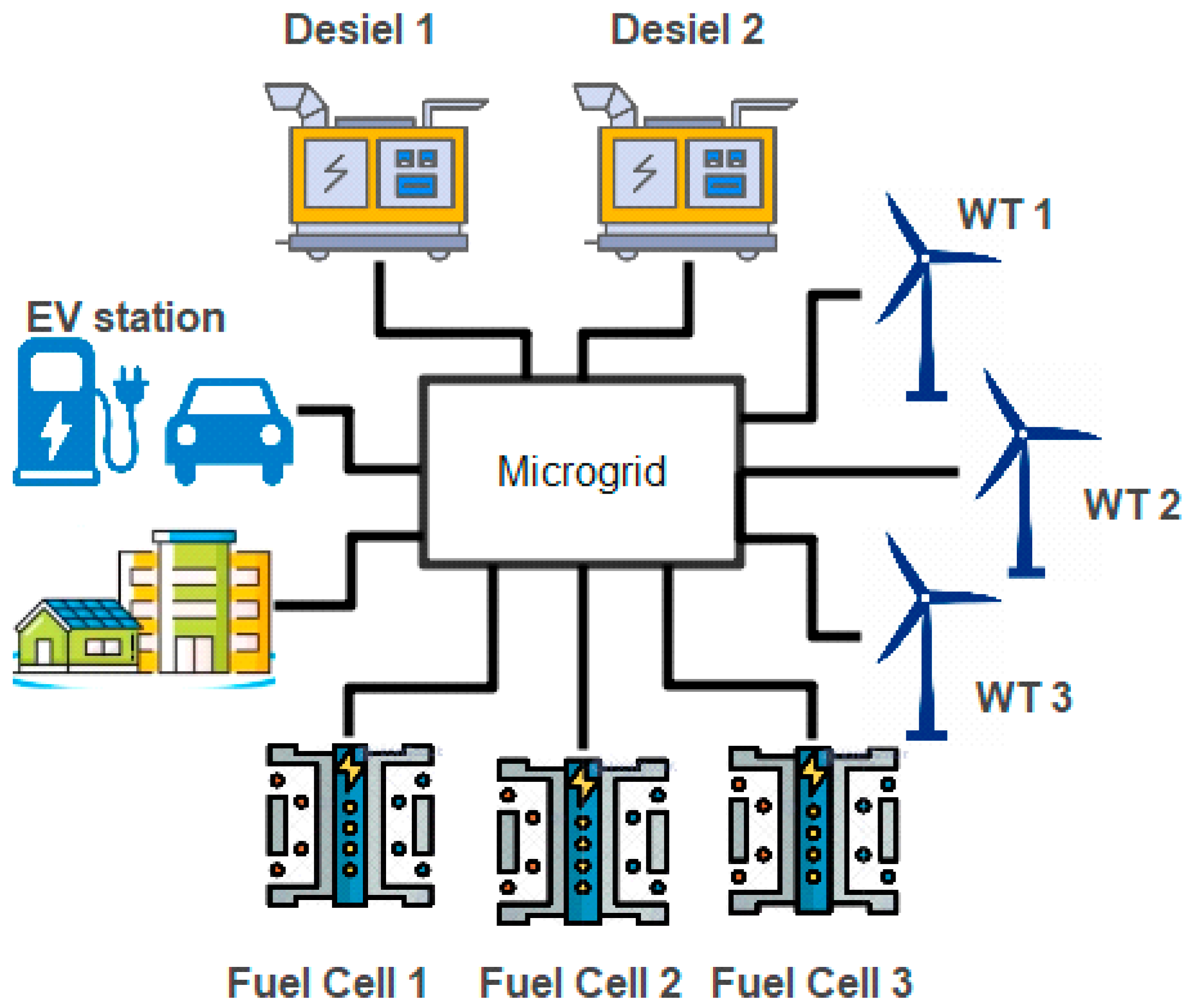
6. Simulation Results
6.1. Case 1: Solving the Energy Management in a Deterministic Condition
6.2. Case 2: Solving the Energy Management with EVs in a Stochastic Condition
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kroposki, B.; Basso, T.; DeBlasio, R. Microgrid standards and technologies. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–4. [Google Scholar]
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M. Microgrids energy management systems: A critical review on methods, solutions, and prospects. Appl. Energy 2018, 222, 1033–1055. [Google Scholar] [CrossRef]
- Monesha, S.; Kumar, S.G.; Rivera, M. Microgrid energy management and control: Technical review. In Proceedings of the 2016 IEEE International Conference on Automatica (ICA-ACCA), Curico, Chile, 19–21 October 2016; pp. 1–7. [Google Scholar]
- Xiang, Y.; Liu, J.; Liu, Y. Robust energy management of microgrid with uncertain renewable generation and load. IEEE Trans. Smart Grid 2015, 7, 1034–1043. [Google Scholar] [CrossRef]
- Ahmed, D.; Ebeed, M.; Ali, A.; Alghamdi, A.S.; Kamel, S. Multi-objective energy management of a micro-grid considering stochastic nature of load and renewable energy resources. Electronics 2021, 10, 403. [Google Scholar] [CrossRef]
- Harsh, P.; Das, D. Energy management in microgrid using incentive-based demand response and reconfigured network considering uncertainties in renewable energy sources. Sustain. Energy Technol. Assess. 2021, 46, 101225. [Google Scholar] [CrossRef]
- Manas, M. Renewable energy management through microgrid central controller design: An approach to integrate solar, wind and biomass with battery. Energy Rep. 2015, 1, 156–163. [Google Scholar]
- Tabar, V.S.; Jirdehi, M.A.; Hemmati, R. Energy management in microgrid based on the multi objective stochastic programming incorporating portable renewable energy resource as demand response option. Energy 2017, 118, 827–839. [Google Scholar] [CrossRef]
- Elsied, M.; Oukaour, A.; Gualous, H.; Hassan, R. Energy management and optimization in microgrid system based on green energy. Energy 2015, 84, 139–151. [Google Scholar] [CrossRef]
- Torkan, R.; Ilinca, A.; Ghorbanzadeh, M. A genetic algorithm optimization approach for smart energy management of microgrids. Renew. Energy 2022, 197, 852–863. [Google Scholar] [CrossRef]
- Hajiamoosha, P.; Rastgou, A.; Bahramara, S.; Sadati, S.M.B. Stochastic energy management in a renewable energy-based microgrid considering demand response program. Int. J. Electr. Power Energy Syst. 2021, 129, 106791. [Google Scholar] [CrossRef]
- Guo, S.; Li, P.; Ma, K.; Yang, B.; Yang, J. Robust energy management for industrial microgrid considering charging and discharging pressure of electric vehicles. Appl. Energy 2022, 325, 119846. [Google Scholar] [CrossRef]
- Gholami, K.; Azizivahed, A.; Arefi, A. Risk-oriented energy management strategy for electric vehicle fleets in hybrid AC-DC microgrids. J. Energy Storage 2022, 50, 104258. [Google Scholar] [CrossRef]
- Gupta, S.; Maulik, A.; Das, D.; Singh, A. Coordinated stochastic optimal energy management of grid-connected microgrids considering demand response, plug-in hybrid electric vehicles, and smart transformers. Renew. Sustain. Energy Rev. 2022, 155, 111861. [Google Scholar] [CrossRef]
- Sedighizadeh, M.; Esmaili, M.; Mohammadkhani, N. Stochastic multi-objective energy management in residential microgrids with combined cooling, heating, and power units considering battery energy storage systems and plug-in hybrid electric vehicles. J. Clean. Prod. 2018, 195, 301–317. [Google Scholar] [CrossRef]
- Abd El-Sattar, H.; Kamel, S.; Hassan, M.H.; Jurado, F. Optimal sizing of an off-grid hybrid photovoltaic/biomass gasifier/battery system using a quantum model of Runge Kutta algorithm. Energy Convers. Manag. 2022, 258, 115539. [Google Scholar] [CrossRef]
- Chen, H.; Ahmadianfar, I.; Liang, G.; Bakhsizadeh, H.; Azad, B.; Chu, X. A successful candidate strategy with Runge-Kutta optimization for multi-hydropower reservoir optimization. Expert Syst. Appl. 2022, 209, 118383. [Google Scholar] [CrossRef]
- Shaban, H.; Houssein, E.H.; Pérez-Cisneros, M.; Oliva, D.; Hassan, A.Y.; Ismaeel, A.A.; AbdElminaam, D.S.; Deb, S.; Said, M. Identification of parameters in photovoltaic models through a runge kutta optimizer. Mathematics 2021, 9, 2313. [Google Scholar] [CrossRef]
- Yousri, D.; Mudhsh, M.; Shaker, Y.O.; Abualigah, L.; Tag-Eldin, E.; Abd Elaziz, M.; Allam, D. Modified interactive algorithm based on Runge Kutta optimizer for photovoltaic modeling: Justification under partial shading and varied temperature conditions. IEEE Access 2022, 10, 20793–20815. [Google Scholar] [CrossRef]
- Jean-Jacques, K.; Roland, A.; Billan, C.; Sharma, P. A Review on Neutrino Oscillation Probabilities and Sterile Neutrinos. Emerg. Sci. J. 2022, 6, 418–428. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, G. A comparative study of fractional-order models for lithium-ion batteries using Runge Kutta optimizer and electrochemical impedance spectroscopy. Control Eng. Pract. 2023, 133, 105451. [Google Scholar] [CrossRef]
- Izci, D.; Ekinci, S.; Mirjalili, S. Optimal PID plus second-order derivative controller design for AVR system using a modified Runge Kutta optimizer and Bode’s ideal reference model. Int. J. Dyn. Control 2022, 11, 1–18. [Google Scholar] [CrossRef]
- Houssein, E.H.; Hassan, H.N.; Samee, N.A.; Jamjoom, M.M. A Novel Hybrid Runge Kutta Optimizer with Support Vector Machine on Gene Expression Data for Cancer Classification. Diagnostics 2023, 13, 1621. [Google Scholar] [CrossRef] [PubMed]
- Suneja, S.; Tiwari, G. Optimization of number of effects for higher yield from an inverted absorber solar still using the Runge-Kutta method. Desalination 1998, 120, 197–209. [Google Scholar] [CrossRef]
- Jana, B.; Mitra, S.; Acharyya, S. Repository and mutation based particle swarm optimization (RMPSO): A new PSO variant applied to reconstruction of gene regulatory network. Appl. Soft Comput. 2019, 74, 330–355. [Google Scholar] [CrossRef]
- Cui, L.; Li, G.; Zhu, Z.; Lin, Q.; Wong, K.-C.; Chen, J.; Lu, N.; Lu, J. Adaptive multiple-elites-guided composite differential evolution algorithm with a shift mechanism. Inf. Sci. 2018, 422, 122–143. [Google Scholar] [CrossRef]
- Kahraman, H.T.; Aras, S.; Gedikli, E. Fitness-distance balance (FDB): A new selection method for meta-heuristic search algorithms. Knowl.-Based Syst. 2020, 190, 105169. [Google Scholar] [CrossRef]
- Aras, S.; Gedikli, E.; Kahraman, H.T. A novel stochastic fractal search algorithm with fitness-distance balance for global numerical optimization. Swarm Evol. Comput. 2021, 61, 100821. [Google Scholar] [CrossRef]
- Guvenc, U.; Duman, S.; Kahraman, H.T.; Aras, S.; Katı, M. Fitness–Distance Balance based adaptive guided differential evolution algorithm for security-constrained optimal power flow problem incorporating renewable energy sources. Appl. Soft Comput. 2021, 108, 107421. [Google Scholar] [CrossRef]
- Sharifi, M.R.; Akbarifard, S.; Qaderi, K.; Madadi, M.R. Developing MSA algorithm by new fitness-distance-balance selection method to optimize cascade hydropower reservoirs operation. Water Resour. Manag. 2021, 35, 385–406. [Google Scholar] [CrossRef]
- Zheng, K.; Yuan, X.; Xu, Q.; Dong, L.; Yan, B.; Chen, K. Hybrid particle swarm optimizer with fitness-distance balance and individual self-exploitation strategies for numerical optimization problems. Inf. Sci. 2022, 608, 424–452. [Google Scholar] [CrossRef]
- Tang, Z.; Tao, S.; Wang, K.; Lu, B.; Todo, Y.; Gao, S. Chaotic Wind Driven Optimization with Fitness Distance Balance Strategy. Int. J. Comput. Intell. Syst. 2022, 15, 46. [Google Scholar] [CrossRef]
- Tabak, A.; Duman, S. Levy Flight and Fitness Distance Balance-Based Coyote Optimization Algorithm for Effective Automatic Generation Control of PV-Based Multi-Area Power Systems. Arab. J. Sci. Eng. 2022, 47, 1–32. [Google Scholar] [CrossRef]
- Cengiz, E.; Yilmaz, C.; Kahraman, H.; Suiçmez, Ç. Improved Runge Kutta optimizer with fitness distance balance-based guiding mechanism for global optimization of high-dimensional problems. Düzce Üniversitesi Bilim Ve Teknol. Derg. 2021, 9, 135–149. [Google Scholar] [CrossRef]
- Dursun, M. Fitness distance balance-based Runge–Kutta algorithm for indirect rotor field-oriented vector control of three-phase induction motor. Neural Comput. Appl. 2023, 35, 13685–13707. [Google Scholar] [CrossRef]
- Bastawy, M.; Ebeed, M.; Ali, A.; Shaaban, M.F.; Khan, B.; Kamel, S. Optimal day-ahead scheduling in micro-grid with renewable based DGs and smart charging station of EVs using an enhanced manta-ray foraging optimisation. IET Renew. Power Gener. 2022, 16, 2413–2428. [Google Scholar] [CrossRef]
- Basu, M.a.; Chowdhury, A. Cuckoo search algorithm for economic dispatch. Energy 2013, 60, 99–108. [Google Scholar] [CrossRef]
- Bastawy, M.; Ebeed, M.; Rashad, A.; Alghamdi, A.S.; Kamel, S. Micro-grid dynamic economic dispatch with renewable energy resources using equilibrium optimizer. In Proceedings of the 2020 IEEE Electric Power and Energy Conference (EPEC), Edmonton, AB, Canada, 9–10 November 2020; pp. 1–5. [Google Scholar]
- Kutta, W. Beitrag zur naherungsweisen integration totaler differentialgleichungen. Z. Math. Phys. 1901, 46, 435–453. [Google Scholar]
- Runge, C. Über die numerische Auflösung von Differentialgleichungen. Math. Ann. 1895, 46, 167–178. [Google Scholar] [CrossRef]
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951. Available online: https://hal.science/hal-03112318/document (accessed on 14 June 2023). [CrossRef]
- Contreras-Reyes, J.E. Fisher information and uncertainty principle for skew-gaussian random variables. Fluct. Noise Lett. 2021, 20, 2150039. [Google Scholar] [CrossRef]
- Atwa, Y.; El-Saadany, E.; Salama, M.; Seethapathy, R. Optimal renewable resources mix for distribution system energy loss minimization. IEEE Trans. Power Syst. 2009, 25, 360–370. [Google Scholar] [CrossRef]
- Ebeed, M.; Aleem, S.H.A. Overview of uncertainties in modern power systems: Uncertainty models and methods. In Uncertainties in Modern Power Systems; Elsevier: Amsterdam, The Netherlands, 2020; pp. 1–34. [Google Scholar]
- Khatod, D.K.; Pant, V.; Sharma, J. Evolutionary programming based optimal placement of renewable distributed generators. IEEE Trans. Power Syst. 2012, 28, 683–695. [Google Scholar] [CrossRef]
- Mooney, C.Z. Monte Carlo Simulation; Sage: London, UK, 1997. [Google Scholar]
- Growe-Kuska, N.; Heitsch, H.; Romisch, W. Scenario reduction and scenario tree construction for power management problems. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; Volume 3, p. 7. [Google Scholar]
- Biswas, P.P.; Suganthan, P.N.; Mallipeddi, R.; Amaratunga, G.A. Optimal reactive power dispatch with uncertainties in load demand and renewable energy sources adopting scenario-based approach. Appl. Soft Comput. 2019, 75, 616–632. [Google Scholar] [CrossRef]
- Ali, A.; Raisz, D.; Mahmoud, K.; Lehtonen, M. Optimal placement and sizing of uncertain PVs considering stochastic nature of PEVs. IEEE Trans. Sustain. Energy 2019, 11, 1647–1656. [Google Scholar] [CrossRef]
- Dhiman, G. MOSHEPO: A hybrid multi-objective approach to solve economic load dispatch and micro grid problems. Appl. Intell. 2020, 50, 119–137. [Google Scholar] [CrossRef]
- Sadati, S.M.B.; Moshtagh, J.; Shafie-Khah, M.; Rastgou, A.; Catalão, J.P. Optimal charge scheduling of electric vehicles in solar energy integrated power systems considering the uncertainties. In Electric Vehicles in Energy Systems: Modelling, Integration, Analysis, and Optimization; Springer: Cham, Swizerlands, 2020; pp. 73–128. [Google Scholar]
- Qian, K.; Zhou, C.; Allan, M.; Yuan, Y. Modeling of load demand due to EV battery charging in distribution systems. IEEE Trans. Power Syst. 2010, 26, 802–810. [Google Scholar] [CrossRef]

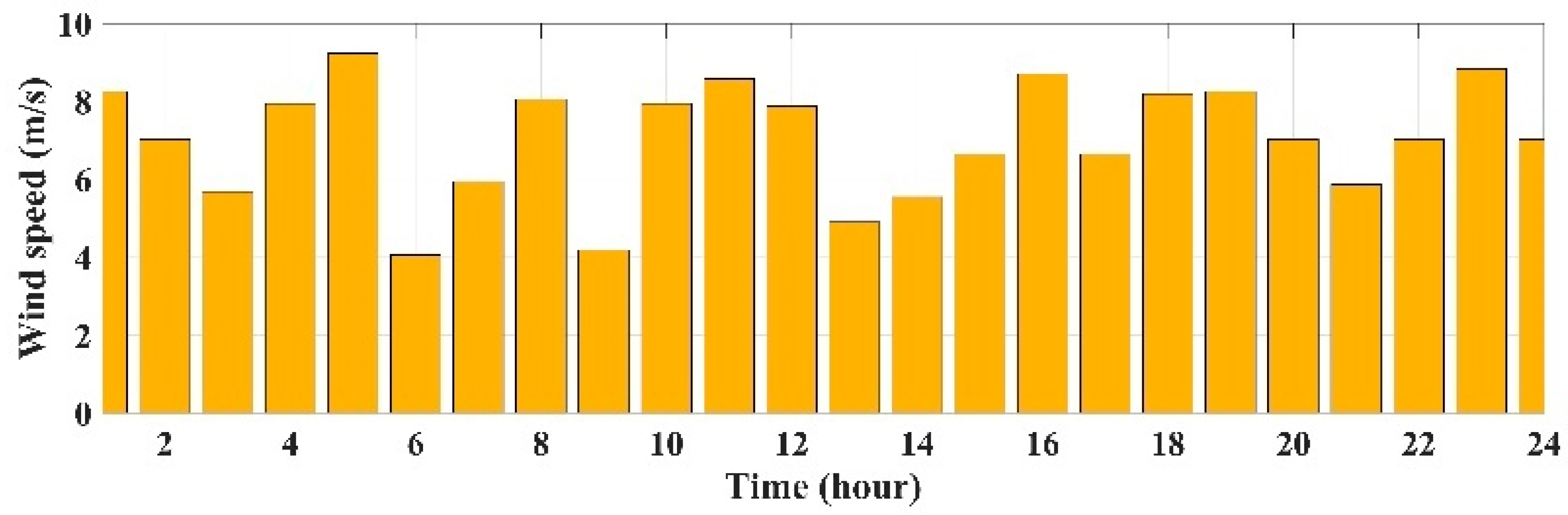
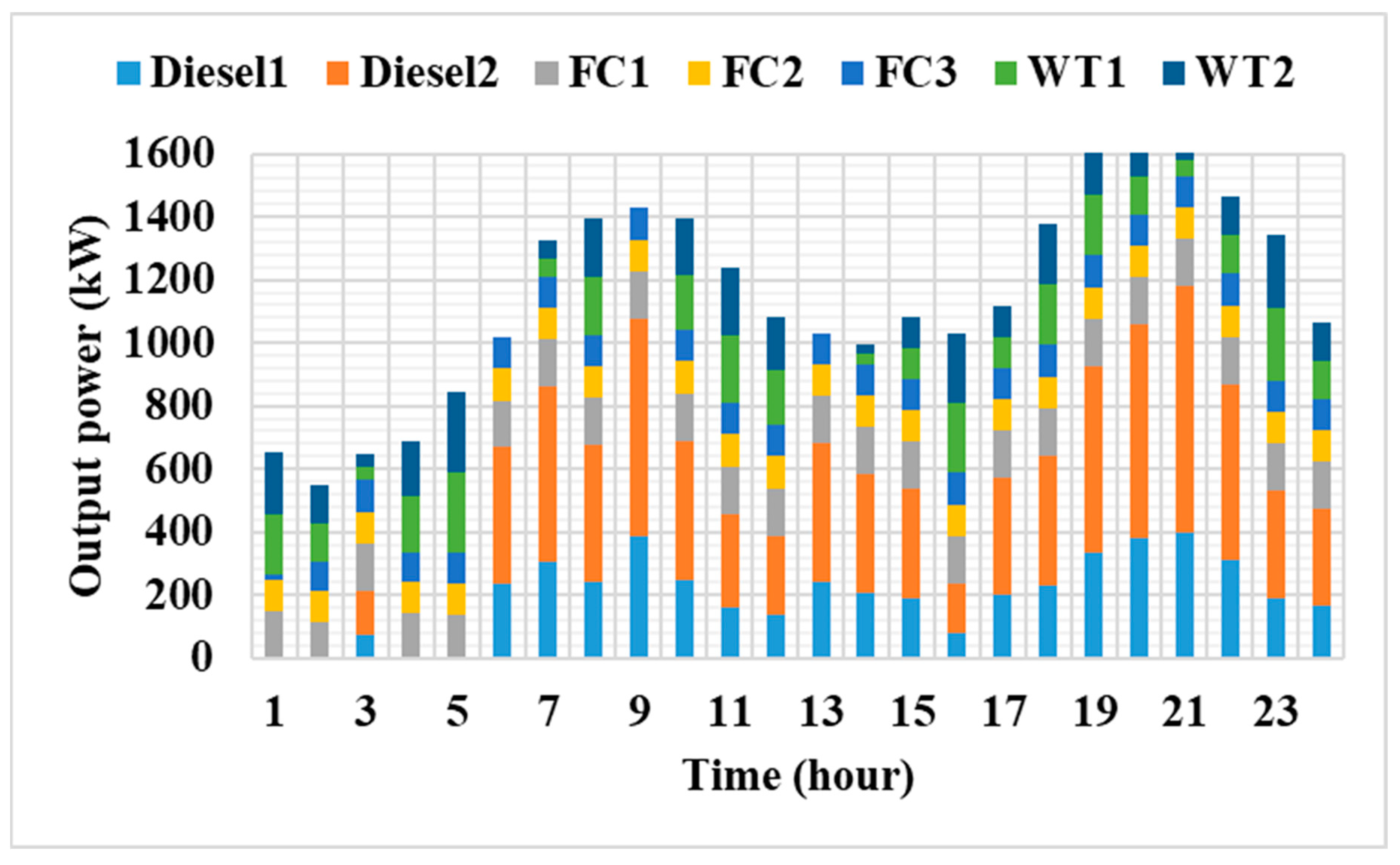
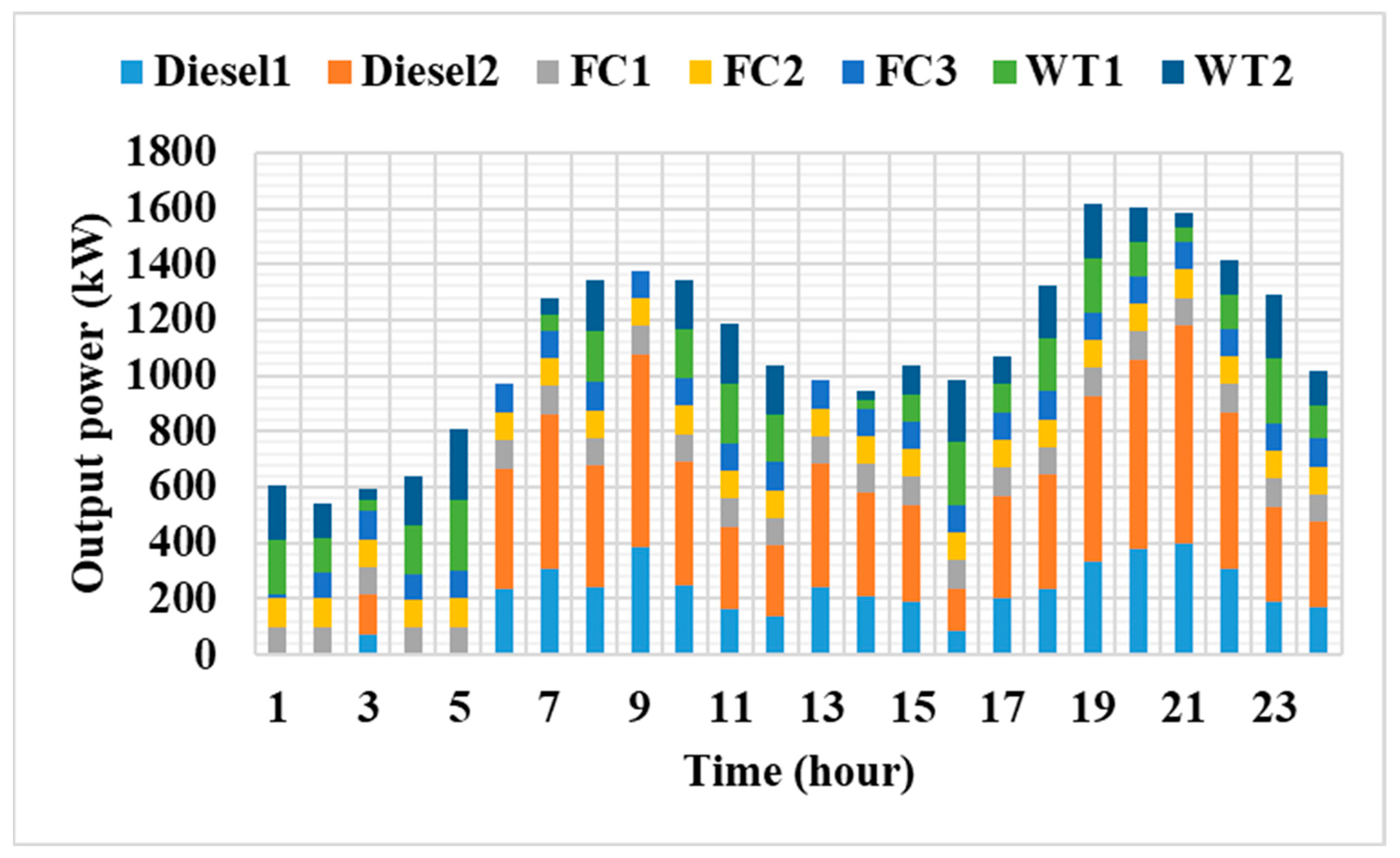





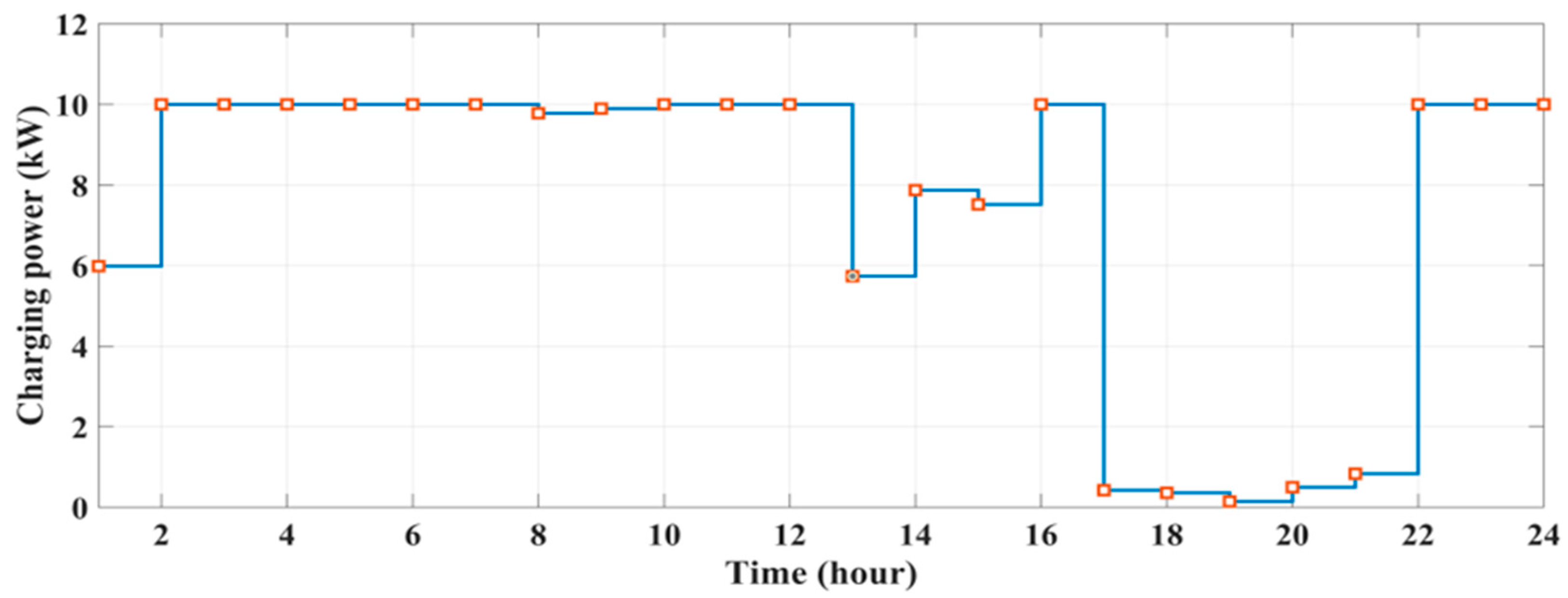

| Generation Type | a (USD/(kWh)2) | b (USD/kWh) | c (USD/h) | (kW) | (kW) | (%) | |||
|---|---|---|---|---|---|---|---|---|---|
| Diesel 1 | 0.0074 | 0.2333 | 0.4333 | 0 | 400 | - | - | - | - |
| Diesel 2 | 0.0042 | 0.1453 | 0.2731 | 0 | 800 | - | - | - | - |
| FC 1 | 0 | 0.05 | 0 | 0 | 150 | - | 90 | ||
| FC 2 | 0 | 0.05 | 0 | 0 | 100 | - | - | - | 90 |
| FC 3 | 0 | 0.07 | 0 | 0 | 100 | - | - | - | 85 |
| WT1 | 0 | 0.022 | 0 | 0 | 300 | 5 | 15 | 10 | - |
| WT2 | 0 | 0.032 | 0 | 0 | 300 | 5 | 15 | 10 | - |
| Algorithm | Improved RUN | RUN | EO [38] | CSA [37] | DE [37] | MOSHEPO [50] |
|---|---|---|---|---|---|---|
| Cost (USD) | 29,893.7746 | 30,779.9573 | 33,100 | 33,824.10 | 33,930.94 | 33,804.53 |
| The reduction of cost v.s. Improved RUN | - | 2.879% | 9.687% | 11.619% | 11.898% | 11.569% |
| Time | Diesel 1 | Diesel 2 | FC 1 | FC 2 | FC 3 | WT 1 | WT 2 | Load | EV Loading |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.00 | 0.06 | 133.94 | 98.76 | 95.78 | 300.00 | 300.00 | 918.54 | 10.00 |
| 2 | 0.07 | 0.00 | 149.99 | 42.21 | 100.00 | 300.00 | 300.00 | 862.27 | 30.00 |
| 3 | 0.10 | 0.00 | 95.68 | 100.00 | 100.00 | 300.00 | 300.00 | 829.84 | 65.94 |
| 4 | 0.06 | 1.22 | 150.00 | 99.99 | 100.00 | 283.54 | 283.54 | 813.42 | 104.93 |
| 5 | 37.58 | 78.14 | 150.00 | 100.00 | 100.00 | 264.36 | 264.36 | 825.26 | 169.17 |
| 6 | 42.97 | 88.98 | 150.00 | 100.00 | 100.00 | 288.67 | 288.67 | 836.88 | 222.41 |
| 7 | 137.52 | 254.20 | 150.00 | 100.00 | 100.00 | 261.36 | 261.36 | 964.94 | 299.50 |
| 8 | 213.75 | 383.18 | 150.00 | 100.00 | 100.00 | 262.55 | 262.55 | 1110.03 | 362.00 |
| 9 | 217.92 | 392.53 | 150.00 | 100.00 | 100.00 | 300.00 | 300.00 | 1213.37 | 347.08 |
| 10 | 196.16 | 360.11 | 150.00 | 100.00 | 100.00 | 300.00 | 300.00 | 1296.35 | 209.93 |
| 11 | 202.09 | 365.88 | 150.00 | 100.00 | 100.00 | 300.00 | 300.00 | 1286.07 | 231.90 |
| 12 | 219.02 | 394.62 | 150.00 | 100.00 | 100.00 | 300.00 | 300.00 | 1307.51 | 256.13 |
| 13 | 354.81 | 634.77 | 150.00 | 100.00 | 100.00 | 70.41 | 70.41 | 1250.52 | 229.88 |
| 14 | 326.14 | 583.71 | 150.00 | 100.00 | 100.00 | 69.98 | 69.98 | 1267.27 | 132.55 |
| 15 | 318.35 | 574.13 | 150.00 | 100.00 | 100.00 | 47.78 | 47.78 | 1236.92 | 101.13 |
| 16 | 287.80 | 518.79 | 150.00 | 100.00 | 100.00 | 41.25 | 41.25 | 1193.02 | 46.06 |
| 17 | 327.87 | 589.26 | 150.00 | 100.00 | 100.00 | 21.89 | 21.89 | 1264.30 | 46.61 |
| 18 | 342.79 | 614.08 | 150.00 | 100.00 | 100.00 | 0.00 | 0.00 | 1268.74 | 38.13 |
| 19 | 335.99 | 601.84 | 150.00 | 100.00 | 100.00 | 0.00 | 0.00 | 1265.47 | 22.37 |
| 20 | 329.77 | 594.85 | 150.00 | 100.00 | 100.00 | 0.00 | 0.00 | 1272.37 | 2.24 |
| 21 | 320.82 | 573.72 | 150.00 | 100.00 | 100.00 | 0.00 | 0.00 | 1244.54 | 0.00 |
| 22 | 301.19 | 542.47 | 150.00 | 100.00 | 100.00 | 0.00 | 0.00 | 1193.66 | 0.00 |
| 23 | 266.34 | 481.23 | 150.00 | 100.00 | 100.00 | 0.00 | 0.00 | 1097.56 | 0.00 |
| 24 | 230.15 | 412.44 | 150.00 | 100.00 | 100.00 | 0.00 | 0.00 | 992.60 | 0.00 |
| Time | Diesel 1 | Diesel 2 | FC 1 | FC 2 | FC 3 | WT 1 | WT 2 | Load | EV Loading |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 4.09 | 10.26 | 110.23 | 99.96 | 99.99 | 300.00 | 300.00 | 918.54 | 5.98 |
| 2 | 1.00 | 3.61 | 129.40 | 65.81 | 99.67 | 300.00 | 300.00 | 862.27 | 30.00 |
| 3 | 4.32 | 2.83 | 119.71 | 72.96 | 99.97 | 300.00 | 300.00 | 829.84 | 69.95 |
| 4 | 3.31 | 0.15 | 149.08 | 100.00 | 98.73 | 283.54 | 283.54 | 813.42 | 104.93 |
| 5 | 44.20 | 71.53 | 150.00 | 100.00 | 100.00 | 264.36 | 264.36 | 825.26 | 169.18 |
| 6 | 48.17 | 83.87 | 149.98 | 99.96 | 99.97 | 288.67 | 288.67 | 836.88 | 222.41 |
| 7 | 141.56 | 250.28 | 149.89 | 99.98 | 99.99 | 261.36 | 261.36 | 964.94 | 299.49 |
| 8 | 204.34 | 384.97 | 150.00 | 100.00 | 100.00 | 262.55 | 262.55 | 1110.03 | 354.38 |
| 9 | 217.61 | 393.21 | 150.00 | 100.00 | 100.00 | 300.00 | 300.00 | 1213.37 | 347.44 |
| 10 | 205.77 | 356.00 | 149.97 | 100.00 | 100.00 | 300.00 | 300.00 | 1296.35 | 215.39 |
| 11 | 216.36 | 352.95 | 149.84 | 100.00 | 100.00 | 300.00 | 300.00 | 1286.07 | 233.08 |
| 12 | 230.87 | 383.41 | 150.00 | 100.00 | 99.90 | 300.00 | 300.00 | 1307.51 | 256.66 |
| 13 | 322.24 | 587.36 | 150.00 | 100.00 | 100.00 | 70.41 | 70.41 | 1250.52 | 149.89 |
| 14 | 333.89 | 581.74 | 150.00 | 100.00 | 100.00 | 69.98 | 69.98 | 1267.27 | 138.32 |
| 15 | 316.79 | 581.80 | 150.00 | 100.00 | 100.00 | 47.78 | 47.78 | 1236.92 | 107.23 |
| 16 | 310.13 | 552.55 | 149.99 | 100.00 | 100.00 | 41.25 | 41.25 | 1193.02 | 102.13 |
| 17 | 316.29 | 556.85 | 150.00 | 100.00 | 100.00 | 21.89 | 21.89 | 1264.30 | 2.62 |
| 18 | 329.68 | 591.25 | 150.00 | 100.00 | 100.00 | 0.00 | 0.00 | 1268.74 | 2.18 |
| 19 | 323.31 | 593.03 | 150.00 | 100.00 | 99.99 | 0.00 | 0.00 | 1265.47 | 0.86 |
| 20 | 327.96 | 597.43 | 149.99 | 100.00 | 100.00 | 0.00 | 0.00 | 1272.37 | 3.01 |
| 21 | 327.59 | 571.94 | 150.00 | 100.00 | 100.00 | 0.00 | 0.00 | 1244.54 | 5.00 |
| 22 | 317.26 | 574.74 | 150.00 | 100.00 | 99.98 | 0.00 | 0.00 | 1193.66 | 48.32 |
| 23 | 291.11 | 494.81 | 150.00 | 99.99 | 100.00 | 0.00 | 0.00 | 1097.56 | 38.35 |
| 24 | 238.78 | 424.13 | 149.99 | 100.00 | 100.00 | 0.00 | 0.00 | 992.60 | 20.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meteab, W.K.; Alsultani, S.A.H.; Jurado, F. Energy Management of Microgrids with a Smart Charging Strategy for Electric Vehicles Using an Improved RUN Optimizer. Energies 2023, 16, 6038. https://doi.org/10.3390/en16166038
Meteab WK, Alsultani SAH, Jurado F. Energy Management of Microgrids with a Smart Charging Strategy for Electric Vehicles Using an Improved RUN Optimizer. Energies. 2023; 16(16):6038. https://doi.org/10.3390/en16166038
Chicago/Turabian StyleMeteab, Wisam Kareem, Salwan Ali Habeeb Alsultani, and Francisco Jurado. 2023. "Energy Management of Microgrids with a Smart Charging Strategy for Electric Vehicles Using an Improved RUN Optimizer" Energies 16, no. 16: 6038. https://doi.org/10.3390/en16166038
APA StyleMeteab, W. K., Alsultani, S. A. H., & Jurado, F. (2023). Energy Management of Microgrids with a Smart Charging Strategy for Electric Vehicles Using an Improved RUN Optimizer. Energies, 16(16), 6038. https://doi.org/10.3390/en16166038







