Validation of Actuator Line Modeling and Large Eddy Simulations of Kite-Borne Tidal Stream Turbines against ADCP Observations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Model
2.1.1. Large Eddy Simulations (LES)
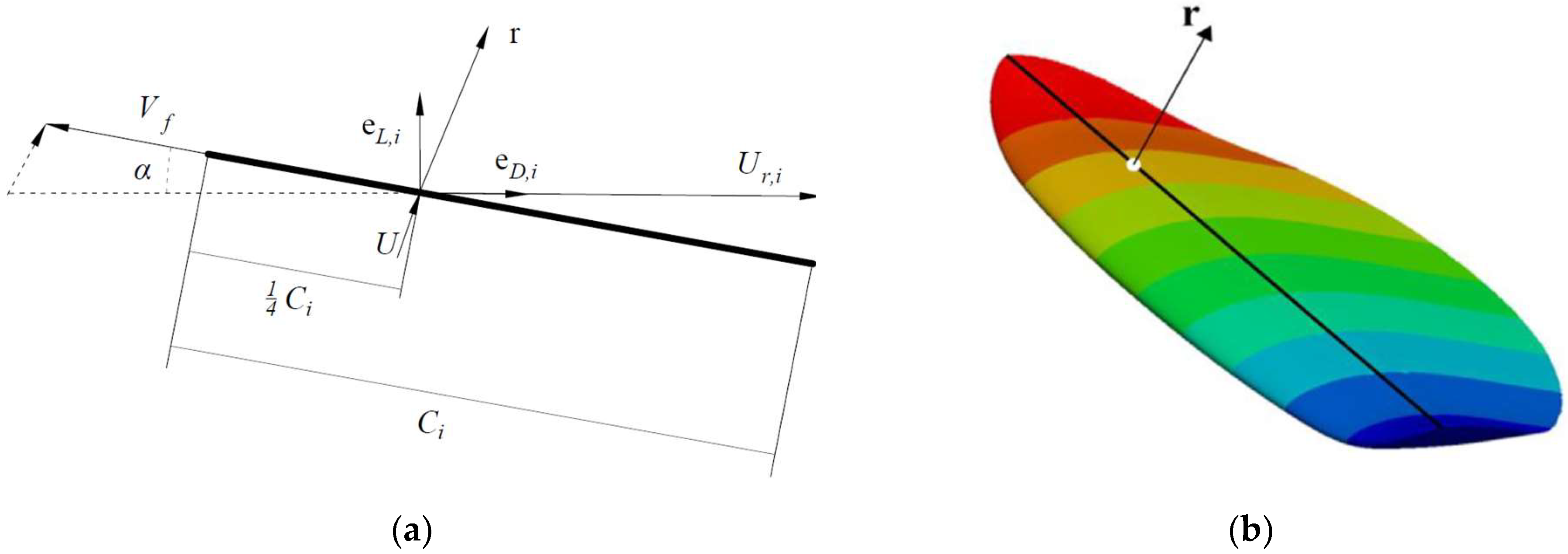
2.1.2. Actuator Line Method (ALM)
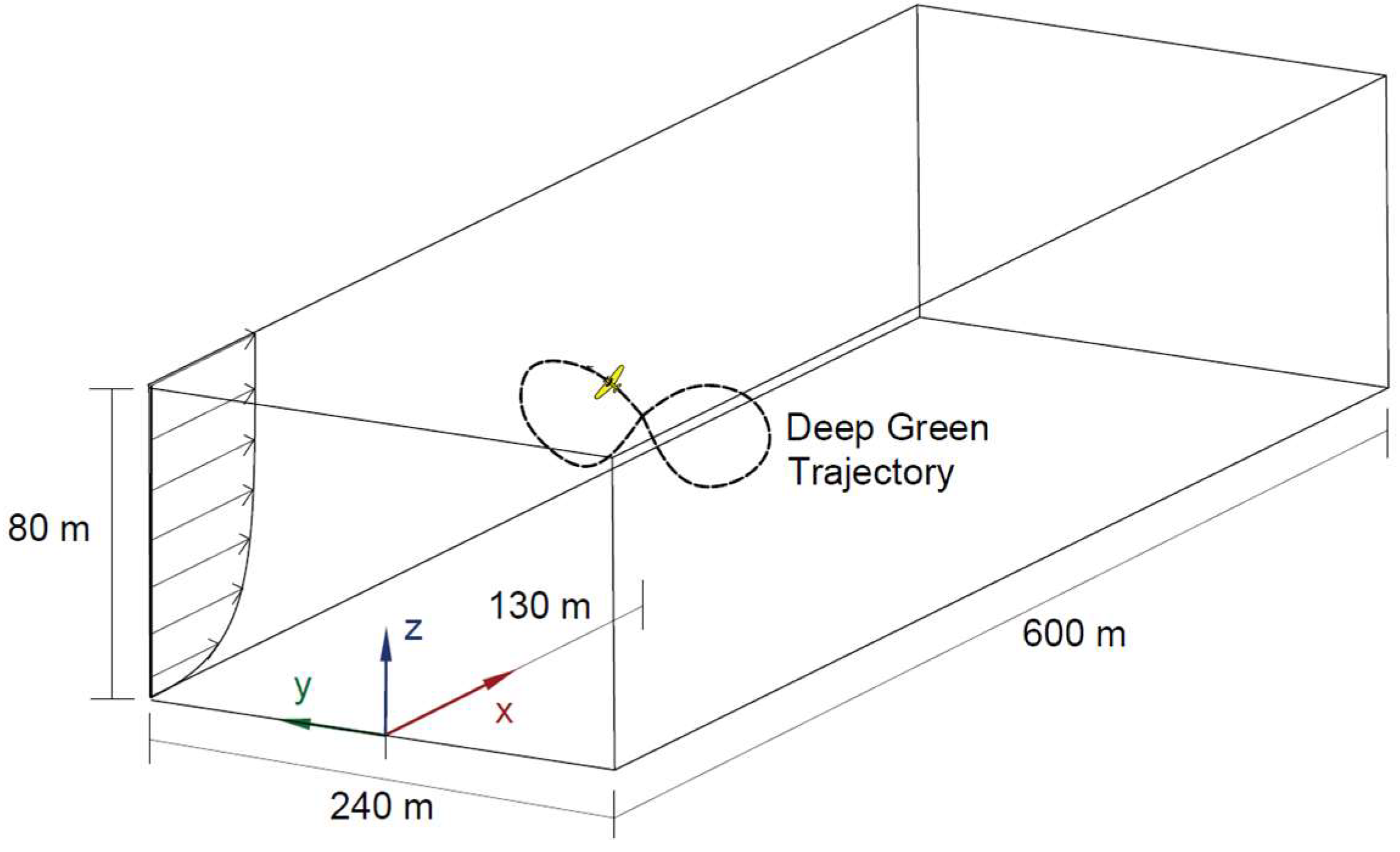
2.1.3. Computational Setup
2.2. ADCP Observations
2.3. Virtual ADCP
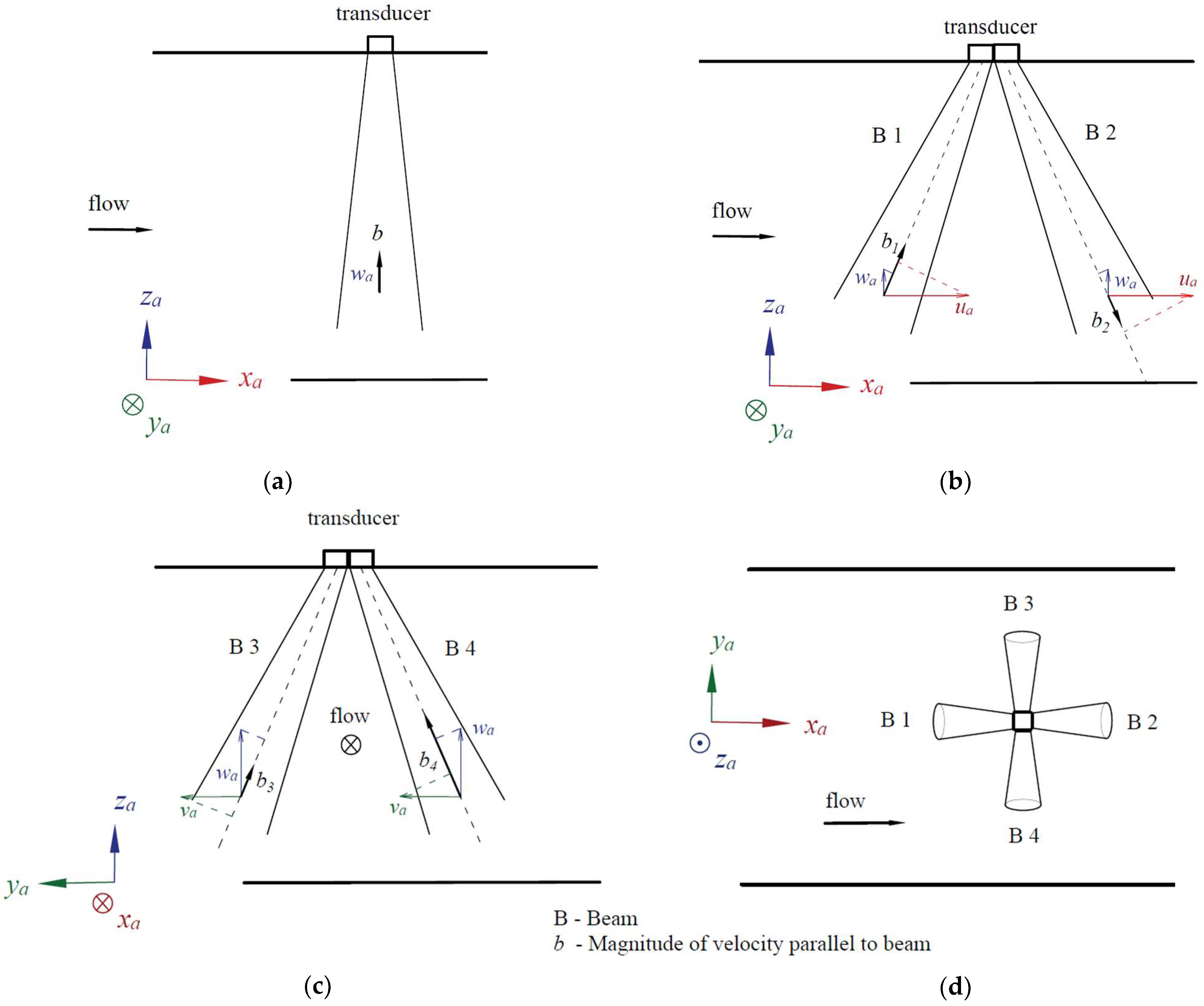
2.3.1. Physical ADCP Working Principles
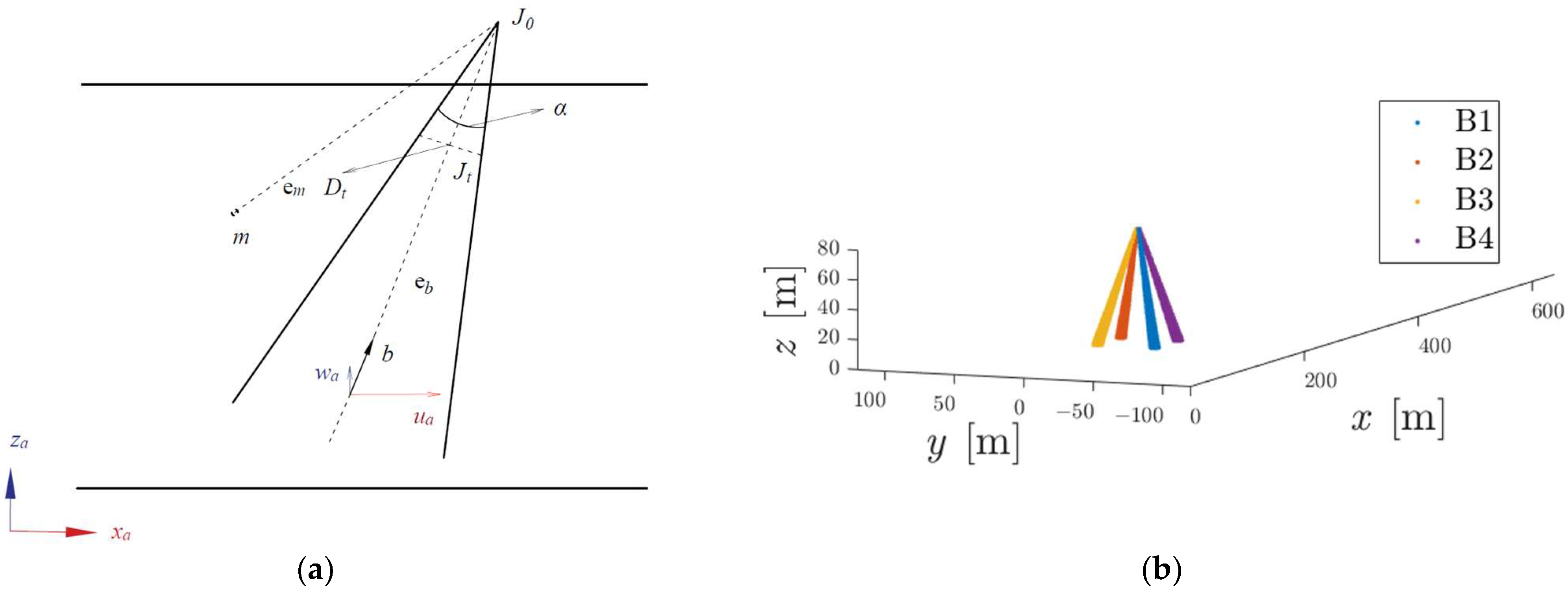
2.3.2. Modeling the Virtual ADCP
2.3.3. Sensitivity Study of the Virtual ADCP
2.4. Turbulence Intensity
3. Results
3.1. Numerical Model
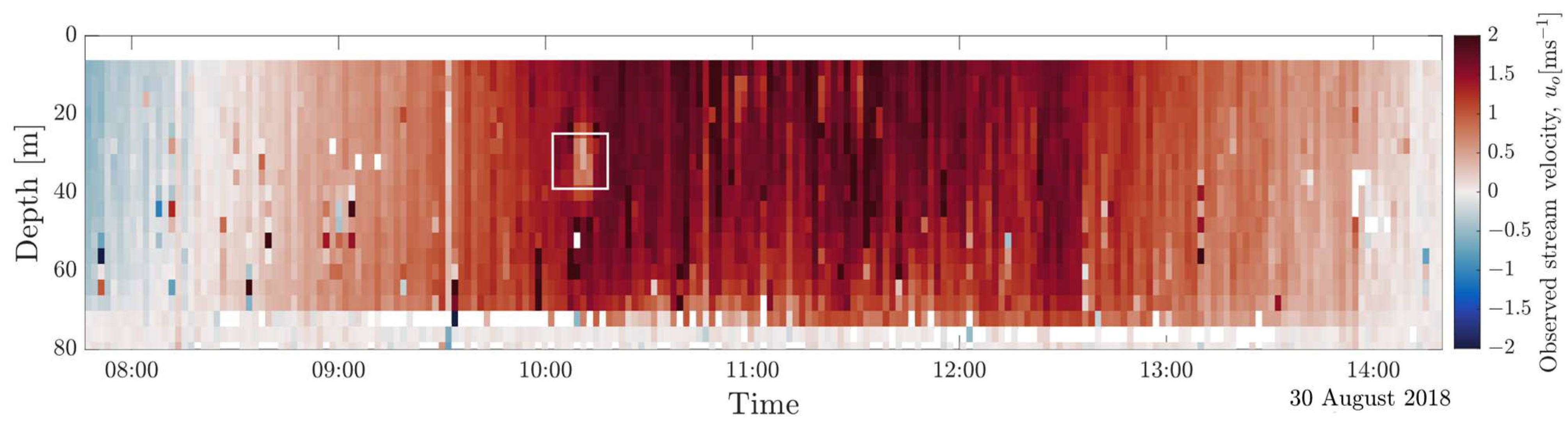
3.2. ADCP Observations
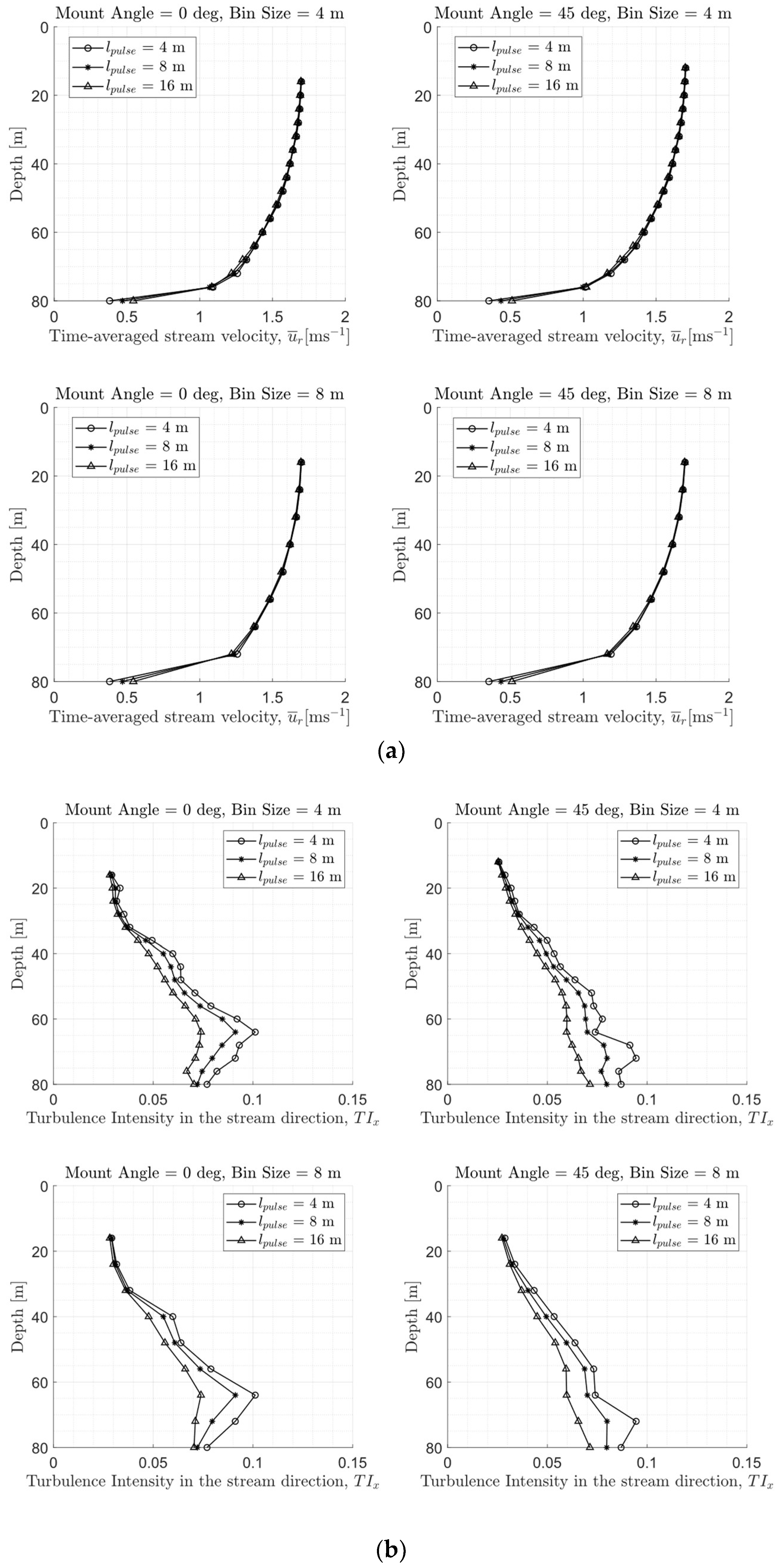
3.3. Sensitivity Study of the vADCP
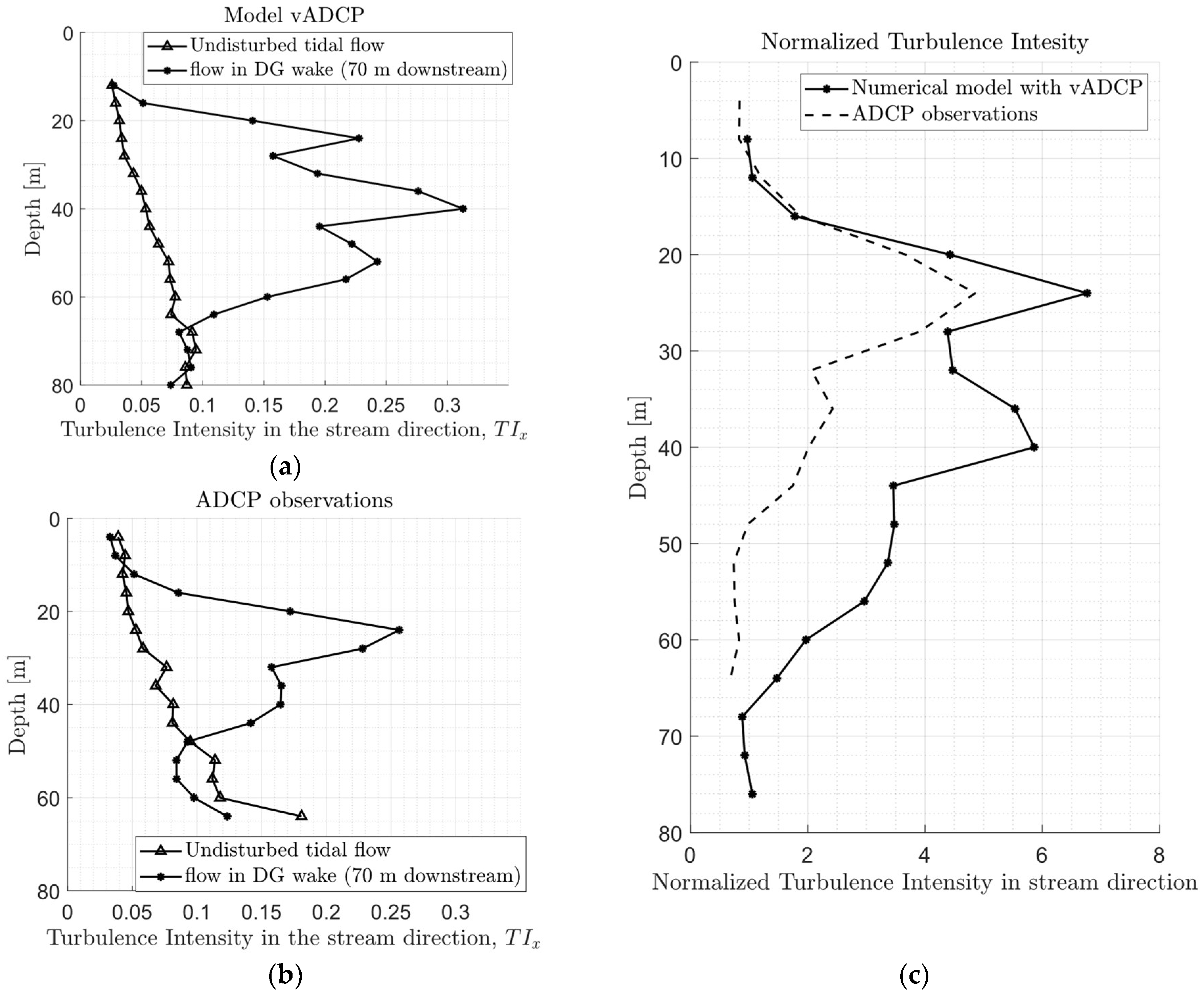
3.4. Comparision of Model Results with Observations
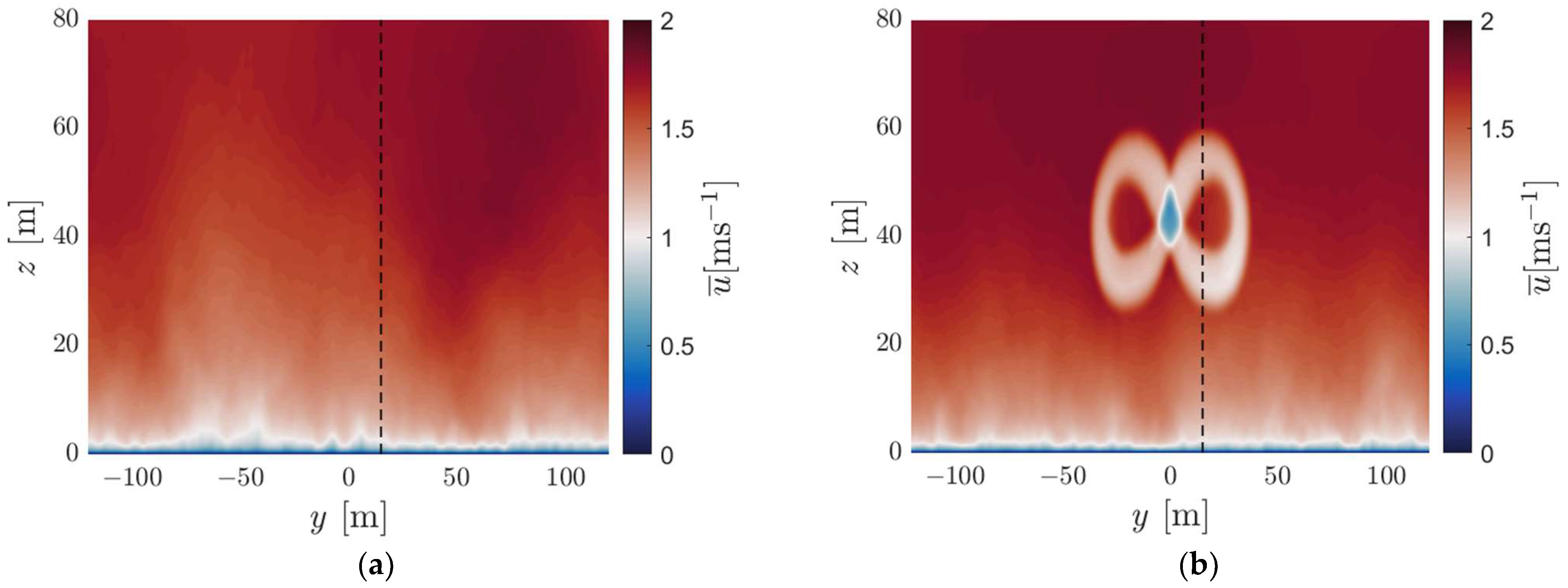
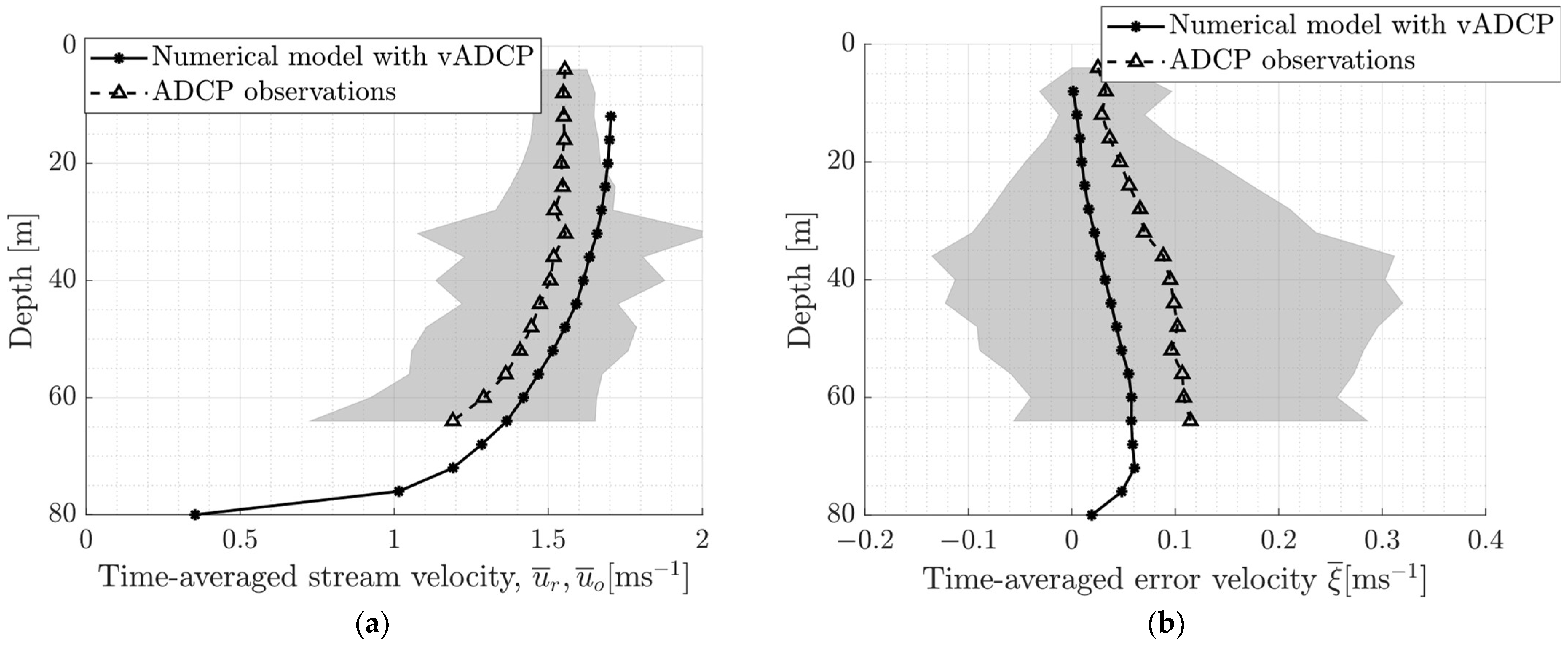
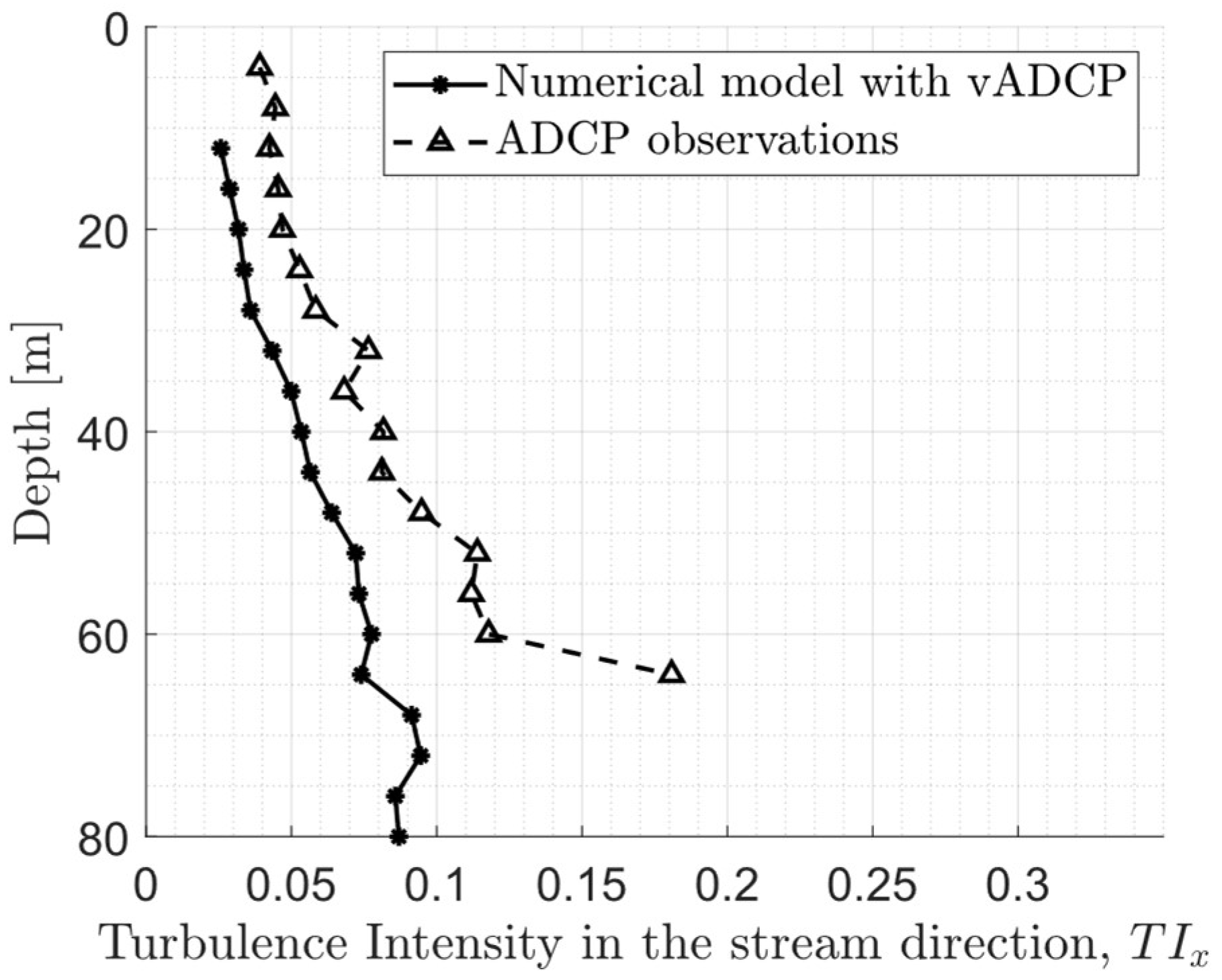
3.4.1. Undisturbed Tidal Flow
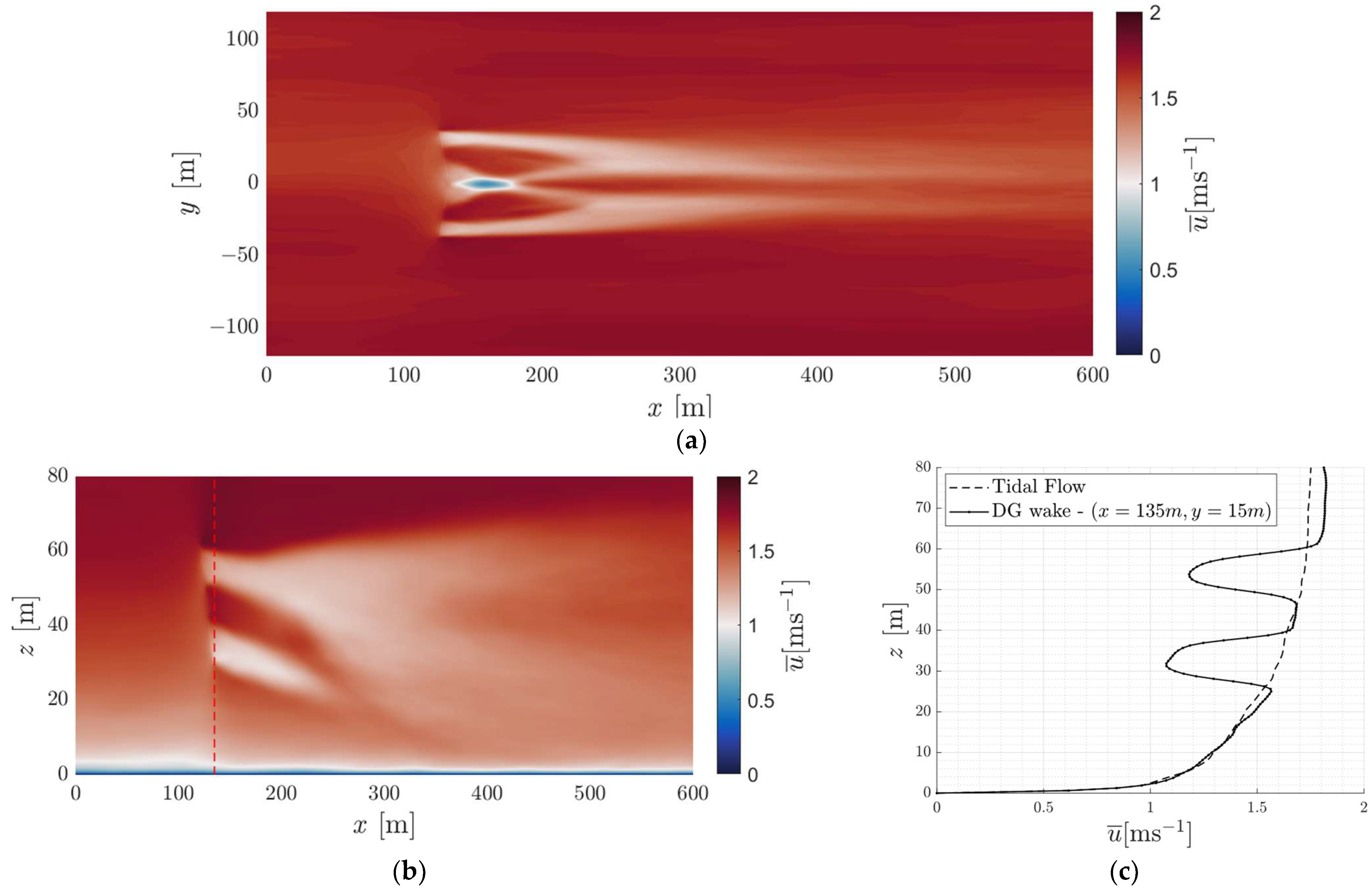
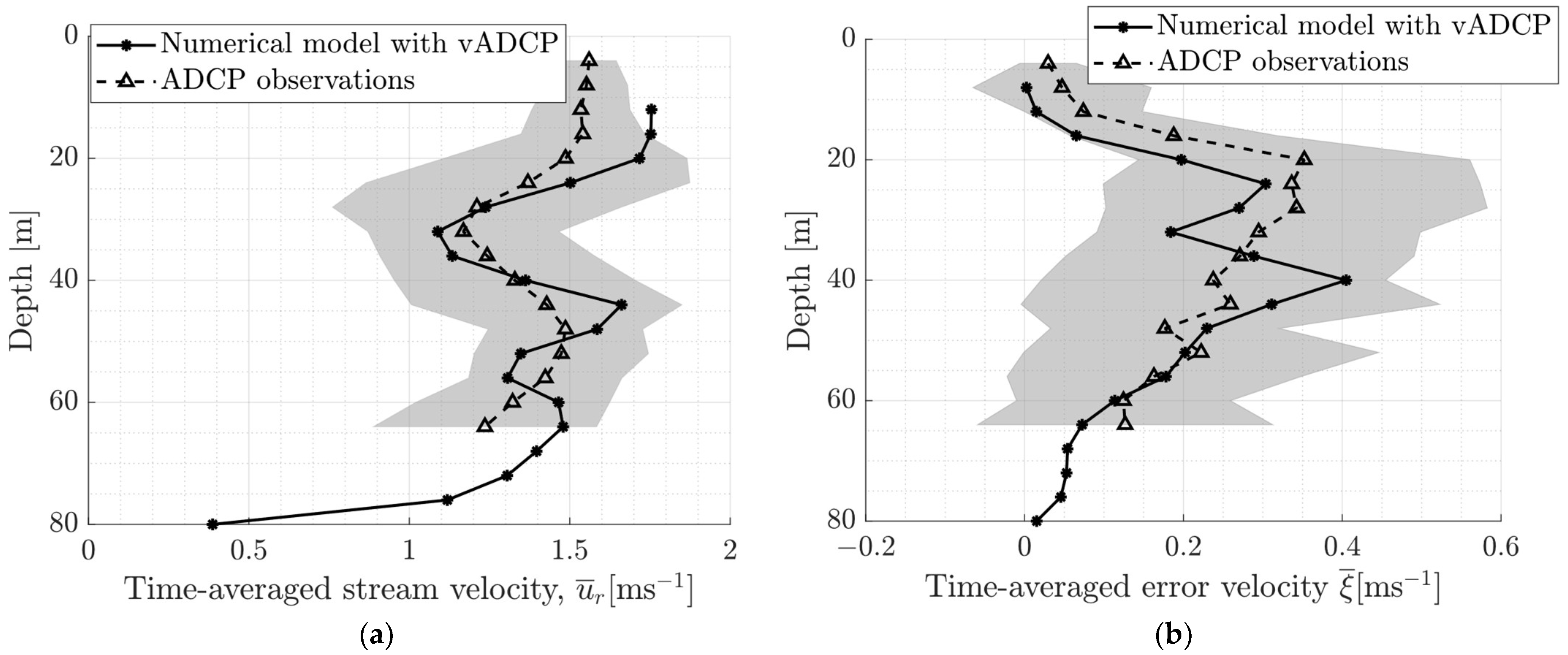
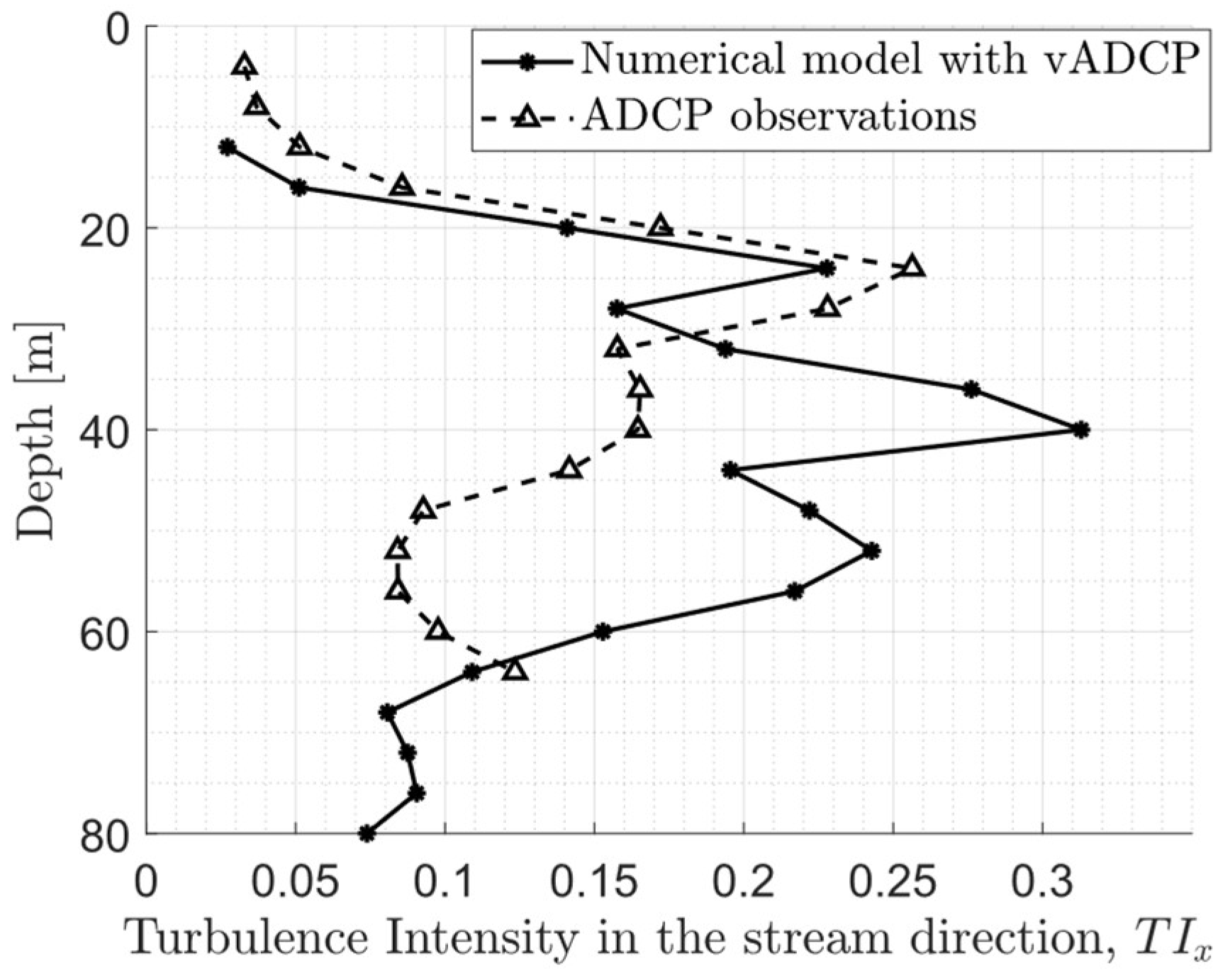
3.4.2. Flow in the Deep Green Wake
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbols | |
| ADCP cell size [m] | |
| ADCP pulse length [m] | |
| Velocities in the model coordinate system in , and directions [ms−1] | |
| Velocities in the ADCP coordinate system [ms−1] | |
| Numerical model coordinate system | |
| ADCP coordinate system | |
| Standard deviation | |
| ADCP error velocity [ms−1] | |
| ADCP mount angle: orientation of beam with respect to the flow [deg] | |
| Abbreviations | |
| ADCP | Acoustic Doppler Current Profiler |
| ALM | Actuator Line Model |
| DG | Deep Green |
| LES | Large Eddy Simulations |
References
- Gerkema, T. An Introduction to Tides; Cambridge University Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Munk, W.; Wunsch, C. Abyssal recipes II: Energetics of tidal and wind mixing. Deep Sea Res. Part I Oceanogr. Res. Pap. 1998, 45, 1977–2010. [Google Scholar] [CrossRef]
- Coles, D.; Angeloudis, A.; Goss, Z.; Miles, J. Tidal Stream vs. Wind Energy: The Value of Cyclic Power When Combined with Short-Term Storage in Hybrid Systems. Energies 2021, 14, 1106. [Google Scholar] [CrossRef]
- Magagna, D.; Monfardini, R. JRC Ocean Energy Status Report 2016 Edition Technology, Market and Economic Aspects of Ocean Energy in Europe; Publications Office of the European Union: Luxembourg, 2016. [Google Scholar]
- Hagerman, G.; Polagye, B.; Bedard, R.; Previsic, M. Methodology for estimating tidal current energy resources and power production by tidal in-stream energy conversion (TISEC) devices. In North American Tidal in Stream Power Feasibility Demonstration Project (TISEC) Devices (Report No. EPRI-TP-001 NA Rev 2); EPRI: Washington, DC, USA, 2006. [Google Scholar]
- Encarnacion, J.I.; Johnstone, C.; Ordonez-Sanchez, S. Design of a Horizontal Axis Tidal Turbine for Less Energetic Current Velocity Profiles. J. Mar. Sci. Eng. 2019, 7, 197. [Google Scholar] [CrossRef]
- Lewis, M.; McNaughton, J.; Márquez-Dominguez, C.; Todeschini, G.; Togneri, M.; Masters, I.; Allmark, M.; Stallard, T.; Neill, S.; Goward-Brown, A.; et al. Power variability of tidal-stream energy and implications for electricity supply. Energy 2019, 183, 1061–1074. [Google Scholar] [CrossRef]
- Milne, I.A.; Day, A.H.; Sharma, R.N.; Flay, R.G.J. The characterisation of the hydrodynamic loads on tidal turbines due to turbulence. Renew. Sustain. Energy Rev. 2016, 56, 851–864. [Google Scholar] [CrossRef]
- Vennell, R.; Funke, S.W.; Draper, S.; Stevens, C.; Divett, T. Designing large arrays of tidal turbines: A synthesis and review. Renew. Sustain. Energy Rev. 2015, 41, 454–472. [Google Scholar] [CrossRef]
- Tedds, S.C.; Owen, I.; Poole, R.J. Near-wake characteristics of a model horizontal axis tidal stream turbine. Renew. Energy 2014, 63, 222–235. [Google Scholar] [CrossRef]
- Nuernberg, M.; Tao, L. Experimental study of wake characteristics in tidal turbine arrays. Renew. Energy 2018, 127, 168–181. [Google Scholar] [CrossRef]
- Lu, Y.; Lueck, R.G. Using a Broadband ADCP in a Tidal Channel. Part I: Mean Flow and Shear. J. Atmos. Ocean. Technol. 1999, 16, 1556–1567. [Google Scholar] [CrossRef]
- Lu, Y.; Lueck, R.G. Using a Broadband ADCP in a Tidal Channel. Part II: Turbulence. J. Atmos. Ocean. Technol. 1999, 16, 1568–1579. [Google Scholar] [CrossRef]
- Bourgoin, A.C.L.; Guillou, S.S.; Thiébot, J.; Ata, R. Turbulence characterization at a tidal energy site using large-eddy simulations: Case of the Alderney Race. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378, 20190499. [Google Scholar] [CrossRef] [PubMed]
- Mcnaughton, J. Tidal Turbine Wake Analysis using Vessel- and Seabed-Mounted ADCPs. In Proceedings of the 5th Oxford Tidal Energy Workshop (OTE 2016), Oxford, UK, 21–22 March 2016. [Google Scholar]
- Schmitt, P.; Elsäßer, B.; Bischof; Starzmann, R. Field testing a full-scale tidal turbine Part 2: In-line Wake Effects. In Proceedings of the European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015. [Google Scholar]
- Jeffcoate, P.; Starzmann, R.; Elsaesser, B.; Scholl, S.; Bischoff, S. Field measurements of a full scale tidal turbine. Int. J. Mar. Energy 2015, 12, 3–20. [Google Scholar] [CrossRef]
- Jensen, N.O. A Note on Wind Generator Interaction; Risø National Laboratory: Roskilde, Denmark, 1983. [Google Scholar]
- Katic, I.; Højstrup, J.; Jensen, N.O. A Simple Model for Cluster Efficiency. In European Wind Energy Association Conference and Exhibition; BT-EWEC’86. Proceedings; A. Raguzzi: Rome, Italy, 1987; Volume 1, pp. 407–410. [Google Scholar]
- Churchfield, M.J. A review of wind turbine wake models and future directions. In Proceedings of the North American Wind Energy Academy Symposium (NAWEA’13), Boulder, CO, USA, 6–8 August 2013. [Google Scholar]
- Jump, E.; Macleod, A.; Wills, T. Review of tidal turbine wake modelling methods: State of the art. Int. Mar. Energy J. 2020, 3, 91–100. [Google Scholar] [CrossRef]
- Sørensen, J.N.; Shen, W.Z. Numerical Modeling of Wind Turbine Wakes. J. Fluids Eng. 2002, 124, 393–399. [Google Scholar] [CrossRef]
- Martínez-Tossas, L.A.; Churchfield, M.J.; Leonardi, S. Large eddy simulations of the flow past wind turbines: Actuator line and disk modeling. Wind Energy 2015, 18, 1047–1060. [Google Scholar] [CrossRef]
- Johansen, J.; Sørensen, N.N.; Michelsen, J.A.; Schreck, S. Detached-eddy simulation of flow around the NREL Phase VI blade. Wind Energy 2002, 5, 185–197. [Google Scholar] [CrossRef]
- Vermeer, L.J.; Sørensen, J.N.; Crespo, A. Wind turbine wake aerodynamics. Prog. Aerosp. Sci. 2003, 39, 467–510. [Google Scholar] [CrossRef]
- Barthelmie, R.J.; Hansen, K.; Frandsen, S.T.; Rathmann, O.; Schepers, J.G.; Schlez, W.; Phillips, J.; Rados, K.; Zervos, A.; Politis, E.S.; et al. Modelling and measuring flow and wind turbine wakes in large wind farms offshore. Wind Energy 2009, 12, 431–444. [Google Scholar] [CrossRef]
- Blondel, F.; Boisard, R.; Milekovic, M.; Ferrer, G.; Lienard, C.; Teixeira, D. Validation and comparison of aerodynamic modelling approaches for wind turbines. J. Phys. Conf. Ser. 2016, 753, 022029. [Google Scholar] [CrossRef]
- Bangga, G.; Lutz, T. Aerodynamic modeling of wind turbine loads exposed to turbulent inflow and validation with experimental data. Energy 2021, 223, 120076. [Google Scholar] [CrossRef]
- Wu, G.; Zhang, L.; Yang, K. Development and Validation of Aerodynamic Measurement on a Horizontal Axis Wind Turbine in the Field. Appl. Sci. 2019, 9, 482. [Google Scholar] [CrossRef]
- Salunkhe, S.; El Fajri, O.; Bhushan, S.; Thompson, D.; O’Doherty, D.; O’Doherty, T.; Mason-Jones, A. Validation of Tidal Stream Turbine Wake Predictions and Analysis of Wake Recovery Mechanism. J. Mar. Sci. Eng. 2019, 7, 362. [Google Scholar] [CrossRef]
- Shahsavarifard, M.; Bibeau, E.L.; Chatoorgoon, V. Effect of shroud on the performance of horizontal axis hydrokinetic turbines. Ocean Eng. 2015, 96, 215–225. [Google Scholar] [CrossRef]
- Sentchev, A.; Thiébaut, M.; Schmitt, F. Impact of turbulence on power production by a free-stream tidal turbine in real sea conditions. Renew. Energy 2019, 147, 1932–1940. [Google Scholar] [CrossRef]
- Fredriksson, S.T.; Broström, G.; Jansson, M.; Nilsson, H.; Bergqvist, B. Large eddy simulation of the tidal power plant deep green using the actuator line method. In Proceedings of the IOP Conference Series: Materials Science and Engineering, First Conference of Computational Methods in Offshore Technology (COTech2017), Stavanger, Norway, 30 November–1 December 2017; Volume 276. [Google Scholar]
- Fredriksson, S.T.; Broström, G.; Bergqvist, B.; Lennblad, J.; Nilsson, H. Modelling Deep Green tidal power plant using large eddy simulations and the actuator line method. Renew. Energy 2021, 179, 1140–1155. [Google Scholar] [CrossRef]
- Draper, M.; Usera, G. Evaluation of the Actuator Line Model with coarse resolutions. J. Phys. Conf. Ser. 2015, 625, 12021. [Google Scholar] [CrossRef]
- Gao, Z.T.; Wang, T.G. Experimental validation and improvement of actuator line model in the large-eddy simulation of wind-turbine wakes. IOP Conf. Ser. Earth Environ. Sci. 2020, 463, 012113. [Google Scholar] [CrossRef]
- Mendoza, V.; Goude, A. Validation of Actuator Line and Vortex Models using Normal Forces Measurements of a Straight-Bladed Vertical Axis Wind Turbine. Energies 2020, 13, 511. [Google Scholar] [CrossRef]
- OpenFOAM. The OpenFOAM Foundation. Available online: https://openfoam.org/ (accessed on 14 August 2023).
- Bachant, P.; Goude, A.; daa-mec; Wosnik, M. turbinesFoam/turbinesFoam: v0.1.1. November 2019. Available online: https://zenodo.org/record/3542301#.ZCbaUspBxaQ (accessed on 14 August 2023).
- De Villiers, E. The Potential of Large Eddy Simulation for the Modeling of Wall Bounded Flows Eugene de Villiers; Imperial College London: London, UK, 2006. [Google Scholar]
- Moeng, C.H.; Sullivan, P.P. NUMERICAL MODELS|Large-Eddy Simulation. In Encyclopedia of Atmospheric Sciences, 2nd ed.; Elsevier: Boulder, CO, USA, 2015; pp. 232–240. [Google Scholar]
- Bachant, P.; Goude, A.; Wosnik, M. Actuator line modeling of vertical-axis turbines. arXiv 2016, arXiv:1605.01449. [Google Scholar]
- Blocken, B.; Stathopoulos, T.; Carmeliet, J. CFD simulation of the atmospheric boundary layer: Wall function problems. Atmos. Environ. 2007, 41, 238–252. [Google Scholar] [CrossRef]
- Muste, M.; Yu, K.; Spasojevic, M. Practical aspects of ADCP data use for quantification of mean river flow characteristics; Part I: Moving-vessel measurements. Flow Meas. Instrum. 2004, 15, 1–16. [Google Scholar] [CrossRef]
- Mueller, D.S. Field Assessment of Acoustic-Doppler Based Discharge Measurements. In Proceedings of the Hydraulic Measurements and Experimental Methods Specialty Conference (HMEM) 2002, Estes Park, CO, USA, 28 July–1 August 2002; pp. 23–31. [Google Scholar]
- Yorke, T.H.; Oberg, K.A. Measuring river velocity and discharge with acoustic Doppler profilers. Flow Meas. Instrum. 2002, 13, 191–195. [Google Scholar] [CrossRef]
- Oberg, K.; Mueller, D.S. Validation of Streamflow Measurements Made with Acoustic Doppler Current Profilers. J. Hydraul. Eng. 2007, 133, 1421–1432. [Google Scholar] [CrossRef]
- P/N 951-6069-00; Acoustic Doppler Current Profiler Principles of Operation—A Practical Primer. Teledyne RD Instruments, Inc.: Poway, CA, USA, 2011.
- Stacey, M.T.; Monismith, S.G.; Burau, J.R. Measurements of Reynolds stress profiles in unstratified tidal flow. J. Geophys. Res. Ocean 1999, 104, 10933–10949. [Google Scholar] [CrossRef]
- Mercier, P.; Thiébaut, M.; Guillou, S.; Maisondieu, C.; Poizot, E.; Pieterse, A.; Thiébot, J.; Filipot, J.-F.; Grondeau, M. Turbulence measurements: An assessment of Acoustic Doppler Current Profiler accuracy in rough environment. Ocean Eng. 2021, 226, 108819. [Google Scholar] [CrossRef]
- Mueller, D.; Abad, J.; García, C.; Gartner, J.; García, M.; Oberg, K. Errors in Acoustic Doppler Profiler Velocity Measurements Caused by Flow Disturbance. J. Hydraul. Eng. 2007, 133, 1411–1420. [Google Scholar] [CrossRef]
- Thiébaut, M.; Filipot, J.F.; Maisondieu, C.; Damblans, G.; Jochum, C.; Kilcher, L.F.; Guillou, S. Characterization of the vertical evolution of the three-dimensional turbulence for fatigue design of tidal turbines. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378, 20190495. [Google Scholar] [CrossRef]
- Thiébaut, M.; Filipot, J.F.; Maisondieu, C.; Damblans, G.; Duarte, R.; Droniou, E.; Guillou, S. Assessing the turbulent kinetic energy budget in an energetic tidal flow from measurements of coupled ADCPs. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378, 20190496. [Google Scholar] [CrossRef]
- Durgesh, V.; Thomson, J.; Richmond, M.C.; Polagye, B.L. Noise correction of turbulent spectra obtained from acoustic doppler velocimeters. Flow Meas. Instrum. 2014, 37, 29–41. [Google Scholar] [CrossRef]
- Nystrom, E.A.; Rehmann, C.R.; Oberg, K.A. Evaluation of Mean Velocity and Turbulence Measurements with ADCPs. J. Hydraul. Eng. 2007, 133, 1310–1318. [Google Scholar] [CrossRef]
- Crismer, J.-B.; Trigaux, F.; Duponcheel, M.; Winckelmans, G. Large-Eddy Simulation of airborne wind energy systems wakes. J. Phys. Conf. Ser. 2023, 2505, 12036. [Google Scholar] [CrossRef]
- Fredriksson, S.T.; Brostrom, G.; Bergqvist, B.; Lennblad, J.; Nilsson, H. Turbulence Characteristics in Tidal Flows Using LES and ALM to Model the Tidal Power Plant Deep Green. In Proceedings of the 4th Asian Wave & Tidal Energy Conference (AWTEC 2018), Taipei, Taiwan, 9–13 September 2018. [Google Scholar]
- Frandsen, S.; Barthelmie, R.; Pryor, S.; Rathmann, O.; Larsen, S.; Højstrup, J.; Thøgersen, M. Analytical modelling of wind speed deficit in large offshore wind farms. Wind Energy 2006, 9, 39–53. [Google Scholar] [CrossRef]
- Ouro, P.; Stoesser, T. Impact of Environmental Turbulence on the Performance and Loadings of a Tidal Stream Turbine. Flow Turbul. Combust. 2019, 102, 613–639. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Transducer width, [m] * | 0.09 |
| Beam width, [deg] * | 3.7 |
| Elevation [deg]—with respect to the water surface * | −70 |
| Direction vector of the beams in the local coordinates * | [−0.2418, −0.2418, −0.9397] |
| [0.2418, 0.2418, −0.9397] | |
| [−0.2418, 0.2418, −0.9397] | |
| [0.2418, −0.2418, −0.9397] | |
| Pulse length [m] | 4, 8, 16 |
| Bin size [m] | 4, 8 |
| Orientation with respect to the flow, [deg] | 0, 45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prabahar, N.S.S.; Fredriksson, S.T.; Broström, G.; Bergqvist, B. Validation of Actuator Line Modeling and Large Eddy Simulations of Kite-Borne Tidal Stream Turbines against ADCP Observations. Energies 2023, 16, 6040. https://doi.org/10.3390/en16166040
Prabahar NSS, Fredriksson ST, Broström G, Bergqvist B. Validation of Actuator Line Modeling and Large Eddy Simulations of Kite-Borne Tidal Stream Turbines against ADCP Observations. Energies. 2023; 16(16):6040. https://doi.org/10.3390/en16166040
Chicago/Turabian StylePrabahar, Nimal Sudhan Saravana, Sam T. Fredriksson, Göran Broström, and Björn Bergqvist. 2023. "Validation of Actuator Line Modeling and Large Eddy Simulations of Kite-Borne Tidal Stream Turbines against ADCP Observations" Energies 16, no. 16: 6040. https://doi.org/10.3390/en16166040
APA StylePrabahar, N. S. S., Fredriksson, S. T., Broström, G., & Bergqvist, B. (2023). Validation of Actuator Line Modeling and Large Eddy Simulations of Kite-Borne Tidal Stream Turbines against ADCP Observations. Energies, 16(16), 6040. https://doi.org/10.3390/en16166040








