Planning of an LVAC Distribution System with Centralized PV and Decentralized PV Integration for a Rural Village
Abstract
:1. Introduction
- Provide a planning tool for the LV distribution network with PV integration that is applicable to developing countries;
- Provide a possible scenario for PV injection into the grid that aligns with current and future regulations;
- Develop a tool using optimization solvers that allows distribution network planners to evaluate the LV topologies and the impact of PV integration on networks;
- Analyze the techno-economic viability of PV integration in an LV distribution network
2. Materials and Methods
2.1. Description Method and Algorithms
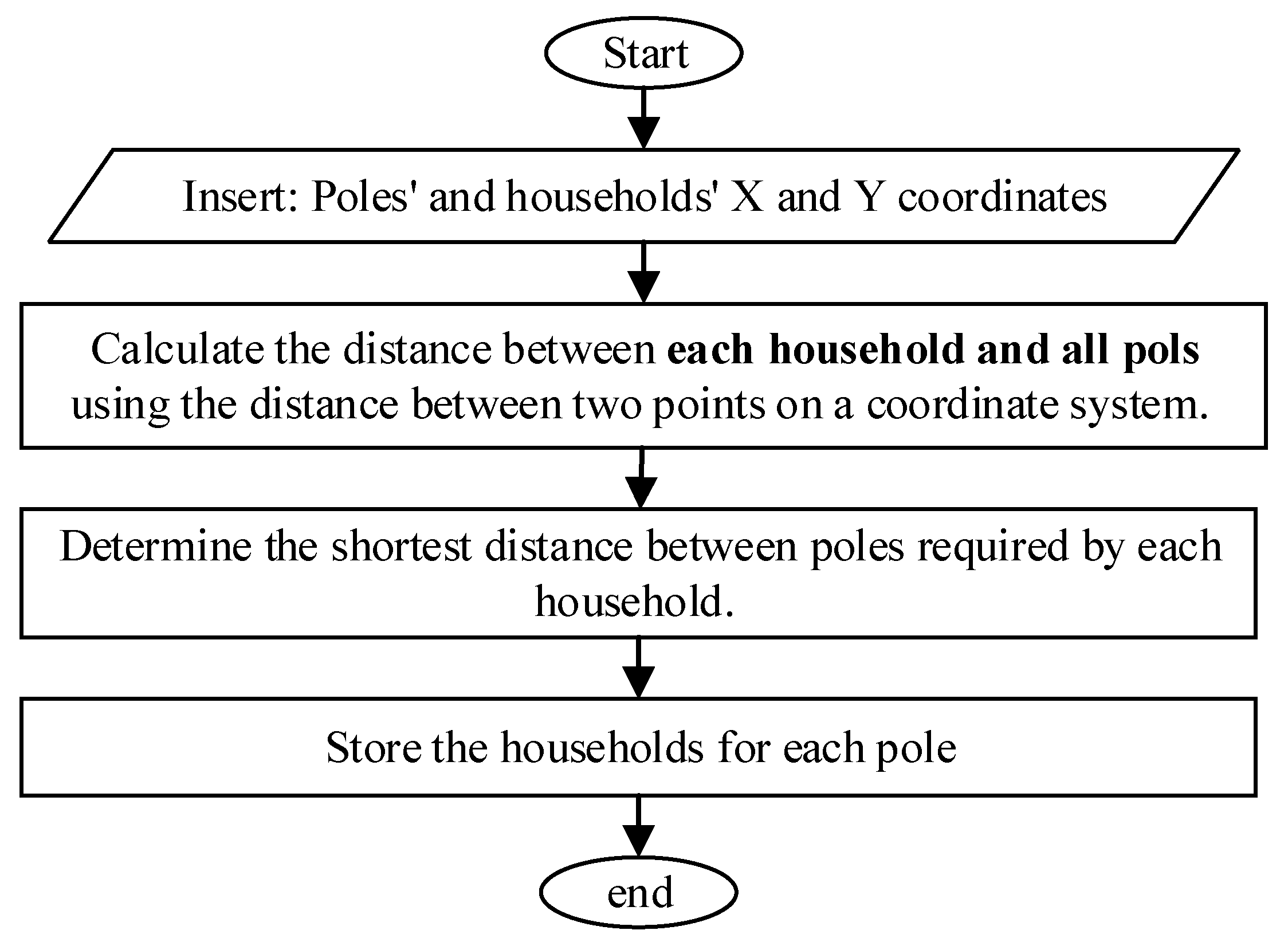
2.1.1. Shortest Path
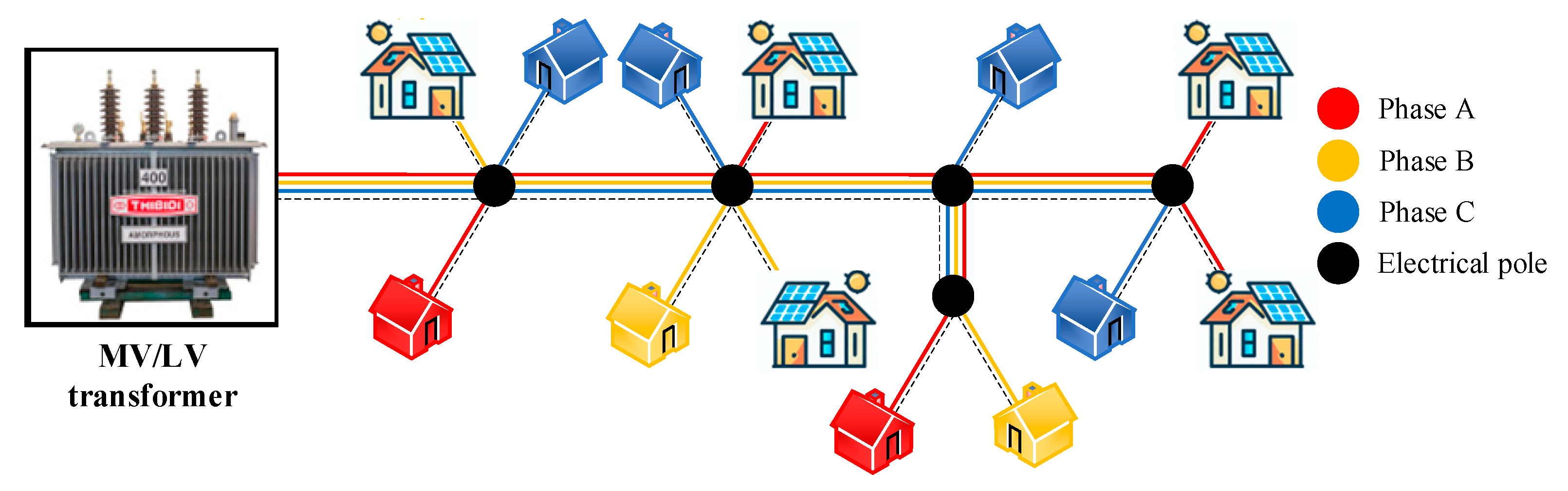
2.1.2. Power Phase Balancing
- Pole balancing (PB): in this case, the concept of single-phase connection of electrical poles is proposed by randomizing its phase connection (possible phase connection of electrical poles: Phase A, B, or C), which is performed using WCA optimization with the objective function of power loss.
- Load balancing (LB): focuses on random single-phases in households (it means that each household has selected the possible phase connections on Phases A, B, or C). It also has the same objective function as pole balancing and is implemented using WCA optimization.
2.1.3. Methods for Energy Loss Minimization
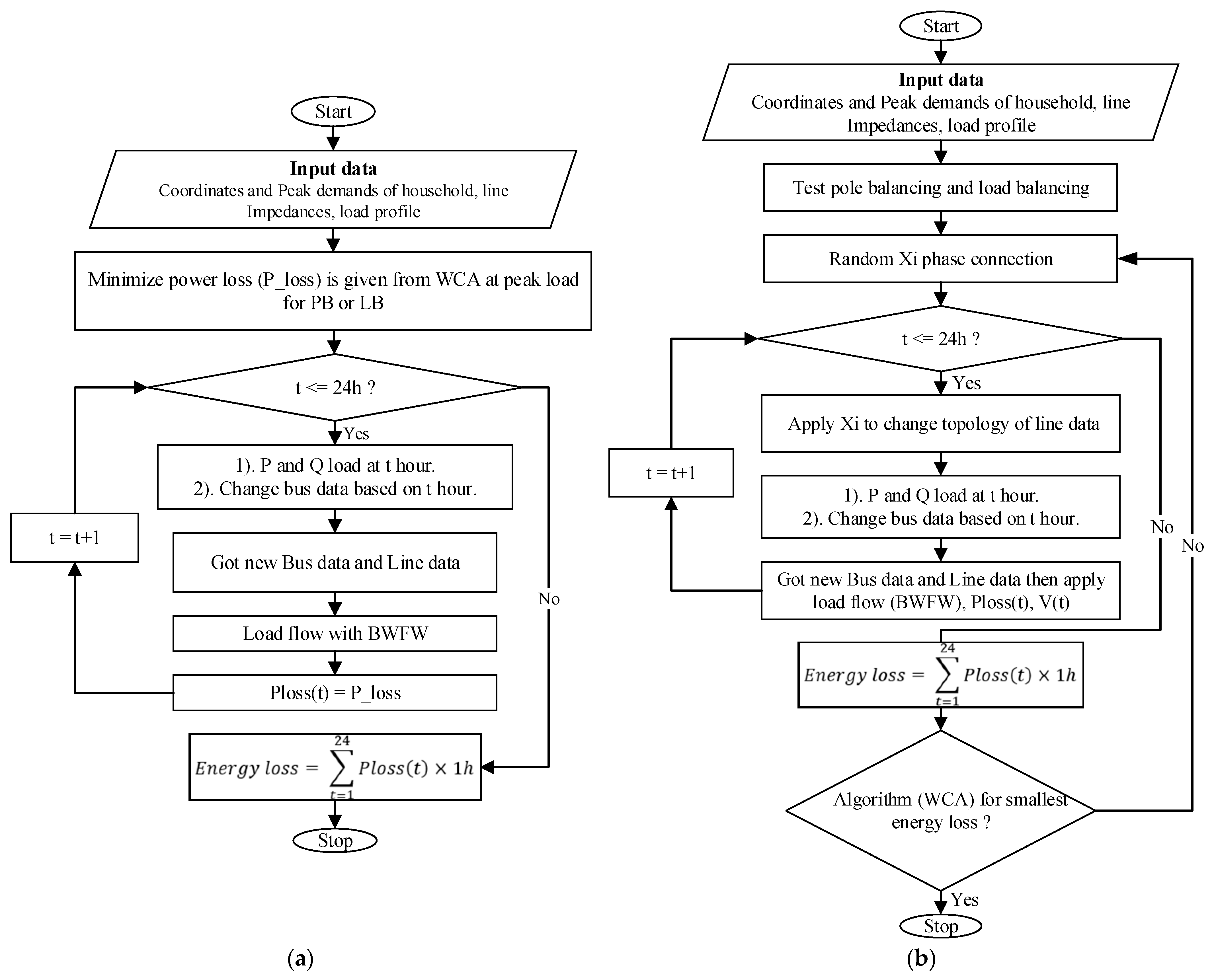
- Method 1: It investigates how to minimize power loss at peak load, and after that, a topology is given for PB and LB at peak load. Additionally, a load profile is performed on this method to attain the energy loss for a day. Figure 4a presents the process of Method 1 as a flow chart. Step 1 begins with the input of coordinates, peak demands of the household, line impedances, and a load profile. Step 2 involves choosing either case pole balancing or load balancing to simulate peak load in this step. Step 3 checks to see if the time is less than 24 h. Step 4 changes bus data based on its load profile. Step 5 obtains new bus data for a given period (t) in hours. Step 6 involves running backward-forward load flow to calculate power loss, voltage, and current. Step 6 then loops back to Step 2 until a certain condition is met. The final step involves calculating the energy loss.
- Method 2: It is a technique that focuses on reducing energy loss during the load profile of a power system using PB and LB to optimize the distribution and balancing of power. This can help to reduce energy costs and improve the efficiency of the power system. Figure 4b shows the flowchart for method 2, which is also used for both PB and LB. The first step involves inputting data such as coordinates (X, Y), peak household demands, line impedances (Z), and a load profile. The second step has case pole and load balancing and selects one to test in this method. The third step is a random phase connection (x) for 24 h. The fourth step focuses on testing LV topology for load profile and x-phase connection by performing load flow (BWFW) to obtain power loss, voltage profile, and current during each hour over 24 h. The fifth step provides a formula to calculate energy loss by summing the power loss of each hour and multiplying it by 1 h. Lastly, WCA optimization is performed to find the smallest energy loss until this condition is met.
2.1.4. PV System Installation
2.1.5. Water Cycle Algorithms (WCA)
- Objective function
- Subjective to:
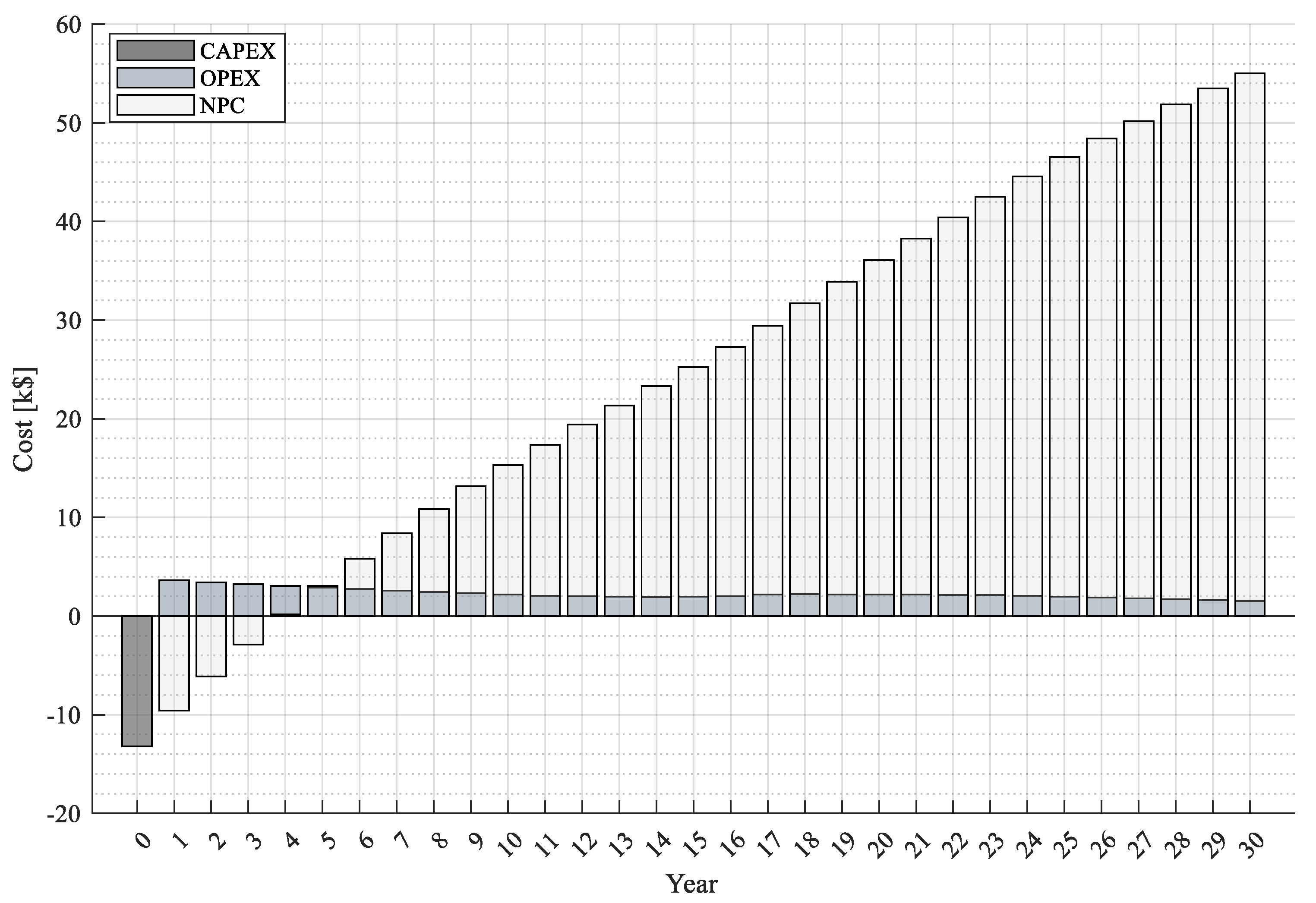
2.1.6. Economic Analysis
- CAPEX, OPEX, and NPC
- Real Discount Rate
2.1.7. Autonomous Operation Time, Energy, and CO2 Emissions
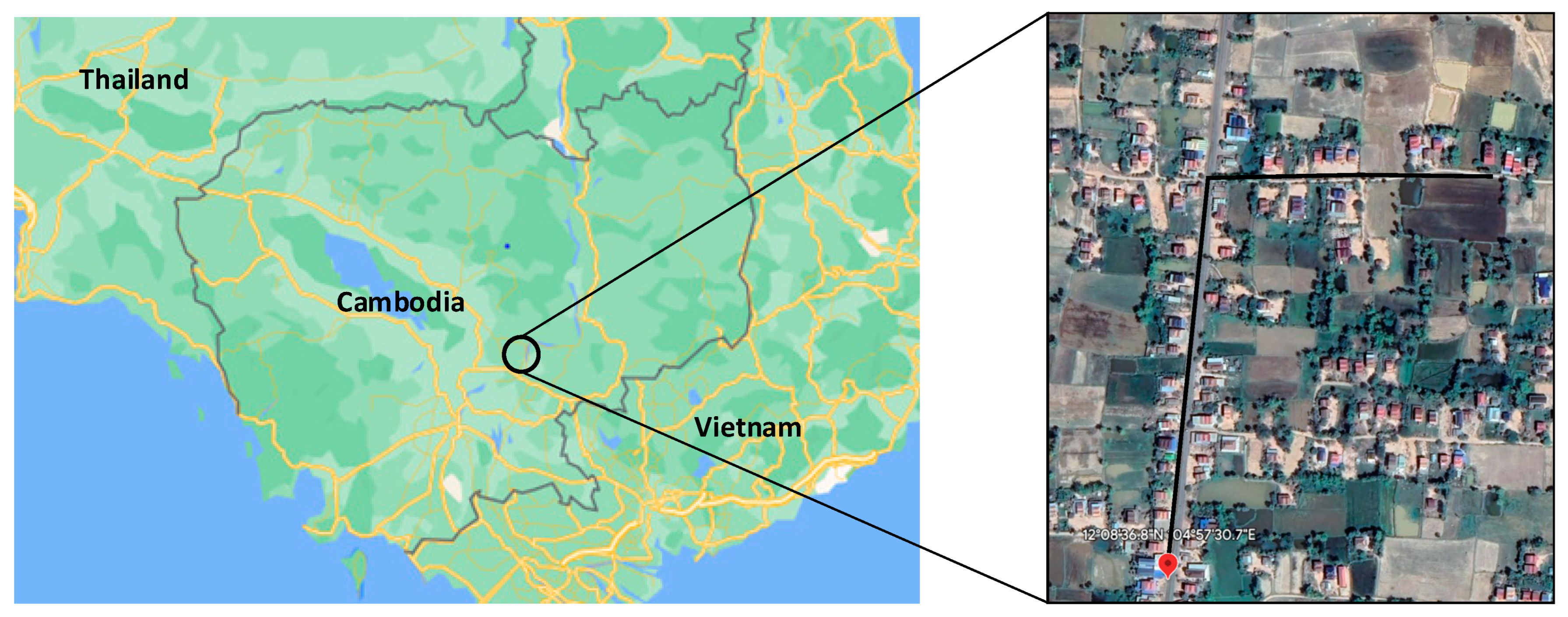
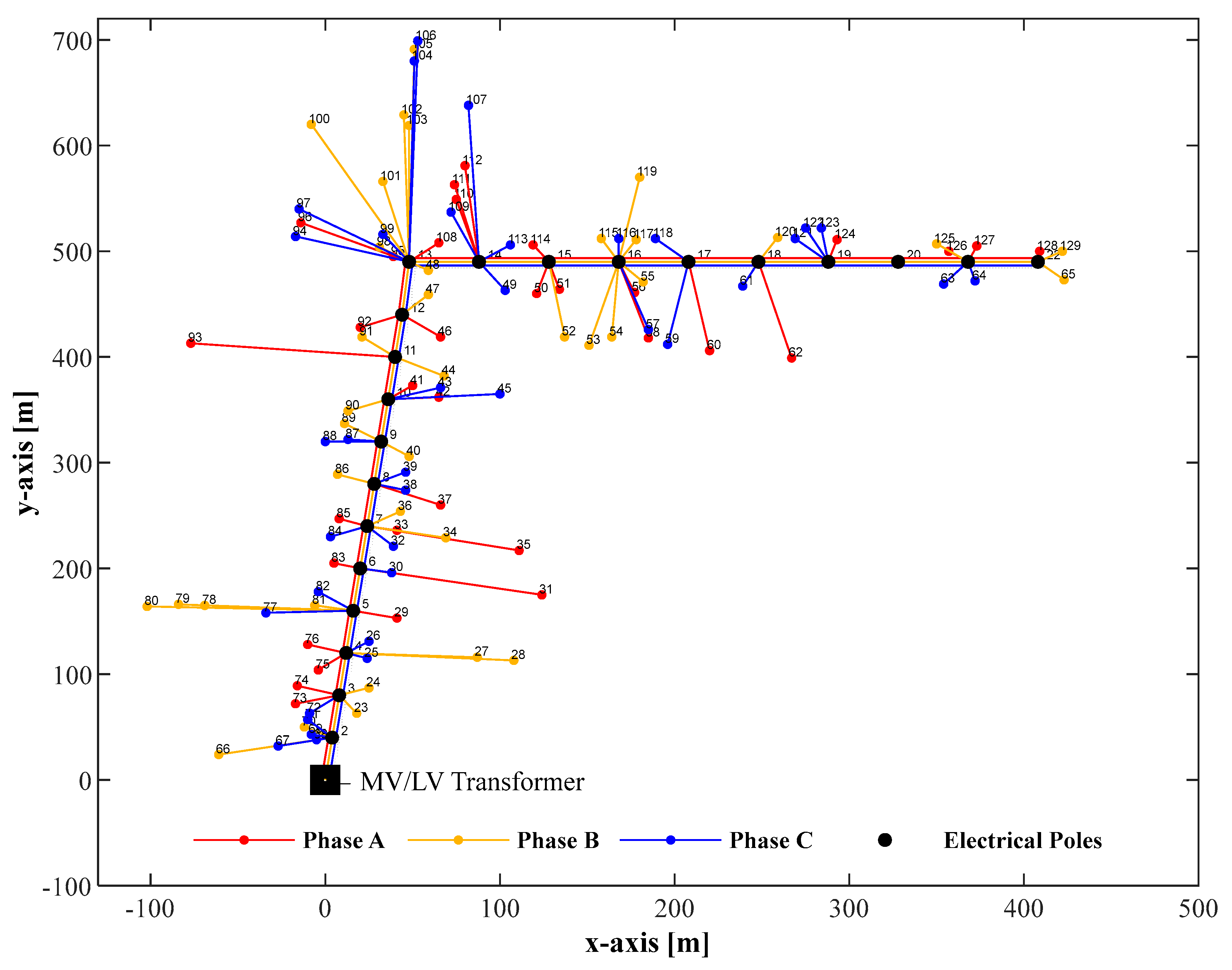
2.2. Case Study
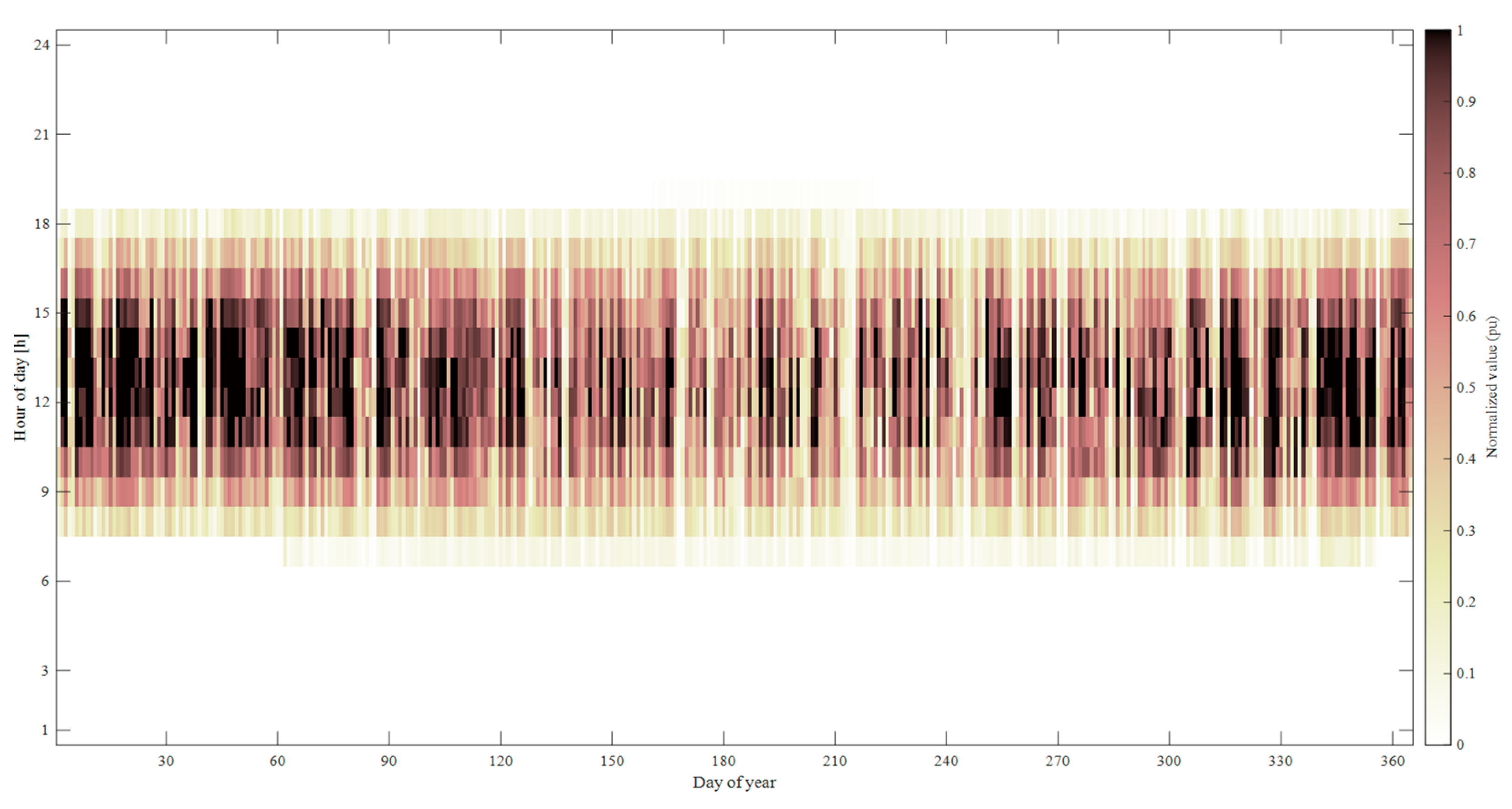
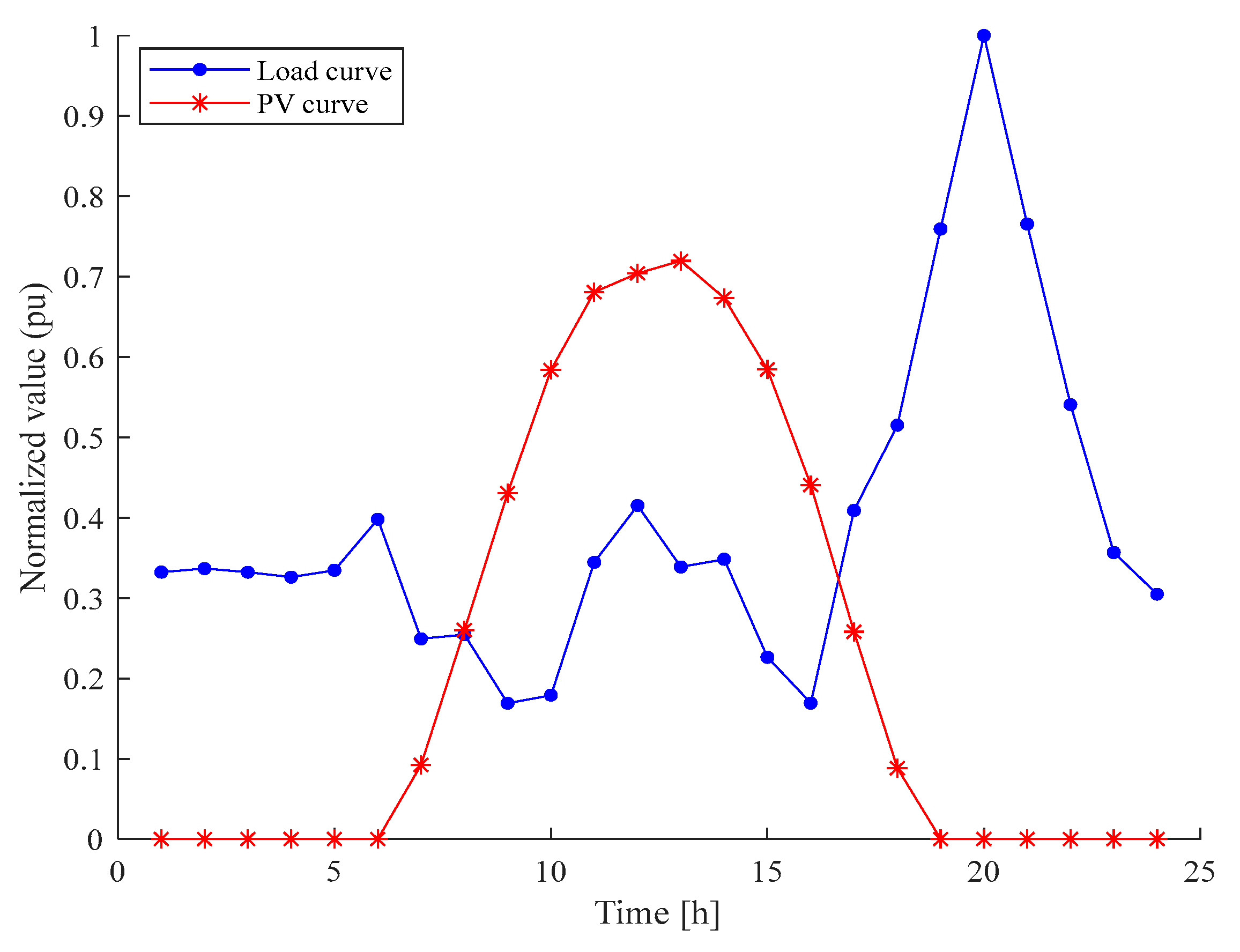
2.2.1. PV Curve and Load Curve
2.2.2. Tariff Payment for MV Feeders and Households in Rural Areas
2.2.3. Input Parameters
3. Simulation Results and Discussion
3.1. Optimal Radial Topology
3.2. CePV and DePV Integration
3.2.1. Scenario 1: Zero Injection
3.2.2. Scenario 2: Injection to the MV Grid without Sell-Back Price
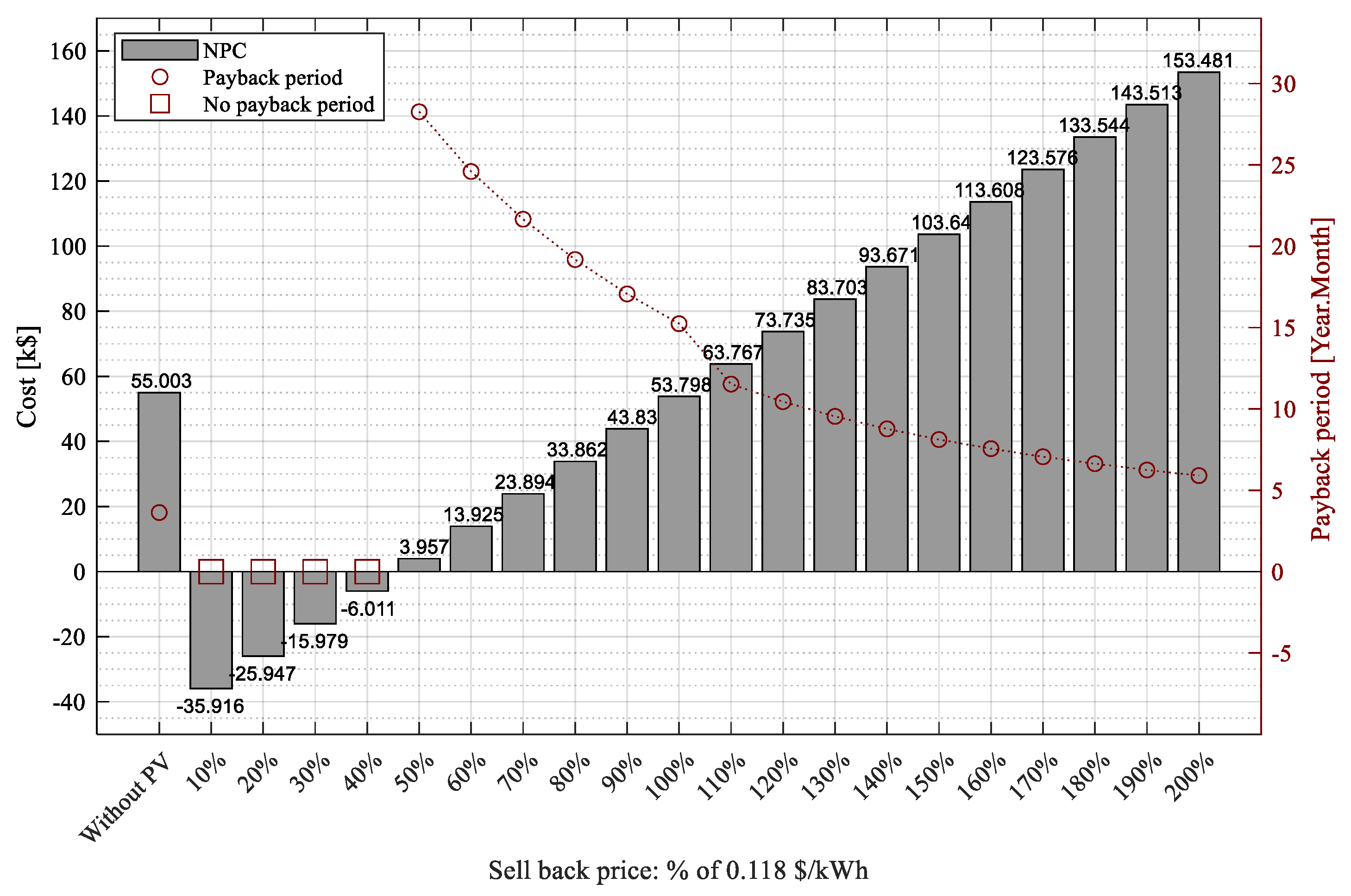
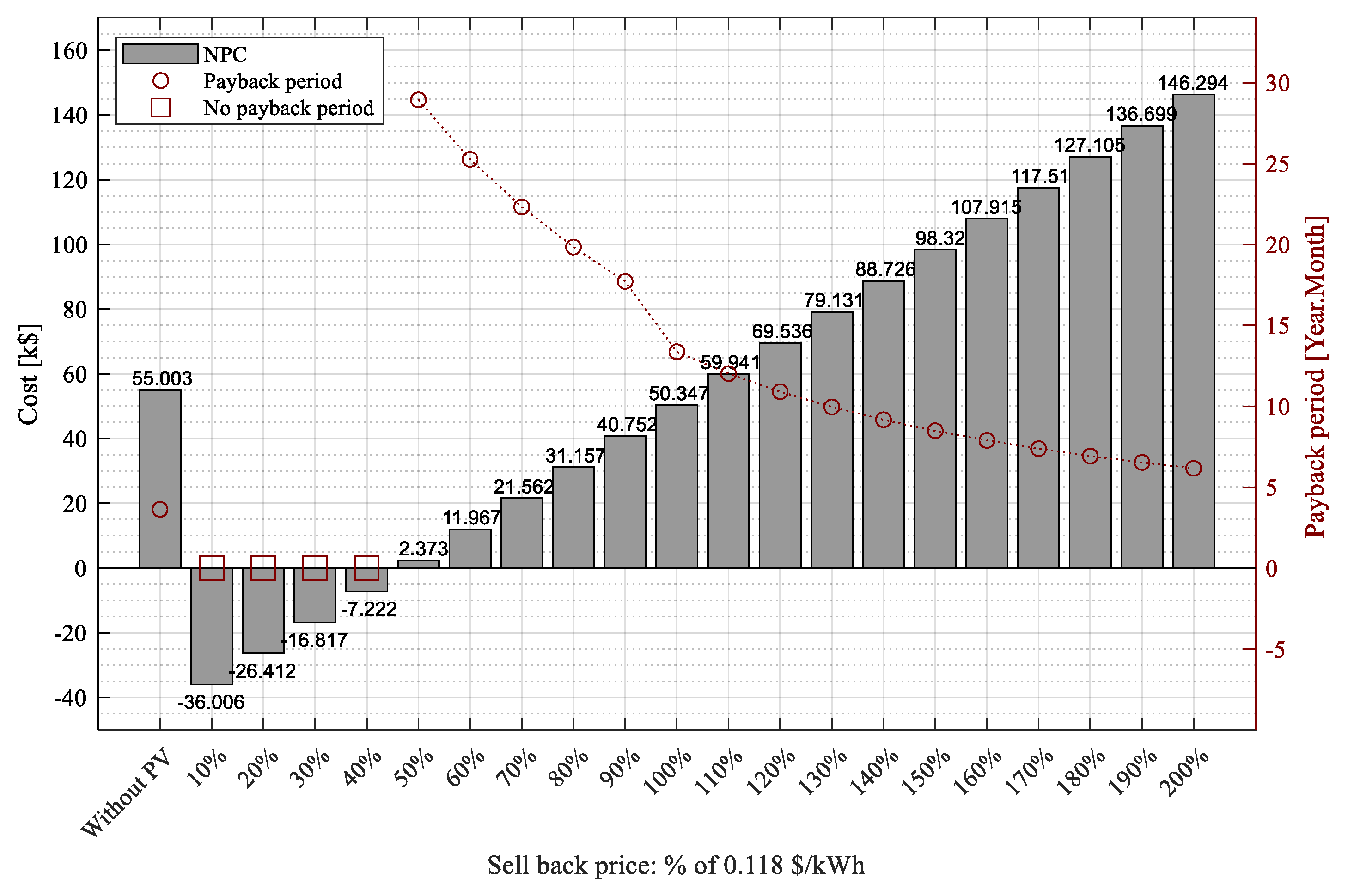
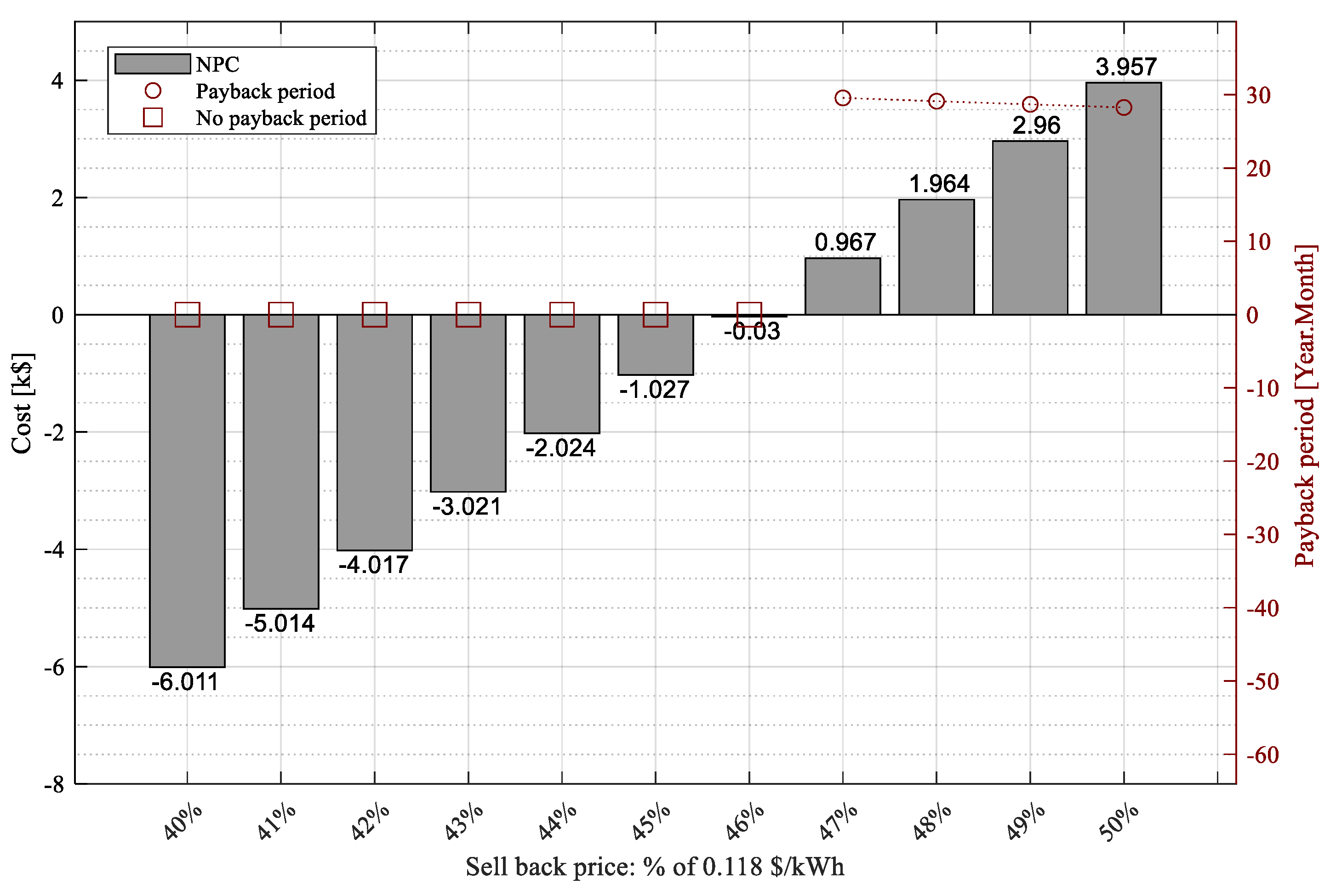
3.2.3. Scenario 3: Injection to the MV Grid with Sell-Back Price
- Strategy 1: Finding the sell-back price to get the profit
- Strategy 2: Minimize the sell-back price to get the profit
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Akinyemi, A.; Musasa, K.; Davidson, I. Analysis of voltage rise phenomena in electrical power network with high concentration of renewable distributed generations. Res. Sq. 2022, 12, 7815. [Google Scholar] [CrossRef] [PubMed]
- Al-Jaafreh, M.A.A.; Mokryani, G. Planning and operation of LV distribution networks: A comprehensive review. IET Energy Syst. Integr. 2019, 1, 133–146. [Google Scholar] [CrossRef]
- Chhlonh, C.; Alvarez-Herault, M.C.; Vai, V.; Raison, B. Comparative planning of LVAC for microgrid topologies with PV-storage in rural areas—Cases study in Cambodia. In Proceedings of the 2022 IEEE PES Innovative Smart Grid Technologies Conference Europe, Novi Sad, Serbia, 10–12 October 2022; pp. 1–5. [Google Scholar]
- Khon, K.; Chhlonh, C.; Vai, V.; Alvarez-Herault, M.C.; Raison, B.; Bun, L. Comprehensive low voltage microgrid planning methodology for rural electrification. Sustainability 2023, 15, 2841. [Google Scholar] [CrossRef]
- Vai, V.; Bun, L. Study on the impact of integrated PV uncertainties into an optimal LVAC topology in a rural village. ASEAN Eng. J. 2020, 10, 79–92. [Google Scholar] [CrossRef]
- Eth, O.; Vai, V.; Bun, L.; Eng, S.; Khon, K. Optimal radial topology with phase balancing in LV distribution system considering energy loss reduction: A case study in Cambodia. In Proceedings of the 2022 4th International Conference on Electrical, Control and Instrumentation Engineering (ICECIE), Kuala Lumpur, Malaysia, 26 November 2022; pp. 1–6. [Google Scholar]
- Jimenez, V.A.; Will, A.L.E.; Lizondo, D.F. Phase reassignment for load balance in low-voltage distribution networks. Int. J. Electr. Power Energy Syst. 2022, 137, 107691. [Google Scholar] [CrossRef]
- Homaee, O.; Mirzaei, M.J.; Najafi, A.; Leonowicz, Z.; Jasinski, M. A practical probabilistic approach for load balancing in data-scarce LV distribution systems using discrete PSO and 2 m + 1 PEM. Int. J. Electr. Power Energy Syst. 2021, 135, 107530. [Google Scholar] [CrossRef]
- You, L.; Vai, V.; Eam, D.; Hem, P.; Heang, S.; Eng, S. Optimal topology of LVAC in a rural village using Water Cycle Algorithms. In Proceedings of the 2022 IEEE International Conference on Power Systems Technology (POWERCON), Kuala Lumpur, Malaysia, 12–14 September 2022; pp. 1–5. [Google Scholar]
- Eam, D.; Vai, V.; You, L.; Hem, P.; Heang, S.; Eng, S. Phase balancing improvement in unbalanced MV distribution systems. In Proceedings of the 2022 19th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Prachuap Khiri Khan, Thailand, 24–27 May 2022; pp. 1–4. [Google Scholar]
- Ibraheem, W.E.; Gan, K.C.; Mohd, M.R. Impact of photovoltaic (PV) systems on distribution networks. Int. Rev. Model. Simul. 2014, 7, 298–310. [Google Scholar]
- Dinh, B.H.; Nguyen, T.T.; Nguyen, T.T.; Pham, T.D. Optimal location and size of photovoltaic systems in high voltage transmission power networks. Ain Shams Eng. J. 2021, 12, 2839–2858. [Google Scholar] [CrossRef]
- Montoya, O.D.; Grisales-Noreña, L.F.; Giral-Ramírez, D.A. Optimal placement and sizing of PV sources in distribution grids using a Modified Gradient-Based Metaheuristic Optimizer. Sustainability 2022, 14, 3318. [Google Scholar] [CrossRef]
- Dakić, P.; Kotur, D. Optimal placement of PV systems from the aspect of minimal power losses in distribution network based on genetic algorithm. Therm. Sci. 2018, 22, 1157–1170. [Google Scholar] [CrossRef]
- Thapar, S. Centralized vs decentralized solar: A comparison study (India). Renew. Energy 2022, 194, 687–704. [Google Scholar] [CrossRef]
- Husein, M.; Chung, I.Y. Optimal design and financial feasibility of a university campus microgrid considering renewable energy incentives. Appl. Energy 2018, 225, 273–289. [Google Scholar] [CrossRef]
- Sackey, D.M.; Amoah, M.; Jehuri, A.B.; Owusu-Manu, D.G.; Acapkovi, A. Techno-economic analysis of a microgrid design for a commercial health facility in Ghana- Case study of Zipline Sefwi-Wiawso. Sci. Afr. 2023, 19, e01552. [Google Scholar] [CrossRef]
- Sharma, S.; Sood, Y.R.; Sharma, N.K.; Bajaj, M.; Zawbaa, H.M.; Turky, R.A.; Turky, S. Modeling and sensitivity analysis of grid-connected hybrid green microgrid system. Ain Shams Eng. J. 2022, 13, 101679. [Google Scholar] [CrossRef]
- Sadollah, A.; Eskandar, H.; Lee, H.K.; Yoo, D.G.; Kim, J.H. Water cycle algorithm: A detailed standard code. SoftwareX 2016, 5, 37–43. [Google Scholar] [CrossRef]
- Eam, D.; Vai, V.; Eng, S.; You, L. Optimizing phase allocation arrangement for a rural lvac distribution system: A case study in Cambodia. In Proceedings of the 2022 4th International Conference on Electrical, Control and Instrumentation Engineering (ICECIE), Kuala Lumpur, Malaysia, 26 November 2022; pp. 1–6. [Google Scholar]
- Uzum, B.; Onen, A.; Hasanien, H.M.; Muyeen, S.M. Rooftop solar PV penetration impacts on distribution network and further growth factors—A comprehensive review. Electronics 2021, 10, 55. [Google Scholar] [CrossRef]
- Karimi, M.; Mokhlis, H.; Naidu, K.; Uddin, S.; Bakar, A.H.A. Photovoltaic penetration issues and impacts in distribution network—A review. Renew. Sustain. Energy Rev. 2016, 53, 594–605. [Google Scholar] [CrossRef]
- EAC. Report on the Decision on Setting the Price List for Electricity for all Types of Consumers Who Buy Electricity from the Substation and from the Distribution Network Originates from the National Network of Private Electricity Suppliers for 2023; Electricity Authority of Cambodia: Phnom Penh, Cambodia, 2023. Available online: https://www.eac.gov.kh/document/tariffdecidelist (accessed on 12 June 2023).
- Vai, V.; Alvarez-Herault, M.C.; Raison, B.; Bun, L. Optimal low-voltage distribution topology with integration of pv and storage for rural electrification in developing countries: A case study of Cambodia. J. Mod. Power Syst. Clean Energy 2020, 8, 531–539. [Google Scholar] [CrossRef]
- NASA. ASDC Processing, Archiving, and Distributing Earth Science Data; NASA Langley Research Center (LaRC): Hampton, VA, USA, 2023. Available online: https://eosweb.larc.nasa.gov/ (accessed on 12 June 2023).
- EAC. Salient Features of Power Development in the Kingdom of Cambodia in 2022; Electricity Authority of Cambodia: Phnom Penh, Cambodia, 2022. Available online: https://www.eac.gov.kh/site/annualreport?lang=en (accessed on 31 December 2022).
- Vai, V.; Eng, S. Study of grid-connected PV system for a low voltage distribution system: A case study of Cambodia. Energies 2022, 15, 5003. [Google Scholar] [CrossRef]
- ADB. Inflation Rate in Asia and the Pacific, Asian Development Outlook (ADO); Asian Development Bank/ERCD: Mandaluyong, Philippines, 2023; Available online: https://data.adb.org/dataset/inflation-rate-asia-and-pacific-asian-development-outlook (accessed on 4 April 2023).
- Our World in Data. Carbon Intensity of Electricity. 2022. Available online: https://ourworldindata.org/grapher/carbon-intensity-electricity (accessed on 12 June 2023).
- IPCC. Technology-Specific Cost and Performance Parameters; The Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2014; Available online: https://www.ipcc.ch/site/assets/uploads/2018/02/ipcc_wg3_ar5_annex-iii.pdf (accessed on 12 June 2023).




| Description | MV Feeder | |
|---|---|---|
| General Tariff | PV Consumer | |
| Capacity charge [$/kW/Month] | - | 3.1 |
| Tariff [$/kWh] | 0.121 | 0.118 |
| Items | Provincial and Rural Areas | |||
|---|---|---|---|---|
| Electricity consumption [kWh/Month] | 0–10 | 11–50 | 51–200 | 201–2000 |
| Tariff [$/kWh] | 0.095 | 0.12 | 0.1525 | 0.1825 |
| Items | Value [Ref.] |
|---|---|
| Planning period [years] | 30 |
| Load growth [%] | 3 [3] |
| Nominal discount rate [%] | 12 [27] |
| Expected inflation rate [%] | 3 [28] |
| Real discount rate [%] | 8.74 |
| PV price [k$/kWp] | 0.6 [3] |
| PV lifetime [Years] | 30 [3] |
| PV inverters [k$/kW] | 0.556 [3] |
| Inverter lifetime [Years] | 15 [3] |
| Inverter efficiency [%] | 95 [3] |
| PV + inverter maintenance cost [k$/kW] | 0.02 [3] |
| LV-2 × 4 mm2 [k$/km] | 0.625 |
| LV-ABC-4 × 120 mm2 [k$/km] | 6.1 |
| Life-cycle CO2 emissions of grid [kg/kWh] | 0.400 [29] |
| Life-cycle CO2 emissions of CePV [kg/kWh] | 0.042 [30] |
| Life-cycle CO2 emissions of DePV [kg/kWh] | 0.066 [30] |
| Items | M1-PB | M1-LB | M2-PB | M2-LB |
|---|---|---|---|---|
| Transformer capacity [kVA] | 160 | 160 | 160 | 160 |
| Length of mainline (4 wires) [m] | 852 | 852 | 852 | 852 |
| Length of secondary (2 wires) [m] | 5105 | 5105 | 5105 | 5105 |
| Max. Voltage [pu] | 1 | 1 | 1 | 1 |
| Min. Voltage [pu] | 0.905 | 0.906 | 0.908 | 0.910 |
| Payback period [Year. Month] | 3.652 | 3.635 | 3.643 | 3.634 |
| Total energy loss [MWh] | 202.421 | 189.958 | 195.471 | 189.274 |
| Energy purchased [MWh] | 7438.712 | 7426.248 | 7431.762 | 7425.564 |
| Cost of energy purchased [k$] | 900.084 | 898.576 | 899.243 | 898.493 |
| CO2 emissions [tons] | 2975.485 | 2970.499 | 2972.705 | 2970.226 |
| CAPEX [k$] | 13.197 | 13.197 | 13.197 | 13.197 |
| OPEX [k$] | 67.815 | 68.180 | 68.018 | 68.199 |
| NPC [k$] | 54.619 | 54.983 | 54.821 | 55.003 |
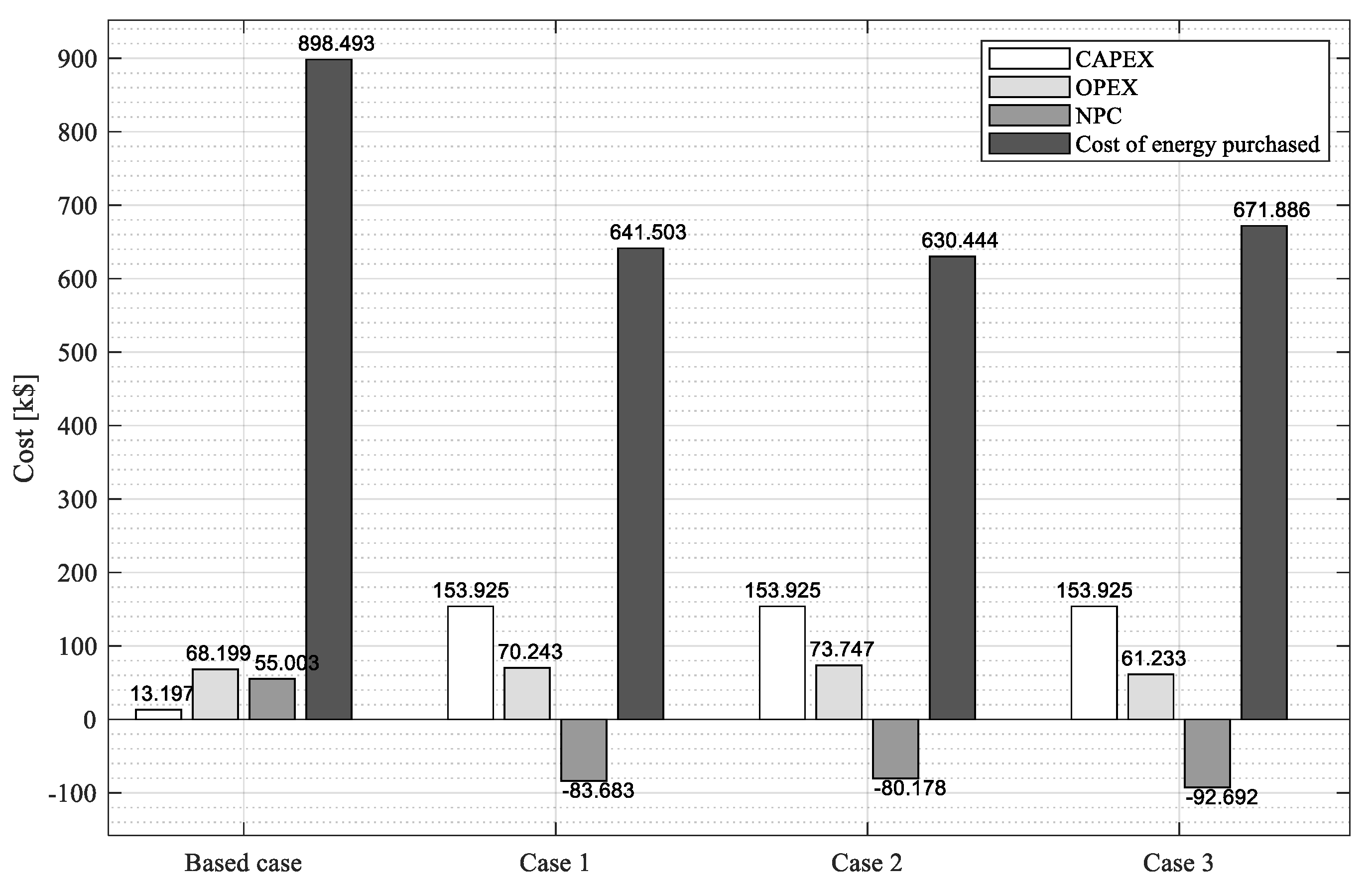
| Items | Base Case | Case 1 | Case 2 | Case 3 |
|---|---|---|---|---|
| PV capacity per HH [kWp] | - | - | 0.828 | 0.828 |
| Number of PV | - | - | 87 | 87 |
| Total PV capacity [kWp] | - | 72 | 72 | 72 |
| Max. Voltage [pu] | 1 | 1 | 1 | 1 |
| Min. Voltage [pu] | 0.910 | 0.910 | 0.910 | 0.910 |
| Payback period [Year. Month] | 3.634 | - | - | - |
| Total energy loss [MWh] | 189.274 | 184.948 | 162.007 | 157.673 |
| Energy purchased [MWh] | 7425.564 | 5301.675 | 5210.281 | 5552.774 |
| PV produced [MWh] | - | 2119.563 | 2188.016 | 1841.189 |
| Cost of energy purchased [k$] | 898.493 | 641.503 | 630.444 | 671.886 |
| CAPEX [k$] | 13.197 | 153.925 | 153.925 | 153.925 |
| OPEX [k$] | 68.199 | 70.243 | 73.747 | 61.233 |
| NPC [k$] | 55.003 | −83.683 | −80.178 | −92.692 |
| Autonomous energy [%] | - | 29 | 30 | 25 |
| CO2 emissions [tons] | 2970.226 | 2254.939 | 2168.381 | 2292.357 |
| CO2 emissions reduction [%] | - | 24 | 27 | 23 |
| Items | Base Case | Case 1 | Case 2 |
|---|---|---|---|
| PV capacity per HH [kWp] | - | - | 0.828 |
| Number of PV | - | - | 87 |
| Total PV capacity [kWp] | - | 72 | 72 |
| Max. Voltage [pu] | 1 | 1 | 1 |
| Min. Voltage [pu] | 0.910 | 0.910 | 0.910 |
| Payback period [Year. Month] | 3.634 | - | - |
| Total Energy loss [MWh] | 189.274 | 188.758 | 252.045 |
| Energy purchased [MWh] | 7425.564 | 5187.568 | 5177.661 |
| PV produced [MWh] | - | 4350.979 | 4350.979 |
| Energy injects to MV grid [MWh] | - | 2113.498 | 2040.305 |
| Cost of energy purchased [k$] | 898.493 | 627.696 | 626.497 |
| CAPEX [k$] | 13.197 | 125.341 | 125.341 |
| OPEX [k$] | 68.199 | 79.457 | 79.740 |
| NPC [k$] | 55.003 | −45.884 | −45.601 |
| Autonomous time [%] | - | 36 | 36 |
| Autonomous energy [%] | - | 59 | 59 |
| CO2 emissions [tons] | 2970.226 | 2362.192 | 2253.805 |
| CO2 emissions reduction [%] | - | 20 | 24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eam, D.; Vai, V.; Chhlonh, C.; Eng, S. Planning of an LVAC Distribution System with Centralized PV and Decentralized PV Integration for a Rural Village. Energies 2023, 16, 5995. https://doi.org/10.3390/en16165995
Eam D, Vai V, Chhlonh C, Eng S. Planning of an LVAC Distribution System with Centralized PV and Decentralized PV Integration for a Rural Village. Energies. 2023; 16(16):5995. https://doi.org/10.3390/en16165995
Chicago/Turabian StyleEam, Dara, Vannak Vai, Chhith Chhlonh, and Samphors Eng. 2023. "Planning of an LVAC Distribution System with Centralized PV and Decentralized PV Integration for a Rural Village" Energies 16, no. 16: 5995. https://doi.org/10.3390/en16165995
APA StyleEam, D., Vai, V., Chhlonh, C., & Eng, S. (2023). Planning of an LVAC Distribution System with Centralized PV and Decentralized PV Integration for a Rural Village. Energies, 16(16), 5995. https://doi.org/10.3390/en16165995












