Comparative Study of Global Sensitivity Analysis and Local Sensitivity Analysis in Power System Parameter Identification

Abstract

In the process of parameter identification, sensitivity analysis is mainly used to determine key parameters with high sensitivity in the model. Sensitivity analysis methods include local sensitivity analysis (LSA) and global sensitivity analysis (GSA). The LSA method has been widely used for power system parameter identification for a long time, while the GSA has started to be used in recent years. However, there is no clear conclusion on the impact of different sensitivity analysis methods on parameter identification results. Therefore, this paper compares and studies the roles that LSA and GSA can play in different parameter identification methods, providing clear guidance for the selection of sensitivity analysis methods and parameter identification methods. The conclusion is as follows. If the identification strategy that only identifies key parameters with high sensitivity is adopted, we recommend still using the existing LSA method. If using a groupwise alternating identification strategy (GAIS) for high- and low-sensitivity parameters, either LSA or GSA can be used. To improve the identification accuracy, it is more important to improve the identification strategy than to change the sensitivity analysis method. When the accuracy of the non-key parameters with low sensitivity cannot be confirmed, using the GAIS is an effective method for ensuring identification accuracy. In addition, it should be noted that the high sensitivity of a parameter does not necessarily mean that the parameter is identifiable, which is revealed by the examples used in this paper.

1. Introduction

Power system research mainly relies on mathematical model-based simulations. The complete simulation model of the power system fuses the models of generation, transmission, distribution, and power consumption equipment. Therefore, the accuracy of various equipment models is a prerequisite for the authenticity of power system simulation results. Since the working principles of electrical equipment are clear, the equations of these equipment models can be considered correct. Therefore, the difficulty of power system modeling is to obtain accurate model parameters. At present, parameter identification is an important way to obtain the true parameter values of the electrical equipment model. Therefore, improving the accuracy of parameter identification is of great significance for power system modeling and simulation.

Parameter identification is essentially an optimization problem that involves finding the optimal values within the parameters’ possible range of values so the model output is as consistent as possible with the measured results. The determination of the parameter value range must conform to the physical background of the parameter but also requires strong engineering judgment. It is very important to determine the identifiability of parameters and their exact value range, otherwise the identification results will have no practical meaning. The current widely used power system parameter identification process is shown in Figure 1. There are three main steps in the process. The first step is to analyze the identifiability of the parameters to ensure that the value of the parameter can be uniquely determined in theory [1,2]. The identifiability can be analyzed by formula derivation [3] or numerical methods based on time-domain sensitivity trajectories [4]. Parameters that are not identifiable do not participate in the identification process. The second step is to analyze the possibility of the accurate identification of the identifiable parameters based on sensitivity. Generally, parameters with high sensitivity are regarded as key parameters in the model and are easy to accurately identify; parameters with low sensitivity are regarded as non-key parameters, and the identification accuracy is usually low. Since there are often many parameters in a model, when all the parameters are identified at the same time, the number of iterations of the identification algorithm needs to be significantly increased as the risk of falling into a locally optimal solution increases. Therefore, in the engineering practice of power system parameter identification, only the key parameters are identified, and the unidentifiable parameters and non-key parameters are usually set to typical values or empirical values [5,6,7,8,9]. The third step is to identify the selected key parameters based on the dynamic response of the electrical equipment under the actual disturbance of the power grid. Parameter identification has been widely used in various electrical equipment in power systems, such as synchronous generators [10,11], excitation controllers [12,13], transmission lines [14,15], electric loads [16], renewable power generation equipment [17,18,19], and energy storage system [20].

From the existing practical application of parameter identification, it can be found that sensitivity analysis plays an important role in the identification process. However, the sensitivity analysis method used in power system parameter identification is mainly trajectory sensitivity, which is a local sensitivity analysis (LSA) method that considers the impact of a single parameter change on the model output. In the family of sensitivity analysis methods, there is also a type of global sensitivity analysis (GSA) method [21,22,23]. The GSA method analyzes the influence of each input or parameter on the model output when all model inputs or parameters change randomly. Compared with LSA, GSA can more comprehensively analyze the impact of the uncertainty of inputs or parameters on model output. The GSA method has a wide range of applications in many disciplines, such as hydrological modeling [24], biomedical science [25], earth system modeling [26], evaluating ecological resilience [27], building performance analysis [28], train traffic scheduling [29], and wind resource assessment [30]. In recent years, the application of GSA methods in power systems has gradually increased, including the analysis of the uncertainty of renewable energy generation [31,32] and its relationship with the reliability of the power system [33], the voltage control of the distribution network [34] and the voltage stability of the transmission grid [35,36,37], the analysis of the maximum load ability of islanded microgrids with distributed generation [38,39], the analysis of the key influencing factors of small disturbance stability [40,41], the analysis of the influence of various parameters on locational marginal prices in electricity market [42], the analysis and optimization of key parameters of power generation system [43,44], the improvement of the power output estimation model [45], and the cost model [46] of wind power generation. In these studies, the variance-based Sobol method was the main GSA method used. However, there are few studies on the use of GSA in power system parameter identification. Reference [47] applies the Sobol method to the parameter identification of the load model. By only identifying the high-sensitivity parameters, the identification difficulty is reduced, and the identification efficiency is improved. Reference [48] also used the Sobol method to analyze the sensitivity of seven parameters in the electrical model of the lithium-ion battery, divided the parameters into three groups according to the sensitivity, and proposed a groupwise alternating identification strategy (GAIS) to iteratively identify the three groups of parameters, achieving a good fit with the experimental data. Compared with the existing method of only identifying high-sensitivity parameters, although the GAIS is more complicated in steps, it has the advantage of not only increasing the number of identification parameters but also improving the identification accuracy, so we believe that this method has a good application future. We used the GAIS in Section 6 and made some improvements to it.

Overall, the use of LSA in power system parameter identification has a long history, and in recent years, GSA has gradually begun to be adopted. However, there is no clear conclusion on the impact of different sensitivity analysis methods on parameter identification results. This paper compares and studies the roles that LSA and GSA can play in different parameter identification methods, providing clear guidance for the selection of sensitivity analysis methods and parameter identification methods. The LSA method used in this paper is the widely used trajectory sensitivity analysis, and the GSA methods used include the Sobol method, Morris method, regional sensitivity analysis, scatter plots, and Andres visualization test. In our research, the Sobol method was implemented by programming, and the other four GSA methods were implemented using an open-source GSA toolbox named SAFE [49,50]. All these sensitivity analysis methods are introduced in Section 2. A generator excitation system model is introduced as a parameter identification object in Section 3. The reason for choosing this model is that the identifiability of its parameters can be analytically analyzed by formula derivation, which is impossible for other complex models. In Section 4, we analyzed the sensitivity of excitation system model parameters using the LSA and GSA methods and compared the differences in the analysis results. In Section 5 and Section 6, we used the traditional parameter identification method shown in Figure 1 and the improved GAIP method proposed in Section 6 for parameter identification, respectively. Following that, we compared and analyzed the selection of sensitivity analysis methods and parameter identification methods from the identification accuracy and other perspectives, and finally provided clear recommendations.

2. Sensitivity Analysis Methods

2.1. Local Sensitivity Analysis Method

The LSA method described below refers to the trajectory sensitivity analysis method, which is a kind of time-domain sensitivity analysis method that is widely used in power system parameter identification. The trajectory sensitivity reflects the change in the dynamic response of the power system or power equipment with the change in a certain parameter. The trajectory sensitivity is the derivative of the trajectory to the parameter [8], as in Equation (1):

$$\frac{\partial y_i(\mathsf{\theta },k)}{\partial {\theta }_i}=\underset{\Delta {\theta }_j\to 0}{\lim }\frac{y_i({\mathsf{\theta }}_{j+},k)-y_i({\mathsf{\theta }}_{j-},k)}{2\Delta {\theta }_j}$$

(1)

where y_i is the ith output of a multiple input multiple output system; k is the index of the sampling point in y_i; θ represents all parameters in the model; θ_j+ represents that the jth parameter θ_j in θ is increased by Δθ_j; θ_j− represents that θ_j is reduced by Δθ_j. In the actual calculation of trajectory sensitivity, the numerical difference method shown in Equation (2) is usually used [8].

$$\frac{\partial [y_i(\mathsf{\theta },k)/y_{i0}]}{\partial [{\theta }_i/{\theta }_{i0}]}=\frac{[y_i({\mathsf{\theta }}_{j+},k)-y_i({\mathsf{\theta }}_{j-},k)]/y_{i0}}{2\Delta {\theta }_j/{\theta }_{i0}}$$

(2)

where θ_j0 is the actual value of θ_j and y_i0 is the steady-state value of y_i(θ, k) when θ_j equals θ_j0.

The analysis result of the trajectory sensitivity shows a curve that changes with time, and it is not convenient to directly compare the parameter sensitivity. Therefore, it is also necessary to calculate the average value of the trajectory sensitivity for the sorting of the sensitivity of each parameter [8], as in Equation (3):

$$S_{ij}=\frac{1}{K}{\displaystyle \sum _{k=1}^K\left|\frac{\partial [y_i(\mathsf{\theta },k)/y_{i0}]}{\partial [{\theta }_j/{\theta }_{j0}]}\right|}$$

(3)

where S_ij represents the sensitivity of the jth parameter to the ith output signal and K is the number of sampling points of the output signal.

Note that there is no absolute standard for the level of sensitivity and that only the relative size can be used to evaluate which parameter has a greater impact on the model output.

2.2. Global Sensitivity Analysis Method

The five GSA methods used in this paper are listed in

Table 1. Five GSA methods used in this paper.

Numerical GSA Method	Visualized GSA Method
Sobol method Morris method	Regional sensitivity analysis Scatter plots Andres visualization test

. The numerical value in the results of the numerical GSA method directly represents the sensitivity of the parameter, which is consistent with the form of the LSA result. The analysis result of a visualized GSA method is an image rather than specific values. The sensitivity of parameters depends on the shape of the graph rather than the value represented by the graph. In the following, a brief explanation of how to interpret the analysis results of each GSA method is given.

2.2.1. Sobol Method

The Sobol method is based on variance decomposition. For a model with n parameters, the Sobol method can calculate the first-order sensitivity to the nth-order sensitivity and the total-order sensitivity. The first-order sensitivity S_i represents the influence of a single parameter on the model output [51] and is calculated as

$$S_i=V\left(E\left(Y|X_i\right)\right)/V\left(Y\right)$$

(4)

where V(·) represents the variance; V(Y) is the unconditional variance in Y when all parameters change; X_i represents a series of possible values of parameter x_i within its value range; E(Y|X_i) represents the average value of Y when the value of x_i is fixed and other parameters except x_i are changed. When calculating the second-order sensitivity S_ij, the values of ith and jth parameters are fixed and other parameters are changed, and the other high-order sensitivities can be deduced by analogy. Sensitivity from the second order to the nth order can be used to analyze the correlation between the parameters. The total-order sensitivity S_Ti is the accumulation of the first-order to the nth-order sensitivity [51] and is calculated as Equation (5).

$$S_{Ti}=S_i+\underset{i}{\Sigma }\underset{j>i}{\Sigma }{S}_{ij}+\underset{i}{\Sigma }\underset{j>i}{\Sigma }\underset{l>j}{\Sigma }{S}_{ijl}+\cdots +S_{123\cdots n}$$

(5)

Note that the relevance of parameters and the identifiability of parameters are not equivalent, so we paid more attention to the first-order sensitivity and total-order sensitivity in parameter identification. If the first-order sensitivity of a parameter is small, it cannot be concluded that its influence must be small because it can also play a role through other related parameters, while if the total-order sensitivity of a parameter is small, the influence of this parameter must be small.

2.2.2. Morris Method

The Morris method is also called the elemental effects test [51]. The elementary effect is calculated as Equation (6).

$$E{E}_i=\frac{Y\left(x_1,\cdots ,x_i+\Delta ,\cdots ,x_k\right)-Y\left(x_1,\cdots ,x_k\right)}{\Delta }$$

(6)

where Δ represents a set of preset changes. Equation (6) is similar to the formula of LSA, but each parameter in Equation (6) is randomly selected. When calculating the elementary effects, only one parameter changes each time. The Morris method counts the mean μ and standard deviation (STD) σ of the elementary effects of each parameter. When the mean value of the elementary effects of a parameter is small, it means that the sensitivity of the parameter is low; when the STD of a parameter is small, it means that the correlation between the parameter and other parameters is weak.

2.2.3. Regional Sensitivity Analysis Method

The SAFE toolbox provides a variant of regional sensitivity analysis (RSA) technology, which is called “RSA based on grouping” [49,50] and is referred to as the RSA method in this paper. The RSA method first divides the parameter samples into a given number of groups according to the output of the model. Each group has an equal number of samples. Following that, the cumulative distribution function (CDF) was calculated for each parameter in each group. When the parameter sensitivity is high, its CDF curves are separated; when the parameter sensitivity is low, its CDF curves are close or even overlapping.

2.2.4. Scatter Plot Method

To draw a scatter plot, the model outputs should be calculated first, corresponding to the parameter samples. The horizontal axis of the one-dimensional scatter plot is the value of a certain parameter, and the vertical axis is the value of the model output. In a one-dimensional scatter plot, if the sensitivity of a certain parameter is high, the graph composed of its scatter points will be regular rather than scattered. To determine the correlation between any two parameters, a two-dimensional scatter plot can be drawn. The horizontal and vertical axes of the two-dimensional scatter plot represent the values of the two parameters, and the values of the model output are represented by different colors. If there is a correlation between the two parameters, the maximum or minimum value of the model output will appear in the two-dimensional scatter diagram as obvious “spots” instead of “color bands” or scattered in the two-dimensional scatter chart [50]. However, the scatter plot method has difficulty evaluating the correlation between three or more parameters.

2.2.5. Andres Visualization Test Method

The Andres visualization test (AVT) is also a kind of scatter plot. The AVT first calculates the following three sets of model output samples [50]:

Y: Model output samples obtained after all parameters have been changed;

Y1: Model output samples obtained by changing all parameters except the i-th parameter;

Y2: Model output samples obtained by changing only the i-th parameter.

If the scatter plot (Y, Y1) aligns along the diagonal line from the lower-left corner to the upper-right corner and the scatter plot (Y, Y2) looks like a horizontal line, this suggests that the i-th input is noninfluential; that is, that the sensitivity of the i-th parameter is low.

Overall, the results of the numerical GSA methods are clearer than those of graphical GSA methods, and it is easy to compare the sensitivities among parameters. The graphical GSA methods are suitable for qualitative analysis.

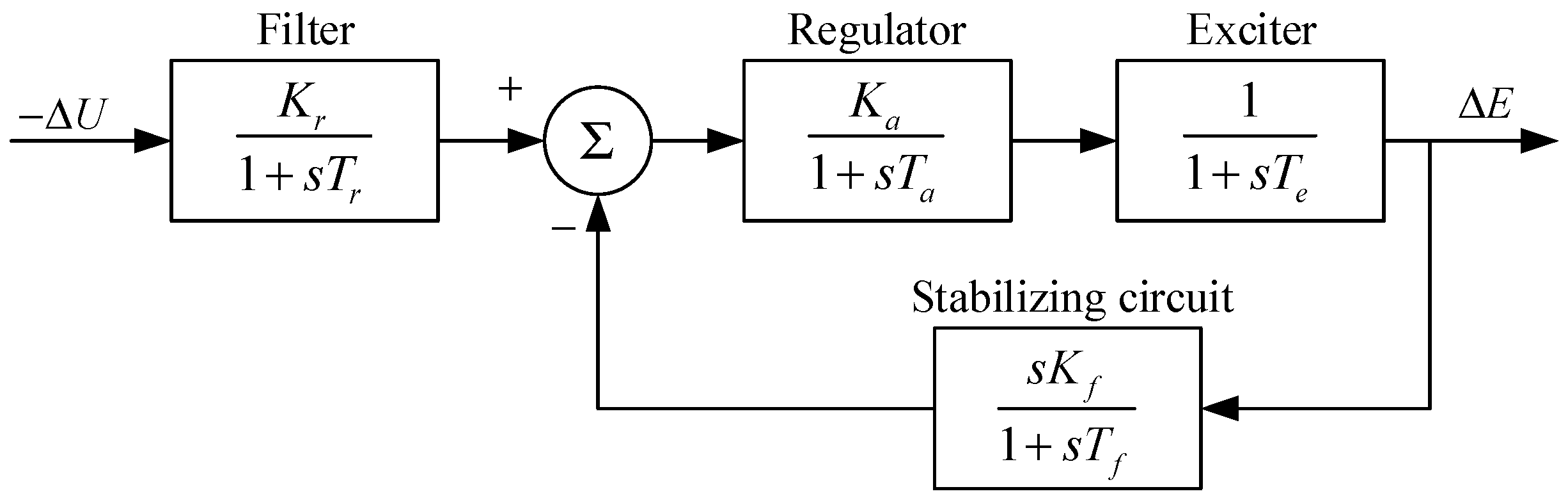
3. Model of Excitation System

There are many types of synchronous generator excitation system models. We took the excitation system model shown in Figure 2 as an example to compare the LSA method and the GSA methods. This model is called Type-I AVR Model in a widely used power system simulation software PSASP V7.35 in China and can be found in the Dynamic Element Model Library User’s Manual of this software. For the convenience of analysis, the saturation elements in the model have been omitted, and the element for calculating the voltage deviation ΔU has been moved before the filter. The input of the model is −ΔU, and the output of the model is the variety of excitation voltages ΔE. There are seven parameters in this model, as listed in

Table 2. Parameters in the model of the excitation system.

Parameter	Symbol	Typical Value
Filter gain	Kr	1.00
Regulator gain	Ka	20.00
Stabilizing circuit gain	Kf	0.04
Filter time constant	Tr	0.04 s
Regulator time constant	Ta	0.04 s
Stabilizing circuit time constant	Tf	0.70 s
Exciter time constant	Te	0.80 s

.

It should be noted that the excitation system model is used as an example not because obtaining the model parameters is difficult in engineering, as many of them can be obtained from the OEM datasheet, but because the identifiability of all parameters of this model can be analytically analyzed by the following formula derivation. Thus, when we discuss the causes of large errors in parameter identification below, we can clearly point out the identification error of which parameter comes from the identifiability problem and that of which parameter comes from the identification method problem. The identification method can be improved; however, the identifiability problem is determined by the model structure and input/output variables. Even if the input/output variables can be changed, they may not be able to solve the identifiability problem.

The identifiability of all parameters in this model is derived as follows:

According to the block diagram shown in Figure 2, the complete transfer function G(s) of the excitation system can be obtained as Equation (7). The expressions of each coefficient in G(s) are shown in Equations (8)–(13).

$$G(s)=\frac{b_{1}s+b_0}{a_4{s}^4+a_3{s}^3+a_2{s}^2+a_{1}s+1}$$

(7)

$$a_4=T_a{T}_e{T}_r{T}_f$$

(8)

$$a_3=T_a{T}_e(T_r+T_f)+(T_a+T_e)T_r{T}_f$$

(9)

$$a_2=T_a{T}_e+(T_r+T_f)(T_a+T_e)+T_r{T}_f+K_f{K}_a{T}_r$$

(10)

$$a_1=(T_a+T_e)+(T_r+T_f)+K_f{K}_a$$

(11)

$$b_1=K_a{K}_r{T}_f$$

(12)

$$b_0=K_a{K}_r$$

(13)

For G(s) in Equation (7), according to the measured data of ΔU and ΔE, the coefficients {a₄, a₃, a₂, a₁, b₁, b₀} can be identified first. Following that, the seven parameters can be solved according to Equations (8)–(13). The identifiability of the seven parameters listed in Table 2 is analyzed through formula derivation as follows.

First, we found that K_aK_r appears only in Equations (12) and (13) and that K_aK_r as a whole can be directly obtained from Equation (13), resulting in values of K_a and K_r that cannot be uniquely determined. Therefore, K_aK_r is identifiable, while neither K_a nor K_r are identifiable.

Then, according to Equations (12) and (13), T_f can be obtained as

$$T_f=b_1/b_0$$

(14)

Substituting Equation (14) into Equations (8) and (11), we obtain

$$T_a{T}_e=a_4{b}_0/T_r{b}_1$$

(15)

$$a_1=(T_a+T_e)+T_r+\frac{b_1}{b_0}+K_f{K}_a$$

(16)

Substituting Equation (15) into Equations (9) and (10), we obtain

$$a_3=\frac{a_4{b}_0}{b_1}+\frac{a_4}{T_r}+\frac{b_1}{b_0}{T}_r(T_a+T_e)$$

(17)

$$a_2=\frac{a_4{b}_0}{b_1{T}_r}+T_r(T_a+T_e)+\frac{b_1}{b_0}[T_r+(T_a+T_e)]+K_f{K}_a{T}_r$$

(18)

According to Equations (16)–(18), the values of T_r, (T_a + T_e), and K_fK_a can be determined as

$$\left\{\begin{array}{l}{T}_r^4-a_1{T}_r^3+a_2{T}_r^2-a_3{T}_r+a_4=0\\ T_a+T_e=\frac{b_0}{b_1}\left(T_r^2-a_1{T}_r+a_2-\frac{a_4{b}_0}{b_1{T}_r}\right)\\ K_f{K}_a=a_1-b_1/b_0-T_r-\left(T_a+T_e\right)\end{array}\right.$$

(19)

In Equation (19), the equation of T_r is a one-variable quaternary equation whose root-finding formula is too complicated to use to analyze the results. Therefore, we adopted numerical analysis. According to the typical values of the parameters listed in Table 2, we can obtain the four roots of T_r as

$$\begin{array}{l}{T}_{r(1)}=2.0417,T_{r(2)}=0.2553\\ T_{r(3)}=0.0430,T_{r(4)}=0.0400\end{array}$$

(20)

Considering that both (T_a + T_e) and K_fK_a should be greater than zero, T_r(1) can be excluded. Considering that the value of T_r is usually in the range of [0.00 s, 0.06 s], T_r(2) is excluded. However, T_r(3) and T_r(4) cannot be further screened. Therefore, we obtained two groups of solutions for Equation (19) as follows:

$$\left\{\begin{array}{l}{T}_r=0.0430\\ T_a+T_e=0.8334\\ K_f{K}_a=0.8036\end{array}\right. \mathrm{or} \left\{\begin{array}{l}{T}_r=0.0400\\ T_a+T_e=0.8400\\ K_f{K}_a=0.8000\end{array}\right.$$

(21)

Considering that the difference between the two solutions in Equation (21) is less than 1%, it is approximately considered that T_r, (T_a + T_e), and K_fK_a are identifiable.

Finally, after the value of (T_a + T_e) is obtained, the values of T_a and T_e can be obtained according to Equation (15). Therefore, both T_a and T_e are identifiable. Although the value of K_fK_a can be obtained, K_fK_a always appears as a whole. Therefore, K_fK_a is identifiable; however, neither K_f nor K_a are identifiable.

In summary, in the excitation system model, the parameters K_aK_r, K_fK_a, T_r, T_a, T_f, and T_e are identifiable, while K_r, K_a, and K_f are unidentifiable. Therefore, we want to emphasize that the high sensitivity of parameters does not mean that parameters can be uniquely identified. The sensitivity analysis results in the next section show that the sensitivities of K_r, K_a, and K_f are significantly higher than other parameters; however, their values cannot be uniquely determined according to the identifiability analysis result. In Section 5 and Section 6, both K_aK_r and K_fK_a are taken as single parameters for identification.

4. Sensitivity Analysis Results

This section will use the LSA method introduced in Section 2.1 and five GSA methods introduced in Section 2.2 to perform sensitivity analysis on the excitation system model parameters introduced in Section 3 and compare the analysis results.

The input used in the following sensitivity analysis is a voltage sag with a duration of 0.2 s and depth of 0.1 p.u.

For GSA, the output of the model is defined as the mean relative error (MRE) between the response of the excitation system with unchanged parameters and the response after parameter changes as follows:

$$\mathrm{MRE}=\frac{1}{N}{\displaystyle \sum _{k=1}^N\left|[y_c\left(k\right)-y_0\left(k\right)]/y_0\left(k\right)\right|}\times 100\%$$

(22)

where N is the number of data points on the excitation system output curve; k is the index of the data point; y₀ is the response with unchanged parameters; y_c is the response after parameter changes; both y₀ and y_c are the sum of the steady-state value of the excitation voltage and the variety of excitation voltage output by the excitation system model.

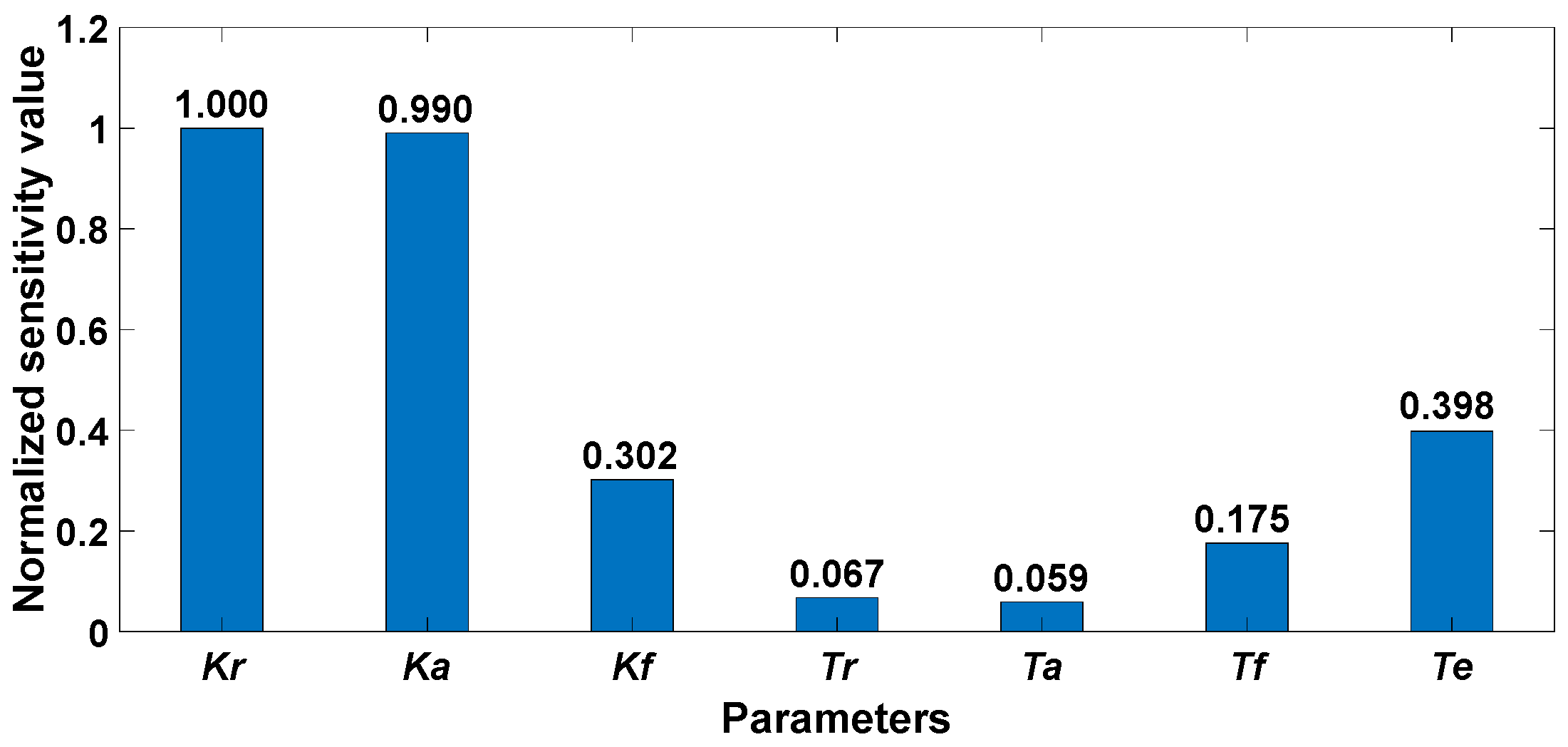
4.1. LSA Results

To facilitate the comparison of the sensitivity of each parameter, we normalized the LSA results based on the maximum sensitivity value. Figure 3 shows the normalized values of the local sensitivity of the seven parameters.

There is no uniform standard for determining the key parameters that need to be identified according to the sensitivity, and it is often determined based on the experience of the researcher. We took 1/10 of the maximum sensitivity as the boundary for distinguishing high and low sensitivity. Therefore, the most sensitive parameters K_r and K_a are definitely recognized as key parameters. Since the sensitivity of K_f, T_f, and T_e is larger than 1/10 of the maximum sensitivity, they are also regarded as key parameters. The sensitivities of T_r and T_a are only approximately 1/15 and 1/16 of the maximum sensitivity, respectively, and they can be regarded as non-key parameters.

4.2. GSA Results

We refer to the typical values of the excitation system parameters in a simulation software named PSASP V7.35 which is developed by China Electric Power Research Institute and set the value ranges of the seven parameters as listed in

Table 3. Value range of the excitation system parameters.

Parameter	Value Range	Parameter	Value Range
Kr	[0.01, 2.00]	Tr	[0, 0.06]
Ka	[1, 100]	Ta	[0, 0.2]
Kf	[0.01, 0.5]	Tf	[0, 2]
		Te	[0, 2]

. When performing GSA, each parameter is set to be uniformly distributed within its value range, and Latin hypercube sampling is used when sampling the parameters, which is a commonly used GSA setting. To ensure the convergence of the analysis results of the numerical GSA methods, the number of parameter samples is 5000. For the graphical GSA methods, the number of parameter samples is 3000, and the generated graphics are clear enough to judge the sensitivity of the parameters.

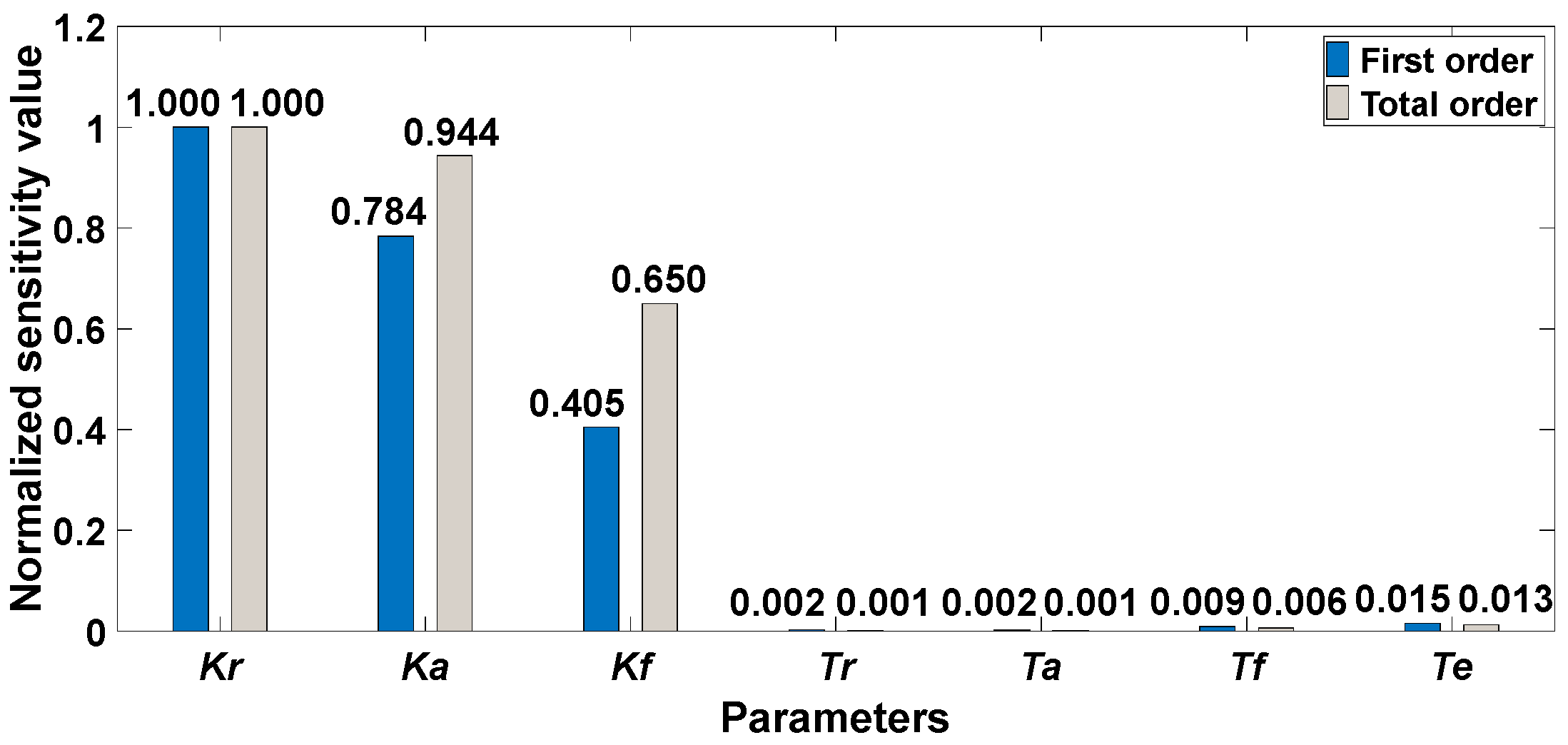
4.2.1. Sobol Method

Figure 4 shows the normalized sensitivity values of the excitation system parameters obtained using the Sobol method. Although the ranking of parameter sensitivity is consistent with the LSA result, the sensitivity difference between the high- and low-sensitivity parameters is significantly greater than the LSA result. For either the first-order sensitivity or the total-order sensitivity, the sensitivity of the three gain parameters K_a, K_r, and K_f is much greater than the sensitivity of the four time constants T_r, T_a, T_f, and T_e; therefore, the three gain parameters can be selected as the key parameters that need to be identified. The difference between the sensitivity of the four time constants and the maximum sensitivity is far greater than 10 times, so they can be considered non-key parameters.

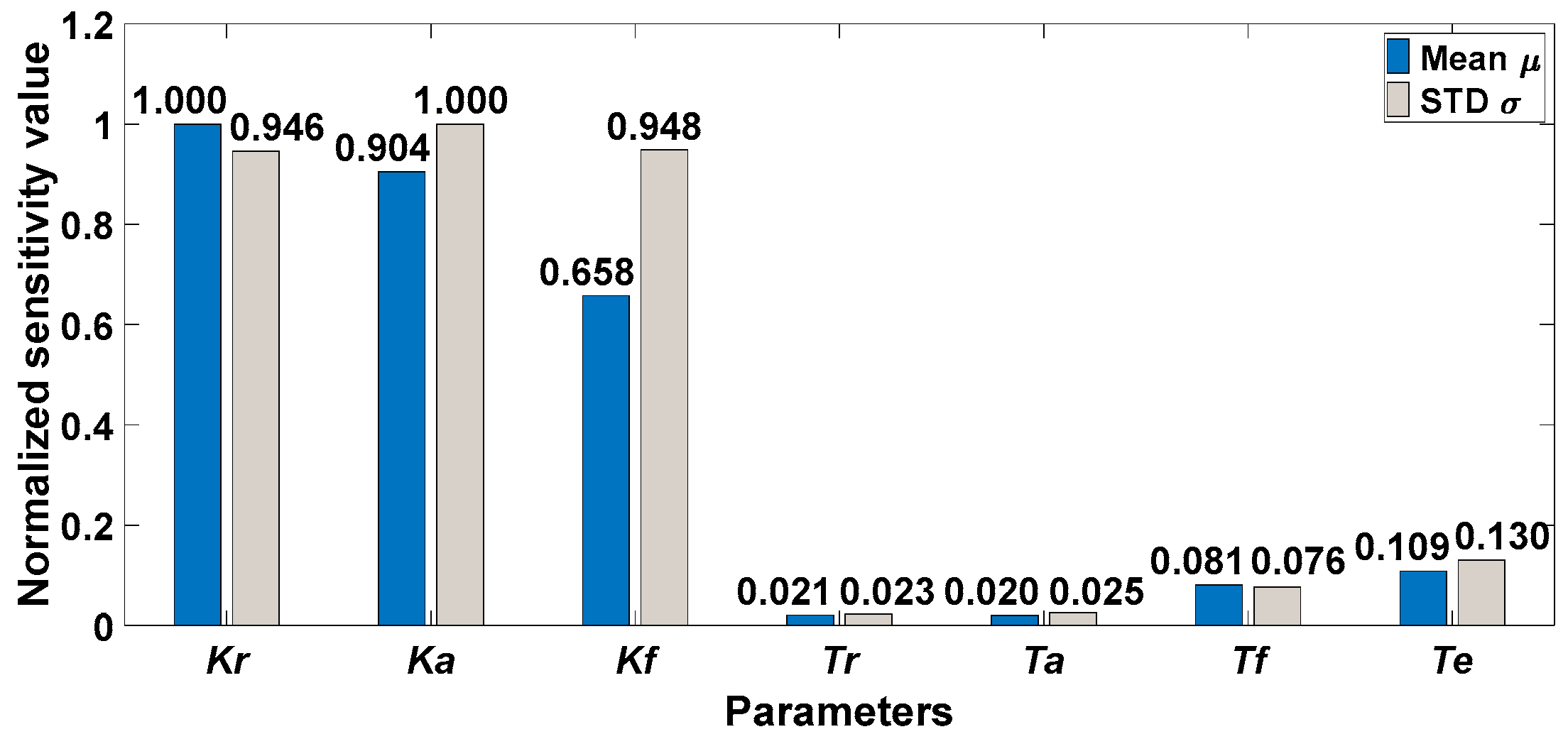
4.2.2. Morris Method

Figure 5 shows the normalized sensitivity values of the excitation system parameters obtained using the Morris method. The sensitivity difference between the high- and low-sensitivity parameters is also several times the result of the LSA method. The ranking of parameter sensitivity is consistent with the results of both the LSA and Sobol methods. In addition to the three gain parameters that should be regarded as key parameters, the difference between the average value and standard deviation of the elementary effects of T_e and the corresponding maximum value is slightly less than 10 times, so T_e can also be regarded as a key parameter.

4.2.3. RSA Method

The analysis result of RSA is shown in Figure 6. According to the RSA analysis method described in Section 3, we also divided the model output into 10 groups to obtain 10 CDF curves for each parameter. Figure 6 shows that the 10 curves of K_r, K_a, and K_f are scattered, especially the curves of K_r and K_a, which represent their high sensitivity. Among the four time constants, the CDF curves of T_r are relatively scattered, but the degree of dispersion is not as good as the three gain parameters, and the CDF curves of other time constants are very close. 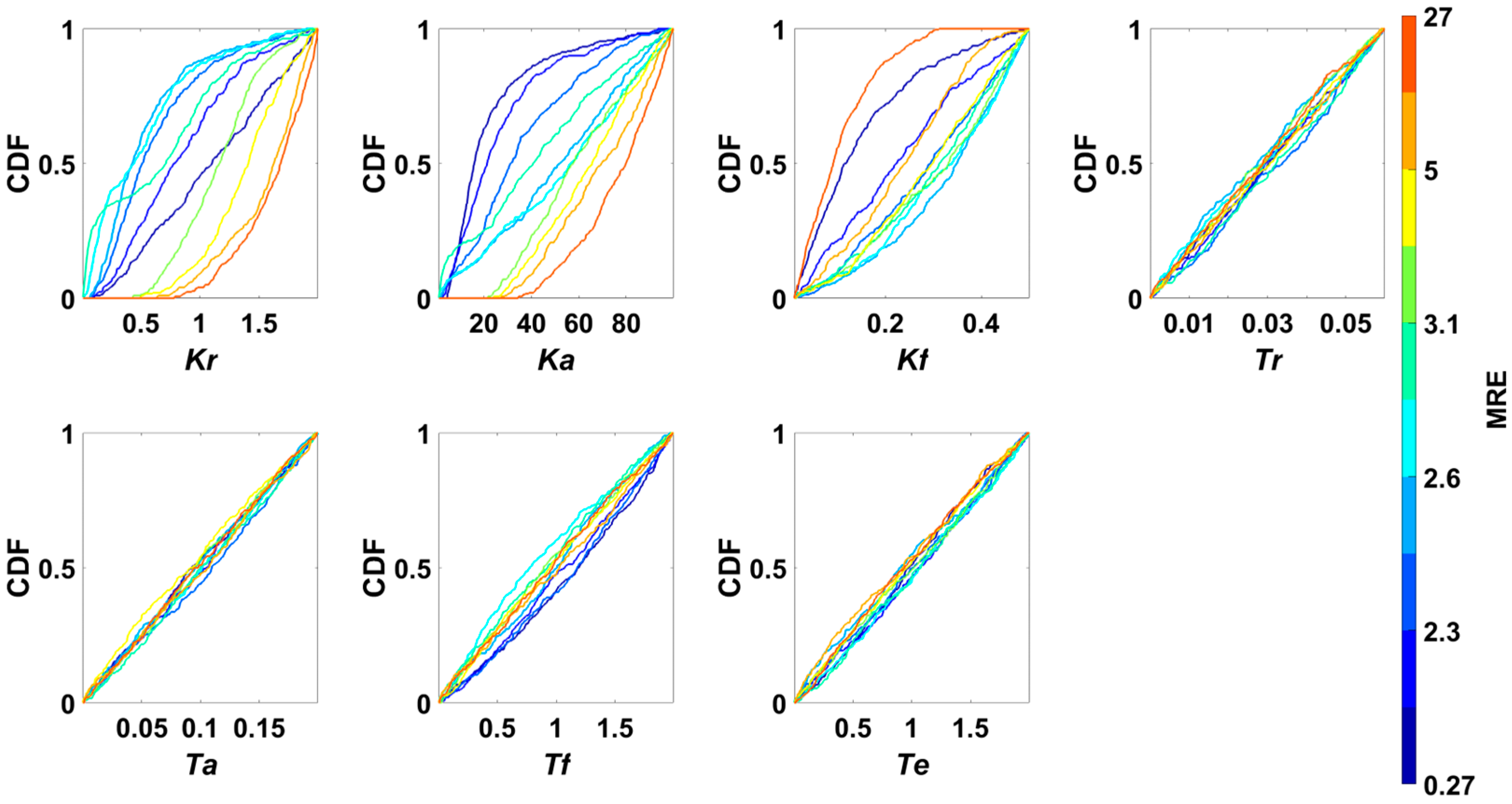Therefore, only three gain parameters can be considered as key parameters from the graph, which is consistent with the results of the Sobol method.

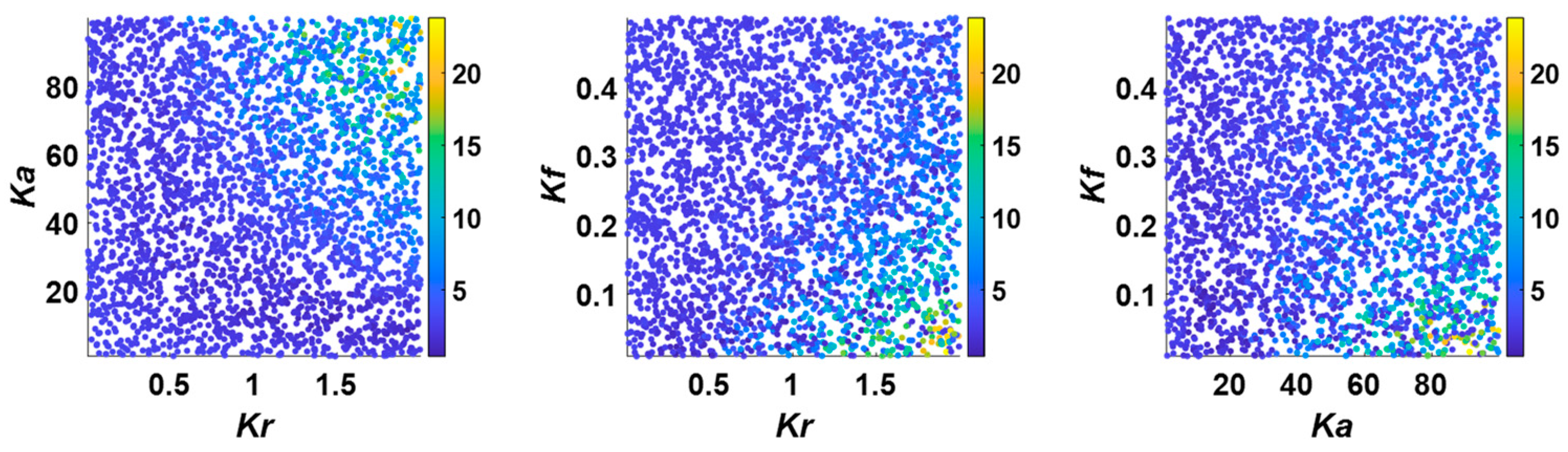
4.2.4. Scatter Plot Method

Figure 7 shows the one-dimensional scatter plot of each parameter of the excitation system. According to the scatter plot interpretation method described in Section 3, the parameters with high sensitivity are still three gain parameters because the relationship between the parameter value and the reduction in the MRE can be clearly seen. Because the scatter plots of the four time constants are very scattered and there is no clear relationship between the parameter values and the MRE value, their sensitivity is low. The above conclusion is consistent with the conclusion derived from the RSA graph.

Two-dimensional scatter plots can be used to reveal the relationship between two parameters. Figure 8 shows the two-dimensional scatter plot of the three gain parameters, where yellow spots can be observed. Taking the two-dimensional scatter plot of K_r–K_a as an example, according to the position of the yellow spot, it can be concluded that the MRE only increases when the values of K_r and K_a approach the upper limit of their value range at the same time. Therefore, there is a correlation between K_r and K_a. Similarly, the correlation between K_a–K_f and K_r–K_f can be analyzed. Because no correlations are found in the two-dimensional scatter plots of other parameters, those graphs are omitted.

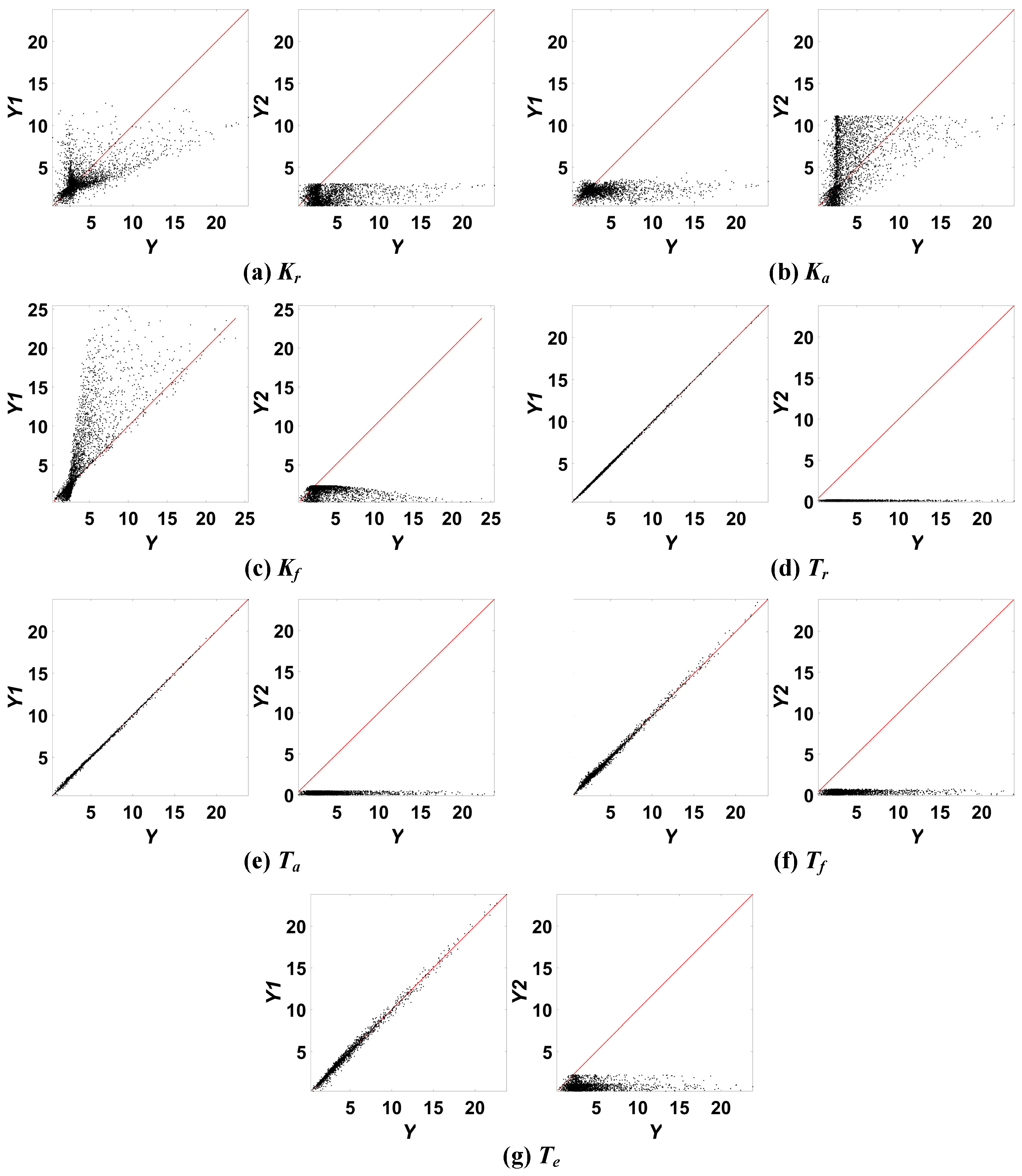
4.2.5. AVT Method

Figure 9 shows the AVT results of all parameters of the excitation system. The graphs of the three gain parameters in the (Y, Y1) scatter plot are obviously asymmetric to the diagonal; in the (Y, Y1) scatter plot, their graphs are not horizontally distributed. In the (Y, Y1) scatter plots of four time constants, the graphs are close to the diagonal; in the (Y, Y2) scatter plot, the graphs of T_r, T_a, and T_f are basically horizontal lines. According to the interpretation method of the AVT results, the sensitivity of the three gain parameters is much greater than that of the four time constants. The sensitivity of T_e is slightly greater than that of the other three time constants.

4.3. Comparison of the LSA and GSA Results

Comparing the use of LSA and GSA, as well as the above analysis results, we can obtain the following conclusions:

• In terms of the amount of calculation, the GSA is far more than that of LSA. The relationship between the number of times that various sensitivity analysis methods calculate the model output, the number of parameters N, and the number of parameter samples N_s is summarized in

  Table 4. Calculation amount of the sensitivity analysis methods.

  Method	Amount of Calculation	Method	Amount of Calculation
  LSA	2 × N	RSA	Ns
  Sobol	(N + 2) × Ns	Scatter plot	Ns
  Morris	(N + 1) × Ns	AVT	Ns

  . If the single calculation of the model output is time-consuming, unless a suitable algorithm is found [52,53], the analysis speed of the GSA method may be unacceptable.
• Both LSA and GSA can be used to distinguish between key and non-key parameters. Although the LSA method and the numerical GSA method have the same parameter-sensitive ordering, the key parameters determined by the two kinds of methods are different. The key parameters in the LSA result are {K_r, K_a, T_e, K_f, T_f}. When integrating the results of the five GSA methods, the key parameter is {K_r, K_a, K_f}. The reason is that the difference in parameter sensitivity is more significant in the GSA results, resulting in fewer key parameters being found.
• Although the analysis process and result display form of the five GSA methods are different, the conclusions are the same. Therefore, there is no need to use multiple GSA methods at the same time. Because the results of numerical methods are clearer and can be used to rank parameter sensitivity, we recommend the numerical GSA method.

We compared the differences in the use and analysis results of LSA and GSA in this section. However, it is difficult to evaluate which method better achieves parameter identification from these two aspects only. In the next two sections, we used different parameter identification strategies to analyze the impact of different key parameter combinations obtained by GSA and LSA on the identification accuracy.

5. Comparison under Existing Parameter Identification Strategy

This section will use the commonly used parameter identification methods to identify the parameters of the excitation system and discuss the effectiveness of various sensitivity analysis methods according to the accuracy of parameter identification.

According to the existing parameter identification process shown in Figure 1, the key parameters are identified, and the non-key parameters take typical values or empirical values. Since the value of the non-key parameters of the actual equipment is not clear, it is difficult to determine how accurate the typical value or the empirical value is. Therefore, we randomly selected non-key parameters within their value ranges and then analyzed the identification results of key parameters.

According to the identifiability analysis result in Section 3, both the K_aK_r and K_fK_a should be identified as a whole, and their accurate values are 20.00 and 0.800, respectively.

A PSO algorithm with linearly decreasing weight coefficients [54] was adopted for parameter identification. The number of particles is 20, the number of iterations is 200, the learning factors C1 and C2 are set to 2, and the weight factor decreases linearly from 0.9 to 0.4. The fitting error index uses the MRE in Equation (22).

5.1. Identification Result According to LSA

According to the LSA results, the key parameters to be identified are K_aK_r, K_fK_a, T_e, and T_f. The non-key parameters T_r and T_a take random values, and their different values have a significant impact on the identification results.

Table 5. Identification results of the excitation system parameters according to LSA.

Result	Parameters						Fitting Error
	* Tr	* Ta	KaKr	KfKa	Tf	Te
1	0.049	0.181	18.54	1.018	0.472	0.546	0.29%
2	0.060	0.077	19.46	0.887	0.626	0.693	0.16%
3	0.056	0.083	19.44	0.890	0.620	0.688	0.16%
4	0.047	0.112	19.26	0.938	0.579	0.629	0.20%
5	0.018	0.106	19.72	0.865	0.626	0.704	0.11%
6	0.056	0.044	19.86	0.837	0.680	0.754	0.05%
7	0.032	0.086	19.71	0.845	0.645	0.735	0.11%
8	0.017	0.050	20.26	0.784	0.712	0.809	0.04%
9	0.050	0.030	19.90	0.815	0.766	0.846	0.07%
10	0.015	0.075	20.00	0.799	0.682	0.789	0.03%
Emin	—	—	0.02%	0.11%	1.78%	1.13%	0.03%
Emax	—	—	7.30%	27.3%	32.6%	31.8%	0.29%
Eavr	—	—	2.19%	8.90%	10.7%	11.5%	0.12%

*: T_r and T_a take random values.

lists the results of 10 identifications. E_min, E_max, and E_avr in Table 5 refer to the minimum, maximum, and average values of the identification errors, respectively.

From the identification results, only the combination of the two highest sensitive parameters K_aK_r has good identification accuracy, while the identification accuracy of other parameters is not good because their average identification error exceeds 10%. Therefore, although the sensitivity of the non-key parameters T_r and T_a is very small, their imprecision has a significant negative impact on the identification accuracy of the key parameters. Although the key parameters in the model can be found through sensitivity analysis, identifying only the key parameters cannot ensure the improvement of identification accuracy. The accuracy of non-key parameters also plays an important role in improving the accuracy of parameter identification.

5.2. Identification Result According to GSA

Combining the results of the five GSA methods, we set the key parameters that need to be identified as K_aK_r and K_fK_a, while T_r, T_a, T_f, and T_e take random values.

Table 6. Identification results of the excitation system parameters according to GSA.

Result	Parameters						Fitting Error
	* Tr	* Ta	* Tf	* Te	KaKr	KfKa
1	0.053	0.200	1.599	1.558	16.04	0.369	0.77%
2	0.032	0.036	0.461	1.995	15.58	0.078	0.69%
3	0.035	0.116	0.045	0.548	16.73	1.198	0.59%
4	0.011	0.169	1.571	1.191	18.25	0.648	0.63%
5	0.048	0.003	0.953	1.625	17.20	0.262	0.46%
6	0.021	0.065	1.315	0.649	18.90	0.984	0.55%
7	0.022	0.043	0.475	1.002	18.99	0.668	0.27%
8	0.042	0.159	1.534	1.503	16.75	0.408	0.68%
9	0.051	0.170	0.539	1.301	16.26	0.501	0.55%
10	0.027	0.123	1.157	0.669	20.07	0.950	0.51%
Emin	—	—	—	—	0.36%	16.5%	0.27%
Emax	—	—	—	—	22.1%	90.3%	0.77%
Eavr	—	—	—	—	12.7%	42.5%	0.57%

*: Tr, Ta, Tf, and Te take random values.

lists the results of 10 identifications. A comparison of the results of Table 5 and Table 6 indicates that since a total of four non-key parameters do not participate in the identification according to the GSA results, the identification accuracy of the two key parameters K_aK_r and K_fK_a is significantly lower than that of the LSA-result-based identification. This result again shows that the accuracy of low-sensitivity parameters cannot be ignored in parameter identification.

5.3. Example of High Sensitivity Not Equating to Identifiability

The derivation of the formula in Section 3 has shown that the single parameters K_r, K_a, and K_f are not uniquely identifiable, and only their products K_aK_r and K_fK_a are uniquely identifiable.

Table 7. The identification results of the three gain parameters of Table 5.

Result	Parameters					Fitting Error
	Kr	Ka	Kf	KaKr	KfKa
1	0.678	27.35	0.037	18.54	1.018	0.29%
2	1.457	13.36	0.066	19.46	0.887	0.16%
3	0.218	89.00	0.010	19.44	0.890	0.16%
4	0.911	21.15	0.044	19.26	0.938	0.20%
5	1.187	16.61	0.052	19.72	0.865	0.11%
6	0.764	26.00	0.032	19.86	0.837	0.05%
7	1.582	12.45	0.068	19.71	0.845	0.11%
8	0.258	78.38	0.010	20.26	0.784	0.04%
9	0.344	57.89	0.014	19.90	0.815	0.07%
10	0.250	79.91	0.010	20.00	0.799	0.03%
Emin	8.92%	5.73%	6.94%	0.02%	0.11%	0.03%
Emax	78.2%	344%	75.0%	7.30%	27.3%	0.29%
Eavr	48.0%	128%	49.3%	2.19%	8.90%	0.12%

shows the identification results of K_r, K_a, and K_f corresponding to the K_aK_r and K_fK_a in Table 5. As can be seen from Table 7, since the errors of K_aK_r and K_fK_a are small, the fitting error of the model output is already small, but the identification results of the three gain parameters K_r, K_a, and K_f are still very scattered. Small model fitting errors but scattered parameter identification results are typical features of identifiability problems, which also proves the correctness of the derivation in Section 3. According to the sensitivity analysis results in Section 4, the sensitivity of parameters K_r, K_a, and K_f is significantly greater than that of other parameters. This example clearly shows that the high sensitivity of a parameter is not equivalent to a parameter being identifiable.

5.4. Discussion of the LSA-Based and GSA-Based Identification Results

By comparing the LSA-based and GSA-based parameter identification results, we found that the small sensitivity of the parameter means that it has only a small impact on the model output. This does not mean that its deviation from the true value has little effect on the identification accuracy of other parameters. Without knowing the exact value of the non-key parameter, when more non-key parameters do not participate in the identification, the possibility of the key parameters being accurately identified decreases. Because GSA amplifies the sensitivity difference between the high- and low-sensitivity parameters, the non-key parameters that are not involved in the identification increase, resulting in a decrease in the identification accuracy of the key parameters.

In general, under the existing identification strategy that identifies only key parameters, GSA does not show advantages over LSA. In the next section, to solve the negative impact of inaccurate non-key parameters on the identification accuracy, a modified groupwise alternating identification method of high- and low-sensitivity parameters was used to compare the effects of LSA and GSA.

6. Comparison under an Alternating Identification Strategy of High- and Low-Sensitivity Parameters

Alternating the identification of high- and low-sensitivity parameters is a novel method, but it is rarely used at present. In this section, some problems in the existing alternate identification method are first improved, and then the improved method is used to identify the excitation system parameters. Finally, the guiding significance of the LSA method and GSA methods for parameter identification is discussed according to the improvement of identification accuracy.

6.1. Process of the Alternating Identification

Reference [48] proposed the GAIS to identify all the parameters in the electric model of Li-ion batteries successfully by alternately identifying parameter groups with different sensitivity levels. We consider the GAIS an effective method to improve the accuracy of parameter identification. We made some modifications to the GAIS to adapt to our research, and the modified GAIS process is shown in Figure 10. The modifications made are as follows:

• Parameter identifiability analysis uses formula derivation or numerical methods [3] instead of the GSA methods. The identifiability analysis results in Section 3 and the sensitivity analysis results in Section 4 clearly show that the high sensitivity of the parameters does not mean that the parameters can be uniquely identified, such as three gain parameters K_r, K_a, and K_f.
• Sensitivity can be analyzed by LSA or GSA. The parameters are divided into only two groups, namely, the high-sensitivity parameter group and the low-sensitivity parameter group. The boundary of the grouping is 1/10 of the highest sensitivity value.
• The initial value of each parameter is obtained by identifying all the parameters at the same time once.
• Alternating identification starts from the low-sensitivity parameter group because, in the first identification of all parameters, the accuracy of the high-sensitivity parameter group is higher than that of the low-sensitivity parameter group.
• The random search of the PSO algorithm does not guarantee that each round of search can obtain a better fitting accuracy of the model output. Therefore, 10 opportunities are set for the identification of each parameter group. If the fitting error cannot be reduced within 10 identification iterations, the entire identification process ends.
• The expected final value of the fitting error is set to less than 0.01%.
• In the following comparison, when the GAIS can at least improve the identification accuracy of all key parameters, the identification is considered successful.

6.2. Application of LSA and GSA in the Alternate Identification Process

We used LSA and GSA to perform the alternating identification process 100 times each. The high- and low-sensitivity parameter grouping results are the same as those in Section 5.

Figure 11 shows the statistical results of many parameters whose identification accuracy can be improved each time in a total of 100 times of alternating identification. We found the following.

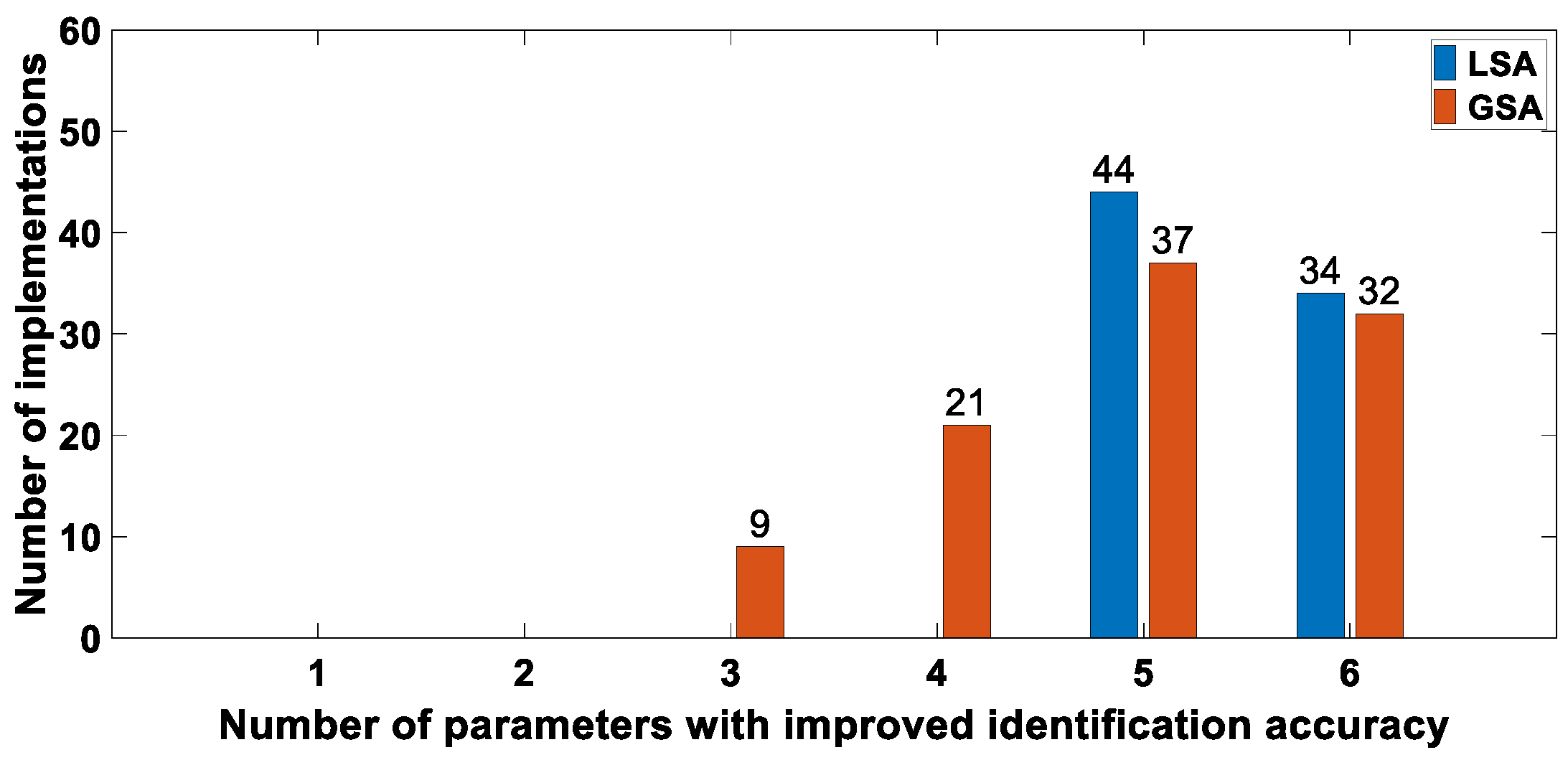
• For parameter groups obtained by LSA, the success rate of GAIS is 78%. In the 100 identifications, the identification accuracy of all parameters was improved in 34 identifications, and the identification accuracy of all key parameters and one non-key parameter was improved in 44 identifications.

  Table 8. Example of the identification results of the GAIS based on the parameter grouping result of LSA.

  Result	Parameters						Fitting Error
  	KaKr	KfKa	Tr	Ta	Tf	Te
  Initial	18.95	0.871	0.034	0.137	0.457	0.688	0.25%
  	5.26%	8.88%	14.4%	242%	34.7%	14.0%
  Final	19.99	0.812	0.052	0.032	0.687	0.778	0.01%
  	0.07%	1.45%	28.7%	20.5%	1.81%	2.72%

  gives an example that only the accuracy of the parameter T_r did not improve, while the identification accuracy of other parameters and the fitting error of the model were significantly improved.
• For parameter groups obtained by GSA, the success rate of GAIS is 99%. In 99 successful identifications, the accuracy of at least three parameters (two key parameters and one non-key parameter) can be improved. The identification accuracy of all parameters is improved in 32 identifications, which is very close to the identification results based on LSA.

  Table 9. Example of the identification results of the GAIS based on the parameter grouping result of GSA.

  Result	Parameters						Fitting Error
  	KaKr	KfKa	Tr	Ta	Tf	Te
  Initial	20.42	0.893	0.031	0.052	0.800	0.812	0.11%
  	2.09%	11.6%	23.8%	30.0%	14.3%	1.49%
  Final	20.03	0.826	0.057	0.028	0.701	0.767	0.01%
  	0.16%	3.19%	42.6%	30.3%	0.12%	4.09%

  gives an example that the identification accuracy of only the three parameters K_aK_r, K_fK_a, and T_f are improved, and the identification accuracy of other parameters remains unchanged or slightly reduced.

Figure 12 shows the statistical results of the identification errors of each parameter in the successful results of groupwise alternating identification. The blue in the figure represents the result of using LSA, and the orange represents the result of using GSA. The length of the line segment represents the range of identification errors, the top-of-the-line segment is the maximum error, the bottom-of-the-line segment is the minimum error, and the circle-on-the-line segment represents the average value of the error. In general, when GAIS is used, the parameter identification accuracy obtained by using LSA or GSA is equivalent, and the average identification error using LSA is slightly better than that using GSA. The ranking of parameter identification accuracy and the ranking of sensitivity (regardless of LSA or GAS) correspond. However, the difference between the parameter identification accuracy and the sensitivity difference of LSA is more compatible. In the GSA results, the sensitivity of the four time constants is much smaller than that of the three gain parameters, but the identification accuracy of T_f and T_e in the identification result is similar to that of K_aK_r and K_fK_a.

The comparison results in this section show that to improve the identification accuracy, it is more important to improve the identification strategy than to change the sensitivity analysis method. When there is a good parameter identification strategy, both GSA and LSA can play a role.

7. Conclusions

Sensitivity analysis plays an important role in the parameter identification of power systems. The use of LSA has a long history, and in recent years, GSA has gradually begun to be adopted. However, there is no clear conclusion on the impact of different sensitivity analysis methods on parameter identification results. Therefore, this paper compares and studies the roles that LSA and GSA can play in different parameter identification methods, providing clear guidance for the selection of sensitivity analysis methods and parameter identification methods. The conclusions are as follows:

• The calculation amount of the GSA methods is much larger than that of the LSA method, especially the numerical GSA methods. The GSA method may be inconvenient to use in a model that takes a long time for a single calculation;
• The results of the five GSA methods on the grouping of high- and low-sensitivity parameters are the same. Because the difference in the high- and low-sensitivity values is more prominent in the GSA results, the grouping results of the key and non-key parameters are different from the LSA method;
• Under the strategy of identifying only key parameters, the identification accuracy based on the GSA is not as good as that based on the LSA when the non-key parameters are inaccurate because the GSA enlarges the difference between high- and low-sensitivity values, resulting in more non-key parameters found;
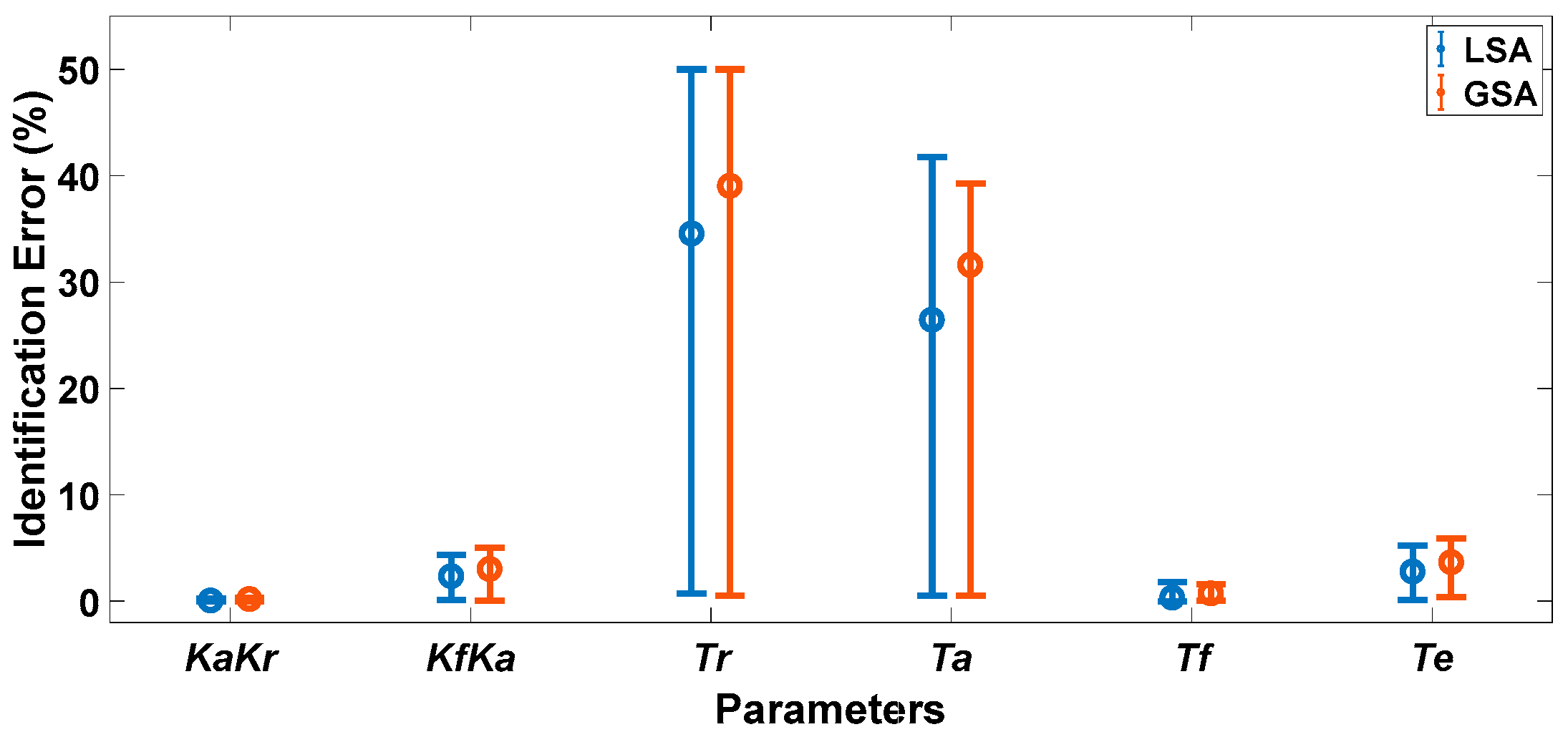
• When the groupwise alternating identification strategy of high- and low-sensitivity parameters is used, the identification accuracy based on the LSA or GSA is equivalent. However, LSA is better than GSA in terms of the corresponding relationship between identification accuracy and sensitivity values.

In summary, for the example used in this paper, both the GSA and LSA can be used to find the key parameters in the model; however, the GSA methods do not show absolute advantages over the LSA method. To improve the identification accuracy, it is more important to improve the identification strategy than to change the sensitivity analysis method. If the identification strategy that identifies only key parameters is adopted, we still recommend using the existing LSA method. If the GAIS of high- and low-sensitivity parameters is adopted, either LSA or GSA can be used. In addition, through the example used, we also want to emphasize that the high sensitivity of a parameter does not prove that this parameter must be identifiable.