Clustering Combined Multi-Objective Optimal Operation of Transmission Systems Considering Voltage Stability

Abstract

In recent years, power systems have undergone major changes called energy transitions during which synchronous generators have been replaced with power electronics-based generation. Therefore, the voltage stability of power systems has become a major concern owing to the absence of synchronous generators. This study proposes multi-objective optimization using the non-dominated sorting genetic algorithm III to achieve optimal reactive power reserve procurement and improve the voltage stability of the overall system. These systematic approaches require high computational power and are unsuitable for the operational frameworks currently used for large-scale power systems. Previous works have rarely considered the local characteristics of reactive power or generation de-commitment with sufficient re-dispatch owing to greater renewable energy integration. We propose a framework for achieving systematic optimization by considering various objective functions while utilizing the regional aspect of reactive power via spectral clustering-based voltage control area (VCA) identification. The proposed method comprises systematic and regional approaches to optimizing systems for voltage stability improvement based on VCAs. The results demonstrate that the proposed method shows satisfactory performance. These results will be helpful for decision making for power system operations in harsher environments with more renewable energy.

1. Introduction

Power systems are undergoing major changes, such as electrification and carbon neutrality, which are causing continuous increases in electricity demand and in the penetration rate of renewable energy sources [1,2]. In these unavoidable situations, increased load with limited investment in transmission facilities and variability in renewable energy generation cause power systems to operate in more stressful conditions and close to their voltage stability limits [3]. To deal with these problems, energy storage systems are an attractive resource; however, they requires additional investment [4].

Reactive power plays an important role in maintaining the voltage stability of a system. It is consumed while active power is delivered to the demand region and operating power facilities. Insufficient supply of the required reactive power may lead to voltage instability; therefore, the appropriate procurement of reactive power reserves is essential for stable system operation [5]. Moreover, because renewable energy sources are replacing the conventional generators that provide most of the reactive power reserves in transmission systems, the shortage of reactive power reserves is a concern. Consequently, the planning and operation of large-scale transmission systems must involve the assessment and optimization of the reactive power reserves of the available generators.

Studies have focused on the reactive power reserves of systems. Various definitions of the generator reactive power reserve (GRPR) were provided according to the maximum limit of the reactive power in [6]. The authors investigated four types of GRPR defined in terms of the constant maximum reactive power, capability curves, the minimum voltage limit and the voltage collapse limit. In [7], the authors suggested that the last two definitions cannot be employed practically because of the difficulties in determining the operating point of the minimum voltage limit and voltage collapse limit in online operations.

To enhance voltage stability, studies focusing on reactive power reserve optimization have been conducted. Although these studies did not consider the local characteristics of the reactive power, they formulated the maximization of the reactive power reserve as an objective function and demonstrated its effectiveness [8,9,10,11,12,13]. Moreover, this aspect was considered in [14,15]. Voltage control areas (VCAs) have been considered when assessing the reactive power reserve; however, the V-Q curve was used to constitute the VCAs and determine the reactive margin in each area [14]. Therefore, a long computation time would be required for large-scale systems. Although VCAs were identified, the focus was only on determining the critical buses in each area [15]. Therefore, this method would not be appropriate to assess the overall voltage stability or that of each area.

A power system partitioning approach has been utilized to establish an efficient operating strategy for large-scale power systems [16]. Moreover, spectral clustering has been used to efficiently partition a system into several areas for operation strategies by utilizing the electrical distance as a clustering criterion [17,18,19].

In addition, optimal reactive power dispatch (ORPD) has also been studied [20,21,22,23]. Owing to the nonlinear nature of the ORPD problem, various heuristic techniques have been applied to solve it [24]. For the heuristic techniques, a non-dominated sorting genetic algorithm (NSGA) called NSGA-III was proposed and its excellent performance was demonstrated [25,26]. This method is particularly appropriate for multi-objective problems owing to its ability to quickly select excellent individuals and ensure the diversity of optimal candidates.

In this study, a framework for clustering combined multi-objective optimal operation is proposed considering voltage instability and the regional characteristics of reactive power. Our proposed method significantly improves the voltage stability margin by obtaining an adequate reactive power reserve while securing the reliability of the system and reducing the operating cost. The proposed framework consists of two stages, where the first and second stages are for the operating strategies of the entire system and of each VCA used by the ORPD, respectively. Each stage uses NSGA-III to determine the optimal solution for handling nonlinear multi-objective problems. Simulations were conducted to demonstrate the effectiveness of the proposed method, and the results are presented. The results show that the proposed method significantly improves the overall voltage stability and the other objective functions. In addition, the results show that the proposed multi-objective operating strategy has superior characteristics, regardless of the multi-objective problem’s inherent trade-offs in relation to each objective function. Also, the proposed framework with a clustering approach reduces the unnecessary complexity of large-scale transmission systems and improves efficiency through appropriate VCA identification by considering the regional characteristics of reactive power.

2. Assessment of the Reactive Power Reserve in Voltage Control Areas

To consider the regional aspect of reactive power, the reactive power reserve was calculated with respect to the VCA. A VCA is a zone that can be used to effectively control the voltage in consideration of this point. As reactive power cannot travel long distances, the voltage is mainly affected by the reactive power from nearby areas; in particular, where the electrical distance is small. Therefore, the VCAs of transmission systems can be identified based on the electrical distance between the nodes [27,28]. Managing reactive power depending on its region by utilizing VCAs may facilitate the efficient maintenance and enhancement of voltage stability.

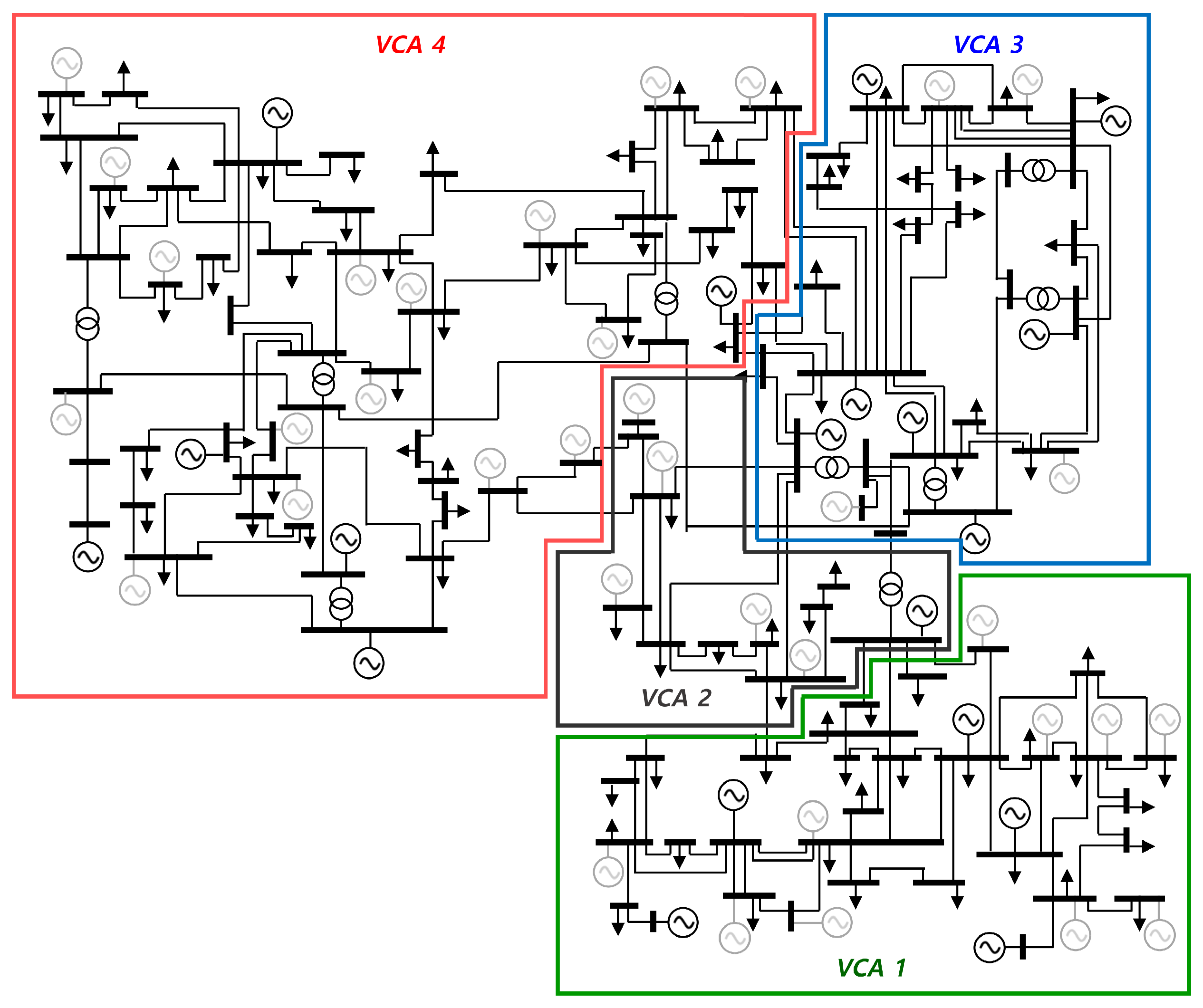
2.1. Identifying Voltage Control Areas

Each VCA consists of electrically coupled buses and is comparatively uncoupled from the other areas. Therefore, it is strongly affected by events in its region but less affected by events in other regions [27,28]. Several partitioning methods have been studied to divide a system into weakly coupled areas based on its voltage sensitivity [29,30,31]. In this study, the VCAs of the system were identified using a two-step approach as follows:

• The electrical distance between nodes was calculated;
• Hierarchical spectral clustering based on electrical distance was conducted.

2.1.1. Derivation of the Electrical Distance

The electrical distance quantifies the electrical inter-connectivity between nodes. Although there are several methods for computing the electrical distance [32], the V-Q sensitivity-based method is mostly used to configure VCAs [17,18,19,27,28,33,34].

Assuming that the active and reactive powers are well decoupled in a highly inductive, large-scale transmission system, the following equations can be derived from the power flow equation:

$$\left[\begin{array}{c}\Delta \mathbf{P}\\ \Delta \mathbf{Q}\end{array}\right]=\left[\begin{array}{cc}{\mathit{J}}_{\mathit{PV}}& {\mathit{J}}_{\mathit{P}\mathit{\theta }}\\ {\mathit{J}}_{\mathit{QV}}& {\mathit{J}}_{\mathit{Q}\mathit{\theta }}\end{array}\right]\left[\begin{array}{c}\Delta \mathbf{V}\\ \Delta \mathit{\theta }\end{array}\right]$$

(1)

$$\Delta \mathbf{Q}={\mathit{J}}_{\mathit{QV}}\Delta \mathbf{V}=[\frac{\partial \mathbf{Q}}{\partial \mathbf{V}}]\Delta \mathbf{V}$$

(2)

where ${\mathit{J}}_{\mathit{QV}}$ denotes the submatrix of the Jacobian matrix. The matrix $[\partial \mathbf{V}/\partial \mathbf{Q}]$, which is called the sensitivity matrix, is the inverse of [$\partial \mathbf{Q}/\partial \mathbf{V}$].

$$[\frac{\partial \mathbf{V}}{\partial \mathbf{Q}}]={[\frac{\partial \mathbf{Q}}{\partial \mathbf{V}}]}^{-1}$$

(3)

The element $[\partial V_i/\partial Q_j]$ represents the voltage variation in the node i in response to reactive power injection in the node j. The degree of voltage coupling between two nodes can be quantified as the attenuation of their voltage fluctuations. The attenuation between node i and node j is defined as

$${\alpha }_{ij}=[\frac{\partial V_i}{\partial Q_j}]/[\frac{\partial V_j}{\partial Q_j}]$$

(4)

The resultant sensitivity-based electrical distance can then finally be calculated, as shown in the following equation, reflecting the concept of distance and symmetry between nodes:

$$D_{ij}=-log({\alpha }_{ij}·{\alpha }_{ji})$$

(5)

As the sensitivity-based electrical distance is calculated by including both the system topology information as well as the voltage magnitude and phase angle information for the node, the operating state of the system can be considered.

2.1.2. Determining VCAs Using Clustering Approach

Based on the derived electrical distance, hierarchical spectral clustering was applied to determine the VCAs. The details of hierarchical spectral clustering are available in [16]. The process of hierarchical spectral clustering is as follows:

1.

Represent the power system as a graph: A power system can be represented as a graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$ whose vertex and edge sets are $\mathcal{V}$ and $\mathcal{E}$, respectively;

2.

Obtain the Laplacian matrix $\mathbf{L}$ and normalized Laplacian matrix ${\mathbf{L}}_{\mathbf{n}}$ of the graph $\mathcal{G}$:

$$\mathbf{L}=\mathbf{D}-\mathbf{W}\mathbf{L}=\mathbf{D}-\mathbf{W}$$

(6)

$${\mathbf{L}}_{\mathbf{n}}={\mathbf{D}}^{-\mathbf{1}/\mathbf{2}}{\mathbf{LD}}^{\mathbf{1}/\mathbf{2}}$$

(7)

Here, W is a weight matrix whose element $w_{ij}$ represents the connectivity between vertices i and j, while D is a diagonal matrix whose element $d_i={\sum }_j{w}_{ij}$. The weight $w_{ij}$ has the following properties.

$$w_{ij}=\frac{1}{D_{ij}},i,j\in \mathcal{V}$$

(8)

$$w_{ij}=0,if(i,j)\notin \mathcal{E}$$

(9)

3.

Perform spectral embedding: Obtain the eigenvalues and eigenvectors of ${\mathbf{L}}_{\mathbf{n}}$, and use the first k eigenvectors of ${\mathbf{L}}_{\mathbf{n}}$ to coordinate the vertices in the Euclidean space ${\mathbb{R}}^k$. Normalize each coordinate so that all vectors have their own norm of 1;

4.

Conduct hierarchical clustering: Calculate the distances between the normalized coordinates of the vertices and cluster them according to their proximity to each other.

It should be noted that the reciprocal of the electrical distance $1/D_{ij}$ was used as $w_{ij}$ to partition the system into VCAs.

The clustering approach for identifying VCAs was verified by simulations using the IEEE 118−bus test system. The electrical distances between the nodes are shown in Figure 1. Figure 1a shows the unsorted results with bus numbers, while Figure 1b shows the sorted results with each cluster $C1,C2,C3,$ and $C4$. These results show the electrical distance relationship for each bus, while the clustering results for the test system topology are shown in Figure 2.

In addition, a pilot bus was utilized to verify whether this clustering result accurately reflected the regional characteristics of the reactive power. The pilot bus for each VCA was selected based on a previous study [35] where the node with the shortest average electrical distance was assigned to a pilot bus, as in the following equation

$$\overline{D_j}=\sqrt{\sum _{i\in G_{VCAk}}{d}_{ij}^2}$$

(10)

where $\overline{D_j}$ denotes the average electrical distance from the controlled node j to the reactive power source nodes $G_{VCAk}$ of VCA k. The numbers of pilot buses for each area were 94, 75, 56, and 30, respectively, which were selected based on a previous study [35]. The VCA verification results, which are shown in Figure 3, indicate that the clustered VCAs were effective regardless of the magnitude of the reactive power injection.

2.1.3. Reactive Power Reserve in Voltage Control Areas

The reactive power reserve is additional available reactive power that contributes to maintaining voltage stability in response to changes in the operating conditions of the system. Therefore, this must be considered to protect the system from disturbance and collapse [5,14]. Thus, the reactive power reserve is considered as a measure of voltage stability that can be utilized to determine the voltage stability margin [1,7]. Furthermore, experiments have proven that the voltage stability of a system can be determined by monitoring the reactive power reserve [5,14].

In this study, the reactive power limit was determined based on the generator capability curve as follows:

$$RP{R}_{Gi}=Q_{Gi}^{Cap.Curve}-Q_{Gi}^{current}$$

(11)

$$Q_{Gi}^{Cap.Curve}=f\left(P_{Gi}\right)$$

(12)

where $RP{R}_{Gi}$, $Q_{Gi}^{Cap.Curve}$, and $Q_{Gi}^{current}$ denote the reactive power reserve, the maximum limit of the reactive power determined by the capability curve, and the current reactive power output of the ith generator, respectively.

3. Proposed Method for Clustering Combined Multi-Objective Optimal Operation

3.1. Overall Framework

Figure 4 shows the overall framework of the proposed method, which is formulated as a two-stage multi-objective optimization problem. In the first stage, the entire systematic operation is optimized by determining the optimal operating points of the generators, including their commitment, active power dispatch, and terminal voltage. It ensures not only economic efficiency and reliability but also the reactive power reserve of the generators. In the second stage, an additional regional optimization of each VCA is performed based on the result of the first stage. In this stage, voltage control devices are utilized to achieve regional efficiency and voltage stabilization, and the system operator can enhance the voltage stability while maintaining a sufficient reactive power reserve.

3.2. Stage 1

In the first stage of the proposed framework, the optimization problem is formulated as follows:

$$Minimize[F_1\left(\mathbf{x}\right),F_2\left(\mathbf{x}\right),F_3\left(\mathbf{x}\right),F_4\left(\mathbf{x}\right)]$$

(13)

$$subjectto{g}_j\left(\mathbf{x}\right)\ge 0,j=1,2,\dots ,J$$

(14)

$$h_k\left(\mathbf{x}\right)=0,k=1,2,\dots ,K$$

(15)

where $F_i$, $g_j$, $h_k$, and $\mathbf{x}$ represent the ith objective function, j-th equality constraints, k-th inequality constraints, and vector of decision variables, respectively.

3.2.1. Decision Variables

The decision variables for the first stage are as follows:

$${\mathbf{x}}^{\mathbf{T}}=[U_{G1},\dots ,U_{G{N}_G},P_{G1},\dots ,P_{G{N}_G},V_{G1},\dots ,V_{G{N}_G}]$$

(16)

where $U_{Gi}$, $V_{Gi}$, and $P_{Gi}$ are the commitment, terminal voltage, and active power output of ith generator, respectively. $N_G$ indicates the number of generators.

3.2.2. Objective Functions

The first objective function is the minimization of active power loss, which affects the overall efficiency of the system. It can be expressed as follows:

$$min{F}_1=\sum P_{Loss}$$

(17)

$$\sum P_{Loss}=\sum _{k=1}^{N_l}{g}_k[V_i^2+V_j^2-2V_i{V}_{j}cos{\theta }_{ij}]$$

(18)

where $N_l$ and $g_k$ denote the number of lines between nodes and the conductance of the line k connecting buses i and j. $V_i$ and $V_j$ are the voltage magnitudes of buses i and j, respectively, while ${\theta }_{ij}$ is the angle difference between bus i and j.

For reliable and high-quality system operation, the bus voltage must be kept within a specific range. The degree to which the voltage profile deviates from the reference value can be measured and it can be improved by minimizing this measurement. It can be expressed as an objective function:

$$min{F}_2=\sum _{i=1}^{N_L}\frac{|V_{Li}-V_{ref,Li}|}{N_L}=\sum _{i=1}^{N_L}\frac{|V_{Li}-1.0|}{N_L}$$

(19)

where $V_{Li}$ and $V_{ref,Li}$ represent the measured and reference values of the i-th load bus voltage, respectively. In this study, 1.0 p.u. was used as the reference value. $N_L$ denotes the number of load buses.

The maximization of the reactive power reserve in each VCA is one of the main features of this study. Equation (20) represents the corresponding objective function. In addition, it can be converted into a minimization objective function, as shown in Equation (21).

$$max{F}_3=min\left(RP{R}_{VCAi}\right)$$

(20)

$$min{F}_3=C_1-min\left(RP{R}_{VCAi}\right)=min(C_1-\left(RP{R}_{VCAi}\right))$$

(21)

where $C_1$ is a constant whose value is large enough for the calculation result to be a value greater than or equal to zero.

In the operation of power systems, both the stability and the economic aspects must be considered. In addition, such systems are strongly dependent on the fuel cost for the generators. The active power dispatch for the generator was determined to minimize the cost without violating its constraints.

$$min{F}_4=Cost=\sum _{i=1}^{N_G}(a_i{P}_{Gi}^2+b_i{P}_{Gi}+c_i)$$

(22)

where $a_i$, $b_i$, and $c_i$ are the coefficients and constant in the cost function for the i-th generator.

3.2.3. Constraints

The constraints can be classified as equality and inequality constraints. The equality constraints are the power flow equations.

$$P_i=V_i\sum _{j=1}^{N_B}{V}_j(G_{ij}cos{\theta }_{ij}+B_{ij}sin{\theta }_{ij})$$

(23)

$$Q_i=V_i\sum _{j=1}^{N_B}{V}_j(G_{ij}sin{\theta }_{ij}-B_{ij}cos{\theta }_{ij})$$

(24)

where $P_i$ and $Q_i$ denote the net active and reactive power injections at the i-th bus, respectively, while $G_{ij}$ and $B_{ij}$ are the conductance and susceptance of the line connecting the buses i and j.

The inequality constraint represents the allowable value and range of each variable as follows:

$$U_{Gi}\in [0,1],i=1,2,\dots ,N_G$$

(25)

$$P_{Gi}^{min}\le P_{Gi}\le P_{Gi}^{max},i=1,2,\dots ,N_G$$

(26)

$$Q_{Gi}^{min}\le Q_{Gi}\le Q_{Gi}^{max},i=1,2,\dots ,N_G$$

(27)

$$V_i^{min}\le V_i\le V_i^{max},i=1,2,\dots ,N_B$$

(28)

$$S_{li}\le S_{li}^{max},i=1,2,\dots ,N_l$$

(29)

where each equation represents a constraint related to the generator commitment $U_{Gi}$, generator active power $P_{Gi}$, reactive power $Q_{Gi}$, bus voltage $V_i$, and thermal limit of line $S_{li}$. $N_B$ denotes the number of buses.

3.3. Stage 2

In the second stage of the proposed framework, the optimal reactive power dispatch considering the reactive power reserve was performed for each VCA. The main difference from stage one was that the dispatch was more concentrated in its area by utilizing its regional voltage-related devices, such as the transformer tap changer and shunt compensators, as well as the generators. In addition, unnecessary complexity can be avoided by utilizing this dividing approach to optimize resources. Therefore, it can be utilized for a shorter operation time-frame compared to the holistic approach. The initial states of commitment and active power dispatch were set at the optimal operating point of the first-stage result. The implementation of the second stage further secures the reactive power reserve and voltage stability of each VCA.

$$Minimize[F_{VCAk,1}\left({\mathit{x}}_{\mathit{VCA},\mathit{k}}\right),F_{VCAk,2}\left({\mathit{x}}_{\mathit{VCA},\mathit{k}}\right),F_{VCAk,3}\left({\mathit{x}}_{\mathit{VCA},\mathit{k}}\right),F_{VCAk,4}\left({\mathit{x}}_{\mathit{VCA},\mathit{k}}\right)]$$

(30)

$$subjectto{g}_j\left({\mathit{x}}_{\mathit{VCA},\mathit{k}}\right)\ge 0,j=1,2,\dots ,J$$

(31)

$$h_k\left({\mathit{x}}_{\mathit{VCA},\mathit{k}}\right)=0,k=1,2,\dots ,K$$

(32)

where $F_{VCAk,i}$, $g_j$, $h_k$, and $\mathbf{x}$ represent the i-th objective function, j-th equality constraint, k-th inequality constraint, and the vector of decision variables, respectively.

3.3.1. Decision Variables

The decision variables of the second stage are as follows.

$${\mathit{x}}^{\mathit{T}}=[V_{VCAk,G1},\dots ,V_{VCAk,G{N}_{VCAk,G}},T_{VCAk,1},\dots ,T_{VCAk,N_{VCAk,T}},Q_{VCAk,C1},\dots ,Q_{VCAk,C{N}_{VCAk,C}}]$$

(33)

where $V_{VCAk,G}$, $T_{VCAk,T}$, and $Q_{VCAk,C}$ are the terminal voltage of the generator, transformer tap ratio, and quantity of shunt compensators in $VCAk$, respectively. $G{N}_{VCAk,G}$, $T{N}_{VCAk,T}$, and $C{N}_{VCAk,C}$ represent the number of generators, tap changing transformers, and shunt compensators, respectively, in $VCAk$.

3.3.2. Objective Functions

The first and second objective functions are nearly the same as those in the first stage, except that we consider only $VCAk$. The objective functions for the second stage are expressed as follows:

$$min{F}_{VCAk,1}=min\left(P_{VCAk,Loss}\right)$$

(34)

$$P_{VCAk,Loss}=\sum _{m=1}^{N_{VCAk,l}}{g}_m(V_i^2+V_j^2-2V_i{V}_{j}cos{\theta }_{ij})$$

(35)

where $N_{VCAk,l}$ represents the number of lines in $VCAk$ and

$$min{F}_{VCAk,2}=\sum _{i=1}^{N_{VCAk,L}}\frac{|V_{Li}-V_{ref,Li}|}{N_{VCAk,L}}=\sum _{i=1}^{N_{VCAk,L}}\frac{|V_{Li}-1.0|}{N_{VCAk,L}}$$

(36)

where $N_{VCAk,L}$ represents the number of controlled buses in $VCAk$.

From the perspective of the VCA, the reactive power reserve of $VCAk$ can be further optimized by searching for the optimal operating point of the generators and reactive power equipment in the area. The objective function of the reactive power reserve in the VCA can be represented as

$$max{F}_{VCAk,3}=RP{R}_{VCAk}$$

(37)

$$min{F}_{VCAk,3}=(C_2-RP{R}_{VCAk})$$

(38)

where $C_2$ is a constant whose value is large enough for the calculation result to be a value greater than or equal to zero.

To assess regional stability, the voltage stability index (VSI) was introduced. The VSI effectively assesses the voltage stability of buses or lines by quantifying their proximity to instability under low computational loads [36,37]. The L-index [36] was utilized to enhance voltage stability. This was achieved by minimizing the largest L-index value in the are of interest.

$$min{F}_{VCAk,4}=max\left(L_i\right)$$

(39)

$$L_i=|1-\sum _{j=1}^{N_G}{Y}_{ij}{V}_j|$$

(40)

$$\left[\begin{array}{c}{I}_G\\ I_L\end{array}\right]=\left[\begin{array}{cc}{I}_{GG}& I_{GL}\\ I_{LG}& I_{LL}\end{array}\right]\left[\begin{array}{c}{V}_G\\ V_L\end{array}\right]$$

(41)

where $I_G$, $I_L$, $V_G$, and $V_L$ represent currents and voltages of the generator and load nodes, respectively.

3.3.3. Constraints

As in the first stage, Equations (24)–(27) are applied as constraints in the second stage. In addition, the upper and lower bounds of the transformer tap settings and reactive power compensators and the L-index constraints are included as constraints.

$$T_{VCAk,i}^{min}\le T_{VCAk,i}\le T_{VCAk,i}^{max},i=1,2,\dots ,N_{VCAk,T}$$

(42)

$$Q_{VCAk,Ci}^{min}\le Q_{VCAk,Ci}\le Q_{VCAk,Ci}^{max},i=1,2,\dots ,N_{VCAk,C}$$

(43)

$$L_j\le 1,j=1,2,\dots ,N_B$$

(44)

where $N_{VCAk,T}$ and $N_{VCAk,C}$ denote the number of tap-changing transformers and reactive power compensators, respectively.

4. Solution for the Proposed Framework

In this study, NSGA-III [25,26] was applied to determine the optimal solution for the proposed framework.

4.1. Non-Dominated Sorting Genetic Algorithm III

NSGA-III is a genetic algorithm that searches for a Pareto optimal solution based on non-dominated sorting. It exhibits promising performance in solving multi-objective optimization problems because, unlike other algorithms, it does not need either a weight for each objective function or additional user-defined parameters to be specified.

The overall process of the NSGA-III is as follows, and more details can be found in [25].

• Set equality/inequality constraints and generate reference points;
• Generate the initial population $P_1$, which becomes the parent population $P_t$ when $t=1$;
• Evaluate the fitness and feasibility of $P_t$;
• Create the offspring population $Q_t$ by recombination and mutation from $P_t$;
• Evaluate the fitness and feasibility of $Q_t$;
• Combine $P_t$ and $Q_t$ ($R_t=P_t\cup Q_t$) and sort $R_t$ according to non-domination levels;
• Choose the best N individuals from $R_t$ according to the non-domination levels and reference point-based selection;
• The N individuals of $P_t$ are transferred to $P_{t+1}$.
• Iterate steps three to eight until t iterations are performed.

The feasibility of the individual affects the creation of the offspring population and the choice of the non-domination level in NSGA-III with constraint handling [26].

4.2. Application of NSGA-III to the Proposed Framework

The procedure for applying NSGA-III to the proposed framework is illustrated in Figure 5. When applying NSGA-III to the framework, initial population generation and final individual selection processes are also performed. In the first stage, a separate process is performed to generate an initial population before starting the iteration. Populations are randomly generated repeatedly until a sufficient number of feasible individuals are obtained. This is done separately because it is difficult to obtain an adequate number of feasible individuals through random generation. Meanwhile, decision making is required to select the final optimal solution from the Pareto optimal solutions based on whether user preferences exist. If user preferences do not exist, the final optimal solution can be determined by selecting a solution close to the ideal point. This is undertaken by normalizing the objective function value of each solution and calculating the distance to the ideal points, all of which are zero. Therefore, in the minimization optimization problem, smaller values are closer to the ideal point. Each objective function value for an individual ranges from 0 to 1, and the ideal solution has all the values of the coordinate 0. This process can be understood better through a case study.

5. Case Studies and Results

This section describes case studies conducted using the proposed framework and presents their results. The simulation environment was the IEEE 118-bus test system shown in Figure 2. Simulations were performed not only to verify the effectiveness of the proposed framework but also to verify its effectiveness in a system with a high level of penetration of renewable energy. A scenario with a 40% increase in renewable energy was utilized to demonstrate that the validity depends on the penetration level [38].

5.1. Base Case

5.1.1. Results of Stage One in the Base Case

The strategy of the first stage was applied to the system, and its results for each objective function are shown in Figure 6. The results demonstrate the effectiveness of the proposed multi-objective optimal operation in the first stage. All objective functions improved as the generations progressed, which indicated that the operating efficiency also improved while obtaining the appropriate reactive power dispatch and reserves to improve the voltage stability. However, as previously mentioned, many optimal solution candidates exist for each generation. Therefore, the appropriate optimal solution must be selected from the Pareto optimal solutions. The results are shown in Figure 7. In this figure, the lines denote the optimal solution candidates, and the blue line represents the optimal solution selected by the optimal candidate-selecting strategy. The values of the resulting objective function are listed in

Table 1. Evaluation results for each objective function with and without the application of the proposed framework.

Case	$\mathbf{\Sigma }{\mathit{P}}_{\mathit{Loss}}$	$\mathit{Avg}\left(\right|{\mathit{V}}_{\mathit{L}}-1\left|\right)$	$\mathit{min}\left({\mathit{RPR}}_{\mathit{VCA}}\right)$	Cost
$Before$	1.3660 p.u.	0.03223 p.u.	158.51 Mvar	491.38
$After$	0.7814 p.u.	0.01538 p.u.	441.31 Mvar	484.26

. The comparison of objective function values before and after optimization reconfirmed that our proposed method was validated. Also, as explained earlier, there was a difference in results of each objective function in Table 1 with best value of each objective function in Figure 6.

In addition, the bus numbers 39, 40, 41, 42, 43, 44, 45, 46, and 72 changed from VCA four to VCA two. The resultant reactive power reserve changes in each area were as follows

Table 2. Changes in reactive power reserves of each area.

Area	VCA 1	VCA 2	VCA 3	VCA 4
$Before$	957.17	158.51	1356.96	988.50
$After$	1556.65	441.31	1000.08	1302.01

.

From these results, it can be confirmed that the overall reactive reserves were well redistributed to obtain an overall improved voltage stability margin for each area.

5.1.2. Results of Stage Two in the Base Case

After the first stage, the reactive devices of each area, such as the reactive power compensator and tap-changed transformer, were utilized with the synchronous generator’s voltage control capability to stabilize each VCA. The optimized results for each area are shown in Figure 8 for VCAs one and two and Figure 9 for VCAs three and four. In addition, comparisons of the results for each area with and without the application of the proposed framework are shown in

Table 3. Stage two results for VCA one with and without the application of the proposed method.

Case	$\mathbf{\Sigma }{\mathit{P}}_{\mathit{Loss}}$	$\mathit{Avg}\left(\right|{\mathit{V}}_{\mathit{L}}-1\left|\right)$	${\mathit{RPR}}_{\mathit{VCA}}$	L-Index
$Before$	0.2075 p.u.	0.01067 p.u.	1556.65 Mvar	0.1240
$After$	0.2094 p.u.	0.01133 p.u.	1580.34 Mvar	0.1128

,

Table 4. Stage two results for VCA two with and without the application of the proposed method.

Case	$\mathbf{\Sigma }{\mathit{P}}_{\mathit{Loss}}$	$\mathit{Avg}\left(\right|{\mathit{V}}_{\mathit{L}}-1\left|\right)$	${\mathit{RPR}}_{\mathit{VCA}}$	L-Index
$Before$	0.06162 p.u.	0.01148 p.u.	441.31 Mvar	0.1259
$After$	0.06624 p.u.	0.009817 p.u.	525.23 Mvar	0.1247

,

Table 5. Stage two results for VCA three with and without the application of the proposed method.

Case	$\mathbf{\Sigma }{\mathit{P}}_{\mathit{Loss}}$	$\mathit{Avg}\left(\right|{\mathit{V}}_{\mathit{L}}-1\left|\right)$	${\mathit{RPR}}_{\mathit{VCA}}$	L-Index
$Before$	0.1077 p.u.	0.01454 p.u.	1000.08 Mvar	0.07456
$After$	0.1040 p.u.	0.01340 p.u.	1093.02 Mvar	0.07494

and

Table 6. Stage two results for VCA four with and without the application of the proposed method.

Case	$\mathbf{\Sigma }{\mathit{P}}_{\mathit{Loss}}$	$\mathit{Avg}\left(\right|{\mathit{V}}_{\mathit{L}}-1\left|\right)$	${\mathit{RPR}}_{\mathit{VCA}}$	L-Index
$Before$	0.2299 p.u.	0.02090 p.u.	1302.01 Mvar	0.1252
$After$	0.2152 p.u.	0.02628 p.u.	1419.68 Mvar	0.1108

.

These results indicate that the overall objective functions for each area improved well. However, in the case of VCA two, less effective results were obtained owing to the inherent trade-off relationship between the objective functions. Also, there were fewer degrees of freedom for control variables such as the reactive power resources and synchronous generators in this area. Therefore, the performance of the proposed framework strongly depends on the operating environment. However, it is evident that the proposed framework is helpful for improving efficiency and the voltage stability margin. In particular, the voltage profiles of almost all buses were improved, which is shown through a comparison before and after the application of the strategy in Figure 10.

5.2. Consideration of High-Level Penetration of Renewable Energy

To consider a more drastic operating environment with more renewable energy, a scenario with a 40% increase in the penetration level of the base case was considered. As mentioned earlier, renewable energy was added to all the PQ buses in proportion to the short-circuit capacity of each bus. The changes in the operating environment were as follow: the total increased renewable energy was 1696.8 MW; the generators of bus numbers 89, 80, and 10 were de-committed; and the real power dispatch of the generator of bus number 66 was reduced from 392 MW to 229.2 MW. The de-commitment and re-dispatch of the generator was determined based on its cost function. Detailed information on the cost functions is provided in Appendix A.

5.2.1. Results of Stage One for High-Level Penetration of Renewable Energy Scenario

The proposed framework was applied to the same system as in the base case. The results of the first stage are shown in Figure 11. As expected, these results demonstrate the effectiveness of the proposed method. All objective functions improved significantly, which implies that our proposed method is valid in more challenging environments with more renewable energy. A comparison of the results obtained with and without the application of the proposed method is shown in

Table 7. Evaluation results for each objective function with and without the application of the proposed method in the high-level penetration of renewable energy scenario.

Case	$\mathbf{\Sigma }{\mathit{P}}_{\mathit{Loss}}$	$\mathit{Avg}\left(\right|{\mathit{V}}_{\mathit{L}}-1\left|\right)$	$\mathit{min}\left({\mathit{RPR}}_{\mathit{VCA}}\right)$	Cost
$Before$	0.9893 p.u.	0.04587 p.u.	0 Mvar	398.03
$After$	0.6187 p.u.	0.01389 p.u.	789.86 Mvar	354.14

. The resulting reactive power reserves for each area are listed in

Table 8. Changes in reactive power reserves of each area with the high-level penetration of renewable energy scenario.

Area	VCA One	VCA Two	VCA Three	VCA Four
$Before$	104.10	0	1436.82	821.47
$After$	1588.38	989.72	807.13	789.86

.

Table 8 shows that there was no available reactive power reserve for VCA two, implying that VCA two had a voltage stability problem owing to an increase in renewable energy without appropriate action. These difficulties are shown through the average of the voltage deviation from its nominal value in Table 7 as well. However, as shown in Table 8, this can be resolved by applying the proposed method. Also, for the voltage profile, significant improvements are shown in Figure 12. It shows that the buses that exceeded the stability limit before were stabilized into the range.

5.2.2. Results of Stage Two in the High-Level Penetration of Renewable Energy Scenario

The results of the proposed method for each area are presented in this section. Comparisons of the results obtained before and after the application of the proposed method are shown in

Table 9. Stage two results with high-level penetration of renewable energy for VCA one with and without the application of the proposed method.

Case	$\mathbf{\Sigma }{\mathit{P}}_{\mathit{Loss}}$	$\mathit{Avg}\left(\right|{\mathit{V}}_{\mathit{L}}-1\left|\right)$	${\mathit{RPR}}_{\mathit{VCA}}$	L-Index
$Before$	0.1493 p.u.	0.00922 p.u.	1588.38 Mvar	0.1223
$After$	0.1398 p.u.	0.01765 p.u.	1610.34 Mvar	0.1180

,

Table 10. Stage two results with high-level penetration of renewable energy for VCA two with and without the application of the proposed method.

Case	$\mathbf{\Sigma }{\mathit{P}}_{\mathit{Loss}}$	$\mathit{Avg}\left(\right|{\mathit{V}}_{\mathit{L}}-1\left|\right)$	${\mathit{RPR}}_{\mathit{VCA}}$	L-Index
$Before$	0.03763 p.u.	0.01923 p.u.	989.72 Mvar	0.05798
$After$	0.03688 p.u.	0.02067 p.u.	1001.47 Mvar	0.05735

,

Table 11. Stage two results with high-level penetration of renewable energy for VCA three with and without the application of the proposed method.

Case	$\mathbf{\Sigma }{\mathit{P}}_{\mathit{Loss}}$	$\mathit{Avg}\left(\right|{\mathit{V}}_{\mathit{L}}-1\left|\right)$	${\mathit{RPR}}_{\mathit{VCA}}$	L-Index
$Before$	0.1834 p.u.	0.009658 p.u.	807.13 Mvar	0.1346
$After$	0.1778 p.u.	0.01295 p.u.	818.13 Mvar	0.1346

and

Table 12. Stage two results with high-level penetration of renewable energy for VCA four with and without the application of the proposed method.

Case	$\mathbf{\Sigma }{\mathit{P}}_{\mathit{Loss}}$	$\mathit{Avg}\left(\right|{\mathit{V}}_{\mathit{L}}-1\left|\right)$	${\mathit{RPR}}_{\mathit{VCA}}$	L-Index
$Before$	0.1978 p.u.	0.01716 p.u.	789.86 Mvar	0.2107
$After$	0.1973 p.u.	0.01908 p.u.	881.46 Mvar	0.2002

for each area. In all cases, improved voltage stability was observed with the use of the VSI. However, as expected, no meaningful results were obtained for VCA two because there were fewer controllable voltage control devices. This reconfirms the results from the first stage. The evaluated values for each objective function, depending on its generation, are shown in Figure 13 and Figure 14. They demonstrate our analysis results well.

6. Conclusions

In this study, a clustering combined multi-objective operation strategy for a large-scale transmission system was proposed to address the increased concern regarding voltage stability. The clustering approach considered the regional characteristics of the reactive power, thereby facilitating more effective reactive power management. Also, its effectiveness was validated through simulations. The proposed multi-objective problem was solved using NSGA-III, and the results demonstrated its superior performance. In addition, to avoid unnecessary complexity and computational demands and to concentrate more on the regional aspect, a two-stage framework was developed that yielded appropriate results for the purpose of each stage. To demonstrate its validity, a normal operating scenario simulation was performed and the corresponding results were presented in this paper. Additionally, a scenario with high-level penetration of renewable energy was considered to demonstrate the approach’s ability to handle more realistic and challenging environments in the near future. The results of both cases show that our proposed method can effectively achieve reliable and stable operation while considering voltage stability. Therefore, this is expected to be helpful for more challenging operating environments for large-scale transmission systems. Future work will focus on utilizing the controllability of renewable energy to improve the overall voltage stability.