Control of an Offshore Wind Farm Considering Grid-Connected and Stand-Alone Operation of a High-Voltage Direct Current Transmission System Based on Multilevel Modular Converters
Abstract
:1. Introduction
Motivation and Contribution of the Work
- (i)
- Mathematical Models: the compilation of a set of linearizing models for MMC-HVDC and WECS units in the synchronous reference frame, allowing for a comprehensive representation of the system’s dynamic behavior, both for grid-connected and stand-alone modes of operation. Furthermore, the study presents a detailed description of the closed-loop transfer functions of the HVDC converters and wind generator units, enabling the design of effective control systems for the overall system. These mathematical models serve as valuable tools for analyzing and optimizing the performance of the interconnected components in various operating conditions.
- (ii)
- Grid-Connected Operation: during grid-connected operation, the control algorithm ensures the proper regulation of the onshore MMC’s DC link voltage while optimizing power generation from the wind turbines. The generating units are controlled to track the maximum power output of the wind turbines, improving the overall system efficiency.
- (iii)
- Stand-Alone Operation: in the event of disconnection from the grid, the control algorithm allows for a smooth transition to stand-alone operation. The onshore converter takes over the AC voltage regulation at the point of common coupling (PCC), ensuring a continuous power supply for local loads. Additionally, the wind generator control adjusts its operation from tracking maximum power to regulating the DC link voltage, preventing excessive power injection into the HVDC link. The pitch angle control of the wind turbines is employed to maintain a fixed generator speed.
- (iv)
- Digital Simulation: the work develops a detailed digital model to analyze the performance of the wind energy system, incorporating wind-generating units, MMC-based rectifier and inverter stations, back-to-back converters, and a 320 /50 DC cable.
- (v)
- Evaluation and Testing: to assess the performance of the proposed control strategy, the developed model is implemented and simulated using the PSCAD/EMTDC program. The system’s dynamic behavior is tested under different scenarios, including grid disconnection, partial loss of a group of wind generating units, and grid reconnection. These simulations provide valuable insights into the system’s performance and validate the control algorithm’s effectiveness.
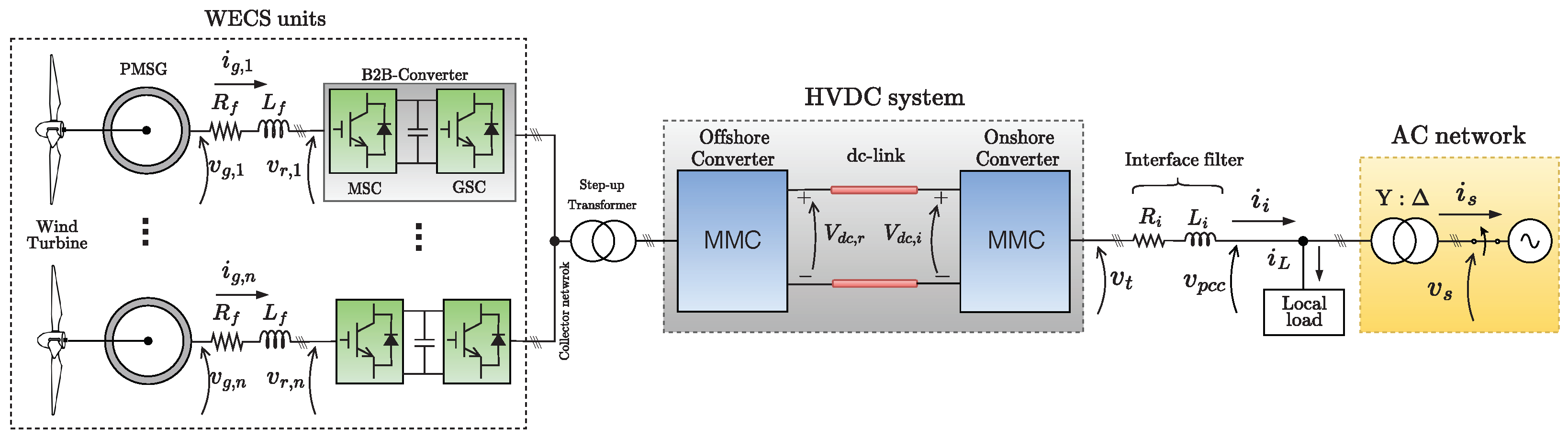
2. Control Strategy for Grid-Connected HVDC
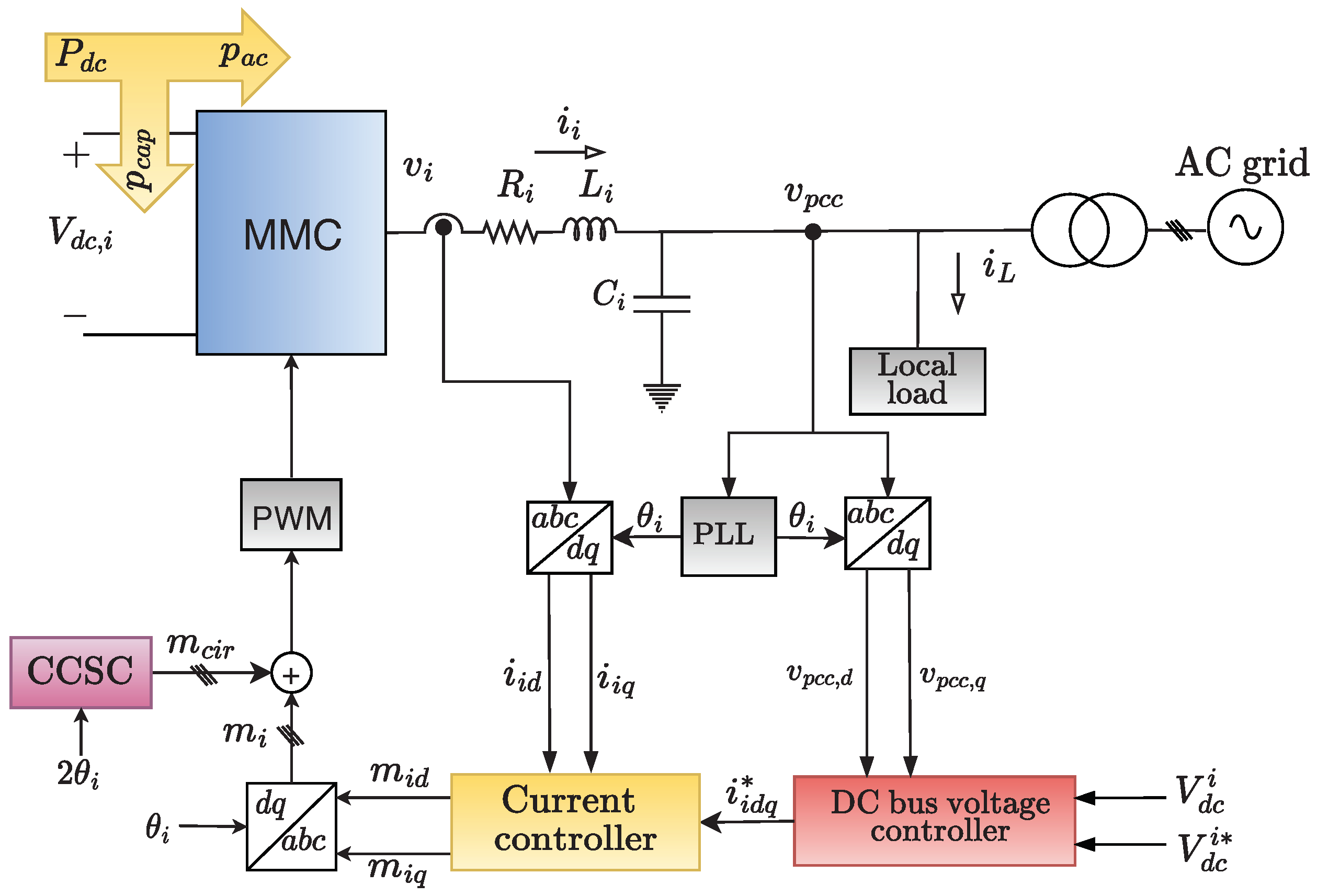
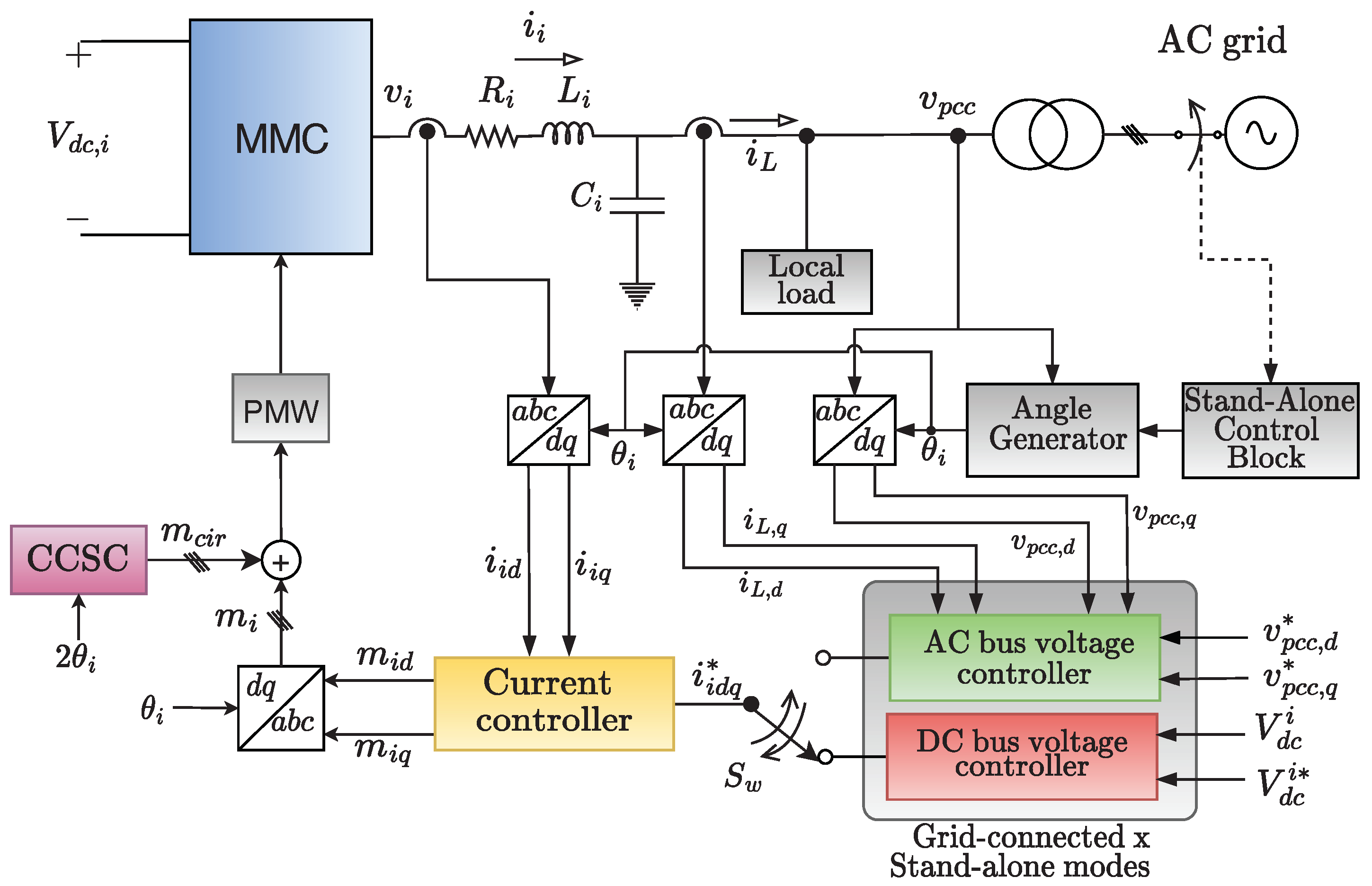
2.1. Onshore MMC Control
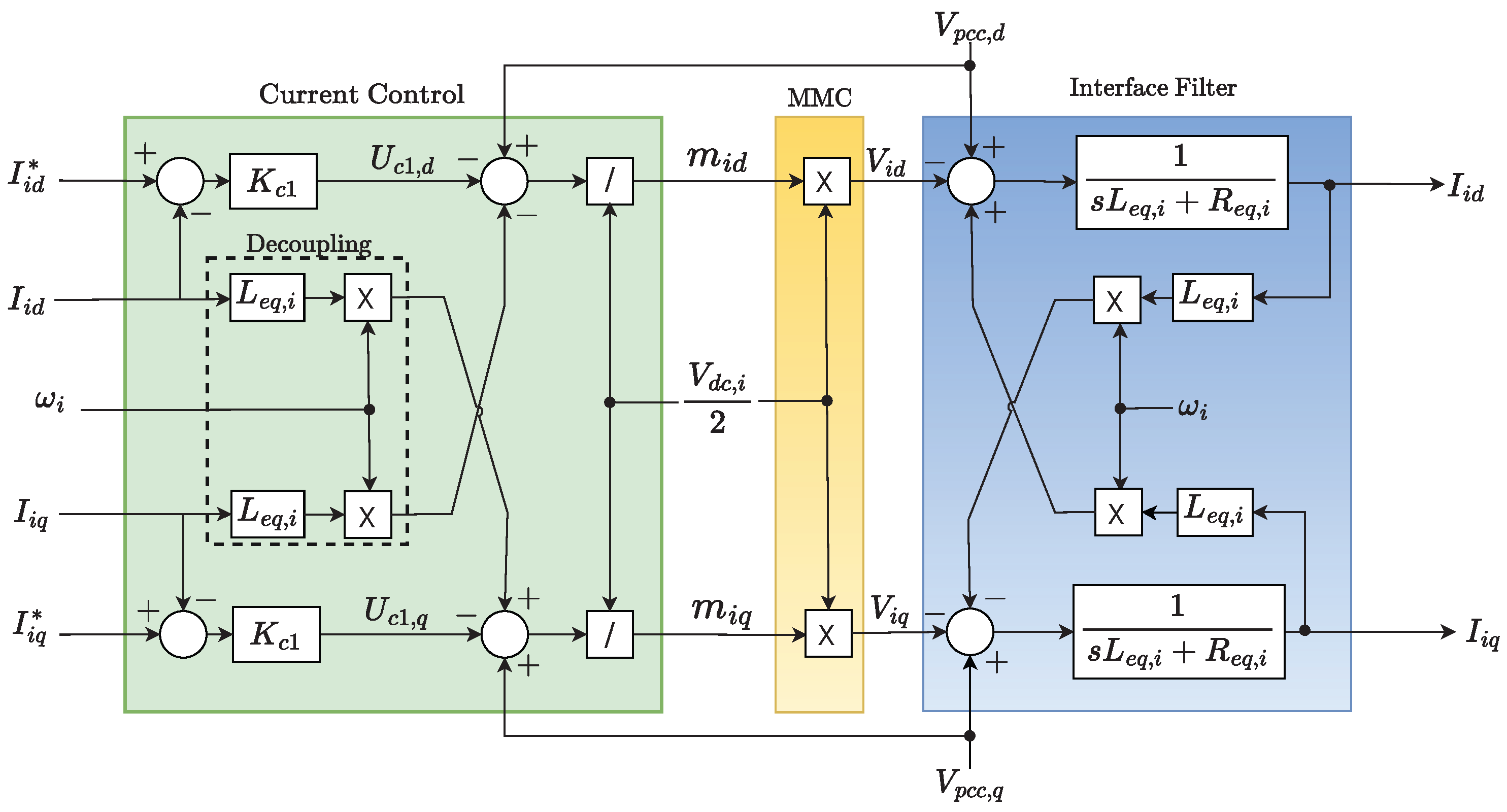
2.1.1. AC Current Control
2.1.2. DC-Link Voltage Control
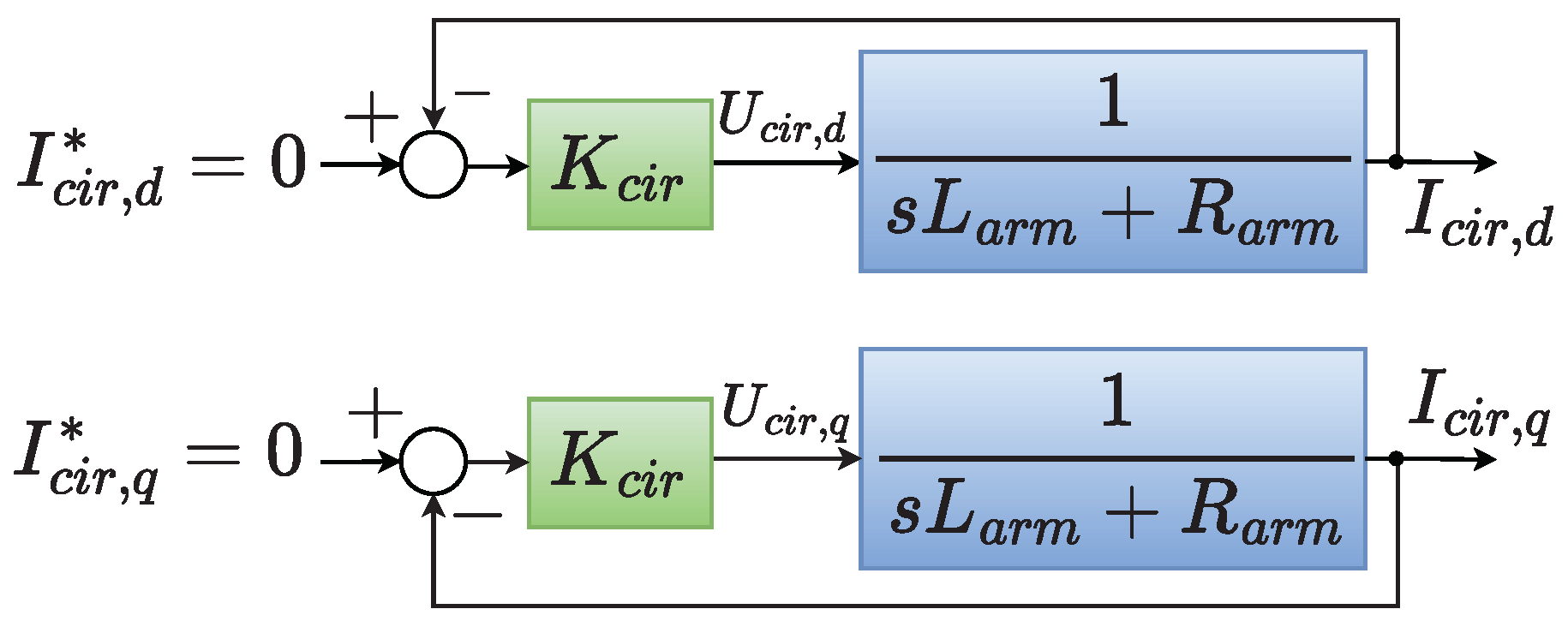
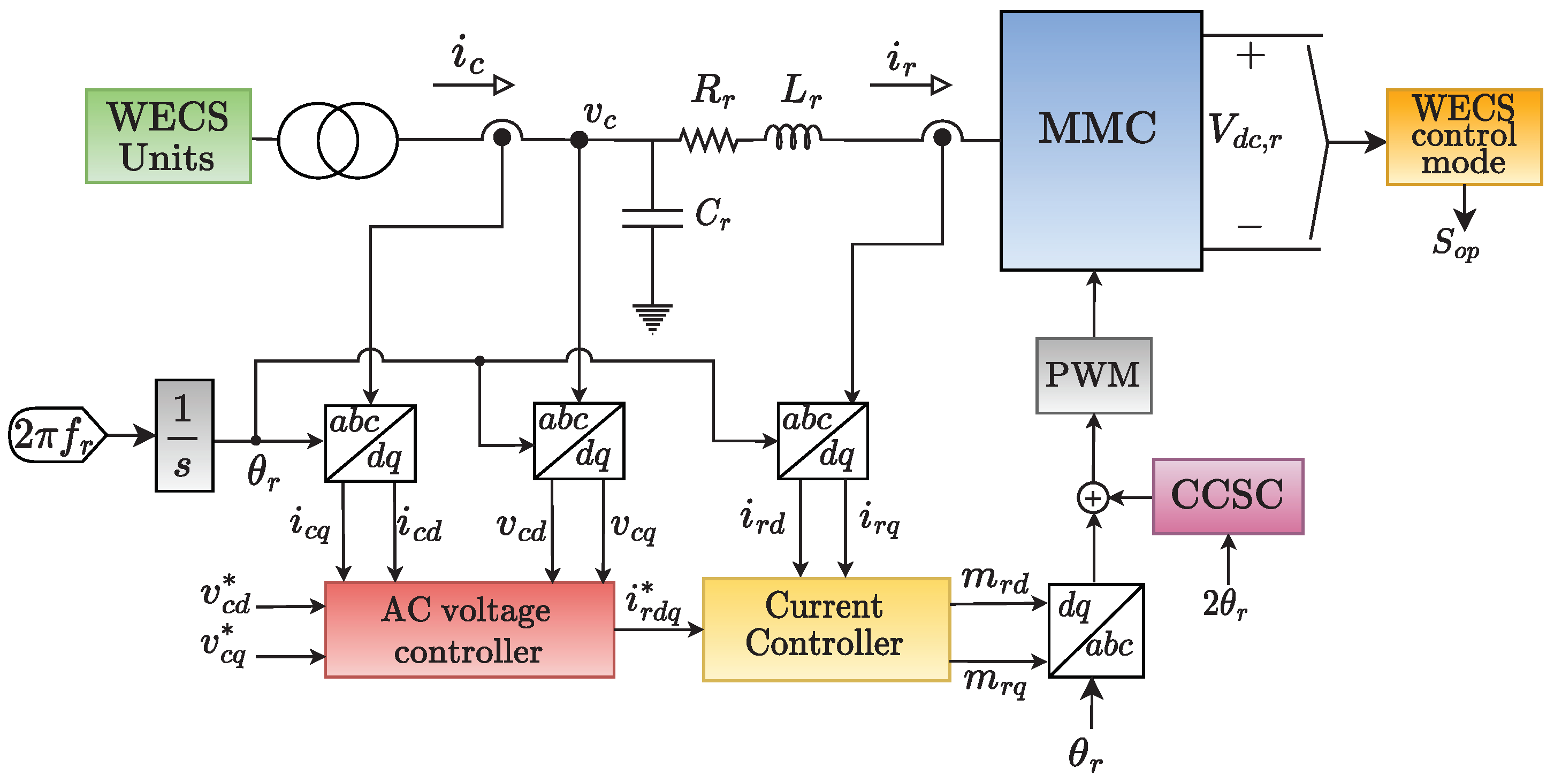
2.1.3. Circulating Current Suppressing Controller
2.2. Offshore MMC Control
2.2.1. AC Current Control
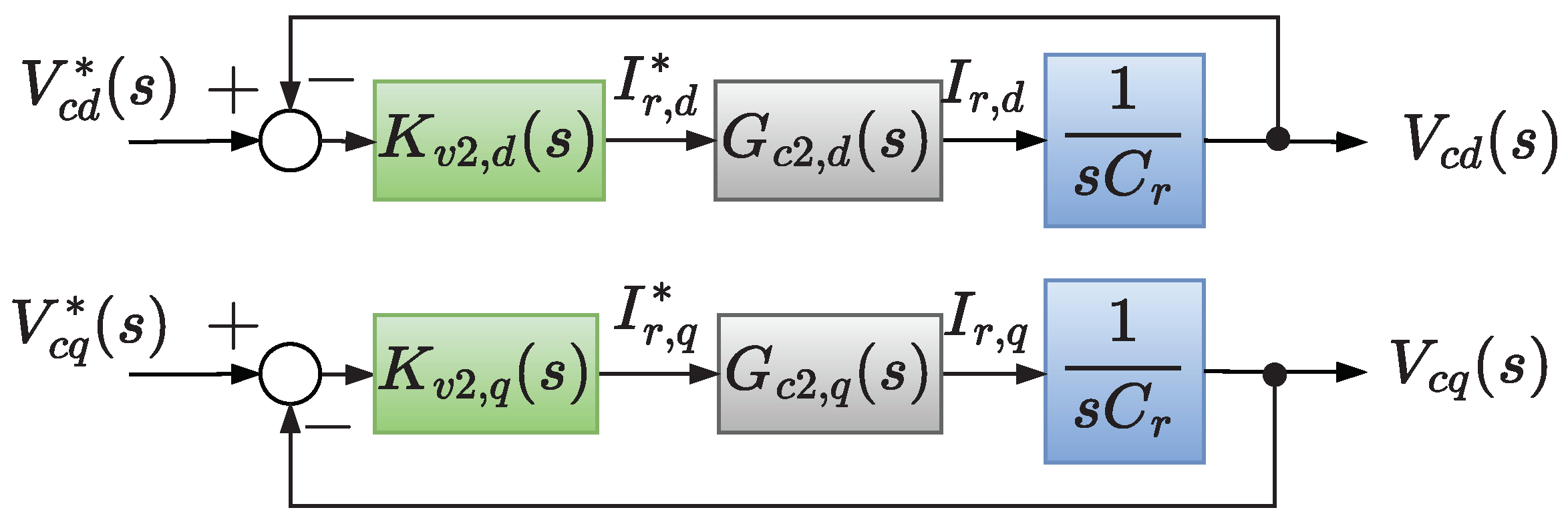
2.2.2. Collector Network Voltage Control
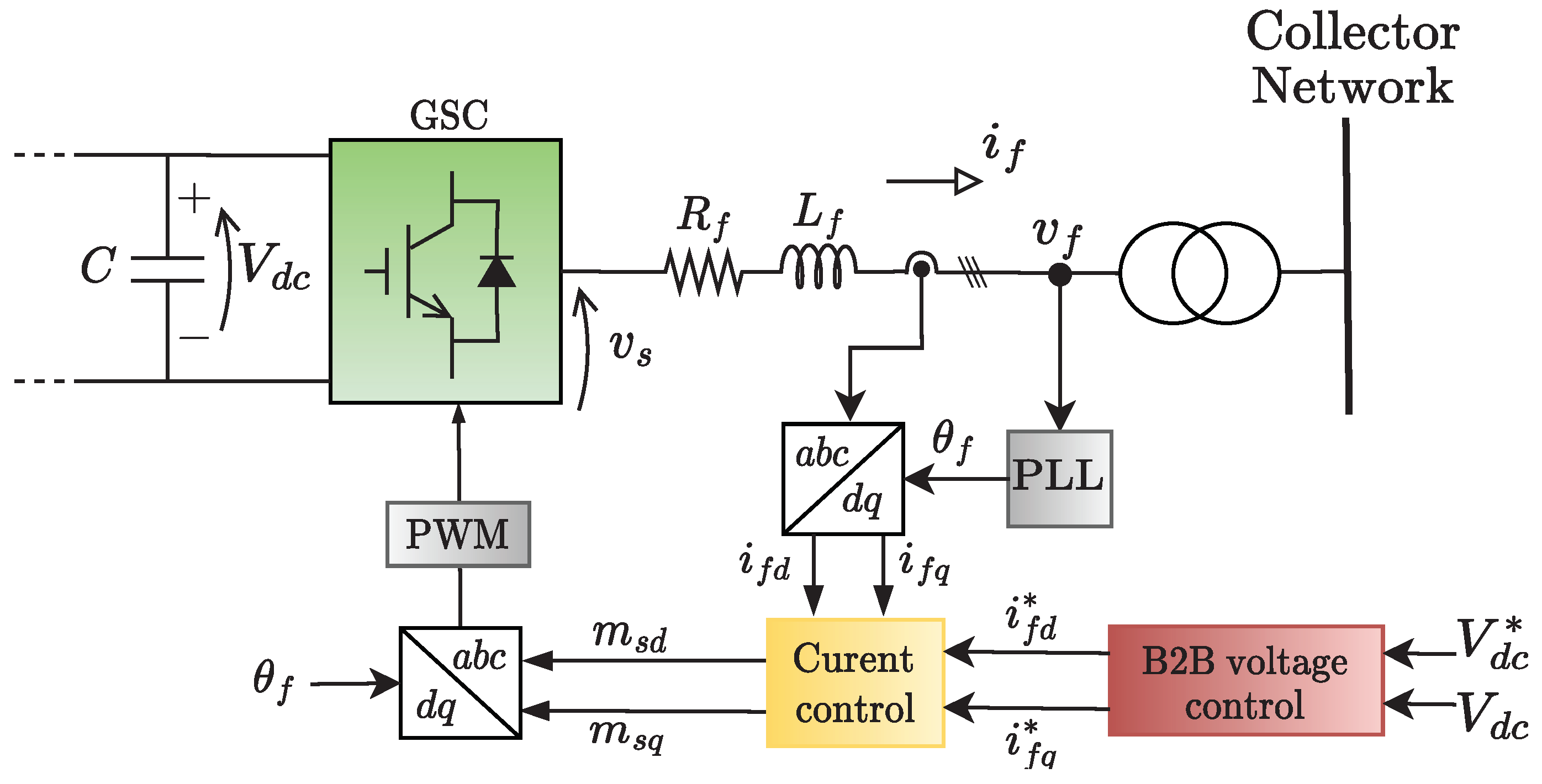
2.3. WEC Grid-Side Converter Control
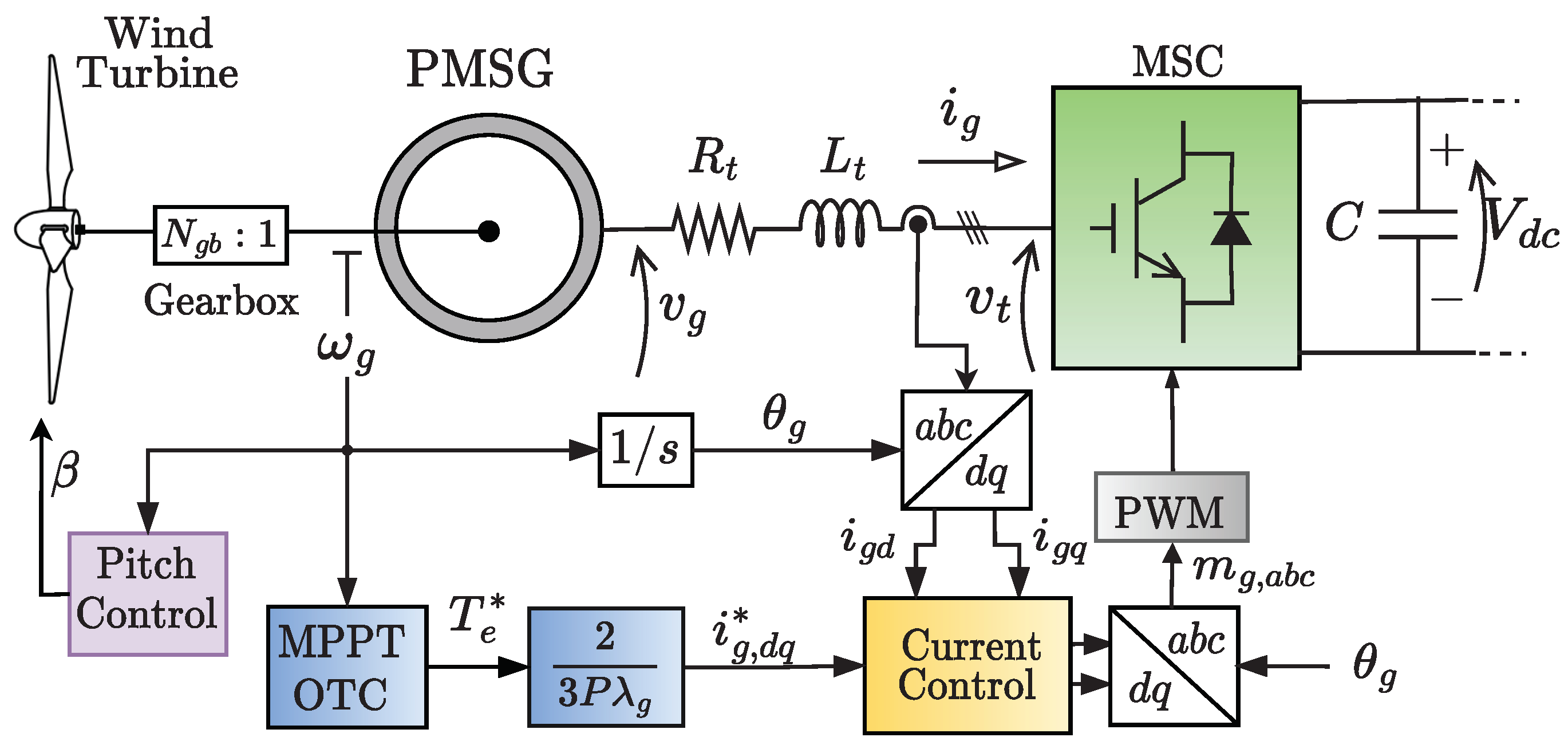
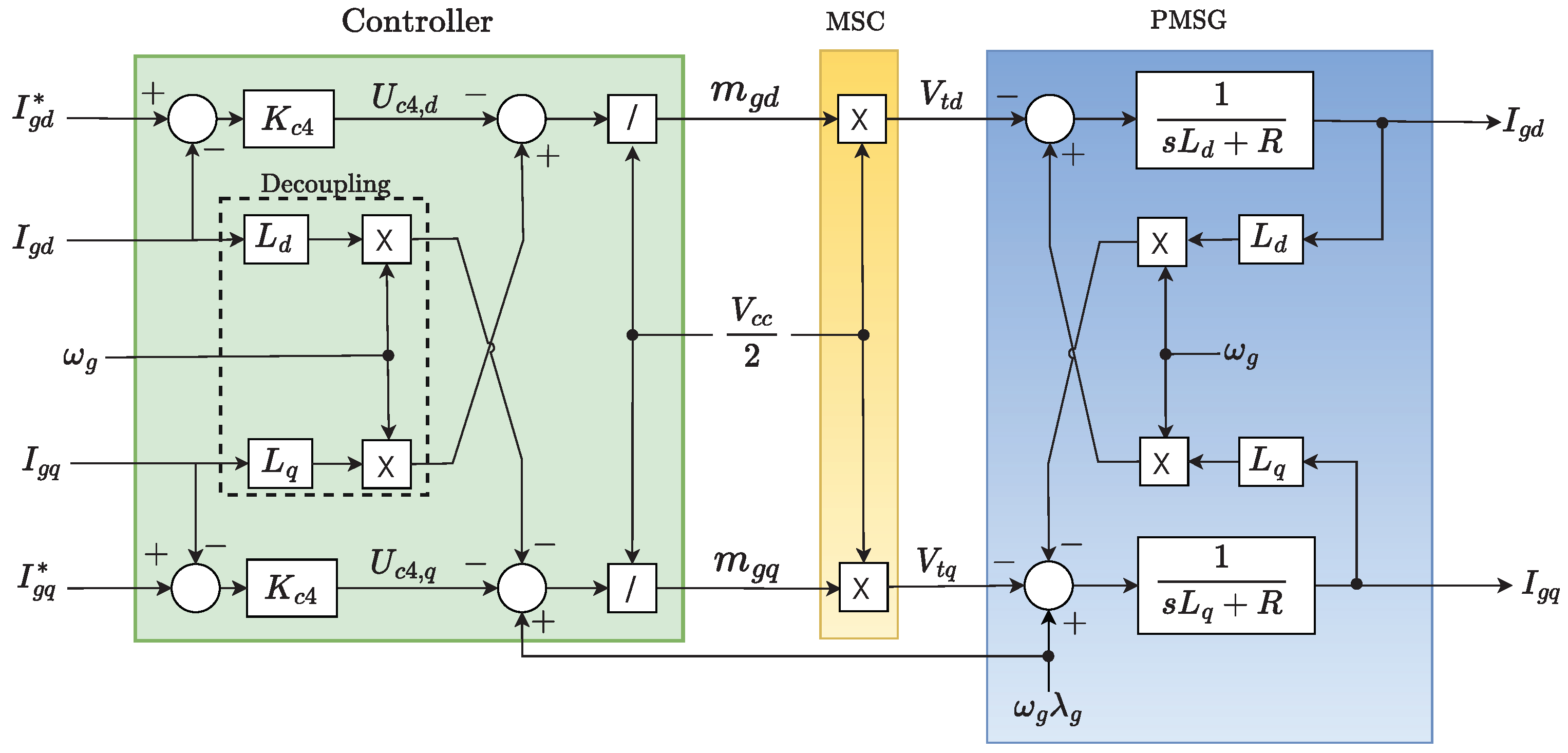
2.4. WEC Machine-Side Converter Control
3. Control Strategy for Stand-Alone HVDC
3.1. Onshore MMC Control
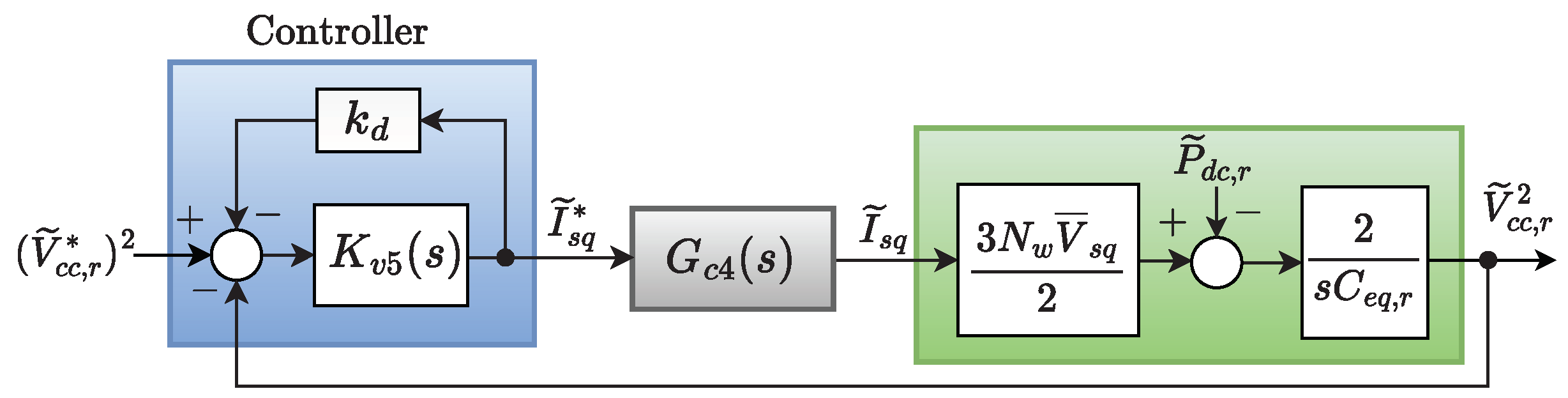
3.2. Control of HVDC-Rectifier DC-Link Voltage with MSC
3.3. Pitch Angle Control
4. Digital Simulation Results
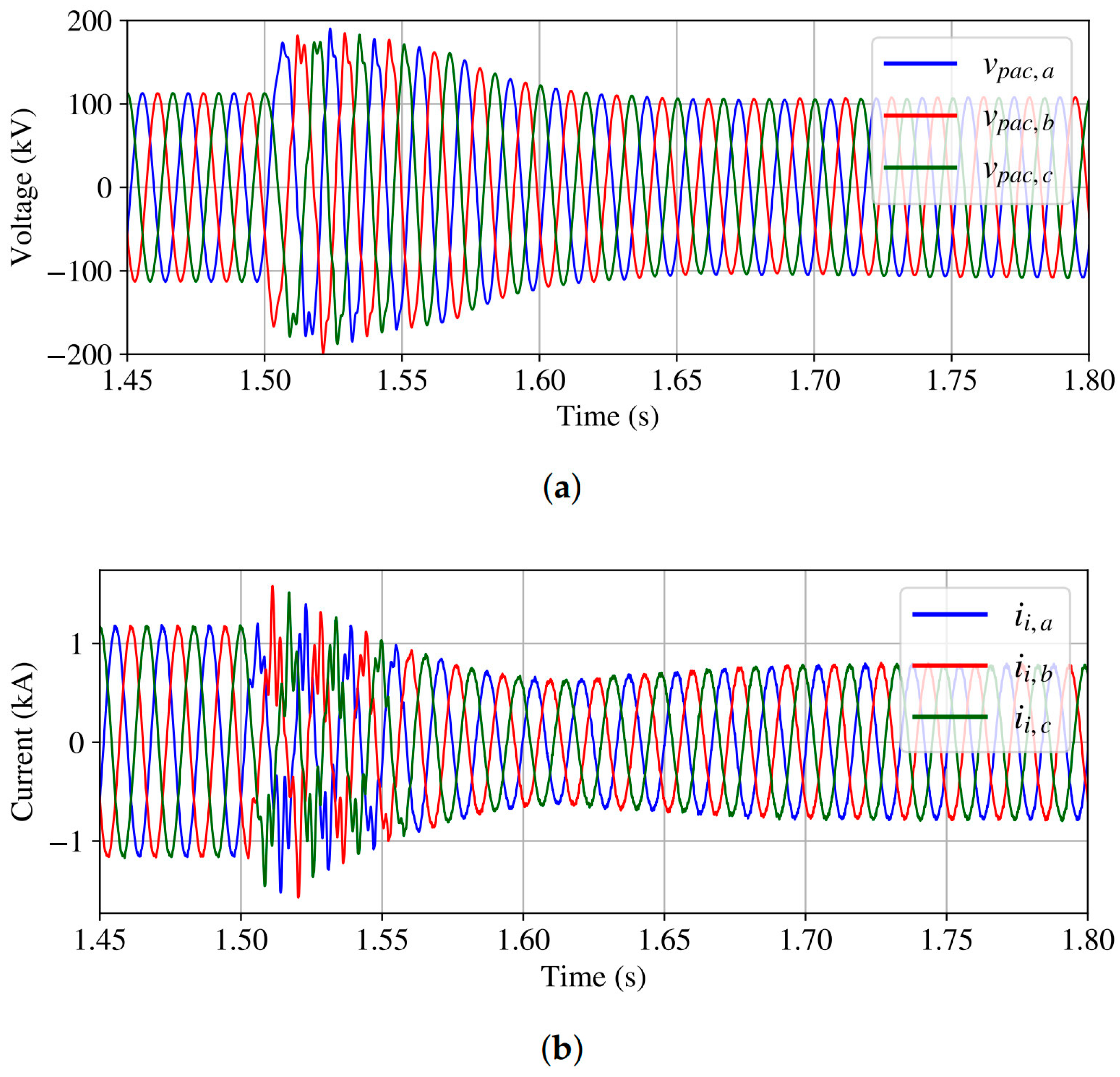
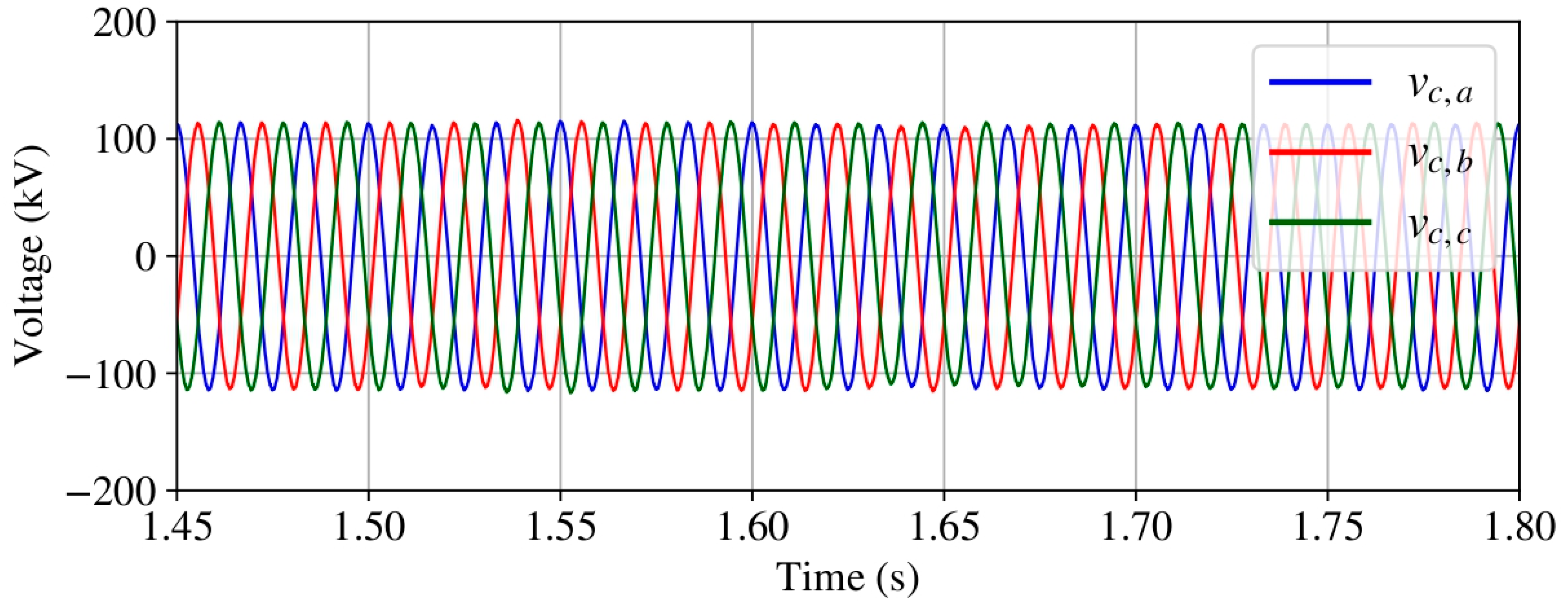
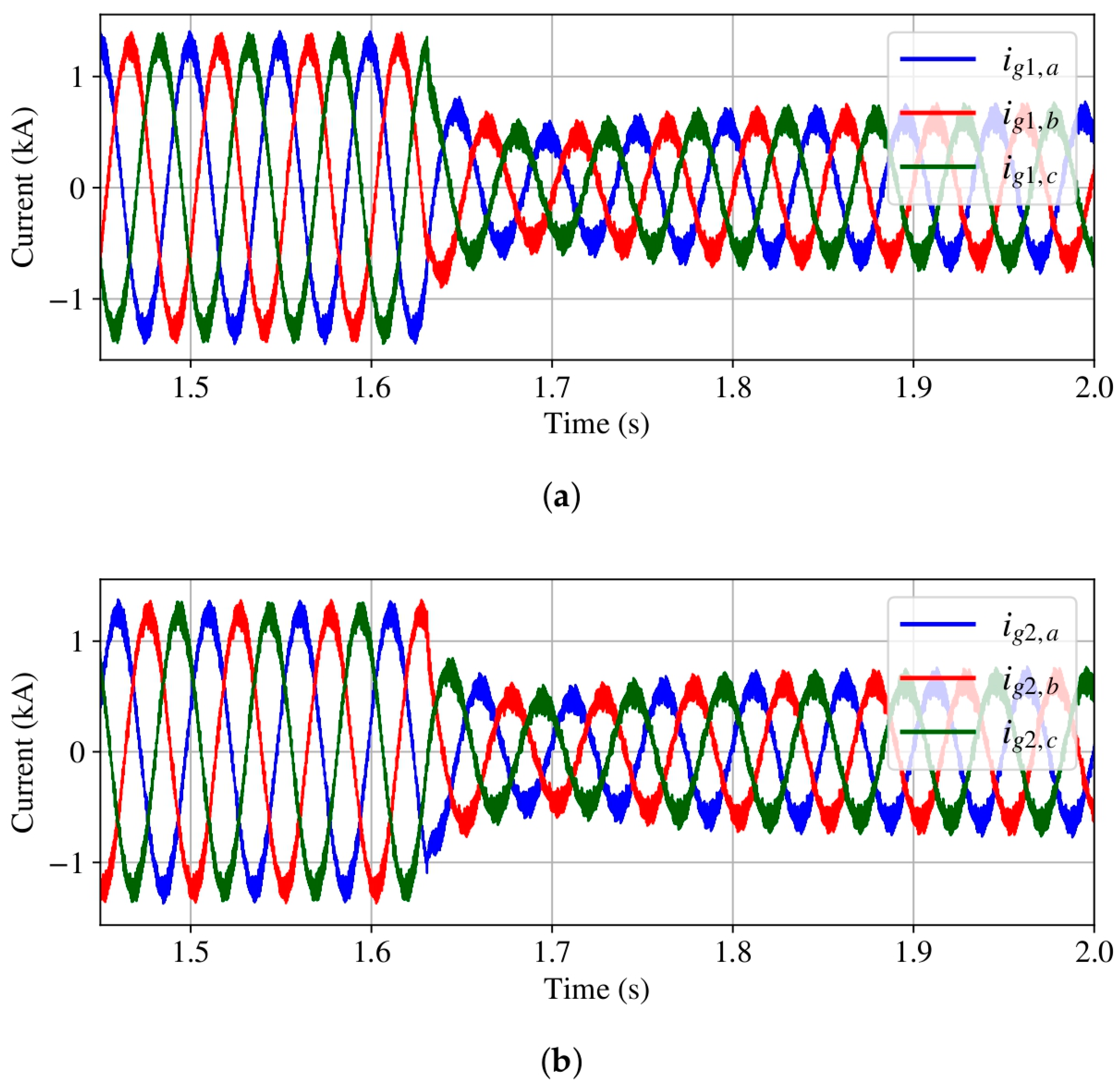
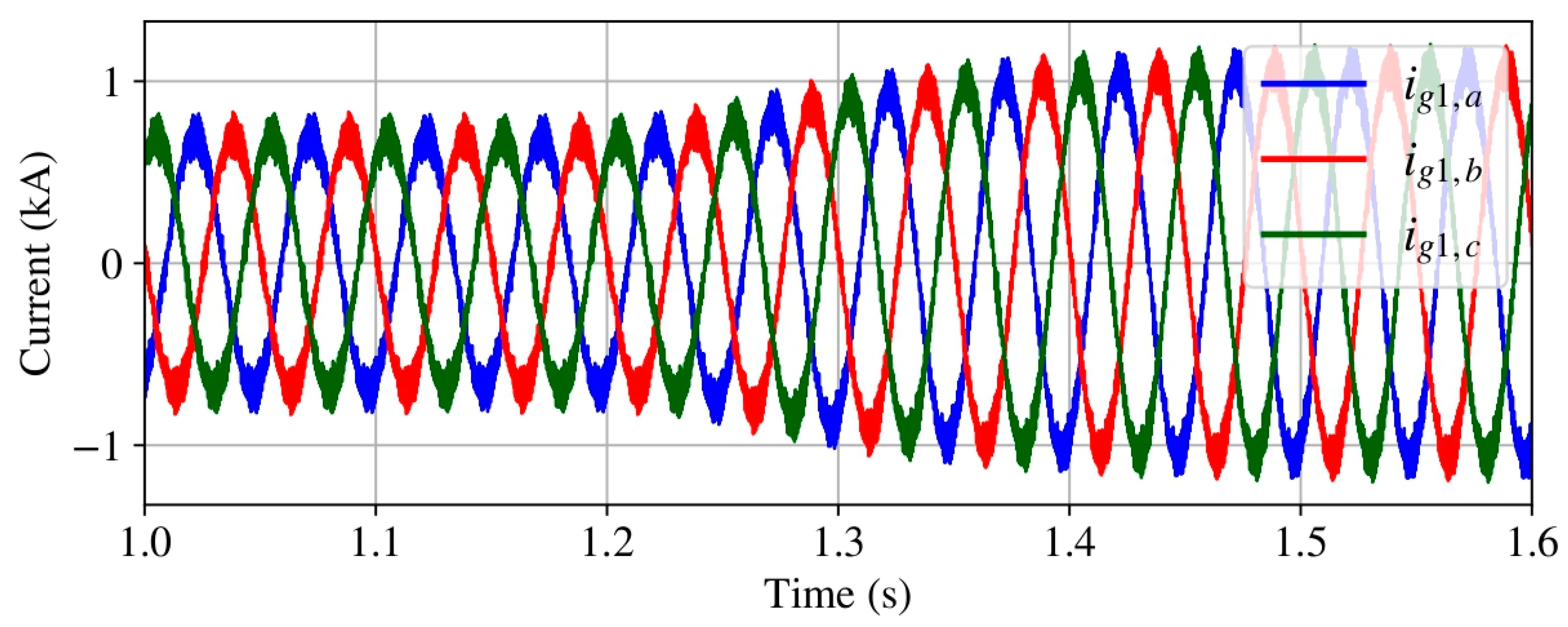
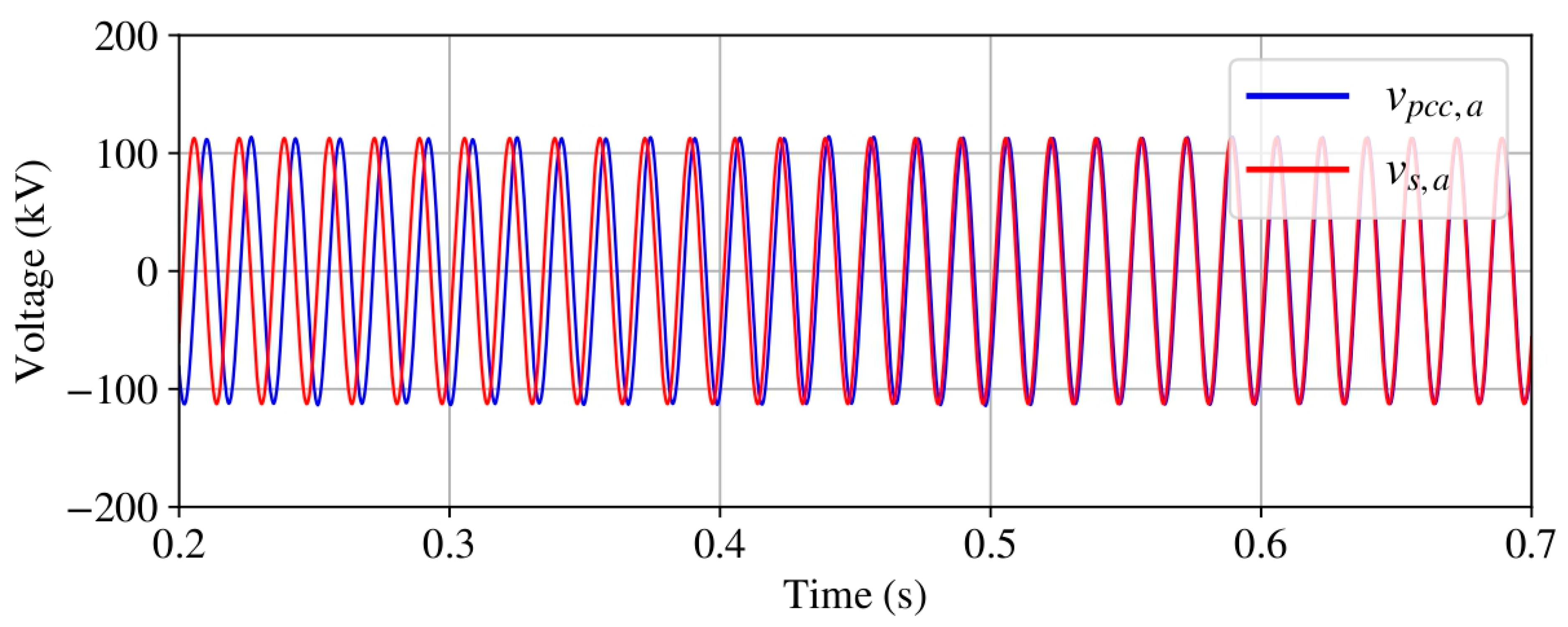
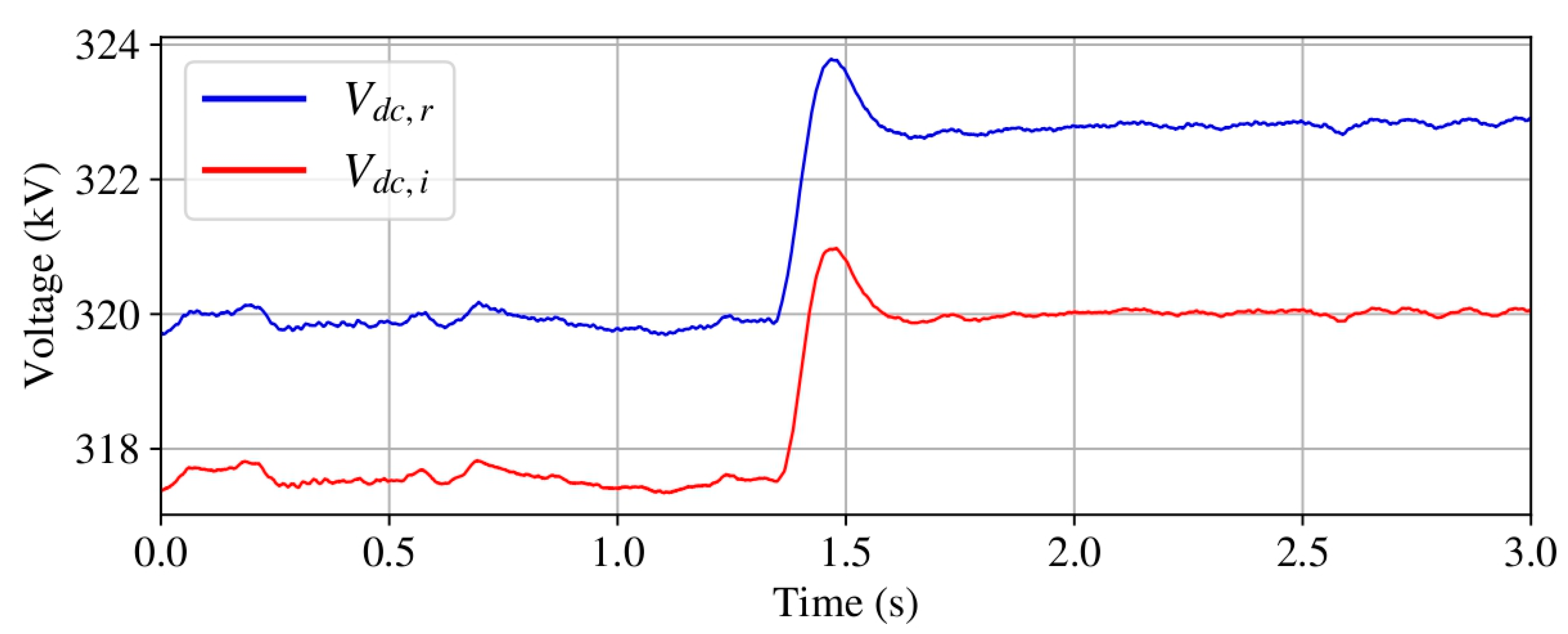
4.1. Case 1: Grid Disconnection
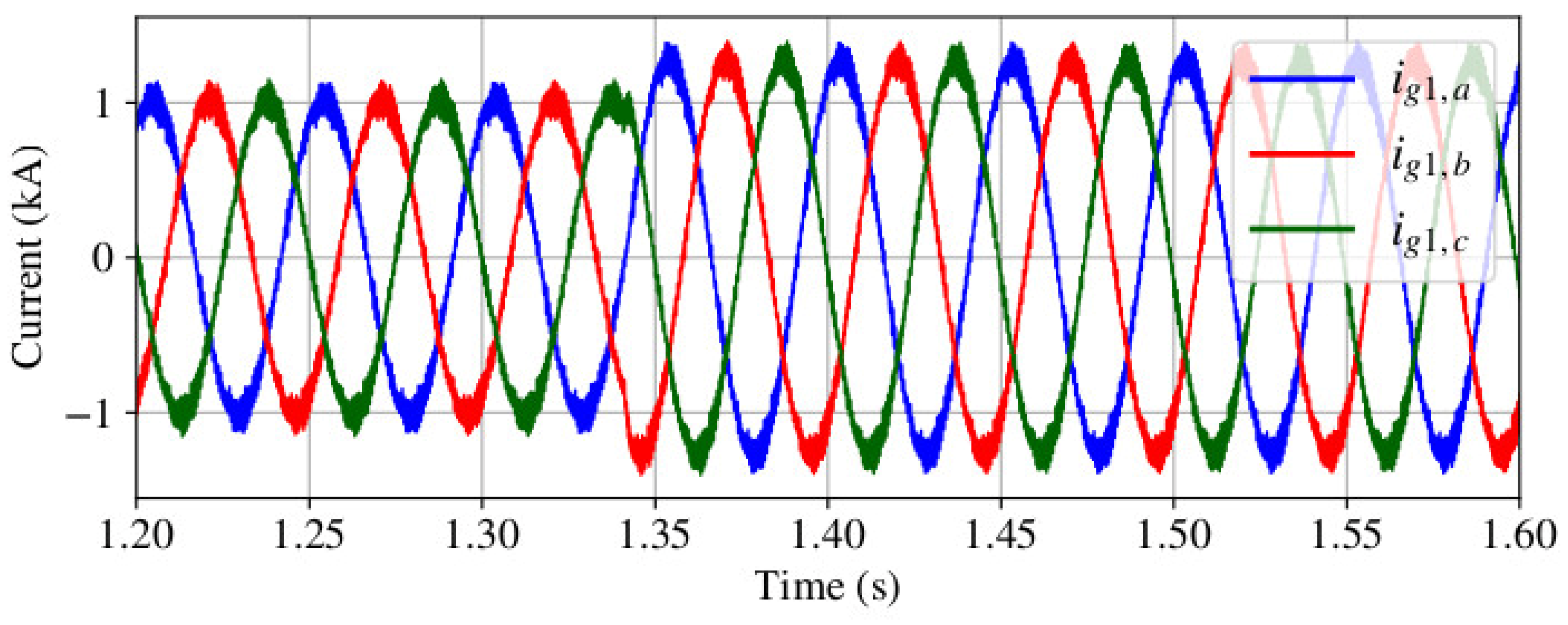
4.2. Case 2: Loss of WECS Units
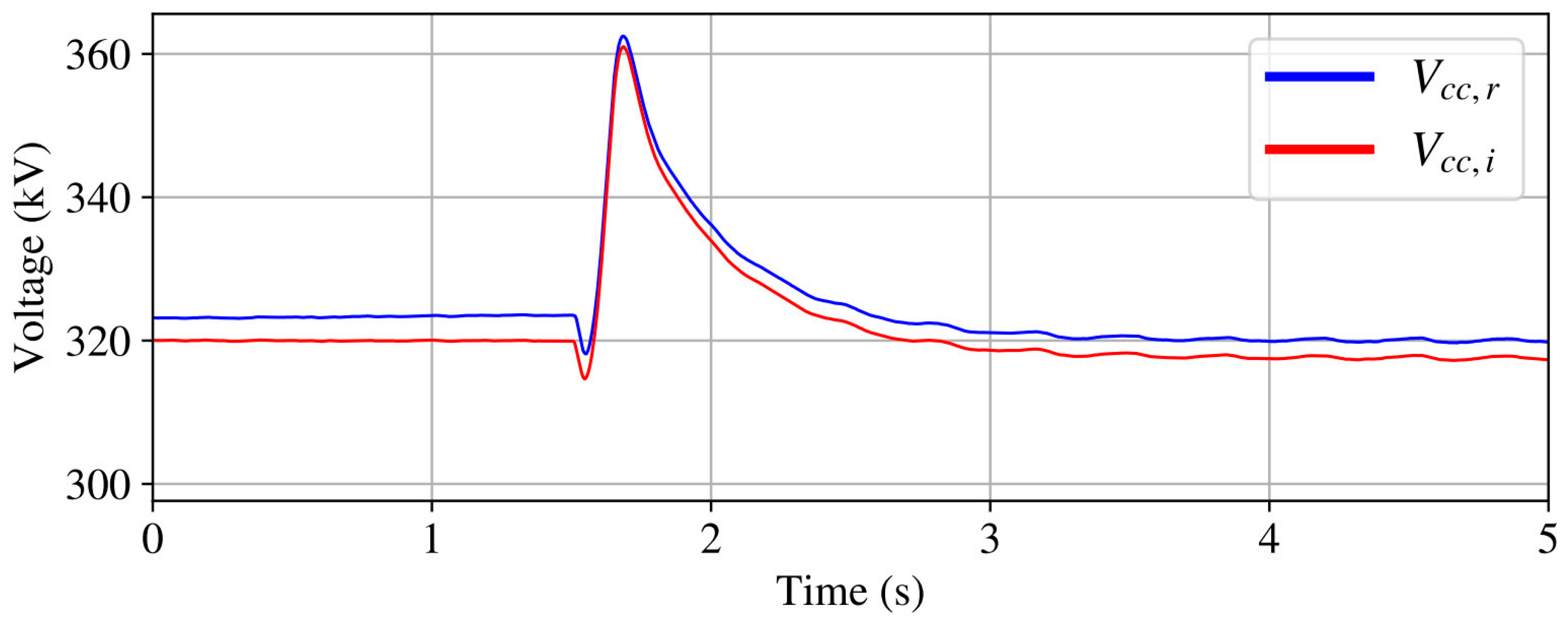
4.3. Case 3: Grid Reconnection
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yaramasu, V.; Wu, B.; Sen, P.C.; Kouro, S.; Narimani, M. High-power wind energy conversion systems: State-of-the-art and emerging technologies. Proc. IEEE 2015, 103, 740–788. [Google Scholar] [CrossRef]
- Anaya-Lara, O.; Campos-Gaona, D.; Moreno-Goytia, E.; Adam, G. Offshore Wind Energy Generation: Control, Protection, and Integration to Electrical Systems; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Pan, W.; Chang, Y.; Chen, H. Hybrid multi-terminal HVDC system for large scale wind power. In Proceedings of the 2006 IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October–1 November 2006; IEEE: Piscatway, NJ, USA, 2006; pp. 755–759. [Google Scholar]
- Andersen, B.R.; Groeman, F.; Alvira, D.; Anaya-Lara, O.; Tang, G.; Hanson, J.; Haeusler, M.; Karoui, K.; Muttik, P.; Nguefeu, S.; et al. Integration of large scale wind generation using HVDC and power electronics. CIGRE Publ. Work. Group B 2009, 4, 2009. [Google Scholar]
- Korompili, A.; Wu, Q.; Zhao, H. Review of VSC HVDC connection for offshore wind power integration. Renew. Sustain. Energy Rev. 2016, 59, 1405–1414. [Google Scholar] [CrossRef] [Green Version]
- Lesnicar, A.; Marquardt, R. An innovative modular multilevel converter topology suitable for a wide power range. In Proceedings of the 2003 IEEE Bologna Power Tech Conference, Bologna, Italy, 23–26 June 2003; IEEE: Piscatway, NJ, USA, 2003; Volume 3, p. 6. [Google Scholar]
- Akagi, H. Classification, terminology, and application of the modular multilevel cascade converter (MMCC). IEEE Trans. Power Electron. 2011, 26, 3119–3130. [Google Scholar] [CrossRef]
- Malinowski, M.; Gopakumar, K.; Rodriguez, J.; Pérez, M.A. A survey on cascaded multilevel inverters. IEEE Trans. Ind. Electron. 2010, 57, 2197–2206. [Google Scholar] [CrossRef]
- Ludois, D.C.; Venkataramanan, G. Simplified terminal behavioral model for a modular multilevel converter. IEEE Trans. Power Electron. 2014, 29, 1622–1631. [Google Scholar] [CrossRef]
- Li, W.; Zhu, M.; Chao, P.; Liang, X.; Xu, D. Enhanced FRT and postfault recovery control for MMC-HVDC connected offshore wind farms. IEEE Trans. Power Syst. 2019, 35, 1606–1617. [Google Scholar] [CrossRef]
- Li, Y.; An, T.; Zhang, D.; Pei, X.; Ji, K.; Tang, G. Analysis and suppression control of high frequency resonance for MMC-HVDC system. IEEE Trans. Power Deliv. 2021, 36, 3867–3881. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, C.; Guo, C. Comparison study of small-signal stability of MMC-HVDC system in different control modes. Int. J. Electr. Power Energy Syst. 2019, 111, 425–435. [Google Scholar] [CrossRef]
- Shi, X.; Yang, R.; Cai, X.; Fang, Z.; Dong, P.; Rao, F. Improved comprehensive energy-based control for MMC-HVDC system. Int. J. Electr. Power Energy Syst. 2023, 145, 108593. [Google Scholar] [CrossRef]
- Belhaouane, M.M.; Ayari, M.; Guillaud, X.; Braiek, N.B. Robust control design of MMC-HVDC systems using multivariable optimal guaranteed cost approach. IEEE Trans. Ind. Appl. 2019, 55, 2952–2963. [Google Scholar] [CrossRef]
- Lourenço, L.F.; Perez, F.; Iovine, A.; Damm, G.; Monaro, R.M.; Salles, M.B. Stability Analysis of Grid-Forming MMC-HVDC Transmission Connected to Legacy Power Systems. Energies 2021, 14, 8017. [Google Scholar] [CrossRef]
- Dadjo Tavakoli, S.; Prieto-Araujo, E.; Sánchez-Sánchez, E.; Gomis-Bellmunt, O. Interaction assessment and stability analysis of the MMC-based VSC-HVDC link. Energies 2020, 13, 2075. [Google Scholar] [CrossRef] [Green Version]
- Chandio, R.H.; Chachar, F.A.; Soomro, J.B.; Ansari, J.A.; Munir, H.M.; Zawbaa, H.M.; Kamel, S. Control and protection of MMC-based HVDC systems: A review. Energy Rep. 2023, 9, 1571–1588. [Google Scholar] [CrossRef]
- Zeng, X.; Liu, T.; Wang, S.; Dong, Y.; Li, B.; Chen, Z. Coordinated control of MMC-HVDC system with offshore wind farm for providing emulated inertia support. IET Renew. Power Gener. 2020, 14, 673–683. [Google Scholar] [CrossRef]
- Jia, K.; Dong, X.; Wen, Z.; Wu, W.; Bi, T. Harmonic injection based fault ride-through control of mmc-hvdc connected offshore wind farms. IEEE Trans. Sustain. Energy 2023, 14, 1796–1806. [Google Scholar] [CrossRef]
- Hossain, M.I.; Abido, M.A. Positive-negative sequence current controller for LVRT improvement of wind farms integrated MMC-HVDC network. IEEE Access 2020, 8, 193314–193339. [Google Scholar] [CrossRef]
- Tu, L.; Yang, Y.; Yang, J.; Sun, T. The Synthetic Inertia Controller for MMC-HVDC Based Offshore Wind Farm Integration. In Proceedings of the 2021 IEEE 1st International Power Electronics and Application Symposium (PEAS), Shanghai, China, 13–15 November 2021; IEEE: Pisctaway, NJ, USA, 2021; pp. 1–4. [Google Scholar]
- Kazemi Golkhandan, R.; Torkaman, H.; Aghaebrahimi, M.R.; Keyhani, A. Load frequency control of smart isolated power grids with high wind farm penetrations. IET Renew. Power Gener. 2020, 14, 1228–1238. [Google Scholar] [CrossRef]
- Kamal, F.; Chowdhury, B. Grid Forming Inverter Control in a Type 4 Wind Turbine for Flexible Power Transfer in an Islanded Microgrid. In Proceedings of the 2021 North American Power Symposium (NAPS), College Station, TX, USA, 14–16 November 2021; IEEE: Pisctaway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Ullah, K.; Basit, A.; Ullah, Z.; Albogamy, F.R.; Hafeez, G. Automatic generation control in modern power systems with wind power and electric vehicles. Energies 2022, 15, 1771. [Google Scholar] [CrossRef]
- Asghar, R.; Riganti Fulginei, F.; Wadood, H.; Saeed, S. A Review of Load Frequency Control Schemes Deployed for Wind-Integrated Power Systems. Sustainability 2023, 15, 8380. [Google Scholar] [CrossRef]
- Yuan, X.; Li, Y. Control of variable pitch and variable speed direct-drive wind turbines in weak grid systems with active power balance. IET Renew. Power Gener. 2014, 8, 119–131. [Google Scholar] [CrossRef]
- Rodriguez, P.; Teodorescu, R.; Candela, I.; Timbus, A.V.; Liserre, M.; Blaabjerg, F. New positive-sequence voltage detector for grid synchronization of power converters under faulty grid conditions. In Proceedings of the Power Electronics Specialists Conference (PESC), Jeju, Republic of Korea, 18–22 June 2006; IEEE: Piscatway, NJ, USA, 2006; pp. 1–7. [Google Scholar]
- Tu, Q.; Xu, Z.; Zhang, J. Circulating current suppressing controller in modular multilevel converter. In Proceedings of the IECON 2010—36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010; IEEE: Piscatway, NJ, USA, 2010; pp. 3198–3202. [Google Scholar]
- Duarte, S.N.; Barbosa, P.G.; Kabalcı, E. Chapter 8—STATCOM and DSTATCOM with modular multilevel converters. In Multilevel Inverters; Kabalcı, E., Ed.; Academic Press: Cambridge, MA, USA, 2021; pp. 209–248. [Google Scholar] [CrossRef]
- Sharifabadi, K.; Harnefors, L.; Nee, H.P.; Norrga, S.; Teodorescu, R. Design, Control, and Application of Modular Multilevel Converters for HVDC Transmission Systems; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Duarte, S.N.; Almeida, P.M.; Barbosa, P.G. Voltage regulation of a remote microgrid bus with a modular multilevel STATCOM. Electr. Power Syst. Res. 2022, 212, 108299. [Google Scholar] [CrossRef]
- Duarte, S.N.; Ghetti, F.T.; de Almeida, P.M.; Barbosa, P.G. Zero-sequence voltage compensation of a distribution network through a four-wire modular multilevel static synchronous compensator. Int. J. Electr. Power Energy Syst. 2019, 109, 57–72. [Google Scholar] [CrossRef]
- Almeida, A.d.O.; Ghetti, F.T.; Ribeiro, A.S.B.; de Almeida, P.M.; Barbosa, P.G. Circulating currents suppression strategies for modular multilevel converter. In Proceedings of the 2017 Brazilian Power Electronics Conference (COBEP), Juiz de Fora, Brazil, 19–22 November 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Duarte, S.N.; Almeida, P.M.; Barbosa, P.G. Voltage compensation in multi-grounded distribution network with a three-phase five-wire DSTATCOM. Electr. Power Syst. Res. 2021, 197, 107310. [Google Scholar] [CrossRef]
- Paulo, M.S. Coordinated Control of an Offshore Wind Farm Considering an MMC-HVDC Transmission System Operating in On-Grid and Off-Grid Modes. Master’s Thesis, Federal University of Juiz de Fora, Juiz de Fora, Brazil, 2023. (In Portuguese). [Google Scholar]
- Wu, B.; Lang, Y.; Zargari, N.; Kouro, S. Power Conversion and Control of Wind Energy Systems; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 76. [Google Scholar]
- Almeida, A.O.; Tomim, M.A.; Almeida, P.M.; Barbosa, P.G. A control strategy for an offshore wind farm with the generating units connected in series with a VSC-HVDC transmission link. Electr. Power Syst. Res. 2020, 180, 106121. [Google Scholar] [CrossRef]
- Almeida, A.O.; Almeida, P.M.; Barbosa, P.G. Design Methodology for the DC Link Current Controller of a Series-Connected Offshore Wind Farm. In Proceedings of the 2022 14th Seminar on Power Electronics and Control (SEPOC), Santa Maria, Brazil, 12–15 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2009. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Zhao, C.; Xiong, Y.; Li, C.; Ji, Y.; An, T. Optimal Design of MMC Levels for Electromagnetic Transient Studies of MMC-HVDC. IEEE Trans. Power Deliv. 2016, 31, 1663–1672. [Google Scholar] [CrossRef]
- Xu, Z.; Xiao, H.; Zhang, Z. Selection methods of main circuit parameters for modular multilevel converters. IET Renew. Power Gener. 2016, 10, 788–797. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering, 5th ed.; Prentice Hall: Hoboken, NJ, USA, 2010. [Google Scholar]
- Duarte, S.N.; Souza, B.C.; Almeida, P.M.; Araujo, L.R.; Barbosa, P.G. Control algorithm for DSTATCOM to compensate consumer-generated negative and zero sequence voltage unbalance. Int. J. Electr. Power Energy Syst. 2020, 120, 105957. [Google Scholar] [CrossRef]
- Ochs, D.S.; Mirafzal, B.; Sotoodeh, P. A Method of Seamless Transitions Between Grid-Tied and Stand-Alone Modes of Operation for Utility-Interactive Three-Phase Inverters. IEEE Trans. Ind. Appl. 2014, 50, 1934–1941. [Google Scholar] [CrossRef]







| Parameter | Value |
|---|---|
| PMSG rated power | 5 |
| PMSG rms voltage | 3 |
| PMSG frequency | 20 |
| PMSG resistance | 9.35 |
| PMSG inductance | 2.2 |
| B2B rated dc voltage | 10 |
| B2B switching frequency | 2.4 |
| B2B transformer turns ratio | 3:33 |
| B2B filter resistance | 5 |
| B2B filter inductance | 2 |
| Gearbox ratio | 10:1 |
| Number of units of the 1st equivalent group | 30 |
| Number of units of the 2nd equivalent group | 15 |
| Parameter | Value |
|---|---|
| MMC dc voltage | 320 |
| Offshore MMC AC voltage | 138 |
| Onshore MMC AC voltage | 138 |
| Number of SM per arm | 18 |
| SM capacitance | 900 |
| Arm resistance | 0.25 |
| Arm inductance | 10.5 |
| MMC switching frequency | 1.26 |
| AC grid voltage | 500 |
| AC grid frequency | 60 |
| Offshore transformer turns ratio | 138:33 |
| Onshore transformer turns ratio | 138:500 |
| AC onshore MMC filter resistance | 0.25 |
| AC onshore MMC filter inductance | 12.8 |
| AC onshore MMC filter capacitance | 10 |
| DC submarine cable length | 50 |
| WECS Group | Parameter | Value |
|---|---|---|
| 1st | Undamped natural frequency () | 20 |
| Damping factor () | 1 | |
| Proportional gain () | ||
| Integral gain () | ||
| Droop gain () | 9.6 | |
| 2nd | Undamped natural frequency () | 20 |
| Damping factor () | 1 | |
| Proportional gain () | ||
| Integral gain () | ||
| Droop gain () | 3.2 |
| Side | Parameter | Value |
|---|---|---|
| Offshore MMC | Undamped natural frequency () | 2000 |
| Damping factor () | 0.7 | |
| Proportional gain () | 50.2 | |
| Integral gain () | 7142.8 | |
| Onshore MMC | Undamped natural frequency () | 2000 |
| Damping factor () | 0.7 | |
| Proportional gain () | 50.2 | |
| Integral gain () | 7142.8 |
| Side | Parameter | Value |
|---|---|---|
| DC link (grid-connected) | Undamped natural frequency () | 20 |
| Damping factor () | 2 | |
| Proportional gain () | ||
| Integral gain () | ||
| AC bus (stand-alone) | Undamped natural frequency () | 20 |
| Damping factor () | 2 | |
| Proportional gain () | 0.0008 | |
| Integral gain () | 0.004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paulo, M.S.; Almeida, A.d.O.; Almeida, P.M.d.; Barbosa, P.G. Control of an Offshore Wind Farm Considering Grid-Connected and Stand-Alone Operation of a High-Voltage Direct Current Transmission System Based on Multilevel Modular Converters. Energies 2023, 16, 5891. https://doi.org/10.3390/en16165891
Paulo MS, Almeida AdO, Almeida PMd, Barbosa PG. Control of an Offshore Wind Farm Considering Grid-Connected and Stand-Alone Operation of a High-Voltage Direct Current Transmission System Based on Multilevel Modular Converters. Energies. 2023; 16(16):5891. https://doi.org/10.3390/en16165891
Chicago/Turabian StylePaulo, Matheus Sene, Andrei de Oliveira Almeida, Pedro Machado de Almeida, and Pedro Gomes Barbosa. 2023. "Control of an Offshore Wind Farm Considering Grid-Connected and Stand-Alone Operation of a High-Voltage Direct Current Transmission System Based on Multilevel Modular Converters" Energies 16, no. 16: 5891. https://doi.org/10.3390/en16165891
APA StylePaulo, M. S., Almeida, A. d. O., Almeida, P. M. d., & Barbosa, P. G. (2023). Control of an Offshore Wind Farm Considering Grid-Connected and Stand-Alone Operation of a High-Voltage Direct Current Transmission System Based on Multilevel Modular Converters. Energies, 16(16), 5891. https://doi.org/10.3390/en16165891







