Dynamic Analysis of a Supercapacitor DC-Link in Photovoltaic Conversion Applications
Abstract
:1. Introduction
2. Materials and Methods
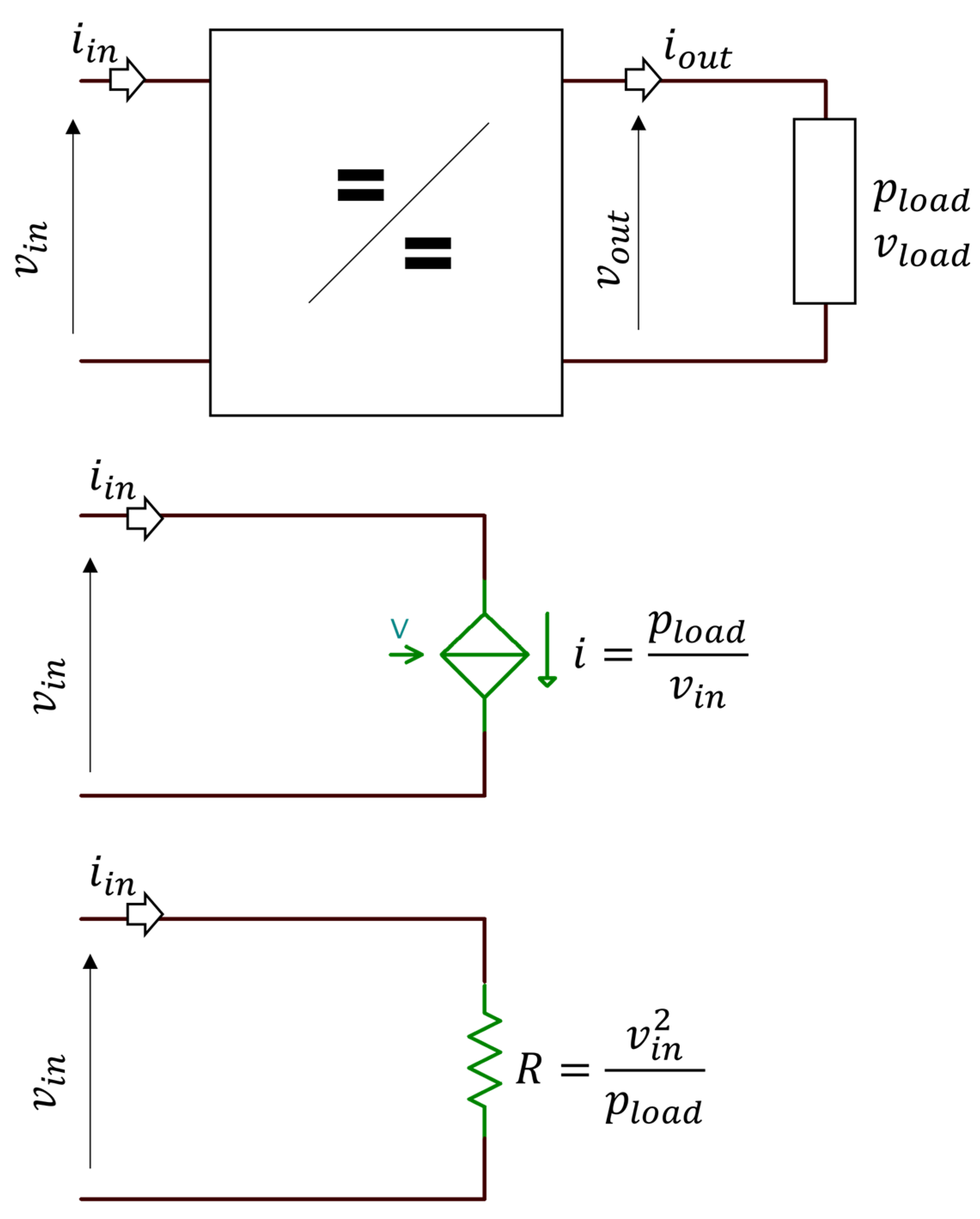
2.1. Modelling for the Blocks of the Conversion Chain
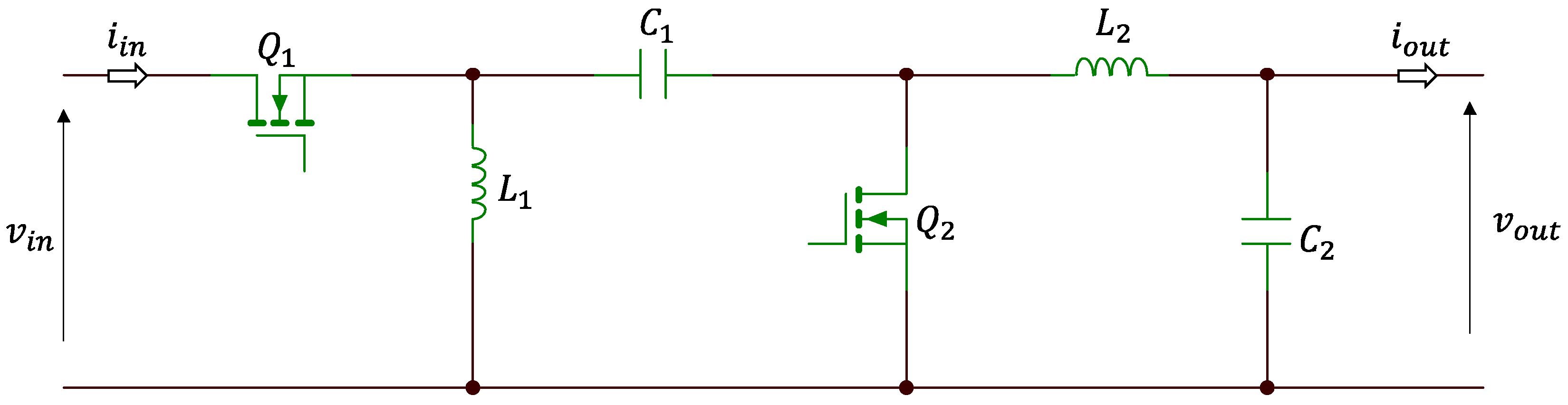
2.2. Full Chain Dynamic Model
2.2.1. Ideal Supercapacitor Dynamic Model (IDSC)
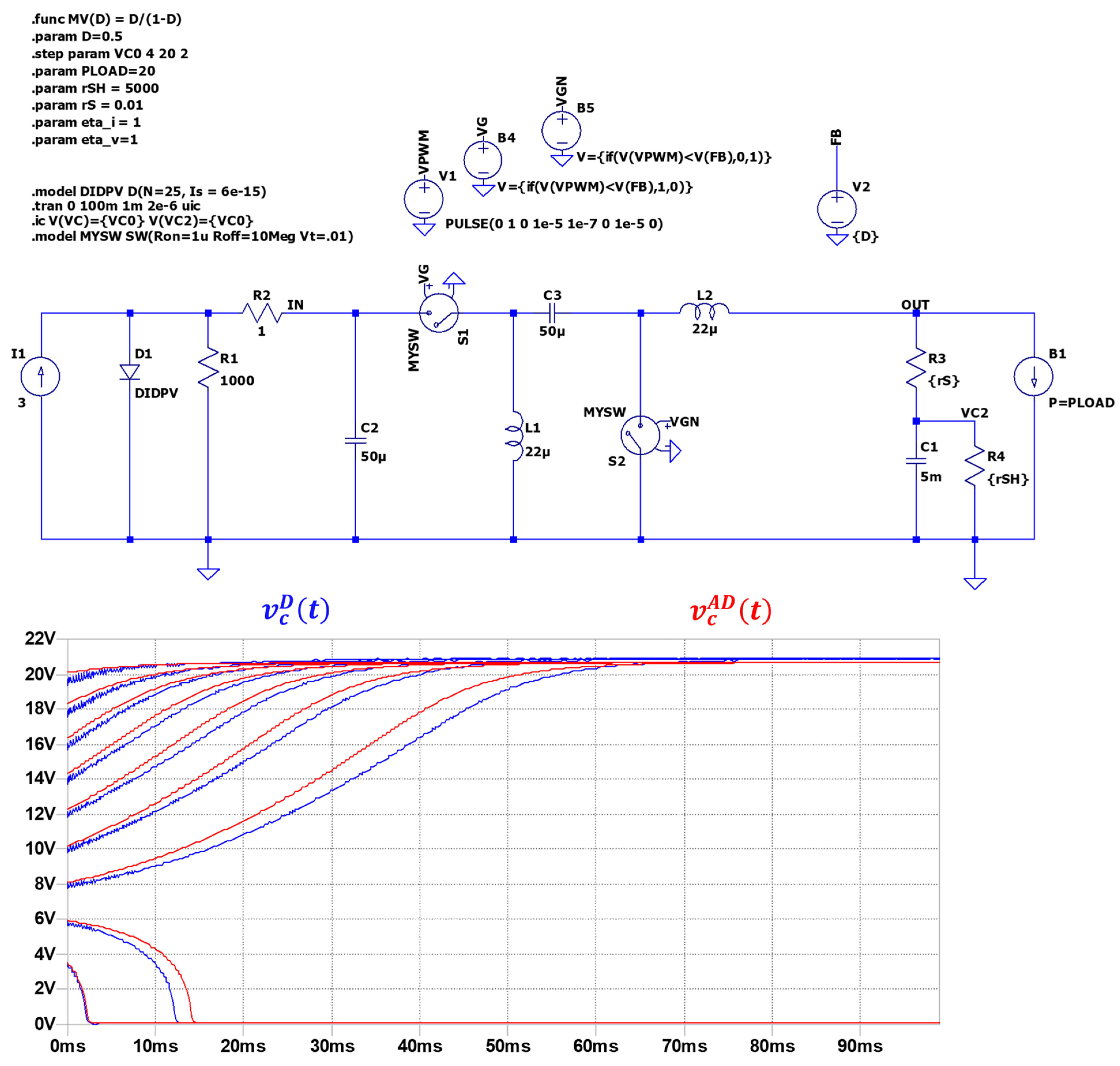
2.2.2. Self-Discharge Supercapacitor Dynamic Model (SDSC)
2.2.3. Full Supercapacitor Dynamic Model (FSC)
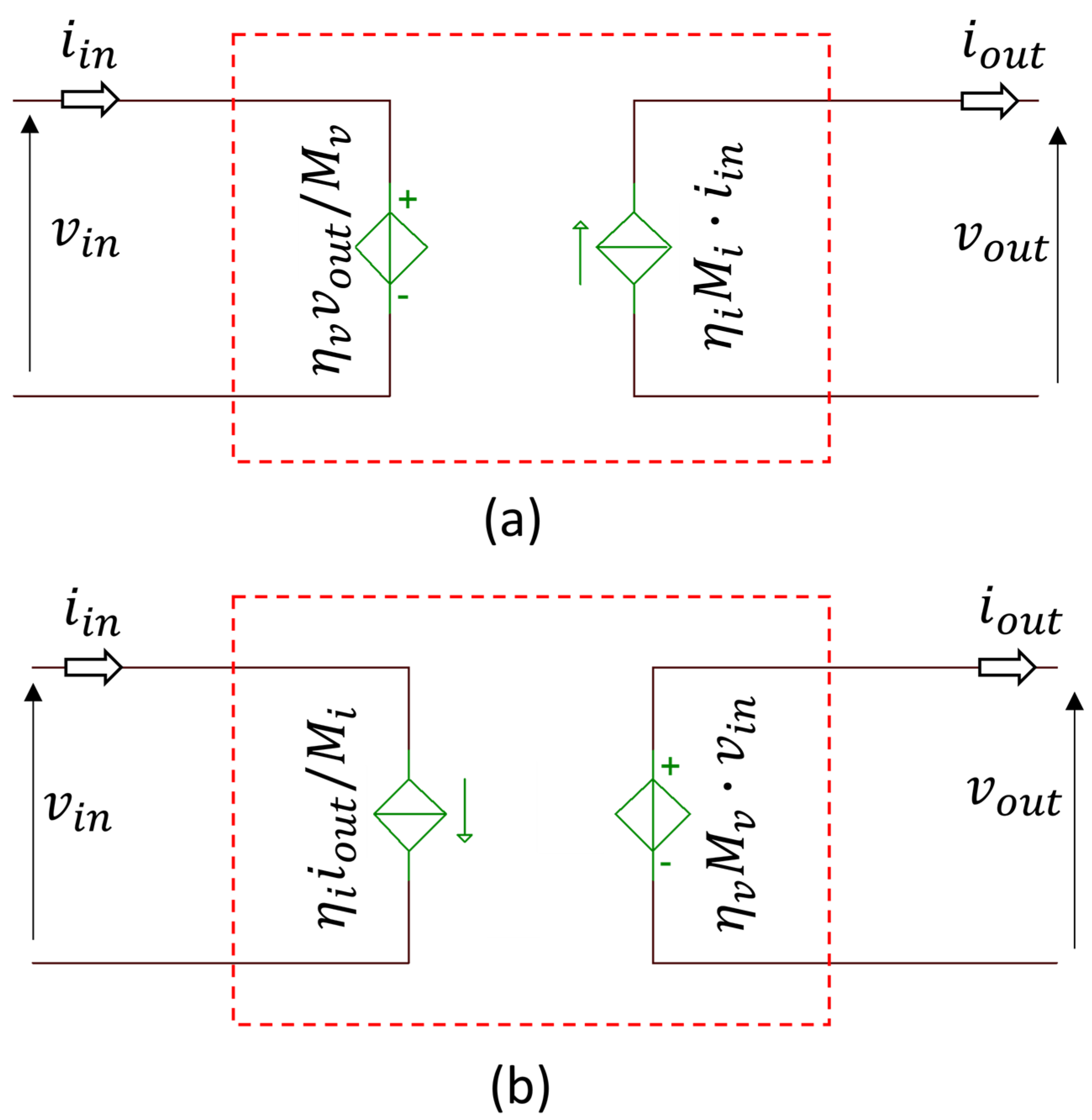
2.3. Equilibrium Points for Final Voltage Charging
2.4. Duty Cycle for Final Voltage Charging
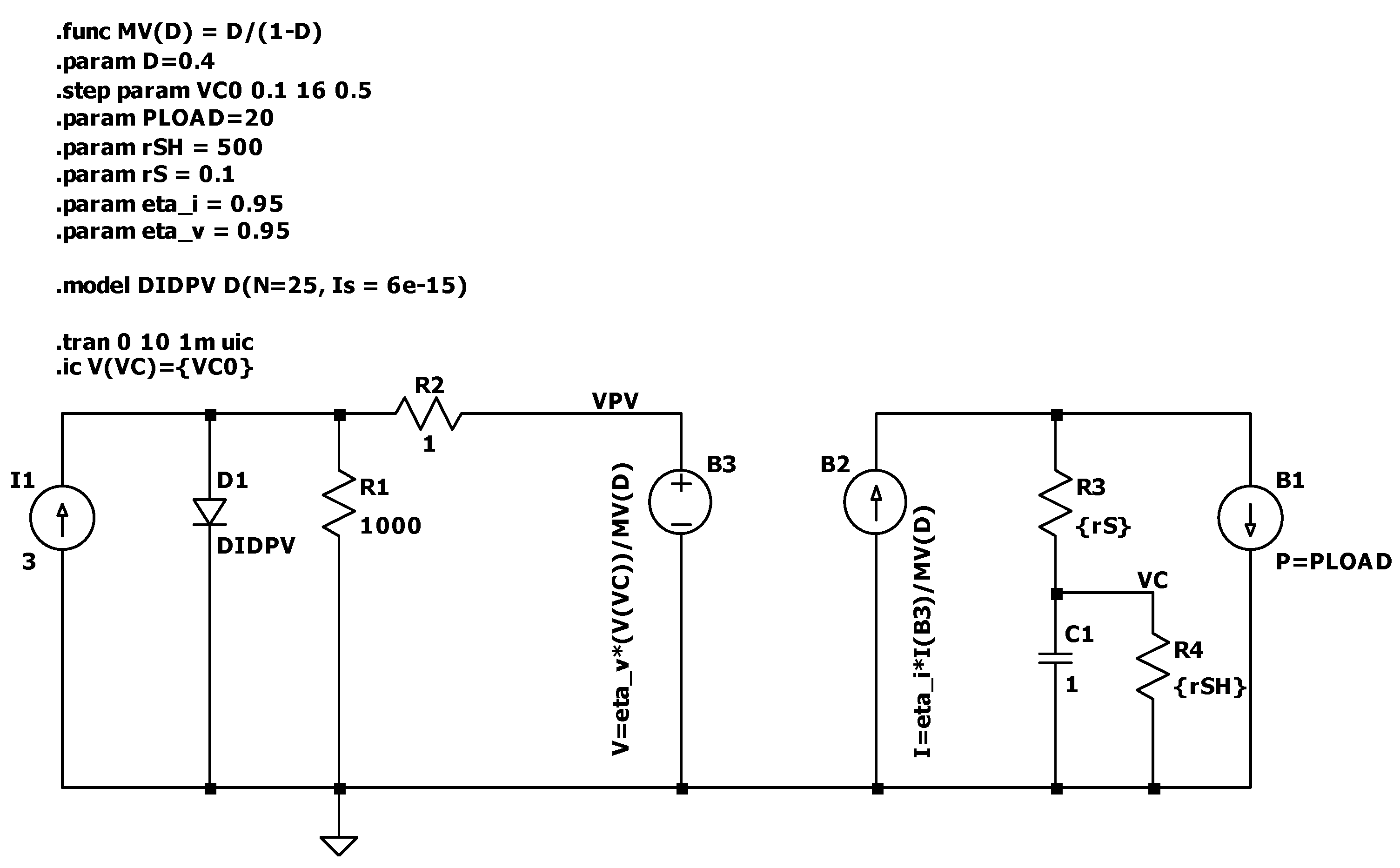
3. Validation Results
3.1. Test A: Final Voltage Charge and Stability Region
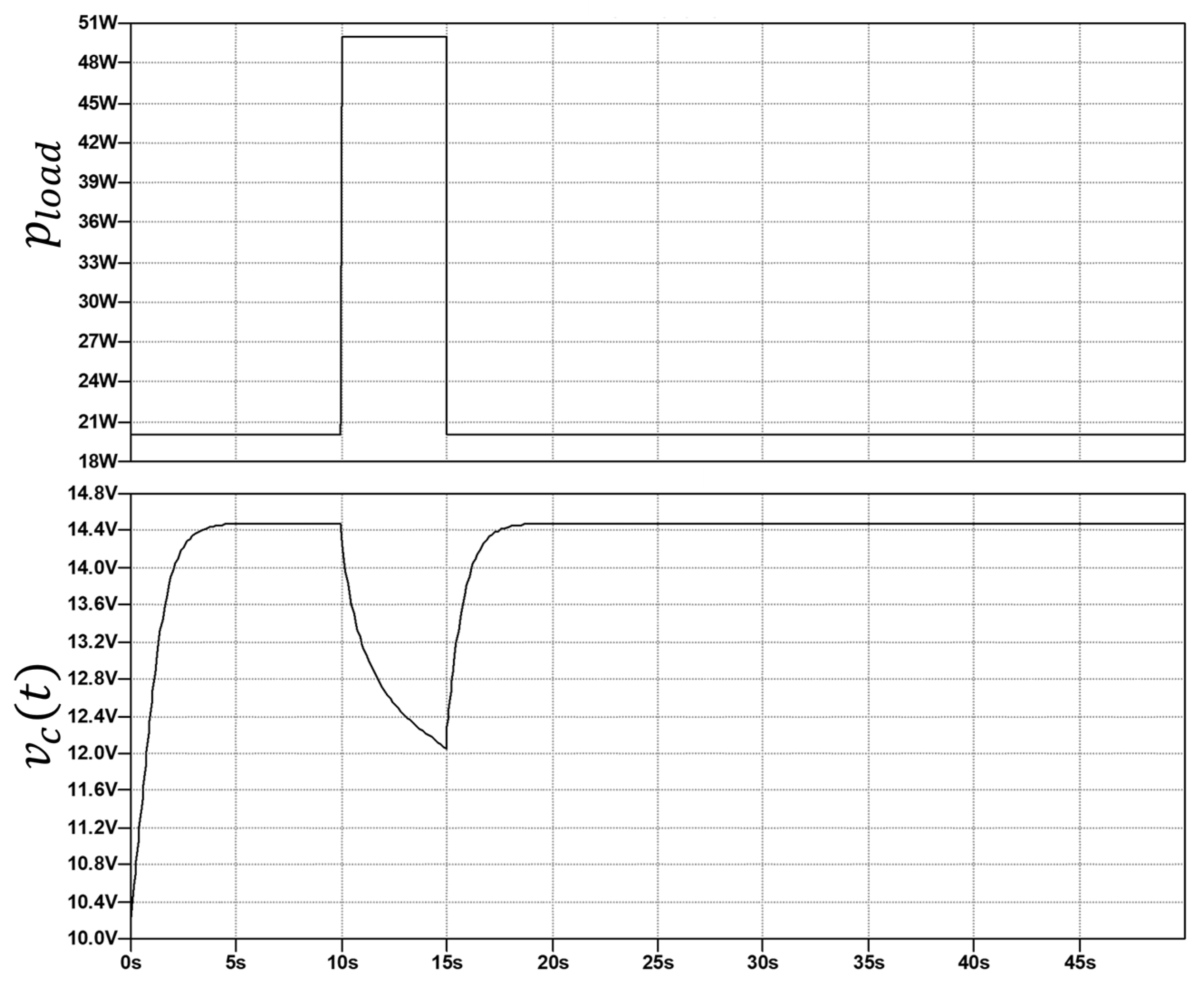
3.2. Test B: Short and Heavy Load Perturbation
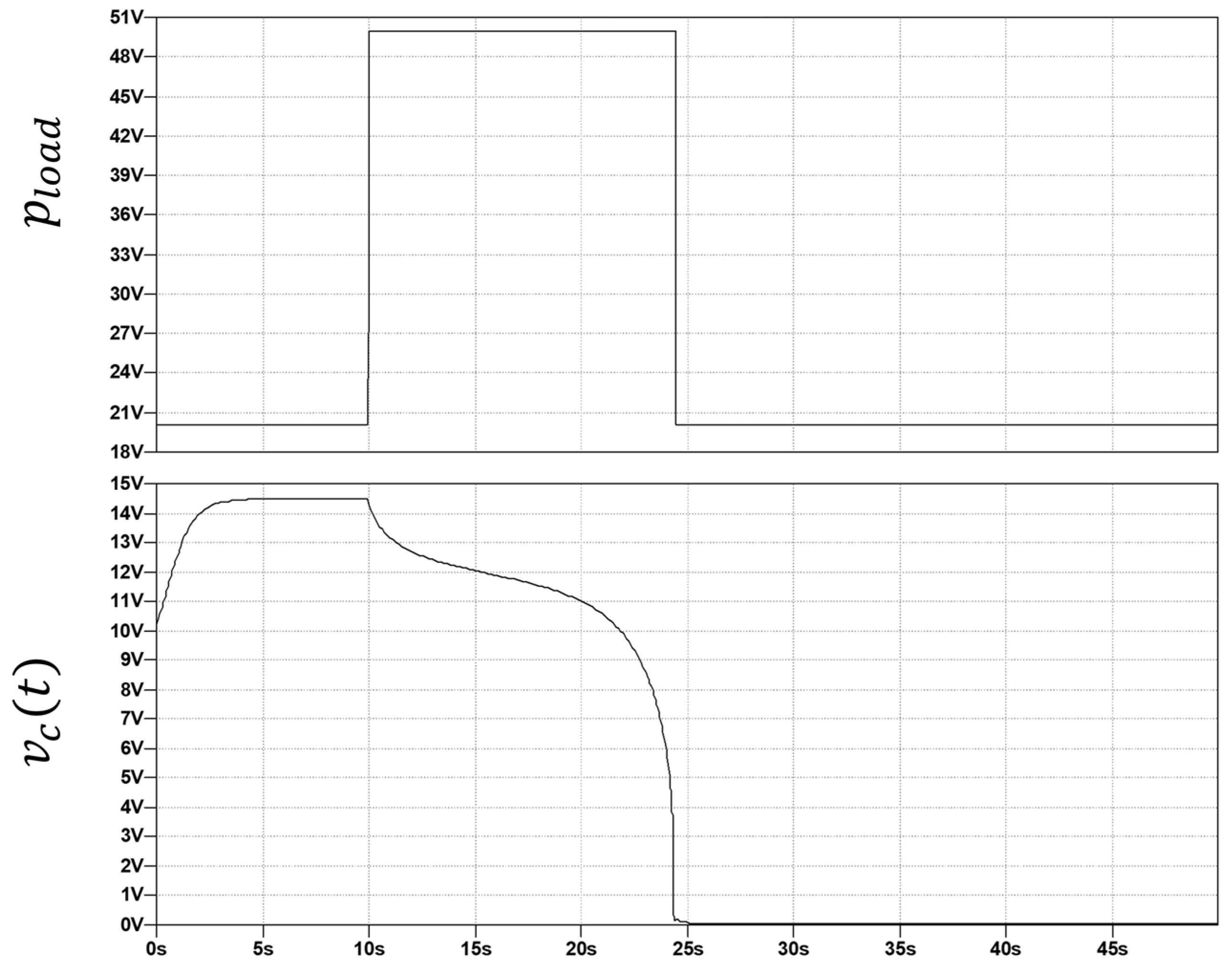
3.3. Test C: Long and Heavy Load Perturbation
3.4. Test D: Dynamic Response
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Corti, F.; Laudani, A.; Lozito, G.M.; Reatti, A. Computationally efficient modeling of DC–DC converters for PV applications. Energies 2020, 13, 5100. [Google Scholar] [CrossRef]
- Azuatalam, D.; Paridari, K.; Ma, Y.; Förstl, M.; Chapman, A.C.; Verbič, G. Energy management of small-scale PV-battery systems: A systematic review considering practical implementation, computational requirements, quality of input data and battery degradation. Renew. Sustain. Energy Rev. 2019, 112, 555–570. [Google Scholar] [CrossRef] [Green Version]
- Sri Revathi, B.; Prabhakar, M. Non isolated high gain DC–DC converter topologies for PV applications—A comprehensive review. Renew. Sustain. Energy Rev. 2016, 66, 920–933. [Google Scholar] [CrossRef]
- Fagiolari, L.; Sampò, M.; Lamberti, A.; Amici, J.; Francia, C.; Bodoardo, S.; Bella, F. Integrated energy conversion and storage devices: Interfacing solar cells, batteries and supercapacitors. Energy Storage Mater. 2022, 51, 400–434. [Google Scholar] [CrossRef]
- Imran, A.; Zhu, Q.; Sulaman, M.; Bukhtiar, A.; Xu, M. Electric-Dipole Gated Two Terminal Phototransistor for Charge-Coupled Device. Adv. Opt. Mater. 2023, 2300910. [Google Scholar] [CrossRef]
- Laudani, A.; Lozito, G.M.; Lucaferri, V.; Radicioni, M.; Fulginei, F.R.; Salvini, A.; Coco, S. An analytical approach for maximum power point calculation for photovoltaic system. In Proceedings of the 2017 European Conference on Circuit Theory and Design, ECCTD 2017, Catania, Italy, 4–6 September 2017. [Google Scholar]
- Kumar, N.; Hussain, I.; Singh, B.; Panigrahi, B.K. Self-Adaptive Incremental Conductance Algorithm for Swift and Ripple-Free Maximum Power Harvesting from PV Array. IEEE Trans. Ind. Inform. 2018, 14, 2031–2041. [Google Scholar] [CrossRef]
- Chiang, S.J.; Shieh, H.J.; Chen, M.C. Modeling and control of PV charger system with SEPIC converter. IEEE Trans. Ind. Electron. 2009, 56, 4344–4353. [Google Scholar] [CrossRef]
- Mohammadinodoushan, M.; Abbassi, R.; Jerbi, H.; Waly Ahmed, F.; Abdalqadir kh ahmed, H.; Rezvani, A. A new MPPT design using variable step size perturb and observe method for PV system under partially shaded conditions by modified shuffled frog leaping algorithm- SMC controller. Sustain. Energy Technol. Assess. 2021, 45, 101056. [Google Scholar] [CrossRef]
- Cossutta, M.; Vretenar, V.; Centeno, T.A.; Kotrusz, P.; McKechnie, J.; Pickering, S.J. A comparative life cycle assessment of graphene and activated carbon in a supercapacitor application. J. Clean. Prod. 2020, 242, 118468. [Google Scholar] [CrossRef]
- Diarra, B.; Zungeru, A.M.; Ravi, S.; Chuma, J.; Basutli, B.; Zibani, I. Design of a photovoltaic system with ultracapacitor energy buffer. Procedia Manuf. 2019, 33, 216–223. [Google Scholar] [CrossRef]
- Pandey, S.; Dwivedi, B.; Tripathi, A. Performance analysis of super capacitor integrated PV fed multistage converter with SMC controlled VSI for varying nonlinear load conditions. Int. J. Eng. Technol. 2018, 7, 174–180. [Google Scholar] [CrossRef] [Green Version]
- Melkia, C.; Ghoudlburk, S.; Soufi, Y.; Maamri, M.; Bayoud, M. Battery-Supercapacitor Hybrid Energy Storage Systems for Stand-Alone Photovoltaic. Rev. Compos. Mater. Av. 2022, 24, 265–271. [Google Scholar] [CrossRef]
- Shchur, I.; Kulwas, D.; Wielgosz, R. Combination of distributed MPPT and distributed supercapacitor energy storage based on cascaded converter in photovoltaic installation. In Proceedings of the 2018 IEEE 3rd International Conference on Intelligent Energy and Power Systems, IEPS 2018, Kharkiv, Ukraine, 10–14 September 2018. [Google Scholar]
- Al-Thabaiti, S.A.; Mostafa, M.M.M.; Ahmed, A.I.; Salama, R.S. Synthesis of copper/chromium metal organic frameworks—Derivatives as an advanced electrode material for high-performance supercapacitors. Ceram. Int. 2023, 49, 5119–5129. [Google Scholar] [CrossRef]
- Mostafa, M.M.M.; Alshehri, A.A.; Salama, R.S. High performance of supercapacitor based on alumina nanoparticles derived from Coca-Cola cans. J. Energy Storage 2023, 64, 107168. [Google Scholar] [CrossRef]
- Gouda, M.S.; Shehab, M.; Helmy, S.; Soliman, M.; Salama, R.S. Nickel and cobalt oxides supported on activated carbon derived from willow catkin for efficient supercapacitor electrode. J. Energy Storage 2023, 61, 106806. [Google Scholar] [CrossRef]
- Gouda, M.S.; Shehab, M.; Soliman, M.M.; Helmy, S.; Salama, R. Preparation and characterization of supercapacitor electrodes utilizing catkin plant as an activated carbon source. Delta Univ. Sci. J. 2023, 6, 255–265. [Google Scholar]
- Zhao, Y.; Xie, W.; Fang, Z.; Liu, S. A Parameters Identification Method of the Equivalent Circuit Model of the Supercapacitor Cell Module Based on Segmentation Optimization. IEEE Access 2020, 19, 92895–92906. [Google Scholar] [CrossRef]
- Corti, F.; Gulino, M.S.; Laschi, M.; Lozito, G.M.; Pugi, L.; Reatti, A.; Vangi, D. Time-domain circuit modelling for hybrid supercapacitors. Energies 2021, 14, 6837. [Google Scholar] [CrossRef]
- Yue, X.; Kiely, J.; Gibson, D.; Drakakis, E.M. Charge-Based Supercapacitor Storage Estimation for Indoor Sub-mW Photovoltaic Energy Harvesting Powered Wireless Sensor Nodes. IEEE Trans. Ind. Electron. 2020, 14, 6837. [Google Scholar] [CrossRef] [Green Version]
- Reatti, A.; Corti, F.; Tesi, A.; Torlai, A.; Kazimierczuk, M.K. Effect of parasitic components on dynamic performance of power stages of DC–DC PWM buck and boost converters in CCM. In Proceedings of the IEEE International Symposium on Circuits and Systems, Sapporo, Japan, 26–29 May 2019. [Google Scholar]
- Kazimierczuk, M.K. Pulse-Width Modulated DC–DC Power Converters; John Wiley & Sons: Hoboken, NJ, USA, 2012; ISBN 9780470773017. [Google Scholar]
- Bronzoni, M.; Colace, L.; De Iacovo, A.; Laudani, A.; Lozito, G.M.; Lucaferri, V.; Radicioni, M.; Rampino, S. Equivalent circuit model for Cu(In,Ga)Se2 solar cells operating at different temperatures and irradiance. Electronics 2018, 7, 324. [Google Scholar] [CrossRef] [Green Version]
- De Soto, W.; Klein, S.A.; Beckman, W.A. Improvement and validation of a model for photovoltaic array performance. Sol. Energy 2006, 80, 78–88. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Roberts, K.; Valluri, S.R. Solar Cells and the Lambert W Function 2016. In Proceedings of the Conference “Celebrating 20 Years of the Lambert W function”, London, ON, Canada, 25–28 July 2016. [Google Scholar]
- Blakesley, J.C.; Castro, F.A.; Koutsourakis, G.; Laudani, A.; Lozito, G.M.; Riganti Fulginei, F. Towards non-destructive individual cell I–V characteristic curve extraction from photovoltaic module measurements. Sol. Energy 2020, 202, 342–357. [Google Scholar] [CrossRef]
- Oommen, S.; Ballaji, A.; Ankaiah, B.; Ananda, M.H. Zeta converter simulation for continuous current mode operation. Int. J. Adv. Res. Eng. Technol. 2019, 10, 2019. [Google Scholar] [CrossRef]
- Chandran, I.R.; Ramasamy, S.; Nallaperumal, C. A high voltage gain multiport zeta-zeta converter for renewable energy systems. Inf. MIDEM 2020, 50, 215–230. [Google Scholar] [CrossRef]
- Song, M.S.; Son, Y.D.; Lee, K.H. Non-isolated bidirectional soft-switching SEPIC/ZETA converter with reduced ripple currents. J. Power Electron. 2014, 14, 649–660. [Google Scholar] [CrossRef] [Green Version]
- Banaei, M.R.; Bonab, H.A.F. A High Efficiency Nonisolated Buck-Boost Converter Based on ZETA Converter. IEEE Trans. Ind. Electron. 2020, 67, 1991–1998. [Google Scholar] [CrossRef]
- Camara, M.B.; Gualous, H.; Gustin, F.; Berthon, A. Design and new control of DC/DC converters to share energy between supercapacitors and batteries in hybrid vehicles. IEEE Trans. Veh. Technol. 2008, 57, 2721–2735. [Google Scholar] [CrossRef]
- Pena, R.A.S.; Hijazi, A.; Venet, P.; Errigo, F. Balancing Supercapacitor Voltages in Modular Bidirectional DC–DC Converter Circuits. IEEE Trans. Power Electron. 2022, 37, 137–149. [Google Scholar] [CrossRef]
- Carpita, M.; De Vivo, M.; Gavin, S. Dynamic modeling of a bidirectional DC/DC interleaved converter working in discontinuous mode for stationary and traction supercapacitor applications. In Proceedings of the SPEEDAM 2012—21st International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Sorrento, Italy, 20–22 June 2012. [Google Scholar]
- Jagadeesh, I.; Indragandhi, V. Comparative Study of DC–DC Converters for Solar PV with Microgrid Applications. Energies 2022, 15, 7569. [Google Scholar] [CrossRef]
- Hole, S.R.; Goswami, A. Das Quantitative analysis of DC–DC converter models: A statistical perspective based on solar photovoltaic power storage. Energy Harvest. Syst. 2022, 9, 113–121. [Google Scholar] [CrossRef]
- Formisano, A.; Hernández, J.C.; Petrarca, C.; Sanchez-Sutil, F. Modeling of pv module and DC/DC converter assembly for the analysis of induced transient response due to nearby lightning strike. Electronics 2021, 10, 120. [Google Scholar] [CrossRef]
- Van De Sande, W.; Ravyts, S.; Alavi, O.; Nivelle, P.; Driesen, J.; Daenen, M. The sensitivity of an electro-thermal photovoltaic DC–DC converter model to the temperature dependence of the electrical variables for reliability analyses. Energies 2020, 13, 2865. [Google Scholar] [CrossRef]
- Karami, Z.; Shafiee, Q.; Sahoo, S.; Yaribeygi, M.; Bevrani, H.; Dragicevic, T. Hybrid Model Predictive Control of DC–DC Boost Converters with Constant Power Load. IEEE Trans. Energy Convers. 2021, 36, 1347–1356. [Google Scholar] [CrossRef]
- Ali, M.S.; Soliman, M.; Hussein, A.M.; Hawash, S.A.F. Robust Controller of Buck Converter Feeding Constant Power Load. J. Control. Autom. Electr. Syst. 2021, 32, 153–164. [Google Scholar] [CrossRef]
- Corti, F.; Laudani, A.; Lozito, G.M.; Reatti, A.; Bartolini, A.; Ciani, L. Model-Based Power Management for Smart Farming Wireless Sensor Networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 2235–2245. [Google Scholar] [CrossRef]
- Santosh Kumar Reddy, P.L.; Obulesu, Y.P.; Singirikonda, S.; Al Harthi, M.; Alzaidi, M.S.; Ghoneim, S.S.M. A Non-Isolated Hybrid Zeta Converter with a High Voltage Gain and Reduced Size of Components. Electronics 2022, 11, 483. [Google Scholar] [CrossRef]
- Rana, M.M.; Uddin, M.; Sarkar, M.R.; Shafiullah, G.M.; Mo, H.; Atef, M. A review on hybrid photovoltaic—Battery energy storage system: Current status, challenges, and future directions. J. Energy Storage 2022, 51, 104597. [Google Scholar] [CrossRef]
- Chibuko, U.; Merdzhanova, T.; Weigand, D.; Ezema, F.; Agbo, S.; Rau, U.; Astakhov, O. Module-level direct coupling in PV-battery power unit under realistic irradiance and load. Sol. Energy 2023, 249, 233–241. [Google Scholar] [CrossRef]
- Lal, V.M.; Parihar, P.S.; Kanimozhi, G. Isolated SEPIC-Based DC–DC Converter for Solar Applications. Smart Grids Smart Cities 2023, 1, 309–322. [Google Scholar]


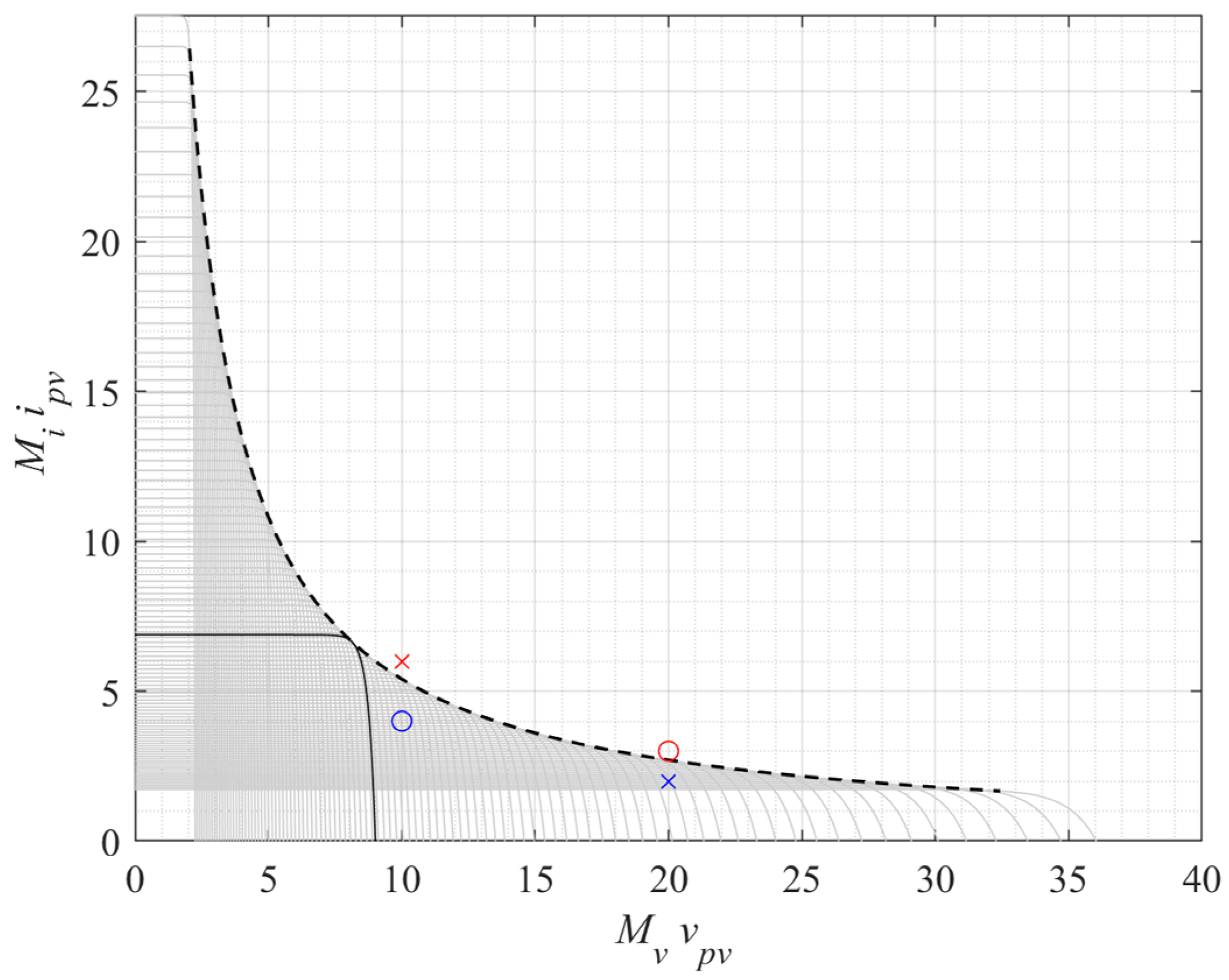

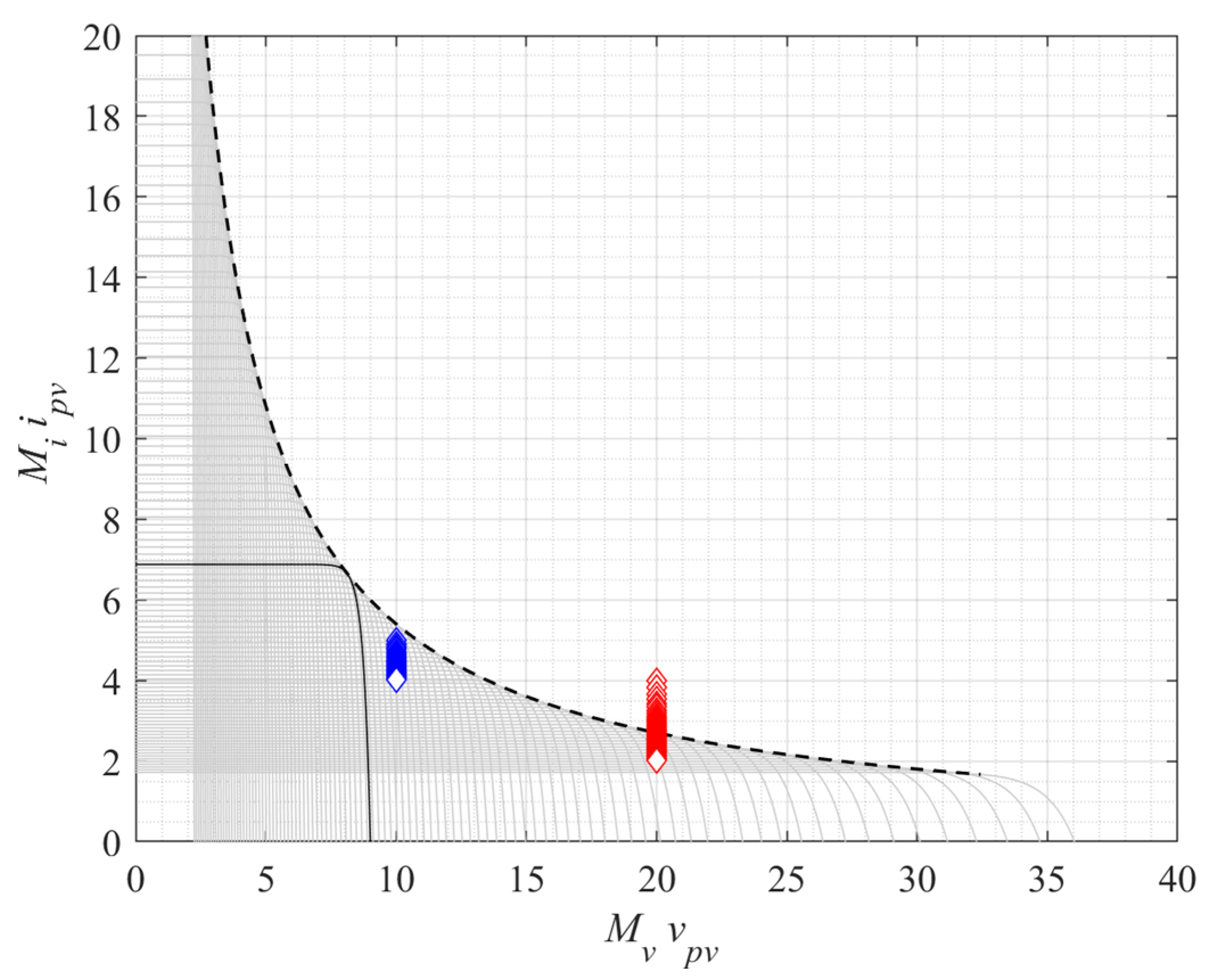



| Symbol | ||
|---|---|---|
| Red Cross | 60 W | 10 V |
| Red Circle | 60 W | 20 V |
| Blue Cross | 40 W | 10 V |
| Blue Circle | 40 W | 20 V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corti, F.; Laudani, A.; Lozito, G.M.; Palermo, M.; Quercio, M.; Pattini, F.; Rampino, S. Dynamic Analysis of a Supercapacitor DC-Link in Photovoltaic Conversion Applications. Energies 2023, 16, 5864. https://doi.org/10.3390/en16165864
Corti F, Laudani A, Lozito GM, Palermo M, Quercio M, Pattini F, Rampino S. Dynamic Analysis of a Supercapacitor DC-Link in Photovoltaic Conversion Applications. Energies. 2023; 16(16):5864. https://doi.org/10.3390/en16165864
Chicago/Turabian StyleCorti, Fabio, Antonino Laudani, Gabriele Maria Lozito, Martina Palermo, Michele Quercio, Francesco Pattini, and Stefano Rampino. 2023. "Dynamic Analysis of a Supercapacitor DC-Link in Photovoltaic Conversion Applications" Energies 16, no. 16: 5864. https://doi.org/10.3390/en16165864
APA StyleCorti, F., Laudani, A., Lozito, G. M., Palermo, M., Quercio, M., Pattini, F., & Rampino, S. (2023). Dynamic Analysis of a Supercapacitor DC-Link in Photovoltaic Conversion Applications. Energies, 16(16), 5864. https://doi.org/10.3390/en16165864











