Energy Storage and Release of Class I and Class II Rocks
Abstract
1. Introduction
2. Rock Materials and Test Methodology
2.1. Rock Description and Sample Preparation
2.2. Test Apparatus and Scheme
3. Mechanical Behavior and Fracture Characteristics of the Rocks
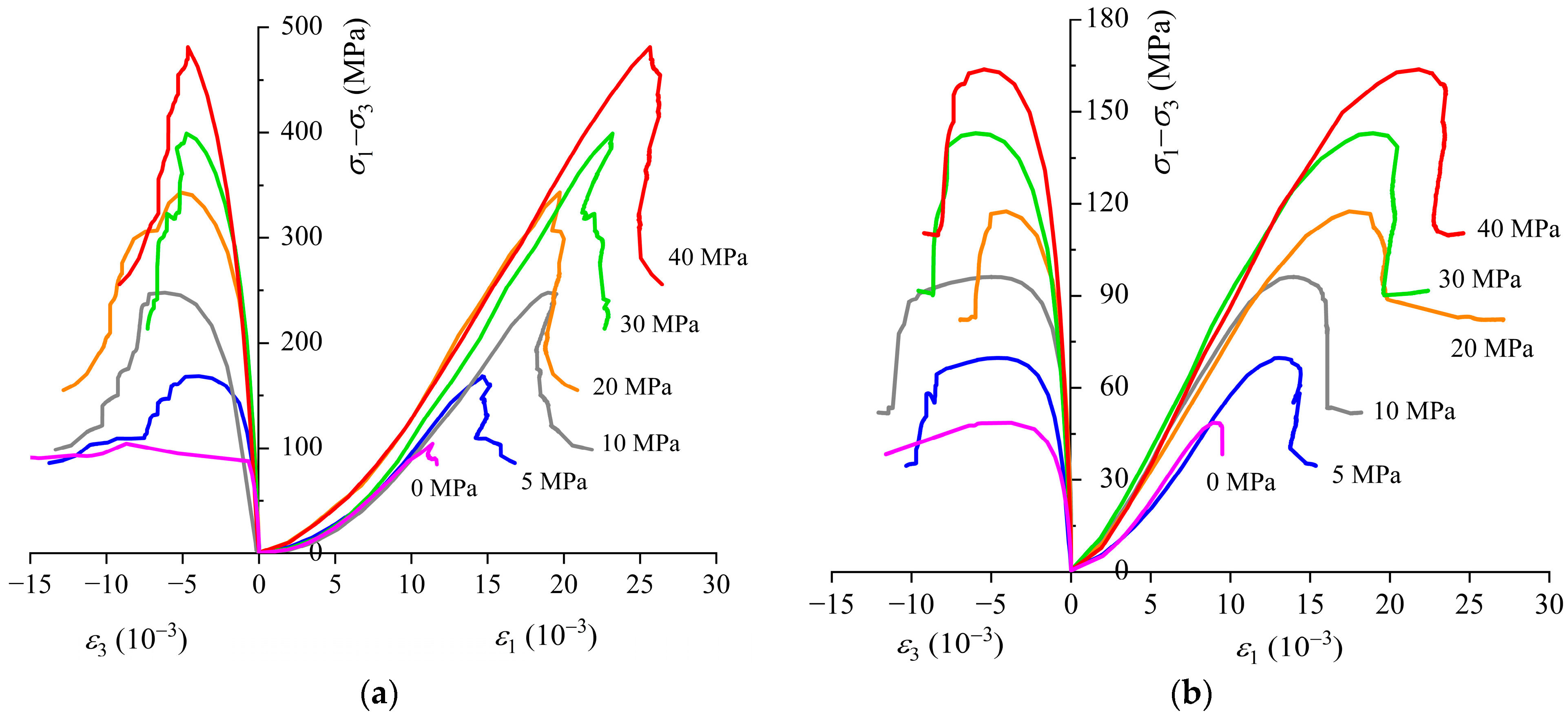
3.1. Granite
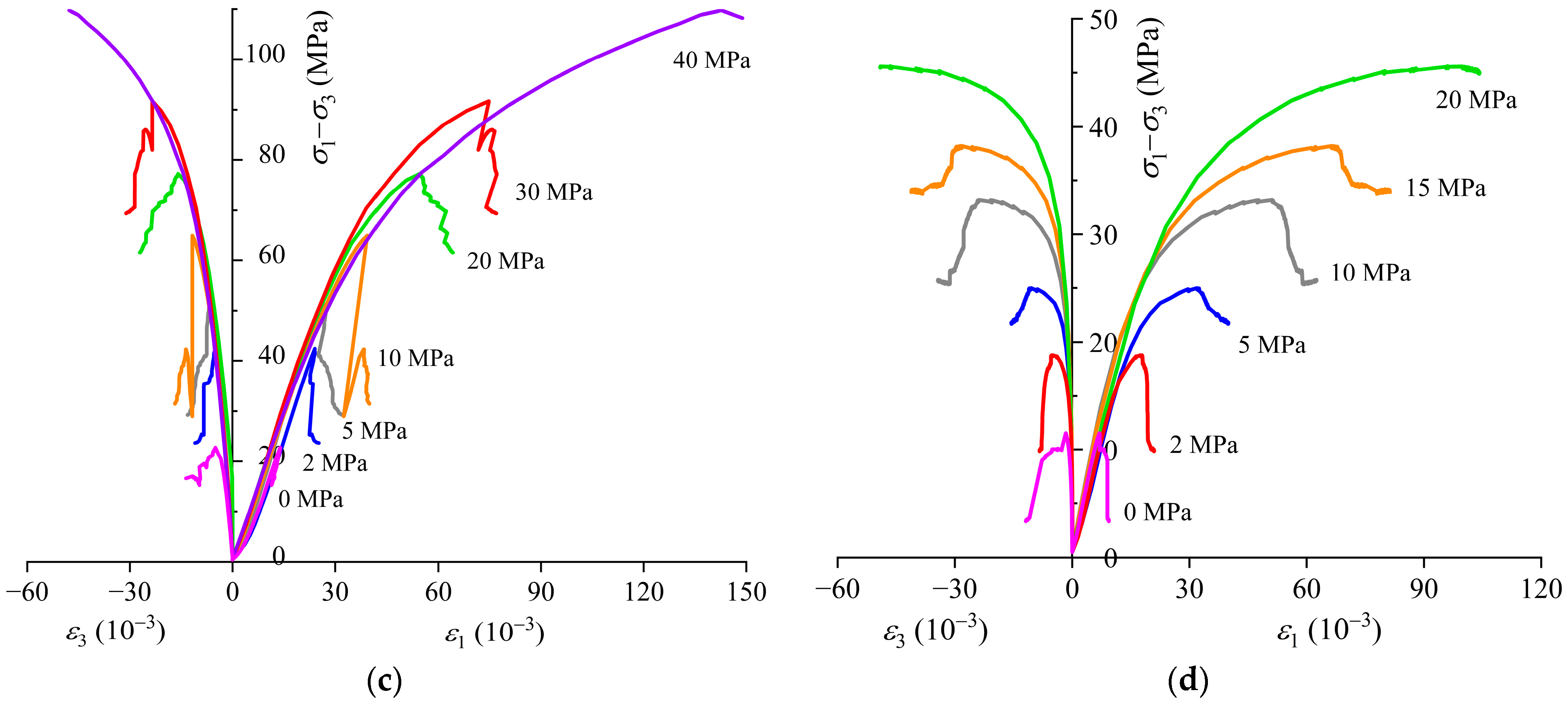
3.2. Red Sandstone
3.3. Coal
3.4. Mudstone
4. Effect of Confinement on Energy Evolution and Energy Parameters
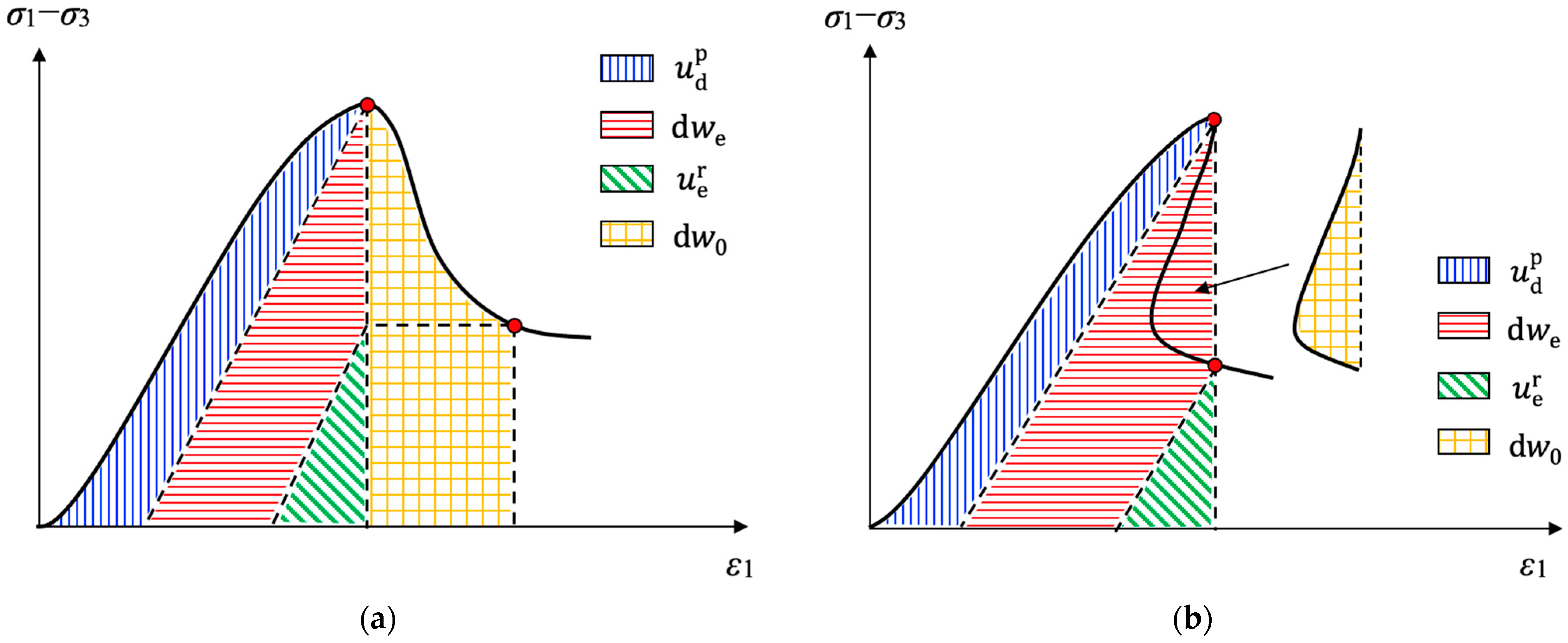
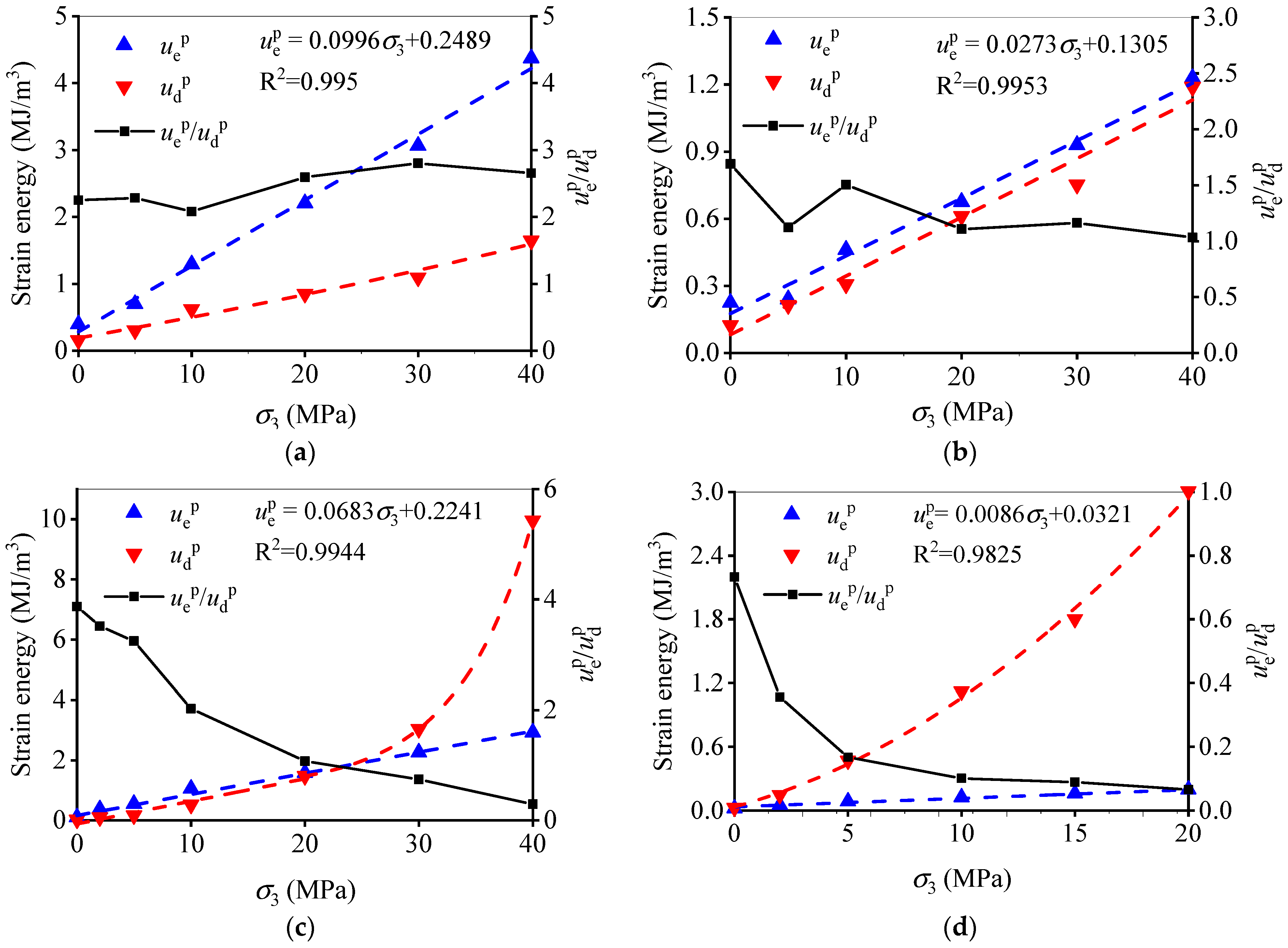
4.1. Estimation of Strain Energy and Energy Portions for Class I and Class II Rocks
4.2. Energy Evolution over Complete Stress–Strain Response of the Rocks
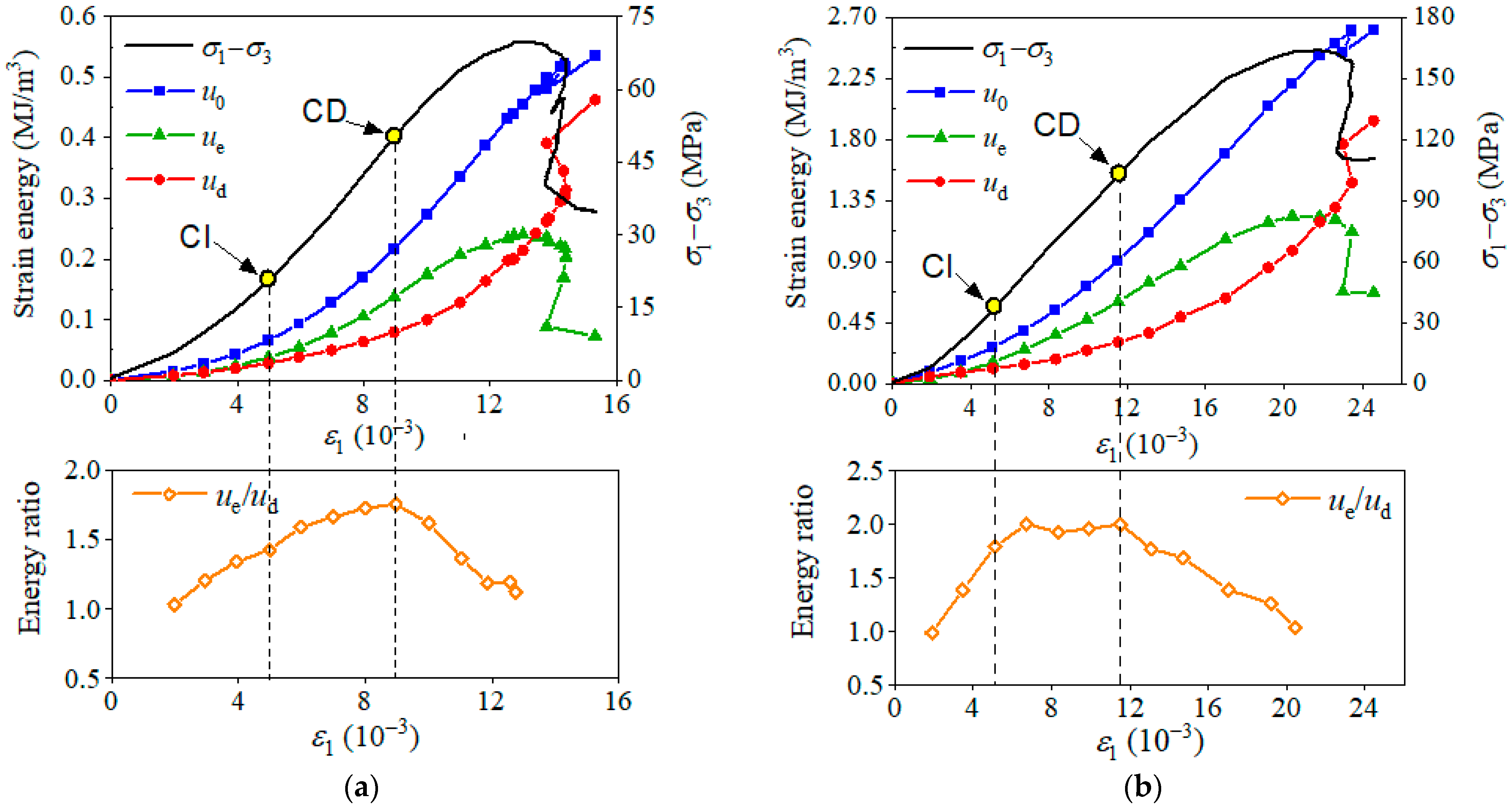
4.2.1. Granite
4.2.2. Red Sandstone
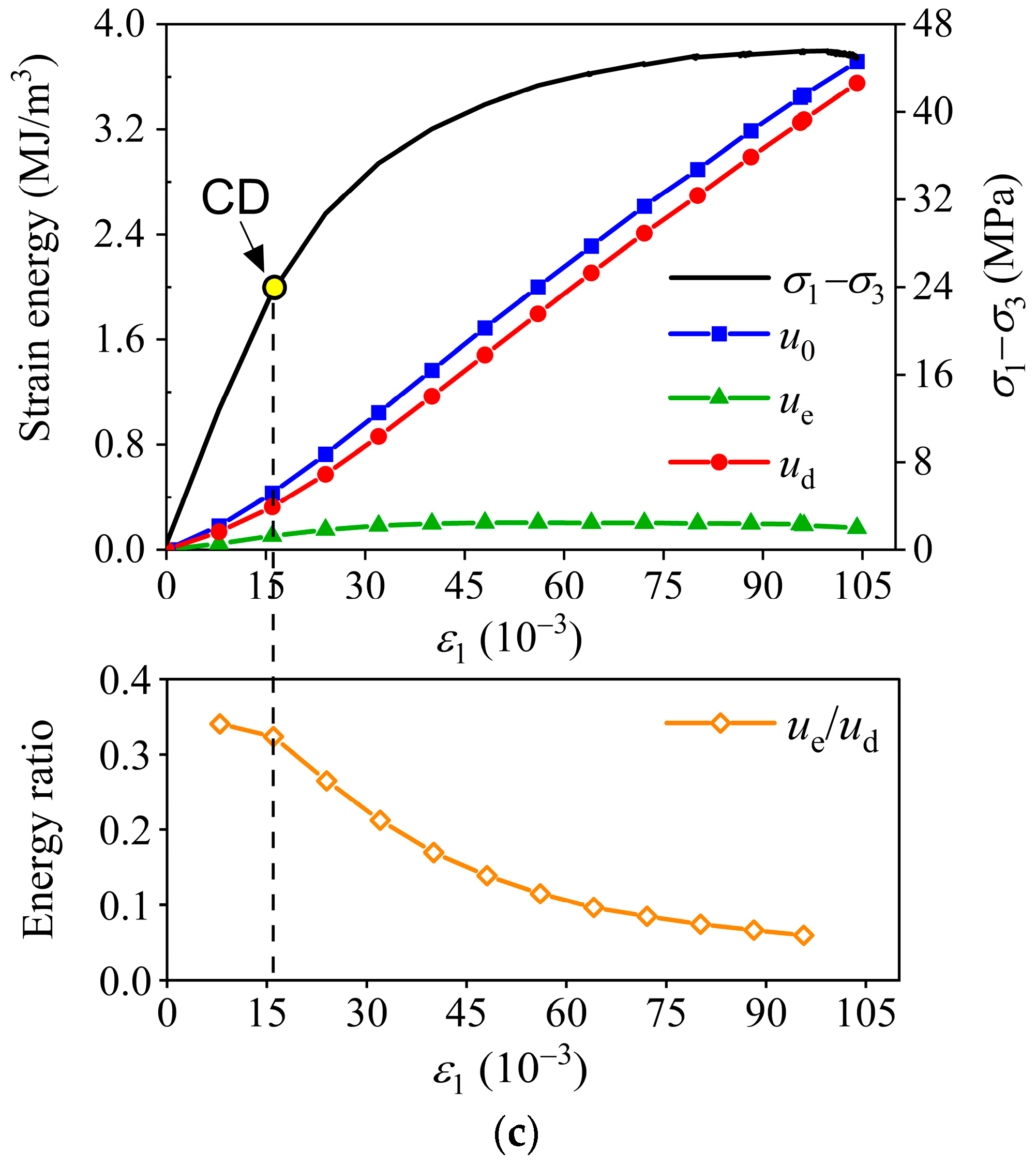
4.2.3. Coal
4.2.4. Mudstone Samples
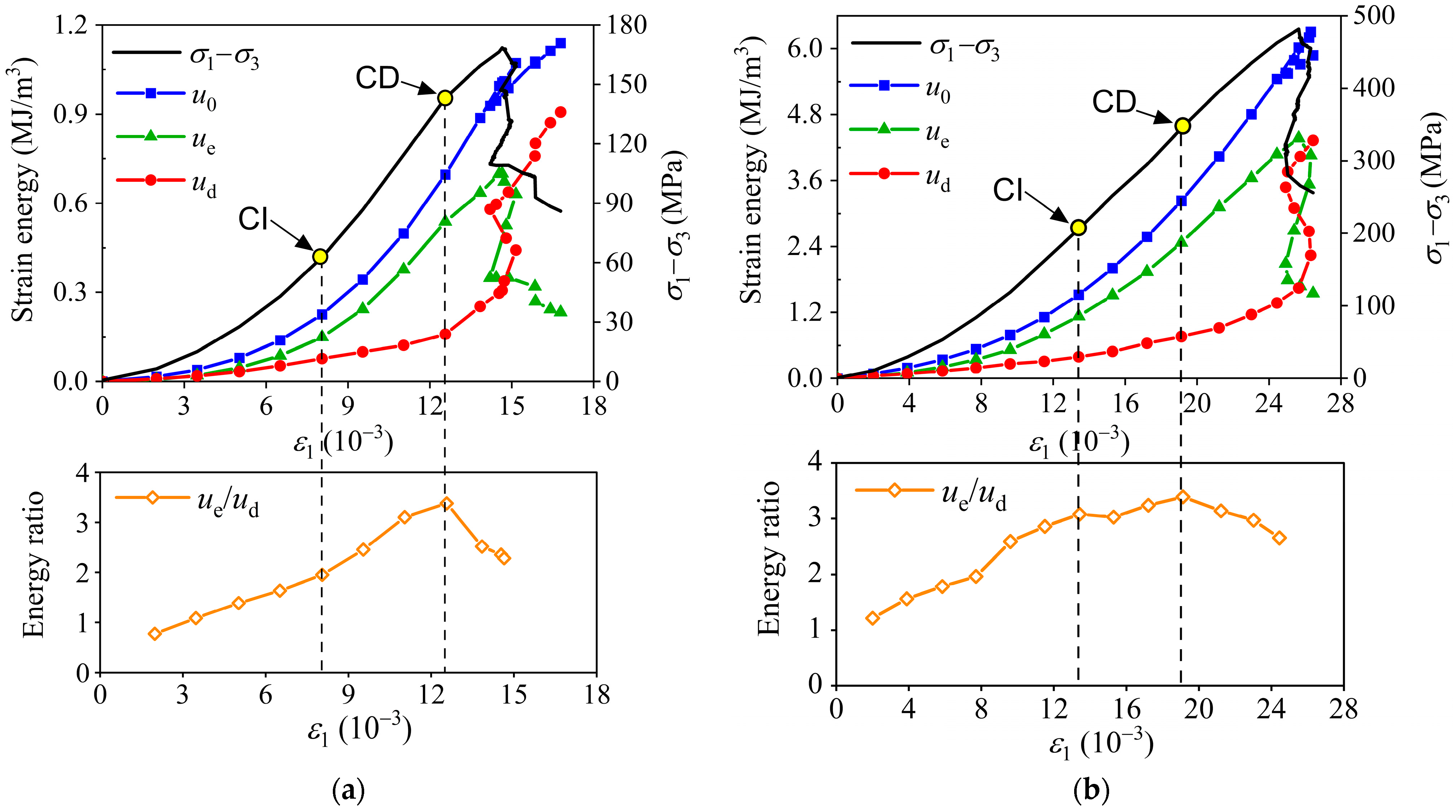
4.2.5. Three Types of Energy Evolution
4.3. Energy Storage and Dissipation of the Rocks
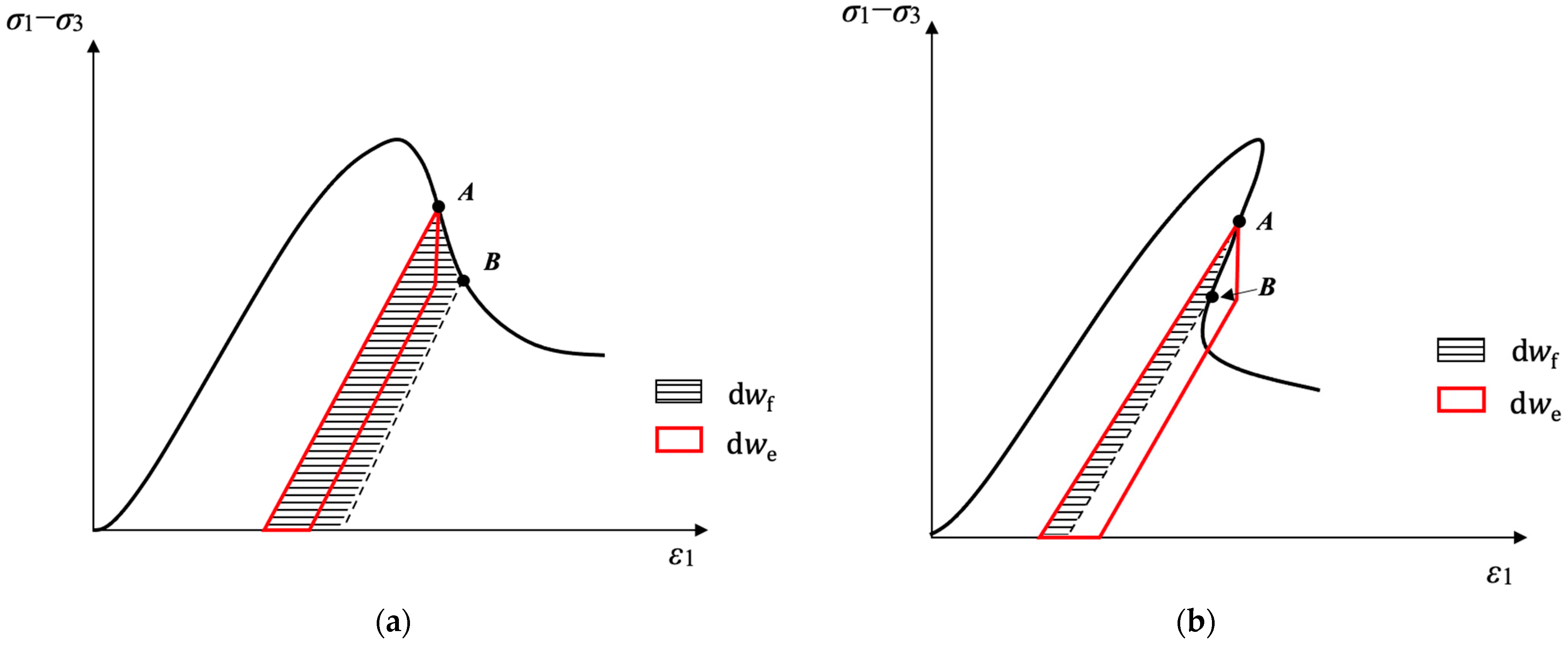
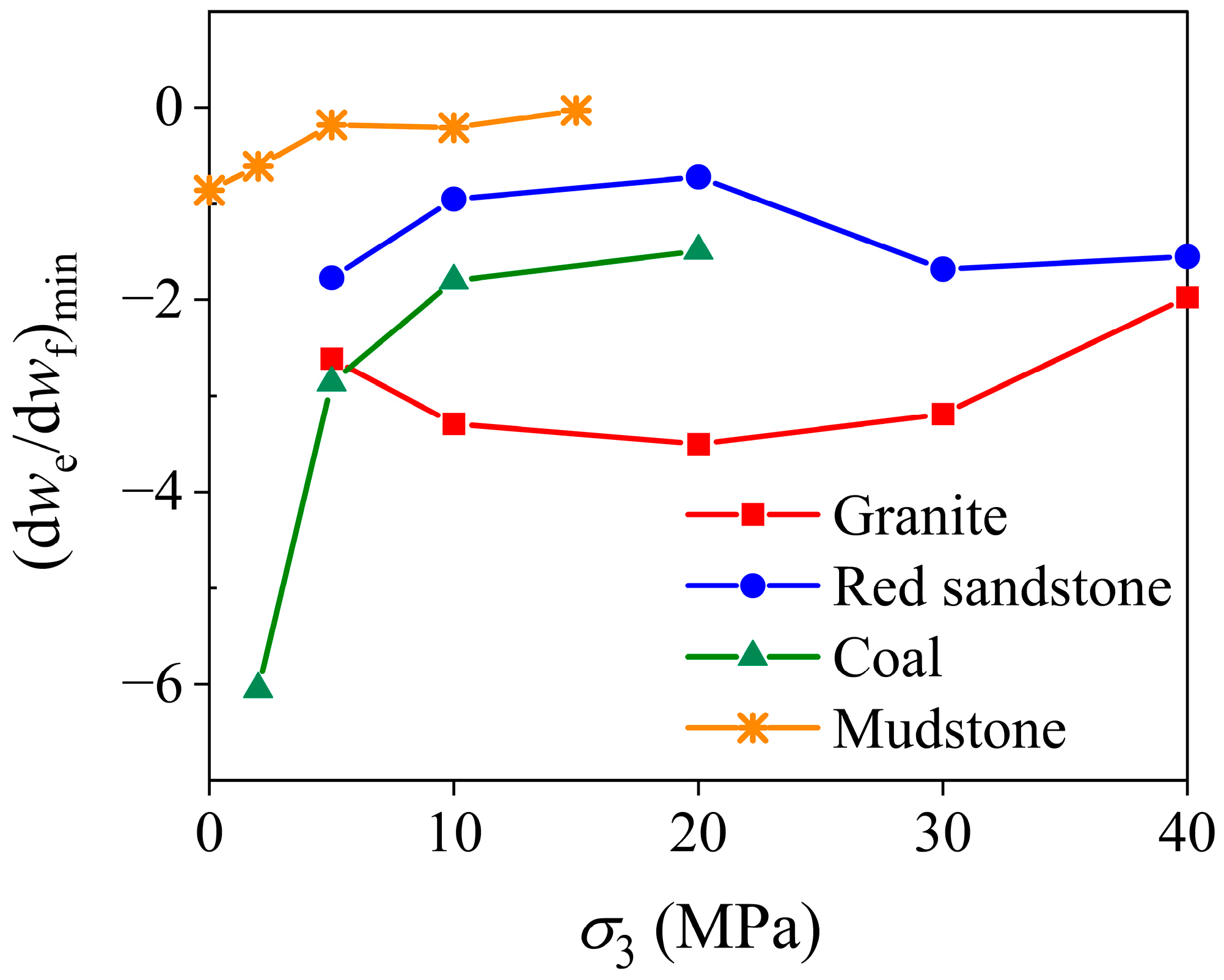
4.4. Post-Peak Energy Release and the Degree of Failure Intensity
5. Discussion
6. Conclusions and Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kaiser, P.K.; Cai, M. Design of rock support system under rockburst condition. J. Rock Mech. Geotech. Eng. 2012, 4, 215–227. [Google Scholar] [CrossRef]
- Mazaira, A.; Konicek, P. Intense rockburst impacts in deep underground construction and their prevention. Can. Geotech. J. 2015, 52, 1426–1439. [Google Scholar] [CrossRef]
- Akdag, S.; Karakus, M.; Nguyen, G.D.; Taheri, A.; Bruning, T. Evaluation of the propensity of strain burst in brittle granite based on post-peak energy analysis. Undergr. Space 2021, 6, 1–11. [Google Scholar] [CrossRef]
- Li, C.C.; Zhao, T.; Zhang, Y.; Wan, W. A study on the energy sources and the role of surrounding rock mass in strain burst. Int. J. Rock Mech. Min. Sci. 2022, 154, 105114. [Google Scholar] [CrossRef]
- Cook, N.G.W.; Hoek, E.; Pretorius, J.P.G.; Ortlepp, W.D.; Salamon, M.D.G. Rock mechanics applied to the study of rockbursts. J. S. Afr. Inst. Min. Metal. 1966, 66, 435–528. [Google Scholar]
- Mitri, H.S.; Tang, B.; Simon, R. FE modelling of mining-induced energy release and storage rates. J. S. Afr. Inst. Min. Metal. 1999, 99, 103–110. [Google Scholar]
- Wang, J.A.; Park, H.D. Comprehensive prediction of rockburst based on analysis of strain energy in rocks. Tunn. Undergr. Space Technol. 2001, 16, 49–57. [Google Scholar] [CrossRef]
- Xie, H.; Li, L.; Peng, R.; Ju, Y. Energy analysis and criteria for structural failure of rocks. J. Rock Mech. Geotech. Eng. 2009, 1, 11–20. [Google Scholar] [CrossRef]
- Huang, D.; Li, Y. Conversion of strain energy in triaxial unloading tests on marble. Int. J. Rock Mech. Min. Sci. 2014, 66, 160–168. [Google Scholar] [CrossRef]
- Meng, Q.; Zhang, M.; Han, L.; Pu, H.; Nie, T. Effects of acoustic emission and energy evolution of rock specimens under the uniaxial cyclic loading and unloading compression. Rock Mech. Rock Eng. 2016, 49, 3873–3886. [Google Scholar] [CrossRef]
- Liang, C.; Wu, S.; Li, X.; Xin, P. Effects of strain rate on fracture characteristics and mesoscopic failure mechanisms of granite. Int. J. Rock Mech. Min. Sci. 2015, 76, 146–154. [Google Scholar] [CrossRef]
- Zhao, K.; Yu, X.; Zhou, Y.; Wang, Q.; Wang, J.; Hao, J. Energy evolution of brittle granite under different loading rates. Int. J. Rock Mech. Min. Sci. 2020, 132, 104392. [Google Scholar] [CrossRef]
- Yan, J.; Gong, F.; Luo, S. Effects of length-to-diameter ratio on energy storage characteristics of rock materials under uniaxial compression. Bull. Eng. Geol. Environ. 2022, 81, 508. [Google Scholar] [CrossRef]
- Li, D.; Sun, Z.; Xie, T.; Li, X.; Ranjith, P.G. Energy evolution characteristics of hard rock during triaxial failure with different loading and unloading paths. Eng. Geol. 2017, 228, 270–281. [Google Scholar] [CrossRef]
- Zhang, L.; Cong, Y.; Meng, F.; Wang, Z.; Zhang, P.; Gao, S. Energy evolution analysis and failure criteria for rock under different stress paths. Acta Geotech. 2021, 16, 569–580. [Google Scholar] [CrossRef]
- Ning, J.; Wang, J.; Jiang, J.; Hu, S.; Jiang, L.; Liu, X. Estimation of crack initiation and propagation thresholds of confined brittle coal specimens based on energy dissipation theory. Rock Mech. Rock Eng. 2018, 51, 119–134. [Google Scholar] [CrossRef]
- Wen, T.; Tang, H.; Huang, L.; Wang, Y.; Ma, J. Energy evolution: A new perspective on the failure mechanism of purplish-red mudstones from the Three Gorges Reservoir area, China. Eng. Geol. 2020, 264, 105350. [Google Scholar] [CrossRef]
- Yang, B.; Xue, L.; Duan, Y. Investigation into energy conversion and distribution during brittle failure of hard rock. Bull. Eng. Geol. Environ. 2022, 81, 114. [Google Scholar] [CrossRef]
- Lu, J.; Yin, G.; Zhang, D.; Gao, H.; Li, C.; Li, M. True triaxial strength failure characteristics of cubic coal and sandstone under different loading paths. Int. J. Rock Mech. Min. Sci. 2020, 135, 104439. [Google Scholar] [CrossRef]
- Arzua, J.; Alejano, L.R. Dilation in granite during servo-controlled triaxial strength tests. Int. J. Rock Mech. Min. Sci. 2013, 61, 43–56. [Google Scholar] [CrossRef]
- Hou, P.Y.; Cai, M. Post-peak stress-strain curves of brittle hard rocks under different loading environment system stiffness. Rock Mech. Rock Eng. 2022, 55, 3837–3857. [Google Scholar] [CrossRef]
- Wawersik, W.R.; Fairhurst, C. A study of brittle rock fracture in laboratory compression experiments. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1970, 7, 561–575. [Google Scholar] [CrossRef]
- Bruning, T.; Karakus, M.; Nguyen, G.D.; Goodchild, D. Experimental study on the damage evolution of brittle rock under triaxial confinement with full circumferential strain control. Rock Mech. Rock Eng. 2018, 51, 3321–3341. [Google Scholar] [CrossRef]
- Zhang, H.; Li, C. Effects of confining stress on the post-failure behaviour and fracture angle of Fauske marble and Iddefjord granite. Rock Mech. Rock Eng. 2019, 52, 1377–1385. [Google Scholar] [CrossRef]
- Wang, H.; Dyskin, A.; Pasternak, E.; Dight, P. Mixed Class I/Class II post-peak curves of mortar models of rock samples. Theor. Appl. Fract. Mech. 2022, 117, 1031178. [Google Scholar] [CrossRef]
- ASTM D7012; Standard Test Methods for Compressive Strength and Elastic Moduli of Intact Rock Core Specimens under Varying States of Stress and Temperatures. ASTM International: West Conshohocken, PA, USA, 2014.
- Martin, C.D.; Chandler, N.A. The progressive fracture of Lac du Bonnet granite. Int. J. Rock. Mech. Min. Sci. Geomech. Abstr. 1994, 31, 643–659. [Google Scholar] [CrossRef]
- Martin, C.D. Strength of Massive Lac du Bonnet Granite around Underground Openings. Ph.D. Thesis, University of Manitoba, Winnipeg, MB, Canada, 1993. [Google Scholar]
- Walton, G.; Hedayat, A.; Kim, E.; Labrie, D. Post-yield strength and dilatancy evolution across the brittle-ductile transition in Indiana limestone. Rock Mech. Rock Eng. 2017, 50, 1691–1710. [Google Scholar] [CrossRef]
- Tarasov, B.; Yves, P. Universal criteria for rock brittleness estimation under triaxial compression. Int. J. Rock Mech. Min. Sci. 2013, 59, 57–69. [Google Scholar] [CrossRef]
- Mogi, K. Pressure dependence of rock strength and transition from brittle fracture to ductile flow. Bull. Earthq. Res. Inst. 1966, 44, 215–232. [Google Scholar]
- Desbois, G.; Hohne, N.; Urai, J.L.; Besuelle, P.; Viggiani, G. Deformation in cemented mudrock (Callovo-Oxfordian Clay) by microcracking, granular flow and phyllosilicate plasticity: Insights from triaxial deformation, broad ion beam polishing and scanning electron microscopy. Solid Earth 2017, 8, 291–305. [Google Scholar] [CrossRef]











| Type of the Rock | Confining Pressure (MPa) | |
|---|---|---|
| Conventional Tests | Cyclic Loading–Unloading Tests | |
| Granite | 0, 5, 10, 20, 30, 40 | 0, 5, 10, 20, 30, 40 |
| Red sandstone | 0, 5, 10, 20, 30, 40 | 0, 5, 10, 20, 30, 40 |
| Coal | 0, 2, 5, 10, 20, 30, 40 | 0, 2, 5, 10, 20, 30, 40 |
| Mudstone | 0, 2, 5, 10, 15, 20 | 0, 2, 5, 10, 15, 20 |
| Type of Rock | Confining Pressure, σ3 (MPa) | (MPa) | Young’s Modulus, E (GPa) | Poisson’s Ratio, μ | CD/Peak Stress | (10−3) | (σ1p − σ3)/σ3 |
|---|---|---|---|---|---|---|---|
| Granite | 0 | 104.38 | 13.74 | 0.09 | 0.84 | 0.36 | - |
| 5 | 173.66 | 18.50 | 0.13 | 0.85 | 0.75 | 33.73 | |
| 10 | 257.87 | 18.91 | 0.19 | 0.88 | 0.90 | 24.79 | |
| 20 | 362.97 | 24.23 | 0.15 | 0.84 | 0.84 | 17.15 | |
| 30 | 429.12 | 24.16 | 0.12 | 0.91 | 0.74 | 13.30 | |
| 40 | 521.36 | 24.27 | 0.16 | 0.84 | 1.25 | 12.03 | |
| Red sandstone | 0 | 48.61 | 7.74 | 0.22 | 0.77 | 0.58 | - |
| 5 | 74.80 | 8.02 | 0.12 | 0.74 | 1.35 | 13.96 | |
| 10 | 106.14 | 8.61 | 0.13 | 0.68 | 1.30 | 9.62 | |
| 20 | 137.55 | 8.78 | 0.09 | 0.77 | 2.21 | 5.88 | |
| 30 | 172.72 | 10.47 | 0.13 | 0.72 | 2.53 | 4.75 | |
| 40 | 203.80 | 9.83 | 0.11 | 0.78 | 3.35 | 4.10 | |
| Coal | 0 | 22.75 | 2.06 | 0.27 | 0.90 | 0.35 | - |
| 2 | 44.44 | 2.15 | 0.22 | 0.82 | 0.42 | 21.22 | |
| 5 | 56.25 | 2.24 | 0.24 | 0.80 | 1.96 | 10.25 | |
| 10 | 74.98 | 1.97 | 0.27 | 0.67 | 4.77 | 6.50 | |
| 20 | 97.25 | 1.99 | 0.28 | 0.65 | 12.72 | 3.86 | |
| 30 | 121.68 | 2.02 | 0.29 | 0.57 | 25.12 | 3.06 | |
| 40 | 149.75 | 1.87 | 0.26 | 0.50 | 83.23 | 2.74 | |
| Mudstone | 0 | 11.52 | 1.79 | 0.08 | 0.63 | 1.39 | - |
| 2 | 20.62 | 1.62 | 0.06 | 0.62 | 7.78 | 9.37 | |
| 5 | 29.78 | 1.55 | 0.06 | 0.63 | 15.42 | 5.00 | |
| 10 | 43.06 | 1.78 | 0.08 | 0.55 | 33.39 | 3.32 | |
| 15 | 52.95 | 1.82 | - | 0.51 | 47.34 | 2.55 | |
| 20 | 65.26 | 1.54 | - | 0.48 | 70.39 | 2.54 |
| Type of Rock | σ3 (MPa) | (MJ/m3) | (MJ/m3) | (MJ/m3) | (MJ/m3) | Type of Energy Evolution |
|---|---|---|---|---|---|---|
| Granite | 5 | 0.699 | 0.306 | 0.350 | 0.332 | I |
| 10 | 1.292 | 0.621 | 0.909 | 0.879 | I | |
| 20 | 2.206 | 0.851 | 1.556 | 1.294 | I | |
| 30 | 3.066 | 1.094 | 1.915 | 1.531 | I | |
| 40 | 4.373 | 1.647 | 2.798 | 2.625 | I | |
| Red sandstone | 5 | 0.240 | 0.201 | 0.157 | 0.219 | II |
| 10 | 0.458 | 0.311 | 0.290 | 0.397 | II | |
| 20 | 0.676 | 0.611 | 0.262 | 0.503 | II | |
| 30 | 0.931 | 0.800 | 0.474 | 0.540 | II | |
| 40 | 1.230 | 1.190 | 0.556 | 0.627 | II | |
| Coal | 2 | 0.378 | 0.107 | 0.229 | 0.203 | I |
| 5 | 0.553 | 0.170 | 0.206 | 0.186 | I | |
| 10 | 1.058 | 0.522 | 0.682 | 0.539 | I | |
| 20 | 1.586 | 1.474 | 0.621 | 1.020 | II | |
| 30 | 2.261 | 3.041 | - | - | II | |
| 40 | 2.930 | 9.959 | - | - | III | |
| Mudstone | 2 | 0.052 | 0.146 | 0.035 | 0.095 | III |
| 5 | 0.088 | 0.524 | 0.021 | 0.185 | III | |
| 10 | 0.123 | 1.217 | 0.038 | 0.263 | III | |
| 15 | 0.160 | 1.802 | 0.022 | 0.515 | III | |
| 20 | 0.198 | 3.007 | - | - | III |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, Y.; Gao, F.; Zhang, Z.; Zheng, W. Energy Storage and Release of Class I and Class II Rocks. Energies 2023, 16, 5516. https://doi.org/10.3390/en16145516
Xing Y, Gao F, Zhang Z, Zheng W. Energy Storage and Release of Class I and Class II Rocks. Energies. 2023; 16(14):5516. https://doi.org/10.3390/en16145516
Chicago/Turabian StyleXing, Yan, Feng Gao, Zhizhen Zhang, and Wenqi Zheng. 2023. "Energy Storage and Release of Class I and Class II Rocks" Energies 16, no. 14: 5516. https://doi.org/10.3390/en16145516
APA StyleXing, Y., Gao, F., Zhang, Z., & Zheng, W. (2023). Energy Storage and Release of Class I and Class II Rocks. Energies, 16(14), 5516. https://doi.org/10.3390/en16145516







