Abstract
In this paper, we describe a comparative analysis of a bus route scheduling problem as part of timetable trips. We consider the current uptake of electric buses as a viable public transportation option that will eventually phase out the diesel-engine-based buses. We note that, with the increasing number of electric buses, the complexity related to the scheduling also increases, especially stemming from the charging requirement and the dedicated infrastructure behind it. The aim of our comparative study is to highlight the brevity with which a multi-agent-system-based scheduling method can be helpful as compared to the classical mixed-integer linear-programming-based approach. The multi-agent approach we design is centralized with asymmetric communication between the master agent, the bus agent, and the depot agent, which makes it possible to solve the multi-depot scheduling problem in almost real time as opposed to the classical optimizer, which sees a multi-depot problem as a combinatorial heuristic NP-hard problem, which, for large system cases, can be computationally inefficient to solve. We test the efficacy of the multi-agent algorithm and also compare the same with the MILP objective designed in harmony with the multi-agent system. We test the comparisons first on a small network and then extend the scheduling application to real data extracted from the public transport of the Maltese Islands.
1. Introduction
The problem of scheduling buses dates back to the 1970s [1]. A proper bus schedule enables both the bus operator and the passengers to plan their trip routines in advance. It is, therefore, important that the buses that deliver public transportation are punctual, and, at the same time, offer a timely and comfortable service. In today’s era, electric buses (EBs) are a growing part of the public transportation fleet, and the proliferation of an EB public transportation network is in line with the future goals of a sustainable society as they are emission-free, and, with an electricity network of high renewable energy share, they also assist in self-consumption from renewable energy sources [2]. Malta (an island country in the European Union) has a singly owned public transport network, known as the Malta Public Transport, that has a total fleet size of 420 buses. While there has been some progress in converting the fuel-powered fleet to battery power, the low number of depots and a highly congested power network are impediments to the fleet becoming fully electric.
The charging of electric buses requires a complex infrastructure, and, unlike smaller electric vehicles that can be charged at a home garage, the transport operators that deploy EBs should also in principle provide easy access to charging availability for the buses that require charging. An issue with EB charging is the total time consumed in the charging process. The two commercially available charging methods offer different time scales in charging. The plug-in-based method, which is more suitable for high-energy-density devices, usually takes up to two hours to charge an EB, whereas pantograph-based charging [3], with a high-power-density charger, offers fast charging for the buses and can fully charge an EB in less than an hour. The size of the depot, therefore, plays a crucial role in determining the hosting capacity of the number of EBs that can charge simultaneously. The depots in island countries such as Malta are generally located as part of the parking and can have the possibility of providing both ‘opportunity’ charging and overnight charging. Opportunity charging can provide partial assistance for the buses as they are fast chargers. It can typically provide the equivalent of 1.91 kWh/km as opposed to the overnight chargers, which provide 1.19 kWh/km [4]. Another issue with the charging of the EBs is the cost, and, therefore, the process of procuring and tendering is also challenging. [5] describes in detail the issues with the procurement process for the charging station for the EU market. The paper analyzed two methods, namely the total cost of ownership and the lifecycle cost analysis (both methods include a variety of costs, such as the vehicle cost, financing cost, tax, labour fee, maintenance, etc.), and concluded that, by embedding the two methods, better planning can be achieved for the procurement of charging stations (or depots) for electric buses.
In a real-time or operational scenario, it is very important for the buses to be aware of the charging levels and, therefore, to be able to communicate with the transport system operator (TSO) about the next available free charging spot/depot in order to reach the depot for charging the bus before the bus is fully discharged. It is also important for the TSO to keep a record of the buses that are in operation, i.e., carrying passengers, and the ones that are deadheading (going towards the depot or vice versa). The presence of multiple depots makes the problem more complex, and sophisticated solutions are necessary to determine the best-case scenario for the buses so that, with the optimal number of buses, the timetabled trips are met, and, in the case of electric buses, the charging demands of the buses are met in addition to meeting the timetabled trip. It is also important that the solution is cost-effective so that, when planning for the future of an ’EB more’ transportation problem, the end customer does not have to face significantly increased pricing. The general approach for this is to take the optimization route to solve the BRSP so that the costs are minimized subject to constraints, such as completion of the trip and preserving the charging times of the bus and, last but not least, guaranteeing all the timetabled trips.
The specific contributions of this paper can be enumerated below:
- The objective of minimizing the usage costs and fixed recharging costs is completed using mixed-integer linear programming;
- A multi-agent solution that is more accommodating to more objectives is proposed in this paper. The solution relies on communication within predefined agents;
- A comparative analysis is conducted between the classical optimization method and the multi-agent-based solution. A toy problem was solved for comparing the two methods. The latter method was then extended to provide the optimal number of buses required for the timetabled trips.
Rest of the paper is organized as follows. A detailed literature review pertaining to the problem is deliberated in Section 2. Section 3 sheds light on the optimization framework that emphasises the above-mentioned cost minimization goals. The multi-agent solution to the BRSP is defined in Section 4, followed by a comparative analysis of the two methods in Section 5. Section 6 concludes the paper.
2. Literature Review
The vehicle scheduling problem (VSP) has been in the limelight within the scientific community for a long time. The VSP essentially means that the schedules are assigned in order to operate public transport in an efficient and cost-effective manner. VSP, especially BRSP, as demonstrated from the depot-based formulation, can be decomposed into two parts, i.e., the single-depot problem and the multi-depot problem. The single-depot problem has the capability to assign buses in a more centralized fashion [6,7]. Especially in [7], a combined forward and reverse auction algorithm was used to schedule the trips. This algorithm ensures that the bus with the highest price bid is chosen first while moving in the forward auctioning, while the unassigned trips bid for another trip. The reverse auctioning, in the same way, is for the bus to obtain trips from the destination back to the source. The caveat with the auctioning method, however, is the issue with convergence whenever there is unintended switching between forward and reverse auctions. As a remedy to this problem, a first-in-first-out rule was proposed in [8]. Here, the timetabled trips are read in terms of available and unavailable intervals, including the forward trips, returning trips, and deadheading trips. However, in the paper, a soft time window was not considered; i.e., whenever a bus arrives at the destination, it immediately begins the successive trip. This limitation was overcome in [9], where the authors proposed an integer linear programming (ILP) approach to incorporate the soft time window in terms of labour regulation constraints. The paper minimizes the driver’s or the vehicle’s idle times, which can be analogous to minimizing the deadheading times or distances.
Single-depot BRSP can cater to multiple types of buses [10]. The classification can vary from the type of fuel and the size of the buses. Differences in each type will alter the BRSP as they will introduce additional constraints to the problem. Albeit environmentally sustainable, the formulation of BRSP with electric buses must include the trip range and also should consider how to plan the recharging trips. Thus, the deadheading trips will also consist of recharging trips. Planning the charge schedule of electric buses will consist of individual vehicle battery characteristics, more specifically, the state of energy. Ref. [11] proposed an optimization method for preserving the state of energy of the electric vehicle batteries in line with the electricity market price signals. The paper, in addition, also considers the time of connection and disconnection, along with the energy required for the next trip, which is an important attribute for the bus operator to be apprised of; however, this paper did not consider the timetable trips of the buses. The lower level of the scheduling problem in [10] had considered similar objectives assuming an electricity market scenario, where the batteries of the electric buses can charge in the case of low energy prices. However, the deficiency in the buses was catered to by the conventional diesel buses, which were also part of the scheduling problem. The integrated operational aspect of the bus route scheduling problem with the network timetable was presented in [12]. To achieve the objective, a Lagrangian relaxation method was proposed to find the constrained shortest path [13], which is a weighted edge problem in order to ascertain the minimum cost-feasible path for a vehicle under operation. A planning methodology to incorporate charging, battery degradation, and a possible shift in the timetable of the buses was discussed in [14]. The paper used a column generation method to minimize the fleet cost. A review on the use of heuristics for scheduling transport (for construction) was presented in [15]. The paper presented a comparison of several algorithms reaching the goal of a sustainable transport measure.
Conventionally, classical optimization methods are applied to the bus route scheduling problem. Various methods of scheduling, varying from minimizing the passenger demand–supply balance to charging and discharging of electric buses within a timetabled environment, are considered in [16,17]. More specifically in line with this paper, the literature [10] proposed bi-level programming to schedule a mixed (electric and diesel) fleet. The bi-level programming being non-Pareto (NP)-hard, i.e., when the Pareto is not equal to the non-Pareto, means that it is not possible to find an optimal polynomial solution [18]. The bi-level problem thereby in [10] was converted into a heuristic problem. However, heuristic solutions do not always guarantee optimality. One approach for an optimal guarantee is to convert the combinatorial framework into a mixed-integer problem. Although this does not necessarily remove the NP-hardness, based on the relaxation applied, the problem can be solved in terms of a mixed-integer linear programming problem, which is a result of applying LP relaxation to the mixed-integer programming (MILP). A case of scheduling electric buses with the help of MILP was proposed in [19,20]. Notably, in [20], the MILPbased approach allows arbitrage, especially during off-peak hours, to charge the electric bus batteries, which satisfies the objective of minimizing the number of buses and the cost of the bus operation, thereby making the problem a mixed-integer one. A similar sequential planning process was described in [21], where a line planning and a vehicle scheduling problem were solved concurrently by converting the sequential problem into a MILP. The same approach of mixed-integer linear programming was also used in [22]. In this paper, apart from the battery capacity optimization, a cost-minimum trade-off was evaluated on the basis of the battery size and the charging profiles of the charging stations. The total number of required charging stations was finally computed for a case study for Berlin.
Evolutionary techniques for optimizing the fleet have also gained importance in the literature. [23] discussed the scheduling of a multiple-sized bus fleet that is fully electric. The genetic algorithm (GA) method was used to optimize the yearly operation costs while gaining insight into an important constraint, that the depot capacity should be respected. The argument provided for using the evolutionary approach was the problem methodology, that only a certain amount of buses can be loaded in a timetable, and that forms a binpacking problem, thereby efficiently solved through GA. On similar lines, a large public transport scheduling procedure was performed in [24]. An improved particle swarm optimization method was used in the paper, comparing the scheduling metrics with the GA method. This platform also provided perspective on costs related to passenger waiting time, which can be an imperative factor in deciding the overall transport costs. The GA method was also used for real-time charging in [25], where the dynamic electricity prices were used as one of the inputs to schedule the charging of the buses. A summary of the various advancements in the BRSP is presented in Table 1.

Table 1.
Summary of literature review.
3. Public Transport Optimization Framework
The public transport optimization framework is designed by converting each trip into a node. These trip nodes () are connected to each other considering the possibility of trips taken by a bus. For this possibility, the average speed of the bus is assumed. Based on this and available time, once a bus has completed a trip, then all the possible trips that can be taken are marked. For example, if a trip can be taken after a trip, then they are connected. In addition, a depot node is considered in triplet to represent starting (), recharging (), and end () points. Here, a bus can start its trip from , recharge at and end at . A toy example of five trip nodes () with their trip timings (–) and one depot is shown in Figure 1. From this example, a separate bus can be allocated for each of the five trips as all the trip nodes have to be completed. Therefore, the maximum number of buses required is five as a separate bus can be allocated for each trip. However, it is not an economical solution and requires an optimization framework for this purpose. From all the trip nodes, a bus can go to for recharging and take another trip. Here, it is logical that, if a bus has taken a trip before going to , then it cannot go back to the same trip and have to take a new trip. Also, if there are no more trips available to take, then a bus will go to . Now, let us understand the connections between the trip nodes. For example, has to start at 540 min, i.e., at 9 a.m., and it takes 14 min to complete this trip, and then a bus will only be available for taking a trip after 544 min. Therefore, it cannot take after ; i.e., a bus is at B at the end of and has to travel from B to A to take the trip . However, it can take , , and . Based on similar logic, all these connections are shown using arrows that represent the possibility of trips based on the time taken for a trip.
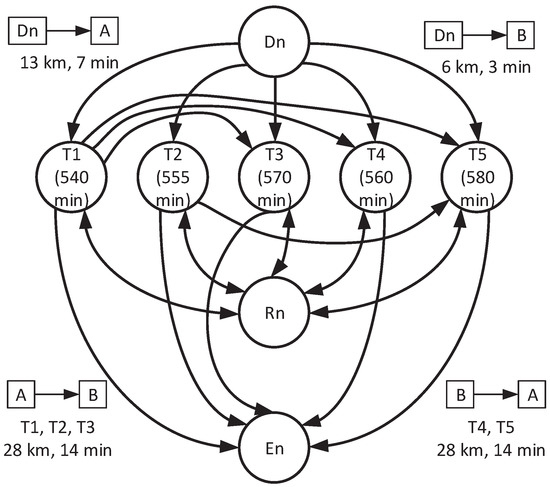
Figure 1.
Toy example: one depot and five trips between points A and B.
For real-world problems, it is not practical to arrive at an economical routing solution only by observing a graph such as Figure 1. Therefore, an optimization framework is proposed and formulated as a mixed-integer linear programming model (MILP) as follows.
Equation (1) represents the objective function (O) that minimizes the overall cost of the bus route scheduling problem, where the first term corresponds to the bus usage cost () and the second term corresponds to the recharging cost (). Here, is the binary variable, which will be one when a bus is used where j is the index of buses that is equal to the maximum number of buses, i.e., equal to the number of trips. is a matrix of binary variables representing the number of connections (l) and number of buses (j). Equation (2) represents a bus arriving at any or that must depart for another trip. Similarly, the sum of all the buses departing from must arrive at , as shown in (3) and (4). Equation (5) represents a trip that must be taken once by any one of the buses. Equation (6) ensures that a bus can take only one connection from to any one . In (7), it is ensured that a bus can only take one trip to an node. Equations (8)–(11) calculate the clock time of every trip. Equation (8) evaluates the time after the completion of trip i connected to , where and represent the timetable for a trip i and time to complete the trip i for the connection l, respectively, which are known quantities. The same is evaluated in (9), where trip i is taken after any . In (10), if a bus is going to , then the time is calculated as the sum of the time at the last completed trip, time to reach (), and time to recharge to a maximum state of charge (SOC), i.e., . In (11), if a bus is taking a trip from , then the time is calculated as the sum of time at and time to complete the trip (). Equations (12) and (13) ensure that the time criteria are satisfied by a bus at every time in minutes. In (12), if a bus is taking a trip after any trip, then the timetable of () should be greater than the time at the last completed trip. Here, M is a large number. The same is satisfied in (13) when a bus is taking a trip after . Similar to time, a variable for SOC () is defined, which represents the remaining distance in kilometres of a bus at the end of connection l. In (14), if a bus is taking a trip from or , then will be the maximum SOC () minus the kilometres travelled to complete a trip (). For the rest of the trips, the remaining SOC will be equal to the SOC at the last completed trip minus the kilometres travelled to complete a trip (), shown in (15). If a bus j is used for taking trips, then only corresponding can be one, shown in (16). Time and SOC variables are limited in (17) and (18), respectively. The binary variables for trips and buses are defined in (19) and (20), respectively.
The optimization framework is a mixed-integer nonlinear problem due to (8)–(11) and (15). However, it can be linearized using the big-M method and converted into a MILP. For example, the linearization of (8) is shown for illustration in (21)–(24). It shows that will be equal to if is equal to . Otherwise, will be equal to if is equal to . Moreover, any professional optimization classical solvers can internally take care of such constraints.
4. Multi-Agent Framework
The electrical vehicle scheduling problem is NP-hard in nature [10]. A multi-agent framework is proposed to solve this problem in a distributed manner. An agent is defined as software that makes decisions as per its own objective and reacts to the environment in which it is situated. A multi-agent system (MAS) [26] is a set of several agents within a similar environment. For the routing and vehicle scheduling problem, three types of agents are defined as follows, which represent the EV, depot, and transport operator.
4.1. Agent Types
There are following three types of agents in the proposed architecture.
4.1.1. Bus Agent (BA)
The BAs are responsible to fulfill the scheduled timetable in coordination with the transport operator. The various attributes of BA are the following: bus ID, current location, available range, maximum battery SOC, charging rate, deadhead, and operating costs.
4.1.2. Depot Agent (DA)
The DAs provide the charging spot and parking space to the BAs. The various attributes of the DA are the following: maximum parking space, maximum charging spot, occupied parking, and charging spots.
4.1.3. Manager Agent (MA)
The MA coordinates with the BAs to realise the timetabled trips on different routes. The various attributes of MA are the following: route number, trip timetable, route start time, and end time.
4.2. Strategies and Tasks of Agents
4.2.1. Strategies and Tasks of MA
MA is designed to schedule the BAs as per the timetable at minimum cost. It has the following tasks and strategies.
- Step 1
- Broadcast the next trip information from the bus timetable to all BAs. The information contains the trip starting time and the route of the trip from starting station to terminating station.
- Step 2
- Receive the operating costs to fulfil the trip from the BAs who can make the trip.
- Step 3
- Dispatch the BA with minimum cost to realise the trip.
4.2.2. Strategies and Tasks of BAs
BAs are designed to make the decision to take the next trip broadcasted by MA based on their current location, time to reach the starting station of the broadcasted trip, and available charge in their battery. The various tasks and strategies are defined as follows
- Step 1
- Receive the message from MA for the next scheduled trip information and starting time.
- Step 2
- Check for the time feasibility to reach the starting station of the scheduled trip from current location. If yes, go to Step 3. Otherwise, do not respond to MA.
- Step 3
- Check for range feasibility that enough range is available to cover the following distances
- Current location to starting station
- Trip distance
- Terminating stop to nearby depot.
If enough range is available, go to Step 4. Otherwise, do not respond to MA and go to Step 5. - Step 4
- Calculate the operating cost to make the scheduled trip and send the cost to MA. Operating cost = deadhead cost + trip cost
- Step 5
- Check if further trips can be realised with the currently available range. If yes, wait at the current location. Otherwise, go to Step 6.
- Step 6
- Communicate with DAs for the parking and charging space availability. Make a decision based on the DAs’ information and go to the nearby available depot for charging.
4.2.3. Strategies and Tasks of DAs
DAs are designed to provide a charging facility and broadcast the available parking space and charging points.
- Step 1
- Receive the message from BAs for parking or charging spots.
- Step 2
- Communicate with BA and provide the information about the available parking and charging space.
- Step 3
- Make the decision about the disconnection of BAs from charging to maintain a minimum waiting time for charging the other BAs.
The functional diagram of the above-proposed architecture and strategies is shown in Figure 2.
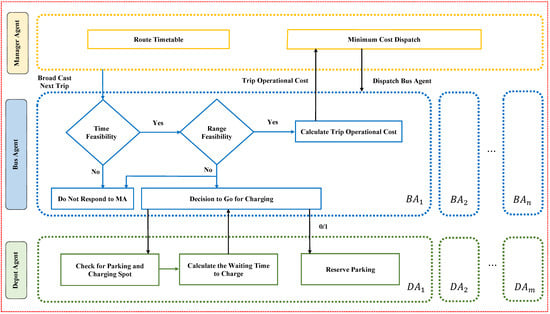
Figure 2.
Multi-agent architecture and strategies.
5. Results and Discussion
A comparative analysis of both frameworks is shown in this section. The results are presented for two small test systems and one partial real-world system from Malta’s public transport network.
5.1. Toy Example: One Depot and Five Trips between Points A and B
The data for this toy example are provided in Figure 1. Here, . One node each is considered , , and as 6, 7, and 8, respectively. This eight-node setup has twentyfour possible connections considering the bidirectional connections as two connections. and are assumed as 2000 and 200, respectively. The timetable () for the trips is 540, 555, 570, 560, and 580, respectively, in minutes. The maximum SOC () is assumed as 100 km. The recharging time to is assumed as 30 min. M is assumed as . The rest of the information can be extracted from the data given in Figure 1.
With this information, the results obtained from both optimization and multi-agent frameworks are the same and presented in Table 2. The optimal number of buses required for this setup is three. Bus 1 takes the following route: . It can be observed that, at , i.e., 6, the bus is fully charged, i.e., km. For taking the trip , i.e., , the bus travels a total distance of 41 km. Therefore, the remaining SOC of the bus at the end of is 59 km. Also, it has to start from at 533 min to reach at 540 min and complete the trip at 554 min. For the trip , i.e., , the bus travels a distance of 28 km. Therefore, the remaining SOC of the bus at the end of is 31 km. At the end of , the bus will be waiting at B for 6 min. Thereafter, it will start travelling to A at 560 min and complete the trip at 574 min. At this time, there are no more trips that this bus can take. Therefore, it will go back to the at 574 min and reach there at 581 min with a remaining SOC of 18 km. Similar observations can be carried out for the other two buses.

Table 2.
Results of optimization and multi-agent framework on the toy example.
The time required by the optimization and multi-agent frameworks is 0.1 s and 0.019 s, respectively. To further investigate, the results are compared with more trips in the following section.
5.2. Single Depot and Fourteen Trips between Points A and B
The graphical data for this example are provided in Figure 3. Here, – corresponds to travel from A to B (up trips), i.e., 12.5 km. Whereas, – corresponds to travel from B to A (down trips), i.e., 12.5 km. One node each is considered , , and as 15, 16, and 17, respectively. This 17-node setup has 140 possible connections. The distances from to A and B are 8 km and 11 km, respectively. It is assumed that the average speed of a bus is 20 km/h. and are assumed as 2000 and 200, respectively. The timetable () for the trips is 300, 460, 620, 780, 940, 1100, 1260, 330, 490, 650, 810, 970, 1130, and 1290, respectively, in minutes. The maximum SOC () is assumed as 100 km. The recharging time to is assumed as 30 min. M is assumed as .
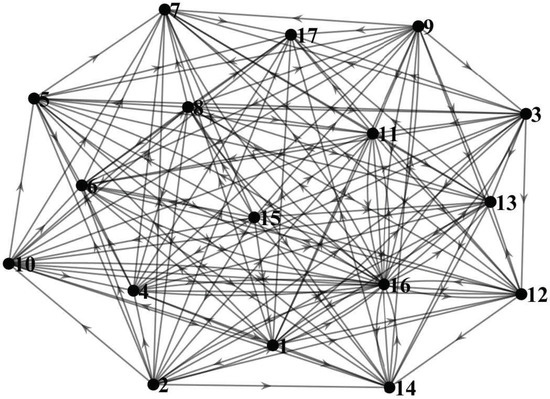
Figure 3.
Single depot and fourteen trips between points A and B.
With this information, the results are obtained in 1779.40 s from the optimization frameworks and are provided in Table 3. The optimal number of buses required for this setup is two. Similar to the example in Section 5.1, the observations can be carried out. However, the uniqueness in this example is that the buses are going to , i.e., 16, for recharging. For example, Bus 2 takes the following route: and so on. It can be observed that, at , i.e., 15, the bus is fully charged at km. For taking the trip , i.e., , the bus travels a total distance of 20.5 km. Therefore, the remaining SOC of the bus at the end of is 79.5 km. Also, it has to start from at 276 min to reach at 300 min and complete the trip at 337.5 min. For trip , i.e., , the bus travels a distance of 12.5 km. Therefore, the remaining SOC of the bus at the end of is 67 km. At the end of , the bus will be waiting at B for 152.5 min. Thereafter, it will start travelling to A at 490 min and complete the trip at 527.5 min. Similarly, the bus will complete the trips to at 817.5 min with a remaining SOC of 29.5 km. At this time, the bus is travelling to , i.e., , taking a total time of 63 min, out of which 33 min are for travelling and 30 min for recharging. Thus, the bus will be available for taking another trip at 880.5 min. The bus is arriving at with a remaining SOC of 18.5 km. However, it is recharging to during this time. Therefore, after taking the trip from , the remaining SOC is 76.5 km, i.e., 100– km. is starting at 970 min, for which this bus is available from 880.5 min onwards and can take this trip. Similar observations can be completed for the other bus.

Table 3.
Results of optimization framework on single depot and fourteen trips problem.
The total distance covered by both buses is 263 km, including operating trip and deadheading distances. The operating trip distance for fourteen trips is 175 km (12.5 each). The deadheading distances are the distances between the depot to stop, stop to the depot, and endpoint of a trip to the start point of the next trip. The deadheading distance with the optimization solution is 88 km.
The multi-agent framework also requires only two buses to fulfil the trips, and the results are provided in Table 4. However, the multi-agent framework takes only 0.0239 s compared to 1779.40 s from the optimization solution. Also, both buses cover only 238 km distance compared to 263 km by the optimization solution. The deadheading distance with the multi-agent solution is 63 km only. Each bus agent takes and trips consecutively. For example, Bus 1 takes the route and so on. Here, the bus takes consecutive trips from up trips (–) and down trips (–), respectively, to avoid deadheading distance. However, the buses are taking two consecutive up or down trips in the optimization solution, which leads to more deadhead distance, as shown in Table 3.

Table 4.
Results of the multi-agent framework on one depot and fourteen trips problem.
As observed from the results of the solved examples by both frameworks, the routes obtained are similar in both cases, with few differences in terms of deadheading distances. However, the run-time of the classical optimizer has increased manifold with the increase in the size of the network. It is due to the increased number of integer variables in the problem by a factor of , where ‘n’ is the number of the binaries associated with the graph. Therefore, for the practical network of Malta, we present the results obtained using the multi-agent framework in the following section.
5.3. Malta’s Public Transport Network
We consider data from Malta’s public transport network [27]. The map version of the routes of interest is shown in Figure 4. The data are cropped to include four bus depots, i.e., Marsa Park and Ride (D1), Luqa (D2), GT (Ghajn Tuffieha) (D3), and Bugibba Bay (D4). Among these depots, the first two depots are closer to all the stations compared to the latter depots. We note that the MAS-based approach can accommodate a multi-depot BRSP, and we harness the potential of the MAS with the above-mentioned depots. We consider the parking capacity per depot to be twenty. For demonstration, the data include 10 bus routes, as shown in Table 5, of Malta, where the public transport system currently relies on diesel-engine-based buses, and has around 10 electric buses currently. These 10 routes have 976 up and down trips [27]. In this study, two types (EV1 and EV2) of electric buses are considered and their details are given in Table 6. In this table, the en route operating cost means that the bus is on a trip and fully loaded. Whereas, the deadheading operating costs signify the operation of the bus without passengers. In addition, it is assumed that there are 40 EV1 buses available with the MA, and the MA can be used to decide the routes. If more buses are required, then the MA will request EV2 buses and decide their routes. Moreover, it is assumed that both types of buses are travelling at a constant speed of 20 km/h while en route and during deadheading. The proposed algorithm is implemented using MATLAB®.
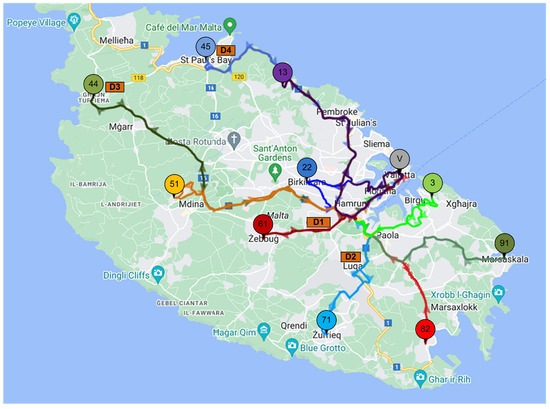
Figure 4.
A pictorial representation of the routes for the analysis.

Table 5.
Ten bus routes considered in this study.

Table 6.
Electric bus data.
With the above setup, the results are obtained for the following four cases and are tabulated in Table 7. The table shows the required total number of buses for each type with their operating cost and total distance travelled. Moreover, their average deadheading, en route, and total distance travelled are shown with their average charging breaks.

Table 7.
Bus route scheduling with MAS: summary of cases.
5.4. Case 1
In this case, it is assumed that, once a bus is returning to the depot after a trip for charging, then it can only accept the next trip after becoming fully charged, i.e., state of charge (SOC) is equal to 100%. Moreover, a startup cost (SC) is assumed for requesting a new bus from a depot. Here, a new bus means that it is being called for a trip for the first time. SC is set equal to the cost of the longest trip for illustration purposes. With this, the total number of buses required is 74. Based on the routes decided by MA for 40 EV1 buses, the operating cost is EUR 7407 and the total distance travelled is 8869.60 km. Moreover, the average distance travelled by EV1 buses is 221.74 km (average en route distance of 206.22 km), with an average of one charging break at the depot. As EV1 buses are exhausted and more buses are required, MA is requesting 34 EV2 buses, with an operating cost of EUR 3825.49 utilised for a total distance of 5548.80 km. The average distance by EV2 buses is 163.20 km, with an average charging break of 1.21. This is due to the lesser range and faster charging rate compared to EV1 buses. Overall, EV1 buses will be utilised first and placed on the nearer depots, which reduces its average deadheading distance to 15.52 km compared to that of EV2 buses, i.e., 24.65 km, placed at farther depots.
5.5. Case 2
This case is the same as Case 1 with SC set to zero. With this, the total number of buses required is 67. Because of zero SC, the MA will utilise EV2 buses first and place them at nearer depots, eventually requiring 27 buses. Due to the shorter range, they are often sent for recharging with an increased average charging break of 1.67 compared to Case 1. Due to this, their operating cost and total distance are increased to EUR 3825.49 and 6309.10 km, thus increasing their average distance and deadheading distance to 233.67 km and 20.50 km, respectively, compared to Case 1. On the other hand, MA is not forcing EV1 buses for more trips, eventually reducing its operating cost to EUR 6660.81 and total distance travelled to 7995.50 km compared to Case 1. This has further led to the reduction in their average distance travelled to 199.89 km, with an average of 0.93 charging break at the depot. Note that the average deadheading distance is increased to 19.79 km due to their placement at farther depots, leading to fewer trips, i.e., an average en route distance of 180.10 km.
5.6. Case 3
This case is the same as Case 1 with SOC set to 80%; i.e., a bus can accept a trip once its SOC is greater than or equal to 80%. Because of the lower SOC requirement, MA requires a smaller number of buses, i.e., 72. Moreover, it can operate EV1 buses for more duration, which has increased its operating cost to EUR 7476.28 and total distance travelled to 8950 km. Thus, they are placed at nearer depots. A slight increase in average distance travelled is observed, i.e., 223.75 km, with average en route and deadheading distances of 208.85 km and 14.90 km, respectively, and an average of one charging break at the depot. The reduction in average deadheading distance is due to relatively lesser charging requirements. For the rest of the duration, MA is requesting 32 EV2 buses with an operating cost of EUR 3769.30 utilised for a total distance of 5471.30 km. The average distance by EV2 buses is 170.98 km, with an average charging break of 1.34 due to the lesser range and faster charging rate compared to EV1 buses. Due to their placement at farther depots, EV2 buses are having higher average deadheading distances, i.e., 27.06 km, compared to EV1 buses.
5.7. Case 4
This case is the same as Case 3 with SC set to zero. With this, the total number of buses required is 65. Because of zero SC, MA can freely utilise EV2 buses by placing them at nearer depots, requiring fewer buses, i.e., 25, at higher operating cost and the total distance of EUR 4080.28 and 5886.90 km, thus increasing their average distance to 235.48 km with an average charging break of 1.76 compared to Case 3. Note that the higher charging breaks are taken at the depot closer to the stations, which eventually reduced their average deadheading distance to 23.17 km. On the other hand, MA is not forcing EV1 buses for more trips, eventually reducing its operating cost to EUR 7040.89 and total distance travelled to 8448.40 km compared to Case 3. This has further led to the reduction in their average distance travelled to 211.21 km with an average of 0.90 charging break at the depot. Note that the average deadheading distance is increased to 19.92 km due to their placement at farther depots, leading to smaller trips, i.e., an average en route distance of 191.30 km.
We note that, for all four cases, the run-time for simulating the entire network as per the data considered did not exceed 2 s, which is in good agreement with solving a near-real-time problem. This is an important virtue if the scheduling problem, especially with multiple depots, looks to accommodate any contingency measures while in operation. However, this problem currently is beyond the scope of our paper.
6. Conclusions
In this work, we introduced a multi-agent framework for scheduling electric-busbased public transport. Our objective in this paper was to determine the minimum number of buses required for a cost-optimal operation while satisfying the charging and passenger levying constraints. We compared the proposed methodology with a mixed-integer linearprogramming-based classical formulation, which attempts to minimize bus usage costs and recharging costs. The observation for the smaller-sized trip revealed that, for five trips, three buses are required for both methods; however, with the multi-agent formulation, the SOC (in kilometres) is greater at the end trip. The latter framework also takes less time to provide the optimal solution. The problem was then extended to a larger problem, and we observed from the 14 trips between the starting and ending nodes that the number of buses required is less, and also the required buses complete the trip with a lesser amount of recharging trips, as can be seen in Table 4. We also observe that the time taken by the optimization framework to converge to a solution was much larger.
We conclude that, for unidirectional bus routes (the ones that are not circular), the multi-agent-based scheduling provides a better performance than the classical optimization, especially for a case when the timetables are known. The framework also ensures a timely convergence to a feasible solution, which we realized was hard to achieve as the trip nodes increased. We also studied a snippet from Malta’s public transport network where we observed the timetabled trips for ten lines and two types of buses (albeit this study can be generalized to any transport network with electric buses), in which we studied case studies involving different startup costs and the energy levels of the buses. The multi-agent approach gave us the flexibility to intake more variables, which made the problem more realistic. Apart from that, as can be seen from the cases, multiple depots were used for the simulations with the proposed approach, which, in the case of the classical optimization approach, is hard to solve because of the high number of variables.
Our work has an important future scope. Multi-agent bus route scheduling takes advantage of quick convergence, and, therefore, contingency, such as the unavailability of a bus driver, can be taken into account by the manager agent in order to make necessary changes to provide a new set of solutions.
Author Contributions
Conceptualization, D.K., B.H. and M.P.; Methodology, S.S. and D.K.; Software, S.S.; Investigation, M.P.; Writing—original draft, S.B.; Visualization, D.K.; Supervision, B.H. and B.A.; Funding acquisition, B.A. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was supported in part by the European Commission’s Horizon 2020 Twinning project, “Networking for Excellence in Electric Mobility Operations (NEEMO)”, Grant number 857484.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Saha, J. An Algorithm for Bus Scheduling Problems. J. Oper. Res. Soc. 1970, 21, 463–474. [Google Scholar] [CrossRef]
- Boren, S. Electric buses’ sustainability effects, noise, energy use, and costs. Int. J. Sustain. Transp. 2020, 14, 956–971. [Google Scholar] [CrossRef]
- ABB. Electric Bus Pantograph Up. Available online: https://new.abb.com/ev-charging/pantograph-up (accessed on 27 May 2023).
- Bakker, S.; Konings, R. The transition to zero-emission buses in public transport—The need for institutional innovation. Transp. Res. Part D Transp. Environ. 2018, 64, 204–215. [Google Scholar] [CrossRef]
- Jagiełło, A.; Wołek, M.; Bizon, W. Comparison of Tender Criteria for Electric and Diesel Buses in Poland—Has the Ongoing Revolution in Urban Transport Been Overlooked? Energies 2023, 16, 4280. [Google Scholar] [CrossRef]
- Teng, J.; Jin, S.; Lai, X.; Chen, S. Vehicle-Scheduling Model for Operation Based on Single-Depot. Math. Probl. Eng. 2015, 2015, 506794. [Google Scholar] [CrossRef]
- Freling, R.; Wagelmans, A.P.M.; Paixão, J.M.P. Models and Algorithms for Single-Depot Vehicle Scheduling. Transp. Sci. 2001, 35, 165–180. [Google Scholar] [CrossRef]
- Zhang, J.; Li, W.; Qiu, F. Optimizing Single-Depot Vehicle Scheduling Problem: Fixed-Interval Model and Algorithm. J. Intell. Transp. Syst. 2015, 19, 215–224. [Google Scholar] [CrossRef]
- Kang, L.; Chen, S.; Meng, Q. Bus and driver scheduling with mealtime windows for a single public bus route. Transp. Res. Part C Emerg. Technol. 2019, 101, 145–160. [Google Scholar] [CrossRef]
- Zhou, G.J.; Xie, D.F.; Zhao, X.M.; Lu, C. Collaborative Optimization of Vehicle and Charging Scheduling for a Bus Fleet Mixed With Electric and Traditional Buses. IEEE Access 2020, 8, 8056–8072. [Google Scholar] [CrossRef]
- Sundstȑom, O.; Binding, C. Optimization Methods to Plan the Charging of Electric Vehicle Fleets; IBM Research: Zurich, Switzerland, 2010. [Google Scholar]
- Xu, X.; Yu, Y.; Long, J. Integrated electric bus timetabling and scheduling problem. Transp. Res. Part C Emerg. Technol. 2023, 149, 104057. [Google Scholar] [CrossRef]
- Wilson, W.; Venkataramanan, M.; Goldberg, J. Introduction to Mathematical Programming; MIT Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Duan, M.; Liao, F.; Qi, G.; Guan, W. Integrated optimization of electric bus scheduling and charging planning incorporating flexible charging and timetable shifting strategies. Transp. Res. Part C Emerg. Technol. 2023, 152, 104175. [Google Scholar] [CrossRef]
- Dasović, B.; Klanšek, U. A Review of Energy-Efficient and Sustainable Construction Scheduling Supported with Optimization Tools. Energies 2022, 15, 2330. [Google Scholar] [CrossRef]
- Meng, G.; Lai, Y.; Yang, F. An Optimal Bus Scheduling Model Based on Mixed-Integer Linear Programming. In Proceedings of the 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 11–13 December 2020; Volume 9, pp. 2200–2204. [Google Scholar]
- Zhang, J.; Jiang, Q.; Pan, A.; Li, T.; Liu, Z.; Zhang, Y.; Jiang, L.; Zhan, X. An Optimal Dispatching Strategy for Charging and Discharging of Electric Vehicles Based on Cloud-Edge Collaboration. In Proceedings of the 2021 3rd Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 26–29 March 2021; pp. 827–832. [Google Scholar]
- Li, W.; Ding, Y.; Yang, Y.; Sherratt, R.S.; Park, J.H.; Wang, J. Parameterized algorithms of fundamental NP-hard problems: A survey. Hum.-Centric Comput. Inf. Sci. 2020, 10, 1–24. [Google Scholar] [CrossRef]
- Sun, B. Optimal Bus Scheduling Considering Operating Costs and Emissions: A Multiple Objective, Mixed Integer Programming Framework. Master’s Thesis, University of Minnesota, Minneapolis, MN, USA, 2015. [Google Scholar]
- Jahic, A.; Plenz, M.; Eskander, M.; Schulz, D. Route Scheduling for Centralized Electric Bus Depots. IEEE Open J. Intell. Transp. Syst. 2021, 2, 149–159. [Google Scholar] [CrossRef]
- Schiewe, P.; Stinzendörfer, M. Integrated Line Planning and Vehicle Scheduling for Public Transport. In Proceedings of the International Network Optimization Conference, Aachen, Germany, 7–10 June 2022. [Google Scholar]
- Kunith, A.; Mendelevitch, R.; Goehlich, D. Electrification of a city bus network—An optimization model for cost-effective placing of charging infrastructure and battery sizing of fast-charging electric bus systems. Int. J. Sustain. Transp. 2017, 11, 707–720. [Google Scholar] [CrossRef]
- Yao, E.; Liu, T.; Lu, T.; Yang, Y. Optimization of electric vehicle scheduling with multiple vehicle types in public transport. Sustain. Cities Soc. 2020, 52, 101862. [Google Scholar]
- Lin, H.; Tang, C. Analysis and Optimization of Urban Public Transport Lines Based on Multiobjective Adaptive Particle Swarm Optimization. IEEE Trans. Intell. Transp. Syst. 2022, 23, 16786–16798. [Google Scholar] [CrossRef]
- Verbrugge, B.; Rauf, A.M.; Rasool, H.; Abdel-Monem, M.; Geury, T.; Baghdadi, M.E.; Hegazy, O. Real-Time Charging Scheduling and Optimization of Electric Buses in a Depot. Energies 2022, 15, 5023. [Google Scholar] [CrossRef]
- Sharma, S.; Bhattacharya, S.; Kiran, D.; Hu, B.; Prandtstetter, M.; Azzopardi, B. A multi-agent framework for scheduling fully electrified public transport. In Proceedings of the 13th Mediterranean Conference on Power Generation, Transmission, Distribution and Energy Conversion (MEDPOWER 2022), Valletta, Malta, 7–9 November 2022; pp. 571–574. [Google Scholar] [CrossRef]
- Malta Public Transport Network Offline Map in PDF. Available online: https://moovitapp.com/index/en-gb/public_transportation-Offline_maps_Malta_Public_Transport_Network-map-Malta-4507-5291 (accessed on 27 May 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).