A Comprehensive Review of Degradation Prediction Methods for an Automotive Proton Exchange Membrane Fuel Cell
Abstract
1. Introduction
1.1. Generality
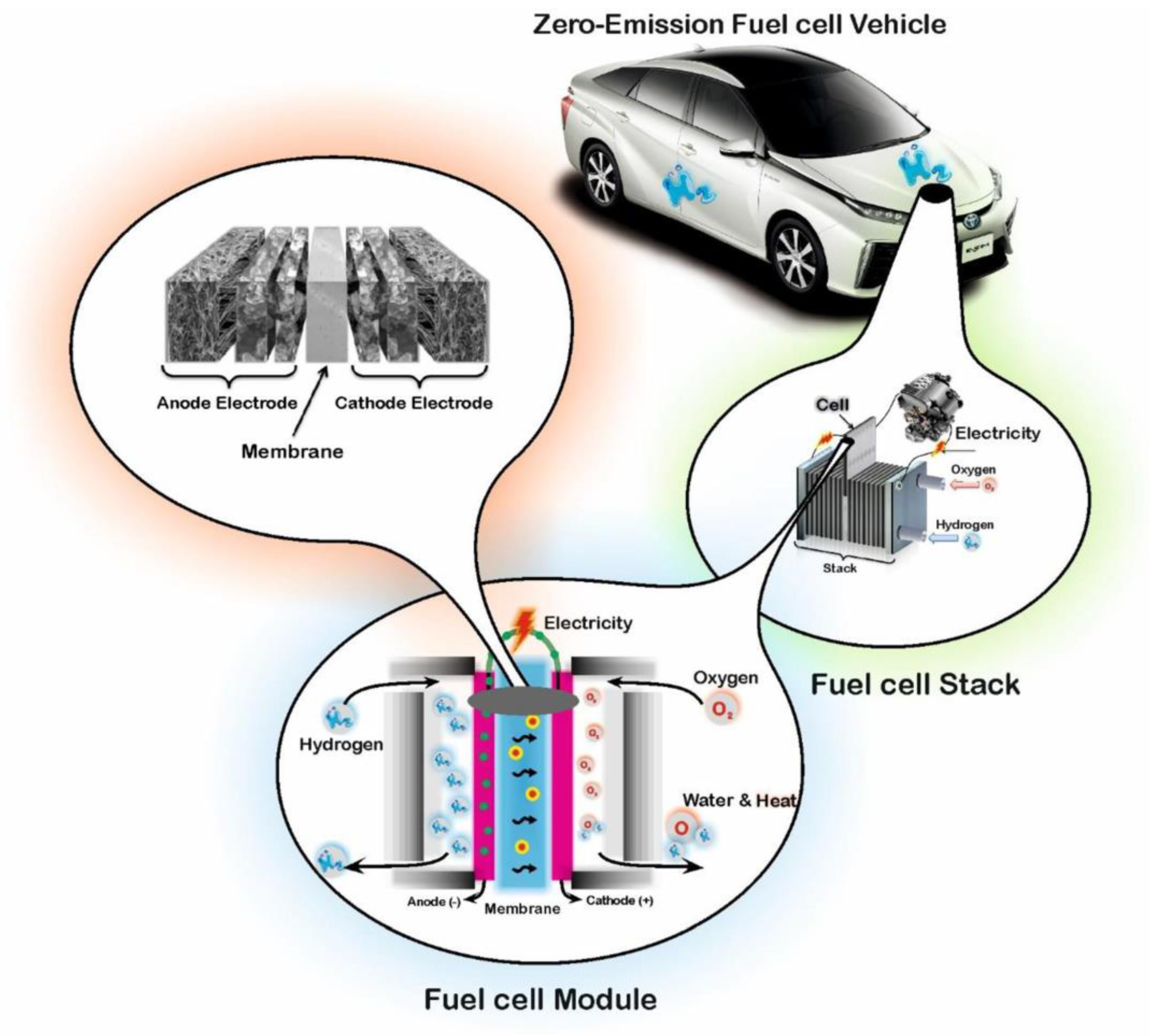
1.2. PEMFC System in Hydrogen Fuel Cell Vehicle
1.3. Performance Degradation of the PEMFC System
- Mechanical degradation: Fuel cells often fail, and this is attributable to material defects and poor structural design and manufacture. Material flaws may generate non-uniform mechanical stresses, fractures, and premature failure. Material flaws, improper structural design, and manufacturing errors produce non-uniform mechanical stresses and fractures. Operating conditions may affect fuel cell components’ physical qualities. Membranes, catalyst layers, etc., shrink or swell depending on the temperature. The non-uniform pressure distribution on components resulting from the cathode-anode pressure difference causes mechanical damage. High and non-uniform mechanical stresses may perforate or shred interfaces between components during cell or stack assembly [9,17].
- Thermal degradation: The fuel cell operating outside the temperature range induces structural changes [18]. PEMFCs work well at 60–80 °C. The glass transition of PFSA polymers causes the severe destruction of conventional Nafion-type membranes around 80–120 °C [19]. One requirement for PEMFCs in automotive applications is the capacity to start at subfreezing temperatures. Notably, in automotive applications, the Department of Energy requires PEMFC stacks and systems to start up and operate at −20 °C to 50% rated power in 30 s using less than 5 MJ of energy [20]. However, the formation and melting of ice during long-term operation at subfreezing temperatures could delaminate the MEA and gas diffusion layers [17].
- Chemical/electrochemical degradation: This is mainly caused by the material’s natural aging, including Pt dissolution and carbon support corrosion/oxidation in the catalyst layers (CLs) and gas diffusion layers (GDL), radial attack in the membrane, and bipolar plate (BBP) corrosion [9]. In addition, contaminants in the fuel and oxidation sources, such as CO, H2S, NH3, etc., may induce catalyst toxicity and affect the catalytic activity, diffusion, and hydrophobic properties [17].
1.4. End-of-Life Definition/Criterion
1.5. Classification of Degradation Modeling Methods
- The model-based method predicts the aging process using mathematical equations. This method does not need a large amount of data. However, it may be computationally expensive, and model construction may be tricky.
- The data-driven method uses collected data to understand the system’s behavior. It detects non-linearities without a degradation model. However, it demands a large amount of data to perform prognostics.
- The hybrid method enhances model learning and improves model uncertainties. However, it may be challenging to design and computationally costly.
2. Performance Degradation Modeling of PEMFC
2.1. Model-Based Approach
2.1.1. Mechanistic Degradation Model
- a.
- Membrane Degradation Mechanism Model
- b.
- Catalyst layer degradation mechanism model
- c.
- GDL degradation mechanism model
- d.
- Summary of mechanistic degradation models
2.1.2. Empirical Model
- a.
- Model development
- b.
- Summary of empirical degradation models
2.1.3. Semi-Empirical Model
- a.
- Model development
- Erev is reversible cell voltage.
- R is gas constant equal to 8:3145 J·mol−1·K−1.
- n is cell number.
- T is stack temperature.
- αa and αc are the charge transfer coefficients at the anode and at the cathode.
- iloss,o represents the initial internal currents within the stack.
- bloss is the aging rate parameter of iloss,o.
- i0a and i0c are the exchange current densities at each electrode.
- Rion,o is the initial ionic resistances.
- bion is the aging rate parameter of Rion,o.
- Ro represents for both electronic and contact resistances.
- bR is aging rate parameter of Ro.
- Bc is an empirical parameter allowing taking into account the effect of water and gas accumulations leading to non-uniform current densities on the electrode.
- DO2 is the diffusivity of oxygen.
- bD is aging rate parameter of DO2.
- I(t) is the time-dependent current.
- A(t) is the active area of the electrode that decreases with the aging given by an exponential form.
- Erev is reversible cell voltage.
- i is operating current density.
- T is fuel cell temperature.
- Ro is initial total resistances of fuel cell.
- A is the Tafel constant.
- B is a concentration constant.
- iL,o is initial limiting current density.
- io is exchange current density.
- Erev is reversible cell voltage.
- i is operating current density.
- T is fuel cell temperature.
- R*o is initial a polarization resistance.
- A is the Tafel constant.
- B is a concentration constant
- iL,o is initial limiting current density.
- io is exchange current density.
- Erev is reversible cell voltage.
- R is internal resistance.
- A is Tafel constant.
- i is operating current density.
- io is exchange current density.
- m1 and m2 are the mass-transfer constants.
- Erev is reversible cell voltage.
- T is fuel cell temperature.
- α is the charge transfer coefficient.
- R is gas constant equal to 8:3145 J·mol−1·K−1.
- i is operating current density.
- Erev is reversible cell voltage.
- R is gas constant equal to 8:3145 J·mol−1·K−1.
- n is cell number.
- T is stack temperature.
- αa and αc are the charge transfer coefficients at the anode and at the cathode.
- i is operating current density.
- ileak,o is initial leaking current density.
- bleak is aging rate parameter of ileak,o.
- ia,ref and ic,ref are referent current density at anode and cathode.
- Rion,o is the initial ionic resistance.
- bion is the aging rate parameter of Rion,o.
- DO2 is the diffusivity of oxygen.
- bD is aging rate parameter of DO2.
- Kc is the concentration loss coefficient.
- aECSA,o is the initial electrochemical active surface area of catalyst layer.
- bECSA is aging rate parameter of aECSA,o.
- mpt is Pt loading.
- b.
- Summary of semi-empirical degradation models
2.1.4. Summary
- Models can easily be implemented and make predictions about the future behavior of PEMFC systems. Simulating the model can be used to explore various scenarios and make informed decisions.
- Models can provide valuable insights into the relationship and interactions between different components of the PEMFC system.
- Models can be used to optimize the PEMFC system by identifying the optimal operating conditions.
- Models do not require a large amount of data. Thus, they can be used to explore different scenarios and hypotheses in online environments before implementing them in real world situations.
- Disadvantages of the model-based approach:
- Models require a good understanding of the behavior and degradation mechanisms of fuel cell systems and their components.
- Creating an accurate and reliable model can be challenging and time-consuming.
- Models need to be validated and verified against experiment data to ensure their accuracy and reliability.
- Models may be limited to the specific conditions under which they were developed. Extrapolating model predictions to different conditions may lead to inaccurate results.
2.2. Data-Driven Approach
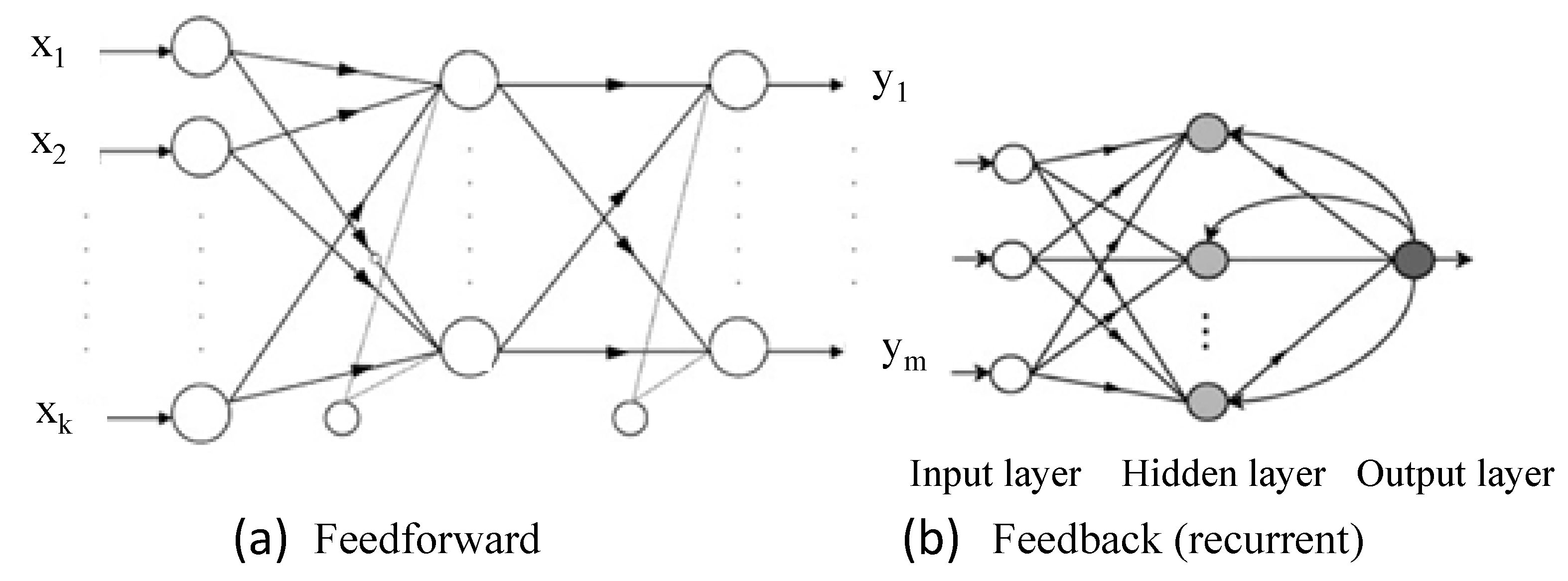
2.2.1. Artificial Neural Network (ANN) Model
- a.
- Back propagation neural network
- b.
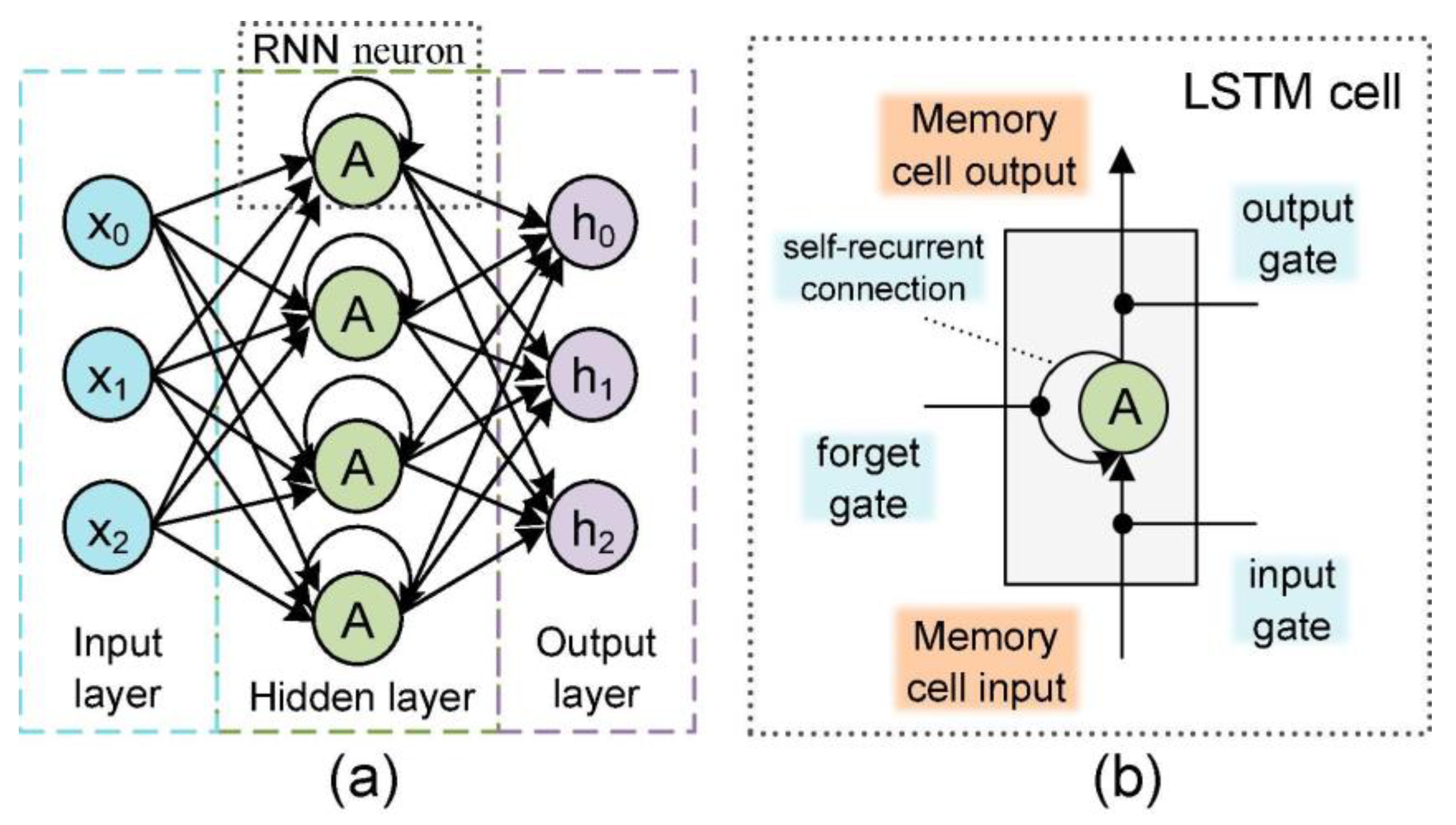
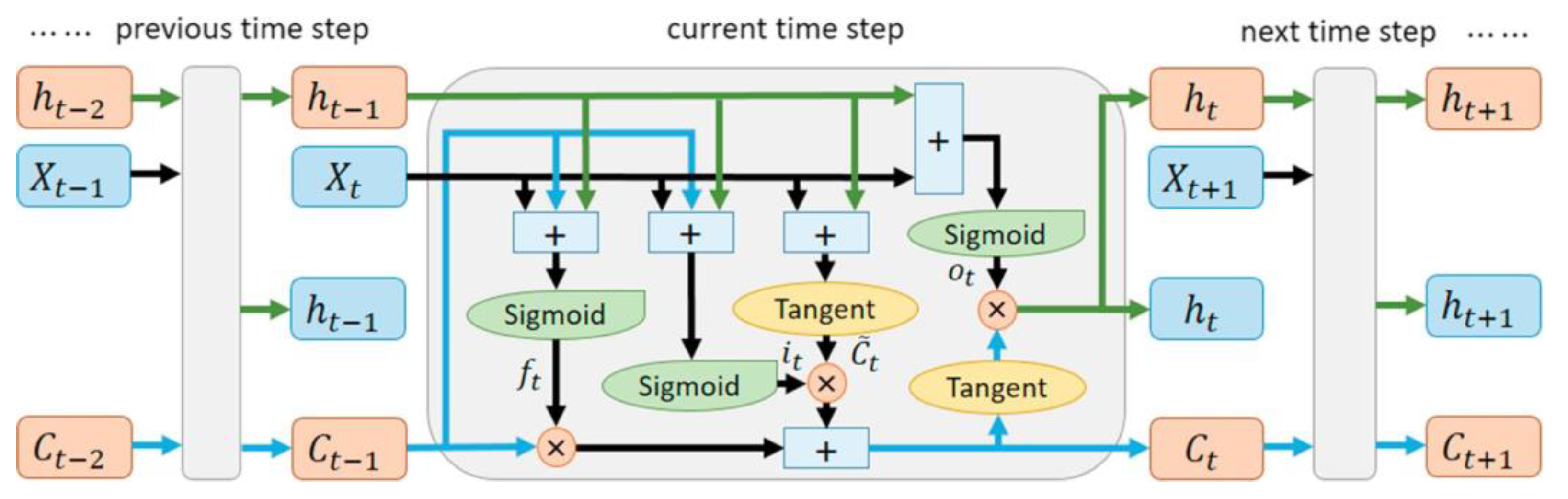
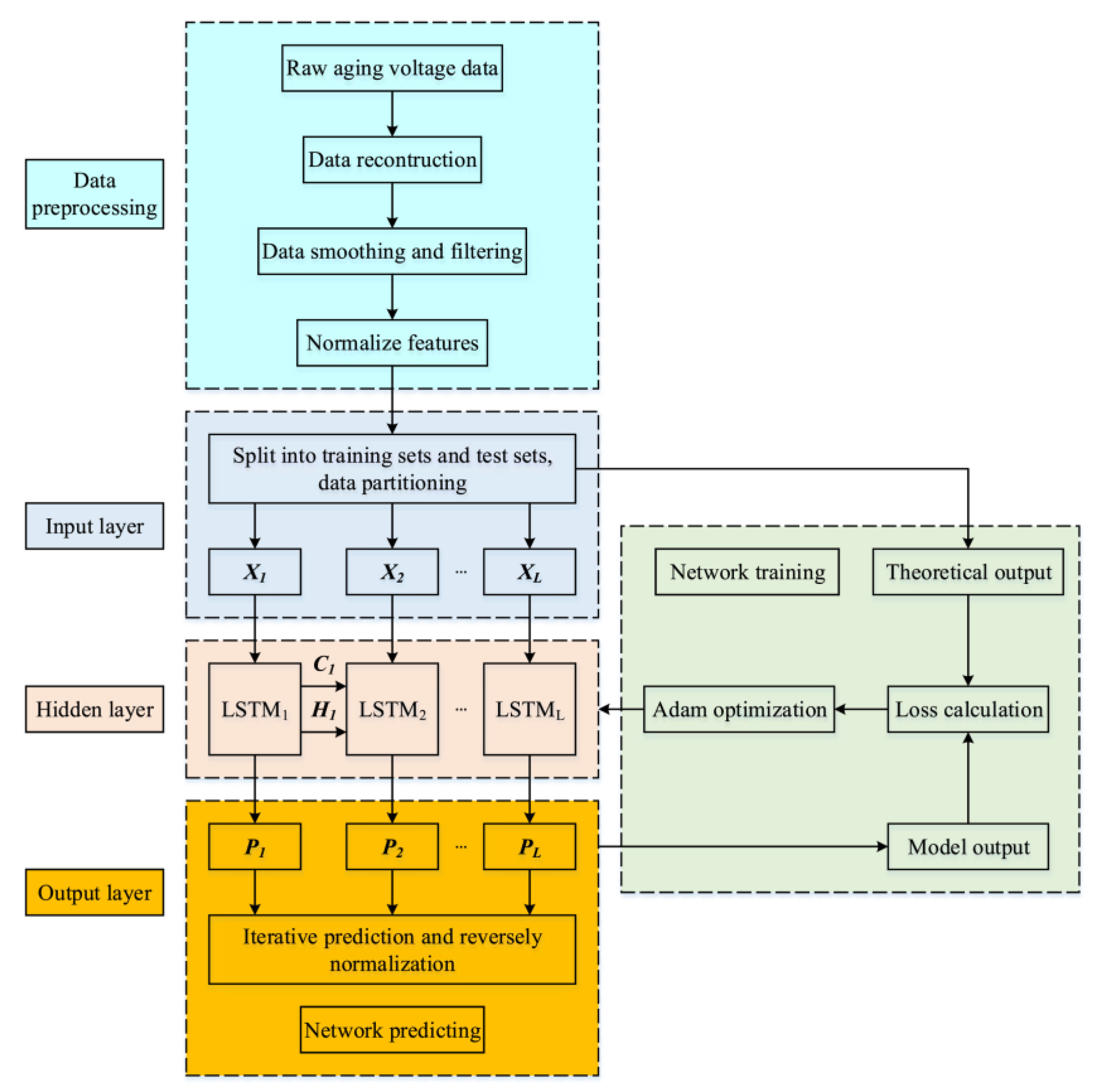
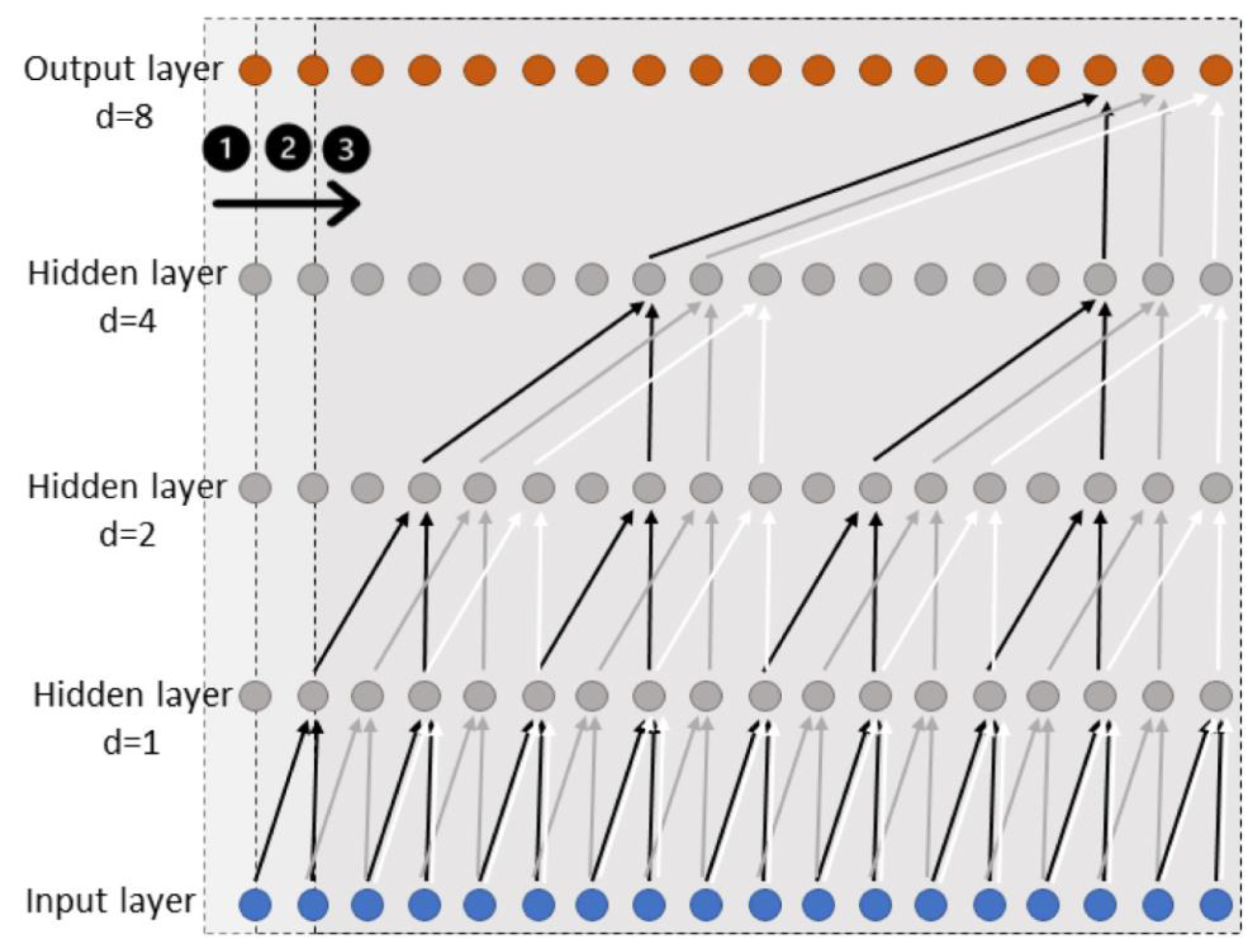
- Long-short-term memory neural network
- c.
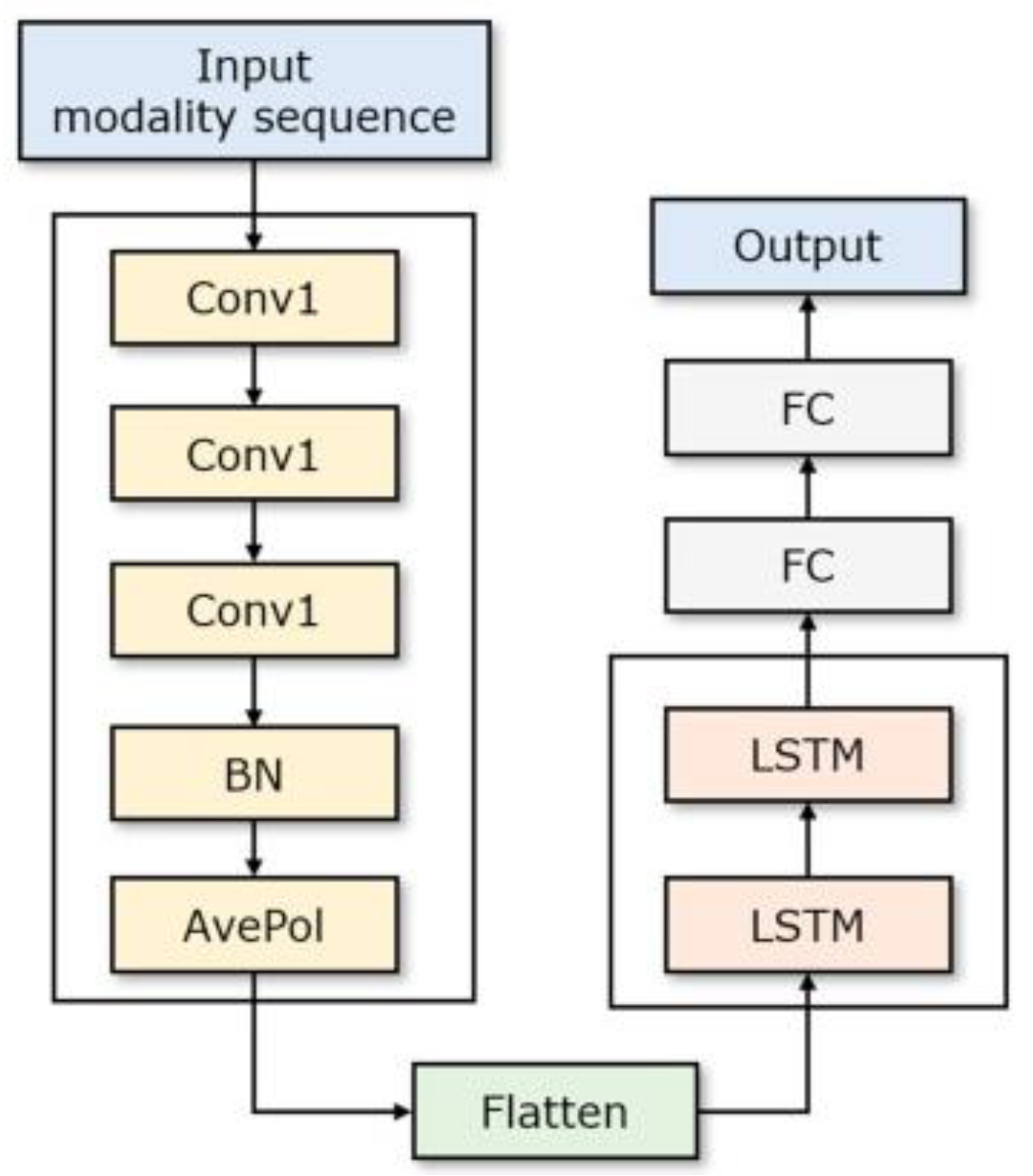
- Convolutional neural network
- d.
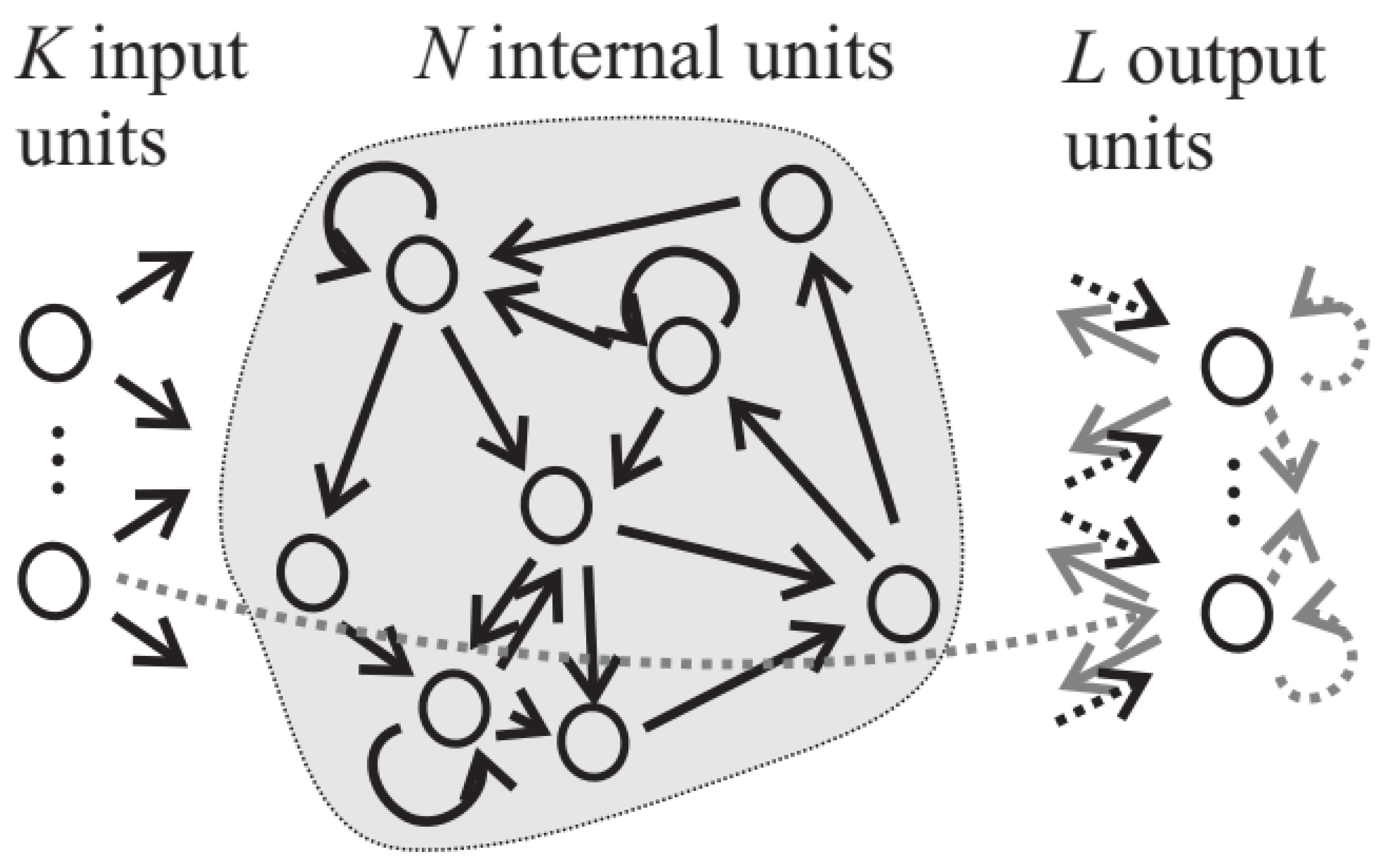
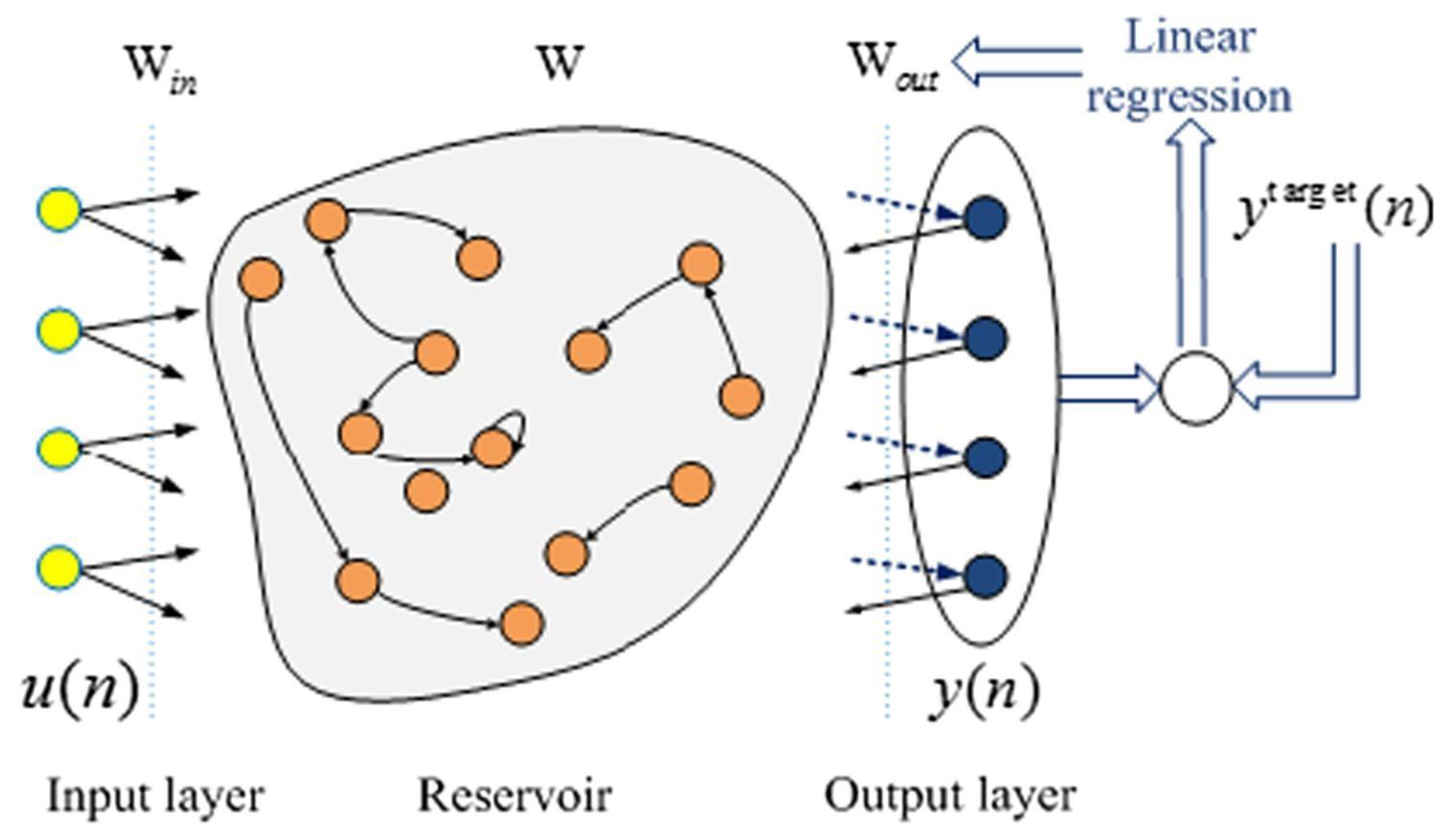
- Echo state network
- e.
- Summary of ANN models
2.2.2. Support Vector Machine Model
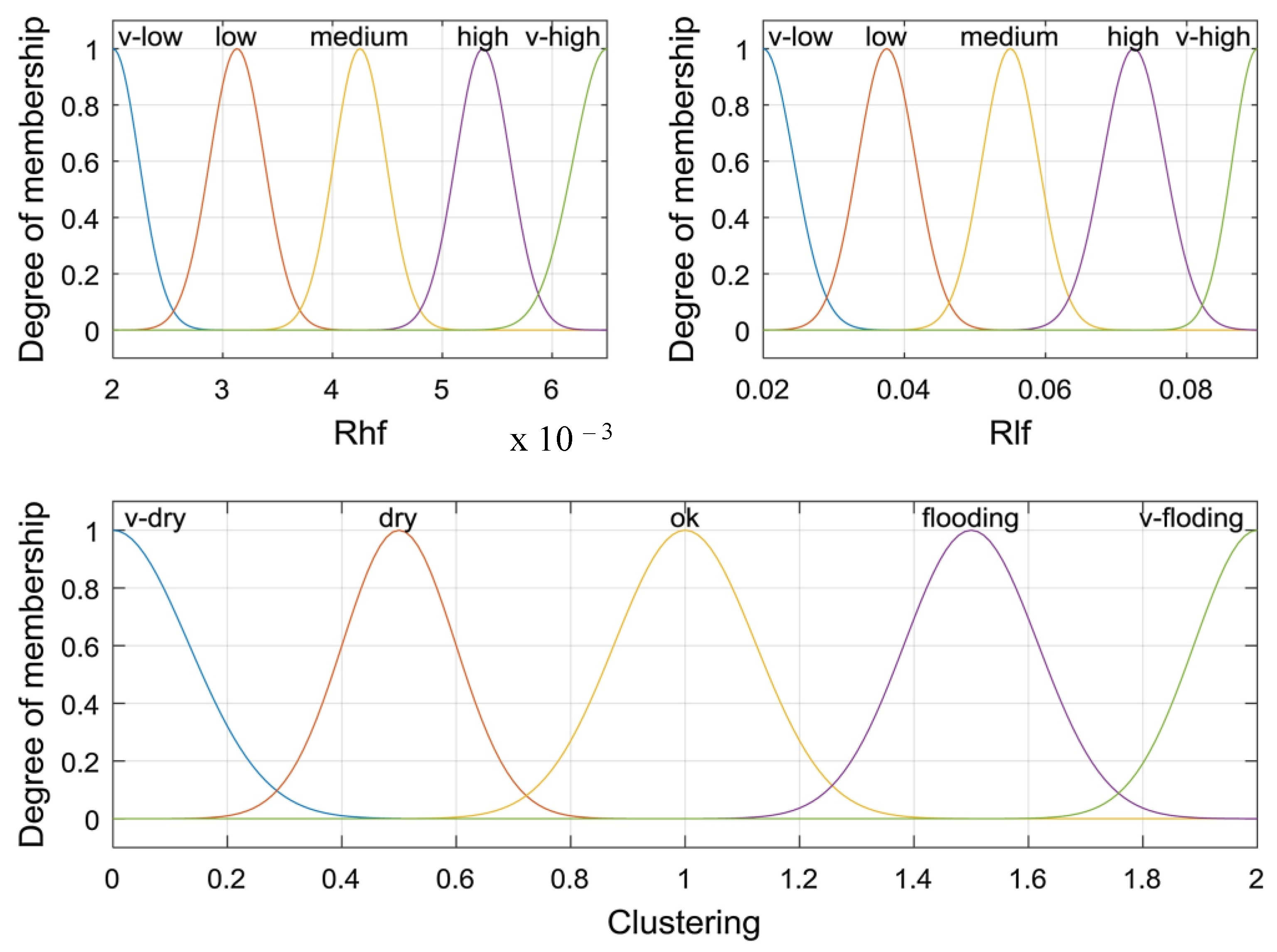
2.2.3. Fuzzy Logic Model
2.2.4. Gaussian Process
2.2.5. Summary
- Data-driven models can make accurate predictions or decisions without requiring a deep understanding of the underlying system. This can be advantageous when dealing with complex systems or when the system dynamics are not well understood.
- Data-driven models can capture complex relationships and interactions between variables, even when the underlying mechanisms are not well understood.
- Data-driven models can be more flexible and adaptable to changing conditions or new data.
- Disadvantages of the data-driven approach:
- Data-driven models often lack interpretability, meaning it can be challenging to understand and explain the reasons behind their predictions or decisions.
- Data-driven models may struggle with extrapolating beyond the range of the available data. They might not accurately predict outcomes in scenarios that differ significantly from the training data.
- The accuracy and reliability of data-driven models heavily depend on the quality, completeness, and representativeness of the input data.
- Data-driven models require access to sufficient and relevant data, which may not always be readily available.
2.3. Hybrid Approach
- (1)
- The model-based approach extracts degradation indexes, then the data-driven approach predicts the degradation trend and estimates the RUL.
- (2)
- Data-driven methods fit the degradation model or measurement data to predict the future degradation trend, then model-based methods estimate the RUL.
- (3)
- Model-based and data-driven methods are applied together. The final degradation results are obtained by weighing each result.
2.3.1. Hybrid Strategy 1
2.3.2. Hybrid Strategy 2
2.3.3. Hybrid Strategy 3
2.3.4. Summary
- By combining the strengths of both model-based and data-driven approaches, hybrid models can potentially offer higher accuracy and reliability in predictions and decisions.
- Hybrid models can effectively model and capture complex and nonlinear relationships between variables. The model-based component can provide an overall degradation trend, while the data-driven component can handle the fine-grained details and nonlinearity present in the data.
- Hybrid models can adapt to different levels of data availability. In cases where data are limited, the model-based component can provide useful insights and predictions. When more data become available, the data-driven component can be integrated to refine and update the model.
- Hybrid models can better generalize new or unseen data compared to data-driven models. The model-based component can improve the model’s ability to make accurate predictions in conditions beyond the training data.
- Disadvantage of hybrid approach:
- Hybrid models can be more complex to develop and implement compared to using a single modeling approach.
- Hybrid models may require more computational resources, especially if the model-based component involves complex mathematical equations or simulations.
- Validating and verifying hybrid models can be more demanding than with single modeling approaches. Ensuring the accuracy and reliability of both components and their integration requires careful testing and comparison with experimental data.
3. Challenges and Prospects
4. Conclusions and Perspectives
- Current studies show that voltage and power are the most reliable indicators of PEMFC age; however, these metrics are indistinct when applied to dynamic conditions. Indeed, the monotonic drop in voltage or power is less visible in dynamic operating situations due to load current uncertainty. Therefore, extracting aging indicators that may be used to make reliable online estimates of PEMFC lifetime with little computational effort is crucial.
- The prediction of the degradation and lifetime of fuel cells plays a significant role in the operation and maintenance of fuel cell vehicles. Thus, there is an immediate need to propose a method for online lifetime prediction under the dynamic responses of the real-world. The main idea is to build mathematical models or “black box” models to quickly forecast the intermediate or long period using real-time collected data of actual running fuel cell vehicles. Despite this progress, online prediction remains a significant obstacle due to the complicated structure of machine learning algorithms, which makes online process implementation difficult. In addition, PEMFCs in electric vehicles operate under complicated conditions due to the rapid changing of electric vehicle operation. Therefore, adaptive prediction methods are necessary for enhanced online prediction accuracy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiao, K.; Xuan, J.; Du, Q.; Bao, Z.; Xie, B.; Wang, B.; Zhao, Y.; Fan, L.; Wang, H.; Hou, Z.; et al. Designing the next Generation of Proton-Exchange Membrane Fuel Cells. Nature 2021, 595, 361–369. [Google Scholar] [CrossRef] [PubMed]
- Itaoka, K.; Saito, A.; Sasaki, K. Public Perception on Hydrogen Infrastructure in Japan: Influence of Rollout of Commercial Fuel Cell Vehicles. Int. J. Hydrogen Energy 2017, 42, 7290–7296. [Google Scholar] [CrossRef]
- Borup, R.L.; Kusoglu, A.; Neyerlin, K.C.; Mukundan, R.; Ahluwalia, R.K.; Cullen, D.A.; More, K.L.; Weber, A.Z.; Myers, D.J. Recent Developments in Catalyst-Related PEM Fuel Cell Durability. Curr. Opin. Electrochem. 2020, 21, 192–200. [Google Scholar] [CrossRef]
- Nguyen, H.L.; Han, J.; Vu, H.N.; Yu, S. Investigation of Multiple Degradation Mechanisms of a Proton Exchange Membrane Fuel Cell under Dynamic Operation. Energies 2022, 15, 9574. [Google Scholar] [CrossRef]
- Wu, H.W. A Review of Recent Development: Transport and Performance Modeling of PEM Fuel Cells. Appl. Energy 2016, 165, 81–106. [Google Scholar] [CrossRef]
- Liu, H.; Chen, J.; Hissel, D.; Lu, J.; Hou, M.; Shao, Z. Prognostics Methods and Degradation Indexes of Proton Exchange Membrane Fuel Cells: A Review. Renew. Sustain. Energy Rev. 2020, 123, 109721. [Google Scholar] [CrossRef]
- Zhao, J.; Li, X.; Shum, C.; McPhee, J. A Review of Physics-Based and Data-Driven Models for Real-Time Control of Polymer Electrolyte Membrane Fuel Cells. Energy AI 2021, 6, 100114. [Google Scholar] [CrossRef]
- Zheng, Z.; Petrone, R.; Péra, M.C.; Hissel, D.; Becherif, M.; Pianese, C.; Yousfi Steiner, N.; Sorrentino, M. A Review on Non-Model Based Diagnosis Methodologies for PEM Fuel Cell Stacks and Systems. Int. J. Hydrogen Energy 2013, 38, 8914–8926. [Google Scholar] [CrossRef]
- Hua, Z.; Zheng, Z.; Pahon, E.; Péra, M.C.; Gao, F. A Review on Lifetime Prediction of Proton Exchange Membrane Fuel Cells System. J. Power Sources 2022, 529, 231256. [Google Scholar] [CrossRef]
- Vichard, L.; Steiner, N.Y.; Zerhouni, N.; Hissel, D. Hybrid Fuel Cell System Degradation Modeling Methods: A Comprehensive Review. J. Power Sources 2021, 506, 230071. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, H.; Brandon, N.P. Gas Diffusion Layer Degradation in Proton Exchange Membrane Fuel Cells: Mechanisms, Characterization Techniques and Modelling Approaches. J. Power Sources 2021, 513, 230560. [Google Scholar] [CrossRef]
- Pan, M.; Pan, C.; Li, C.; Zhao, J. A Review of Membranes in Proton Exchange Membrane Fuel Cells: Transport Phenomena, Performance and Durability. Renew. Sustain. Energy Rev. 2021, 141, 110771. [Google Scholar] [CrossRef]
- Okonkwo, P.C.; Ben Belgacem, I.; Emori, W.; Uzoma, P.C. Nafion Degradation Mechanisms in Proton Exchange Membrane Fuel Cell (PEMFC) System: A Review. Int. J. Hydrogen Energy 2021, 46, 27956–27973. [Google Scholar] [CrossRef]
- Tzelepis, S.; Kavadias, K.A.; Marnellos, G.E.; Xydis, G. A Review Study on Proton Exchange Membrane Fuel Cell Electrochemical Performance Focusing on Anode and Cathode Catalyst Layer Modelling at Macroscopic Level. Renew. Sustain. Energy Rev. 2021, 151, 111543. [Google Scholar] [CrossRef]
- Dafalla, A.M.; Wei, L.; Habte, B.T.; Guo, J.; Jiang, F. Membrane Electrode Assembly Degradation Modeling of Proton Exchange Membrane Fuel Cells: A Review. Energies 2022, 15, 9247. [Google Scholar] [CrossRef]
- Raeesi, M.; Changizian, S.; Ahmadi, P.; Khoshnevisan, A. Performance Analysis of a Degraded PEM Fuel Cell Stack for Hydrogen Passenger Vehicles Based on Machine Learning Algorithms in Real Driving Conditions. Energy Convers. Manag. 2021, 248, 114793. [Google Scholar] [CrossRef]
- Nguyen, H.L.; Han, J.; Nguyen, X.L.; Yu, S.; Goo, Y.M.; Le, D.D. Review of the Durability of Polymer Electrolyte Membrane Fuel Cell in Long-Term Operation: Main Influencing Parameters and Testing Protocols. Energies 2021, 14, 4048. [Google Scholar] [CrossRef]
- Hissel, D.; Pera, M.C. Diagnostic & Health Management of Fuel Cell Systems: Issues and Solutions. Annu. Rev. Control 2016, 42, 201–211. [Google Scholar]
- Yu, S.; Jung, D. Thermal Management Strategy for a Proton Exchange Membrane Fuel Cell System with a Large Active Cell Area. Renew. Energy 2008, 33, 2540–2548. [Google Scholar] [CrossRef]
- Büchi, F.N.; Inaba, M.; Schmidt, T.J. Polymer Electrolyte Fuel Cell Durability; Springer: New York, NY, USA, 2009; ISBN 9780128114599. [Google Scholar]
- Jouin, M.; Bressel, M.; Morando, S.; Gouriveau, R.; Hissel, D.; Péra, M.C.; Zerhouni, N.; Jemei, S.; Hilairet, M.; Ould Bouamama, B. Estimating the End-of-Life of PEM Fuel Cells: Guidelines and Metrics. Appl. Energy 2016, 177, 87–97. [Google Scholar] [CrossRef]
- Mayur, M.; Gerard, M.; Schott, P.; Bessler, W.G. Lifetime Prediction of a Polymer Electrolyte Membrane Fuel Cell under Automotive Load Cycling Using a Physically-Based Catalyst Degradation Model. Energies 2018, 11, 2054. [Google Scholar] [CrossRef]
- Futter, G.A.; Latz, A.; Jahnke, T. Physical Modeling of Chemical Membrane Degradation in Polymer Electrolyte Membrane Fuel Cells: Influence of Pressure, Relative Humidity and Cell Voltage. J. Power Sources 2019, 410–411, 78–90. [Google Scholar] [CrossRef]
- Ferreira, R.B.; Falcão, D.S.; Pinto, A.M.F.R. Simulation of Membrane Chemical Degradation in a Proton Exchange Membrane Fuel Cell by Computational Fluid Dynamics. Int. J. Hydrogen Energy 2021, 46, 1106–1120. [Google Scholar] [CrossRef]
- Singh, R.; Sui, P.C.; Wong, K.H.; Kjeang, E.; Knights, S.; Djilali, N. Modeling the Effect of Chemical Membrane Degradation on PEMFC Performance. J. Electrochem. Soc. 2018, 165, F3328–F3336. [Google Scholar] [CrossRef]
- Hasan, M.; Chen, J.; Waldecker, J.R.; Santare, M.H. Predicting Fatigue Lifetimes of a Reinforced Membrane in Polymer Electrolyte Membrane Fuel Cell Using Plastic Energy. J. Power Sources 2022, 539, 231597. [Google Scholar] [CrossRef]
- Zhou, X.; Qiu, D.; Peng, L.; Lai, X. Numerical and Experimental Characterization of Gas Permeation through Membranes with Consideration of Mechanical Degradation in Proton Exchange Membrane Fuel Cells. J. Power Sources 2023, 556, 232489. [Google Scholar] [CrossRef]
- Zhang, X.; Pisu, P. Prognostic-Oriented Fuel Cell Catalyst Aging Modeling and Its Application to Health-Monitoring and Prognostics of a PEM Fuel Cell. Int. J. Progn. Health Manag. 2014, 5, 1–16. [Google Scholar] [CrossRef]
- Darling, R.M.; Meyers, J.P. Kinetic Model of Platinum Dissolution in PEMFCs. J. Electrochem. Soc. 2003, 150, A1523. [Google Scholar] [CrossRef]
- Li, Y.; Moriyama, K.; Gu, W.; Arisetty, S.; Wang, C.Y. A One-Dimensional Pt Degradation Model for Polymer Electrolyte Fuel Cells. J. Electrochem. Soc. 2015, 162, F834–F842. [Google Scholar] [CrossRef]
- Holby, E.F.; Morgan, D. Application of Pt Nanoparticle Dissolution and Oxidation Modeling to Understanding Degradation in PEM Fuel Cells. J. Electrochem. Soc. 2012, 159, B578–B591. [Google Scholar] [CrossRef]
- Polverino, P.; Pianese, C. Model-Based Prognostic Algorithm for Online RUL Estimation of PEMFCs. In Proceedings of the 2016 3rd Conference on Control and Fault-Tolerant Systems (SysTol), Barcelona, Spain, 7–9 September 2016; IEEE Computer Society: Washington, DC, USA, 2016; pp. 599–604. [Google Scholar]
- Koltsiva, E.M.; Vasilenko, V.A.; Shcherbakov, A.I.; Fokina, E.A.; Bogdanovskaya, V.A. Mathematical Simulation of PEMFC Platinum Cathode Degradation Accounting Catalyst’s Nanoparticles Growth. Chem. Eng. Trans. 2018, 70, 1303–1308. [Google Scholar] [CrossRef]
- Jahnke, T.; Baricci, A.; Rabissi, C.; Casalegno, A. Erratum: Physical Modeling of Catalyst Degradation in Low Temperature Fuel Cells: Platinum Oxidation, Dissolution, Particle Growth and Platinum Band Formation [J. Electrochem. Soc., 167, 013523 (2020)]. J. Electrochem. Soc. 2020, 167, 149001. [Google Scholar] [CrossRef]
- Moein-Jahromi, M.; Kermani, M.J. Three-Dimensional Multiphase Simulation and Multi-Objective Optimization of PEM Fuel Cells Degradation under Automotive Cyclic Loads. Energy Convers. Manag. 2021, 231, 113837. [Google Scholar] [CrossRef]
- Zheng, W.; Xu, L.; Hu, Z.; Zhao, Y.; Li, J.; Ouyang, M. Dynamic Modeling of Pt Degradation and Mitigation Strategies in Polymer Electrolyte Membrane Fuel Cells. eTransportation 2022, 12, 100171. [Google Scholar] [CrossRef]
- Tang, M.; Zhang, S.; Chen, S. Pt Utilization in Proton Exchange Membrane Fuel Cells: Structure Impacting Factors and Mechanistic Insights. Chem. Soc. Rev. 2022, 51, 1529–1546. [Google Scholar] [CrossRef]
- Tang, M.; Shan, Q.; Liu, Y.; Chen, S. Pt Loading-Dependent Transport Kinetics and Effectiveness of Pt in Proton Exchange Membrane Fuel Cells. J. Power Sources 2023, 567, 232966. [Google Scholar] [CrossRef]
- Jahnke, T.; Futter, G.; Latz, A.; Malkow, T.; Papakonstantinou, G.; Tsotridis, G.; Schott, P.; Gérard, M.; Quinaud, M.; Quiroga, M.; et al. Performance and Degradation of Proton Exchange Membrane Fuel Cells: State of the Art in Modeling from Atomistic to System Scale. J. Power Sources 2016, 304, 207–233. [Google Scholar] [CrossRef]
- Li, H.; Zhao, H.; Tao, B.; Xu, G.; Gu, S.; Wang, G.; Chang, H. Pt-Based Oxygen Reduction Reaction Catalysts in Proton Exchange Membrane Fuel Cells: Controllable Preparation and Structural Design of Catalytic Layer. Nanomaterials 2022, 12, 4173. [Google Scholar] [CrossRef]
- Seidenberger, K.; Wilhelm, F.; Schmitt, T.; Lehnert, W.; Scholta, J. Estimation of Water Distribution and Degradation Mechanisms in Polymer Electrolyte Membrane Fuel Cell Gas Diffusion Layers Using a 3D Monte Carlo Model. J. Power Sources 2011, 196, 5317–5324. [Google Scholar] [CrossRef]
- Pauchet, J.; Prat, M.; Schott, P.; Kuttanikkad, S.P. Performance Loss of Proton Exchange Membrane Fuel Cell Due to Hydrophobicity Loss in Gas Diffusion Layer: Analysis by Multiscale Approach Combining Pore Network and Performance Modelling. Int. J. Hydrogen Energy 2012, 37, 1628–1641. [Google Scholar] [CrossRef]
- Pei, P.; Chang, Q.; Tang, T. A Quick Evaluating Method for Automotive Fuel Cell Lifetime. Int. J. Hydrogen Energy 2008, 33, 3829–3836. [Google Scholar] [CrossRef]
- Chen, H.; Pei, P.; Song, M. Lifetime Prediction and the Economic Lifetime of Proton Exchange Membrane Fuel Cells. Appl. Energy 2015, 142, 154–163. [Google Scholar] [CrossRef]
- Jouin, M.; Gouriveau, R.; Hissel, D.; Péra, M.C.; Zerhouni, N. Prognostics of PEM Fuel Cell in a Particle Filtering Framework. Int. J. Hydrogen Energy 2014, 39, 481–494. [Google Scholar] [CrossRef]
- Jouin, M.; Gouriveau, R.; Hissel, D.; Péra, M.-C.; Zerhouni, N.; Member, S.; Zerhouni Member, N. Joint Particle Filters Prognostics for PEMFC Power Prediction at Constant Current Solicitation. IEEE Trans. Reliab. 2016, 65, 336–349. [Google Scholar] [CrossRef]
- Chen, K.; Laghrouche, S.; Djerdir, A. Fuel Cell Health Prognosis Using Unscented Kalman Filter: Postal Fuel Cell Electric Vehicles Case Study. Int. J. Hydrogen Energy 2019, 44, 1930–1939. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, Y.; Sun, C. Remaining Useful Life Prediction for Proton Exchange Membrane Fuel Cell Using Stochastic Fusion Filtering. IFAC PapersOnLine 2018, 51, 158–162. [Google Scholar] [CrossRef]
- Jouin, M.; Gouriveau, R.; Hissel, D.; Péra, M.C.; Zerhouni, N. Degradations Analysis and Aging Modeling for Health Assessment and Prognostics of PEMFC. Reliab. Eng. Syst. Saf. 2016, 148, 78–95. [Google Scholar] [CrossRef]
- Sharaf, O.Z.; Orhan, M.F. An Overview of Fuel Cell Technology: Fundamentals and Applications. Renew. Sustain. Energy Rev. 2014, 32, 810–853. [Google Scholar] [CrossRef]
- Zhou, D.; Wu, Y.; Gao, F.; Breaz, E.; Ravey, A.; Miraoui, A. Degradation Prediction of PEM Fuel Cell Stack Based on Multiphysical Aging Model with Particle Filter Approach. IEEE Trans. Ind. Appl. 2017, 53, 4041–4052. [Google Scholar] [CrossRef]
- Bressel, M.; Hilairet, M.; Hissel, D.; Ould Bouamama, B. Extended Kalman Filter for Prognostic of Proton Exchange Membrane Fuel Cell. Appl. Energy 2016, 164, 220–227. [Google Scholar] [CrossRef]
- Yue, M.; Li, Z.; Roche, R.; Jemei, S.; Zerhouni, N. Degradation Identification and Prognostics of Proton Exchange Membrane Fuel Cell under Dynamic Load. Control Eng. Pract. 2022, 118, 104959. [Google Scholar] [CrossRef]
- Wang, P.; Liu, H.; Chen, J.; Qin, X.; Lehnert, W.; Shao, Z.; Li, R. A Novel Degradation Model of Proton Exchange Membrane Fuel Cells for State of Health Estimation and Prognostics. Int. J. Hydrogen Energy 2021, 46, 31353–31361. [Google Scholar] [CrossRef]
- Bressel, M.; Hilairet, M.; Hissel, D.; Ould Bouamama, B. Remaining Useful Life Prediction and Uncertainty Quantification of Proton Exchange Membrane Fuel Cell under Variable Load. IEEE Trans. Ind. Electron. 2016, 63, 2569–2577. [Google Scholar] [CrossRef]
- Zhang, D.; Baraldi, P.; Cadet, C.; Yousfi-Steiner, N.; Bérenguer, C.; Zio, E. An Ensemble of Models for Integrating Dependent Sources of Information for the Prognosis of the Remaining Useful Life of Proton Exchange Membrane Fuel Cells. Mech. Syst. Signal. Process. 2019, 124, 479–501. [Google Scholar] [CrossRef]
- Mao, L.; Jackson, L.; Jackson, T. Investigation of Polymer Electrolyte Membrane Fuel Cell Internal Behaviour during Long Term Operation and Its Use in Prognostics. J. Power Sources 2017, 362, 39–49. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, K.; Zhao, H.; Li, J.; Sheng, X.; Yin, Y.; Du, Q.; Zu, B.; Han, L.; Jiao, K. Degradation Prediction of Proton Exchange Membrane Fuel Cell Stack Using Semi-Empirical and Data-Driven Methods. Energy AI 2023, 11, 100205. [Google Scholar] [CrossRef]
- Ohenoja, M.; Leiviskä, K. Observations on the Parameter Estimation Problem of Polymer Electrolyte Membrane Fuel Cell Polarization Curves. Fuel Cells 2020, 20, 516–526. [Google Scholar] [CrossRef]
- Pan, R.; Yang, D.; Wang, Y.; Chen, Z. Performance Degradation Prediction of Proton Exchange Membrane Fuel Cell Using a Hybrid Prognostic Approach. Int. J. Hydrogen Energy 2020, 45, 30994–31008. [Google Scholar] [CrossRef]
- Shahraki, A.F.; Parkash Yadav, O.; Liao, H. A Review on Degradation Modelling and Its Engineering Applications. Int. J. Perform. Eng. 2017, 13, 299–314. [Google Scholar] [CrossRef]
- Chen, K.; Laghrouche, S.; Djerdir, A. Degradation Prediction of Proton Exchange Membrane Fuel Cell Based on Grey Neural Network Model and Particle Swarm Optimization. Energy Convers. Manag. 2019, 195, 810–818. [Google Scholar] [CrossRef]
- Chen, K.; Laghrouche, S.; Djerdir, A. Aging Prognosis Model of Proton Exchange Membrane Fuel Cell in Different Operating Conditions. Int. J. Hydrogen Energy 2020, 45, 11761–11772. [Google Scholar] [CrossRef]
- Chen, K.; Laghrouche, S.; Djerdir, A. Health State Prognostic of Fuel Cell Based on Wavelet Neural Network and Cuckoo Search Algorithm. ISA Trans. 2021, 113, 175–184. [Google Scholar] [CrossRef] [PubMed]
- Ma, R.; Yang, T.; Breaz, E.; Li, Z.; Briois, P.; Gao, F. Data-Driven Proton Exchange Membrane Fuel Cell Degradation Predication through Deep Learning Method. Appl. Energy 2018, 231, 102–115. [Google Scholar] [CrossRef]
- Theodoridis, S. Neural Networks and Deep Learning. In Machine Learning, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 901–1038. [Google Scholar] [CrossRef]
- Liu, J.; Li, Q.; Chen, W.; Yan, Y.; Qiu, Y.; Cao, T. Remaining Useful Life Prediction of PEMFC Based on Long Short-Term Memory Recurrent Neural Networks. Int. J. Hydrogen Energy 2019, 44, 5470–5480. [Google Scholar] [CrossRef]
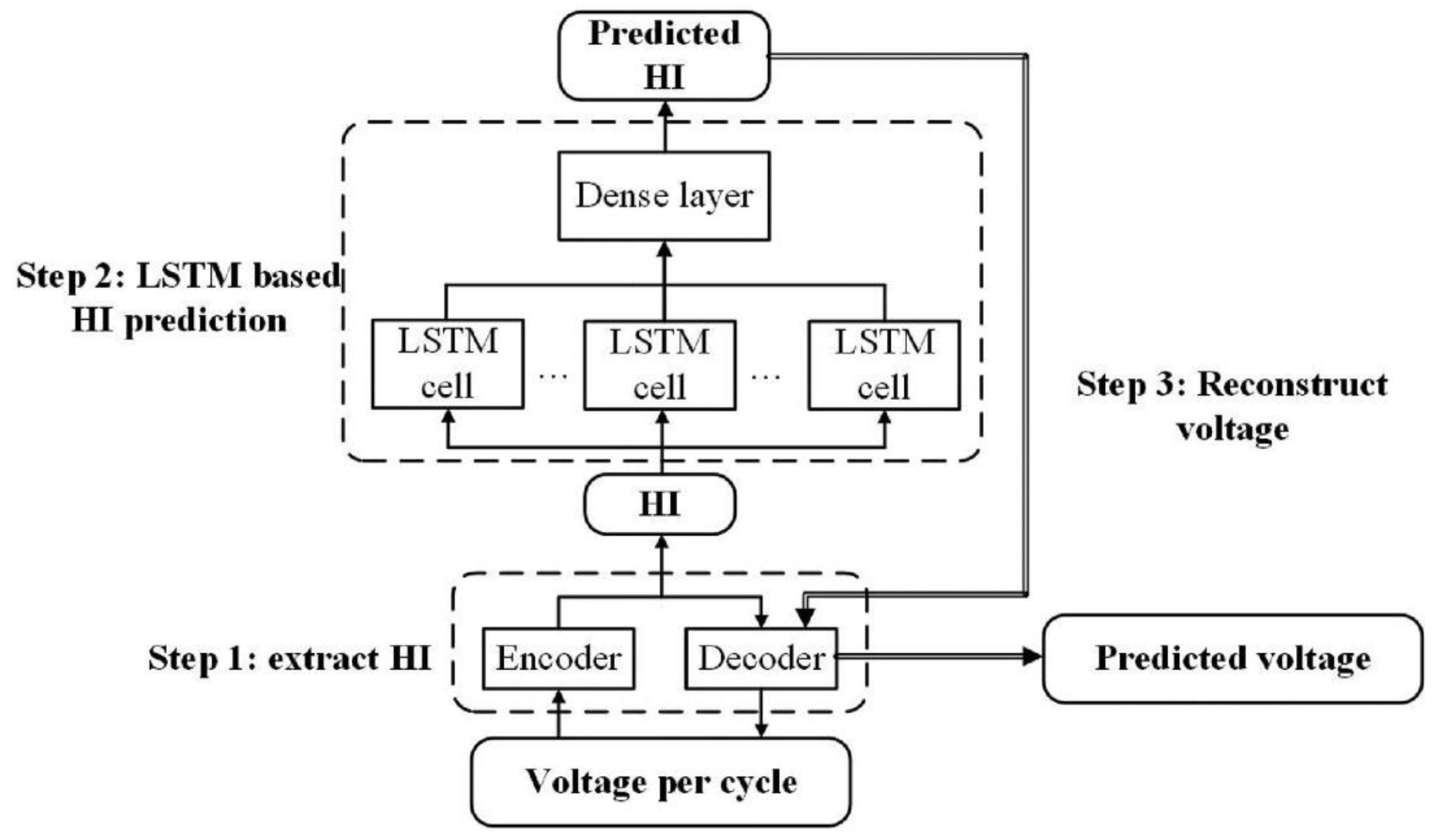
- He, K.; Liu, Z.; Sun, Y.; Mao, L.; Lu, S. Degradation Prediction of Proton Exchange Membrane Fuel Cell Using Auto-Encoder Based Health Indicator and Long Short-Term Memory Network. Int. J. Hydrogen Energy 2022, 47, 35055–35067. [Google Scholar] [CrossRef]
- Zuo, B.; Cheng, J.; Zhang, Z. Degradation Prediction Model for Proton Exchange Membrane Fuel Cells Based on Long Short-Term Memory Neural Network and Savitzky-Golay Filter. Int. J. Hydrogen Energy 2021, 46, 15928–15937. [Google Scholar] [CrossRef]
- Yezerska, K.; Dushina, A.; Sarabakha, A.; Wagner, P.; Dyck, A.; Wark, M. Model-Based Degradation Prediction on Impedance Data and Artificial Neural Network for High-Temperature Polymer Electrolyte Membrane Fuel Cells after Hydrogen Starvation. Int. J. Hydrogen Energy 2022, 47, 29495–29504. [Google Scholar] [CrossRef]
- Wang, C.; Li, Z.; Outbib, R.; Dou, M.; Zhao, D. A Novel Long Short-Term Memory Networks-Based Data-Driven Prognostic Strategy for Proton Exchange Membrane Fuel Cells. Int. J. Hydrogen Energy 2022, 47, 10395–10408. [Google Scholar] [CrossRef]
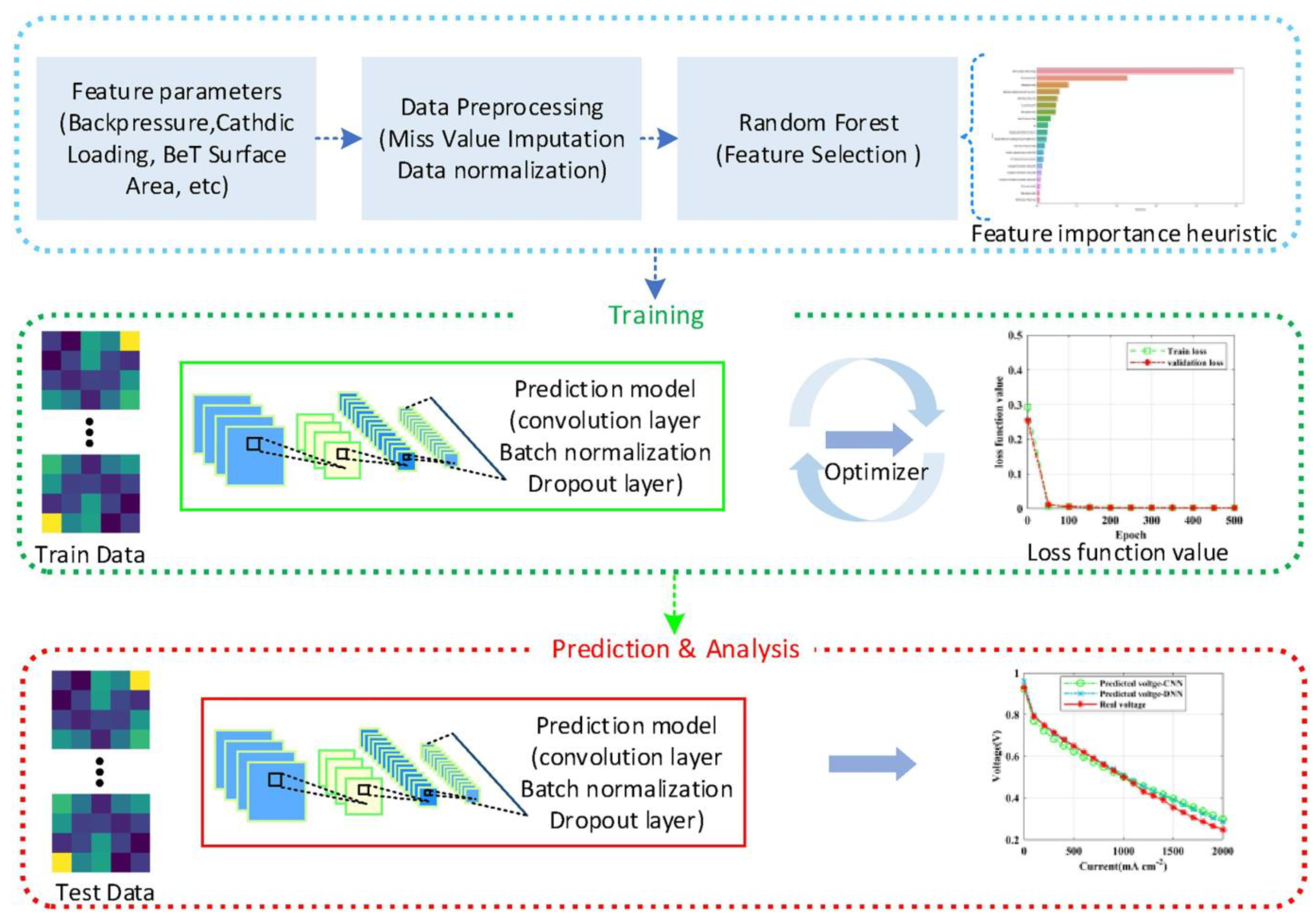
- Huo, W.; Li, W.; Zhang, Z.; Sun, C.; Zhou, F.; Gong, G. Performance Prediction of Proton-Exchange Membrane Fuel Cell Based on Convolutional Neural Network and Random Forest Feature Selection. Energy Convers. Manag. 2021, 243, 114367. [Google Scholar] [CrossRef]
- Benaggoune, K.; Yue, M.; Jemei, S.; Zerhouni, N. A Data-Driven Method for Multi-Step-Ahead Prediction and Long-Term Prognostics of Proton Exchange Membrane Fuel Cell. Appl. Energy 2022, 313, 118835. [Google Scholar] [CrossRef]
- Wilberforce, T.; Alaswad, A.; Garcia–Perez, A.; Xu, Y.; Ma, X.; Panchev, C. Remaining Useful Life Prediction for Proton Exchange Membrane Fuel Cells Using Combined Convolutional Neural Network and Recurrent Neural Network. Int. J. Hydrogen Energy 2022, 48, 291–303. [Google Scholar] [CrossRef]
- Sun, B.; Liu, X.; Wang, J.; Wei, X.; Yuan, H.; Dai, H. Short-Term Performance Degradation Prediction of a Commercial Vehicle Fuel Cell System Based on CNN and LSTM Hybrid Neural Network. Int. J. Hydrogen Energy 2022, 48, 8613–8628. [Google Scholar] [CrossRef]
- Morando, S.; Jemei, S.; Hissel, D.; Gouriveau, R.; Zerhouni, N. ANOVA Method Applied to Proton Exchange Membrane Fuel Cell Ageing Forecasting Using an Echo State Network. Math. Comput. Simul. 2017, 131, 283–294. [Google Scholar] [CrossRef]
- Mezzi, R.; Yousfi-Steiner, N.; Péra, M.C.; Hissel, D.; Larger, L. An Echo State Network for Fuel Cell Lifetime Prediction under a Dynamic Micro-Cogeneration Load Profile. Appl. Energy 2021, 283, 116297. [Google Scholar] [CrossRef]
- Morando, S.; Jemei, S.; Hissel, D.; Gouriveau, R.; Zerhouni, N. Proton Exchange Membrane Fuel Cell Ageing Forecasting Algorithm Based on Echo State Network. Int. J. Hydrogen Energy 2017, 42, 1472–1480. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, T.; Xiao, F.; Zhang, R. Degradation Prediction Model of PEMFC Based on Multi-Reservoir Echo State Network with Mini Reservoir. Int. J. Hydrogen Energy 2022, 47, 40026–40040. [Google Scholar] [CrossRef]
- Hua, Z.; Zheng, Z.; Péra, M.C.; Gao, F. Remaining Useful Life Prediction of PEMFC Systems Based on the Multi-Input Echo State Network. Appl. Energy 2020, 265, 114791. [Google Scholar] [CrossRef]
- Han, I.S.; Chung, C.B. Performance Prediction and Analysis of a PEM Fuel Cell Operating on Pure Oxygen Using Data-Driven Models: A Comparison of Artificial Neural Network and Support Vector Machine. Int. J. Hydrogen Energy 2016, 41, 10202–10211. [Google Scholar] [CrossRef]
- Legala, A.; Zhao, J.; Li, X. Machine Learning Modeling for Proton Exchange Membrane Fuel Cell Performance. Energy AI 2022, 10, 100183. [Google Scholar] [CrossRef]
- Wu, Y.; Breaz, E.; Gao, F.; Miraoui, A. A Modified Relevance Vector Machine for PEM Fuel-Cell Stack Aging Prediction. IEEE Trans. Ind. Appl. 2016, 52, 2573–2581. [Google Scholar] [CrossRef]
- Wu, Y.; Breaz, E.; Gao, F.; Paire, D.; Miraoui, A. Nonlinear Performance Degradation Prediction of Proton Exchange Membrane Fuel Cells Using Relevance Vector Machine. IEEE Trans. Energy Convers. 2016, 31, 1570–1582. [Google Scholar] [CrossRef]
- Chen, K.; Badji, A.; Laghrouche, S.; Djerdir, A. Polymer Electrolyte Membrane Fuel Cells Degradation Prediction Using Multi-Kernel Relevance Vector Regression and Whale Optimization Algorithm. Appl. Energy 2022, 318, 119099. [Google Scholar] [CrossRef]
- Rubio, G.A.; Agila, W.E. A Fuzzy Model to Manage Water in Polymer Electrolyte Membrane Fuel Cells. Processes 2021, 9, 904. [Google Scholar] [CrossRef]
- Mammar, K.; Saadaoui, F.; Laribi, S. Design of a PEM Fuel Cell Model for Flooding and Drying Diagnosis Using Fuzzy Logic Clustering. Renew. Energy Focus 2019, 30, 123–130. [Google Scholar] [CrossRef]
- Rezazadeh, S.; Mehrabi, M.; Pashaee, T.; Mirzaee, I. Using Adaptive Neuro-Fuzzy Inference System (ANFIS) for Proton Exchange Membrane Fuel Cell (PEMFC) Performance Modeling. J. Mech. Sci. Technol. 2012, 26, 3701–3709. [Google Scholar] [CrossRef]
- Wilberforce, T.; Olabi, A.G. Performance Prediction of Proton Exchange Membrane Fuel Cells (PEMFC) Using Adaptive Neuro Inference System (ANFIS). Sustainability 2020, 12, 4952. [Google Scholar] [CrossRef]
- Silva, R.E.; Gouriveau, R.; Jemeï, S.; Hissel, D.; Boulon, L.; Agbossou, K.; Yousfi Steiner, N. Proton Exchange Membrane Fuel Cell Degradation Prediction Based on Adaptive Neuro-Fuzzy Inference Systems. Int. J. Hydrogen Energy 2014, 39, 11128–11144. [Google Scholar] [CrossRef]
- Liu, H.; Chen, J.; Hissel, D.; Su, H. Short-Term Prognostics of PEM Fuel Cells: A Comparative and Improvement Study. IEEE Trans. Ind. Electron. 2019, 66, 6077–6086. [Google Scholar] [CrossRef]
- Sun, K.; Esnaola, I.; Okorie, O.; Charnley, F.; Moreno, M.; Tiwari, A. Data-Driven Modeling and Monitoring of Fuel Cell Performance. Int. J. Hydrogen Energy 2021, 46, 33206–33217. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, J. Prognostics of PEM Fuel Cells Based on Gaussian Process State Space Models. Energy 2018, 149, 63–73. [Google Scholar] [CrossRef]
- Tang, L.; Yang, X.; Gao, J.J.; Huang, J.; Cui, J.R. Adaptive Gaussian Process Regression Based Remaining Useful Life Prediction of PEMFC Incorporating an Improved Health Indicator. In Proceedings of the 2022 IEEE 11th Data Driven Control and Learning Systems Conference, DDCLS 2022, Chengdu, China, 3–5 August 2022; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2022; pp. 1080–1085. [Google Scholar]
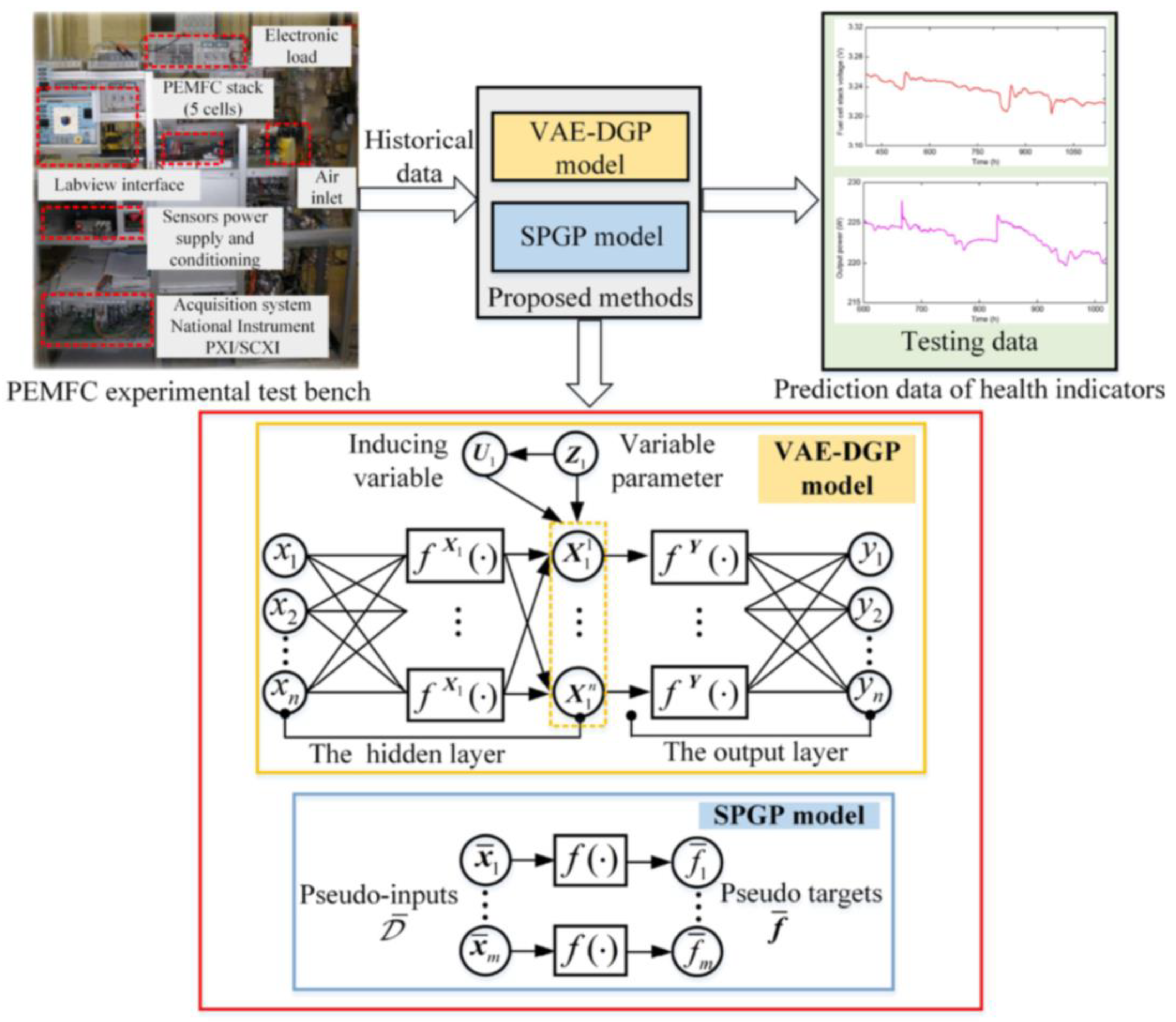
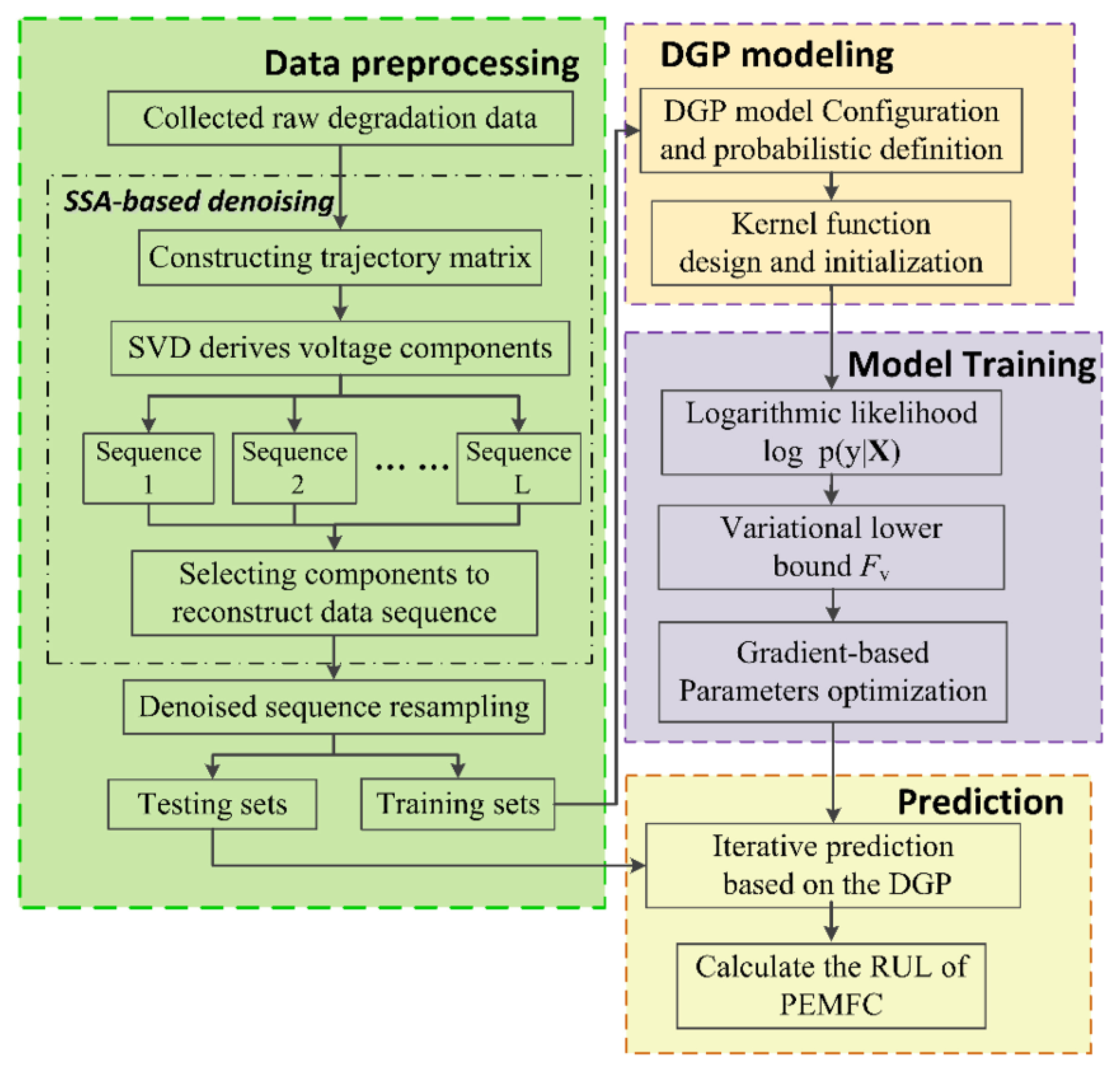
- Xie, Y.; Zou, J.; Peng, C.; Zhu, Y.; Gao, F. A Novel PEM Fuel Cell Remaining Useful Life Prediction Method Based on Singular Spectrum Analysis and Deep Gaussian Processes. Int. J. Hydrogen Energy 2020, 45, 30942–30956. [Google Scholar] [CrossRef]
- Deng, H.; Hu, W.; Cao, D.; Chen, W.; Huang, Q.; Chen, Z.; Blaabjerg, F. Degradation Trajectories Prognosis for PEM Fuel Cell Systems Based on Gaussian Process Regression. Energy 2022, 244, 122569. [Google Scholar] [CrossRef]
- Zhou, D.; Al-Durra, A.; Zhang, K.; Ravey, A.; Gao, F. Online Remaining Useful Lifetime Prediction of Proton Exchange Membrane Fuel Cells Using a Novel Robust Methodology. J. Power Sources 2018, 399, 314–328. [Google Scholar] [CrossRef]
- Wang, C.; Dou, M.; Li, Z.; Outbib, R.; Zhao, D.; Liang, B. A Fusion Prognostics Strategy for Fuel Cells Operating under Dynamic Conditions. eTransportation 2022, 12, 100166. [Google Scholar] [CrossRef]
- Cheng, Y.; Zerhouni, N.; Lu, C. A Hybrid Remaining Useful Life Prognostic Method for Proton Exchange Membrane Fuel Cell. Int. J. Hydrogen Energy 2018, 43, 12314–12327. [Google Scholar] [CrossRef]
- Liu, H.; Chen, J.; Hissel, D.; Su, H. Remaining Useful Life Estimation for Proton Exchange Membrane Fuel Cells Using a Hybrid Method. Appl. Energy 2019, 237, 910–919. [Google Scholar] [CrossRef]
- Zhou, D.; Gao, F.; Breaz, E.; Ravey, A.; Miraoui, A. Degradation Prediction of PEM Fuel Cell Using a Moving Window Based Hybrid Prognostic Approach. Energy 2017, 138, 1175–1186. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, H.-L.; Lee, S.-M.; Yu, S. A Comprehensive Review of Degradation Prediction Methods for an Automotive Proton Exchange Membrane Fuel Cell. Energies 2023, 16, 4772. https://doi.org/10.3390/en16124772
Nguyen H-L, Lee S-M, Yu S. A Comprehensive Review of Degradation Prediction Methods for an Automotive Proton Exchange Membrane Fuel Cell. Energies. 2023; 16(12):4772. https://doi.org/10.3390/en16124772
Chicago/Turabian StyleNguyen, Huu-Linh, Sang-Min Lee, and Sangseok Yu. 2023. "A Comprehensive Review of Degradation Prediction Methods for an Automotive Proton Exchange Membrane Fuel Cell" Energies 16, no. 12: 4772. https://doi.org/10.3390/en16124772
APA StyleNguyen, H.-L., Lee, S.-M., & Yu, S. (2023). A Comprehensive Review of Degradation Prediction Methods for an Automotive Proton Exchange Membrane Fuel Cell. Energies, 16(12), 4772. https://doi.org/10.3390/en16124772