1. Introduction
The phenomenon of climate change is having an increasing impact on everyday life, as can be seen from the rising average temperatures and number of extreme meteorological events. While future scenarios are looking dire [
1], it is encouraging to see that awareness on the matter has been generally increasing—especially among young generations, who are worried by long-term impact of climate change [
2]—as has the acceptance that fighting against climate change requires combined actions of individuals to be successful [
3]. Mobility plays and will play an important role in the climate change fight: transportation accounts for more than one-quarter of CO
2 emissions worldwide [
4] and is particularly relevant in the EU, where its share of CO
2 is 45% [
5]. However, car commuters are not willing to change their habits and move to public transportation or bike [
6], with a 70% share not willing to renounce to their own car for the daily commute. The attitude toward private transportation, paired with the awareness of the climate change issue, makes a fertile terrain for the penetration of electric vehicles (EVs). This technology, however, presents severe limitations in terms of costs, charging time and range.
It is indeed well known that while the higher cost is still a major factor, even potential buyers who could afford to purchase an EV are nevertheless discouraged because of the so-called range anxiety [
7], i.e., the fear of exhausting the battery during travel before reaching the destination. To mitigate the effects of this phenomenon, it is possible to install larger batteries to increase the range of the vehicle and to position more charging stations. In the current scenario, the long time to recharge along with the small number of stations opens a major role for prior route planning and station selection in order to build a more confident attitude toward EVs in traditional car users.
Car manufactures make free planners available online; these include Tesla’s “Go Anywhere” [
8], Volkswagen’s “E-route planner” [
9] and Porsche’s “Charge Map” [
10]. Third party developers offer similar free services, such as “EVNavigation” [
11], “ABRP: A Better Route Planner” [
12], “Zap Map” [
13] or “PlugShare” [
14]. It is obvious that route planners must be robust and reliable in order to improve the trust of car users in EVs. As a matter of fact, for route planning to be reliable, several aspects have to be taken into consideration, such as battery degradation through aging, cabin heating and cooling, driving style, traffic conditions, number of passengers and road grading.
To obtain robust solutions, a verification on the reachability of the charging stations is needed. A simple approach is to perform a check between the road distance from the station and the range of the vehicle, reduced by a factor related to the vehicle speed [
15]. Other solutions are based on the computation of the energy needed to reach the station either through the definition of an energy-per-distance factor per every road segment of the route according to the speed [
16] or through the estimation of the resisting power contributions (drag, rolling resistance, slope) [
17]. More accurate estimations of the energy consumption are presented in [
18,
19,
20]—although only the latter of the three uses the energy estimation to perform route planning, while the other two use it to depict the set of points that are reachable by an EV. However, the planner proposed by [
20] bases the energy estimation on statistical data to define speed and acceleration profiles and therefore does not account for the driving style of the user, a factor which heavily influences vehicle range.
An additional aspect that plays a major role is cabin conditioning, which strictly depends on weather. Indeed, both low and high temperatures severely reduce the range of EVs through the increase in power demand linked to the activation of heating, ventilation and air conditioning (HVAC) systems [
20]. While traditional vehicles can warm the cabin with heat from the internal combustion engine (ICE), EVs are forced to draw power from the battery. Another considerable factor is the availability of charging stations.
The aforementioned charging time and station scarcity compared to gas pumps require that this factor be considered in planning a route for an EV. It is possible that the stations which are selected as best by the route planner are occupied upon arrival, causing a significant waiting time for the user. The influence of this factor is already well known and considered in the literature: the route planning approach proposed in [
17] exploits real-time knowledge of which charging stations are occupied, current SoC of the vehicle charging and charging power. The planner is able to predict when occupied chargers will be free and can use this information to plan the best route in terms of minimum total time. A similar approach is used in [
21], with the difference being that information does not come from the real-time monitoring of charging stations but from the EVs themselves, which announce to a central database their desire to recharge at a specific station at a particular time.
None of the planners present in the literature, however, mention the effect of the battery’s state of health (SoH) degradation and driving style on EV range. It is therefore evident that in the current state of the art, a solution considering all these range-reducing factors and accounting for station occupancy is missing.
To fill this gap, the route planning proposed in this paper aims at providing a tool to consider the main factors affecting EV range, such as battery SoH, external temperature, number of passengers, driving style and station occupancy. These factors are considered as follows: (a) battery SoH through reduction of battery capacity and increase of its internal resistance, (b) external temperature through the definition of additional power required by the HVAC system, (c) number of passengers through the increase in vehicle mass and adjustments on HVAC working, (d) driving style through vehicle speed and acceleration, and (e) station occupancy through emulation of a live availability checking system.
Besides the combination of all range affecting factors, which in themselves represent a novel approach, additional innovative aspects with respect to the current literature are proposed. The first one is related to route selection. Conventional planners are based on the Dijkstra algorithm [
22] as a solution to generate the best route. However, this algorithm does not consider energetic aspects: it is not verified that the energy on board is sufficient to reach the selected station. To overcome this limitation and increase planning reliability and robustness, in the technique proposed in this paper, the Dijkstra algorithm is complemented with a routine comparing the energy available on the vehicle with the energy needed to reach the stations. The route is built as a series of subroutes connecting the selected stations, and Dijkstra’s algorithm is used only to find the fastest route to each station.
The method for the selection of the stations themselves represents a further novelty proposed by this paper. This problem is typically solved in the literature by searching for stations around the direct nonstop route, hereinafter defined as the "Baseline route”, in two ways. One is to look only at stations in the radius of 5 km from the Baseline route [
15], another is to suggest the best stations in a close range when the battery SoC falls below a specific threshold during the trip [
23]. These strategies aim at reducing, as much as possible, the time lost by leaving the main road [
24] but present the following drawbacks: (1) after having left the main route to reach a charging station, it might be more convenient to take a completely new route instead of driving back to the Baseline as done by [
15]; (2) for range anxiety reasons, EV users would not accept driving until the car finds a suitable charging station, as proposed by [
23], but want to plan stops before starting. To overcome these issues, the proposed solution uses a reward function which considers battery SoC, charging station power, distance between the stop and the Baseline route and energy consumption to reach the station. Moreover, after the selection of each station, the route is recomputed to evaluate whether it is convenient to drive back to the previous best route.
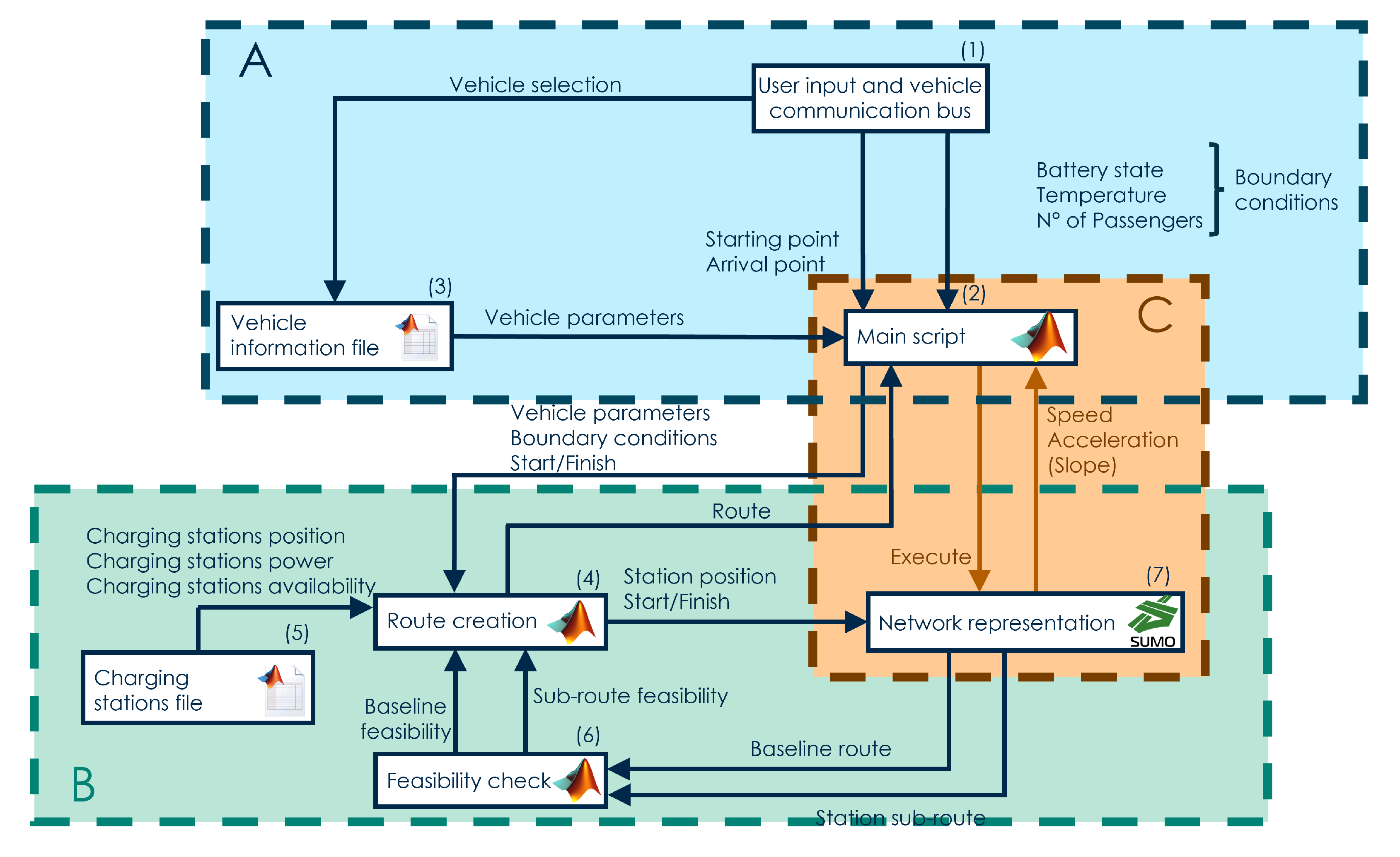
The proposed approach is tested in simulation by means of a framework which results from the interaction between Matlab and Simulation of Urban MObility (SUMO) [
25]. SUMO is an open-source, microscopic and continuous traffic simulation package designed to handle large networks and was developed by the German Aerospace Center [
26]. It is used here to generate possible routes between starting and arrival point and perform the simulation needed to evaluate the selected route. The evaluation of the proposed method’s effectiveness for devising the resulting route considers two metrics: (a) number of cases in which travel is conducted successfully, i.e., the condition in which battery SoC is always above the lower SoC threshold set by the user; and (b) the amount by which SoC violates this threshold. Tests were conducted that considered a set of eight couples of starting and arrival points and eighteen boundary condition configurations. These configurations included 3 different vehicle classes: (a) a grand touring sedan, (b) a small city car, and (c) a compact SUV. The impact of the energetic considerations on route planning reliability was measured by comparing the results of the proposed planner with those of standard planner that selects charging stations based on the nominal range. Obtained results show that the first metric moves from 44% (standard) to 93% (proposed method). The second moves from −13.1% (standard) to −1.1% (proposed method).
To summarize, the contributions offered by this paper are as follows: (a) the introduction in route planning of the combination of range-affecting factors including battery SoH, number of passengers, HVAC consumption, driving style and charging station occupancy; (b) improvement of planning reliability and robustness through completion of the Dijkstra algorithm with a routine comparing the energy available on the vehicle with the energy needed to reach the stations; and (c) a novel station selection method to minimize time loss through a cost function that rewards stations close to the route and at high charging power.
The paper is organized as follows:
Section 2 explains the methodology followed in the route planner definition;
Section 3 presents the algorithms for route generation and charging stations selection;
Section 4 explains the evaluation phase design through the selection of the travel missions;
Section 5 presents the obtained results;
Section 6 closes the paper with the conclusions drawn from the results.
4. Travel Mission Dataset and Route Evaluation Procedure
A travel mission is defined as the union of starting and arrival points and boundary conditions (temperature, number of passengers, battery SoH, battery SoC threshold, driving style). The dataset of missions is the result of the combination of eight pairs and eighteen boundary condition configurations.
The set of starting–arrival points, listed below, are selected to be as far as possible so that EVs need to stop at least once to recharge, with the exception of direction H, which is built to verify that the planner recognizes when the Baseline direct route is feasible.
case A: (45.544 N, 10.212 E)–(44.310 N, 8.485 E). Length: 256 km.
case B: (44.396 N, 7.555 E)–(45.707 N, 9.765 E). Length: 304 km.
case C: (44.809 N, 10.323 E)–(45.706 N, 7.675 E). Length: 277 km.
case D: (45.065 N, 7.673 E)–(44.332 N, 9.332 E). Length: 199 km.
case E: (45.142 N, 10.034 E)–(45.111 N, 7.299 E). Length: 245 km.
case F: (45.556 N, 8.067 E)–(44.285 N, 10.301 E). Length: 319 km.
case G: (45.470 N, 7.878 E)–(44.298 N, 8.467 E). Length: 194 km.
case H: (45.057 N, 9.701 E)–(45.439 N, 8.631 E). Length: 122 km.
The
couple positions in the network are shown in
Figure 3.
The eighteen boundary condition configurations are created with three different vehicles being considered: (1) vehicle A, a grand touring vehicle with 5 seats, weighing 2200 kg and with over 90 kWh of total battery energy; (2) vehicle B, a small city car with four seats, weighing 1200 kg and with around 30 kWh of battery energy; and (3) vehicle C, a small-sized SUV with five seats, weighing around 1500 kg and with over 50 kWh of battery energy. The configurations are designed to highlight the effects of the external temperature, battery SoH, number of passengers and driving style on the planned route. Moreover, as the grand touring vehicle and the compact SUV also offer also the possibility to perform a fast charge of the battery, three configurations highlight the impact of a station’s maximum charging power on the reward function. The boundary condition configurations are presented in
Table 3.
Planned routes are evaluated by means of two metrics. (a) The first is a classification on the feasibility of the planned route. This metric returns three possible results: (1) success, in which the route allows the vehicle to reach the destination respecting the constraint on the minimum SoC imposed by the user; (2) near miss, in which the route allows the vehicle to reach the destination, but the SoC falls below minimum SoC desired by the user, with bad effects on battery SoH; and (3) critical failure, in which the vehicle SoC falls below 0 during the travel and the route is unfeasible. (b) The second metric is the computation of the SoC violation when the first metric is a near miss by means of Equation (
9).
In critical failures, the amount of the violation is not meaningful since the battery is completely discharged, while in successes, there is no violation by definition. The metrics are obtained through a Matlab–SUMO cosimulation. The first simulates the vehicle to obtain the battery SoC profile, while the second simulates the network and retrieves vehicle speed and acceleration. First, the initial subroute is performed, and resistant forces acting on the vehicle are computed. Speed accounts for stops at crossroads, traffic lights and reduced speed on sharp turns, differently from what happens in the feasibility check previously described. Once the vehicle reaches the desired station, the subroute is completed, and the recharge routine is performed. The simulation proceeds with the following subroutes until the vehicle reaches the final destination. As a first approximation, the results presented in the following section are obtained via the simplified vehicle model used for the feasibility check. While the feasibility check has to be performed thousands of times to plan the route, the cosimulation has to be performed only once. Therefore, it is possible to improve the accuracy of the cosimulation through more complex vehicle and battery models, as stated in
Section 2.4.
A further step in the refinement of the energy estimation and the tuning of
K parameter would be the validation of the simulated results through repetition of the travel on real roads with constant monitoring of the EV. The instantaneous speed could be measured by means of Kalman filters [
39] and used to compare the effective energy consumption as measured from on-board BMS to the energy consumption estimated by the planner for a vehicle following the measured speed profile.
5. Results
This section presents the results obtained by the proposed planning method and compares them to a planning method—hereinafter defined as the“standard”—that does not account for any range-reducing factor but selects the stations according to the nominal EV range adjusted by the SoC lower threshold without performing any energy estimation. To ensure that the results comparison displayed the robustness increase provided by the proposed planner, the two planners were built around the same station selection procedure and cost function, and the generated routes were evaluated through cosimulation with the same vehicle model. The planning methods were compared through the two metrics previously introduced: (1) success rate, i.e., the percentage of routes planned whose cosimulation ends with the vehicle reaching the destination without the SoC falling below the threshold set by the user; (2) SoC threshold violation, i.e., the amount of SoC which is discharged below the user set threshold in a near miss. A comparison of the first metric between the standard (a) and the proposed (b) planner is shown in
Figure 4 as a function of different range-affecting factors and the overall numerical results are presented in
Table 4.
The overall results relative to the first metric are presented in point (1) of
Figure 4, and the improvement in the robustness of the planned algorithm is noticeable. The routes planned by the standard algorithm (a) achieve success in fewer than half of the scenarios, and almost one in five routes ends with the vehicle fully discharged along the route. On the contrary, the proposed planner (b) does not incur any critical failure, and the success rate more than doubles (from 44% to 93%). The critical failure through full discharge appears mainly in cases with the sport driving style.
Sport driving style is indeed the factor with the heaviest impact on standard route planner reliability, as is evident from point (2), which shows that the standard planning method does not achieve successful travels in cases of sport driving style (Tests 6, 7 and 9 from
Table 3). Moreover, in two=thirds of these scenarios, the route selected by the standard planner causes the car to run out of battery before reaching the destination.
The factor with the second heaviest impact on the reliability of the standard planner is the SoH degradation of the battery. The reduction in capacity and the consequent reduction in vehicle range are not considered by the standard planner, and this led to a share of 78% of near misses and failures in the considered scenarios (Tests 5, 7, 9, 14, 15 and 18). The results of these scenarios with the standard and the proposed planner are shown in point (3). The success rate increased from 23% with the standard planner to 85% with the proposed planner. Moreover, the share of cases where the charging stations were insufficient (8%) consist of four cases of Test 15, where the city car is placed in its most severe conditions, with an average driving style, battery degradation to 90%, cold outside temperature and three passengers. With such boundary conditions, the proposed planner could not find a feasible route on four out of eight test routes because of the lack of stations along the highways.
The number of passengers was the third-most-impacting factor on the reliability of the standard planner, which achieved a success rate of 30% in the considered scenarios (Tests 3, 7, 9, 13 and 15). The comparison between the results of the standard planner and the proposed planner in these scenarios is presented in point (4). The success rate increased from 30% to 80%, demonstrating that the proposed planner is robust with respect to the number of passengers.
Finally, the external temperature is the least failure-affecting factor in the standard planner. The scenarios in which the external temperature caused a significant power demand by the HVAC systems (Tests 2, 3, 7, 9, 11, 12 and 15) saw a 41% success rate by the standard planner, which increased to 88% with the proposed planner, as can be seen from point (5).
Other than improving the robustness in presence of factors reducing vehicle range, the proposed planner presents better results compared to the standard one even in conditions where no range-affecting factors are present, i.e., Tests 1, 8, 10 and 16. The success rate doubles from 50% to 100%, so all routes generated by the proposed planner are listed as successes.
As the focus of this work is on the increase in robustness of the route-planning algorithm, the total time required for the travel is not considered as a metric. Therefore, it might happen that a route planned with the standard algorithm results in faster travel, as a lower number of recharges is required. The more robust battery management is achieved through a higher number of stops, but the overall time duration of the travel does not change significantly. The comparison between the time duration of the travels generated by the two planners is presented in
Figure 5.
For the average driving style, routes found by the proposed route planner take 15.6% longer to be completed when neither the standard nor the proposed planner violates the lower SoC threshold. The situation is reversed in scenarios with the eco driving style (Tests 11–14). These scenarios are tested with Vehicle B (small city car), as such a car can not follow an aggressive speed profile in real life. Out of the thirty-two travels planned in Tests 11–14, in twenty-four cases (75%), the proposed planner outperforms the standard planner without violating the lower SoC threshold. The energy estimation allows for the selection of the charging stations that are outside of the nominal range because of the lower speed, and therefore the proposed planner requires fewer stopping times, leading to a reduction of the time the route takes to be completed. In seven of the thirty-two cases, the proposed planner is outperformed by the standard planner; that is, the route created by the proposed planner takes longer to be completed. Finally, in a single case, the route generated by the proposed planner violates the threshold, while the standard planner respects it. Overall, the success rate is better for the standard planner (100%) than for the proposed planner (96.9%) in this subset of cases, but the only near miss obtained by the proposed planner has a violation of the SoC constraint by −4.6%. Overall, the proposed planner generates routes which are completed in 15.4% less time.
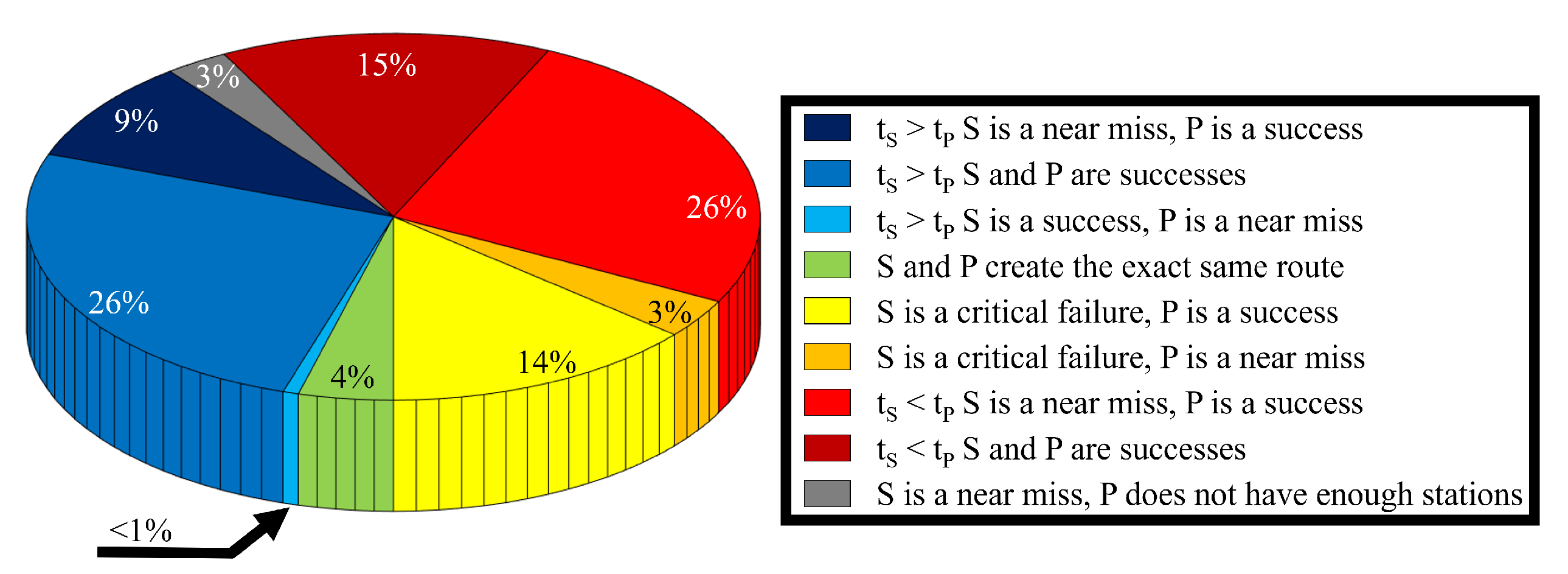
Figure 6 shows side by side the routes generated by the standard (a) and the proposed planner (b) in driving missions that are relevant for their results. The first point of
Figure 6 compares the SoC profiles on
case A, Test 1. It is evident how the need for more charging stops does not translate into a longer route, as the stations are selected close to the Baseline route to minimize time loss. The second, third and fourth points of
Figure 6, instead, show cases in which the proposed planner requires a detour from the Baseline route. Case (2) refers to the driving mission conducted on
case B, Test 1, where the proposed planner requires leaving the motorway to stop for the last recharge. On the other hand, the standard planner requires a single stop further down the route, but—to do so– -it overdischarges the battery by 10% SoC. Case (3) refers to the driving mission conducted on
case B, Test 7, where the proposed planner requires a total change of route from the Baseline. This is the product of the recomputation of the direct route every time a station is selected, as in that case, it is more efficient to generate a whole new route instead of driving back to the Baseline route. Case (4) refers to the driving mission conducted on
case F, Test 7, where the proposed planner requires to deviate twice from the Baseline route. The first deviation requires driving through the urban road network after leaving the highway to perform a recharge. This deviation would not be advantageous in real life, where urban roads are severely congested, and the speed of their traffic is significantly lower than the nominal speed limit, but the planner currently does not account for traffic congestion. The second deviation is required since the best station among those from which the destination is reachable is far from the Baseline route, and all of the stations present in the cluster located to its north along the Baseline route are too far from the destination. It is important to highlight that in both case (3) and (4), the standard planner is outperformed by the proposed planner, as the former experiences critical failures with the battery fully discharged. This can be seen in the maps of
Figure 6 relative to cases (2), (3) and (4), where the SoC profile disappears along the way, leaving the Baseline route visible (in black).
Cases (5) and (6) refer to cases in which the driving mission involves the eco driving styles, which allows the proposed planner to select stations that are outside of the nominal EV range. This advantage concretizes in two ways, respectively shown in case (5) and (6): (1) the selection of farther charging stations that avoids excessive detours as the one done for the second and the last stop of case (5) ( case D, Test 11) and (2) the selection of fewer stations (4 instead of 3) for case (6) ( case F, Test 14) to reduce the total travel duration. However, compared to what occurs with the standard planner, the lower number of stations does not come at the cost of the generate route reliability, with a 96.3% success rate in the eco driving style subset.
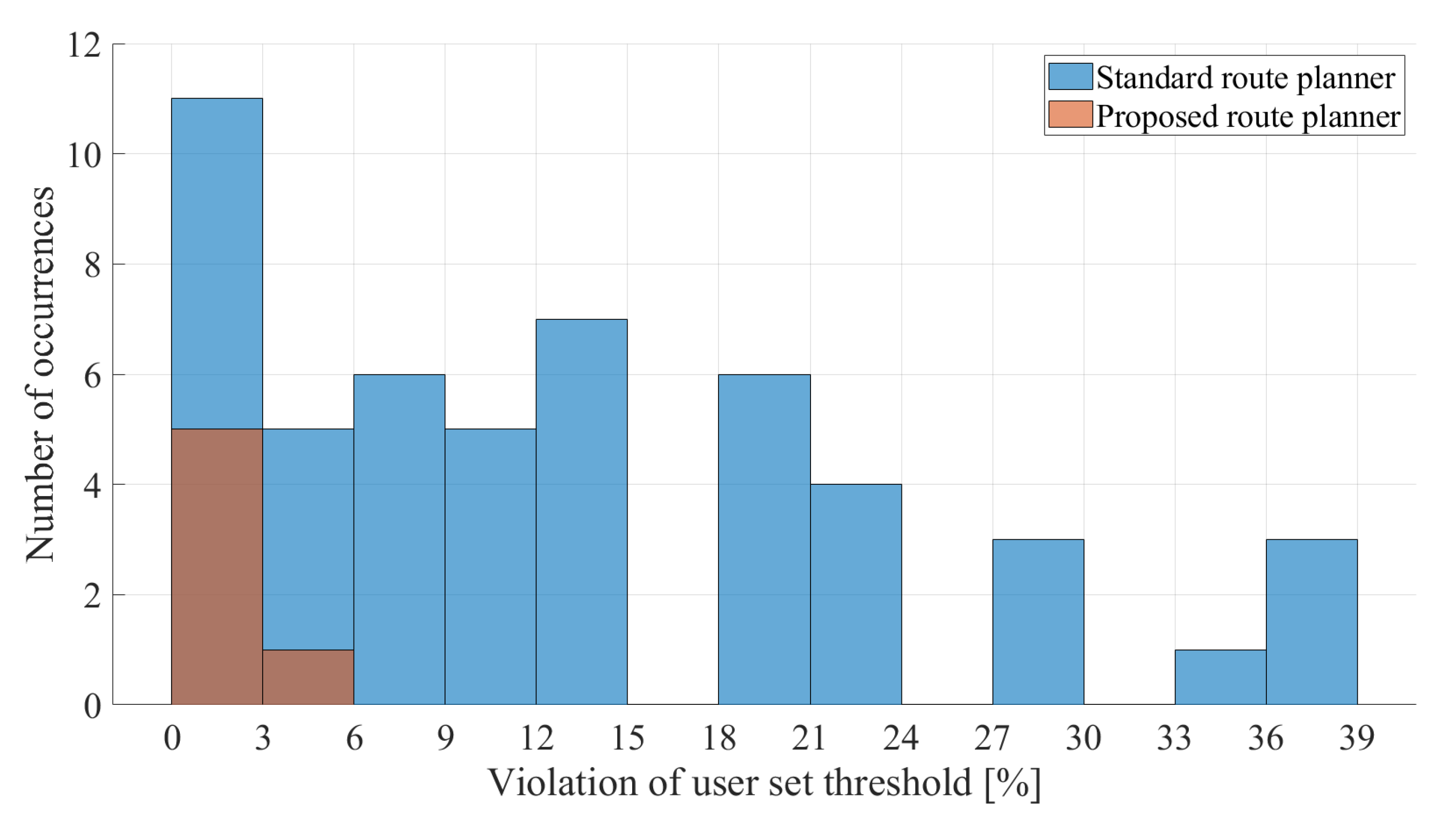
The second metric is deeply linked with the first one, as a higher success rate leads to a smaller amount of travel missions with a SoC threshold violation. This phenomenon is presented in
Figure 7, where the distribution of the magnitude of the violation is shown. The total amount of violations is significantly lower for the proposed planner, as the near miss percentage drops from 38% to 4%. It is important to point out that the magnitude of the violation is also reduced by the adoption of the proposed planner. The most common amount of violation is the (0 ÷ 3)% band for both planners, but no travel run on a route generated by the proposed planner over-discharges by more than 6%. Instead, in several occurrences the standard planner violated the SoC threshold by almost 40%. As 40% is the lower threshold in most of the boundary conditions settings, it is evident that such violations almost constitute a critical failure. Overall, the average SoC threshold violation moves from −13.1% to −1.1%, thanks to the adoption of the proposed planner.
6. Conclusions
This paper proposed a route planning method for EVs accounting for driving style, battery SoH degradation, number of passengers and external temperature. It builds the route through the progressive selection of charging stations with a cost function which favors the most powerful charging stations and the stations which detour less from the Baseline route.
The reachability of the selected stations is checked by means of energy estimation instead of nominal vehicle range comparison. This facilitates taking into account the aforementioned factors, which are not considered if the stations are only tested for the nominal EV range. The route testing is conducted via Matlab–SUMO cosimulation instead of real-life on-road tests because of the large amount of driving missions to be performed.
The routes are evaluated through two metrics based on SoC profile: share of routes completed without violating the SoC constraints and the amount of violation on such SoC constraints.
To evaluate the improvement in robustness offered by the energetic estimation, the proposed planning method was tested against a standard planning method, which uses the same cost function to select the stations but only considers nominal EV range. Results show that the success rate increased from 44% to 93%, and the violation on the SoC constraint increased from −13.1% to −1.1%.
Future steps for the development of this route planning method include refinements on the evaluation procedure and the introduction of more range-affecting factors into the route planner.
Regarding the evaluation procedure, a more precise vehicle and battery model could be introduced to more accurately represent the SoC profile during the travel, and real-life tests could be run to experimentally validate the cosimulation evaluation procedure.
Additional range-affecting factors that can be introduced as a future development include the following: (a) the introduction of altimetric values in the map, as the planner is designed to account for them, but the road network was considered as flat; (b) the definition of wind speed and direction across the map to obtain a more accurate definition of the aerodynamic drag; and (c) the introduction of traffic congestion coefficients, representing the speed at which traffic flows on each portion of network instead of the maximum speed to optimize the total travel time accounting also for traffic jams.
Finally, the route planning method proposed here would be improved by the introduction of live information services, such as live weather monitoring to better detail HVAC impact, real-time traffic updates to adapt the traffic congestion coefficients and monitoring of charging stations to obtain information about the charging station availability in real-time instead of simulating it.