Material Balance Method and Dynamic Pressure Monitoring for Water-Bearing Gas Reservoirs with CO2 Injection
Abstract
1. Introduction
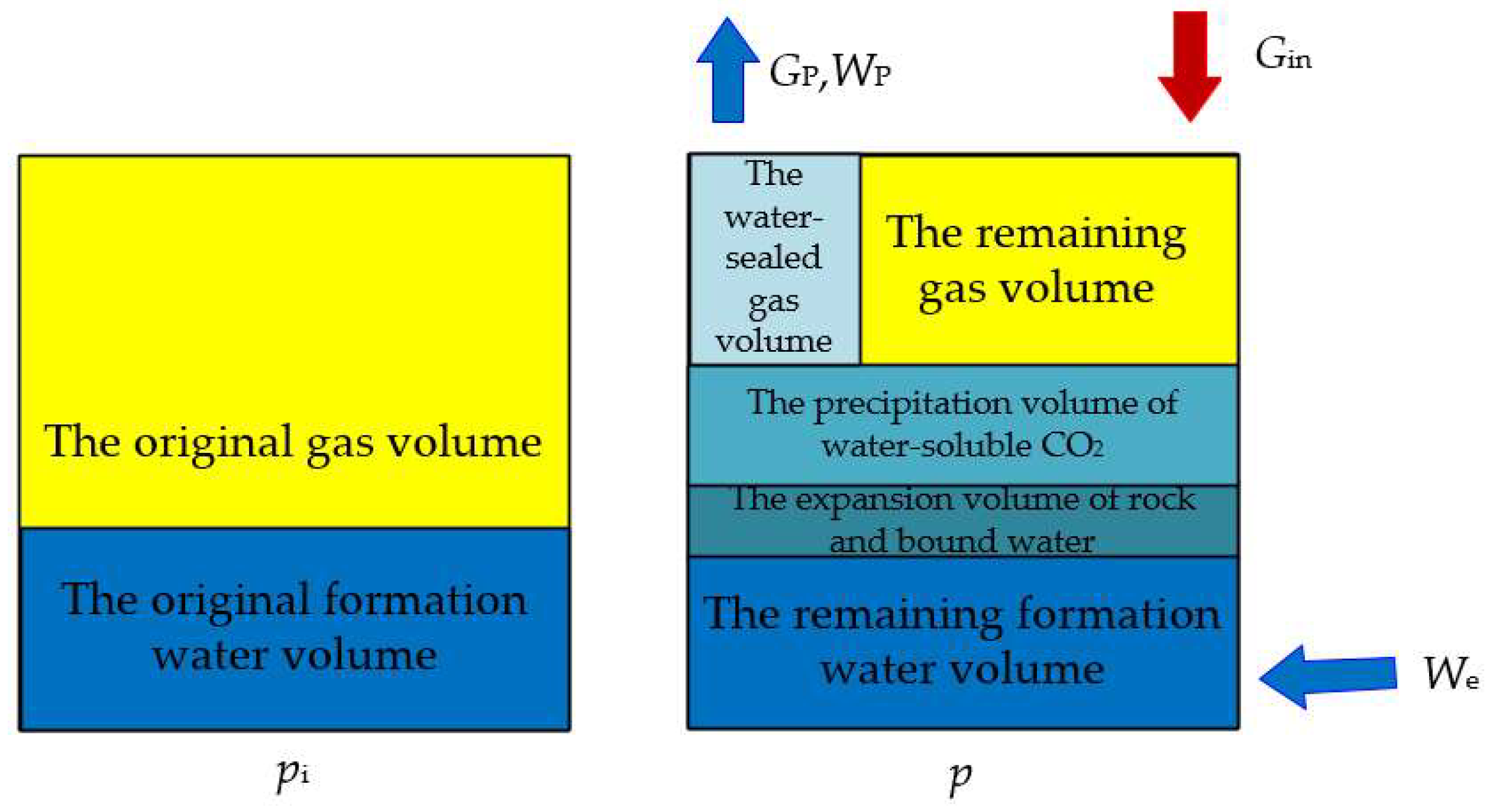
2. Physical Model
3. Mathematical Model
3.1. Derivation of Mathematical Model
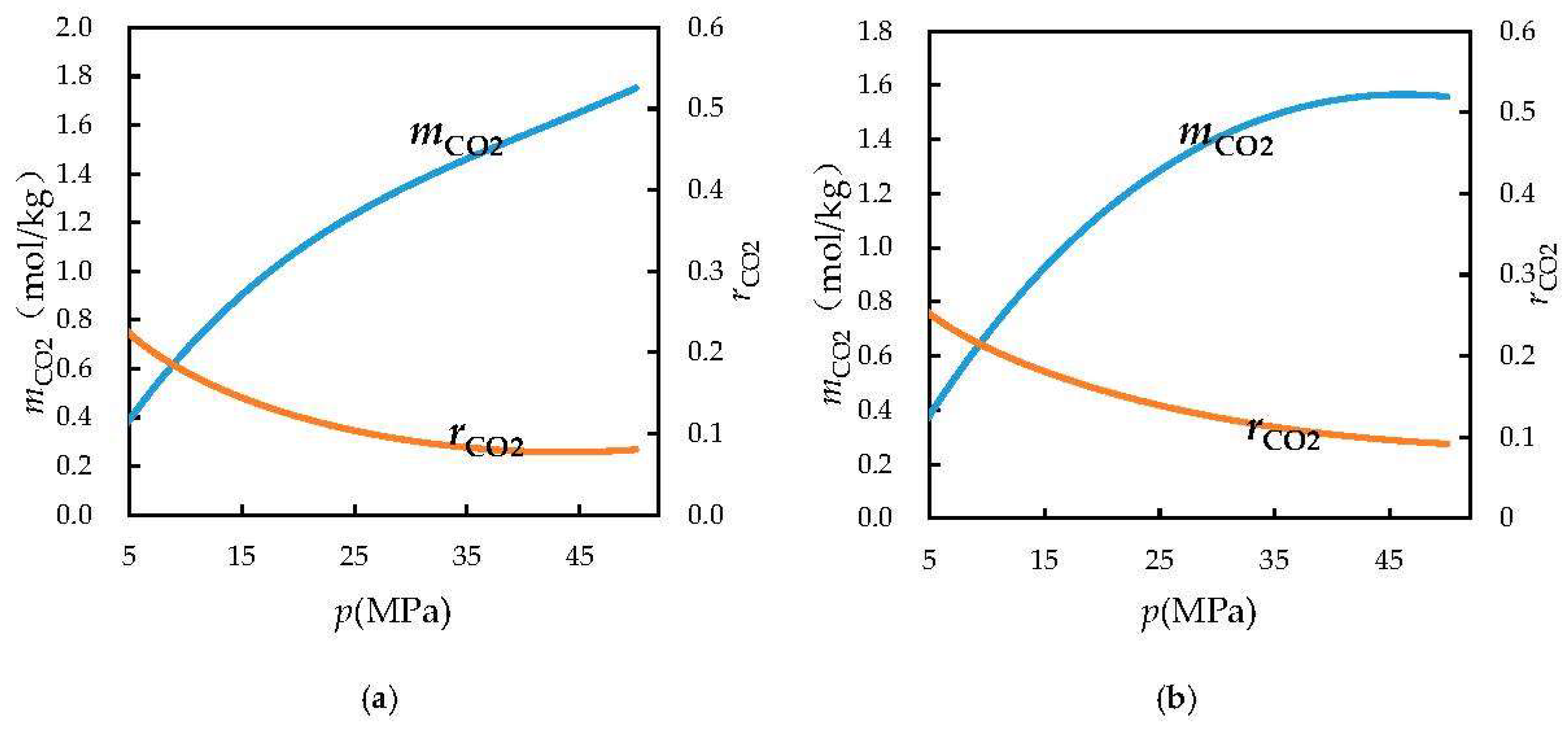
3.2. Calculation of Ratio of Dissolved Carbon Dioxide to Water
3.3. Solution of the Mathematical Model
- Let p0 = pi;
- Let the initial value of Gin be 0;
- Obtain the values of , Z, and by substituting p0; combine Gp, G, Swi, Sgi, Cf, Cw, A, and ω and substitute them into the right part of Equation (18); then calculate the pressure on the left part of Equation (18), and let the pressure be p1;
- Obtain the values of , Z1, and by substituting p1; combine Gp, G, Swi, Sgi, Cf, Cw, A, and ω and substitute them into the right part of Equation (18); then, calculate the pressure on the left part of Equation (18), and let the pressure be p2;
- Make p2 equal to p0;
- Repeat steps (3)–(5) until p2 − p1 < 0.0001;
- Output the value of p at this point;
- Increase Gin by 0.1 and repeat steps (3)–(8) until the formation pressure reaches the overlying formation pressure (ps; assuming that ps = 1.1pi);
- On the basis of the value of Gin and the corresponding value of p, changes in formation pressure during carbon dioxide injection can be characterized.
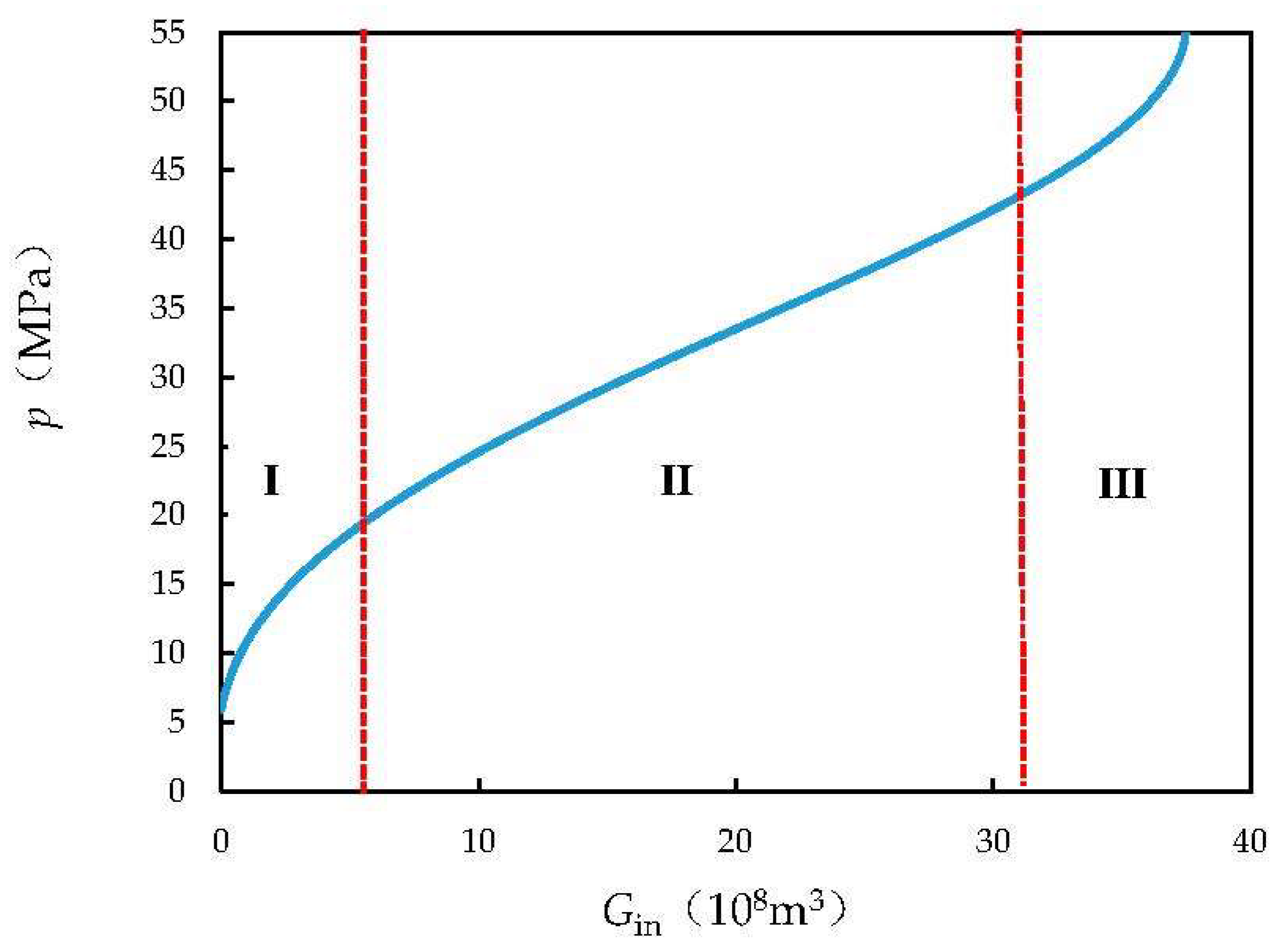
4. Results and Discussion
5. Instance Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Che, X.; Yi, X.; Dai, Z.; Zhang, Z.; Zhang, Y. Application and Development Countermeasures of CCUS Technology in China’s Petroleum Industry. Atmosphere 2022, 13, 1757. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Miao, X.; Gan, M.; Li, X. Geochemistry in geologic CO2 utilization and storage: A brief review. Adv. Geo-Energy Res. 2019, 3, 304–313. [Google Scholar] [CrossRef]
- Bachu, S.; Gunter, W.; Perkins, E. Aquifer disposal of CO2: Hydrodynamic and mineral trapping. Energy Convers. Manag. 1994, 35, 269–279. [Google Scholar] [CrossRef]
- Baines, S.J.; Worden, R.H. Geological Storage of Carbon Dioxide; Special Publications; Geological Society: London, UK, 2004; Volume 233, pp. 1–6. [Google Scholar]
- Gilfillan, S.M.; Ballentine, C.J.; Holland, G.; Blagburn, D.; Lollar, B.S.; Stevens, S.; Schoell, M.; Cassidy, M. The noble gas geochemistry of natural CO2 gas reservoirs from the Colorado Plateau and Rocky Mountain provinces, USA. Geochim. Cosmochim. Acta 2008, 72, 1174–1198. [Google Scholar] [CrossRef]
- Xu, T.; Tian, H.; Zhu, H.; Cai, J. China actively promotes CO2 capture, utilization and storage research to achieve carbon peak and carbon neutrality. Adv. Geo-Energy Res. 2022, 6, 1–3. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, L.; Hu, R.; Cai, J. Subsurface multiphase reactive flow in geologic CO2 storage: Key impact factors and characterization approaches. Adv. Geo-Energy Res. 2022, 6, 179–180. [Google Scholar] [CrossRef]
- Al-Abri, A.; Sidiq, H.; Amin, R. Mobility ratio, relative permeability and sweep efficiency of supercritical CO2 and methane injection to enhance natural gas and condensate recovery: Coreflooding experimentation. J. Nat. Gas Sci. Eng. 2012, 9, 166–171. [Google Scholar] [CrossRef]
- Andersen, P.Ø. Carbon capture utilization and storage (CCUS) in tight gas and oil reservoirs. J. Nat. Gas Sci. Eng. 2020, 81, 103458. [Google Scholar] [CrossRef]
- Chima, F.U.; Mengdi, S.; Zhejun, P.; Mehdi, O.; Bo, L.; Yanran, X.; Agwom, I.M.; Happiness, I.U.; Mohammed, D.A.; Baolin, Y. An insight into CO2 sequestration and EGR in Longmaxi and Niutitang shale formations via experimental analysis. Fuel 2022, 324, 124776. [Google Scholar]
- Eshkalak, M.O.; Al-Shalabi, E.W.; Sanaei, A.; Aybar, U.; Sepehrnoori, K. Simulation study on the CO2-driven enhanced gas recovery with sequestration versus the re-fracturing treatment of horizontal wells in the U.S. unconventional shale reservoirs. J. Nat. Gas Sci. Eng. 2014, 21, 1015–1024. [Google Scholar] [CrossRef]
- Biagi, J.; Agarwal, R.; Zhang, Z. Simulation and optimization of enhanced gas recovery utilizing CO2. Energy 2016, 94, 78–86. [Google Scholar] [CrossRef]
- Song, Z.; Song, H.; Cao, Y.; Killough, J.; Leung, J.; Huang, G.; Gao, S. Numerical research on CO2 storage efficiency in saline aquifer with low-velocity non-Darcy flow. J. Nat. Gas Sci. Eng. 2015, 23, 338–345. [Google Scholar] [CrossRef]
- Saptharishi, P.; Makwana, M. Technical and Geological review of Carbon dioxide Geo Sequestration along with analysis and study of various Monitoring Techniques. In Proceedings of the International Petroleum Technology Conference, Bangkok, Thailand, 15–17 November 2011. [Google Scholar]
- Oppert, S.; Adachi, J.; Thornton, D.; Royle, A. Monitoring technology to enable characterization of CCUS reservoirs. In Proceedings of the SEG/AAPG International Meeting for Applied Geoscience & Energy, Houston, TX, USA, 28 August–1 September 2022. [Google Scholar]
- Fibbi, G.; Del Soldato, M.; Fanti, R. Review of the Monitoring Applications Involved in the Underground Storage of Natural Gas and CO2. Energies 2023, 16, 12. [Google Scholar] [CrossRef]
- Seshia, A.A.; Neill, F. MEMS-based gravity imaging for CO2 storage monitoring. In Proceedings of the SEG/AAPG International Meeting for Applied Geoscience & Energy, Houston, TX, USA, 28 August–1 September 2022. [Google Scholar]
- Montes-Hernandez, G.; Pérez-López, R.; Renard, F.; Nieto, J.; Charlet, L. Mineral sequestration of CO2 by aqueous carbonation of coal combustion fly-ash. J. Hazard. Mater. 2009, 161, 1347–1354. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Yin, X.; Winterfeld, P.H.; Wu, Y.-S. A fully coupled thermal-hydrological-mechanical-chemical model for CO2 geological sequestration. J. Nat. Gas Sci. Eng. 2016, 28, 280–304. [Google Scholar] [CrossRef]
- Celia, M.A.; Nordbotten, J.M. Practical modeling approaches for geological storage of carbon dioxide. Groundwater 2009, 47, 627–638. [Google Scholar] [CrossRef]
- Stein, M.H.; Ghotekar, A.L.; Avasthi, S. CO2 sequestration in a depleted gas field: A material balance study. In Proceedings of the SPE EUROPEC/EAGE Annual Conference and Exhibition, Barcelona, Spain, 14–17 June 2010; OnePetro: Richardson, TX, USA, 2010. [Google Scholar]
- Teng, H.; Masutani, S.; Kinoshita, C.; Nihous, G. Solubility of CO2 in the ocean and its effect on CO2 dissolution. Energy Convers. Manag. 1996, 37, 1029–1038. [Google Scholar] [CrossRef]
- Spycher, N.; Pruess, K.; Ennis-King, J. CO2-H2O mixtures in the geological sequestration of CO2. Assessment and calculation of mutual solubilities from 12 to 100 C and up to 600 bar. Geochim. Cosmochim. Acta 2003, 67, 3015–3031. [Google Scholar] [CrossRef]
- Ellis, A.; Golding, R. The solubility of carbon dioxide above 100 degrees C in water and in sodium chloride solutions. Am. J. Sci. 1963, 261, 47–60. [Google Scholar] [CrossRef]
- Hu, J.; Duan, Z.; Zhu, C.; Chou, I.-M. PVTx properties of the CO2–H2O and CO2–H2O–NaCl systems below 647 K: Assessment of experimental data and thermodynamic models. Chem. Geol. 2007, 238, 249–267. [Google Scholar] [CrossRef]
- Yan, W.; Huang, S.; Stenby, E.H. Measurement and modeling of CO2 solubility in NaCl brine and CO2–saturated NaCl brine density. Int. J. Greenh. Gas Control 2011, 5, 1460–1477. [Google Scholar] [CrossRef]
- Mohammadian, E.; Hamidi, H.; Asadullah, M.; Azdarpour, A.; Motamedi, S.; Junin, R. Measurement of CO2 solubility in NaCl brine solutions at different temperatures and pressures using the potentiometric titration method. J. Chem. Eng. Data 2015, 60, 2042–2049. [Google Scholar] [CrossRef]
- Salaheddine, C.; Pezhman, A.; Pascal, T.; Christophe, C.; Antonin, C.; Jerome, C.; Patrice, P. Measurements and Modeling of High-Pressure O2 and CO2 Solubility in Brine (H2O + NaCl) between 303 and 373 K and Pressures up to 36 MPa. J. Chem. Eng. Data 2021, 66, 609–620. [Google Scholar]
- King, M.; Mubarak, A.; Kim, J.; Bott, T. The mutual solubilities of water with supercritical and liquid carbon dioxides. J. Supercrit. Fluids 1992, 5, 296–302. [Google Scholar] [CrossRef]
- Zheng, D.-Q.; Guo, T.-M.; Knapp, H. Experimental and modeling studies on the solubility of CO2, CHC1F2, CHF3, C2H2F4 and C2H4F2 in water and aqueous NaCl solutions under low pressures. Fluid Phase Equilibria 1997, 129, 197–209. [Google Scholar] [CrossRef]
- Bando, S.; Takemura, F.; Nishio, M.; Hihara, E.; Akai, M. Solubility of CO2 in aqueous solutions of NaCl at (30 to 60) C and (10 to 20) MPa. J. Chem. Eng. Data 2003, 48, 576–579. [Google Scholar] [CrossRef]
- Duan, Z.; Sun, R. An improved model calculating CO2 solubility in pure water and aqueous NaCl solutions from 273 to 533 K and from 0 to 2000 bar. Chem. Geol. 2003, 193, 257–271. [Google Scholar] [CrossRef]
- Duan, Z.; Sun, R.; Zhu, C.; Chou, I.-M. An improved model for the calculation of CO2 solubility in aqueous solutions containing Na+, K+, Ca2+, Mg2+, Cl−, and SO42−. Mar. Chem. 2006, 98, 131–139. [Google Scholar] [CrossRef]
- Chang, Y.-B.; Coats, B.K.; Nolen, J.S. A compositional model f or CO2 floods including CO2 solubility in water. In Proceedings of the Permian Basin Oil and Gas Recovery Conference, Midland, TX, USA, 27–29 March 1996; OnePetro: Richardson, TX, USA, 1996. [Google Scholar]
- Kiepe, J.; Horstmann, S.; Fischer, K.; Gmehling, J. Experimental determination and prediction of gas solubility data for CO2 + H2O mixtures containing NaCl or KCl at temperatures between 313 and 393 K and pressures up to 10 MPa. Ind. Eng. Chem. Res. 2002, 41, 4393–4398. [Google Scholar] [CrossRef]
- Sun, H.; Cao, W.; Li, J.; Jia, W.; Li, Y.; Wu, Y.; Zhu, S.; Fu, X.; Yang, M.; Meng, G. A material balance based practical analysis method to improve the dynamic reserve evaluation reliability of ultra-deep gas reservoirs with ultra-high pressure. Nat. Gas Ind. B 2021, 8, 79–87. [Google Scholar] [CrossRef]
- Zhang, L.; He, Y.; Guo, C.; Yu, Y. Dynamic Material Balance Method for Estimating Gas in Place of Abnormally High-Pressure Gas Reservoirs. Lithosphere 2021, 2021, 6669012. [Google Scholar] [CrossRef]
- Carter, R.; Tracy, G. An improved method for calculating water influx. Trans. AIME 1960, 219, 415–417. [Google Scholar] [CrossRef]
- Jiao, Y.; Xia, J.; Liu, P.; Zhang, J.; Li, B.; Tian, Q.; Wu, Y. New material balance analysis method for abnormally high-pressured gas-hydrocarbon reservoir with water influx. Int. J. Hydrogen Energy 2017, 42, 18718–18727. [Google Scholar] [CrossRef]
- Tan, X.; Peng, G.; Li, X.; Chen, Y.; Xu, X.; Kui, M.; Li, Q.; Yang, G.; Xiao, H. Material balance method and classification of non-uniform water invasion mode for water-bearing gas reservoirs considering the effect of water sealed gas. Nat. Gas Ind. B 2021, 8, 353–358. [Google Scholar] [CrossRef]
- Hawthorne, S.B.; Miller, D.J.; Holubnyak, Y.; Harju, J.A.; Kutchko, B.G.; Strazisar, B.R. Experimental investigations of the effects of acid gas (H2S/CO2) exposure under geological sequestration conditions. Energy Procedia 2011, 4, 5259–5266. [Google Scholar] [CrossRef]
- Feng, Y.; Hu, S.; Liu, X.; Luo, G.; Zhu, G. Prevention and disposal technologies of gas hydrates in high-sulfur gas reservoirs containing CO2. J. Nat. Gas Sci. Eng. 2014, 19, 344–349. [Google Scholar] [CrossRef]
- Xiong, W.; Zhu, Z.; Gao, S. Material balance equation of waterflooding gas reservoir considering trapped gas. Pet. Drill. Tech. 2012, 40, 93–97. [Google Scholar]
- Van der Meer, L.G.H. The K12-B CO2 injection project in The Netherlands. In Geological Storage of Carbon Dioxide (CO2); Woodhead Publishing: Sawston, UK, 2013; pp. 301–327. [Google Scholar] [CrossRef]


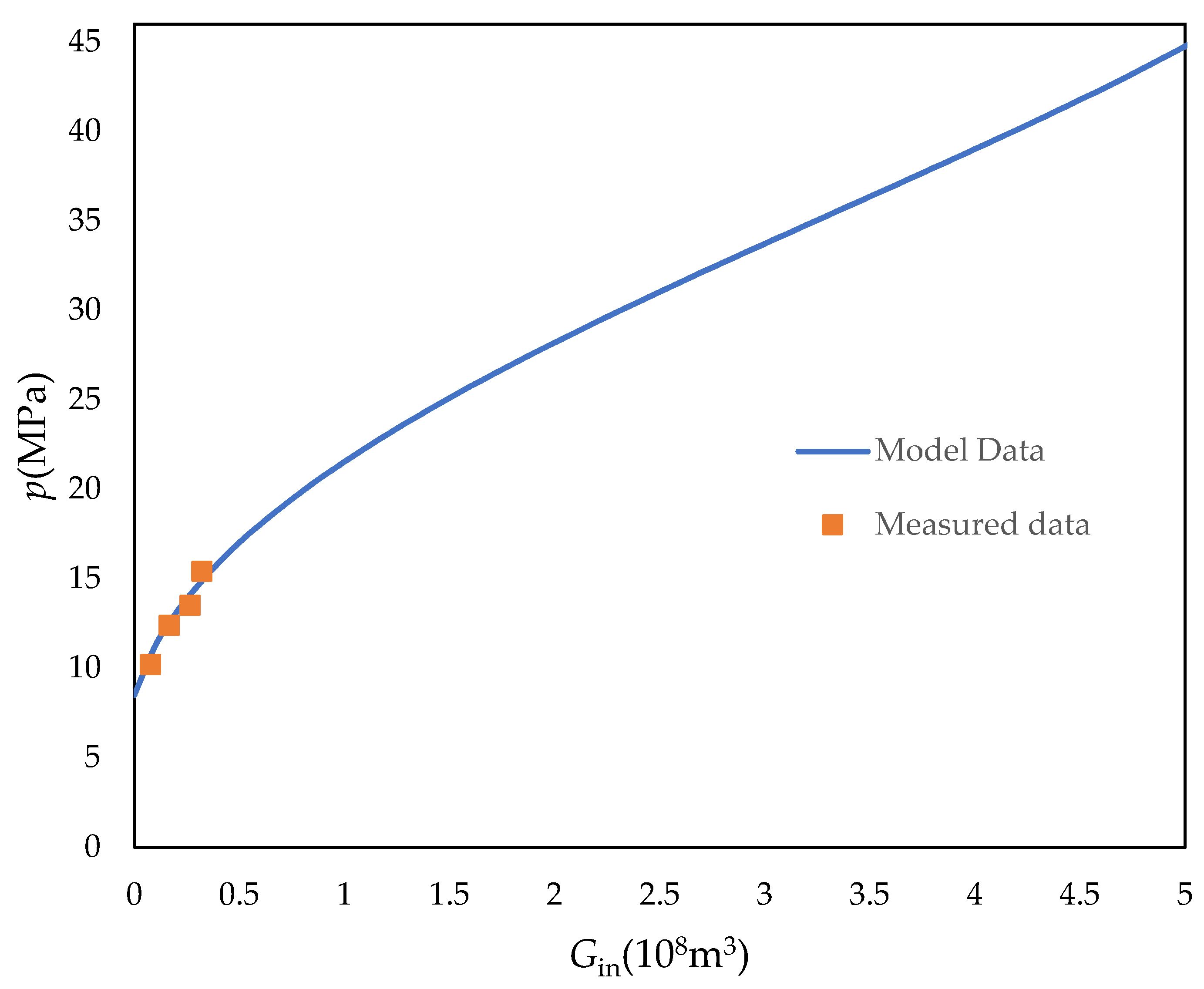
| Date (Year) | Injection Time (d) | Average Injection Rate (m3/d) | Injection Volume (108 m3) | Cumulative Injection Volume (108 m3) | Average Formation Pressure (MPa) |
|---|---|---|---|---|---|
| 2005~2006 | 300 | 26,000 | 0.0780 | 0.0780 | 10.2 |
| 2006~2007 | 330 | 27,000 | 0.0891 | 0.1671 | 12.4 |
| 2008~2009 | 350 | 28,500 | 0.0997 | 0.2668 | 13.5 |
| 2009~2010 | 200 | 28,000 | 0.0560 | 0.3228 | 15.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, X.; Shi, J.; Hui, D.; Li, Q.; Wu, T. Material Balance Method and Dynamic Pressure Monitoring for Water-Bearing Gas Reservoirs with CO2 Injection. Energies 2023, 16, 4592. https://doi.org/10.3390/en16124592
Tan X, Shi J, Hui D, Li Q, Wu T. Material Balance Method and Dynamic Pressure Monitoring for Water-Bearing Gas Reservoirs with CO2 Injection. Energies. 2023; 16(12):4592. https://doi.org/10.3390/en16124592
Chicago/Turabian StyleTan, Xiaohua, Jiajia Shi, Dong Hui, Qiu Li, and Tingting Wu. 2023. "Material Balance Method and Dynamic Pressure Monitoring for Water-Bearing Gas Reservoirs with CO2 Injection" Energies 16, no. 12: 4592. https://doi.org/10.3390/en16124592
APA StyleTan, X., Shi, J., Hui, D., Li, Q., & Wu, T. (2023). Material Balance Method and Dynamic Pressure Monitoring for Water-Bearing Gas Reservoirs with CO2 Injection. Energies, 16(12), 4592. https://doi.org/10.3390/en16124592







