A Survey on the Shortcomings of the Current Rate of Penetration Predictive Models in Petroleum Engineering
Abstract
1. Introduction
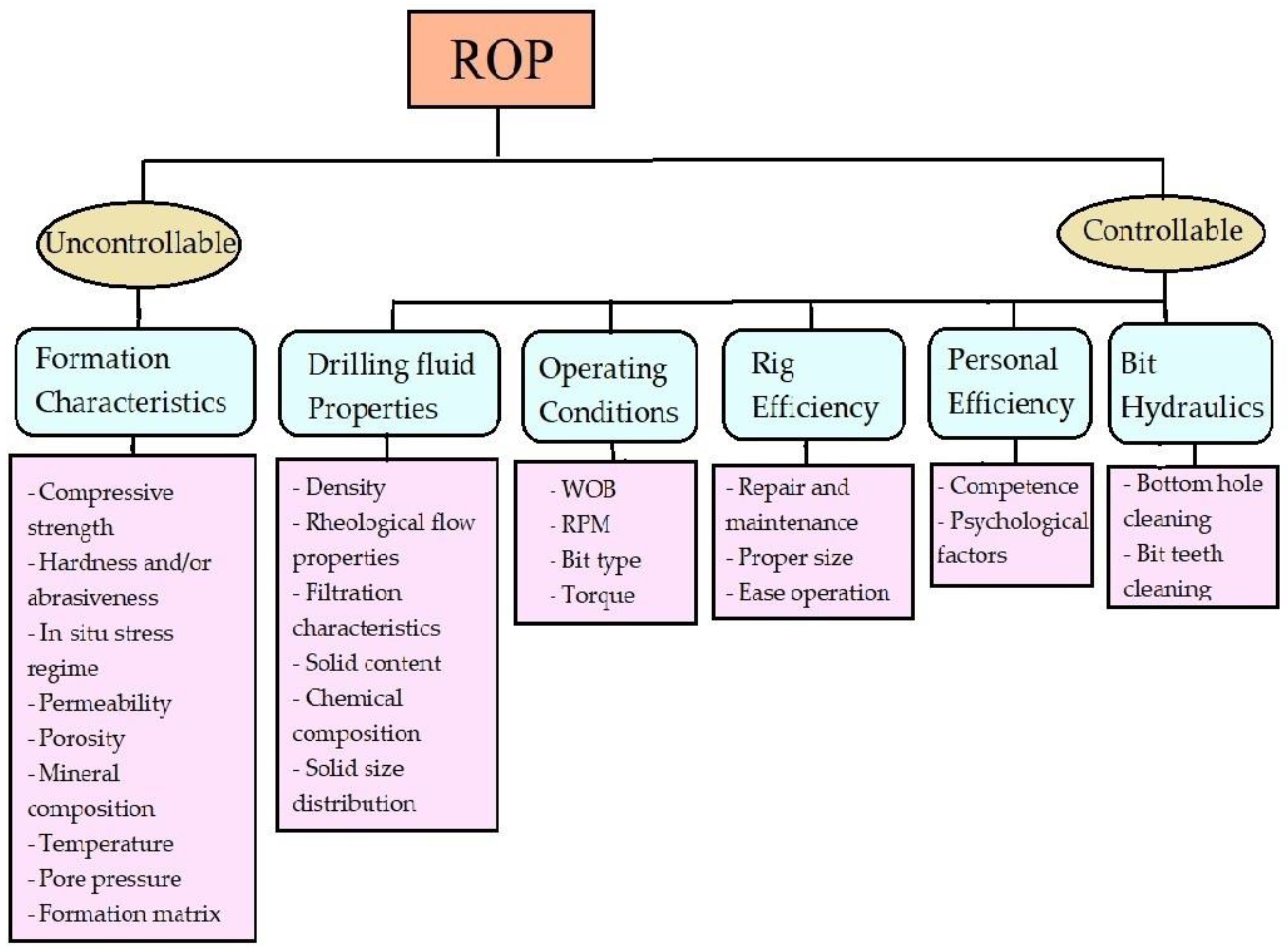
2. Contributing Factors on the ROP
2.1. Formation Characteristics
2.2. Mud Properties
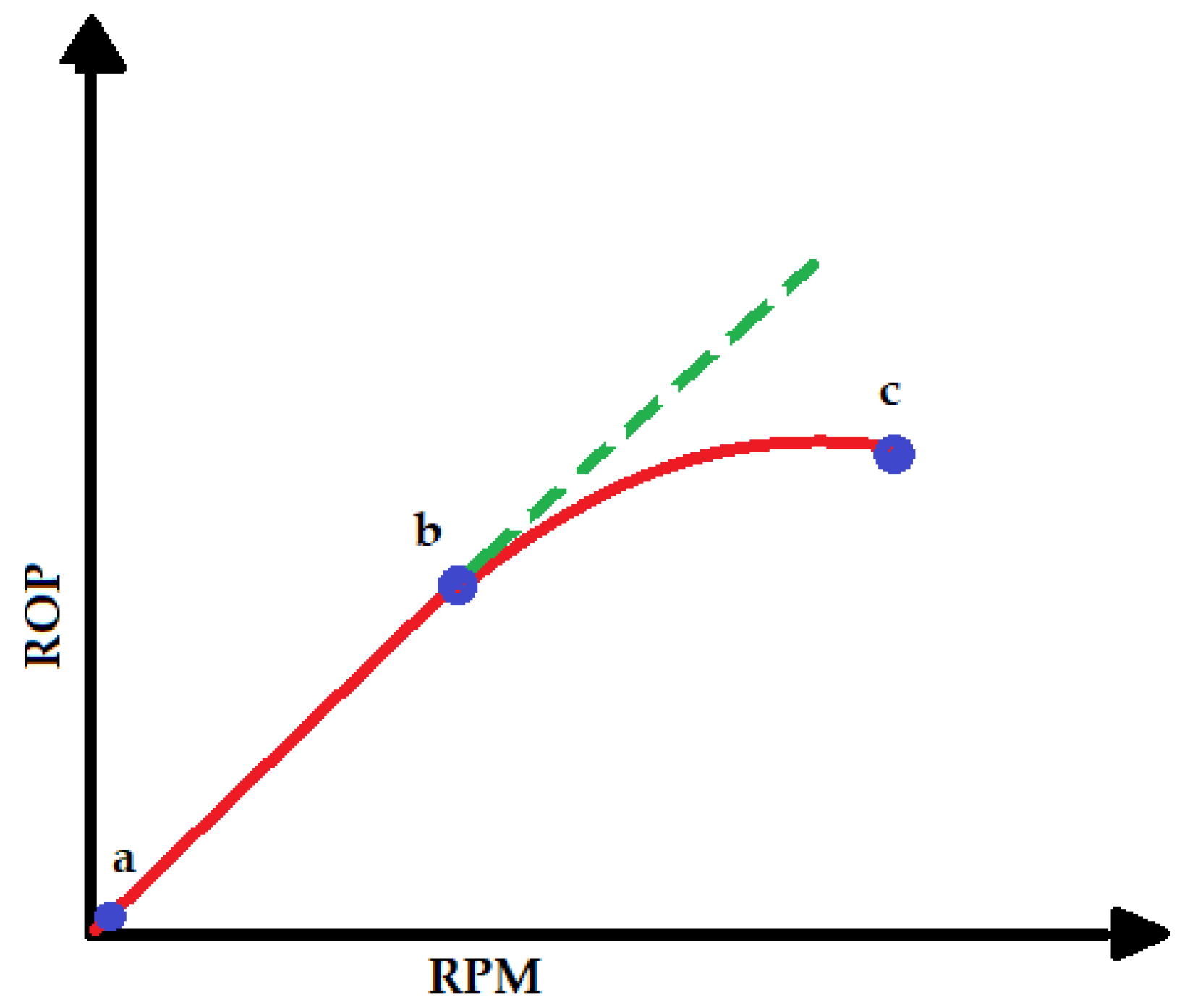
2.3. Bit Operating Conditions
2.4. Bit Hydraulics
2.5. Personal Efficiency
2.6. Rig Efficiency
3. The ROP Models
3.1. Empirical ROP Models
3.1.1. Review on Empirical ROP Models
3.1.2. Analysis of the Empirical ROP Models
3.1.3. Shortcomings and Limitations of Existing Empirical ROP Models
- Rock permeability represents the capacity of rock to allow fluid to move through the rock pores. In nature, such fluid is water, brine, oil, etc. During drilling operations, the bit cutters break the rock, and, simultaneously, the mud pressure prevents the pore fluid from flowing into the well space. In a microscopic perspective, the bit pushes the pore fluid back through two mechanisms [74]. In the first mechanism, the mud pushes back the pore fluid directly, thereby driving it to flow backwards. This mechanism is dominantly governed by the bit-rotation speed. In the second mechanism, the pores are compressed by bit cutters, and, consequently, the pore fluid is squeezed away from the bottom hole. This mechanism is mainly governed by rock diffusivity which is directly related to the rock permeability. Therefore, since the rock permeability changes, the ROP is altered [74]. Thus, it is suggested that more investigations on the relations between rock permeability and the ROP are conducted to improve the previous empirical models or to develop new ones;
- The second less-frequent factor is the coefficient of cuttings concentration which can be utilized as an indicator of the cuttings volume accumulated at the bottom hole. This factor is especially determining in the ROP during drilling of directional wells. As mentioned in the previous section, with the increasing demands for production from unconventional reservoirs, directional (horizontal and inclined) drilling has markedly increased; however, some features of past ROP models were considered only for vertical wells. Thus, it is essential to account for those features in ROP models developed for directional wellbores. The coefficient of cuttings concentration is such an essential factor.
- The third parameter is rock hardness. Rock hardness can be defined as the rock resistance to drilling. In other words, rock hardness is reciprocal of drillability. Some researchers have linked hardness with drilling speed; other researchers related the hardness to the amount of energy required for cutting a unit volume of rock [76]. Rock hardness is mainly dependent on the hardness of the minerals, grain size, grain shape, grain distribution, and cementation material. The silica content of the rock greatly affects the rock hardness. Although other resistive features, such as compressive strength and rock abrasiveness, have been adopted more frequently in ROP models, the inclusion of rock hardness into ROP models seems to be necessary;
- Temperature is another factor influencing the penetration rate. The bit brecks the rock under a thermo–hydro–mechanical condition. During the drilling operation, the bit penetrates the deeper formations with different thermal conditions. The heat changes the poroelastic properties of the rocks as well as the characteristics of the pore fluid [63,64]. One of those important poroelastic parameters is Biot’s coefficient. When the temperature changes, Biot’s coefficient varies and has an impact on the effective stress applied on the rock at the bottom hole. As a matter of consequence, the rock compression or shear strength changes, thereby influencing the ROP. Hence, the impact of temperature should be regarded in ROP models, especially using inclusion of Biot’s coefficient as a temperature-dependent factor.
3.2. Data-Driven ROP Models
| Reference | AI Technique | Input Parameters |
|---|---|---|
| Bilgesu, 1997 [97] | ANN | drillability; formation abrasiveness; rotary time; bearing wear; torque; tooth wear; WOB; pump rate; RPM. |
| Moran, 2010 [103] | ANN | formation strength; formation abrasiveness; bit weight; RPM; drilling fluid weight; rock gense. |
| Jahanbakhshi, 2012 [29] | ANN | mud type; pressure differential; hydraulic power of the bit; hydraulics; bit wear; depth; RPM; pump pressure; WOB; formation density; bit type; ECD; 10 min gel strength of drilling fluid; wellbore diameter; early gel strength of drilling fluid; drillability; drilling fluid’s yield point; permeability; drilling fluid’s plastic viscosity; porosity. |
| Amar and Ibrahim, 2012 [79] | ANN | pore fluid pressure; RPM; depth; ECD; Reynolds number function; tooth wear; WOB. |
| Alarfaj et al., 2012 [104] | ANN | Reynolds number; depth; WOB; RPM; tooth wear; gradient of pore pressure; ECD. |
| Cui et al., 2014 [105] | ANN | apparent viscosity; unconfined compressive strength; mud density; RPM; bit geometry; WOB; bit type; gross hours drilled; drillability constant. |
| Bodaghi, 2015 [100] | SVM | viscosity; mud weight; tooth wear; pump rate; bit geometry; formation; deviation of well; RPM; depth. |
| Mantha and Samuel, 2016 [36] | Hybrid system | RPM; flow rate; WOB. |
| Shi et al., 2016 [99] | ANN, ELM | mud properties; formation; RPM; geomechanical characteristics; WOB; hydraulics. |
| Amer, 2017 [106] | ANN | WOB; mud weight; bit gense; mineralogy; IADC codes; drill-pipe pressure; bit size; mud pump; bit condition; torque; depth; RPM; TVD. |
| Abdulmalek et al., 2018 [37] | SVM | yield point; WOB; solid; RPM; funnel viscosity; flow rate; plastic viscosity; standpipe pressure; mud density; torque. |
| Yavari et al., 2018 [39] | Hybrid system | WOB and RPM. |
| Anemangely, 2018 [33] | Hybrid system | RPM; WOB; shear wave slowness; compressional wave slowness; flow rate. |
| Ahmed et al., 2018 [99] | ANN, ELM, SVM, and LS-SVR | depth; flow rate; WOB; RPM; torque; standpipe pressure; mud weight; bit diameter. |
| Hegde et al., 2018 [38] | Hybrid system | RPM; UCS; flow rate; WOB. |
| Gan et al., 2019 [40] | ANN | seismic velocity; depth; torque; WOB; RPM; drillability; depth; mud density. |
| Elkatatny, 2021 [107] | Hybrid system | UCS; WOB; drill-pipe pressure; RPM; flow rate; torque; mud density; gamma ray; bit design; total flow area. |
| Lawal, 2021 [108] | ANN | density; porosity; point load index. |
| Mahdi, 2021 [98] | ANN | flow rate; WOB; RPM; bit diameter; standpipe pressure. |
| Sobhi et al., 2022 [35] | Hybrid system | depth; Reynolds number; WOB; tooth wear; ECD; RPM. |
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- De Oliveira, L.S.R.; Nascimento, A.; Mantegazini, D.Z.; Nascimento, N. Drilling optimization of petroleum wells: A data analysis of the drilling fluid flow-rate influence in ROP. Lat. Am. J. Energy Res. 2021, 8, 59–66. [Google Scholar] [CrossRef]
- Bourgoyne, A.T.; Millheim, K.K.; Chenevert, M.E.; Young, F.S. Applied Drilling Engineering; Society of Petroleum Engineers Richardson: Richardson, TX, USA, 1986. [Google Scholar]
- Bourgoyne, A.T.; Young, F.S. A Multiple Regression Approach to Optimal Drilling and Abnormal Pressure Detection. Soc. Pet. Eng. J. 1974, 14, 371–384. [Google Scholar] [CrossRef]
- Youcefi, M.R.; Hadjadj, A.; Bentriou, A.; Boukredera, F.S. Rate of penetration modeling using hybridization extreme learning machine and whale optimization algorithm. Earth Sci. Inform. 2020, 13, 51–68. [Google Scholar] [CrossRef]
- Edalatkhah, S.; Rasoul, R.; Hashemi, A. Bit selection optimization using artificial intelligence systems. Pet. Sci. Technol. 2010, 28, 1946–1956. [Google Scholar] [CrossRef]
- Protodyakonov, M.M. Mechanical properties and drillability of rocks. In Proceedings of the 5th Symposium Rock Mechanics; University of Minnesota: Minneapolis, MN, USA, 1963. [Google Scholar]
- Paone, J.; Madson, D.; Bruce, W.E. Drillability Studies-Laboratory Percussive Drilling; No. 7300-7309; US Department of the Interior, Bureau of Mines: Washington, DC, USA, 1969. [Google Scholar]
- Tandanand, S.; Unger, H.F. Drillability Determination: A Drillability Index for Percussion Drills; US Department of the Interior, Bureau of Mines: Washington, DC, USA; University of Michigan: Ann Arbor, MI, USA, 1975; Volume 8073. [Google Scholar]
- Pathankar, G.B.; Misra, A. critical appraisal of the Protodyakonov Index. Int. J. Rock Mech. Min. Sci. 1976, 13, 249–251. [Google Scholar] [CrossRef]
- Rabia, H. Oilwell Drilling Engineering: Principles and Practise; Graham & Tromtman: Gaihersburg, MD, USA, 1985. [Google Scholar]
- Bond, D.F. The optimization of PDC bit selection using sonic velocity profiles present in the Timor Sea. SPEDE 1990, 5, 135–142. [Google Scholar]
- Perrin, V.P.; Mensa-Wilmot, G.; Alexander, W.L. Drilling index-a new approach to bit performance evaluation. In Proceedings of the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 4–6 March 1997. [Google Scholar] [CrossRef]
- Graham, J.W.; Muench, N.L. Analytical determination of optimum bit weight and rotary speed combinations. In Proceedings of the in Fall Meeting of the Society of Petroleum Engineers of AIME, Dallas, TX, USA, 4–7 October 1959. [Google Scholar] [CrossRef]
- Maurer, W.C. The “Perfect—Cleaning” Theory of Rotary Drilling. J. Pet. Technol. 1962, 14, 1270–1274. [Google Scholar] [CrossRef]
- Galle, H.B.; Woods, E.M. Best Constant Weight and Rotary Speed for Rotary Rock Bits. Hughes Tool, Co.: New York, NY, USA, 1963. [Google Scholar]
- Bingham, M.G. A New Approach to Interpreting Rock Drill-Ability; Petroleum Pub. Co.: Oklahoma, OK, USA, 1965. [Google Scholar]
- Teale, R. The Concept of Specific Energy in Rock Drilling. Int. J. Rock Mech. Min. 1965, 2, 57–73. [Google Scholar] [CrossRef]
- Eckel, J.R. Microbit studies of the effect of fluid properties and hydraulics on drilling rate. J. Pet. Technol. 1967, 19, 541–546. [Google Scholar] [CrossRef]
- Eren, T.; Ozbayoglu, M.E. Real-time drilling rate of penetration performance monitoring. In Proceedings of the Offshore Mediterranean Conference and Exhibition, Ravenna, Italy, 23 March 2011. [Google Scholar]
- Warren, T.M. Drilling Model for Soft-Formation Bits. J. Pet. Technol. 1981, 33, 963–970. [Google Scholar] [CrossRef]
- Warren, T.M. Factors Affecting Torque for a Roller Cone Bit. J. Pet. Technol. 1984, 36, 1500–1508. [Google Scholar] [CrossRef]
- Al-Betairi, E.A.; Moussa, M.M.; Al-Otaibi, S. Multiple regression approach to optimize drilling operations in the Arabian Gulf area. SPE Drill. Eng. 1988, 3, 83–88. [Google Scholar] [CrossRef]
- Maidla, E.E.; Ohara, S. Field Verification of Drilling Models and Computerized Selection off Drill Bit, WOB, and Drillstring Rotation. SPE Drill. Eng. 1991, 6, 189–195. [Google Scholar] [CrossRef]
- Hareland, G.; Rampersad, P.R. Drag-bit model including wear. In Proceedings of the SPE Latin America/Caribbean Petroleum Engineering Conference, Buenos Aires, Argentina, 27–29 April 1994. [Google Scholar] [CrossRef]
- Motahhari, H.R.; Hareland, G.; James, J.A. Improved drilling efficiency technique using integrated PDM and PDC bit parameters. J. Can. Pet. Technol. 2010, 49, 45–52. [Google Scholar] [CrossRef]
- Hareland, G.; Wu, A.; Rashidi, B.; James, J.A. A new drilling rate model for tricone bits and its application to predict rock compressive strength. In Proceedings of the 44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27 June 2010. [Google Scholar]
- Alum, M.A.; Egbon, F. Semi-analytical models on the effect of drilling fluid properties on rate of penetration (ROP). In Proceedings of the Nigeria Annual International Conference and Exhibition, Abuja, Nigeria, 30 July–3 August 2011. [Google Scholar] [CrossRef]
- Moazzeni, A.R.; Khamehchi, E. Rain optimization algorithm (roa): A new metaheuristic method for drilling optimization solutions. J. Pet. Sci. Eng. 2020, 195, 107512. [Google Scholar] [CrossRef]
- Jahanbakhshi, R.; Keshavarzi, R.; Jafarnezhad, A. Real-time prediction of rate of penetration during drilling operation in oil and gas wells. In Proceedings of the 46th US Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 24 June 2012. [Google Scholar]
- Bataee, M.; Irawan, S.; Kamyab, M. Artificial neural network model for prediction of drilling rate of penetration and optimization of parameters. J. Jpn. Pet. Inst. 2014, 57, 65–70. [Google Scholar] [CrossRef]
- Kahraman, S. Estimating the Penetration Rate in Diamond Drilling in Laboratory Works Using the Regression and Artificial Neural Network Analysis. Neural Process. Lett. 2016, 43, 523–535. [Google Scholar] [CrossRef]
- Hegde, C.; Daigle, H.; Millwater, H.; Gray, K. Analysis of Rate of Penetration (ROP) Prediction in Drilling Using Physics-Based and Data-Driven Models. J. Pet. Sci. Eng. 2017, 159, 295–306. [Google Scholar] [CrossRef]
- Anemangely, M.; Ramezanzadeh, A.; Tokhmechi, B.; Molaghab, A.; Mohammadian, A. Drilling rate prediction from petrophysical logs and mud logging data using an optimized multilayer perceptron neural network. J. Geophys. Eng. 2018, 15, 1146–1159. [Google Scholar] [CrossRef]
- Elkatatny, S. Development of a new rate of penetration model using self-adaptive differential evolution-artificial neural network. Arab. J. Geosci. 2019, 12, 19. [Google Scholar] [CrossRef]
- Sobhi, I.; Dobbi, A.; Hachana, O. Prediction and analysis of penetration rate in drilling operation using deterministic and metaheuristic optimization methods. J. Pet. Explor. Prod. Technol. 2022, 12, 1341–1352. [Google Scholar] [CrossRef]
- Mantha, B.; Samuel, R. ROP optimization using artificial intelligence techniques with statistical regression coupling. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, UAE, 26–28 September 2016. [Google Scholar] [CrossRef]
- Abdulmalek, A.S.; Salaheldin, E.; Abdulazeez, A.; Mohammed, M.; Abdulwahab, Z.A.; Mohamed, I.M. Prediction of rate of penetration of deep and tight formation using support vector machine. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 23 April 2018. [Google Scholar] [CrossRef]
- Hegde, C.; Soares, C.; Gray, K. September. Rate of penetration (ROP) modeling using hybrid models: Deterministic and machine learning. In Proceedings of the Unconventional Resources Technology Conference, Houston, TX, USA, 23–25 July 2018. [Google Scholar] [CrossRef]
- Yavari, H.; Sabah, M.; Khosravanian, R.; Wood, D. Application of an adaptive neuro-fuzzy inference system and mathematical rate of penetration models to predicting drilling rate. Iran. J. Oil Gas Sci. Technol. 2018, 7, 73–100. [Google Scholar] [CrossRef]
- Gan, C.; Cao, W.; Wu, M.; Liu, K.Z.; Chen, X.; Hu, Y.; Ning, F. Two-level intelligent modeling method for the rate of penetration in complex geological drilling process. Appl. Soft Comput. 2019, 80, 592–602. [Google Scholar] [CrossRef]
- Dunlop, J.; Isangulov, R.; Aldred, W.D.; Sanchez, H.A.; Flores, J.L.; Herdoiza, J.A.; Belaskie, J.; Luppens, J.C. Increased rate of penetration through automation. In Proceedings of the SPE/IADC Drilling Conference and Exhibition, Amsterdam, The Netherlands, 1–3 March 2011. [Google Scholar] [CrossRef]
- Stelzer, C. Drillpipe Failure and Its Prediction Doctoral Dissertation; University of Leoben: Leoben, Austria, 2007. [Google Scholar]
- Hegde, C.; Gray, K.E. Use of Machine Learning and Data Analytics to Increase Drilling Efficiency for Nearby Wells. J. Nat. Gas Sci. Eng. 2017, 40, 327–335. [Google Scholar] [CrossRef]
- Hoseinie, S.H.; Ataei, M.; Osanloo, M. A new classification system for evaluating rock penetrability. Int. J. Rock Mech. Min. Sci. 2009, 46, 1329–1340. [Google Scholar] [CrossRef]
- Knez, D.; Calicki, A. Looking for a New Source of Natural Proppants in Poland. J. Bull. Pol. Acad. Sci. Tech. Sci. 2018, 66, 3–8. [Google Scholar] [CrossRef]
- Knez, D.; Mazur, S. Simulation of Fracture Conductivity Changes due to Proppant Composition and Stress Cycles. J. Pol. Miner. Eng. Soc. 2019, 2, 231–234. [Google Scholar]
- Niyazi, B. Determination of drillability of some natural stones and their association with rock properties. Sci. Res. Essays 2011, 6, 382–387. [Google Scholar] [CrossRef]
- Kuesel, T.R.; King, E.H.; Bickel, J.O. Tunnel Engineering Handbook; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Howarth, D.F. Experimental study on the relationship between rock texture and mechanical performance. Trans. Inst. Min. Metall. Sect. A 1986, 95, 41–45. [Google Scholar]
- Hoseinie, S.H.; Aghababaei, H.; Pourrahimian, Y. Development of a new classification system for assessing of rock mass drillability index (RDi). Int. J. Rock Mech. Min. Sci. 2008, 45, 1–10. [Google Scholar] [CrossRef]
- Knez, D.; Wiśniowski, R.; Owusu, W.A. Turning Filling Material into Proppant for Coalbed Methane in Poland—Crush Test Results. Energies 2019, 12, 1820. [Google Scholar] [CrossRef]
- Kumar, S.; Murthy, V.M.S.R. Experimental studies on drill penetration rate prediction in coal measure rocks through Cerchar hardness index tests. J. Mines Met. Fuels 2014, 62, 88–95. [Google Scholar] [CrossRef]
- Kumar, S.; Murthy, V.M.S.R. Predicting penetration rate for rotary blast hole drills in surface coal mines—An approach. In Proceedings of the 6th National Seminar on Surface Mining (NSSM), Indian School of Mines, Dhanbad, India, 10–11 January 2014. [Google Scholar]
- Khalilidermani, M.; Knez, D.; Zamani, M.A.M. Empirical Correlations between the Hydraulic Properties Obtained from the Geoelectrical Methods and Water Well Data of Arak Aquifer. Energies 2021, 14, 5415. [Google Scholar] [CrossRef]
- Knez, D.; Rajaoalison, H. Land Subsidence Assessment for Wind Turbine Location in the South-Western Part of Madagascar. Energies 2022, 15, 4878. [Google Scholar] [CrossRef]
- Knez, D.; Khalilidermani, M. A Review of Different Aspects of Off-Earth Drilling. Energies 2021, 14, 7351. [Google Scholar] [CrossRef]
- Knez, D.; Zamani, M.A.M. A Review of the Geomechanics Aspects in Space Exploration. Energies 2021, 14, 7522. [Google Scholar] [CrossRef]
- Mitchell, R.F.; Miska, S.Z. Fundamentals of Drilling Engineering; Society of Petroleum Engineers: Richardson, TX, USA, 2011; ISBN 978-1-61399-951-6. [Google Scholar] [CrossRef]
- Hossain, M.E.; Al-Majed, A.A. Fundamentals of Sustainable Drilling Engineering; Wiley: Hoboken, NJ, USA, 2015; pp. 374–412. [Google Scholar] [CrossRef]
- Knez, D.; Khalilidermani, M.; Zamani, M.A.M. Water Influence on the Determination of the Rock Matrix Bulk Modulus in Reservoir Engineering and Rock-Fluid Coupling Projects. Energies 2023, 16, 1769. [Google Scholar] [CrossRef]
- Knez, D.; Zamani, M.A.M. Empirical Formula for Dynamic Biot Coefficient of Sandstone Samples from South-West of Poland. Energies 2021, 14, 5514. [Google Scholar] [CrossRef]
- Zamani, M.A.M.; Knez, D. A New Mechanical-Hydrodynamic Safety Factor Index for Sand Production Prediction. Energies 2021, 14, 3130. [Google Scholar] [CrossRef]
- Rajaoalison, H.; Knez, D.; Zlotkowski, A. Changes of Dynamic Mechanical Properties of Brine-Saturated Istebna Sandstone under Action of Temperature and Stress. Przemysł Chem. 2019, 98, 801–804. [Google Scholar]
- Knez, D.; Rajaoalison, H. Discrepancy between Measured Dynamic Poroelastic Parameters and Predicted Values from Wyllie’s Equation for Water-Saturated Istebna Sandstone. Acta Geophys. 2021, 69, 673–680. [Google Scholar] [CrossRef]
- Young, F.S., Jr. Computerized Drilling Control. J. Pet. Technol. 1969, 21, 483–496. [Google Scholar] [CrossRef]
- Reza, M.R.; Alcocer, C.F. A unique computer simulation model well drilling: Part I-the reza drilling model. In Proceedings of the SPE California Regional Meeting, Oakland, CA, USA, 2–4 April 1986. [Google Scholar] [CrossRef]
- Ziaja, M.B.; Miska, S. Mathematical model of the diamond-bit drilling process and its practical application. Soc. Pet. Eng. J. 1982, 22, 911–922. [Google Scholar] [CrossRef]
- Osgouei, R.E. Rate of Penetration Estimation Model for Directional and Horizontal Wells; Middle East Technical University: Ankara, Turkey, 2007. [Google Scholar]
- Kirencigil, E. Numerical Modelling of the Hydraulic of the Drilling Process Using PDC Drill Bit; Graduate Faculty of the University of Akron: Akron, OH, USA, 2017. [Google Scholar]
- Boyun, G.; Gefei, L. Applied Drilling Circulation Systems (Hydraulic, Calculations and Models); Gulf Publishing Company: Houston, TX, USA, 2011; ISBN 978-0-12-381957-4. [Google Scholar]
- Langston, J.W. A Methtid of Utilizing Existing Information To optimize Drilling Procedures. J. Pet. Technol. 1966, 18, 677–686. [Google Scholar] [CrossRef]
- Khalilidermani, M.; Knez, D. A Survey of Application of Mechanical Specific Energy in Petroleum and Space Drilling. Energies 2022, 15, 3162. [Google Scholar] [CrossRef]
- Nearly All New U.S. Crude Oil and Natural Gas Wells Are Horizontal or Directional. Available online: https://www.eia.gov/todayinenergy/detail.php?id=52138 (accessed on 15 March 2023).
- Miska, S.Z.; Mitchell, R.F.; Ozbayoglu, E.M. Drilling Engineering: Advanced Applications and Technology, 1st ed.; McGraw Hill: New York, NY, USA, 2022. [Google Scholar]
- Chen, X.; Fan, H.; Guo, B.; Gao, D.; Wei, H.; Ye, Z. Real-time prediction and optimization of drilling performance based on a new mechanical specific energy model. Arab. J. Sci. Eng. 2014, 39, 8221–8231. [Google Scholar] [CrossRef]
- Hardness and Toughness of Rocks. Available online: https://www.911metallurgist.com/hardness-toughness-rocks/ (accessed on 11 April 2023).
- Mendes, J.R.P.; Fonseca, T.C.; Serapião, A. Applying a genetic neuro-model reference adaptive controller in drilling optimization. World Oil 2007, 228, 29–36. [Google Scholar]
- Paiaman, A.M.; Al-Askari, M.G.; Salmani, B.; Al-Anazi, B.D.; Masihi, M. Effect of drilling fluid properties on rate of penetration. Nafta 2009, 60, 129–134. [Google Scholar]
- Amar, K.; Ibrahim, A. Rate of Penetration Prediction and Optimization Using Advances in Artificial Neural Networks, a Comparative Study. In Proceedings of the 4th International Joint Conference on Computational Intelligence, Barcelona, Spain, 5–7 October 2012; SciTePress—Science and Technology Publications: Barcelona, Spain, 2012; pp. 647–652. [Google Scholar]
- Sultan, M.A.; Al-Kaabi, A.U. Application of neural network to the determination of well-test interpretation model for horizontal wells. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Melbourne, Australia, 8–10 October 2002. [Google Scholar] [CrossRef]
- Abtahi, A. Bit Wear Analysis and Optimization for Vibration Assisted Rotary Drilling (VARD) Using Impregnated Diamond Bits. Doctoral Dissertation, Memorial University of Newfoundland, St. John’s, NL, Canada, 2011. [Google Scholar]
- Hamrick, T.R. Optimization of Operating Parameters for Minimum Mechanical Specific Energy in Drilling; West Virginia University: Morgantown, WV, USA, 2011. [Google Scholar]
- Bahari, A.; Baradaran Seyed, A. Drilling cost optimization in a hydrocarbon field by combination of comparative and mathematical methods. Pet. Sci. 2009, 6, 451–463. [Google Scholar] [CrossRef]
- Anemangely, M.; Ramezanzadeh, A.; Tokhmechi, B. Determination of constant coefficients of Bourgoyne and Young drilling rate model using a novel evolutionary algorithm. J. Min. Environ. 2017, 8, 693–702. [Google Scholar] [CrossRef]
- Elkatatny, S. New approach to optimize the rate of penetration using artificial neural network. Arab. J. Sci. Eng. 2018, 43, 6297–6304. [Google Scholar] [CrossRef]
- Minghui, W.; Gensheng, L.; Huaizhong, S.; Shuaishuai, S.; Zhaokun, L.; Yi, Z. Theories and Applications of Pulsed-Jet Drilling with Mechanical Specific Energy. SPE J. 2016, 21, 303–310. [Google Scholar] [CrossRef]
- Dupriest, F.E.; Koederitz, W.L. Maximizing Drill Rates with Real-Time Surveillance of Mechanical Specific Energy. In Proceedings of the SPE Annual Technical Conference and Exhibition, Amsterdam, The Netherlands, 23 February 2005. [Google Scholar]
- Knez, D. Stress State Analysis in Aspect of Wellbore Drilling Direction. Arch. Min. Sci. 2014, 59, 71–76. [Google Scholar] [CrossRef]
- Bello, O.; Teodoriu, C.; Yaqoob, T.; Oppelt, J.; Holzmann, J.; Obiwanne, A. Application of artificial intelligence techniques in drilling system design and operations: A state of the art review and future research pathways. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Lagos, Nigeria, 2–4 August 2016. [Google Scholar] [CrossRef]
- Pollock, J.; Stoecker-Sylvia, Z.; Veedu, V.; Panchal, N.; Elshahawi, H. Machine learning for improved directional drilling. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2018. [Google Scholar] [CrossRef]
- Zakharov, L.A.; Martyushev, D.A.; Ponomareva, I.N. Predicting dynamic formation pressure using artificial intelligence methods. J. Min. Inst. 2022, 253, 23–32. [Google Scholar] [CrossRef]
- Angelini, E.; Ludovici, A. CDS evaluation model with neural networks. J. Serv. Sci. Manag. 2009, 2, 15. [Google Scholar] [CrossRef]
- Monjezi, M.; Dehghani, H. Evaluation of effect of blasting pattern parameters on back break using neural networks. Int. J. Rock Mech. Min. Sci. 2008, 45, 1446–1453. [Google Scholar] [CrossRef]
- Lippmann, R.P. An introduction to computing with neural nets. IEEE Assp Mag. 1987, 4, 4–22. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Ahmed, O.; Adeniran, A.; Samsuri, A. Drilling; Intech Open: London, UK, 2018. [Google Scholar] [CrossRef]
- Bilgesu, H.I.; Tetrick, L.T.; Altmis, U.; Mohaghegh, S.; Ameri, S. A New Approach for the Prediction of Rate of Penetration (ROP) Values. In Proceedings of the SPE Annual Technical Conference and Exhibition, Lexington, KY, USA, 22 October 1997; p. SPE-39231-MS. [Google Scholar]
- Mahdi, D.S. Predicting Drilling Rate of Penetration Using Artificial Neural Networks. In Proceedings of the 4th International Conference on Engineering Sciences (ICES 2020), Kerbala, Iraq, 5–6 December 2020. [Google Scholar] [CrossRef]
- Shi, X.; Liu, G.; Gong, X.; Zhang, J.; Wang, J.; Zhang, H. An efficient approach for real-time prediction of rate of penetration in offshore drilling. Math. Probl. Eng. 2016, 2016, 3575380. [Google Scholar] [CrossRef]
- Bodaghi, A.; Ansari, H.R.; Gholami, M. Optimized support vector regression for drillingrate of penetration estimation. Open Geosci. 2015, 7, 870–879. [Google Scholar] [CrossRef]
- Noshi, C.I.; Schubert, J.J. The role of machine learning in drilling operations; a review. In Proceedings of the SPE/AAPG Eastern Regional Meeting, Pittsburgh, PA, USA, 7–11 October 2018. [Google Scholar] [CrossRef]
- Mostafaei, K.; Maleki, S.; Mahmoudi, M.Z.A.; Knez, D. Risk management prediction of mining and industrial projects by support vector machine. Resour. Policy 2022, 78, 102819. [Google Scholar] [CrossRef]
- Moran, D.; Ibrahim, H.; Purwanto, A.; Osmond, J. Sophisticated ROP prediction technologies based on neural network delivers accurate drill time results. In Proceedings of the IADC/SPE Asia Pacific Drilling Technology Conference and Exhibition, Ho Chi Minh City, Vietnam, 1–3 November 2010. [Google Scholar] [CrossRef]
- AlArfaj, I.; Khoukhi, A.; Eren, T. Application of advanced computational intelligence to rate of penetration prediction. In Proceedings of the in UKSim/AMSS European Symposium on Computer Modeling and Simulation, Malta, Malta, 14–16 November 2012. [Google Scholar] [CrossRef]
- Cui, M.; Sun, M.C.; Zhang, J.; Kang, K.; Luo, Y. Maximizing drilling performance with real-time surveillance system based on parameters optimization algorithm. Adv. Pet. Explor. Dev. 2014, 8, 15–24. [Google Scholar]
- Amer, M.M.; Dahab, A.S.; El-Sayed, A.A.H. An ROP predictive model in Nile delta area using artificial neural networks. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 24–27 April 2017. [Google Scholar] [CrossRef]
- Elkatatny, S. Real-time prediction of rate of penetration while drilling complex lithologies using artificial intelligence techniques. Ain Shams Eng. J. 2021, 12, 917–926. [Google Scholar] [CrossRef]
- Lawal, A.I.; Kwon, S.; Onifade, M. Prediction of rock penetration rate using a novel antlion optimized ANN and statistical modelling. J. Afr. Earth Sci. 2021, 182, 104287. [Google Scholar] [CrossRef]
- Ansari, H.R.; Sarbaz Hosseini, M.J.; Amirpour, M. Drilling rate of penetration prediction through committee support vector regression based on imperialist competitive algorithm. Carbonates Evaporites 2017, 32, 205–213. [Google Scholar] [CrossRef]
- Rajaoalison, H.; Knez, D.; Zamani, M.A.M. A Multidisciplinary Approach to Evaluate the Environmental Impacts of Hydrocarbon Production in Khuzestan Province, Iran. Energies 2022, 15, 8656. [Google Scholar] [CrossRef]
- Fowell, R.J.; Mcfeat-Smith, I. Factors Influencing the Cutting Performance of a Selective Tunnelling Machine. In Proceedings of the First International Symposium on Tunnelling; Jones, J.M., Ed.; IMM: London, UK, 1976; Available online: https://pascal-francis.inist.fr/vibad/index.php?action=getRecordDetail&idt=PASCAL7780338404 (accessed on 11 April 2023).
- Wilbur, L. Rock Tunnels. In Tunnel Engineering Handbook; Bichel, J.O., Kuesel, T.R., Eds.; Van Nostrand Reinhold Company: New York, NY, USA, 1982. [Google Scholar]
- Bieniawski, Z.T. Engineering Rock Mass Classifications: A Complete Manual for Engineers and Geologists in Mining, Civil, and Petroleum Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1989; pp. 40–47. ISBN 0-471-60172-1. [Google Scholar]
- Barton, N.; Lien, R.; Lunde, J.J.R.M. Engineering classification of rock masses for the design of tunnel support. Rock Mech. 1974, 6, 189–236. [Google Scholar] [CrossRef]






| Reference | Controllable Factors | Uncontrollable Factors | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WOB | RPM | TVD | B | ρf | Q | Pm | S | Ab | E | Pp | T | Pe | Awell | ||||||
| Maurer, 1962 [14] | × | × | × | × | |||||||||||||||
| Galle and Woods, 1963 [15] | × | ||||||||||||||||||
| Bingham, 1965 [16] | × | × | × | × | |||||||||||||||
| Bourgoyne and Young, 1974 [3] | × | × | × | × | × | × | × | × | × | × | × | × | |||||||
| Warren (perfect model), 1981 [6] | × | × | × | × | |||||||||||||||
| Warren (imperfect model), 1984 [7] | × | × | × | × | × | × | × | ||||||||||||
| Reza and Alcocer, 1986 [64] | × | × | × | × | × | × | × | × | × | × | |||||||||
| Hareland and Rampersad, 1994 [24] | × | × | × | × | × | × | × | × | × | × | |||||||||
| Osgouei, 2007 [5] | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | ||||
| Reference | Bit Type | Well Direction | ||
|---|---|---|---|---|
| Roller-Cone Bit | Fixed-Cutter Bit | Vertical | Directional | |
| Maurer, 1962 [14] | × | × | ||
| Galle and Woods, 1963 [15] | × | × | ||
| Bingham, 1965 [16] | × | × | ||
| Bourgoyne and Young, 1974 [3] | × | × | ||
| Warren (perfect model), 1981 [6] | × | × | ||
| Warren (imperfect model), 1984 [7] | × | × | ||
| Reza and Alcocer, 1986 [64] | × | × | × | |
| Hareland and Rampersad, 1994 [24] | × | × | ||
| Osgouei, 2007 [5] | × | × | × | × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalilidermani, M.; Knez, D. A Survey on the Shortcomings of the Current Rate of Penetration Predictive Models in Petroleum Engineering. Energies 2023, 16, 4289. https://doi.org/10.3390/en16114289
Khalilidermani M, Knez D. A Survey on the Shortcomings of the Current Rate of Penetration Predictive Models in Petroleum Engineering. Energies. 2023; 16(11):4289. https://doi.org/10.3390/en16114289
Chicago/Turabian StyleKhalilidermani, Mitra, and Dariusz Knez. 2023. "A Survey on the Shortcomings of the Current Rate of Penetration Predictive Models in Petroleum Engineering" Energies 16, no. 11: 4289. https://doi.org/10.3390/en16114289
APA StyleKhalilidermani, M., & Knez, D. (2023). A Survey on the Shortcomings of the Current Rate of Penetration Predictive Models in Petroleum Engineering. Energies, 16(11), 4289. https://doi.org/10.3390/en16114289







