Evaluation of Voltage-Matched 2T Multi-Junction Modules Based on Monte Carlo Ray Tracing
Abstract
1. Introduction
2. Optical Model
- When the ray is traveling through an absorbing medium, an absorption probability is calculated, with being the absorption coefficient defined by Lambert–Beer’s Law and , where is the angle between and the direction. A random number is generated to determine whether the ray is actually absorbed into the current layer or not. In the former case, a new iteration is initialized, whereas in the latter case, the position of the ray is updated and the iteration continues;
- When the ray reaches an interface, reflection and transmission probabilities are calculated from the Fresnel Equation [6] and a random number is generated to determine if the ray is reflected or transmitted. In the former case, the ray remains in the current layer and its direction is updated according to [17]; in the latter case, the layer is changed, and the ray direction is updated according to [17];
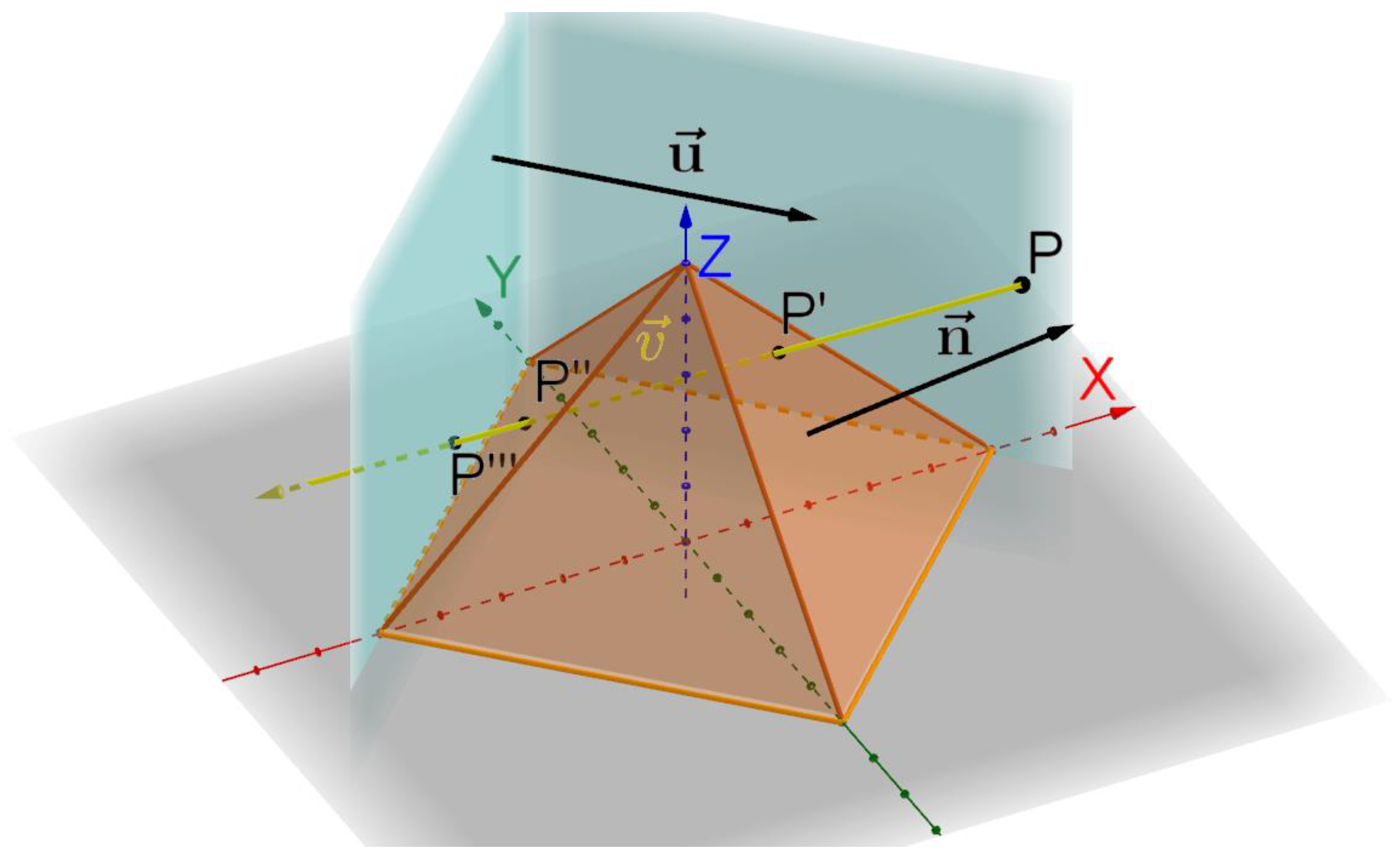
- When the ray approaches a pyramid, that is, when is in the range of the values of the points of the pyramid, the intersections between the and the faces of the pyramid and of the unit cell are calculated, if present. The closest point is selected, and, if the ray is traveling through an absorbing medium, a new absorption event is carried out as described above, with . If the ray has not been absorbed and lies on the pyramid, a new reflection/transmission event is carried out, whereas if lies on the face of the unit cell, periodic boundary conditions are applied and the position is updated as , where is the unit vector perpendicular to the face pointing inwards and is the length of the edge of the base of the pyramid. The geometry of this step is summarized in Figure 2;
- If the ray travels from one surface of the Si layer to the other without being absorbed, its and will be randomized with respect to the pyramid of the new surface. This step reflects the fact that the position of pyramids obtained through chemical etching of Si is not correlated with the two surfaces of the layer;
- If the ray is in one of the two semi-infinite air layers and is traveling away from the system, it is considered either reflected (if ) or transmitted (if ), and a new iteration is initialized.
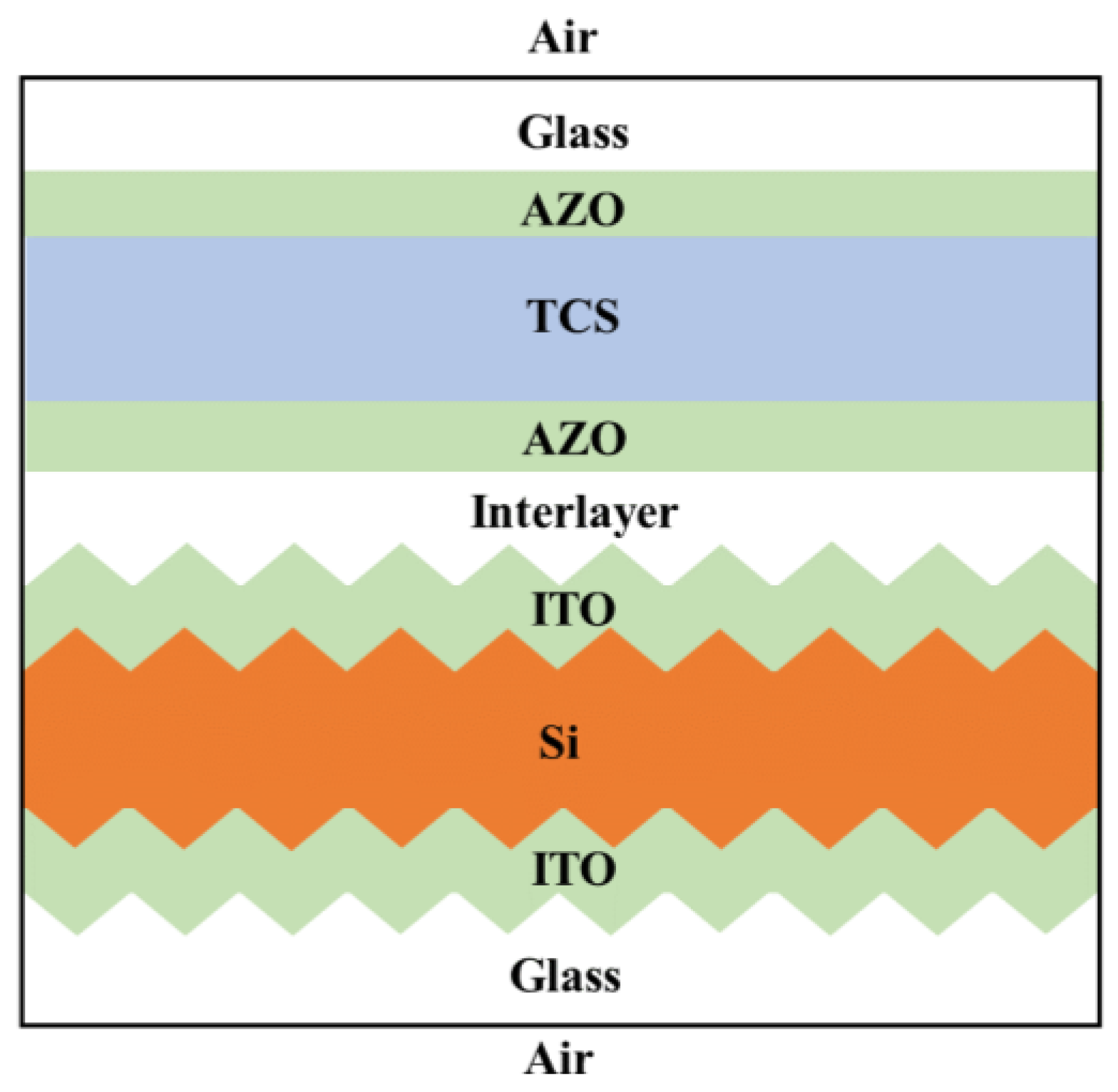
3. Electrical Model
4. Results and Discussion
4.1. VM2T Module Optimization
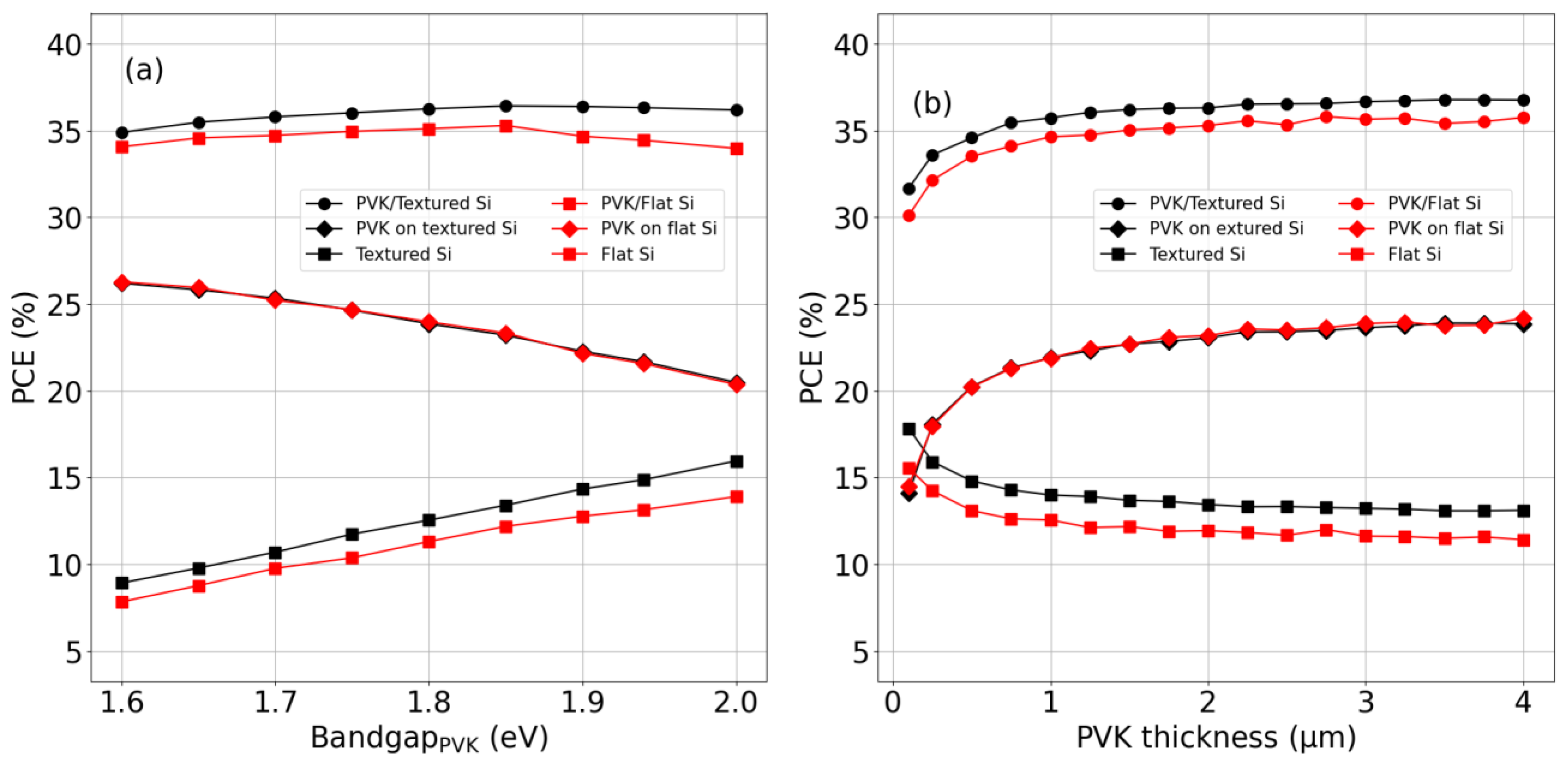
4.2. VM2T PVK/Si Module Analysis
5. State-of-the-Art Module Efficiencies
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fraunhofer Institute for Solar Energy Systems, ISE; PSE Projects GmbH. Photovoltaics Report (fraunhofer.de). Available online: https://www.ise.fraunhofer.de/content/dam/ise/de/documents/publications/studies/Photovoltaics-Report.pdf (accessed on 21 October 2022).
- Yu, Z.J.; Fisher, K.C.; Holman, Z.C. Evaluation of spectrum-splitting dichroic mirrors for PV mirror tandem solar cells. In Proceedings of the 2015 IEEE 42nd Photovoltaic Specialist Conference (PVSC), New Orleans, LA, USA, 14–19 June 2015. [Google Scholar] [CrossRef]
- Werner, J.; Niesen, B.; Ballif, C. Perovskite/Silicon Tandem Solar Cells: Marriage of Convenience or True Love Story?—An Overview. Adv. Mater. Interfaces 2018, 5, 1700731. [Google Scholar] [CrossRef]
- Wu, Y.; Kostuk, R.K. Two-junction holographic spectrum-splitting microconcentrating photovoltaic system. J. Photonics Energy 2017, 7, 17001. [Google Scholar] [CrossRef]
- Scuto, A.; Corso, R.; Leonardi, M.; Milazzo, R.G.; Privitera, S.M.S.; Colletti, C.; Foti, M.; Bizzarri, F.; Gerardi, C.; Lombardo, S.A. Outdoor performance of GaAs/bifacial Si heterojunction four-terminal system using optical spectrum splitting. Sol. Energy 2022, 241, 483–491. [Google Scholar] [CrossRef]
- Saleh, B.E.; Teich, M.C. Fundamentals of Photonics; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Nishigaki, Y.; Nagai, T.; Nishiwaki, M.; Aizawa, T.; Kozawa, M.; Hanzawa, K.; Kato, Y.; Sai, H.; Hiramatsu, H.; Hosono, H.; et al. Extraordinary strong band-edge absorption in distorted chalcogenide perovskites. Sol. RRL 2020, 4, 1900555. [Google Scholar] [CrossRef]
- Fashina, A.; Kana, M.G.Z.; Soboyejo, W.O. Optical reflectance of alkali-textured silicon wafers with pyramidal facets: 2D analytical model. J. Mater. Res. 2015, 30, 904–913. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, Y.; Wang, Y.; Chen, W.; Wu, J.; Zhao, Y.; Du, X. Optical properties of a random inverted pyramid textured silicon surface studied by the ray tracing method. Sol. Energy 2019, 186, 392–397. [Google Scholar] [CrossRef]
- Reiners, N.; Blieske, U. SMARTI—An Open Source Matlab Ray Tracing Tool for Solar Cell and Module Optics. In Proceedings of the 2018 7th International Energy and Sustainability Conference (IESC), Cologne, Germany, 17–18 May 2018. [Google Scholar] [CrossRef]
- Holst, H.; Winter, M.; Vogt, M.R.; Bothe, K.; Köntges, M.; Brendel, R.; Altermatt, P.P. Application of a New Ray Tracing Framework to the Analysis of Extended Regions in Si Solar Cell Modules. Energy Procedia 2013, 38, 86–93. [Google Scholar] [CrossRef]
- Rafiee, M.; Ahmed, H.; Chandra, S.; Sethi, A.; McCormack, S.J. Monte Carlo ray tracing modelling of multi-crystalline silicon photovoltaic device enhanced by luminescent material. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), Waikoloa, HI, USA, 10–15 June 2018. [Google Scholar]
- LIGHTHOUSE. Wafer Ray Tracer (pvlighthouse.com.au). Available online: https://www2.pvlighthouse.com.au/calculators/wafer%20ray%20tracer/wafer%20ray%20tracer.html (accessed on 14 April 2023).
- Essig, S.; Allebé, C.; Remo, T.; Geisz, J.F.; Steiner, M.A.; Horowitz, K.; Barraud, L.; Ward, J.S.; Schnabel, M.; Descoeudres, A.; et al. Raising the one-sun conversion efficiency of III–V/Si solar cells to 32.8% for two junctions and 35.9% for three junctions. Nat. Energy 2017, 2, 1–9. [Google Scholar] [CrossRef]
- Schulze, P.S.C.; Bett, A.J.; Bivour, M.; Caprioglio, P.; Gerspacher, F.M.; Kabaklı, Ö.Ş.; Richter, A.; Stolterfoht, M.; Zhang, Q.; Neher, D.; et al. 25.1% High-Efficiency Monolithic Perovskite Silicon Tandem Solar Cell with a High Bandgap Perovskite Absorber. Sol. RRL 2020, 4, 2000152. [Google Scholar] [CrossRef]
- Campbell, P.; Green, M.A. Light trapping properties of pyramidally textured surfaces. J. Appl. Phys. 1987, 62, 243–249. [Google Scholar] [CrossRef]
- De Greve, B. Reflections and refractions in ray tracing. Retrived Oct. 2006, 16, 2014. [Google Scholar]
- Green, M.A. Self-consistent optical parameters of intrinsic silicon at 300K including temperature coefficients. Sol. Energy Mater. Sol. Cells 2008, 92, 1305–1310. [Google Scholar] [CrossRef]
- Papatryfonos, K.; Angelova, T.; Brimont, A.; Reid, B.; Guldin, S.; Smith, P.R.; Tang, M.; Li, K.; Seeds, A.J.; Liu, H.; et al. Refractive indices of MBE-grown AlxGa (1 − x) As ternary alloys in the transparent wavelength region. AIP Adv. 2021, 11, 025327. [Google Scholar] [CrossRef]
- E Treharne, R.; Seymour-Pierce, A.; DuRose, K.; Hutchings, K.; Roncallo, S.; Lane, D. Optical Design and Fabrication of Fully Sputtered CdTe/CdS Solar Cells. J. Phys. Conf. Ser. 2011, 286, 012038. [Google Scholar] [CrossRef]
- Leem, J.W.; Yu, J.S. Influence of oblique-angle sputtered transparent conducting oxides on performance of Si-based thin film solar cells. Phys. Status Solidi (a) 2011, 208, 2220–2225. [Google Scholar] [CrossRef]
- Minoura, S.; Maekawa, T.; Kodera, K.; Nakane, A.; Niki, S.; Fujiwara, H. Optical constants of Cu (In, Ga) Se2 for arbitrary Cu and Ga compositions. J. Appl. Phys. 2015, 117, 195703. [Google Scholar] [CrossRef]
- Höhn, O.; Tucher, N.; Bläsi, B. Theoretical study of pyramid sizes and scattering effects in silicon photovoltaic module stacks. Opt. Express 2018, 26, A320–A330. [Google Scholar] [CrossRef]
- Standard Tables for Reference Solar Spectral Irradiances: Direct Normal and Hemispherical on 37° Tilted Surface (astm.org). Available online: https://www.astm.org/g0173-03r20.html (accessed on 22 December 2022).
- Shockley, W.; Queisser, H.J. Detailed Balance Limit of Efficiency of p-n Junction Solar Cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Richter, A.; Werner, F.; Cuevas, A.; Schmidt, J.; Glunz, S. Improved Parameterization of Auger Recombination in Silicon. Energy Procedia 2012, 27, 88–94. [Google Scholar] [CrossRef]
- Raja, W.; De Bastiani, M.; Allen, T.G.; Aydin, E.; Razzaq, A.; Rehman, A.U.; Ugur, E.; Babayigit, A.; Subbiah, A.S.; Isikgor, F.H.; et al. Photon recycling in perovskite solar cells and its impact on device design. Nanophotonics 2021, 10, 2023–2042. [Google Scholar] [CrossRef]
- Linss, V.; Dietsch, T.; Baumann, J.; Graupner, U.; Hoß, J.; Linke, J.; Lossen, J.; Polzin, J.I.; Mack, S.; Nagel, H.; et al. Single Sided High Throughput Sputter Process Technology for In-Situ Doped n-Type Amorphous Silicon Layers for High Efficiency TOPCon Solar Cells. In Proceedings of the 39th European Photovoltaic Solar Energy Conference and Exhibition, Milan, Italy, 26–30 September 2022; pp. 202–207. [Google Scholar]
- Monokroussos, C.; Salis, E.; Etienne, D.; Zhang, X.; Dittmann, S.; Friesen, G.; Morita, K.; Stang, J.; Herbrecht, T.; Fakhfouri, V.; et al. Electrical characterization intercomparison of high-efficiency c-Si modules within Asian and European laboratories. Prog. Photovolt. Res. Appl. 2019, 27, 603–622. [Google Scholar] [CrossRef]
- Basore, P.A. Multidimensional Fourier-Series Solution of the Quasi-Neutral Drift–Diffusion Equations. IEEE J. Photovolt. 2020, 10, 905–911. [Google Scholar] [CrossRef]
- Fell, A.; Fong, K.C.; McIntosh, K.R.; Franklin, E.; Blakers, A.W. 3-D Simulation of Interdigitated-Back-Contact Silicon Solar Cells With Quokka Including Perimeter Losses. IEEE J. Photovolt. 2014, 4, 1040–1045. [Google Scholar] [CrossRef]
- Varache, R.; Leendertz, C.; Gueunier-Farret, M.; Haschke, J.; Muñoz, D.; Korte, L. Investigation of selective junctions using a newly developed tunnel current model for solar cell applications. Sol. Energy Mater. Sol. Cells 2015, 141, 14–23. [Google Scholar] [CrossRef]
- Liu, Y.; Ahmadpour, M.; Adam, J.; Kjelstrup-Hansen, J.; Rubahn, H.-G.; Madsen, M. Modeling Multijunction Solar Cells by Nonlocal Tunneling and Subcell Analysis. IEEE J. Photovolt. 2018, 8, 1363–1369. [Google Scholar] [CrossRef]
- Jhuma, F.A.; Shaily, M.Z.; Rashid, M.J. Towards high-efficiency CZTS solar cell through buffer layer optimization. Mater. Renew. Sustain. Energy 2019, 8, 6. [Google Scholar] [CrossRef]
- Yaşar, S.; Kahraman, S.; Çetinkaya, S.; Apaydın, Ş.; Bilican, I.; Uluer, I. Numerical thickness optimization study of CIGS based solar cells with wxAMPS. Optik 2016, 127, 8827–8835. [Google Scholar] [CrossRef]
- Canino, M.; Boldrini, V.; Rizzoli, R.; Centurioni, E.; Maurizi, A.; Lombardo, S.; Terrasi, A.; Summonte, C. TCO Optimization of c-Si Heterojunction Solar Cells for Tandem Architecture by Optical Simulation. In Proceedings of the 38th European Photovoltaic Solar Energy Conference and Exhibition, Online, 6–10 September 2021; pp. 501–504. [Google Scholar] [CrossRef]
- Yoon, H.P.; Haney, P.M.; Yoon, Y.; An, S.; Basham, J.I.; Zhitenev, N.B. Local photocarrier dynamics in CdTe solar cells under optical and electron beam excitations. In Proceedings of the 2015 IEEE 42nd Photovoltaic Specialist Conference (PVSC), New Orleans, LA, USA, 14–19 June 2015. [Google Scholar]
- Brown, G.; Faifer, V.; Pudov, A.; Anikeev, S.; Bykov, E.; Contreras, M.; Wu, J. Determination of the minority carrier diffusion length in compositionally graded Cu(In,Ga)Se2 solar cells using electron beam induced current. Appl. Phys. Lett. 2010, 96, 022104. [Google Scholar] [CrossRef]
- Hu, Z.; Lin, Z.; Su, J.; Zhang, J.; Chang, J.; Hao, Y. A review on energy band-gap engineering for perovskite photovoltaics. Sol. RRL 2019, 3, 1900304. [Google Scholar] [CrossRef]
- Lucarini, V.; Saarinen, J.J.; Peiponen, K.E.; Vartiainen, E.M. Kramers-Kronig Relations in Optical Materials Research; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; Volume 110. [Google Scholar]
- Yu, Z.J.; Leilaeioun, M.; Holman, Z. Selecting tandem partners for silicon solar cells. Nat. Energy 2016, 1, 16137. [Google Scholar] [CrossRef]
- Li, X.; Xu, Q.; Yan, L.; Ren, C.; Shi, B.; Wang, P.; Mazumdar, S.; Hou, G.; Zhao, Y.; Zhang, X. Silicon heterojunction-based tandem solar cells: Past, status, and future prospects. Nanophotonics 2020, 10, 2001–2022. [Google Scholar] [CrossRef]
- Green, M.A.; Dunlop, E.D.; Hohl-Ebinger, J.; Yoshita, M.; Kopidakis, N.; Bothe, K.; Hinken, D.; Rauer, M.; Hao, X. Solar cell efficiency tables (Version 60). Prog. Photovolt. Res. Appl. 2022, 30, 687–701. [Google Scholar] [CrossRef]
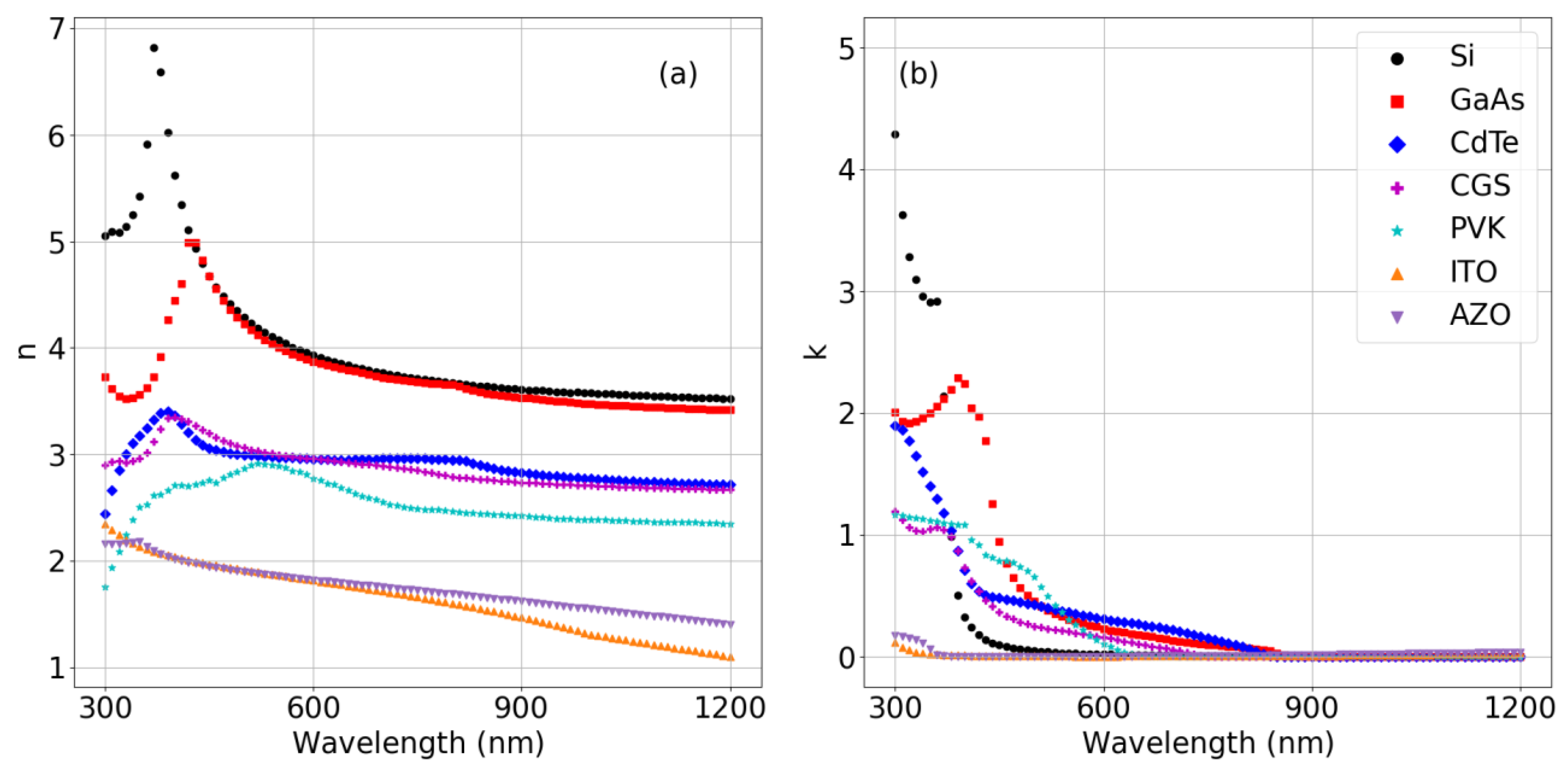
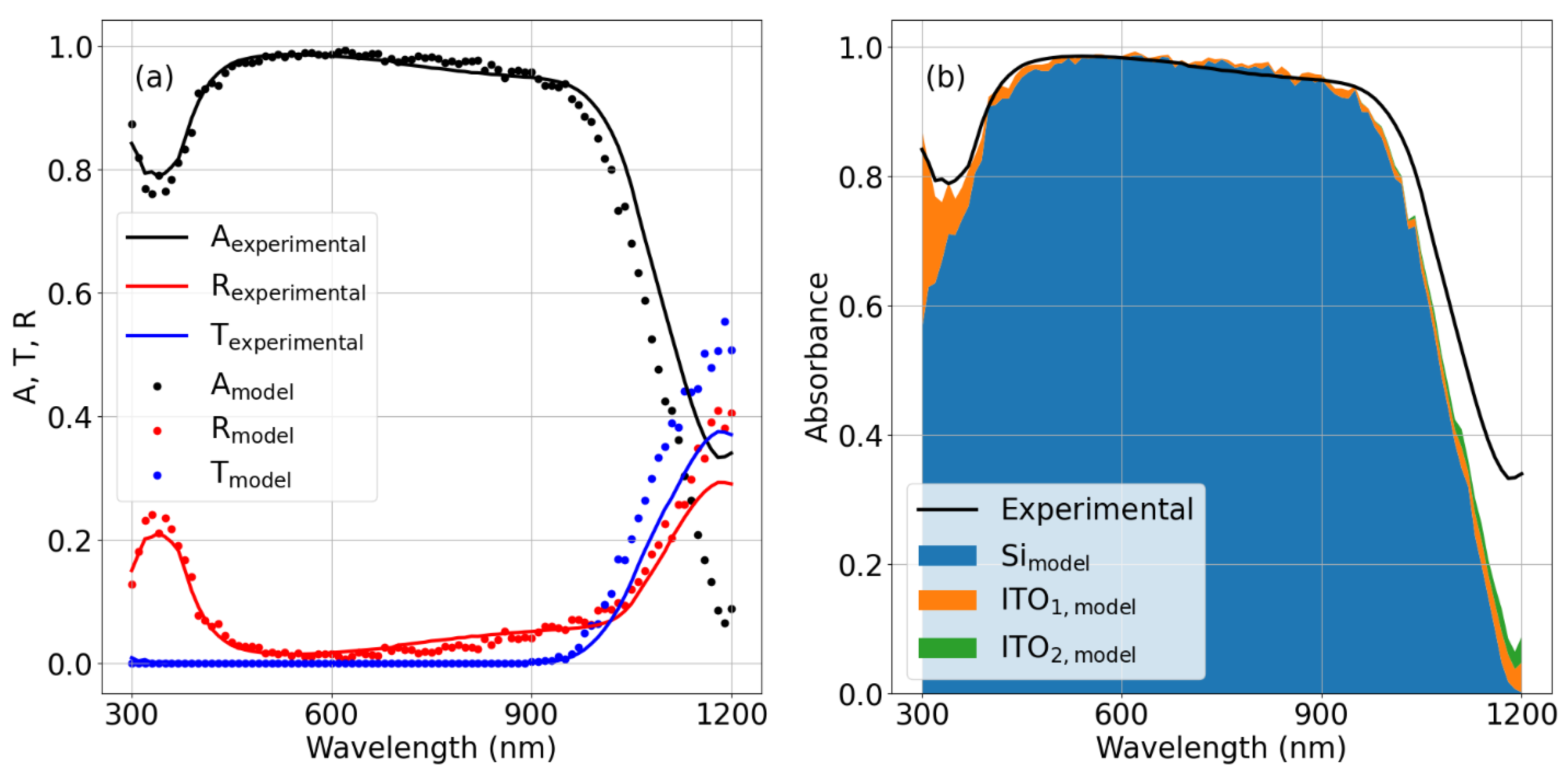
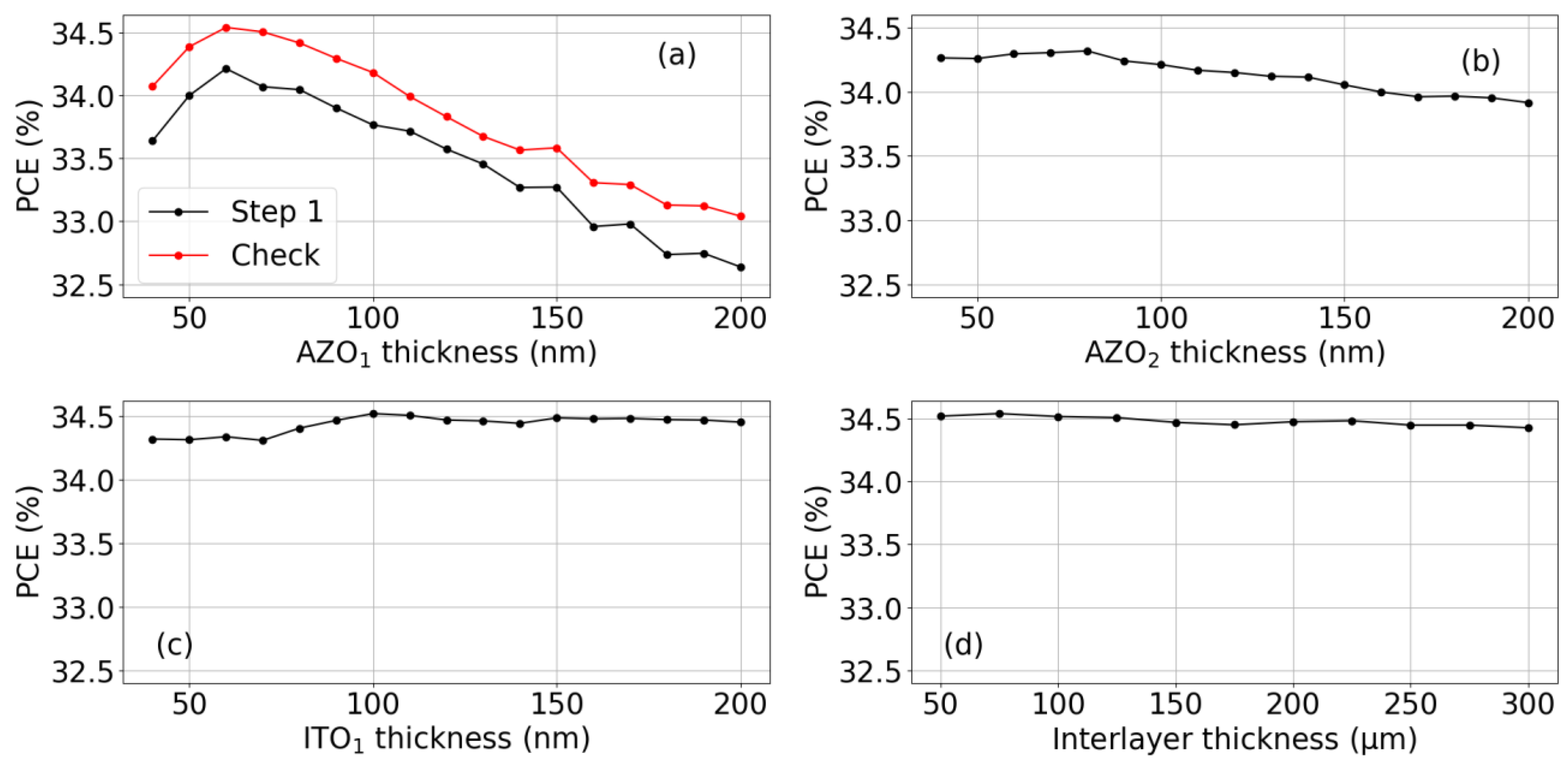
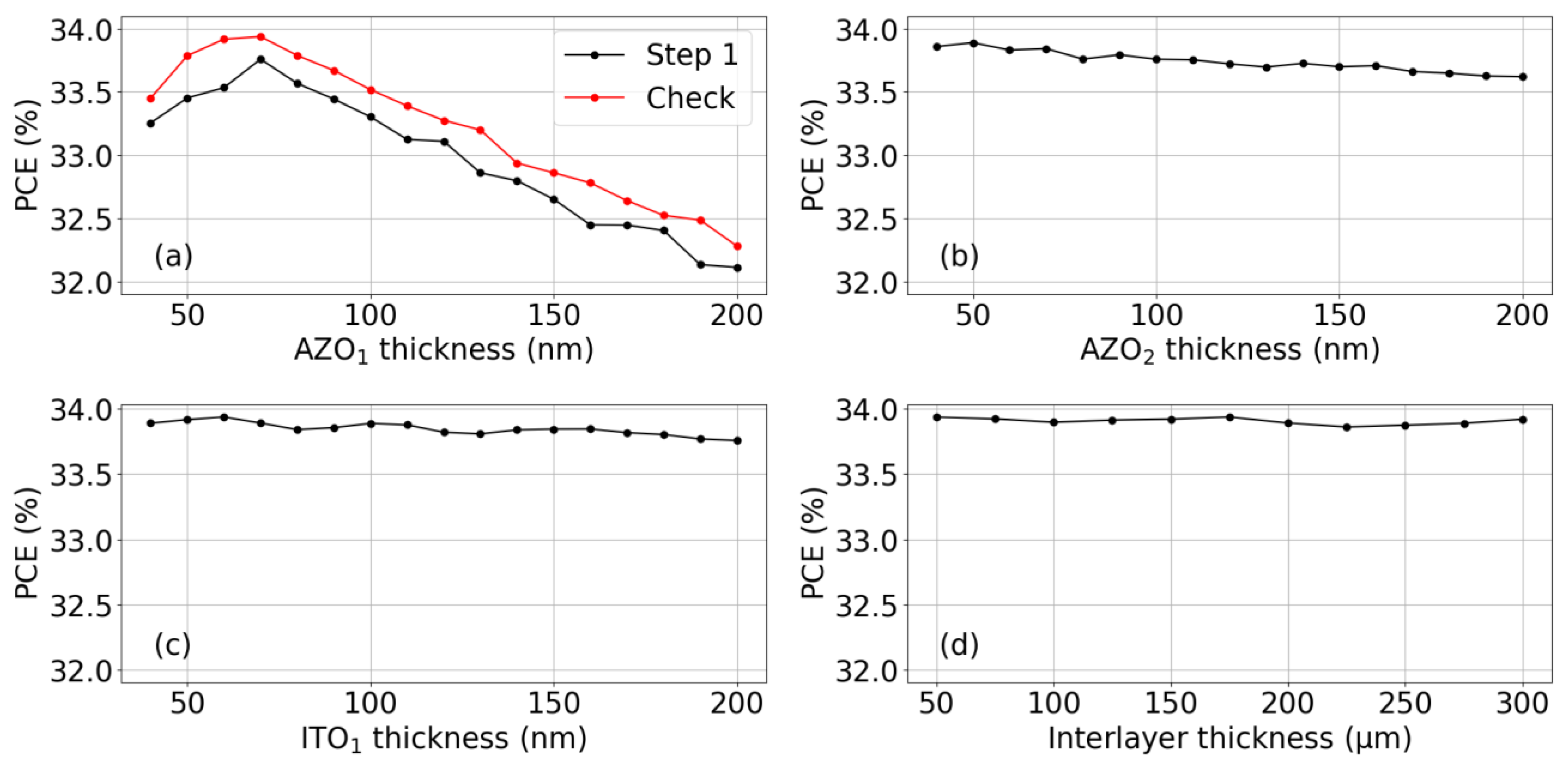
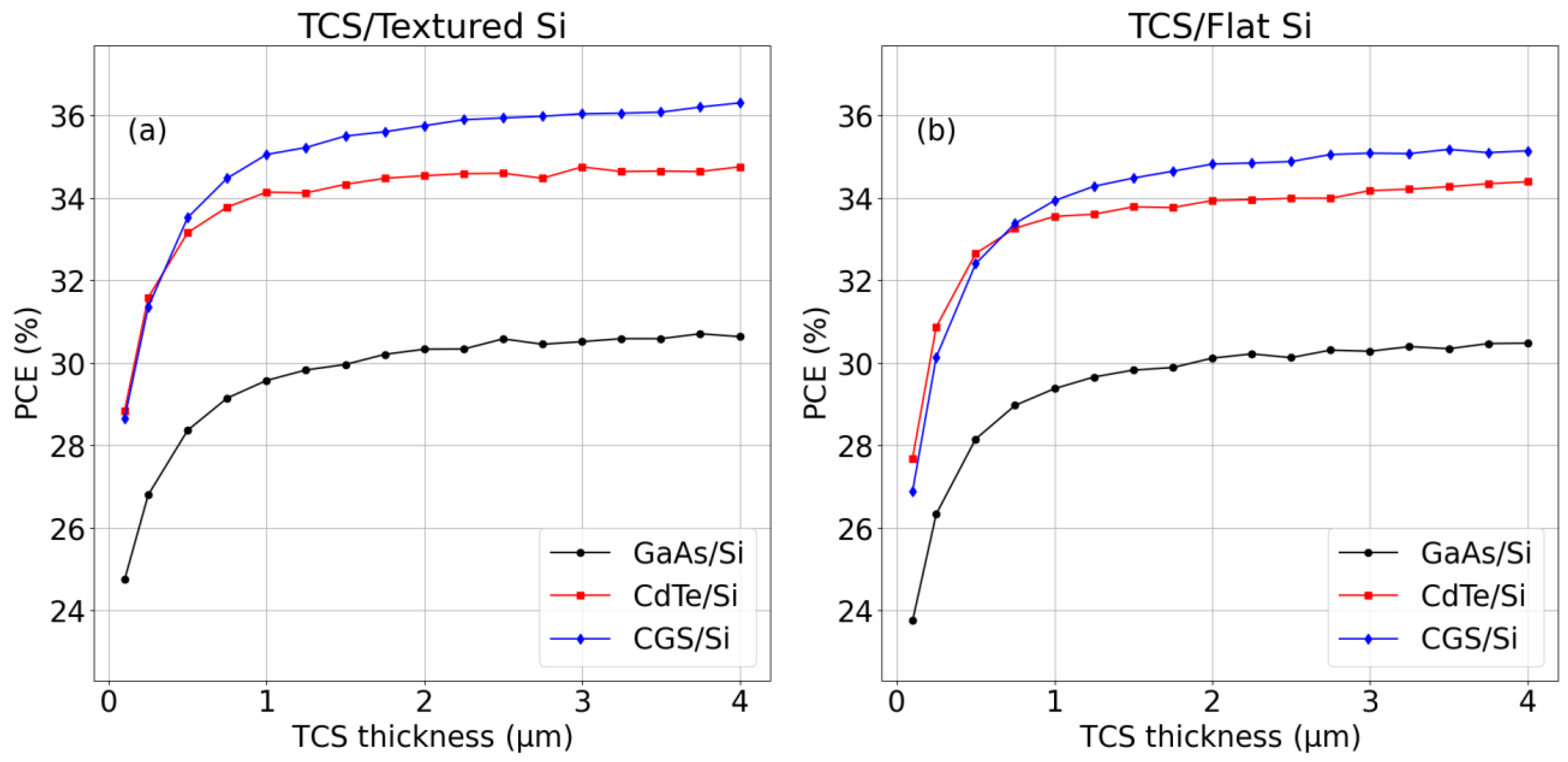
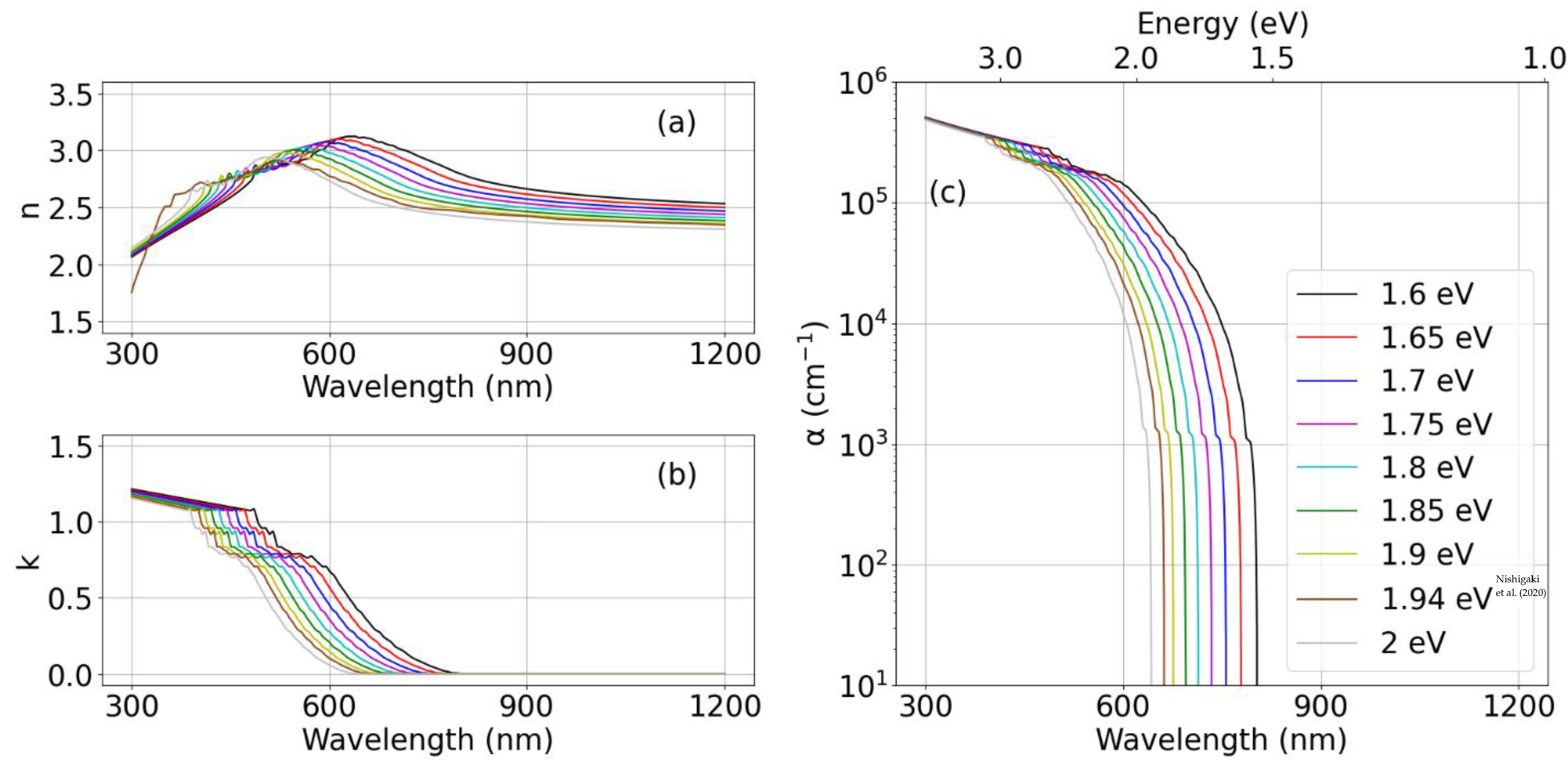
| Semiconductor | Bandgapthis work (eV) | Bandgapliterature (eV) | VOC,SA (V) | VOC,SQ (V) | TDC |
|---|---|---|---|---|---|
| Si | 1.12 | - | 0.738 | 0.860 | 0.858 |
| GaAs | 1.42 | - | 1.1272 | 1.144 | 0.985 |
| CdTe | 1.5 | - | 0.875 | 1.215 | 0.720 |
| CuIn1-xGaxSe2 | 1.7 (x = 1) | 1.08 | 0.734 | 0.822 | 0.893 |
| PVK | 1.85 | 1.67 | 1.213 | 1.374 | 0.883 |
| Module | PCETCS,SA (%) | PCEVM2T,SQ (%) | PCEVM2T,SA (%) | ||
|---|---|---|---|---|---|
| GaAs/Si | 50 | 44 | 29.1 | 30.51 | 29.45 |
| CdTe/Si | 48 | 57 | 21.0 | 34.53 | 25.24 |
| CGS/Si | 42 | 40 | 23.35 | 36.07 | 31.74 |
| PVK/Si | 38 | 37 | 23.7 | 36.77 | 34.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corso, R.; Leonardi, M.; Milazzo, R.G.; Scuto, A.; Privitera, S.M.S.; Foti, M.; Gerardi, C.; Lombardo, S.A. Evaluation of Voltage-Matched 2T Multi-Junction Modules Based on Monte Carlo Ray Tracing. Energies 2023, 16, 4292. https://doi.org/10.3390/en16114292
Corso R, Leonardi M, Milazzo RG, Scuto A, Privitera SMS, Foti M, Gerardi C, Lombardo SA. Evaluation of Voltage-Matched 2T Multi-Junction Modules Based on Monte Carlo Ray Tracing. Energies. 2023; 16(11):4292. https://doi.org/10.3390/en16114292
Chicago/Turabian StyleCorso, Roberto, Marco Leonardi, Rachela G. Milazzo, Andrea Scuto, Stefania M. S. Privitera, Marina Foti, Cosimo Gerardi, and Salvatore A. Lombardo. 2023. "Evaluation of Voltage-Matched 2T Multi-Junction Modules Based on Monte Carlo Ray Tracing" Energies 16, no. 11: 4292. https://doi.org/10.3390/en16114292
APA StyleCorso, R., Leonardi, M., Milazzo, R. G., Scuto, A., Privitera, S. M. S., Foti, M., Gerardi, C., & Lombardo, S. A. (2023). Evaluation of Voltage-Matched 2T Multi-Junction Modules Based on Monte Carlo Ray Tracing. Energies, 16(11), 4292. https://doi.org/10.3390/en16114292








