Abstract
The precise prediction of power estimates of wind–solar renewable energy sources becomes challenging due to their intermittent nature and difference in intensity between day and night. Machine-learning algorithms are non-linear mapping functions to approximate any given function from known input–output pairs and can be used for this purpose. This paper presents an artificial neural network (ANN)-based method to predict hybrid wind–solar resources and estimate power generation by correlating wind speed and solar radiation for real-time data. The proposed ANN allows optimization of the hybrid system’s operation by efficient wind and solar energy production estimation for a given set of weather conditions. The proposed model uses temperature, humidity, air pressure, solar radiation, optimum angle, and target values of known wind speeds, solar radiation, and optimum angle. A normalization function to narrow the error distribution and an iterative method with the Levenberg–Marquardt training function is used to reduce error. The experimental results show the effectiveness of the proposed approach against the existing wind, solar, or wind–solar estimation methods. It is envisaged that such an intelligent yet simplified method for predicting wind speed, solar radiation, and optimum angle, and designing wind–solar hybrid systems can improve the accuracy and efficiency of renewable energy generation.
1. Introduction
With the increase in the need for energy due to industrial development and high living standards, the whole world is looking for cheap and reliable energy resources. In previous years, renewable energy attracted extraordinary popularity because of the decrease in material costs, technological advancements, environment-friendliness quality, and favorable government policies [1]. Today, more efficient solar panels are still costly and it is more effective to use a hybrid system consisting of wind turbines and solar panels. Such hybrid systems consist of photovoltaic (PV) modules, a controller, a battery, and an inverter for AC output. Limited energy resources from coal and hydro are pushing the world to search for new energy resources that can overcome this situation. The increasing prices of fossil fuels have accelerated the trend of renewable energy. In addition, traditional fossil fuels have a significant impact on climate change and cause global warming [2]. On the other hand, wind and solar energies are available everywhere with various strengths and the whole world is shifting towards renewable resources. The capacity factor of wind turbines depends largely on two factors: the size of rotors and blades to cover a wider area and their placement at a higher altitude for attaining steady wind blows [3]. These factors, coupled with higher costs, reduce the usability of bigger sized turbines and encourage the use of more than one smaller turbine to achieve a similar capacity factor. Small turbines minimize costs and improve efficiency, as they may work at lower altitudes and with lesser wind speeds to start production.
Substantial work has been carried out on the use of solar energy to heat water in solar guizers and distill water. Conventional solar-operated systems still use only heat from the sun to perform actions. Solar-still systems are one of the most popular systems that use heat from the sun for water distillation. Conventional stills are of many types, such as the single effect, multi-effect, double slope, and wick [4]. The process used for this type of distillation consists of evaporating polluted water and then condensing its vapors in separate basins [5]. The efficiency level of solar-still systems has reached about 50% but a loss of 14% is very common due to bad insulation or degradation with time. In addition, increasing wind speeds decrease the efficiency by 2%. These days, only 5–10% of power is produced from wind and solar [6].
Energy from wind has been used since ancient times, where the harvested energy was utilized for different purposes such as crushing grains and pumping water. Nowadays this is again recharged, as it provides contamination-free energy. The framework used for the conversion of wind energy into mechanical power to run a generator is called a wind turbine. The model consists of multiple horizontal-axis turbines with solar panels instead of a single turbine with greater capacity because the rated wind speed for smaller turbines is less compared to larger turbines. In comparison with large wind turbines, multiple smaller wind turbines show better performance. This was concluded when two different types of wind–solar hybrid systems were set up with the same output power in Tianjin [7]. The power output of both systems was compared by measuring and simulating results in TRNSYS software (Version 18). The results showed that a wide range of wind speeds in multi-turbine wind–solar hybrid systems produce more power than the reference. Similarly, the power generated from the reference system increased by 18.6%, 53.7%, and 31% when used in other cities such as Shenyang, Guangzhou, and Shanghai, respectively [7]. Multiple turbines mean more than one turbine connected on the same or multiple poles but connected with the same system to provide power collectively. Furthermore, if one talks about a hybrid system, then this means an enhancement in reliability as compared to a standalone wind or solar system and this feature increases more in the case of multiple turbines. If one turbine fails because of any damage then the system is not significantly affected [8,9].
According to the International Renewable Energy Agency (IRENA), global renewable power capacity was 3064 GW by the end of 2021. With a 1230 GW capacity, hydropower contributed the greatest share of the world’s total. With a combined 88% of all net renewable additions in 2021, solar and wind energy remained the leaders in renewable capacity increases [10]. Thus, it is apparent from the report by IRENA and several other researchers [11,12] that wind–solar hybrid power generation is a growing trend in the energy sector. This technology combines two renewable energy sources, wind and solar power, to generate electricity. However, with the help of machine learning, the performance of this hybrid system can be optimized by predicting weather conditions and adjusting their output, accordingly [13]. Today, methodologies for learning-based modeling are used to create exact forecast models for renewable energy sources. Techniques using computational intelligence (CI) have been acknowledged as efficient ways to create and improve renewable energy generation. The energy complexity is dependent on the quantity of the data and parameters, both of which need to be carefully examined. Many studies have evaluated offshore wind energy but the research on wind-energy classification and wind-power-plant location is still a challenge, as larger wind turbines require installation sites with high wind speeds and these turbines are harmful to birds as well. The idea of multiple turbines presented in this study is the solution to this problem.
More machine-learning and artificial-intelligence techniques have been applied in forecasting as computer processing speeds have increased. Machine-learning algorithms typically produce better outcomes than statistical and physical forecasting methods [14]. However, the training process for machine learning requires a lot of data, and it is simple to overfit a model with a lot of variation in the training data [15]. It is possible to anticipate the production of wind and solar energy independently, and then one can simply add up the regional power. As solar and wind energy complement one another, when wind turbines and solar power plants are erected in a power plant or region, the combined use of solar and wind data can increase forecast accuracy [16,17].
2. Literature Review
Wind turbines convert the kinetic energy in the wind into mechanical power; the mechanical power can be used for specific tasks such as grinding grain or pumping water or a generator can convert this mechanical power into electricity to power homes, businesses, schools, and the like. Wind turbines come in many different sizes, from very large utility-scale turbines which generate electricity for large numbers of people to small turbines which are used to power a single home or business. However, it has been found that since the start of solar-hybrid power generation, the need for energy optimization has been apparent from the losses discussed in the research by [18]. It is impossible to predict the output of a renewable energy plant with perfect accuracy; however, a reasonable accuracy is achievable [19]. The wind and sun might be more intense in some places than others. The grid receives frequency management and voltage assistance from diesel power generators. It is possible for intermittent renewable energy generators to do this, but it will cost more money. Only the sun or the wind may be used as variable sources of renewable energy. Research conducted by [19] assesses several deep-learning (DL) and machine-learning (ML) algorithms used in the production of solar and wind energy. A new taxonomy is also used to investigate and assess the performance of the related approaches. Additionally, it provides thorough, cutting-edge approaches for assessing the effectiveness of the provided procedures. In a different article [20], a photovoltaic/wind turbine/batteries system is designed and optimised for the Bejaia (Algeria) location, a Mediterranean region with a wealth of renewable energy sources. The study employs Homer Pro software to identify the ideal design for the hybrid system under investigation and uses solar irradiation and wind speed as inputs. The recommended optimisation method is fuzzy logic control (FLC)-based. The main points and objectives of the study may be summed up as follows: a significant rise in renewable energy, resulting in reduced strain on the batteries in PV/wind systems. A novel technique using an artificial neural network is suggested in another paper [21] for a hybrid energy system. To improve power quality and reduce total harmonic distortion (THD), a controller for an artificial neural network is deployed. Simulink is employed for the proposed system, and its performance is examined under various operational conditions. The authors of [22] describe a power management method based on an artificial deep neural network (DNN) for a photovoltaic (PV) system with Li-ion batteries and a supercapacitor (SC) hybrid energy storage system (HESS). In this study, which is based on an artificial neural network, the energy management controllers for a photovoltaic hybrid power system with such a power supply are described. Using a traditional PV system, the effectiveness of the proposed power management approach is shown and confirmed for extending the life of Li-ion batteries. In order to meet the energy requirements of residential users and improve the performance of electrical networks, ref. [23] develops an enhanced control system using artificial neural network (ANN) ideas. The Levenberg–Marquardt algorithm provides connectivity in this method’s multi-level feedback network (MLFN), which allows data and calculations to flow from input to output in a predetermined manner. In a house that was installed in Bouismail, Algeria, during a summer week with suitable weather, the effectiveness of the suggested neural network based on a home-energy management system (NNHEMS) is demonstrated. Results show that by reducing energy usage by 24.6%, the proposed NNHEMS could manage energy in this solar home optimally.
Data-mining techniques are becoming increasingly popular in the wind energy sector, like many others. Utilizing predictive data-mining strategies can lead to cost savings in contemporary wind turbines [24]. In [25], a data-mining approach is applied in the operation and maintenance of wind turbines through the use of various machine-learning algorithms for condition monitoring. The research discovers correlations between signals recorded at different parts of the wind turbine, even with a limited sample size. The concept is demonstrated through a case study using SCADA data from an offshore wind farm. Another recent paper [24] finds that incorporating environmental factors such as relative humidity, ambient temperature, and wind speed into data-mining analysis helps predict the potential failures in key components of wind turbines, such as the gearbox, generator, and pitch and yaw system. The authors use both supervised and unsupervised data mining techniques to process wind turbine data and recommended timely component replacements to increase wind-turbine availability. The authors of [26] conduct an analysis of icing measurements from a cold-weather site. An interesting approach presented in [27] utilizes the autoregressive integrated moving average (ARIMA) model to forecast solar irradiance, taking into account the logarithmic value of the observed solar irradiance. Another method is [28], which compares the accuracy of the ARIMA model and a neural network model for short-term wind-speed forecasting and finds that the ARIMA model performs better. The researchers in [29] employ the auto-regressive moving average (ARMA) and wavelet transform to predict wind speed as part of planning a wind power system. On the other hand, the authors of [30] propose a time-series regression with the Box–Jenkins ARMA model to predict solar radiation.
Deep-learning methods have become increasingly popular recently and have been used widely to solve classification and regression problems. In [31], it is shown that deep-learning methods have an advantage compared to shallow methods in extracting the underlying natural structures and abstract features of data, making them a promising choice for wind-speed forecasting. In recent times, deep-learning methods such as the deep belief network (DBN) and long short-term memory (LSTM) have been used to establish wind-speed prediction models. The approach adopted in [32] proposes a DBN-based wind-speed prediction model, which is found to be accurate and stable through case studies. The authors of [33] develop an efficient wind-speed model using the DBN and transfer learning. An interesting method presented in [34] introduces an LSTM-based wind-speed forecasting model which demonstrates satisfactory prediction performance. The authors of [35] investigate the impact of certain features on the accuracy of wind-speed and wind-power prediction. The data collected from wind turbines is mapped to a grid space referred to as a ’scene’. The scene time series is a multi-channel image which represents the spatial and temporal characteristics of wind in a particular area and time. Based on these images, the researchers develop a prediction model using a convolutional neural network (CNN) to extract features. The results show that the proposed model outperforms existing methods and that wind speed is easier to predict than wind power, as the latter is dependent on the specific characteristics of the wind turbine. The approach presented in [36] also uses two-dimensional data, which represent multiple temporal wind speeds at multiple locations, as inputs for their day-ahead wind-speed forecasting model. The structure and hyperparameters of the CNN model are optimized using the Taguchi method, resulting in a highly accurate model.
From the literature, and feasibility reports [37,38,39,40], it is apparent that there are still substantial obstacles in the way of mainstream adoption of renewable energy. Some of these have to do with solar and wind energy, while others are tied to the transportation, laws, and market restrictions of the day. The cost of creating and installing facilities such as solar or wind farms is now the biggest and best-known obstacle to the adoption of renewable energy. To properly utilize renewable sources, a sizable amount of extra transmission infrastructure is required. Despite a booming industry, an overstocking problem was caused by the significant rise in panel output. As the number of wind–solar hybrid energy-generating systems rises, it will be essential to find more appropriate, industry-specific methodologies to improve accuracy and give the world various financial and environmental benefits. These systems have the potential to reduce losses in energy production and increase efficiency. Since there are still some losses associated with these systems that need to be addressed. In this paper, we discuss various losses in wind–solar hybrid energy-generation systems and how machine learning can be used to reduce these losses, and how systems can be optimized for better efficiency.
Most academics agree that incorporating datasets increases prediction performance [41]; nonetheless, the relationship between such elements and prediction output varies by area. To conclude, further comparison experiments must be conducted to illustrate the influence of integrating certain meteorological information on the model’s performance. It is not possible to create a forecasting model for every area. In this paper, the region of Thatta, a city in Pakistan’s Sindh province which is well-known for its capacity to produce renewable energy, primarily from wind and solar sources, is studied for real-time hybrid wind–solar resource assessment and power estimation. Thatta has a mean wind speed of around 6.5 m per second at a height of 100 m above sea level, according to the Global Wind Atlas. This indicates Thatta’s potential for producing wind energy is tremendous [42]. Thatta has tremendous potential for solar-energy generation in addition to wind energy [43]. With a daily average solar radiation of about 5.5 kWh/, the city has a high solar irradiance. This implies that Thatta has great potential for solar-energy production, especially when solar panels are installed. More thorough investigations and analysis are needed in order to pinpoint Thatta’s precise wind and solar energy-generating potential. The precise locations and features of possible wind and solar energy projects, as well as other environmental and regulatory considerations that may have an influence on energy output, would all be taken into account in these analyses [44]. This is where this research using artificial neural networks plays a role in predicting the wind and solar power-generation capacity of Thatta.
The desire to cut greenhouse-gas emissions and move towards a more sustainable energy future has made it more crucial than ever to integrate renewable energy sources, including wind and solar, into the electrical grid. Renewable energy sources can be unpredictable and variable, which makes it difficult to integrate them into the system. To run the system effectively and use renewable energy sources to their full potential, accurate real-time assessments of the available wind and solar resources and power estimation are essential. Real-time hybrid wind–solar resource assessment and power estimation have been developed using an artificial neural network (ANN)-based method to solve this problem. This method trains an ANN to predict the availability of wind and solar resources in real time and estimate their power output using past data on weather and energy production. This method uses ANNs to identify intricate correlations between weather and energy production that might not be immediately obvious when using conventional statistical methods. This method’s real-time hybrid wind–solar resource evaluation and power estimation can help with efficient grid management and increased use of renewable energy sources, paving the way for a more efficient and sustainable energy future. The primary benefit of ANN is its capacity to analyze and handle non-linearity in data pertaining to wind power generation.
3. Proposed Method
The methodology for an ANN-based wind–solar hybrid system can be divided into the following steps.
- Data collection: The first step is to gather relevant data on wind and solar energy production. This data can be obtained from various sources, including meteorological data, weather forecasts, and actual wind and solar power-production data from existing wind and solar farms. The data used for our model was collected for first 200 days of 2022.
- Data preprocessing: The collected data must be preprocessed to remove any outliers, inconsistencies, and missing values. This step is crucial for ensuring the accuracy of any machine-learning model. The training dataset was normalized to fall between [0] and [1].
- Feature selection: The next step is to select the relevant features that are most indicative of wind and solar energy production. This can be performed by using various feature-selection techniques, such as correlation analysis and mutual information. Weibull distribution was utilized in our model to assess product dependability, model failure rates, and life data.
- Model selection: Based on the selected features, a suitable machine-learning model must be chosen. This can be a regression model, decision tree, random forest, or neural network, among others. The choice of the model depends on the complexity of the data, the number of features, and the desired prediction accuracy. The model chosen in this study was artificial neural network (ANN) due to its capacity to analyze and handle non-linearity in data pertaining to wind–solar power generation.
- Model training: The selected model must be trained on the preprocessed data using an appropriate training algorithm, such as gradient descent or backpropagation. The model must be trained until the prediction accuracy is satisfactory. The proposed model utilizes a feedforward back propagation neural network (FFBPN-net) [45]. The primary reason for the selection of a feed-forward back propagation network (FFBPN) is to discover and map the connections between inputs and outputs. In order to attain the least amount of error, a system’s weight values and threshold values are also adjusted using the FFBPN learning rule. The model was trained on FFBPN Equation (1) until the required criteria were met.where wki is the weight link value between the neuron and the variable, is the variable’s initial value, and xk is its updated value. The logsig activation function in Equation (2) was used between the input layer and the hidden layer.The linear function was used as an activation function between the hidden and output layer, as it just returns the value without making any changes to the weighted sum of the input.
- Model validation: The trained model must be validated using a validation dataset to ensure that the model is not overfitting the training data. This step is crucial to ensure that the model can generalize well to the unseen data. In our model, the training set and testing set were split at a ratio of 0.7 to 0.3.
- Model deployment: Once the model has been trained and validated, it can be deployed in the wind–solar hybrid system. The model can be used to predict wind and solar energy production for a given set of weather conditions and to optimize the operation of the hybrid system.
- Model monitoring and maintenance: The performance of the deployed model must be monitored regularly, and any necessary updates or improvements must be made to ensure that the model continues to perform well over time. Mean absolute percentage error (MAPE) is the most widely used performance measure for energy-generation prediction models, which is also used in this study.
A suitable topology and architecture of AN-net are employed for the prediction of wind speed shown in Figure 1, which can be used for the estimation of power from multiple turbines, as required in the design of the wind–solar hybrid system. The purpose was to improve the accuracy level in design and reduce the maintenance cost as well as losses. AN-nets are used in many different fields such as signal processing [46], feature extraction [47] and optimization [48].
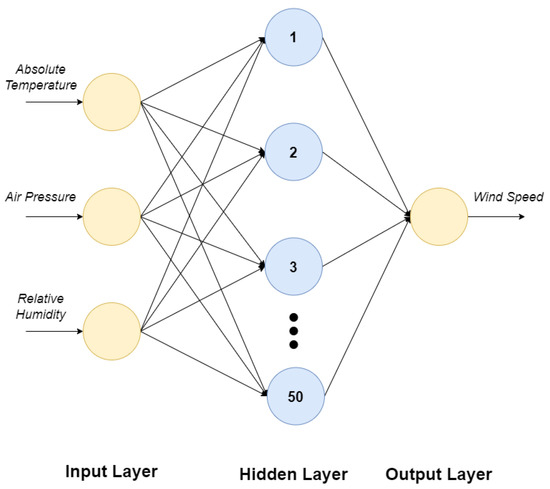
Figure 1.
Architecture of the AN-Net used.
As shown in Figure 1, the structure proposed in this study is a fully connected feedforward back propagation neural network (FFBPN-net). AN-nets consist of three types of layers named input layer, hidden layers, and output layer. The input layer is responsible for collecting input data from the user while the output layer provides processed results. The number of input and output neurons depends on the number of input parameters and target values in each provided example, respectively. The computational process takes place in hidden layers because of the weights which are updated; this process is called training. Furthermore, training can be supervised (training with inputs and outputs provided) and unsupervised type (training with inputs only). The data is split for training and test purposes in different ratios; however, a 0.7 to 0.3 ratio is most common.
3.1. Levenberg–Marquardt vs. Gauss Newton
The Levenberg–Marquardt algorithm (D. Marquardt, 1963) was developed by Kenneth Levenberg and Donald Marquart and converges solutions for non-linear problems. This algorithm is popular for fast convergence of small- and medium-sized problems and is more robust than Gauss–Newton. Handling multiple free parameters which are not even known properly is also a plus point of the Levenberg–Marquardt training algorithm. Even if initial weights are called by a random function, it can find the optimal solution easily.
3.2. Data Used for Training and Validation
Data for training and validation was collected from Thatta in Pakistan, which is known for being a suitable location for wind power plants due to high wind speeds all through the year [49]. However, it also has a high potential for solar power plants; a few have already been installed in Gharo, Thatta. Thus, the dataset was chosen carefully for locations that provide an ideal situation for wind–solar hybrid power plants.
3.2.1. Temperature
The degree of hotness and coldness of air is known as air temperature. It is directly proportional to the energy held in the air. In all regions, air temperature increases during the day and decreases at night. This temperature has a great effect on the climate of the region and that is the reason it is used by scientists to track climate change. Air temperature has a significant effect on creating high- or low-pressure regions at any location, which affects the airspeed. Wind speed and direction are somehow affected by Coriolis force and surface friction but are neglected in this study as this effect is not dominant in the case of wind speed and has a greater effect on wind direction. In the northern hemisphere, Coriolis force causes wind deflection clockwise around high-pressure regions and anti-clockwise in the case of low-pressure regions. Similarly, the opposite case occurs in the case of the southern hemisphere.
3.2.2. Air Pressure
Air pressure is the weight of the air column at any point. At high elevations, there is less air above the surface than at sea level, which means there is less air pressure at high altitudes. Changes in pressure indicate the weather conditions; a low-pressure system is associated with being cloudy and wetter while a high-pressure system is associated with clear and dry conditions.
3.2.3. Relative Humidity
All types of air contain some water vapors and the amount of water vapors changes from place to place and time to time during the year due to evaporation from water resources and the respiration of plants. Relative humidity decreases when water vapors condense to form small drops of liquid water, clouds, and water droplets. Evaporation and condensation becoming the same is known as saturation at that temperature. An increase in humidity means the number of suspended particles in the air is increased, which has the positive effect of driving the wind turbine; however, at the same time, heavier air initially requires a higher pressure gradient to be moved. Furthermore, dry air density can be calculated by the ideal gas law; however, in reality, air contains some moisture at every temperature meaning the humid-air partial pressure of water vapors is required to be added to the ideal gas law.
where P is air pressure, shows air density, T is absolute temperature and R is the general gas constant.
The value of the general gas constant for dry air is 287.05 J/(kg·K). The dry-air density and relative humidity of the first six months of 2022 are shown in Figure 2 and Figure 3, respectively.
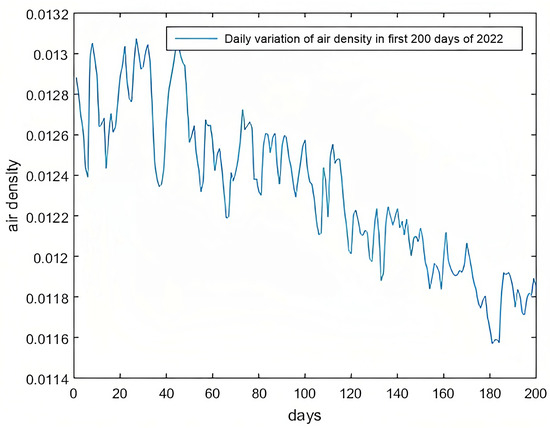
Figure 2.
Dry-air density trends.
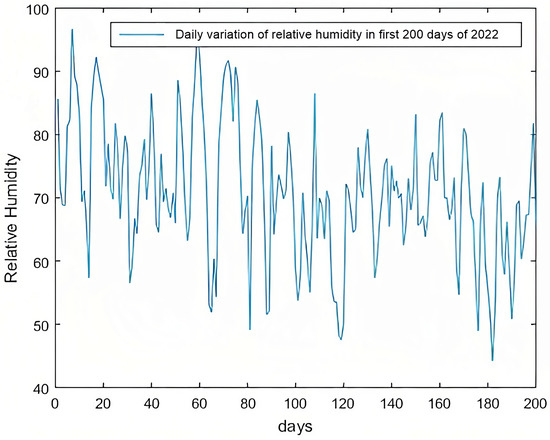
Figure 3.
Relative-humidity trends.
3.3. Weibull Distribution
Different types of distributions are used for different purposes. More commonly used distributions include the normal distribution, Rayleigh’s distribution, Bernoulli’s distribution, Poisson distribution, and Weibull distribution. The Weibull curve is very popular in prediction but there are certain limitations. The first problem of the Weibull curve is its limitation concerning the data type. For the Weibull curve to be used, it is recommended to check whether the data fit the Weibull distribution or not. A dataset of 50 random data points with 1.2 and 1.5 as values of shape and scale parameters, respectively, is generated. The straight-line graph confirms that the data fit the Weibull distribution as shown in Figure 4.
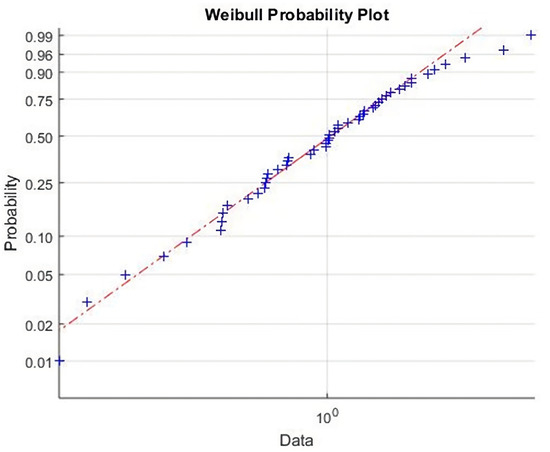
Figure 4.
Weibull probability plot.
Once the data type is confirmed, the probability distribution function can be written as
where K is the size parameter, C is shape parameter, and V is wind speed.
Weibull probability distribution and cumulative distribution functions can be used only if the values of shape and size parameters are known. Several different methods can be used to find these parameters such as the maximum likelihood method, empirical method, modified maximum likelihood method, and energy pattern factor method, etc. Maximum frequent wind speed can be found by
While maximum energetic wind speed is
3.4. Wind-Speed Prediction Using ANN
A fully connected feed-forward back-propagation neural network with a single hidden layer and a suitable number of neurons at the input, hidden, and output layers was used. The number of neurons in the hidden layer was changed from 25 to 50 and 500 to see the effect on the results. The learn gradient descent learning function with momentum weight (GDM) was used as an adaptation function. The mean square error (MSE) was used as a performance function while the transfer function used for the hidden layer was Logarithmic-Sigmoid (Logsig). Figure 5 shows the predicted wind speed (m/s) from above mentioned ANN architecture.
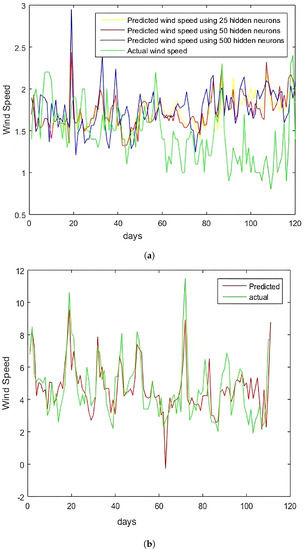
Figure 5.
(a) Comparison of predicted wind speeds (at 12-h intervals) using different hidden neurons, and (b) predicted wind speeds (daily basis) using optimized hidden neurons and layers.
As is clear from Figure 5a, increasing the number of neurons does not show any improvement in efficiency and it is advised to optimize the number of neurons, hidden layers, and the number of epochs according to data type. In the above case, results are improved while increasing neurons from 25 to 50. A further increase to 100 neurons does not improve results. Similarly, the results with 500 neurons are much higher than the actual. Figure 5b shows daily prediction using optimized hidden neurons, layers, and activation functions. Here, MAPE is used, which is a metric for assessing accuracy by calculating the sum of the absolute forecast errors divided by the actual values for each period. It measures errors based on the relative percentage of the forecasted values. A lower MAPE value indicates better predictive accuracy, with zero being the ideal target. Table 1 shows the comparison between different available research articles.

Table 1.
Performance comparison.
Clearly, from Table 1, studies achieve relatively high levels of MAPE for wind-speed prediction and solar prediction; however, our model achieved a lower MAPE compared to other wind–solar hybrid models. The inputs used in the studies are similar, with wind speed, direction, temperature, and pressure being common variables. Some studies also include relative humidity or solar radiation as additional inputs. More input variables does not guarantee an optimal solution; thus, to calculate the optimum function in ANNs, it is essential to make a careful choice of input variables. In addition, the use of feature selection is necessary in the case of wind–solar energy generation prediction. The results obtained through the proposed model achieve a low MAPE of 2.08%, because of the use of Weibull distribution on data, learn GDM as adaptation function, MSE as performance function, and Tansig transfer function. The most important parameter for achieving high accuracy is the use of accurate data and training with the optimized model for such data, and that is exactly what increases the accuracy.
4. Wind–Solar Hybrid System Modeling
Wind–solar hybrid systems combine solar photovoltaic cells and wind turbines to produce power from both solar and wind energy. The following are some features of such systems:
- An uninterrupted power supply is ensured by the combination of two or more energy-generating technologies and the integration of energy storage technology.
- Enhanced dependability: installing two or more energy systems improves the system’s dependability.
- Reduced carbon footprint by using fewer fossil fuels; hybrid systems have a smaller carbon impact.
Wind turbines, solar photovoltaic cells, controllers, batteries, inverters, AC and DC loads, etc., make up the bulk of a wind and solar hybrid system, as shown in Figure 6. The novelty of the proposed model lies in the prediction of wind speeds for increased power production after installation or location selection before installation. The optimum angle of inclination helps in maximizing the power generated through photovoltaic panels by moving the panels towards the sun throughout the power generation. The model provides lower MAPE, as shown in Table 1, thus allowing for accurate predictions resulting in a greater amount of power generation.
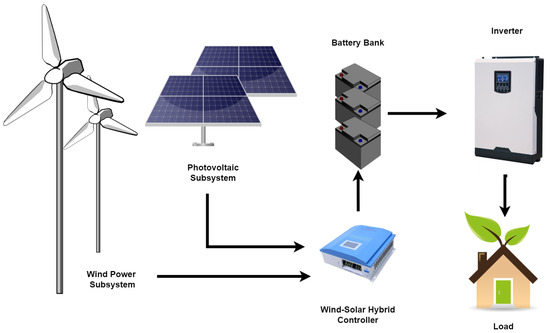
Figure 6.
Wind–solar hybrid system overview.
4.1. Solar-Panel-Array Modeling
Solar panels interconnected to produce power is called a solar array. A software named hybrid optimization of multiple energy resources (HOMER) is an optimization tool which is used to design micropower systems. It basically optimizes the capacity of items using techno-economic analysis. In this software, a wide range of optimization can be performed in fields of solar energy systems, wind energy systems, hydro energy systems, and conventional generator systems, which can be modeled and optimized. The output of the photovoltaic cell in HOMER can be calculated using Equation (7).
where is the output of array, is the rated capability, f is the degradation factor as a percentage, is solar radiation incident to the array in , shows solar radiation under standard conditions, is the temperature coefficient in %C, is the panel temperature, and indicates the panel temperature under standard conditions.
is normally taken as 1 . The radiations in the first five months of the year 2022 are given in Figure 7.
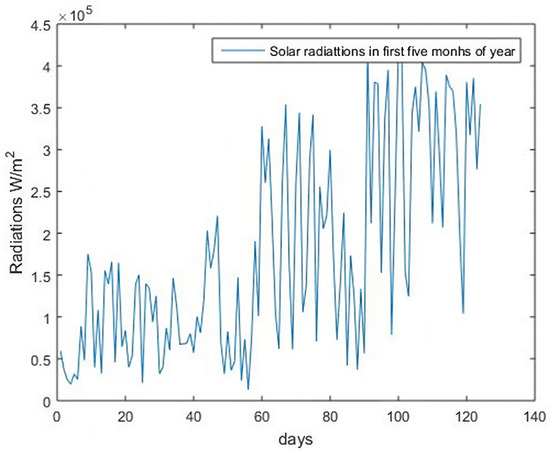
Figure 7.
Solar radiations in January–May 2022.
The efficiency of solar panels decreases with temperature and if no solar tracking system is used then the solar panels are held to a suitable inclination which is fixed. In this study, the suitable inclination angles for every month are discussed in Table 2. In addition, if there are alternating load types then converters can be used which convert AC into DC by a process called rectification.

Table 2.
Optimum angle and solar irradiance for each month.
4.2. Solar Radiance
To find the optimal angle of inclination, the solar energy received on 1 panel at different instances of the year at different angles (between 0–90) is derived with the help of simple integral calculations. The value of the optimum is given in Table 2. Using these angles, one can achieve maximum output from solar panels.
4.3. Power Produced by Wind Turbines
To calculate wind speed, there are three steps. The first step is to find the wind speed approaching the turbine using a logarithmic law which is used to find the air speed at a hub height. Then, the generated output of the turbine is calculated through a comparison of the characteristic curve provided by the manufacturer, measured wind speed, and standard air density at a height equal to the hub height. Finally, the final output is adjusted for the actual air density. Wind speed at the corresponding hub height is calculated as:
where is the wind speed at the hub height in m, V is the wind speed in m/s, f is the degradation factor as a percentage, is the hub height, H is the height of the wind-speed measurement point and is the logarithmic law exponent.
The actual output of the wind turbine is calculated by adjusting actual air density conditions using
In the above Equation, is the air density in kg/m, is the standard air density under standard atmospheric conditions, is the power produced by a wind turbine in under the standard conditions used by the turbine power curve, which is provided by manufacturers in Figure 8, below.
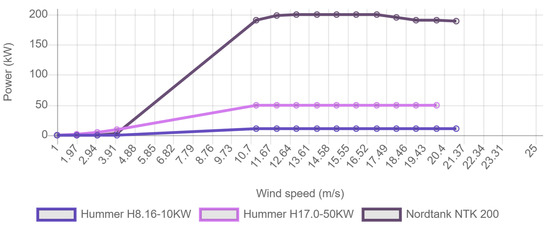
Figure 8.
Power vs wind speed curve for different rated wind turbines.
As mentioned previously, the is the density of air in , its value is 1.225 at standard conditions; A is the swept area of the wind-turbine blades in , which can be calculated by rotor diameter; and v is the upstream air speed in m/s. It is clear from the equation that wind power is cubic proportional to wind speed. The wind density measured at various locations is less diverse in nature as compared to wind speed. The wind-power capacity is proportional to the wind speed throughout the year [57]. Figure 8 provides a useful visualization of the relationship between the wind speed and power output of different turbines with a rated capacity of 10 kW, 50 kW, and 200 kW. The data required for this comparison was provided by [58]. The 11 m/s wind speed is required for rated outputs 10, 50, and 200 kW wind turbines and produces almost little to no power during 0–4 m/s wind speeds. Turbines are bound and are not allowed to produce power higher than that for which they are designed to avoid failures and this is achieved by adjusting blade angles. From this, it is apparent that the installation of wind turbines should only be carried out at locations with a minimum wind speed of 4 m/s, and a maximum of nearly 21 m/s, while the average should be around 11 m/s. However, these values can change depending on the design of the wind turbines. Furthermore, safety mechanisms in the case of high wind speed are necessary as well. Our model can help in the prediction of such high wind speeds.
5. Conclusions
Wind–solar hybrid systems are the most suitable type of energy extraction system from renewable energy resources and can address the energy shortage, which occurred due to development in the modern world. Hybrid systems are not only environmentally friendly but are more reliable than any other standalone system, as evident from the literature review. In this study, a fully connected feed-forward back-propagation neural network with a single hidden layer and a suitable number of neurons at the input, hidden, and output layers were used to predict the wind speed and optimum angle for PV panels with an MAPE of 2.08%. The number of neurons in the hidden layer was set to 50 after seeing no improvement after further increases. The learn gradient descent learning function with momentum weight (GDM) was used as an adaptation function and logsig as an activation function. However, it is to be noted that the accuracy is dependent on the reliability of the training data that is used to train the Levenberg–Marquardt (LM) training function. A trained LM function converges better and shows better results than Gauss–Newton; however, still, flaws in data and network design can compromise the accuracy of results. By predicting the wind speeds, optimal power generation through wind turbines is achieved along with protection from high wind speeds. In addition, optimum angle prediction allows for optimal power generation through PV panels.
Author Contributions
Conceptualization, I.S. and M.S.F.; Data curation, M.S.F. and H.K.; Formal analysis, I.S. and H.K.; Funding acquisition, I.d.l.T.D.; Investigation, J.C.G.; Methodology, H.K.; Project administration, I.d.l.T.D. and Y.M.; Resources, I.d.l.T.D.; Software, Y.M. and J.C.G.; Supervision, I.A.; Validation, J.C.G. and I.A.; Visualization, Y.M.; Writing—original draft, I.S. and M.S.F.; Writing—review and editing, I.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the European University of the Atlantics.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Kumar, R.; Bansal, H.O. Shunt active power filter: Current status of control techniques and its integration to renewable energy sources. Sustain. Cities Soc. 2018, 42, 574–592. [Google Scholar] [CrossRef]
- Agency, I.E. Energy, Climate Change and Environment: 2016 Insights; International Energy Agency: Paris, France, 2016. [Google Scholar]
- Chang, T.P.; Liu, F.J.; Ko, H.H.; Cheng, S.P.; Sun, L.C.; Kuo, S.C. Comparative analysis on power curve models of wind turbine generator in estimating capacity factor. Energy 2014, 73, 88–95. [Google Scholar] [CrossRef]
- Fath, H.E. Solar distillation: A promising alternative for water provision with free energy, simple technology and a clean environment. Desalination 1998, 116, 45–56. [Google Scholar] [CrossRef]
- Kumar, K.V.; Bai, R.K. Performance study on solar still with enhanced condensation. Desalination 2008, 230, 51–61. [Google Scholar] [CrossRef]
- Maalej, A. Solar still performance. Desalination 1991, 82, 197–205. [Google Scholar] [CrossRef]
- Huang, Q.; Shi, Y.; Wang, Y.; Lu, L.; Cui, Y. Multi-turbine wind-solar hybrid system. Renew. Energy 2015, 76, 401–407. [Google Scholar] [CrossRef]
- Celik, A.; Muneer, T.; Clarke, P. An investigation into micro wind energy systems for their utilization in urban areas and their life cycle assessment. Proc. Inst. Mech. Eng. Part A J. Power Energy 2007, 221, 1107–1117. [Google Scholar] [CrossRef]
- Chen, H.C. Optimum capacity determination of stand-alone hybrid generation system considering cost and reliability. Appl. Energy 2013, 103, 155–164. [Google Scholar] [CrossRef]
- International Renewable Energy Agency. Renewable Capacity Statistics 2022. Available online: https://www.irena.org/publications/2022/Apr/Renewable-Capacity-Statistics-2022 (accessed on 21 December 2022).
- Cameron, L.; Van Der Zwaan, B. Employment factors for wind and solar energy technologies: A literature review. Renew. Sustain. Energy Rev. 2015, 45, 160–172. [Google Scholar] [CrossRef]
- Eid, A.; Kamel, S.; Abualigah, L. Marine predators algorithm for optimal allocation of active and reactive power resources in distribution networks. Neural Comput. Appl. 2021, 33, 14327–14355. [Google Scholar] [CrossRef]
- Pombo, D.V.; Bindner, H.W.; Spataru, S.V.; Sørensen, P.E.; Rygaard, M. Machine learning-driven energy management of a hybrid nuclear-wind-solar-desalination plant. Desalination 2022, 537, 115871. [Google Scholar] [CrossRef]
- Abdmouleh, Z.; Alammari, R.A.; Gastli, A. Review of policies encouraging renewable energy integration & best practices. Renew. Sustain. Energy Rev. 2015, 45, 249–262. [Google Scholar]
- Hong, T.; Wang, P. Fuzzy interaction regression for short term load forecasting. Fuzzy Optim. Decis. Mak. 2014, 13, 91–103. [Google Scholar] [CrossRef]
- Heydari, A.; Garcia, D.A.; Keynia, F.; Bisegna, F.; De Santoli, L. A novel composite neural network based method for wind and solar power forecasting in microgrids. Appl. Energy 2019, 251, 113353. [Google Scholar] [CrossRef]
- Han, S.; Qiao, Y.H.; Yan, J.; Liu, Y.Q.; Li, L.; Wang, Z. Mid-to-long term wind and photovoltaic power generation prediction based on copula function and long short term memory network. Appl. Energy 2019, 239, 181–191. [Google Scholar] [CrossRef]
- Ali, S.; Jang, C.M. Evaluation of PV-wind hybrid energy system for a small island. In Wind Solar Hybrid Renewable Energy System; IntechOpen: London, UK, 2019. [Google Scholar]
- Abualigah, L.; Zitar, R.A.; Almotairi, K.H.; Hussein, A.M.; Abd Elaziz, M.; Nikoo, M.R.; Gandomi, A.H. Wind, solar, and photovoltaic renewable energy systems with and without energy storage optimization: A survey of advanced machine learning and deep learning techniques. Energies 2022, 15, 578. [Google Scholar] [CrossRef]
- Mezzai, N.; Belaid, S.; Rekioua, D.; Rekioua, T. Optimization, design and control of a photovoltaic/wind turbine/battery system in Mediterranean climate conditions. Bull. Electr. Eng. Inform. 2022, 11, 2938–2948. [Google Scholar] [CrossRef]
- Susmitha, P.; Parventhan, K.; Umamaheswari, S. Artificial Neural Network Control for Solar—Wind Based Micro Grid. In Proceedings of the 2022 IEEE 2nd Mysore Sub Section International Conference (MysuruCon), Mysuru, India, 16–17 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Sahoo, S.; Amirthalakshmi, T.M.; Ramesh, S.; Ramkumar, G.; Dhanraj, J.A.; Ranjith, A.; Obaid, S.A.; Alfarraj, S.; Kumar, S.S. Artificial Deep Neural Network in Hybrid PV System for Controlling the Power Management. Int. J. Photoenergy 2022, 2022, 9353470. [Google Scholar] [CrossRef]
- Drir, N.; Chekired, F.; Rekioua, D. An integrated neural network for the dynamic domestic energy management of a solar house. Int. Trans. Electr. Energy Syst. 2021, 31, e13227. [Google Scholar] [CrossRef]
- Reder, M.; Yürüşen, N.Y.; Melero, J.J. Data-driven learning framework for associating weather conditions and wind turbine failures. Reliab. Eng. Syst. Saf. 2018, 169, 554–569. [Google Scholar] [CrossRef]
- Colone, L.; Reder, M.; Tautz-Weinert, J.; Melero, J.J.; Natarajan, A.; Watson, S.J. Optimisation of data acquisition in wind turbines with data-driven conversion functions for sensor measurements. Energy Procedia 2017, 137, 571–578. [Google Scholar] [CrossRef]
- Pedersen, M.C.; Sørensen, H.; Swytink-Binnema, N.; Martinez, B.; Condra, T. Measurements from a cold climate site in Canada: Boundary conditions and verification methods for CFD icing models for wind turbines. Cold Reg. Sci. Technol. 2018, 147, 11–21. [Google Scholar] [CrossRef]
- Reikard, G. Predicting solar radiation at high resolutions: A comparison of time series forecasts. Sol. Energy 2009, 83, 342–349. [Google Scholar] [CrossRef]
- Palomares-Salas, J.; De La Rosa, J.; Ramiro, J.; Melgar, J.; Aguera, A.; Moreno, A. ARIMA vs. Neural networks for wind speed forecasting. In Proceedings of the 2009 IEEE International Conference on Computational Intelligence for Measurement Systems and Applications, Hong Kong, China, 11–13 May 2009; pp. 129–133. [Google Scholar]
- Li, H.; Li, R.; Zhao, Y. Wind speed forecasting based on autoregressive moving average- exponential generalized autoregressive conditional heteroscedasticity-generalized error distribution (ARMA-EGARCH-GED) model. Int. J. Phys. Sci. 2011, 6, 6867–6871. [Google Scholar]
- Hejase, H.A.; Assi, A.H. Time-series regression model for prediction of mean daily global solar radiation in Al-Ain, UAE. Int. Sch. Res. Not. 2012, 2012, 412471. [Google Scholar] [CrossRef]
- Wang, H.Z.; Li, G.Q.; Wang, G.B.; Peng, J.C.; Jiang, H.; Liu, Y.T. Deep learning based ensemble approach for probabilistic wind power forecasting. Appl. Energy 2017, 188, 56–70. [Google Scholar] [CrossRef]
- Wang, H.; Wang, G.; Li, G.; Peng, J.; Liu, Y. Deep belief network based deterministic and probabilistic wind speed forecasting approach. Appl. Energy 2016, 182, 80–93. [Google Scholar] [CrossRef]
- Hu, Q.; Zhang, R.; Zhou, Y. Transfer learning for short-term wind speed prediction with deep neural networks. Renew. Energy 2016, 85, 83–95. [Google Scholar] [CrossRef]
- Liu, H.; Mi, X.W.; Li, Y.F. Wind speed forecasting method based on deep learning strategy using empirical wavelet transform, long short term memory neural network and Elman neural network. Energy Convers. Manag. 2018, 156, 498–514. [Google Scholar] [CrossRef]
- Yu, R.; Liu, Z.; Li, X.; Lu, W.; Ma, D.; Yu, M.; Wang, J.; Li, B. Scene learning: Deep convolutional networks for wind power prediction by embedding turbines into grid space. Appl. Energy 2019, 238, 249–257. [Google Scholar] [CrossRef]
- Hong, Y.Y.; Satriani, T.R.A. Day-ahead spatiotemporal wind speed forecasting using robust design-based deep learning neural network. Energy 2020, 209, 118441. [Google Scholar] [CrossRef]
- Ding, Z.; Hou, H.; Yu, G.; Hu, E.; Duan, L.; Zhao, J. Performance analysis of a wind-solar hybrid power generation system. Energy Convers. Manag. 2019, 181, 223–234. [Google Scholar] [CrossRef]
- Wind Energy Technologies Office. Wind Market Reports: 2022 Edition. Available online: https://www.energy.gov/eere/wind/wind-market-reports-2022-edition (accessed on 21 December 2022).
- International Energy Agency. Solar PV—Analysis. 2022. Available online: https://www.iea.org/reports/solar-pv (accessed on 21 December 2022).
- International Energy Agency. Next Generation Wind and Solar Power (Full Report). 2022. Available online: https://www.iea.org/reports/next-generation-wind-and-solar-power-full-report (accessed on 21 December 2022).
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Alternative Energy Development Board (AEDB). Current Status of Solar PV Power Projects. 2023. Available online: https://www.aedb.org/ae-technologies/solar-power/solar-current-status (accessed on 4 April 2023).
- Alternative Energy Development Board (AEDB). Current Status of Wind Power Projects. Available online: https://www.aedb.org/ae-technologies/wind-power/wind-current-status (accessed on 4 April 2023).
- Brody, S.D.; Zahran, S.; Vedlitz, A.; Grover, H. Examining the relationship between physical vulnerability and public perceptions of global climate change in the United States. Environ. Behav. 2008, 40, 72–95. [Google Scholar] [CrossRef]
- Shaik, N.B.; Pedapati, S.R.; Taqvi, S.A.A.; Othman, A.R.; Dzubir, F.A.A. A Feed-Forward Back Propagation Neural Network Approach to Predict the Life Condition of Crude Oil Pipeline. Processes 2020, 8, 661. [Google Scholar] [CrossRef]
- Shafi, I.; Ahmad, J.; Shah, S.I.; Kashif, F.M. Techniques to obtain good resolution and concentrated time-frequency distributions: A review. EURASIP J. Adv. Signal Process. 2009, 2009, 673539. [Google Scholar] [CrossRef]
- Pavlić, B.; Bera, O.; Vidović, S.; Ilić, L.; Zeković, Z. Extraction kinetics and ANN simulation of supercritical fluid extraction of sage herbal dust. J. Supercrit. Fluids 2017, 130, 327–336. [Google Scholar] [CrossRef]
- Shafi, I.; Noman, M.; Gohar, M.; Ahmad, A.; Khan, M.; Din, S.; Ahmad, S.H.; Ahmad, J. An adaptive hybrid fuzzy-wavelet approach for image steganography using bit reduction and pixel adjustment. Soft Comput. 2018, 22, 1555–1567. [Google Scholar] [CrossRef]
- Weather Spark. Climate and Average Weather Year Round in Thatta, Pakistan. 2022. Available online: https://weatherspark.com/y/106464/Average-Weather-in-Thatta-Pakistan-Year-Round (accessed on 21 December 2022).
- Gupta, A.; Bansal, A.; Roy, K. Solar energy prediction using decision tree regressor. In Proceedings of the 2021 5th International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 6–8 May 2021; pp. 489–495. [Google Scholar]
- Xia, X.; Wang, X. A Novel Hybrid Model for Short-Term Wind Speed Forecasting Based on Twice Decomposition, PSR, and IMVO-ELM. Complexity 2022, 2022, 4014048. [Google Scholar] [CrossRef]
- Kani, S.P.; Ardehali, M. Very short-term wind speed prediction: A new artificial neural network–Markov chain model. Energy Convers. Manag. 2011, 52, 738–745. [Google Scholar] [CrossRef]
- Grassi, G.; Vecchio, P. Wind energy prediction using a two-hidden layer neural network. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2262–2266. [Google Scholar] [CrossRef]
- Khatib, T.; Mohamed, A.; Sopian, K.; Mahmoud, M. Solar energy prediction for Malaysia using artificial neural networks. Int. J. Photoenergy 2012, 2012, 419504. [Google Scholar] [CrossRef]
- Barua, P.; Barua, R. Machine learning based solar energy forecasting and wind-solar based hybrid grid arrangement at Patenga coastal area, Bangladesh. In Proceedings of the 2021 IEEE International Conference on Power, Electrical, Electronic and Industrial Applications (PEEIACON), Dhaka, Bangladesh, 3–4 December 2021; pp. 53–57. [Google Scholar]
- Sanjari, M.J.; Gooi, H.B.; Nair, N.K.C. Power generation forecast of hybrid PV–wind system. IEEE Trans. Sustain. Energy 2019, 11, 703–712. [Google Scholar] [CrossRef]
- Lei, M.; Shiyan, L.; Chuanwen, J.; Hongling, L.; Yan, Z. A review on the forecasting of wind speed and generated power. Renew. Sustain. Energy Rev. 2009, 13, 915–920. [Google Scholar] [CrossRef]
- Bauer, L.; Matysk, S. Compare Power Curves of Wind Turbines. 2023. Available online: https://en.wind-turbine-models.com/powercurves (accessed on 4 April 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).