Optimized Fractional Maximum Power Point Tracking Using Bald Eagle Search for Thermoelectric Generation System
Abstract
1. Introduction
- For the first time, optimized determination of fractional PID parameters based on the BES to gain the most from the flexibility and achieve accurate and fast tracking is suggested.
- Performance comparisons between the proposed BES method and the featured algorithms in the literature, such as ant lion optimizer (ALO), equilibrium optimizer (EO), cuckoo search (CS), and whale optimization algorithm (WOA), are introduced in this paper. Moreover, statistical tests to fairly compare various employed metaheuristic algorithms are introduced in this paper.
- Both fast tracking and zero oscillations around MPP are achieved.
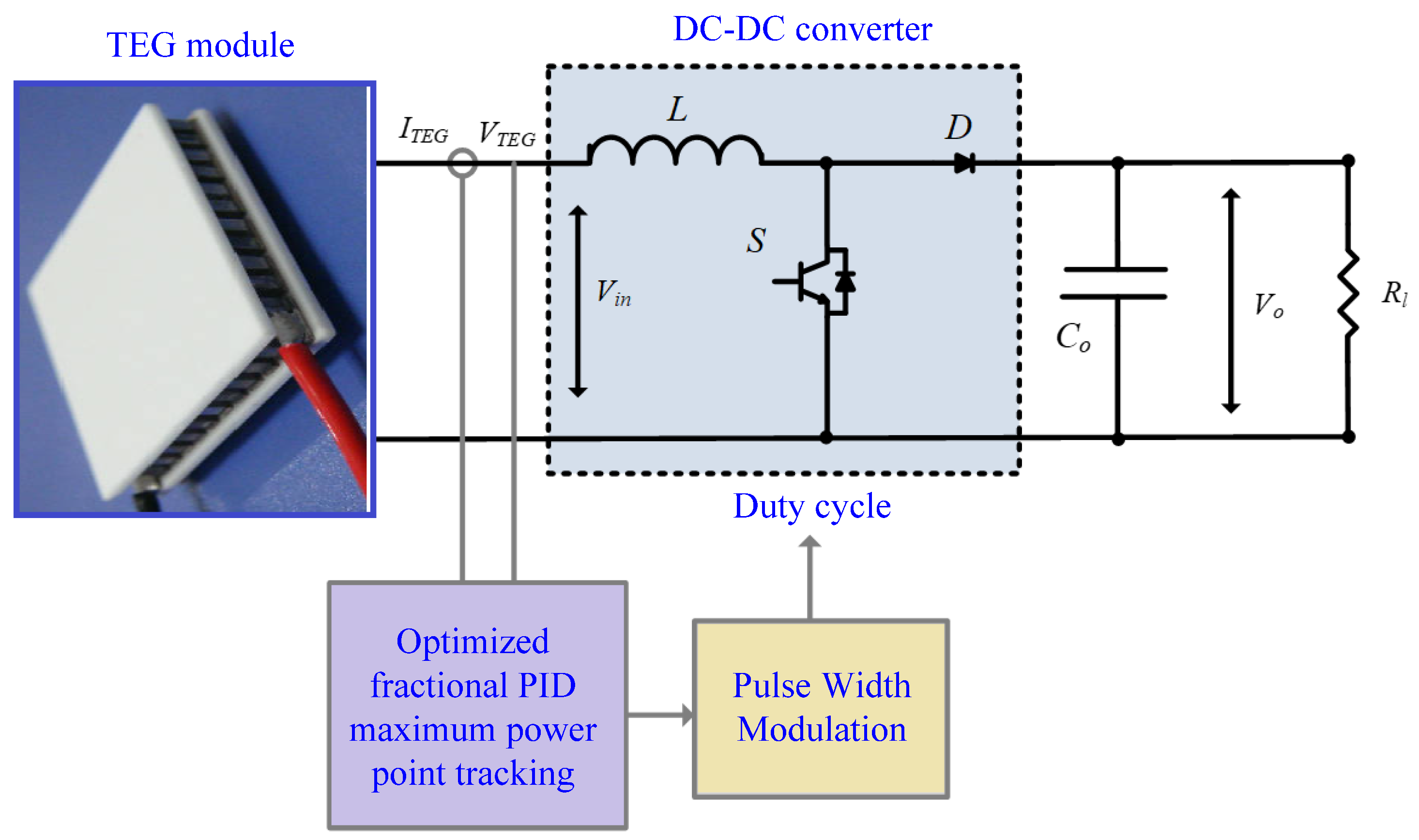
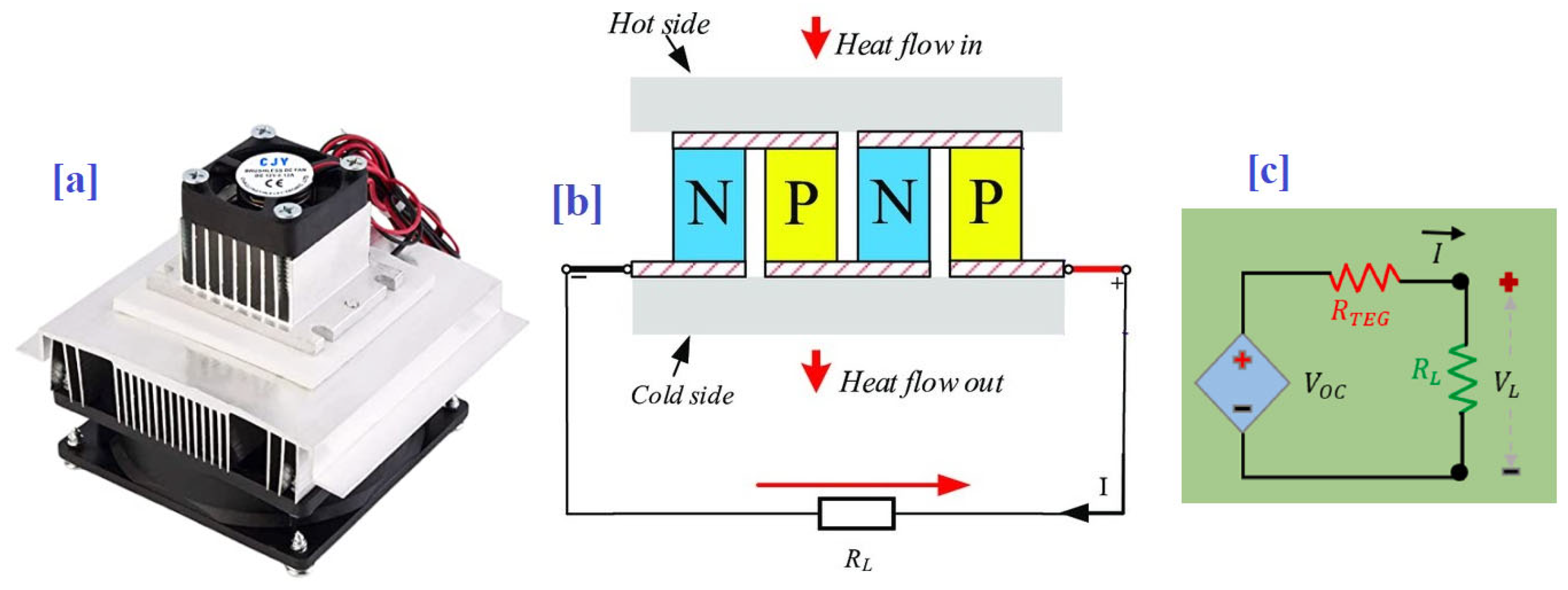
2. Thermoelectric Generation System
3. Maximum Power Point Tracking
3.1. Perturb and Observe Algorithm
- The algorithm measures the TEG’s power at the current operating point.
- It then introduces a small perturbation, usually by increasing or decreasing the converter duty cycle or the current to the load, and measures the resulting change in output power.
- If the output power increases, the algorithm moves the operating point in the same direction as the perturbation to continue searching for the MPP. Otherwise, if the output power decreases, the algorithm returns to the previous operating point and introduces a perturbation in the opposite direction.
- The process is reiterated continually to follow changes in the MPP due to varying environmental conditions, such as temperature and irradiance.
3.2. Incremental Resistance Method
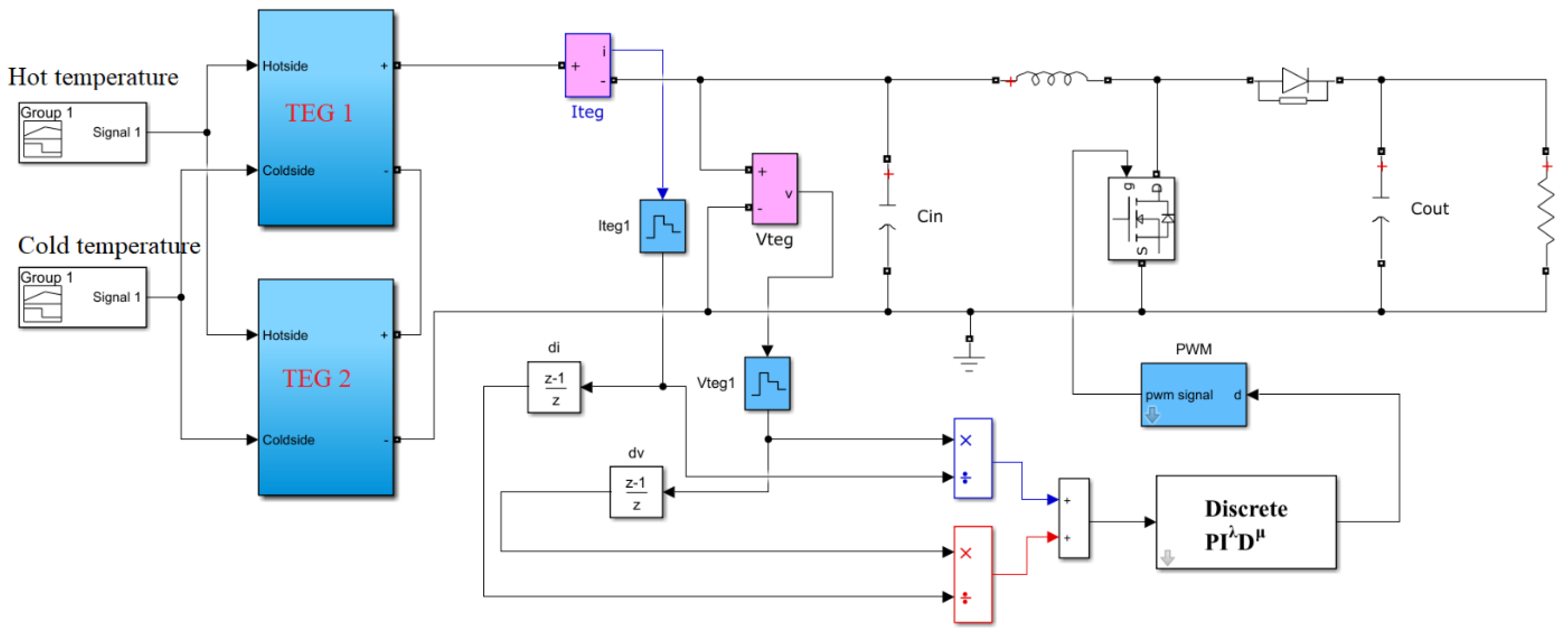
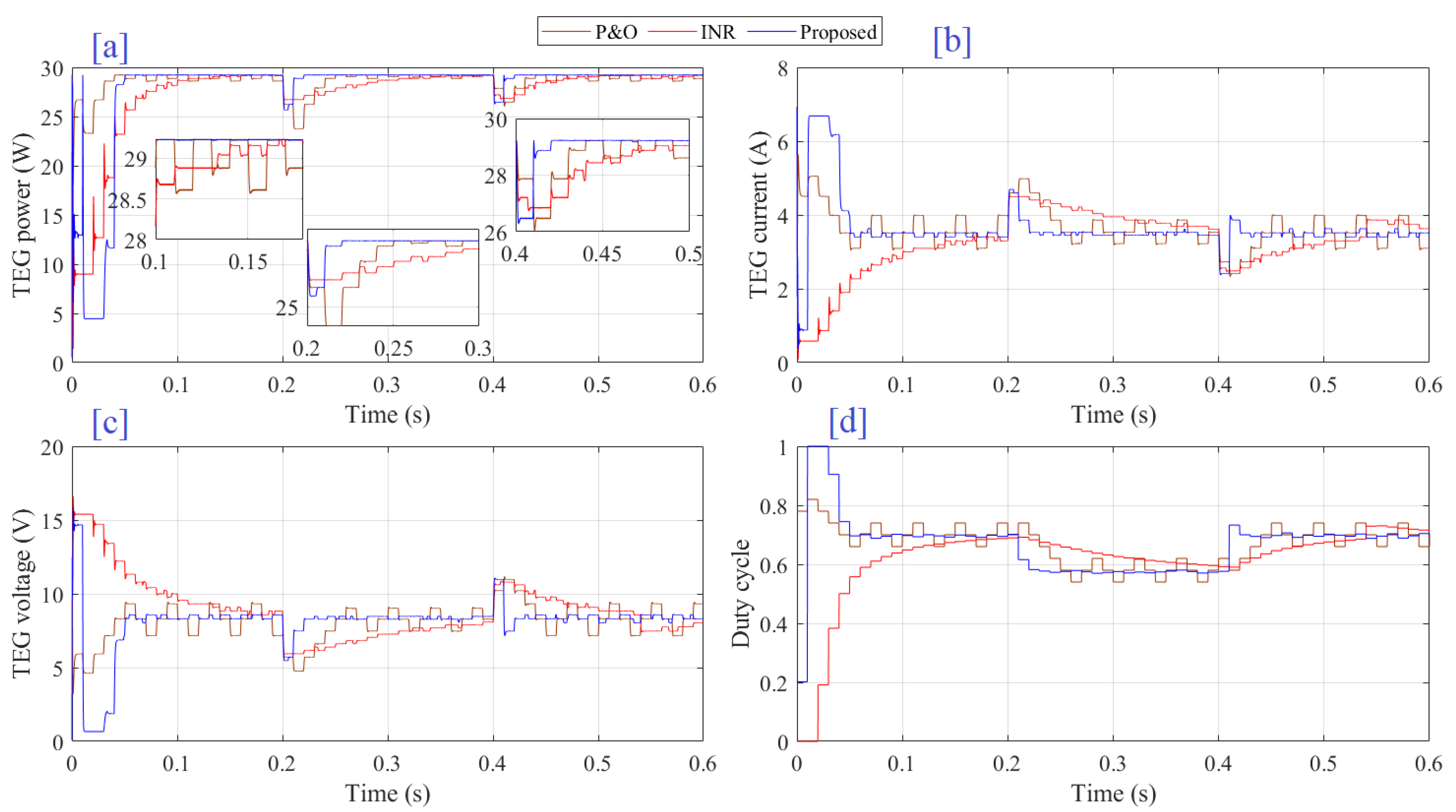
3.3. Optimized Fractional PID-Based INR
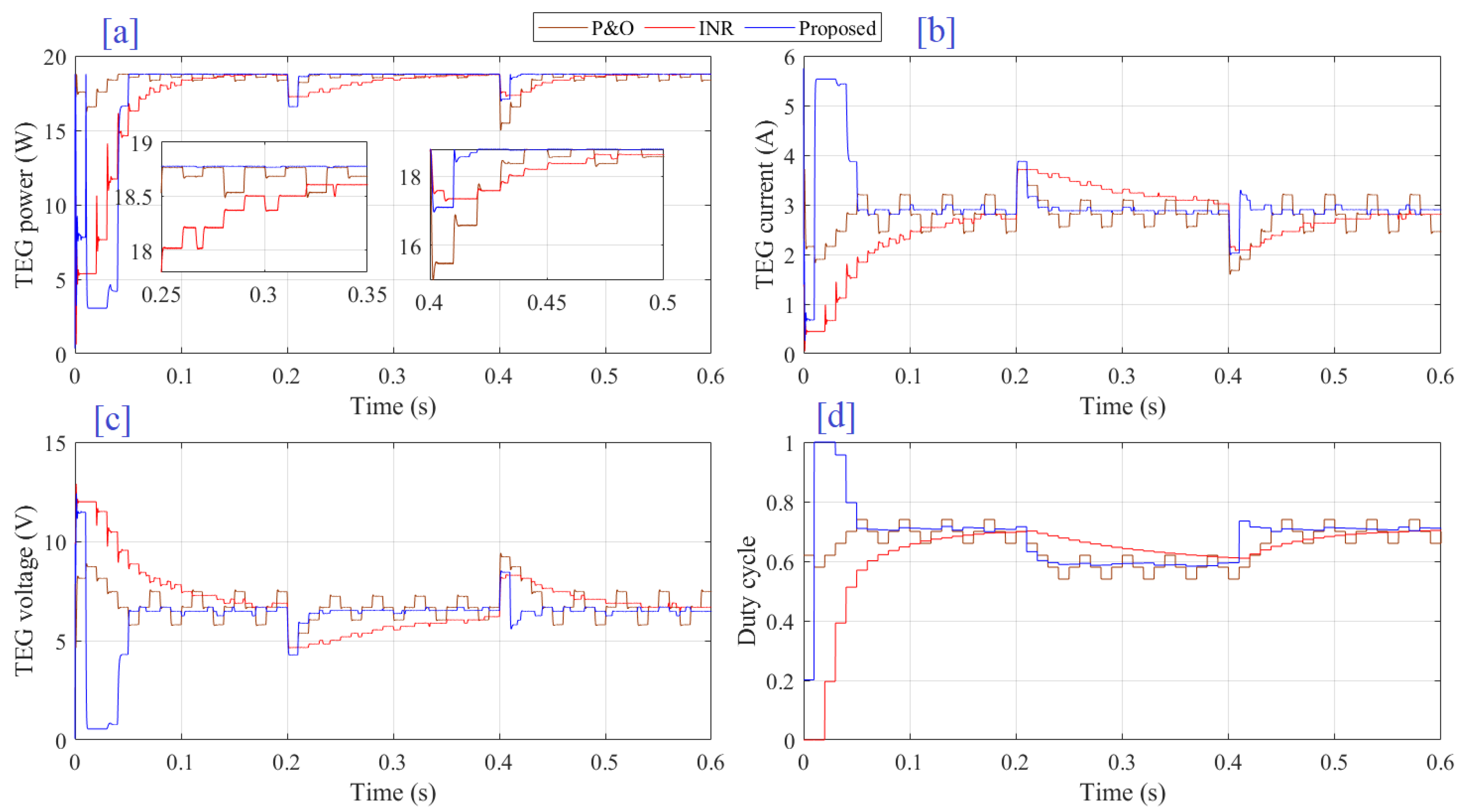
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Olabi, A.G.; Wilberforce, T.; Elsaid, K.; Sayed, E.T.; Maghrabie, H.M.; Abdelkareem, M.A. Large scale application of carbon capture to process industries—A review. J. Clean. Prod. 2022, 362, 132300. [Google Scholar] [CrossRef]
- Sayed, E.T.; Olabi, A.G.; Alami, A.H.; Radwan, A.; Mdallal, A.; Rezk, A.; Abdelkareem, M.A. Renewable Energy and Energy Storage Systems. Energies 2023, 16, 1415. [Google Scholar] [CrossRef]
- Abdelkareem, M.A.; Mahmoud, M.S.; Elsaid, K.; Sayed, E.T.; Wilberforce, T.; Al-Murisi, M.; Maghrabie, H.M.; Olabi, A.G. Prospects of Thermoelectric Generators with Nanofluid. Therm. Sci. Eng. Prog. 2022, 29, 101207. [Google Scholar] [CrossRef]
- Champier, D. Thermoelectric generators: A review of applications. Energy Convers. Manag. 2017, 140, 167–181. [Google Scholar] [CrossRef]
- Aranguren, P.; Roch, A.; Stepien, L.; Abt, M.; von Lukowicz, M.; Dani, I.; Astrain, D. Optimized design for flexible polymer thermoelectric generators. Appl. Therm. Eng. 2016, 102, 402–411. [Google Scholar] [CrossRef]
- Jouhara, H.; Żabnieńska-Góra, A.; Khordehgah, N.; Doraghi, Q.; Ahmad, L.; Norman, L.; Axcell, B.; Wrobel, L.; Dai, S. Thermoelectric generator (TEG) technologies and applications. Int. J. Thermofluids 2021, 9, 100063. [Google Scholar] [CrossRef]
- Kaibe, H.; Makino, K.; Kajihara, T.; Fujimoto, S.; Hachiuma, H. Thermoelectric generating system attached to a carburizing furnace at Komatsu Ltd. Awazu Plant. AIP Conf. Proc. 2012, 1449, 524–527. [Google Scholar]
- Aranguren, P.; Astrain, D.; Pérez, M.G. Computational and experimental study of a complete heat dissipation system using water as heat carrier placed on a thermoelectric generator. Energy 2014, 74, 346–358. [Google Scholar] [CrossRef]
- Olabi, A.G.; Al-Murisi, M.; Maghrabie, H.M.; Yousef, B.A.A.; Sayed, E.T.; Alami, A.H.; Abdelkareem, M.A. Potential applications of thermoelectric generators (TEGs) in various waste heat recovery systems. Int. J. Thermofluids 2022, 16, 100249. [Google Scholar] [CrossRef]
- Montecucco, A.; Siviter, J.; Knox, A.R. A Combined Heat and Power System for Solid-fuel Stoves Using Thermoelectric Generators. Energy Procedia 2015, 75, 597–602. [Google Scholar] [CrossRef]
- Wang, W.; Cionca, V.; Wang, N.; Hayes, M.; O’Flynn, B.; O’Mathuna, C. Thermoelectric energy harvesting for building energy management wireless sensor networks. Int. J. Distrib. Sens. Netw. 2013, 9, 232438. [Google Scholar] [CrossRef]
- Baranowski, L.L.; Snyder, G.J.; Toberer, E.S. Concentrated solar thermoelectric generators. Energy Environ. Sci. 2012, 5, 9055–9067. [Google Scholar] [CrossRef]
- Hasan, M.N.; Nafea, M.; Nayan, N.; Mohamed Ali, M.S. Thermoelectric Generator: Materials and Applications in Wearable Health Monitoring Sensors and Internet of Things Devices. Adv. Mater. Technol. 2022, 7, 2101203. [Google Scholar] [CrossRef]
- Olabi, A.G.; Rezk, H.; Sayed, E.T.; Awotwe, T.; Alshathri, S.I.; Abdelkareem, M.A. Optimal Parameter Identification of Single-Sensor Fractional Maximum Power Point Tracker for Thermoelectric Generator. Sustainability 2023, 15, 5054. [Google Scholar] [CrossRef]
- Valera, Á.; Rodrigo, P.M.; Ceballos, M.A.; Almonacid, F.; Fernández, E.F. Design, manufacturing and indoor/outdoor testing of a hybrid thermoelectric-concentrator photovoltaic mono-module at unprecedented ultra-high concentration levels. Sol. Energy Mater. Sol. Cells 2023, 254, 112269. [Google Scholar] [CrossRef]
- Rodrigo, P.M.; Valera, A.; Fernández, E.F.; Almonacid, F.M. Annual Energy Harvesting of Passively Cooled Hybrid Thermoelectric Generator-Concentrator Photovoltaic Modules. IEEE J. Photovolt. 2019, 9, 1652–1660. [Google Scholar] [CrossRef]
- Salman, S.; Ai, X.; Wu, Z. Design of a P-&-O algorithm based MPPT charge controller for a stand-alone 200W PV system. Prot. Control Mod. Power Syst. 2018, 3, 25. [Google Scholar]
- Jately, V.; Azzopardi, B.; Joshi, J.; Venkateswaran, V.B.; Sharma, A.; Arora, S. Experimental Analysis of hill-climbing MPPT algorithms under low irradiance levels. Renew. Sustain. Energy Rev. 2021, 150, 111467. [Google Scholar] [CrossRef]
- Putri, R.I.; Wibowo, S.; Rifa’i, M. Maximum Power Point Tracking for Photovoltaic Using Incremental Conductance Method. Energy Procedia 2015, 68, 22–30. [Google Scholar] [CrossRef]
- Mandal, R.; Chatterjee, K. Chapter 10—Application and optimization of a robust fractional-order FOPI-FOPID automatic generation controller for a multiarea interconnected hybrid power system. In Fractional Order Systems and Applications in Engineering; Baleanu, D., Balas, V.E., Agarwal, P., Eds.; Academic Press: Cambridge, MA, USA, 2023; pp. 175–197. [Google Scholar]
- Petráš, I. Chapter Three—Fractional-order control: New control techniques. In Fractional Order Systems; Radwan, A.G., Khanday, F.A., Said, L.A., Eds.; Academic Press: Cambridge, MA, USA, 2022; Volume 1, pp. 71–106. [Google Scholar]
- Raj, A.; Praveen, R.P. Highly efficient DC-DC boost converter implemented with improved MPPT algorithm for utility level photovoltaic applications. Ain Shams Eng. J. 2022, 13, 101617. [Google Scholar] [CrossRef]
- Jaziri, N.; Boughamoura, A.; Müller, J.; Mezghani, B.; Tounsi, F.; Ismail, M. A comprehensive review of Thermoelectric Generators: Technologies and common applications. Energy Rep. 2020, 6, 264–287. [Google Scholar] [CrossRef]
- Markowski, P.M. Multilayer thick-film thermoelectric microgenerator based on LTCC technology. Microelectron. Int. 2016, 33, 155–161. [Google Scholar] [CrossRef]
- Hewawasam, L.S.; Jayasena, A.S.; Afnan, M.M.M.; Ranasinghe, R.A.C.P.; Wijewardane, M.A. Waste heat recovery from thermo-electric generators (TEGs). Energy Rep. 2020, 6, 474–479. [Google Scholar] [CrossRef]
- Ruzaimi, A.; Shafie, S.; Hassan, W.Z.W.; Azis, N.; Ya’acob, M.E.; Elianddy, E.; Aimrun, W. Performance analysis of thermoelectric generator implemented on non-uniform heat distribution of photovoltaic module. Energy Rep. 2021, 7, 2379–2387. [Google Scholar]
- Fathy, A.; Rezk, H.; Yousri, D.; Houssein, E.H.; Ghoniem, R.M. Parameter Identification of Optimized Fractional Maximum Power Point Tracking for Thermoelectric Generation Systems Using Manta Ray Foraging Optimization. Mathematics 2021, 9, 2971. [Google Scholar] [CrossRef]
- Ahmed, E.M.; Shoyama, M. Scaling factor design based variable step size incremental resistance maximum power point tracking for PV systems. J. Power Electron. 2012, 12, 164–171. [Google Scholar] [CrossRef]
- El-Khazali, R. Fractional-order PIλDμ controller design. Comput. Math. Appl. 2013, 66, 639–646. [Google Scholar] [CrossRef]
- Ho, Y.C.; Pepyne, D.L. Simple Explanation of the No-Free-Lunch Theorem and Its Implications. J. Optim. Theory Appl. 2002, 115, 549–570. [Google Scholar] [CrossRef]
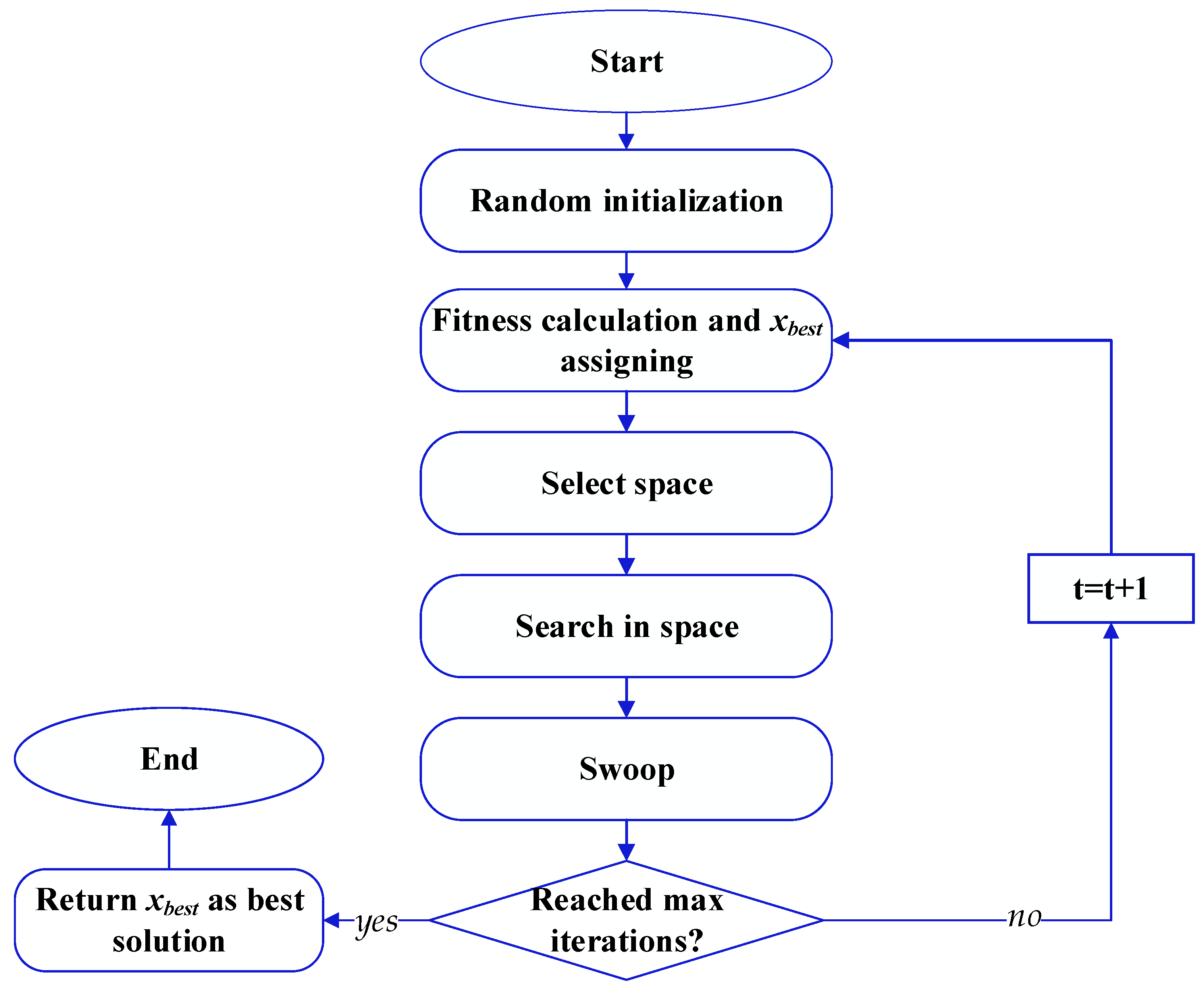
- Alsattar, H.A.; Zaidan, A.A.; Zaidan, B.B. Novel meta-heuristic bald eagle search optimisation algorithm. Artif. Intell. Rev. 2020, 53, 2237–2264. [Google Scholar] [CrossRef]
- Mirjalili, S. The Ant Lion Optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Shehab, M.; Khader, A.T.; Al-Betar, M.A. A survey on applications and variants of the cuckoo search algorithm. Appl. Soft Comput. 2017, 61, 1041–1059. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
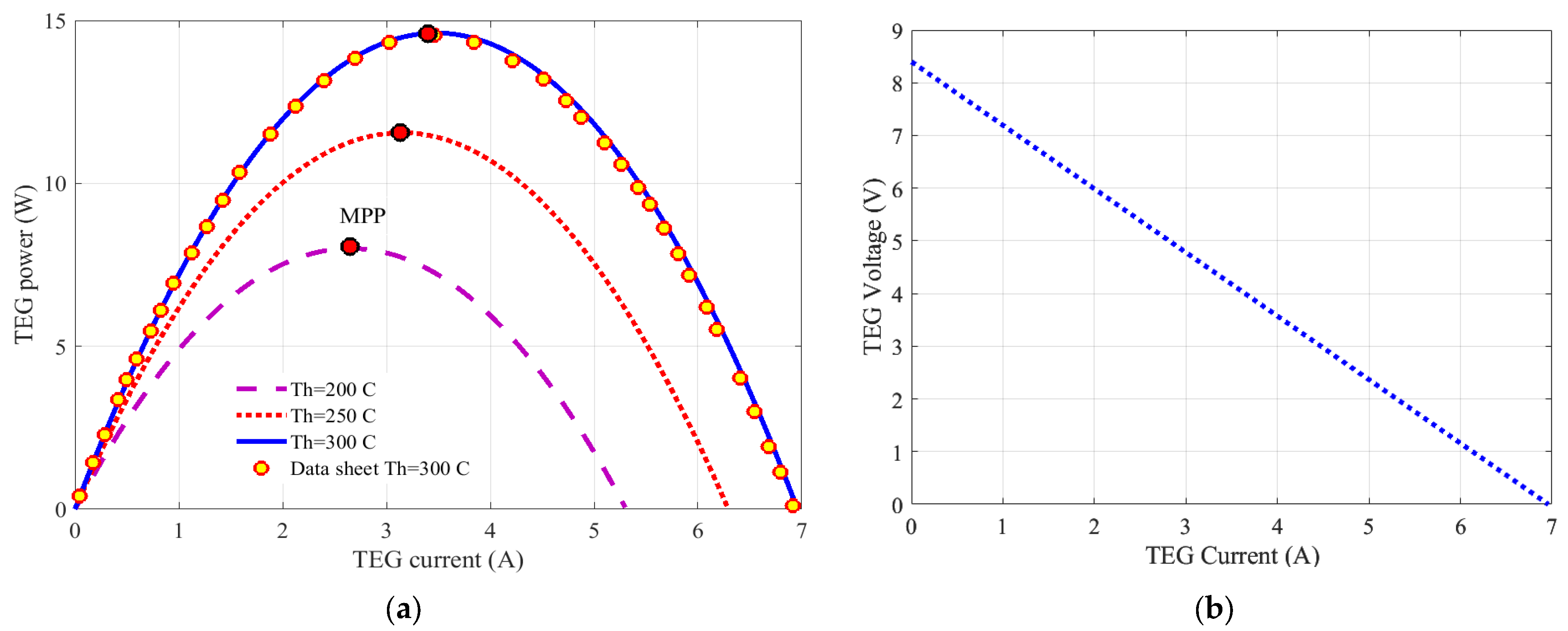

| Characteristics | Unit | Specification | |
|---|---|---|---|
| Temp. (hot side) | °C | 300 | 250 |
| Temp. (cold side) | °C | 30 | 50 |
| OCV “Open circuit voltage” | Volt | 8.4 | 6.56 |
| Load | |||
| resistance (Matched) | Ohm | 1.2 | 1.13 |
| voltage (Matched) | Volt | 4.2 | 3.25 |
| current (Matched) | Ampere | 3.4 | 2.88 |
| power (Matched) | Watt | 14.6 | 9.4 |
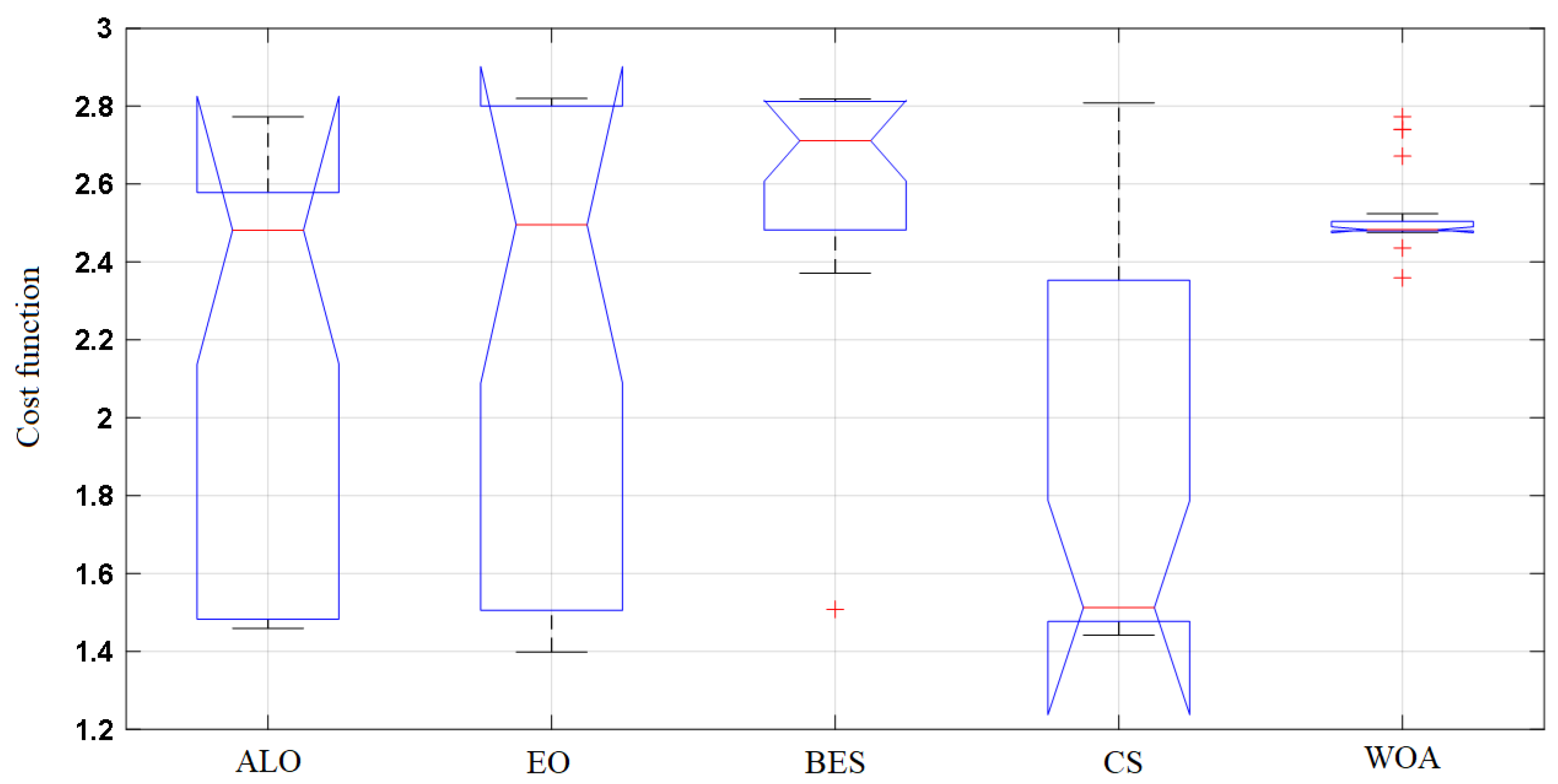
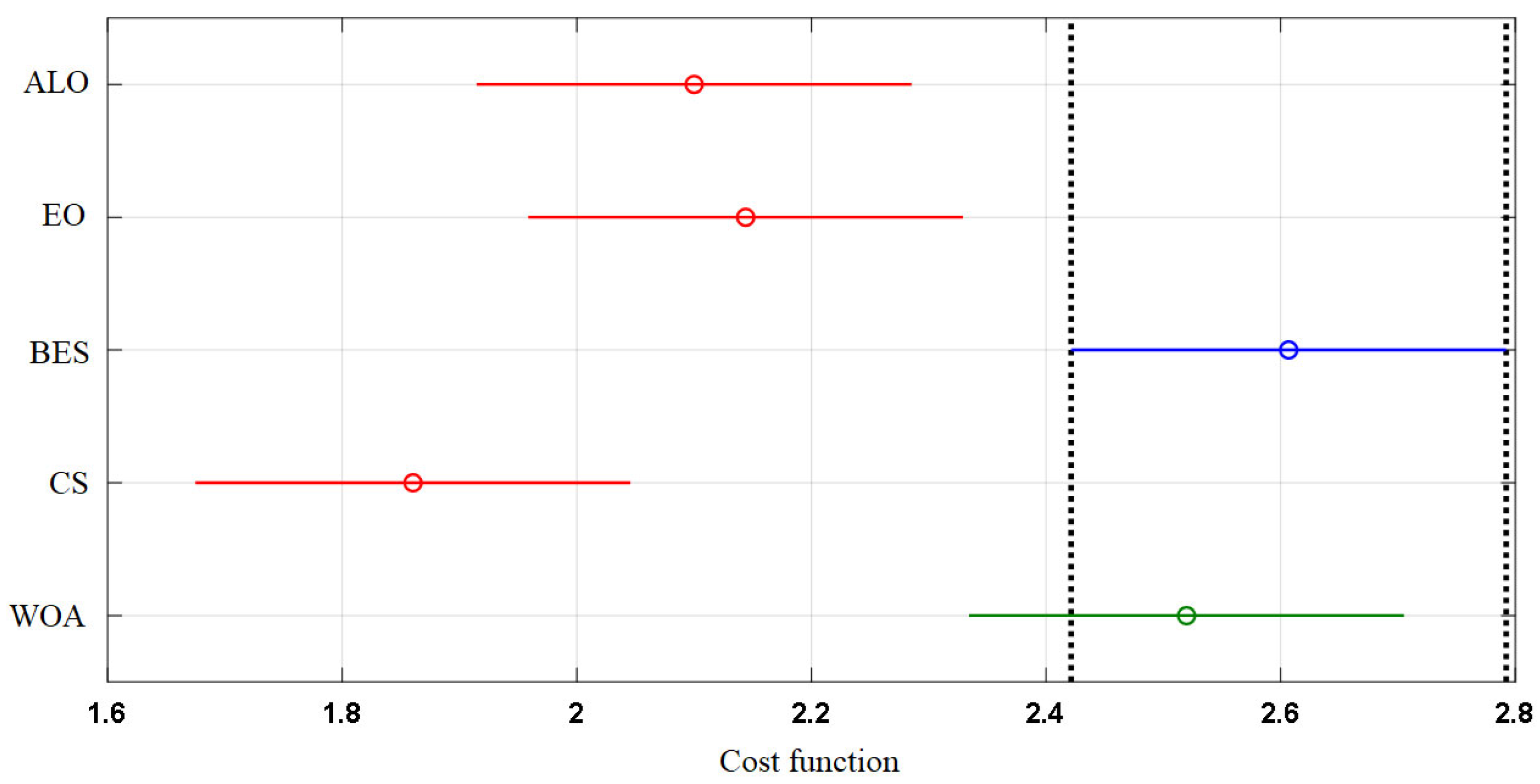
| Parameter | ALO | EO | BES | CS | WOA |
|---|---|---|---|---|---|
| Proportional gain | 0.001 | 0.006701 | 0.001 | 0.008929 | 0.001419 |
| Integral gain | 0.960709 | 1.88613 | 1.884123 | 2 | 1.011736 |
| Order of integrator | 0.483217 | 0.656843 | 0.648258 | 0.680298 | 0.543252 |
| Derivative gain | 0.001 | 0.001314 | 0.001 | 0.001 | 0.001197 |
| Order of derivative | 0.001 | 0.125633 | 0.362192 | 0.427855 | 0.001138 |
| Best | 2.773 | 2.82 | 2.819 | 2.808 | 2.773 |
| Worst | 1.459 | 1.399 | 1.508 | 1.441 | 2.359 |
| Average | 2.1 | 2.144 | 2.607 | 1.86 | 2.52 |
| STD | 0.559 | 0.637 | 0.278 | 0.52 | 0.098 |
| Median | 2.482 | 2.495 | 2.711 | 1.513 | 2.483 |
| variance | 0.312 | 0.406 | 0.077 | 0.27 | 0.01 |
| Efficiency | 74.504 | 76.061 | 92.484 | 66 | 89.396 |
| Run | ALO | EO | BES | CS | WOA | Run | ALO | EO | BES | CS | WOA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.459 | 1.459 | 2.81 | 1.497 | 2.482 | 14 | 2.557 | 1.505 | 2.482 | 1.441 | 2.501 |
| 2 | 1.464 | 2.806 | 2.481 | 2.808 | 2.48 | 15 | 1.465 | 2.804 | 2.81 | 1.495 | 2.436 |
| 3 | 1.489 | 1.399 | 1.508 | 1.471 | 2.483 | 16 | 2.491 | 1.477 | 2.809 | 2.037 | 2.492 |
| 4 | 1.505 | 2.504 | 2.496 | 1.515 | 2.481 | 17 | 2.549 | 2.797 | 2.489 | 1.471 | 2.481 |
| 5 | 2.405 | 2.82 | 2.812 | 1.459 | 2.512 | 18 | 2.763 | 1.508 | 2.479 | 1.477 | 2.497 |
| 6 | 1.459 | 2.807 | 2.481 | 1.514 | 2.524 | 19 | 2.523 | 1.505 | 2.812 | 1.499 | 2.476 |
| 7 | 2.483 | 1.465 | 2.808 | 1.502 | 2.481 | 20 | 1.487 | 2.811 | 2.711 | 1.516 | 2.741 |
| 8 | 2.773 | 2.799 | 2.492 | 2.352 | 2.487 | 21 | 1.471 | 2.772 | 2.819 | 1.495 | 2.493 |
| 9 | 2.642 | 1.517 | 2.815 | 1.477 | 2.359 | 22 | 1.487 | 2.793 | 2.812 | 2.789 | 2.479 |
| 10 | 1.469 | 1.518 | 2.371 | 2.356 | 2.479 | 23 | 2.482 | 1.465 | 2.485 | 2.301 | 2.485 |
| 11 | 2.712 | 1.508 | 2.482 | 2.556 | 2.481 | 24 | 2.485 | 2.812 | 2.817 | 2.804 | 2.672 |
| 12 | 1.491 | 1.508 | 2.795 | 1.513 | 2.739 | 25 | 2.682 | 2.74 | 2.818 | 2.686 | 2.478 |
| 13 | 2.703 | 2.495 | 2.475 | 1.471 | 2.773 |
| Source | df | SS | MS | F | Prob |
|---|---|---|---|---|---|
| Columns | 4 | 9.640 | 2.410 | 10.76 | 1.133 × 10−7 |
| Error | 120 | 26.874 | 0.224 | ||
| Total | 124 | 36.514 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rezk, H.; Olabi, A.G.; Ghoniem, R.M.; Abdelkareem, M.A. Optimized Fractional Maximum Power Point Tracking Using Bald Eagle Search for Thermoelectric Generation System. Energies 2023, 16, 4064. https://doi.org/10.3390/en16104064
Rezk H, Olabi AG, Ghoniem RM, Abdelkareem MA. Optimized Fractional Maximum Power Point Tracking Using Bald Eagle Search for Thermoelectric Generation System. Energies. 2023; 16(10):4064. https://doi.org/10.3390/en16104064
Chicago/Turabian StyleRezk, Hegazy, Abdul Ghani Olabi, Rania M. Ghoniem, and Mohammad Ali Abdelkareem. 2023. "Optimized Fractional Maximum Power Point Tracking Using Bald Eagle Search for Thermoelectric Generation System" Energies 16, no. 10: 4064. https://doi.org/10.3390/en16104064
APA StyleRezk, H., Olabi, A. G., Ghoniem, R. M., & Abdelkareem, M. A. (2023). Optimized Fractional Maximum Power Point Tracking Using Bald Eagle Search for Thermoelectric Generation System. Energies, 16(10), 4064. https://doi.org/10.3390/en16104064









