Abstract
The emerging smart-grid and microgrid concept implementation into the conventional power system brings complexity due to the incorporation of various renewable energy sources and non-linear inverter-based devices. The occurrence of frequent power outages may have a significant negative impact on a nation’s economic, societal, and fiscal standing. As a result, it is essential to employ sophisticated monitoring and measuring technology. Implementing phasor measurement units (PMUs) in modern power systems brings about substantial improvement and beneficial solutions, mainly to protection issues and challenges. PMU-assisted state estimation, phase angle monitoring, power oscillation monitoring, voltage stability monitoring, fault detection, and cyberattack identification are a few prominent applications. Although substantial research has been carried out on the aspects of PMU applications to power system protection, it can be evolved from its current infancy stage and become an open domain of research to achieve further improvements and novel approaches. The three principal objectives are emphasized in this review. The first objective is to present all the methods on the synchro-phasor-based PMU application to estimate the power system states and dynamic phenomena in frequent time intervals to observe centrally, which helps to make appropriate decisions for better protection. The second is to discuss and analyze the post-disturbance scenarios adopted through better protection schemes based on accurate and synchronized measurements through GPS synchronization. Thirdly, this review summarizes current research on PMU applications for power system protection, showcasing innovative breakthroughs, addressing existing challenges, and highlighting areas for future research to enhance system resilience against catastrophic events.
1. Introduction
In the conventional power grid, the energy management system (EMS) and Supervisory Control and Data Acquisition (SCADA) system can afford the steady state view of the power system with high data flow latency [1]. The critical issue in adopting a better protection scheme with these setups is the inability to measure the phase angles of the bus voltage and current in real-time in a synchronized way [2]. The instant dynamic behavior assessment with faster monitoring and measurement is essential for a reliable, protective, and secure operation. The transformation to the smart grid concept of the modern power system needs faster monitoring, more accurate, and synchronized phasor measurement of electrical parameters to achieve the above objective with the use of a Global Positioning System (GPS) to power system operation [3]. Among many emerging devices to facilitate better system monitoring, measurement, and signal communication, PMUs are very attractive in comparison due to the ability to provide the phasor signals in microseconds with accuracy and a faster way through the GPS [4,5,6]. The application of the PMUs in the system network facilitates tracking grid dynamics in real-time, obtaining data for wide-area monitoring, assessing the state estimation, predicting system failure, helping to plan energy delivery proactively, and providing improved protection and control [7,8,9]. Due to this perspective of the PMUs, research of the application of the PMUs in power systems is up-and-coming with many research gaps to handle the solution issues and challenges, particularly to power system protection. The objective of this review includes WAMS-based power network protection, PMU measurement for enhancing power grid monitoring and protection, fault monitoring, localization and detection, and PMU-based state and security estimation.
The conventional measurements were asynchronously reported in 2–5 s intervals [1]. This time interval limited the capabilities of monitoring and measurement operation for the quick and correct decision to provide a secure protective operation in real-time. The introduction of PMU enhances the power system monitoring and subsequent control and protection aspects in many ways, according to the intent of the application [10]. The measuring features such as the fast reporting rate (50–100 measurements/s), synchronization of measurements through GPS signals, measurements of frequency and frequency rate of change, and the provision of phase measurements (instead of only magnitude measurements) are the significant factors to put together the PMUs as the critical enablers for real-time measurement and protection. Firstly, even a wide power network can be fully or partially observable by PMUs, which helps monitor power systems dynamically to take corrective solutions for steady and stable operation even under abnormal conditions [11]. Secondly, the integration of PMUs is optimally restructured along with the current SCADA system to establish the wide-area monitoring and protection system (WAMPS) [8]. This will provide real-time visualization of the system variation and improve the capabilities of WAMPS for dynamic state estimator, phase angle monitoring, oscillation detection and monitoring, and voltage stability [11,12]. This, in turn, considerably improves many crucial operational benefits such as enhancing reliability by reducing the number of blackouts and power cuts, cost-effective power system operation, and extensively allowing the integration of RESs in the smart power system [9]. Thirdly, the uncertainties associated with renewable energy sources (RESs), electrical energy storage (EES), electric vehicle charging (EVC), and changes in load scenarios make control and protection more challenging [11]. Wide-area monitoring with PMUs can overcome new challenges in the operation, planning, protection, and control of distribution and transmission grids to enhance flexibility for the system operation [9]. In addition, the new fast communication technologies support the WAMPS’s fast access to power grid information. The PMU application to the power transmission and distribution sector is indispensable and needs further research to enhance the protection to make the system secure and reliable.
The installations of PMUs in intelligent grid systems reach for distributed and hierarchical controlled WAMS that facilitate various monitoring, protection, and control applications [13]. The conventional protection schemes restrict the distance relays to operate for faults occurring between the location of the concerned relay and the related reach point [14]. It remains unaffected in the cases of all the faults outside this domain, leading to unreliable and insecure protection for the system. The WAMS technology based on the PMUs’ synchronized phasor measurement brings a better solution to the above issue [9]. Secondly, a wide-area differential protection (WADP) can be established with the PMUs’ measurement to suit the shipboard applications’ needs. Thirdly, a secured, coordinated, and synchronized backup protection can be established to function as an intelligent processing system. In a nutshell, WAMS with the PMUs’ measurement provide the grid dynamic state in terms of angular and voltage stability and transfer capacity at different instances on various transmission and distribution systems to control and regulate the power flow satisfying the constraints related to the grid parameters, integrating various protection schemes and identifying corrective actions with an accurate decision [12]. Lastly, the security of both the transmission and distribution sector is reasonably necessary with the provision of the WAMS to cope with the deregulated and restructured power system. Overall, WAMS facilitate a developed intelligent grid of adaptive islanding, a secure and self-healing system.
Even though very few review articles have been published recently, as shown in Table 1, a proper, concise review confined to PMU application to grid protection aspects is yet to present for the researchers and power engineers. Few review research articles mention the broad scope of PMUs and WAMS with their possible applications. This article extensively discusses and analyzes PMUs’ utilization in the power system protection domain at the transmission and distribution levels. The significant contributions of this study can be enumerated as follows:
- It emphasizes various applications of PMUs to provide better protection and secure microgrid systems. The investigations were conducted on protection aspects only.
- The ideas and newness in the proposed PMU-based backup protection schemes by various researchers are systematically presented along with their pros and fault detection times.
- This review provides an overview of the standards for installing, testing, and designing PMUs in power system protection.
- The research gaps are extensively summarized to provide the futuristic scope of the PMU-based protection scheme design and formulation.

Table 1.
Recent literature review papers on PMU-based protection.
Table 1.
Recent literature review papers on PMU-based protection.
| Ref. No. | Title | Highlights | Shortcomings |
|---|---|---|---|
| [1] | A Comprehensive Survey on Phasor Measurement Unit Applications in Distribution Systems |
|
|
| [10] | D-PMU based applications for emerging active distribution systems: A review |
|
|
| [13] | Synchro-phasor measurement applications and optimal PMU placement:A review |
|
|
| [2] | A Survey on the Micro-Phasor Measurement Unit in Distribution Networks |
|
|
The remaining part of the manuscript is organized as follows: Section 2 addresses the various aspects of PMUs and WAMS, looking at their architecture, design, operation, and implementation. Section 3 depicts different issues and challenges related to PMU application, particularly for protection aspects. Section 4 summarizes various PMU-based protection methods, including backup protection. Section 5 presents several applications of PMUs. Section 6 and Section 7 enumerate the standards and the future scope, respectively. Finally, Section 8 ends with the concluding remarks from the work performed on the PMU application for protection to date.
2. PMU and WAMS for Power System Protection
This section presents the basic principle of PMUs and WAMS technology operation and how it improves power system monitoring and protection. Moreover, researchers have conducted studies on several monitoring and protection techniques that employ PMUs, as demonstrated by the comparative publication statistics illustrated in Figure 1, on an annual basis. A distribution pie chart of articles published in various journals covering PMU and protection applications is available, as shown in Figure 2.
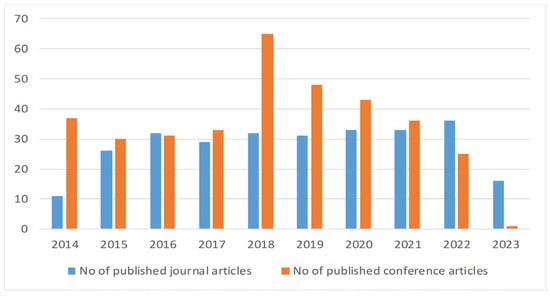
Figure 1.
Annual publication data on PMU-based protection.
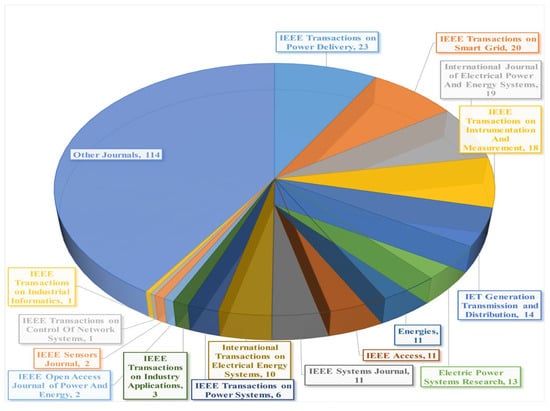
Figure 2.
PMU-based protection schemes in various academic publications.
2.1. Phasor
A phasor is a mathematical representation of a sinusoidal wave quantity in which the complex number’s modulus represents the cosine/sine wave’s amplitude, and the angle represents the cosine/sine wave’s phase angle. Using phasors simplifies the analysis of circuits and systems that involve sinusoidal wave quantities, making it easier to perform calculations and visualize the relationships between different signals [15,16].
A sinusoidal signal is generally represented as follows:
The phasor representation of this expression is represented by the following:
Here, Xm and are denoted as the peak value of the sinusoid and the signal’s phase angle, respectively. The phase angle measurement is regarded as positive when measured in an anti-clockwise direction from the positive real axis. It relies on the frequency inherent in the phasor representation. For different signals to be represented in the same phasor diagram, they must have the same frequency. Still, input signals may not remain stationary in real-time conditions, as shown in Figure 3. A finite data window is used to consider the input signals to address this. PMUs require at least one period of the input signal’s fundamental frequency in the data window [8]. However, when non-harmonic and harmonic components are present, the frequency is not necessarily the same as the fundamental frequency. Thus, PMUs use frequency tracking algorithms to separate the fundamental frequency components and estimate the fundamental frequency period before measuring the phasor.
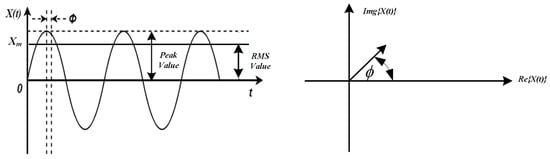
Figure 3.
Synchro-phasor representation.
2.2. Synchro-Phasor and PMUs
A PMU is a tool used to calculate the phase angle and magnitude of a grid-wide electrical quantity (such as voltage or current) using a standard time reference. The time synchronization is given by a GPS and according to some protocols such as the IEEE 1588 Precision Time Protocol [17]. This enables synchronized real-time measurements of several distant places on the grid and helps to provide a wide-area monitoring and signal retrieval system. PMUs can quickly take samples from a waveform and rebuild the phasor quantity, which consists of measurements of both the angle and magnitude. These resulting measurements are known as the synchro-phasor data. These time-synchronized observations are crucial to analyze the power system from a control, protection, and energy management point of view to smooth the whole system’s operation.
Figure 4 depicts the operational block diagram of a PMU. It processes information quickly and accurately and estimates the phasors and timestamps of the incoming signals. The anti-aliasing filter eliminates signal elements whose frequency is equal to/higher than half the Nyquist rate. An analog-to-digital converter (A/D converter) converts the input voltage and current phasors from analog to digital AC signals. A phase-locked oscillator (PLO) transforms the GPS one pulse/sec signal into a series of high-frequency pulses (HFP). The phasor microprocessor performs the phasor computations, and the resulting phasors are merged to provide positive sequence readings. The information from the GPS and clock is eventually used to tag the phasors. At last, by using a modem, the ultimate phasor value is sent to a data center [13].
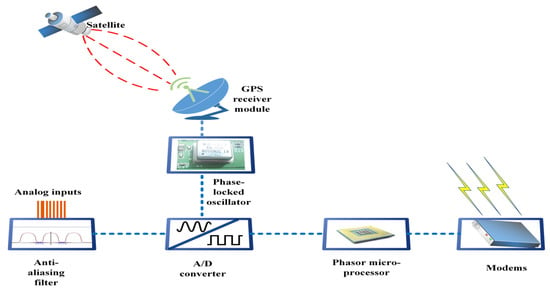
Figure 4.
The principle of operation of PMUs as suggested initially at Virginia Tech., USA (Blacksburg, VA, USA).
2.3. Synchro-Phasor-Based Communication
Communication features are required for applications that demand phasor data in isolated locations. In each communication activity, two data flow components are crucial [18,19]. The first factor is channel capacity (the rate of data change that could be maintained on the current dataset), calculated in kilobits per second or megabits per second. The second factor is latency, which is the interval between the creation of data and its availability for use by the intended purpose [20]. There are two basic categories of communication networks, including wired (e.g., telephonic line, overhead line, coaxial lines, power line communication (PLC), optical fiber) and wireless (e.g., Wi-Fi, radio frequency, satellite, microwaves). Wired networks may be divided into star and mesh networks [21,22]. Figure 5 represents an overall view of the synchro-phasor-based communication network.
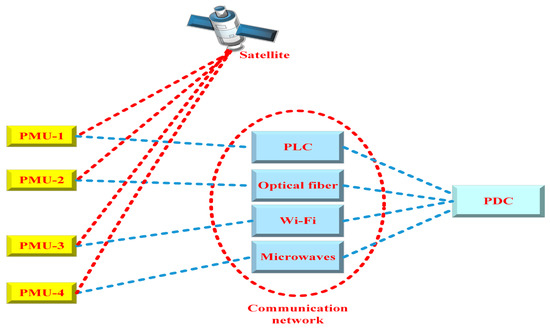
Figure 5.
Synchro-phasor-based communication network.
A star network is one in which all communication nodes are connected to the central node. However, additional communication cables and towers are required to establish such a network. Furthermore, real-world power systems, such as NASPInet, have already adopted star networks [23]. On the other hand, a mesh network is a network whose communication topology resembles a network of power lines. It can utilize power line communication (PLC) technology [24] and has proven to be effective in the past [25,26]. Depending on the physical communication medium, the PMU data transfer modes may be categorized [27]. Leased line connections (LLC) were one of the earliest forms of communication for these uses. Switched telephone circuits (STC) are also viable if transfer latency is not critical. Additionally, traditional electric utility communication techniques, including PLC and microwave links, have been widely adopted and are still prevalent in many current applications [20].
Despite the challenges such as noise, signal loss, and attenuation, PLC remains a feasible option for PMU communications at medium and low voltage distribution levels due to its low cost, easy accessibility, and widespread deployment. However, the latest fifth-generation (5G) mobile services are considered the most promising alternative for PMU communications in the future. With a transfer rate of 20 gigabits per second (Gbps), 5G is almost 100 times faster than 4G, enabling advanced wireless broadband, extensive machine-type communications, and ultra-reliable low-latency communications [28]. Although this technology has not been deployed in functioning power systems, its security must be ensured for future applications. Lastly, fiber-optic networks are the preferred medium today because they have unmatched channel capacity, rapid data transmission speeds, and resistance to electromagnetic interference.
2.4. Synchro-Phasor-Based Wide-Area Measuring System (WAMS)
Power systems are evolving due to the increased renewable energy production, open access to transmission networks, and deregulation of the electrical industry. The functioning of electrical power systems is under strain due to this reality, which increases the need to enhance the control and protection systems provided by WAMS based on PMU [29]. The critical elements of WAMS are phasor data concentrators (PDCs), communication networks, and PMUs, as shown in Figure 6.
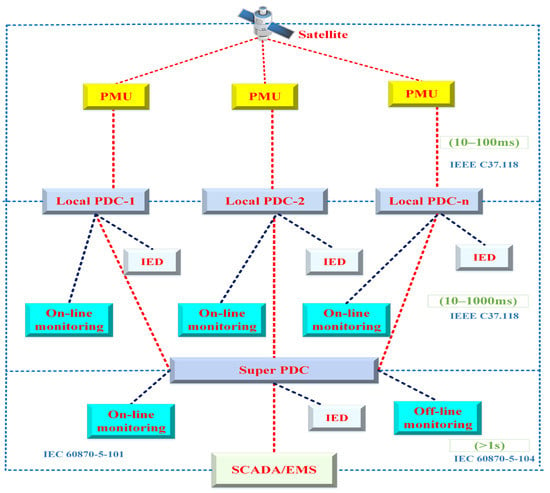
Figure 6.
Hierarchical architecture of WAMS.
In the hierarchically constructed WAMS, the PDC arranges the phasors by the GPS timestamps using the measured output data from PMUs [30]. The PMUs collect and transmit critical information about the power system, such as voltage, current, frequency, and rate of change of frequency (ROCOF), using the IEEE C37.118.2 or IEC 61850-90-5 standards. These data are then received by nearby PDCs (within 10 ms–100 ms), which synchronize and distribute them to super PDCs. The PDCs are responsible for monitoring, storing, and analyzing the received data and detecting and responding to faults in the system [31]. Additionally, it may utilize intelligent electronic devices (IEDs), such as protective relays, switches, and capacitor banks, to quickly respond to disturbances and ensure the stability and security of the power system at both the distribution and transmission levels. However, transferring all the data from the synchro-phasor network to the SCADA or EMS is not required, as receiving higher-level online alerts is sufficient. According to a suggestion in [1], the future of synchro-phasor networks involves using the IEC 61850-90-5 standard for efficient communication between all network components, replacing the current IEEE C37.118.2 standard. Furthermore, rapid relay communication can be achieved using the IEC 61850 standard. This approach allows for additional data review at a later time while ensuring quick and reliable communication between all components of the synchro-phasor network.
2.5. Synchro-Phasor-Based Load Shedding
Currently, power systems are operated closer to their stability limits, mainly due to the deregulation of the electricity markets and the rise in electrical energy demand. However, due to significant disturbances, such as tripped generators or transmission line faults [32], the following active and reactive power unbalance can ultimately cause substantial simultaneous voltage and frequency variations along with instability. As a result, there is a greater chance that the entire system could collapse [33]. Load shedding is a technique that can prevent system collapse by shedding some of the load demand when there is an imbalance between the power generation and load demand, as shown in Figure 7. The technique can be represented as follows [34]:
where represents the weight of the load; represents that load j needs to be shed.
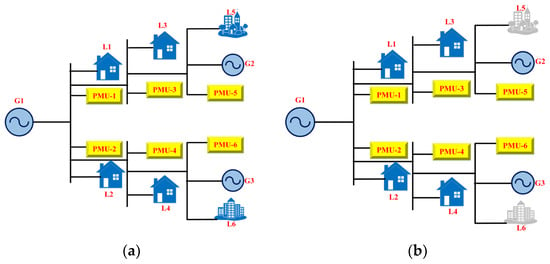
Figure 7.
A simplified load-shedding scenario (a) before and (b) after.
The technique is classified into two main categories based on the objectives and measurements; these include under-frequency load shedding (UFLS) and under-voltage load shedding (UVLS) [35]. In the past, various under-frequency load shedding (UFLS) methods have been developed and can be broadly categorized into classic, adaptive, semi-adaptive, and algorithmic approaches [36,37]. In conventional UFLS methods, relays use locally measured frequency as input and continuously compare it against predetermined thresholds. The key benefits of these systems are simplicity, ease of operation, and reliability. However, they can also have drawbacks, such as treating steep and gradual frequency gradients equally, potentially resulting in excess or insufficient load shedding [38]. The enormous scope is suitable for the use of PMUs to develop a new methodology for optimal load shedding to prevent voltage and frequency instability phenomena with proper power regulation by adopting the concept of WAMS.
PMUs are a potentially effective solution for improving UFLS [39,40,41], as they can provide highly accurate frequency and ROCOF measurements with synchronized time information [42]. However, the reliability of PMU-based measurements may be affected by time-varying conditions and transient events since they rely on a static signal model [43,44]. Therefore, the control scheme should consider the potential measurement uncertainty [45,46]. A new approach was proposed in reference [47] to address the above challenges. This approach utilizes synchro-phasor reading obtained from PMUs to calculate the absolute frequency and ROCOF. The novel approach employs two sets of ROCOF criteria to calculate the load that must be shed and initiates the load shedding. This approach results in a more sensitive system that can handle quick dynamics in a modern power network (MPN). However, adopting PMUs improves the estimate and monitoring rate accuracy, offering a more effective solution for UFLS in MPN. In addition, in [48], a method is suggested to address measurement errors, communication failure, and time delays. The above factors are incorporated into the problem formulation to make the results more accurate and reflective of real-world scenarios. Finally, [49] proposes an approach that considers the connections across load buses and is robust to PMU failure and communication delay, further improving the load-shedding solution’s effectiveness. Lastly, PMU is also very helpful in creating credible and practical tools for UVLS issues that may successfully minimize voltage collapse [50,51,52]. In addition, references [53,54] discuss the problem of voltage collapse in power systems due to high reactive power mismatch. However, the above methods are unsuitable for dynamic real-time conditions and an open research field for power engineers.
3. Issues and Challenges of PMU-Based Protection
Recently, many suggestions have been proposed to adopt a secure, reliable, and self-protective capability for the intelligent transmission and distribution sector. However, integrating WAMS and PMUs with the traditional protection scheme and topology raises many inherent critical issues and challenges in real-time, including the following:
- The architecture of wide-area protection systems (WAPS): The architecture of WAPS needs to be designed to provide adaptive relaying for primary protection and long-term voltage instability at the local stage of operation. The frequency instability, angular instability, and control coordination need to be considered for small-signal stability at the global stage of operation. A proper architecture can enhance the system security, improve the speed of information exchange between components, and provide high system reliability [55].
- Dynamic and nonlinear loading: The dynamics of loads and electric vehicle charging in the distribution sector can cause frequency instability. However, they are not substantially considered in frequency instability protection measures based on WAMS. The protection scheme must focus on the dynamic and nonlinear loading characteristics through WAPS [56].
- Overreaching distance relay zones: Overreaching distance relay zones under stressed abnormal conditions can lead to cascaded tripping and blackouts. WAMS-based anticipatory adaptive relaying schemes may be a better solution for handling these situations in the future [57].
- Operational uncertainties of FACT devices: The series of connected FACT devices have a critical impact on the distance protection of the transmission lines due to their associated operational uncertainties. WAMS-based flexible protection schemes can be designed to handle the uncertainties related to distance protection and acquire the control parameters of FACTS devices in a brief period [4].
- Optimal PMU placement: Without a comprehensive plan for wide-area protection, there is a lack of optimal PMU placement that can provide complete observability of the power system. Proper PMU placement is essential to detect and prevent different types of instabilities and uncertainties in the system [57].
- Time delays: Time delays during information exchange and transfer in PMUs can impact the accuracy and effectiveness of WAPS. Proper measures must be taken to handle time delays accurately and correctly through real-time adaptive identification techniques [57].
- GPS spoof attacks: GPS spoof attacks can influence PMU timestamps by injecting counterfeit GPS signals into the antenna of the PMU’s time reference receiver. This can violate the PMU’s maximum phase error and inaccurate signaling for protection and control. Mitigation strategies must be developed to prevent GPS spoof attacks [58,59].
- Calibration of PMUs: Characterizing PMUs according to prescribed measurement standards is essential to ensure the reliability and consistency of the operation and control of WAPS. The calibration of PMUs under steady-state conditions traceable to prescribed standards is necessary [60].
- False data injection attacks (FDIA): Cybersecurity is a significant concern for intelligent power grids, and FDIA can cause operational, physical, and economic damage. Continuous cyber-physical system monitoring is essential to achieve secure and reliable operations under cyber threats. The WAPS should be designed to prevent and detect FDIA research gaps, aiming for a better solution to these factors [61].
- Role of PMUs in inverter-based resources: PMUs can be crucial in monitoring and controlling power systems that incorporate inverter-based resources, especially relevant in regions with high resource penetration. However, this deployment also presents challenges, such as the high cost of PMUs, the need for precise time synchronization, and a lack of standardization that may create interoperability issues. Nevertheless, PMUs also present opportunities, including real-time monitoring and control that can improve power system stability and reliability and more precise information to enhance inverter-based resource performance [62].
4. PMU-Based Protection Methods
Synchro-phasor measurements have revolutionized the field of power system protection by providing highly accurate and time-synchronized phasor data. This data detects and responds to various power system events, including faults, out-of-step conditions, and other abnormal operating conditions. To address these abnormal conditions, the synchro-phasor has provided several solutions to the above protection problems in power systems. They have enabled the development of sophisticated protection schemes such as adaptive out-of-step protection (OSP), differential protection, and backup protection, which rely on accurate and time-synchronized phasor data to detect and respond to power system events [3].
Differential protection is a commonly used protection scheme in power systems. It protects power transformers, generators, and other critical equipment from damage due to internal faults. It relies on measuring the difference in current flowing into and out of a protected zone. When a fault occurs within the zone, the current balance is disrupted, and the differential relay detects the fault and initiates a trip signal to disconnect the equipment. Adaptive OSP protects power system generators from damage due to the loss of synchronism, which can occur when two generators are connected to the same power system with unsynchronized rotational speeds. Lastly, backup protection is used as a secondary protection scheme to protect against equipment failures or the malfunction of primary protection systems. The schemes rely on synchro-phasor measurements to detect and isolate faults quickly and accurately, ensuring the power system remains stable and reliable.
4.1. Backup Protection
With the emergence of interlinked power systems, systemic disruptions (e.g., transmission line faults, blackout events) inside the power system may create an inexorably problematic situation for the power industry. To prevent the deterioration of the power grid, protection and control measures must be taken to recover the system to normal operating conditions. Generally, primary and backup protection is used to protect the transmission lines [63,64]. Conventional backup protection is mainly performed based on independent judgment following local data. Furthermore, conventional backup protection cannot adjust to varying loading scenarios and fault impedance [65]. As a result, symmetrical disturbances cannot be detected from other loading conditions, including load invasion, power swing, and generator breakdowns [66].
Additionally, backup protection may operate incorrectly, leading to cascading failures or blackout events [66,67]. The implementation of phasor measurement units (PMUs) in power systems has recently been widely acknowledged. The voltage and current synchro-phasor are delivered by PMUs using GPS. Researchers are proposing wide-area backup protection (WABP) schemes that utilize data collected from various points in the grid to detect transmission line faults. There are three significant categories documented in WABP research [68]. The first involves using electrical quantity parameters, the second involves WABP based on the protection relay device’s switching status information, and the third category combines electrical quantity and circuit breaker/protective relay operating information.
Figure 8 depicts a schematic diagram of WABP consisting of a protection device (PD) that detects the network’s electrical properties and transfers the data to the regional network’s system protection center (SPC). After that, SPC examines the data and runs the protective algorithm to decide whether or not a defect has occurred. Once a defect is discovered, the SPC sends a trip order to the appropriate circuit breaker, isolating the faulty area of the network. Table 2 depicts the backup protection approaches recommended by many authors in recent years, and a detailed examination of these techniques is covered in the following sections.
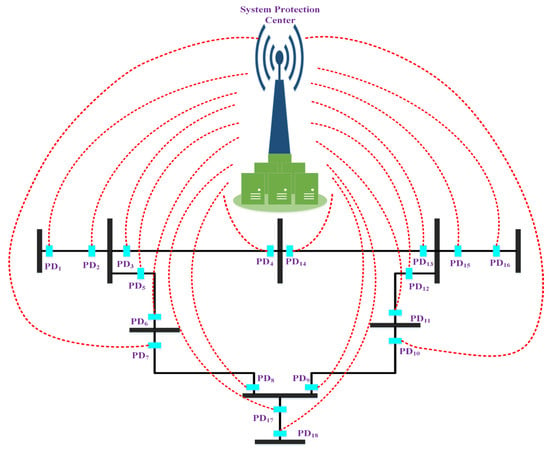
Figure 8.
Architecture of WABP.
4.1.1. WABP Scheme Based on Electrical Quantity Parameters
This scheme consists of WABP based on information on electrical parameters, such as the evaluation of the fault voltage [69], the comparison of the sequence current phase and amplitude, the comparison of the voltage and current composite directional component [70,71,72], and the cumulative impedance comparison algorithm. As mentioned above, the schemes can realize WABP by gathering wide-area data without modifying the typical backup protection architecture. However, by comparing the variation of electrical quantity between the calculated and estimated values to a certain threshold, the defective line was successfully located, as shown in Figure 9.
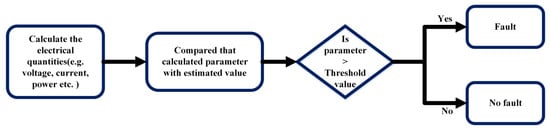
Figure 9.
Block diagram of WABP scheme based on electrical quantity.
Identifying a faulty transmission line was achieved by analyzing variations in the positive-sequence current angles across all transmission lines. To determine the bus closest to the defective line, [72] analyzed the positive-sequence voltage (PSV) magnitudes of the buses and calculated the absolute difference in the positive-sequence current (PSC) angles at both ends of each line connected to the identified bus. However, this method has limitations, particularly for high impedance faults where the measurement of the bus voltage magnitude may be low, leading to insignificant differences in current angles. Several alternative techniques have been proposed to address this limitation. For example, a unique WABP algorithm was proposed in [70] to identify faulty branches based on the steady-state fault component.
In contrast, another special WABP algorithm based on fault component voltage distribution was suggested in [69]. Later, ref. [73] proposed a WABP scheme based on PSV readings to determine the location of the damaged line. At the same time, the Koopman analysis was used in another study to generate WABP and detect the faulty line based on the PMU data, but it has a high computational burden [74]. Further, reference [75] introduced a novel WABP algorithm that does not consider system variables such as transmission line impedance, but only uses the phasor data of voltages and currents, which was proven effective. In [76], a decentralized method was presented to detect and clear transmission line faults in power systems. This approach utilizes the gain in momentum data of all generators and PSV magnitudes to identify the susceptible protection zone and the nearest bus to the fault.
Moreover, the techniques described in references [72,73,74,75,76] do not address two crucial factors, wide-area fault detection and location for cross-country and evolving faults. In this direction, a novel WABP scheme was proposed in [68] to handle the associated issues. The scheme requires only a limited number of synchronized PMUs, making it a cost-effective solution for power systems. The main drawback of all these schemes is that they need a lot of observations and relevant data, such as transmission line voltage and current. As a result, when examining the real-time implementation in a large region, such schemes could be both costly and challenging.
4.1.2. WABP Scheme Based on Switching Status of Protection Relay
This scheme consists of WABP based on switching information and updates, such as WABP-based genetic and fault tolerance algorithm [77]. Several techniques are suggested in [78,79,80,81]; these backup protection principle schemes are framed by observing and analyzing the switching status of the protection device, as demonstrated in Figure 10.
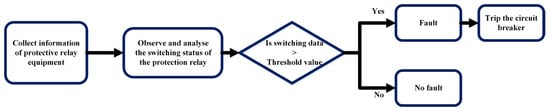
Figure 10.
Block diagram of WABP scheme based on the status of circuit breaker.
In [78], the authors used broad-area data, such as the statuses and operations of conventional protection relays, to detect faults through the collaboration between intelligent agents. Another backup protection scheme, outlined in [79], relies on the status of primary and auxiliary protective relays and circuit breakers to simplify the settings and avert cascading trips. In [80], the authors suggested a comprehensive backup protection scheme that considers the contribution of all established distance relays across the network, utilizing a protection fitness function. While [81] presented a backup protection approach that relies on the status of the distance relay’s second and third zones, its key restrictions include higher end-to-end latencies and data congestion at the phasor data concentrator (PDC). The main drawback of these schemes is that they frequently need the circuit breaker’s status, which could make them impracticable and expensive.
4.1.3. WABP Scheme Based on Electrical Quantity and Switching Status of Protection Relay
In this study, novel methods for the transmission line backup protection are provided by employing synchro-phasor measurements. These schemes consist of WABP based on data on electrical parameters and the operational status of protective devices. The above methods are suggested to be implemented into two phases at the predefined buses. The first stage involves identifying the fault and strained circumstances. However, in the second phase, the defective line is cut off from the electrical supply, as shown in Figure 11.
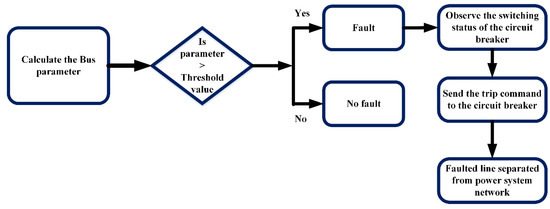
Figure 11.
Block diagram of WABP scheme based on the bus data and circuit breaker status.
In [82], a synchro-phasor state estimator’s residual vector is utilized to detect faults and improve the security of the present remote backup protection scheme. In contrast, ref. [83] proposed a WABP technique for transmission lines that operate based on synchronized data and the actions of third-zone distance relays. The proposed algorithm offers a significant advantage over other wide-area methods, requiring fewer synchronized devices. Therefore, the proposed algorithm represents a valuable contribution to the backup protection of power transmission lines, as it can achieve accurate results using fewer synchronized devices. Furthermore, ref. [84] proposed a novel WABP strategy based on device detection to address the device failure issue. This strategy is valuable to the power system protection field, as it can efficiently and reliably locate faults and provide backup protection.
In summary, the above method proposes innovative approaches to enhance the security and reliability of power systems through backup protection. However, utilizing wide-area information, synchronized data, and device detection techniques are significant advancements that can significantly improve the accuracy and effectiveness of backup protection strategies. These contributions are crucial in ensuring the stability and efficiency of power systems, which are essential for the modern world’s functioning. The major drawback is that the strategy’s effectiveness may be limited to communication failures or delays.

Table 2.
Backup protection scheme.
Table 2.
Backup protection scheme.
| Ref. No. | Contribution | Detection Time |
|---|---|---|
| [85] |
| 65–95 ms |
| [86] |
| 403 ms |
| [87] |
| 400 ms |
| [88] |
| 740 ms |
| [89] |
| - |
| [90] |
| 50 ms |
| [91] |
| 20 ms |
| [92] |
| 0.48 ms |
| [93] |
| 300 ms |
| [94] |
| 140 ms |
| [95] |
| 12 ms |
| [96] |
| 81 ms |
| [97] |
| 50 ms |
5. Synchro-Phasor-Based Application in Transmission and Distribution System
The real-time management of power systems necessitates using fast and synchronized data collection and processing techniques. PMUs, with their synchronized timing and high-frequency sampling capabilities, play a crucial role in analyzing the complicated dynamics of the power system. These measurements also assist in detecting system abnormalities and implementing prompt corrective actions. Despite these benefits, minor variations in voltage phasors at different buses in the distribution system must also be accounted for, as they are crucial in achieving better control and protection. Extensive research has been conducted in this field. The following sections outline the applications of synchro-phasor measurements in transmission and distribution systems, as shown in Figure 12.
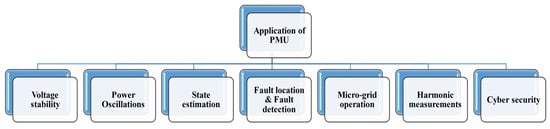
Figure 12.
Applications of PMU.
5.1. Voltage Stability
Voltage stability refers to the capability of a system to sustain its voltage levels after a disturbance occurs. This concept is typically divided into two categories, short-term voltage stability and long-term voltage stability, which are differentiated based on the type and duration of the disturbance [98]. The system voltage stability margin (VSM) is expressed as follows:
where represents the maximum loading point and represents the current operating point.
Traditionally, only SCADA and EMS data were used to monitor the P–V and Q–V curves, but a model-free technique was developed in [13] to measure the voltage magnitude. In [99], a new strategy was designed to improve the accuracy and speed of measuring the voltage magnitude, which is essential in addressing voltage instability and preventing blackouts. However, this approach involves using WAMS and optimizing parallel processes with guidelines to minimize calculation times. Later, an innovative approach was proposed to estimate the voltage stability margin in a power grid to enhance operators’ awareness [100]. This method utilizes PMUs and incorporates a preprocessing technique for PMU measurements to eliminate any inconsistency or uncertainty due to random load disturbances. This approach promises to provide a reliable and accurate estimation of the voltage stability margin, which is crucial for ensuring a power system’s safety and stable operation. In [101], a new technique for monitoring voltage stability in a transmission system was introduced. This method was developed by combining the impedance matching method and the previous local identification of voltage emergency technique (LIVET). The proposed method can detect voltage instability soon after it occurs by monitoring the changes in the active power transfer. A novel multi-bus voltage stability index was introduced in [102]. This index can calculate the stability margin and the load-shedding percentage. Several voltage stability evaluations were conducted under various operating conditions [103,104,105,106,107,108,109]. Table 3 depicts some recent research on voltage stability using PMU data.

Table 3.
Application of PMU on voltage stability.
5.2. Power Oscillations
Distance relay failure contributes significantly to most cascaded blackouts worldwide [27]. Severe disruptions such as faults and load failure may cause the system to experience power swings (PSs) or power oscillations (POs) [110]. The swing equation can be expressed as follows [111]:
where represents power angle; and shows the actual and angular velocity, respectively; and are the mechanical and electrical power; H is the inertia constant; and D is the damping coefficient.
Depending on the severe disturbances, POs can either be stable (synchronous generators maintain synchronism) or unstable (synchronous generators lose synchronism) [112]. During stable power oscillation (SPO), blocking the performance of the distance relay is desirable. On the other hand, alternative events are offered during unstable power oscillation (UPO). Depending on the location, the distance relay could block or trip in the first event. In the second event, the distance relay could be plugged (close to the electrical center) and proceed by forcing separation at a different system site [113]. However, UPOs can cause significant changes in the voltage and current, which can be hazardous for the operation of the power grid. In addition to that, UPOs can also cause the failure of specific protective systems, such as distance and under-impedance relays, leading to widespread blackouts and cascading outages. The above issues highlight the importance of detecting and mitigating UPOs in power systems to ensure the stability and reliability of the power grid [114].
To maintain the stability of the power grid, an out-of-step (OOS) prevention mechanism is provided, which includes pole slip protection (PSP) of synchronous generators, exceptional security, additional control, power swing blocking (PSB) of distance protection, and OOS tripping in transmission networks [114]. The above mechanism works to detect and prevent OOS events, ensuring the stability and reliability of the power grid. However, conventional blind-based schemes, such as pole slip protection (PSP) for synchronous generators, face limitations in differentiating between stable and unstable swings and require a detailed stability study for their implementation [115]. Other techniques, such as the rate of change of impedance and resistance [115], changing the zone shape of distance relays [116], and the swing-center voltage (SCV) method [117], were also reported, but have limitations such as requiring extensive stability studies or being applicable only for two-source equivalent systems.
Various techniques were proposed in the power system industry to prevent out-of-step (OOS) events and detect POs to ensure stable operation and prevent blackouts [116]. These include the frequency of voltage value-based approaches [116], pattern recognition-based strategies [117,118,119], admittance trajectory-based methods [120], the relative speed of a hypothetical identical machine [121], PMU information-based methods [122,123], and predictive analysis-based methods [124]. These methods aim to distinguish stable power swings from unstable ones, increase the protection system’s reliability and security, and reduce false tripping and communication failure. However, each method has its limitations and challenges, such as the requirement for a vast amount of training data, improvement in filter design, and the necessity for PMU information. Table 4 tabulates some recent research on power oscillation using PMU data.

Table 4.
Application of PMU on power oscillation.
5.3. State Estimation
Power system state estimation (PSSE), a crucial real-time application, typically happens every 30 s. An appropriate SE provides the necessary input data so that operators can learn about the security and dependability of the system and, at the same time, achieve the capability to reduce capital expenditures. The SE involves calculating the amplitude of the bus voltage and phase angles by utilizing redundant active and reactive power injection data [132]. However, the estimation can be performed using several SE techniques. All approaches often use the same measurement items, the foundation for establishing the algorithm’s goal function. The SE measuring model that is most frequently employed is the following:
where y is the measurement vector entered into the SE method, x represents the selected state variables, and h(x) and e represent the measurement function and error vectors, respectively. Since poor SE performance can have severe financial and practical repercussions, much research has already been conducted to enhance SE performance, and numerous strategies have been suggested in this article.
Conventionally, the data measurement is asynchronous, resulting in static state estimation (SSE). The following have been explored through SSE: (i) the enhancement that was obtained when PMUs were introduced and multiplied; (ii) the ideal placement and positioning of PMUs to provide high reliability, the identification of incorrect data, and the detection of system element issues; (iii) the inclusion of PMUs in the estimation technique, such as by immediately replacing the actual values inside the state variables; (iv) calculating the weights attached to these PMUs; and (v) the advantages of PMUs for enhancing data security [132]. However, synchro-phasor technology allows for dynamic state estimation (DSE), providing real-time information about the voltage magnitude and phase angle at each node in the power system. This approach provides a more accurate and dynamic understanding of the system’s state, enabling better decision making and control [133].
Several studies have shown the benefits of using PMU data with an extended Kalman filter (EKF) for online state and parameter estimation. References [134,135] demonstrated the potential applications of this approach. References [136,137] used the EKF to estimate a single-machine infinite bus system’s generator states, unknown inputs, and dynamic states. References [138,139] proposed using an ensemble Kalman filter (EnKF) for simultaneous state and parameter estimation and the use of an extended particle filter (EPF) for dynamic state estimation, respectively. The main disadvantage of these methods is the lower sampling rate. A comparative study based on dynamic state estimation was suggested to address this above issue in [140].
Later, an SE method for the distribution system was deployed in reference [141]. This method offers several advantages, including low latency and high state estimation frame rates. In [132], a novel hybrid power system static state estimation (SE) method was introduced, which utilizes PMU observations as a multivariate time series and incorporates existing time and cross-correlation through VAR models. Additionally, the process provides better confidence intervals, and has the ability to anticipate the power state and detect sudden biases, resulting in more robust state estimation. Despite the attempts to capture the dynamic conditions of the power system through various methods, the challenge of decentralized processing and decoupling with power plant controls persists. To overcome this, ref. [142] proposed an EKF technique that features decentralized processing and decoupling with power plant controls. Even with noise, the framework accurately estimates the states, outputs, and unknown inputs. It was also demonstrated that the above method was resistant to generator component errors and efficient in various situations. In [143], a new method that combined SCADA and PMU measurements was presented. It shows a significantly reduced computing time compared to existing approaches, especially in large-scale networks with multiple faulty SCADA measurements in PMU observable areas. Reference [144] proposed an improved dynamic state estimation scheme. The scheme’s performance was evaluated by considering the impact of probabilistic communication interruptions and delays, ensuring robustness and reliability in real-world conditions. The centralized approach integrates and aggregates information from multiple sources, providing a more comprehensive and accurate state estimate reference. Table 5 presents some recent research on SE using PMU data.

Table 5.
Application of PMU on state estimation.
5.4. Fault Location and Fault Detection
Fault location is the process of determining the location of a fault in an electrical power grid. PMU-based approaches were proposed to prevent widespread power outages or other disruptions. These PMUs provide real-time voltage, current, and frequency readings, allowing the electrical power system to be fully observable at all times, thereby assisting system analysts in identifying faults quickly and avoiding blackouts. The faulty bus model can be expressed as follows:
where n = bus number; PSVnbf = positive sequence voltage (before fault); and PSVnaf = positive sequence voltage (after fault).
However, to further improve the efficiency of the protection system, it is recommended to use the WAMS, which provide a more effective backup protection scheme.
The WAMS feature PMUs equipped with intelligent electronic devices and synchronized data from both ends of the transmission lines [158,159]. It is essential to accurately identify faulty transmission lines and perform a dynamic security analysis of the power system to enhance protection through PMUs [160]. Implementing the differential protection philosophy based on Kirchhoff’s laws is also crucial to demonstrate the efficiency of PMUs in protecting transmission lines [161]. The study conducted in [70] was one of the first studies to develop a differential protection scheme for a 33 kV transmission line and substation, using numerical relays and incorporating GPS synchronization to streamline the sample data. Moreover, the recursive algorithm for updating phasors was found to increase the estimation errors over time due to the continuous nature of electrical power systems (EPS). To effectively monitor and protect EPS, it is crucial to have an accurate synchronization of phasors and a precise measurement of the phase angles. The phase angles of the voltages and currents play a crucial role in defining the location of the faults in the transmission line when using a minimum positive-sequence voltage as a backup for traditional protection systems. This information can then be used to classify faulty buses. In addition, the use of Wavelet and Fourier transform for fault classification in transmission lines was discussed in reference [162]. Reference [163] proposed a method that detects and classifies transmission line faults using only PMU data from the generator bus. The methodology employed PMU readings from a single bus voltage for the whole grid, decreasing the price and complexity of the surveillance system. Recently, there has been an increase in the use of artificial intelligence (AI) or machine learning (ML) techniques for fault diagnosis, including detection, identification, and localization of faults in power transmission networks [164]. Table 6 tabulates recent research on fault location and detection using PMU data.

Table 6.
Application of PMU on fault location and fault detection.
5.5. Microgrid Operation
Microgrids can operate in two different modes, islanded mode and grid-connected mode. The microgrid is connected to the main power grid in the grid-connected mode and can import or export electricity as needed. This mode allows the microgrid to take advantage of the benefits of the main grid, such as the backup power and access to additional energy resources. In GC mode, the microgrid must maintain a stable frequency and voltage to ensure the reliable operation of connected loads and to avoid any negative impact on the main power grid [174]. Using PMUs, the microgrid can monitor the power system parameters and quickly detect any changes or disturbances in the grid.
Islanding is a situation that occurs when a portion of an electrical power grid becomes disconnected from the primary grid, forming an isolated island. This can occur due to several factors, including equipment failures, natural disasters, or cyberattacks. Islanding can pose a significant threat to the stability of the power grid, leading to unanticipated power outages and other system disruptions. It is crucial to employ effective islanding detection methods to mitigate this problem. PMUs were identified as a potential solution for islanding detection. PMUs are specialized hardware devices that track and gauge the electrical power grid, providing instantaneous voltage, current, and frequency measurements. By utilizing these measurements, PMUs can detect when a portion of the grid becomes disconnected from the primary grid and initiate an alert or another appropriate response.
To transfer data between PMUs in smart grids, different communication technologies such as wire lines, fiber-optic cables, 4G/5G networks, and power line communication are utilized [175]. PMUs provide time-synchronized signals from various locations in the microgrids (MG), which are particularly crucial when there is an increased installation of DGs [176]. PMU-based detection is a remote technique that offers fast, reliable, and precise islanding detection in different operating conditions. Even if a circuit breaker (CB) open is detected, the DG can still operate in islanded mode if there is a sufficient generation-load balance [177]. However, relying solely on local measurements reduces the ability to control DGs, which limits flexibility in active distribution system management. Therefore, gathering system component parameters to achieve resilient and stochastic energy management in MGs is crucial, which can be accomplished through PMU measurements [178].
Synchronized measurements obtained from multiple PMU sites are instrumental in accurately detecting islanding events in MGs [179,180]. By analyzing power system variables such as voltage phasor, current phasor, frequency, and ROCOF, operators can make decisions and prevent threats to the system. However, the reporting rate of PMUs can be extremely high, with 60 to 120 frames per second for various variables, resulting in massive amounts of data that need to be processed [181]. Identifying an actual islanding event from embedded dynamics in the MGs is a daunting task that requires sophisticated techniques such as multivariate statistical methods, including independent component analysis, principal component analysis (PCA), and partial least squares to compress the data. PCA is a technique that reduces correlation among the observed variables without significantly losing data by reducing the input data dimension [182]. The PCA model is updated as new data arrives to achieve a more accurate detection since the power network data is subjected to change over time. PCA has been utilized in various studies for islanding detection [183,184,185,186]. Table 7 tabulates recent research on islanding detection using PMU data.

Table 7.
Application of PMU on islanding detection.
5.6. Harmonic Measurements
Monitoring and controlling harmonic distortions are critical in power system management, particularly in power distribution systems. With the increasing power of electronic devices, nonlinear loads, and inverter-based energy resources, the importance of this task has increased in recent years. Such equipment can introduce harmonic distortions, which may compromise the dependability and security of power distribution systems by causing conductor overheating or interfering with power protection systems. Hence, utilities must monitor and control harmonic levels in power distribution systems to prevent pollution and ensure secure and reliable operation. However, PMUs offer high-speed and accurate harmonic measurements that enable power system operators to identify and analyze harmonic distortion problems in real-time. By measuring the amplitude and frequency of harmonics, PMUs can provide valuable information to power system operators to identify the source of harmonic distortions and take corrective actions. For every harmonic injection, the total harmonic vector error (TVE) for the nth harmonic order is expressed as follows:
A novel algorithm for calculating harmonic phasors using PMUs based on the principle of fundamental phasor calculation was proposed in [195]. By accurately calculating harmonic phasors, this algorithm enables the efficient utilization of PMU calculation resources and enhances the overall functionality of PMUs in power system monitoring and control. In [196], two estimation techniques were developed from recent PMU-based applications by examining their estimation results using a real-world measurement dataset. While a novel harmonic phasor estimator for P-class PMUs was proposed in [197], it was found that the technique suffered from the inter harmonic injection. A phasor signal processing model was proposed to overcome this issue, which involves adding a preprocessing filtering step before PMUs [198]. This step incorporates estimating signal parameters using either the estimation of signal parameters via rotational invariance techniques (ESPRIT) or the matrix pencil (MP) algorithm for signal processing. In addition, a design for a PMU using a PXI modulator and GPS receivers for accurate harmonic synchro-phasor measurement in distribution networks was presented in [199]. The presented PMU prototype and measurement procedures can help improve the performance and efficiency of distribution grids, which are essential for the reliable and cost-effective integration of renewable energy sources and other distributed energy resources. Table 8 depicts recent research on harmonic measurement using PMU data.

Table 8.
Application of PMU on harmonic measurement.
5.7. Cybersecurity
In recent years, PMUs have been applied to the field of cybersecurity, as they have the potential to detect and respond to cyberattacks on power systems. In December 2015, over 200,000 customers were impacted by cyberattacks that targeted three electric distribution companies in Ukraine [205]. The cyberattack detection model is expressed as follows:
where P = the positive number of attack PMUs; N = the number of safe PMUs.
Several approaches have investigated the use of PMUs in cybersecurity, focusing on detecting irregularities and suspicious behavior in real-time. An approach for detecting the manipulation of PMU data involves utilizing transmission line parameters, including shunt admittance and series impedance, as they remain constant and can help identify potential attacks and recover the correct data [206,207]. However, this approach requires the placement of PMUs on every bus on the grid, which can be costly. Time synchronization attacks are also typical attacks that can affect the accuracy of voltage and current phase angle measurements, resulting in adverse impacts on power system operations such as fault localization, voltage stability detection, and line parameter identification [208]. Detecting such attacks can be achieved using various methods, including cross-layer defense mechanisms [209], data-driven models [210], and phasor measurement analysis [211]. In addition to attack detection, several methods exist for recovering accurate data once a cyberattack has been detected. For instance, a new framework was proposed for restoring missing PMU measurements. However, its efficacy remains untested during transient power system operation [212]. Table 9 tabulates recent research on cybersecurity using PMU data.

Table 9.
Application of PMU on cybersecurity.
6. Standards
The IEEE Standards for PMUs provide guidelines for designing, installing, and testing PMUs used in power systems. The standards specify communication protocols, performance requirements, and testing procedures for synchro-phasors, including PMUs, which are essential for the accurate and reliable measurement of power system dynamics. The standards also provide recommendations for hardware, software, and communication protocols for PMUs and power system stabilizers (PSSs) and define communication protocols for PMUs used in distributed energy resource (DER) systems. The IEEE standards ensure that the PMUs and synchro-phasors from different manufacturers can communicate and work together effectively, providing a common framework for designing, installing, and testing. Table 10 depicts the advantages and limitations of the following IEEE standards:

Table 10.
Advantages and limitations of IEEE standard.
- IEEE Std 1344-1995: This was the first synchro-phasor standard formulated for measurement and communication specifications, emphasizing achieving better interoperability among PMUs [219].
- IEEE C37.118-2005: This standard was developed to address the limitations of IEEE Std 1344-1995, specifically regarding the performance of PMUs at off-nominal frequencies. This standard restricts the frequency deviation of off-nominal frequency inputs within a range from the nominal frequency [220].
- IEEE Std C37.118.1-2011: This standard identifies the measurement of electrical parameters such as synchro-phasor, frequency, and ROCOF under steady-state and dynamic conditions. It also includes compliance requirements and evaluation methods and defines P and M classes as two performance classes for PMUs [221].
- IEEE Std C37.118.1a-2014: This standard is a revision to IEEE Std C37.118.1-2011 and aims to eliminate specific limitations, mainly frequency, and ROCOF measurements. It also corrects latency and measurement discrepancies and refines ramp tests to guarantee repeatable results while evaluating PMUs with anti-aliasing filters [222].
- IEEE C37.244-2013: This standard defines the functional, performance, and communication needs of power dispatching centers (PDCs) to provide better system monitoring, protection, and control. It includes an information annex on report rate conversion and filtering issues and outlines various tests and test methodologies to ensure protocol support, cybersecurity, and communication media compatibility [223].
7. Future Scope
- Integrating PMUs with other grid monitoring and control technologies, such as SCADA systems, could enhance the capabilities of PMUs in detecting and responding to cyberattacks and other threats to the power grid. Future work could explore the integration of PMUs with AI and ML algorithms, enabling automatic and real-time detection and response to cyber threats.
- The research can be conducted on developing more secure PMUs resistant to cyberattacks and hacking, ensuring the reliability and stability of the electrical power grid. This could involve using advanced encryption techniques and secure communication protocols to protect the data transmitted by PMUs and develop secure firmware and software resistant to malware and other security threats.
- Harmonic measurement can be used to monitor and analyze the performance of renewable energy systems, such as wind turbines and solar photovoltaic systems, which are known to produce significant harmonic distortion. By detecting and addressing these issues, the performance of these systems can be improved, leading to better energy production and efficiency.
- To boost the overall effectiveness and dependability of the power system, islanding detection technology might be used with control strategies such as load shedding and islanding control. This may lessen the effects of islanding occurrences and increase the power system’s resistance to faults and disturbances.
- The islanding approach may be further examined from the cybersecurity perspective, particularly regarding possible attacks and weaknesses. Through the identification of potential threats and the development of mitigation techniques, the security of the power system may be improved.
- Developing an AI model for identifying fault detection and replacing lost or defective information with correct information is a complex task that requires expertise in data science and ML.
- One of the primary goals of system state estimation is to accurately determine the state variables of the power system, such as voltage and phase angle. In the future, researchers can work toward developing more accurate and reliable PMUs that can provide more precise measurements and improve the accuracy of system state estimation.
8. Conclusions
PMUs are advanced instruments designed to measure voltage and current phasors in electric power systems accurately. Due to their high precision and accuracy, they have become widely used in transmission and distribution networks for various purposes, including power system protection. With the increasing use of AI and ML techniques in power systems, PMUs are expected to become increasingly essential. This paper explains the operating principle and various applications of PMUs in terms of their capability to establish a better protective system using other established technologies. It also highlights the numerous benefits of PMU data in areas such as backup protection, voltage monitoring, power swing detection, state estimation, harmonic measurements, and cybersecurity. The thorough discussions and analyses reflect that using PMUs improves network reliability, resiliency, cost savings, and environmental safety, and provides a better protection system.
Author Contributions
Conceptualization, B.K.S., M.M., and P.K.R.; methodology, B.K.S. and P.K.R.; software, C.B.; validation, C.B., M.M., and P.K.R.; formal analysis, B.K.S.; investigation, C.B.; resources, P.K.R.; data curation, C.B.; writing—original draft preparation, C.B., P.K.R., and B.K.S.; writing—review and editing, C.B., B.K.S., and P.K.R.; visualization, M.M.; supervision, B.K.S. and P.K.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hojabri, M.; Dersch, U.; Papaemmanouil, A.; Bosshart, P. A comprehensive survey on phasor measurement unit applications in distribution systems. Energies 2019, 12, 4552. [Google Scholar] [CrossRef]
- Dusabimana, E.; Yoon, S.G. A survey on the micro-phasor measurement unit in distribution networks. Electronics 2020, 9, 305. [Google Scholar] [CrossRef]
- Phadke, A.G.; Bi, T. Phasor measurement units, WAMS, and their applications in protection and control of power systems. J. Mod. Power Syst. Clean Energy 2018, 6, 619–629. [Google Scholar] [CrossRef]
- Arefin, A.A.; Baba, M.; Singh, N.S.S.; Nor, N.B.M.; Sheikh, M.A.; Kannan, R.; Abro, G.E.M.; Mathur, N. Review of the Techniques of the Data Analytics and Islanding Detection of Distribution Systems Using Phasor Measurement Unit Data. Electronics 2022, 11, 2967. [Google Scholar] [CrossRef]
- Singh, B.; Sharma, N.K.; Tiwari, A.N.; Verma, K.S.; Singh, S.N. Applications of phasor measurement units (PMUs) in electric power system networks incorporated with FACTS controllers. Int. J. Eng. Sci. Technol. 2011, 3, 2967. [Google Scholar] [CrossRef]
- Hagan, T.; Senaratne, D.; Meier, R.; Cotilla-Sanchez, E.; Kim, J. Implementing Power System Protection Algorithms in a Digital Hardware-in-the-Loop Substation. IEEE Open Access J. Power Energy 2022, 10, 270–282. [Google Scholar] [CrossRef]
- Bertsch, J.; Carnal, C.; Karlson, D.; McDaniel, J.; Vu, K. Wide-area protection and power system utilization. Proc. IEEE 2005, 93, 997–1003. [Google Scholar] [CrossRef]
- Cruz, M.A.; Rocha, H.R.; Paiva, M.H.; Segatto, M.E.; Camby, E.; Caporossi, G. An algorithm for cost optimization of PMU and communication infrastructure in WAMS. Int. J. Electr. Power Energy Syst. 2019, 106, 96–104. [Google Scholar] [CrossRef]
- De La Ree, J.; Centeno, V.; Thorp, J.S.; Phadke, A.G. Synchronized phasor measurement applications in power systems. IEEE Trans. Smart Grid 2010, 1, 20–27. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, L.; Li, J. D-PMU based applications for emerging active distribution systems: A review. Electr. Power Syst. Res. 2020, 179, 106063. [Google Scholar] [CrossRef]
- Seferi, Y.; Cetina RG, Q.; Blair, S.M. Review of PMU algorithms suitable for real-time operation with digital sampled value data. In Proceedings of the 2021 IEEE 11th International Workshop on Applied Measurements for Power Systems (AMPS), Virtual, 29 September–1 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Asprou, M. Synchronized measurement technology: A blessing for power systems [Trends in Future I&M]. IEEE Instrum. Meas. Mag. 2017, 20, 25–42. [Google Scholar]
- Joshi, P.M.; Verma, H.K. Synchrophasor measurement applications and optimal PMU placement: A review. Electr. Power Syst. Res. 2021, 199, 107428. [Google Scholar] [CrossRef]
- Khandare, B.B.; Deshmukh, B.T. A literature review on wide area protection technique using PMU. In Proceedings of the 2017 International Conference on Energy, Communication, Data Analytics and Soft Computing (ICECDS), Chennai, India, 1–2 August 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1449–1454. [Google Scholar]
- Usman, M.U.; Faruque, M.O. Applications of synchrophasor technologies in power systems. J. Mod. Power Syst. Clean Energy 2019, 7, 211–226. [Google Scholar] [CrossRef]
- Martin, K.E. Synchrophasor measurements under the IEEE standard C37. 118.1-2011 with amendment C37. 118.1 a. IEEE Trans. Power Deliv. 2015, 30, 1514–1522. [Google Scholar] [CrossRef]
- Carta, A.; Locci, N.; Muscas, C.; Pinna, F.; Sulis, S. GPS and IEEE 1588 synchronization for the measurement of synchrophasors in electric power systems. Comput. Stand. Interfaces 2011, 33, 176–181. [Google Scholar] [CrossRef]
- Khatib, A.R.A. Internet-Based Wide Area Measurement Applications in Deregulated Power Systems. Doctoral Dissertation, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2002. [Google Scholar]
- Snyder, A.F.; Ivanescu, D.; HadjSaid, N.; Georges, D.; Margotin, T. Delayed-input wide-area stability control with synchronized phasor measurements and linear matrix inequalities. In Proceedings of the 2000 Power Engineering Society Summer Meeting (Cat. No. 00CH37134), Como, Italy, 27 July 2000; IEEE: Piscataway, NJ, USA, 2000; Volume 2, pp. 1009–1014. [Google Scholar]
- Phadke, A.G.; Thorp, J.S. Synchronized Phasor Measurements and Their Applications; Springer: New York, NY, USA, 2008; Volume 1, p. 81. [Google Scholar]
- Ye, F.; Bose, A. Multiple communication topologies for pmu-based applications: Introduction, analysis and simulation. IEEE Trans. Smart Grid 2020, 11, 5051–5061. [Google Scholar] [CrossRef]
- Li, G.W.; Ju, W.Y.; Shi, D.Y. Functional vulnerability assessment of SCADA network. In Proceedings of the 2012 Asia-Pacific Power and Energy Engineering Conference, Shanghai, China, 27–29 March 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–4. [Google Scholar]
- Myrda, P.T.; Koellner, K. Naspinet-the internet for synchrophasors. In Proceedings of the 2010 43rd Hawaii International Conference on System Sciences, Honolulu, HI, USA, 5–8 January 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–6. [Google Scholar]
- Galli, S.; Scaglione, A.; Wang, Z. For the grid and through the grid: The role of power line communications in the smart grid. Proc. IEEE 2011, 99, 998–1027. [Google Scholar] [CrossRef]
- Aquilue, R.; Gutierrez, I.; Pijoan, J.L.; Sanchez, G. High-voltage multicarrier spread-spectrum system field test. IEEE Trans. Power Deliv. 2009, 24, 1112–1121. [Google Scholar] [CrossRef]
- Pighi, R.; Raheli, R. On multicarrier signal transmission for high-voltage power lines. In Proceedings of the International Symposium on Power Line Communications and Its Applications, Vancouver, BC, Canada, 6–8 April 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 32–36. [Google Scholar]
- Horowitz, S.H.; Phadke, A.G.; Henville, C.F. Power System Relaying; John Wiley Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- What Is 5G: Everything You Need to Know about 5G: 5G FAQ: Qualcomm. Wireless Technology & Innovation. (n.d.). Retrieved 22 February 2023. Available online: https://www.qualcomm.com/5g/what-is-5g#Whatis5G? (accessed on 25 March 2023).
- Bobba, R.B.; Dagle, J.; Heine, E.; Khurana, H.; Sanders, W.H.; Sauer, P.; Yardley, T. Enhancing grid measurements: Wide area measurement systems, NASPInet, and security. IEEE Power Energy Mag. 2011, 10, 67–73. [Google Scholar] [CrossRef]
- Fesharaki, F.H.; Hooshmand, R.A.; Khodabakhshian, A. Simultaneous optimal design of measurement and communication infrastructures in hierarchical structured WAMS. IEEE Trans. Smart Grid 2013, 5, 312–319. [Google Scholar] [CrossRef]
- Borlase, S. (Ed.) . Smart Grids: Infrastructure, Technology, and Solutions; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Abdelwahid, S.; Babiker, A.; Eltom, A.; Kobet, G. Hardware implementation of an automatic adaptive centralized underfrequency load shedding scheme. IEEE Trans. Power Deliv. 2014, 29, 2664–2673. [Google Scholar] [CrossRef]
- Tang, J.; Liu, J.; Ponci, F.; Monti, A. Adaptive load shedding based on combined frequency and voltage stability assessment using synchrophasor measurements. IEEE Trans. Power Syst. 2013, 28, 2035–2047. [Google Scholar] [CrossRef]
- Xu, J.; Xie, B.; Liao, S.; Yuan, Z.; Ke, D.; Sun, Y.; Li, X.; Peng, X. Load shedding and restoration for intentional island with renewable distributed generation. J. Mod. Power Syst. Clean Energy 2021, 9, 612–624. [Google Scholar] [CrossRef]
- Monti, A.; Muscas, C.; Ponci, F. Phasor Measurement Units and Wide Area Monitoring Systems; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Amraee, T.; Darebaghi, M.G.; Soroudi, A.; Keane, A. Probabilistic under frequency load shedding considering RoCoF relays of distributed generators. IEEE Trans. Power Syst. 2017, 33, 3587–3598. [Google Scholar] [CrossRef]
- HaesAlhelou, H.; Hamedani-Golshan, M.E.; Njenda, T.C.; Siano, P. Wide-area measurement system-based optimal multi-stage under-frequency load-shedding in interconnected smart power systems using evolutionary computing techniques. Appl. Sci. 2019, 9, 508. [Google Scholar]
- Derviškadić, A.; Zuo, Y.; Frigo, G.; Paolone, M. Under frequency load shedding based on PMU estimates of frequency and ROCOF. In Proceedings of the 2018 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Sarajevo, Bosnia and Herzegovina, 15 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Karimi, M.; Wall, P.; Mokhlis, H.; Terzija, V. A new centralized adaptive underfrequency load shedding controller for microgrids based on a distribution state estimator. IEEE Trans. Power Deliv. 2016, 32, 370–380. [Google Scholar] [CrossRef]
- Rudez, U.; Mihalic, R. WAMS-based underfrequency load shedding with short-term frequency prediction. IEEE Trans. Power Deliv. 2015, 31, 1912–1920. [Google Scholar] [CrossRef]
- Jegarluei, M.R.; Cortés, J.S.; Azizi, S.; Terzija, V. Wide-area event identification in power systems: A review of the state-of-the-art. In Proceedings of the 2022 International Conference on Smart Grid Synchronized Measurements and Analytics (SGSMA), Split, Croatia, 24–26 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–7. [Google Scholar]
- IEEE Std C37 118.1-2011; IEEE Standard for Synchrophasor Measurements for Power Systems–Amendment 1: Modification of Selected Performance Requirements. IEEE Std C37. 118.1 a-2014 (Amendment to IEEE Std C37. 118.1-2011). IEEE: Piscataway, NJ, USA, 2014.
- Phadke, A.G.; Kasztenny, B. Synchronized phasor and frequency measurement under transient conditions. IEEE Trans. Power Deliv. 2008, 24, 89–95. [Google Scholar] [CrossRef]
- Frigo, G.; Colangelo, D.; Derviškadić, A.; Pignati, M.; Narduzzi, C.; Paolone, M. Definition of accurate reference synchrophasors for static and dynamic characterization of PMUs. IEEE Trans. Instrum. Meas. 2017, 66, 2233–2246. [Google Scholar] [CrossRef]
- Roscoe, A.J.; Dyśko, A.; Marshall, B.; Lee, M.; Kirkham, H.; Rietveld, G. The case for redefinition of frequency and ROCOF to account for AC power system phase steps. In Proceedings of the 2017 IEEE International Workshop on Applied Measurements for Power Systems (AMPS), Liverpool, UK, 20–22 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Frigo, G.; Derviškadić, A.; Zuo, Y.; Paolone, M. PMU-based ROCOF measurements: Uncertainty limits and metrological significance in power system applications. IEEE Trans. Instrum. Meas. 2019, 68, 3810–3822. [Google Scholar] [CrossRef]
- Zuo, Y.; Frigo, G.; Derviškadić, A.; Paolone, M. Impact of synchrophasor estimation algorithms in ROCOF-based under-frequency load-shedding. IEEE Trans. Power Syst. 2019, 35, 1305–1316. [Google Scholar] [CrossRef]
- Golpira, H.; Bevrani, H.; Messina, A.R.; Francois, B. A data-driven under frequency load shedding scheme in power systems. IEEE Trans. Power Syst. 2022, 38, 1138–1150. [Google Scholar] [CrossRef]
- Bekhradian, R.; Sanaye-Pasand, M.; Mahari, A. Adaptive Wide-Area Load Shedding Scheme Based on the Sink and Source Concept to Preserve Power System Stability. IEEE Syst. J. 2022, 17, 503–512. [Google Scholar] [CrossRef]
- Glavic, M.; Van Cutsem, T. Wide-area detection of voltage instability from synchronized phasor measurements. Part I: Principle. IEEE Trans. Power Syst. 2009, 24, 1408–1416. [Google Scholar] [CrossRef]
- Gu, W.; Wan, Q. Linearized voltage stability index for wide-area voltage monitoring and control. Int. J. Electr. Power Energy Syst. 2010, 32, 333–336. [Google Scholar] [CrossRef]
- Mahari, A.; Seyedi, H. A wide area synchrophasor-based load shedding scheme to prevent voltage collapse. Int. J. Electr. Power Energy Syst. 2016, 78, 248–257. [Google Scholar] [CrossRef]
- Modarresi, J.; Gholipour, E.; Khodabakhshian, A. A new undervoltage load shedding method to reduce active power curtailment. Int. Trans. Electr. Energy Syst. 2017, 27, e2291. [Google Scholar] [CrossRef]
- Adewole, A.C.; Tzoneva, R.; Apostolov, A. Adaptive under-voltage load shedding scheme for large interconnected smart grids based on wide area synchrophasor measurements. IET Gener. Transm. Distrib. 2016, 10, 1957–1968. [Google Scholar] [CrossRef]
- Phadke, A.G.; Wall, P.; Ding, L.; Terzija, V. Improving the performance of power system protection using wide area monitoring systems. J. Mod. Power Syst. Clean Energy 2016, 4, 319–331. [Google Scholar] [CrossRef]
- Liu, W.; Lin, Z.; Wen, F.; Ledwich, G. A wide area monitoring system based load restoration method. IEEE Trans. Power Syst. 2013, 28, 2025–2034. [Google Scholar] [CrossRef]
- Itiki, R.; Libonati, F.; Burgués, H.; Martini, M.; Essakiappan, S.; Manjrekar, M.; Bai, L.; Di Santo, S.G. A proposed wide-area stabilization system through a large-scale fleet of electric vehicles for grid. Int. J. Electr. Power Energy Syst. 2022, 141, 108164. [Google Scholar] [CrossRef]
- Shepard, D.P.; Humphreys, T.E.; Fansler, A.A. Evaluation of the vulnerability of phasor measurement units to GPS spoofing attacks. Int. J. Crit. Infrastruct. Prot. 2012, 5, 146–153. [Google Scholar] [CrossRef]
- Fan, Y.; Zhang, Z.; Trinkle, M.; Dimitrovski, A.D.; Song, J.B.; Li, H. A cross-layer defense mechanism against GPS spoofing attacks on PMUs in smart grids. IEEE Trans. Smart Grid 2014, 6, 2659–2668. [Google Scholar] [CrossRef]
- Hu, Y.; Novosel, D. Progresses in PMU testing and calibration. In Proceedings of the 2008 Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Nanjing, China, 6–9 April 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 150–155. [Google Scholar]
- Ahmed, A.; Krishnan, V.V.G.; Foroutan, S.A.; Touhiduzzaman; Rublein, C.L.; Srivastava, A.K.; Wu, Y.; Hahn, A.; Suresh, S. Cyber physical security analytics for anomalies in transmission protection systems. IEEE Trans. Ind. Appl. 2019, 55, 6313–6323. [Google Scholar] [CrossRef]
- Chamorro, H.R.; Gomez-Diaz, E.O.; Paternina, M.R.A.; Andrade, M.A.; Barocio, E.; Rueda, J.L.; Gonzalez-Longatt, F.; Sood, V.K. Power system coherency recognition and islanding: Practical limits and future perspectives. IET Energy Syst. Integr. 2023, 5, 1–14. [Google Scholar] [CrossRef]
- Phadke, A.G.; Thorp, J.S. Computer Relaying for Power Systems; John Wiley Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Anderson, P.M.; Henville, C.F.; Rifaat, R.; Johnson, B.; Meliopoulos, S. Power System Protection; John Wiley Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- Adamiak, M.; Apostolov, A.; Begovic, M.; Henville, C.; Martin, K.; Michel, G.; Phadke, A.; Thorp, J. Wide area protection—Technology and infrastructures. IEEE Trans. Power Deliv. 2006, 21, 601–609. [Google Scholar] [CrossRef]
- Horowitz, S.H.; Phadke, A.G. Third zone revisited. IEEE Trans. Power Deliv. 2005, 21, 23–29. [Google Scholar] [CrossRef]
- Tan, J.C.; Crossley, P.A.; McLaren, P.G.; Gale, P.F.; Hall, I.; Farrell, J. Application of a wide area backup protection expert system to prevent cascading outages. IEEE Trans. Power Deliv. 2002, 17, 375–380. [Google Scholar] [CrossRef]
- Saber, A.; Emam, A.; Elghazaly, H. Wide-area backup protection scheme for transmission lines considering cross-country and evolving faults. IEEE Syst. J. 2018, 13, 813–822. [Google Scholar] [CrossRef]
- He, Z.; Zhang, Z.; Chen, W.; Malik, O.P.; Yin, X. Wide-area backup protection algorithm based on fault component voltage distribution. IEEE Trans. Power Deliv. 2011, 26, 2752–2760. [Google Scholar] [CrossRef]
- Ma, J.; Li, J.; Thorp, J.S.; Arana, A.J.; Yang, Q.; Phadke, A.G. A fault steady state component-based wide area backup protection algorithm. IEEE Trans. Smart Grid 2011, 2, 468–475. [Google Scholar] [CrossRef]
- Nayak, P.K.; Pradhan, A.K.; Bajpai, P. Wide-area measurement-based backup protection for power network with series compensation. IEEE Trans. Power Deliv. 2014, 29, 1970–1977. [Google Scholar] [CrossRef]
- Eissa, M.M.; Masoud, M.E.; Elanwar, M.M.M. A novel back up wide area protection technique for power transmission grids using phasor measurement unit. IEEE Trans. Power Deliv. 2009, 25, 270–278. [Google Scholar] [CrossRef]
- Zare, J.; Aminifar, F.; Sanaye-Pasand, M. Communication-constrained regionalization of power systems for synchrophasor-based wide-area backup protection scheme. IEEE Trans. Smart Grid 2015, 6, 1530–1538. [Google Scholar] [CrossRef]
- Dubey, R.; Samantaray, S.R.; Panigrahi, B.K.; Venkoparao, V.G. Koopman analysis based wide-area back-up protection and faulted line identification for series-compensated power network. IEEE Syst. J. 2016, 12, 2634–2644. [Google Scholar] [CrossRef]
- Mirhosseini, S.S.; Akhbari, M. Wide area backup protection algorithm for transmission lines based on fault component complex power. Int. J. Electr. Power Energy Syst. 2016, 83, 1–6. [Google Scholar] [CrossRef]
- Jena, M.K.; Samantaray, S.R.; Panigrahi, B.K. A new decentralized approach to wide-area back-up protection of transmission lines. IEEE Syst. J. 2017, 12, 3161–3168. [Google Scholar] [CrossRef]
- Ma, J.; Liu, C.; Thorp, J.S. A wide-area backup protection algorithm based on distance protection fitting factor. IEEE Trans. Power Deliv. 2015, 31, 2196–2205. [Google Scholar] [CrossRef]
- Tong, X.; Wang, X.; Wang, R.; Huang, F.; Dong, X.; Hopkinson, K.M.; Song, G. The study of a regional decentralized peer-to-peer negotiation-based wide-area backup protection multi-agent system. IEEE Trans. Smart Grid 2013, 4, 1197–1206. [Google Scholar] [CrossRef]
- Li, Z.; Yin, X.; Zhang, Z.; He, Z. Wide-area protection fault identification algorithm based on multi-information fusion. IEEE Trans. Power Deliv. 2013, 28, 1348–1355. [Google Scholar]
- Yu, F.; Booth, C.; Dysko, A.; Hong, Q. Wide-area backup protection and protection performance analysis scheme using PMU data. Int. J. Electr. Power Energy Syst. 2019, 110, 630–641. [Google Scholar] [CrossRef]
- Chen, M.; Wang, H.; Shen, S.; He, B. Research on a distance relay-based wide-area backup protection algorithm for transmission lines. IEEE Trans. Power Deliv. 2016, 32, 97–105. [Google Scholar] [CrossRef]
- Navalkar, P.V.; Soman, S.A. Secure remote backup protection of transmission lines using synchrophasors. IEEE Trans. Power Deliv. 2010, 26, 87–96. [Google Scholar] [CrossRef]
- Sharafi, A.; Sanaye-Pasand, M.; Aminifar, F. Transmission system wide-area back-up protection using current phasor measurements. Int. J. Electr. Power Energy Syst. 2017, 92, 93–103. [Google Scholar] [CrossRef]
- Li, W.; Tan, Y.; Li, Y.; Cao, Y.; Chen, C.; Zhang, M. A new differential backup protection strategy for smart distribution networks: A fast and reliable approach. IEEE Access 2019, 7, 38135–38145. [Google Scholar] [CrossRef]
- Zare, J.; Aminifar, F.; Sanaye-Pasand, M. Synchrophasor-based wide-area backup protection scheme with data requirement analysis. IEEE Trans. Power Deliv. 2014, 30, 1410–1419. [Google Scholar] [CrossRef]
- Neyestanaki, M.K.; Ranjbar, A.M. An adaptive PMU-based wide area backup protection scheme for power transmission lines. IEEE Trans. Smart Grid 2015, 6, 1550–1559. [Google Scholar] [CrossRef]
- Nougain, V.; Jena, M.K.; Panigrahi, B.K. Decentralised wide-area back-up protection scheme based on the concept of centre of reactive power. IET Gener. Transm. Distrib. 2019, 13, 4551–4557. [Google Scholar] [CrossRef]
- Samantaray, S.R.; Sharma, A. Enhancing performance of wide-area back-up protection scheme using PMU assisted dynamic state estimator. IEEE Trans. Smart Grid 2018, 10, 5066–5074. [Google Scholar]
- Abd el-Ghany, H.A. Optimal PMU allocation for high-sensitivity wide-area backup protection scheme of transmission lines. Electr. Power Syst. Res. 2020, 187, 106485. [Google Scholar] [CrossRef]
- Ahmadinia, M.; Sadeh, J. A modified wide-area backup protection scheme for shunt-compensated transmission lines. Electr. Power Syst. Res. 2020, 183, 106274. [Google Scholar] [CrossRef]
- Azizi, S.; Liu, G.; Dobakhshari, A.S.; Terzija, V. Wide-area backup protection against asymmetrical faults using available phasor measurements. IEEE Trans. Power Deliv. 2019, 35, 2032–2039. [Google Scholar] [CrossRef]
- Chavez, J.J.; Kumar, N.V.; Azizi, S.; Guardado, J.L.; Rueda, J.; Palensky, P.; Terzija, V.; Popov, M. PMU-voltage drop based fault locator for transmission backup protection. Electr. Power Syst. Res. 2021, 196, 107188. [Google Scholar] [CrossRef]
- Samantaray, S.R. A differential voltage-based wide-area backup protection scheme for transmission network. IEEE Syst. J. 2021, 16, 520–530. [Google Scholar]
- Harish, A.; Prince, A.; Jayan, M.V. Fault Detection and Classification for Wide Area Backup Protection of Power Transmission Lines Using Weighted Extreme Learning Machine. IEEE Access 2022, 10, 82407–82417. [Google Scholar] [CrossRef]
- Jegarluei, M.R.; Dobakhshari, A.S.; Azizi, S. Reducing the computational complexity of wide-area backup protection in power systems. IEEE Trans. Power Deliv. 2022, 37, 2421–2424. [Google Scholar] [CrossRef]
- Shazdeh, S.; Golpîra, H.; Bevrani, H. A PMU-based back-up protection scheme for fault detection considering uncertainties. Int. J. Electr. Power Energy Syst. 2023, 145, 108592. [Google Scholar] [CrossRef]
- Jegarluei, M.R.; Aristidou, P.; Azizi, S. Wide-Area backup protection against asymmetrical faults in the presence of renewable energy sources. Int. J. Electr. Power Energy Syst. 2023, 144, 108528. [Google Scholar] [CrossRef]
- Goh, H.H.; Chua, Q.S.; Lee, S.W.; Kok, B.C.; Goh, K.C.; Teo, K.T.K. Evaluation for voltage stability indices in power system using artificial neural network. Procedia Eng. 2015, 118, 1127–1136. [Google Scholar] [CrossRef]
- Li, H.; Bose, A.; Venkatasubramanian, V.M. Wide-area voltage monitoring and optimization. IEEE Trans. Smart Grid 2015, 7, 785–793. [Google Scholar] [CrossRef]
- Su, H.Y.; Liu, C.W. Estimating the voltage stability margin using PMU measurements. IEEE Trans. Power Syst. 2015, 31, 3221–3229. [Google Scholar] [CrossRef]
- Vournas, C.D.; Lambrou, C.; Mandoulidis, P. Voltage stability monitoring from a transmission bus PMU. IEEE Trans. Power Syst. 2016, 32, 3266–3274. [Google Scholar] [CrossRef]
- Kamel, M.; Karrar, A.A.; Eltom, A.H. Development and application of a new voltage stability index for on-line monitoring and shedding. IEEE Trans. Power Syst. 2017, 33, 1231–1241. [Google Scholar] [CrossRef]
- Mandoulidis, P.; Vournas, C. A PMU-based real-time estimation of voltage stability and margin. Electr. Power Syst. Res. 2020, 178, 106008. [Google Scholar] [CrossRef]
- Safavizadeh, A.; Kordi, M.; Eghtedarnia, F.; Torkzadeh, R.; Marzooghi, H. Framework for real-time short-term stability assessment of power systems using PMU measurements. IET Gener. Transm. Distrib. 2019, 13, 3433–3442. [Google Scholar] [CrossRef]
- Gao, H.; Cai, G.; Yang, D.; Wang, L. Real-time long-term voltage stability assessment based on eGBDT for large-scale power system with high renewables penetration. Electr. Power Syst. Res. 2023, 214, 108915. [Google Scholar] [CrossRef]
- Guddanti, K.P.; Matavalam AR, R.; Weng, Y. PMU-based distributed non-iterative algorithm for real-time voltage stability monitoring. IEEE Trans. Smart Grid 2020, 11, 5203–5215. [Google Scholar] [CrossRef]
- Hur Rizvi, S.M.; Kundu, P.; Srivastava, A.K. Hybrid voltage stability and security assessment using synchrophasors with consideration of generator Q-limits. IET Gener. Transm. Distrib. 2020, 14, 4042–4051. [Google Scholar] [CrossRef]
- Kumar, S.; Tyagi, B.; Kumar, V.; Chohan, S. PMU-based voltage stability measurement under contingency using ANN. IEEE Trans. Instrum. Meas. 2021, 71, 1–11. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, W.; Chen, J.; Wang, L. PMU-based voltage stability prediction using least square support vector machine with online learning. Electr. Power Syst. Res. 2018, 160, 234–242. [Google Scholar] [CrossRef]
- Jena, M.K.; Panigrahi, B.K. Transient potential power based supervisory zone-1 operation during unstable power swing. IEEE Syst. J. 2018, 13, 1823–1830. [Google Scholar] [CrossRef]
- Cai, G.; Wang, B.; Yang, D.; Sun, Z.; Wang, L. Inertia estimation based on observed electromechanical oscillation response for power systems. IEEE Trans. Power Syst. 2019, 34, 4291–4299. [Google Scholar] [CrossRef]
- Machowski, J. Selectivity of power system protections at power swings in power system. Acta Energetica 2012, 4, 96–123. [Google Scholar]
- Machowski, J.; Lubosny, Z.; Bialek, J.W.; Bumby, J.R. Power System Dynamics: Stability and Control; John Wiley Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Desai, J.P.; Makwana, V.H. Phasor measurement unit incorporated adaptive out-of-step protection of synchronous generator. J. Mod. Power Syst. Clean Energy 2020, 9, 1032–1042. [Google Scholar] [CrossRef]
- Gao, Z.D.; Wang, G.B. A new power swing block in distance protection based on a microcomputer-principle and performance analysis. In Proceedings of the 1991 International Conference on Advances in Power System Control, Operation and Management, APSCOM-91, Hong Kong, China, 5–8 November 1991; IET: London, UK, 1991; pp. 843–847. [Google Scholar]
- So, K.H.; Heo, J.Y.; Kim, C.H.; Aggarwal, R.K.; Song, K.B. Out-of-step detection algorithm using frequency deviation of voltage. IET Gener. Transm. Distrib. 2007, 1, 119–126. [Google Scholar] [CrossRef]
- Sriram, C.; Kumar, D.R.; Raju, G.S. Blocking the distance relay operation in third zone during power swing using polynomial curve fitting method. In Proceedings of the 2014 International Conference on Smart Electric Grid (ISEG), Guntur, India, 19–20 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–7. [Google Scholar]
- Nayak, P.K.; Pradhan, A.K.; Bajpai, P. Secured zone 3 protection during stressed condition. IEEE Trans. Power Deliv. 2014, 30, 89–96. [Google Scholar] [CrossRef]
- Chothani, N.G.; Bhalja, B.R.; Parikh, U.B. New support vector machine-based digital relaying scheme for discrimination between power swing and fault. IET Gener. Transm. Distrib. 2014, 8, 17–25. [Google Scholar] [CrossRef]
- Jafari, R.; Moaddabi, N.; Eskandari-Nasab, M.; Gharehpetian, G.B.; Naderi, M.S. A novel power swing detection scheme independent of the rate of change of power system parameters. IEEE Trans. Power Deliv. 2014, 29, 1192–1202. [Google Scholar] [CrossRef]
- Kang, D.; Gokaraju, R. A new method for blocking third-zone distance relays during stable power swings. IEEE Trans. Power Deliv. 2016, 31, 1836–1843. [Google Scholar] [CrossRef]
- Kundu, P.; Pradhan, A.K. Wide area measurement based protection support during power swing. Int. J. Electr. Power Energy Syst. 2014, 63, 546–554. [Google Scholar] [CrossRef]
- GhanizadehBolandi, T.; Haghifam, M.R.; Khederzadeh, M. Real-time monitoring of zone 3 vulnerable distance relays to prevent maloperation under load encroachment condition. IET Gener. Transm. Distrib. 2017, 11, 1878–1888. [Google Scholar] [CrossRef]
- Lavand, S.A.; Soman, S.A. Predictive analytic to supervise zone 1 of distance relay using synchrophasors. IEEE Trans. Power Deliv. 2016, 31, 1844–1854. [Google Scholar] [CrossRef]
- Patel, B.; Bera, P.; nee Dey, S.H. A novel method to distinguish internal and external faults during power swing. IEEE Trans. Power Deliv. 2020, 36, 2595–2605. [Google Scholar] [CrossRef]
- Nazari, A.A.; Razavi, F.; Fakharian, A. A new power swing detection method in power systems with large-scale wind farms based on modified empirical-mode decomposition method. IET Gener. Transm. Distrib. 2022, 17, 1204–1215. [Google Scholar] [CrossRef]
- Alnassar, Z.; Nagarajan, S.T. Analysis of Oscillations during Out-of-Step Condition in Power Systems. Int. Trans. Electr. Energy Syst. 2023, 2023, 4303491. [Google Scholar] [CrossRef]
- Tealane, M.; Kilter, J.; Popov, M.; Bagleybter, O.; Klaar, D. Online detection of out-of-step condition using PMU-determined system impedances. IEEE Access 2022, 10, 14807–14818. [Google Scholar] [CrossRef]
- Rao, J.T.; Bhalja, B.R.; Andreev, M.; Malik, O.P. Discrimination between in-zone and out-of-zone faults during power swing condition using synchrophasor data. Int. J. Electr. Power Energy Syst. 2023, 146, 108769. [Google Scholar]
- El-Sayed LM, A.; Ibrahim, D.K.; Gilany, M.I. Enhancing distance relay performance using wide-area protection for detecting symmetrical/unsymmetrical faults during power swings. Alex. Eng. J. 2022, 61, 6869–6886. [Google Scholar] [CrossRef]
- Cheng, Y.; Foggo, B.; Yamashita, K.; Yu, N. Missing Value Replacement for PMU Data via Deep Learning Model With Magnitude Trend Decoupling. IEEE Access 2023, 11, 27450–27461. [Google Scholar] [CrossRef]
- Chakhchoukh, Y.; Vittal, V.; Heydt, G.T. PMU based state estimation by integrating correlation. IEEE Trans. Power Syst. 2013, 29, 617–626. [Google Scholar] [CrossRef]
- Johnson, T.; Moger, T. Latest Trends in Electromechanical Dynamic State Estimation for Electric Power Grid. In Proceedings of the 2022 3rd International Conference for Emerging Technology (INCET), Belgaum, India, 27–29 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Huang, Z.; Du, P.; Kosterev, D.; Yang, S. Generator dynamic model validation and parameter calibration using phasor measurements at the point of connection. IEEE Trans. Power Syst. 2013, 28, 1939–1949. [Google Scholar] [CrossRef]
- Fan, L.; Wehbe, Y. Extended Kalman filtering based real-time dynamic state and parameter estimation using PMU data. Electr. Power Syst. Res. 2013, 103, 168–177. [Google Scholar] [CrossRef]
- Ghahremani, E.; Kamwa, I. Dynamic state estimation in power system by applying the extended Kalman filter with unknown inputs to phasor measurements. IEEE Trans. Power Syst. 2011, 26, 2556–2566. [Google Scholar] [CrossRef]
- Ghahremani, E.; Kamwa, I. Online state estimation of a synchronous generator using unscented Kalman filter from phasor measurements units. IEEE Trans. Energy Convers. 2011, 26, 1099–1108. [Google Scholar] [CrossRef]
- Zhou, N.; Huang, Z.; Li, Y.; Welch, G. Local sequential ensemble Kalman filter for simultaneously tracking states and parameters. In Proceedings of the 2012 North American Power Symposium (NAPS), Champaign, IL, USA, 9–11 September 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–6. [Google Scholar]
- Zhou, N.; Meng, D.; Lu, S. Estimation of the dynamic states of synchronous machines using an extended particle filter. IEEE Trans. Power Syst. 2013, 28, 4152–4161. [Google Scholar] [CrossRef]
- Zhou, N.; Meng, D.; Huang, Z.; Welch, G. Dynamic state estimation of a synchronous machine using PMU data: A comparative study. IEEE Trans. Smart Grid 2014, 6, 450–460. [Google Scholar] [CrossRef]
- Pignati, M.; Popovic, M.; Barreto, S.; Cherkaoui, R.; Flores, G.D.; Le Boudec, J.Y.; Mohiuddin, M.; Paolone, M.; Romano, P.; Sarri, S.; et al. Real-time state estimation of the EPFL-campus medium-voltage grid by using PMUs. In Proceedings of the 2015 IEEE Power Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 18–20 February 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–5. [Google Scholar]
- Ghahremani, E.; Kamwa, I. Local and wide-area PMU-based decentralized dynamic state estimation in multi-machine power systems. IEEE Trans. Power Syst. 2015, 31, 547–562. [Google Scholar] [CrossRef]
- Wu, T.; Chung, C.Y.; Kamwa, I. A fast state estimator for systems including limited number of PMUs. IEEE Trans. Power Syst. 2017, 32, 4329–4339. [Google Scholar] [CrossRef]
- Paul, A.; Kamwa, I.; Joos, G. Centralized dynamic state estimation using a federation of extended Kalman filters with intermittent PMU data from generator terminals. IEEE Trans. Power Syst. 2018, 33, 6109–6119. [Google Scholar] [CrossRef]
- Prasad, S.; Kumar, D.V. Trade-offs in PMU and IED deployment for active distribution state estimation using multi-objective evolutionary algorithm. IEEE Trans. Instrum. Meas. 2018, 67, 1298–1307. [Google Scholar] [CrossRef]
- Shereen, E.; Delcourt, M.; Barreto, S.; Dán, G.; Le Boudec, J.Y.; Paolone, M. Feasibility of time-synchronization attacks against PMU-based state estimation. IEEE Trans. Instrum. Meas. 2019, 69, 3412–3427. [Google Scholar] [CrossRef]
- Jovicic, A.; Jereminov, M.; Pileggi, L.; Hug, G. A linear formulation for power system state estimation including RTU and PMU measurements. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), Bucharest, Romania, 29 September–2 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Kabiri, M.; Amjady, N. A new hybrid state estimation considering different accuracy levels of PMU and SCADA measurements. IEEE Trans. Instrum. Meas. 2018, 68, 3078–3089. [Google Scholar] [CrossRef]
- Lin, C.; Wu, W.; Guo, Y. Decentralized robust state estimation of active distribution grids incorporating microgrids based on PMU measurements. IEEE Trans. Smart Grid 2019, 11, 810–820. [Google Scholar] [CrossRef]
- Gholami, M.; Abbaspour, A.; Moeini-Aghtaie, M.; Fotuhi-Firuzabad, M.; Lehtonen, M. Detecting the location of short-circuit faults in active distribution network using PMU-based state estimation. IEEE Trans. Smart Grid 2019, 11, 1396–1406. [Google Scholar] [CrossRef]
- Muscas, C.; Pegoraro, P.A.; Sulis, S.; Pau, M.; Ponci, F.; Monti, A. New Kalman filter approach exploiting frequency knowledge for accurate PMU-based power system state estimation. IEEE Trans. Instrum. Meas. 2020, 69, 6713–6722. [Google Scholar] [CrossRef]
- Dobakhshari, A.S.; Azizi, S.; Abdolmaleki, M.; Terzija, V. Linear LAV-based state estimation integrating hybrid SCADA/PMU measurements. IET Gener. Transm. Distrib. 2020, 14, 1583–1590. [Google Scholar] [CrossRef]
- Jovicic, A.; Hug, G. Linear state estimation and bad data detection for power systems with RTU and PMU measurements. IET Gener. Transm. Distrib. 2020, 14, 5675–5684. [Google Scholar] [CrossRef]
- Khalili, R.; Abur, A. PMU-based decoupled state estimation for unsymmetrical power systems. IEEE Trans. Power Syst. 2021, 36, 5359–5368. [Google Scholar] [CrossRef]
- De Oliveira-De Jesus, P.M.; Rodriguez, N.A.; Celeita, D.F.; Ramos, G.A. PMU-based system state estimation for multigrounded distribution systems. IEEE Trans. Power Syst. 2020, 36, 1071–1081. [Google Scholar] [CrossRef]
- Dobakhshari, A.S.; Abdolmaleki, M.; Terzija, V.; Azizi, S. Robust hybrid linear state estimator utilizing SCADA and PMU measurements. IEEE Trans. Power Syst. 2020, 36, 1264–1273. [Google Scholar] [CrossRef]
- Basumallik, S.; Ma, R.; Eftekharnejad, S. Packet-data anomaly detection in PMU-based state estimator using convolutional neural network. Int. J. Electr. Power Energy Syst. 2019, 107, 690–702. [Google Scholar] [CrossRef]
- Mekhamer, S.F.; Abdelaziz, A.Y.; Ezzat, M.; Abdel-Salam, T.S. Fault location in long transmission lines using synchronized phasor measurements from both ends. Electr. Power Compon. Syst. 2012, 40, 759–776. [Google Scholar] [CrossRef]
- Abdelaziz, A.Y.; Mekhamer, S.F.; Ezzat, M. Fault location of uncompensated/series-compensated lines using two-end synchronized measurements. Electr. Power Compon. Syst. 2013, 41, 693–715. [Google Scholar] [CrossRef]
- Mukherjee, R.; De, A. Real-time dynamic security analysis of power systems using strategic PMU measurements and decision tree classification. Electr. Eng. 2021, 103, 813–824. [Google Scholar] [CrossRef]
- Hauer, J.F. Validation of phasor calculations in the macrodyne PMU for California-Oregon transmission project tests of March 1993. IEEE Trans. Power Deliv. 1996, 11, 1224–1231. [Google Scholar] [CrossRef]
- Abdollahi, A.; Seyedtabaii, S. Comparison of fourierwavelet transform methods for transmission line fault classification. In Proceedings of the 2010 4th International Power Engineering and Optimization Conference (PEOCO), Shah Alam, Malaysia, 23–24 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 579–584. [Google Scholar]
- Gopakumar, P.; Reddy MJ, B.; Mohanta, D.K. Transmission line fault detection and localisation methodology using PMU measurements. IET Gener. Transm. Distrib. 2015, 9, 1033–1042. [Google Scholar] [CrossRef]
- Bakdi, A.; Bounoua, W.; Guichi, A.; Mekhilef, S. Real-time fault detection in PV systems under MPPT using PMU and high-frequency multi-sensor data through online PCA-KDE-based multivariate KL divergence. Int. J. Electr. Power Energy Syst. 2021, 125, 106457. [Google Scholar] [CrossRef]
- Bansal, Y.; Sodhi, R. PMUs Enabled Tellegen’s Theorem-Based Fault Identification Method for Unbalanced Active Distribution Network Using RTDS. IEEE Syst. J. 2020, 14, 4567–4578. [Google Scholar] [CrossRef]
- Cui, Q.; Weng, Y. Enhance high impedance fault detection and location accuracy via μ-PMUs. IEEE Trans. Smart Grid 2019, 11, 797–809. [Google Scholar] [CrossRef]
- Sharma, N.K.; Samantaray, S.R. Assessment of PMU-based wide-area angle criterion for fault detection in microgrid. IET Gener. Transm. Distrib. 2019, 13, 4301–4310. [Google Scholar] [CrossRef]
- Khan, M.Q.; Ahmed, M.M.; Haidar, A.M. An accurate algorithm of PMU-based wide area measurements for fault detection using positive-sequence voltage and unwrapped dynamic angles. Measurement 2022, 192, 110906. [Google Scholar] [CrossRef]
- Liu, G.; Li, X.; Wang, C.; Chen, Z.; Chen, R.; Qiu, R.C. Hessian Locally Linear Embedding of PMU Data for Efficient Fault Detection in Power Systems. IEEE Trans. Instrum. Meas. 2022, 71, 1–4. [Google Scholar] [CrossRef]
- Aloghareh, F.H.; Jannati, M.; Shams, M. A deep long Short-Term memory based scheme for Auto-Reclosing of power transmission lines. Int. J. Electr. Power Energy Syst. 2022, 141, 108105. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Khodayar, M.E. Graph-based faulted line identification using micro-PMU data in distribution systems. IEEE Trans. Smart Grid 2020, 11, 3982–3992. [Google Scholar] [CrossRef]
- Gilanifar, M.; Cordova, J.; Wang, H.; Stifter, M.; Ozguven, E.E.; Strasser, T.I.; Arghandeh, R. Multi-task logistic low-ranked dirty model for fault detection in power distribution system. IEEE Trans. Smart Grid 2019, 11, 786–796. [Google Scholar] [CrossRef]
- Shadi, M.R.; Ameli, M.T.; Azad, S. A real-time hierarchical framework for fault detection, classification, and location in power systems using PMUs data and deep learning. Int. J. Electr. Power Energy Syst. 2022, 134, 107399. [Google Scholar] [CrossRef]
- Sarangi, S.; Biswal, C.; Sahu, B.K.; Rout, P.K. Active Islanding Detection and Analysis of Total Harmonic Distortion for Inverter-Interfaced Microgrid Based on High-Frequency Signal Installation. In Proceedings of the 2022 1st International Conference on Sustainable Technology for Power and Energy Systems (STPES), Srinagar, India, 4–6 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Kim, J.S.; Kim, C.H.; Oh, Y.S.; Cho, G.J.; Song, J.S. An islanding detection method for multi-RES systems using the graph search method. IEEE Trans. Sustain. Energy 2020, 11, 2722–2731. [Google Scholar] [CrossRef]
- Kabalci, Y. A survey on smart metering and smart grid communication. Renew. Sustain. Energy Rev. 2016, 57, 302–318. [Google Scholar] [CrossRef]
- Franco, R.; Sena, C.; Taranto, G.N.; Giusto, A. Using synchrophasors for controlled islanding—A prospective application for the Uruguayan power system. IEEE Trans. Power Syst. 2012, 28, 2016–2024. [Google Scholar] [CrossRef]
- Sankar, A.; Sunitha, R. Synchrophasor data driven islanding detection, localization and prediction for microgrid using energy operator. IEEE Trans. Power Syst. 2021, 36, 4052–4065. [Google Scholar]
- Samantaray, S.R.; Kamwa, I.; Joos, G. Phasor measurement unit based wide-area monitoring and information sharing between micro-grids. IET Gener. Transm. Distrib. 2017, 11, 1293–1302. [Google Scholar] [CrossRef]
- Werho, T.; Vittal, V.; Kolluri, S.; Wong, S.M. A potential island formation identification scheme supported by PMU measurements. IEEE Trans. Power Syst. 2015, 31, 423–431. [Google Scholar] [CrossRef]
- Brahma, S.; Kavasseri, R.; Cao, H.; Chaudhuri, N.R.; Alexopoulos, T.; Cui, Y. Real-time identification of dynamic events in power systems using PMU data, and potential applications—Models, promises, and challenges. IEEE Trans. Power Deliv. 2016, 32, 294–301. [Google Scholar] [CrossRef]
- Barocio, E.; Pal, B.C.; Fabozzi, D.; Thornhill, N.F. Detection and visualization of power system disturbances using principal component analysis. In Proceedings of the 2013 IREP Symposium Bulk Power System Dynamics and Control-IX Optimization, Security and Control of the Emerging Power Grid, Madison, WI, USA, 29–31 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–10. [Google Scholar]
- Rafferty, M.; Liu, X.; Laverty, D.M.; McLoone, S. Real-time multiple event detection and classification using moving window PCA. IEEE Trans. Smart Grid 2016, 7, 2537–2548. [Google Scholar] [CrossRef]
- Liu, X.; Laverty, D.M.; Best, R.J.; Li, K.; Morrow, D.J.; McLoone, S. Principal component analysis of wide-area phasor measurements for islanding detection—A geometric view. IEEE Trans. Power Deliv. 2015, 30, 976–985. [Google Scholar] [CrossRef]
- Guo, Y.; Li, K.; Laverty, D.M.; Xue, Y. Synchrophasor-based islanding detection for distributed generation systems using systematic principal component analysis approaches. IEEE Trans. Power Deliv. 2015, 30, 2544–2552. [Google Scholar] [CrossRef]
- Muda, H.; Jena, P. Phase angle-based PC technique for islanding detection of distributed generations. IET Renew. Power Gener. 2018, 12, 735–746. [Google Scholar] [CrossRef]
- Gayathry, V.; Sujith, M. Machine learning based synchrophasor data analysis for islanding detection. In Proceedings of the 2020 International Conference for Emerging Technology (INCET), Belgaum, India, 5–7 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Ali, W.; Ulasyar, A.; Mehmood, M.U.; Khattak, A.; Imran, K.; Zad, H.S.; Nisar, S. Hierarchical control of microgrid using IoT and machine learning based islanding detection. IEEE Access 2021, 9, 103019–103031. [Google Scholar] [CrossRef]
- Kumar, G.P.; Jena, P. Pearson’s correlation coefficient for islanding detection using micro-PMU measurements. IEEE Syst. J. 2020, 15, 5078–5089. [Google Scholar] [CrossRef]
- Shukla, A.; Dutta, S.; Sadhu, P.K. An island detection approach by μ-PMU with reduced chances of cyber attack. Int. J. Electr. Power Energy Syst. 2021, 126, 106599. [Google Scholar] [CrossRef]
- Chauhan, K.; Sodhi, R. A distribution-level PMU enabled Teager-Kaiser energy based islanding detector. Electr. Power Syst. Res. 2021, 192, 106964. [Google Scholar] [CrossRef]
- Laverty, D.M.; Duggan, C.; Hastings, J.C.; Morrow, D.J. Islanding detection by phase difference method using a low cost quasi-PMU. IET Gener. Transm. Distrib. 2021, 15, 3302–3314. [Google Scholar] [CrossRef]
- Dua, G.S.; Tyagi, B.; Kumar, V. Microgrid Differential Protection Based On Superimposed Current Angle Employing Synchrophasors. IEEE Trans. Ind. Inform. 2022, 1–9. [Google Scholar] [CrossRef]
- Som, S.; Dutta, R.; Gholami, A.; Srivastava, A.K.; Chakrabarti, S.; Sahoo, S.R. Dpmu-based multiple event detection in a microgrid considering measurement anomalies. Appl. Energy 2022, 308, 118269. [Google Scholar] [CrossRef]
- Li, S.; Sun, Y.; Qin, S.; Shi, F.; Zhang, H.; Xu, Q.; Xie, W.; Zhang, Y. PMU-based harmonic phasor calculation and harmonic source identification. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Frigo, G.; Derviškadić, A.; Pegoraro, P.A.; Muscas, C.; Paolone, M. Harmonic phasor measurements in real-world PMU-based acquisitions. In Proceedings of the 2019 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Auckland, New Zealand, 20–23 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Chen, L.; Zhao, W.; Wang, F.; Huang, S. Harmonic phasor estimator for P-class phasor measurement units. IEEE Trans. Instrum. Meas. 2019, 69, 1556–1565. [Google Scholar] [CrossRef]
- Bernard, L.; Goondram, S.; Bahrani, B.; Pantelous, A.A.; Razzaghi, R. Harmonic and interharmonic phasor estimation using matrix pencil method for phasor measurement units. IEEE Sens. J. 2020, 21, 945–954. [Google Scholar] [CrossRef]
- Carta, A.; Locci, N.; Muscas, C. A PMU for the measurement of synchronized harmonic phasors in three-phase distribution networks. IEEE Trans. Instrum. Meas. 2009, 58, 3723–3730. [Google Scholar] [CrossRef]
- Sun, Y.; Li, S.; Xu, Q.; Xie, X.; Jin, Z.; Shi, F.; Zhang, H. Harmonic contribution evaluation based on the distribution-level PMUs. IEEE Trans. Power Deliv. 2020, 36, 909–919. [Google Scholar] [CrossRef]
- Castello, P.; Laurano, C.; Muscas, C.; Pegoraro, P.A.; Toscani, S.; Zanoni, M. Harmonic synchrophasors measurement algorithms with embedded compensation of voltage transformer frequency response. IEEE Trans. Instrum. Meas. 2020, 70, 9001310. [Google Scholar] [CrossRef]
- Chen, L.; Farajollahi, M.; Ghamkhari, M.; Zhao, W.; Huang, S.; Mohsenian-Rad, H. Switch status identification in distribution networks using harmonic synchrophasor measurements. IEEE Trans. Smart Grid 2020, 12, 2413–2424. [Google Scholar] [CrossRef]
- Ahmadi-Gorjayi, F.; Mohsenian-Rad, H. A Physics-Aware MIQP Approach to Harmonic State Estimation in Low-Observable Power Distribution Systems Using Harmonic Phasor Measurement Units. IEEE Trans. Smart Grid 2022, 14, 2111–2124. [Google Scholar] [CrossRef]
- Aligholian, A.; Mohsenian-Rad, H. GraphPMU: Event Clustering via Graph Representation Learning Using Locationally-Scarce Distribution-Level Fundamental and Harmonic PMU Measurements. IEEE Trans. Smart Grid 2022. [Google Scholar] [CrossRef]
- Liang, G.; Weller, S.R.; Zhao, J.; Luo, F.; Dong, Z.Y. The 2015 Ukraine blackout: Implications for false data injection attacks. IEEE Trans. Power Syst. 2016, 32, 3317–3318. [Google Scholar] [CrossRef]
- Pal, S.; Sikdar, B.; Chow, J.H. Classification and detection of PMU data manipulation attacks using transmission line parameters. IEEE Trans. Smart Grid 2017, 9, 5057–5066. [Google Scholar] [CrossRef]
- Wang, X.; Shi, D.; Wang, J.; Yu, Z.; Wang, Z. Online identification and data recovery for PMU data manipulation attack. IEEE Trans. Smart Grid 2019, 10, 5889–5898. [Google Scholar] [CrossRef]
- Xue, A.; Xu, F.; Xu, J.; Chow, J.H.; Leng, S.; Bi, T. Online pattern recognition and data correction of PMU data under GPS spoofing attack. J. Mod. Power Syst. Clean Energy 2020, 8, 1240–1249. [Google Scholar] [CrossRef]
- Liang, H.; Zhu, L.; Yu, F.R.; Wang, X. A Cross-Layer Defense Method for Blockchain Empowered CBTC Systems Against Data Tampering Attacks. IEEE Trans. Intell. Transp. Syst. 2022, 24, 501–515. [Google Scholar] [CrossRef]
- Yasinzadeh, M.; Akhbari, M. Detection of PMU spoofing in power grid based on phasor measurement analysis. IET Gener. Transm. Distrib. 2018, 12, 1980–1987. [Google Scholar] [CrossRef]
- Shereen, E.; Dán, G. Model-based and data-driven detectors for time synchronization attacks against PMUs. IEEE J. Sel. Areas Commun. 2019, 38, 169–179. [Google Scholar] [CrossRef]
- Gao, P.; Wang, M.; Ghiocel, S.G.; Chow, J.H.; Fardanesh, B.; Stefopoulos, G. Missing data recovery by exploiting low-dimensionality in power system synchrophasor measurements. IEEE Trans. Power Syst. 2015, 31, 1006–1013. [Google Scholar] [CrossRef]
- Kamal, M.; Farajollahi, M.; Mohsenian-Rad, H. Analysis of cyber attacks against micro-PMUs: The case of event source location identification. In Proceedings of the 2020 IEEE Power Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 17–20 February 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar]
- Li, Q.; Li, F.; Zhang, J.; Ye, J.; Song, W.; Mantooth, A. Data-driven cyberattack detection for photovoltaic (PV) systems through analyzing micro-PMU data. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 431–436. [Google Scholar]
- Ghafouri, M.; Au, M.; Kassouf, M.; Debbabi, M.; Assi, C.; Yan, J. Detection and mitigation of cyber attacks on voltage stability monitoring of smart grids. IEEE Trans. Smart Grid 2020, 11, 5227–5238. [Google Scholar] [CrossRef]
- Chakhchoukh, Y.; Lei, H.; Johnson, B.K. Diagnosis of outliers and cyber attacks in dynamic PMU-based power state estimation. IEEE Trans. Power Syst. 2019, 35, 1188–1197. [Google Scholar] [CrossRef]
- Khalafi, Z.S.; Dehghani, M.; Khalili, A.; Sami, A.; Vafamand, N.; Dragičević, T. Intrusion detection, measurement correction, and attack localization of PMU networks. IEEE Trans. Ind. Electron. 2021, 69, 4697–4706. [Google Scholar] [CrossRef]
- Elimam, M.; Isbeih, Y.J.; Azman, S.K.; ElMoursi, M.S.; Al Hosani, K. Deep Learning-Based PMU Cyber Security Scheme Against Data Manipulation Attacks With WADC Application. IEEE Trans. Power Syst. 2022, 38, 2148–2161. [Google Scholar] [CrossRef]
- Martin, K.; Benmouyal, G.; Adamiak, M.; Begovic, M.; Burnett, R.; Carr, K.; Cobb, A.; Kusters, J.; Horowitz, S.; Jensen, G.; et al. IEEE standard for synchrophasors for power systems. IEEE Trans. Power Deliv. 1998, 13, 73–77. [Google Scholar] [CrossRef]
- Martin, K.E.; Hamai, D.; Adamiak, M.G.; Anderson, S.; Begovic, M.; Benmouyal, G.; Brunello, G.; Burger, J.; Cai, J.Y.; Dickerson, B.; et al. Exploring the IEEE standard C37. 118–2005 synchrophasors for power systems. IEEE Trans. Power Deliv. 2008, 23, 1805–1811. [Google Scholar] [CrossRef]
- Martin, K.E.; Brunello, G.; Adamiak, M.G.; Antonova, G.; Begovic, M.; Benmouyal, G.; Bui, P.D.; Falk, H.; Gharpure, V.; Goldstein, A.; et al. An overview of the IEEE standard C37. 118.2—Synchrophasor data transfer for power systems. IEEE Trans. Smart Grid 2014, 5, 1980–1984. [Google Scholar] [CrossRef]
- Löper, M.; Trummal, T.; Kilter, J. Analysis of the applicability of PMU measurements for power quality assessment. In Proceedings of the 2018 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Sarajevo, Bosnia and Herzegovina, 21–25 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Huang, C.; Li, F.; Zhou, D.; Guo, J.; Pan, Z.; Liu, Y.; Liu, Y. Data quality issues for synchrophasor applications Part I: A review. J. Mod. Power Syst. Clean Energy 2016, 4, 342–352. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).