Abstract
The European Union’s vision for energy transition not only foresees decarbonization of the electricity sector, but also requires commitment across different sectors such as gas, heating, and cooling through an integrated approach. It also sets local energy communities at the center of the energy transition as a bottom-up approach to achieve these ambitious decarbonization goals. The energy hub is seen as a promising conceptual model to foster the optimization of multi-carrier energy systems and cross-sectoral interaction. Especially in the context of local energy communities, the energy hub concept can enable the optimal design, management, and control of future integrated and digitalized networks where multiple energy carriers operate seamlessly and in complementarity with each other. In that sense, the optimal design and operation of energy hubs are of critical importance, especially under the effect of multiple objectives taking on board not only technical, but also other aspects that would enable the sustainability of local energy communities, such as economic and environmental. This paper aims to provide an in-depth review of the literature surrounding the existing state-of-the-art approaches that are related to the design and operation optimization of energy hubs by also exploring their interaction with the external network and multiple markets. As the planning and operation of an energy hub is a multifaceted research topic, this paper covers issues such as the different optimization methods, optimization problems formulation including objective functions and constraints, and the hubs’ optimal market participation, including flexibility mechanisms. By systematizing the existing literature, this paper highlights any limitations of the approaches so far and identifies the need for further research and enhancement of the existing approaches.
1. Introduction
1.1. The Background and the Sector Coupling Need
The European Union (EU) set ambitious environmental and energy goals to design a low-carbon energy system by the middle of the 21st century. The EU Climate and Energy Framework aims to reduce greenhouse gas (GHG) emissions by 55% by 2030, improve the share of renewable electricity by 32%, and improve energy efficiency by 32.5%. These goals can be achieved through the development of integrated energy systems that foster the protection of the environment and the creation of market-oriented energy services, while guaranteeing security, reliability, and resilience of the energy supply [1].
The basic idea of an integrated energy system is to switch from a single energy carrier to multiple energy carriers to take advantage of the synergistic effects of interactions to increase the efficiency of the energy resources used [2]. The integrated energy systems concept was introduced in the European Technology & Innovation Platforms Smart Networks for Energy Transition (ETIP SNET) Vision 2050 [3]. Their main feature is the integrated management of various carriers beyond electricity including heating, cooling, hydrogen, and mobility. In detail, this system can be seen as a “system of systems,” where various energy carriers coexist in an integrated infrastructure that is supported by the electrical system. Therefore, electrical networks are coupled with gas, heating, and cooling networks and this integration is made possible through energy conversion processes and storage of different types. This sector coupling is related to both the linking energy carriers with each other, and to end-use sectors including residential, tertiary, industry, and transportation. With this in mind, different types of energy technologies are managed with strong synergy to meet multi-energy needs, and the services can be supplied by the most convenient sector and related carrier. In addition, the increase in efficiency in the use of energy resources achieved thanks to the exploitation of synergies among energy carriers can lead to the reduction of renewable energy sources (RES) curtailment [4]. For instance, power-to-X technologies can act as a reservoir for excess electricity, using available energy in a cyclic and cost-effective manner. Integrating electricity and gas/hydrogen sectors (power-to-gas, power-to-hydrogen) will help exploit and retrofit existing gas infrastructures for renewable energy transport, thereby reducing the needs to expand power transmission through the storage of gas to deal with the seasonal changes in supply and demand of renewable energy. In fact, the gas generated with RES can be a resource as a low-carbon back-up capacity to supply electricity in power plants or fuel cells when there is no availability of other RES. Power-to-heat technologies such as heat pumps (HPs) allow achieving efficient heating and cooling processes of buildings from both energetic and economic points of view through the reduction of primary energy consumption. If thermal storage is coupled with HPs, it could allow for a change in thermal energy production in the event of an excess of renewable electricity.
Based on this premise, sector coupling is today considered a key to responding to the needs of the energy system, which is characterized by strong electrification of final consumption and high penetration of RES. This will bring several challenges for the operation of the power system, which in principle would need additional flexibility, reinforcement, and new investments for the transmission and distribution networks.
In the longer term, PRIMES (price-induced market equilibrium system) model results [5] show that 70% of the gas mixture could be renewable by 2050 [6], and this can be achieved only through sector coupling [7]. Further deployment of RES in collaboration and coordination with emerging technologies such as HPs or hydrogen production and storage from other carriers than electricity is considered more critical than ever for decarbonizing the whole energy system, as seen in the RePowerEU plan [8].
1.2. The Energy Hub Concept at the Service of Need
Due to the importance of sector coupling solutions, the energy hub (EH) concept, which allows the coupling/integration of different carriers at a local level, has been drawing researchers’ attention in recent years. An EH is a conceptual unit where multiple energy carriers can be converted, conditioned, stored, and consumed. EHs can exchange energy at their interfaces, e.g., with electricity and natural gas external networks, and provide certain required energy services such as power, heating, cooling, mobility services, ancillary services, etc. Within the hub, energy is converted and conditioned by technologies such as combined heat and power (CHP), transformers, power electronic devices, compressors, heat exchangers, and storage, among others [9]. A series of technical, economic, and environmental advantages of the EH concept is summarized in Table 1, making EHs a perfect fit for the architectural concept basis of the future integrated grids.

Table 1.
An overview of energy hubs’ advantages.
The energy technologies that are implementable and are building blocks of EHs can be classified as seen in [10]:
- Distributed generation technologies: renewable technologies to decarbonize energy supply systems;
- “End-user” sector coupling technologies: energy conversion technologies for the electrification of the end-uses that enable the flexibility of end-users/prosumers to be activated;
- “Cross-vector” sector coupling technologies: technologies that allow the integration of multiple energy carriers. The main technology that can be easily implemented in most energy hubs is the CHP, which can be installed both at the prosumer level (buildings, shopping centers, industries) and at the city/neighborhood level (district heating);
- Energy storage technologies of different energy carriers (electrical, thermal, mobility).
1.3. The Need for This Review and Its Contribution
The optimal design, operation, and interconnection of different energy carriers result in cost-efficient uses of local resources, aiming at maximizing the efficiency of the energy conversion processes. On top of that, EHs hosting storage facilities enable conversion to a greater extent between different energy carriers and thus offer higher demand-side flexibility potential. Therefore, optimal design and operation of the EHs are of primary importance to maximize their advantages. This especially holds true within the context of integrated local energy communities (ILECs). Within ILECs, a set of energy users need to agree on common choices in terms of satisfying their energy needs, maximizing the benefits derived from this collegial approach, thanks to the implementation of different multi-carrier technologies and the optimized management of energy flows. The optimal design and operation of such complex systems is a non-trivial task due to several aspects. For instance, for the design phase, the interest of developers in achieving a system configuration with the lowest costs might conflict with one of the EU energy legislations in public welfare in terms of sustainability of the energy supply, and this would require a multi-objective approach for guaranteeing the economic and environmental sustainability of such solutions. On the other hand, operation optimization is also challenging, not only for the need to consider multiple and conflicting objectives, but also to capture the interaction between energy carriers (e.g., electricity, heat, cooling, etc.) while satisfying the time-varying user demands. Last but not least, the interaction with external networks and multiple markets is also a key topic for EHs to optimize their benefits for larger systems.
So far, several reviews related to the EHs have been produced, but most of them are focused on the technical aspects of the configuration and the conversion technologies included in the EHs [11,12,13]. For instance, reference [14] focuses only on the aspects of the storage facilities and the flexibility that they have to offer within the EH, whereas reference [15] addresses the different demand response (DR) schemes served by EHs. Reference [16] touches upon the modeling of EHs based on multi-objective optimization for their design and operation without relating to an external framework such as the grid or the market, as it focuses on the uncertainty’s impact. Reference [17] reviews the management techniques of the EHs, although it excludes heuristic methods. This means that the optimal operation of the EHs in relation to external factors such as the networks and the markets also under a multi-objective approach has not been systematized before or carefully reviewed.
The latter is significantly important to consider in the real context of an ILEC’s planning and operation, where the multi-objective approach can foster different drivers such as technical, social, environmental, etc., along with the market interaction, on which the sustainability of the business cases relies. To overcome this existing review gap, the contribution of this paper is to present a comprehensive review related to the planning and operation of EHs holistically, considering a wide set of transversal aspects listed below:
- Analysis of the technologies and energy carriers in EHs;
- Analysis of the design and operation optimization of EHs, considering the full chain of relevant topics, i.e., problem formulation with constraints, objective functions overview, multi-objective approach and solution methodologies, solvers and modeling frameworks considering heuristic methods, uncertainty, and risk aversion, management of flexibility sources, and simulation methods for electric vehicles (EVs);
- Analysis of the EHs’ interaction with multiple markets, from energy and balancing markets to peer-to-peer (P2P) markets, along with business models and interaction of EHs with the external network; and
- Analysis of collateral aspects such as temporal and spatial scopes.
For the analyzed aspects, limitations of the existing approaches and methodologies are also discussed, along with the need for further research and enhancement.
This paper is structured as follows. Section 2 presents the methodology used for this review. Section 3 presents a detailed analysis of EHs configuration in the literature. Section 4 analyzes the objective functions for optimal design and operation of EHs, while Section 5 and Section 6 review the constraints and the optimization problems modeling for EHs, respectively. Section 7 presents the multi-objective optimization approach and methods. Section 8 focuses on heuristic models, while Section 9 provides an overview of optimization solvers and modeling environments. Section 10 focuses on uncertainties and risk aversion. Section 11 offers insights related to the interaction of EHs with external networks and multiple markets, with a key focus on P2P architectures and related markets. Section 12 presents the business landscape of EHs. Section 13 analyzes collateral concerns when setting up the operation frameworks of an EH, and Section 14 concludes the paper and summarizes limitations or gaps found in the current literature, while also providing insights on research pathways.
2. The Methodology Used for This Review Paper
In order to perform this systematic review, the following methodology with related steps has been adopted:
- Collect all the documents related to optimization problems, including multi-objective approaches, multi-carrier energy systems, and EHs configurations. In detail, 128 related documents were collected from the most popular and impactful research repositories of the research and innovation (R&I) community;
- Identify a list of topics of interest to focus on. The EH concept is a multi-faceted research question that entails different topics to be further investigated. Therefore, an exhaustive list of 18 topics of interest that are related to EHs has been developed. Within this list, the topics have been further categorized as “setting the background” topics or/and “research and innovation” topics. Background topics are the ones that formulate the state of the art of this review and establish the baseline knowledge of this effort, whereas “research and innovation” topics are classified as such to formulate further innovation pathways and the research questions that are analyzed in detail. Of course, a topic can be characterized as both “background” and “research and innovation”;
- An extensive review of the topics for each of the documents in order to capture the holistic approach of this review and the connection of EHs with the external framework, such as the networks, the market, and the business models; and
- Compilation of brief reports per topic for both state-of-the-art and innovation approaches before developing this review.
Figure 1 presents the methodology steps with the list of topics.
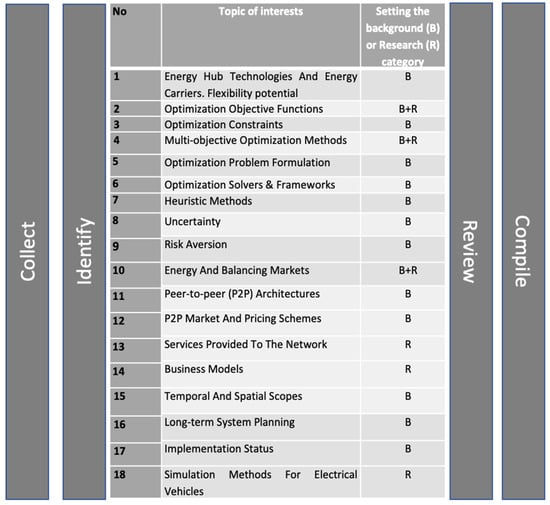
Figure 1.
The methodology of performing this review.
In addition, Figure 2 presents a graph capturing the distribution of the topics against the current works in the literature. From the blocks below, we can derive what has been mentioned earlier, i.e., the gaps in the literature in addressing the interaction of the EHs with the networks, markets, and business-model-related topics. It is also seen that no paper—research or review—has yet addressed all topics at the same time, thereby highlighting the main novelty of the current work.
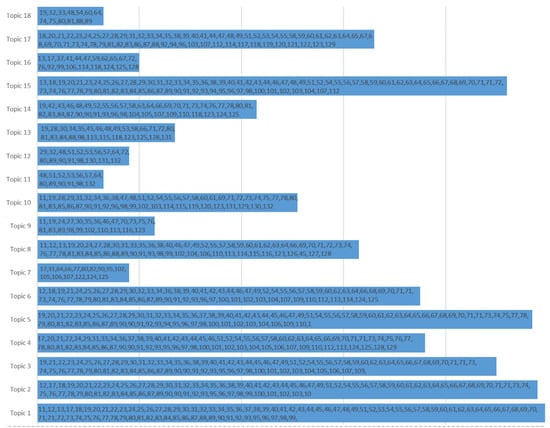
Figure 2.
Matrix of analyzed works in the literature vs. topics.
Table 2 shows the distribution of the related papers throughout the years. It is evident that in the last years, the multi-carrier energy approach has resulted in more scientific work around the topic of EHs.

Table 2.
The distribution of the literature through the years.
3. The EH Configuration in the Literature
As it is important for the optimization of both design and operation, this section provides a detailed overview of the EH configuration that is mainly seen in the literature focusing on carriers and different technologies. Special mention is given to storage technologies and the demand flexibility potential under such configurations.
3.1. Energy Carriers of an EH
In all reviewed papers, electricity is considered the backbone carrier. Then, the electricity carrier is combined with other energy carriers such as natural gas, heating, cooling, hydrogen, and/or domestic hot water. Table 3 shows the distribution of the energy carrier combinations throughout the analyzed works in the literature. It can be observed that the electricity carrier is mostly combined with heating and cooling.

Table 3.
Combination of considered energy carriers in the literature.
3.2. Cluster of EHs
Some papers in the literature [11,17,46,47] also discuss the benefits and challenges related to the integration of the energy carriers and the creation of a network of interconnected EHs identified as clusters of EHs.
The main benefits of such a clustering are as follows:
- Advanced security of energy supply;
- Increased provision of system services to neighboring systems, such as balancing and ancillary services;
- Reduced RES curtailment and therefore reduced GHG emissions;
- Increased system reliability;
- Increased load flexibility;
- Self-sufficiency and minimization of costs related to energy exchange with the upper grid.
On the other hand, the main challenges identified when integrating energy carriers and interconnecting of EHs that need to be addressed are specified below:
- Cost of the required infrastructure and the connecting technologies;
- The ownership of the interconnected networks has to be adequately defined;
- Advanced communication, data acquisition, and management infrastructure is needed for the optimum operation of the interconnected networks;
- The high initial investment with a long time for payback;
- Lack of cases and proper business models;
- Lack of regulations regarding functionalities and operation, including roles and responsibilities;
- Public acceptance of the interconnection and interaction between the EHs.
3.3. Energy Conversion Technologies
Different energy carrier conversion technologies are considered in the literature. Regarding heating and cooling carriers, the most considered technologies are CHPs [14,19,21,22,23,24,25,26,27,28,29,30,31,32] and gas-fired boilers [14,19,20,21,23,24,25,27,29,31,32]. As far as hydrogen technology is concerned, most papers consider hydrogen production through electrolysis [18,20]. For example, hydrogen produced by electrolysis can be used to produce methane via a methanation process, which can then be injected into the natural gas network [28]. Other thermal generation technologies considered are HPs [21,22,27,29,32] and chillers [21,26,29,32]. When it comes to the electricity carrier, both RES and conventional energy technologies may well be considered. In most cases, the largest amount of energy comes from RES [22,40,41,48], including photovoltaic systems (PV), wind turbines, solar thermal, and biomass. Energy generation technologies of the electricity carrier interact with the generation technologies of other energy carriers and can be combined with other generation technologies such as diesel generators, natural gas generators, and fuel cells. In addition, power-to-gas (P2G) is considered in [23], while gas-fired generation is also included in [49]. Hydrogen by means of fuel cells is used to produce not only electricity, but also thermal energy, as seen in [50]. In Table 4, the distribution of the different technologies per carrier is shown with a detailed overview of the existing literature.

Table 4.
The distribution of technologies per carrier based on the existing literature.
In Figure 3, a general configuration of an EH, including different energy carriers and their respective conversion technologies, is presented.
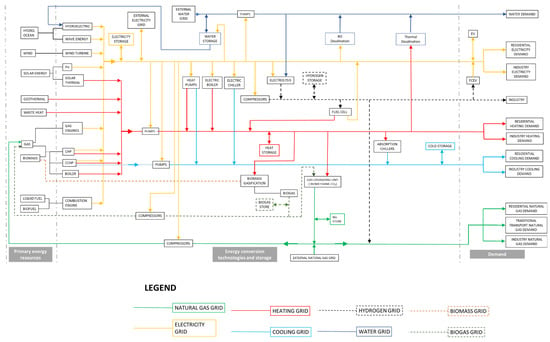
Figure 3.
The general configuration of an EH.
3.4. Energy Storage and Flexibility Potential
As already mentioned in the previous sections, the EH concept is characterized by high flexibility potential that can be derived from storage or loads of different carriers. Regarding the storage facilities, in most of the reviewed papers [71,72,73,74,75,76,77,78,79], the configurations include at least electrical storage capabilities, combining other forms of storage in several cases, such as thermal storage and natural gas storage for providing better flexibility potential. Electrical storage may include any type of battery, EV, plug-in hybrid electric vehicle (PHEV), compressed air energy storage (CAES), or pumped hydro storage (PHS). In addition, fuel cells with hydrogen (H2) storage are considered for storage purposes in some cases, as seen in [58,70]. In other cases, hot water storage for heating purposes has been employed in [69,80].
Table 5 shows the combination of storage facilities per carrier for the complete list of the literature.

Table 5.
Storage facilities per carrier based on the existing literature.
From the reviewed papers, a specific focus is found on the concept of flexibility of different energy carriers of an EH. Very often, the supply-side flexibility is managed using only storage systems, such as a battery or thermal storage [41,43,51,54,55,58,79,89]. However, some of this research has been constrained in terms of supply-side flexibility because of the loose coupling of various energy carriers that were structured within their EH. For example, in some research, the CHP plant was the only technology that interacted with both the electricity and heating carrier [62].
On the other hand, in several works, demand-side flexibility is addressed by considering incentive-based programs and energy-price strategies [26,37] such as time-of-use electricity price or time-of-day unit price for electricity for demand response [19,25,32,42,43,78,82,90]. In these cases, EVs and batteries are considered, but their collaboration strategy with other co-existing storage facilities in the EH is of primary importance.
The literature on EHs flexibility also focuses on flexibility coming from residential assets, i.e., appliances. Regarding the appliances (apart from the non-interruptible ones), three types that offer flexibility are analyzed: shiftable appliances, shapeable appliances, and thermostatically controlled appliances. Shiftable appliances are flexible and can shift consumption between time intervals. The operation of these appliances can be shifted to off-peak periods without affecting the consumer’s comfort, such as washing machines and dishwashers [91,92]. Shapeable appliances are flexible appliances that can change their shape to store energy or minimize their consumption (the latter is known as interruptible load) [65]. Finally, thermostatically controlled appliances are the appliances that can be controlled by a thermostat, such as heating and cooling loads in buildings. The main objective of this control is the minimization of energy consumption [81].
As already seen, the EHs concept can cover much more than just a residential building and thus their flexibility assets. For example, an EH can cover a whole region under the ILEC concept exploiting flexibility from the different assets of the carriers that can be communally owned.
3.5. Flexibility Potential of EVs
Many different approaches are present in the literature dealing with the simulation and modeling of EVs within the EH environment for exploiting their flexibility potential. Functions foreseen, such as controllable charging/discharging and vehicle-to-X operation (V2X) representing the flexibility potential, and how they are modeled, may have a significant impact on the obtained results. Therefore, a major challenge when dealing with modeling plug-in EVs (PEVs) or PHEVs is the representation of the vehicles’ availability and energy use while they are away. Indeed, those factors are dependent on the users’ behavior and habits.
PEVs can be represented either as loads under the grid-to-vehicle (G2V) or as distributed storage when equipped with V2X technology. Therefore, in most cases, EVs and PHEVs are modeled as batteries, as in [45,75,82]; as a part of a large-size equivalent battery, as in [76]; as different peers in a bilateral trading system based on P2P, as in [48]; as a part of the end-users’ load profile, as [89]; or as a flexible/shapeable load for electrical networks, as in [65,81].
Another major concern when modeling EVs is the availability of data and energy use, as well as their availability and status during the day. Some works assume that the vehicles depart and arrive at given times [32,60]. For example, in [60], EVs are assumed to be plugged out at 8 a.m. (approximately full battery) and plugged in at 4 p.m. (quite empty). From 4 p.m. to 8 a.m., the battery can store electric energy when it is more convenient (during low-price hours) and uses its energy during high-price hours. In order to ensure that at 8 a.m., the EV has a good charge level, a dissatisfaction term is considered that is directly proportional to the difference between the maximum level of charge and the level of charge at 8 a.m. Other works divide the PEVs into clusters [54], each with specific characteristics: (1) battery capacity, (2) arrival and departure times at/from the charging stations, (3) the state-of-charge (SOC) at the arrival time, and (4) the SOC desired at the departure time. Some works, such as [33], use a probabilistic approach representing the EVs’ availability by a normal distribution and a probability function based on survey data. In addition, these data are used in a stochastic model predictive control (MPC) to control the local energy system, allowing for planning for the EV availability with refined scenarios for each hour. In [19], the uncertainty of the time intervals during which the EV owners are at home and can therefore charge or discharge the EV battery is considered by means of a Monte Carlo approach. The daily driving distance of each EV is modeled as a log-normal distribution function, whereas the home arrival and departure times of each EV are modeled as a normal distribution.
3.6. Key Challenges for the EH Configuration in the Literature
Through the analysis of the literature on the EH configuration, it is perceived that some key challenges arise which must be addressed to achieve their efficient and reliable operation. The most important key challenges are presented below:
- Limited connection between various energy sectors/carriers. Although may diverse carriers can be present in the different EHs structures, the interconnectivity among them is low in many cases. This means that the full potential of employing the advantages of the integration as described in the introduction remains unused.
- Limited economic incentives in order to encourage the use of flexibility, focusing only on the electricity carrier. This results in a limited number of technologies participating in flexibility management, such as batteries, whereas the thermal part and their flexibility potential are neglected in most cases;
- Management or/and pricing schemes of other energy carriers beyond electricity. This results in more complex and decentralized schemes for energy carriers other than electricity that are now not represented;
- The inclusion of EVs in ILECs can make their management more difficult. Even if there is some coordination, there will always be several more constraints than for a simple battery storage system;
- The stochastic nature of EV operation that intertwines with behavioral aspects can affect the stability of the system as well in case of high EV penetration.
4. Objective Functions for Optimal Design and Operation of EHs
The optimal configuration for a multi-energy system is a complex problem due to the wide variety of technology options, energy price variations, and significant daily and annual fluctuations in energy consumption. Additionally, as environmental issues are becoming increasingly important in the analysis of these systems, they should also be taken on board through the appropriate variables and constraints. However, conflicting objective functions may arise when it comes to such a complex problem.
The literature discusses different optimization approaches leading to single or multi-objective functions with mostly having a twofold focus, i.e., minimization of system cost and environmental emissions (mostly CO2 reduction). In detail, a significant part of the analyzed papers aims to minimize several objective functions. In most cases, multi-objective optimization problems have at least two different objectives. The first one is cost-related, and the second one is usually environmental-related, e.g., CO2 emissions reduction and the maximum integration of RES. Moreover, most EHs use electricity and gas as energy carriers, and their coordination is performed through an optimization model in which both economic and environmental objectives may be considered. Representative references are discussed below.
The following references explore multi-objective optimization approaches for energy systems. References [40,42,70] focus on minimizing energy costs and CO2 emissions. References [44,54,58,59,62,93,94] also prioritize CO2 emissions reduction as the primary objective, but with different secondary objectives such as minimizing total annual costs, including investment, operation, and maintenance costs, maximizing profits for the energy system operator, and minimizing energy costs. Reference [77] prioritizes economic targets, followed by a second objective related to system reliability. Reference [78] presents a non-dominated sorting genetic algorithm for optimizing both economic benefits and energy efficiency. Reference [79] details a fuzzy multi-objective decision and two-stage adaptive robust optimization method. Reference [82] proposes a fuzzy decision-making approach to minimize procurement costs and carbon emissions for interconnected energy systems. Reference [84] aims to strike a balance between operational costs and exergy efficiency using a three-stage optimization process. Reference [95] seeks to minimize the operational cost of interconnected energy systems, as well as the amount of freshwater used. Finally, reference [96] proposes a multi-objective optimization problem to minimize the operational cost and total emissions of an energy system. While using multiple objectives in problem formulation can lead to better outcomes, it can also increase complexity, as objectives may conflict and require trade-offs.
On the other hand, some papers present a single-objective optimization problem. When it comes to single-objective optimization functions, the minimization of cost, be it investment cost or operation cost, is dominant. The maximization of revenues for the different actors of the energy value chain is also a common pursuit. Therefore, works such as [23,32,41,57,81,92,97,98,99,100] aim to minimize the operational cost of the EH, while, for instance, Refs. [28,29] deal with the minimization of total investment and operating costs. These representative papers are included here for the sake of completeness.
In summary, Table 6 shows the complete list of references with multi-objective optimization functions, while Table 7 presents the full list of references with single-objective optimization functions.

Table 6.
Objective functions in multi-objective optimization of EHs in the literature.

Table 7.
Objective functions in single-objective optimization of EHs in the literature.
The objective function is the key factor of any optimization problem and defines its general target and the influencing parameters and variables. In the analyzed works, the main objective is—in most cases—related to economic targets expressed as the maximization of revenues or profits or, similarly, the minimization of the costs (capital and operational) and the minimization of energy losses.
In a single-objective optimization problem, the space of solutions is usually easily identifiable since there is a unique optimal solution. The introduction of an additional objective function in an optimization problem (multi-objective optimization) and the requirement of simultaneous optimization between each other results in both an increase in the number of solutions (the best solution is not one but many) and difficulty in accurately determining the space of the solutions.
5. Optimization Problem Constraints
Constraints have a central role in optimization problems. Indeed, they limit the solution space while defining the choice and/or operation of the components of the modeled system. In energy system modeling, they are used to determine the performance characteristics and limitations of the considered energy conversion and storage technologies and of the elements through which the energy carriers are transported and distributed. They also regulate the interaction between the system and the considered commodity, grid services, and ancillary markets. Due to the complexity of the interaction of the active resources in the EHs and the surrounding energy systems, it is necessary to define a set of physical, technical, economic, and environmental constraints that allow delimiting the optimization problem to viable search space.
Therefore, this section aims to discuss the equality and inequality constraints that have been used in the analyzed optimization problems in the literature so far. The constraints can be classified into four categories: technology constraints, network constraints, market constraints, and other constraints.
Technology constraints can be divided into three different subcategories, as can be seen in Table 8. Specifically, these are operational constraints, design constraints, and selection of the technologies in the EH configuration. Most of the reviewed papers use operational constraints, while fewer papers use design constraints in conjunction with operational constraints. As seen in [41,43,44,85], it mainly depends on whether the optimization problem aim is focused on the operation or design of an EH. Some constraints simply describe technology modeling in terms of their efficiency and capacity limits, as seen in [85]. Other models are more detailed for the various technologies that they consider. Commonly modeled technologies include PV [23,27,57], wind turbine [23,57], electric chiller [32,57], solar thermal [59], absorption chiller [32,57], gas boiler [10,27,46], gas turbine [59], diesel generator [50], fuel cell [50], CHP [27,50,56], and HPs [27,56]. Storage technologies are also common, such as batteries [23,27,32,57,99], or other electricity storage, such as compressed air [32], heat storage [32], and hydrogen storage [56]. Other conversion technologies, such as P2G, can also be found in [32]. In addition to the technologies that convert or store energy, some works also add details to the modeling of loads. The EVs, which act either as load or storage, are often modeled as in [32,81]. A major reason to include detailed modeling of the loads is to consider their flexibility potential. Shiftable loads are modeled in [32,92], while [81] makes a distinction between non-interruptible and thermostatically controlled appliances.

Table 8.
Technology constraints.
Network constraints are presented in Table 9 and are divided into three subcategories. The network constraints represent mainly import and export limits to the different grids or markets [32,57]. Other network-related restrictions, such as the difference in temperature between the inlet and outlet of heat pipes and gas or power flow equations, can also be found, though more rarely [22]. Some models use a constraint to explicitly forbid simultaneous import and export, as seen in [57]. Reference [92] includes a constraint representing the possibility for the grid operator to limit their export to the electric grid if there are grid security concerns. The network flow constraints include the limits of energy flow, limits of imported/exported energy, and use of the share of the network between the energy providers and users, etc., as in [19,21,23,24,25,27,32,36,39,40,41,42,43,44,47,50,51,52,54,55,56,57,58,59,62,65,67,68,69,70,71,72,74,75,76,78,79,82,83,84,85,88,90,91,93,94,101,102,103,104,105], the transmission limits, which mainly include boundaries of active and reactive power in transmission lines, and gas flow equations in active and passive pipelines [46,49,54,97,101], and finally, the nodal limitations at EH level [19,22,27,30,49,86,88,90,92,106].

Table 9.
Network constraints.
Market constraints are presented in Table 10, and they are less commonly encountered in the reviewed documents. They are sometimes used to represent the estimation of the internal price in models, including P2P energy sharing. Other types of market constraints include the constraint of not buying and selling energy in the same period [36,57,85], the revenue from selling electricity by-products on the spot market [86], and the internal price of electricity [81,92].

Table 10.
Market constraints.
Other types of constraints used in optimization models of EHs are presented in Table 11, and they include inequality constraints about the trading participants and the platform service charge, the established target for the RES penetration levels, and the ε-constraint (parametric optimization method) and integer cut constraints (ICC).

Table 11.
Other constraints.
The identification of constraints is a critical step when formulating the optimization problem of the EHs due to the complexity of the system itself. The literature shows that the identification of operational constraints is dominant for both the EH per se and for the efficient operation of the upper grid. In most optimization models, the objectives of the problem formulation are transformed into operational constraints. It needs to be highlighted that only a few papers combine both the operational and design constraints of the EHs. This is an important consideration to be taken, especially when setting up an EH or planning its expansion. Constraints should be carefully identified when considering the interaction of the EHs with other parties, such as the markets or other EHs as well. So far, this has been considered only for one type of interaction, i.e., one type of electricity market, thereby neglecting different types or gas markets. This makes the problem formulation more demanding, but it is needed for a realistic representation of the EHs’ role.
6. Optimization Problems Modeling
Based on the reviewed works, it is found that some papers formulate the optimization problem as a linear programming (LP) model, but most of them formulate the optimization problems using a mixed-integer linear programming (MILP) or mixed-integer nonlinear programming (MINLP) approach. Others present both linear and nonlinear problems (MILP&MINLP) formulation. A detailed discussion of MILP, MINLP, and MILP&MINLP approaches follows.
6.1. MILP
MILP problems are LP problems that include integer variables but are much harder to solve. Binary variables are the most widely used type of integer variable in MILP problems. These types of problems usually employ solution techniques, such as branch- and bound or branch and cut, to obtain the optimal value. Binary variables can be used for several purposes. In some cases, they represent a yes/no investment decision for a particular technology, e.g., by easily considering fixed investment costs in the objective function. In addition, these variables can also be employed to decide on the status (on/off) of an energy conversion technology in each period of the problem’s time horizon. Similarly, they can be used to consider start-up costs and minimum uptime or downtime of an energy conversion technology. Sometimes, binary variables are used to control investment in grid connection and ensure no simultaneous import and export of electricity from/to the upper grid. Restricting the number of binary variables permits limiting the computation time.
Several papers address the problem of EH optimization using MILP formulations, such as [19,20,21,22,23,26,27,28,30,31,32,33,34,35,47,50,63,67,68,72,74,81,82,90,95,104,105,111,112,113,114,115,117,118,119,120,121]. In particular, Ref. [19] presents a MILP model to minimize the EH’s total cost. A similar approach -that also considers the optimal size of an EH- is seen in [20]. The authors of [21] formulate the optimal sizing problem of a multi-energy urban EH as a multi-objective MILP problem aimed at minimizing both costs and carbon emissions. Authors in [22] give an overview of the integrated electricity and heat systems (IEHS) modeling and solution methods for optimal operation and compare the main differences between the possible solutions. Authors in [27,32] propose a planning model for a multi-energy microgrid formulated as a MILP problem, while in [28], the day-ahead scheduling of an electricity–hydrogen–gas–heat integrated energy system (EHGHS) is formulated as a scenario-based MILP problem. In [33], the day-ahead scheduling of an EH is formulated as a MILP problem aimed at minimizing the system’s operation cost. The MILP problem is solved on a rolling horizon basis under a model predictive control strategy so as to cope with uncertainty. In [34], a MILP formulation for the optimal design of an industrial manufacturer’s EH is used. In [35], a MILP formulation for the optimal operation of an EH under different electricity, heating, and cooling scenarios is considered. In [68], authors use binary variables to control investment in a grid connection and ensure no simultaneous import and export of electricity through a MILP approach.
On the other hand, in [111], a MILP framework is proposed for the robust optimization of smart multi-energy districts under uncertainty with different energy conversion and storage technologies (e.g., PV, EHP, CHP, electric and thermal energy storage, and gas boilers) and detailed integrated electricity, heat, and gas network mathematical models. In [90], a MILP model of an EH considering CHPs, HPs, air conditioners (ACs), EVs, RES, and community energy storage (CES) is presented, with the main objective of minimizing the overall operating cost of the system. The authors of [114] use a MILP formulation for the optimal operation of an EH considering downside risk constraints. References [115,117,118] use MILP formulations for the optimal design of EHs from scratch, i.e., with no predetermined system structure, carriers, or technologies mix. Reference [105] proposes a robust MILP (RMILP) model for optimizing the operation of an EH. In [63], the potential for improvement of a residential multi-carrier microgrid is analyzed via scenario-based simulations under different management strategies.
6.2. MINLP
MINLP problems are still very challenging today, especially if they are non-convex, i.e., the objective functions and/or constraints are defined by non-convex functions. Usually, MINLP problems are relaxed and reformulated as, e.g., mixed-integer second-order cone programming (MISOCP), mixed-integer quadratically constrained (MIQCP), and MILP problems and solved by appropriate decomposition techniques. Several works in the literature formulate the optimization problem as an MINLP problem due to the nonlinear nature of the objective functions and/or constraints, such as [23,25,36,46,49,70,76,96,97,102,106,107,108,109,110,122]. In particular, Ref. [25] defines the network-constrained scheduling problem of an EH as an MINLP problem, which is reformulated as an MISOCP problem and solved by the use of the partial surrogate cuts method. In [36], an MINLP model for the day-ahead scheduling of electricity and natural gas networks is presented by considering three downward EHs and a P2G system. An MINLP model is developed in [49] with a multi-objective approach to finding trade-off solutions between maximizing RES penetration and minimizing costs in the optimal scheduling of an EH. The authors in [97] present a nonlinearly constrained optimization problem to optimize the couplings/connections among the different networks of an EH. The authors highlight the usual complications that may appear when using MINLP formulations, such as the solution dependency of the initial values of variables or the large number of suboptimal solutions that are not all technically reasonable or feasible. The necessary procedures to overcome the problems mentioned above usually require ad hoc solutions that cannot be implemented elsewhere. The authors in [102] formulate the day-ahead scheduling problem of four urban EHs as an MINLP problem, which is reformulated as an MISOCP problem, which in turn, is decomposed into a second-order cone programming (SOCP) problem and a mixed-integer quadratic programming (MIQP) problem. These problems are solved sequentially and iteratively, using the results of each program as input variables to the other. In [122], an MINLP model is developed for the multi-objective operation optimization of an EH consisting of district heating, cooling, and electricity networks interconnected among them. The presented methodology is general enough to be applied to several objective functions, and in the case study, operating costs and carbon emissions are considered objectives.
6.3. MILP & MINLP
In the literature, there are also several works formulating the optimization problem by using a mixed approach based on both MILP and MINLP. Among the analyzed works using this approach, in [24], the multi-objective optimization problem is solved in two stages, in the first stage through a MILP and in the second stage through an MINLP. In [65], the optimization problem is defined through a SOCP relaxation. In [83], all the mathematical expressions in the optimization problem are formulated as linear equations. However, the employed solution method uses a meta-heuristic model (bacterial foraging optimization) to solve the problem. In [84], the optimization problem for the day-ahead dispatch is formulated as a MILP model, whereas the intraday scheduling is formulated as a nonlinear model. In [88], the optimization problem is formulated as an MINLP model. In [92], a bi-level optimization model is employed. The upper level is not formulated via an objective function but is solved through an iterative algorithm. The authors in [123] analyze the optimal scheduling of a coupled electrical–natural gas network feeding a distributed electrical load in a combined day-ahead market and real-time operating conditions. The problem is formulated via a data-driven distributionally robust optimization (DDRO), considering wind data uncertainty. On the other hand, reference [124] reviews existing optimization techniques and their applications in power systems, focusing on multi-objective optimization in power system planning.
Table 12 summarizes all screened documents according to the approach used to formulate the optimization problems.

Table 12.
Modeling approaches used for the optimization problems formulation in the existing literature.
6.4. Key Challenges for the Optimization Problems Modeling
From the reviewed papers, it emerges that MILP formulations are the most widely used for the design and operation optimization of EHs. Nevertheless, some variables that may be present in EHs respond to a nonlinear behavior, e.g., power flow variables, and to non-convexities, e.g., commitment status of energy conversion and storage units. The accurate representation of the physical phenomena taking place in the energy conversion and storage units of an EH and of their design and operational decisions may require the use of MINLP formulations. As already mentioned, the solution to MINLP problems is a challenging and computationally hard task. Usually, MINLP problems are relaxed and reformulated as MIQCP, MISOCP, or MILP problems and solved using proper decomposition techniques. The solutions of such approaches are not guaranteed to be optimal, nor do they represent with precision some physical phenomena taking place in the energy conversion and storage units of the multi-carrier energy system. To summarize, in the context of EHs, very detailed models of energy technologies and energy flows cannot be the best solution to adopt since they limit the effectiveness of the optimization models and methods employed to solve the problem. It is, therefore, necessary to find a good trade-off between model fidelity and the complexity of the optimization process.
7. Multi-Objective Optimization Problems and Methods
The design and management of EHs need to respond to different stakeholders’ participation requirements and preferences. Therefore, the objectives are usually formulated from different perspectives and can be in conflict with each other. For instance, an economic optimization that serves developers’ needs cannot ensure that the EH configuration or the operation strategies obtained are optimal from an environmental point of view that would serve the energy community’s needs. This intrinsic conflict existing between different objectives calls for the need to establish a multi-objective approach when dealing with the optimal design and operation of EHs.
In practice, in the context of a multi-objective problem, obtaining a unique solution is only possible if the objectives do not conflict with each other, but in most real cases, this does not happen, and there are multiple aims represented by objective functions, which need to be traded off. Due to the multiple objectives, there is no single optimal solution but a set of non-inferior solutions (a 1D set for two objectives, a 2D set for three objectives, etc.). This set defines the so-called Pareto front, and it can be used to assess solutions by the relative meaning of the objectives. Non-inferior solutions are solutions where one objective cannot be improved without making another objective worse.
In order to identify a single solution for the multi-objective problem for the design or operation of an EH, two steps need to be followed, i.e., the optimization and the decision-making steps. According to the order used for these steps, two methods are derived as specified below [107]:
- The preference-based approach in which the decision-making is performed before the optimization. This approach requires a good knowledge of the preferences of decision-makers that need to be respected in the optimization problem formulation. Quantifying these preferences is a challenge;
- The second approach is considered ideal. The optimization is performed before the decision-making. This approach is more desirable than the previous one, as it is less subjective and leaves the final decision to the decision-makers.
In many cases, the multi-objective problem is simplified into a single-objective problem by modifying the objective function or combining specific constraints. In this case, a second objective is added to the first one thanks to a conversion factor. For example, in [34,97], where multi-energy systems are investigated, emission minimization is included in the cost minimization models. Another option is represented by the epsilon constraint method, as seen in [72,85]. In detail, a primary objective is employed, while the other objectives are converted into inequality constraints where the right-hand side is a factor that is wide-ranging to obtain various solutions. Meta-heuristic models can also be applied for multi-objective optimization [125], but they do not guarantee the optimality (non-inferiority for multi-objective problems) of the solutions found.
From the analysis of the relevant literature, the most used method for multi-objective optimization problems in EHs is the weighted-sum method, as in [66,86,101]. This method combines the different objectives into a weighted sum. The weighting factor can be varied from 0–1 to obtain the Pareto front with the best possible trade-off solutions between two objectives. In addition, objectives can be normalized, as seen in [86,101], to simplify the process and the knowledge of the weights. This method allows for the use of the second, ideal approach described earlier, with the identification of the Pareto front through the optimization process. Therefore, the final choice is left to decision-makers to make informed choices and select an appropriate solution on the Pareto front from a wider range of alternatives.
The various multi-objective optimization methodologies analyzed in the literature are categorized in Table 13.

Table 13.
Multi-objective optimization methods used in the context of EHs in the literature.
Based on the conducted analysis, the main limitations related to the multi-optimization methods described in the previous table are reported below.
The most important limitation of the Ɛ-constraints method and compromise programming method lies within the need to transform multi-objective problems into single-objective problems based on good knowledge of the decision-makers. The most common approach, as shown in Table 12, is the weighted-sum method, thanks to the ease and straightforward way of obtaining multiple points on the Pareto-optimal front. In this case, the challenge is the selection of a weighting criterion ensuring that the points are spread evenly on the Pareto front. Taking into account the nature of different flexibility resources present in EHs, the method which transforms the multi-objective problem into a single-objective problem to be easily solved could be considered.
Definitively, choosing the most suitable method depends on the complexity and scale of the problem. In this case, the challenge in deciding the best methodology to solve a multi-objective optimization problem is to perform a detailed study of the algorithms and the characteristics of the problem before applying the optimization approach. In particular, the selected method must always find and provide all Pareto-optimal solutions, consider weights to express preferences, as well as employ the utopia point or its approximation.
8. Heuristic Methods
A heuristic method can be defined as a procedure for solving a well-defined mathematical problem by an intuitive approach in which the structure of the problem can be interpreted and exploited intelligently to obtain a reasonable solution. Heuristic methods, unlike optimization methods discussed in previous sections, are not able to guarantee the optimality of the decisions but can, if designed and tuned correctly, provide enough adequate solutions faster and/or with fewer computational resources than by using an optimization model. For example, Ref. [124] mentions its utilization in power systems contexts, with a special focus on multi-objective optimization for power system planning. The heuristic methods discussed in this literature review are categorized into simple heuristics and meta-heuristics, as shown in Table 14 below.

Table 14.
Categorization of heuristic methods.
Simple heuristics come in the form of local search, greedy algorithms, and/or hill climbers. Meta-heuristics try to go beyond the local search for the best solution. Many of them are based on some biological metaphor, are bio-inspired, and are in the form of genetic algorithms (GA) and evolutionary algorithms (EA), simulated annealing, tabu search, ant colony, hybrid algorithms, fuzzy programming, neural networks, etc. A meta-heuristic creates a set of candidate solutions (population), checks the value of the objective function for each of them, and applies a heuristic for generating a second population. The heuristic varies between the methods but is often based on the most promising elements of the previous generation. Those steps are repeated until a stop criterion is satisfied. Meta-heuristics can be applied to planning problems, as seen in [31]. There, the robust planning of the energy system of an EH is tackled using quantum particle swarm optimization (QPSO). This meta-heuristic is also compared to the performances of PSO and GA approaches and shows the superiority of the proposed method in terms of convergence speed and global search ability. Similarly, Ref. [125] uses an elitist GA (a variant of NSGA-II) in a multi-objective planning problem. The objective considered is minimizing the primary energy demand and investment costs for RES installation in a building.
In [67], a fuzzy inference system has been used to solve the energy storage system (ESS) scheduling problem in the microgrid energy management (MGEM) system. Reference [78] developed a multi-strategy gravitational search algorithm (MSGA-II) for optimizing the operation of integrated energy systems with electro-thermal DR mechanisms. In [83], a modified bacterial foraging optimization (MBFO) is used to solve the ESS scheduling problem considering the economic and environmental objective functions simulating the trade-off between conflicting objectives. In [96,109], a variation of a fuzzy decision-making method is proposed, merged with the well-known modified teaching–learning-based optimization algorithm.
In P2P systems, energy sharing has the potential to facilitate local energy balance and self-sufficiency. In [81], an evaluation of the performance of some P2P energy-sharing systems based on a multiagent-based simulation framework was performed. In order to facilitate the convergence of the algorithm, two heuristic techniques were considered: a step length control and a learning process involvement.
Other methods are used in the context of local energy markets, such as centralized/decentralized optimization, hybrid, continuous trading, auction-based, etc. [99]. They specifically occur when modeling multiple agents competing in a market or in decentralized or distributed approaches, such as in [65], where different optimization models such as the alternating direction method of multipliers (ADMM), Stackelberg game, and Nash game approaches were utilized.
The environmental/economic dispatch problem involves conflicting objectives, and it is known to be highly constrained, as already mentioned. In order to tackle this challenge, a method combining traditional optimization and a meta-heuristic method is presented in [103]. It combines convex optimization and meta-heuristics in a method named scenario-based branch and bound. This method is used to obtain reliable solutions in a model predictive-based MINLP with coupled timesteps. The meta-heuristic used is a modified version of the real coded genetic algorithm (RCGA) that is chosen over GA because it converges faster. The meta-heuristic is used to solve single steps independently, and their compatibility over the prediction horizon is checked afterward. In [106], a hybrid multi-objective optimization algorithm is presented based on particle swarm optimization (PSO) and differential evolution (DE). They showed the effectiveness and potential of the algorithm, comparing it with different techniques reported in the literature and by the application to the standard IEEE 30-bus test system.
Reference [107] mentions that these problems are usually difficult to solve using traditional mathematical methods, therefore EA is a good alternative. EA handles sets of possible solutions simultaneously and, as a result, permits the identification of several solutions of the Pareto front at once. Hence, EA is recognized as a natural way of solving multi-objective problems efficiently.
Heuristic/meta-heuristics methods can also be used in various aspects related to EHs, for example, for the operation/control of the EHs, as they are often able to handle problems in a shorter computational time. Reference [108] uses a modified teaching–learning-based optimization algorithm for solving the optimal power flow problem in multi-carrier energy systems, while reference [110] solves optimal energy flow problems (OEF) via a multi-agent genetic algorithm (MAGA) for decomposing the multi-carrier optimal power flow (OPF) problem into separate OPF problems.
A summary of the utilized heuristics methods per reference can be seen in Table 15.

Table 15.
Heuristic methods used in the context of EHs in the literature.
As already mentioned in the limitations of the previous section, in a multi-carrier energy system, the operation management considering multi-objective functions is a large-size problem and, in general, is nonlinear, non-convex, non-smooth, and of high dimension. Employing different mathematical techniques in such problems could lead to being trapped in local minima. Hence, a well alternative to deal with large-size problems is to use evolutionary techniques. However, a significant limitation when using heuristics techniques to solve multi-objective optimization problems is the complexity of setting up their parameters to afford an efficient performance. Along with this, the fact that it is not possible to obtain the optimal solution with these techniques is the main issue to consider when employing them.
9. Optimization Solvers and Modeling Environments
Based on the literature review, the most used optimization modeling environments and solvers with related optimization algorithms in EH contexts are summarized in Table 16. It is found that researchers employ more proprietary software (MATLAB, GAMS, LINGO, X-press, IBM ILOG CPLEX) than open-source (CVXPY) tools to formulate, create, configure, and solve the proposed optimization problems. Table 15 shows that most works use MATLAB as a framework for modeling their approaches due to its capability to handle both linear and nonlinear problems through its proprietary optimization tools. However, other works combine MATLAB as an interface with other modeling environments such as GAMS or YALMIP to implement the optimization models, using commercial solvers such as CPLEX or GUROBI to solve them. A few papers also formulate their models in environments developed under Python language such as CVXPY or RLLab, the latter for developing and evaluating reinforcement learning algorithms, with the limitation that larger models are hardly handled by open-source solvers, e.g., GLPK, IPOPT, CBC, ECOS, SCIP, etc., leading to an infeasible convergence or getting stuck in local minima. Therefore, using a particular modeling environment strongly depends on the expertise of the researcher, development time, ease of model implementation, and maintenance. As the environments enable the user to express complex algebraic expressions concisely, they employ more memory than an optimization application programming interface (API), e.g., CPLEX or GUROBI object-oriented Python API, to create the model.

Table 16.
Optimization solvers with related optimization algorithms and modeling environments used in EH contexts in the literature.
10. Uncertainties and Risk Aversion
10.1. Uncertainties
When considering uncertainties in the context of EHs, most of the analyzed research has considered the behavior of variable renewable energy (VRE), be it wind or PV, or the variations in consumption patterns among different users, be it by the representation of electrical and/or thermal loads. Added to this, some of the works have also considered variations in the market energy price. There is some research focusing also on thermal load uncertainties. In order to categorize these references according to the uncertainties that were tackled, a summary is provided in Table 17.

Table 17.
Uncertainties in the context of EHs in the literature.
In order to consider uncertainties in the problem formulation, different methodologies have been proposed in the literature that can be divided into three categories, as explained in [108], which are as follows:
- Stochastic optimization discretizes the continuous stochastic parameters into a tree of scenarios, whose nodes of uncertainty are assumed to be known;
- Robust optimization defines the solution according to more adverse scenarios regardless of the probability of occurrence;
- Chance-constrained optimization introduces probabilistic constraints for obtaining a trade-off between the optimal value and the robustness of the solution.
Among the analyzed references, the most frequent methodology uses stochastic optimization models. From these, the utilization of the Monte Carlo simulations [19,20,36,40,46,57,59,71,82,85] has stood out as the most common way of dealing with uncertainties, which randomly samples scenarios from historical data or probability distributions, albeit other sampling methods have also been utilized, as in [94] with Latin hypercube sampling or [111] with the average sampling approximation. In the latter, the authors propose a two-stage framework that combines a stochastic optimization model and robust techniques to identify solutions to the problem that are robust and flexible in terms of uncertainty. In the case of [33], a two-step approach is used for the operation of an EH, using stochastic optimization in the first step and an MPC strategy in the second step. The authors in [114] propose a stochastic optimization combined with a novel risk assessment approach called the downside risk constraints method for the modeling of the risk imposed by uncertain parameters.
Robust optimization techniques are found in the works [30,31]. The authors of [30] consider the uncertainty of each variable through a suitable uncertainty set or prediction interval that is defined as a function of the forecast value and the forecast error. The authors consider different degrees of robustness and different magnitudes of the forecast error. In [31], the authors use a robust method based on a QPSO approach for solving the optimization problem.
As for chance-constrained optimization, the authors of [50] solve the optimization problem using a distributionally robust chance-constrained model. Further, the authors of [67] made a forecast of uncertain parameters that were then used in a fuzzy inference system to make charging and discharging decisions for an ESS with the goal of simplifying the optimization of the energy system.
10.2. Risk Aversion
Risk-averse formulations interpolate between the classical expectation-based stochastic and minimax optimal control. This means that they are flexibly managing uncertainty from the worst case up to the expected (risk-neutral). In this way, risk-averse problems aim at hedging against extreme events of low probability without being overly conservative. There are two main approaches followed in dealing with this issue in the literature:
- The first one considers risk metrics that provide a grade of risk to moderate the decision;
- The second one is through distributionally robust optimization.
In general, the decision-maker may trade performance for safety by interpolating between the conventional stochastic and worst-case formulations looking forward to robustness to load and renewable power prediction errors.
In [71], the presence of uncertainties in the zero-carbon multi-energy system (ZCMES) influences its scheduling performance and brings some particular operational risks. Thus, in the operational-cost objective function, Markowitz’s mean-variance theory is employed to simultaneously minimize and maintain a balance between economy and risk.
The information gap decision theory (IGDT) is a practical strategy with no need for a probability distribution function of the uncertain parameters that models the positive and negative aspects of uncertainty based on the known and unknown information. For example, in [84], positive and negative outcomes that may cause risk are modeled using two functions of information gap decision theory called robustness and opportunity functions. In [74], IGDT may be used either from risk-averse or risk-seeking perspectives. In risk-averse IGDT, the decision-maker would be satisfied if the cost is equal to or less than a pre-specified critical value.
Reference [114] presents a stochastic model for risk assessment that utilizes a flexible methodology to mitigate risks associated with uncertain environments. This is achieved by slightly increasing the operational costs, as demonstrated in various tables that compare the operation costs of the hybrid energy system (HES) under different scenarios with the risk control parameter.
In addition, data-driven solutions are utilized to coordinate the scheduling of multi-energy coupled systems (MECS) by taking into account the correlation and distribution characteristics of uncertainties. This approach reduces the conservativeness of decision-making and improves the operation reliability of coordination scheduling for MECS. Reference [123] employs the data-driven robust optimization (DDRO) method to address uncertainties while obtaining less conservative minimum cost solutions.
The table below (Table 18) presents the risks with the associated parameters, as seen in the literature.

Table 18.
Risks and related parameters in the context of EHs in the literature.
10.3. Key Challenges in Handling Uncertainties and Risk Aversion
To handle uncertainty in the context of EHs, scenario-based optimization (SO) and robust optimization (RO) methods are dominant. However, they provide certain challenges. SO needs to utilize scenarios while considering the probability of them occurring. Otherwise, the end-up solutions can be conservative and/or their costs suboptimal. RO assumes known uncertainties per node. However, treating the uncertainties from different sources independently leads to over-conservative strategies as well. By combining the advantages of SO and RO, the distributionally robust optimization (DRO) methods can be promising when solving optimization problems with uncertainties (renewable generation and loads). There are different approaches to solving these kinds of problems, typically by reducing the constraints formulation to be solved via MILP, where the distribution information is useful to obtain a less conservative solution. These data-driven approaches can be combined with risk-averse methods to identify realistic and operationally efficient solutions.
11. Interaction of EHs with Multiple Markets and Networks
The aim of this section is to analyze the interactions of EHs with external entities and markets, which include not only the existing power grid and gas utility networks, but also thermal networks and, in some cases, other neighboring EHs.
The exchanged energy and the involved external networks differ between the analyzed literature, depending—to a great extent—on the existing energy carriers and local resources of the EH. In the review papers [11,13,17], it is possible to gain a general idea of the entities with which different EHs can interact. EHs can exchange energy among them (electricity, gas, thermal, and hydrogen) through external networks, as seen in [58]. In contrast, EHs can also send and receive electrical and thermal energy between each other (named transactive energy) without considering any utility or third-party network, as seen in [88]. However, most of the revised literature considers the interaction of a unique EH with at least one external network and energy market. In [129,130], the EH through the aggregator role interacts with more than one different operator and provides multi-energy bids to participate in multiple energy markets.
These energy exchanges could be performed efficiently by means of the conventional wholesale markets, P2P markets, and/or other kinds of market mechanisms that allow the exchange of different forms of energy other than electricity (natural gas, fuel, thermal energy, and hydrogen). Due to the higher complexity of coupling and integration of the EH with the external grids, synergies with multiple markets, and novel operational schemes should be further investigated.
11.1. Involvement of EHs in Multiple Wholesale Markets
According to the literature, two approaches are mainly followed to consider the interaction of the EHs with the surroundings and can be evaluated from the market and the network perspective. The market approach refers to the monetary/financial energy transactions between the EH and the surrounding energy system or market of interest, while the network approach is limited to the physical interaction and constraints regarding the amount of energy exchange between those two main systems.
By focusing on the technical network-constrained approach, it is included in the strategy of optimal coordination of flexible resources to maintain reliability and stability in EHs’ operation. Still, most of the literature within the EHs’ scope has been focused on demonstrating an optimal operation of such resources, where market rules were scarcely designed or omitted altogether [67,71].
In this first network approach, the optimization models have to impose technical constraints associated with the electrical and gas networks, such as [19,23,30,36,49,96,97,116,123], and load balancing to guarantee the stability, operational security, and energy balance of the EHs. On top of these, in [129,130], technical constraints for heat networks are also considered. These constraints include power and energy balance at the electrical point of common coupling (PCC), an admissible voltage range, transmission line capacity, and operational limits related to the gas sub-network. For example, in [123], economic costs have been considered, such as generation cost, start-up/shutdown cost, upward/downward reserve cost, and real-time operation cost (regulation cost, curtailment/shedding penalties), where a co-optimization between the power system and the natural gas system is presented. Similarly, in [116], the electric power, natural gas, and district heating systems are coordinated to achieve the optimal economical operation of the whole system (energy and reserve scheduling) with minimum wind curtailment, both in the day-ahead and real-time stages. In [130], possible energy imbalances and reserve shortages due to network violations are minimized for the combined space of multi-carrier systems. In [49], the model for optimal scheduling of P2G and gas-fired generation (GfG) is evaluated on the IEEE standard power transmission grid integrated with a gas transmission grid that would form an EH. Reference [25] proposes a network-constrained optimal scheduling model for a power distribution network and district heating network (DHN) with consideration of the DR, in which gas is imported upstream for thermal needs covering. More details regarding the involved constraints are reported in previous Section 4.
There is another trend of research that assesses the impact of the interaction of the considered EHs with the electrical distribution grids in terms of grid stability or performance, but not from a market perspective. Grid integration level (GIL) is evaluated in [79], where a strong interaction via importing/exporting electrical power in large quantities may result in a destabilization and performance degradation of the grid, and it can reduce the economic performance of the EH with high GIL rates. In [49], the renewable penetration level into the EH and optimal scheduling of P2G and GfG is decided by the grid operator considering the cost that comes with it. Other works evaluate and solve these grid issues inside the EH and not under the upstream utility network perspective. In [116], simultaneous energy and reserve scheduling is performed to minimize the operation costs, while accommodation of wind power production is achieved through reserves in the second stage (real time). In [123], the power output and up/down reserve capacity of gas-fired units is determined in the day-ahead scheduling stage in the multi-energy coupled system for handling wind power uncertainty, which influences the operation feasibility of the gas system and the availability of reserve of gas-fired units in real time. In both works [116,123], the reserve availability is used to manage uncertainties inside EHs, but not as a network service to the grid. Reference [66] estimates the ancillary service fees and other chargers Inside the EHs, depending on the energy schedule, but does not apply the issue upstream in the utility grid.
Hereafter, the market approach is presented in-depth, covering the wholesale electricity markets consecutively, balancing/grid services, gas market/trading, and DR mechanisms.
As for the literature that has been studied, EHs participate in the day-ahead electricity market (DAM), considering variable costs and/or different timeframes. A single EH is usually connected to the utility grid at the PCC, assuming the existence of the wholesale market [25,26,31,39,50,57,58,63,66,68,70,72,74,78,79,82,83,85,86,88,94,97,104,114,119,120,125]. The interaction with the DAM can be asymmetric by considering energy imports exclusively, as in [27,30,33,40,44], or the EH is enabled to import energy and excess export energy [100] to the wholesale market, as in [19,28,32,35,49,54,55,69,84,93]. In the latest case, the energy exports can be the result of surplus generation from a CHP in [86], the available electrical flexibility of DERs in [55], or EVs in vehicle-to-grid (V2G) operations [54]. Reference [88] addresses multi-EHs operation to minimize grids’ cost of operation and carbon emission through electricity price signal. Reference [40] provides a stochastic model for the optimal operation scheduling of a DER system, including renewables, considering economic and environmental aspects. In [54], local multi-energy systems cover the electricity and thermal needs of a building cluster with a fleet of PHEVs, where DERs are dispatched (including optimized charging/discharging strategies of PHEVs) in order to maximize the operator’s profit while also reducing CO2 emissions. Reference [63] addresses hourly scheduling for a multi-apartment residential microgrid operation.
Other works also cover the design stage, for instance, in [32], where a planning model is presented for a multi-energy microgrid that supplies the electricity, heating, and cooling loads, including flexible demands and hydrogen energy storage. Reference [68] addresses the optimal microgrid design, including optimal technology portfolio, placement, and dispatch, for multi-energy microgrids, including annualized investment costs of discrete and continuous technologies, the total cost of electricity purchase inclusive of carbon taxation, demand charges, electricity export revenues, and generation cost for electrical, heating, or cooling technologies. The interaction of thermal or electricity carriers between multiple EHs is presented in [57], where a non-profit entity named the local market operator (LMO) trades various forms of energy in local P2P markets between EHs and manages the aggregated demand-–supply curves in the wholesale and thermal district markets. Despite the fact that the majority of the models consider electricity markets to purchase or sell electricity, authors use historical day-ahead electricity prices to model the electricity market in its simplest version, as seen, for example, in [86,104]. Usually, the fluctuation of hourly wholesale electricity prices has a direct influence on the objective functions, in contrast to [79], where the electricity price is considered relatively stable.
After the DM, the intraday market (IDM) is represented as the second stage, where deviations from the DAM schedule and operation can be corrected in the IDM. Not many works consider electricity markets closer to operation, such as IDM or real-time markets [27,50,66,84,116,123]. The market interaction is modeled in [19,103] through the day-ahead and real-time prices, but wholesale electricity markets are not addressed for each timeframe. In contrast, Ref. [103] aims to reduce energy utilization from the utility grid through a real-time price-based DR scheme. Similarly, in [19], the EH is allowed to purchase or sell electricity so as to meet its own electricity and heat demand and to minimize the cost, in which the uncertainties of “real-time prices” are highly correlated to the DAM prices. In [27], the intraday schedule is adjusted (such as increasing the purchase of electricity and gas) to reduce the energy differences between the supply and demand inside the multi-energy system.
IDM is incorporated in [66] via real-time pricing data for both electricity import and export (wholesale electricity prices, distribution and transmission charges, and other ancillary service fees), according to different projections of grid carbon intensity and cost. Reference [50] proposes a chance-constrained problem designed for DAM EH energy management with multiple uncertainties and taking account of risks in intraday real-time transactions. The electricity and gas purchases are optimized and presented at daily and intraday timeframes. Reference [84] considers a multi-stage optimization with three temporal horizons: day-ahead dispatch with 1 h resolution and intraday operation with 15 min and 5 min beforehand scheduling intervals to adjust short-term cost and efficiency based on forecast updates of local generation and load. This market design representation is closer to the realistic market dispatch. Reference [35] proposes a robust chance-constrained framework for optimal EH management in the presence of uncertainties, where the time resolutions of 60 min, 30 min, 15 min, and 1 min have been simulated to present a close-to-real operation model. Additionally, local electricity markets are presented as a mechanism to deal with uncertainty in prices, demand, and renewable production, which usually use an intraday timescale and only a few combined multiple timeframes [99]. Reference [130] optimizes an aggregator’s portfolio by considering the technical constraints of the networks (electricity, gas, heat) and it enables trading in day-ahead electricity, natural gas, green hydrogen, and carbon markets, considering their intraday activation of the bidding as well.
Figure 4 illustrates the common timeline for energy scheduling of the wholesale electricity markets: day-ahead and intraday, including temporal horizon and discretization.
Figure 4.
Day-ahead and intraday schedule.
Apart from the wholesale electricity markets, other ancillary services should be considered as well in favor of network operators, such as grid congestion, reserve, balancing markets, frequency control, or voltage regulation. In this regard, reference [99] reports different TSO-DSO coordination schemes to solve balancing problems and grid congestion at the local level. Nevertheless, ancillary or grid services are hardly considered in the literature under the scope of EHs [49,65,131]. In [131], the participation of a distributed multi-energy system in providing ancillary services for the reserve market is assessed as a function of the economic parameters (availability fee and exercise fee), while maintaining the end-use energy demand at a constant level and thus without affecting the consumers’ comfort. The availability and exercise fees are established by the market operator rules. A P2G system is proposed in [36] to increase system flexibility, contribute to the supply of the network load in contingent events, and prevent the loss of the excessive power generated by the wind turbine. In [65], the network operator is in charge of operating the controllable energy resources to perform real-time grid management while maintaining the grid’s stability after the P2P and day-ahead scheduling.
Additionally, DR mechanisms [37] (via incentives, mainly via time-of-use (TOU) tariffs [25,58,70]) are mostly included to provide flexible EH operation. However, these studies do not model the DR mechanisms from the market or network operation point of view.
The DR is addressed in the literature as follows: electrical and thermal demand response programs for shiftable loads are included in [19], the day-ahead and real-time demand-based prices during peak periods are considered in [103], shifting loads from high-price times to low-price times to reduce operational costs are modeled in [88], shiftable and transferrable loads are considered during peak demand to the off-peak periods in [71], deferrable and critical loads are also included in [26], electrical V2G flexibility from PHEVs is provided in the wholesale market in [54], fast ramping capabilities (fast ramp up- and downtime) are provided by PEM electrolyzer in [34], and the available electrical flexibility of DERs is modeled in [55]. TOU tariffs to end-users and white certificates (WC), derived from the Italian incentive scheme, are included in [93] for CHPs oriented to primary energy saving. Additionally, in [58], the TOU prices and the transmission and distribution costs are distributed among end-users. In [120], electricity-load shifting, and flexible electrical heating/cooling supply are included, and it demonstrates the effectiveness of the planning and design method to show the influence of nodal energy prices. Following another approach, Ref. [29] considers the EH participating in DR programs by changing its behavior in response to a TOU tariff. Reference [119] incorporates responsive thermal and electrical loads, and their effects on EH planning (optimal configuration and sizing) are investigated. Furthermore, Ref. [82] addresses TOU prices to end-users as an incentive scheme to reduce their operational costs by shifting load from high- to low-price times, while in [78], both electrical and thermal loads enhance the flexibility of demand-side load management based on users’ comfort. In [27], emergency measures such as power curtailment and load shedding have to be taken for real-time adjustment. Other commodities may be considered as well, such as gas trading [19,23,25,27,28,30,31,33,35,36,39,40,44,49,54,55,57,58,70,72,74,78,79,82,83,84,85,88,93,97,104,116,119,120,123,125]. However, the upstream gas network is only modeled by means of a gas price, not as an internal or external gas network.
In contrast, the downstream electricity and gas sub-networks inside or between the EHs are presented in [23,36,49,96,97,116,123], in view of the growing influence of RES in power systems and the mutual effects of the gas and electricity networks. For example, several EHs connected to a 33-bus radial distribution network and a 14-node gas network are considered in [36], where the internal system operator defines upper transaction limits for each EH in its day-ahead operation. Afterward, each EH optimizes its own operation in the wholesale markets. P2G is also studied in [49,116], and incorporating hydrogen into the gas network is studied in [23]. In [44], thermal needs are exchanged between different local energy communities through a common thermal network, while hot water exchange and gas tariff schemes are included in [70].
Table 19 summarizes the literature and the interaction considered with the external entities.

Table 19.
Interaction of EHs with multiple markets in the literature and information available.
11.2. P2P Markets
In the literature, three main P2P architectures [48,53,99] are proposed in the context of EHs according to how the decisions of the energy trading process are taken and their communication characteristics.
In a centralized P2P architecture, a central coordinator dictates the energy transactions and their prices among the peers in the community. The decision-making process is generally based on an optimization algorithm aimed at maximizing the overall benefit of the community. Peers only communicate with the coordinator, as seen in Figure 5. Once the transactions have been made effective, the central coordinator is in charge of distributing the obtained revenues among the participants [36,37]. The coordinator also acts as an intermediary between the community and the rest of the system. For instance, Ref. [52] proposes a novel centralized P2P energy trading model named operator-oriented P2P trading to lower the barriers to entering into the transaction while accommodating various customers. The operator decides the marginal/trading price and trading schedules that are defined with the objective of maximizing the social welfare given by the sum of the profits of all participants. In [65], another centralized P2P architecture is proposed for the real-time operation of the distribution network where the network operator has direct control over the DERs of crowdsources. The objective is to minimize the generator’s cost function in addition to the thermal losses and crowdsources’ disutility function designed to compensate for the inconvenience caused by rescheduling shapeable load. Reference [90] defines a centralized system that searches for optimization of the electricity and gas costs of a neighborhood, including technologies such as CHPs, HPs, heating, ventilation and air-conditioning (HVACs), EVs, and RES.
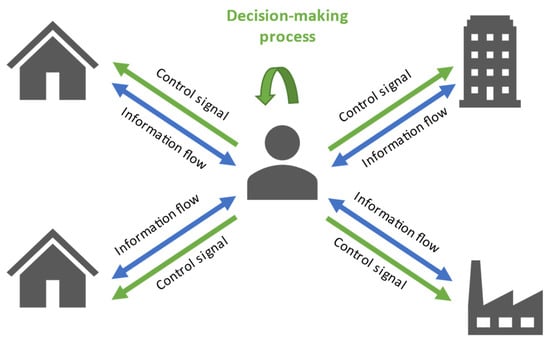
Figure 5.
Centralized P2P architecture.
In a decentralized P2P architecture, peers can directly communicate with each other and negotiate energy transactions among themselves without the involvement of a central coordinator. The decision-making process for defining the amount of energy exchanged and the price is taken by each peer, generally based on an optimization algorithm to minimize its individual electricity costs or maximize its revenues, as shown in Figure 6. In addition to the centralized architecture described above, Reference [65] also proposes a solution based on a decentralized architecture for the day-ahead operation in which direct energy trading between crowdsources is carried out. These energy transactions are included within the optimization algorithm of the network operator as constraints. Reference [51] defines a decentralized architecture where customers can trade and exchange energy with other customers. All customers can communicate with each other using a two-way communication system. The optimization is based on two stages. The first stage allows a decision on whether a customer should participate or not in the P2P energy-sharing trading system based on the maximization of social welfare. The second stage allows for maximizing the payoff of the involved customers. Reference [91] considers a fully decentralized P2P system where smart energy buildings can share energy among themselves without the need to have a coordinator. A two-stage P2P energy-sharing strategy for a building cluster is developed. In the first stage, the optimal energy-sharing profiles of the buildings aim to minimize the total social energy cost. In the second stage, the clearing prices are calculated based on mutual energy sharing via a non-cooperative game.
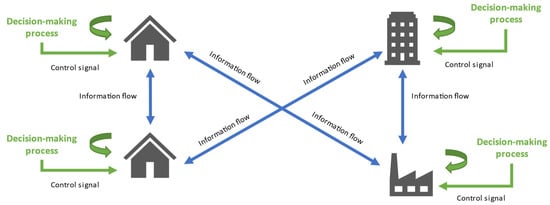
Figure 6.
Decentralized P2P architecture.
In a distributed P2P architecture, a coordinator communicates with each peer and manages a local energy trading market set for the transactions among them. However, in contrast to a centralized P2P architecture, the coordinator does not have control over the amount of energy exchanged. It just tries to influence participating peers by sending suitable price signals. Each peer carries out the optimization process according to the received internal P2P market signal sent by the coordinator to minimize its individual electricity costs or maximize its individual revenues within the P2P energy-sharing system. It represents a hybrid approach between centralized and decentralized P2P architectures, as shown in Figure 7. For example, Ref. [81] proposes a distributed architecture where the operator only provides a local market platform with necessary functions, in which all the prosumers trade or share energy with each other in order to maximize their own benefits individually. Hence, prosumers have full authority over their distributed energy resources (DERs), eliminating the need for any supplementary incentives to encourage prosumer participation. The article proposes three distinct pricing approaches for determining the P2P market’s internal trading price: the supply and demand ratio (SDR), mid-market rate (MMR), and bill sharing (BS).
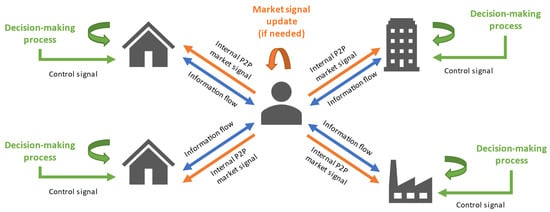
Figure 7.
Distributed P2P architecture.
In [92], a P2P architecture is proposed, consisting of two types of agents: (i) P2P PV prosumers who trade energy among themselves, and (ii) an energy-sharing provider (ESP) responsible for coordinating the sharing activities. The ESP interacts with the utility grid by purchasing the required electricity or selling excess power production of the energy-sharing zone using a dynamic internal pricing model within the EH. In [56], a P2P distributed architecture is defined, utilizing blockchain technology to implement transactions. The transaction process involves four stages: (i) customer demand forecasting, (ii) initiation of the transaction, (iii) security check, and (iv) trading execution. In [57], a distributed P2P architecture is considered, where EHs participate in a local market managed by the LMO. EHs also have access to district markets (electricity utility, gas utility, district heating, district cooling) where they can trade various forms of energy. However, EHs prioritize exchanging the maximum energy in local markets due to more beneficial market clearing prices for both buyers and sellers.
Some other studies focused on the P2P electricity market and its pricing structure in which peers are able to sell their excess production and trade for a better electricity price than the one offered by the retailer, as seen in [41,42,43,44,54,58,62,93]. Table 20 shows the key factors among the three P2P architectures.

Table 20.
Comparison of P2P architectures in the EH context.
A centralized P2P architecture offers several advantages, such as maximizing the total welfare of the community and providing better support for grid operator services. However, it may have higher management complexity and computational burden, particularly when many peers are involved. Additionally, confidentiality concerns may arise as prosumers need to share all information with the central coordinator. On the other hand, a decentralized P2P architecture enables prosumers to have complete control over their DERs and make decisions at the prosumer level. This architecture is also highly scalable. In contrast, as there is no coordinator, the overall welfare of the community is less optimized. Distributed P2P architecture shares the advantages of the previous two architectures. There exists a coordinator that, through sending suitable price signals, influences the participation of the prosumers while the decision-making process is still maintained at the prosumer level. The amount of information to be exchanged with the coordinator is less than in a centralized architecture, so prosumers can better maintain their privacy. It is very scalable and more compatible with the existing regulatory framework [48,53,99]. This architecture requires the definition of a suitable pricing mechanism by the coordinator to manage the internal energy trading market. Different approaches can be applied for the calculation of internal prices, such as (i) SDR, where the internal trading price is defined as a piecewise function [81,92]; (ii) MMR, where the internal trading price is set as the average of retail and export prices [81]; (iii) BS, where a pro-rata cost-sharing mechanism is defined in which the income and cost of each participant are proportional to its electricity production and consumption throughout the time horizon [81]; and (iv) auction-based pricing strategy, where EHs independently decide on the amount and price of energy to be traded in the local markets and express their interest in local trading through submitting their offers/bids to the coordinator [57,99].
11.3. Key Challenges for the Interaction of EHs with Multiple MARKETS and Networks
Several limitations and challenges are identified regarding the interaction of EHs with multiple markets. Firstly, although there are studies in the literature that consider electrical and gas networks, their approach does not elaborate and implement extensive market rules and constraints. In most cases, electrical and gas networks are referred to as internal EH or between EHs networks, without considering the upstream utility grids and associated market model. Therefore, there is a lack of studies that integrate grid distribution models and complex market mechanisms between several EHs.
Secondly, although most models consider electricity markets to purchase or sell electricity, authors use historical day-ahead electricity prices to model the electricity market in its simplest version. Additionally, few published articles consider electricity markets closer to operation, such as IDM or real-time markets, needed to adjust EH supply and demand under intrinsic uncertainty. In conclusion, a clear market framework is not presented (i.e., the framework of the European single market), which should include the main features of market mechanisms such as market bids, closure times, market clearing process, real-time power setpoint, or grid needs. There is a lack of sensible and realistic interaction with energy markets or upward networks. A further necessary step would be the specific-country analysis for a more realistic cost-benefit scenario.
Thirdly, several key challenges have been identified regarding thermal and gas networks. Most research papers usually have common characteristics as follows: (i) well-known natural gas price signal; (ii) natural gas or other fuel is only bought to satisfy the local thermal needs; and (iii) heating and cooling networks (if modeled) are only considered inside the EHs, and a central control is implemented to purchase and sell electricity in the utility grid. Regarding (i), in fact, only natural gas price and thermal load are considered in the optimized operation of the EHs in most papers, but without any gas market structure, gas transactions, gas scarcity, or shortage. According to (ii), gas or thermal energy is purchased according to internal EH needs. Moreover, hydrogen as an energy carrier is not commonly included in the EHs. Nowadays, a bidirectional electricity carrier is most common to purchase renewable generation, whereas bidirectional flows should be enabled for all energy carriers. Regarding (iii), thermal needs are mostly satisfied with internal heating and cooling networks fed by natural gas or other fossil fuel, but existing thermal or gas infrastructure downstream of the EH is not modeled.
Fourthly, DR is widely addressed, although it should be oriented more toward the upstream grid needs. In contrast, ancillary grid services are hardly considered in the literature under the scope of EHs to support the upstream utility network. After the consulted literature, the reserve market established by the market operator rules is conducted in [131] and to support contingent events in [36]. Few other research papers solve grid problems inside the EH without any market design, i.e., reserve availability [116,123] provided by a conventional generator to manage uncertainties inside EHs, but not to provide valuable services to the upstream grid. In conclusion, further research is required on how EHs may interact with multiple energy markets, assuming knowledge of grid network constraints, considering the market design, and evaluating mutual coupling with other energy vectors and markets.
Based on the reviewed literature on P2P, it is concluded that the establishment of a P2P energy-sharing mechanism benefits both prosumers, which can reduce their electricity bill and allow them to benefit from cleaner energy, and the system, which can obtain new sources of flexibility contributing to reducing peak load and improving system security through the participation in ancillary service markets [53]. However, there are several challenges that should be tackled to implement a P2P system efficiently.
The adoption of feasible and effective optimization algorithms and pricing schemes within the P2P system to automatize energy transactions is challenging. In the centralized architecture, there might be scalability problems with the optimization algorithm if many peers are involved because it could require a high computational effort to reach the optimal solution. In the distributed one, the proper P2P pricing mechanism should be adopted to incentivize prosumers’ participation and help to maximize the overall welfare of the community. Several pricing schemes proposed in the literature can show convergence problems, such as SDR, MMR, and BS. These are based on iterative bidding processes in which the bids provided by the prosumers change in response to the dynamic internal price. It is possible that the energy bids and internal price values do not converge to a fixed point after a finite number of iterations. Therefore, it is necessary to implement mechanisms that ensure the convergence of these algorithms in the required time. It is essential that the implemented optimization algorithms include models that accurately simulate the behavior of the flexible resources and, therefore, can identify the available flexibility under different control actions in an accurate way. This represents a challenge since the flexibility depends on many factors, several of them subject to a high degree of uncertainty (e.g., end-users’ behavior, weather conditions, etc.).
12. Business Models of EHs
From the reviewed works, it emerges that business models are mostly based on the different objectives of the systems under study. Many works focus on a single objective, usually consisting of the minimization of the cost of the energy carriers involved or of the total investment or operating cost of the systems. Among others, Ref. [19] aims to reduce the total cost of an EH by deciding on the electrical and thermal load dispatch, for electricity, heat generation, and storage units, to meet a specific electricity and heat demand at a minimum cost. The EH is allowed for such a purpose as to purchase/sell electricity from/to the upper grid. In [56], the business model aims to minimize the total energy expenditure of all individual customers in the microgrid. Similarly, in [65], the main objective is to minimize electricity costs by employing local resources from the community energy system in a way that does not violate any network constraints. In [75], the model employs a transactive energy scheme as a business model. Each building tends to charge more for the energy supplies to other buildings and pay less for the energy demands from other buildings; therefore, the clearing prices should be equilibrium prices such that each building will pay/charge for the energy demands/supplies. The objective is to minimize the daily operation cost, considered to be composed of three parts: net electricity purchasing cost, gas purchasing cost, and carbon emission cost. In [105,108], the business model is focused on the reduction of the total operating cost, while in [111], it is based on the reduction of the expected time-ahead energy costs.
Many works deal with two or more objectives, considering economic objectives associated with the minimization of the cost of emissions, cost of power loss, and CO2 emissions. For instance, in [70], the business model is focused on the minimization of energy cost with the minimization of environmental impact, which is assessed in terms of CO2 emissions, while in [97,109,110], the business model is focused on reducing the total cost of generation and environmental emissions.
Relating to the literature on energy markets and P2P schemes, in [48], three business models are discussed: C2C (consumer-to-consumer), on which a distributed P2P scheme would be based; B2C (business-to-consumer), which could portray a traditional scheme in which the consumer buys electricity from the retailer; and B2B (business-to-business), which would imply an exchange between different commercial entities. Regarding P2P energy trading, in [52], the business model is focused on the maximization of profits (P2P energy trading). In [57], the EHs have access to district markets, in which they can trade various forms of energy. Additionally, they have access to a local market, which allows the EHs to trade energy among themselves in a P2P market. EHs first try to exchange the maximum energy in the local markets because market clearing prices are assumed to be more beneficial for both seller and buyer EHs than the prices of district markets. As noted in [99], business models for energy sharing via local electricity markets are still very rarely put into commercial practice. This work presents the existing barriers in current regulatory frameworks focusing on the Portuguese energy market after analyzing the P2P energy-sharing business model of the project Community S (S stands for sharing, solar, storage, sustainable, and smart).
Table 21 summarizes the business models for all analyzed works.

Table 21.
Business model per reference.
Based on the reviewed papers, the business models of EHs have as a basis the reduction of the energy cost and/or of the total investment and operating costs of the EHs. In some papers, the reduction of the carbon emission cost is taken into consideration as well. In most cases, business models are limited to the electricity carrier, some include gas or heat, and they rarely focus on multi-carrier technical aspects such as the inclusion of additional energy carriers.
Relating to the literature on energy markets and P2P schemes, it emerges that business models are mostly limited to a single energy carrier, which is electricity, or do not go in-depth into the specificities of other energy markets. Therefore, the main challenge is to provide innovative business models that could reflect the different energy carriers present in the EHs and the synergies among them. This means fully exploiting the potential to participate in different markets, considering their specificities.
13. Other Collateral Concerns
13.1. Temporal Scope for the Operation Optimization of EHs
This section discusses the time horizons and time resolution that the analyzed works in the literature consider for the operation optimization of the EHs. The most commonly used time horizon among the papers considered in this study is either one year or one day, depending on the scope of the optimization. Many documents use one year [31,38,41,44,47,48,49,58,62,63,68,69,70,71,72,85,86,89,93,95,104,113,115,125] and focus on long-term energy system planning. However, this is not always performed in the same way. Indeed, a complete year can be too computationally challenging, and some models reduce the complexity by representing a year with representative days. The number of representative days varies depending on the model; references [41,44,71] simplify the annual scope by the use of one representative day per season, while [62] uses one week per month to study the whole year. Reference [68] uses three days for each month in a year corresponding to weekday, weekend, and peak, while [70,85,101] use only three typical days in total. Models with a stronger operational focus use more detailed descriptions and may choose only to use a horizon of one day, such as [19,23,24,25,28,29,30,33,34,40,42,43,46,48,50,54,55,57,61,74,75,80,83,84,90,92,94,96,98,102,105,114,116,123].
Other models need to account for the future trends in price and demands, e.g., using a longer horizon, five years, in the case of [64,66]. In addition, Ref. [66] compares the use of 4 day-types (summer weekday, summer weekend, winter weekday, and winter weekend) and 39 day-types (weekdays, Saturday, and Sunday for 13 periods for every 4 weeks). Finally, some documents use particular horizons, for example, seven weeks, as in [60].
In addition to the time horizon, the literature adequately describes the time resolution used in the various cases. The most common temporal resolution is one hour, as in [19,20,21,23,25,26,28,29,30,36,38,40,42,43,46,47,49,50,54,55,57,60,61,63,67,68,72,74,75,77,79,80,83,90,92,94,98,102,104,105,113,115,123,125]. An hourly resolution allows the capture of some of the variability in the demand and renewable generation and also fits well with the structure of the day-ahead markets. Nevertheless, Refs. [35,66,103] use a half-hourly resolution, as it is the time resolution in the UK’s DAM. Even finer resolutions can also be rarely found. For example, Refs. [112,116,122] use 15 min, Refs. [65,91] use a time resolution between 5 and 15 min, Ref. [35] uses a time resolution of 1 min, and Ref. [87] uses a time resolution of half a minute. The greater the granularity, the deeper the level of detail that increases the reliability and accuracy of the model, although this causes higher computational efforts. In fact, some models use a lower resolution as a way to reduce the computational burden; for example, Ref. [101] uses 2 h, Ref. [86] 4 h, and Ref. [85] divides each day into 6 periods which do not have to be the same length.
Table 22 summarizes the different temporal resolutions used in the analyzed works in the literature dealing with the operation optimization of EHs.

Table 22.
Temporal resolutions used in the analyzed works in the literature dealing with the operation optimization of EHs.
13.2. Spatial Scope for the Design and Operation Optimization of EHs
The spatial scope varies greatly between models due to different goals, locations, technologies, and sectors (e.g., residential, industrial, commercial sectors) of the EH. In addition, it is not always reported precisely in the analyzed works and can focus on different types of information: for instance, some documents report a geographical location while others provide a physical description of the local system, and others provide no information at all.
Many models focus solely on an individual energy system, be it a single building ([66,125]) or a single area (neighborhood) [72,74,75,97,104,105]. The number of buildings can vary greatly, e.g., 4 in [101], 6 in [85], 25 in [113], and 29 in [47]. A few models focus more on the interaction between different energy systems inside a larger one. For example, in [46], 4 smart EHs are included in the IEEE 33-bus network. Similarly, the model presented in [36] is applied in a 33-bus radial distribution network and a 14-node gas network, 3 smart EHs, and a P2G system. The IEEE 30-bus network is also used in [96] with 5 generators, 4 tap-transformers, and 2 shunt capacitors.
A different approach Is taken in [86,90], where authors consider a grid of interconnected nodes. The microgrid considered in the latter has 21 nodes, 6 of which are EHs, each comprising a natural gas boiler, a CHP unit, an HP, and a heat storage unit. In other nodes of the microgrid, there are three wind generators, two batteries, and electrical loads.
Table 23 summarizes the different spatial scopes used in the reviewed papers found in the literature.

Table 23.
Spatial scopes used in the analyzed works in the literature dealing with the design and operation optimization of EHs.
14. Discussion and Conclusions
14.1. Summary of Challenges and Limitations
This review paper presents the optimal design and operation of EHs and their interaction with external networks and multiple markets, tackling all aspects of this multi-faceted theme.
Based on the reviewed literature, there are some important limitations and challenges related to the EH configuration that need to be addressed in order to optimize the planning and operation of such systems in the future, especially considering the RePowerEU plan objectives. Past research papers focus mainly on the electricity carrier as a backbone while limited other carriers and conversion technologies are considered in single studies. The optimal placement of the different energy technologies in the EH is an important aspect of the design optimization of EHs, especially in the case of thermal storage, whose location in a DHN can impact thermal losses and, therefore, energy consumption and related costs and emissions. However, in many cases, it is not addressed.
Also, based on the literature findings, the MILP approach is the most widely used to optimize the design and operation of multi-carrier energy systems. Nevertheless, some of the different variables that may be present in EHs respond to a nonlinear behavior, e.g., power flow variables, and to non-convexities, e.g., commitment status of energy conversion and storage units. The accurate representation of the physical phenomena taking place in the energy conversion and storage units of a multi-carrier energy system and of their design and operational decisions may require the use of MINLP formulations. Of course, the solution to MINLP problems is still today a challenging and computationally hard task, especially when the configuration is complex, as said. Usually, MINLP problems are relaxed and reformulated as MIQCP, MISOCP, or MILP problems and solved using proper decomposition techniques. However, very detailed models of energy technologies can limit the effectiveness of the optimization models and methods used to solve the problem, and a good compromise should be found between model fidelity and the complexity of the optimization process. As for the use of multi-objective approaches aimed at finding good compromise solutions that satisfy the needs of the different stakeholders taking part in the decision-making process of EHs, an ideal approach should be used where the optimization is performed before the decision-making. In this way, the final decision to select the trade-off between conflicting objectives on the Pareto front is left to the decision-maker.
Regarding the EHs’ interaction with the markets, the most important limitation found in the literature is that ancillary grid services are hardly considered under the scope of EHs to support the upstream utility network. The day-ahead wholesale market is the most usual, but only a few papers consider intraday or real-time scheduling. Therefore, there is a lack of sensible and realistic interaction with markets or upward utility networks beyond EHs. A second limitation found in the studied works is the lack of a real electricity market setting in the EHs’ interaction. Generally, when selling/purchasing electricity in the day-ahead electricity spot market, the EH or a proxy acting on EH’s behalf, e.g., a market agent, must submit selling/buying bids before the market gate closure (usually the day before the electricity delivery/withdrawal). In between the gate closure time of the day-ahead electricity spot market and the time of delivery of the energy cleared in such a market, several intraday electricity markets are celebrated where the market agent representing the EH can submit selling or buying bids to modify the generation schedule of the day-ahead electricity spot market or the previous intraday market. This setting is mainly disregarded by the literature so far, whereas it has been partly addressed by the latest [130] where day-ahead and real-time optimization strategies have been combined for an aggregator representing multi-energy assets. Of course, more actors under different realistic business models shall be investigated along with different market settings, e.g., balancing, P2P, etc. The third limitation found in the revised works is analogous to the second one but refers to the natural gas market setting. Natural gas supply and consumption are also negotiated in day-ahead and intraday markets or sessions. The time horizon and temporal resolution of the day-ahead and intraday gas market sessions are not the same as those of the day-ahead and intraday electricity markets. Gas imbalances are also computed in the gas market. The gas sold/purchased in each market or market session in which the agent has participated is settled at the market clearing price (usually marginal), whereas the excess/deficit gas imbalances are cleared at the imbalance price (usually different for excess and deficit imbalances). Again, reference [130] considers not only electricity markets, but also the day-ahead gas market through multi-energy biddings. Still, the gas intraday is not considered, and thus none of the revised papers have considered the entire process so far. All papers—where the gas price is considered—use a single gas price, presumably corresponding to the day-ahead gas market price. The uncertainty of gas prices is not considered in any of the revised papers.
Finally, regarding the P2P markets, there are fruitful studies in the literature on the maximization of social welfare and increase in individual profits, which allow users to negotiate the excess electricity that is being produced as well as to choose who they are going to buy it from. Still, the interaction between users with other outside actors is either reduced to the minimum that is needed or nonexistent.
14.2. Research Pathways
Overall, EH is a promising concept that could serve the energy transition under the cross-sectoral view that is needed. Based on the findings, there is a need for studying realistic approaches, e.g., proper configuration, market interaction, actors’ interaction, etc., so that EHs potential can be unfolded. In detail:
- Different types of EH configurations with a wide range of conversion technologies that compile general solutions and can be replicable and scalable should be considered. Energy storage and its flexibility potential are of high importance, and EHs’ future configuration models need to consider the optimization of their sizing and placement, including potential alternative means of storage such as EVs and hydrogen. On top of that, as the interaction of different energy carriers affects the nonlinearity and nonconvexity of the problem, a more complex configuration shall lead to higher sensitivity of initial conditions that affect the problem formulation and solution. This challenge should be faced as the integrated grid approach needs the high interconnection of many different carriers;
- The optimization of the design and operation of an EH is a complicated task that has been considered in the past under different prisms as already analyzed. It is also well established that in order to address the needs of the most related actors in an EH, the multi-objective approach is the way forward. What is the most challenging so far is the accurate representation of physical phenomena that would add complexity to an already multi-faceted problem. Therefore, it seems that the optimization of design and operation should be tackled in layers and in a distributed way with loops of interaction that would allow the different layers to be in accordance. The layers could address physical carriers and/or hierarchical layers of governance where the complexity is built based on the pursuit of the actors involved. As an example, distributed optimization could be dealt with within the EH on the prosumers’ side while being in good collaboration with the central optimization at the central level of the ILEC. An example of this innovative approach is tested under the approach proposed in the eNeuron H2020 project (November 2020–October 2024, ID: 957779), which has the main goal to develop an innovative toolbox for the optimal design and operation of local energy communities, integrating DERs and multiple energy carriers at different scales;
- Last but not least, regarding the EHs’ interaction with the markets, a further necessary step would be the specific-country cost–benefit analysis feeding sustainable business models. Moreover, further research is required on how EHs may interact with multiple energy markets, assuming knowledge of grid network constraints, considering the market design, and evaluating mutual coupling with other energy carriers and markets, including gas markets. Especially for P2P markets, when considering users’ interaction, local but centralized resources, as well as different energy carriers, should be involved. A good baseline for further investigation under the EH scope could be the consideration of the electricity–carbon integrated P2P market as presented in [132].
Author Contributions
Conceptualization, C.P., M.D.S. and G.G.; methodology, C.P.; validation, C.P., M.D.S. and G.G.; formal analysis, C.P., M.D.S., C.C., M.C., V.P., A.F.C.B., A.G.-G., N.R. and G.G.; writing—original draft preparation, C.P., M.D.S., C.C., M.C., V.P., A.F.C.B., A.G.-G., N.R. and G.G.; writing—review and editing, C.P., M.D.S., C.C., M.C., V.P., A.F.C.B., A.G.-G., N.R. and G.G.; supervision, C.P., M.D.S. and G.G.; funding acquisition, C.P., M.D.S. and G.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been carried out within the eNeuron project that has received funding from the European Union’s Horizon 2020 Research and Innovation Programme under Grant Agreement No. 957779.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviation
| Acronym | Meaning | Acronym | Meaning |
| AC | Air conditioners | LMO | Local market operator |
| ADMM | Alternating direction method of multipliers | LP | Linear programming |
| B2B | Business-to-business | MAGA | Multi-agent genetic algorithm |
| B2C | Business-to-consumer | MBFO | Modified bacterial foraging optimization |
| BS | Bill sharing | MECS | Multi-energy coupled systems |
| C2C | Consumer-to-consumer | MES | Multi-energy system |
| CAES | Compressed air energy storage | MGEM | Microgrid energy management |
| CD | Crowding distance | MILP | Mixed-integer linear programming |
| CES | Community energy storage | MINLP | Mixed-integer nonlinear programming |
| CHP | Combined heat and power | MIQCP | Mixed-integer quadratically constrained |
| DAM | Day-ahead electricity market | MISOCP | Mixed-integer second-order cone programming |
| DDRO | Data-driven distributionally robust optimization | MMR | Mid-market rate |
| DE | Differential evolution | MOEA | Multi-objective evolutionary algorithms |
| DER | Distributed energy resource | MO-MFEA-II | Multi-objective multifactorial evolutionary algorithm II |
| DHN | District heating network | MPC | Model predictive control |
| DRO | Distributionally robust optimization | MSGA-II | Multi-strategy gravitational search algorithm |
| DRP | Demand response programs | MTLBO | Modified teaching–learning-based optimization algorithm |
| EA | Evolutionary algorithms | NR | Non-dominated rank |
| EH | Energy hub | NSGA | Non-dominated sorting genetic algorithm |
| EHGHS | Electricity–hydrogen–gas heat integrated energy system | nZED | Net-zero energy districts |
| ESP | Energy-sharing provider | O&M | Operation and maintenance |
| ESS | Energy storage system | OEF | Optimal energy flow |
| ETIP SNET | European Technology & Innovation Platforms Smart Networks for Energy Transition | P2G | Power-to-gas |
| EU | European Union | P2P | Peer-to-peer |
| EV | Electric vehicle | PCC | Point Of common coupling |
| GA | Genetic algorithms | PCM | Phase change materials |
| GfG | Gas-fired generation | PHEV | Plug-in hybrid electric vehicle |
| GHG | Greenhouse gas | PRIMES | Price-induced narket equilibrium system |
| GIL | Grid integration level | PSO | Particle swarm optimization |
| HER | Heat-to-electricity ratio | PV | Photovoltaic |
| HES | Hybrid energy system | QPSO | Quantum particle swarm optimization |
| HP | Heat pump | RCGA | Real coded genetic algorithm |
| HVAC | Heating, ventilation, and air-conditioning | RES | Renewable energy sources |
| ICC | Integer cut constraints | RMILP | Robust MILP |
| IDM | Intraday market | SDR | Supply and demand ratio |
| TOU | Time of use | ||
| IGDT | Information gap decision theory | V2G | Vehicle-to-grid |
| ILECs | Integrated local energy communities | VIKOR | Vlsekriterijumska optimizacija i kompromisno resenj multi-criteria decision-making method |
| KPI | Key performance indicator | VRE | Variable renewable energy |
| LAES | Liquid air energy storage | WC | White certificates |
| LEC | Local energy community | ZCMES | Zero-carbon multi-energy system |
References
- Available online: https://ec.europa.eu/clima/policies/strategies/2030_en (accessed on 10 April 2022).
- Di Somma, M.; Graditi, G. Challenges and opportunities of the energy transition and the added value of energy systems integration. In Technologies for Integrated Energy Systems and Networks; Wiley: Hoboken, NJ, USA, 2022; pp. 1–14. [Google Scholar] [CrossRef]
- Rinaldi, R.; Losa, I.; De Nigris, M.; Prata, R.; Albu, M.; Kulmala, A.; Samovich, N.; Iliceto, A.; Amann, G.; Pastor, R.; et al. ETIP SNET VISION 2050 Integrating Smart Networks for the Energy Transition: Serving Society and Protecting the Environment. In Proceedings of the CIRED 2019, Madrid, Spain, 3–6 June 2019; p. 175. [Google Scholar] [CrossRef]
- Di Somma, M.; Graditi, G. Integrated Energy Systems: The Engine for Energy Transition. In Technologies for Integrated Energy Systems and Networks; Wiley: Hoboken, NJ, USA, 2022; pp. 15–40. [Google Scholar] [CrossRef]
- Available online: https://ec.europa.eu/clima/policies/strategies/analysis/models_en (accessed on 6 February 2023).
- Jägemann, C.; Fürsch, M.; Hagspiel, S.; Nagl, S. Decarbonizing Europe’s power sector by 2050—Analyzing the economic implications of alternative decarbonization pathways. Energy Econ. 2013, 40, 622–636. [Google Scholar] [CrossRef]
- Available online: https://ec.europa.eu/energy/en/news/commission-proposes-new-rules-consumer-centred-cleanenergy-transition (accessed on 4 May 2023).
- Available online: https://ec.europa.eu/info/strategy/priorities-2019-2024/european-green-deal/repowereu-affordable-secure-and-sustainable-energy-europe_en#documents (accessed on 14 June 2022).
- Geidl, M.; Koeppel, G.; Favre-Perrod, P.; Klockl, B.; Andersson, G.; Frohlich, K. Energy hubs for the future. IEEE Power Energy Mag. 2007, 5, 24–30. [Google Scholar] [CrossRef]
- Comodi, G.; Spinaci, G.; Di Somma, M.; Graditi, G. Transition Potential of Local Energy Communities. In Technologies for Integrated Energy Systems and Networks; Wiley: Hoboken, NJ, USA, 2022; pp. 275–304. [Google Scholar] [CrossRef]
- Mohammadi, M.; Noorollahi, Y.; Mohammadi-Ivatloo, B.; Yousefi, H. Energy hub: From a model to a concept—A review. Renew. Sustain. Energy Rev. 2017, 80, 1512–1527. [Google Scholar] [CrossRef]
- Guelpa, E.; Bischi, A.; Verda, V.; Chertkov, M.; Lund, H. Towards future infrastructures for sustainable multi-energy systems: A review. Energy 2019, 184, 2–21. [Google Scholar] [CrossRef]
- Mancarella, P. MES (multi-energy systems): An overview of concepts and evaluation models. Energy 2014, 65, 1–17. [Google Scholar] [CrossRef]
- Mohammadi-Ivatloo, B.; Jabari, F. Jabari, Operation, Planning, and Analysis of Energy Storage Systems in Smart Energy Hubs; Springer International Publishing: Manhattan, NY, USA, 2018. [Google Scholar]
- Papadimitriou, C.; Anastasiadis, A.; Psomopoulos, C.; Vokas, G. Demand response schemes in energy hubs: A comparison study. Energy Procedia 2019, 157, 939–944. [Google Scholar] [CrossRef]
- Lasemi, M.A.; Arabkoohsar, A.; Hajizadeh, A.; Mohammadi-Ivatloo, B. A comprehensive review on optimization challenges of smart energy hubs under uncertainty factors. Renew. Sustain. Energy Rev. 2022, 160, 112320. [Google Scholar] [CrossRef]
- Mohammadi, M.; Noorollahi, Y.; Mohammadi-Ivatloo, B.; Hosseinzadeh, M.; Yousefi, H.; Khorasani, S.T. Optimal management of energy hubs and smart energy hubs—A review. Renew. Sustain. Energy Rev. 2018, 89, 33–50. [Google Scholar] [CrossRef]
- Akhtari, M.R.; Baneshi, M. Techno-economic assessment and optimization of a hybrid renewable co-supply of electricity, heat and hydrogen system to enhance performance by recovering excess electricity for a large energy consumer. Energy Convers. Manag. 2019, 188, 131–141. [Google Scholar] [CrossRef]
- Lu, X.; Liu, Z.; Ma, L.; Wang, L.; Zhou, K.; Feng, N. A robust optimization approach for optimal load dispatch of community energy hub. Appl. Energy 2020, 259, 114195. [Google Scholar] [CrossRef]
- Petkov, I.; Gabrielli, P.; Spokaite, M. The impact of urban district composition on storage technology reliance: Trade-offs between thermal storage, batteries, and power-to-hydrogen. Energy 2021, 224, 120102. [Google Scholar] [CrossRef]
- Cannata, N.; Cellura, M.; Longo, S.; Montana, F.; Sanseverino, E.R.; Luu, Q.L.; Nguyen, N.Q. Multi-objective optimization of urban microgrid energy supply according to economic and environmental criteria. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, Q.; Wen, J.; Lin, Z.; Fang, F.; Chen, Q. Optimal operation of integrated electricity and heat system: A review of modeling and solution methods. Renew. Sustain. Energy Rev. 2021, 135, 110098. [Google Scholar] [CrossRef]
- Ghanbari, A.; Karimi, H.; Jadid, S. Optimal planning and operation of multi-carrier networked microgrids considering multi-energy hubs in distribution networks. Energy 2020, 204, 117936. [Google Scholar] [CrossRef]
- Bidgoli, M.M.; Karimi, H.; Jadid, S.; Anvari-Moghaddam, A. Stochastic electrical and thermal energy management of energy hubs integrated with demand response programs and renewable energy: A prioritized multi-objective framework. Electr. Power Syst. Res. 2021, 196, 107183. [Google Scholar] [CrossRef]
- Chen, H.; Liu, M.; Liu, Y.; Lin, S.; Yang, Z. Partial surrogate cuts method for network-constrained optimal scheduling of multi-carrier energy systems with demand response. Energy 2020, 196, 117119. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, D.; Wang, S.; Wu, T. Standardized modelling and economic optimization of multi-carrier energy systems considering energy storage and demand response. Energy Convers. Manag. 2019, 182, 126–142. [Google Scholar] [CrossRef]
- Yong, W.; Wang, J.; Lu, Z.; Yang, F.; Zhang, Z.; Wei, J.; Wang, J. Day-ahead dispatch of multi-energy system considering operating conditions of multi-energy coupling equipment. Energy Rep. 2021, 7, 100–110. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, J.; Liu, B. Stochastic optimal dispatching strategy of electricity-hydrogen-gas-heat integrated energy system based on improved spectral clustering method. Int. J. Electr. Power Energy Syst. 2021, 126, 106495. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Ahmarinejad, A.; Javadi, M.S.; Catalão, J.P. Two-stage stochastic framework for energy hubs planning considering demand response programs. Energy 2020, 206, 118124. [Google Scholar] [CrossRef]
- Shams, M.H.; Shahabi, M.; MansourLakouraj, M.; Shafie-Khah, M.; Catalão, J.P. Adjustable robust optimization approach for two-stage operation of energy hub-based microgrids. Energy 2021, 222, 119894. [Google Scholar] [CrossRef]
- Shahrabi, E.; Hakimi, S.M.; Hasankhani, A.; Derakhshan, G.; Abdi, B. Developing optimal energy management of energy hub in the presence of stochastic renewable energy resources. Sustain. Energy Grids Netw. 2021, 26, 100428. [Google Scholar] [CrossRef]
- Nosratabadi, S.M.; Hemmati, R.; Gharaei, P.K. Optimal planning of multi-energy microgrid with different energy storages and demand responsive loads utilizing a technical-economic-environmental programming. Int. J. Energy Res. 2021, 45, 6985–7017. [Google Scholar] [CrossRef]
- Guo, X.; Bao, Z.; Yan, W. Stochastic model predictive control based scheduling optimization of multi-energy system considering hybrid CHPs and EVs. Appl. Sci. 2019, 9, 356. [Google Scholar] [CrossRef]
- Preston, N.; Maroufmashat, A.; Riaz, H.; Barbouti, S.; Mukherjee, U.; Tang, P.; Wang, J.; Haghi, E.; Elkamel, A.; Fowler, M. How can the integration of renewable energy and power-to-gas benefit industrial facilities? From techno-economic, policy, and environmental assessment. Int. J. Hydrog. Energy 2020, 45, 26559–26573. [Google Scholar] [CrossRef]
- Javadi, M.S.; Lotfi, M.; Nezhad, A.E.; Anvari-Moghaddam, A.; Guerrero, J.M.; Catalao, J.P.S. Optimal Operation of Energy Hubs Considering Uncertainties and Different Time Resolutions. IEEE Trans. Ind. Appl. 2020, 56, 5543–5552. [Google Scholar] [CrossRef]
- Hosseini, S.; Ahmarinejad, A. Stochastic framework for day-ahead scheduling of coordinated electricity and natural gas networks considering multiple downward energy hubs. J. Energy Storage 2021, 33, 102066. [Google Scholar] [CrossRef]
- Vahid-Ghavidel, M.; Javadi, M.S.; Gough, M.; Santos, S.F.; Shafie-Khah, M.; Catalão, J.P. Demand response programs in multi-energy systems: A review. Energies 2020, 13, 4332. [Google Scholar] [CrossRef]
- Ye, Y.; Qiu, D.; Wu, X.; Strbac, G.; Ward, J. Model-Free Real-Time Autonomous Control for a Residential Multi-Energy System Using Deep Reinforcement Learning. IEEE Trans. Smart Grid 2020, 11, 3068–3082. [Google Scholar] [CrossRef]
- Di Somma, M.; Yan, B.; Bianco, N.; Graditi, G.; Luh, P.; Mongibello, L.; Naso, V. Operation optimization of a distributed energy system considering energy costs and exergy efficiency. Energy Convers. Manag. 2015, 103, 739–751. [Google Scholar] [CrossRef]
- Di Somma, M.; Graditi, G.; Heydarian-Forushani, E.; Shafie-Khah, M.; Siano, P. Stochastic optimal scheduling of distributed energy resources with renewables considering economic and environmental aspects. Renew. Energy 2018, 116, 272–287. [Google Scholar] [CrossRef]
- Di Somma, M.; Yan, B.; Bianco, N.; Graditi, G.; Luh, P.; Mongibello, L.; Naso, V. Multi-objective design optimization of distributed energy systems through cost and exergy assessments. Appl. Energy 2017, 204, 1299–1316. [Google Scholar] [CrossRef]
- Di Somma, M.; Yan, B.; Bianco, N.; Luh, P.B.; Graditi, G.; Mongibello, L.; Naso, V. Multi-objective operation optimization of a Distributed Energy System for a large-scale utility customer. Appl. Therm. Eng. 2016, 101, 752–761. [Google Scholar] [CrossRef]
- Di Somma, M.; Caliano, M.; Graditi, G.; Pinnarelli, A.; Menniti, D.; Sorrentino, N.; Barone, G. Designing of Cost-Effective and Low-Carbon Multi-Energy Nanogrids for Residential Applications. Inventions 2020, 5, 7. [Google Scholar] [CrossRef]
- Foiadelli, F.; Nocerino, S.; Di Somma, M.; Graditi, G. Optimal Design of der for Economic/Environmental Sustainability of Local Energy Communities. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018. [Google Scholar] [CrossRef]
- Nasir, M.; Jordehi, A.R.; Matin, S.A.A.; Tabar, V.S.; Tostado-Véliz, M.; Mansouri, S.A. Optimal operation of energy hubs including parking lots for hydrogen vehicles and responsive demands. J. Energy Storage 2022, 50, 104630. [Google Scholar] [CrossRef]
- Majidi, M.; Zare, K. Integration of smart energy hubs in distribution networks under uncertainties and demand response concept. IEEE Trans. Power Syst. 2019, 34, 566–574. [Google Scholar] [CrossRef]
- Orehounig, K.; Evins, R.; Dorer, V. Integration of decentralized energy systems in neighbourhoods using the energy hub approach. Appl. Energy 2015, 154, 277–289. [Google Scholar] [CrossRef]
- Sousa, T.; Soares, T.; Pinson, P.; Moret, F.; Baroche, T.; Sorin, E. Peer-to-peer and community-based markets: A comprehensive review. Renew. Sustain. Energy Rev. 2019, 104, 367–378. [Google Scholar] [CrossRef]
- Khani, H.; Sawas, A.; Farag, H.E. An estimation–Based optimal scheduling model for settable renewable penetration level in energy hubs. Electr. Power Syst. Res. 2021, 196, 107230. [Google Scholar] [CrossRef]
- Cao, J.; Yang, B.; Zhu, S.; Ning, C.; Guan, X. Day-ahead chance-constrained energy management of energy hub: A distributionally robust approach. CSEE J. Power Energy Syst. 2021, 8, 812–825. [Google Scholar] [CrossRef]
- Jiang, A.; Yuan, H.; Li, D. A two-stage optimization approach on the decisions for prosumers and consumers within a community in the Peer-to-peer energy sharing trading. Int. J. Electr. Power Energy Syst. 2021, 125, 106527. [Google Scholar] [CrossRef]
- Heo, K.; Kong, J.; Oh, S.; Jung, J. Development of operator-oriented peer-to-peer energy trading model for integration into the existing distribution system. Int. J. Electr. Power Energy Syst. 2021, 125, 106488. [Google Scholar] [CrossRef]
- Tushar, W.; Yuen, C.; Saha, T.K.; Morstyn, T.; Chapman, A.C.; Alam, M.J.E.; Hanif, S.; Poor, H.V. Peer-to-peer energy systems for connected communities: A review of recent advances and emerging challenges. Appl. Energy 2021, 282, 116131. [Google Scholar] [CrossRef]
- Di Somma, M.; Ciabattoni, L.; Comodi, G.; Graditi, G. Managing plug-in electric vehicles in eco-environmental operation optimization of local multi-energy systems. Sustain. Energy Grids Netw. 2020, 23, 100376. [Google Scholar] [CrossRef]
- Di Somma, M.; Graditi, G.; Siano, P. Optimal Bidding Strategy for a DER Aggregator in the Day-Ahead Market in the Presence of Demand Flexibility. IEEE Trans. Ind. Electron. 2018, 66, 1509–1519. [Google Scholar] [CrossRef]
- Huang, H.; Nie, S.; Lin, J.; Wang, Y.; Dong, J. Optimization of peer-to-peer power trading in a microgrid with distributed PV and battery energy storage systems. Sustainability 2020, 12, 923. [Google Scholar] [CrossRef]
- Khorasany, M.; Najafi-Ghalelou, A.; Razzaghi, R.; Mohammadi-Ivatloo, B. Transactive energy framework for optimal energy management of multi-carrier energy hubs under local electrical, thermal, and cooling market constraints. Int. J. Electr. Power Energy Syst. 2021, 129, 106803. [Google Scholar] [CrossRef]
- Maroufmashat, A.; Sattari, S.; Roshandel, R.; Fowler, M.; Elkamel, A. Multi-objective Optimization for Design and Operation of Distributed Energy Systems through the Multi-energy Hub Network Approach. Ind. Eng. Chem. Res. 2016, 55, 8950–8966. [Google Scholar] [CrossRef]
- Petkov, I.; Gabrielli, P. Power-to-hydrogen as seasonal energy storage: An uncertainty analysis for optimal design of low-carbon multi-energy systems. Appl. Energy 2020, 274, 115197. [Google Scholar] [CrossRef]
- Rayati, M.; Sheikhi, A.; Ranjbar, A.M. Optimising operational cost of a smart energy hub, the reinforcement learning approach. Int. J. Parallel Emergent Distrib. Syst. 2015, 30, 325–341. [Google Scholar] [CrossRef]
- Sogabe, T.; Malla, B.; Hioki, T.; Takahashi, K. Multi-carrier energy hub management through deep deterministic policy gradient over continuous action space. In Proceedings of the 33rd Annual Conference of the Japanese Society for Artificial Intelligence, Niigata, Japan, 4–7 June 2019; pp. 3–6. [Google Scholar] [CrossRef]
- Buoro, D.; Casisi, M.; De Nardi, A.; Pinamonti, P.; Reini, M. Multicriteria optimization of a distributed energy supply system for an industrial area. Energy 2013, 58, 128–137. [Google Scholar] [CrossRef]
- Comodi, G.; Giantomassi, A.; Severini, M.; Squartini, S.; Ferracuti, F.; Fonti, A.; Cesarini, D.N.; Morodo, M.; Polonara, F. Multi-apartment residential microgrid with electrical and thermal storage devices: Experimental analysis and simulation of energy management strategies. Appl. Energy 2015, 137, 854–866. [Google Scholar] [CrossRef]
- Zou, H.; Tao, J.; Elsayed, S.K.; Elattar, E.E.; Almalaq, A.; Mohamed, M.A. Stochastic multi-carrier energy management in the smart islands using reinforcement learning and unscented transform. Int. J. Electr. Power Energy Syst. 2021, 130, 106988. [Google Scholar] [CrossRef]
- Wang, S.; Taha, A.F.; Wang, J.; Kvaternik, K.; Hahn, A. Energy Crowdsourcing and Peer-to-Peer Energy Trading in Blockchain-Enabled Smart Grids. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1612–1623. [Google Scholar] [CrossRef]
- Alvarado, D.C.; Acha, S.; Shah, N.; Markides, C.N. A Technology Selection and Operation (TSO) optimisation model for distributed energy systems: Mathematical formulation and case study. Appl. Energy 2016, 180, 491–503. [Google Scholar] [CrossRef]
- Murty, V.V.S.N.; Kumar, A. Multi-objective energy management in microgrids with hybrid energy sources and battery energy storage systems. Prot. Control Mod. Power Syst. 2020, 5, 2. [Google Scholar] [CrossRef]
- Mashayekh, S.; Stadler, M.; Cardoso, G.; Heleno, M. A mixed integer linear programming approach for optimal DER portfolio, sizing, and placement in multi-energy microgrids. Appl. Energy 2017, 187, 154–168. [Google Scholar] [CrossRef]
- Liu, J.; Xu, Z.; Wu, J.; Liu, K.; Guan, X. Optimal planning of distributed hydrogen-based multi-energy systems. Appl. Energy 2021, 281, 116107. [Google Scholar] [CrossRef]
- Ren, H.; Zhou, W.; Nakagami, K.; Gao, W.; Wu, Q. Multi-objective optimization for the operation of distributed energy systems considering economic and environmental aspects. Appl. Energy 2010, 87, 3642–3651. [Google Scholar] [CrossRef]
- Alabi, T.M.; Lu, L.; Yang, Z. A novel multi-objective stochastic risk co-optimization model of a zero-carbon multi-energy system (ZCMES) incorporating energy storage aging model and integrated demand response. Energy 2021, 226, 120258. [Google Scholar] [CrossRef]
- Gabrielli, P.; Gazzani, M.; Martelli, E.; Mazzotti, M. Optimal design of multi-energy systems with seasonal storage. Appl. Energy 2018, 219, 408–424, Correction in Appl. Energy 2018, 212, 720. [Google Scholar] [CrossRef]
- Heendeniya, C.B.; Sumper, A.; Eicker, U. The multi-energy system co-planning of nearly zero-energy districts – Status-quo and future research potential. Appl. Energy 2020, 267, 114953. [Google Scholar] [CrossRef]
- Jordehi, A.R.; Javadi, M.S.; Shafie-Khah, M.; Catalão, J.P. Information gap decision theory (IGDT)-based robust scheduling of combined cooling, heat and power energy hubs. Energy 2021, 231, 120918. [Google Scholar] [CrossRef]
- Ma, T.; Wu, J.; Hao, L. Energy flow modeling and optimal operation analysis of the micro energy grid based on energy hub. Energy Convers. Manag. 2017, 133, 292–306. [Google Scholar] [CrossRef]
- Maroufmashat, A.; Taqvi, S.T.; Miragha, A.; Fowler, M.; Elkamel, A. Modeling and optimization of energy hubs: A comprehensive review. Inventions 2019, 4, 50. [Google Scholar] [CrossRef]
- Roberts, J.J.; Cassula, A.M.; Silveira, J.L.; Bortoni, E.D.C.; Mendiburu, A.Z. Robust multi-objective optimization of a renewable based hybrid power system. Appl. Energy 2018, 223, 52–68. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, Y.; Song, F.; Ma, Y.; Qi, C.; Huang, F.; Xing, J.; Zhang, F. Economic and efficient multi-objective operation optimization of integrated energy system considering electro-thermal demand response. Energy 2020, 205, 118022. [Google Scholar] [CrossRef]
- Yan, R.; Wang, J.; Lu, S.; Ma, Z.; Zhou, Y.; Zhang, L.; Cheng, Y. Multi-objective two-stage adaptive robust planning method for an integrated energy system considering load uncertainty. Energy Build. 2021, 235, 110741. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Asadi, S. Optimal operation of multi-carrier energy networks with gas, power, heating, and water energy sources considering different energy storage technologies. J. Energy Storage 2020, 31, 101574. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, J.; Long, C. Evaluation of peer-to-peer energy sharing mechanisms based on a multiagent simulation framework. Appl. Energy 2018, 222, 993–1022. [Google Scholar] [CrossRef]
- Salehi, J.; Namvar, A.; Gazijahani, F.S. Scenario-based Co-Optimization of neighboring multi carrier smart buildings under demand response exchange. J. Clean. Prod. 2019, 235, 1483–1498. [Google Scholar] [CrossRef]
- Motevasel, M.; Seifi, A.R.; Niknam, T. Multi-objective energy management of CHP (combined heat and power)-based micro-grid. Energy 2013, 51, 123–136. [Google Scholar] [CrossRef]
- Li, P.; Guo, T.; Abeysekera, M.; Wu, J.; Han, Z.; Wang, Z.; Yin, Y.; Zhou, F. Intraday multi-objective hierarchical coordinated operation of a multi-energy system. Energy 2021, 228, 120528. [Google Scholar] [CrossRef]
- Karmellos, M.; Georgiou, P.; Mavrotas, G. A comparison of methods for the optimal design of Distributed Energy Systems under uncertainty. Energy 2019, 178, 318–333. [Google Scholar] [CrossRef]
- Rieder, A.; Christidis, A.; Tsatsaronis, G. Multi criteria dynamic design optimization of a small scale distributed energy system. Energy 2014, 74, 230–239. [Google Scholar] [CrossRef]
- Bollenbacher, J.; Rhein, B. Optimal configuration and control strategy in a multi-carrier-energy system using reinforcement learning methods. In Proceedings of the 2017 International Energy and Sustainability Conference, Farmingdale, NY, USA, 19–20 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Pakdel, M.J.V.; Sohrabi, F.; Mohammadi-Ivatloo, B. Multi-objective optimization of energy and water management in networked hubs considering transactive energy. J. Clean. Prod. 2020, 266, 121936. [Google Scholar] [CrossRef]
- Bartolini, A.; Carducci, F.; Muñoz, C.B.; Comodi, G. Energy storage and multi energy systems in local energy communities with high renewable energy penetration. Renew. Energy 2020, 159, 595–609. [Google Scholar] [CrossRef]
- Çiçek, A.; Şengör, I.; Erenoğlu, A.K.; Erdinç, O. Decision making mechanism for a smart neighborhood fed by multi-energy systems considering demand response. Energy 2020, 208, 118323. [Google Scholar] [CrossRef]
- Cui, S.; Wang, Y.-W.; Xiao, J.-W. Peer-to-peer energy sharing among smart energy buildings by distributed transaction. IEEE Trans. Smart Grid 2019, 10, 6491–6501. [Google Scholar] [CrossRef]
- Liu, N.; Yu, X.; Wang, C.; Li, C.; Ma, L.; Lei, J. Energy-Sharing Model with Price-Based Demand Response for Microgrids of Peer-to-Peer Prosumers. IEEE Trans. Power Syst. 2017, 32, 3569–3583. [Google Scholar] [CrossRef]
- Roberto, R.; De Iulio, R.; Di Somma, M.; Graditi, G.; Guidi, G.; Noussan, M. A multi-objective optimization analysis to assess the potential economic and environmental benefits of distributed storage in district heating networks: A case study. Int. J. Sustain. Energy Plan. Manag. 2019, 20, 5–20. [Google Scholar] [CrossRef]
- Wu, T.; Bu, S.; Wei, X.; Wang, G.; Zhou, B. Multitasking multi-objective operation optimization of integrated energy system considering biogas-solar-wind renewables. Energy Convers. Manag. 2021, 229, 113736. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, L.; Chhabra, P.; Garud, S.S.; Aditya, K.; Romagnoli, A.; Comodi, G.; Magro, F.D.; Meneghetti, A.; Kraft, M. A novel methodology for the design of waste heat recovery network in eco-industrial park using techno-economic analysis and multi-objective optimization. Appl. Energy 2016, 184, 88–102. [Google Scholar] [CrossRef]
- Shabanpour-Haghighi, A.; Seifi, A.R. Multi-objective operation management of a multi-carrier energy system. Energy 2015, 88, 430–442. [Google Scholar] [CrossRef]
- Geidl, M.; Andersson, G. Operational and structural optimization of multi-carrier energy systems. Eur. Trans. Electr. Power 2006, 16, 463–477. [Google Scholar] [CrossRef]
- Fonseca, M.N.; Pamplona, E.D.O.; de Queiroz, A.R.; Valerio, V.E.D.M.; Aquila, G.; Silva, S.R. Multi-objective optimization applied for designing hybrid power generation systems in isolated networks. Sol. Energy 2018, 161, 207–219. [Google Scholar] [CrossRef]
- Bjarghov, S.; Loschenbrand, M.; Ibn Saif, A.U.N.; Pedrero, R.A.; Pfeiffer, C.; Khadem, S.K.; Rabelhofer, M.; Revheim, F.; Farahmand, H. Developments and Challenges in Local Electricity Markets: A Comprehensive Review. IEEE Access 2021, 9, 58910–58943. [Google Scholar] [CrossRef]
- Sadeghi, H.; Rashidinejad, M.; Moeini-Aghtaie, M.; Abdollahi, A. The energy hub: An extensive survey on the state-of-the-art. Appl. Therm. Eng. 2019, 161, 114071. [Google Scholar] [CrossRef]
- Li, L.; Mu, H.; Li, N.; Li, M. Economic and environmental optimization for distributed energy resource systems coupled with district energy networks. Energy 2016, 109, 947–960. [Google Scholar] [CrossRef]
- Xu, D.; Wu, Q.; Zhou, B.; Li, C.; Bai, L.; Huang, S. Distributed Multi-Energy Operation of Coupled Electricity, Heating, and Natural Gas Networks. IEEE Trans. Sustain. Energy 2019, 11, 2457–2469. [Google Scholar] [CrossRef]
- Dan, M.; Srinivasan, S.; Sundaram, S.; Easwaran, A.; Glielmo, L. A Scenario-Based Branch-and-Bound Approach for MES Scheduling in Urban Buildings. IEEE Trans. Ind. Inform. 2020, 16, 7510–7520. [Google Scholar] [CrossRef]
- Fazlollahi, S.; Mandel, P.; Becker, G.; Maréchal, F. Methods for multi-objective investment and operating optimization of complex energy systems. Energy 2012, 45, 12–22. [Google Scholar] [CrossRef]
- Najafi-Ghalelou, A.; Nojavan, S.; Zare, K.; Mohammadi-Ivatloo, B. Robust scheduling of thermal, cooling and electrical hub energy system under market price uncertainty. Appl. Therm. Eng. 2019, 149, 862–880. [Google Scholar] [CrossRef]
- Gong, D.-W.; Zhang, Y.; Qi, C.-L. Environmental/economic power dispatch using a hybrid multi-objective optimization algorithm. Int. J. Electr. Power Energy Syst. 2010, 32, 607–614. [Google Scholar] [CrossRef]
- Alarcon-Rodriguez, A.; Ault, G.; Galloway, S. Multi-objective planning of distributed energy resources: A review of the state-of-the-art. Renew. Sustain. Energy Rev. 2010, 14, 1353–1366. [Google Scholar] [CrossRef]
- Shabanpour-Haghighi, A.; Seifi, A.R. Energy Flow Optimization in Multicarrier Systems. IEEE Trans. Ind. Inform. 2015, 11, 1067–1077. [Google Scholar] [CrossRef]
- Shabanpour-Haghighi, A.; Seifi, A.R.; Niknam, T. A modified teaching–learning based optimization for multi-objective optimal power flow problem. Energy Convers. Manag. 2014, 77, 597–607. [Google Scholar] [CrossRef]
- Moeini-Aghtaie, M.; Abbaspour, A.; Fotuhi-Firuzabad, M.; Hajipour, E. A decomposed solution to multiple-energy carriers optimal power flow. IEEE Trans. Power Syst. 2013, 29, 707–716. [Google Scholar] [CrossRef]
- Cesena, E.A.M.; Mancarella, P. Energy Systems Integration in Smart Districts: Robust Optimisation of Multi-Energy Flows in Integrated Electricity, Heat and Gas Networks. IEEE Trans. Smart Grid 2018, 10, 1122–1131. [Google Scholar] [CrossRef]
- Nicholson, M. Smart Grids. In The Power Makers’ Challenge; Springer: Berlin/Heidelberg, Germany, 2012; pp. 119–121. [Google Scholar] [CrossRef]
- Ghorab, M. Energy hubs optimization for smart energy network system to minimize economic and environmental impact at Canadian community. Appl. Therm. Eng. 2019, 151, 214–230. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, Q.; Cheng, W.; Nojavan, S.; Jermsittiparsert, K. Risk-constrained optimal operation of fuel cell/photovoltaic/battery/grid hybrid energy system using downside risk constraints method. Int. J. Hydrogen Energy 2020, 45, 14108–14118. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, N.; Zhuo, Z.; Kang, C.; Kirschen, D. Mixed-integer linear programming-based optimal configuration planning for energy hub: Starting from scratch. Appl. Energy 2018, 210, 1141–1150. [Google Scholar] [CrossRef]
- Turk, A.; Wu, Q.; Zhang, M.; Østergaard, J. Day-ahead stochastic scheduling of integrated multi-energy system for flexibility synergy and uncertainty balancing. Energy 2020, 196, 117130. [Google Scholar] [CrossRef]
- Ma, T.; Wu, J.; Hao, L.; Lee, W.-J.; Yan, H.; Li, D. The optimal structure planning and energy management strategies of smart multi energy systems. Energy 2018, 160, 122–141. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, N.; Yang, J.; Wang, Y.; Kang, C. Optimal configuration planning of multi-energy systems considering distributed renewable energy. IEEE Trans. Smart Grid 2017, 10, 1452–1464. [Google Scholar] [CrossRef]
- Qiu, Z.; Wang, B.; Huang, J.; Xie, Z. Optimal configuration and sizing of regional energy service company’s energy hub with integrated demand response. IEEJ Trans. Electr. Electron. Eng. 2019, 14, 383–393. [Google Scholar] [CrossRef]
- Pan, G.; Gu, W.; Wu, Z.; Lu, Y.; Lu, S. Optimal design and operation of multi-energy system with load aggregator considering nodal energy prices. Appl. Energy 2019, 239, 280–295. [Google Scholar] [CrossRef]
- Comodi, G.; Bartolini, A.; Carducci, F.; Nagaranjan, B.; Romagnoli, A. Achieving low carbon local energy communities in hot climates by exploiting networks synergies in multi energy systems. Appl. Energy 2019, 256, 113901. [Google Scholar] [CrossRef]
- Capone, M.; Guelpa, E.; Verda, V. Multi-objective optimization of district energy systems with demand response. Energy 2021, 227, 120472. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Shu, S.; Zheng, F.; Huang, Z. A data-driven distributionally robust optimization model for multi-energy coupled system considering the temporal-spatial correlation and distribution uncertainty of renewable energy sources. Energy 2020, 216, 119171. [Google Scholar] [CrossRef]
- Grond, M.O.W.; Luong, N.H.; Morren, J.; Slootweg, J.G. Multi-objective optimization techniques and applications in electric power systems. In Proceedings of the 2012 47th International Universities Power Engineering Conference (UPEC), Uxbridge, UK, 4–7 September 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; De Masi, R.F.; De Stasio, C.; Mauro, G.M.; Vanoli, G.P. Multi-objective optimization of the renewable energy mix for a building. Appl. Therm. Eng. 2016, 101, 612–621. [Google Scholar] [CrossRef]
- Arteconi, A.; Ciarrocchi, E.; Pan, Q.; Carducci, F.; Comodi, G.; Polonara, F.; Wang, R. Thermal energy storage coupled with PV panels for demand side management of industrial building cooling loads. Appl. Energy 2017, 185, 1984–1993. [Google Scholar] [CrossRef]
- Good, N.; Karangelos, E.; Navarro-Espinosa, A.; Mancarella, P. Optimization Under Uncertainty of Thermal Storage-Based Flexible Demand Response With Quantification of Residential Users’ Discomfort. IEEE Trans. Smart Grid 2015, 6, 2333–2342. [Google Scholar] [CrossRef]
- Cesena, E.A.M.; Loukarakis, E.; Good, N.; Mancarella, P. Integrated Electricity– Heat–Gas Systems: Techno–Economic Modeling, Optimization, and Application to Multienergy Districts. Proc. IEEE 2020, 108, 1392–1410. [Google Scholar] [CrossRef]
- Coelho, A.; Iria, J.; Soares, F.; Lopes, J.P. Real-time management of distributed multi-energy resources in multi-energy networks. In Sustainable Energy, Grids and Networks; Elsevier: Amsterdam, The Netherlands, 2023; Volume 34, p. 101022. [Google Scholar] [CrossRef]
- Coelho, A.; Iria, J.; Soares, F. Network-secure bidding optimization of aggregators of multi-energy systems in electricity, gas, and carbon markets. Appl. Energy 2021, 301, 117460. [Google Scholar] [CrossRef]
- Mancarella, P.; Chicco, G.; Capuder, T. Arbitrage opportunities for distributed multi-energy systems in providing power system ancillary services. Energy 2018, 161, 381–395. [Google Scholar] [CrossRef]
- Li, J.; Ge, S.; Xu, Z.; Liu, H.; Li, J.; Wang, C.; Cheng, X. A network-secure peer-to-peer trading framework for electricity-carbon integrated market among local prosumers. Appl. Energy 2023, 335, 120420. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).