Optimal Allocation and Size of Renewable Energy Sources as Distributed Generations Using Shark Optimization Algorithm in Radial Distribution Systems

Abstract

The need for energy has significantly increased in the world in recent years. Various research works were presented to develop Renewable Energy Sources (RESs) as green energy Distributed Generations (DGs) to satisfy this demand. In addition, alleviating environmental problems caused by utilizing conventional power plants is diminished by these renewable sources. The optimal location and size of the DG-RESs significantly affect the performance of Radial Distribution Systems (RDSs) through the fine bus voltage profile, senior power quality, low power losses, and high efficiency. This paper investigates the use of PV (photovoltaic) and (Wind Turbine) WT systems as a DG source in RDSs. This investigation is presented via the optimal location and size of the PV and WT systems, which are the most used DG sources. This optimization problem aims to maximize system efficiency by minimizing power losses and improving both voltage profile and power quality using White Shark Optimization (WSO). This algorithm emulates the attitude of great white sharks when foraging using their senses of hearing and smell. It confirms the balance between exploration and exploitation to discover optimization that is considered as the main advantage of this approach in attaining the global minimum. To assess the suggested approach, three common RDSs are utilized, namely, IEEE 33, 69, and 85 node systems. The results prove that the applied WSO approach can find the best location and size of the RESs to reduce power loss, ameliorate the voltage profile, and outlast other recent strategies. Adding more units provides a high percentage of reducing losses by at least 93.52% in case of WTs, rather than 52.267% in the case of PVs. Additionally, the annual saving increased to USD 74,371.97, USD 82,127.257, and USD 86,731.16 with PV penetration, while it reached USD 104,872.96, USD 116,136.57, and USD 155,184.893 with WT penetration for the 33, 69, and 85 nodes, respectively. In addition, a considerable enhancement in the voltage profiles with the growth of PV and WT units was confirmed. The ability of the suggested WSO for feasible implementation was validated and inspected by preserving the restrictions and working constraints.

1. Introduction

Owing to being the cheapest and easiest to construct, radial distributed systems (RDSs) are frequently employed in sparsely populated areas. In these systems, a single power source provides electricity to many customers; yet, they have several drawbacks [1]. One of these disadvantages is that a power outage, short circuit, or damaged power line will cut off energy to the entire line and that power cannot be restored until it is rectified. Another drawback is the increasing power losses that would reduce the efficiency, which has a detrimental effect on the economy [2].

Using compensators is one of the primary remedies for these disadvantages [1,2,3,4]. Many compensators are used in RDSs to ameliorate voltage profile, improve power quality, reduce power loss, and increase the reserve of generation [3,4]. The principle of operation for these compensators is to support the reactive power of the system. Inserting some distributed generations (DGs), especially those that are based on renewable energy sources (RESs), is another important approach. DGs are distributed, flexible, and more adaptable technologies that are positioned near the load. They reduce the power transmitted through the transmission lines, which results in a reduction in the amount of power lost in the transmission lines and an increase in efficiency. One of the primary benefits of adopting DG-RESs is to provide customers with reliable, cost-effective, and environmentally friendly power [5].

RESs’ integration into the electrical grid has emerged as a critical remedy for the increasing load demand as well as environmental concerns. Many RESs were incorporated into the electrical grid, including Solar PV, wind, and fuel cells [6]. Using RESs as DG benefits the functioning of the electricity system in three ways: environmentally, economically, and technically [7,8]. Additionally, the quality of the distribution power systems may be improved by installing RESs in the appropriate place with a sufficient capacity, which can boost the voltage profile and reduce network power losses [8,9,10,11].

Studies have shown that integrating DGs in improper locations and with good sizes might cause a reverse flow of power toward the distribution substation. The system may experience overloads as a result, increasing system losses [12]. Several studies in this area have recently concentrated on proposing an optimal location and size of DG implantation methods. These studies focused on proposing an approach for selecting the optimal size of the DG in distribution systems, for example, novel power stability indexes [13], lowest voltage buses [14], most sensitive buses [15], and solving multi-objective functions [16]. Most of these works used some optimization techniques to solve the optimal location and size issues for DGs. Genetic Algorithm [17], Particle Swarm Optimization [18,19], Modified Bacterial Foraging Optimization [20], Bat Approach [21], Invasive Weed Optimization [22], Water Cycle Algorithm [23], Ant Colony Algorithm [24,25], Modified Teaching–Learning-based Optimization Algorithm [26], Hybrid Big Bang–Big Crunch Approach [27], Gray Wolf Optimization [28], Cuckoo Search Algorithm [29,30,31], Heuristic Methods [32], Chaotic Symbiotic Organisms Search Algorithm [33], and Marine Predators Optimizer [34] were introduced to deal with the DG placement process. Using three typical radial systems, IEEE 33 [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51], 69 [52,53,54,55,56,57,58,59,60,61], and 85 [62,63,64,65] systems, these studies attempted to identify the optimum position and size of DGs in RDSs taking voltage support and minimal power losses into consideration. These studies were successful in determining the ideal position and size, while taking into consideration the voltage level and power losses. The option still exists to address this optimization problem using more recent optimization methods than those described in [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65]. As a result, the current work presents a novel optimization approach for figuring out the best placement and size of DGs in RDSs, while taking into account reducing net losses and enhancing voltage profiles under all requirements and limitations for the optimization assignment. This new optimization approach is called White Shark Optimizer (WSO) [66,67].

WSO is one of the most recent nature-inspired algorithms that emulates the successful behavior of white sharks when foraging in the depths of the ocean to survive while depending on their senses of smell and hearing [68]. WSO has distinct advantages for optimization tasks, such as flexibility in dealing with various types of problems, simplicity, robustness, speed, and accuracy to find solutions [69]. It confirms its supremacy in various fields, which are addressed in [70,71,72,73]. The optimization of RESs via WSO has not been believed yet. This motivates us to promote WSO to handle this task. It is applied to detect the optimum allocations and capacity of DG in RDSs. The results of the WSO are compared with distinct algorithms to discover its notability in resolving the process of optimum allocations and the capacity of DGs, thus lowering the real power losses and attenuating the voltage profiles.

The contributions of this article are as follows:

• The most advisable values of the weight factors of the developed objective function are discovered.
• WSO as a successful optimization tool to handle the issue of the optimum position and size of PVs and WTs in RDSs is adopted to reduce power losses and reinforce the system voltage profile.
• The economic charge is examined to find the power losses and net savings after placing the DGs in the standard IEEE 33, 69, and 85 point systems. Moreover, the voltage stability index (VSI) is inspected for all RDSs.
• The sensibleness of the method for real implementation has been validated and investigated by calculation of the losses and voltage profile before and after installing the DG strategy with achieving the restrictions and working constraints.

This article is arranged as follows: the suggested WSO is discussed in Section 2; then, the developed objective function is addressed in Section 3; the outcomes and discussion are developed in Section 4, and finally, Section 5 presents the conclusion.

2. White Shark Optimizer

This section explains the proposed WSO mathematical models for foraging and prey-tracking. Although the senior white shark can mark prey in the depths of the ocean, there is no understanding of the position of the food resource in a specific investigation.

2.1. Inspiration

The WSO algorithm simulates the dynamic attitude of white sharks as they possess many intrinsic features. White sharks are among the most adaptable predators as they are distinguished hunters with powerful muscles, amazing eyesight, well-contrasted vision with a strong sense of smell, giant jaws, and sharp, pointed teeth. The shark ambushes its prey and tries to dash its prey using sudden and powerful deadly blows. Great white sharks adopt collective behavior when hunting prey using their distinct swimming methods and senses, such as smelling the odor of their prey and good hearing.

2.2. Track Victim

White sharks, similar to any living creature, roam the ocean looking for prey and change their positions according to the location of their prey using all their senses to track and locate them. Figure 1 shows some of their combined and integrated senses.

Figure 1. Various white shark’s senses.

First, great white sharks possess an amazing sense of hearing that they utilize to explore large spaces when looking for prey using their strong sense of smell to scout the whole zone and every potential location of the victim [66,67,68,69,70].

2.3. Exploration

Great white sharks use their unfamiliar sense of hearing to search for prey in large areas, as they hear through the two sidelines along their bodies. These duo lines may distinguish any variations in the water pressure as evidence of the prey’s movements. The water pressure changes caused by the turbulence created by prey attract the sharks’ attention to swim towards it. Sharks possess organs that detect the tiny electromagnetic fields generated by the locomotion of prey taking into account the speed and drift of the waves during their turbulent movements, so they can accurately detect the site of the prey in addition to its size. Then, the shark moves towards the prey in an undulating movement that can be represented by the following arithmetical formulation [66]:

$$v=x\cdot f$$

(1)

where $v$ is the wave motion speed, $x$ is the wavelength that indicates the distance covered in an undulating motion that a white shark travels to complete a whole revolution, and $f$ symbolizes the frequency of the wave activity that equals the inverse of the number of revolutions per second.

2.4. Exploitation

Great white sharks use their strong sense of smell to explore possible places in their field to find prey, and when the white shark approaches its victim, its sense of smell functions in an exceptional manner. When the shark approaches, its sense of smell develops exponentially to precisely determine the location of its prey; the following constant acceleration motion equation may be employed [66]:

$$x=x_i+v_i\Delta t+\frac{1}{2}a{(\Delta t)}^2$$

(2)

where $x$ is the updated white shark location, $x_i$ is the initial location, $v_i$ is the premier velocity, $\Delta t$ is the time interval between the new and initial white shark locations, and $a$ is a fixed acceleration factor.

Most prey leave behind their scent after leaving a location; therefore, great white sharks cannot find their prey when this smell is present. They must randomly search nearby and distant areas using their distinct senses, such as sight, hearing, and smell [70,71,72,73].

2.5. Algorithm Steps

White sharks must search the ocean depths on a large scale to locate their prey using three behaviors:

(1) Their activity toward their prey depends on the frequency of the waves that occur due to the turbulent motion caused by the prey, taking advantage of the senses of hearing and smell.

(2) Randomly seeking prey in the depths of the ocean, where great white sharks’ move toward the location of prey while remaining close to it.

(3) The attitude of the white shark in determining the nearest prey.

The great white shark employs a school-fish attitude and moves toward the closest ideal prey.

2.6. Initialization of WSO

The approach starts by assuming a random set of initial solutions at the beginning of the used optimization process as a population-based approach. The population size of $n$ white sharks where each white shark location indicates an elected solution is expressed by Equation (3) [66]:

$$\omega =\left[\begin{array}{ccccc}{\omega }_1^1& {\omega }_2^1& \cdots & \cdots & {\omega }_d^1\\ {\omega }_1^2& {\omega }_2^2& \cdots & \cdots & {\omega }_d^2\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ {\omega }_1^n& {\omega }_2^n& \cdots & \cdots & {\omega }_d^n\end{array}\right]$$

(3)

where $\omega$ represents the site of white sharks in the inspection area, $d$ defines a variable number for the process, and ${\omega }_d^i$ assigns the site of the $i^{th}$ white shark in the $d^{th}$ dimension. The premier population is determined by the following equation [72]:

$${\omega }_j^i=l_j+r\times (u_j-l_j)$$

(4)

where ${\omega }_j^i$ is the $i^{th}$ white shark in $j^{th}$, $u_j$ and $l_j$ symbolize the superior and minimal limits of the inspection area in the $j^{th}$ size, and $r$ is a random value in [0–1].

The benefit of every elected solution for every novel white shark position was evaluated based on the fitness charge function. If the location was better than the current one, the current location was renewed, unless the white shark stayed in its location.

2.7. Movement Speed toward Prey

The survival instinct of white sharks makes them spend most of their time tracking and hunting prey using all methods of hunting based on their unusual senses, such as hearing, sight, and smell. The white shark locates its prey based on the frequency of the waves caused by the prey while moving; the white shark exhibits an undulating movement towards the prey represented by the following formula [72]:

$$v_{k+1}^i=\mu \left[v_k^i+p_1\left({\omega }_{gbes{t}_k}-{\omega }_k^i\right)\times c_1+p_2\left({\omega }_{best}^{v_k^i}-{\omega }_k^i\right)\times c_2\right]$$

(5)

where $i=1,2,\dots ..,n,$ is the index of white sharks for $n$ populations, $v_{k+1}^i$ is the $i^{th}$ white shark’s new speed vector in the ${(k+1)}^{th}$ step, $v_k^i$ is the $i^{th}$ white shark’s actual speed vector in the $k^{th}$ step, ${\omega }_{gbes{t}_k}$ is the comprehensive best location vector observed at a great distance by any white shark in the $k^{th}$ generation, ${\omega }_k^i$ is the $i^{th}$ white shark’s actual location vector in the $k^{th}$ step, ${\omega }_{best}^{v_k^i}$ is the $i^{th}$ best discovered location vector marked for the herd, and $v_i$ is the $i^{th}$ index vector of the white sharks with a superior location, as in Equation (6), where $c_1$ and $c_2$ are regularly random values with the domain [0–1]; $p_1$ and $p_2$ are the white shark’s values that control ${\omega }_{gbes{t}_k}$ and ${\omega }_{best}^{v_k^i}$, as shown in Equations (7) and (8), $\mu$ is the shrinkage agent used to analyze the white shark’s convergence attitude, as in Equation (9).

$$v=\left[n\times rand(1,n)\right]+1$$

(6)

where $rand(1,n)$ is a regularly random vector with the domain [0–1].

$$p_1=p_{max}+(p_{max}-p_{min})\times e^{-{(4k/K)}^2}$$

(7)

$$p_2=p_{min}+(p_{max}-p_{min})\times e^{-{(4k/K)}^2}$$

(8)

where $k$ and $K$ are the instant and supreme generations, respectively, $p_{min}$ and $p_{max}$ are the initial and dependent velocities for the perfect movements of the white sharks. The amounts of $p_{min}$ and $p_{max}$ are set as 0.5 and 1.5, respectively [72].

$$\mu =\frac{2}{\left|2-\tau -\sqrt{{\tau }^2-4\tau }\right|}$$

(9)

where $\tau$ is the acceleration value that is set to be 4.125 [72].

2.8. Movement toward Optimum Kill

Great white sharks spend a great amount of their time locating their prey, and when the motion of the waves is caused by their prey or if they smell it, they head towards it; however, in some cases, the prey vacates its site, leaving behinds its smell, and then the white shark moves randomly, according to the following formula [72,73]:

$${\omega }_{k+1}^i=\{\begin{array}{c}{\omega }_k^i\cdot \neg \oplus {\omega }_o+u\cdot a+l\cdot b; rand<mv\\ {\omega }_k^i+v_k^i/f; rand\ge mv\end{array}$$

(10)

where ${\omega }_{k+1}^i$ is the new vector location of the $i^{th}$ white shark in the ${(k+1)}^{th}$ generation, $\neg$ is a negation operator, and $a$ and $b$ are presented in Equations (11) and (12) as one-dimensional binary vectors. $l$ and $u$ are the minimum and maximum limits of the search era. ${\omega }_o$ is defined as a logical vector, as presented by Equation (13). $\oplus$ is a bitwise XOR operation. The frequency of the wave movement $f$ is defined by Equation (14). $rand$ is a random value with the domain [0–1]; $mv$ is the motion force that increases with iterations and is defined by Equation (15) [72].

$$a=sgn({\omega }_k^i-u)>0$$

(11)

$$b=sgn({\omega }_k^i-l)>0$$

(12)

$${\omega }_o=\oplus (a,b)$$

(13)

$$f=f_{min}+\frac{f_{max}-f_{min}}{f_{max}+f_{min}}$$

(14)

where $f_{min}$ and $f_{max}$ are the lower and superior frequencies of the wave movement, and are taken as 0.07 and 0.75, respectively, after testing [72,73].

$$mv=\frac{1}{\left(a_0+e^{(K/2-k)/a_1}\right)}$$

(15)

where $a_0$ and $a_1$ are positive values that represent the exploration and exploitation of nature [72].

2.9. Motion toward the Great White Shark

A great white shark’s location close to its prey is evaluated by the following equation [66]:

$${{\omega }^{\prime }}_{k+1}^i={\omega }_{gbes{t}_k}+r_1{\overrightarrow{D}}_{\omega }sgn(r_2-0.5) r_3<S_s$$

(16)

where ${{\omega }^{\prime }}_{k+1}^i$ is the new $i^{th}$ white shark’s location regarding the prey, $sgn(r_2-0.5)$ indicates either 1 or −1 for the search direction, the parameters $r_1,r_2,\mathrm{and}{r}_3$ are random values that fill in [0, 1], ${\overrightarrow{D}}_{\omega }$ is the distance between white shark and its prey and is presented in Equation (17), and $S_s$ indicates the strength of the senses of sight and smell, which are realized as displayed in Equation (18) [72,73].

$${\overrightarrow{D}}_{\omega }=\left|rand\times \left({\omega }_{gbes{t}_k}-{\omega }_k^i\right)\right|$$

(17)

where ${\omega }_k^i$ is the white shark’s current location regarding ${\omega }_{gbes{t}_k}$.

$$S_s=\left|1-e^{(-a_2\times k/K)}\right|$$

(18)

where $a_2$ is a positive value that represents the exploration and exploitation factors and is taken as 0.0005 [72].

2.10. Fish-School Attitude

To imitate the nature of the school of white sharks, the first two optimal resolutions were maintained, and then the location of the other white sharks was updated regarding the best locations, according to the following formula [66]:

$${\omega }_{k+1}^i=\frac{{\omega }_k^i+{{\omega }^{\prime }}_{k+1}^i}{2\times rand}$$

(19)

Equation (19) shows that white sharks position themselves in accordance with the best site, very close to the prey. The great white sharks reach their location and thus the best position of the great white sharks is somewhere within the investigation zone, very close to the optimum prey. The flowchart of the WSO is shown in Figure 2.

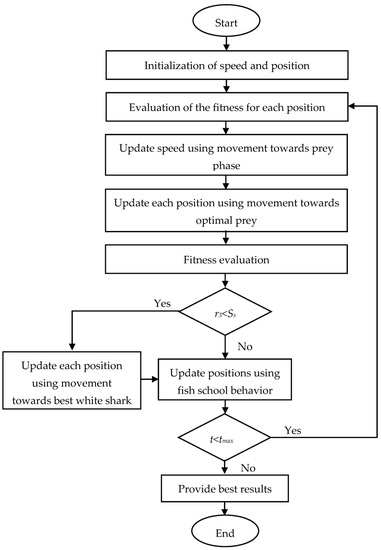
Figure 2. Flowchart of WSO.

3. Objective Charge Function

The developed objective charge function was exercised to reduce the power losses and to improve the voltage profiles and VSIs. The DG sites and their capacities can be found optimally by resolving the subsequent objective charge function [10]:

$$F_t=w_1\cdot o{f}_1+w_2\cdot o{f}_2+w_3\cdot o{f}_3$$

(20)

where $o{f}_1$ displays the minimization in real losses, and it can be realized as shown in the subsequent equation:

$$o{f}_1=\frac{{\displaystyle \sum _{i=1}^L{(P_{Lineloss}(i))}_{afterDG}}}{{\displaystyle \sum _{i=1}^L{(P_{Lineloss}(i))}_{beforeDG}}}$$

(21)

$o{f}_2$ offers the refinement of the voltage profiles and it may be extracted using the following equation:

$$o{f}_2=\frac{{\displaystyle \sum _{i=1}^N{\left|V_i-V_{i,ref}\right|}_{afterDG}}}{{{\displaystyle \sum _{i=1}^N\left|V_i-V_{i,ref}\right|}}_{beforeDG}}$$

(22)

$o{f}_3$ presents the amelioration of the VSI. Then, it can be addressed as:

$$o{f}_3=\frac{1}{VSI{(k)}_{afterDG}}$$

(23)

where the VSI is organized as Equation (2):

$$VSI(k)=\left|V_i\right|{}^4-4{(P_k\cdot X_{ik}-Q_k\cdot R_{ik})}^2-4(P_k\cdot R_{ik}+Q_k\cdot X_{ik})\cdot \left|V_i\right|{}^2$$

(24)

$w_1$, $w_2$, and $w_3$ are weighting factors. The sum of the weights specific to all sharks can add up to one [10], as can be observed in the following equation:

$$w_1+w_2+w_3=1$$

(25)

To provide the most suitable values of three weighted parameters, various settings for these parameters were obtained, where $w_1$ should be greater than $w_2$ and $w_3$, as discussed in [42]. The most appropriate values of these parameters were discovered by installing a single DG in a 33-node RDS, and then the optimization process via WSO was performed. The results for various weighting parameters and the corresponding values of the cost function are presented in Table 1. The best cost function was found when the weighting parameters were 0.5, 0.1, and 0.4. This result is proven, compared with the setting in [42]. Therefore, these values were used for all the systems in this study.

Table 1. Effect of various values of the weighting parameters in Equation (20).

${\mathit{w}}_{\mathbf{1}}$	${\mathit{w}}_{\mathbf{2}}$	${\mathit{w}}_{\mathbf{3}}$	Cost Function
0.5	0.1	0.4	0.317
0.5	0.2	0.3	0.362
0.5	0.3	0.2	0.407
0.5	0.4	0.1	0.452
0.5	0.25	0.25	0.385
0.6	0.1	0.3	0.365
0.6	0.2	0.2	0.41
0.6	0.3	0.1	0.455
0.6	0.25	0.15	0.432
0.6	0.15	0.25	0.387
0.7	0.1	0.2	0.412
0.7	0.2	0.1	0.457
0.7	0.15	0.15	0.435
0.8	0.1	0.1	0.46

3.1. Equality and Inequality Restrictions

Equation (20) is optimized while achieving the following equality and inequality restrictions.

3.1.1. Equality Restriction

Power-conservation restrictions

The algebraic expression for the incoming and outgoing power flows over the RDSs could be equalized [10]; thus:

$$P_{Swing}+{\displaystyle \sum _{i=1}^{N_{DG}}{P}_{DG}(i)}={\displaystyle \sum _{i=1}^L{P}_{Lineloss}(i)+{\displaystyle \sum _{q=1}^{N}Pd(q)}}$$

(26)

$$Q_{Swing}+{\displaystyle \sum _{i=1}^{N_{DG}}{Q}_{DG}(i)}={\displaystyle \sum _{i=1}^L{Q}_{Lineloss}(i)+{\displaystyle \sum _{q=1}^{N}Qd(q)}}$$

(27)

3.1.2. Inequality Restrictions

Voltage restriction

The rate of voltage at every node must be restricted by the following Equation:

$$V_{min}\le \left|V_i\right|\le V_{max}$$

(28)

where $V_{min},V_{max}$ are considered as 0.90 and 1.05 p.u, respectively, as specified in [3,4].

DG limit restrictions

To prohibit an inverse power flow, the installed size of DGs in the grid were restricted so as not to exceed the power provided by the substation [10].

$${\displaystyle \sum _{i=1}^{N_{DG}}{P}_{DG}(i)}\le \frac{3}{4}\times \left[{\displaystyle \sum _{i=1}^L{P}_{Lineloss}(i)+{\displaystyle \sum _{q=1}^{N}Pd(q)}}\right]$$

(29)

$${\displaystyle \sum _{i=1}^{N_{DG}}{Q}_{DG}(i)}\le \frac{3}{4}\times \left[{\displaystyle \sum _{i=1}^L{Q}_{Lineloss}(i)+{\displaystyle \sum _{q=1}^{N}Qd(q)}}\right]$$

(30)

$$P_{DG}^{min}\le P_{DG}(i)\le P_{DG}^{max}$$

(31)

$$Q_{DG}^{min}\le Q_{DG}(i)\le Q_{DG}^{max}$$

(32)

Line Capacity Restriction

The power of any line should be less than its rating amount, as shown by Equations (1) and (2)

$$S_{Li}\le S_{Li(rated)}$$

(33)

4. Outcomes and Discussion

The superiority of the developed WSO was investigated for distinct RDSs. The outcomes of 33, 69, and 85 bus RDSs are discussed in detail, below. The developed approach was executed via MATLAB.

4.1. The 33-Node Test System

The first studied case through WSO was a 33-node system. Figure 3 displays the schema of the system that contains prime feeders and three sides. This system possesses a net demand of 3720 kW and 2300 kVar at a voltage scale of 12.66 kV. The superiority of the developed WSO to detect the best allocations and capacity of PVs and WTs was proved, compared to those found in [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51]. Table 1 explains the influences of establishing various figures of PVs and WTs on system attitudes.

Figure 3. IEEE 33-node distribution grid.

In Figure 4, the voltage profile is promoted after using the developed WSO to obtain the optimum placements and capacities of PVs and WTs. It was clear that the power loss, percentage reduction, yearly savings, charge of losses, and VSIs improved by increasing the number of DGs, as presented in Table 2. If the energy loss charge of USD 0.06 was selected in the investigation, the cost of losses and annual energy savings were USD 54,027.212 and USD 56,863.87 via the suggested WSO by the penetration of 2600 kW for bus 6, while they were USD 34,238.95 and USD 76,652.129 for 2550 kVA with a power factor of 0.825. Additionally, the results are better for the WT rather than PV penetration due to the attainability of reactive power generation, as presented in Table 2.

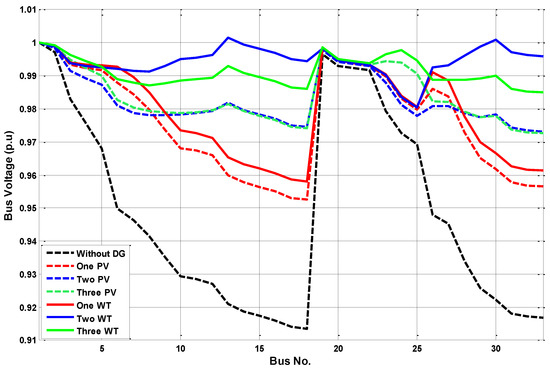
Figure 4. Voltage profiles of the 33-node grid for various values of DGs.

Table 2. Outcomes for the 33-node grid.

Items	Without DG	DG (kVA/p.f)
		1 PV	2 PVs	3 PVs
Net losses (kW)	210.98	102.7915	82.6	69.4808
Loss reduction (%)	-	51.28	60.85	67.068
Lower voltage/bus	0.9134/18	0.9525/18	0.9732/33	0.9726/33
Net DG/p.f/bus	-	2600/1/6	850/1/13 1191.1/1/30	790/1/13 1070/1/24 1080/1/30
VSI	25.887	28.8655	29.4794	29.6384
Charge of losses (USD)	110,891.08	54,027.212	43,414.56	36,519.1085
Saving (USD/year)	-	56,863.87	67,476.52	74,371.9715
		1 WT	2 WTs	3 WTs
Net losses (kW)	210.98	65.1426	28.4	11.45
Loss reduction (%)	-	69.124	86.54	94.57
Lower voltage/bus	0.9134	0.9581/18	0.9803/25	0.985/33
Net DG/p.f/bus	-	2550/0.825/6	945/0.9/13 1550/0.73/30	800/0.88/13 1100/0.9/24 1200/0.73/30
VSI	25.887	29.2610	30.8679	30.4412
Charge of losses (USD)	110,891.08	34,238.95	14,927.04	6018.12
Saving (USD/year)	-	76,652.129	95,964.04	104,872.96

4.1.1. Outcomes for Establishing 1 Unit in the 33-Node Grid

For a single DG establishment, the optimum siting and capacity were obtained using WSO, as presented in Table 3. Node 6 is the best site for PV establishment with a capacity of 2600 kW, while a capacity of 2550 kVA with a p.f of 0.825 was required for the WT establishment. The power losses were diminished to 102.7915 kW with a percentage reduction of 51.28%, and the lower voltage exceeded from 0.9134 to 0.9525 p.u using PV. Additionally, much better results were obtained using a WT rather than PV. The cost of losses and annual savings for both the PV and WT are presented in Table 2. The developed WSO can discover less power losses than other algorithms [35,36,37,38,39,40,41,42,43] from 0.2615 to 39.5485 kW. Likewise, the corresponding values represented the enhancement level from 0.2537% to 27.78% for the PV-type system. Furthermore, these values ranged from 2.6874 to 16.2874 kW and the corresponding values represent the enhancement level from 3.96% to 20% for the WT-type system, as compared with [41,42,44]. Additionally, the effect of DGs establishing voltage profiles is introduced in Figure 4.

Table 3. Outcomes for establishing 1 DG in the 33-node grid.

DG Type	Mechanism	Year	DG Installation		Power Loss (kW)		Lower Voltage
			Size (Kva/p.f)	Bus	Value	Percentage
PV	Without		-	-	210.98	-	0.9134
	GA [35]	2017	2580/1	6	105.481	48.21	NR
	EVPSO [36]	2013	763/1	11	140.19	33.55	0.9284
	PSOPC [36]	2013	1000/1	15	136.75	35.18	0.9318
	AEPSO [36]	2013	1200/1	14	131.43	37.7	0.9347
	ADPSO [36]	2013	1210/1	13	129.53	38.60	0.9348
	DAPSO [36]	2013	1212/1	8	127.17	39.7	0.9349
	Analytical [37]	2006	2490/1	6	111.24	47.27	NR
	GA [38]	2010	2380/1	6	132.64	37.13	NR
	[39]	2013	1000/1	18	142.34	33.29	0.9311
	ALOA [40]	2017	2450/1	6	103.053	51.15	0.9503
	ALOA [41]	2018	1542.67/1	30	125.161	40.67	0.9272
	ROA [42]	2021	2590.2/1	6	111.027	47.37	0.7886
	HHO [42]	2021	2590.2/1	6	111.03	47.3717	NR
	HGSO [42]	2021	2616.8/1	6	111.038	47.3703	NR
	ECOA [43]	2021	1000/1	30	127.28	39.67	0.9285
	Proposed	-	2600/1	6	102.7915	51.28	0.9525
WT	ALOA [41]	2018	2238.8/0.87	6	71.75	65.99	0.9528
	GWO [44]	2019	1000/0.8011	30	81.43	61.404	NR
	ROA [42]	2021	2558.4/0.82	6	67.83	67.85	NR
	Proposed	-	2550/0.825	6	65.1426	69.123	0.9581

4.1.2. Outcomes for Establishing Two DGs in the 33-Node System

The validation of the suggested WSO for searching the optimum site and capacity of DGs with two units of penetration was inspected. Nodes 13 and 30 were the best sites for the DG composition. The power losses were reduced to 82.6 kW with a percentage of 60.85%, and the lower voltage increased to 0.9732 p.u for the PV with capacities of 850 and 1191.1 kW, respectively. Additionally, inserting two WTs with capacities of 945 and 1550 kVA with p.f values of 0.9 and 0.73, respectively, reduced losses to 28.4 kW with a percentage of 86.54%, and the lower bus voltage increased to 0.9803 p.u. The yearly savings were USD 67,476.52 and USD 95,964.04 for the PV and WT, respectively, as recorded in Table 2. Moreover, the suggested approach provided the best outcomes in terms of power loss, reduced percentage of losses, and lower voltages, as compared to [35,36,38,42,43,44], as shown in Table 4. Furthermore, the effect of the composition of two PVs and WTs on the voltage profiles is presented in Figure 4.

Table 4. Outcomes for establishing 2 units in the 33-node grid.

DG Type	Mechanism	Year	DG Installation		Power Loss (kW)		Lower Voltage
			Size (kVA)/p.f	Bus	Value	Percentage
-	Without		-	-	210.98	-	0.9134
PV	GA [35]	2017	837.5/1	13	82.7	60.8	0.96846
			1212.2/1	29
	PSOPC [36]	2013	916/1	8	111.45	47.17	0.9418
			767/1	12
	EVPSO [36]	2013	540/1	14	108.05	48.78	0.9457
			569/1	31
	AEPSO [36]	2013	600/1	14	106.38	49.57	0.9447
			600/1	29
	ADPSO [36]	2013	550/1	15	106.24	49.64	0.9467
			621/1	30
	DAPSO [36]	2013	1227/1	13	95.93	54.53	0.9651
			738/1	32
	GA [38]	2010	1718/1	6	96.580	54.22	NR
			840/1	8
	ROA [42]	2021	851.5/1	13	87.165	58.68	0.96
			1157.6/1	30
	HHO [42]	2021	855.93/1	13	87.1682	58.684	NR
			1150.6/1	30
	HGSO [42]	2021	1128.8/1	11	89.999	57.342	NR
			806.199/1	30
	ECOA [43]	2021	893/1	10	86.55	58.977	0.9629
			1000/1	30
	Proposed		850/1	13	82.6	60.85	0.9732
			1191.1/1	30
WT	ALOA [41]	2018	1039.5/0.862	13	30.9251	85.34	NR
			1463/0.837	30
	ROA [42]	2021	858.4/0.91	13	28.50	86.49	NR
			1089.09/0.7	30
	GWO [44]	2019	861/0.8742	10	32.17	84.75	NR
			1000/0.8091	30
	Proposed		945/0.9	13	28.4	86.539	0.9803
			1550/0.73	30

4.1.3. Outcomes for Establishing Three DGs in 33-Node System

The efficacy of the suggested WSO for detecting the optimum siting and capacity of DGs for three locations of PVs and WTs was investigated. Nodes 13, 24, and 30 were the best locations for the DG compositions. With capacities of 790, 1070, and 1080 kW for the PV-type system, the power losses were reduced to 69.4808 kW with a percentage of 67.068%. With capacities of 800, 1100, and 1200 kVA for the WT-type system with p.f values of 0.88, 0.9, and 0.73, respectively, the power losses were reduced to 11.45 kW with a percentage of 94.57%, which was much better than the PV installation. The yearly savings were USD 104,872.96 for the WT, which was better than USD 74,371.9715 for the PV system, as presented in Table 2. The lower voltage increased to 0.985 p.u with the WT, while it was 0.9726 p.u with the PV system. Moreover, the suggested approach produced the best outcome in terms of reducing power loss, improving the percentage of losses, and enhancing lower voltages, as recorded in Table 5, compared to [42,43,44,45,46,47,48,49,50,51]. Furthermore, the effect of DG installations on the voltage profiles is presented in Figure 4.

Table 5. Outcomes for establishing three DGs in 33-node grid.

DG Type	Mechanism	Year	DG Installation		Power Loss (kW)		Minimum Voltage
			Size (kVA)/p.f	Bus	Value	Percentage
-	Without		-	-	210.98	-	0.9134
PV	QOSIMBO_Q [45]	2016	801.6/1	13	72.8	65.49	NR
			1090.6/1	24
			1054.2/1	30
	QOCSOS [46]	2020	801.7/1	13	72.7869	65.5	NR
			1091.3/1	24
			1053.7/1	30
	CSCA [47]	2020	871/1	13	71.94	65.9	NR
			1091.5/1	24
			954.1/1	30
	HHO [48]	2020	775.5/1	14	72.79	65.5	NR
			1080.8/1	24
			1066.7/1	30
	SFSA [49]	2018	802/1	13	72.785	65.5	NR
			1092/1	24
			1053.7/1	30
		2014	880.8/1	12	74.101	64.88	NR
			1059.2/1	24
			1059.2 /1	30
	I-GWO [51]	2022	758/1	14	70.64	66.51	NR
			1073/1	24
			1099/1	30
	ROA [42]	2021	790.3/1	14	72.786	65.5	0.96
			870/1	24
			1119.51/1	30
	HGSO [42]	2021	919.2/1	12	83.981	60.19	NR
			1237.1/1	27
			504.8/1	24
	ECOA [43]	2021	737.6/1	14	74.6	64.64	0.9666
			651.8/1	25
			1070.5/1	30
	COA [43]	2021	709.6/1	14	76	63.977	0.9637
			595.4/1	25
			997.2/1	30
	Proposed		790/1	13	69.4808	67.068	0.9726
			1070/1	24
			1080/1	30
WT	ROA [42]	2021	793.8/0.9	13	11.74	94.43	NR
			1069.9/0.9	24
			1029.8/0.71	30
	GWO [44]	2019	1000/0.8122	13	13.68	93.5	NR
			789/0.8726	24
			997/0.8659	30
	Proposed		800/0.88	13	11.45	94.57	0.985
			1100/0.9	24
			1200/0.73	30

4.2. Simulation Results for the IEEE-69 Bus RDS

The second studied case via the WSO approach was a 69-bus system. Figure 5 displays the system graph that consists of major feeders and seven branches. This system has a net load of 3800 kW and 2690 kVAr at 12.6 kV. It is clear that the power loss reduced while the percentage reduction, yearly saving, voltage, and VSI improved with increasing numbers of DGs, as presented in Table 6. Additionally, the systems with WT penetrations presented superior results than with the PV penetration, due to the use of both active and reactive powers.

Figure 5. IEEE 69-node distribution grid.

Table 6. Outcomes for the 69-node grid.

Items	Without DG	With DG (kVA/p.f)
		1 PV	2 PVs	3 PVs
Net losses (kW)	224.94	81.5033	70.4556	68.6857
Loss reduction (%)	-	63.766	68.678	69.465
Lower voltage/bus	0.9102	0.9685/27	0.9828/65	0.9836/65
Net DG/p.f/bus	-	1890/1/61	525/1/17 1775/1/61	480/1/11 380/1/17 1740/1/61
VSI	61.2379	64.5914	65.8988	66.1004
Cost of losses (USD)	118,228.46	42,838.1345	37,031.463	36,101.203
Saving (USD/year)	-	75,390.325	81,196.996	82,127.257
		1 WT	2 WTs	3 WTs
Net losses (kW)	224.94	23.1551	6.98	3.98
Loss reduction (%)	-	89.7	96.89	98.23
Lower voltage/bus	0.9102	0.9718/27	0.9851/65	0.9878/65
Net DG/p.f/bus	-	2250/0.82/61	680/0.83/17 1795/0.814/61	528/0.81/11 527/0.83/17 1800/0.814/61
VSI	61.2379	65.3928	66.6257	66.9666
Cost of losses (USD)	118,228.46	12,170.32	3668.688	2091.888
Saving (USD/year)	-	106,058.14	114,559.77	116,136.57

4.2.1. Outcomes for Establishing One DG in the 69-Node Grid

For a single DG composition, the optimal allocation and capacity were obtained via the WSO. Table 6 summarizes the developed outcomes for installing a single DG. Node 61 was the best site for the DG composition. With a capacity of 1890 kW for the PV-type system, a reduction in the real power losses to 81.5033 kW occurred, which indicated a 63.766% reduction. The yearly saving was USD 75,390.325 and the minimum voltage increased to 0.9685 p.u. For the WT-type system with a capacity of 2250 kVA with a p.f of 0.82, the power loss decreased to 23.1551 kW with educed reduction to 89.7%, a net saving of USD 106,058.14, and a voltage lowered to 0.9718 p.u, as reported in Table 6. Additionally, the developed WSO presented better outcomes in terms of power losses and the percentage minimizations of power losses, as recorded in Table 7, compared to [35,42,43,44,52,53,54,55,56,57,58]. Furthermore, the effect of the DG composition on the voltage profiles is presented in Figure 6.

Table 7. Outcomes for establishing one DG in the 69-node grid.

DG Type	Mechanism	Year	DG Installation		Power Loss (kW)
			Size (kVA/p.f)	Bus	Amount	Percentage
-	Without	-	-	-	224.94	-
PV	ABC [52]	2011	1900/1	61	83.31	62.96
	GA [35]	2017	1872/1	61	83.18	63.02
	Analytical [37]	2006	1810/1	61	81.54	63.64
	Analytical [53]	2009	1807.8/1	61	92	59.1
	Grid search [53]	2009	1876.1/1	61	83	63.1
	GA [54]	2009	1794/1	61	83.4252	62.91
	PSO [55]	2010	1337.8/1	61	83.206	63.01
	CSA [56]	2012	2000/1	61	83.8	62.74
	SGA [56]	2012	2300/1	61	89.4	60.3
	PSO [56]	2012	2000/1	61	83.8	62.75
	MTLBO [26]	2013	1819.691/1	61	83.323	62.95
	BB-BC [57]	2015	1872.5/1	61	83.2246	63
	ALOA [58]	2018	1800/1	61	81.776	63.645
	ROA [42]	2021	1872.7/1	61	83.19	63.01
	HHO [42]	2021	1901/1	61	83.24	62.99
	HGSO [42]	2021	1890/1	61	83.25	62.99
	ECOA [43]	2021	1000/1	61	111.56	50.40
	Proposed		1890/1	61	81.5033	63.766
WT	ALOA [41]	2018	2227.9/0.82	61	23.1622	89.7
	ROA [42]	2021	1828.47/0.814	61	23.1681	89.7
	GWO [44]	2019	1000/0.8	61	58.8	73.86
	Proposed		2250/0.82	61	23.1551	89.706

Figure 6. Voltage profile of the 69-node grid.

4.2.2. Outcomes for Establishing Two DGs in the 69-Node Grid

For two DG compositions, the optimal site and capacity were achieved by the WSO, as shown in Table 8. Nodes 17 and 61 were the best sites for PV compositions with capacities of 525 and 1775 kW, respectively. The power loss reduced to 70.4556 kW, with a percentage minimization of 68.678%. For WTs with capacities of 680 and 1795 kVA and p.f values of 0.83 and 0.814, respectively, the power loss reduced to 6.98 kW with percentage losses of 96.89%. The yearly savings increased to USD 81,196.996 and USD 114,559.77 and the lower voltage was updated to 0.9828 p.u and 0.9851 for PVs and WTs, respectively, as displayed in Table 6. Additionally, the developed WSO discovered less power losses than the others presented in Table 8, increasing from 0.2944 to 13.7774 kW. Likewise, the corresponding values enhanced from 0.4161% to 16.356% for the PV-type system. Moreover, these values ranged from 0.21 to 16.25 kW, and the corresponding values enhanced from 2.92% to 69.8% for the WT-type system. Furthermore, the effect of DG penetration on the voltage profiles is presented in Figure 6.

Table 8. Outcomes for establishing two DGs in the 69-node grid.

DG Type	Mechanism		DG Installation		Power Loss (kW)
			Size (kVA/p.f)	Bus	Value	Percentage
-	Without		-	-	224.94	-
PV	GA [38]	2010	1777/1	61	71.7912	68.08
			555/1	11
	GA [54]	2009	6/1	1	84.233	62.55
			1794/1	62
	CSA [56]	2012	600/1	22	76.4	66
			2100/1	61
	SGA [56]	2012	1000/1	17	82.9	63.1
			2400/1	61
	PSO [56]	2012	700/1	14	78.8	64.97
			2100/1	62
	MTLBO [26]	2013	519.705/1	17	71.776	68.09
			1732.004/1	61
	ALOA [58]	2018	538.777/1	17	70.750	68.547
			1700/1	61
	ROA [42]	2021	531.48/1	17	71.674	68.13
			1781.5/1	61
	HHO [42]	2021	814/1	12	72.52	67.76
			1735.3/1	61
	HGSO [42]	2021	502/1	17	72.9	67.59
			1998/1	61
	ECOA [43]	2021	1000/1	61	83.34	62.95
			863/1	62
	Proposed		525/1	17	70.4556	68.678
			1775/1	61
WT	ALOA [58]	2018	726.637/0.83	17	20.9342	90.69
			1500/0.8	61
	ROA [42]	2021	432.3717/0.7	17	7.19	96.80
			1750.06/0.8195	61
	GWO [44]	2019	1000/0.8	61	23.28	89.65
			820/0.8328	62
	Proposed		680/0.83	17	6.98	96.89
			1795/0.814	61

4.2.3. Outcomes of the 69-Bus System and Three DGs

The optimum site and capacity values were obtained using WSO, as seen in Table 9, for three DG installations. Nodes 11, 17, and 61 were the best sites for DG compositions with sizes of 480, 380, and 1740 kW for PV and 528, 527, and 1800 kVA with p.f values of 0.81, 0.83, and 0.814 for WTs. The power losses decreased to 68.6857 and 3.98 kW, with percentage increases of 69.465% and 98.23% for PVs and WTs, respectively. The yearly saving increased to USD 82,127.257 and USD 116,136.57 and the lower voltage was updated to 0.9836 and 0.9878 p.u for PVs and WTs, respectively, as presented in Table 6. Compared with [42,43,44,45,46,47,48,49,59,60,61], WSO produces better outcomes in terms of power losses and the percentage attenuation of power, as indicated in Table 9. Furthermore, the effect of DG compositions on voltage profiles is presented in Figure 6.

Table 9. Outcomes for establishing three DGs in the 69-node system.

DG Type	Mechanism	Year	DG Installation		Power Loss (kW)
			Size (kVA/p.f)	Bus	Value	Percentage
-	Without		-	-	224.94	-
PV	SFSA [49]	2018	527.3/1	11	69.428	69.14
			380.5/1	18
			1719.8/1	61
	QOSIMBO_Q [45]	2016	833.6/1	9	71.00	68.44
			451.1/1	18
			1500/1	61
	CSCA-64 [47]	2020	365.9/1	17	70.07	68.86
			1675.8/1	61
			652.5/1	67
	IHHO [48]	2020	527.2/1	11	69.41	69.15
			382.5/1	17
			1719.4/1	61
	QOCSOS [46]	2020	526.9/1	11	69.4284	69.14
			380.3/1	18
			1719/1	61
	BFOA [59]	2014	295.4/1	27	75.23	66.55
			1345.1/1	61
			447.6/1	65
	LSFSA [60]	2013	420.4/1	18	77.1	65.72
			1331.1/1	60
			429.8/1	65
	CABC [61]	2015	538.1/1	17	71.59	68.17
			1200/1	61
			535/1	64
	ROA [42]	2021	526.9147/1	11	69.42553	69.135
			380.3464/1	18
			1718.8/1	61
	HHO [42]	2021	467.148/1	12	70.01	68.88
			346.77/1	15
			1734.2/1	61
	HGSO [42]	2021	598.634/1	15	72.338	67.84
			1796.9/1	61
			200/1	57
	COA [43]	2021	343.9/1	19	72.5	67.769
			1438.8/1	61
			285.5/1	64
	SFO [43]	2021	358.3/1	19	72.7	67.68
			30/1	50
			1732.3/1	61
	Proposed		480/1	11	68.6857	69.465
			380/1	17
			1740/1	61
WT	ROA [42]	2021	508.44/0.836	11	4.2	98.13
			370.25/0.819	18
			1670.84/0.8102	61
	GWO [44]	2019	523/0.8294	18	7.27	96.76
			1000/0.8191	61
			723/0.802	62
	Proposed		528/0.81	11	3.98	98.23
			527/0.83	17
			1800/0.814	61

4.3. The 85-Node Test System

Figure 7 presents a graph of the 85-bus system. The loss without compensation was 315.714 kW. The lower voltage was 0.8743 p.u. at node 54. The yearly charge was calculated as USD 165,939.3. The optimal locations, sizing of the PVs and WTs, minimum voltage, VSI, cost of losses, and yearly savings are presented in Table 10 for various numbers of PVs and WTs. It was obvious that the power loss, percentage reduction, annual saving, voltage, and VSI improved with increasing the numbers of PVs and WTs, as presented in Table 10. Additionally, the level of enhancement was better in the case of WT penetration than the PV due to the generation of complex power. Table 11 shows a comparison between the developed algorithm and other recent works. It is clear that the implementation of WSO is more distinguished in solving the studied optimization process, compared with [43,62,63,64,65]. Furthermore, the effects of DG compositions on voltage profiles are presented in Figure 8.

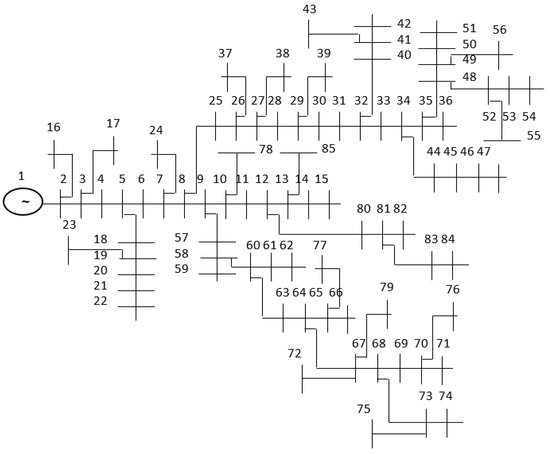
Figure 7. The graph of the 85-node grid.

Table 10. Outcomes for the 85-node grid.

Items	Without DG	With DG (kVA/p.f)
		1 PV	2 PVs	3 PVs
Net losses (kW)	315.714	214.1204	157.4592	150.7008
Loss reduction (%)	-	32.18	50.126	52.267
Minimum voltage/bus	0.8743/54	0.9175/76	0.9443/76	0.9543/76
Net DG/p.f/bus	-	1000/1/55	1100/1/9 900/1/34	950/1/9 730/1/33 440/1/61
VSI	57.7845	67.1635	72.6946	73.1184
Cost of losses (USD)	165,939.3	112,541.168	82,760.55	79,208.3405
Saving (USD/year)	-	53,397.62	83,178.75	86,731.16
		1 WT	3 WTs
Net losses (kW)	315.714	141.4474	20.4612
Loss reduction (%)	-	55.197	93.52
Minimum voltage/bus	0.8743/54	0.9255/76	0.9790/54
Net DG/p.f/bus	-	1250/0.7/55	1200/0.7/9 860/0.7/33 780/0.7/61
VSI	57.7845	69.6909	79.7560
Cost of losses (USD)	165,939.3	74,344.7534	10,754.40
Saving (USD/year)	-	91,594.55	155,184.893

Table 11. Outcomes for establishing various DGs in the 85-node grid.

DG Type	Mechanism	Year	DG Installation		Power Loss (kW)
			Size (kVA/p.f)	Bus	Value	Percentage
-	Without		-	-	315.714	-
One PV	WOA [62]	2018	910.075/1	54	227.105	28.06
	WOA [63]	2017	946.347/1	55	224.049	29.03
	Proposed		1000/1	55	214.1204	32.18
Three PVs	WCA [64]	2020	838.085/1	53	235.592	25.378
			837.995/1	54
			837.328/1	63
	WCA [64]	2020	838.093/1	12	152.583	51.67
			838.093/1	48
			838.093/1	67
	WCA [64]	2020	838.093/1	46	246.568	21.9
			838.093/1	47
			838.093/1	69
	MFF [65]	2019	1000/1	9	151.79	51.92
			700/1	33
			500/1	61
	COA [43]	2021	831.2/1	34	152.2	51.79
			677.9/1	67
			421.9/1	80
	SFO [43]	2021	354.6/1	12	153.6	51.348
			1059.2/1	32
			568.6/1	72
	Proposed		1000/1	9	149.7321	52.573
			800/1	33
			500/1	61
3 WTs	WCA [64]	2020	957.82/0.8	10	21.056	93.331
			800.62/0.8	34
			606.95/0.8	67
	Proposed		1200/0.7	9	20.4612	93.519
			860/0.7	33
			780/0.7	61

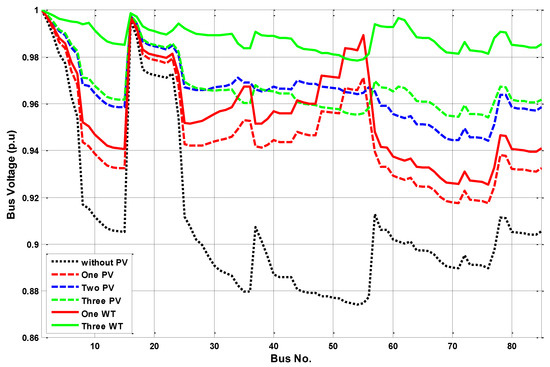
Figure 8. Voltage profile of the 85-node grid.

5. Conclusions

In this article, the WSO was applied successfully to obtain the optimal site and capacity of DGs in distinct RDSs. The process was designed as an optimization case concerned with power losses, voltage profiles, and VSIs. The outcomes were compared to those found using other approaches. The main conclusions of this paper were:

• A multi-objective function was developed with an accurate choice of weighting factors to reduce the net power losses and improve the voltage profiles and VSIs of various RDSs.
• WT installation provides much better results compared with PVs.
• As the number of penetrated DGs was increased to three units, the percentages of power losses increased to 94.57%, 98.23%, and 93.52% for WTs, while these percentages were 67.068%, 69.465%, and 52.267% for PVs for 33, 69, and 85, respectively.
• With the increasing number of penetrated DGs, the rate of improvement in the percentage of loss reductions decreased. These rates were 63.766, 4.912, and 0.787 for PV, which was less than 89.7, 7.19, and 1.34, respectively, for WTs used for the 69-node system.
• The notability of WSO was assured, compared to other recent studies, in terms of power losses. The enhancement reached 27.78%, 70%, and 39.27% for the three used systems.

The implementation of the developed approach to considerable-level RDSs with other RESs and unbalanced systems is the future concern of this study.