Compressed Air Energy Storage System with Burner and Ejector

Abstract

The timescale of the energy-release process of an energy storage system has put forward higher requirements with the increasing proportion of new energy power generation in the power grid. In this paper, a new type of compressed-air energy storage system with an ejector and combustor is proposed in order to realize short-timescale and long-timescale energy-release processes under the non-supplementary combustion condition and ejector supplementary combustion condition, respectively. A simulation model of the new system is established in APROS software. The results of this study show that the new system can realize continuous power output when energy storage and energy release operate simultaneously, and especially when the ejector coefficient is 0.8 and burner thermal power is 10 MW, the power-generation time is 12.45 h and the total generated power is 140,052 kW∙h, which are 15.6 and 17.5 times greater those of the short-timescale condition, respectively. In summary, the compressed-air energy storage system with an ejector and combustor that is proposed in this paper can flexibly meet the demands of multiple timescales’ power generation.

1. Introduction

In recent years, the clean and low-carbon process of energy utilization is accelerating, and the scale of new energy power generation, such as wind power and photovoltaic power, is growing larger and larger in China [1]. According to the data of the China National Energy Bureau, the installed capacity of wind power and solar power was about 330 million kW and 320 million kW, respectively, by the end of February 2022. However, new energy power generation, such as wind power and photovoltaic power, has the characteristics of strong intermittence, volatility, and randomness [2], which may have adverse effects on the power quality, safety, and stability of the power systems [3].

Large-scale electric energy storage technology is one of the effective ways to solve the above problems [4]. It has been validated that equipping a large amount of energy storage systems can effectively stabilize the gap and volatility of new energy power generation [5]. The energy storage systems will release energy to supplement the power generation when new energy power generation is insufficient, which can ensure the power balance, safe, and stable operation of power grid. Additionally, they will store energy to ensure that the new energy is consumed when the new energy generation is surplus. At present, the main types of large-scale clean power energy storage are pumped storage, compressed-air energy storage (CAES) [6], electrochemical energy storage [7], etc., and their typical rated power and maximum output time [8,9,10] are shown in

Table 1. Typical rated power and maximum output time of various energy storage systems [8,9,10].

Types	Typical Rated Power	Continuous Response Time
Electrochemical energy storage	1 kW~50 MW	1 min~4 h
Pumped storage	100~2000 MW	2~8 h
Compressed-air energy storage	500 kW~300 MW	1–26 h
Flywheel energy storage	5 kW~5 MW	15 s~15 min
Superconducting magnetic energy storage	0.01~1 MW	ms~15 min
Supercapacitor	0.01~1 MW	1 s~15 min

. It can be seen that the longest continuous response time (that is, output power time) is 1–26 h of compressed-air energy storage.

The CAES system has the advantages of a large capacity, low pollution, moment of inertia, long storage cycle, etc. [11], and scholars and researchers have been widely concerned with it because of its broad development prospects. [12]. Since Stal Laval proposed to use underground caves to realize compressed-air energy storage in 1949 [13], domestic and foreign scholars have carried out a lot of research and practice [14] and established a number of CAES commercial power stations and demonstration projects [15]. At present, there are many types of CAES systems, which can be divided into supplementary combustion and non-combustion CAES systems from the perspective of auxiliary combustion [16]. The supplementary combustion CAES system has the advantages of strong reliability, stability, and good flexibility, but the disadvantage is obviously, e.g., consumption of fossil energy and emission of greenhouse gas. Two large-scale CAES power plants have been put into commercial operation in the world, namely the Huntorf power plant in Germany and the McIntosh power plant in the United States [17], both of which are supplementary combustion CAES systems. Compared with the supplementary combustion CAES system, the non-combustion CAES system has no supplementary combustion process, and the heat required in the energy-release stage mainly comes from the compression heat generated by the air-compression process in the energy-storage stage, so it has advantages of being environmentally friendly and pollution free [18,19]. At present, all the CAES demonstration projects in China adopt non-combustion CAES. The advanced adiabatic compressed-air energy storage (AA-CAES) power station of 50 MW in Feicheng, Shandong Province, was put into commercial operation in September 2021, and it is the first CAES commercial power station in China [20]. In the same month, the national demonstration project of 60 MW salt-cave CAES power generation system in Jintan, Jiangsu Province, successfully implemented a grid connection test [21].

As shown in Figure 1, the AA-CAES system is a typical non-combustion CAES system, and it includes two stages, namely energy storage and energy release [22]. In the energy-storage stage, air is compressed by compressors and stored in a storage tank. In the energy-release stage, compressed air enters a turbine from the gas storage tank, expands and releases energy to drive the synchronous generator to generate electricity, and then exhaust air is discharged into atmosphere [23].

At present, the research on the application of CAES system mainly focuses on two aspects, one is to participate in the source network coupling of grid load frequency regulation and improve the reliability of power supply on the grid side. Kamyar et al. [24] proposed a new design method of CAES system based on the performance requirements of the Ontario power grid by analyzing the actual operation data of a whole year. Based on the characteristics of the CAES system, Wen et al. [25] constructed its primary frequency modulation function and analyzed and set its dead zone, governor droop, clearance, and other parameters, which laid a foundation for CAES to participate in primary frequency modulation of power grid. Yang et al. [26] put forward a load rejection control strategy for an AA-CAES expansion generator by adding a shutoff valve between adjacent expansion units to effectively prevent speed rise. AmirReza. et al. [27] proposed a cogeneration system composed of CAES, organic Rankine cycle, and absorption–compression refrigeration cycle. Considering the multi-generation characteristics of the AA-CAES power plant, Li et al. [28] constructed the joint dispatching constraint model of cooling, heating, and power multi-energy flow for the AA-CAES power station. Hesamoddin et al. [29] proposed a two-stage mathematical optimization model for optimizing the day-ahead operation of generation units, as well as CAESs, in energy and reserve markets in a stochastic way.

The other aspect is to couple with the source storage of new energy power stations, such as wind energy and photovoltaic, on the generation side. Deng et al. [30] proposed a control strategy of a wind-storage combined system on the basis of power stabilization and verified its feasibility by simulation. Amirreza et al. [31] researched an absorption-recompression refrigeration system with CAES and wind turbines, which employed a CAES system to compensate the further energy consumption of the vapor compressor. Alirahmi et al. [32] proposed and thoroughly investigated a novel efficient and environmentally friendly hybrid energy production/storage system comprising a compressed-air energy storage, and the system has an exergy round trip efficiency of 60.4% and a total cost rate of 117.5 $/GJ. Li et al. [33] studied the operation optimization strategy of the wind-storage combined system, considering the dynamic characteristics and operation constraints of CAES. Li et al. [34] studied a grid-connected power-optimization strategy that integrates wind energy and a low-temperature CAES, which can balance the fluctuation of wind energy by reducing energy storage capacity and ensure continuous and stable output power to power grid.

As mentioned above, the current research studies of the AA-CAES system are all based on a single timescale operation, which can only meet the requirements of storing energy when new energy power generation is surplus and releasing energy in a short timescale when new energy power generation is not enough. Nevertheless, the long-timescale fluctuation of new energy and the extreme conditions of zero power generation have a growing impact on the power system with the rapid development of new energy and the increasing proportion of installed capacity. Although increasing the capacity of energy storage system is an important method to effectively solve this problem, it will lead to high system cost and low utilization.

In consideration of the demands of multiple timescales’ power generation and economy, a novel AA-CAES system with two main components, namely an ejector and a burner, is proposed in this paper. This system has three operating modes, including a short-timescale mode with adiabatic non-supplementary combustion condition, a long-timescale mode with ejector-supplementary combustion condition, and a continuous-output mode with energy storage and energy release operating simultaneously, which can flexibly adapt to the requirements of multiple timescales’ energy release. In addition, a simulation model of the new system was established based on APROS software, and the characteristics of the three operating modes are analyzed.

2. Architecture of Energy Storage System

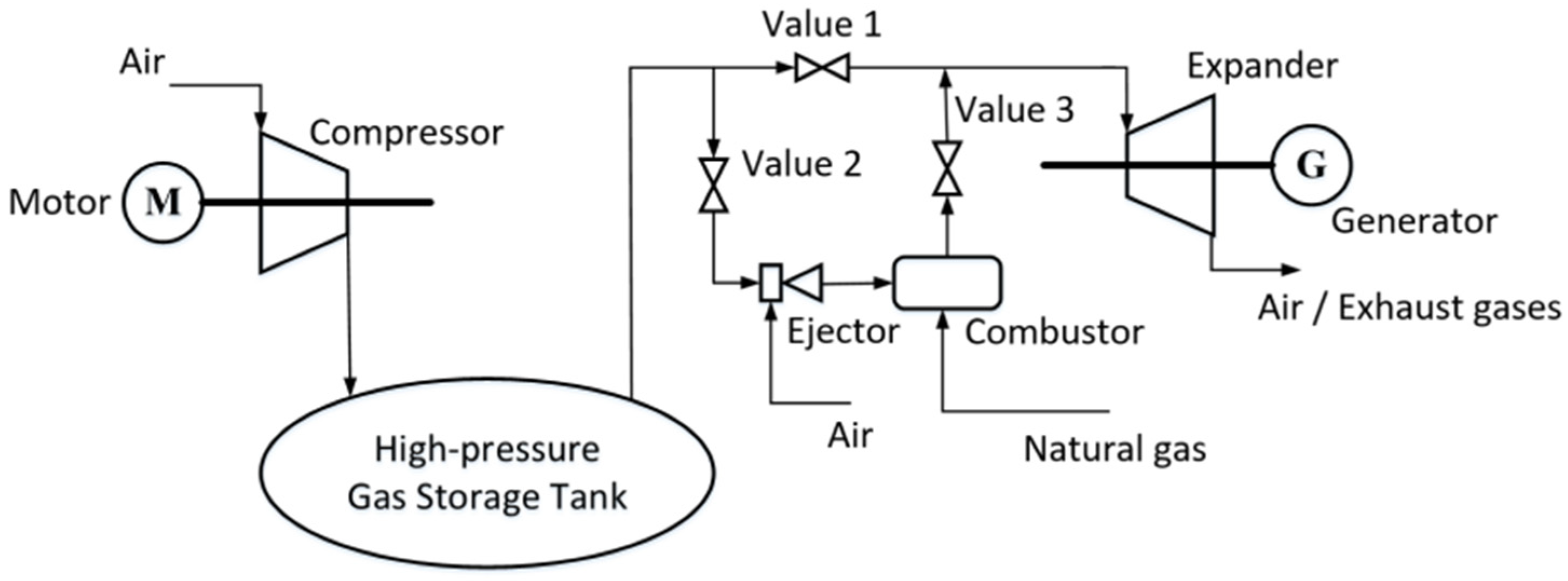
2.1. Compressed-Air Energy Storage System with Ejector and Combustor

Based on the AA-CAES system, this paper proposes a new CAES system with an ejector and combustor which can release energy in multi-timescales. Its system architecture is shown in Figure 2. The system is composed of a compression energy storage subsystem, a gas storage subsystem, and an expansion energy-release subsystem. Among them, the compression energy storage subsystem is composed of multistage compressors and motors; the gas storage subsystem is a high-pressure gas storage tank; and the expansion energy-release subsystem is composed of an ejector, a combustor, multistage expanders, and a generator.

In this study, a simulation model of the new CAES system with an ejector and burner is established based on APROS software [35,36]. Considering the characteristics of the CAES system with supplemental combustion and the relevant operating parameters of a 10 MW advanced CAES system demonstration project in Bijie, China [36,37], the detailed design parameters [19,36] are shown in

Table 2. Basic design parameters for the new CAES system.

Parameters	Units	Value
Energy-Release Power	MW	10
Energy-Release Pressure	MPa	7
Maximum Storage Pressure	MPa	10
Gas Storage Tank Volume	m3	6000
Ambient Pressure	MPa	0.1
Ambient Temperature	K	298
10 MW Release Time	s	2880
Hot Tank Temperature	K	403
Hot Tank Pressure	MPa	0.4
Cold Tank Temperature	K	298
Cold Tank Pressure	MPa	0.1
Compressor Motor Power	MW	10
Burner Thermal Power	MW	20
Burner Fuel	/	Natural Gas
Fuel Calorific Value	MJ/Nm3	36.22
Electric Power Consumed by Other Auxiliary Machines of Energy Storage Subsystem	MW	1.5
Electric Power Consumed by Other Auxiliary Machines of Energy-Release Subsystem	MW	1.5
Generator Power	MW	30

.

In this paper, a short-timescale simulation method is adopted, and the operation parameters of each expander are shown in

Table 3. Operation parameters in the mode of short timescale.

Expander Stages	Unit	1	2	3	4
Inlet Pressure	MPa	7	2.46	0.853	0.283
Outlet Pressure	MPa	2.48	0.873	0.303	0.1
Inlet Temperature	°C	82	82	82	82
Outlet Temperature	°C	14.4	7.6	10.0	18.0
Pressure Loss in Heat Exchanger	MPa	0.02	0.02	0.02	0.02
Air Flow Rate	kg/s	34.7	34.7	34.7	34.7
Expansion Ratio	/	2.82	2.82	2.82	2.82
Isentropic Efficiency	/	0.88	0.88	0.88	0.88
Output power	MW	2.536	2.786	2.691	2.358
speed	r/min	3 000	3 000	3 000	3 000

.

2.2. Mathematic Model

2.2.1. Expander

The air-expansion process is generally regarded as a polytropic process in the expander, and the output power of the expander [38,39] is calculated as follows:

$$W_i=\frac{k}{k-1}m{R}_{\mathrm{g}}{T}_i^{\mathrm{in}}{\eta }_i\left(1-{\beta }_i^{\frac{1-k}{k}}\right),i=1,2,\cdots M$$

(1)

where $W_i$ is the output power of the ith expanders, $\mathrm{kW}$; $m$ is the air mass flow, $\mathrm{kg}/\mathrm{s}$; $k$ is the air adiabatic index; $R_{\mathrm{g}}$ is the gas constant; $T_i^{\mathrm{in}}$ is the intake temperature of the $i$th stage expander,$\mathrm{K}$; ${\eta }_i$ is the adiabatic efficiency of the $i$th stage expander; and ${\beta }_i$ is the expansion ratio of the $i$th stage expander.

2.2.2. Heat Exchanger

In the AA-CAES power generation system, heat exchangers and expanders are arranged in a series. After air flows into the heat exchanger, the heat exchange between the air and tube-wall [36] is as follows:

$$Q_{\mathrm{h}}=A_{\mathrm{h}}\left(T_{\mathrm{h}}-T_{\mathrm{w}}\right)/\left(\delta /2K_{\mathrm{w}}+1/{\alpha }_{\mathrm{h}}\right)$$

(2)

The heat exchange between heat-transfer medium and pipe-wall is as follows:

$$Q_{\mathrm{c}}=A_{\mathrm{c}}\left(T_{\mathrm{c}}-T_{\mathrm{w}}\right)/\left(\delta /2K_{\mathrm{w}}+1/{\alpha }_{\mathrm{c}}\right)$$

(3)

where $\delta$ is the thickness of the tube-wall, $\mathrm{m}$; $T_{\mathrm{w}}$ is the average temperature of the tube-wall, $\mathrm{K}$; $T_{\mathrm{h}}$ is the air temperature inside the tube-wall, $\mathrm{K}$; $T_{\mathrm{c}}$ is the average temperature of the heat-transfer medium, $\mathrm{K}$; $K_{\mathrm{w}}$ is the thermal conductivity of the tube-wall, $\mathrm{W}/\left(\mathrm{m}·\mathrm{K}\right)$; ${\alpha }_{\mathrm{c}} \mathrm{and} {\alpha }_{\mathrm{h}}$ are the convective heat-transfer coefficients of the inner and outer tube-walls, respectively, $\mathrm{W}/\left({\mathrm{m}}^2·\mathrm{K}\right)$; and $A_{\mathrm{c}} \mathrm{and} A_{\mathrm{h}}$ are the areas of the inner and outer tube-walls, respectively, ${\mathrm{m}}^2$.

2.2.3. Gas Storage Tank

In the energy-release stage, the discharge process of the gas storage tank is a polytropic process. According to the mass and energy balance equations, the change rules of gas in the gas storage tank during the discharge process [40] can be obtained as follows:

$$\frac{\mathrm{d}p}{\mathrm{d}t}=\frac{R_{\mathrm{g}}}{V{c}_{\mathrm{v}}}\left[\frac{\mathrm{d}m}{\mathrm{d}t}{c}_{\mathrm{p}}{T}_{\mathrm{ac}}-h_{\mathrm{a}}A\left(T_{\mathrm{ac}}-T_{\mathrm{a}}\right)\right],$$

(4)

$$\frac{\mathrm{d}{T}_{\mathrm{ac}}}{\mathrm{d}t}=\frac{T_{\mathrm{ac}}}{m}\left(k-1\right)\frac{\mathrm{d}m}{\mathrm{d}t}-\frac{1}{m{c}_{\mathrm{v}}}{h}_{\mathrm{a}}A\left(T_{\mathrm{ac}}-T_{\mathrm{a}}\right),$$

(5)

where $p$ is the air pressure of the gas storage tank, $\mathrm{Pa}$; $V$ is the volume of the gas storage tank, ${\mathrm{m}}^3$; $c_{\mathrm{p}}$ is the air-specific heat at constant pressure,$\mathrm{kJ}/\mathrm{kg}·\mathrm{K}$; $c_{\mathrm{v}}$ is the air-specific heat at constant volume, $\mathrm{kJ}/(\mathrm{kg}·\mathrm{K})$; $h_{\mathrm{a}}$ is the convective heat transfer coefficient of the gas storage tank, $\mathrm{kW}/\left({\mathrm{m}}^2·\mathrm{K}\right)$; $A$ is the internal surface area of the gas storage tank, ${\mathrm{m}}^2$; $m$ is the air mass in the gas storage tank, $\mathrm{kg}$; $T_{\mathrm{a}}$ is the wall temperature of the gas storage tank, $\mathrm{K}$; and $T_{\mathrm{ac}}$ is the air temperature in the gas storage tank, $\mathrm{K}$.

2.2.4. Regulating Valve

The flow equation of the regulating valve [41] is as follows:

$$m_{\mathrm{s}}=\epsilon C_{\mathrm{s}}f\left(\mu \right)\sqrt{\rho \Delta p},$$

(6)

where $m_{\mathrm{s}}$ is the outlet air flow rate of regulating valve, $\mathrm{kg}/\mathrm{s}$; $\epsilon$ is the fluid compressibility, $C_{\mathrm{s}}$ is the valve admittance, $f\left(\mu \right)$ is the characteristic function of the regulating valve, and $\rho$ is the inlet air density of the regulating valve.

3. Energy Storage Condition

The compression energy-storage subsystem of CAES system has the same system architecture and operation mode under the conditions of energy release at different timescales.

In the stage of energy storage, the air is compressed into high-pressure compressed air by the compressor and stored in the high-pressure gas storage tank to realize the conversion of electric energy to internal energy. The judgment conditions for the completion of compressed-air preparation and the end of the energy-storage phase are as follows:

$$\left\{\begin{array}{c}p=p_{\mathrm{e}}\\ t=t_{\mathrm{s}}\end{array}\right\},$$

(7)

where $p$ is the pressure of high-pressure gas storage tank, $p_{\mathrm{e}}$ is the rated pressure of gas storage tank, $t$ is the operation time, and $t_{\mathrm{s}}$ is the end time of energy storage stage.

The end time $t_{\mathrm{s}}$ of energy storage stage is dispatched by the power grid, which is determined according to the peak regulation demand of power grid and dispatched through the day-ahead scheduling plan.

The power consumption of the $i$th compressor is defined as follows:

$$P_{\mathrm{c}i}=G_{\mathrm{c}i}\left(h_{\mathrm{c}i,\mathrm{out}}-h_{\mathrm{c}i,\mathrm{in}}\right)$$

(8)

where $P_{\mathrm{c}i}$ is the power consumption of the $i$th compressor, $G_{\mathrm{c}i}$ is the air mass flow of the $i$th compressor during energy storage process, and $h_{\mathrm{c}i,\mathrm{in}}$ and $h_{\mathrm{c}i,\mathrm{out}}$ are the specific enthalpies of inlet and outlet of the $i$th compressor.

The total power consumption of compressor motor can be expressed as follows:

$$P_m=\frac{P_c}{{\eta }_m\times {\eta }_{\mathrm{c}}}=\frac{G_{\mathrm{c}}\times {{\displaystyle \sum }}_{i=1}^m\left(h_{\mathrm{c}i,\mathrm{out}}-h_{\mathrm{c}i,\mathrm{in}}\right)}{{\eta }_m\times {\eta }_{\mathrm{c}}}$$

(9)

where $P_m$ is the power consumption of compressor motor, $P_{\mathrm{c}}$ is the total power consumption of compressor motor, $G_{\mathrm{c}}$ is the air mass flow of compressor, ${\eta }_m$ is the motor efficiency, ${\eta }_{\mathrm{c}}$ is the compressor efficiency, and $m$ is the number of compressors.

4. Multi-Timescale Energy-Release Condition

In this paper, the short-timescale power-generation condition is defined as a power-generation time less than 6 h, the long-term scale power-generation condition is defined as a power-generation time between 6 and 30 h, and the continuous-output condition is defined as continuous uninterrupted power generation.

The compressed-air energy storage system with an ejector and combustor has three operation modes in the energy-release stage that can flexibly adapt to three power-generation conditions, namely short timescale, long timescale, and continuous output. The three operating conditions of the energy-release stage of the system are discussed below.

4.1. Short-Timescale Condition

Under the short-timescale condition, the CAES system operates in adiabatic non-supplementary combustion mode.

4.1.1. Energy-Release Stage

The CAES system starts the process of air expansion to generate electricity when electric energy in the power grid is in short supply. As shown in Figure 1, the compressed air enters the expander from the high-pressure gas storage tank to expand and drive the generator to generate electricity by opening Valve 1, closing Valve 2 and Valve 3, sequentially. The compressed air after the work of the upper stage enters the heat exchanger for heating, and then it enters the expander of the next stage for power generation and is discharged into atmosphere after multistage expansion.

The generating power, $P_{\mathrm{t}i}$, of the $i$th expander is defined as follows:

$$P_{\mathrm{t}i}=\frac{G_{\mathrm{t}i}\times \left(h_{\mathrm{t}i,\mathrm{in}}-h_{\mathrm{t}i,\mathrm{out}}\right)}{3600}$$

(10)

where $G_{\mathrm{t}i}$ is the air mass flow of the $i$th expander, and $h_{\mathrm{t}i,\mathrm{in}}$ and $h_{\mathrm{t}i,\mathrm{out}}$ are the specific enthalpies of inlet and outlet of the $i$th expander.

The total generating power, $P_{\mathrm{g}}$, of the CAES system can be expressed as Equation (11):

$$P_{\mathrm{g}}=P_{\mathrm{t}}\times {\eta }_{\mathrm{g}}\times {\eta }_{\mathrm{t}}=G_{\mathrm{g}}{{\displaystyle \sum }}_{i=1}^m\left(h_{\mathrm{t}i,\mathrm{in}}-h_{\mathrm{t}i,\mathrm{out}}\right)\times {\eta }_{\mathrm{g}}\times {\eta }_{\mathrm{t}}$$

(11)

where $P_{\mathrm{t}}$ is the total generating power of expanders, $G_{\mathrm{g}}$ is the air mass flow of expanders in short scale, ${\eta }_{\mathrm{g}}$ is the generator efficiency, ${\eta }_{\mathrm{t}}$ is the expander efficiency, and $m$ is the number of expanders.

4.1.2. Timescale Determination

The determination of timescale is mainly related to parameters such as the volume, temperature, and pressure of the high-pressure gas storage tank.

To simplify the calculation, the following assumptions need to be made in this paper:

(1)

The compressed air is an ideal gas;

(2)

The gas loss at the pipes and valves are ignored;

(3)

The temperature change in the process of compression and depressurization of gas storage device is not considered. (The energy storage system has a heat-exchange device, so the internal temperature change of gas storage device is ignored and regarded as an isothermal expansion process.)

According to the ideal gas law, the relationship between the state parameters of gas storage device at the initial time in the energy storage stage is as follows:

$$p_{\mathrm{c},\mathrm{s}}V=m_{\mathrm{c},\mathrm{s}}R{T}_{\mathrm{c},\mathrm{s}}$$

(12)

where $p_{\mathrm{c},\mathrm{s}}$ is the air pressure at the initial time, $V$ is the volume of gas storage device, $m_{\mathrm{c},\mathrm{s}}$ is the air mass at the initial time, and $T_{\mathrm{c},\mathrm{s}}$ is the air temperature at the initial time.

The state parameters of gas storage device at the end time can be expressed as follows:

$$p_{\mathrm{c},\mathrm{f}}V=m_{\mathrm{c},\mathrm{f}}R{T}_{\mathrm{c},\mathrm{f}}$$

(13)

where $p_{\mathrm{c},\mathrm{f}}$ is the air pressure at the end time, $m_{\mathrm{c},\mathrm{f}}$ is the air mass at the end time, and $T_{\mathrm{c},\mathrm{f}}$ is the air temperature at the end time and is equal to $T_{\mathrm{c},\mathrm{s}}$.

Equations (12) and (13) can be subtracted to obtain Equation (14):

$$V\left(p_{\mathrm{c},\mathrm{f}}-p_{\mathrm{c},\mathrm{s}}\right)=\mathsf{\Delta }mR{T}_{\mathrm{c},\mathrm{s}}$$

(14)

where $\Delta m$ is the total mass of compressed air produced by compressor during energy storage process.

According to the total mass of compressed air and the mass flow of compressor under the rated working conditions, the time, $t_{\mathrm{c}}$, of the energy storage process can be expressed as follows:

$$t_{\mathrm{c}}=\frac{V\left(p_{\mathrm{c},\mathrm{f}}-p_{\mathrm{c},\mathrm{s}}\right)}{R{T}_{\mathrm{c},\mathrm{s}}{G}_{\mathrm{c}}},$$

(15)

Similarly, we derive the working time, $t_{\mathrm{g}}$, of the energy-release process as follows:

$$t_{\mathrm{g}}=\frac{V\left(p_{\mathrm{g},\mathrm{s}}-p_{\mathrm{g},\mathrm{f}}\right)}{R{T}_{\mathrm{g},\mathrm{s}}{G}_{\mathrm{g}}},$$

(16)

where $p_{\mathrm{g},\mathrm{s}}$ is the air pressure at the initial time, $p_{\mathrm{g},\mathrm{f}}$ is the air pressure at the end time, and $T_{\mathrm{c},\mathrm{s}}$ is the air temperature at the initial time.

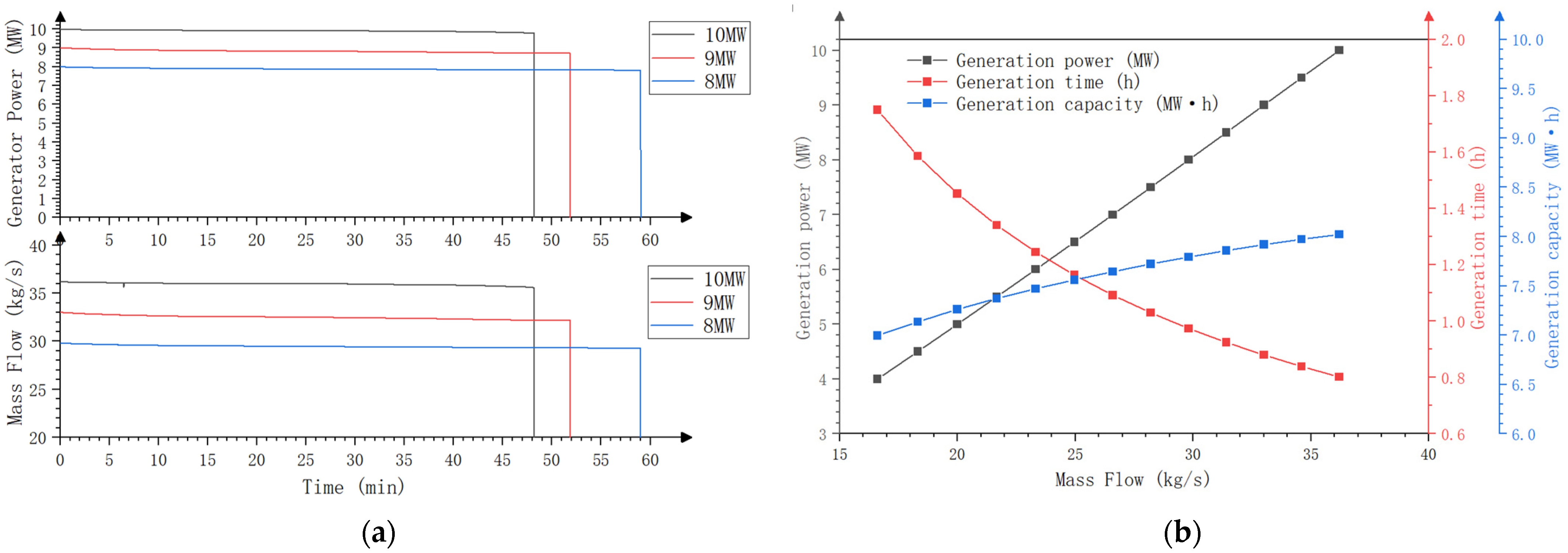
4.1.3. Simulation Analysis

As shown in Figure 3a, with the mass flow of compressed air decreased, the generator power decreases, while the working time of the energy-release process, $t_{\mathrm{g}}$, is increased. Moreover, the relations of different mass flows of compressed air with the generator power, power-generation capacity, and power-generation time are shown in Figure 3b. The compressed air flow is inversely proportional to the power-generation time. Because the total quality of the workable working medium in the gas storage tank is constant, the power-generation capacity tends to decrease with the decrease of the compressed air flow.

4.2. Long-Timescale Condition

The working condition of the power consumption and energy-storage stage in the long timescale is the same as that in the short timescale.

4.2.1. Energy-Release Stage

As shown in Figure 2, the ambient air is inhaled into the ejector to increase the flow when the high-pressure compressed air passes through the injector by closing Valve 1 and opening Valve 2 and Valve 3, sequentially. By adding natural gas into the combustor for mixed combustion, the temperature, pressure, and expansion work capacity of the compressed air are increased. Finally, the pressurized and heated air enters the turbine and drives the generator to generate electricity, realizing the conversion of internal energy to electrical energy.

This model improves the power-generation capacity through two means. One is to increase the air-mass flow of the expander through the ejector, and the other is to increase the temperature and pressure of the working air through the external combustor. Air enthalpy is positively correlated with air temperature and pressure; that is, raising the enthalpy of working air inlet could increase the enthalpy drop of air inlet and outlet of expander.

4.2.2. Ejector Model

The structure diagram of the ejector is shown in Figure 4.

According to the mass-balance equations, the total mass balance [42] is calculated as follows:

$$G_{\mathrm{g}}^{\prime }+G_{\mathrm{e}}=G_{\mathrm{t}}$$

(17)

The suction coefficient of the ejector is defined [42] as follows:

$$\gamma =\frac{G_{\mathrm{e}}}{G_{\mathrm{g}}^{\prime }}$$

(18)

where $G_{\mathrm{g}}^{\prime }$ is the mass flow rate of compressed air, and $G_{\mathrm{e}}$ is the mass flow rate of atmosphere air.

Therefore, after high-pressure compressed air passes through the ejector, its mass flow rate changes as follows:

$$G_{\mathrm{t}}=G_{\mathrm{g}}^{\prime }\left(1+\gamma \right)$$

(19)

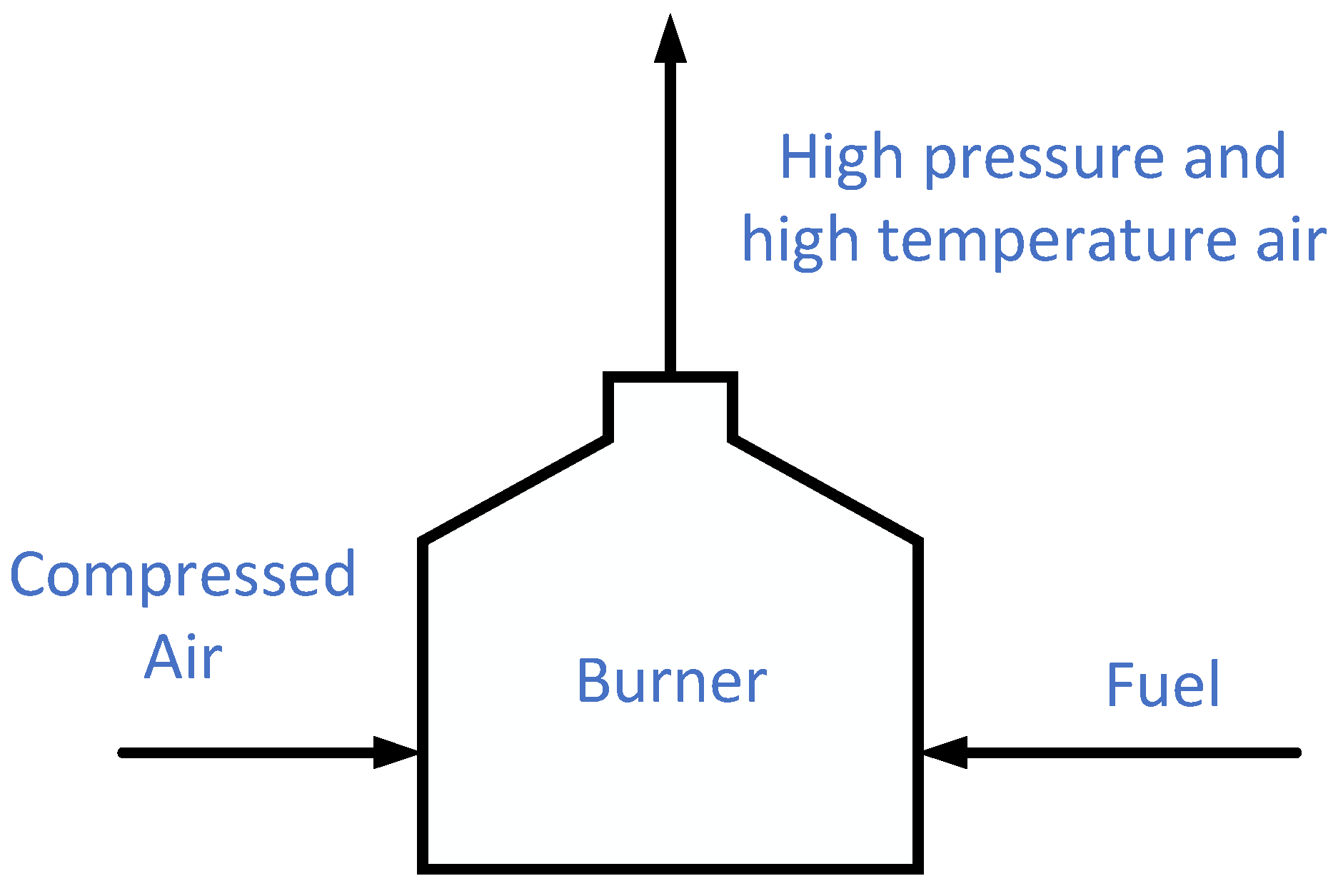
4.2.3. Combustor Model

The structure diagram of the combustor is shown in Figure 5.

In this paper, the new system uses natural gas as the fuel of burner, and its calorific value is 36.22 $\mathrm{MJ}/{\mathrm{Nm}}^3$. The energy changes after burning with natural gas are as follows [43]:

$$Q_{\mathrm{b}}=Q_{\mathrm{Fuel}}\times {\eta }_{\mathrm{b}}$$

(20)

where $Q_{\mathrm{b}}$ is the thermal power output of the combustor, $Q_{\mathrm{Fuel}}$ is the thermal power of burning natural gas, and ${\eta }_{\mathrm{b}}$ is the conversion efficiency of the combustor.

Therefore, under the long-timescale condition, the generating power of the energy-release generation stage is as follows:

$$P_{\mathrm{g}}^{\prime }=\frac{(G_{\mathrm{g}}^{\prime }\left(1+\gamma \right)\times {{\displaystyle \sum }}_{i=1}^m(h_{\mathrm{t}i,\mathrm{in}}^{\prime }-h_{\mathrm{t}i,\mathrm{out}}^{\prime })+Q_b)}{3600}\times {\eta }_{\mathrm{g}}\times {\eta }_{\mathrm{t}}$$

(21)

where $P_{\mathrm{g}}^{\prime }$ is the generating power of the energy-release generation stage.

4.2.4. Timescale Determination

There are two aspects to prolonging the energy-release time in this mode: one is to increase the working air flow rate from $G_{\mathrm{g}}^{\prime }$ to $G_{\mathrm{g}}^{\prime }\left(1+\gamma \right)$ through the ejector, and the other is to increase its capacity for work through combustion. When the output power is constant at the rated power of the expansion generator, reducing the compressed-air consumption per unit output power can increase the time of the power generation:

$$P_{\mathrm{g}}^{\prime }=P_{\mathrm{g}}$$

(22)

$$G_{\mathrm{g}}^{\prime }=\frac{G_{\mathrm{g}}{{\displaystyle \sum }}_{i=1}^m\left(h_{\mathrm{t}i,\mathrm{in}}-h_{\mathrm{t}i,\mathrm{out}}\right)-Q_b}{\left(1+\gamma \right)\times {{\displaystyle \sum }}_{i=1}^m\left(h_{\mathrm{t}i,\mathrm{in}}^{\prime }-h_{\mathrm{t}i,\mathrm{out}}^{\prime }\right)}$$

(23)

Compressed-air energy that can perform expansion work in the high-pressure gas storage tank is constant, so we can obtain the following:

$$G_{\mathrm{g}}^{\prime }{t}_{\mathrm{g}}^{\prime }=G_{\mathrm{g}}{t}_{\mathrm{g}}$$

(24)

$$t_{\mathrm{g}}^{\prime }=G_{\mathrm{g}}\frac{\left(1+\gamma \right)\times {{\displaystyle \sum }}_{i=1}^m\left(h_{\mathrm{t}i,\mathrm{in}}^{\prime }-h_{\mathrm{t}i,\mathrm{out}}^{\prime }\right)}{G_{\mathrm{g}}{{\displaystyle \sum }}_{i=1}^m\left(h_{\mathrm{t}i,\mathrm{in}}-h_{\mathrm{t}i,\mathrm{out}}\right)-Q_b}{t}_g$$

(25)

$$W_{\mathrm{g}}^{\prime }=\left(1+\gamma \right)\frac{h_{\mathrm{J},\mathrm{in}}}{h_{\mathrm{J},\mathrm{mix}}}{W}_{\mathrm{g}}+Q_{\mathrm{b}}{t}_{\mathrm{g}}^{\prime }$$

(26)

where $t_{\mathrm{g}}^{\prime }$ is the working time of the energy-release process under the long-timescale condition, and $W_{\mathrm{g}}^{\prime }$ is the generation capacity during the energy-release process under the long-timescale condition.

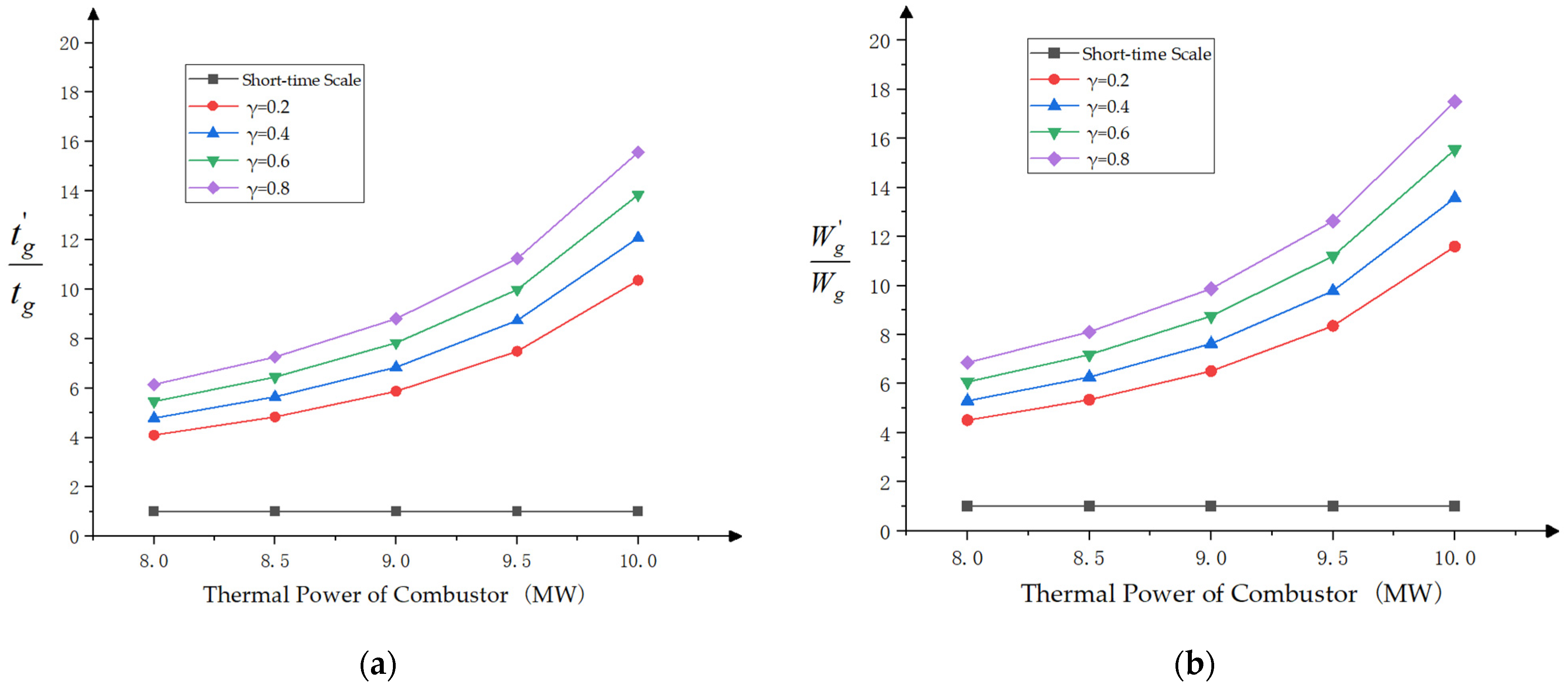
4.2.5. Simulation Analysis

From Equations (25) and (26), it can be seen that the power-generation capacity and power-generation time in a long timescale are affected by the ejection coefficient of the ejector and the thermal power of the burner, and their relationships are shown in Figure 6a,b. It can be seen from Figure 6a,b that, when the ejector coefficient is 0.2 and the burner thermal power is 8 MW, the power-generation time is 3.28 h and the power-generation capacity is 36,114.3 kW·h, which are 4.1 and 4.5 times that of the short-timescale conditions, respectively. When the ejector coefficient and burner thermal power are increased to 0.8 and 10 MW, the power-generation time and power-generation capacity increase by 8.35 h and 103,937.7 kW·h, which are 15.6 and 17.5 times that of those of the short-timescale conditions, respectively.

Under the condition of the long timescale, increasing the ejection coefficient can increase the power-generation time and power-generation capacity of the system. When the compressed-air mass available in the gas storage tank and the flow rate after passing through the jet are constant, increasing the ejection coefficient will make the air flow into the jet decrease and prolong the power-generation time. The power-generation time and power-generation capacity will increase with the increase of the burner thermal power. This is because increasing the burner thermal power will lead to the specific enthalpy of the intake air of the first-stage expander increasing, thus reducing the compressed air flow required to achieve the rated power. Meanwhile, compared with the ejector coefficient, the change of burner thermal power has a more obvious influence on the power-generation time and power-generation capacity.

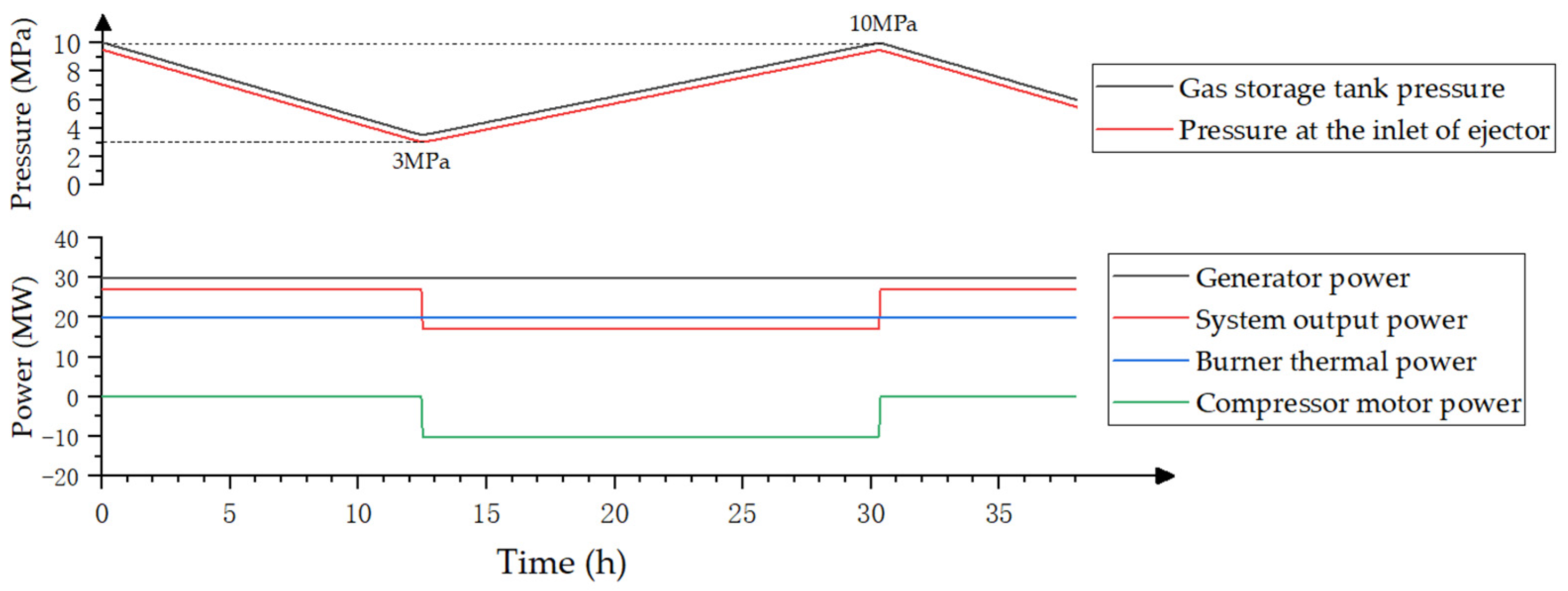
4.3. Continuous-Output Condition

The continuous-output condition is that the energy-storage stage and energy-release stage are carried out simultaneously. The energy-storage stage can provide high-pressure compressed air for the energy-release stage, while the generator provides electricity energy for the energy-storage subsystem. The power-generation capacity of the whole system is improved by increasing the air mass flow of the expander through the ejector and increasing the air enthalpy at the inlet of the expander by burning natural gas in the external burner.

4.3.1. Constraint Conditions

The construction of continuous-output conditions needs to meet the following constraints:

$$\{\begin{array}{c}{P}_{\mathrm{g}}^{″}>P_{\mathrm{u}}\\ G_{\mathrm{g}}^{″}<G_{\mathrm{c}}\\ p_{\mathrm{p}}>p_{\mathrm{g},\lim }\end{array}$$

(27)

where $P_{\mathrm{g}}^{″}$ is the generating power of the energy-release subsystem, $P_{\mathrm{u}}$ is the system power consumption, $G_{\mathrm{g}}^{″}$ is the air mass flow of compressed air into the jet, $G_{\mathrm{c}}$ is the air mass flow at the outlet of the last-stage compressor, $P_{\mathrm{p}}$ is the pressure of high-pressure gas storage tank, and $P_{\mathrm{g},\lim }$ is the minimum working pressure of the ejector.

Through the above constraints, it is ensured that the mass flow rate of the working air consumed by the ejector is less than or equal to the mass flow rate at the outlet of the last-stage compressor, so that the system has working air that can meet the continuous operating conditions. Meanwhile, it ensures that the ejector can work normally and prevents the ejector from not forming an entrainment effect due to a too-low working pressure.

The generating power of the energy-release subsystem is the same as that under the long-timescale condition:

$$P_{\mathrm{g}}^{″}=P_{\mathrm{g}}^{\prime }=\frac{\left(G_{\mathrm{g}}^{″}\left(1+\gamma \right)\times {{\displaystyle \sum }}_{i=1}^m\left(h_{\mathrm{t}i,\mathrm{in}}^{″}-h_{\mathrm{t}i,\mathrm{out}}^{″}\right)+Q_{\mathrm{b}}\right)}{3600}\times {\eta }_{\mathrm{g}}\times {\eta }_{\mathrm{t}}$$

(28)

The power consumption of the whole system is as follows:

$$P_{\mathrm{u}}=P_{\mathrm{m}}+{\displaystyle \sum }{P}_{\mathrm{o},\mathrm{m}}+{\displaystyle \sum }{P}_{\mathrm{o},\mathrm{g}}$$

(29)

where $P_{\mathrm{o},\mathrm{m}}$ is the electric power consumed by other auxiliaries in the energy-storage subsystem, and $P_{\mathrm{o},\mathrm{g}}$ is the electric power consumed by other auxiliaries in the energy-release subsystem.

The system’s generating power is as follows:

$$P_{\mathrm{s}}=P_{\mathrm{g}}^{″}-P_{\mathrm{u}}$$

(30)

where $P_{\mathrm{u}}$ is the generating power of the whole system.

4.3.2. Simulation Analysis

Under continuous-output conditions, the compression energy-storage subsystem, gas-storage subsystem, and expansion energy-release subsystem are all put into operation, and their operating parameters are shown in Figure 7. During the duration of 0–12.45 h, the system operates under the long-timescale condition, and the system’s output power is 27 MW. When the air pressure at the inlet of the ejector drops to 3 MPa, the compression energy-storage subsystem is put into operation, and gas storage tank’s pressure rises. The system operates under continuous-output conditions, and the compressor’s motor power is 10 MW, so that the system’s output power drops to 17 MW. When the gas storage tank’s pressure rises to 10 MPa again, the compression energy-storage subsystem stops running.

5. Conclusions

The current literature has identified the CAES as a potentially important part of coupling renewable energy generation and low-carbon power grids. The extreme conditions of the long timescale’s fluctuation and zero-power generation of the new energy power generation require that the CAES system has the ability to generate electricity on multiple timescales. The existing commercial CAES systems cannot meet the needs of multi-timescale power generation well compared to the system studied in this paper. The AA-CAES system can only meet the needs of short-timescale power generation. The supplementary combustion CAES system can meet the needs of short-timescale and long-timescale power generation, but it will cause pollution problems in the short-timescale power generation due to supplementary combustion compared to the system studied here.

In this paper, a new type of compressed-air energy-storage system with an injector and burner was established. The simulation analysis was carried out under short-timescale, long-timescale, and continuous-output conditions, sequentially. Several conclusions were obtained:

(1)

The new system can meet the needs of multiple timescales under different operating conditions. The energy-storage stage of the new system is consistent with that of the AA-CAES system, and there are three operation modes in the energy-release stage which can flexibly adapt to three power-generation conditions: short timescale, long timescale, and continuous output.

(2)

Under the short-timescale condition, the ejector and combustor are not put into operation, and the CAES system operates as adiabatic compression/expansion processes, which do not need to burn natural gas and are environmentally friendly.

(3)

Under medium- and long-timescale conditions, the ejector and combustor are put into operation to prolong the duration of the power generation, so that the new system can meet the needs of long-timescale power generation. Moreover, the power-generation duration and capacity of the system improve with the increase of the ejector coefficient and burner thermal power. When the ejector coefficient is 0.8 and the burner thermal power is 10 MW, the power-generation time is 12.45 h, and the power-generation capacity is 140,052 kW∙h, which are 15.6 and 17.5 times that of the short-timescale conditions, respectively.

(4)

Under the continuous-output condition, the energy-storage system and energy-release system operate at the same time. The energy-storage subsystem provides high-pressure compressed air for the energy-release stage, while the generator provides electricity for the energy-storage subsystem. By selecting equipment parameters according to the constraint conditions, the new system can realize continuous power output.