Abstract
Cold climate regions have great potential for wind power generation. The available wind energy in these regions is about 10% higher than in other regions due to higher wind speeds and increased air density. However, these regions usually have favorable icing conditions that lead to ice accumulation on the wind turbine blades, which in turn increases the weight of the blades and disrupts local airflow, resulting in a reduction in wind turbine performance. Considering this problem, plasma actuators have been proposed as devices for simultaneous flow control and deicing. These devices transfer momentum to the local airflow, improving the aerodynamic performances of the turbine blades while producing significant thermal effects that can be used to prevent ice formation. Considering the potential application of plasma actuators for simultaneous flow control and deicing, it is very important to investigate the thermal effects induced by these devices. However, due to the significant electromagnetic interference generated by the operation of these devices, there is a lack of experimental techniques that can be used to analyze them. In the current work, a background-oriented Schlieren system was developed and is presented as a new experimental technique for the thermal characterization of the plasma-induced flow. For the first time, the induced flow temperatures are characterized for plasma actuators with different dielectric materials and different dielectric thicknesses. The results demonstrate that, due to the plasma discharge, the temperature of the plasma-induced flow increases with the increase of the applied voltage and may achieve temperatures five times higher than the room temperature, which proves the potential of plasma actuators for deicing applications. The results are presented and discussed with respect to the potential application of plasma actuators for simultaneous flow control and deicing of wind turbine blades.
1. Introduction
Cold regions at very high altitudes are generally very attractive for wind power generation. These regions usually present larger wind speeds and higher air densities at lower temperatures and conditions that result in about 10% more available wind energy than in other regions [1,2,3,4]. Due to these optimal conditions, nowadays, about a quarter of the world’s wind turbines are installed in cold climate regions [5,6]. However, these regions are prone to ice formation that gradually accumulates on the wind turbine blades and considerably reduces the wind turbine performance [7,8]. It is estimated that, depending on the icing duration, icing accumulation on the wind turbine blades can be responsible for 50% of power loss per year [9]. In addition to the power losses, ice accretion also increases the maintenance costs of wind turbines due to the creation of unbalanced loads, which deteriorates the components and shortens their lifetime [10].
In these circumstances, various types of ice protection systems have been studied and developed over the years [4,9]. Dielectric barrier discharge (DBD) plasma actuators are recent technologies proposed for ice protection systems [11,12,13]. These electronic devices have been studied throughout the years as active flow control means [14,15,16,17]; however, lately, several authors have demonstrated that they produce considerable thermal effects that can be used for deicing or ice prevention purposes [18,19,20,21]. When the actuator is supplied with a high voltage and high-frequency signal, the adjacent air is ionized and the charged particles are accelerated downstream. As a result, the actuator imparts a body force on the adjacent air, which is pulled toward the surface and accelerated downstream, tangentially to the actuator surface [22,23]. Besides this aerodynamic plasma effect, plasma actuators also generate significant thermal effects. In fact, only a very small fraction of the power applied to the actuator is transferred to the adjacent air as kinetic energy while the larger percentage is dissipated as heat. When a dielectric is under the action of an alternating electric field, as is the case with DBD plasma actuators, part of the power is dissipated as dielectric heating due to the phenomenon of dielectric hysteresis, which is similar to hysteresis in ferromagnetic materials. In addition, during the plasma discharge, a significant percentage of energy is also dissipated by elastic collisions of electrons, vibrational excitations, collisions between ions and neutral molecules, and thermal energy transferred from electrons to neutral particles [24]. Due to these thermal phenomena, plasma actuators locally release a large amount of heat, which increases the surface temperature to levels considerably higher than the water freezing temperature, making ice formation and/or accumulation impossible. In addition, researchers also demonstrated the possibility of using them as ice capacitive sensors and, therefore, when integrated into ice protection systems, these devices allow for performing active flow control, deicing, and ice detection operations [25,26,27]. Within this framework, various authors focused on the study of the thermal characteristics of plasma actuators and their application for deicing and ice prevention accumulation. However, in a few studies, researchers reported difficulties in studying these devices and a lack of experimental techniques for that purpose, due to the magnitudes of high voltage required for their operation and subsequent generation of high electromagnetic interference [24,28]. Considering this, the current work aims to present and implement a background-oriented schlieren (BOS) technique as an alternative tool for thermal characterization of the flow induced by plasma actuators.
Although Schlieren techniques started to be implemented in the seventeenth century, the pioneering works employing the background-oriented schlieren method were only reported at the beginning of the 2000s [29]. Dalziel et al. [30] presented novel techniques based on the Schlieren method for accurate density field measurements and Raffel et al. [31] implemented a technique, based on the same principles, for density field visualization of blade tip vortex interactions from a helicopter in hover flight. Meanwhile, Richard et al. [32,33] presented the principle and applications of a background-oriented schlieren method and used it to investigate the details of the blade–vortex interactions of two different helicopters in flight. In the meantime, Meier [34] introduced the technique as a computerized schlieren measurement method based on the refractive index variations of a propagation medium. As explained in the above-mentioned works, in its simplest form, the BOS method uses only a randomly dotted background and a camera. The camera is used to capture high-resolution images with and without refractive disturbances of the medium in between the two. The images are then post-processed using specific software that reveals the small distortions of the background due to refraction, which in turn allows estimating the density gradients in terms of the magnitude and direction.
After these initial studies introduced the BOS technique, this method continued to be used throughout the years by several different authors. Venkatakrishnan and Meier [35,36] applied the BOS technique for density measurements of complex underexpanded jet flow and axisymmetric supersonic flow over a cone cylinder. Goldhahn and Seume [37] acquired the three-dimensional density information of a and investigated the sensitivity, accuracy, and resolution of the implemented double-free air jet BOS method. They explained that the sensitivity depends mostly on the focal length of the lens, positioning of the phase shift object, and the smallest detectable displacement in the background. On the other hand, the resolution depends on the interrogation window used for the cross-correlation algorithm. Later, Atcheson et al. [38] analyzed the impacts of different background patterns and different optical flow algorithms for the displacement vector analysis and demonstrated that the performances of BOS systems can be considerably improved through a combination of optical flow algorithms and multiscale backgrounds. In turn, Hargather and Settles [39] compared the BOS method with two quantitative schlieren methods, the lens-calibrated standard schlieren and the rainbow schlieren, and concluded that the BOS technique produces good results and requires a cheaper apparatus than the remaining methods.
Considering the potential of the BOS technique, throughout the years, this optical method has been used for studies within different applications, including the analysis of the shock wave propagation from explosions [40], underwater shock waves [41,42], heat transfer processes [43,44,45], air leakage [46], and flame-induced flow [47,48], among others [49,50,51,52,53,54]. Recently, the BOS measurement technique began to be used for density field quantification of the DBD flow induced by plasma actuators. Biganzoli et al. [55], in a short note published in 2015, introduced the possibility of adopting the BOS technique for studying the capabilities of surface dielectric barrier discharges; however, this technique was only applied on a detailed analysis of DBD plasma actuators a few years later in the work carried out by Komuro et al. [56]. In this work, the authors investigated the spatiotemporal changes in the absolute density promoted by a plasma actuator operating at different voltage levels. However, they only obtained the density gradients and quantified the plasma-induced temperature field. Later, Kaneko et al. [57,58] investigated the effects of the depth of field, wall surface, and background image deformation on measurements of the near-surface density field in DBD plasma actuators. They also investigated the errors associated with the measurements of density variation fields generated by plasma actuators and confirmed that the BOS technique allows for obtaining valid results. Once again, in this work, the authors obtained the density gradients but not the temperature field. Recently, Emori et al. [59] used the background-oriented schlieren method for density field measurement of DBD plasma actuators operating in burst mode.
As we can see, although the background-oriented schlieren is a powerful technique for fluid flow density measurements, studies implementing this method for DBD plasma actuator analyses are scarce. Nevertheless, the BOS technique is a non-intrusive method that does not cause any disturbance in the small-scale plasma-induced flow. On the other hand, plasma actuators generate high electromagnetic interferences, which affect the operation of several conventional measurement techniques, such as temperature measurements with thermocouples. This is a problem that can be overtaken with the BOS technique, which is an optical method and, thus, is not affected by the high electromagnetic interference generated in the plasma discharge. In addition, by applying the methodology presented by Guo et al. [60], the density fields obtained with the BOS technique can be used to reconstruct the temperature field of the plasma-induced flow. Considering this, in the current study, the BOS method was implemented for thermal analysis of the plasma-induced flow by DBD plasma actuators and, for the first time, the temperature of the plasma-induced flow was experimentally obtained. The BOS system was used to obtain the density field variations of the plasma-induced flow and a short Matlab algorithm was used to numerically compute the temperature field. Before implementing this methodology to the plasma-induced flow analysis, the convective flow generated by two distinct flames was analyzed by this method and validated with results obtained with thermocouple measurements. After the validation of the BOS technique for flow temperature reconstruction, plasma actuators were fabricated with different dielectric thicknesses and materials and were experimentally tested. The different actuators were tested in terms of electrical parameters, induced flow velocity, and by implementing the BOS technique (also in terms of induced flow temperature field). The plasma-induced flow temperature fields constitute new results that have not been reported before in the literature and which allow evaluating the thermal impacts of plasma actuators on the adjacent flow. The results are presented and discussed considering the application of plasma actuators for simultaneous active flow control and deicing of wind turbine blades operating in cold climates.
2. Experimental Setup and Methods
In the current work, the experimental setup contains all the elements needed to implement the BOS technique and those needed to operate and characterize the different dielectric barrier discharge plasma actuators. Figure 1 presents a schematic and a photo of the experimental setup used.
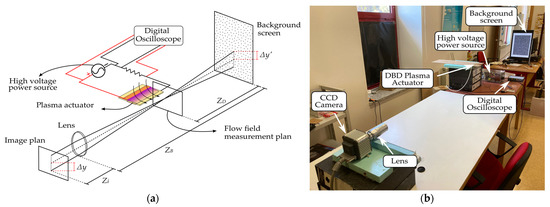
Figure 1.
Experimental setup (a) schematic of the implemented BOS method; (b) photo of the equipment used.
For implementing the background-oriented Schlieren technique, we used a CCD camera model, C10600-10B ORCA-R2, with a 2/3” CCD sensor coupled to a lens model Schneider TELE-XENAR 4,0/150 CM 120, which allows capturing images with a resolution of . The background originated with a conventional computer screen of 24” that produces a synthetic image containing 900,000 particles randomly distributed. The distances used between the various elements of our BOS system are the results of a calibration process involving several laboratory tests, which aimed to set up the system with the optimized distances for the visualization of the flow induced by the various phase objects. The BOS system has a 3.7 m overall length and the distances are the following: ZD = 2.15 m, which corresponds to the distance between the background and the phase object, ZB = 3.55 m, which corresponds to the distance between the background and the lens and Zi = 0.15 m, which corresponds to the lens length. In Figure 1, ∆y’ represents the displacement of the background spots due to the density gradients in the measurement plan, and ∆y is the displacement calculated in the obtained images by using a cross-correlation analysis.
Initially, a pair of images with and without the influence of the phase object was captured using the camera and then analyzed through a cross-correlation measurement based on the PIV method. The interrogation window was pixels with a 50% step in order to increase the resolution and as suggested by Guo et al. [60]. After obtaining the particle displacement fields through the cross-correlation analysis, the reconstruction of the density field is then based on the solution of Poisson’s equation, described as follows:
where ∆x and ∆y represent the particle’s displacements in both directions, horizontal and vertical, in relation to the variables x and y, n is the refractive index inside the phase object and n0 is the refractive index of the medium. Poisson’s equation is solved by Liebmann’s numerical method and is used for the solution of the refractive index n. This solution is obtained by imposing Neumann boundary conditions at the inlet and outlet sides and Dirichlet boundary conditions on the two other sides. Then, using the Gladstone–Dale relation, described by Equation (2), the density field is obtained.
K is the coefficient of Gladstone–Dale, which has a value of approximately 2.27 × 10−4 m3/kg for air and lights with wavelengths in the visible spectrum, as we can see in the literature [36,56,57,60]. Furthermore, if the condition of the ideal gas is considered, we can also obtain the temperature field according to the following equation:
In which p is the pressure, R is the constant of the perfect gases, which is approximately 287 J/kg·K, and T is the temperature. Since the ambient conditions are known, the following relation can give us the temperature field of the phase object as follows:
In which is the density of the environment and T0 is the ambient temperature. In order to validate the background-oriented schlieren system, a type K thermocouple connected to an Arduino Uno was used to measure the temperature of the convective flow generated by different objects. This K thermocouple presents an uncertainty of ±2.2 °C and can be used to measure temperatures in a range of −200 to 1260 °C.
Regarding the DBD plasma actuators fabricated and tested in the current work, they were 10 cm in length and 5 cm in width, and the electrodes were made of 0.08 mm thick copper tape (9 cm in length). Figure 2 presents a schematic and a photo of the fabricated plasma actuators. The exposed electrode is 1 cm in width and the embedded electrode is 2 cm in width to ensure that it does not limit the plasma discharge extension. The electrodes are asymmetrically disposed of in such a way that they generate a plasma discharge at a length of 8 cm. For analyzing the influence of the dielectric thickness on the plasma-induced flow temperature, plasma actuators with thicknesses of 0.3 mm, 0.6 mm, and 1.02 mm were fabricated by overlapping several layers of Kapton tape. Furthermore, for understanding the influences of different dielectric materials on the plasma-induced flow temperatures, plasma actuators were fabricated with 1 mm of thickness of PIB rubber, Teflon, and PMMA materials, which are widely used materials as dielectric barrier discharge layers. To estimate the power consumption of these actuators, the electric current method, described in the literature [61,62], was used, in which a resistor with an impedance of 100 Ω and 1% tolerance was placed between the covered electrode and ground. The actuators were operated by using an AC high voltage power source model “PVM 500”; a digital oscilloscope model “PicoScope 5443 A” was used to acquire the electrical signals of the system.
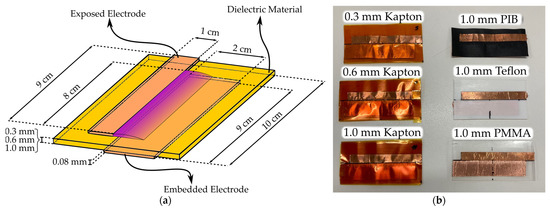
Figure 2.
Plasma actuators tested (a) schematic of the plasma actuator’s dimensions; (b) photo of the fabricated plasma actuators.
3. Results
In this section, the experimental results are presented and discussed. Firstly, the reconstructed temperature fields of two different convective flows are shown and compared with our thermocouple measurements and state-of-the-art results. After the BOS system validation, the electrical and mechanical characterization of the plasma actuators is exposed for different dielectric thicknesses and materials. Finally, we present the temperature fields obtained for the different actuators with our proposed BOS technique; we considered the possible application of these devices for flow control and deicing in wind turbines.
3.1. Background-Oriented Schlieren Method Validation
The validation of our background-oriented schlieren setup was done by using two elementary phase objects. The validation was performed using the same methodology as Guo et al. [60] by applying the BOS method to reconstruct the temperature field of the convective flow produced by a burning candle and comparing it with results measured by a thermocouple. In addition, in order to have a second validation for different temperature ranges, the validation was also performed for the convective flow resultant from the flame of a blow torch. Figure 3 presents the temperature fields obtained with the BOS method for the convective flow generated by the flame of a candle and a blow torch. The temperature fields were obtained at a distance of 0.15 m from the bottom of the candle and 0.07 m from the nozzle of the torch, to ensure that the light emitted from the flame produced by each object did not affect the measurement. The results were obtained at a room temperature T0 of 298.15 K (25 °C).
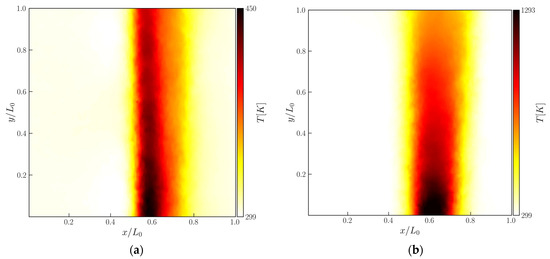
Figure 3.
Temperature field obtained by the implemented background-oriented schlieren method for two different convective flows (a) burning candle; (b) blow torch.
As expected, in Figure 3, we observe that the larger temperature gradients were found in the centerlines of the convective flows produced by the two different flames. In addition, larger temperatures were found at the bottom of the measurement plan for y/L0 = 0, since this region is closer to the flame, and gradually decreases along the vertical direction. Although we cannot quantitatively compare our results with the results obtained by Guo et al. [60] since there is ambiguity on the type of candles used, we verify that our results demonstrate a similar temperature distribution and that the convective flow temperature field presents the same order of magnitudes. Since the larger temperature gradients are found in the centerlines of the convective flows, a type K thermocouple was used to measure the convective flow temperature in this region for different points along the vertical direction. The temperature measurements obtained with the thermocouple and the corresponding temperature values obtained with the BOS technique, for the two different convective flows, are presented in Table 1.

Table 1.
Comparison between the thermocouple temperature measurements and the reconstructed temperature field obtained by the BOS technique.
As we can see from Table 1, the results obtained with the thermocouple are consistent with the results extracted from the BOS temperature field. The relative error between the thermocouple measurement and the BOS method results for the different points was estimated and the highest value found was about 7%. With this in mind, we can conclude that the BOS technique is well-calibrated and allows us to obtain accurate temperature field estimations with an average error lower than 7%. Although we are going to use the BOS method to quantify the temperature field of the plasma-induced flow, this type of validation could not be applied to the plasma flow, since the high electromagnetic interference generated in the plasma region does not allow measuring the flow temperature with thermocouples or other temperature sensor devices. However, with the results obtained here for two different convective flows free of electromagnetic interference, we can conclude that the BOS-implemented setup will allow us to accurately quantify the plasma-induced flow temperatures.
3.2. Electrical and Mechanical Characterizations of Plasma Actuators
Before applying the BOS technique for the temperature characterization of the flow induced by plasma actuators, the various plasma actuators with different thicknesses and different dielectric materials were characterized in terms of electrical and fluid mechanical parameters. First, the electric current method was applied for obtaining the voltage and current waveforms and, with that, the actuator power consumption, which is plotted for different voltage levels in Figure 4. The current and voltage waveforms were acquired over 12 AC voltage signals with a sampling rate of 125 MS/s and a vertical resolution of 14 bits. Considering the acquisition parameters and the accuracy of the oscilloscope and the low uncertainty of the resistor, the uncertainty of the electrical power consumption results presented in Figure 4 is lower than 2%.
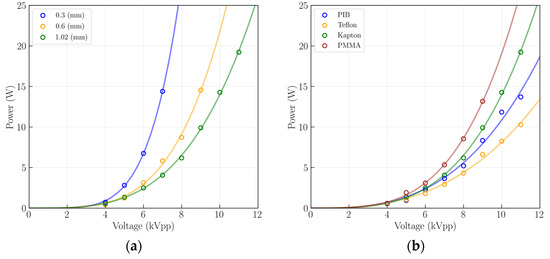
Figure 4.
Power consumption curves obtained for different input voltage levels and a frequency of 24 kHz for dielectric layers made of (a) Kapton with different thicknesses; (b) different materials with 1 mm of thickness.
As we can see from Figure 4, the electrical power consumption increases with the increase of the applied voltage and it can reach values from 1 to 20 W, depending on the applied voltage, dielectric thickness, and dielectric material. Figure 4a demonstrates that with the increase in thickness, the power consumed by the actuator for the same voltage level decreases. This behavior is congruent with the results reported in the literature [24] and is also related to the increase in the breakdown voltage due to the thickness increase. In order words, when the dielectric thickness increases, the voltage level required to ignite the plasma increases as well, and, thus, the actuator will only consume larger levels of power for higher applied voltage magnitudes. From the results presented in Figure 4b, we observe that the type of dielectric material also influences the power consumption behavior. From the tested materials, we observed that PMMA consumes higher levels of power at the same applied voltage, followed by Kapton, PIB rubber, and Teflon actuators.
To analyze the fluid mechanical characteristics of the different dielectric barrier discharge plasma actuators, conventional Pitot tube measurements were performed. The velocity measurements were performed at a distance of 1.5 cm from the exposed electrode since, according to the literature; this is the region where the induced flow velocities are larger [63,64]. The velocity was acquired within 10 s for each vertical point, at a sampling rate of one sample per second, and in order to reduce the error; the final results were obtained by averaging the acquired samples. Figure 5 shows the velocity profiles experimentally obtained for actuators with different thicknesses and dielectric materials with the corresponding errors calculated by the standard deviation of the mean. The velocity profiles for actuators with different dielectric thicknesses of Kapton operating at 7 kVpp and 24 kHz are shown in Figure 5a. This specific applied voltage was chosen because it was the largest value supported by the 0.3 mm actuator of Kapton. For the comparison between different dielectric materials, the velocity profiles are shown for an applied voltage of 9 kVpp since this was the largest value supported by the actuator made of PMMA. The velocity profile-fitting curves were computed using the method described in Nunes-Pereira et al. [65].
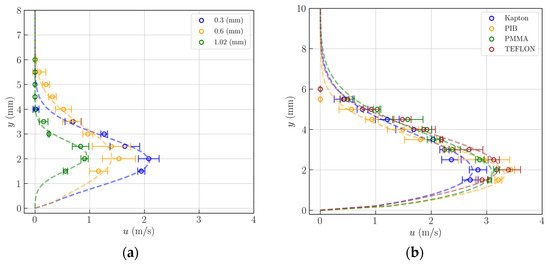
Figure 5.
Induced flow velocity profiles obtained for different plasma actuators operating at a frequency of 24 kHz for actuators made of (a) Kapton with different dielectric thicknesses operating at 7 kVpp; (b) different dielectric materials with 1 mm of thickness operating at 9 kVpp.
From the velocity profiles, we verify that, at the same applied voltage, thinner actuators induce larger flow velocities. However, during the experiments, we also noticed that thin actuators were more prone to quick degradation; for example, the 0.3 mm actuator could not operate at voltages higher than 7 kVpp without failing. For the actuators made of different dielectric materials, we verified that by operating at the same voltage level, the actuators made of PIB and Teflon were able to induce higher flow velocities, followed by the actuators of PMMA and Kapton. Regardless of the type of dielectric material and thickness, the plasma flow was induced in a region very close to the surface and the maximum velocities were achieved up to 2 mm from the surface.
To further extend the fluid mechanical analysis, the mechanical power and efficiencies of the different actuators were calculated as explained in [63,66]. The obtained results are presented in Table 2. It is worth mentioning that although the values of mechanical power and efficiency are significantly low, they are in line with the reported values found in the literature [63,64].

Table 2.
Comparison between the thermocouple temperature measurements and the reconstructed temperature field obtained by the BOS technique.
From Table 2, we can verify that the actuators with lower thicknesses allowed for achieving higher flow-induced velocities at the same applied voltages. However, we can also verify that higher efficiencies were achieved when actuators operated at larger voltage levels, and since the thinner actuators could not support these voltage levels without suffering significant degradation, the mechanical efficiencies achieved with thin actuators were smaller. Moreover, the maximum-induced flow velocities were achieved with Teflon and PIB rubber actuators, which presented close maximum velocity values at different applied voltages. The PMMA actuator also allowed inducing flow velocities with similar magnitudes to PIB and Teflon actuators; however, it showed quick degradation for larger voltage levels and, thus, we could only test it up to 9 kVpp without burning. In terms of mechanical efficiency, we verified that the power consumed by the actuator had a great impact on it. Due to that, and since the Teflon actuator presented lower power consumption values, the Teflon actuator allowed obtaining considerably larger mechanical efficiencies than the remaining actuators.
3.3. Flow-Induced Temperature Characterization
As explained, considering the potential of DBD plasma actuators for simultaneous deicing and flow control on wind turbine blades, it is important to study the thermal effects induced by these devices. For that purpose, the convective flow produced by the different plasma actuators was experimentally analyzed with the BOS method, and the temperature field of the plasma-induced flow was estimated. In Figure 6, we present the temperature field contours obtained for actuators made of Kapton with different dielectric thicknesses, operating at 7 kVpp and 24 kHz.
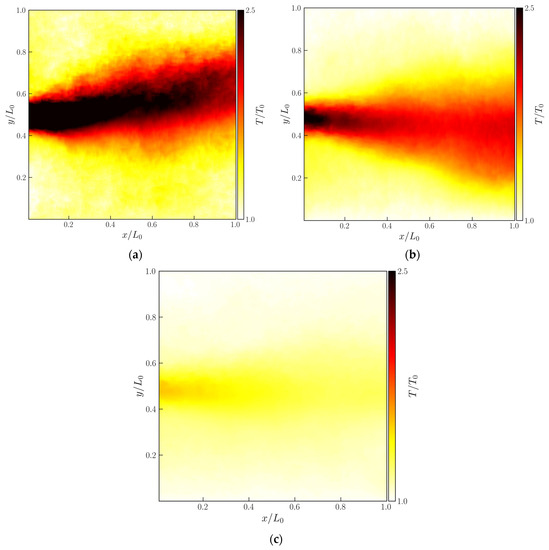
Figure 6.
Plasma-induced flow temperature field, at a steady state, for actuators made of Kapton with different dielectric thicknesses, (a) 0.3 mm; (b) 0.6 mm; (c) 1.02 mm, all operating at 7 kVpp and 24 kHz.
As we observed in the previous section, actuators with smaller thicknesses have a lower breakdown voltage level and, thus, can ignite the plasma at lower applied voltages. Due to that, they present larger power consumption compared to thicker actuators operating at the same applied voltage. On the other hand, we know that from the power consumed by the actuator, a large percentage of power is dissipated as heat, and only a very small percentage is converted as kinetic energy. Thus, actuators with larger power consumption should dissipate a larger amount of power as heat. This trend is clearly observed in Figure 6, in which we verify that, for the same applied voltage and frequency, the thinnest actuator induces considerably higher temperature levels. When the actuator thickness is increased, the induced flow temperature reduces, as well as the impact of the actuator on the adjacent air temperature field.
In order to understand the influences of different dielectric materials on the plasma-induced flow temperature, the actuators made of different dielectric materials were also analyzed with the BOS method. The plasma-induced flow temperature results obtained for actuators made of different dielectric materials operating at 9 kVpp and 24 kHz are presented in Figure 7.
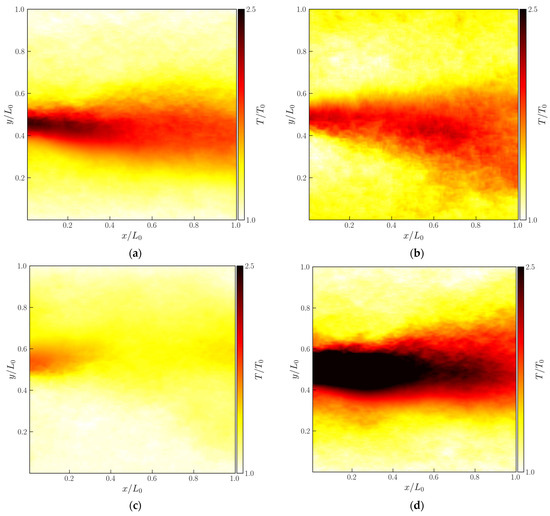
Figure 7.
Plasma-induced flow temperature field, at steady state, for actuators with 1 mm thickness of, (a) Kapton; (b) PIB rubber; (c) Teflon. (d) PMMA. All operating at 9 kVpp and 24 kHz.
From the analysis of Figure 7, once again we verify that the trend observed in the power consumption is reflected in the plasma-induced temperature fields. Since the PMMA actuator consumes larger power and allows for achieving higher temperatures than the remaining actuators operating at the same applied voltage and frequency. On the opposite side, we verify that the Teflon actuator, since it presents lower power consumption levels, induces a convective flow with smaller temperature magnitudes. Considering this and the fluid mechanical results, we may conclude that although PMMA material is associated with lower mechanical efficiencies, it allows for inducing velocities closer to those obtained with the remaining actuators and it induces considerably higher convective flow temperatures, which can be beneficial for deicing and ice control applications.
For a better understanding of the thermal behavior of the plasma-induced flow, the maximum temperatures achieved by the various actuators were obtained for different applied voltage levels. These results are shown in Figure 8.
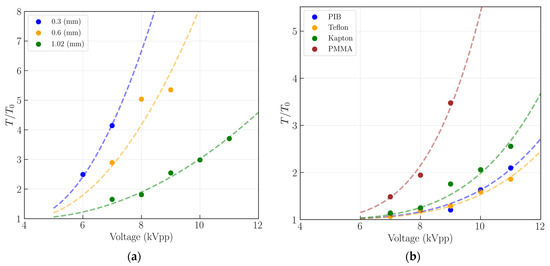
Figure 8.
Plasma-induced flow–maximum temperatures achieved operating at different voltage levels and a frequency of 24 kHz for the actuators made of (a) Kapton with different dielectric thicknesses; (b) different dielectric materials with a thickness of 1 mm.
From Figure 8, we observe that by disregarding the applied voltage level, thinner actuators induce higher maximum flow temperatures and, at the same operating voltage, the plasma-induced flow temperature decreases for larger dielectric thicknesses. These results are completely concordant with the results reported by Rodrigues et al. [18,19] where the authors measured the actuator surface temperature and concluded that the actuator surface temperature decreases with the increase in the dielectric thickness. Since the plasma heat is simultaneously dissipated to the dielectric layer and adjacent air, it is logical that both the surface temperature and induced flow follow the same trend. Comparing the different dielectric materials, we conclude that PMMA leads to the highest maximum temperatures, followed by the Kapton actuator, PIB rubber actuator, and, lastly, the Teflon actuator. Interestingly, this trend is also concordant with the surface temperature results reported in the work by Abdollahzadeh et al. [27].
Considering the results obtained in the current study, we may conclude that for deicing purposes, the use of thinner dielectrics is beneficial since they allow for achieving higher convective flow temperatures than thicker actuators operating at the same voltage level. However, thinner actuators degrade faster and cannot operate at high voltage levels, presenting lower mechanical efficiencies. On the other hand, from the comparison of different dielectric materials, we verified that the PMMA actuator allows for achieving considerably higher-induced flow temperatures than the remaining tested materials. Nevertheless, the PMMA, similar to the thinnest actuator, showed quicker degradation and had to operate at lower voltage levels than the actuators made of different dielectric materials. This behavior suggests that the temperature achieved in the actuator surface and induced flow have direct contributions to the actuator degradation and higher surface/flow temperatures lead to quicker actuator degradation.
4. Conclusions
The current work demonstrated the feasibility of the BOS method for the thermal characterization of plasma-induced flow. The BOS experimental setup was calibrated and validated with two different convective flows and it was demonstrated that the BOS method allows for accurately quantifying the temperature fields of convective flows. Considering the potential of plasma actuators for deicing and ice prevention applications and the importance of studying the thermal effects produced by these devices, the BOS method was applied to analyze actuators with different dielectric thicknesses and materials. The present work demonstrated that since the BOS is an optical method, it is not affected by the electromagnetic interference generated by the plasma discharge region and, thus, is a suitable technique for plasma-induced flow thermal characterization.
Plasma actuators with different dielectric thicknesses and materials were studied. From the electrical analysis, we concluded that the power consumption increases with the increase of the applied voltage and it can reach values from 1 to 20 Watts, depending on the applied voltage, dielectric thickness, and dielectric material. In addition, we observed that with the increase of the thickness, the power consumed by the actuator, operating at the same voltage level, decreased. The type of dielectric material also influenced the power consumption behavior. From the tested materials, we observed that the PMMA consumed higher levels of power, at the same applied voltage, followed by Kapton, PIB rubber, and Teflon actuators. From the velocity measurements, we verified that thinner actuators induced the largest flow velocities, and the actuators made of PIB and Teflon were able to induce higher flow velocities, followed by the actuator of the PMMA and Kapton. Furthermore, we verified that higher efficiencies were achieved when actuators operated at larger voltage levels, and since thinner actuators cannot support these voltage levels without quick degradation, the mechanical efficiencies achieved with thin actuators were smaller. Moreover, the largest mechanical efficiencies were obtained with the actuator made of Teflon since it is a material that allows for inducing the highest velocity magnitudes with less power consumption.
By applying the BOS method, the plasma-induced flow temperature field was quantified. We verified that the thinner actuators generated and induced flow with higher temperature magnitudes than thicker actuators. We also concluded that the power consumption of the actuator was directly related to the flow temperatures produced. Therefore, since the PMMA actuator consumes larger power, it allows for achieving higher temperatures compared to the remaining actuators when operating at the same applied voltage and frequency. On the opposite side, we verified that the Teflon actuator induced a convective flow with quite smaller temperature magnitudes. Considering this, and also considering the fluid mechanical results, we may conclude that although PMMA material is associated with lower mechanical efficiencies, it allows for inducing velocities closer to the ones obtained with the remaining actuators and it induces considerably higher convective flow temperatures, which can be beneficial for deicing and ice control applications. Nevertheless, similar to the thinnest actuator, the PMMA showed quicker degradation and had to operate at lower voltage levels than the remaining actuators made of different dielectric materials. This behavior suggests that the temperature achieved in the actuator surface and induced flow have direct contributions to the actuator’s degradation and higher surface/flow temperatures reduce the actuator’s lifetime.
Author Contributions
Conceptualization, M.M. and F.R.; methodology, M.M. and F.R.; software, M.M., S.C. and G.S.; validation M.M.; investigation, M.M., F.R., S.C. and G.S.; writing—original draft preparation, M.M. and F.R.; writing—review and editing, M.M., F.R., S.C., G.S. and J.P.; supervision, J.P.; project administration, J.P.; funding acquisition, F.R., S.C. and J.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by C-MAST (Center for Mechanical and Aerospace Science and Technology), FCT research unit no. 151, project grant number UID/00151/2020 (F.R.), and by FCT, Foundation for Science and Technology, I.P., through the individual research grant number 2020.04517.BD (S.C.).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ali, Q.S.; Kim, M.-H. Design and performance analysis of an airborne wind turbine for high-altitude energy harvesting. Energy 2021, 230, 120829. [Google Scholar] [CrossRef]
- Fortin, G.; Perron, J.; Ilinca, A. Behaviour and modeling of cup anemometers under icing conditions. In Proceedings of the International Workshop on Atmospheric Icing of Structures, Montreal, QC, Canada, 12–16 June 2005. [Google Scholar]
- Manatbayev, R.; Baizhuma, Z.; Bolegenova, S.; Georgiev, A. Numerical simulations on static Vertical Axis Wind Turbine blade icing. Renew. Energy 2021, 170, 997–1007. [Google Scholar] [CrossRef]
- Parent, O.; Ilinca, A. Anti-icing and de-icing techniques for wind turbines: Critical review. Cold Reg. Sci. Technol. 2011, 65, 88–96. [Google Scholar] [CrossRef]
- Tao, T.; Liu, Y.; Qiao, Y.; Gao, L.; Lu, J.; Zhang, C.; Wang, Y. Wind turbine blade icing diagnosis using hybrid features and Stacked-XGBoost algorithm. Renew. Energy 2021, 180, 1004–1013. [Google Scholar] [CrossRef]
- Stoyanov, D.; Nixon, J.; Sarlak, H. Analysis of derating and anti-icing strategies for wind turbines in cold climates. Appl. Energy 2021, 288, 116610. [Google Scholar] [CrossRef]
- Wang, Q.; Yi, X.; Liu, Y.; Ren, J.; Li, W.; Wang, Q.; Lai, Q. Simulation and analysis of wind turbine ice accretion under yaw condition via an Improved Multi-Shot Icing Computational Model. Renew. Energy 2020, 162, 1854–1873. [Google Scholar] [CrossRef]
- Cheng, X.; Shi, F.; Liu, Y.; Liu, X.; Huang, L. Wind turbine blade icing detection: A federated learning approach. Energy 2022, 254, 12441. [Google Scholar] [CrossRef]
- Wei, K.; Yang, Y.; Zuo, H.; Zhong, D. A review on ice detection technology and ice elimination technology for wind turbine. Wind Energy 2020, 23, 433–457. [Google Scholar] [CrossRef]
- Yirtici, O.; Tuncer, I.H. Aerodynamic shape optimization of wind turbine blades for minimizing power production losses due to icing. Cold Reg. Sci. Technol. 2021, 185, 103250. [Google Scholar] [CrossRef]
- Liu, Y.; Kolbakir, C.; Hu, H.; Hu, H. A comparison study on the thermal effects in DBD plasma actuation and electrical heating for aircraft icing mitigation. Int. J. Heat Mass Transf. 2018, 124, 319–330. [Google Scholar] [CrossRef]
- Abdollahzadeh, M.; Rodrigues, F.; Pascoa, J. Simultaneous ice detection and removal based on dielectric barrier discharge actuators. Sens. Actuators A Phys. 2020, 315, 112361. [Google Scholar] [CrossRef]
- Rodrigues, F.F.; Abdollahzadeh, M.; Pascoa, J.; Pires, L. Influence of Exposed Electrode Thickness on Plasma Actuators Performance for Coupled Deicing and Flow Control Applications. In Proceedings of the Fluids Engineering Division Summer Meeting, Virtual, 10–12 August 2021; American Society of Mechanical Engineers, Fluids Engineering Division: New York, NY, USA, 2021; Volume 3. [Google Scholar] [CrossRef]
- Benmoussa, A.; Páscoa, J.C. Enhancement of a cycloidal self-pitch vertical axis wind turbine performance through DBD plasma actuators at low tip speed ratio. Int. J. Thermofluids 2023, 17, 100258. [Google Scholar] [CrossRef]
- Benmoussa, A.; Páscoa, J.C. Performance improvement and start-up characteristics of a cyclorotor using multiple plasma actuators. Meccanica 2021, 56, 2707–2730. [Google Scholar] [CrossRef]
- Pendar, M.-R.; Páscoa, J.C. Numerical Investigation of Plasma Actuator Effects on Flow Control Over a Three-Dimensional Airfoil With a Sinusoidal Leading Edge. J. Fluids Eng. 2022, 144, 081208. [Google Scholar] [CrossRef]
- Pendar, M.R.; Pascoa, J. Study of the Plasma Actuator Effect on the Flow Characteristics of an Airfoil: An LES Investigation. SAE Int. J. Adv. Curr. Pract. Mobil. 2021, 3, 1206–1215. [Google Scholar] [CrossRef]
- Rodrigues, F.F.; Pascoa, J.C.; Trancossi, M. Experimental Analysis of Dielectric Barrier Discharge Plasma Actuators Thermal Characteristics under External Flow Influence. J. Heat Transf. 2018, 140, 102801. [Google Scholar] [CrossRef]
- Rodrigues, F.F.; Pascoa, J.C.; Trancossi, M. Experimental Thermal Characterization of DBD Plasma Actuators. In ASME 2017 International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2017; Volume 1. [Google Scholar] [CrossRef]
- Kolbakir, C.; Hu, H.; Liu, Y.; Hu, H. An experimental study on different plasma actuator layouts for aircraft icing mitigation. Aerosp. Sci. Technol. 2020, 107, 106325. [Google Scholar] [CrossRef]
- Abdollahzadehsangroudi, M.; Pascoa, J.; Rodrigues, F. System for ice detection/prevention and flow control based on the impression of sliding plasma actuators with dielectric discharge barrier. WO2018060830A1, 25 September 2017. [Google Scholar]
- Rodrigues, F.; Páscoa, J.; Dias, F.; Abdollahzadehsangroudi, M. Plasma Actuators for Boundary Layer Control of Next Generation Nozzles. In ASME 2015 International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2015; pp. 1–2015. [Google Scholar] [CrossRef]
- Rodrigues, F.F.; Mushyam, A.; Pascoa, J.C.; Trancossi, M. A new plasma actuator configuration for improved efficiency: The stair-shaped dielectric barrier discharge actuator. J. Phys. D Appl. Phys. 2019, 52, 385201. [Google Scholar] [CrossRef]
- Rodrigues, F.; Pascoa, J.; Trancossi, M. Heat generation mechanisms of DBD plasma actuators. Exp. Therm. Fluid Sci. 2018, 90, 55–65. [Google Scholar] [CrossRef]
- Rodrigues, F.; Abdollahzadeh, M.; Pascoa, J.C.; Oliveira, P.J. An experimental study on segmented-encapsulated electrode dielectric-barrier-discharge plasma actuator for mapping ice formation on a surface: A conceptual analysis. J. Heat Transf. 2020, 143, 011701. [Google Scholar] [CrossRef]
- Rodrigues, F.F.; Nunes-Pereira, J.; Abdollahzadeh, M.; Pascoa, J.; Lanceros-Mendez, S. Comparative Evaluation of Dielectric Materials for Plasma Actuators Active Flow Control and Heat Transfer Applications. In Proceedings of the Fluids Engineering Division Summer Meeting, Virtual, 10–12 August 2021; American Society of Mechanical Engineers: New York, NY, USA, 2021; Volume 3. [Google Scholar] [CrossRef]
- Abdollahzadeh, M.; Rodrigues, F.; Nunes-Pereira, J.; Pascoa, J.; Pires, L. Parametric optimization of surface dielectric barrier discharge actuators for ice sensing application. Sens. Actuators A Phys. 2022, 335, 113391. [Google Scholar] [CrossRef]
- Tirumala, R.; Benard, N.; Moreau, E.; Fenot, M.; Lalizel, G.; Dorignac, E. Temperature characterization of dielectric barrier discharge actuators: Influence of electrical and geometric parameters. J. Phys. D Appl. Phys. 2014, 47, 255203. [Google Scholar] [CrossRef]
- Raffel, M. Background-oriented schlieren (BOS) techniques. Exp. Fluids 2015, 56, 60. [Google Scholar] [CrossRef]
- Dalziel, S.B.; Hughes, G.O.; Sutherland, B.R. Whole-field density measurements by ‘synthetic schlieren’. Exp. Fluids 2000, 28, 322–335. [Google Scholar] [CrossRef]
- Raffel, M.; Richard, H.; Meier, G.E.A. On the applicability of background oriented optical tomography for large scale aerodynamic investigations. Exp. Fluids 2000, 28, 477–481. [Google Scholar] [CrossRef]
- Richard, H.; Raffel, M.; Rein, M.; Kompenhans, J.; Meier, G.E.A. Demonstration of the applicability of a Background Oriented Schlieren (BOS) method. In Laser Techniques for Fluid Mechanics; Springer: Berlin/Heidelberg, Germany, 2002; pp. 145–156. [Google Scholar] [CrossRef]
- Richard, H.; Raffel, M. Principle and applications of the background oriented schlieren (BOS) method. Meas. Sci. Technol. 2001, 12, 1576–1585. [Google Scholar] [CrossRef]
- Meier, G. Computerized background-oriented schlieren. Exp. Fluids 2002, 33, 181–187. [Google Scholar] [CrossRef]
- Venkatakrishnan, L. Density Measurements in an Axisymmetric Underexpanded Jet by Background-Oriented Schlieren Technique. AIAA J. 2005, 43, 1574–1579. [Google Scholar] [CrossRef]
- Venkatakrishnan, L.; Meier, G.E.A. Density measurements using the Background Oriented Schlieren technique. Exp. Fluids 2004, 37, 237–247. [Google Scholar] [CrossRef]
- Goldhahn, E.; Seume, J. The background oriented schlieren technique: Sensitivity, accuracy, resolution and application to a three-dimensional density field. Exp. Fluids 2007, 43, 241–249. [Google Scholar] [CrossRef]
- Atcheson, B.; Heidrich, W.; Ihrke, I. An evaluation of optical flow algorithms for background oriented schlieren imaging. Exp. Fluids 2009, 46, 467–476. [Google Scholar] [CrossRef]
- Hargather, M.J.; Settles, G.S. A comparison of three quantitative schlieren techniques. Opt. Lasers Eng. 2012, 50, 8–17. [Google Scholar] [CrossRef]
- Hargather, M.J. Background-oriented schlieren diagnostics for large-scale explosive testing. Shock Waves 2013, 23, 529–536. [Google Scholar] [CrossRef]
- Hayasaka, K.; Tagawa, Y.; Liu, T.; Kameda, M. Optical-flow-based background-oriented schlieren technique for measuring a laser-induced underwater shock wave. Exp. Fluids 2016, 57, 179. [Google Scholar] [CrossRef]
- Yamamoto, S.; Tagawa, Y.; Kameda, M. Application of background-oriented schlieren (BOS) technique to a laser-induced underwater shock wave. Exp. Fluids 2015, 56, 93. [Google Scholar] [CrossRef]
- Vinnichenko, N.A.; Uvarov, A.V.; Plaksina, Y.Y. Combined study of heat exchange near the liquid–gas interface by means of Background Oriented Schlieren and Infrared Thermal Imaging. Exp. Therm. Fluid Sci. 2014, 59, 238–245. [Google Scholar] [CrossRef]
- Michalski, Q.; Parejo, C.J.B.; Claverie, A.; Sotton, J.; Bellenoue, M. An application of speckle-based background oriented schlieren for optical calorimetry. Exp. Therm. Fluid Sci. 2018, 91, 470–478. [Google Scholar] [CrossRef]
- Rajshekhar, G.; Ambrosini, D. Multi-scale approach for analyzing convective heat transfer flow in background-oriented Schlieren technique. Opt. Lasers Eng. 2018, 110, 415–419. [Google Scholar] [CrossRef]
- Boudreaux, P.; Venkatakrishnan, S.; Iffa, E.; Hun, D. Application of reference-free natural background–oriented schlieren photography for visualizing leakage sites in building walls. Build. Environ. 2022, 223, 109529. [Google Scholar] [CrossRef]
- Su, C.; Bai, J. Measurement of the neutral plane of an internal fire whirl using the background-oriented Schlieren technique for a vertical shaft model of a high-rise building. Measurement 2016, 78, 151–167. [Google Scholar] [CrossRef]
- Grauer, S.J.; Unterberger, A.; Rittler, A.; Daun, K.J.; Kempf, A.M.; Mohri, K. Instantaneous 3D flame imaging by background-oriented schlieren tomography. Combust. Flame 2018, 196, 284–299. [Google Scholar] [CrossRef]
- Vinnichenko, N.A.; Pushtaev, A.V.; Plaksina, Y.Y.; Uvarov, A.V. Measurements of liquid surface relief with moon-glade background oriented Schlieren technique. Exp. Therm. Fluid Sci. 2020, 114, 110051. [Google Scholar] [CrossRef]
- Becher, L.; Voelker, C.; Rodehorst, V.; Kuhne, M. Background-oriented schlieren technique for two-dimensional visualization of convective indoor air flows. Opt. Lasers Eng. 2020, 134, 106282. [Google Scholar] [CrossRef]
- Porta, D.; Echeverría, C.; Stern, C.; Rendón, P.L. Visualization of a shock wave travelling inside a rectangular duct using the background-oriented schlieren method. Wave Motion 2022, 114, 102999. [Google Scholar] [CrossRef]
- Vinnichenko, N.A.; Pushtaev, A.V.; Plaksina, Y.Y.; Uvarov, A.V. Natural convection flows due to evaporation of heavier-than-air fluids: Flow direction and validity of using similarity of temperature and vapor density fields. Exp. Therm. Fluid Sci. 2019, 106, 1–10. [Google Scholar] [CrossRef]
- Hayasaka, K.; Tagawa, Y. Mobile visualization of density fields using smartphone background-oriented schlieren. Exp. Fluids 2019, 60, 171. [Google Scholar] [CrossRef]
- Shimazaki, T.; Ichihara, S.; Tagawa, Y. Background oriented schlieren technique with fast Fourier demodulation for measuring large density-gradient fields of fluids. Exp. Therm. Fluid Sci. 2022, 134, 110598. [Google Scholar] [CrossRef]
- Biganzoli, I.; Capone, C.; Barni, R.; Riccardi, C. Note: Background Oriented Schlieren as a diagnostics for airflow control by plasma actuators. Rev. Sci. Instrum. 2015, 86, 026103. [Google Scholar] [CrossRef]
- Komuro, A.; Ogura, N.; Ito, M.; Nonomura, T.; Asai, K.; Ando, A. Visualization of density variations produced by alternating-current dielectric-barrier-discharge plasma actuators using the background-oriented schlieren method. Plasma Sources Sci. Technol. 2019, 28, 055002. [Google Scholar] [CrossRef]
- Kaneko, Y.; Nishida, H.; Tagawa, Y. Background-oriented schlieren measurement of near-surface density field in surface dielectric-barrier-discharge. Meas. Sci. Technol. 2021, 32, 125402. [Google Scholar] [CrossRef]
- Kaneko, Y.; Emori, K.; Nakano, A.; Oshio, Y.; Shimazaki, T.; Tagawa, Y.; Nishida, H. Study for application of background oriented schlieren method to flow induced by DBD plasma actuator. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; American Institute of Aeronautics and Astronautics: Reston, VA, USA. [Google Scholar] [CrossRef]
- Emori, K.; Kaneko, Y.; Nishida, H. Classification of flow-field patterns in burst-mode actuation of a dielectric-barrier-discharge plasma actuator. Phys. Fluids 2022, 34, 023601. [Google Scholar] [CrossRef]
- Guo, G.-M.; Liu, H. Density and temperature reconstruction of a flame-induced distorted flow field based on background-oriented schlieren (BOS) technique. Chin. Phys. B 2017, 26, 064701. [Google Scholar] [CrossRef]
- Rodrigues, F.F.; Pascoa, J.C.; Trancossi, M. Analysis of Innovative Plasma Actuator Geometries for Boundary Layer Control. In ASME 2016 International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Ashpis, D.; Laun, M.; Griebeler, E. Progress toward accurate measurements of power consumption of DBD plasma actuators. In Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. [Google Scholar] [CrossRef]
- Pons, J.; Moreau, E.; Touchard, G. Asymmetric surface dielectric barrier discharge in air at atmospheric pressure: Electrical properties and induced airflow characteristics. J. Phys. D Appl. Phys. 2005, 38, 3635–3642. [Google Scholar] [CrossRef]
- Rodrigues, F.F.; Pascoa, J.C. Implementation of stair-shaped dielectric layers in micro- and macroplasma actuators for increased efficiency and lifetime. J. Fluids Eng. 2020, 142, 104502. [Google Scholar] [CrossRef]
- Nunes-Pereira, J.; Rodrigues, F.F.; Abdollahzadehsangroudi, M.; Páscoa, J.C.; Lanceros-Mendez, S. Improved performance of polyimide Cirlex-based dielectric barrier discharge plasma actuators for flow control. Polym. Adv. Technol. 2021, 33, 1278–1290. [Google Scholar] [CrossRef]
- Rodrigues, F.F.; Pascoa, J.C.; Trancossi, M. Experimental Analysis of Alternative Dielectric Materials for DBD Plasma Actuators. In ASME 2018 International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 1. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).