A Quantum Approach to the Problem of Charging Electric Cars on a Motorway

Abstract

In this paper, the problem of charging electric motor vehicles on a motorway is considered. Charging points are located alongside the motorway. It is assumed that there are a number of vehicles on a given section of a motorway. In the motorway, there are several nodes, and for each vehicle, the entering and the leaving nodes are known, as well as the time of entrance. For each vehicle, we know the total capacity of its battery, and the current amount of energy in the battery when entering the motorway. It is also assumed that for each vehicle, there is a finite set of speeds it can use when traveling the motorway. The speed is chosen when entering the motorway, and cannot be changed before reaching the charging station. For each speed, there is given a corresponding power usage; the higher the speed, the larger the power usage. Each vehicle can only use one charger, and when its battery is full, the amount of energy is sufficient for reaching the outgoing node. We look for a feasible solution to the problem, i.e., a solution in which no vehicle has to wait for a charger. The problem is formulated as a problem of scheduling independent, nonpreemptable jobs in parallel, unrelated machines under an additional doubly constrained resource, which is power. Quantum approaches to solve the defined problem are proposed. They use the quantum approximate optimization algorithm and the quantum annealing technique. A computational experiment is presented and discussed. Some conclusions and directions for future research are given.

1. Introduction

The interest in electric motor vehicles (EMVs) in the world is growing rapidly. According to the report of the Polish Alternative Fuels Association [1], from May 2021 to May 2022, the number of electric passenger cars in Poland increased by 81% (currently 48,883 vehicles), the number of electric buses increased by 43% (currently 762), and the number of motorcycles and scooters by 37% (currently 14,464). In total, approximately 26,000 more electric vehicles appeared on Polish roads than in the previous year. The number of generally accessible charging stations also increased by 47% (currently 2232). An additional premise for the increased interest in EMVs is the ban on the sale of new vehicles with internal combustion engines from the year 2035. It is one of the key elements of the implementation of the so-called European Green Deal, which aims, among other things, to achieve net-zero greenhouse gas emissions. Of course, to achieve this, it is necessary not only to reduce the number of vehicles emitting carbon dioxide, but also to increase the amount of energy obtained from renewable energy sources.

This paper focuses not so much on the emissivity, but on the comfort of EMV users. Facilitating the use and operation of a vehicle for an individual user may naturally contribute to a faster change in the preferences of purchasing a particular type of vehicle, and thus a faster technological transformation in the field of transport. The problem of scheduling EMV battery charging is not new and has been discussed many times in many publications.

In [2,3], the problem of scheduling the battery charging process is considered. In the adopted model, it is assumed that during charging, the power consumption decreases linearly with time from a certain known initial value. The available power is a doubly constrained resource, in an amount not enough to charge all the batteries simultaneously. In [4], the use of an evolutionary algorithm to find the scheduling of drone-charging tasks in a multi-station charging station is considered.

In their article [5], Hahnsang and Kang propose the principles of planning activities aimed at extending the operation time and life of the battery. A weighted-k round robin (kRR) scheduling framework is designed. It consists of an adaptive filter and the kRR scheduler, whose task is to plan the number of parallel connected cells to be discharged while taking advantage of the recovery effect and also plan the load between k cells. The obtained result is up to 56% longer battery life and 50% more resistance to failures.

Mitici et al. [6] discuss problems related to planning flights by electric planes between airports. The authors develop an optimization model, thanks to which they create a flight schedule for electric aircraft. The schedule determines when the batteries are to be charged, the optimal charging time, when they are to be replaced with spare ones, and the optimal number of charging and replacement stations. The developed model enables three times more round trips than the size of the fleet. The included bi-linear charging profiles are divided into fast (up to 0–90%) and slow (90–100%) charging.

Xiaoqi et al. [7] consider the problem of battery replacement stations and charging the batteries at the stations. Their goal is to minimize charging costs while meeting the current demand for immediate battery replacement. In their research, they use the generalized Benders decomposition algorithm. The same algorithm is used by You et al. [8], who study the problem of planning the replacement of electric bus batteries.

Schaden et al. [9] considered the problem of charging at a single charging station with respect to current time-dependent electricity cost and vehicle state of charge. They found that the problem can be efficiently solved with only 1.5% error approximating concave power functions with piecewise linear functions.

In [10], Yang et al. described a model for choosing the best charging station on a highway for a single EMV. They found that using global information causes shorter waiting times than using only local information.

Del Razo et al. [11] proposed a modified version of the A* algorithm to schedule generated EMVs driving on a German highway connecting Berlin and Munich. Their work also enable dynamic changes to the schedule so that traffic can be accounted.

This article differs from the ones above mentioned, first of all, by taking a modern approach to solving a computationally difficult scheduling problem. This approach guarantees short solution times and is attractive due to the low cost of energy used to perform the calculations. The considerations are narrowed down to the section of the motorway where traffic flows only one way. On the modeled motorway section, there are many clearly ordered motorway junctions and a limited, usually small, number of charging points. The increase in the number of EMVs in use and long charging times pose the risk of large queues at charging points at stations. In the proposed approach, the aim is to prevent the arising of queues, and if this is impossible, to minimize their length or waiting times for charging to start. The proposed model is a relatively faithful reflection of reality, although, like every model, it includes some simplifications. Nevertheless, the scheduling problem formulated on its basis remains a difficult problem from a computational point of view. This means that to solve it, it is rational to use approximate algorithms, the effectiveness of which most often depends on the time of calculations, and thus on the amount of energy used to perform them. Therefore, in order to solve the considered problem, we propose to use quantum computers that can reveal their advantages over classical computers when used to solve problems of a combinatorial nature. Examples of such successful implementations of algorithms on quantum computers are reported in many studies. Ajagekar and You [12] generally discuss many applications of quantum computers and compare them computationally to classical computers. In their research, they focus on planning energy systems and notice that quantum computers achieve better solutions in a much shorter time than classical computers. The authors emphasize, however, that not every optimization problem can be solved by quantum computers today. Faugler [13] notices the enormous potential of using quantum computing in the energy sector, where the complexity of computations is high and the dynamics of the modeled processes require quick adaptation to the existing situation. An important advantage of quantum computing is the possibility of building ecological energy management systems on its basis. Quantum computers were also used to calculate the charging of plug-in hybrid electric vehicles using the quantum annealing algorithm [14]. The quantum annealing method itself is becoming more and more popular and used for scheduling problems, e.g., nursing roster [15,16].

In this work, the hypothesis that quantum computers can be used to solve difficult, complex and real scheduling problems is verified with a specific example. The above hypothesis is tested experimentally with the use of two quantum computer architectures. The research was carried out on quantum computers from D-Wave Systems and IBM.

The paper is organized as follows. The problem formulation is given in Section 2. Section 3 presents our quantum approach. The computational experiment is described in Section 4, and its results are presented in Section 5. Section 6 is devoted to a discussion on the obtained results. Finally, some conclusions and final remarks are given in Section 7.

2. Problem Formulation

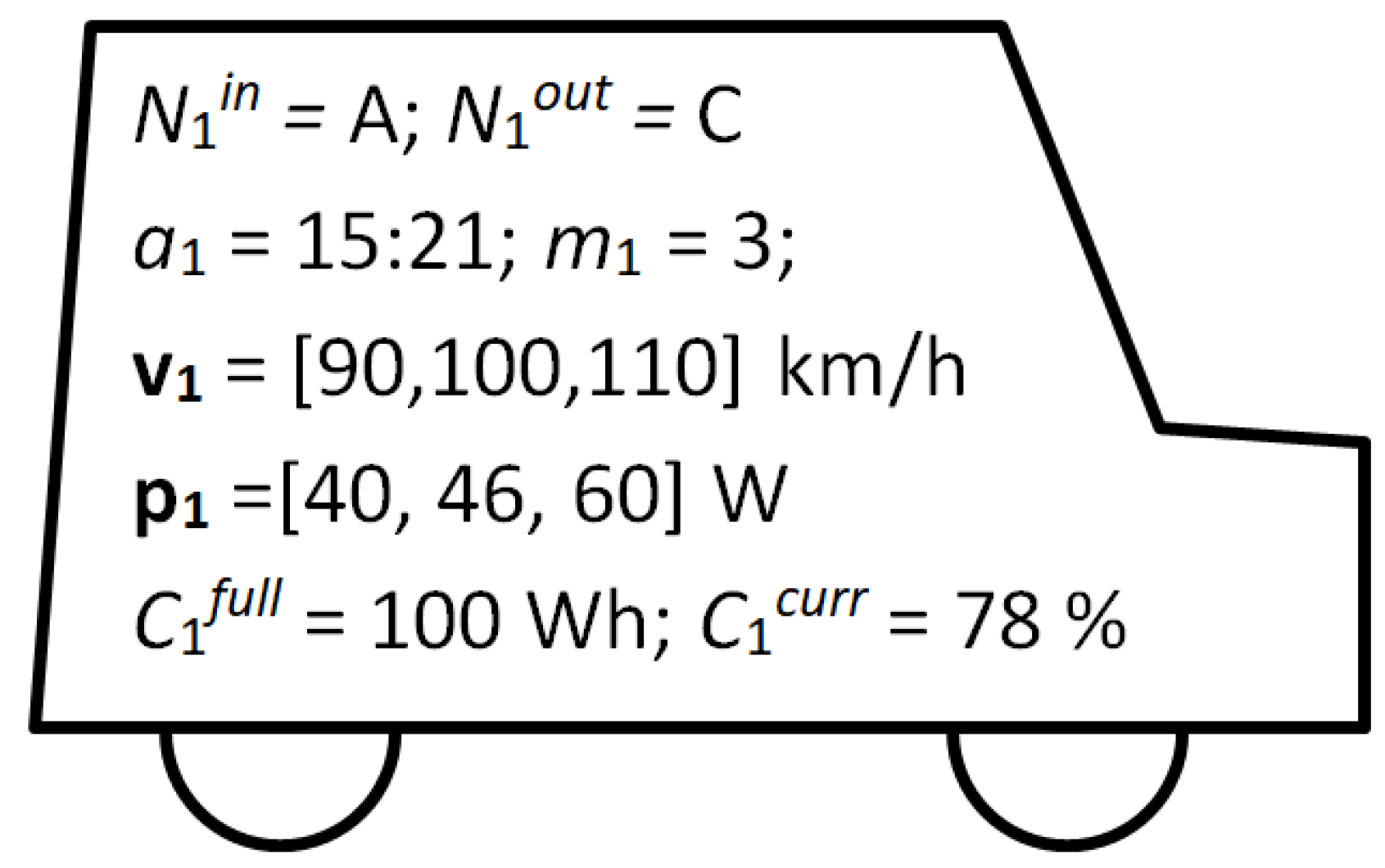
2.1. Problem Description and Parameters

In this section, we will formulate the problem of searching for the conflict-free order of charging vehicles on a chosen motorway section as a deterministic problem of scheduling jobs on machines. Let us start with a formal description of the problem and its parameters.

Given is a set of EMVs that are to drive through the motorway section, and need charging within this section. Each charging operation is divided into two phases:

• Phase I—reaching the charging point (station).
• Phase II—the process of charging the EMV’s battery.

We define the motorway section M as a sequence of r nodes $M=(A,B,\dots ,X)$, where A is the start node, and X is the end node of the section. For each node its distance from the start node A is known, and denoted as $D_k^N>0,k=2,\dots ,r$, where, obviously, $D_1^N=0$. We use the superscript N to distinguish between node distance and charging station distance, where we use S in the superscript. There are s charging stations over the section M. For each station $j,j=1,2\dots ,s$, the following parameters are defined:

• $D_j^S$—distance between charging station j and the start node A.
• $b_j$—number of chargers at station j.
• $B_{jl}$—l-th charger at station $j,l=1,2,\dots ,b_j$.
• $P_{jl}$—available power of charger $B_{jl}$.

Furthermore, there are n EMVs on the motorway section M. We assume that we know the node where the EMV enters the motorway, the node where it leaves, as well as the time of entrance. We also know the total capacity of its battery, and the current amount of energy in the battery when entering the motorway. Moreover, we will assume that for each EMV, there is a finite set of speeds it can use when traveling the motorway. The speed is chosen when entering the motorway, and cannot be changed until reaching the charging station. For each speed, there is given a corresponding power usage; the higher the speed, the larger the power usage. Consequently, we can speak about driving modes, where a mode represents a relation between the speed of EMV and its power usage. Summarizing, for i-th EMV, $i=1,2,\dots ,n$, the following parameters are known:

• $N_i^{in}$—entrance (ingoing) node.
• $N_i^{out}$—outgoing node.
• $a_i$—arrival time of EMV i, i.e., the time of entering the motorway through node $N_i^{in}$.
• $C_i^{full}$—total capacity of the battery of EMV i.
• $C_i^{curr}$—current amount of energy in the battery of EMV i.
• $m_i$—number of driving modes “speed/power usage”.
• ${\mathbf{v}}_i$—vector of available speeds, ${\mathbf{v}}_i=[v_{i1},v_{i2},\dots ,v_{i{l}_i}]$.
• ${\mathbf{p}}_i$—vector of corresponding power usages, ${\mathbf{p}}_i=[p_{i1},p_{i2},\dots ,p_{i{m}_i}]$.

As we can see, $C_i^{def}=C_i^{full}-C_i^{curr}$ is the energy deficit of EMV i, the amount of energy needed for its battery to be fully charged.

An example of data describing an EMV is shown in Figure 1.

Let us notice that the power usage function of an EMV, expressed by the “speed/power usage” modes, is nonlinear, and, usually, convex. If the function was linear, the energy consumed per distance unit as well as charging time would be both constant. In contrast, the more realistic, nonlinear power usage function does not assume constant distance/speed power usage, which, for example, might lead to the situation where, driving with a particular speed, the EMV may be unable to arrive at some stations because of the lack of energy. This indication, together with having all the data about the motorway infrastructure, can be utilized to define at the stage of processing a set of feasible (i.e., reachable) charging stations for each driving mode of an EMV. Notice that for each mode, this number may be different since the power usage function is nonlinear.

We further assume that the charging operations are independent, i.e., there are no precedence relations between EMVs, as well as nonpreemptable, i.e., the charging process in phase II cannot be interrupted (the battery is being charged without preemptions until it is full). We also make the following additional assumptions:

• Each EMV can charge its battery only once, i.e., when the battery is full after phase II, the amount of energy is sufficient for reaching the outgoing node.
• For each EMV, there exists at least one available speed for which the number of feasible charging stations is greater than 0.
• Operations in phase I can be performed fully in parallel, i.e., we do not assume any limited capacity of the motorway, accidents, traffic jams, etc.
• Each charging process is done by using exactly one charger.
• The charging time in phase II is linearly dependent on the energy deficit $C_i^{def}$ in the battery.

From the problem point of view, EMVs that can travel through the highway without charging are not of interest because they require no attention or alterations to the proposed solution. On the other hand, it would be tedious for EMV drivers to charge many times, even if it would result in reduced travel time. Therefore, we decided for a trade-off and, by assumption (1), allow only a single charging. Additionally, the assumption (2) assures that there are no instances for which we know already in the preprocessing step that there is no feasible solution. We further simplify the problem with assumptions (3) and (4). Current batteries charge linearly up to some threshold near being fully charged, after which the charging process slows down. As we noted in the assumption (5), we approximate it with linear dependence; however, we are aware of the fact that the faithful reproduction of the charging process would eliminate some solutions.

We look for a feasible solution of the problem, i.e., a solution in which no EMV has to wait for a charger. To this end, for each EMV, we have to define its mode, i.e., speed and corresponding power usage (fixed between the entrance node and the charging point) and its charging point, i.e., charging station or charger which, we will discuss in points Section 2.3.1 and Section 2.3.2 such that the time gap between the end of phase I and the beginning of phase II is equal to 0. To improve the readability of the rest of the paper, the term “EMV instance” will mean the assignment of both a specific driving mode and charging point to an EMV vehicle.

2.2. Classification of the Problem in the Classical Scheduling Theory

The problem formulated in Section 2.1 can be treated as a decision problem of scheduling (charging) jobs on parallel, unrelated machines. Each job corresponds to an operation of charging the battery of a single EMV. Jobs can be performed in various execution modes defined by pairs: available speed of the EMV and its corresponding power usage. Each machine corresponds to a single charging point. For each couple (machine, execution mode), the following two parameters can be calculated and set:

• Ready time $r_i$ of job i, calculated as the sum of arrival time $a_i$ of EMV i and the duration $d_i^I$ of phase I for this EMV (i.e., the time needed for reaching the charging point): $r_i=a_i+d_i^I$.
• Execution time of job i, i.e., the duration $d_i^{II}$ of phase II (the length of the charging process) for the corresponding EMV.

We look for such an allocation of jobs to machines (vehicles to charging points) that guarantees zero time gap between phase I and phase II for each EMV, i.e., no vehicle waits to start the charging process. The problem is NP-hard as a generalization of the problem of scheduling independent, nonpreemptable jobs in parallel, unrelated machines (see, for example, [17]).

A similar problem is considered in [18]. The authors study the unrelated parallel machine scheduling problem where the processing time of a job is based on resource allocation and the jobs are delivered in batches with unlimited batch capacity. A mathematical model is presented for minimizing the total weighted penalties of tardiness and earliness, resource allocation, and batch delivery costs with idle time and machine eligibility constraints. Three metaheuristic algorithms, including modified ant colony optimization (MACO), genetic algorithm (GA), and a hybrid algorithm based on the hybridization of MACO and GA, are proposed to solve the problem.

2.3. Charging Point Models

Let us now consider two options of defining the charging point. The applied model will then have an influence on, among others, the chance of finding a feasible solution.

2.3.1. Charger as a Charging Point

In the first, natural option, each charging point corresponds to a single charger with its unique parameters, in particular, the available charging power. Under this assumption, in an instance of the problem, the number of unrelated machines can be very large, which has a strong impact on the size of potential solutions and results in a huge computer memory requirements by the elaborated scheduling algorithm. An example of a motorway infrastructure in this case is presented in Figure 2.

2.3.2. Station as a Charging Point

A possible method of reducing the memory usage could be making some assumptions exceeding classical formulations of machine scheduling problems. Namely, if in the same location j (at the same charging station), there is a certain number of identical chargers ($P_{jl}=P_j$ for $l=1,...,b_j$), a set of such chargers may be treated as a single multi-functional machine able to perform several jobs in parallel. Such a machine is characterized by an additional parameter—the number of terminals (see parameter $b_j$ in Section 2.1) defining the maximum number of jobs that can be processed simultaneously. Such an assumption can result in significant reduction of memory used by the scheduling algorithm; however, it may also reduce the chance of finding a feasible solution by the algorithm. It follows from that fact that the time of execution of a set of jobs by such a multi-functional machine is determined by the processing time of the longest jobs. As a result, some machines may not be fully loaded, and some idle times may occur.

An example of a motorway infrastructure in this case is presented in Figure 3.

3. Quantum Approach

Due to recent advancements in building real quantum hardware, especially in the past few years, quantum computation and quantum information have rapidly accelerated not only as a field of science, but also as a field of technology. Many researchers invest their time to make quantum computers useful in the current noisy intermediate scale quantum (NISQ) era, because they believe that quantum approaches can soon achieve significant advantages over classical computing in computation time, solution quality or energy usage. This is mainly due to exploiting superposition and entanglement phenomena. In short, having n qubits in superposition allows to perform simple computations simultaneously on up to $2^n$ possible states, while adding entanglement allows to make more complex computations, where two or more states depend on one another.

In the current NISQ era, there are two leading approaches which give exposure to the quantum realm: the gate-model architecture and the quantum annealing. The gate model paradigm is to use universal set of basis gates to encode any possible function [19]. Moreover, by the Solovay–Kitaev theorem, any arbitrary qubit gate can be approximated to some accuracy using the polylogarithmic number of these gates [20]. The nice properties do not come with no cost however, as it remains a difficulty to build many-qubit fault-tolerant quantum computers. The most advanced in the technology seems to be the IBM company, which bases its quantum-chip technology on Josephson junctions cooled to near absolute zero temperatures. Currently reaching up to 127 qubits [21], they still suffer from noise, decoherence gate and measurement errors, which all lead to useless final measurements when the quantum circuit is too long.

The quantum-annealing-based devices are an attempt to build more powerful and accurate quantum computers at the cost of their universality. Their architecture restricts computation to a single type of algorithm—quantum annealing—which in and of itself is a technique with very broad applications. To make a problem solvable by quantum annealing, it has to be transformed to a QUBO formulation, which stands for quadratic unconstrained binary optimization. In short, it is a notation which assigns penalties to binary variables (representing qubits), as well as to pairs of them. Assigning rewards is also possible by setting a penalty to a negative value. We assume that the variable is selected when its respective qubit’s state after measurement is 1. To implement problem constraints, we can assign penalties for selecting a single variable by controlling its superposition state to tilt toward value 0. A penalty for selecting two variables is implemented using entanglement. The bigger penalty there is for selecting a pair of variables; the more strongly their qubits are entangled, therefore the less likely they are to both be measured in the same state.

3.1. Conflict Avoidance Problem

An ideal situation on the motorway would allow every EMV to start charging its battery as soon as the vehicle arrives at the station. In that way, the users would waste no time waiting in the queue. Simultaneously, this would result in the chargers being used to their full potential, as less waiting time means more dense charging schedules.

In order to avoid waiting in queue, the problem we try to implement using a quantum computer is a conflict avoidance problem.

Due to the nature of the quantum computer, our approach will detect potential conflicts between each pair of vehicles, taking into account all their possible driving modes. By definition, conflicts only occur at specific charging points. At a single charging point, however, all potential conflict situations between each pair of vehicles using the motorway must be considered.

The number of potential conflicts between two vehicles $i_1$ and $i_2$ (at a given charging point), therefore, depends on the number of their driving modes $m_{i_1}$ and $m_{i_2}$, respectively. Thus, at each charging point reachable by both EMVs, $m_{i_1}\times m_{i_2}$, different conflict situations should be checked. If a certain charging point was reachable by all EMVs traveling in any of the m driving modes, the number of possible different conflict matches (or lack thereof) to all vehicles would be $2^{n\times m}$. If you further consider that there are many such charging points, the exponent of this number is increased by an additional factor—number of charging points.

In order to find a feasible solution of the problem, for each EMV, it is necessary to choose such a driving mode and such a charging point that ensure that there are no charging conflicts along the entire stretch of motorway. If we denote by $x_{ijk}$ a binary variable that takes the value 1 when the i-th EMV moving in k-th driving mode is charged at station j, a one-hot constraint should be fulfilled:

$$\sum _j\sum _k{x}_{i,j,k}=1\mathrm{for}\mathrm{all}i=1,2,...,n$$

(1)

Now we can move on to one of the key elements of our algorithm, which is the conflict matrix.

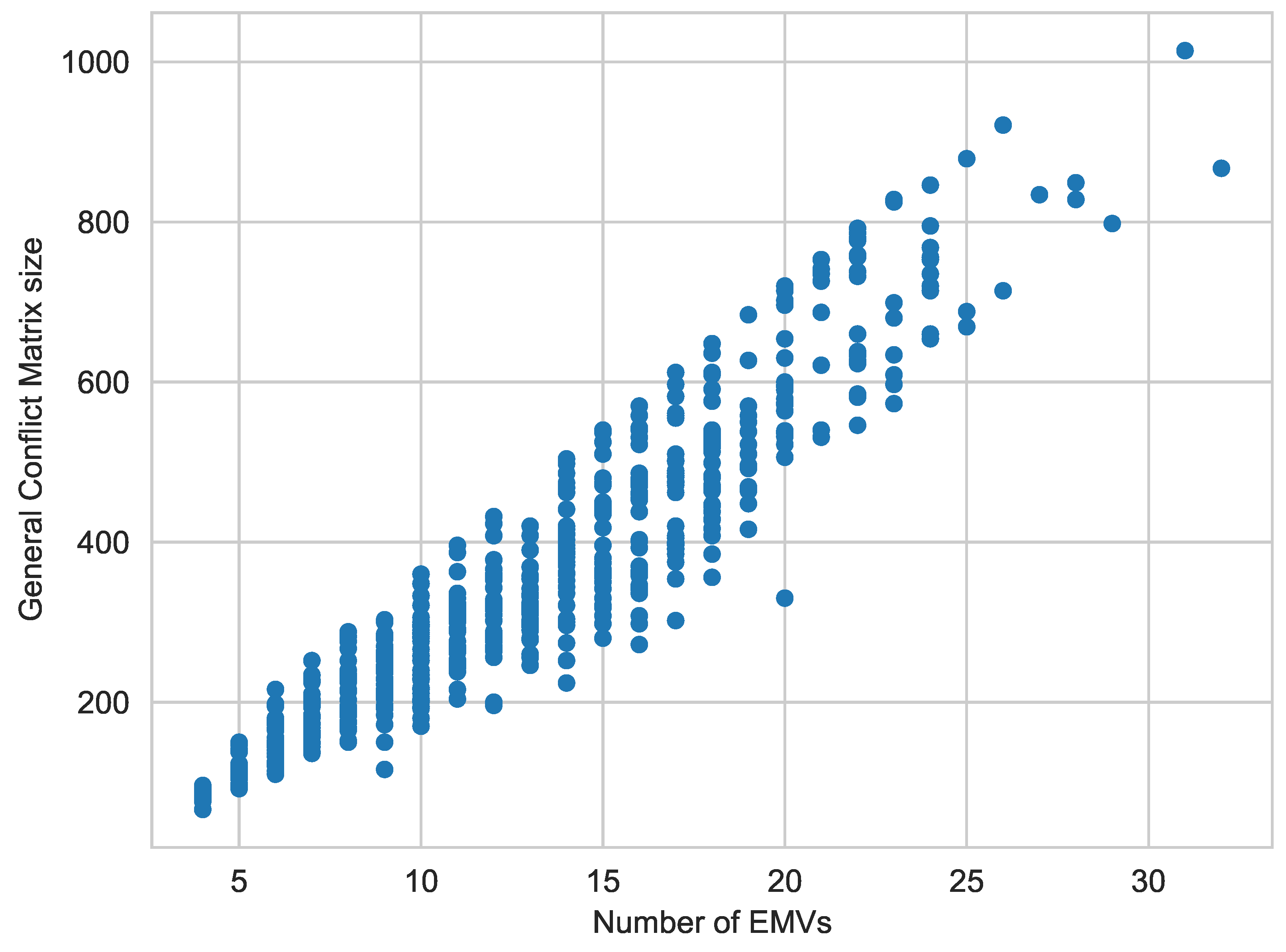
3.2. Conflict Matrix

The set of conflicts between each pair of vehicles moving in different driving modes is most conveniently represented in a binary array—the Conflict Matrix (CM). For a single charging point, this array is a two-dimensional upper triangular matrix of the form shown in Figure 4.

The maximum size of the 2D CM can be calculated as

$$\sum _{i=1}^n\sum _{k=1}^{m_i}1\times \sum _{i=1}^n\sum _{k=1}^{m_i}1$$

(2)

Different types of conflict situations between two EMV’s are depicted in Figure 4:

• Orange “1”—conflict because the charging point is unreachable by one of the EMVs moving in the selected driving mode;
• Black “1”—conflict because of charging at the charging point at the same time;
• Green “0”—no conflict.

Before the CM is fed to the quantum computer, all columns and rows representing driving modes leading to unreachable charging points can be removed. It allows to reduce the matrix size. Of course, the two-dimensional CM must be expanded to include a third dimension in which all charging points are represented. The 3D CM representing potential conflicts at all charging point is shown in Figure 5.

In the paper, we consider two different definitions of a charging point. The consequence of their application is discussed below.

3.2.1. Conflict Matrix for Charger as a Charging Point

The most general way to represent conflicts at each potential charging point is to include all individual chargers in the conflict matrix. We will call the so-constructed matrix the general conflict matrix (GCM). In this case, the solution to the problem is feasible when such a driving mode and charger can be found in the GCM for each EMV, guaranteeing the lack of conflict. The size of such a matrix is not greater than

$$\sum _{i=1}^n\sum _{k=1}^{m_i}1\times \sum _{i=1}^n\sum _{k=1}^{m_i}1\times \sum _{j=1}^s\sum _{l=1}^{b_j}1$$

(3)

This representation of conflicts has its advantages and disadvantages. Its advantage is that it allows detecting feasible solutions in which an EMV sequence is being charged on one of the chargers, even though charging is going on all the time on other chargers of the same station. Such a situation is shown in Figure 6.

Its disadvantage, on the other hand, is that the 3D CM constructed in this way (GCM) unnecessarily contains redundant information about conflicts on chargers from the same location.

3.2.2. Conflict Matrix for Station as a Charging Point

Smaller 3D conflict matrices, and consequently fewer necessary calculations, can be obtained by taking into account the fact that some stations are equipped with multiple identical chargers. In this case, you can limit yourself to detecting conflicts at the station, aggregating information from individual chargers. In practice, this looks like counting the conflicts of pairs of EMVs at a given station. If each EMV at a station j containing $b_j$ chargers is in conflict with no more than $b_j-1$ other EMVs, the solution is considered feasible. The size of the conflict matrix (in this case, called the station conflict matrix—SCM) so constructed is

$$\sum _{i=1}^n\sum _{k=1}^{m_i}1\times \sum _{i=1}^n\sum _{k=1}^{m_i}1\times s$$

(4)

This approach—while useful due to lower memory occupancy and shorter time of necessary calculations—does not allow to find some feasible solutions of the problem. The feasible solution in Figure 7 is treated as infeasible in this case, since EMVs 1, 4 and 5 are in conflict with more than three other EMVs.

A feasible solution correctly recognized by “the station as charging point” rule is shown in Figure 8.

3.3. Gate-Based Approach and QAOA Algorithm

Mathematically a quantum state is typically represented as a superposition of the two basis states written in Dirac bracket notation:

$$|\psi \rangle =a|0\rangle +b|1\rangle$$

(5)

where the complex numbers a and b are called the amplitudes of the basis states satisfying normalization constraint $\sqrt{a^2+b^2}$ = 1. In contrast to classical computing, a qubit before measurement can be in any proportion between its basis states. After the measurement, a qubit collapses into one of them. The squared amplitudes describe the probabilities of a qubit to collapse into $|0\rangle$ or $|1\rangle$ after Z-basis measurement. This comes directly from the measurement and projection properties followed by their formal definitions [19]. A many-qubit state can be written using the tensor product. As a consequence, the number of base states and the number of amplitudes raise exponentially,

$$a_0|00\dots 00\rangle +a_1|00\dots 01\rangle +\cdots +a_{2^n}|11\dots 11\rangle$$

(6)

where n is the number of qubits, and we write $|00\dots 00\rangle$ as an abbreviation of a tensor product.

In quantum mechanics, the evolution of a quantum state can be always described with a unitary operator U

$${\psi }^{\prime }=U|\psi \rangle$$

(7)

This has some important consequences, e.g., that a quantum operation is always reversible. Strongly connected to the the unitary evolution is the notion of a Hamiltonian, which, in quantum mechanics, describes the total energy of a quantum system. In quantum computing, the Hamiltonian often acts as an expected value operator. Its size is $2^n\times 2^n$, where n is the number of qubits, and it can be interpreted as a map assigning a value to each of the $2^n$ basis states. The expected value of the Hamiltonian is called energy and can be written as

$$E=\langle \psi \left|H\right|\psi \rangle$$

(8)

From now on, we will use the term ‘energy’ to both indicate the expected value and the energy in batteries. Their meaning should naturally come from the context. Hamiltonians, together with parametrized unitaries, are often used in a special family of hybrid quantum–classical algorithms, which are able to solve combinatorial optimization problems, namely variational algorithms. The approach is to construct such a circuit and find such parameters so that the expectation value of a user-defined Hamiltonian is minimum. The user-defined Hamiltonian acts as a function which aggregates both the cost function as well as the constraints.

To tackle the problem of conflict-free EMV charging, as a hybrid quantum–classical variational algorithm, we use the quantum approximate optimization algorithm (QAOA) [22]. QAOA is an algorithm that tries to approximate continuous-time quantum adiabatic evolution [23], which states that if we change the time-dependent Hamiltonian slowly enough, a system will remain in its eigenstate. Mathematically, the adiabatic evolution can be written as

$$H\left(t\right)=(1-t)H_M+t{H}_C$$

(9)

In QAOA, we often call $H_M$ a mixer Hamiltonian, and $H_C$ is a cost Hamiltonian. $H_M$ is usually composed of Pauli-X gates so that the quantum state can be easily prepared as an equal superposition of the basis states using Hadamard gates. The slow enough evolution is performed using Trotter–Suzuki approximation, and hence the final form of QAOA is

$$|{\psi }_p(\overrightarrow{\gamma },\overrightarrow{\beta })\rangle =e^{-i{\beta }_p{H}_M}{e}^{-i{\gamma }_p{H}_C}\dots e^{-i{\beta }_1{H}_M}{e}^{-i{\gamma }_1{H}_C}{|+\rangle }^{\otimes n}$$

(10)

The $|+\rangle$ denotes equal superposition, and p is a key parameter of QAOA, which defines the length of the circuit, and thus the approximation quality. The longer the circuit is, the better the solution can be, but it is harder to optimize the variational parameters $\beta$ and $\gamma$. This trade-off is especially visible when working on a real NISQ hardware, as the noise prevents from taking advantage of longer circuits.

We can see that the role of $H_C$ in QAOA is twofold. Firstly, by the adiabatic theorem, it defines the building blocks of the circuit. Secondly, by being the expected value operator, we can treat it as a function to minimize.

3.4. Gate-Based Hamiltonian Formulation

Due to technological limitations, we will limit the implementation of the Gate-based approach only to the “station as a charging point” model. We established the one-hot constraint (1) in Section 3.1. Additional constraints arise from the need to avoid conflicts and are based on information stored in the SCM. Since the cost Hamiltoniain $H_C$ is a function that aggregates constraints, we need to convert them accordingly. Every Boolean function can be represented as a sum of Pauli-Z clauses [24]. Following the recipe, we can write the one-hot constraint as a 1-in-n function, or rather its negation, as we are minimizing the expected value, selecting only one instance of the same EMV

$$H_{\mathrm{one}-\mathrm{hot}}=\sum _{i}1-in-n(x_{i,1,1},\dots ,x_{i,s,l_i})$$

(11)

where 1-in-n is derived with the Fourier transform as in [24].

Likewise, we define the conflict Hamiltonian. Firstly, let us define a set containing all EMVs possibly conflicted with a EMV i driving in mode j and charging at a station k

$$S_{i,j,k}=\{x_{i^{\prime }{j}^{\prime }{k}^{\prime }}:SCM(i,j,k)\left(i^{\prime }{j}^{\prime }{k}^{\prime }\right)=1\}$$

(12)

Since we are interested only in those situations where the number of EMVs simultaneously charging at a station is greater than available chargers, we define a collection S containing only these $S_{i,j,k}$ with cardinality greater than $b_j$

$$S=\{S_{i,j,k}:|S_{i,j,k}|>b_j\}$$

(13)

To prevent more than $b_j$ EMVs to arrive at a station at the same time, it is sufficient to prevent $b_j+1$ EMVs to arrive, so we define a set P of such possible combinations:

$$P=\left\{\left(\genfrac{}{}{0pt}{}{s}{b_j}\right)\forall s\in S\right\}$$

(14)

The set P can be easily interpreted as a sum of logic AND functions preventing more than $b_j$ EMVs to simultaneously charge at that station:

$$H_{\mathrm{conflict}}=\sum _{p\in P}\frac{1}{2^{\left|p\right|}}\prod _{x_{i^{\prime }{j}^{\prime }{k}^{\prime }}\in p}(I-Z_{i^{\prime }{j}^{\prime }{k}^{\prime }})$$

(15)

where $Z_{i^{\prime }{j}^{\prime }{k}^{\prime }}$ is applied on a qubit assigned to $x_{i^{\prime }{j}^{\prime }{k}^{\prime }}$.

Having the constraints converted, we can construct the final Hamiltonian as

$$H_C=H_{\mathrm{one}-\mathrm{hot}}+H_{\mathrm{conflict}}$$

(16)

3.5. Quantum Annealing

Quantum-annealing-based solutions also utilize Hamiltonians to formulate optimization problems. The problem’s energy landscape is described by the following equation:

$$H=\sum _i{\mathbf{Q}}_{i,i}{\mathbf{x}}_i+\sum _{i<j}{\mathbf{Q}}_{i,j}{\mathbf{x}}_i{\mathbf{x}}_j$$

(17)

where $Q_{i,j}$ are entries of upper-triangular $\mathbf{Q}$ matrix (18) and $x_i$ is a state i-th qubit ended up in after measurement. The $\mathbf{Q}$ matrix is used to control the degree of qubit superposition imbalances and entanglement strengths.

$$\left[\begin{array}{cccc}{Q}_{11}& Q_{12}& \cdots & Q_{1n}\\ 0& Q_{22}& \cdots & Q_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & Q_{mn}\end{array}\right]$$

(18)

The upper-triangular matrix Q is constructed from the state Hamiltonian.

Every entry on the main diagonal of the $\mathbf{Q}$ matrix describes how much energy the solution will gain if a given variable is selected. The selection of a variables is in fact a qubit being measured as 1. Every other entry of the $\mathbf{Q}$ matrix describes how much energy the solution will gain if two qubits end up in the same state. For example, if $Q_{i,j}=2$, the solution’s energy will rise by 2 if both $x_i$ and $x_j$ are selected. Positive values in $\mathbf{Q}$ matrix act as penalties for the model. It is also possible to assign negative penalties to encourage the QPU to select a given variable.

3.6. Quantum Annealing Hamiltonian Formulation

After the GCM (or SCM) is created, we apply several constraints to quantum variables, ensuring that the final result represents a feasible solution to the EMV conflict avoidance problem. Every qubit represents a selection of its corresponding EMV instance. The qubit representing j-th instance of i-th vehicle is denoted as $q_{i,j}$.

The first restriction applied to qubits is a one-hot constraint (1). We group all qubits describing instances of the same EMV, sum their values and require that their sum be equal to one. This way, the selection of just one EMV instance (charging point and driving mode) is ensured:

$$H_{\mathrm{one}-\mathrm{hot}}=\sum _{i=1}^n\left({(1-\sum _{j=1}^s\sum _{k=1}^{m_i}\sum _l^{b_j}{x}_{i,j,k,l})}^2\right)$$

(19)

where n is a number of vehicles, $m_i$ is a number of driving modes of vehicle i, s is a number of available stations, and $b_j$ is a number of chargers available on station k. Every time the QPU chooses more (or less) than one instance of every EMV, the solution’s energy increases exponentially.

The second part of the problem Hamiltonian ensures the minimization of conflicts during charging. The equation differs depending on whether we treat each charger as a separate charging point:

$$H_{\mathrm{conflict}}=\sum _{j=1}^s\sum _{l=1}^{b_j}\left(\sum _{i=1}^n\sum _{k=1}^{m_i}\sum _{i^{\prime }=i+1}^n\sum _{k^{\prime }=k+1}^{m_i}{x}_{i,(j,l),k}\ast x_{i^{\prime },(j,l),k^{\prime }}\ast \mathrm{GCM}(i,(j,l),k)(i^{\prime },(j,l),k^{\prime })\right)$$

(20)

or each station as a collection of chargers:

$$H_{\mathrm{conflict}}=\sum _{j=1}^s\left(\sum _{i=1}^n\sum _{k=1}^{m_i}\sum _{i^{\prime }=i+1}^n\sum _{k^{\prime }=k+1}^{m_i}{x}_{i,j,k}\ast x_{i^{\prime },j,k^{\prime }}\ast \mathrm{SCM}(i,j,k)(i^{\prime },j,k^{\prime })\right)>b_j$$

(21)

Note that Equation (21), for the cost of being less precise, contains fewer variables, which means greater problems can be embedded on QPU chips:

$$H_C=H_{\mathrm{one}-\mathrm{hot}}+H_{\mathrm{conflict}}$$

(22)

The final Hamiltonian incorporates both one-hot constraint and conflict constraint. It is possible to apply weights to those Hamiltonian in order to regulate their impact, but experiments showed that an equal representation results in a robust optimization.

3.7. Note on Energy

Looking at the Hamiltonians defined in both quantum techniques, we can see that they correlate to the number of constraints that failed to be met. Even though the energy value is not proportional to the number of unresolved conflicts, it can be interpreted as such. The key point is to understand that minimizing the Hamiltonian energy directly improves the solution.

4. Computational Experiment

4.1. Assumptions

To confirm the usefulness of quantum approaches for solving the practical problem considered in this work, a number of computational experiments were carried out. The assumptions for the experiments were matched to the current strong technological limitations (small number of available qubits) of available quantum computers. More attractive due to the size of the possible instances of the problem is the DWave quantum computer, so more experiments were carried out for the QUBO algorithm. A more general conflict matrix, GCM, and “charger as a charging point” model, were used in all experiments for this case. A test instance generator was implemented specifically for the purpose of these experiments.

The second quantum technology presented above—the gate-based architecture (and QAOA algorithm)—was tested only on an instance limited in size. Due to the small capacity of currently available gate-model-based quantum computers, only one set of toy-size experiments was conducted. The experiments instance included part of the A4 motorway (described below), but only 5 EMVs were considered. Moreover, we decided to utilize a smaller version of the conflict matrix, SCM, and consequently the “station as charging point” method for the conflict avoidance problem.

All experiments assumed a convex function of EMV power usage while driving—an assumption that reflects the actual dependence of power consumption on vehicle speed. In the experiment for the real section of the motorway, precise tabular data specified for two specific EMV models were adopted. As for the available EMVs types, in the experiments with QAOA, we follow ref. [25], wherein two types of vehicles are described: Mitsubishi i-MiEV with 16kWh battery capacity and Nissan Leaf with 24 kWh battery capacity.

However, due to the limitations of quantum computers, a relatively small number of driving modes were assumed in all experiments. For example, it resulted in only 18 EMV instances (for 5 EMVs) in the QAOA experiment.

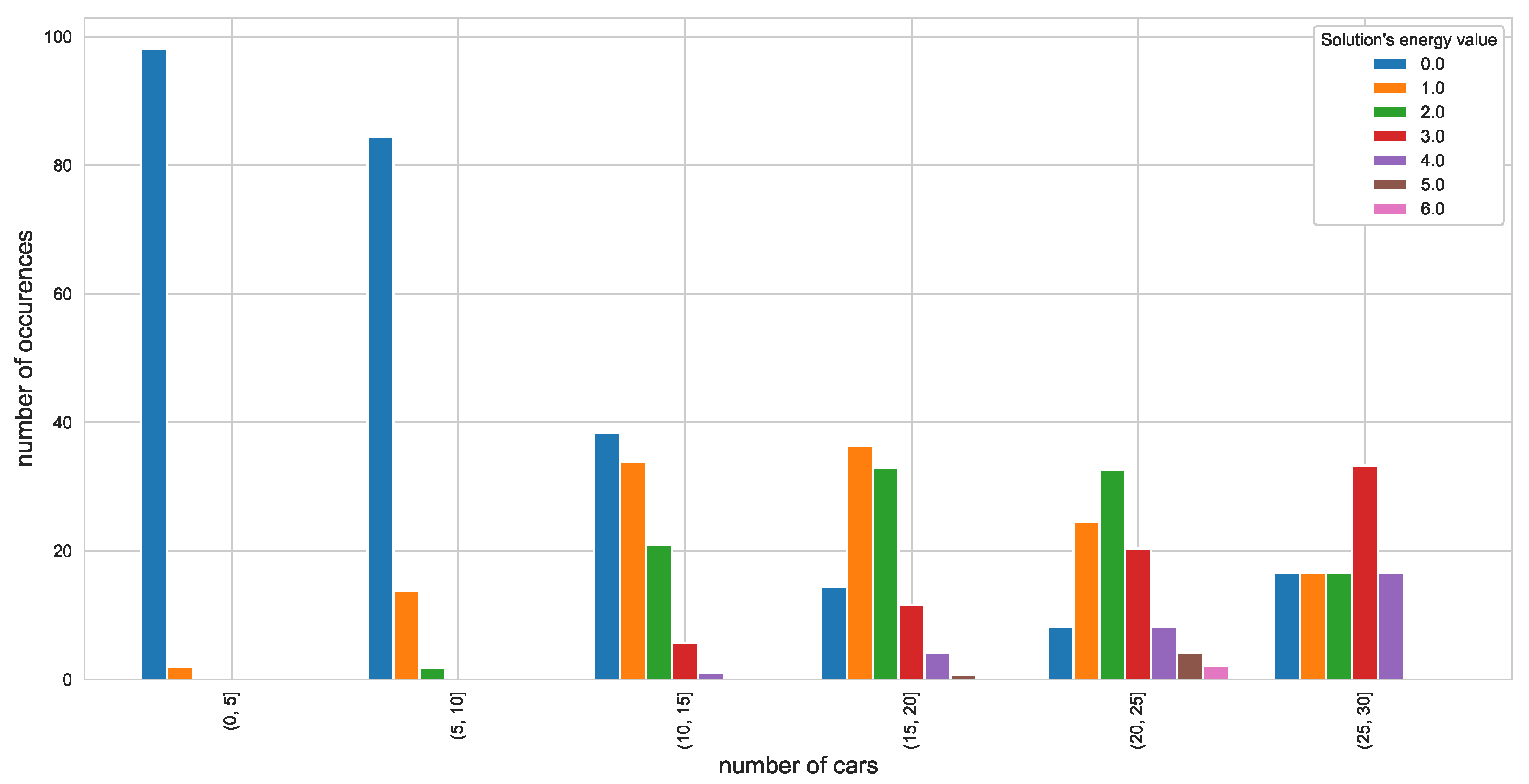
4.2. Test Instances—Generator

As for a dataset for our implementation of the QUBO algorithm, we decided to write our own instance generator. The process of generating a complete instance comprises three steps. Firstly, the motorway is generated. The key parameters of the motorway are its length, number of stations (or alternatively, station frequency), number of nodes (alternatively, their frequency) and chargers in each station. Secondly, EMV types are generated. Each EMV has different battery capacity ($C_i^{full}\in [10,30]$ kWh, $i=1,2,...,n$) as well as an individual vector of power usages corresponding to global vector of available speeds ($p_{i{m}_i}\in [80,250]$ kWh/km, $i=1,2,...,n$). We set the vector so that the energy consumption raises with the EMV speed. In the last step, EMVs entering and leaving the motorway are randomly selected. Their amount of energy when entering a motorway is also randomly selected. In this step, we can control the difficulty of an instance by changing two parameters: density, which defines the overall occupation of charging station and simulation time, which defines size of the instance. The range of parameter values that affect the size of GCM is given below:

• $s\in \{1,2,...,25\}$
• $b_j\in \{2,3\}$, $j=1,2,...,s$
• $n\in \{3,4,...,33\}$
• $m_i=6$, $i=1,2,...,n$.

The instance generator is designed so that every instance is guaranteed to have at least one feasible solution. If all the EMVs travel with their lowest speed, there is always a schedule such that there is no conflict at the charging stations. Note that this does not mean that there are other feasible solutions in which EMVs can travel with higher speed.

4.3. Exemplary Practical Instance

Our instance generator allows for the generation of numerous instances of different kinds. The problem of choosing an optimal location for the charging infrastructure is interesting in itself, and has been widely studied, e.g., [26]. Since we are considering only motorways, we can make an assumption that gas stations will be naturally transforming themselves into charging stations, as the basic infrastructure, such as exits or parking spaces, are already there.

In order to get closer to real data, in some experiments, we will be considering the A4 motorway, which is currently the longest motorway in Poland (669 km) and it is a part of the European route E40. We will be considering a section of the motorway between two big polish cities: 104 km route in direction from Katowice to Krakow. The section characteristics [27] are as follows:

• $r=18$ nodes
• $s=4$ gas stations which we will interpret as charging stations.
• We will assume each charging station has 2 terminals in total.

4.4. Runtime Environment

All of the experiments with the QUBO algorithm were obtained using D-wave’s Advantage 4.1 computer with the pure binary quadratic model (BQM) representation. This means that the entirety of the problem’s solution computation was performed on a quantum computer. The only preprocessing done was the problem’s embedding on an Advantage chip and mapping problem variables to qubits.

The experiments for QAOA were run on a 27-qubit quantum machine: ibmq_toronto (32 Quantum Volume, 1.8 k circuit layers operations per second).

5. Results

Two sets of instances were used in our experiments with QAOA. To acquire Figure 9, Figure 10 and Figure 11, we used artificially constructed (using the implemented generator) instances of motorways with varying number of EMVs utilizing the motorway. Figure 12 represents data from a part of the A4 motorway located in the south of Poland.

The height of the bars of figures is an average value from different instances of the problem, grouped by the number of cars (Figure 9 and Figure 12) or the size of the general conflict matrix (Figure 10) As seen in Figure 9 and Figure 10, the quality of the solution depends on the instance’s number of EMVs and the size of the corresponding GCM. This result is hardly surprising, as number of qubits used in the computation is determined by the size of the GCM.

In Figure 11, the distribution of the dependence of the GCM size on the value of the parameter n (the number of EMVs) is presented. It confirms that the number of EMVs is highly correlated with the GCM size in our experiments.

In addition to data on the efficiency of the tested algorithm in finding solutions to the considered problem, the computation times on the quantum computer seem equally interesting. Below, we present the mean timing values:

• QPU_SAMPLING_TIME: 1.97 s
• QPU_ANNEAL_TIME_PER_SAMPLE: 20.0 µs
• QPU_READOUT_TIME_PER_SAMPLE: 156.20 µs
• QPU_ACCESS_TIME: 1.98 s
• QPU_ACCESS_OVERHEAD_TIME: 107.13 ms
• QPU_PROGRAMMING_TIME: 15.07 ms
• QPU_DELAY_TIME_PER_SAMPLE: 20.54 µs
• POST_PROCESSING_OVERHEAD_TIME: 1.12 ms
• TOTAL_POST_PROCESSING_TIME: 8.59 ms.

The values were obtained directly from the D-wave’s leap platform. The precise meaning of those metrics may be found in [28], where many helpful tutorials and guides are included.

In the experiments with a gate-based model of a quantum computation (QAOA), we tried to study the effect of the length of the circuit on the chance of finding feasible solutions to the considered problem. We show the results for QAOA for different circuit length (from $p=1$ to $p=5$) in Figure 13. We can see that the highest chance of measuring optimal solution is when using circuit of length 2. After that, the noise issues disturb the optimization process. We can also observe, that for $p=2$, the probability of measuring the feasible solution is around $0.5\%$, which is several times better than drawing a random bitstring. The computational times (classical and quantum computation) for different circuit length are the following:

• $p=1$: 1 h 7 m 7 s
• $p=2$: 1 h 10 m 59 s
• $p=3$: 1 h 19 m 3 s
• $p=4$: 1 h 29 m 31 s
• $p=5$: 1 h 35 m 29 s.

6. Discussion

We were looking for the assignment of the appropriate speed and charging point to EMV traveling on the motorway so that no one has to wait for the charging process to start after reaching the station. We considered two models of vehicle charging points:

• A set of independent chargers (probably some of them at the same station).
• A set of charging stations with several identical chargers.

In the first case, we treat each charger separately and search for conflicts consisting in connecting more than one vehicle to the same charger at the same time. This is a more accurate approach to the problem under consideration. In the second case, we enable charging a number of vehicles in parallel at the same station. As described earlier, such an approach, despite the lower memory consumption, causes the rejection of acceptable solutions due to the detection of a greater number of conflicts (Figure 7). However, we use this approach because of the limited technological capabilities of quantum computers (low capacity) and the limited time of computing. Minimizing the number of variables and simplifying the conflict matrix allows finding feasible solutions for instances of the greater size.

In the graphs provided in Section 5, the parameter solution energy value should be interpreted as a value proportional to the number of unresolved conflicts at charging points. As a result of the experiments, the expected effect was observed—the more EMV, the more potential conflicts and the more difficult it is to find a feasible solution to the conflict avoidance problem. It can be assumed that in these cases, an acceptable solution does not exist. However, it should be taken into account that the tested algorithms should be considered as heuristics, which do not guarantee finding the sought solutions to the problem. Their great advantage, however, is the short computation time (evident for the QUBO case) and low energy consumption for computation.

At the current level of quantum technology development, larger instances of the problem can be solved on D-wave computers. It should be noted that in our experiments, we used BQM only—a purely quantum model of computation. The D-wave company provides another way of solution computation using hybrid (both quantum and classical computing). The constraint quadratic model (CQM) allows for defining inequality constraints, as well as many other utilities. What is more, this model type is required to use hybrid computing in which the problem is first divided into sub-problems and only then solved, piece by piece, on a purely quantum machine. This approach allowed us to reliably solve similar instances containing 40 EMVs (compared to BQM’s 10). Unfortunately, as the computing time on D-wave machines is highly limited, we could only run a handful of experiments.

The problem we are discussing can be developed toward an optimization problem. We will notice that when using the discussed method of work, one can consider the problem, among others, of minimizing the travel time assuming one or more charges or minimizing the energy consumption of all tested vehicles. Another limitation that can be taken into account is the limitation of the power or energy available at specific charging stations, which would further reduce the number of vehicles charged at the same time.

7. Conclusions

In this paper, a problem of charging batteries of EMVs driving on a motorway was considered. The problem was formulated in terms of the deterministic scheduling theory. We looked for a feasible solution in which no EMV has to wait for starting the process of charging its battery. Two quantum computing approaches were proposed to attack the problem—gate-based approach (QAOA) and quantum annealing (QA). A computational experiment was designed and carried out in order to evaluate the efficiency of the proposed quantum algorithms. It can be seen that quantum technology is just developing, but its use is already becoming real and useful. With the assumed considerable limitations, the obtained results are still several times better than the random results.

The results show that the quality of the solution is strongly related to the number of variables (number of EMVs, charging stations, and driving modes). Due to the limitations of quantum machines and access to them, we managed to perform only one test instance with tangible results. The obtained result leaves us an open path for further experiments on this topic, as soon as there are more possibilities for the use of quantum computers.

Let us notice that although our model contains some simplifications (e.g., a discrete number of driving modes defined by available speeds), it can still be useful in practice. Decisions made by such a centralized scheduling module can achieve an advantage over a set of decisions made autonomously by EMV drivers. It has all the information coming from monitoring systems on the motorway, as well as from the vehicles themselves. This may enable to synchronize and optimize the entire process of charging the fleet of EMVs which an individual driver is not capable of doing. Nowadays, there are already technical means sufficient to carry out the entire process. Additionally, despite the fact that the situation on a motorway is very dynamic and, generally, it would require online scheduling, the quantum computing power may be enough to apply the batch scheduling approach and solve the problem for a fleet of EMVs currently present on a considered motorway section. This approach will become practically more applicable in the near future when quantum computers become more powerful.

Future research can go in several directions. First of all, the considered problem can be generalized in many different ways. Possible extensions may include generalizations of the EMV model, motor way infrastructure, and/or charging process assumptions. In this paper, we only analyzed a decision (deconfliction) problem. On its basis, various optimization problems can be formulated in which different objective functions may be studied, e.g., minimization of the total (or mean) flow time, total waiting time, the number of waiting EMVs, and energy consumption. Additionally, from the computational point of view, various extensions of the experiment are possible, including solving bigger instances and comparing quantum approaches to some classical ones, e.g., involving local search metaheuristics.