Ellipsoidal Design of Robust Stabilization of Power Systems Exposed to a Cycle of Lightning Surges Modeled by Continuous-Time Markov Jumps
Abstract
:1. Introduction
1.1. Brief Review
- (1)
- topological randomness (e.g., line faults);
- (2)
- parametric randomness (e.g., in the state matrix coefficients, which is caused by the parameters changes in the system equipment);
- (3)
- exogenous stochastic disturbances, such as variations in wind turbine mechanical power inputs.
1.2. The Most Important Contributions
- SDE modeling of a multi-machine system under a succession of lightning surges by continuous-time Markov jumps (representing the topology uncertainty) + external disturbance (representing the stochastic parameter uncertainty).
- A new sufficient condition for stochastic stability is derived where the external disturbance is rejected by minimizing the volume of the invariant (attractive) ellipsoid.
- A simple design of the excitation control is presented.
- The proposed design’s efficacy is tested on a 3-machine 6-bus power system.
1.3. Structure of the Paper
1.4. Notation
- denotes the n-dimensional Euclidean space;
- is the space of real matrices of dimension ;
- refers to the Euclidean vector norm;
- The probability space with the sample space -algebra F of subsets of the sample space, and probability measure are represented by the notation ;
- signifies the expectation operator;
- For continuous-time systems, is a time-homogeneous semi-Markov process with the right continuous trajectories and takes values in a finite set with stationary transition probabilitieswhere , and is the transition rate from mode i at time t to mode j at time , satisfying for all
2. Problem Formulation
2.1. A Multi-Machine System’s Dynamic Model
2.2. Continuous-Time Markov Model of Power System Subject to a Sequence of Lightning Strikes
3. Problem Solution
3.1. Closed-Loop System
3.2. Main Result
4. Optimal Feedback Gain Selection
4.1. Optimization Problem Formulation
4.2. Transformation of the Optimization Problems under MNIs Constrains to the Problem with LMIs
5. Numerical Example
- The example below is solved numerically for ,
5.1. Optimal Parameters
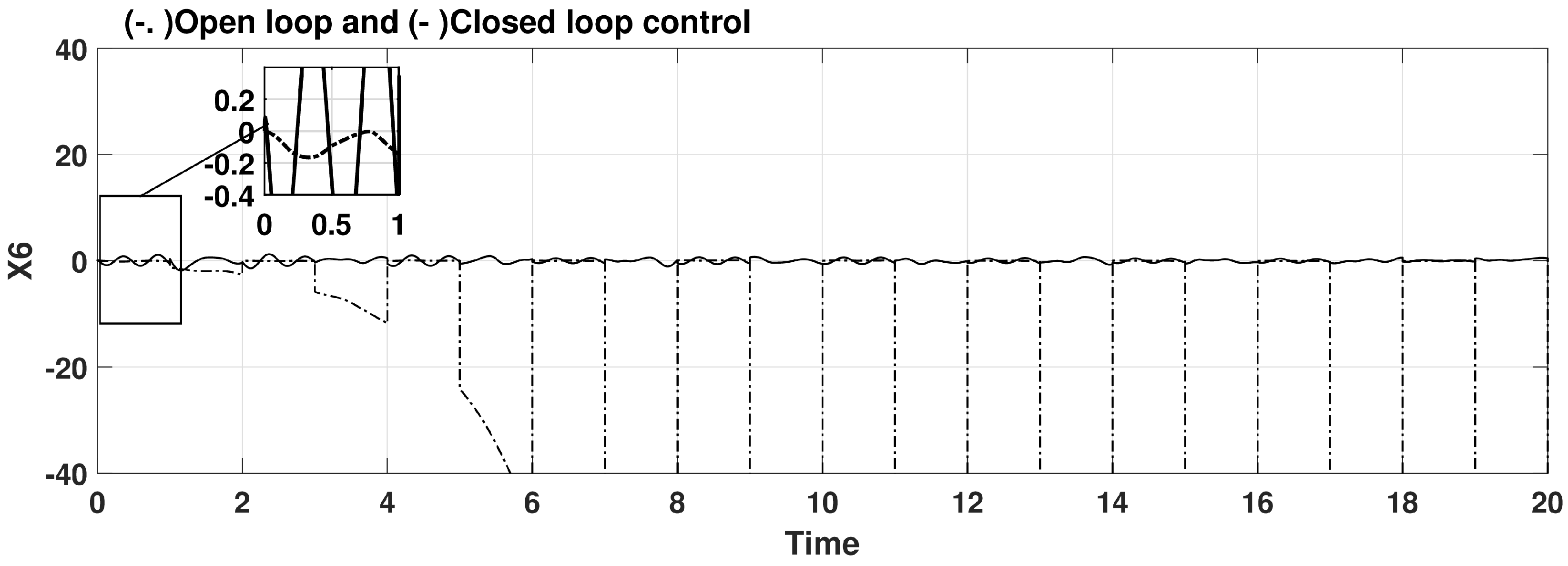
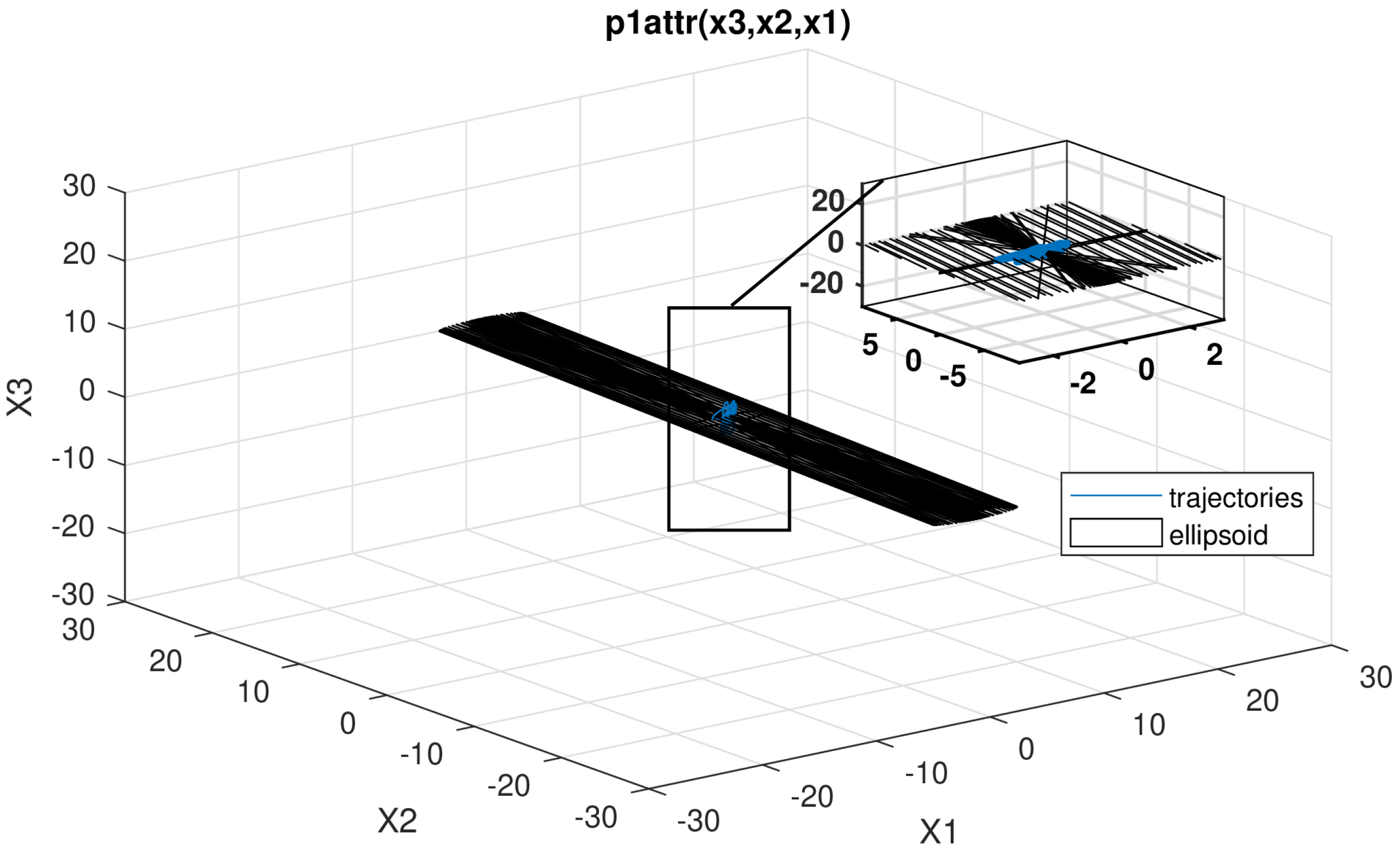
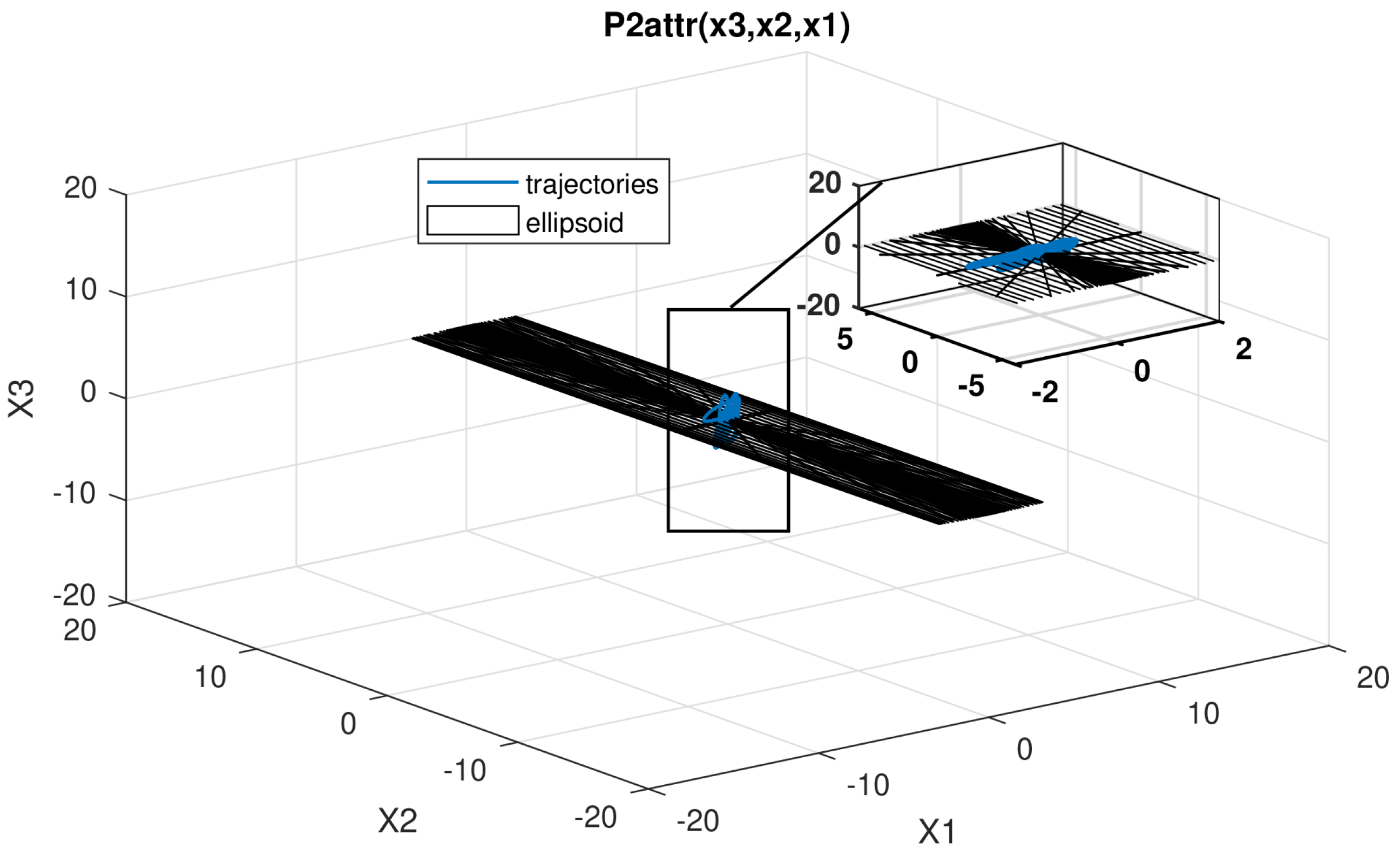
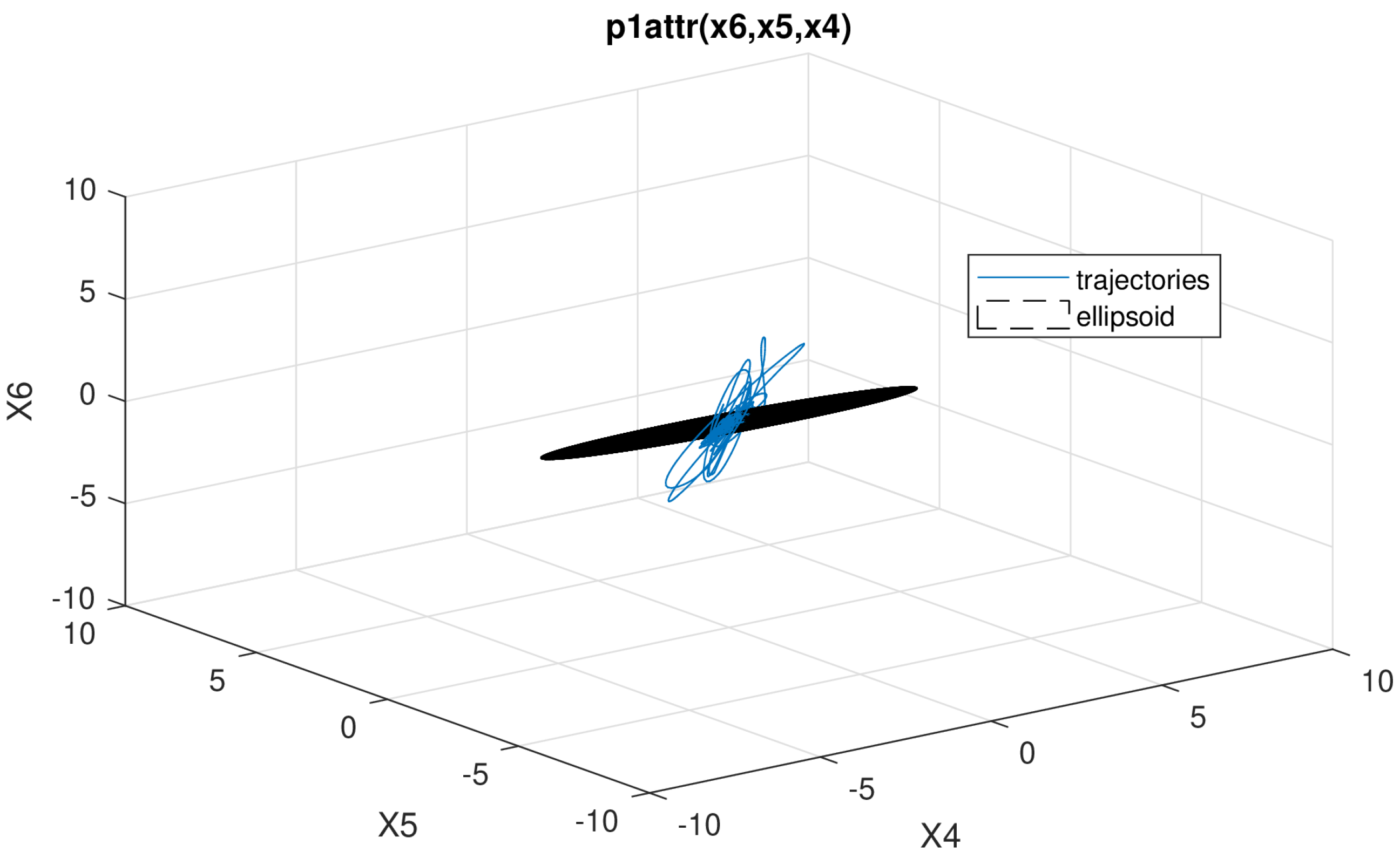
5.2. Illustrating Figures
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| the i-th generator’s power angle (); | |
| the i-th generator’s relative speed; | |
| the speed of the synchronous generator; | |
| the mechanical input power; | |
| the active electrical power; | |
| the reactive electrical power; | |
| the inertia constant (in seconds); | |
| the quadrature axis’s transient EMF; | |
| the EMF in the quadrature axis; | |
| the excitation coil’s equivalent EMF; | |
| the transient short circuit time constant in the direct axis, ; | |
| the current along the direct axis; | |
| the quadrature axis current; | |
| the i-th generator’s terminal voltage; | |
| the i-th row and j-th column element of the nodal susceptance matrix at the internal nodes | |
| after eliminating all physical buses; | |
| the reactance along the direct axis; | |
| the quadrature axis reactance; | |
| the transient reactance along the direct axis; | |
| the transient reactance along the quadrature axis. |
Appendix A. Stability of Continuous-Time Itô-Type Stochastic Differential Equations with Jumping Parameters
Appendix A.1. General Model Description
Appendix A.2. Lyapunov Function Analysis
Appendix A.3. Linear Model Case
Appendix A.4. Stability Analysis for a Linear System with Jumping Parameters
References
- Machowski, J.; Lubosny, Z.; Bialek, J.W.; Bumby, J.R. Power System Dynamics: Stability and Control; John Wiley&Sons: Croydon, UK, 2020. [Google Scholar]
- El-Sheikhi, F.A.; Soliman, H.M.; Ahshan, R.; Hossain, E. Regional pole placers of power systems under random failures/repair Markov jumps. Energies 2021, 14, 1989. [Google Scholar] [CrossRef]
- Soliman, H.M.; Elshafei, A.L.; Shaltout, A.A.; Morsi, M.F. Robust power system stabilizer. IEE Proc. Gener. Distrib. 2000, 147, 285–291. [Google Scholar] [CrossRef]
- Soliman, H.M.; Dabroum, A.; Mahmoud, M.S.; Soliman, M. Guaranteed-cost reliable control with regional pole placement of a power system. J. Frankl. Inst. 2011, 348, 884–898. [Google Scholar] [CrossRef]
- Derbel, N.; Ghommam, J.; Zhu, Q. Diagnosis, Fault Detection & Tolerant Control; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Soliman, H.M.; Yousef, H.A. Saturated robust power system stabilizers. Int. J. Electr. Power Energy Syst. 2015, 73, 608–614. [Google Scholar] [CrossRef]
- Yousef, H.; Soliman, H.M.; Albadi, M. Nonlinear power system excitation control using adaptive wavelet networks. Neurocomputing 2017, 30, 302–311. [Google Scholar] [CrossRef]
- Soliman, H.M.; El Metwally, K.A. Robust pole placement for power systems using two-dimensional membership fuzzy constrained controllers. IET Gener. Transm. Distrib. 2017, 11, 3966–3973. [Google Scholar] [CrossRef]
- Soliman, M.; Elshafei, A.L.; Bendary, F.; Mansour, W. Robust decentralized PID-based power system stabilizer design using an ILMI approach. Electr. Power Syst. Res. 2008, 80, 1488–1497. [Google Scholar] [CrossRef]
- Soliman, M. Robust non-fragile power system stabilizer. Int. J. Electr. Power Energy Syst. 2015, 64, 626–634. [Google Scholar] [CrossRef]
- Soliman, M. Parameterization of robust three-term power system stabilizers. Electr. Power Syst. Res. 2014, 17, 172–184. [Google Scholar] [CrossRef]
- Nwankpa, C.O.; Shahidehpour, S.M.; Schuss, Z.A. stochastic approach to small disturbance stability analysis. IEEE Trans. Power Syst. 1992, 7, 1519–1528. [Google Scholar] [CrossRef]
- Rueda, J.L.; Colome, D.G.; Erlich, I. Assessment and enhancement of small signal stability considering uncertainties. IEEE Trans. Power Syst. 2009, 24, 198–207. [Google Scholar] [CrossRef]
- Chung, C.Y.; Wang, K.W.; Tse, C.T.; Bian, X.Y.; David, A.K. Probabilistic eigenvalue sensitivity analysis and PSS design in multimachine systems. IEEE Trans. Power Syst. 2003, 18, 1439–1445. [Google Scholar] [CrossRef]
- Ugrinovskii, V.; Pota, H.R. Decentralized control of power systems via robust control of uncertain Markov jump parameter systems. Int. J. Control. 2005, 78, 662–677. [Google Scholar] [CrossRef]
- Ma, J.; Wang, S.; Qiu, Y.; Li, Y.; Wang, Z.; Thorp, J.S. Angle stability analysis of power system with multiple operating conditions considering cascading failure. IEEE Trans. Power Systems 2017, 32, 873–882. [Google Scholar] [CrossRef]
- Soliman, H.; Shafiq, M. Robust stabilisation of power systems with random abrupt changes. IET Gener. Distrib. 2015, 9, 2159–2166. [Google Scholar] [CrossRef]
- Ju, P. Fundamentals of Stochastic Dynamics. In Stochastic Dynamics of Power Systems; Springer: Singapore, 2019. [Google Scholar]
- Duffy, D.G. Advanced Engineering Mathematics with MATLAB®, 3rd ed.; Chapman and Hall/CRC: New York, NY, USA, 2016. [Google Scholar]
- Yuan, B.; Zhou, M.; Li, G.; Zhang, X.P. Stochastic small-signal stability of power systems with wind power generation. IEEE Trans. Power Syst. 2014, 30, 1680–1689. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, Y.; Wei, Z.; Sun, G.; Wu, X. Robust H∞ load frequency control of multi-area power system with time delay: A sliding mode control approach. IEEE/CAA J. Autom. 2017, 5, 610–617. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Y. Stochastic Small Signal Interval Stability of Power Systems with Asynchronous Wind Turbine Generators. Math. Probl. Eng. 2018, 2018, 7617394. [Google Scholar] [CrossRef]
- Kuppusamy, S.; Joo, Y.H.; Kim, H.S. Asynchronous Control for Discrete-Time Hidden Markov Jump Power Systems. IEEE Trans. Cybern. 2021, 52, 9943–9948. [Google Scholar] [CrossRef]
- Soliman, H.M.; Alazki, H.; Poznyak, A.S. Robust stabilization of power systems subject to a series of lightning strokes modeled by Markov jumps: Attracting ellipsoids approach. J. Frankl. Inst. 2022, 35, 3389–3404. [Google Scholar] [CrossRef]
- Poznyak, A.S.; Alazki, H.; Soliman, H.M. Invariant-set design of observer-based robust control for power systems under stochastic topology and parameters changes. Int. J. Electr. Power Energy Syst. 2016, 131, 107–112. [Google Scholar] [CrossRef]
- Poznyak, A.; Polyakov, A.; Azhmyakov, V. Attractive Ellipsoids in Robust Control; Birkhauser: Boston, MA, USA, 2014. [Google Scholar]
- Alazki, H.; Hernández, E.; Ibarra, J.; Poznyak, A. Attractive ellipsoid method controller under noised measurements for SLAM. Int. Control. Autom. Syst. 2017, 15, 2764–2775. [Google Scholar] [CrossRef]
- Saadat, H. The Power System and Electric Power Generation, 3rd ed.; PSA Publishing: Alexandria, VA, USA, 2010; pp. 154–196. [Google Scholar]
- Feng, X.; Loparo, K.A.; Ji, Y.; Chizeck, H.J. Stochastic stability properties of jump linear systems. IEEE Trans. Automatic Control. 1992, 37, 38–53. [Google Scholar] [CrossRef]
- Hou, Z.; Luo, J.; Shi, P.; Nguang, S.K. Stochastic stability of Ito differential equations with semi-Markovian jump parameters. IEEE Trans. Autom. Control. 2006, 51, 1383–1387. [Google Scholar] [CrossRef]
- Khasminskii, R. Stochastic Stability of Differential Equations; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
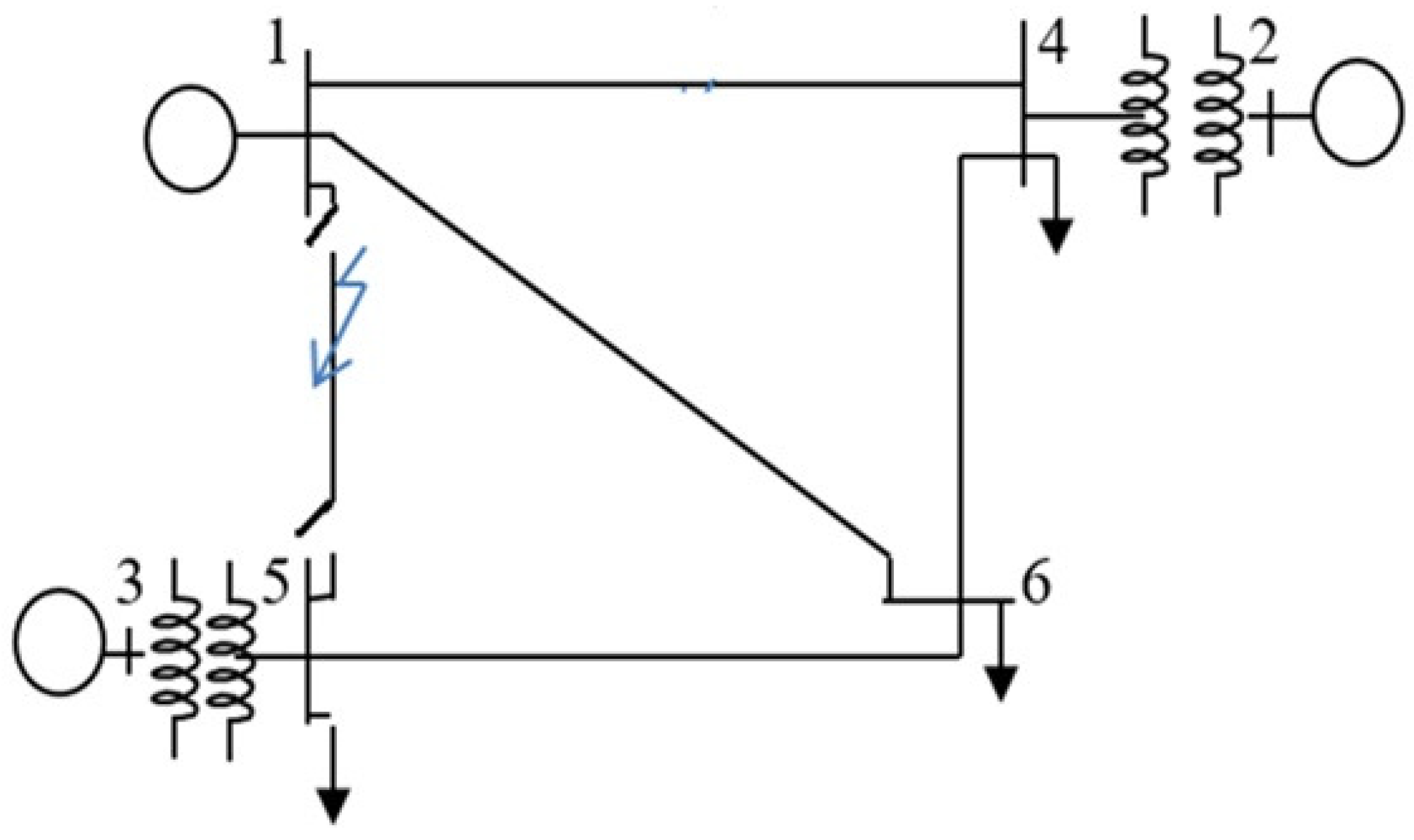
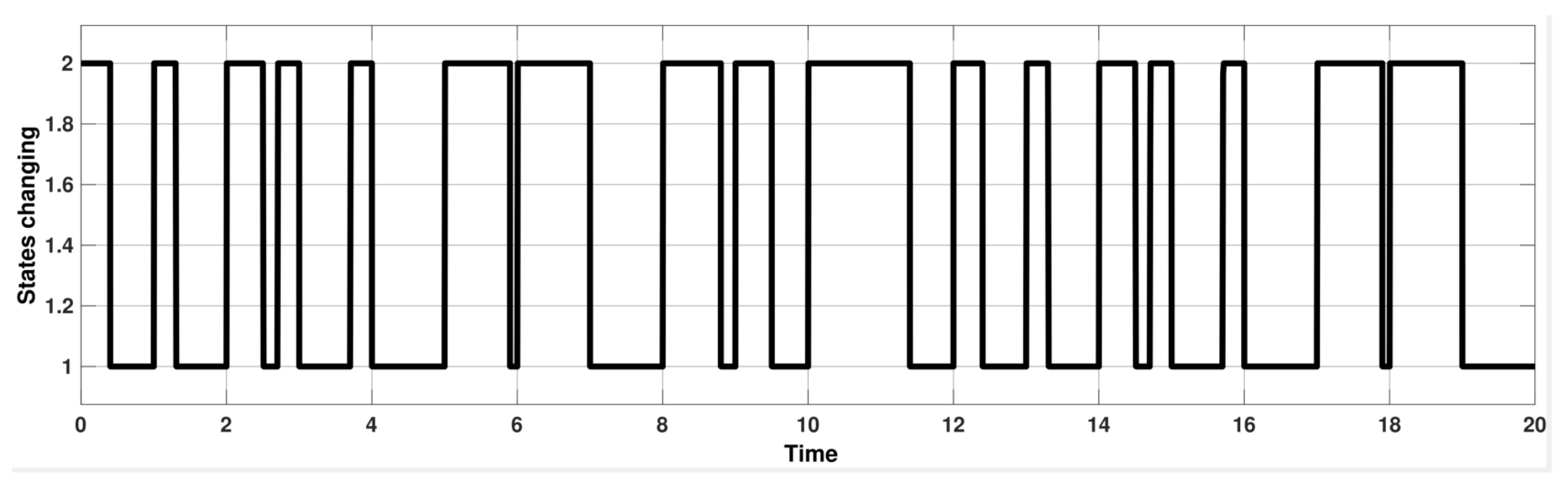

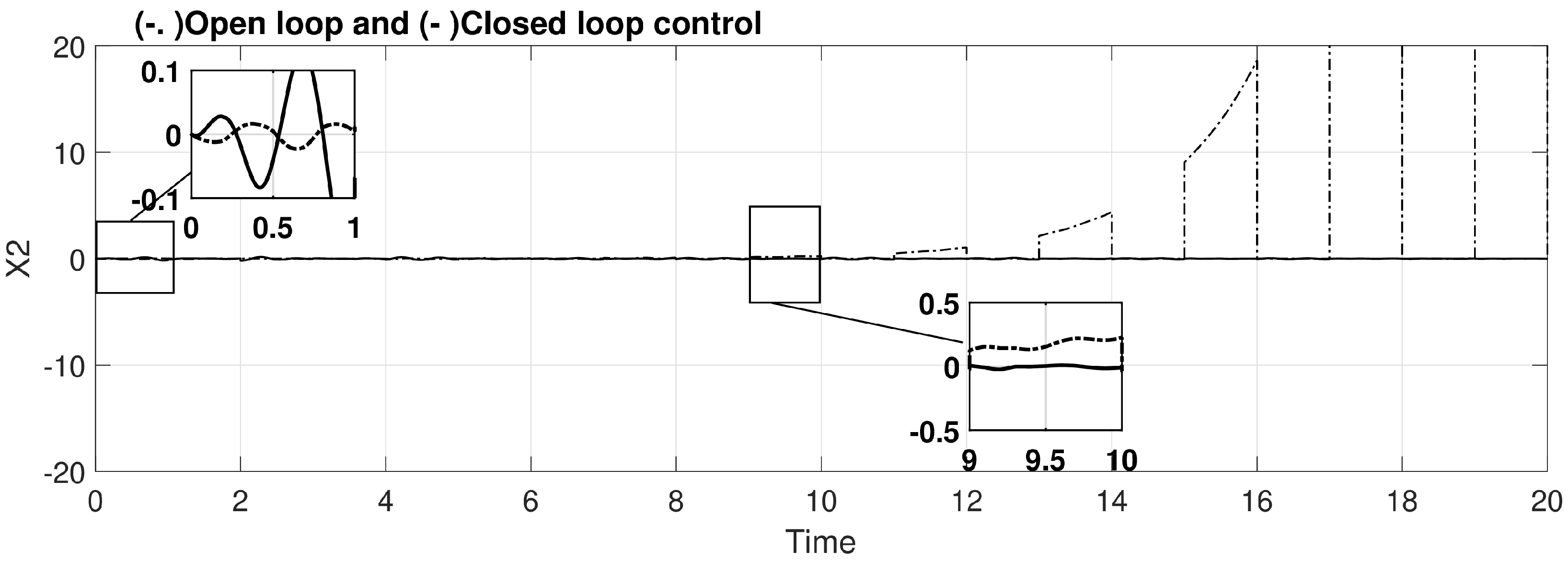


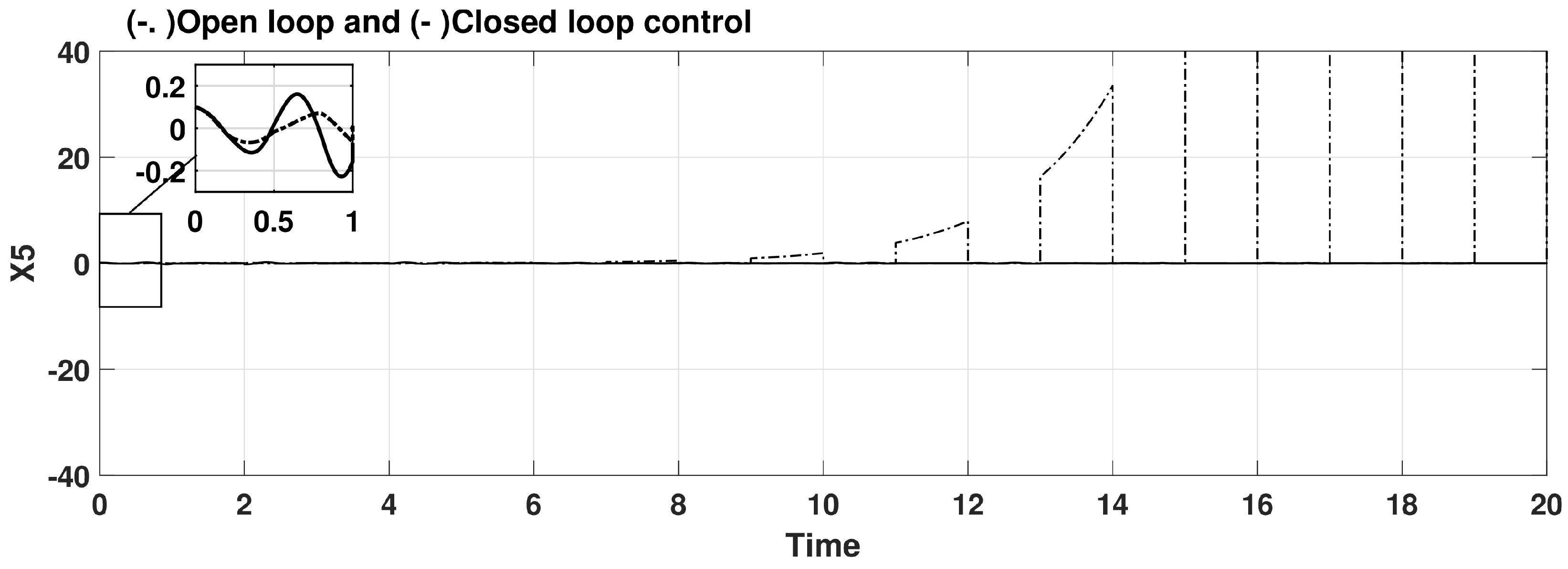

| Bus # | 1 | 2 | 3 | 4 | 5 | 6 |
| Gen- | 150 | 100 | ||||
| Load- | 0 | 0 | 0 | 100 | 90 | 160 |
| Load- | 0 | 0 | 0 | 70 | 30 | 110 |
| 0.8, 0.8, 0.2 | 1.3, 1.3, 0.15 | 0.9, 0.9, 0.25 | ||||
| 9 | 5.8 | 6 | ||||
| H | 20 | 4 | 5 | |||
| Bus # | Bus # | |||||
| 1 | 4 | 0.035 | 0.025 | 0.0065 | ||
| 1 | 5 | 0.025 | 0.105 | 0.0045 | ||
| 1 | 6 | 0.04 | 0.215 | 0.0055 | ||
| 3 | 4 | 0 | 0.035 | 0 | ||
| 3 | 5 | 0 | 0.042 | 0 | ||
| 4 | 6 | 0.028 | 0.125 | 0.0035 | ||
| 5 | 6 | 0.026 | 0.175 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poznyak, A.; Alazki, H.; Soliman, H.M.; Ahshan, R. Ellipsoidal Design of Robust Stabilization of Power Systems Exposed to a Cycle of Lightning Surges Modeled by Continuous-Time Markov Jumps. Energies 2023, 16, 414. https://doi.org/10.3390/en16010414
Poznyak A, Alazki H, Soliman HM, Ahshan R. Ellipsoidal Design of Robust Stabilization of Power Systems Exposed to a Cycle of Lightning Surges Modeled by Continuous-Time Markov Jumps. Energies. 2023; 16(1):414. https://doi.org/10.3390/en16010414
Chicago/Turabian StylePoznyak, Alexander, Hussain Alazki, Hisham M. Soliman, and Razzaqul Ahshan. 2023. "Ellipsoidal Design of Robust Stabilization of Power Systems Exposed to a Cycle of Lightning Surges Modeled by Continuous-Time Markov Jumps" Energies 16, no. 1: 414. https://doi.org/10.3390/en16010414
APA StylePoznyak, A., Alazki, H., Soliman, H. M., & Ahshan, R. (2023). Ellipsoidal Design of Robust Stabilization of Power Systems Exposed to a Cycle of Lightning Surges Modeled by Continuous-Time Markov Jumps. Energies, 16(1), 414. https://doi.org/10.3390/en16010414







