Experimental Investigation on the Vector Characteristics of Concentrated Solar Radiation Flux Map
Abstract
1. Introduction
2. Experimental Details
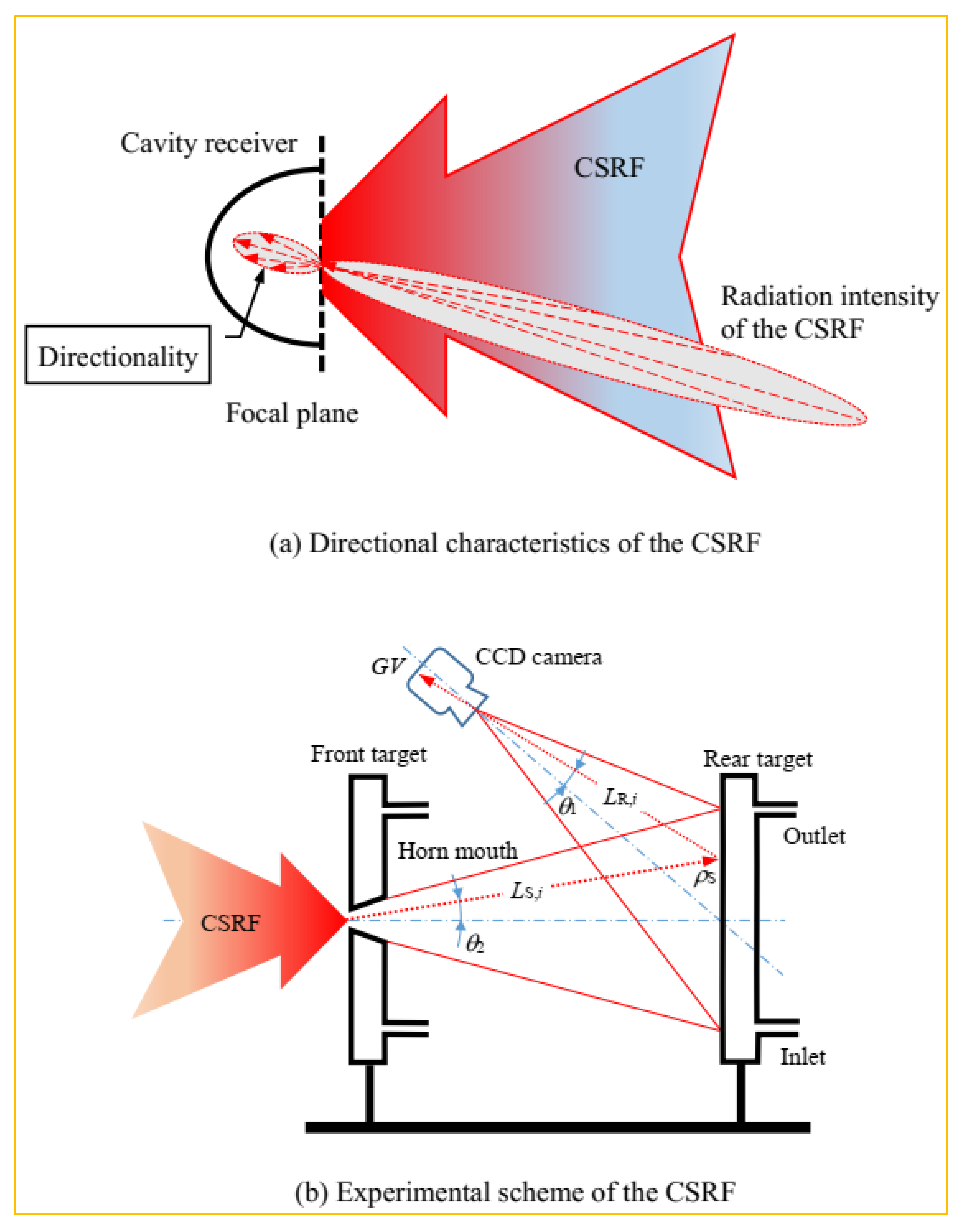
2.1. Experimental Method
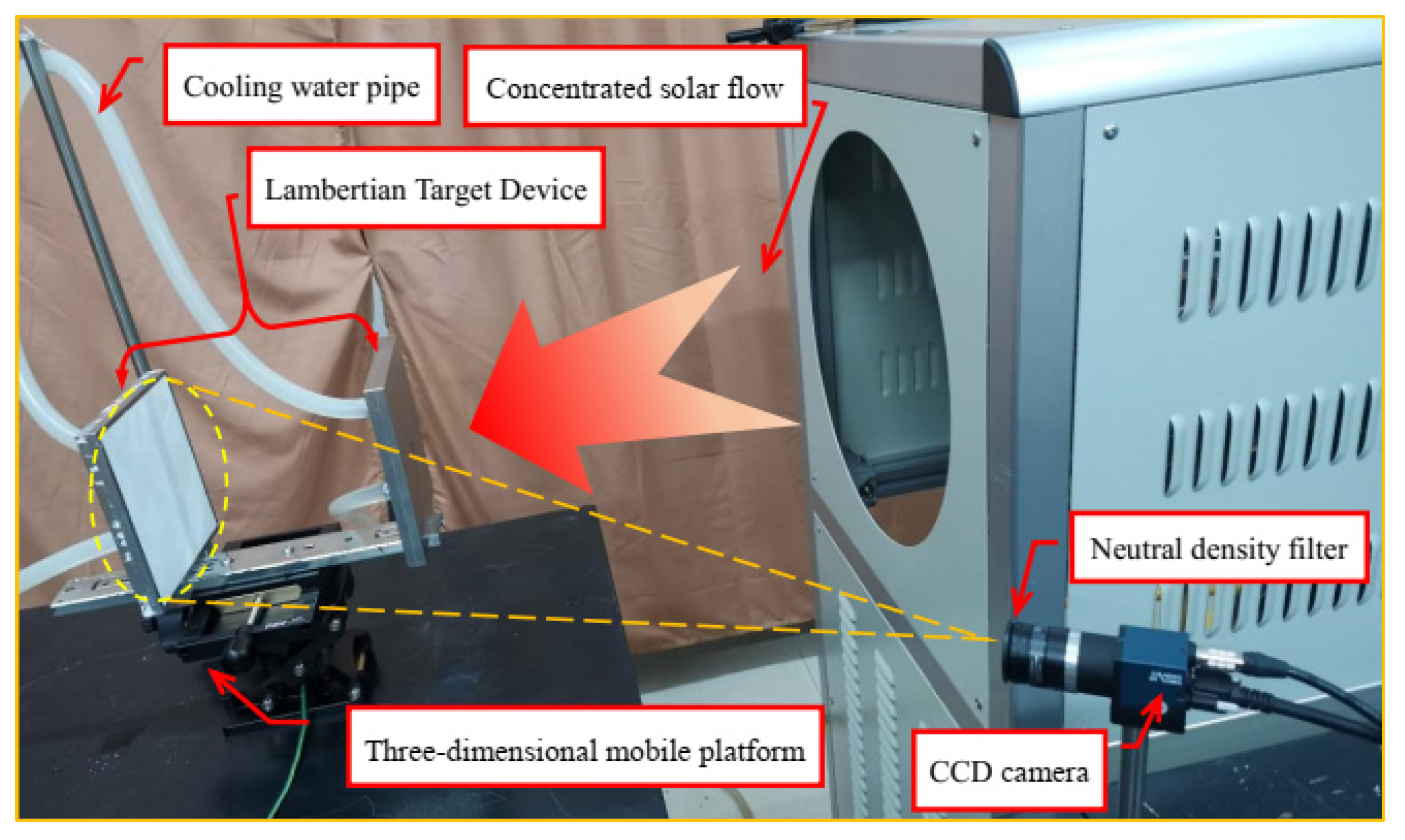
2.2. Experimental Apparatus
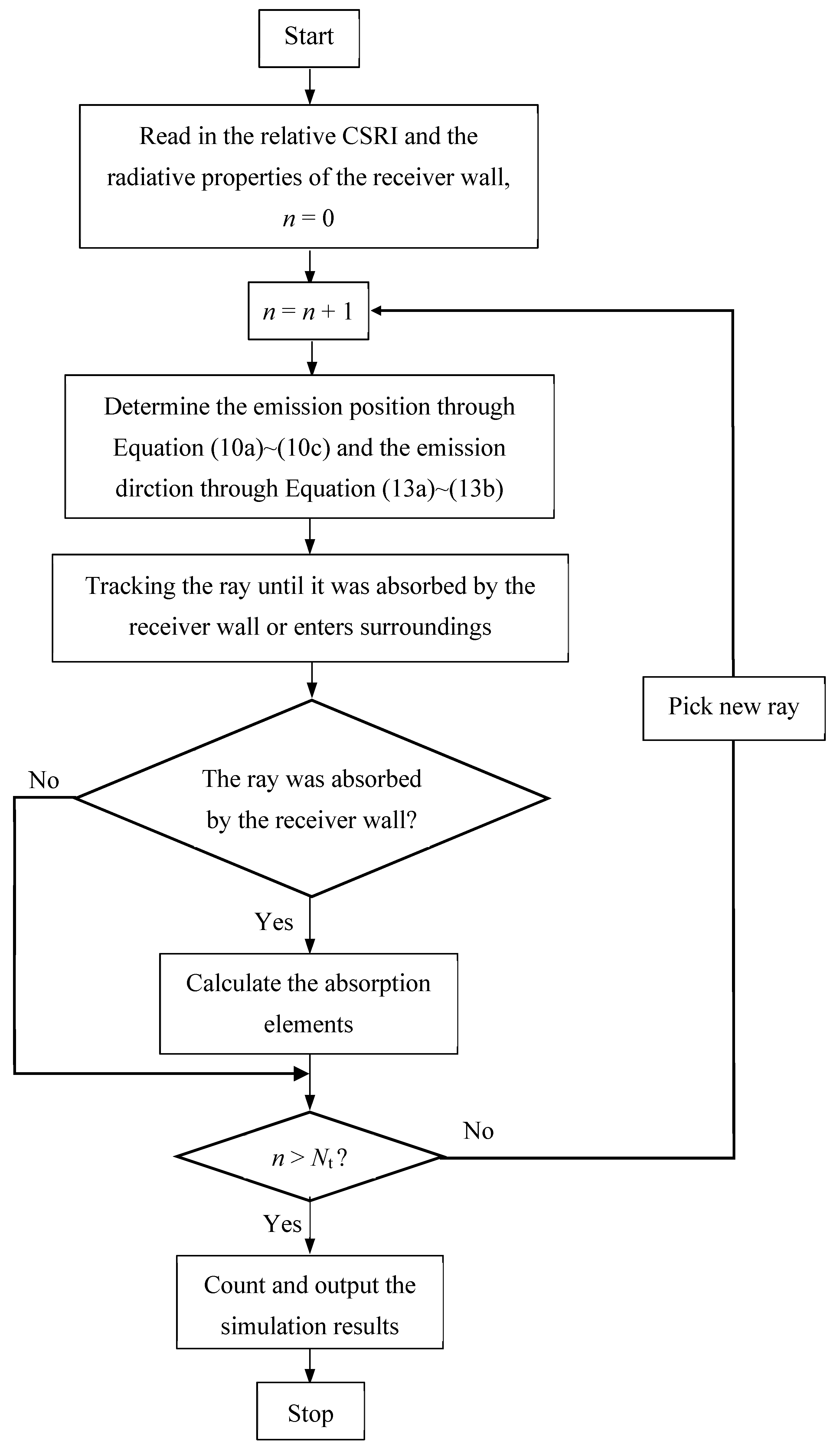
3. MCRTM Method Coupled with Experimental CSRF on the Focal Plane
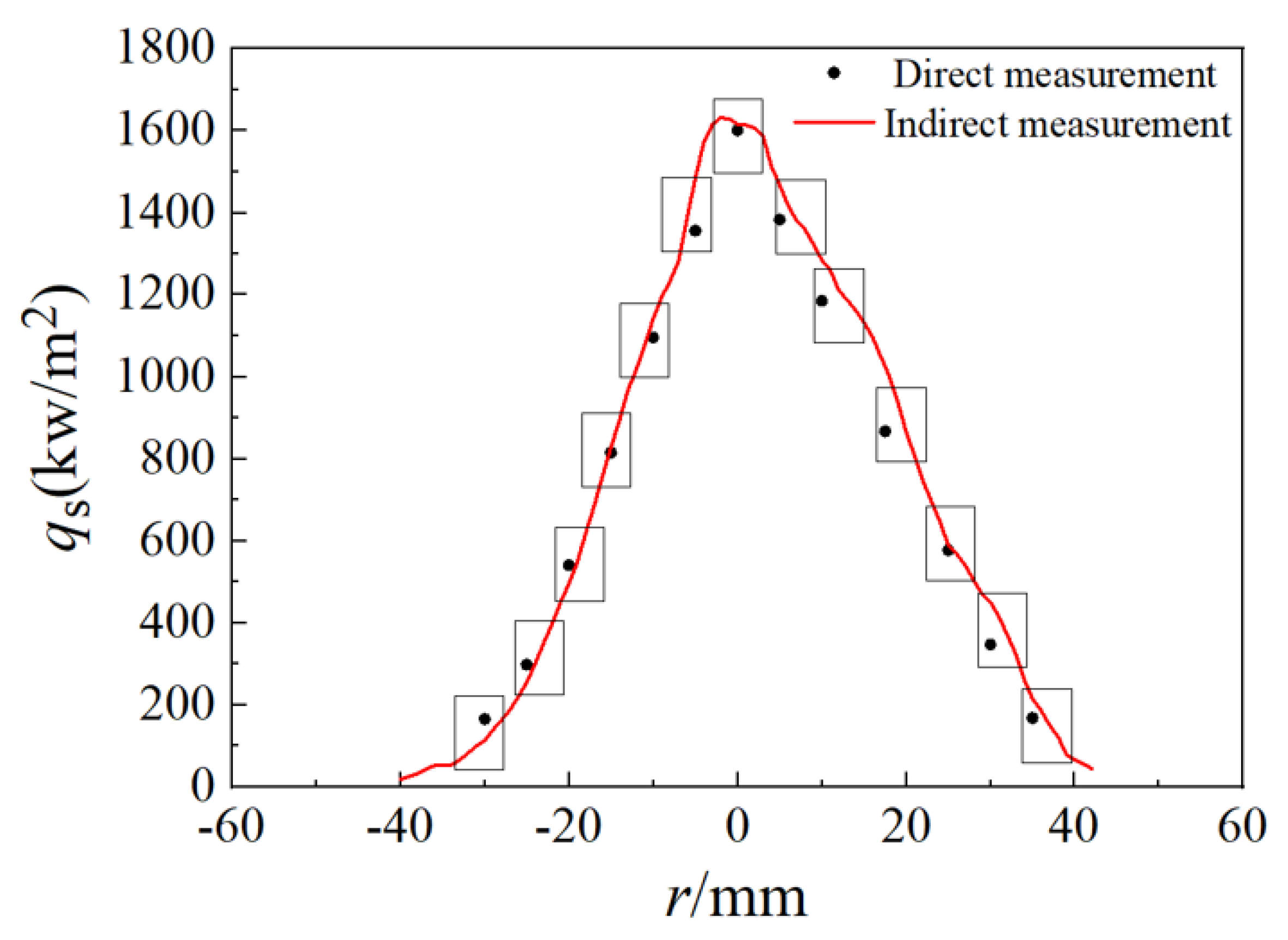
4. Measurement Results and Experimental Verification
4.1. Composite Measurement of the CSRF Density Distributions
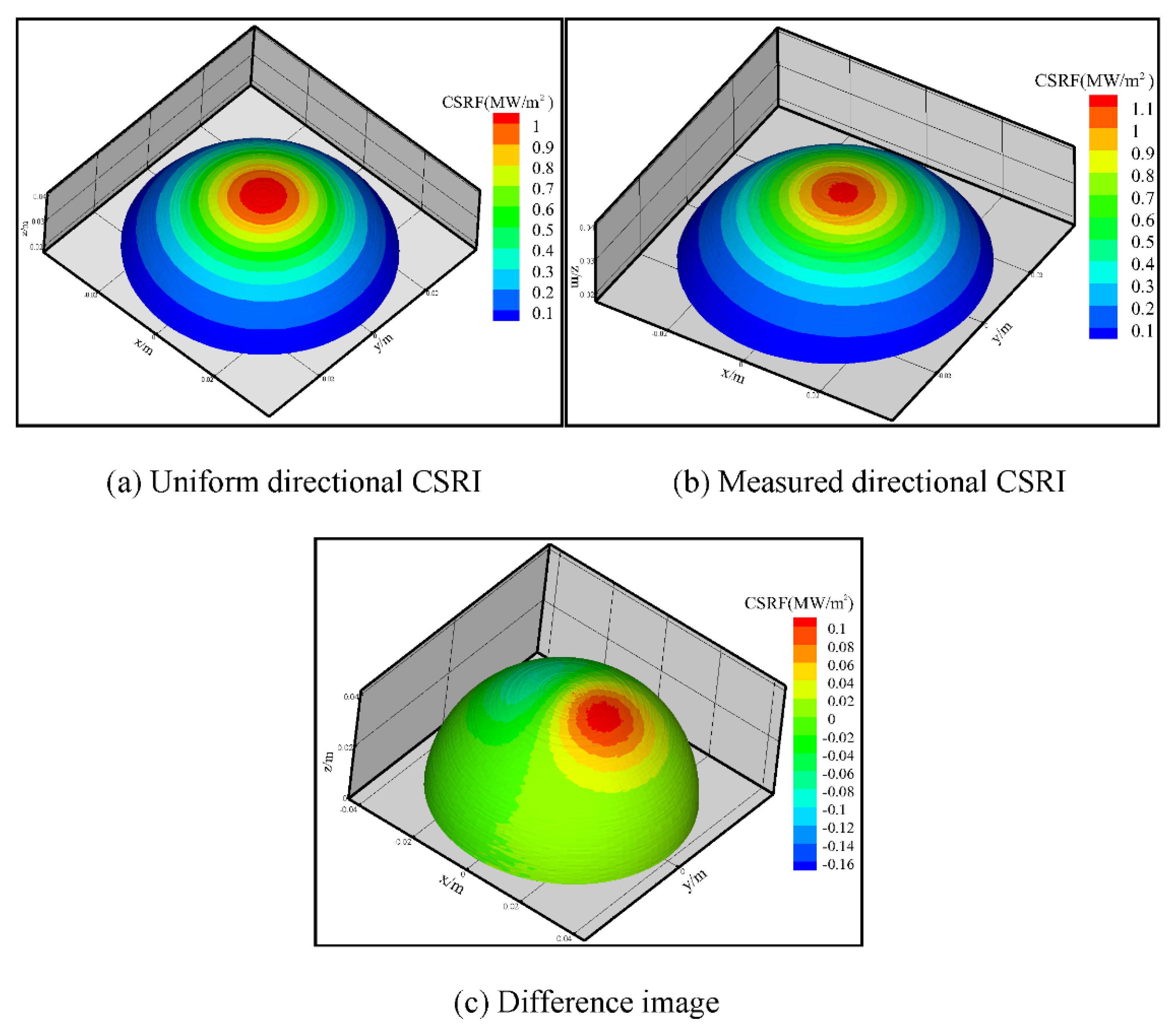
4.2. The Directional Characteristics of the CSRF
4.3. Influences of the Directional CSRI on Thermal Conditions of the Cavity Receiver
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| ac,bc | fitting coefficients of the CCD camera |
| GV | gray value of the CCD camera |
| fs | transmittance of the neutral density filter |
| hx | size of the rear target surface along x axis |
| hy | size of the rear target surface along y axis |
| Is | concentrated solar radiative intensity(CSRI), W/(m2·sr) |
| Relative CSRI, | |
| LS,(i,j) | incoming solar radiant intensity of the rear target at grid (i, j), W/m2 |
| l | spacing between the front and rear target, m |
| Nx | pixel number of the rear target surface image along x axis |
| Ny | pixel number of the rear target surface image along y axis |
| qs | spatial distribution of the CSRF, w/m2 |
| x | x-direction coordinate, m |
| y | y-direction coordinate, m |
| r | emission radius for the solar ray, m |
| r0 | radius of the CSRF spot, m |
| R | correlation coefficient of the fitting functions |
| Rφ, Rr, Rβ, Rθ | random number uniformly distributed between zero and one |
| Greek symbols | |
| θ | zenith angle |
| β | circumferential angle |
| ΔA | area of surface element, m2 |
| ΔΩ | solid angle of surface element, sr |
| ΔAHM | area of the horn mouth, m2 |
| μ | total uncertainty |
| μA | type A uncertainty |
| μB | type B uncertainty |
| ρs | reflectivity of the lambertian target |
| Subscripts | |
| s | solar radiation |
| i, j | surface element |
| 0 | emission positon |
| Abbreviations | |
| CSRF | concentrated solar radiation flux |
| CSRI | concentrated solar radiative intensity |
| MCRTM | Monte-Carlo ray-tracing method |
| CCD | Charge coupled Device |
References
- Ávila-Marín, A.L. Volumetric receivers in solar thermal power plants with central receiver system technology: A review. Sol. Energy 2011, 85, 891–910. [Google Scholar] [CrossRef]
- Avila-Marin, A.L.; Fernandez-Reche, J.; Martinez-Tarifa, A. Modelling strategies for porous structures as solar receivers in central receiver systems: A review. Renew. Sustain. Energy Rev. 2019, 111, 15–33. [Google Scholar] [CrossRef]
- Cagnoli, M.; Froio, A.; Savoldi, L.; Zanino, R. Multi-scale modular analysis of open volumetric receivers for central tower CSP systems. Sol. Energy 2019, 190, 195–211. [Google Scholar] [CrossRef]
- Patil, V.R.; Kiener, F.; Grylka, A.; Steinfeld, A. Experimental testing of a solar air cavity-receiver with reticulated porous ceramic absorbers for thermal processing at above 1000 °C. Sol. Energy 2021, 214, 72–85. [Google Scholar] [CrossRef]
- Ballestrin, J. A non-water-cooled heat flux measurement system under concentrated solar radiation conditions. Sol. Energy 2002, 73, 159–168. [Google Scholar] [CrossRef]
- Röger, M.; Herrmann, P.; Ulmer, S.; Ebert, M.; Prahl, C.; Göhring, F. Techniques to Measure Solar Flux Density Distribution on Large-Scale Receivers. J. Sol. Energy Eng. 2014, 136, 031013–1–031013–10. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Q.; Lei, J.; Liu, F. Design and characterization of the non-uniform solar flux distribution measurement system. Appl. Therm. Eng. 2019, 150, 294–304. [Google Scholar] [CrossRef]
- Ulmer, S.; Lüpfert, E.; Pfänder, M.; Buck, R. Calibration corrections of solar tower flux density measurements. Energy 2004, 29, 925–933. [Google Scholar] [CrossRef]
- Krueger, K.R.; Lipinski, W.; Davidson, J.H. Operational performance of the university of minnesota 45 kWe High-Flux Solar Simulator. J. Sol. Energy Eng. 2013, 135, 044501.1–044501.4. [Google Scholar] [CrossRef]
- Li, J.; Gonzalez-Aguilar, J.; Pérez-Rábago, C.; Zeaiter, H.; Romero, M. Optical analysis of a hexagonal 42kWe high-flux solar simulator. Energy Procedia 2014, 57, 590–596. [Google Scholar] [CrossRef]
- Sarwar, J.; Georgakis, G.; LaChance, R.; Ozalp, N. Description and characterization of an adjustable flux solar simulator for solar thermal, thermochemical and photovoltaic applications. Sol. Energy 2014, 100, 179–194. [Google Scholar] [CrossRef]
- Levêque, G.; Bader, R.; Lipiński, W.; Haussener, S. Experimental and numerical characterization of a new 45 kWel multisource high-flux solar simulator. Opt. Express 2016, 24, A1360–A1373. [Google Scholar] [CrossRef] [PubMed]
- Aichmayer, L.; Wang, W.; Garrido, J.; Laumert, B. Experimental flux measurement of a high-flux solar simulator using a Lambertian target and a thermopile flux sensor. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2016. [Google Scholar]
- Ballestrín, J.; Monterreal, R. Hybrid heat flux measurement system for solar central receiver evaluation. Energy 2004, 29, 915–924. [Google Scholar] [CrossRef]
- Xiao, J.; Wei, X.; Gilaber, R.N.; Zhang, Y.; Li, Z. Design and characterization of a high-flux non-coaxial concentrating solar simulator. Appl. Therm. Eng. 2018, 145, 201–211. [Google Scholar] [CrossRef]
- Xiao, J.; Yang, H.; Wei, X.; Li, Z. A novel flux mapping system for high-flux solar simulators based on the indirect method. Sol. Energy 2019, 179, 89–98. [Google Scholar] [CrossRef]
- Modest, M. Radiative Heat Transfer; Academic Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Shuai, Y.; Xia, X.L.; Tan, H.P. Radiation performance of dish solar concentrator/cavity receiver systems. Sol. Energy 2008, 82, 13–21. [Google Scholar] [CrossRef]
- Chen, X.; Xia, X.L.; Liu, H.; Li, Y.; Liu, B. Heat transfer analysis of a volumetric solar receiver by coupling the solar radiation transport and internal heat transfer. Energy Convers. Manag. 2016, 114, 20–27. [Google Scholar] [CrossRef]
- Ali, M.; Rady, M.; Attia, M.A.; Ewais, E.M. Consistent coupled optical and thermal analysis of volumetric solar receivers with honeycomb absorbers. Renew. Energy 2020, 145, 1849–1861. [Google Scholar] [CrossRef]
- Garcia, P.; Ferriere, A.; Bezian, J.J. Codes for solar flux calculation dedicated to central receiver system applications—A comparative review. Sol. Energy 2008, 82, 189–197. [Google Scholar] [CrossRef]
- He, Y.L.; Cui, F.Q.; Cheng, Z.D.; Li, Z.Y.; Tao, W.Q. Numerical simulation of solar radiation transmission process for the solar tower power plant_ From the heliostat field to the pressurized volumetric receiver. Appl. Therm. Eng. 2013, 61, 583–595. [Google Scholar] [CrossRef]
- Daabo, A.M.; Mahmoud, S.; Al-Dadah, R.K. The optical efficiency of three different geometries of a small scale cavity receiver for concentrated solar applications. Appl. Energy 2016, 179, 1081–1096. [Google Scholar] [CrossRef]
- Daabo, A.M.; Ahmad, A.; Mahmoud, S.; Al-Dadah, R.K. Parametric analysis of small scale cavity receiver with optimum shape for solar powered closed Brayton cycle applications. Appl. Therm. Eng. 2011, 31, 3377–3386. [Google Scholar] [CrossRef]
- Kasaeian, A.; Kouravand, A.; Rad, M.A.V.; Maniee, S.; Pourfayaz, F. Cavity receivers in solar dish collectors: A geometric overview. Renew. Energy 2021, 169, 53–79. [Google Scholar] [CrossRef]
- Du, S.; He, Y.L.; Yang, W.W.; Liu, Z.B. Optimization method for the porous volumetric solar receiver coupling genetic algorithm and heat transfer analysis. Int. J. Heat Mass Transf. 2018, 122, 383–390. [Google Scholar] [CrossRef]
- Barreto, G.; Canhoto, P.; Collares-Pereira, M. Three-dimensional CFD modelling and thermal performance analysis of porous volumetric receivers coupled to solar concentration systems. Appl. Energy 2019, 252, 113433. [Google Scholar] [CrossRef]
- Kribus, A. Optical performance of conical windows for concentrated solar radiation. J. Sol. Energy Eng. 1994, 116, 47–52. [Google Scholar] [CrossRef]
- Karni, J.; Kribus, A.; Ostraich, B.; Kochavi, E. A high-pressure window for volumetric solar receivers. J. Sol. Energy Eng. 1998, 120, 101–107. [Google Scholar] [CrossRef]
- Timinger, A.; Spirkl, W.; Kribus, A.; Ries, H. Optimized secondary concentrators for a partitioned central receiver system. Sol. Energy 2000, 69, 153–162. [Google Scholar] [CrossRef]
- Xia, X.L.; Dai, G.L.; Shuai, Y. Experimental and numerical investigation on solar concentrating characteristics of a sixteen-dish concentrator. Int. J. Hydrogen Energy 2012, 37, 18694–18703. [Google Scholar] [CrossRef]
- Wang, K.; He, Y.L.; Qiu, Y.; Zhang, Y. A novel integrated simulation approach couples MCRT and Gebhart methods to simulate solar radiation transfer in a solar power tower system with a cavity receiver. Renew. Energy 2016, 89, 93–107. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, G.; Zhuang, Y.; Wang, X.; Chen, X.; Sun, C.; Du, S. Experimental Investigation on the Vector Characteristics of Concentrated Solar Radiation Flux Map. Energies 2023, 16, 136. https://doi.org/10.3390/en16010136
Dai G, Zhuang Y, Wang X, Chen X, Sun C, Du S. Experimental Investigation on the Vector Characteristics of Concentrated Solar Radiation Flux Map. Energies. 2023; 16(1):136. https://doi.org/10.3390/en16010136
Chicago/Turabian StyleDai, Guilong, Ying Zhuang, Xiaoyu Wang, Xue Chen, Chuang Sun, and Shenghua Du. 2023. "Experimental Investigation on the Vector Characteristics of Concentrated Solar Radiation Flux Map" Energies 16, no. 1: 136. https://doi.org/10.3390/en16010136
APA StyleDai, G., Zhuang, Y., Wang, X., Chen, X., Sun, C., & Du, S. (2023). Experimental Investigation on the Vector Characteristics of Concentrated Solar Radiation Flux Map. Energies, 16(1), 136. https://doi.org/10.3390/en16010136






