Effect of Gaskets Geometry on the Performance of a Reverse Electrodialysis Cell
Abstract
1. Introduction
- Cell design and components (materials, equipment and cell geometry);
- Hydrodynamics (flow distribution, pressure drop);
- Mass transport (mass distribution);
- Energy transport (potential and current distribution).
- Thickness of the gaskets. Flow velocities are higher within thinner compartments, and this can reduce the formation of dead zones and generate a more uniform flow distribution [18];
- Spacers characteristics. Filament spacing, diameter, arrangement, and angle affect the flow pattern, velocity distribution, flow regime, pressure drops, and mass transport [6];
- Gaskets geometry. The geometry of the gasket can influence the distribution of the solutions in the compartments; this promotes fluid mixing, reducing polarization phenomena and electrical resistance [18].
2. Materials and Methods
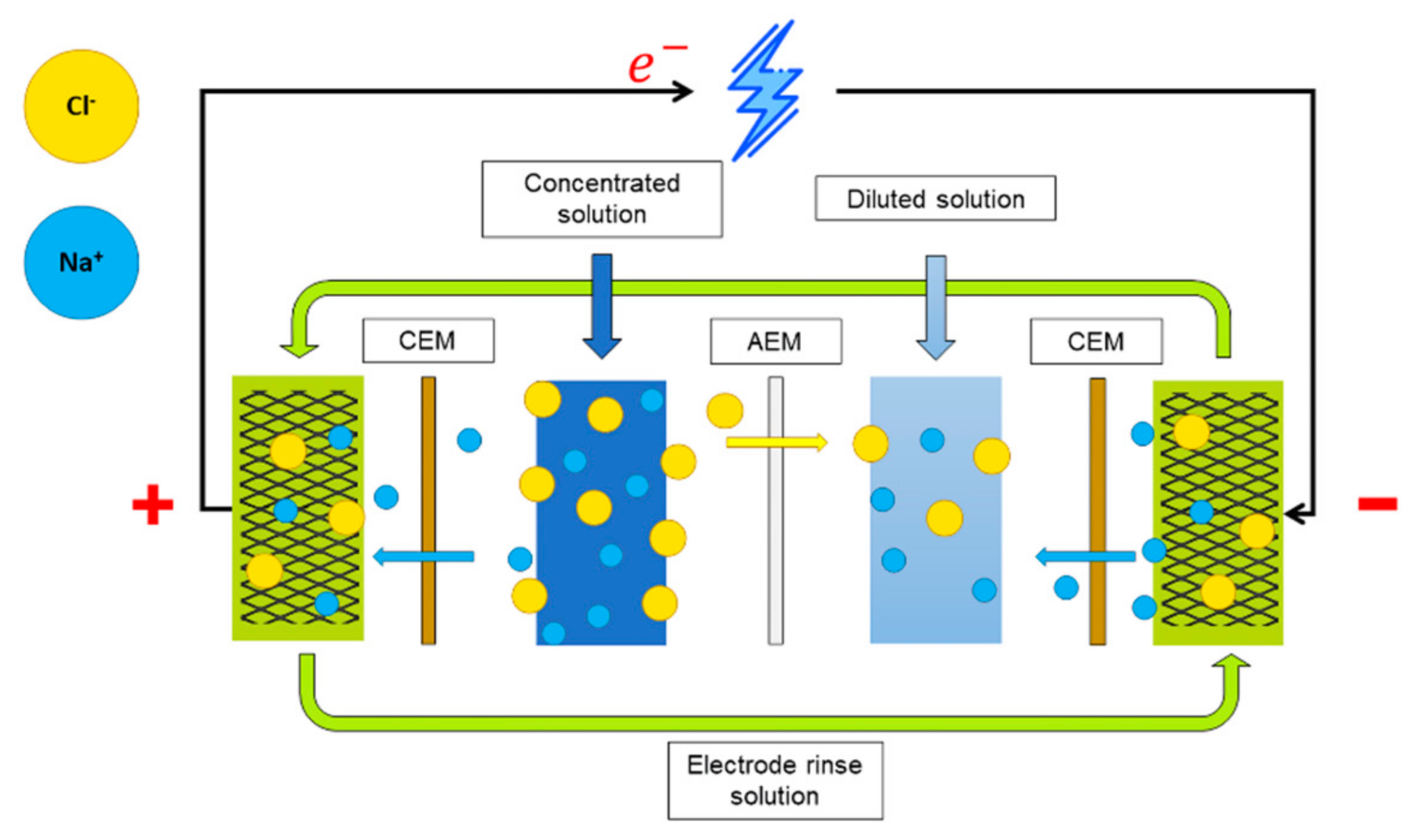
2.1. Reverse Electrodialysis Cell
2.2. Feed Solutions
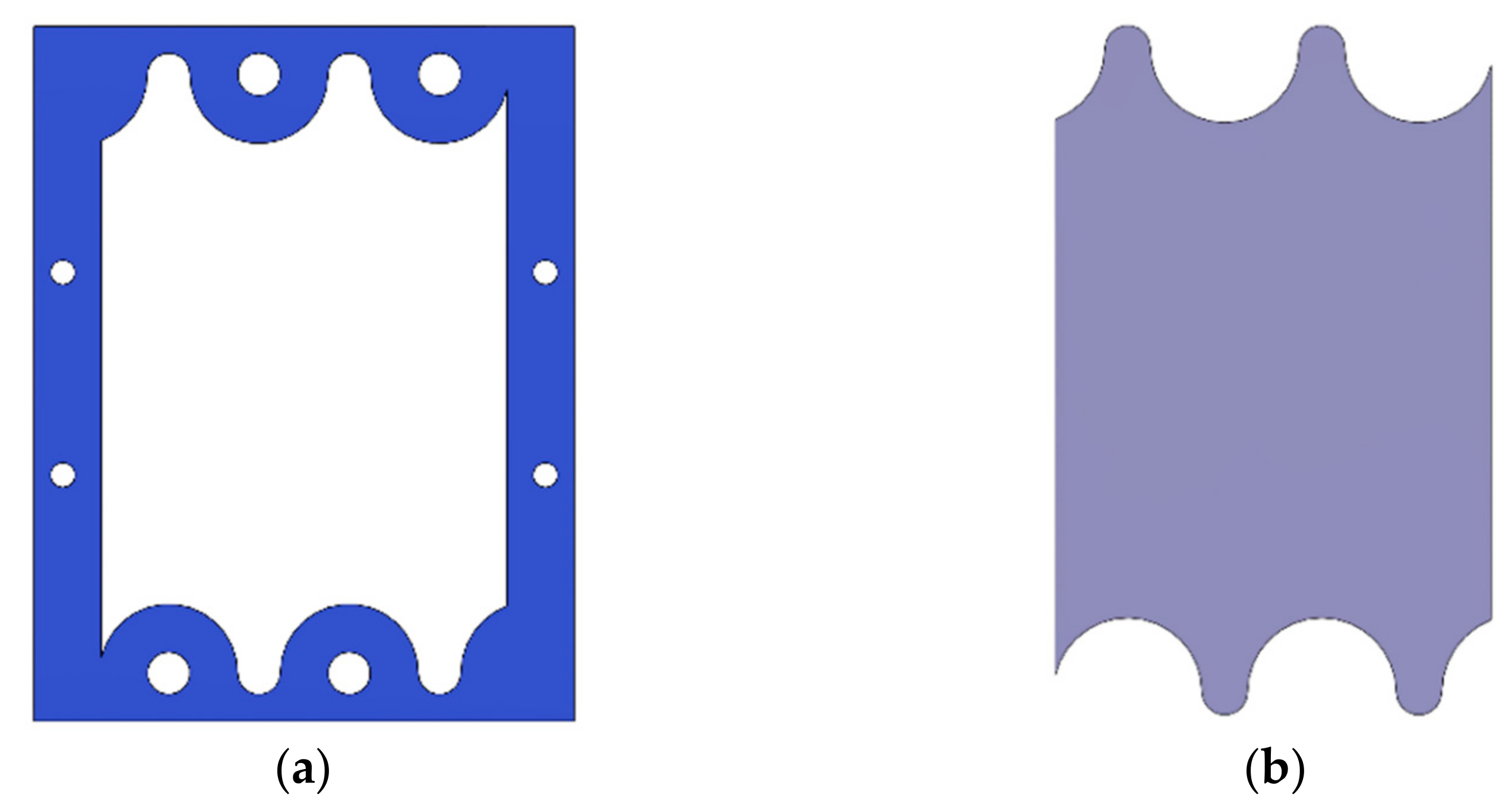
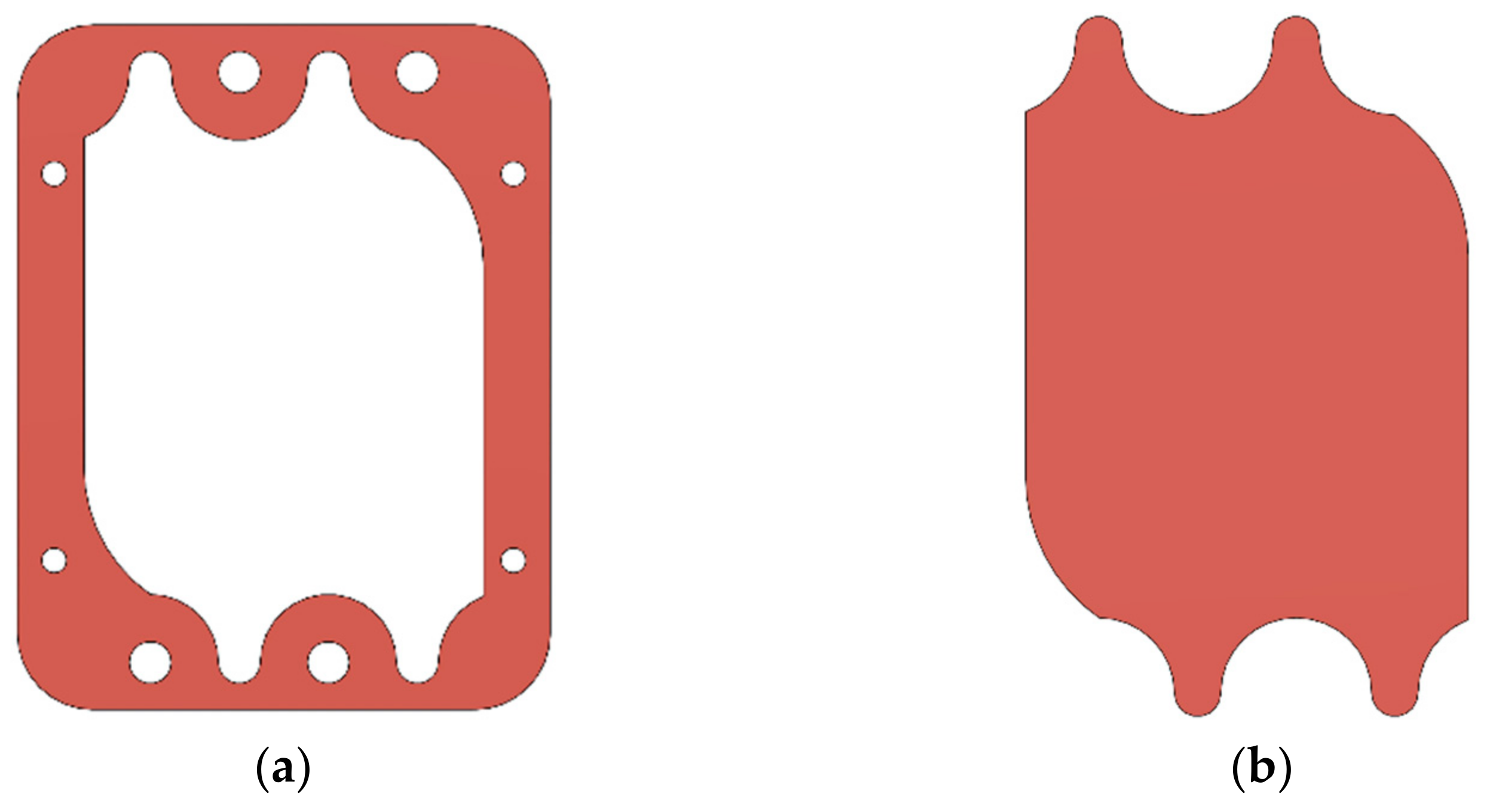
2.3. Gasket Geometry
2.4. Gaskets Optimization
2.5. Calculations and Measurement of Parameters
3. Results
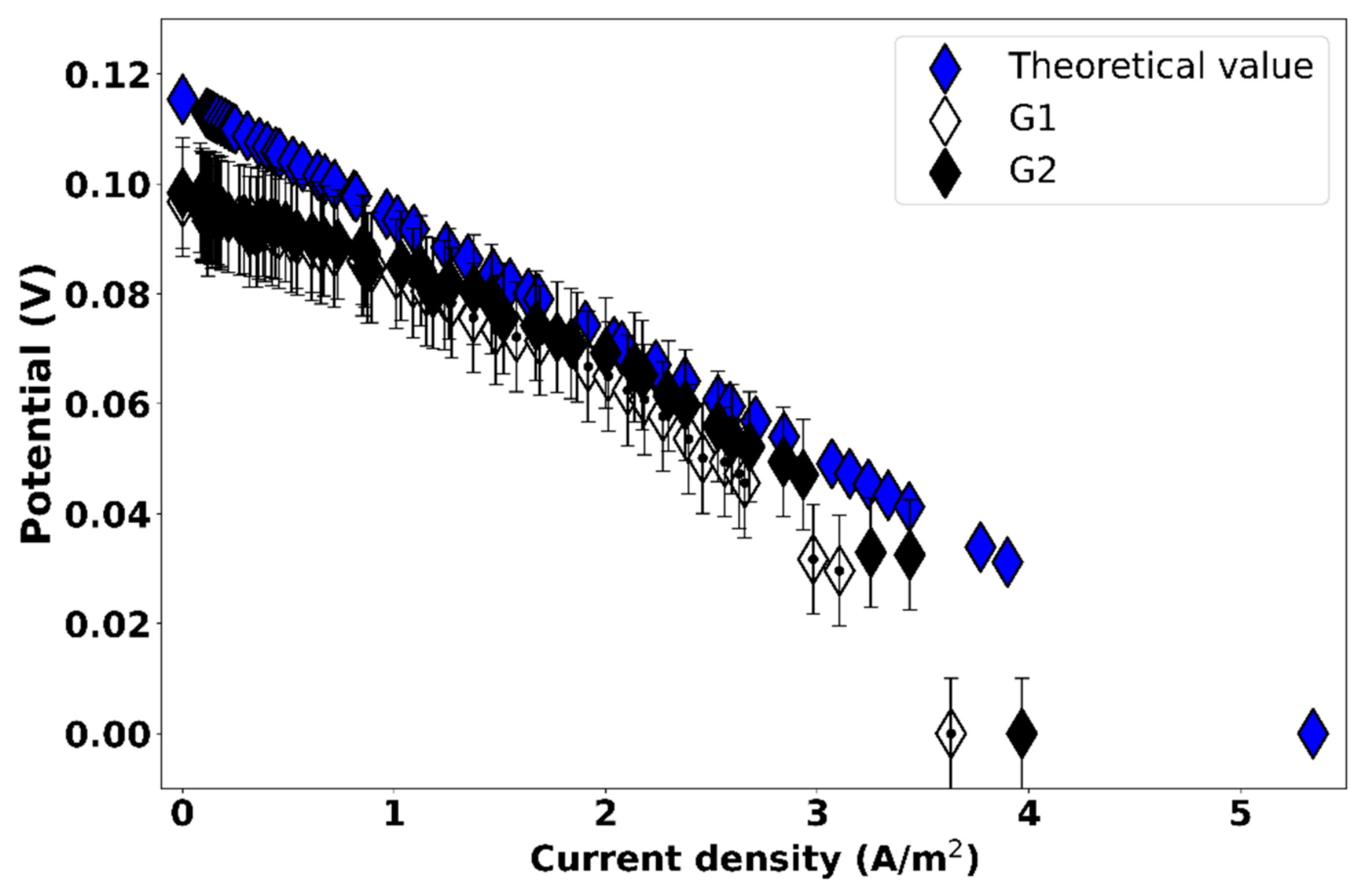
3.1. Effect of Gasket Geometry on the Potential of the RED Cell
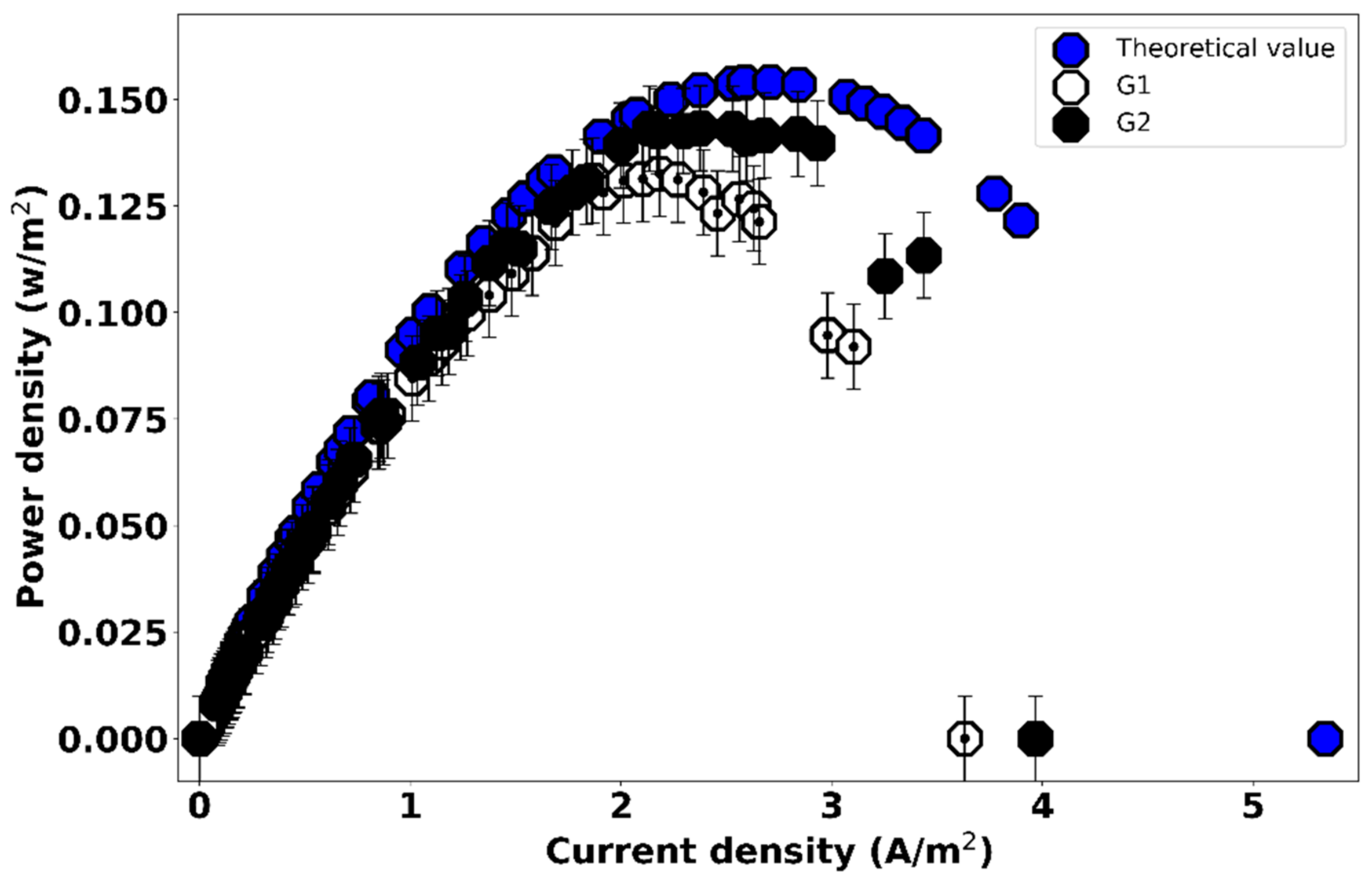
3.2. Effect of Gasket Geometry on the Power Output of the RED Cell
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Coleman Gilstrap, M. Renewable Electricity Generation from Salinity Gradients Using Reverse Electrodialysis. August 2013, p. 37. Available online: http://hdl.handle.net/1853/49031 (accessed on 31 January 2022).
- Cipollina, A.; Micale, G. Sustainable Energy from Salinity Gradients; Elsevier/Woodhead Publishing: Duxford, UK, 2016. [Google Scholar] [CrossRef]
- Veerman, J.; Saakes, M.; Metz, S.J.; Harmsen, G.J. Electrical power from sea and river water by reverse electrodialysis: A first step from the laboratory to a real power plant. Environ. Sci. Technol. 2010, 44, 9207–9212. [Google Scholar] [CrossRef] [PubMed]
- Altıok, E.; Kaya, T.Z.; Güler, E.; Kabay, N.; Bryjak, M. Performance of reverse electrodialysis system for salinity gradient energy generation by using a commercial ion exchange membrane pair with homogeneous bulk structure. Water 2021, 13, 814. [Google Scholar] [CrossRef]
- Cervantes-Alcalá, R.; Miranda-Hernández, M. Flow distribution and mass transport analysis in cell geometries for redox flow batteries through computational fluid dynamics. J. Appl. Electrochem. 2018, 48, 1243–1254. [Google Scholar] [CrossRef]
- Gurreri, L.; Tamburini, A.; Cipollina, A.; Micale, G.; Ciofalo, M. Flow and mass transfer in spacer-filled channels for reverse electrodialysis: A CFD parametrical study. J. Membr. Sci. 2016, 497, 300–317. [Google Scholar] [CrossRef]
- Tanaka, Y. Concentration polarization in ion-exchange membrane electrodialysis—The events arising in a flowing solution in a desalting cell. J. Membr. Sci. 2003, 216, 149–164. [Google Scholar] [CrossRef]
- Strathmann, H. Electrodialysis, a mature technology with a multitude of new applications. Desalination 2010, 264, 268–288. [Google Scholar] [CrossRef]
- Vermaas, D.A.; Saakes, M.; Nijmeijer, K. Doubled power density from salinity gradients at reduced intermembrane distance. Environ. Sci. Technol. 2011, 45, 7089–7095. [Google Scholar] [CrossRef]
- Gurreri, L.; Tamburini, A.; Cipollina, A.; Micale, G.; Ciofalo, M. CFD prediction of concentration polarization phenomena in spacer-filled channels for reverse electrodialysis. J. Membr. Sci. 2014, 468, 133–148. [Google Scholar] [CrossRef]
- Veerman, J.; Saakes, M.; Metz, S.J.; Harmsen, G.J. Reverse electrodialysis: A validated process model for design and optimization. Chem. Eng. J. 2011, 166, 256–268. [Google Scholar] [CrossRef]
- Mei, Y.; Tang, C.Y. Recent developments and future perspectives of reverse electrodialysis technology: A review. Desalination 2018, 425, 156–174. [Google Scholar] [CrossRef]
- He, W.; Zhang, X.; Liu, J.; Zhu, X.; Feng, Y.; Logan, B.E. Microbial fuel cells with an integrated spacer and separate anode and cathode modules. Environ. Sci. Water Res. Technol. 2016, 2, 186–195. [Google Scholar] [CrossRef]
- Noack, J.; Roznyatovskaya, N.; Herr, T.; Fischer, P. The Chemistry of Redox-Flow Batteries. Angew. Chem. Int. Ed. 2015, 54, 9776–9809. [Google Scholar] [CrossRef] [PubMed]
- Chamoun, M. Rechargeable Aqueous Batteries Based on Available Resources Investigation and Development towards Efficient Battery Performance. 2019. Available online: http://urn.kb.se/resolve?urn=urn:nbn:se:su:diva-163154 (accessed on 31 January 2022).
- Rivera, F.F.; Pérez, T.; Castañeda, L.F.; Nava, J.L. Mathematical modeling and simulation of electrochemical reactors: A critical review. Chem. Eng. Sci. 2021, 239, 116622. [Google Scholar] [CrossRef]
- Długołecki, P.; Dąbrowska, J.; Nijmeijer, K.; Wessling, M. Ion conductive spacers for increased power generation in reverse electrodialysis. J. Membr. Sci. 2010, 347, 101–107. [Google Scholar] [CrossRef]
- He, Z.; Gao, X.; Zhang, Y.; Wang, Y.; Wang, J. Revised spacer design to improve hydrodynamics and anti-fouling behavior in reverse electrodialysis processes. Desalin. Water Treat. 2016, 57, 28176–28186. [Google Scholar] [CrossRef]
- Post, J.W.; Hamelers, H.V.M.; Buisman, C.J.N. Energy recovery from controlled mixing salt and fresh water with a reverse electrodialysis system. Environ. Sci. Technol. 2008, 42, 5785–5790. [Google Scholar] [CrossRef] [PubMed]
- Cruz-Díaz, M.R.; Laureano, A.; Rodríguez, F.A.; Arenas, L.F.; Pijpers, J.J.H.; Rivero, E.P. Modelling of flow distribution within spacer-filled channels fed by dividing manifolds as found in stacks for membrane-based technologies. Chem. Eng. J. 2021, 423, 130232. [Google Scholar] [CrossRef]
- Mehdizadeh, S.; Yasukawa, M.; Abo, T.; Kakihana, Y.; Higa, M. Effect of spacer geometry on membrane and solution compartment resistances in reverse electrodialysis. J. Membr. Sci. 2019, 572, 271–280. [Google Scholar] [CrossRef]
- Veerman, J.; Saakes, M.; Metz, S.J.; Harmsen, G.J. Reverse electrodialysis: Evaluation of suitable electrode systems. J. Appl. Electrochem. 2010, 40, 1461–1474. [Google Scholar] [CrossRef]
- Vermaas, D.A. Energy Generation from Mixing Salt Water and Fresh Water. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2014. [Google Scholar] [CrossRef][Green Version]
- Tedesco, M.; Hamelers, H.V.M.; Biesheuvel, P.M. Nernst-Planck transport theory for (reverse) electrodialysis: I. Effect of co-ion transport through the membranes. J. Membr. Sci. 2016, 510, 370–381. [Google Scholar] [CrossRef]
- Hong, J.G.; Zhang, B.; Glabman, S.; Uzal, N.; Dou, X.; Zhang, H.; Wei, X.; Chen, Y. Potential ion exchange membranes and system performance in reverse electrodialysis for power generation: A review. J. Membr. Sci. 2015, 486, 71–88. [Google Scholar] [CrossRef]
- Moya, A.A. A Nernst-Planck analysis on the contributions of the ionic transport in permeable ion-exchange membranes to the open circuit voltage and the membrane resistance in reverse electrodialysis stacks. Electrochim. Acta 2017, 238, 134–141. [Google Scholar] [CrossRef]
- Luo, T.; Abdu, S.; Wessling, M. Selectivity of ion exchange membranes: A review. J. Membr. Sci. 2018, 555, 429–454. [Google Scholar] [CrossRef]
- Kedem, O.; Katchalsky, A. A physical interpretation of the phenomenological coefficients of membrane permeability. J. Gen. Physiol. 1961, 45, 143–179. [Google Scholar] [CrossRef] [PubMed]
- Auclair, B.; Nikonenko, V.; Larchet, C.; Métayer, M.; Dammak, L. Correlation between transport parameters of ion-exchange membranes. J. Membr. Sci. 2002, 195, 89–102. [Google Scholar] [CrossRef]
- Nikonenko, V.; Zabolotsky, V.; Larchet, C.; Auclair, B.; Pourcelly, G. Mathematical description of ion transport in membrane systems. Desalination 2002, 147, 369–374. [Google Scholar] [CrossRef]

| Parmeters | CEM | AEM |
|---|---|---|
| Thickness (µm) | 135 | 125 |
| Electical resistance (Ω cm2) | 2.7 | 1.3 |
| Selectivity (%) | 92 | 92 |
| Ion exchange capacity (mol/g) | 1.4 | 1.4 |
| Parameters | Concentrated Solution | Dilute Solution |
|---|---|---|
| Concentration (M) | 0.6 | 0.05 |
| Conductivity (mS/cm) | 49.6 | 5.2 |
| Flow rate (mL/min) | 10 | 10 |
| Velocity (m/s) | 0.01 | 0.01 |
| Temperature (°C) | 20 | 20 |
| Measurement | Open Circuit Voltage (V) | Short Circuit Current (A/m2) | Cell Resistance (Ω) |
|---|---|---|---|
| Theoretical calculation | 0.1154 | 5.34 | 2.16 |
| G1 | 0.0967 | 3.63 | 2.66 |
| G2 | 0.0983 | 3.97 | 2.48 |
| Measurement | Power Density (W/m2) | Optimum Current Density (A/m2) |
|---|---|---|
| Theoretical calculation | 0.1541 | 2.71 |
| G1 | 0.1326 (±0.02) | 2.18 |
| G2 | 0.1433 (±0.06) | 2.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sandoval-Sánchez, E.; De la Cruz-Barragán, Z.; Miranda-Hernández, M.; Mendoza, E. Effect of Gaskets Geometry on the Performance of a Reverse Electrodialysis Cell. Energies 2022, 15, 3361. https://doi.org/10.3390/en15093361
Sandoval-Sánchez E, De la Cruz-Barragán Z, Miranda-Hernández M, Mendoza E. Effect of Gaskets Geometry on the Performance of a Reverse Electrodialysis Cell. Energies. 2022; 15(9):3361. https://doi.org/10.3390/en15093361
Chicago/Turabian StyleSandoval-Sánchez, Elier, Ziomara De la Cruz-Barragán, Margarita Miranda-Hernández, and Edgar Mendoza. 2022. "Effect of Gaskets Geometry on the Performance of a Reverse Electrodialysis Cell" Energies 15, no. 9: 3361. https://doi.org/10.3390/en15093361
APA StyleSandoval-Sánchez, E., De la Cruz-Barragán, Z., Miranda-Hernández, M., & Mendoza, E. (2022). Effect of Gaskets Geometry on the Performance of a Reverse Electrodialysis Cell. Energies, 15(9), 3361. https://doi.org/10.3390/en15093361









