Detection of Stator Winding Faults in PMSMs Based on Second Harmonics of Phase Instantaneous Reactive Powers
Abstract
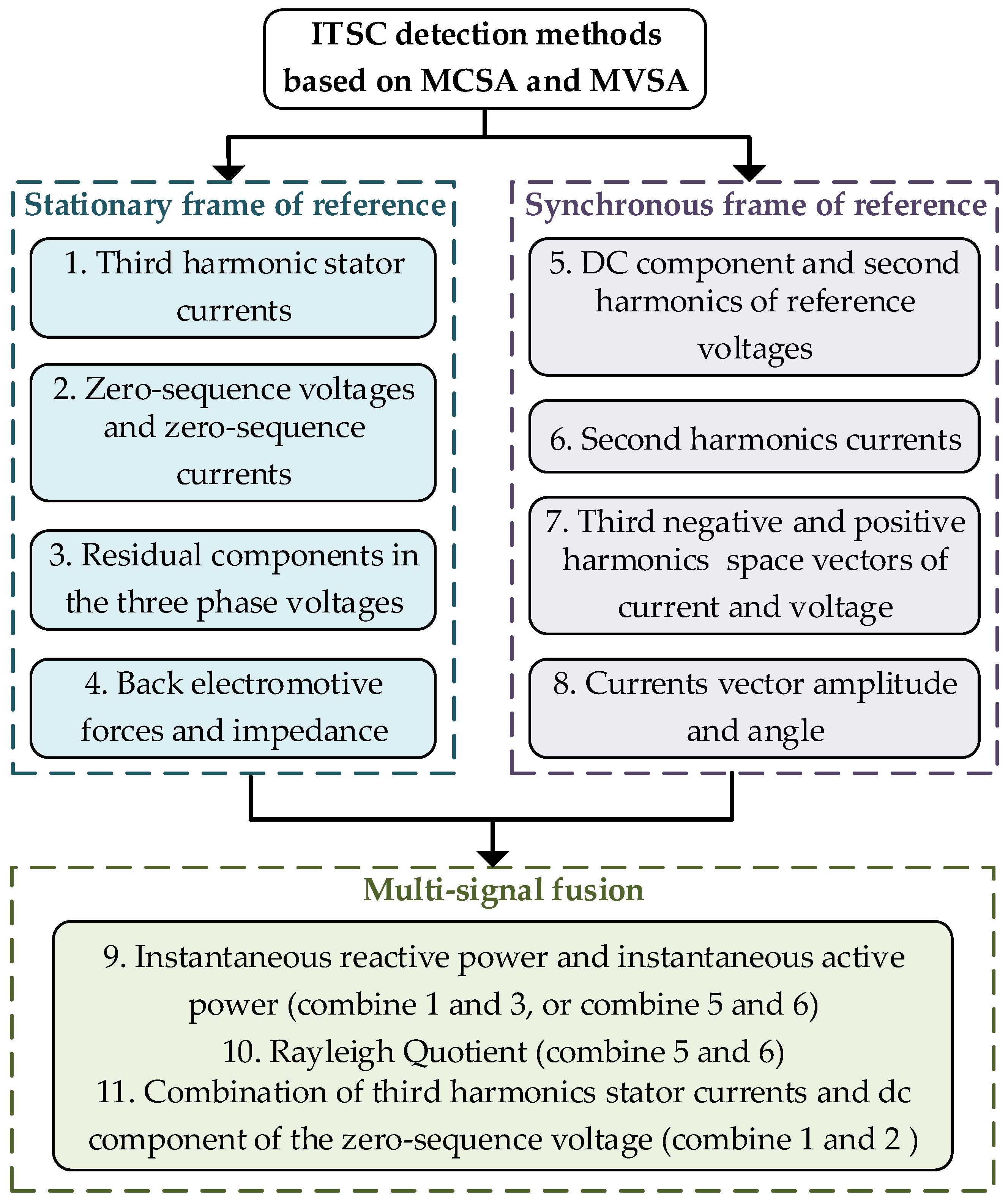
:1. Introduction
2. Reactive Power Signature Analysis
2.1. Instantaneous Reactive Power Definition
2.2. ITSC Characterization
2.2.1. Case of Healthy PMSMs
2.2.2. Case of Faulty PMSMs
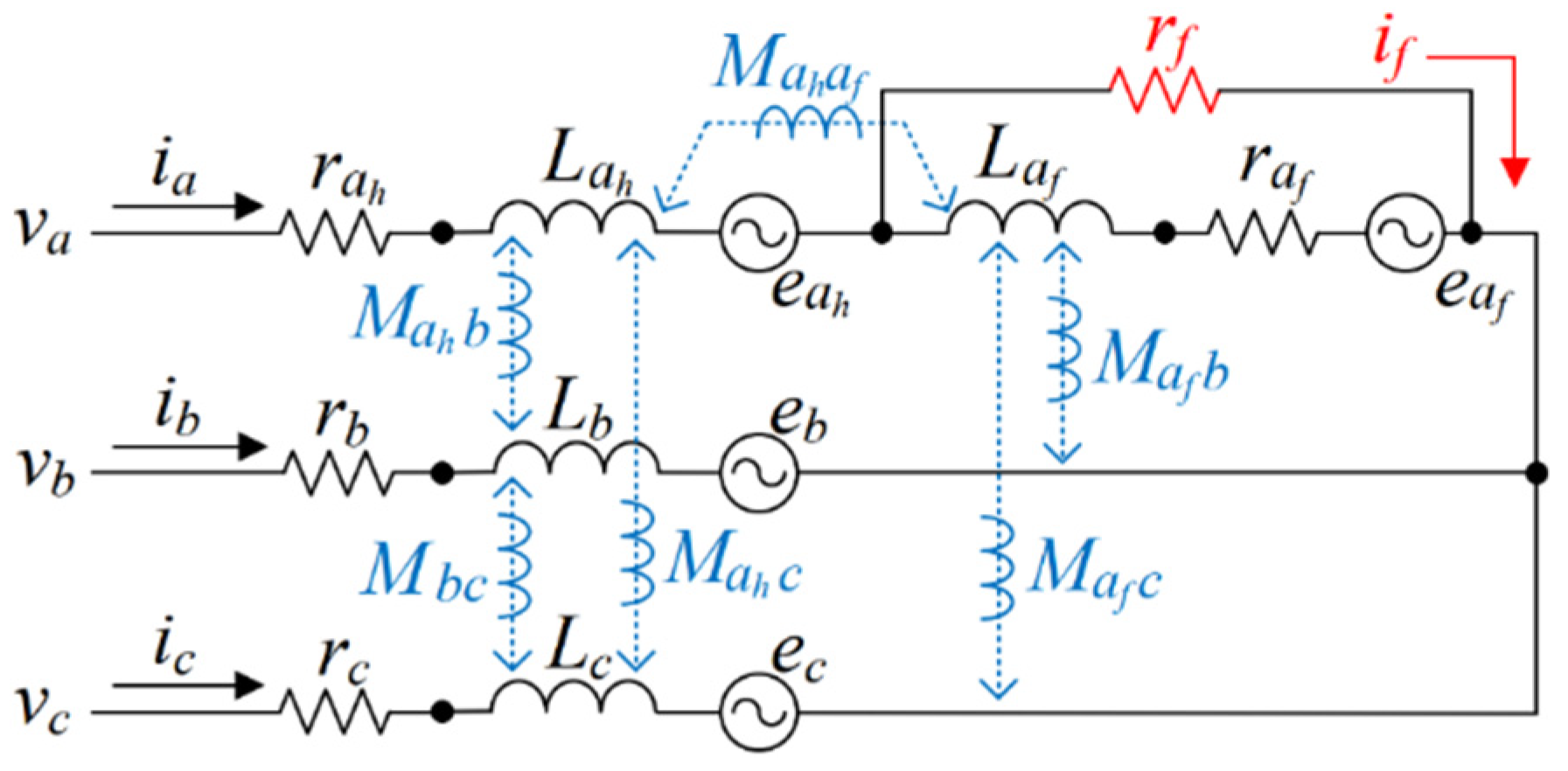
3. Fault Model and Simulation
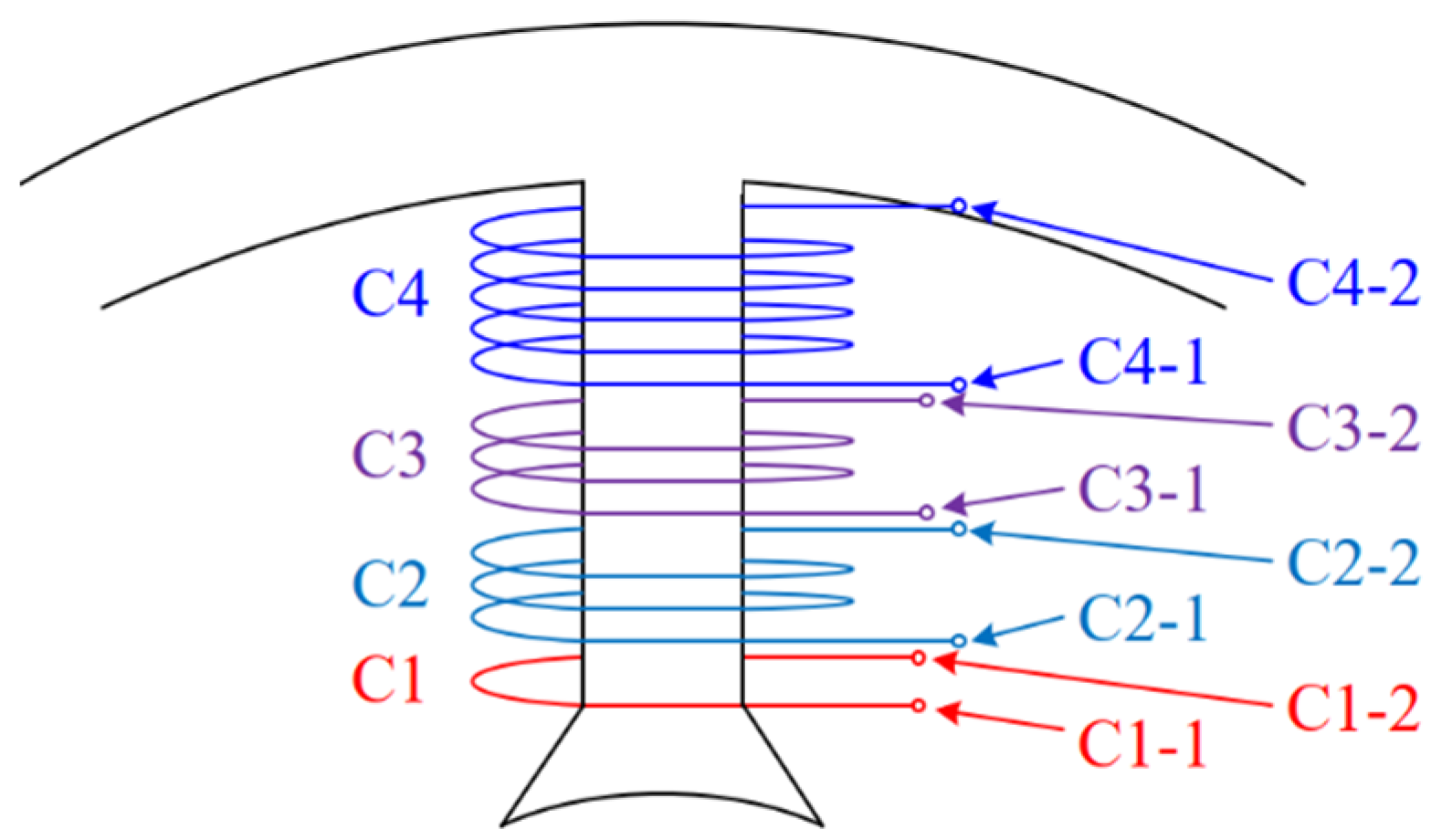
3.1. Voltage Equations of Faulty PMSM
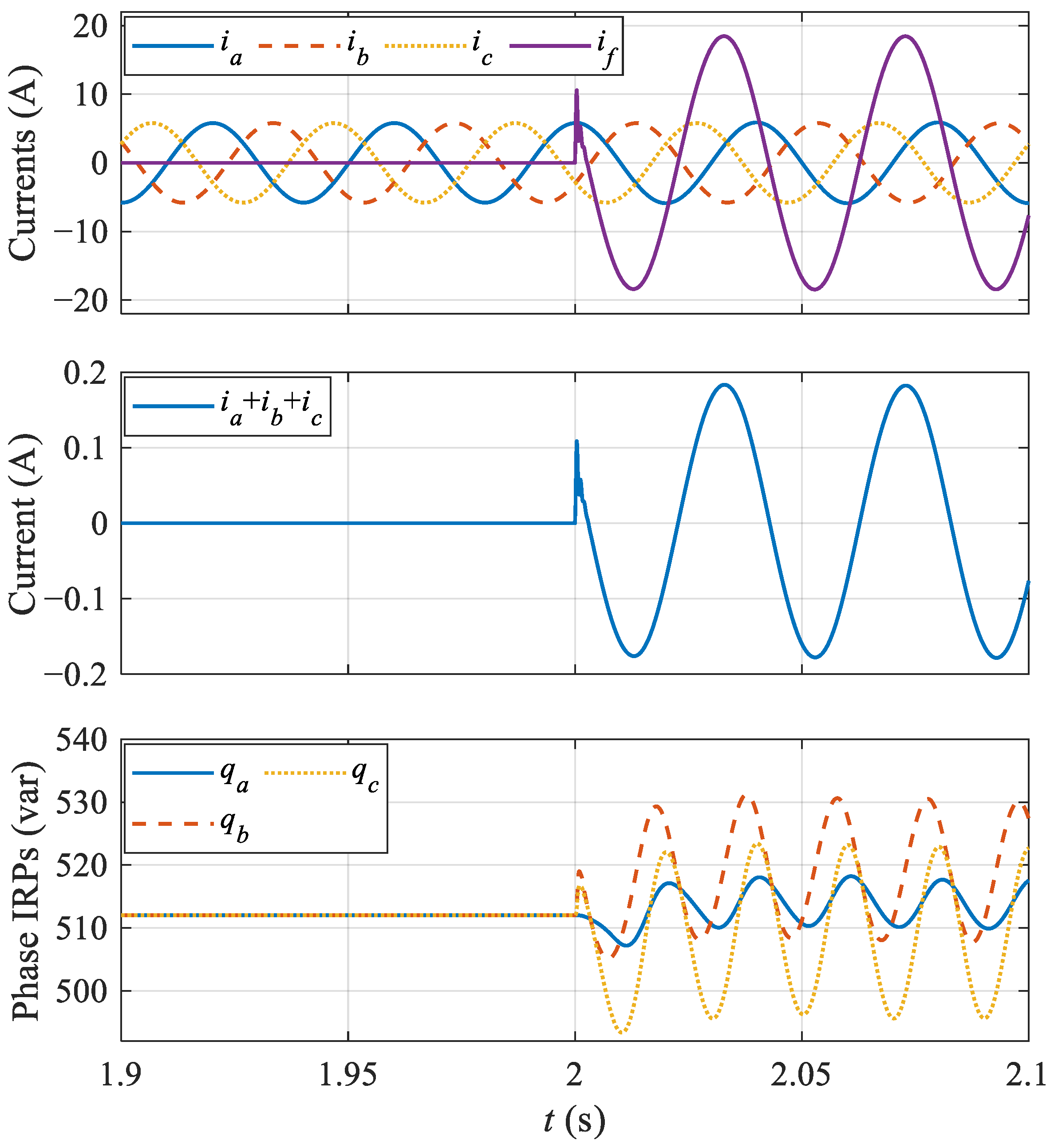
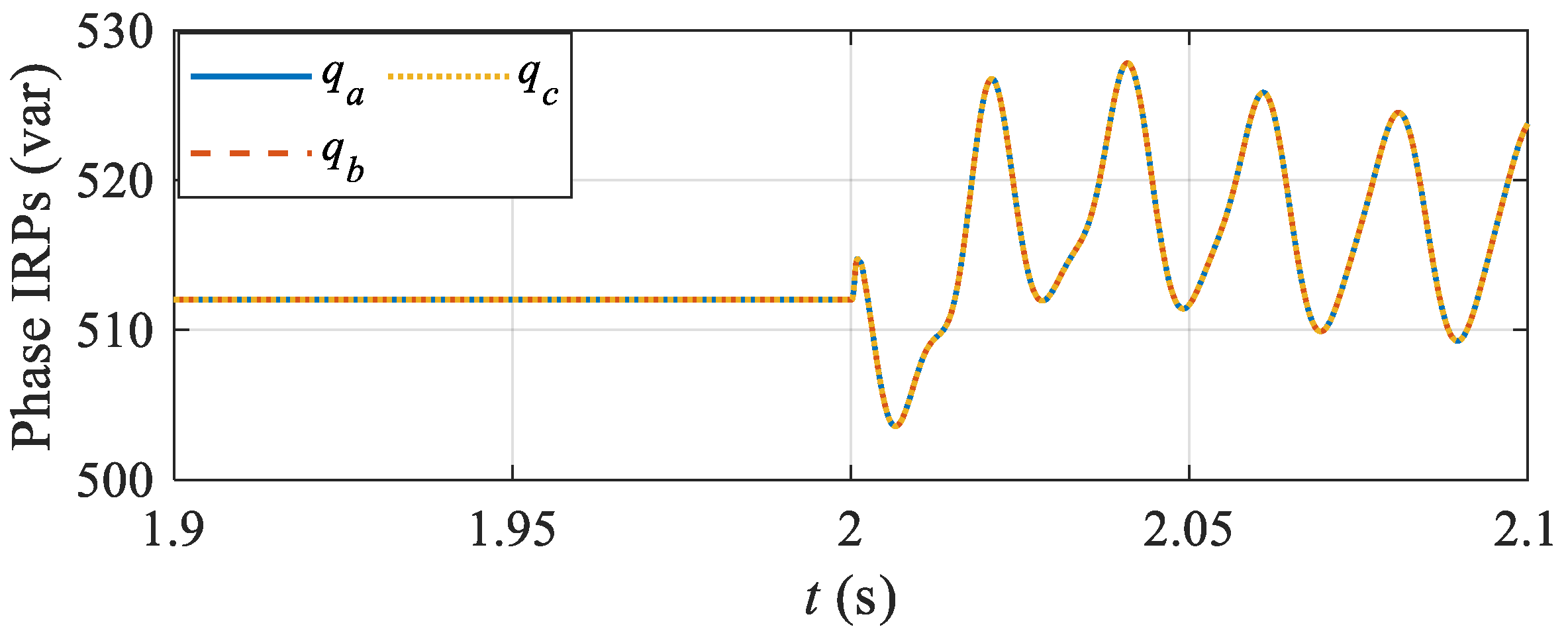
3.2. Simulation Results
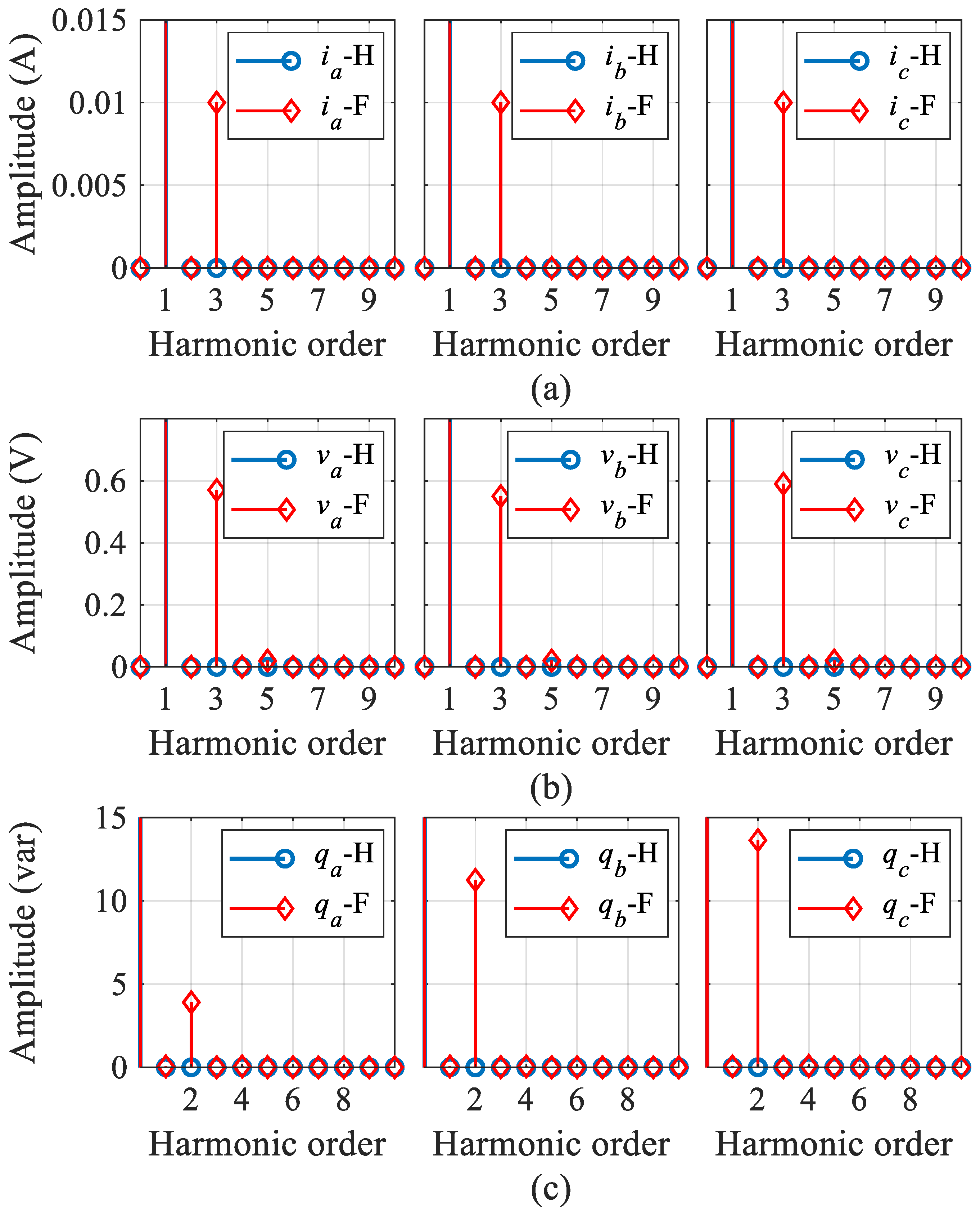
3.3. Fault Feature Analysis
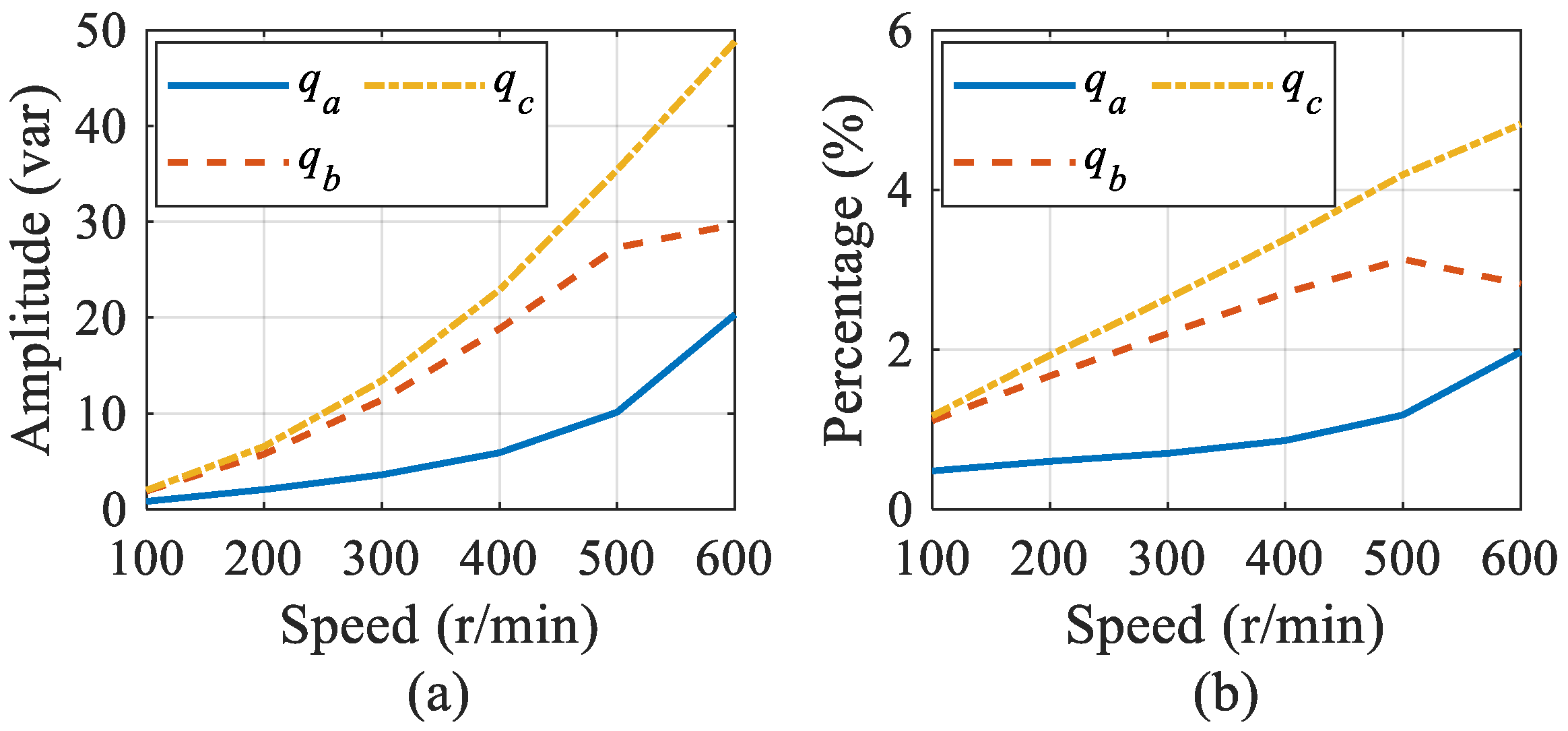
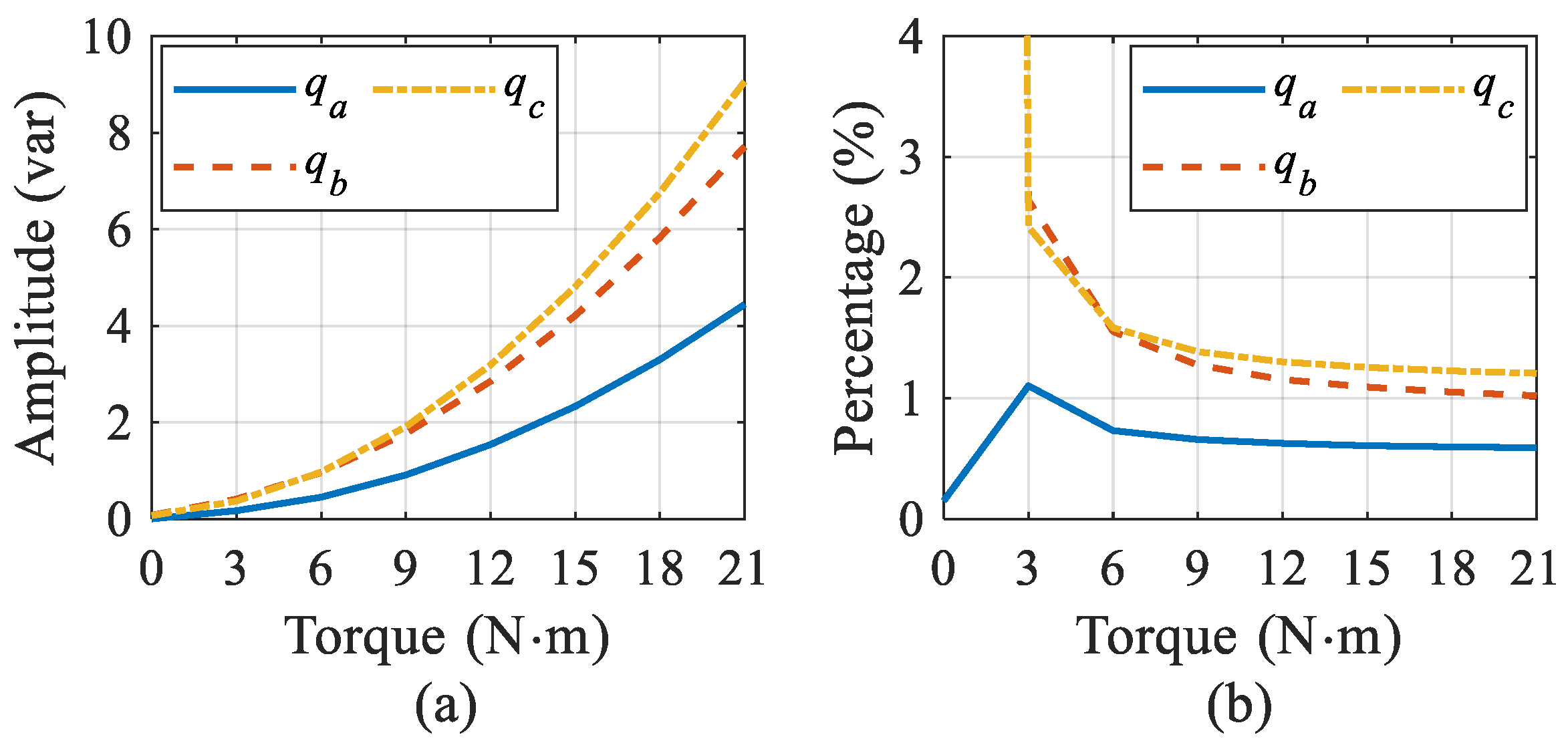
3.4. ITSCs Detection at Different Operating Conditions
4. Experimental Validation
4.1. Fault Feature Analysis in Experiments
4.2. Performance of Proposed Indicator
4.3. Online Fault Detection Algorithm
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Drif, M.; Cardoso, A.J.M. Stator Fault Diagnostics in Squirrel Cage Three-Phase Induction Motor Drives Using the Instantaneous Active and Reactive Power Signature Analyses. IEEE Trans. Ind. Inform. 2014, 10, 1348–1360. [Google Scholar] [CrossRef]
- Foster, S.N.; Cintron-Rivera, J.G.; Strangas, E.G. Detection of incipient stator winding faults in PMSMs with single-layer fractional slot concentrated windings. Electr. Power Syst. Res. 2016, 131, 231–243. [Google Scholar] [CrossRef]
- Ebrahimi, B.M.; Faiz, J. Feature Extraction for Short-Circuit Fault Detection in Permanent-Magnet Synchronous Motors Using Stator-Current Monitoring. IEEE Trans. Power Electron. 2010, 25, 2673–2682. [Google Scholar] [CrossRef]
- Faiz, J.; Exiri, A.H.; Nejadi-Koti, H. Current-based inter-turn short circuit fault modeling in permanent magnet synchronous machine using magnetic equivalent circuit model. In Proceedings of the 10th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Bydgoszcz, Poland, 1–29 June 2016. [Google Scholar]
- Saavedra, H.; Saavedra, J.-C.; Riba, U.J.-R.; Rome-ral, L. Detection of interturn faults in PMSMs with different winding configurations. Energy Convers. 2014, 79, 534–542. [Google Scholar] [CrossRef]
- Hang, J.; Zhang, J.; Cheng, M. Online Interturn Fault Diagnosis of Permanent Magnet Synchronous Machine Using Zero-Sequence Components. IEEE Trans. Power Electron. 2015, 30, 6731–6741. [Google Scholar] [CrossRef]
- Boileau, T.; Leboeuf, N.; Nahid-Mobarakeh, B.; Meibody-Tabar, F. Synchronous demodulation of control voltages for stator interturn fault detection in PMSM. IEEE Trans. Power Electron. 2013, 28, 5647–5654. [Google Scholar] [CrossRef]
- Ahn, G.; Lee, J.; Park, C.H.; Youn, M.; Youn, B.D. Inter-turn short circuit fault detection in permanent magnet synchronous motors based on reference voltage. In Proceedings of the IEEE 12th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Toulouse, France, 27–30 August 2019. [Google Scholar]
- Moon, S.; Jeong, H.; Lee, H.; Kim, S.W. Detection and classification of demagnetization and interturn short faults of IPMSMs. IEEE Trans. Ind. Electron. 2017, 64, 9433–9441. [Google Scholar] [CrossRef]
- Qi, Z.; Liang, Y. Evaluating the stator winding inter-tern short circuit fault of permanent magnet motor using FEA combined with experiment. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014. [Google Scholar]
- Sarikhani, A.; Mohammed, O.A. Inter-Turn Fault Detection in PM Synchronous Machines by Physics-Based Back Electromotive Force Estimation. IEEE Trans. Ind. Electron. 2013, 60, 3472–3484. [Google Scholar] [CrossRef]
- Haddad, R.Z.; Strangas, E.G. On the accuracy of fault detection and separation in permanent magnet synchronous machines using MCSA/MVSA and LDA. IEEE Trans. Energy Convers. 2016, 31, 924–934. [Google Scholar] [CrossRef]
- Moon, S.; Jeong, H.; Lee, H.; Kim, S.W. Interturn short fault diagnosis in a PMSM by voltage and current residual analysis with the faulty winding model. IEEE Trans. Energy Convers. 2018, 33, 190–198. [Google Scholar] [CrossRef]
- Çira, F.; Arkan, M.; Gümüş, B.; Goktas, T. Analysis of stator inter-turn short-circuit fault signatures for inverter-fed permanent magnet synchronous motors. In Proceedings of the IECON 42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016. [Google Scholar]
- Du, B.; Wu, S.; Han, S.; Cui, S. Interturn fault diagnosis strategy for interior permanent magnet synchronous motor of electric vehicles based on digital signal processor. IEEE Trans. Ind. Electron. 2016, 63, 1694–1706. [Google Scholar] [CrossRef]
- Qi, Y.; Zafarani, M.; Akin, B. A diagnosis procedure in standstill mode for inter turn short circuit faults of PMSMs through modified self-commissioning. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016. [Google Scholar]
- Huang, S.; Aggarwal, A.; Strangas, E.G.; Li, K.; Niu, F.; Huang, X. Robust Stator Winding Fault Detection in PMSMs With Respect to Current Controller Bandwidth. IEEE Trans. Power Electron. 2021, 36, 5032–5042. [Google Scholar] [CrossRef]
- Urresty, J.; Riba, J.; Romeral, L. Diagnosis of Interturn Faults in Pmsms Operating under Nonstationary Conditions by Applying Order Tracking Filtering. IEEE Trans. Power Electron. 2013, 28, 507–515. [Google Scholar] [CrossRef]
- Wang, B.; Wang, J.; Griffo, A.; Sen, B. Stator turn fault detection by second harmonic in instantaneous power for a triple-redundant fault-tolerant PM drive. IEEE Trans. Ind. Electron. 2018, 65, 7279–7289. [Google Scholar] [CrossRef] [Green Version]
- Eltabach, M.; Charara, A.; Zein, I. A comparison of external and internal methods of signal spectral analysis for broken rotor bars detection in induction motors. IEEE Trans. Ind. Electron. 2004, 51, 107–121. [Google Scholar] [CrossRef]
- Abadi, M.B. Detection of stator and rotor faults in a DFIG based on the stator reactive power analysis. In Proceedings of the IECON 40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014. [Google Scholar]
- Huang, S.; Strangas, G.; Li, K.; Niu, F. Detection of inter-turn short-circuit faults in PMSMs based on instantaneous reactive power. In Proceedings of the 7th International Conference on Reliability of Electrical Products and Electrical Contacts, Suzhou, China, 4–6 November 2019. [Google Scholar]
- Drif, M.; Cardoso, A.J.M. The use of the instantaneous-reactive-power signature analysis for rotor-cage-fault diagnostics in three-phase induction motors. IEEE Trans. Ind. Electron. 2009, 56, 4606–4614. [Google Scholar] [CrossRef]
- Jeong, I.; Hyon, B.J.; Nam, K. Dynamic Modeling and Control for SPMSMs With Internal Turn Short Fault. IEEE Trans. Power Electron. 2013, 28, 3495–3508. [Google Scholar] [CrossRef]
- Lee, Y.; Habetler, T.G. A phase variable simulation model for interior PM synchronous motor drives with stator turn faults. In Proceedings of the 12th International Power Electronics and Motion Control Conference, Portoroz, Slovenia, 30 August–1 September 2006. [Google Scholar]

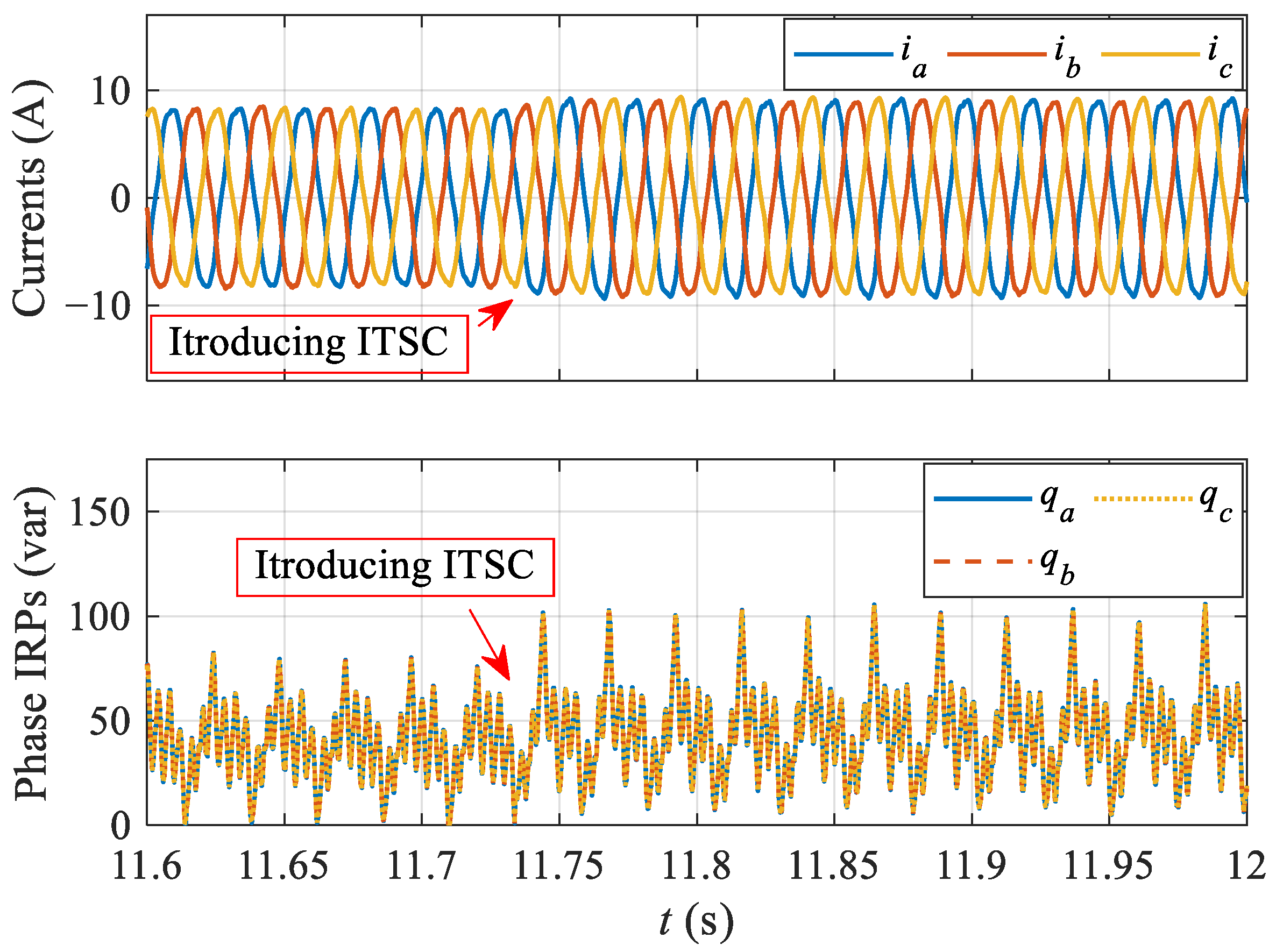
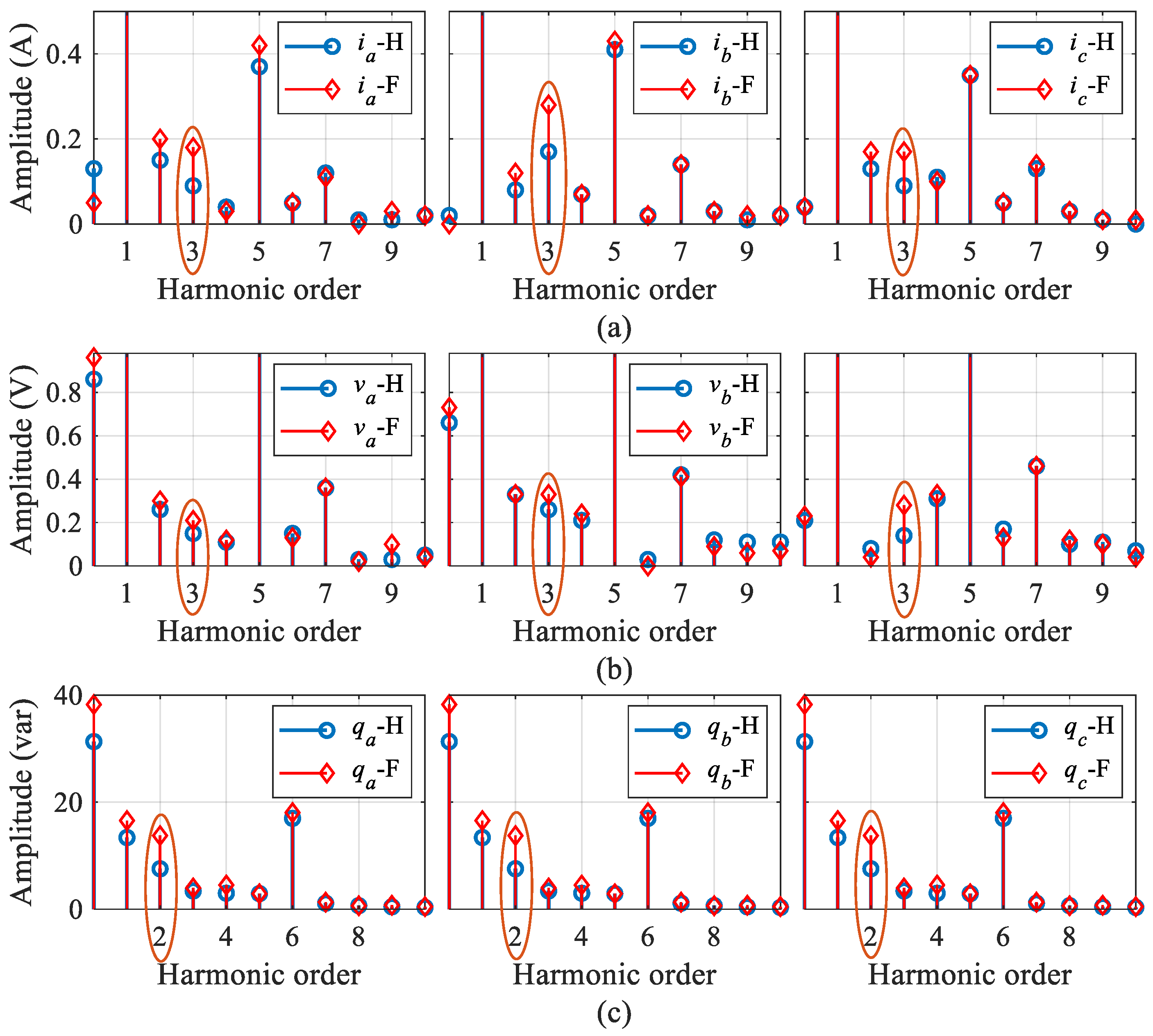


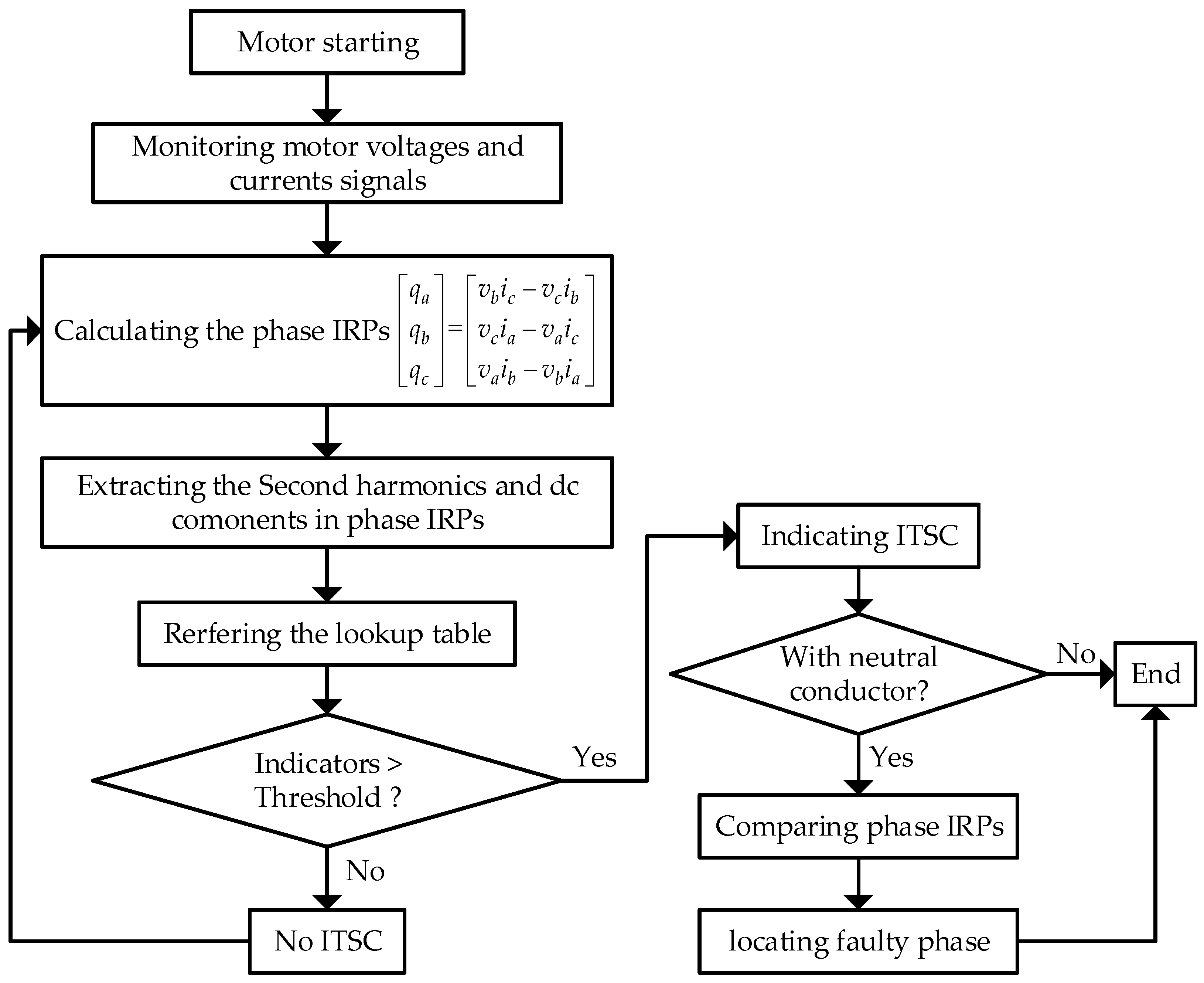
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Number of phases | 3 | Number of Slots/Poles | 12/10 |
| Rated phase current Irms | 18 A | Turns of Phase Ntotal | 300 |
| Rated line voltage Vrms | 480 V | Phase Resistance rs | 1.5 Ω |
| Base speed | 800 r/min | Phase Inductance Ls | 112 mH |
| Magnet flux λpm | 0.23 Wb | Mutual Inductance Ms | ≈0 mH |
| Currents | Voltages | IRPs | |||
|---|---|---|---|---|---|
| ia | 0.19 | va | 0.5 | qa | 0.76 |
| ib | 0.18 | vb | 0.51 | qb | 2.17 |
| ic | 0.18 | vc | 0.53 | qc | 2.68 |
| Currents | Voltages | IRPs | |||
|---|---|---|---|---|---|
| ia | 1.92 | va | 0.48 | qa | 35.96 |
| ib | 3.04 | vb | 0.73 | qb | 35.96 |
| ic | 1.88 | vc | 0.61 | qc | 35.96 |
| Detection Methods | Signal-to-Noise Ratio | Robustness to Speed | Capability of Fault Location |
|---|---|---|---|
| Method based on the third harmonic stator voltages | Low | Low | √ |
| Method based on the third harmonic stator currents | Low | Low | √ |
| Method based on the second harmonic IRPs | Medium | Low | × |
| The proposed methods | High | High | √ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, S.; Bi, Z.; Sun, Z.; Aggarwal, A.; Huang, X.; Wu, L.; Niu, F. Detection of Stator Winding Faults in PMSMs Based on Second Harmonics of Phase Instantaneous Reactive Powers. Energies 2022, 15, 3248. https://doi.org/10.3390/en15093248
Huang S, Bi Z, Sun Z, Aggarwal A, Huang X, Wu L, Niu F. Detection of Stator Winding Faults in PMSMs Based on Second Harmonics of Phase Instantaneous Reactive Powers. Energies. 2022; 15(9):3248. https://doi.org/10.3390/en15093248
Chicago/Turabian StyleHuang, Shaopo, Zhenguo Bi, Zhaojia Sun, Anmol Aggarwal, Xiaoyan Huang, Lijian Wu, and Feng Niu. 2022. "Detection of Stator Winding Faults in PMSMs Based on Second Harmonics of Phase Instantaneous Reactive Powers" Energies 15, no. 9: 3248. https://doi.org/10.3390/en15093248
APA StyleHuang, S., Bi, Z., Sun, Z., Aggarwal, A., Huang, X., Wu, L., & Niu, F. (2022). Detection of Stator Winding Faults in PMSMs Based on Second Harmonics of Phase Instantaneous Reactive Powers. Energies, 15(9), 3248. https://doi.org/10.3390/en15093248






