1. Introduction
The output of PV systems is highly variable, especially due to the stochastic formation and movement of clouds in the sky. Energy storage and generation forecasts are the two most important and widely adapted strategies to mitigate the adverse impact of highly variable renewable energy production for the stability of an electricity grid [
1]. Accurate PV power forecasting has become a critical factor not only in the overall effective management of electricity grids; it also provides financial benefits in energy market trading, supporting effective decision making based on forecast data.
Accurate and optimized forecasting models based on the use of on-site measurements and data from weather forecast providers are needed [
2].
The output of PV power plants mainly depends on solar irradiance (W/m2) falling on the PV panel. Therefore, global horizontal irradiance (GHI) is the most important input parameter in most PV power prediction systems, and increasing effort is currently spent on research on forecasting of GHI as a basis for PV power forecasts. Different input data and forecasting models are used depending on the forecast horizon.
Numerical methods are based on the actual atmospheric conditions. The dynamic process of weather evolution in a given period is estimated using equations based on fluid thermodynamics [
3]. Numerical weather data and satellite images are typically used as input variants for this method. The Global Forecast System (GFS), the European Centre for Medium-Range Forecasts (ECMWF), the North American Mesoscale Model (NAM) and Weather Research Forecast (WRF) are all examples of numerical weather prediction (NWP) approaches [
4]. They can be classified as global (worldwide) or mesoscale (local) models based on the area of simulated atmosphere [
5].
At a 6 h refresh rate and 1–3 h granularity, these models often yield forecasts for multiple variables important for predicting solar radiation, with forecast horizons ranging from 24 to 72 h or longer. Spatial resolution of these models is variable, and on average, each forecast grid cell is on a scale of a few to hundreds of square kilometers. The quality of NWP forecast is limited by the quality and horizon of the model utilized. Proprietary models, such as satellite-based models or total sky imager models based on cloud cover and cloud motion vectors, are also used to further enhance forecast accuracy. The latest detailed study of solar power forecasting, its dependence on meteorology and grid implications is presented by Yang et al. [
6].
Current forecasting methods are based on the individual or small groups of time series. The model parameters for each time series are derived independently from previous observations. Different factors, such as autocorrelation structure, trend, seasonality and other explanatory variables, determine the selection of a particular model. Based on the model dynamics, the fitted model is then utilized to predict the time series into the future. These models also have a scope of probabilistic forecasts through simulation or closed-form expressions for the predictive distributions. Box–Jenkins methodology [
7] is widely used for this class of forecasting.
However, instead of predicting individual or a limited number of time series, a new form of forecasting challenge has emerged in recent years, involving forecasting a huge number of related time series [
8]. PV power forecasting is one such example that involves time series forecasting of GHI, temperature and several other parameters. In such a case, a large amount of historical data on similar, linked time series can be used to make predictions. Using historical data not only allows for fitting of more complex and potentially more accurate models, but it can also attenuate the time and intensive manual feature-engineering and model-selection steps required by the classical techniques [
8].
A plethora of forecasting methodologies for PV power systems has recently been developed and published in the literature. One approach for categorizing forecast methodologies is based on the forecast horizon, which is the amount of time between the actual time and the effective period of prediction [
9].
The second classification is based on the forecasting method, which can be statistical or time-series-based, physical, hybrid or ensemble. Statistical approaches are based on a set of observations of one or more parameters taken at a successive sequence of times [
10].
Regression methods and persistence methods (primarily used as a standard to test other models) are examples of statistically based forecasters. These methods rely primarily on historical data and do not require any information about PV systems or their installation site. Models such as the autoregressive integrated moving average (ARIMA) work well with non-stationary time series [
11]. The drawback of statistical regression models or time series ARIMA models is that they are computationally more intensive and require continuous times series historical data.
According to several reviews, artificial neural network (ANN)-based forecasting is one of the most effective methods. ANNs can capture sharp changes in the input–output relationship due to varying environmental conditions [
12] compared with statistical or time series models. However, the fundamental disadvantage is that ANNs necessitate a vast amount of data for training. Any erroneous or insufficient initial data can compromise the predictability of the findings and the accuracy with which the model parameters are chosen. ANNs outperform conventional statistical methods in terms of accuracy and adaptability under intermittent meteorological conditions [
12]. A hybrid approach has been applied to enhance the forecasting accuracy of ML and ANN methods by using statistical post processing in conjunction with weather clustering assessment for day-ahead PV power forecasting [
13]. Recent publications have also shown interest in forecasting accuracy with varying spatial distribution of PV plants. Various ML models have been compared and examined in terms of technical and economic performance for point forecast with spatial distribution [
14].
In this work, the evaluation and comparison of various statistical regression models (SK-Learn linear regression, ridge regression, elastic net), time series models (SARIMAX, Facebook Prophet (FBP)) and ML (gradient boosting (GB), extreme gradient boost (XGB), random forest (RF)) are presented, and forecast equations are derived using GEKKO optimization tool based on the irradiance classification approach to cluster the dataset. The purpose of irradiance classification is to improve on the forecast accuracy, as the irradiance distribution pattern randomly depends on the type and height of clouds. The mentioned models are explained in detail in
Section 3. The main contributions of this paper are twofold: (1) The forecast-equation-derived method can be adapted to any location and any technology by deriving the regressive coefficients. (2) This work empirically demonstrates that ML models work better in highly variable cloud conditions; in future, with larger datasets, such models can be used with GEKKO to build a better ensemble model.
2. Materials and Methods
2.1. PV System Description
The ground measurement data employed in this analysis were taken from the PV system of the University of Applied Sciences Upper Austria (FHOOE). The university building is in Wels, Austria (latitude 48.17° N, longitude 14.03° E, elevation 317 m). The system is composed of five types of PV technologies: copper indium selenide (CIS), amorphous silicon (a-Si), cadmium telluride (CdTe), polycrystalline silicon (p-Si) and monocrystalline silicon (c-Si).
Figure 1 shows images of the rooftop PV system, as well as the solar radiation measurement station.
The output power of the mono-Si PV system, which is used for the modelling analysis in this paper, is described in
Table 1.
2.2. Forecasting Methodology
The PV power forecast is based on GHI (W/m
2) and temperature (°C) forecasts with hourly resolution and a forecast horizon of 72 h ahead. These meteorological forecasts (“Blue Forecast”) are provided by Blue Sky Wetteranalysen [
15]. The Blue Forecast is an automated local weather forecasting tool developed based on statistical methods and meteorological knowhow to correct global GFS-NWP models with historical ground measurements from local weather stations. Local characteristics and conditions such as orography, terrain and climatological factors are used in the model, along with other meteorological features, to enhance the accuracy of global NWP.
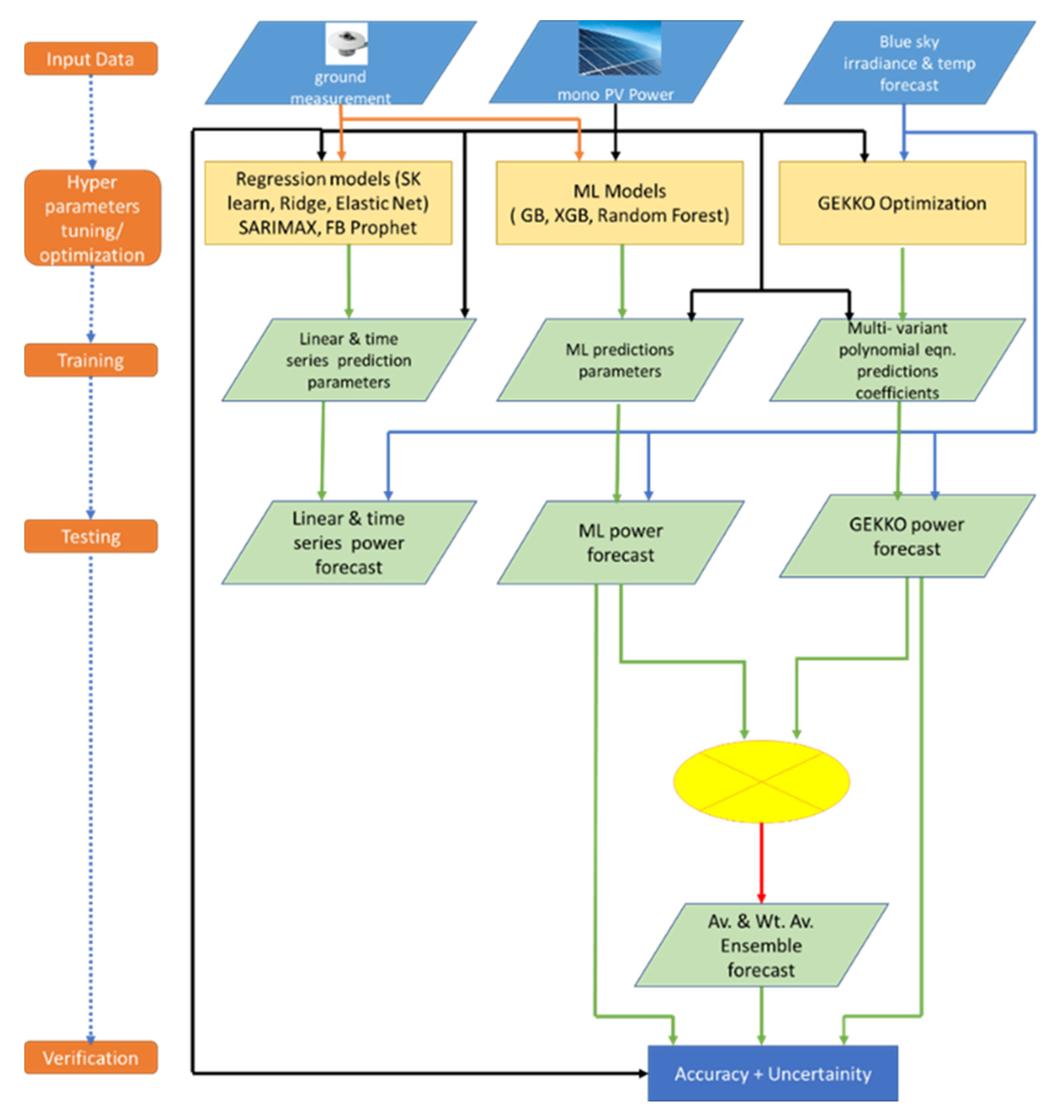
The methodology adopted for this study and the basic steps of the modelling and evaluation algorithm to evaluate power forecast are shown in
Figure 2.
The rolling cross-validation approach is used because time series data have a temporal structure, and the data cannot be randomly mixed in a fold while preserving the structure [
16].
2.3. Performance Metrics
There are several parameters and metrics used for the evaluation of any solar energy forecasting model to assess the accuracy of the forecasting methods. The three most widely used metrics for forecast accuracy are the mean bias error (MBE), the mean absolute error (MAE) and the root mean square error (RMSE) [
17]. The relative MAE (rMAE) and relative RMSE (rRMSE) are calculated by dividing the respective metrics by the average value of the observed parameter, and the normalized metrics (nMAE and nRMSE) are normalized to the maximum variable (power in this case) under consideration.
RMSE is better suited to applications such as grid operation and stability, where high errors are critical [
18], whereas MAE is more suited to applications such as day-ahead markets, which have linear costs relative to error [
19]. MAE is used as the benchmark metric when calculating the weight factor for a weighted-average ensemble model, as it is appropriate for application with linear cost functions, with the primary goal of day-ahead forecasting with hourly resolution.
The skill score is an important parameter used to evaluate the performance of any model by comparing it with a reference model, which is typically a persistence model in the case of solar forecasting. Mathematically, the skill score (SS) of the forecast is defined by the following equation [
20]:
where score can be MAE or RMSE.
Specific metrics, such as accuracy, bias, reliability, calibration and sharpness are used for the validation of probabilistic forecasts [
21]. Accuracy and bias for point forecasts can also be used for probabilistic forecasts. However, reliability and sharpness are important properties specific to probabilistic forecasts. The similarity between a priori forecast probability and a posteriori observed frequency is measured by reliability. If a forecast appears to be derived from the same distribution as the observation, it is considered reliable. The ability of a forecast to focus the probabilistic information about future outcome(s) is characterized as sharpness. Sharpness is a property of the forecast alone, and its assessment does not involve the observations. Therefore, it is recommended practice that any model’s reliability be supported with a sharpness assessment, as otherwise, prediction distribution mis-specifications may go undetected [
22].
2.3.1. Probability Integral Transform
Probability integral transform (PIT) is a commonly used metric for reliability. It is performed by converting data values modeled as random variables from any continuous distribution to random variables with a standard uniform distribution [
23]. If a random variable (forecast power),
, has a continuous distribution for which the cumulative distribution function is
, then the random variable,
, defined as
has a uniform distribution. Therefore, a uniform PIT histogram means that the forecasting model is perfectly reliable. The shape of the PIT histogram gives information about the reliability index, e.g., a convex U-shaped PIT histogram means overconfident forecasts with an excessively narrow prediction interval, whereas a concave inverse U-shaped PIT histogram means underconfident forecasts with a too widely dispersed forecast distribution and prediction interval [
24].
2.3.2. Continuous Ranked Probability Scores
Continuous ranked probability score (CRPS) accounts for the overall accuracy, reliability and sharpness of the forecasts. It is widely used in weather forecasting and atmospheric science, as it allows for comparison of actual results with the whole prediction distribution instead of just comparing to the mean prediction distribution. The standard way to calculate CRPS is given by the integral [
25]:
where
is the cumulative distribution function (CDF) of the probabilistic forecast for the
ith value, whereas
is the CDF of the corresponding ground measurement. Equation (2) has a severe limitation due to the inherent slowness of calculating such an integral for a large database. Gneiting et al. [
24] suggested a closed-form solution for a Gaussian distribution, as per the following equation:
2.3.3. Brier Score
The Brier score (BS) is another extensively used skill score that allows for verification and comparison of probabilistic forecasts of dichotomous events. It is defined by the following equation:
where
and
are the respective probabilities of predicted power and observed power that would exceed a fixed threshold.
BS is also negatively oriented, and
BS = 0 implies a perfect forecast.
2.4. Database Clustering
The collected GHI and on-site power data measurements are of 10 min resolution and include night hours. For forecasting purposes, the data are averaged to hourly resolution. The PVLIB irradiance clear sky index is used to calculate the clear sky index [
26]. The clear sky index is the ratio of global to clear sky global irradiance.
Negative and non-finite clear sky index values are truncated to zero. A maximum value of the clear sky index of 2.0 is applied to account for over-irradiance events typically seen in sub-hourly data due to cloud enhancement and refraction phenomena [
26].
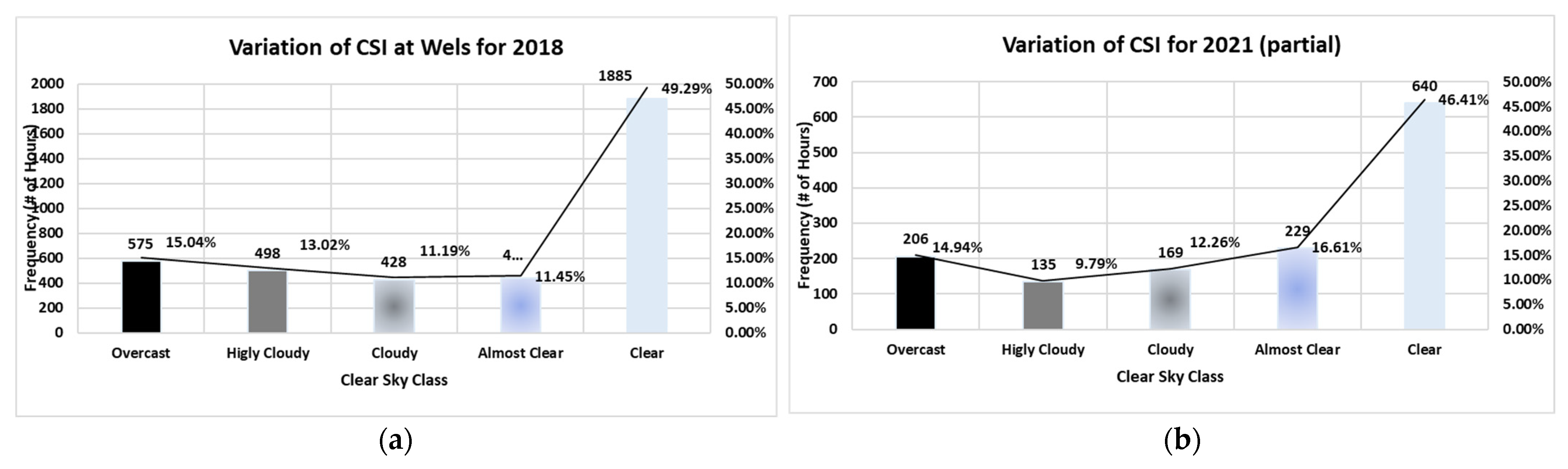
We adopted a novel method of classifying the clear sky index into five clusters depending on the value of clearness index,
, based on the observation of hourly distribution,
, from annual data of Wels for 2018 and the current year trend, as shown in
Figure 3. The criteria for the classification of different clusters is illustrated in
Table 2.
The forecast meteorological data of GHI and temperature are used from 1 May 2021 onwards on a daily basis for 72 h forecast horizon.
The GHI data collected are duly checked and validated. However, pyranometers are highly sensitive to dust, which can lead to an underestimation of GHI. This could possibly lead to a limitation for the lower boundary data of each bin falling into an adjacent lower bin.
There have been calibration and cable problems at the site due to which gaps in the measured data are noted. The recorded ground measurement data used for training and testing are for the periods listed in
Table 3. All the models are tested for 96 days during the period, starting from 1 May 2021 until 30 September 2021 for three-days-ahead forecast, and the results are divided into 24 h, 48 h and 72 h forecast horizons for analysis.
As the GHI and PV production is 0 for hours before sunrise and after sunsets, these values are excluded from the testing phase by applying a filtering of the data, where is the solar zenith angle. is used in all models as one of the key variables in training and testing, as it strongly influences the GHI.
Month, day of the month, hour of the day, year and season are added as additional feature values, as they define the seasonality of GHI.
GHI, temperature and values are scaled, whereas all other variables are employed as feature values (binary 0 or 1) in machine learning and linear regression models for training and testing. For GEKKO optimization to derive the equations, forecast values of GHI, temperature and are used without scaling.
The Fourier transform series are added as features to handle the multiple seasonality. This converts a time and signal function into a frequency and power function. This provides information about which frequencies make up the signal and how strong they are [
27]. Fourier transform aids in seeing through the noise and determining which frequencies are important in the real data.
Multiple Fourier series with different k terms in the form of and are added, with k value of 5 for each season of the year, hour of the day and week of the year as additional feature values for training and testing ML and times series models.
3. Models
In this study, various statistical linear regression, time series and machine learning models were analyzed and compared to allow for higher degrees of model complexity. This also helps to identify and to model dependency structures. The decision to use these techniques over the many other ML methods is based on a comparison of the models to find the best fit, as well as the possibility of merging them to form ensemble models to increase forecast accuracy. Although different energy forecast models have already been compared [
28], the focus of this paper is on improving forecast accuracy through the formulation of prediction equations under different clusters of the clear sky index. Furthermore, the probabilistic forecast of the three best-performing models is evaluated as a measure of uncertainty, and the resulting quantile forecasts are evaluated by different probabilistic forecasting skill scores. The different models applied in this study are:
3.1. Linear Regression
This is the simplest form of a regression model, where the target value is the linear combination of the features [
29].
Equation (6) fits a linear model with coefficients = () to minimize the residual sum of squares between the observed and anticipated targets in the dataset.
The coefficients
are determined using least square estimation (LSE), which minimizes the following cost function:
3.2. Ridge Regression
Ridge regression is used to estimate the coefficients of multiple regression models, where independent variables are highly correlated [
30]. Placing a penalty on the size of the coefficients overcomes some of the issues with regular least squares. The ridge coefficients minimize a penalized residual sum of squares.
A ridge-regularized cost function has two components, i.e., the error term and the regularized term, as illustrated in Equation (8).
The loss is nothing but an error term (first term on the RHS of Equation (8)), followed by a regularized term, λ is a hyperparameter to tune or a balancing factor and β is the sum of squared coefficients. The penalty term (second term on the RHS of Equation (8)) is controlled by changing λ, where λ = 0 implies using only the error term with any penalty, and high value of λ implies the penalty leading to the reduction in the magnitude of coefficients. It is imperative to choose an optimal λ value.
3.3. Elastic Net
LASSO means ‘least absolute shrinkage selector operator’ and is a linear model that estimates sparse coefficients. The key difference between the LASSO and ridge regression is that LASSO employs the absolute value of coefficients and sets redundant feature coefficients to zero, making it easier to choose the best features.
Elastic net is a fusion of the ridge and LASSO regression techniques. Elastic net regression uses shrinkage to prevent overfitting by minimizing a modified cost function:
The second term on the RHS of Equation (9) represents LASSO penalty (L1), whereas the third term represents the ridge penalty (L2), and and control shrinkage of L1 and L2, respectively.
In a situation with a larger dataset with 500 or more variables, ridge regression only reduces the magnitude of coefficients; if LASSO is used, then reduces coefficients of redundant features to zero (feature selection), which leads to loss of information. Therefore, it is recommended to use elastic net, as it performs well on large datasets. and are hyperparameters to be tuned by the user.
3.4. SARIMAX
The seasonal ARIMA (SARIMA) model is a generalized form of the ARIMA model that is used to handle seasonality in data. SARIMA uses seasonal autoregressive (AR), moving average (MA) and differencing elements in the model to explicitly deal with seasonality in data. SARIMA is used to model non-stationary series or data that do not oscillate around the same mean, variance or co-variance. As the GHI data (and hence PV power) are not stationary because they has a trend (changing mean) and seasonality, which means that the covariance function does depend on time. The most common way to identify stationarity (or its absence) is by testing a dataset for stationarity with the Dicky Fuller test [
31], which tests for a unit root. Basically, if the
p-value of the test is too small (i.e., less than 0.05, achieving 95% confidence), the hypothesis that the data are non-stationary is rejected, and data are assumed to be stationary. The standard method of differencing the dataset is adopted to ensure stationarity and then integrated by the same order in as that used in the case of SARIMAX. This model can identify trends and seasonality, which makes it so important.
SARIMAX is seasonal ARIMA with exogenous regressors, which allows it to incorporate the impacts of external factors into the model via an exogenous regressor term. The general form of the SARIMAX model,
, is mathematically represented by Equation (10) [
32], where:
p: is the order of the AR term.
d: order of differencing to make the data stationary.
q: order of the MA term.
P: order of the seasonal AR term.
D: order of the seasonal differencing to make the data stationary.
Q: order of the seasonal MA term.
S: number of periods in a season.
denotes the value of the series at time t.
… denote observations of the exogenous variables.
, … is the coefficient value for the k-th exogenous (explanatory) input variable.
, … is the weight of the nonseasonal autoregressive terms.
, … is the weight of the seasonal autoregressive terms.
, … is the weight of the nonseasonal moving average terms.
, … is the weight of the seasonal moving average terms.
denotes the backshift operator such that
denotes the white noise terms.
3.5. Facebook Prophet
Facebook Prophet uses a decomposable time series model with three main model components: trend, seasonality and holidays. They are combined in the following Equation [
33]:
where:
: piecewise linear or logistic growth curve for modeling non-periodic changes in time series;
: periodic changes (e.g., weekly/yearly seasonality);
: effects of holidays (user-provided) with irregular schedules;
: error term, accounting for any unusual changes not accommodated by the model.
Using time as a regressor, FBP tries to fit several linear and non-linear functions of time as components. Instead of directly examining the time-based dependence of each observation inside a time series, FBP addresses the forecasting problem as a curve-fitting exercise.
3.6. Random Forest
Leo Breiman and Adele Cutler introduced and patented random forest (RF), which aggregates the output of numerous decision trees to arrive at a single outcome [
34]. However, this concept was first proposed in the literature by Ho [
35], who employed a consensus of trees generated in random subspaces of the features.
Bagging is a technique to minimize the variance of an estimated prediction function [
36]. Bagging works well for high-variance, low-bias procedures. The same regression trees are fit several times to bootstrap-sampled versions of the training data and average the result in case of regression. For classification problems, a committee of trees vote for the projected class.
RF is a significant refinement and expansion of bagging in which a large number of uncorrelated trees is built and then averaged. RF performs similarly to boosting in many problems, but is easier to train and tune, which makes it widely popular and easy to implement in several applications.
The RF algorithm has three critical hyperparameters that need to be tuned before training, viz., node size, the number of trees and number of feature samples. RF classifiers can be used thereafter to solve for regression or classification problems [
37].
Classification in RF is performed using ensemble methodology, consisting of collection of decision trees. The training data are fed with a replacement, called the bootstrap sample, to train various decision trees. The correlation among decision trees is reduced by introducing further randomness through feature bagging, thereby adding more diversity. This dataset contains observations and features that will be chosen at random during the splitting of nodes [
37].
The RF system relies on various decision trees. Every decision tree consists of decision nodes, leaf nodes and a root node. Each tree’s leaf node represents the final output produced by that particular decision tree. The prediction depends on the type of problem, e.g., for a regression task, the individual decision trees will be averaged, and for a classification task, a majority vote, i.e., the most frequent categorical variable, will yield the predicted class. The out-of-bag (oob) sample is then eventually used for cross-validation and prediction [
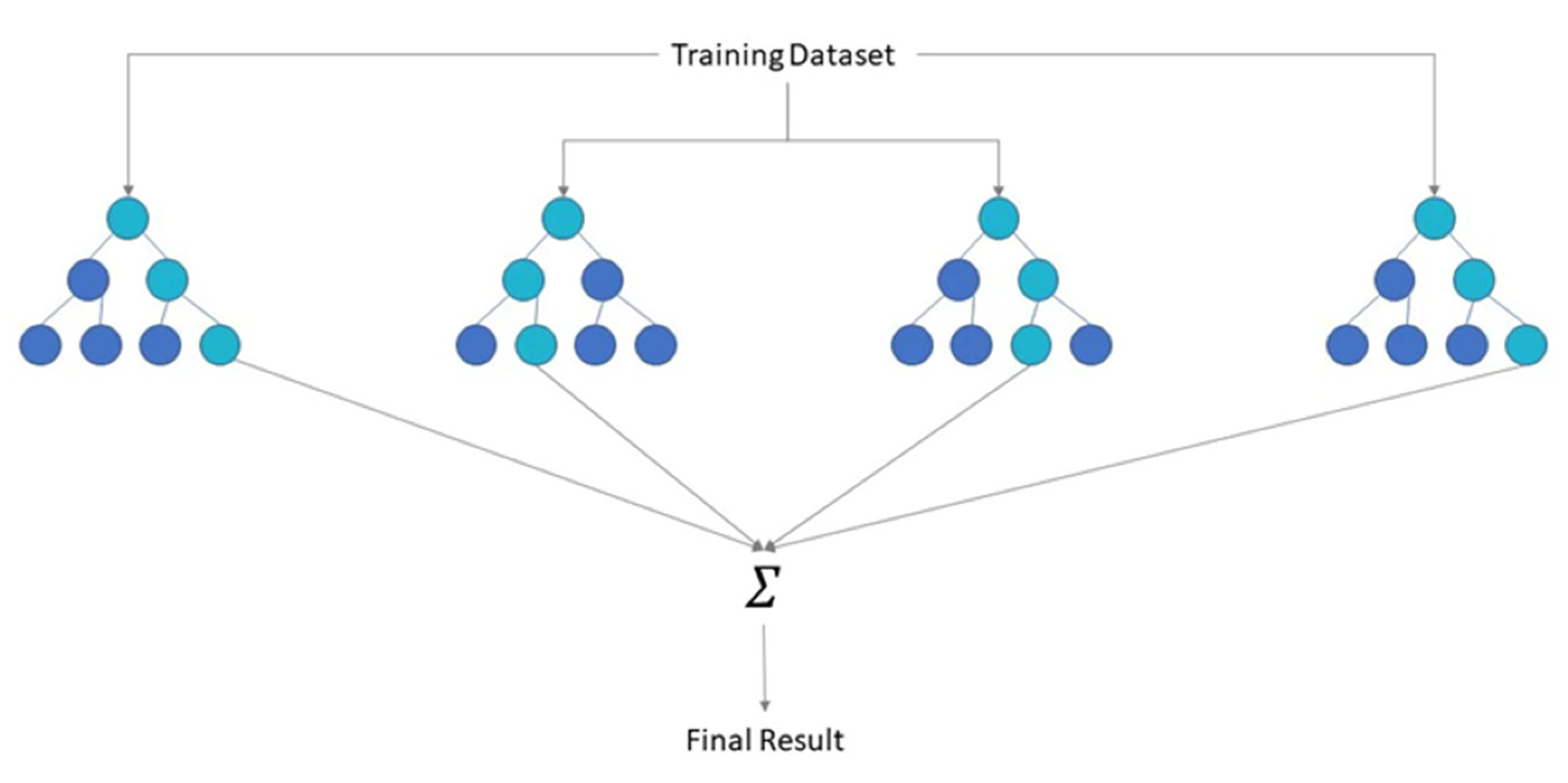
37]. The functioning of RF is illustrated in
Figure 4.
The essential algorithm for RF applies bagging bootstrap aggregation of the trees. In other words, the primary goal is to average many noisy but approximately unbiased models and hence reduce the variance.
Given a training set, X = x1, …, xn, with responses Y = y1, …, yn, bagging repeatedly (N times) selects a random sample with replacement of the training set and fits trees to these samples:
For n = 1, …., N.
Sample, with replacement, n training examples from X, Y; (Xn, Yn)
Create a classification or regression tree fn and train it on Xn, Yn
After training, the predictions for unknown samples,
x’, are calculated by averaging the predictions from all the separate regression trees on
x’ [
37]:
In case of classification, the same task is performed by a majority vote.
The standard deviation of the predictions from all of the individual regression tress on
x’ is used to measure the forecast uncertainty [
38]:
RF uses a modified tree-learning method to select a random subset of new introduced features at each candidate split in the learning process besides the bagging approach. The reason for doing this is to inject decorrelation among the trees. The study examines how bagging and random subspace projection lead to accuracy gains under various scenarios [
39].
Variable m is chosen before each split for a classification in such a way that m ≤ p of the input variables at random as candidates for splitting.
Typical values for
m are
or as low as 1. In practice, the best value for these parameters depends on the problem and are usually treated as tuning parameters. The following recommendations are widely used [
40]:
For a classification problem, the default value of m is , and the smallest node size is 1;
The default value for m is p/3, and the minimum node size is 5 for a regression problem.
3.7. Gradient Boosting
Boosting algorithms were originally introduced for classification problems [
40], and subsequently, a statistical viewpoint of boosting was introduced, connecting the algorithm to the loss function [
41]. The key approach is to iteratively merge many simple models, known as “weak learners”, to produce a “strong learner” with higher forecast accuracy [
41]. Boosting was further extended to the regression problem by introducing the gradient boosting machines (GBM) method [
42].
Gradient boosting (GB) is a machine learning model that uses the gradient descent optimization method on boosting technique classification, regression and prediction in supervised learning. Boosting differs from RF in that it sequentially constructs an ensemble by training a new weak base learner model (most commonly a decision tree) with respect to the error of the entire ensemble learned so far, as opposed to RF, which depends on simple averaging of models in the ensemble. The error value of a weak classifier is marginally better than that of a random guess. The boosting technique repeats the application of this classifier on modified data, and all predictions are aggregated using a weighted majority vote to obtain a final prediction [
43].
In typical supervised learning, given a dataset,
, where output variable y and vector of input variable
x = (
x1,
x2, …,
xn), related to each other by some probabilistic distribution function, the objective is to reconstruct functional dependence
x y with an estimate,
, such that the specified loss function,
, is minimized:
Once
is initialized as constant, the GB algorithm [
42] proceeds with the iteration of:
Fitting a base learner (or a week learner, e.g., tree) regression model, , to pseudo-residuals, i.e., training the model using the training dataset and predicting zi from the covariates of xi;
Computation of multiplier γ by solving the following one-dimensional problem to choose a gradient descent step size as:
The algorithm determines the direction and the gradient in which it needs to improve at each iteration to fit the data and select a particular model.
The trees are iteratively fitted to the residuals using GB to optimize any arbitrary differentiable loss function, such as the squared error cost function, where the negative gradient is equal to the residuals [
44].
The GBM algorithm performs better if at each iterative step, the contribution of the added decision tree is shrunk by using a shrinkage parameter,
α, also known as the learning rate, which ranges between 0 and 1. This helps to constrain the fitting procedure and address the overfitting problem [
45].
3.8. Extreme Gradient Boosting
Extreme gradient boosting (XGB) is comparable to GBM in that it uses the same gradient boosting technique to construct an ensemble of trees [
46]. There are, however, important differences and a few advantages of XGB over GBM [
47], such as:
- ▪
Regularization: XGB offers additional regularization hyperparameters that provide added protection against overfitting.
- ▪
Early stopping: XGB implements early stopping, allowing for stopping of the process of modelling when additional trees offer no improvement.
- ▪
Parallel Processing: It is particularly difficult to parallelize GBM because of its sequential nature. XGB has introduced methods to support GPU and Spark compatibility, which enables the use of distributed parallel processing to fit gradient boosting.
- ▪
Loss functions: Using specific objective and evaluation criteria, users can define and optimize gradient boosting models in XGB.
- ▪
Continue with existing model: A user can train an XGB model, save the results and later return to that model and continue building onto the results, thereby allowing continued training of the model without starting from scratch.
- ▪
Different base learners: Most GBM implementations are built with decision trees, but XGB also provides boosted generalized linear models.
The XGB algorithm proceeds with the following iterations once is initialized as constant using Equation (14):
Fitting a base learner (or a week learner, e.g., tree) regression model, , to pseudo-residuals, i.e., training the model using the training dataset by solving the following optimization problem:
A detailed overview, implementation suggestion and hyperparameter tuning for GBM and XGB are presented by Boehmke [
47].
3.9. GEKKO
GEKKO is a mixed-integer and differential algebraic equation optimization software tool. It provides large-scale solvers for linear, quadratic, nonlinear and mixed-integer programming (LP, QP, NLP, MILP, MINLP). Data reconciliation, real-time optimization, dynamic modeling, and nonlinear predictive control are some of the modes of operation [
48,
49].
GEKKO is a package that includes the ability to run model-predictive control, dynamic parameter estimation, real-time optimization and parameter update for dynamic models in real-time applications. It provides an algebraic modeling language (AML) for solving optimization problems in simple object-oriented, equation-based models to interface with powerful built-in optimization solvers [
48].
GEKKO uses nonlinear approaches in model development, dynamic data reconciliation and dynamic optimization to meet research and industrial application objectives [
50].
The interface between advanced solvers and human users is generally facilitated by AML. Variable limits, constraint functions and bounds, goal functions, and first and second derivatives of the functions, all in consistent array format, are required by high-end, off-the-shelf gradient-based solvers. AMLs make the process easier by allowing the model to be written in a straightforward, user-friendly manner. AML takes in a model (constraints) and an optimization goal [
48].
The GEKKO optimization tool solves a problem in the form Equation (24) using AML design.
By tuning and optimizing the state variables,
, and inputs,
, the objective function in Equation (24) is minimized. The inputs,
u, typically include variables such as measured disturbances, unmeasured disturbances, control actions, feed-forward values and parameters. The solver determines these parameters to minimize the objective function,
J. Differential or algebraic equations, which include equality constraints (
f) and inequality constraints (
g), are used based on the application to solve the state variables,
[
48].
A detailed overview of GEKKO with nine different modes of operation for different solutions and applications is presented in [
48].
The basic set of variable types includes constants, parameters and variables (with initial values and bounds). Fixed variables (FV) inherit parameters but have the possibility to add a degree of freedom, and they remain constant over the horizon. The built-in optimizer implicitly solves all user-defined equations simultaneously. Equations are discretized across the entire time horizon in dynamic modes, and all time points are solved at the same time [
48].
The following settings are applied in the optimization algorithm in this study to estimate the multivariate polynomial coefficients to derive the equation between PV power output as a function of forecast GHI, forecast temperature, forecast clear-sky index and :
Variable type: fixed variable;
Equation: user-defined;
Optimization simulation type: non-dynamic steady state;
Estimation: model parameter update ;
Measure power value to provide an initial guess: ;
APOPT solver: , as the number of degrees of freedom is less than 2000.
After multiple iterations with various equation formats, the following forecast equation is generated:
where:
= Forecast power;
= Forecast GHI;
= Forecast temperature;
= ;
= Forecast clear-sky index.
Five sets of coefficients of Equation (25) optimized and derived using GEKKO for different sky conditions by applying clustering on forecast clear-sky index as per
Table 2 are listed in
Table 4.
3.10. Ensemble Model
As illustrated in
Section 4, the performance of linear and time series regression models is much lower than that of ML models and GEKKO; therefore, only RF, RF with Fourier, GB, XGB and GEKKO models are considered for the evaluation of average and weighted averaged ensemble models. In an average ensemble model, the average forecast of each individual model is evaluated under different clusters based on the forecast value of clear sky index, i.e.,
In the weighted average ensemble, the weight of each model performance is first evaluated for different clusters by using the inverse value of MAE, e.g., the weight of RF forecast:
where IMAE = 1/MAE.
The weighted average ensemble forecast is then evaluated on an hourly basis for each cluster based on the forecast value of clear sky index as:
4. Results and Discussion
4.1. Overview and Analysis
In this section, the evaluation of the power forecasts obtained by the different models described in
Section 3 is presented, and a comparison of different methods is performed to assess which models perform best under given conditions. This is followed by a more detailed analysis with respect to the performance of the forecasts for different clear sky index clusters, as well as monthly forecasts. Finally, information on the variation in performance of each model with increased forecast horizon and the probabilistic forecast for the best performing models is provided.
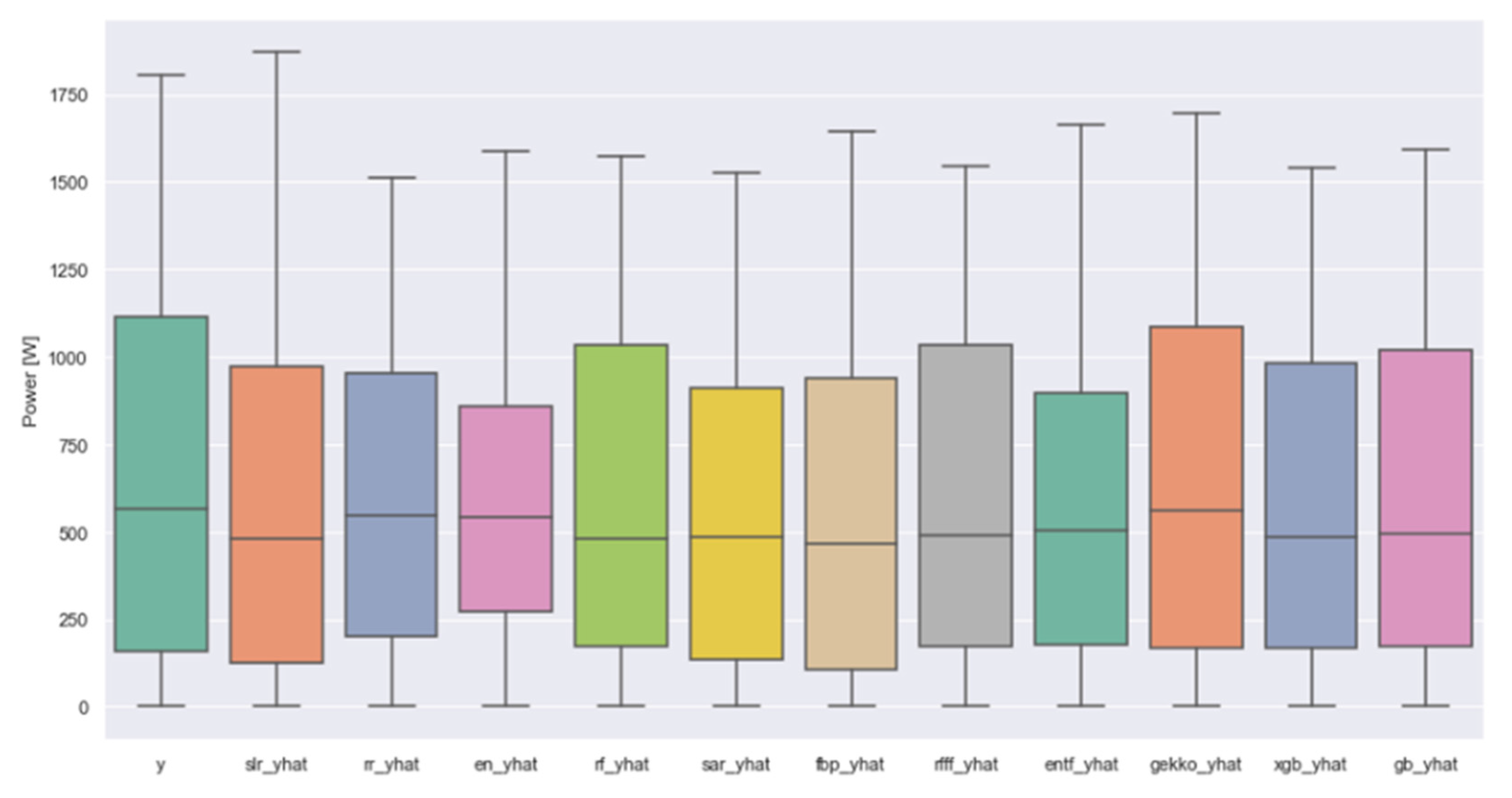
Figure 5 shows the box plot for the aggregate forecast data for different models compared with the actual measured value (y) and
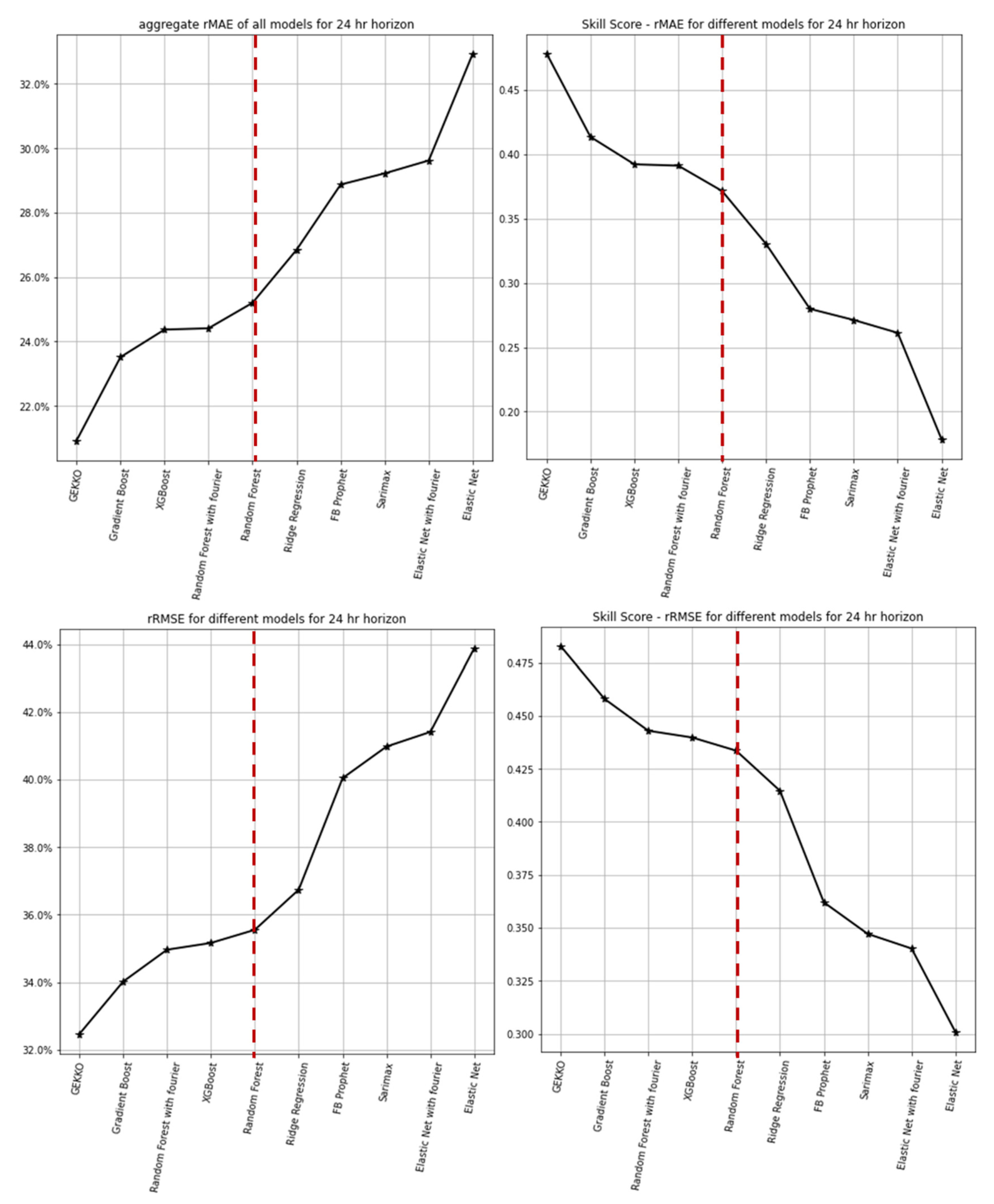
Figure 6 shows rMAE and rRMSE and associated skill scores for a 24 h forecast horizon for the entire test period. It is evident that GEKKO outperforms all the models both in rMAE (20.9%) and rRMSE (32.4%), with the skill score of both indices close to 0.48.
Linear regression models SKlearn, ridge and elastic net and time series models SARIMAX and FBP did not perform well. These models apparently require continuous data without any serious gaps, and as such, their forecast performance deteriorated due to gaps in the measured data, as explained in
Section 3.3. Solar power is not a linear function of the GHI, and as such, the performance of the linear models deteriorates compared with ML and polynomial regressions models. Furthermore, as the purpose is to build a robust forecast model with minimal dependence on historical data, the focus lies on further analysis of the five best-performing models, i.e., GEKKO, GB, XGB, RF and RFF.
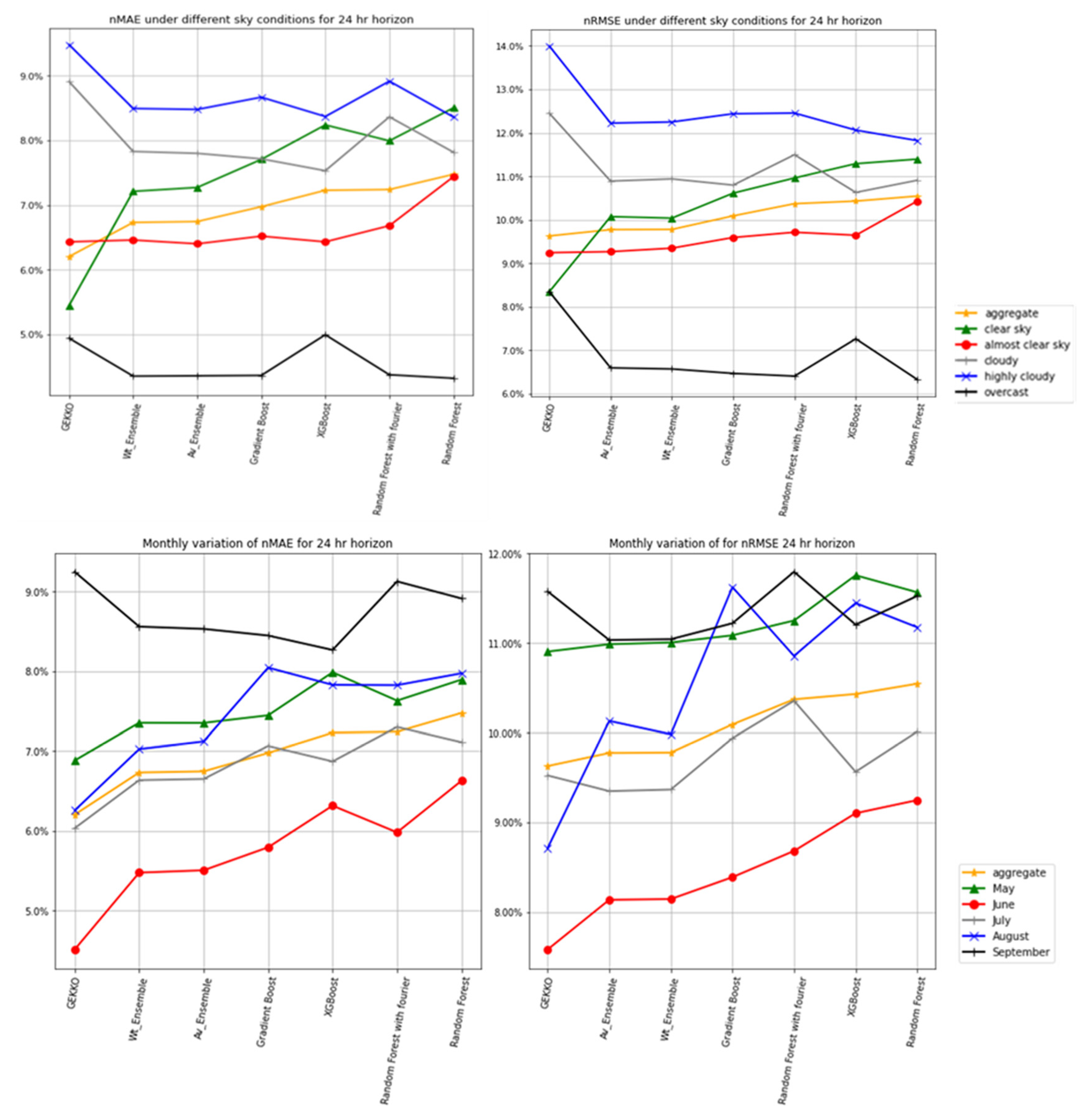
Figure 7 shows important metrics under different clear sky conditions and the aggregate during the whole test period. Normalized indices are calculated by dividing the respective metrics by installed power capacity, i.e., 2200 W.
It is evident that overall (aggregate), GEKKO outperforms all other models for all metrics. Furthermore, GEKKO outperforms other models under clear sky and almost clear sky conditions, i.e., for clear sky index ≥0.7, whereas the weighted average ensemble model performs the best under cloudy, highly cloudy and overcast conditions, i.e., under clear sky index <0.7. The performance of ML models (GB, XGB, RF) is close, with the advantage of introducing multiple Fourier transform series as additional features evident from the fact that RF with Fourier performs better than RF, especially under highly variable cloudy and highly cloudy conditions.
The month-wise analysis shows results in line with expectations that all models perform better than the aggregated model during summer (June and July), as there are more instances of clear sky hours during these months compared to other months (May, Aug, Sept), where the performance of all the models drop compared to the aggregate model.
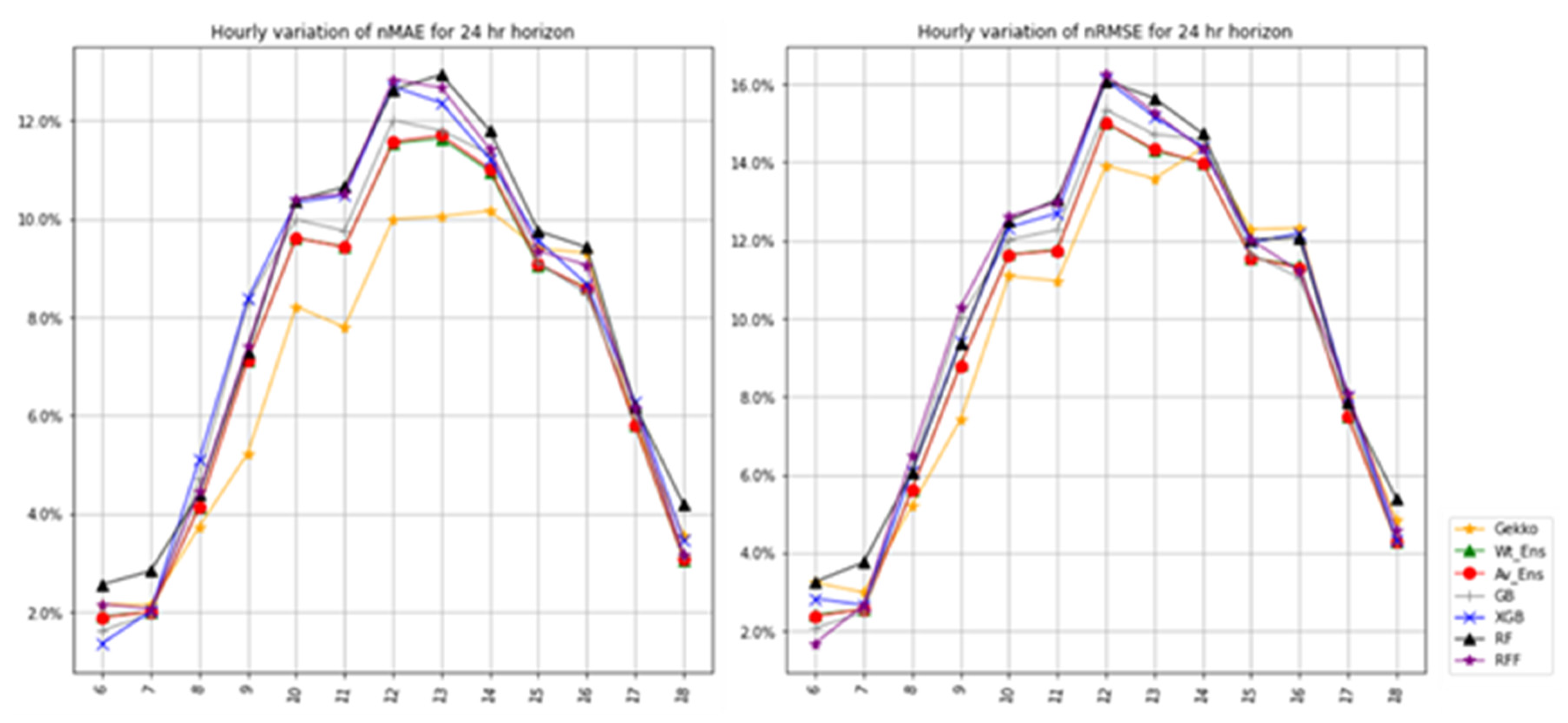
It is evident from hourly variation analysis of metrics (
Figure 8) that GEKKO outperforms all the models from 8:00 to 14:00 h, followed by the weighted and average ensemble models. The performance of GEKKO is relatively poor in the early morning hours from 6:00 to 8:00 h. This is corroborated by the analysis of the distribution of the forecast clear sky index, which shows a higher density of forecast,
, during the period. The statistical difference in the performance of all the models is insignificant from 16:00 to 18:00 h.
Figure 9 illustrates the variation in aggregate nMAE and nRMSE of different models for 24 h, 48 h and 72 h forecast horizons. As anticipated, the forecasting error rises as the forecast horizon increases for all metrics.
Detailed analysis of
Figure 9 shows that the drop in performance of GEKKO is much higher compared with that of other models. The nMAE for GEKKO increases by 11% and 26%, whereas for all other models, the increase in nMAE is around 7% and 19% for 48 h and 72 h forecast horizons, respectively, compared to a 24 h forecast horizon. A similar observation is made on the other scores. This is because the coefficients in
Table 3 derived for GEKKO are based on the forecast data for a 24 h horizon, and the same coefficients and equations are used to forecast for 48 h and 72 h horizons, as the main purpose of this study is to forecast for a 24 h horizon. Nevertheless, GEKKO still performs better than other models for 48 and 72 h horizons.
4.2. Probabilistic Forecast
The forecasting accuracy of PV power greatly depends on the forecasting quality of meteorological parameters, particularly on GHI and temperature. Therefore, uncertainty is bound to play a major role in forecasting of power because of the associated uncertainty in meteorological parameters due to the stochastic nature of weather conditions. Probabilistic forecasting is therefore very important in quantifying the forecast uncertainty by delivering not only the deterministic forecast but also a full predictive distribution.
A probabilistic forecast enables users to adapt their decisions based on additional uncertainty information. For example, the uncertainty in forecast estimates is critical in determining the best bidding approach for a microgrid with a high proportion of renewable energy sources [
51]. A study showed that probabilistic forecast for day-ahead energy bidding of an Italian wind farm can result in a 23% increase in the annual profit in comparison to point forecasts [
52].
A point forecast with a confidence interval is desirable to show the claimed accuracy [
53]. For a reasonably large sample size, an
x% confidence interval, by definition, gives the probability that future ground measured data will fall in
x% confidence interval for the forecast under simulated conditions, with an assumption that the model is correct. Statistically, it is defined as [
53]:
The lower and upper quantile limits for the 95% confidence interval are calculated using a t distribution for GEKKO and weighted ensemble probabilistic forecast comparison and analysis. GB is one of several ML models that can be adapted to predict quantiles. The GB tree-boosting algorithm predicts α quantile with an appropriate quantile cost function and hence can be used for quantile regression [
54]. As the primary focus of this work is to compare the probabilistic forecasts of the models, quantile GB is also used to predict two quantiles, i.e., 0.05 and 0.95.
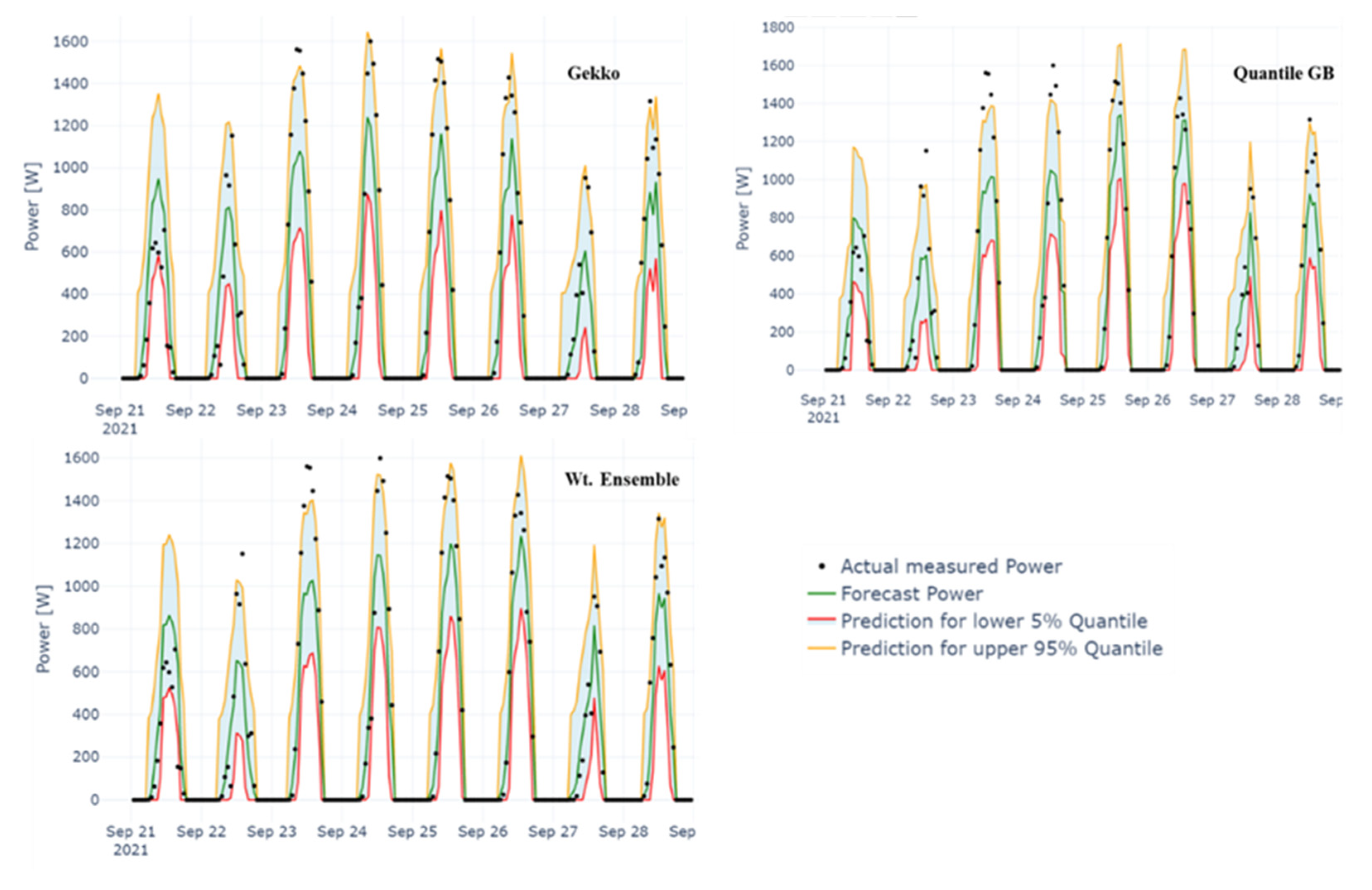
Figure 10 shows the intraday time series plot of forecast with a 95% confidence interval for a 24 h forecast horizon, along with measured power for eight consecutive days starting at 21 September 2021 for the three models under consideration for probabilistic forecast. The light-blue shaded region between the red and orange lines is the 95% confidence interval. The statistical analysis shows that 90.6% of the ground-measured data fall within the 95% confidence interval of GEKKO, whereas the same is 89.8% and 88.3% for weighted average ensemble and GB, respectively. There is also a statistically significant higher percentage of absolute errors in the lower quantile for all three models.
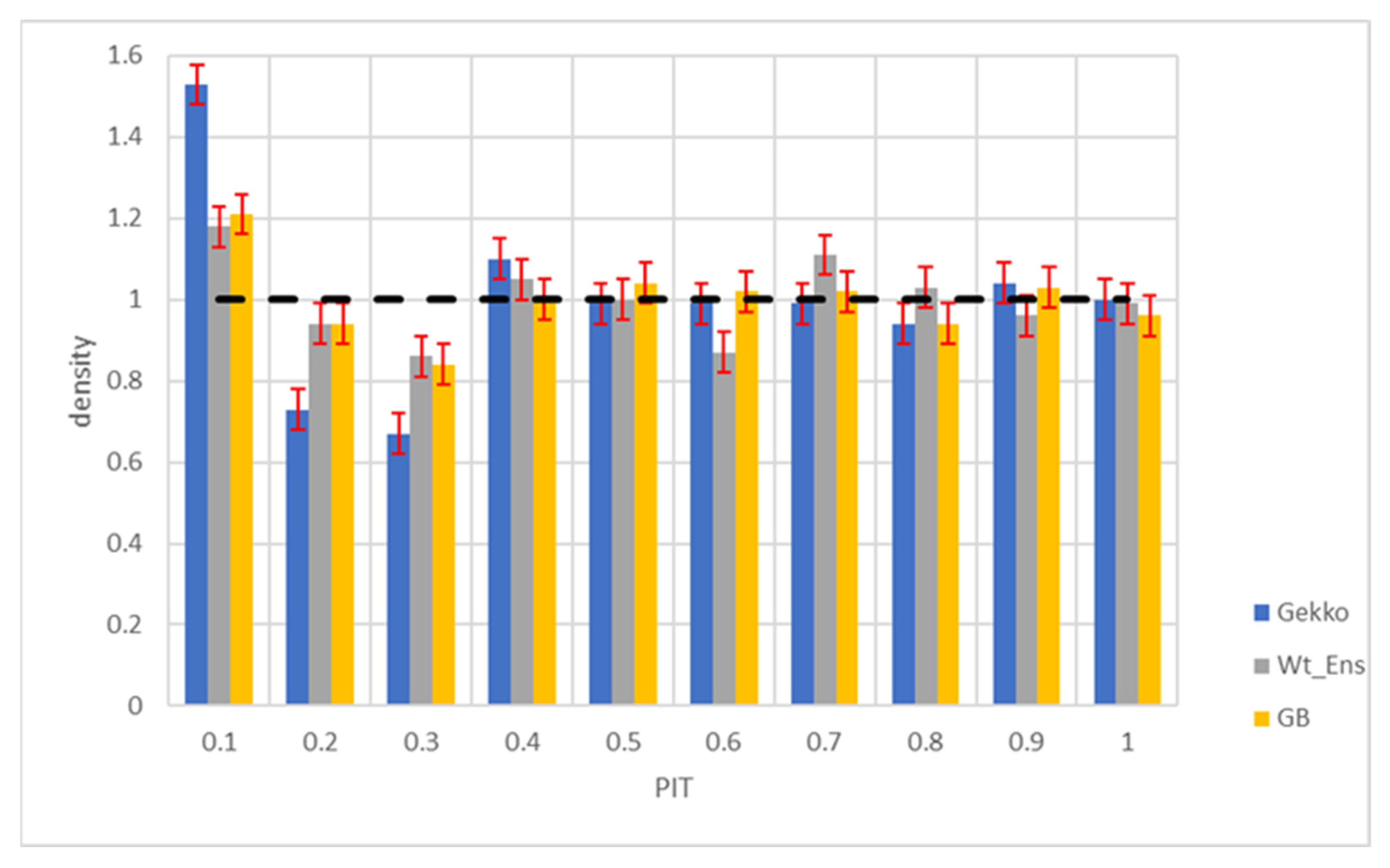
Figure 11 shows the PIT histograms of GEKKO, weighted ensemble and GB models with a 95% confidence interval for each bin shown as a red error bar, with the dashed line representing significant level 1 of uniform distribution. The high value on the first bin for all the models suggests that these models underestimate the lower quantile. The performance of GEKKO is almost 100% uniform in bins 0.5–1.0, suggesting its excellent reliability skill in the respective quantiles.
Figure 12a shows the relative CRPS (rCRPS) of three models for overall and different sky conditions. rCRPS is calculated by dividing the CRPS score by the average value of observed power in the corresponding cluster for better resolution and visualization. The difference in the overall rCRPS score of all the models is statistically insignificant, with all models close to 0.475. However, it is evident that GEKKO performs significantly better compared with the two other models for
, whereas weighted average ensemble has better CRPS for
, and the statistical difference between weighted average ensemble and GB is insignificant.
The rCRPS of the three models is shown as a function of the time of the day in
Figure 12b. The rCRPS of GEKKO is significantly lower for 70% of the hours of the day.
Although the models under evaluation forecast a continuous variable, BS is used to compare the performance of the models to predict common and rare events. In this study, BS is calculated for two rare events and one normal event:
Rare event R1, where is lower than its 10% percentile;
Rare event R2, where is higher than its 90% percentile;
Normal event N1, where is higher than its 50% percentile.
The threshold value is kept at 0.5 of the maximum power value in each cluster for BS evaluation, as per the standard practice.
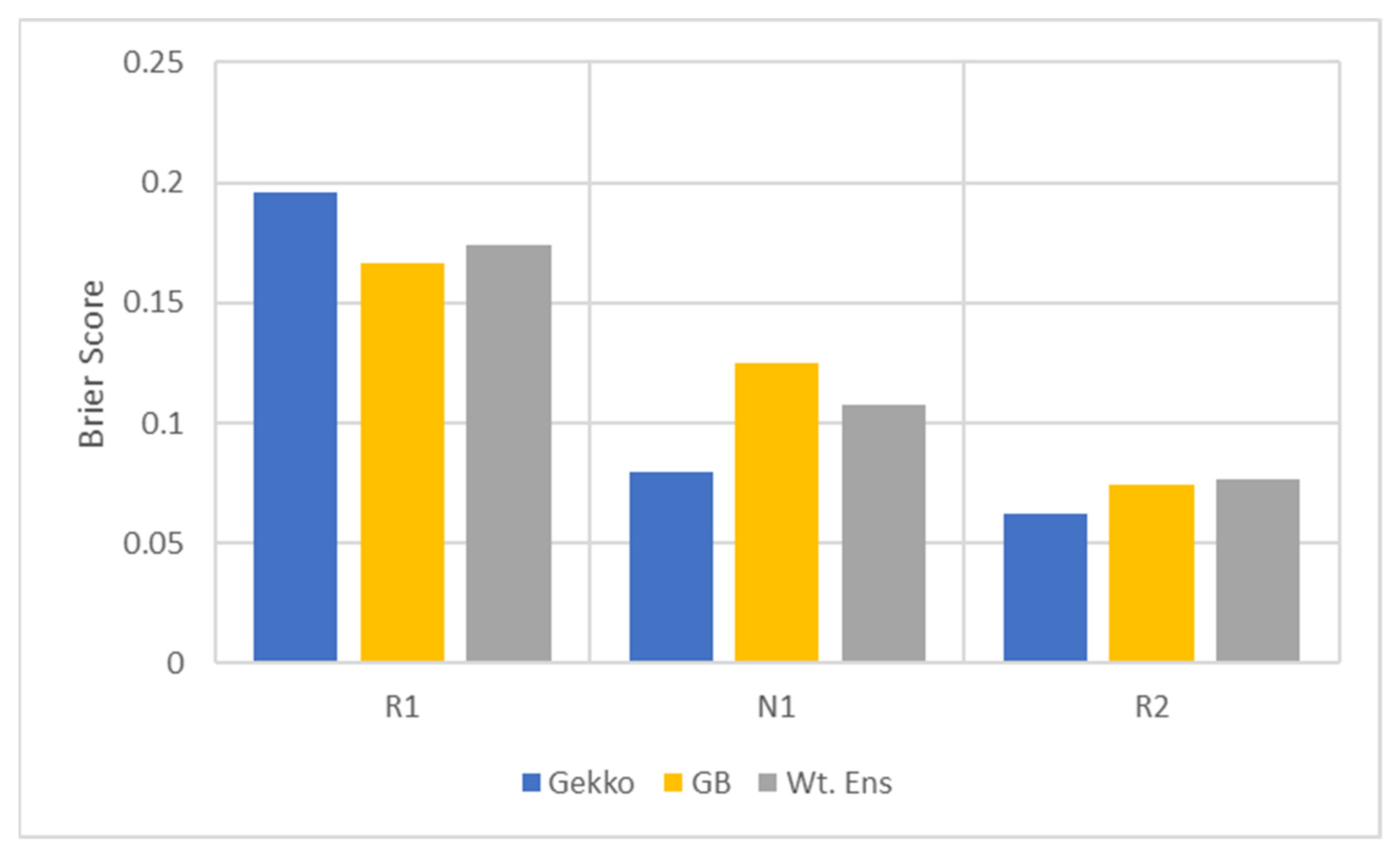
Overall values of BS for three events, as shown in
Figure 13, show statistically significant differences for the three models. GEKKO is more skilled for the normal event, N1, as well as for higher
event R2. However, the performance of GEKKO drops significantly for R1, where GB seems to perform better, suggesting it is better at predicting extreme low power to some degree.
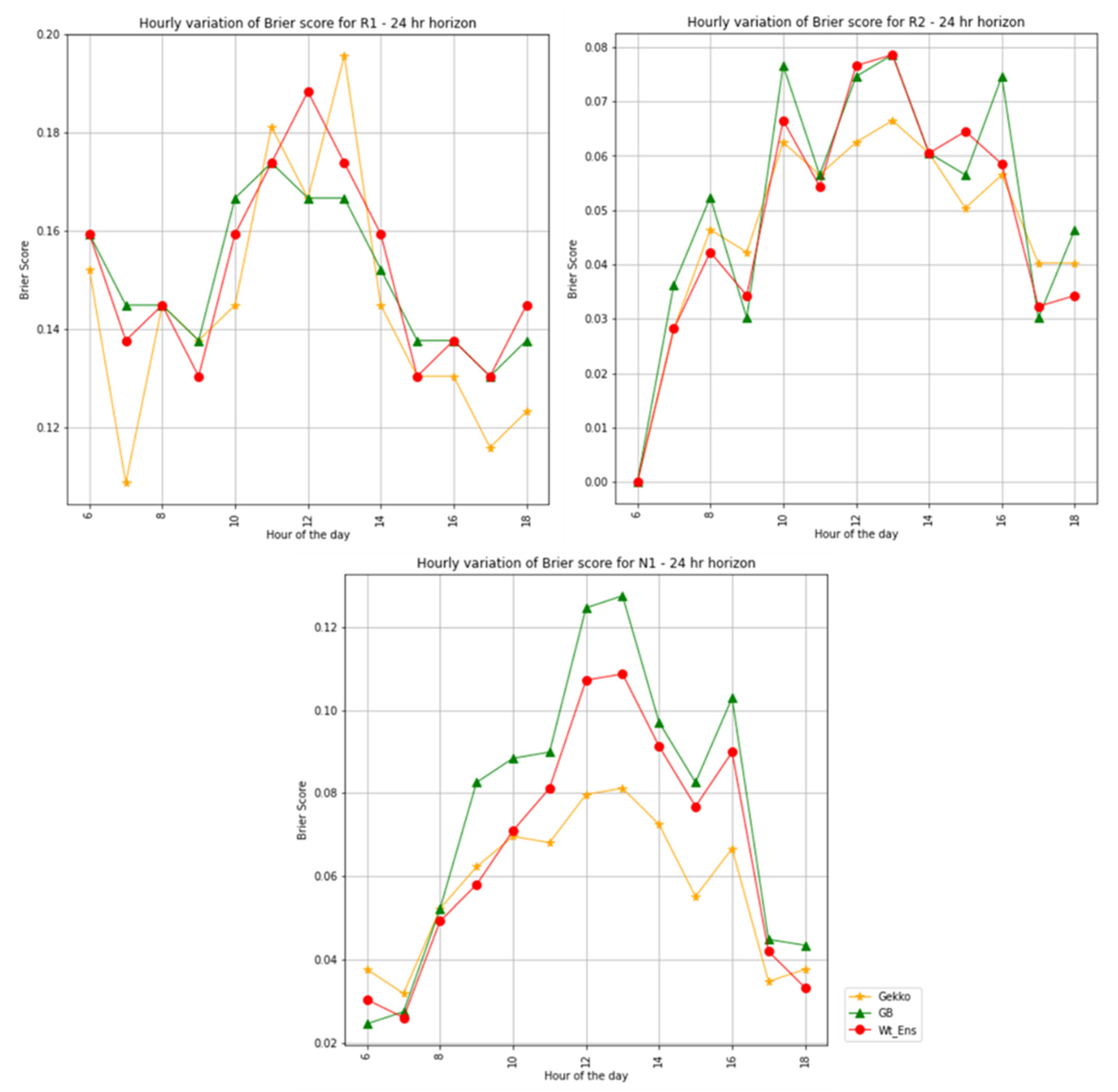
The BS of the three models is shown as a function of the time of day for each event in
Figure 14. GEKKO is apparently more skilled for common event N1, and the difference between GEKKO and weighted average ensemble is significant for 54% of the hours of the day, from 11:00 to 17:00 h. The performance of GEKKO is mostly lower compared to the other models for event R1; however, its performance improves significantly for event R2 for higher power hours of the day, from 11:00 to 15:00 h.
5. Conclusions and Outlook
The accurate and reliable forecasting of PV energy production has gained tremendous importance and dynamics in recent years from both a research and economic point of view due to a rapidly growing integration of solar energy into the power grid. In this study, the prediction of PV energy based on meteorological variables is presented, which are available from meteorological data providers. A study was performed to evaluate the impact of different cloud conditions by classifying the clear sky index into clusters to enhance the forecast performance. As benchmark models, several linear regression models and time series models were applied and compared to evaluate the possible gains in applying computationally more demanding models. Several ML models were used and compared for both deterministic and probabilistic forecasts because solar power possesses nonlinear properties.
In this paper, we also proposed a novel method based on GEKKO-optimized polynomial regression forecast methodology. The overall results show that the proposed GEKKO-based methodology works better than any other model, even under central European cloudy conditions. The forecasting accuracy can be further increased for tropical countries and southern Europe because of the large proportion of clear sky data in such datasets.
Further improvement in GEKKO forecast is possible by optimizing regressive coefficients under cloudy and overcast sky conditions with larger datasets. This methodology is also verified and applied for other PV technologies, such as copper indium selenide (CIS), amorphous silicon (a-Si), cadmium telluride (CdTe) and polycrystalline silicon (p-Si) and can be adapted for any location. The forecasting performance beyond a 24-h horizon can be improved by optimizing the GEKKO model to separately derive coefficients for respective forecast horizons. Different ML models show significant improvements, especially under cloudy to overcast sky conditions. The quantile loss study presented in
Section 4.2 can be further extended in quantile gradient boosting (QGB) and other ML models, such as analog ensemble models, to build a more robust probabilistic procedure. Forecasting accuracy can be further leveraged in QGB by penalizing the model for overestimating or underestimating, thereby enhancing the forecasting accuracy. This study shows the potential of applying various ML methods with limited input and logical clustering methodology but nonetheless with promising forecasting results for PV energy.