An Impedance Matching Solution to Increase the Harvested Power and Efficiency of Nonlinear Piezoelectric Energy Harvesters †
Abstract
1. Introduction
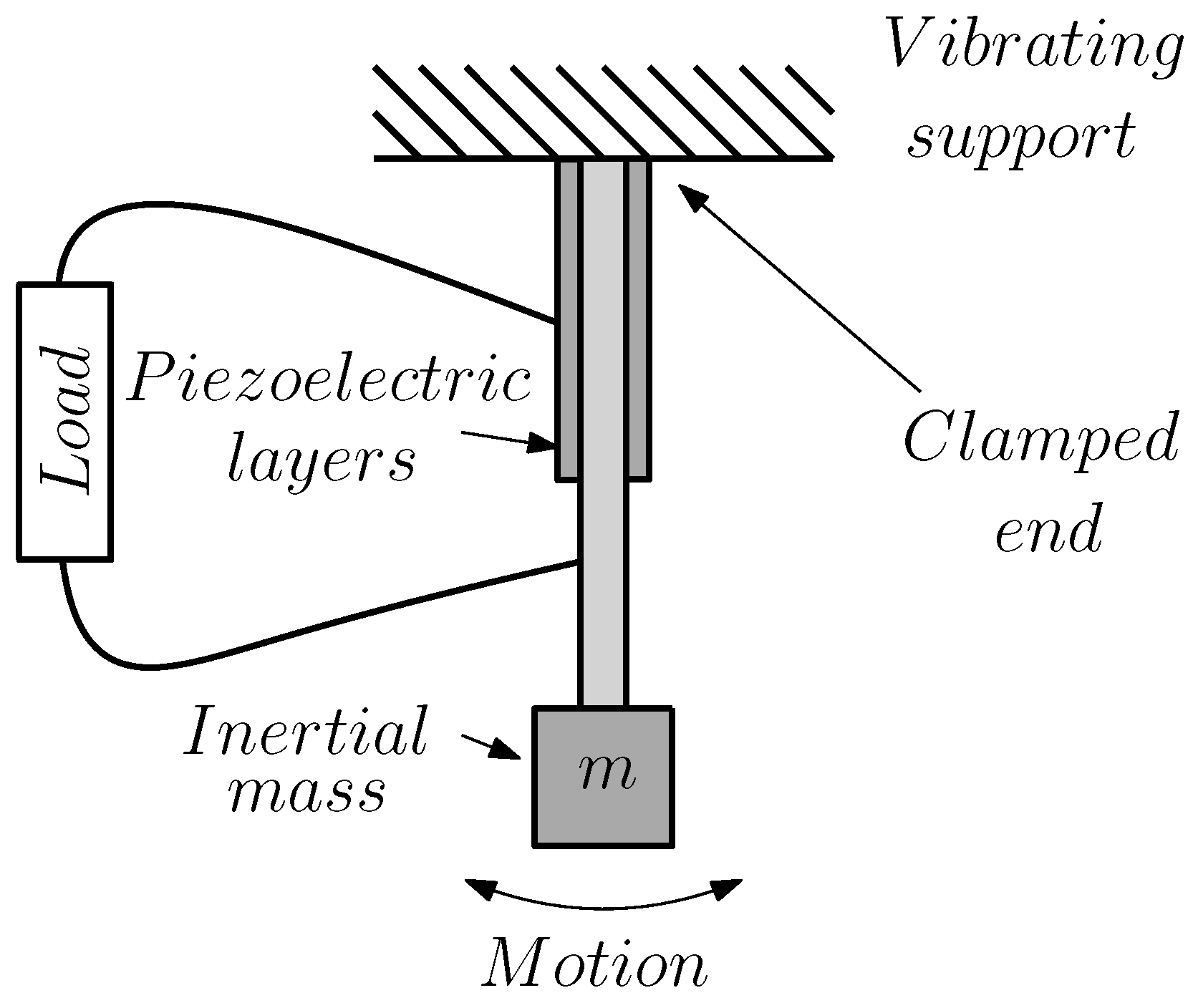
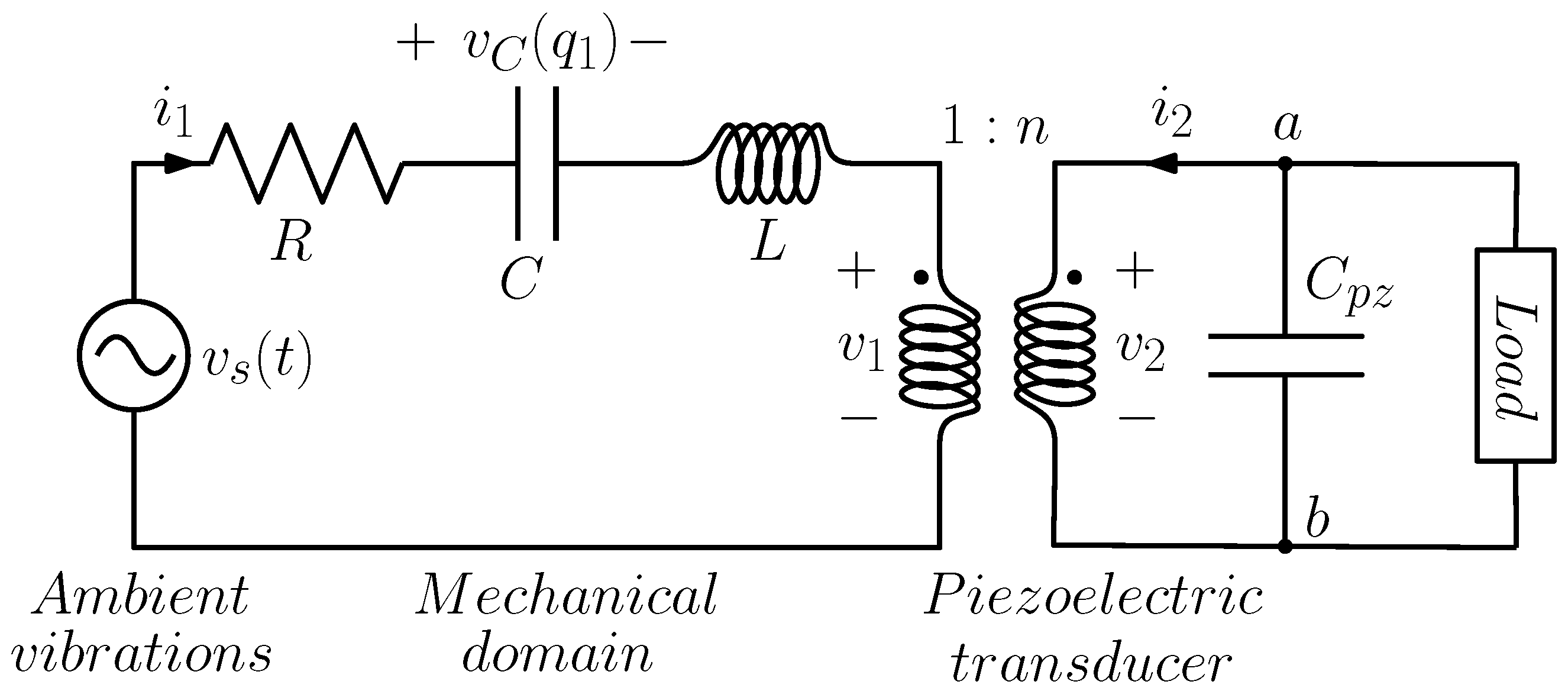
2. Piezoelectric Energy Harvester Modeling
3. Linear Harvester, Impedance Matching and Maximum Power Transfer
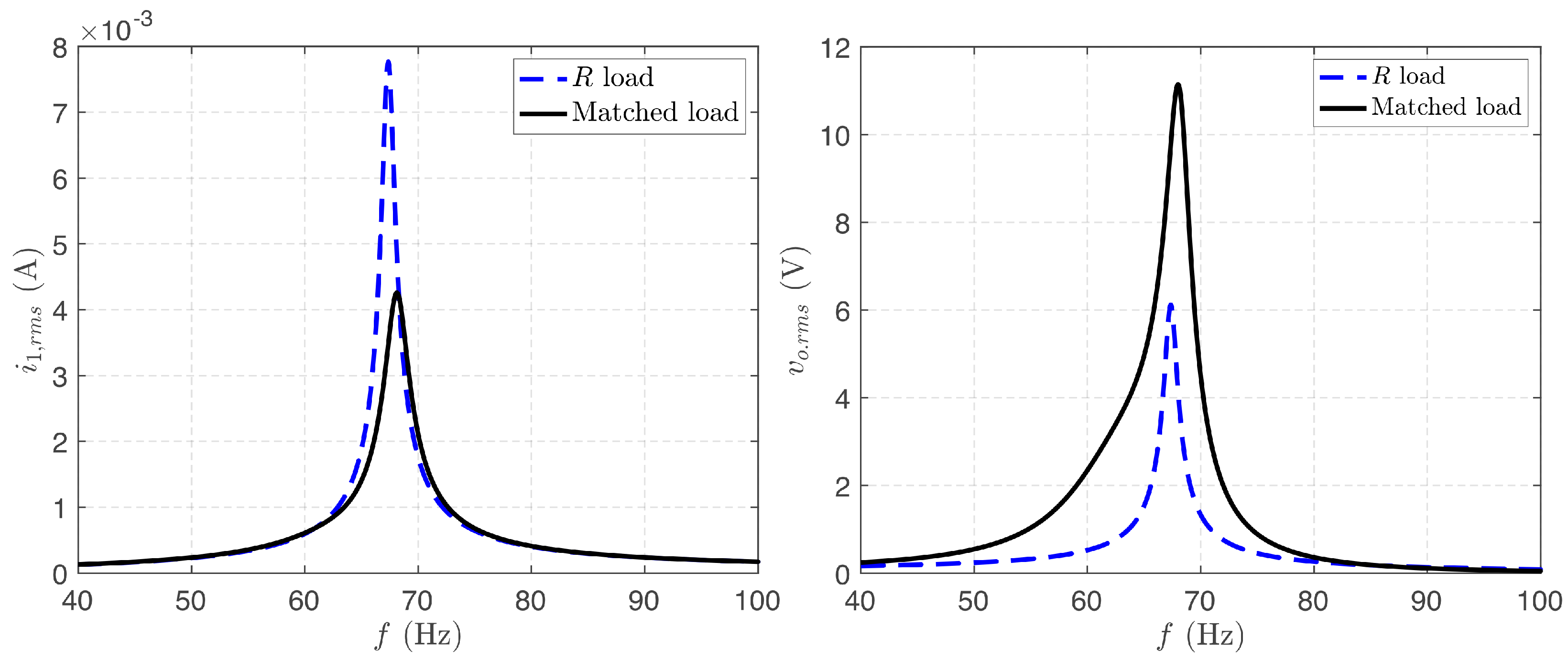
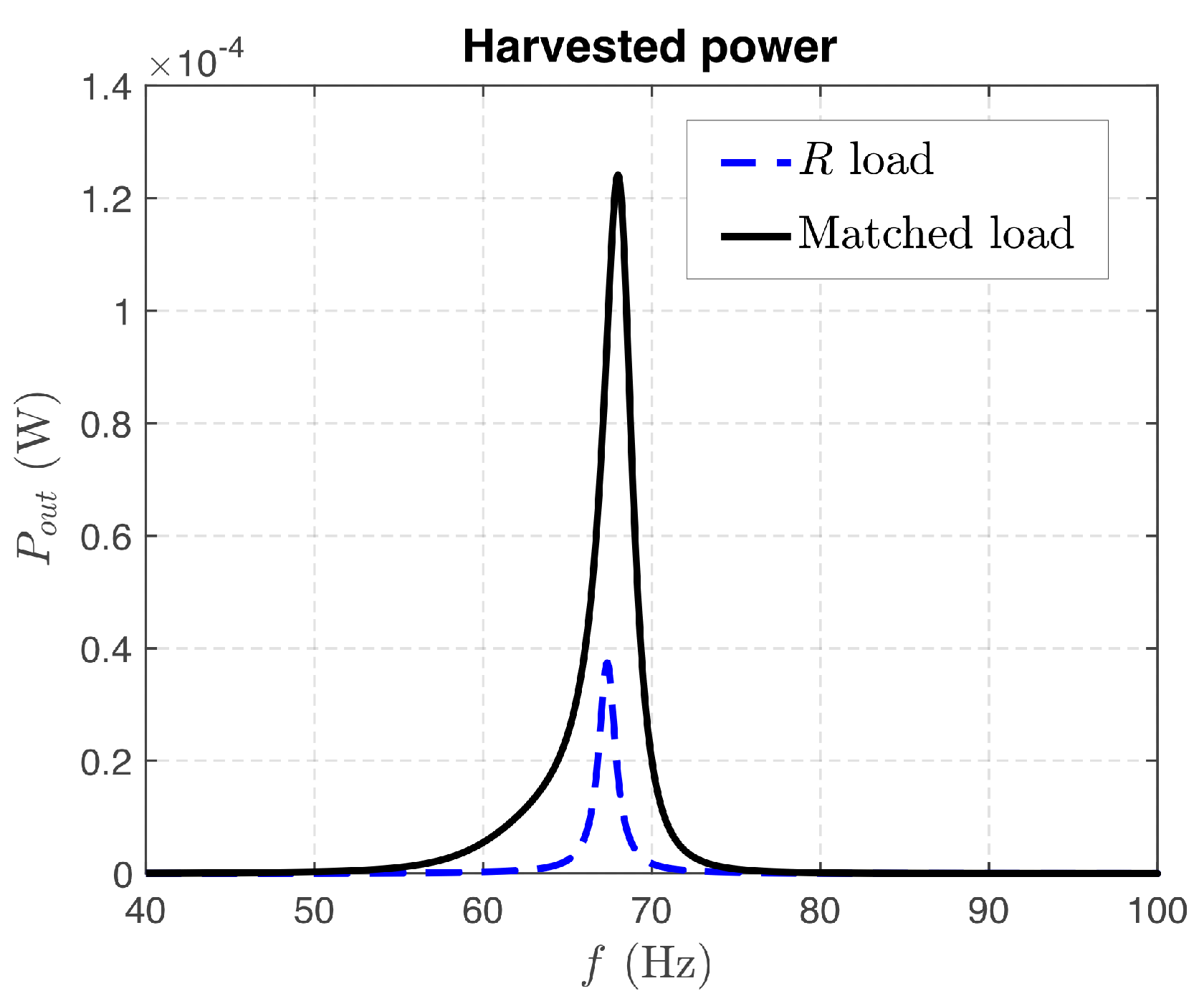
3.1. Resistive Load
3.2. Matched Load
4. Nonlinear Energy Harvester Analysis
4.1. The Harmonic Balance Technique
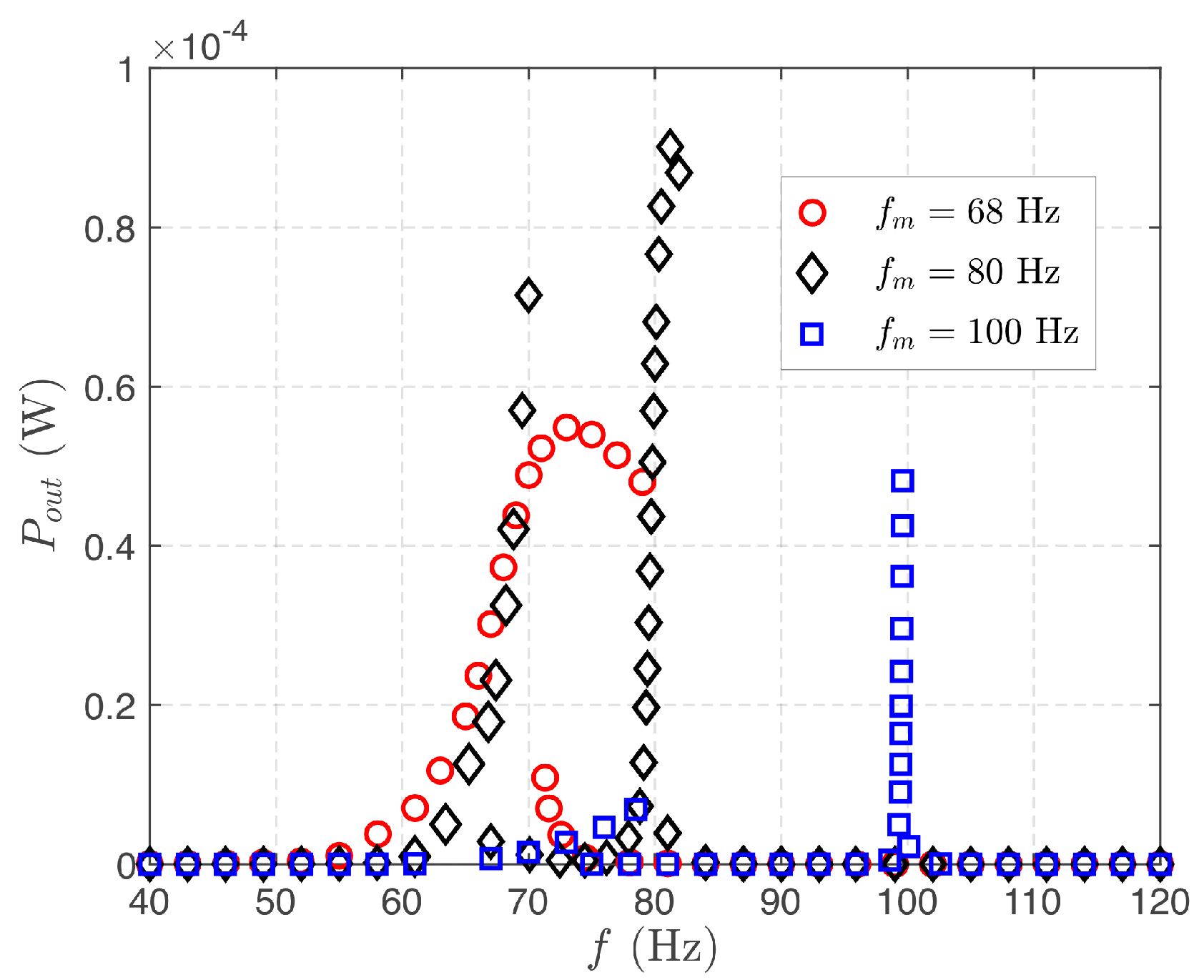
4.2. Nonlinear Piezoelectric Energy Harvester Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Roundy, S.; Wright, P.K.; Rabaey, J.M. Energy Scavenging for Wireless Sensor Networks; Springer: Boston, MA, USA, 2003. [Google Scholar]
- Paradiso, J.A.; Starner, T. Energy scavenging for mobile and wireless electronics. IEEE Pervasive Comput. 2005, 4, 18–27. [Google Scholar] [CrossRef]
- Beeby, S.P.; Tudor, M.J.; White, N. Energy harvesting vibration sources for microsystems applications. Meas. Sci. Technol. 2006, 17, R175. [Google Scholar] [CrossRef]
- Mitcheson, P.; Yeatman, E.; Rao, G.; Holmes, A.; Green, T. Energy Harvesting From Human and Machine Motion for Wireless Electronic Devices. Proc. IEEE 2008, 96, 1457–1486. [Google Scholar] [CrossRef]
- Lu, X.; Wang, P.; Niyato, D.; Kim, D.I.; Han, Z. Wireless Networks with RF Energy Harvesting: A Contemporary Survey. IEEE Commun. Surv. Tutor. 2015, 17, 757–789. [Google Scholar] [CrossRef]
- Khaligh, A.; Zeng, P.; Zheng, C. Kinetic energy harvesting using piezoelectric and electromagnetic technologies—State of the art. IEEE Trans. Ind. Electron. 2009, 57, 850–860. [Google Scholar] [CrossRef]
- Vocca, H.; Neri, I.; Travasso, F.; Gammaitoni, L. Kinetic energy harvesting with bistable oscillators. Appl. Energy 2012, 97, 771–776. [Google Scholar] [CrossRef]
- Wen, X.; Yang, W.; Jing, Q.; Wang, Z.L. Harvesting broadband kinetic impact energy from mechanical triggering/vibration and water waves. ACS Nano 2014, 8, 7405–7412. [Google Scholar] [CrossRef]
- Fu, Y.; Ouyang, H.; Davis, R.B. Nonlinear dynamics and triboelectric energy harvesting from a three-degree-of-freedom vibro-impact oscillator. Nonlinear Dyn. 2018, 92, 1985–2004. [Google Scholar] [CrossRef]
- Shin, Y.H.; Choi, J.; Kim, S.J.; Kim, S.; Maurya, D.; Sung, T.H.; Priya, S.; Kang, C.Y.; Song, H.C. Automatic resonance tuning mechanism for ultra-wide bandwidth mechanical energy harvesting. Nano Energy 2020, 77, 104986. [Google Scholar] [CrossRef]
- Wang, Z.; Du, Y.; Li, T.; Yan, Z.; Tan, T. A flute-inspired broadband piezoelectric vibration energy harvesting device with mechanical intelligent design. Appl. Energy 2021, 303, 117577. [Google Scholar] [CrossRef]
- Cottone, F.; Vocca, H.; Gammaitoni, L. Nonlinear energy harvesting. Phys. Rev. Lett. 2009, 102, 080601. [Google Scholar] [CrossRef] [PubMed]
- Gammaitoni, L.; Neri, I.; Vocca, H. Nonlinear oscillators for vibration energy harvesting. Appl. Phys. Lett. 2009, 94, 164102. [Google Scholar] [CrossRef]
- Mann, B.P.; Sims, N.D. Energy harvesting from the nonlinear oscillations of magnetic levitation. J. Sound Vib. 2009, 319, 515–530. [Google Scholar] [CrossRef]
- Gammaitoni, L.; Neri, I.; Vocca, H. The benefits of noise and nonlinearity: Extracting energy from random vibrations. Chem. Phys. 2010, 375, 435–438. [Google Scholar] [CrossRef]
- Daqaq, M.F. Response of uni-modal Duffing-type harvesters to random forced excitations. J. Sound Vib. 2010, 329, 3621–3631. [Google Scholar] [CrossRef]
- Bonnin, M.; Traversa, F.L.; Bonani, F. Analysis of influence of nonlinearities and noise correlation time in a single-DOF energy-harvesting system via power balance description. Nonlinear Dyn. 2020, 100, 119–133. [Google Scholar] [CrossRef]
- Daqaq, M.F. On intentional introduction of stiffness nonlinearities for energy harvesting under white Gaussian excitations. Nonlinear Dyn. 2012, 69, 1063–1079. [Google Scholar] [CrossRef]
- Xu, M.; Li, X. Two-step approximation procedure for random analyses of tristable vibration energy harvesting systems. Nonlinear Dyn. 2019, 98, 2053–2066. [Google Scholar] [CrossRef]
- Daqaq, M.F.; Crespo, R.S.; Ha, S. On the efficacy of charging a battery using a chaotic energy harvester. Nonlinear Dyn. 2020, 99, 1525–1537. [Google Scholar] [CrossRef]
- Yan, Z.; Sun, W.; Hajj, M.R.; Zhang, W.; Tan, T. Ultra-broadband piezoelectric energy harvesting via bistable multi-hardening and multi-softening. Nonlinear Dyn. 2020, 100, 1057–1077. [Google Scholar] [CrossRef]
- Bonnin, M.; Traversa, F.L.; Bonani, F. On the application of circuit theory and nonlinear dynamics to the design of highly efficient energy harvesting systems. In Proceedings of the 2021 International Conference on Smart Energy Systems and Technologies (SEST), Vaasa, Finland, 6–8 September 2021. [Google Scholar] [CrossRef]
- Brufau-Penella, J.; Puig-Vidal, M. Piezoelectric energy harvesting improvement with complex conjugate impedance matching. J. Intell. Mater. Syst. Struct. 2009, 20, 597–608. [Google Scholar] [CrossRef]
- Abdelmoula, H.; Abdelkefi, A. Ultra-wide bandwidth improvement of piezoelectric energy harvesters through electrical inductance coupling. Eur. Phys. J. Spec. Top. 2015, 224, 2733–2753. [Google Scholar] [CrossRef]
- Huang, D.; Zhou, S.; Litak, G. Analytical analysis of the vibrational tristable energy harvester with a RL resonant circuit. Nonlinear Dyn. 2019, 97, 663–677. [Google Scholar] [CrossRef]
- Yu, T.; Zhou, S. Performance investigations of nonlinear piezoelectric energy harvesters with a resonant circuit under white Gaussian noises. Nonlinear Dyn. 2021, 103, 183–196. [Google Scholar] [CrossRef]
- Bonnin, M.; Traversa, F.L.; Bonani, F. Leveraging circuit theory and nonlinear dynamics for the efficiency improvement of energy harvesting. Nonlinear Dyn. 2021, 104, 367–382. [Google Scholar] [CrossRef]
- IEEE Std 1859-2017; IEEE Standard on Piezoelectricity. IEEE: Minneapolis, MN, USA, 1988. [CrossRef]
- Priya, S.; Inman, D.J. Energy Harvesting Technologies; Springer: Boston, MA, USA, 2009; Volume 21. [Google Scholar]
- Ghanem, R.G.; Spanos, P.D. Stochastic Finite Elements: A Spectral Approach; Courier Corporation: North Chelmsford, MA, USA, 2003. [Google Scholar]
- Yang, Y.; Tang, L. Equivalent circuit modeling of piezoelectric energy harvesters. J. Intell. Mater. Syst. Struct. 2009, 20, 2223–2235. [Google Scholar] [CrossRef]
- Kundert, K.S.; Sangiovanni-Vincentelli, A.L.; White, J.K. Steady-State Methods for Simulating Analog and Microwave Circuits; Springer: Boston, MA, USA, 2010. [Google Scholar]
- Bonnin, M.; Traversa, F.; Bonani, F. Efficient spectral domain technique for the frequency locking analysis of nonlinear oscillators. Eur. Phys. J. Plus 2018, 133, 246. [Google Scholar] [CrossRef]
- Traversa, F.L.; Bonani, F.; Donati Guerrieri, S. A frequency-domain approach to the analysis of stability and bifurcations in nonlinear systems described by differential-algebraic equations. Int. J. Circuit Theory Appl. 2008, 36, 421–439. [Google Scholar] [CrossRef]
- Farkas, M. Periodic Motions; Springer Nature: New York, NY, USA, 1994. [Google Scholar]
- Cappelluti, F.; Traversa, F.L.; Bonani, F.; Donati Guerrieri, S.; Ghione, G. Large-Signal Stability of Symmetric Multibranch Power Amplifiers Exploiting Floquet Analysis. IEEE Trans. Microw. Theory Tech. 2013, 61, 1580–1587. [Google Scholar] [CrossRef]
- Traversa, F.; Bonani, F. Frequency-domain evaluation of the adjoint Floquet eigenvectors for oscillator noise characterisation. IET Circuits Devices Syst. 2011, 5, 46. [Google Scholar] [CrossRef]
- Traversa, F.L.; Bonani, F. Improved harmonic balance implementation of Floquet analysis for nonlinear circuit simulation. AEU Int. J. Electron. Commun. 2012, 66, 357–363. [Google Scholar] [CrossRef][Green Version]

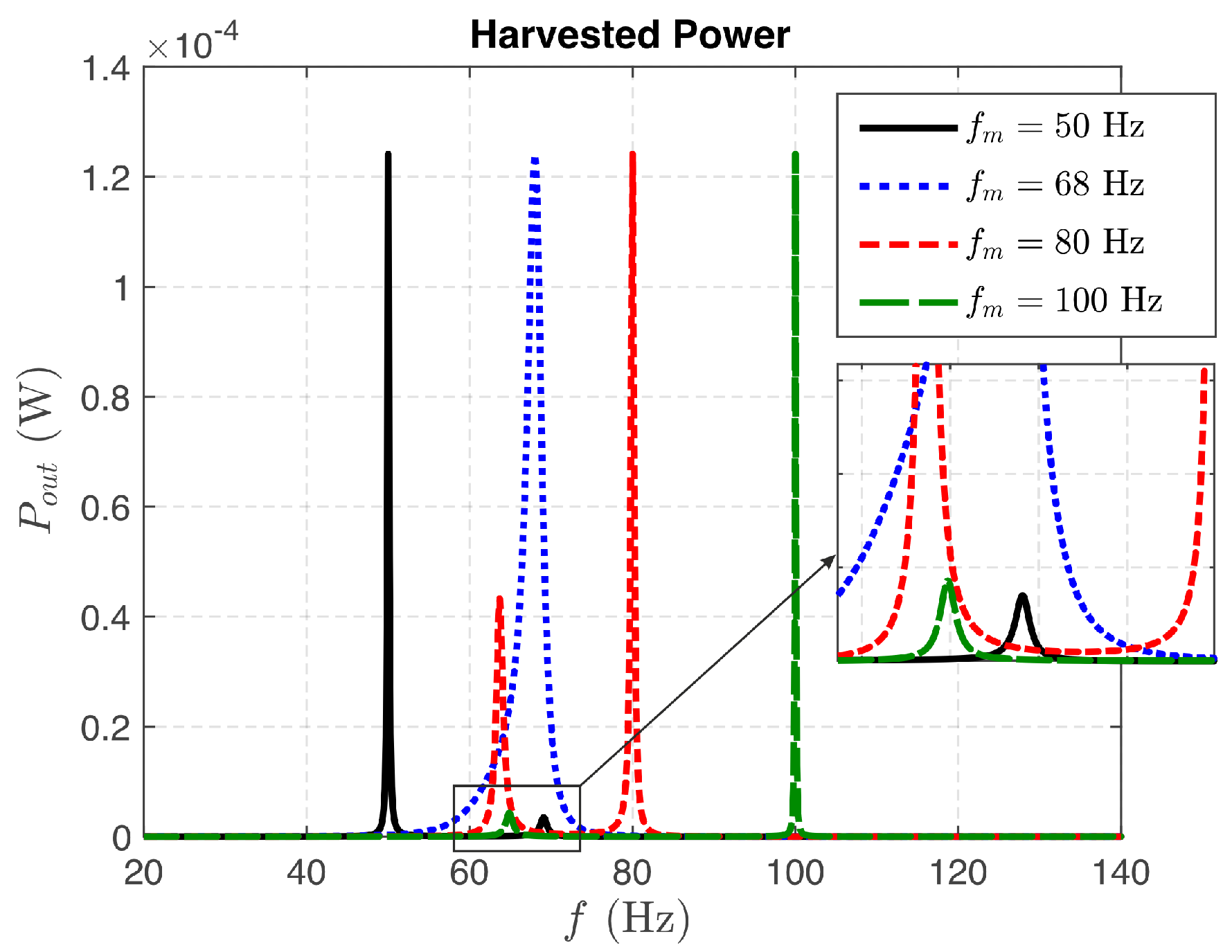
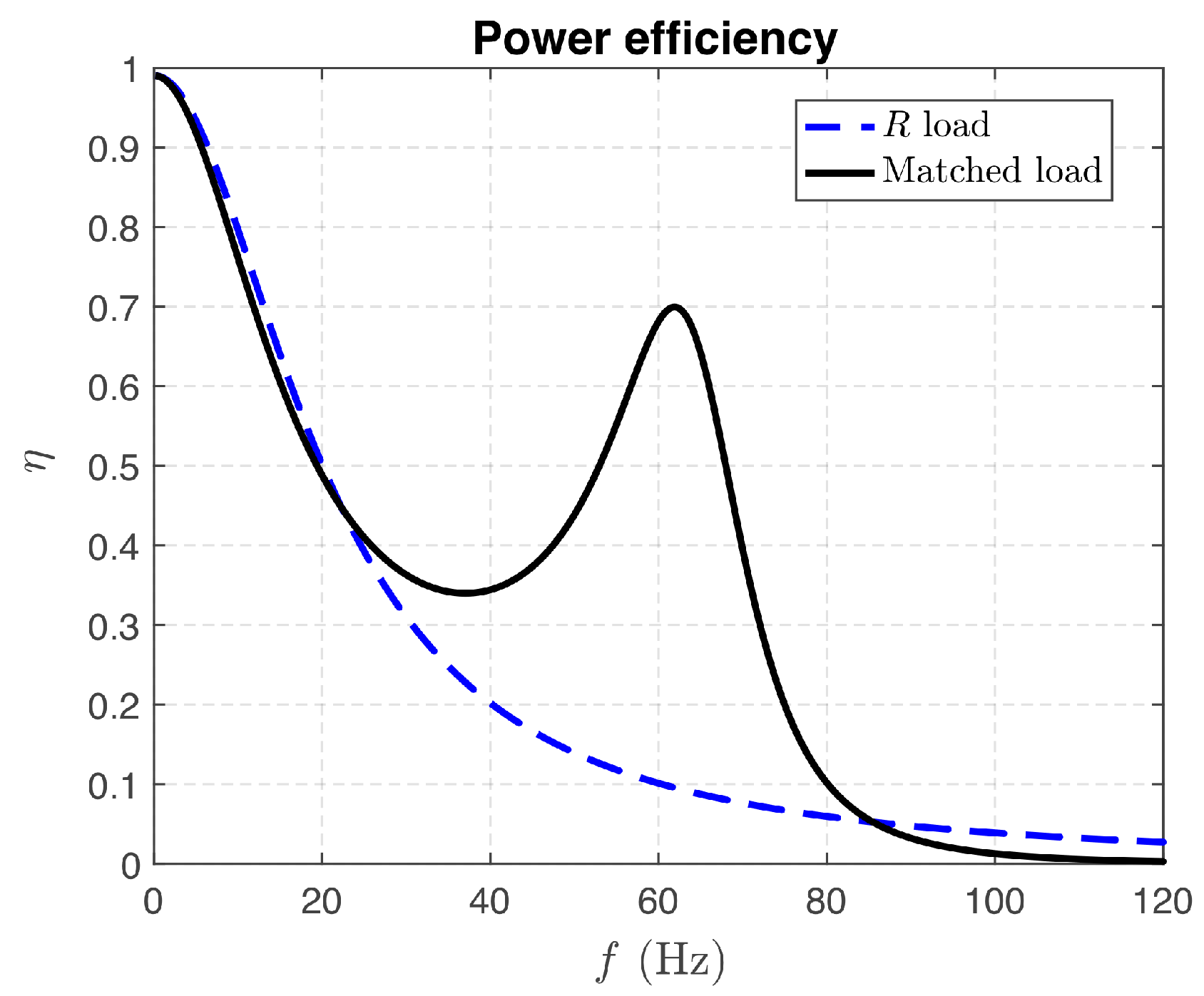

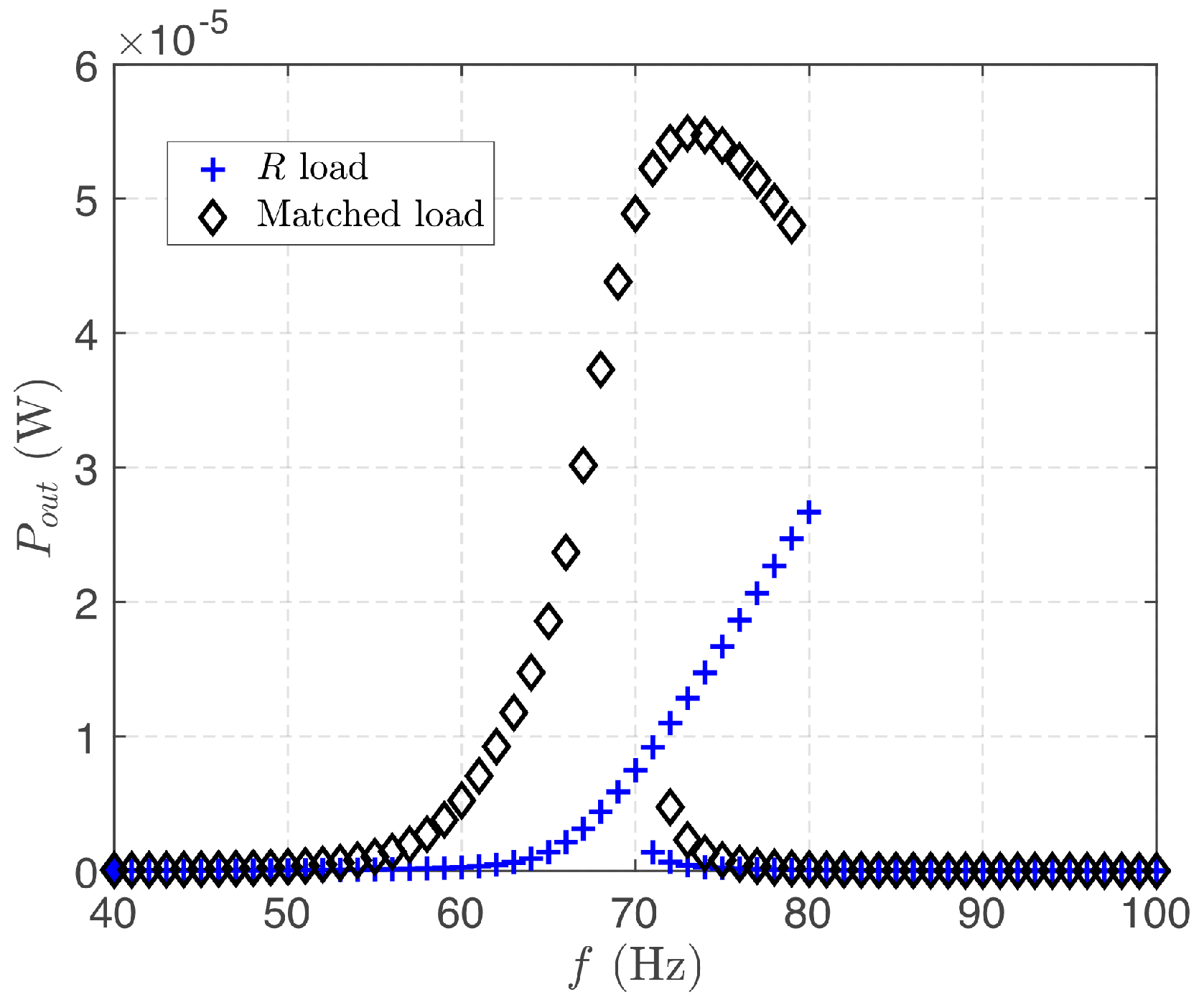
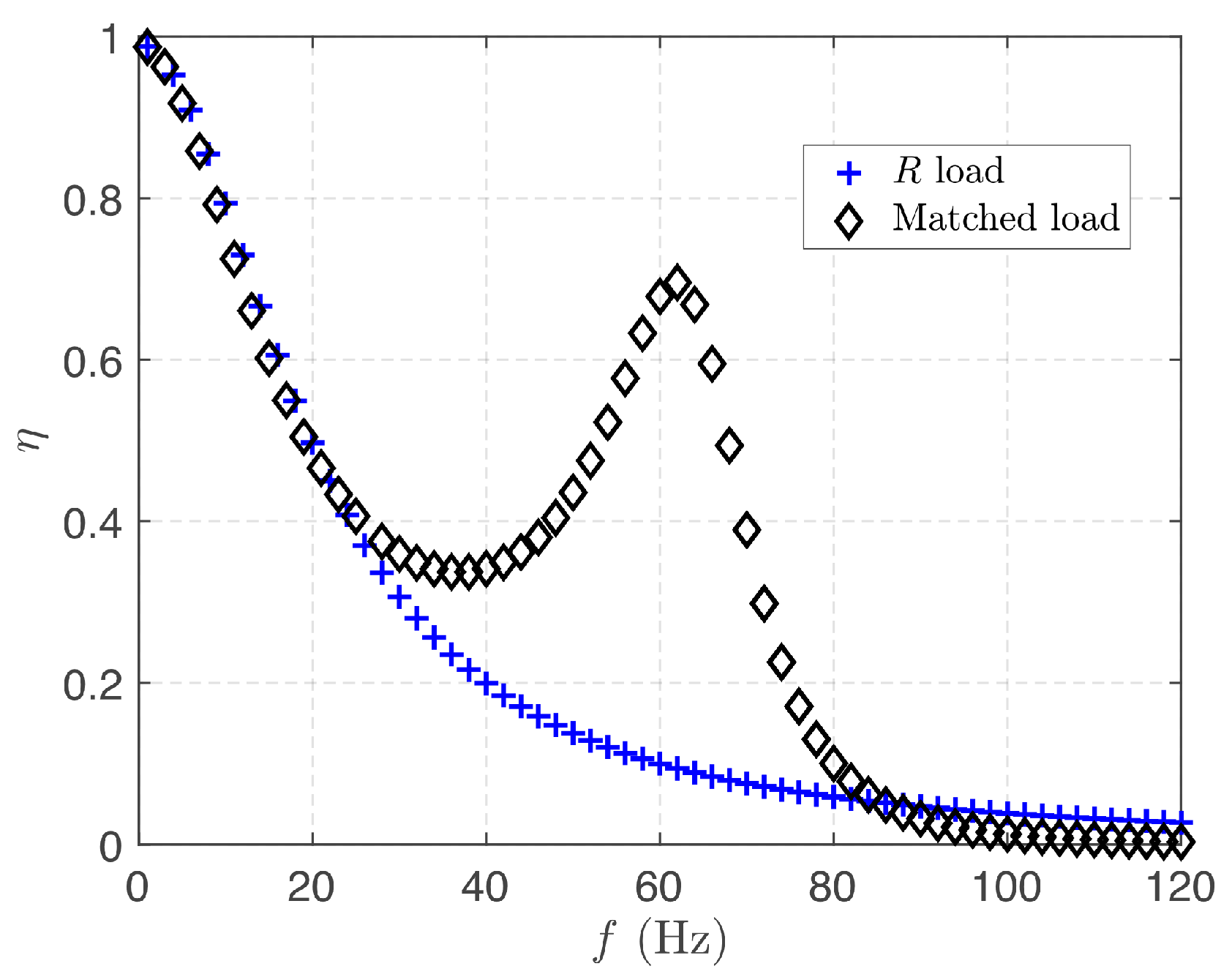
| Parameter | Value |
|---|---|
| R | 6.9366 |
| C | 5.874 F |
| L | 1 H |
| 80.08 nF | |
| 1 M | |
| n | 37.4254 |
| 83.0 mV |
| Matching Frequency | |||
|---|---|---|---|
| 50 Hz | 112.5157 H | 34.7505 H | 291.53 nF |
| 68 Hz | 170.3708 H | 447.9216 H | 11.764 nF |
| 80 Hz | 55.4050 H | 23.7563 H | 166.58e nF |
| 100 Hz | 32.9385 H | 6.4850 H | 390.59 nF |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonnin, M.; Traversa, F.L.; Bonani, F. An Impedance Matching Solution to Increase the Harvested Power and Efficiency of Nonlinear Piezoelectric Energy Harvesters. Energies 2022, 15, 2764. https://doi.org/10.3390/en15082764
Bonnin M, Traversa FL, Bonani F. An Impedance Matching Solution to Increase the Harvested Power and Efficiency of Nonlinear Piezoelectric Energy Harvesters. Energies. 2022; 15(8):2764. https://doi.org/10.3390/en15082764
Chicago/Turabian StyleBonnin, Michele, Fabio L. Traversa, and Fabrizio Bonani. 2022. "An Impedance Matching Solution to Increase the Harvested Power and Efficiency of Nonlinear Piezoelectric Energy Harvesters" Energies 15, no. 8: 2764. https://doi.org/10.3390/en15082764
APA StyleBonnin, M., Traversa, F. L., & Bonani, F. (2022). An Impedance Matching Solution to Increase the Harvested Power and Efficiency of Nonlinear Piezoelectric Energy Harvesters. Energies, 15(8), 2764. https://doi.org/10.3390/en15082764






