Development of a Predicting Model for Calculating the Geometry and the Characteristic Curves of Pumps Running as Turbines in Both Operating Modes
Abstract
:1. Introduction
- -
- The inability of the distribution networks to reach rural settlements. The latter were therefore forced to produce energy independently, also using inverted flow pumps.
- -
- The use of power electronics: the adjustment of the machine using inverters makes it possible to obtain acceptable efficiencies for a range of different flow rates (previously the adjustments were manual and only hydraulic).
- -
- Lower costs compared to a normal hydraulic turbine, especially for small units, below 50 kW;
- -
- Simplicity of installation and maintenance;
- -
- The wide range of models available on the market.
- -
- The absence of guide vanes, which excludes the possibility of making hydraulic adjustments;
- -
- The lower efficiency compared to a well-designed hydraulic turbine, especially in the off-design conditions;
- -
- The lack of information about the characteristic curves for the turbine, as the manufacturer of the machine supplies only those for the pump.
State of the Art
- Simple statistical correlations that aim to establish a connection between the point of better efficiency (BEP) in pump operation and that in turbine operation. In more detail, from the examination of the position of the BEP points in the pump and turbine operation, of machines for which these are known, laws are derived which can then be used to predict the location of the BEP of a new machine. For example, Child [13], Sharma [14], Alatorre [15], and Stepanoff [16] combine the best head ratio and the best flow ratio with respect to the total efficiency of the pump; Hancock [17] correlates these reports to the total efficiency of the turbine; Schmield [18] relates these relationships to the hydraulic efficiency of the pump; and Grover [19] and Hergt [20] relate these ratios to the characteristic speed of the turbine.
- The PAT performance prediction method using specific speed, where flow rate and head are expressed as a function of specific speed [21]. Different expressions of specific speeds are used, which are gradually refined and improved to ensure better accuracy of the results. Some examples are as follows: Derakshan applied the dimensionless specific speed to obtain different relations, valid for centrifugal pumps with specific speed ns < 60 [22]; Nautiyal proposed an additional parameter through which it is possible to obtain the trend of the prevalence and the flow rate [23]; Singh proposed a correlation based on experimentation performed on a sample of 13 pumps and subsequently applied it to the pump under examination, thus obtaining the relationship between the specific speed in turbine operation and that in pump operation [24]; Tan, by testing the hydraulic performance of centrifugal pumps, used both in direct and reverse operation, obtained different linear relationships between the pump and turbine parameters [25]; Stefanizzi established a relationship between specific speed under pump and turbine mode, based on data obtained from the performance of 27 pumps, and subsequently it used to predict the performance of 11 new PATs [26].
- Empirical correlations: Derakshan’s [27] methodology proposes head–flow and power–flow polynomial curves, interpolated on the available PAT sample. These polynomials are dimensionless based on the values of the flow rate, head, and power of the PAT at the BEP and can be used in a universal way for predicting the curves of head, power, and efficiency versus flow rate for any machine.
- One-dimensional model: Venturini [28] developed a prediction model based on the physics of the machine and consisting in the use of loss coefficients and specific parameters, through an optimization procedure, which is applied to the machine operating as a pump and subsequently as a turbine.
- Numerical analysis and CFD, for axial flow centrifugal pumps, which allow reconstructing, through a structured step-by-step methodology, the characteristic curve in pump mode, and subsequently in turbine mode, and predicting the behavior of the fluid inside the turbomachinery [29].
- For commercial centrifugal radial flow pumps, through computer numerical simulations, a methodology has been developed that makes it possible to predict the characteristic curves, in both operating modes, with errors of less than 10% compared to the mathematical model [30]. The operating conditions of the site are then obtained, providing a methodology that allows the choice of the most suitable turbomachine to obtain electricity in those areas that do not have access to it, exploiting small hydroelectric resources.
2. Materials and Methods
2.1. Fluid Dynamic Model
2.1.1. Pump Operation
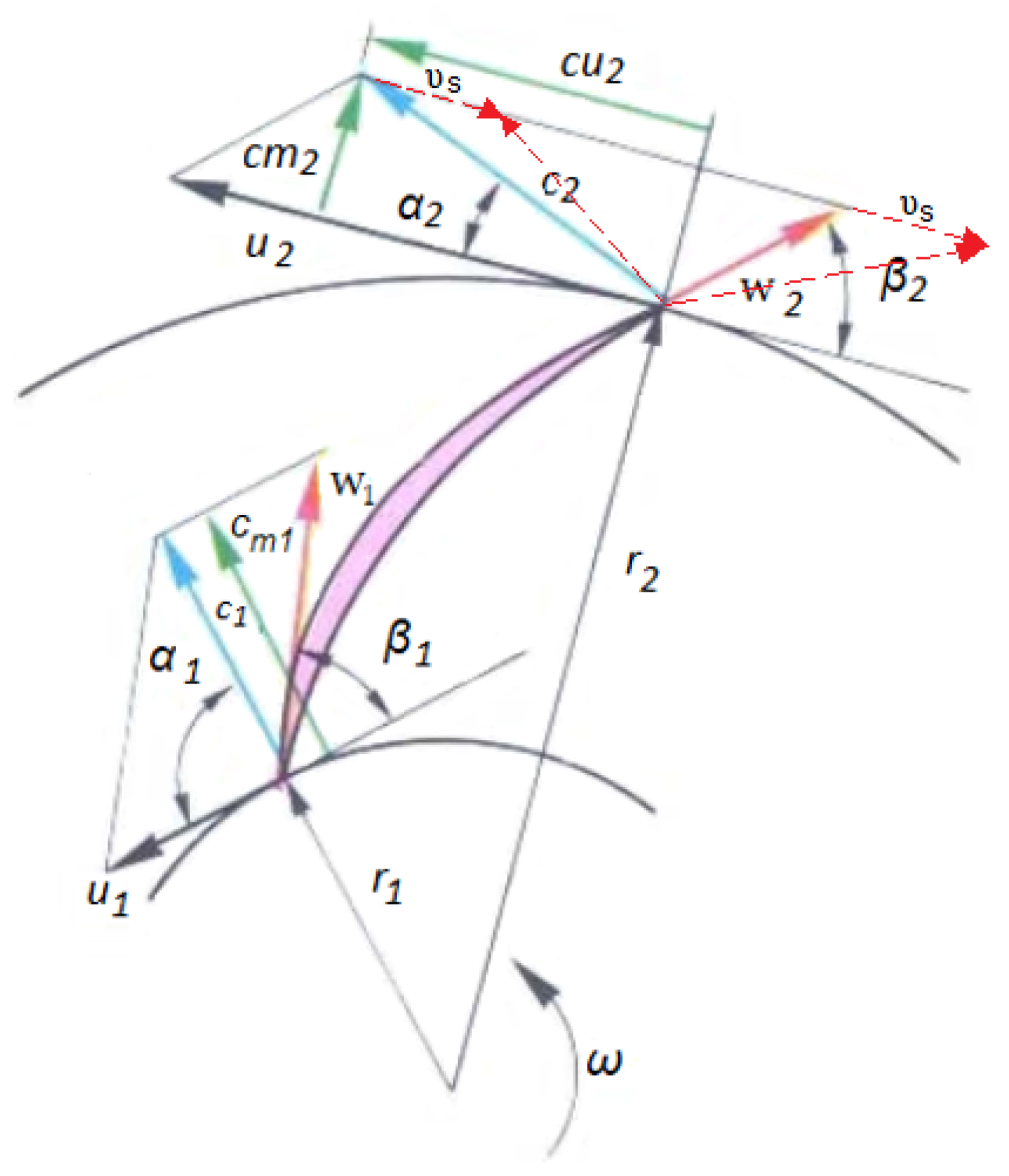
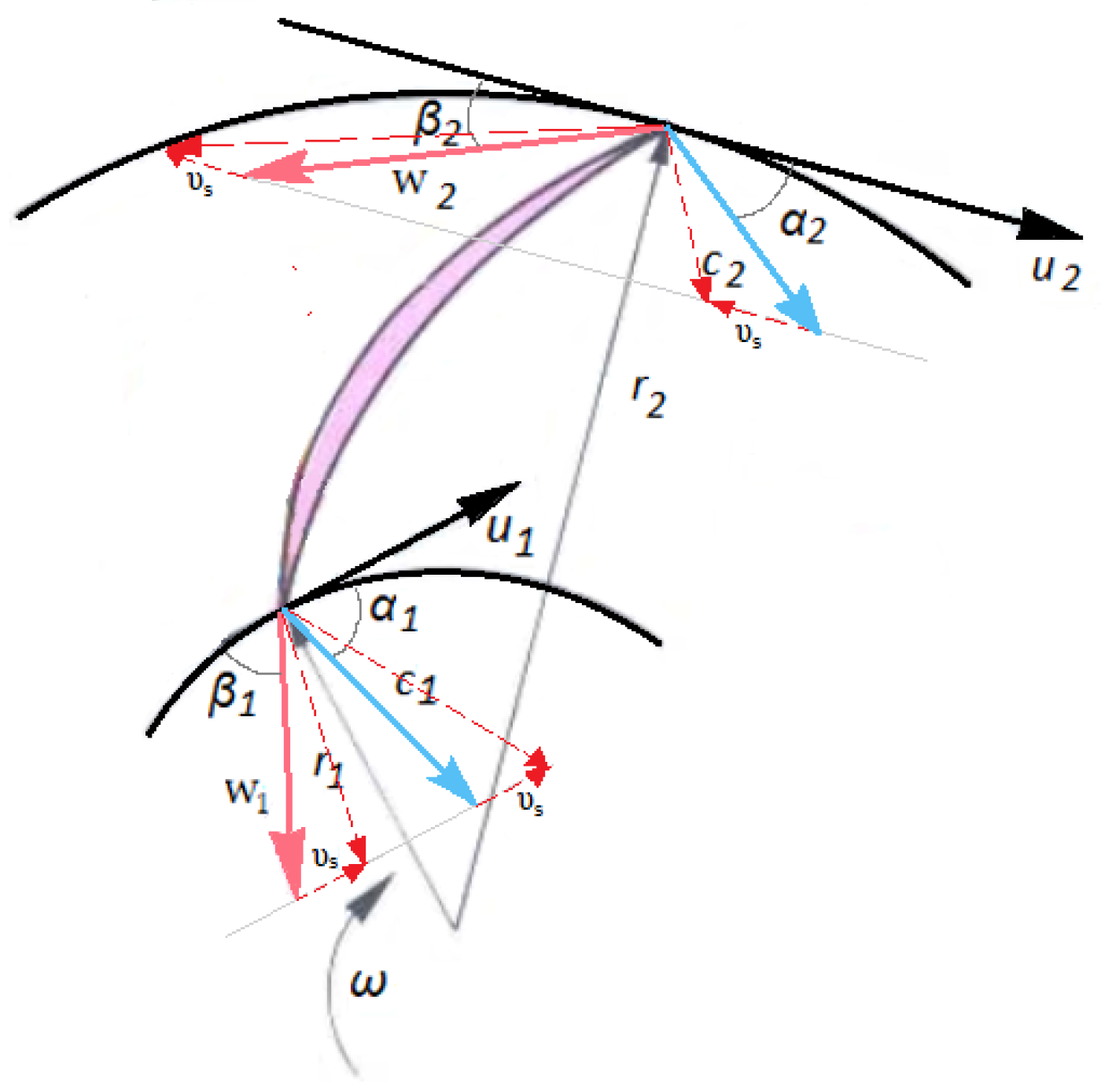
Velocity Triangles
- -
- Stodola [37,38] assumes that the motion of the fluid at the exit of the impeller is the sum of a main flow, which is guided by the blades, and of a vortex, having a rotation speed equal in modulus but in the opposite direction to that of the impeller. The diameter to which this vortex refers corresponds to the minimum passage section at the exit of the impeller.
- -
- -
- Busemann [39,40] considered radial impellers having thick blades in an infinitesimal logarithmic spiral, which transforms into a rectilinear array made of infinite foil profile planes of infinitesimal thickness. Furthermore, he assumed that the upstream machine elements downstream of the rotor are sufficiently distant to have no effect on the behavior of the fluid in the mobile blade.
- -
- Qiu, Mallikarachchi, and Anderson [41,42], who analyzed the various computation models of the slip factor present in the literature, realized their application limits. Based on this analysis procedure, they obtained a unitary formulation of the slip coefficient, which considers both the geometry of the impeller and the flow conditions. This model was derived from the studies of Eckardt [43], who believed that the rotation speed of the vortex was not equal to the rotation speed of the impeller but depended on the blade load, that is, the difference in relative speed between the face under pressure and that in the blade depression.
- -
- -
- Wiesner carried out an in-depth study on the correlations that existed in the literature in that year (1967) to verify which was the most reliable and which provided results as close as possible to those obtained experimentally. From this study, he found that Busemann’s correlation [39,40] is the most reliable if applied to pumps with centrifugal impellers.
Hydraulic Losses
2.1.2. Turbine Operation
Velocity Triangles
- -
- Inlet: For the calculation of the velocities, reference is made to their average value.
- -
- Volute: For this component, a free vortex distribution is hypothesized, and this assumption is confirmed in the experimental analyses carried out by some researchers.
- -
Hydraulic Losses
2.2. Geometric Model
- -
- Flow rate and head relative to the best efficiency conditions (Q, Hm);
- -
- Rotational speed at which the machine must work (n);
- -
- Head at the shut-off (Hmo);
- -
- Absorbed power at the point of best efficiency (Pe);
- -
- Height of the machine (h2);
- -
- External diameter of the impeller (d2).
2.2.1. Calculation of the Shaft Diameter
2.2.2. Sizing of the Inlet Section
- -
- The blade tip diameter, d1p, is obtained through an interpolation function, of order two, which correlates the blade tip diameter with the specific speed, that is
- -
- The internal diameter of impeller inlet d1m is assumed with design criteria, considering that the shaft must be housed in the impeller hub. It is determined as follows:
- -
- The inlet angle of the relative velocity vector, β1p, was obtained by imposing that, in correspondence with the design conditions, the geometric angle is equal to the real angle. This evaluation of the angle of entry is aimed at minimizing, under design conditions, the losses due to shocks. For a correct evaluation of the meridian speed, both the volumetric efficiency ηv and the real transit area must be considered. The real transit area considers the overall dimension factor of the blades which in turn depends on the angle β1p. It is clear that there is a need to resort to a recursive procedure for the evaluation of β1p.
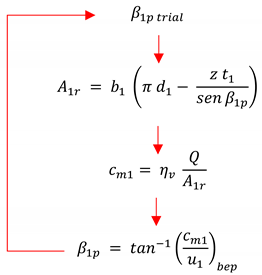
- -
- The width of the inlet blade, b1: Indicating with θ the inclination of the blade edge with respect to the radial direction, the length of the incoming blade was obtained as follows:
2.2.3. Determination of the Geometry of the Seals
2.2.4. Determination of the Number of Blades and the Angle β2p
2.2.5. Calculation of the Blade width at the Outlet
2.2.6. Sizing of the Volute
2.2.7. Sizing of the Final Diffuser
2.2.8. Impeller–Case Distance sd
2.3. Measurement of Geometric Parameters
- -
- External diameter (d1);
- -
- Eye diameter of the impeller (d2);
- -
- External blade width (b1);
- -
- Blade width at the eye of the impeller (b2);
- -
- Outflow angle relative to the external diameter (β1);
- -
- Outflow angle relative to the eye of the impeller (β2).
- -
- To calculate the exit angle β2 (angle relative to the high-pressure area), it was verified that the profile of the impeller blades in the radial plane was approximated by a logarithmic spiral, using a probe mounted in the spindle of the milling machine to reconstruct its shape. The equation of the logarithmic spiral in polar coordinates r, θ (where r is the generic radius of the profile in a radial plane and θ is the angle that this radius forms with the axis of the machine always in the radial plane) is as follows:
- -
- To determine the angle β1, it is required that in correspondence with the design conditions (BEP point) there is a correspondence between the geometric angle and the flow angle.
3. Results
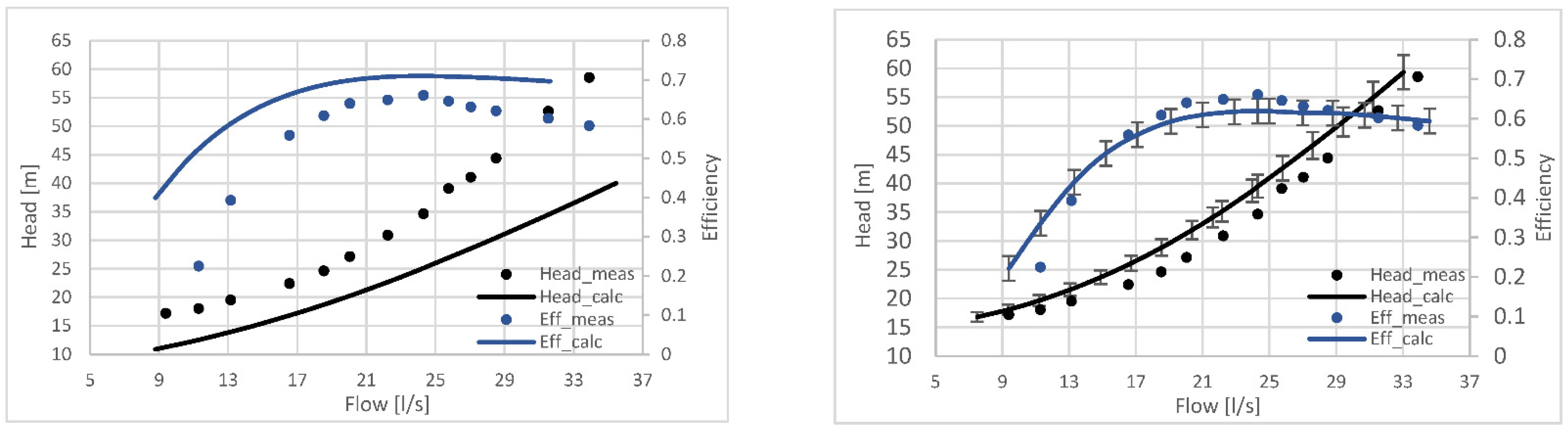
3.1. Results of the Fluid Dynamics Model
- -
- Oscillations of the rotation speed;
- -
- Instability in the torque applied to the motor shaft;
- -
- Instability in the head from the turbine or in the flow rate processed;
- -
- Cavitation due to the presence of low suction pressures;
- -
- Water hammer, which stresses both the piping system and the mechanical parts of the PAT.
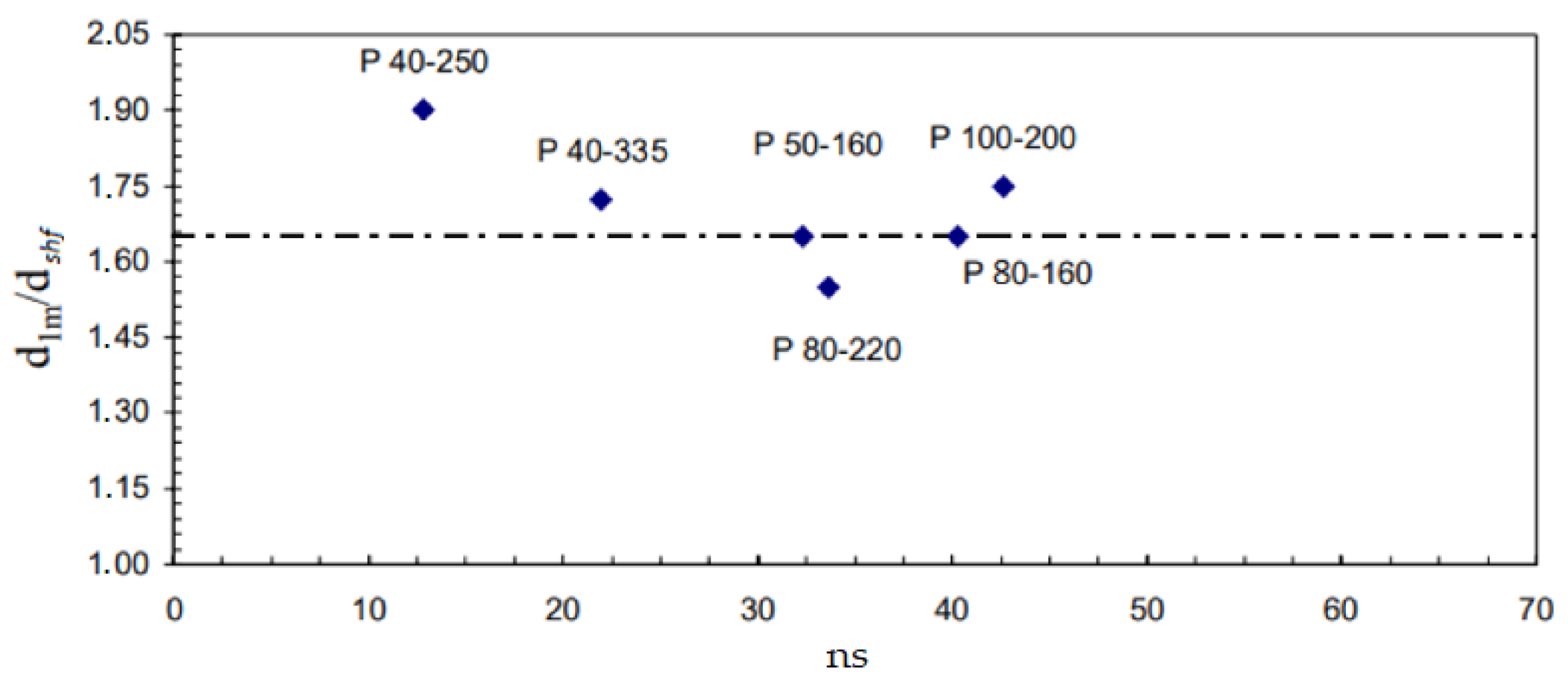
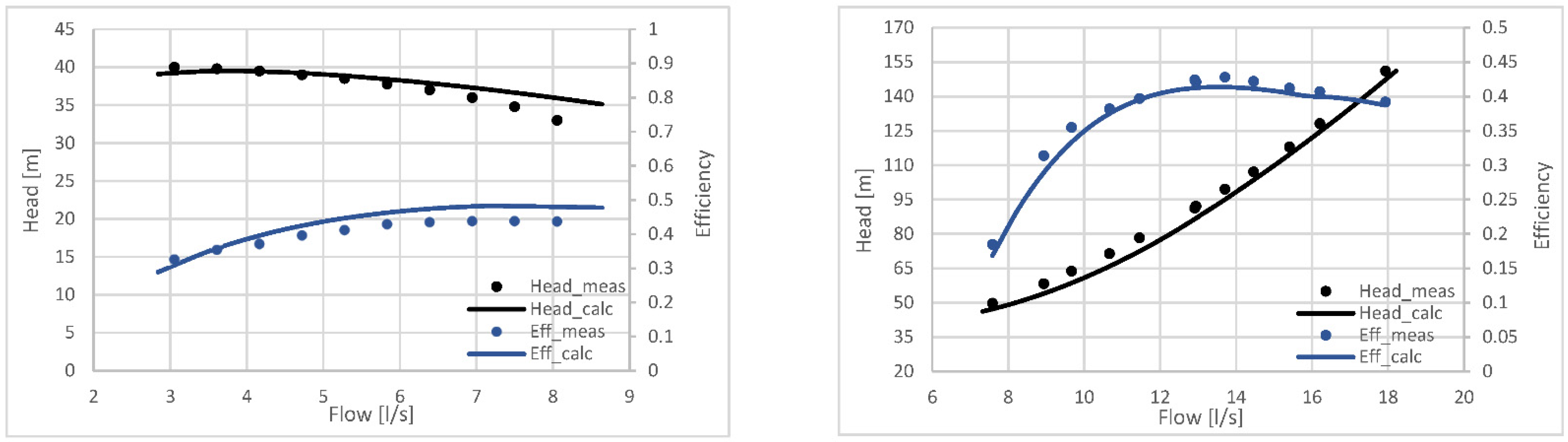
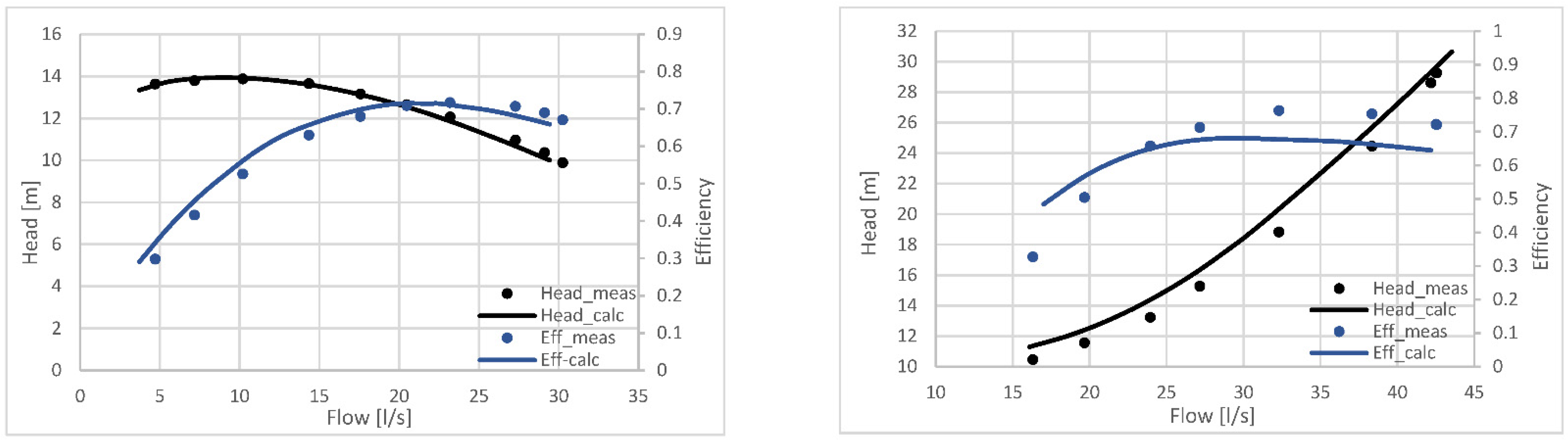
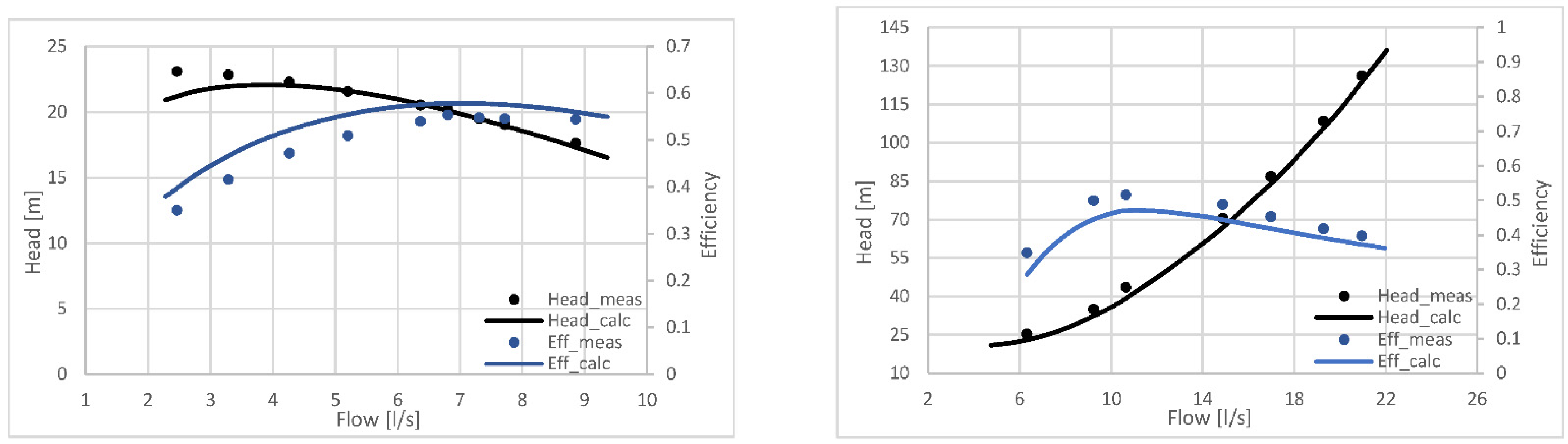
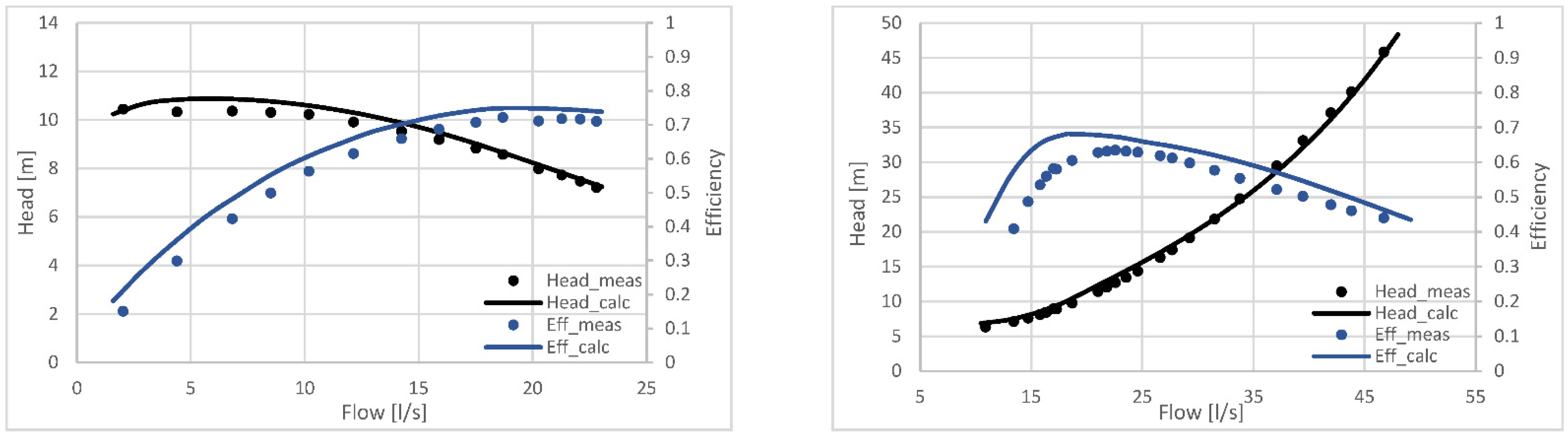
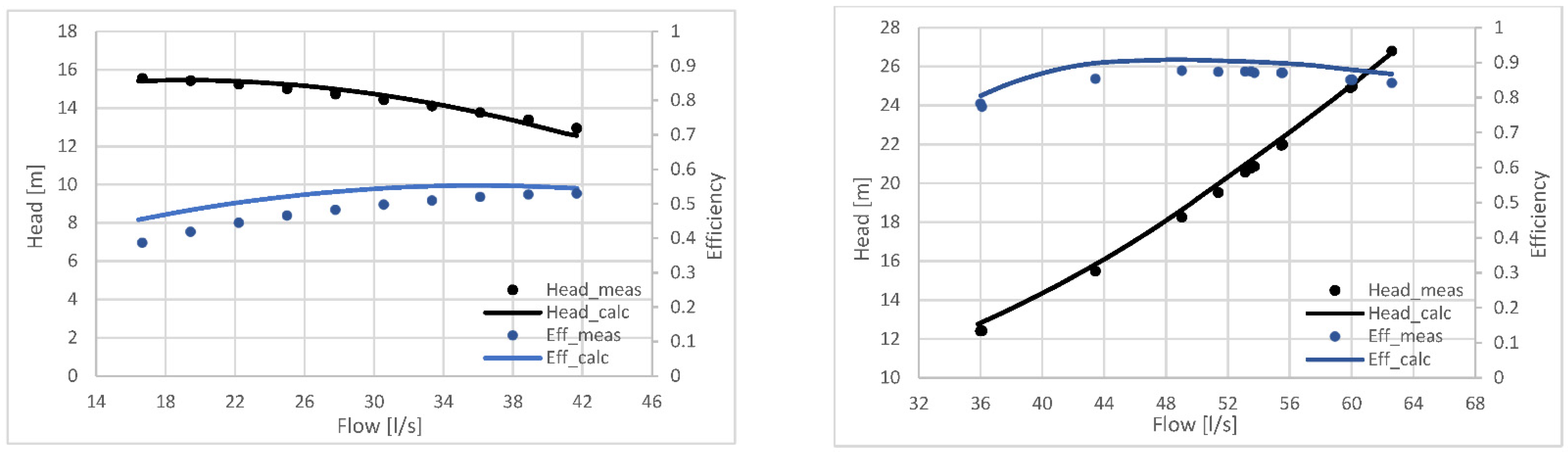
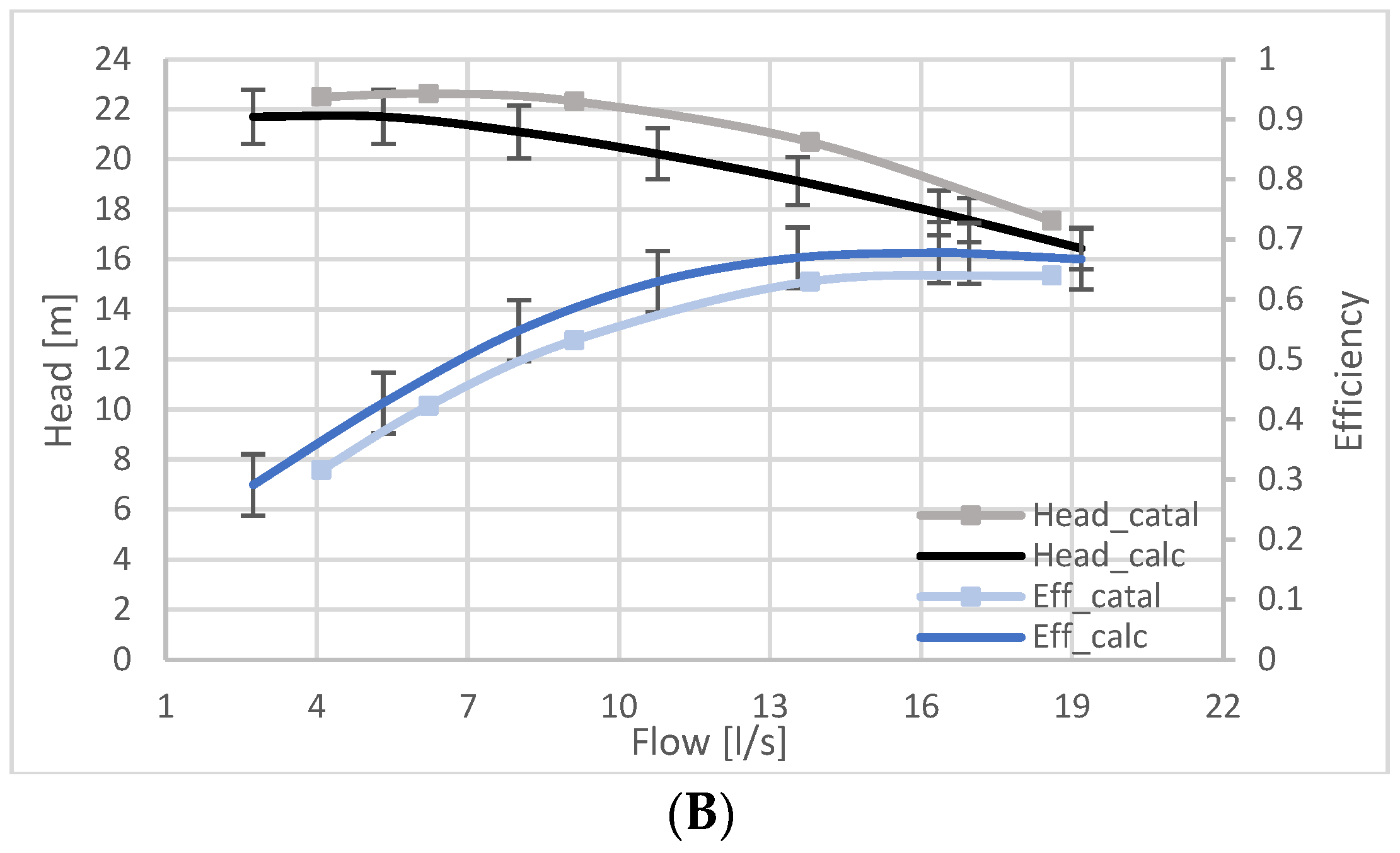
3.2. Results of the Geometric Model
4. Sensitivity Analysis
- -
- Hub diameter d1m;
- -
- Width of the blades entering the impeller b1;
- -
- Suction diameter d0;
- -
- Width and height of the volute hv, b;
- -
- Impeller exit angle β2;
- -
- Height of the blades exiting the impeller b2.
- -
- QP/T meas: flow rate to BEP measured on the bench;
- -
- QP/T calc: flow rate to the BEP calculated by the model;
- -
- HP/T meas: head at BEP measured on the bench;
- -
- HP/T calc: head at BEP calculated by the model.
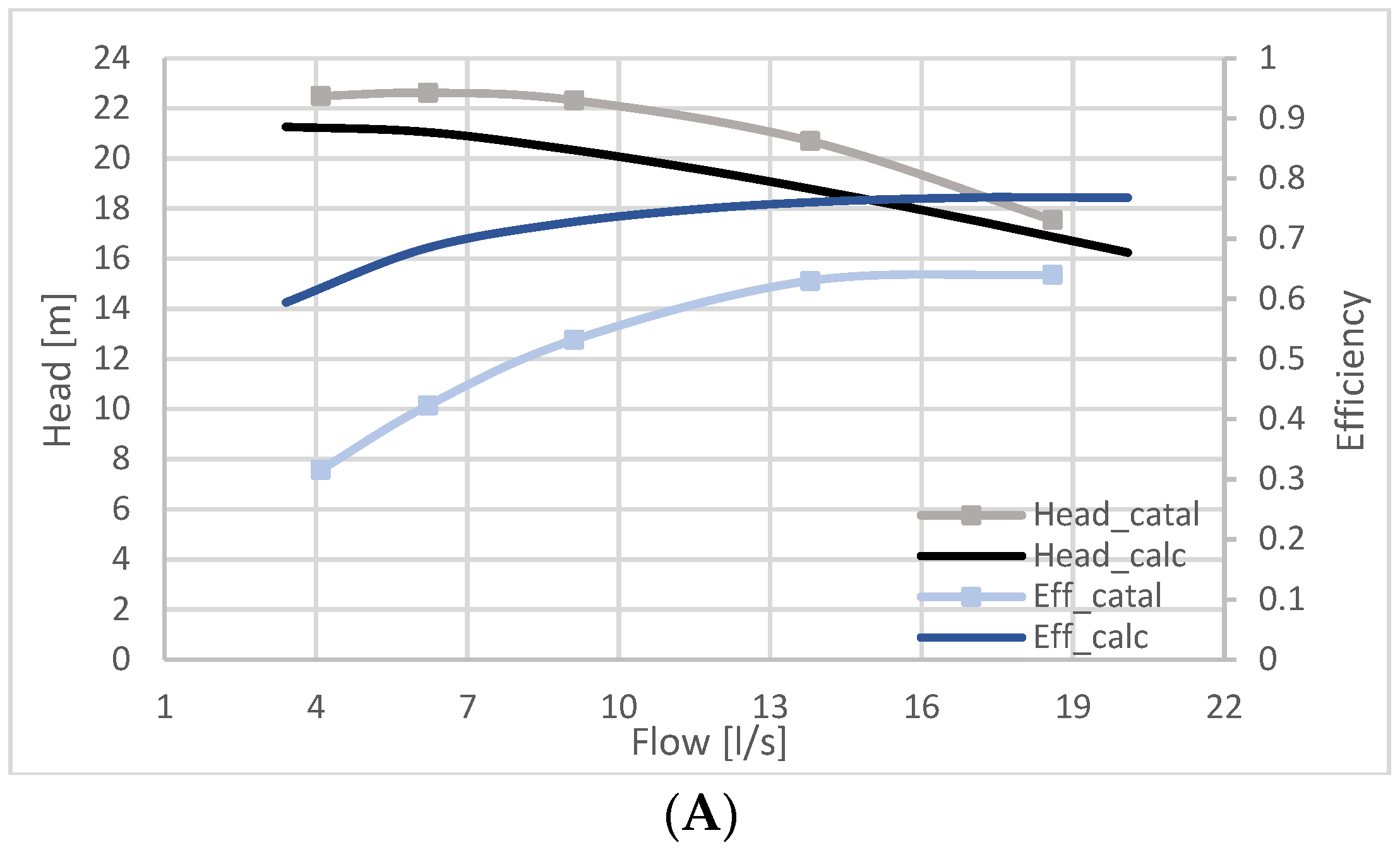
5. Procedure for Predicting the Performance of a Generic Pump
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| A | generic area |
| Ab,f | back/front leakage passage area |
| Aθmj | inlet area of the jth volute sector |
| A1, 2 | passage area at different points of the impeller |
| A1r, 2r | real passage area at different points of impeller |
| A3 | diffusion region passage area |
| A4 | volute final section area |
| A5 | final diffuser inlet passage area |
| b1, 2 | width at different points of impeller |
| b3 | vaneless diffuser width |
| b4 | final section volute width |
| b5 | final section diffuser width |
| c1, 2, 3, 4 | absolute fluid velocities at different points of PAT |
| cm1, m2, m3 | meridional velocities at different points of PAT |
| cu1, u2, u3, u4 | peripheral velocities at different points of PAT |
| cl | radial clearance of the seal |
| d | generic diameter |
| do | impeller eye diameter |
| d1, d2, d3 | diameter at different points of PAT |
| deq | equivalent hydraulic diameter |
| dshf | shaft diameter |
| df | diameter of the front seal |
| db | diameter of the rear seal |
| Eff_meas | measured efficiency |
| Eff_catal | catalog efficiency |
| Eff_calc | calculated efficiency |
| h4, 5 | heights at different points of the final diffuser |
| hv | volute throat section height |
| H | head |
| He | head at BEP of the pump |
| Hm | real head |
| Head_meas | measured real head |
| Head_catal | catalog real head |
| Head_calc | calculated real head |
| Hmo | head at the shut-off |
| Hth | theoretical head (Euler’s head) |
| HBEP | head at BEP of the PAT |
| Kv | volute velocity coefficient |
| Ld | diffuser length |
| n | rotational speed |
| ns | characteristic speed |
| sd | clearance between the impeller and the case |
| P | power |
| Pe | maximum pump power |
| Q | flow rate |
| Qe | flow rate at BEP of the pump |
| Qs | leakage flow |
| QBEP | flow rate at BEP of the PAT |
| R4 | final section volute radius |
| t1, 2 | vane thickness |
| u1, 2 | peripheral velocities at different points of impeller |
| wu1, u2 | peripheral components of relative velocity |
| wm1, m2 | meridional components of relative velocity |
| w∞ | average relative velocity |
| z | number of blades |
| Greek letters | |
| α2 | absolute flow angle in the vaneless diffuser |
| αd | final diffuser opening angle |
| β | inclination of relative flow to peripheral direction |
| β1f, 2f | relative flow direction |
| β1p, 2p | blades angles at different points of impeller |
| ΔScl | lateral surface area |
| ΔSinn | increment of inner wall surface |
| ΔScp | increment of peripheral volute surface |
| z | dynamic loss coefficient |
| η | efficiency |
| ηcalc | calculated efficiency |
| ηH | hydraulic efficiency |
| ηD | disc efficiency |
| ηv | volumetric efficiency |
| ηtot | total efficiency |
| ηmeas | measured efficiency |
| θ | inclination of blade to radial direction |
| λ | friction coefficient |
| λj | friction coefficient of a segment of volute |
| μ | leakage flow coefficient |
| υ | kinematic viscosity |
| ξ1, 2 | vanes blockage factor |
| ξd | localized drag coefficient |
| ρ | density of water |
| τa | torsional stress |
| ϕ | capacity coefficient |
| ω | angular velocity |
References
- Williams, A.A. Pumps as Turbines a User’s Guide; Intermediate Technology Publications: Bradford, UK, 1995. [Google Scholar] [CrossRef]
- Barbarelli, S.; Amelio, M.; Florio, G. Experimental activity at test rig validating correlations to select pumps running as turbines in microhydro plants. Energy Convers. Manag. 2017, 149, 781–797. [Google Scholar] [CrossRef]
- Thoma, D.; Kittredge, C. Centrifugal pumps operated under abnormal conditions. J. Power Sources 1931, 73, 881–884. [Google Scholar]
- Patelis, M.; Kanakoudis, V.; Gonelas, K. Pressure management and energy recovery capabilities using Pats. Procedia Eng. 2016, 162, 503–510. [Google Scholar] [CrossRef]
- Lima, G.M.; Luvizotto, E., Jr.; Brentan, B.M. Selection of Pumps as Turbines Substituting Pressure Reducing Valves. Procedia Eng. 2017, 186, 676–683. [Google Scholar] [CrossRef]
- Barbarelli, S.; Amelio, M.; Florio, G.; Scornaienchi, N.M. Procedure Selecting Pumps Running as Turbines in Micro Hydro Plants. Procedia Eng. 2017, 126, 549–556. [Google Scholar] [CrossRef]
- Barbarelli, S.; Nastasi, B. Tides and Tidal Currents—Guidelines for Site and Energy Resource Assessment. Energies 2021, 14, 6123. [Google Scholar] [CrossRef]
- Barbarelli, S.; Florio, G.; Amelio, M.; Scornaienchi, N.M. Preliminary performance assessment of a novel onshore system recovering energy from tidal currents. Appl. Energy 2018, 224, 717–730. [Google Scholar] [CrossRef]
- Agarwal, T. Review of pump as turbine (PAT) for micro-hydropower. Int. J. Emerg. Technol. Adv. Eng. 2012, 2, 163–169. [Google Scholar]
- Williams, A.A. Pumps as turbines for low-cost micro hydro power. Renew. Energy 1996, 9, 1227–1234. [Google Scholar] [CrossRef]
- Barbarelli, S.; Florio, G.; Scornaienchi, N.M. Developing of a Small Power Turbine Recovering Energy from low Enthalpy Steams or Waste Gases: Design, Building and Experimental Measurements. Therm. Sci. Eng. Prog. 2018, 6, 346–354. [Google Scholar] [CrossRef]
- Barbarelli, S.; Florio, G.; Zupone, G.L.; Scornaienchi, N.M. First techno-economic evaluation of array configuration of self-balancing tidal kinetic turbines. Renew. Energy 2018, 129, 183–200. [Google Scholar] [CrossRef]
- Childs, S.M. Convert pumps to turbines and recover HP. Hydrocarb. Process. Pet. Refin. 1962, 41, 173–174. [Google Scholar]
- Sharma, K.R. Small Hydroelectric Project-Use of Centrifugal Pumps as Turbines; Kirloskar Electric Co.: Bangalore, India, 1985. [Google Scholar]
- Alatorre-Frenk, C.; Thomas, T.H. The pumps as Turbine’s approach to small hydropower. In Proceedings of the World congress on Renewable energy, Reading, UK, 23–28 September 1990. [Google Scholar]
- Stepanoff, A.J. Centrifugal and Axial Flow Pumps; John Wiley: New York, NY, USA, 1957; p. 276. [Google Scholar]
- Hancock, J.W. Centrifugal pumps or water turbine. Pipeline News 1963, 6, 25–27. [Google Scholar]
- Schmield, E. Serien-Kreiselpumpen im Turbinenbetrieb; Pumpentagung: Karlsruhe, Germany, 1988. [Google Scholar]
- Grover, K.M. Conversion of Pump to Turbines; GSA Inter Corp.: Katonah, NY, USA, 1980. [Google Scholar]
- Lewinsky-Kesslitz, H.P. Pumpen als Turbinen fur Kleinkraftwerke. Wasserwirtschaft 1987, 77, 531–537. [Google Scholar]
- Liu, M.; Tan, L.; Cao, S. Performance Prediction and Geometry Optimization for Application of Pump as Turbine: A Review. Front. Energy Res. 2022, 9, 818118. [Google Scholar] [CrossRef]
- Derakhshan, S.; Nourbakhsh, A. Experimental Study of Characteristic Curves of Centrifugal Pumps Working as Turbines in Different Specific Speeds. Exp. Therm. Fluid Sci. 2008, 32, 800–807. [Google Scholar] [CrossRef]
- Nautiyal, H.; Kumar, A.; Yadav, S. Experimental Investigation of Centrifugal Pump Working as Turbine for Small Hydropower Systems. Energy Sci. Technol. 2011, 1, 79–86. [Google Scholar]
- Singh, P.; Nestmann, F. Internal Hydraulic Analysis of Impeller Rounding in Centrifugal Pumps as Turbines. Exp. Therm. Fluid Sci. 2011, 35, 121–134. [Google Scholar] [CrossRef]
- Tan, X.; Engeda, A. Performance of Centrifugal Pumps Running in Reverse as Turbine: Part Ⅱ-Systematic Specific Speed and Specific Diameter Based Performance Prediction. Rev. Energy 2016, 99, 188–197. [Google Scholar] [CrossRef]
- Stefanizzi, M.; Torresi, M.; Fortunato, B.; Camporeale, S.M. Experimental Investigation and Performance Prediction Modeling of a Single Stage Centrifugal Pump Operating as Turbine. Energy Procedia 2017, 126, 589–596. [Google Scholar] [CrossRef]
- Derakhshan, S.; Kasaeian, N. Optimization, Numerical, and Experimental Study of a Propeller Pump as Turbine. ASME J. Energy Resour. Technol. 2011, 136, 012005. [Google Scholar] [CrossRef]
- Venturini, M.; Manservigi, L.; Alvisi, S.; Simani, S. Development of a physics-based model to predict the performance of pumps as turbines. Appl. Energy 2018, 231, 343–354. [Google Scholar] [CrossRef]
- Penagos-Vásquez, D.; Graciano-Uribe, J.; Torres, E. Characterization of a Commercial Axial Flow PAT Through a Structured Methodology Step-by-Step. CFD Lett. 2022, 14, 1–19. [Google Scholar] [CrossRef]
- Vásquez, D.P.; Uribe, J.G.; García, S.V.; del Rio, J.S. Characteristic Curve Prediction of a Commercial Centrifugal Pump Operating as a Turbine Through Numerical Simulations. J. Adv. Res. Fluid Mech. Therm. Sci. 2021, 83, 153–169. [Google Scholar] [CrossRef]
- Graciano-Uribe, J.; Sierra, J.; Torres-López, E. Instabilities and Influence of Geometric Parameters on the Efficiency of a Pump Operated as a Turbine for Micro Hydro Power Generation: A Review. J. Sustain. Dev. Energy Water Environ. Syst. 2021, 9, 1–23. [Google Scholar] [CrossRef]
- Omidi, M.; Liu, S.J.; Mohtaram, S.; Lu, H.T.; Zhang, H.C. Improving Centrifugal Compressor Performance by Optimizing the Design of Impellers Using Genetic Algorithm and Computational Fluid Dynamics Methods. Sustainability 2019, 11, 5409. [Google Scholar] [CrossRef] [Green Version]
- Morabito, A.; Vagnoni, E.; Di Matteo, M.; Hendrick, P. Numerical investigation on the volute cutwater for pumps running in turbine mode. Renew. Energy 2021, 175, 807–824. [Google Scholar] [CrossRef]
- Nejadali, J. Analysis and evaluation of the performance and utilization of regenerative flow pump as turbine (PAT) in Pico-hydropower plants. Energy Sustain. Dev. 2021, 64, 103–117. [Google Scholar] [CrossRef]
- Barbarelli, S.; Amelio, M.; Florio, G. Predictive model estimating the performances of centrifugal pumps used as turbines. Energy 2016, 107, 103–121. [Google Scholar] [CrossRef]
- Neumann, B. The Interaction between Geometry and Performance of a Centrifugal Pump; Mechanical Engineering Publications: London, UK, 1991. [Google Scholar]
- Lobnanoff, V.S. Centrifugal Pumps–Design and Applications, 2nd ed.; Gulf Publishing Company: Houston, TX, USA, 1992. [Google Scholar]
- Stodola, A. Steam and Gas Turbines; McGraw-Hill: New York, NY, USA, 1945. [Google Scholar]
- Japikse, D.; Marscher, W.D.; Furst, R.B. Centrifugal Pump Design and Performance; Concepts ETI: Wilder, VT, USA, 1997. [Google Scholar]
- Micheli, D.; Pinamonti, P. La valutazione del fattore di scorrimento nel dimensionamento di ventilatori centrifughi a pale rovesce. In 42° Congresso Nazionale ATI; CLEUP Editore: Padova PD, Italy, 1987; Volume 2, p. III-13. [Google Scholar]
- De Bellis, V. Simulazione Monodimensionale Stazionaria e non Stazionaria di Turbocompressori per la Sovralimentazione di MCI. Napoli, 30 November 2011. Available online: http://www.fedoa.unina.it/id/eprint/8894 (accessed on 22 September 2021).
- Qiu, X.; Mallikarachchi, C.; Anderson, M. A new slip factor model for axial and radial impellers. In Turbo Expo: Power for Land, Sea, and Air; ASME: Montreal, Canada, 2007; Volume 47950, pp. 957–966. [Google Scholar]
- Eckardt, D. Flow Field Analysis of Radial and Backswept Centrifugal Compressor Impellers, Part 1: Flow Measurement using a Laser Velocimeter. In Proceedings of the Twenty-fifth Annual International Gas Turbine Conference and Exhibit and Twenty-second Annual Fluids Engineering Conference, New Orleans, LA, USA, 9–13 March 1980; (A80-36101 14-34). American Society of Mechanical Engineers: New York, NY, USA, 1979; pp. 77–86. [Google Scholar]
- Balje, O. Turbomachines; John Wiley & Sons: New York, NY, USA, 1981. [Google Scholar]
- Cristian, F. Sviluppo di una Metodologia di Progettazione Integrata per il Dimensionamento di Macchine Operatrici a Flusso Centrifugo; Università degli studi di Ferrara: Ferrara, Italy, 2012. [Google Scholar]
- Worster, R.C. The Effects of Skin Friction and Roughness on the Losses in Centrifugal Pump Volutes. BHRA Fluid Engineering Centre, Publication No. RR-557; Cranfield: Bedford, UK, 1957. [Google Scholar]
- Perdite di Carico Nelle Condotte. Available online: https://www.edutecnica.it/macchine/carico/carico.htm (accessed on 15 December 2021).
- Van den Braembussche, R.A. Flow in Radial Turbomachines; Lecture Series 1996−01; Von Karman Institute for Fluid Dynamics: Rhode Saint Genèse, Belgium, 1996. [Google Scholar]
- Rohlik, H.E. Radial Inflow Turbines. NASA SP 1975, 290, 279–306. [Google Scholar]
- Whitfield, A.; Baines, N.C. Design of Radial Turbomachines; Longman Scientific & Technical, Ltd.: Harlow, UK, 1990. [Google Scholar]
- Worster, R.C. The flow in volutes and its effect on centrifugal pump performance. Proc. ImechE 1957, 177–843. [Google Scholar] [CrossRef]
- Amelio, M.; Barbarelli, S.; Schinello, D. Review of Methods Used for Selecting Pumps as Turbines (PATs) and Predicting their Characteristic Curves. Energies 2020, 13, 6341. [Google Scholar] [CrossRef]
- Fanizzi, L. Scienza & Inquinamento: Le Perdite di Carico nei Circuiti Idraulici. ECOACQUE. 2014. Available online: http://www.ecoacque.it/phocadownload/le%20perdite%20di%20carico%20nei%20circuiti%20idraulici.pdf (accessed on 15 December 2021).
- Idel’cick, E. Memento des Pertes de Charge; Eyrolles Edition: Paris, France, 1986. [Google Scholar]

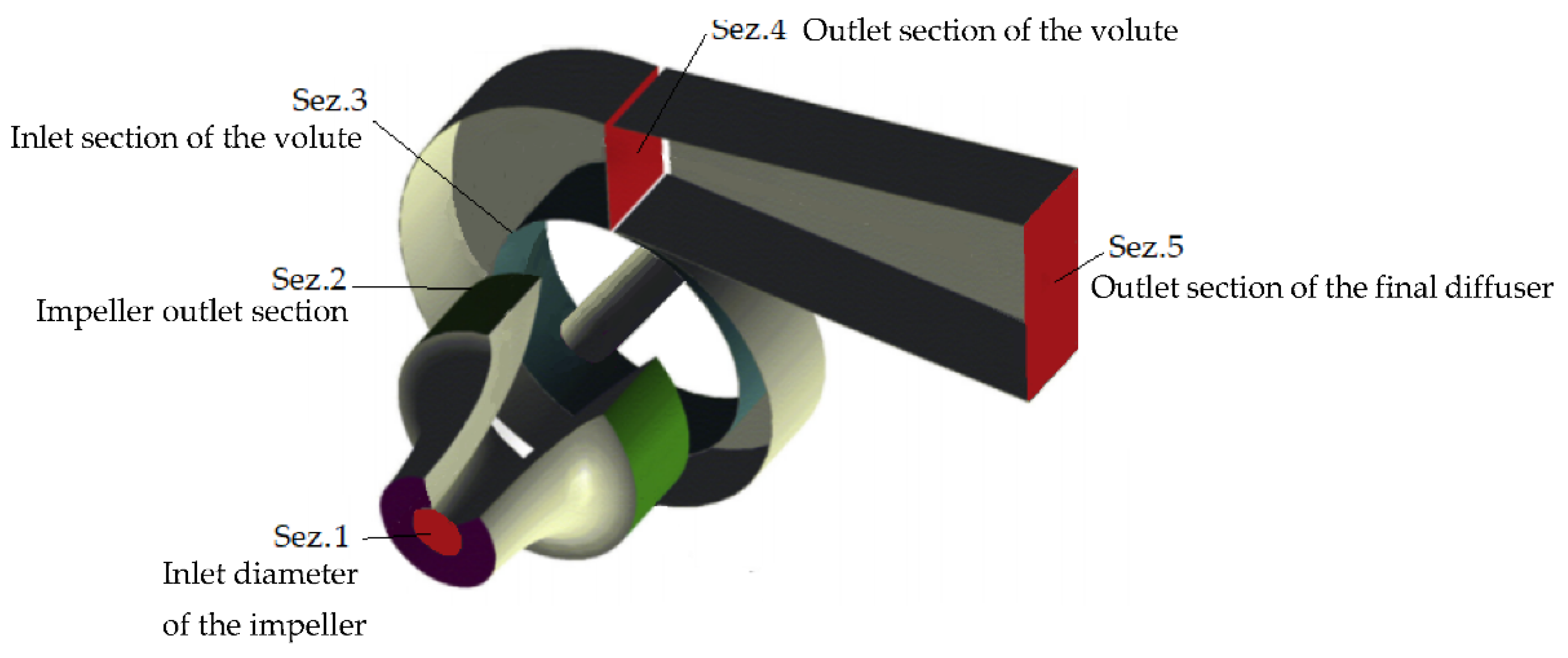


| Impeller | |
| Vaneless diffuser | |
| Volute | |
| Final diffuser |
| Inlet | ||
| Impeller | Shock losses | |
| Wake losses | ||
| Vaneless diffuser | Instantaneous expansion losses | |
| Volute | Mixing losses | |
| Final diffuser | Diffusion losses 1 | |
| Diffuser | Inlet losses | |
| Impeller | Inlet losses | |
| Shock losses 1 | ||
| Instantaneous expansion losses | ||
| Volute | Diffusion losses | |
| Outlet 2 | ||
| Pumps | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 40-335 | 40-250 | 80-220 | 50-160 | 80-160 | 100-200 | |||||||
| Meas | Calc | Meas | Calc | Meas | Calc | Meas | Calc | Meas | Calc | Meas | Calc | |
| d0 (mm) | 72.5 | 82.4 | 65 | 65.6 | 115 | 95.6 | 77.1 | 73.4 | 120 | 87.5 | 143 | 114 |
| d1m (mm) | 49.9 | 40.2 | 37.74 | 35.9 | 50 | 45.4 | 34 | 29.6 | 42 | 35 | 50 | 51 |
| d1 (mm) | 60.9 | 61.3 | 51.37 | 50.8 | 57 | 70.5 | 50 | 51.5 | 81 | 61.2 | 62 | 82.4 |
| df (mm) | 84.75 | 107.3 | 84.75 | 85.5 | 134.75 | 124.5 | 89.75 | 95.6 | 135 | 114 | 159.75 | 148.4 |
| d3 (mm) | 338 | 251.2 | 282 | 273 | 230 | 234.3 | 185 | 186.2 | 185 | 187.3 | 224 | 234.3 |
| db (mm) | 139.7 | 108.2 | 99.76 | 86.2 | 150 | 125.5 | 90 | 96.4 | 135 | 114.9 | 150 | 149.6 |
| b1 (mm) | 7.2 | 27.5 | 8.89 | 11.5 | 50 | 32.7 | 32 | 28.6 | 62 | 34.3 | 61 | 41.1 |
| b2 (mm) | 10 | 16.1 | 8 | 7.3 | 25 | 21.2 | 16 | 16.5 | 25 | 21.1 | 32.5 | 28.7 |
| b3 (mm) | 16 | 28.2 | 8 | 14.7 | 42.5 | 37.2 | 26 | 28.8 | 35 | 37 | 61 | 50.3 |
| b (mm) | 26 | 24 | 24 | 27 | 49 | 66 | 67 | 42 | 87 | 47 | 55 | 93.6 |
| β1p (°) | 20.49 | 43.83 | 38.58 | 51.9 | 17.53 | 42.75 | 26.36 | 41.38 | 23.7 | 43 | 20 | 38.97 |
| β2p (°) | 24 | 23 | 20 | 23 | 28.26 | 27 | 26 | 26 | 23.7 | 26 | 26 | 27 |
| t1 (mm) | 4 | 4 | 4 | 4 | 2 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| t2 (mm) | 4 | 4 | 4 | 4 | 2 | 4 | 4 | 4 | 5 | 4 | 4 | 4 |
| b5 (mm) | 40 | 64.2 | 89 | 52.6 | 80 | 89 | 50 | 89.9 | 84 | 63 | 89 | 114.5 |
| cl (mm) | 0.125 | 0.125 | 0.25 | 0.125 | 0.15 | 0.125 | 0.25 | 0.125 | 0.25 | 0.125 | 0.55 | 0.25 |
| sd (mm) | 7 | 9 | 17 | 9 | 9 | 9 | 21 | 9 | 9 | 9 | 15 | 9 |
| Ld (mm) | 97 | 131.5 | 98 | 95 | 90 | 170 | 102 | 93 | 137 | 136.5 | 91 | 170 |
| QP | HP | QT | HT | |
|---|---|---|---|---|
| d1m | * | *** | *** | *** |
| b1 | * | * | ** | **** |
| d0 | ** | *** | **** | **** |
| hv, b | **** | *** | *** | **** |
| b2 | ** | *** | * | * |
| b2 | ** | **** | ** | ** |
| hv, b (m) | Δ% Variation | hv, b (m) | Qp meas | Qp calc | E% | Hp meas | Hp calc | E% | QT meas | QT calc | E% | HT meas | HT calc | E% |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.024 | −5.0% | 0.023 | 26 | 25.1 | 3.6% | 35 | 29.90 | 14.7% | 49.3 | 45.9 | 7.0% | 99.5 | 109.0 | −9.5% |
| 0.024 | −2.5% | 0.023 | 26 | 26.0 | 0.0% | 35 | 30.30 | 13.5% | 49.3 | 47.3 | 4.0% | 99.5 | 105.1 | −5.6% |
| 0.024 | 0.0% | 0.024 | 26 | 26.0 | 0.0% | 35 | 31.10 | 11.1% | 49.3 | 48.8 | 1.1% | 99.5 | 101.5 | −2.0% |
| 0.024 | 2.5% | 0.025 | 26 | 27.2 | −4.6% | 35 | 31.20 | 10.9% | 49.3 | 50.2 | −1.8% | 99.5 | 98.2 | 1.4% |
| 0.024 | 5.0% | 0.025 | 26 | 28.3 | −9.0% | 35 | 31.30 | 10.6% | 49.3 | 51.7 | −4.8% | 99.5 | 95.0 | 4.5% |
| hv, b (m) | Δ% Variation | hv, b (m) | Qp meas | Qp calc | E% | Hp meas | Hp calc | E% | QT meas | QT calc | E% | HT meas | HT calc | E% |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.027 | −5.0% | 0.026 | 25 | 25.0 | 0.0% | 20 | 19.90 | 3.8% | 38.3 | 37.6 | 1.8% | 43.7 | 49.0 | −12.2% |
| 0.027 | −2.5% | 0.026 | 25 | 25.0 | 0.0% | 20 | 19.70 | 1.7% | 38.3 | 38.7 | −1.0% | 43.7 | 47.3 | −8.4% |
| 0.027 | 0.0% | 0.027 | 25 | 25.0 | 0.0% | 20 | 20.00 | 0.0% | 38.3 | 39.8 | −3.7% | 43.7 | 45.9 | −5.0% |
| 0.027 | 2.5% | 0.028 | 25 | 25.4 | −1.6% | 20 | 20.20 | −0.8% | 38.3 | 41.2 | −7.4% | 43.7 | 44.9 | −2.9% |
| 0.027 | 5.0% | 0.028 | 25 | 26.4 | −5.7% | 20 | 20.10 | −0.4% | 38.3 | 42.3 | −10.2% | 43.7 | 43.6 | 0.1% |
| hv, b (m) | Δ% Variation | hv, b (m) | Qp meas | Qp calc | E% | Hp meas | Hp calc | E% | QT meas | QT calc | E% | HT meas | HT calc | E% |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.066 | −5.0% | 0.063 | 100 | 100.0 | 0.0% | 14.4 | 14.28 | 0.8% | 123 | 117.68 | 4.3% | 20.0 | 20.7 | −3.3% |
| 0.066 | −2.5% | 0.064 | 100 | 100.0 | 0.0% | 14.4 | 14.35 | 0.3% | 123 | 120.66 | 1.9% | 20.0 | 20.2 | −1.1% |
| 0.066 | 0.0% | 0.066 | 100 | 100.0 | 0.0% | 14.4 | 14.41 | −0.1% | 123 | 122.64 | 0.3% | 20.0 | 19.6 | 1.9% |
| 0.066 | 2.5% | 0.068 | 100 | 100.0 | 0.0% | 14.4 | 14.46 | −0.4% | 123 | 124.63 | −1.3% | 20.0 | 19.1 | 4.6% |
| 0.066 | 5.0% | 0.069 | 100 | 100.0 | 0.0% | 14.4 | 14.51 | −0.8% | 123 | 126.61 | −2.9% | 20.0 | 18.6 | 7.2% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbarelli, S.; Pisano, V.; Amelio, M. Development of a Predicting Model for Calculating the Geometry and the Characteristic Curves of Pumps Running as Turbines in Both Operating Modes. Energies 2022, 15, 2669. https://doi.org/10.3390/en15072669
Barbarelli S, Pisano V, Amelio M. Development of a Predicting Model for Calculating the Geometry and the Characteristic Curves of Pumps Running as Turbines in Both Operating Modes. Energies. 2022; 15(7):2669. https://doi.org/10.3390/en15072669
Chicago/Turabian StyleBarbarelli, Silvio, Vincenzo Pisano, and Mario Amelio. 2022. "Development of a Predicting Model for Calculating the Geometry and the Characteristic Curves of Pumps Running as Turbines in Both Operating Modes" Energies 15, no. 7: 2669. https://doi.org/10.3390/en15072669
APA StyleBarbarelli, S., Pisano, V., & Amelio, M. (2022). Development of a Predicting Model for Calculating the Geometry and the Characteristic Curves of Pumps Running as Turbines in Both Operating Modes. Energies, 15(7), 2669. https://doi.org/10.3390/en15072669








