An Analytic Hierarchy Process for Selecting Battery Equalization Methods
Abstract
1. Introduction
1.1. Main Issues and Characteristics of Battery Cells
1.2. Objectives and Contributions
1.3. Related Work
2. Cell Equalization Methods
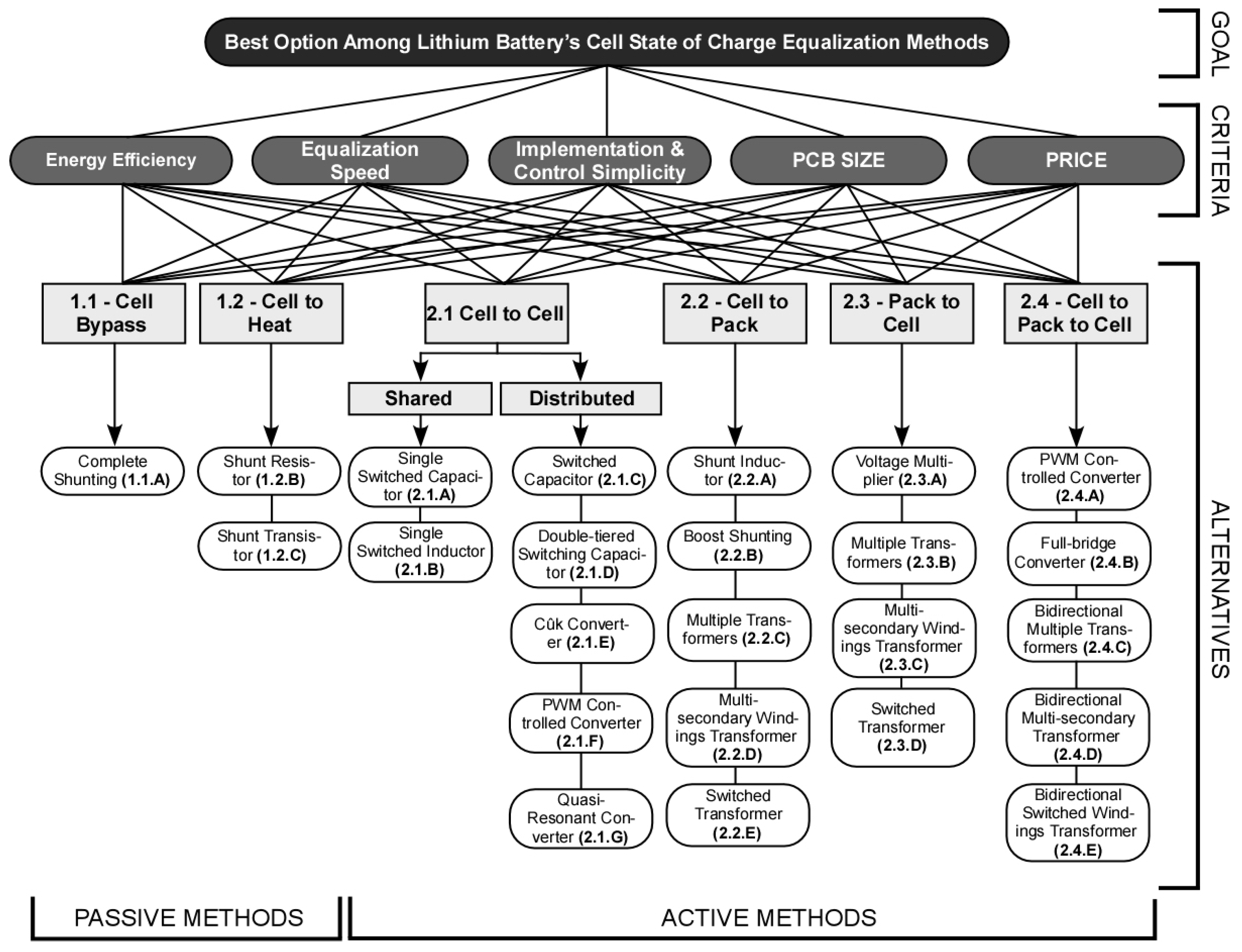
- Passive methods: [1.1] Cell Bypass (CB), [1.2] Cell-to-heat (CH);
- Active methods: [2.1] Cell-to-Cell Shared (CCS) or Distributed (CCD), [2.2] Cell-to-Pack (CP), [2.3] Pack-to-Cell (PC), and [2.4] Cell-to-Pack-to-Cell (CPC).
3. Method: Analytic Hierarchy Process
- 1.
- Define the problem and the decision that needs to be made. In the presented work, the problem consists in selecting a battery SoC equalization circuit for a given application. Next a hierarchy model is established based on an analysis of the problem. A decision hierarchy is built from the top with the decision goal, the criteria that will be used to evaluate the fulfillment of the goal, and a set of design alternatives (see Figure 1). In this work, there are five design criteria [energy efficiency , equalization speed , implementation simplicity , hardware size , and price ]; and there are 24 alternatives or methods for the SoC equalization circuit as presented in Figure 1;
- 2.
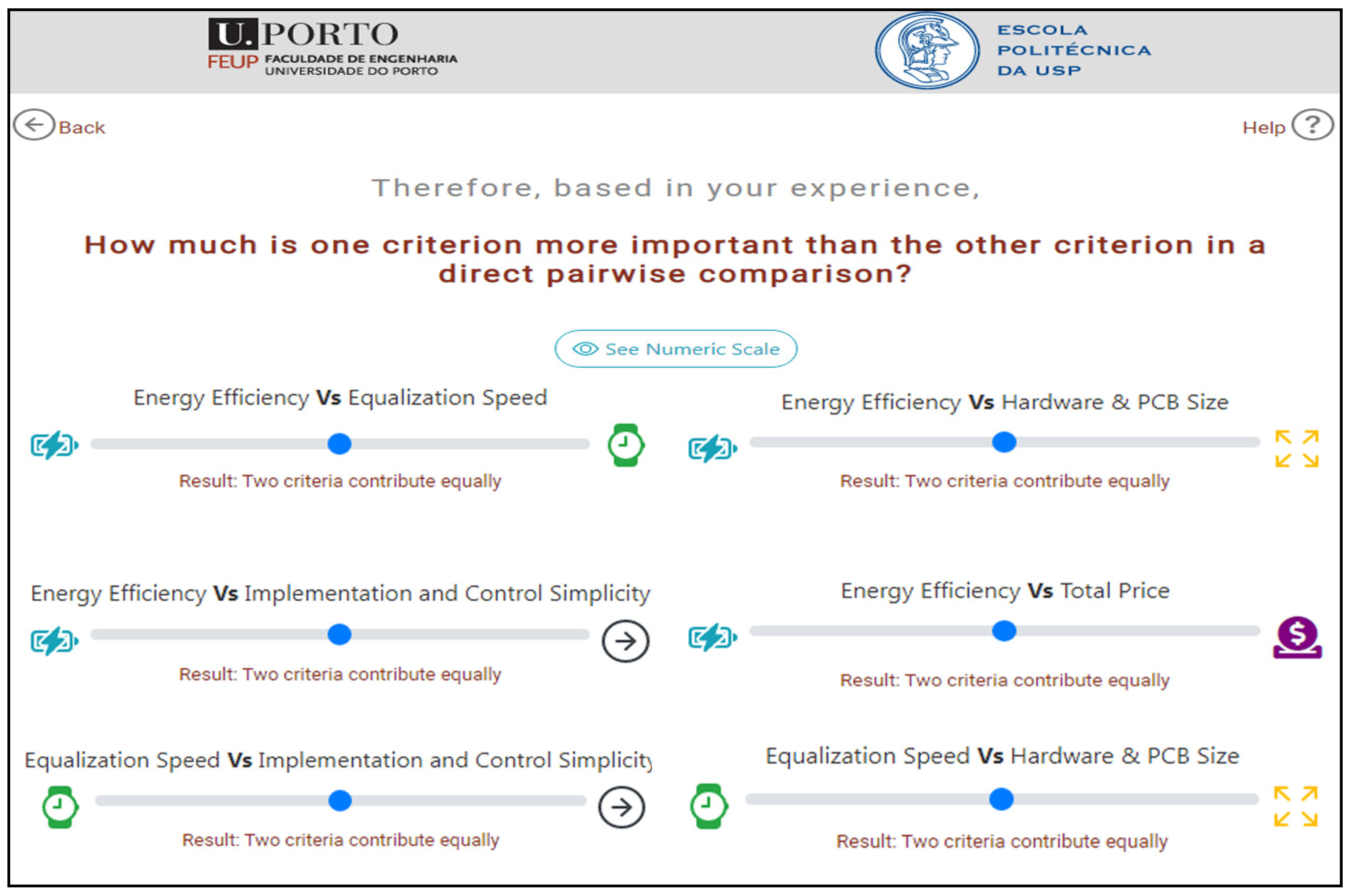
- Pairwise comparison matrices are formed among the design criteria. Each element in the pairwise comparison matrix depicts an individual judgment of the relative importance between the pair of and the design criteria using the ratio scale method shown in Table 1. In the presented work, a worldwide survey collected experts’ opinions to define this judgment. The importance between the same opposite pair, e.g., the and the factors, must be the inverse of the and the ratio scale as shown in Table 2. For example, following the scales shown in Table 1, the expert can strongly favor the price over the speed in their pairwise comparison judgment, yielding ; and ;
- 3.
- To give the relative weights of criteria, each eigenvalue of the eigenvector (λ) must be calculated using the geometric mean at the criterion data set of the pairwise comparison matrix ) formed at the previous step. Thefore, the individual components of λ, denoted , are defined as:
- 4.
- Calculate the criteria vector [] by summing the rows of :
- 5.
- Determine the weight vector . The priorities obtained from the pairwise comparison matrix ) are used to define the importance of each criterion toward the decision goal. The components of the weight vector () are proportional to :
- 6.
- Calculate the maximum eigenvalue using and the criteria vector []:
- 7.
- Compilation of the alternative matrix . Given a specific SoC equalization circuit ( 24]), each criterion () must be evaluated on a scale of 1 to 9. For this research work, the scale was defined as bigger is better for energy efficiency () and equalization speed (); and, it was defined as smaller is better for implementation effort (simplicity) (), hardware size (), and price ();
- 8.
- Normalization of the alternative matrix ( to obtain a global scale in a range of 0 to 1 for every alternative of the matrix (. The normalization techniques must be done before the values being used to calculate the AHP decision profile matrix (δ), and they must consist of dividing every entry in a vector by its magnitude to create a vector of length one known as the unit vector [32]. The normalized value for each entry is calculated as:
- 9.
- Still, from a descriptive point of view, it will be important to develop a common understanding among the criteria; and, for this purpose, sometimes an additional harmonization process is required before calculating the normalized alternative matrix (. This step should be executed only if the specific criterion ( was defined to be better as smaller per the value on the AHP scale is (see step 7). Harmonization involves improving comparability of similar measures collected by separate databases and different individuals. Thus, these criteria were first harmonized accordingly to Equation (7) and then the normalization process occurred according to Equation (8);
- 10.
- The consistency of judgments is checked. The AHP also calculates an inconsistency index to reflect the consistency of decision makers’ judgements during the evaluation phase. The consistency index (CI) and the consistency ratio (CR) are measured for each pairwise comparison matrix. CI is defined as:where and are the maximum eigenvalue and the quantity of design criteria, respectively. The judgment is consistent only if ; otherwise, the judgment should be revised. The CR is defined as:where is a set of given average random consistency indices—given by [38] and illustrated at Table 3, which is an index whose value varies according to the quantity of design criteria defined for AHP, and it can be obtained using statistical calculations [36]. If is no larger than 10%, the inconsistency of judgments is acceptable. Otherwise, the judgments need to be revised [39];
- 11.
- Finally, as Equation (11) demonstrates, the AHP decision profile matrix (δ) can be calculated as the sum of products between the normalized alternative matrix ( and the weight vector calculated at step 5.
4. Results and Discussion
- We considered a road vehicle with 100 lithium iron phosphate cells in series with a total nominal voltage of 320 V, a common battery pack configuration used in today’s electric vehicles;
- Every SoC equalization method should be able to transfer or dissipate up to 10 Ah of electric charge between the cells or the battery pack;
- The price and the PCB Size criteria will be calculated equally between all methods according to assumptions 1 and 2 above.
4.1. Survey
- () Implementation and Control Simplicity VS. () Hardware and PCB Size;
- () Implementation and Control Simplicity VS. () Total Price;
- () Energy Efficiency VS. () Implementation and Control Simplicity;
- () Energy Efficiency VS. () Hardware and PCB Size;
- () Energy Efficiency VS. () Total Price;
- () Energy Efficiency VS. () Equalization Speed;
- () Hardware and PCB Size VS. () Total Price;
- () Equalization Speed VS. () Implementation and Control Simplicity;
- () Equalization Speed VS. () Hardware and PCB Size;
- () Equalization Speed VS. () Total Price.
4.2. Hardware Size () and Price () Alternative Matrix
4.3. Alternative Matrix Normalization
4.4. Overall Comparison—Decision Profile Matrix
4.5. Discussion
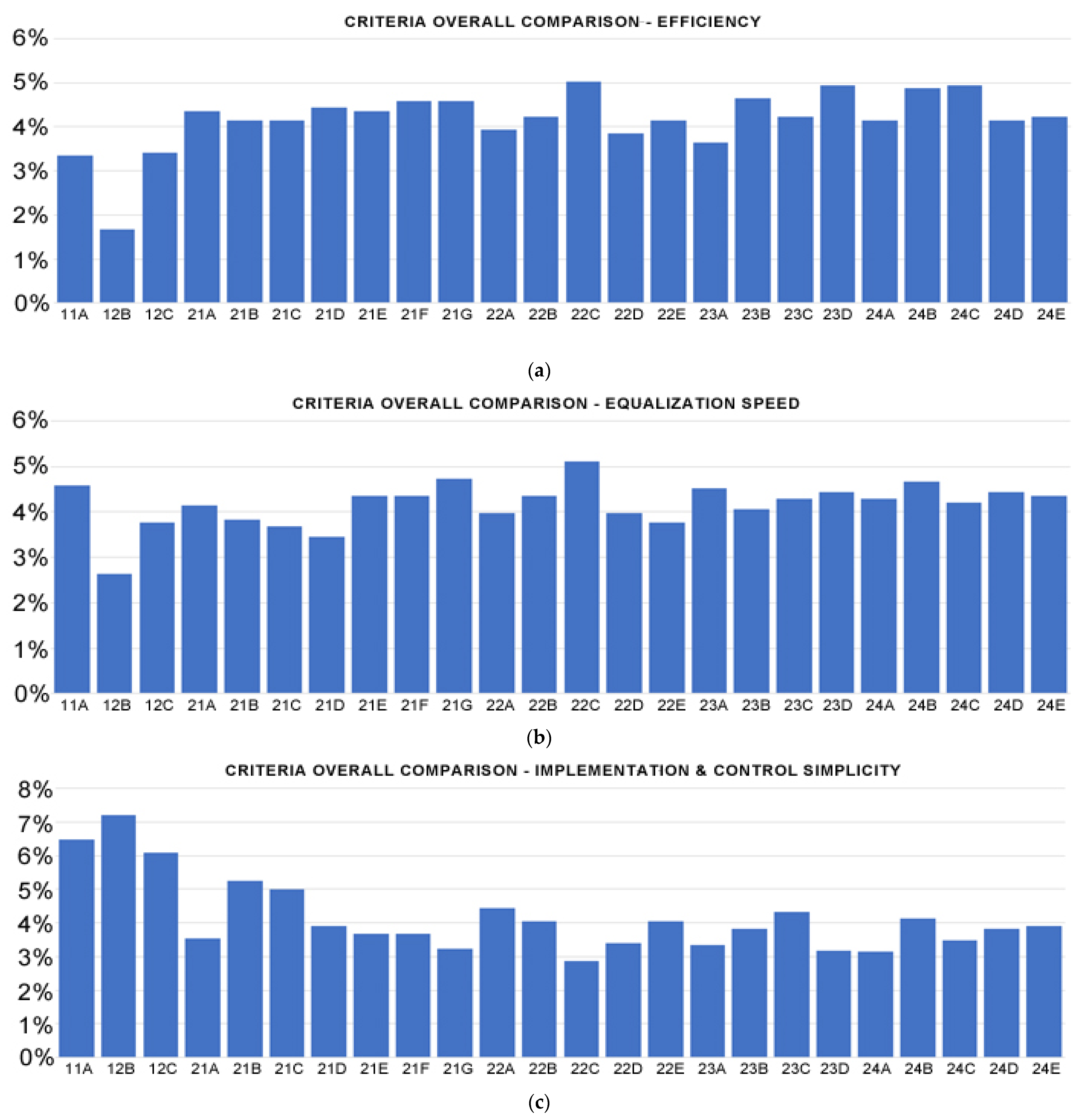
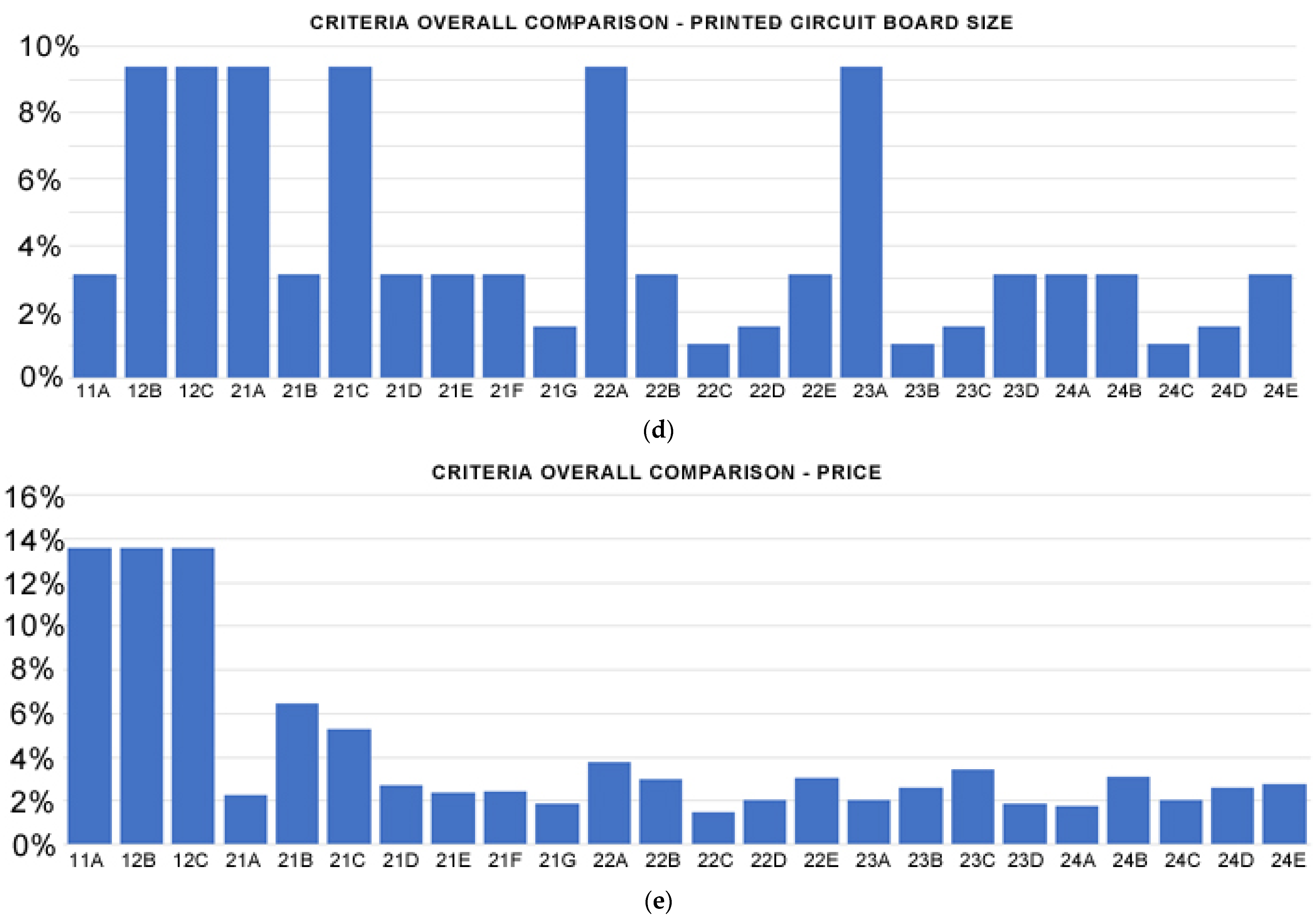
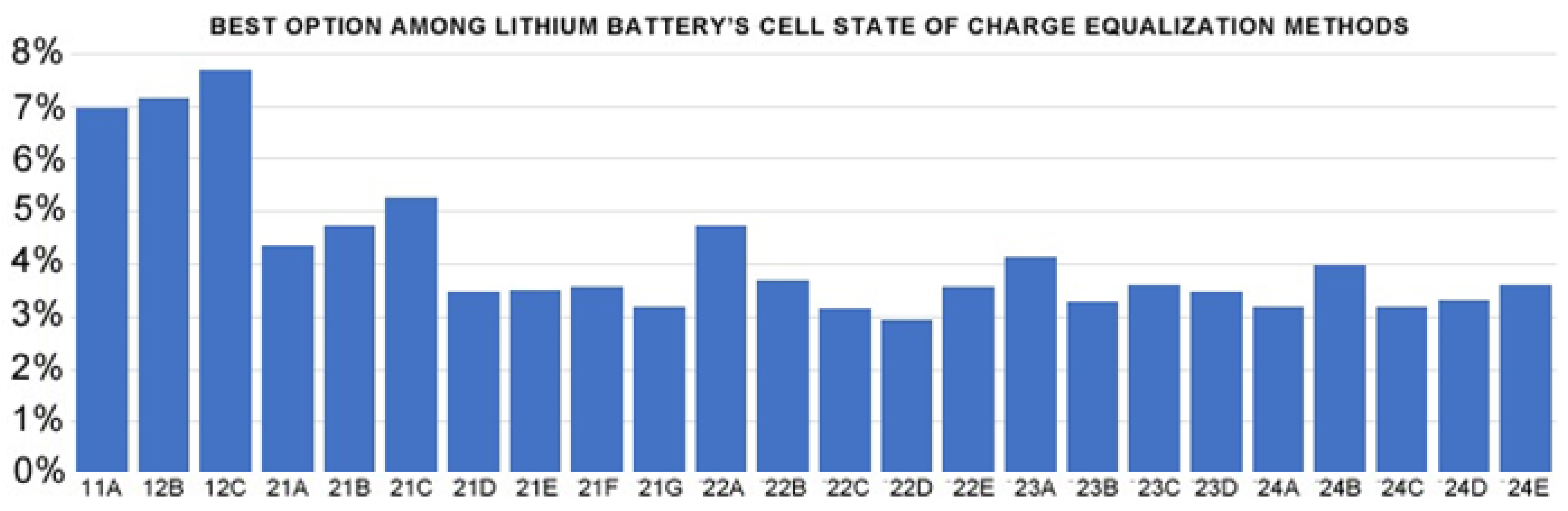
- Energy efficiency and equalization speed are very similar across all equalization methods, varying between 3% and 5% (Figure 4a,b). In contrast, PCB size and price present the widest variation. They present values between 2% and 12% (Figure 4d,e). These last two metrics are the main differentiating factors in equalization methods. This result is, in some way, expected as price is usually one of the main factors in industry applications;
- Among all equalization methods, the Cell to Heat—Shunt Resistor (Index 1.2 B) has the worst energy efficiency and equalization speed, although this method has the best implementation and control simplicity;
- Active equalization methods (index 2.x.x) show an average score from 3 to 5% with the math average at 3.72% (see Figure 5), which is significantly less than the passive methods (index 1.x.x) which provide scores > 6.95%. Among active balancing methods, the Cell to Pack—Multi-secondary Windings Transformer (Index 2.2.D) demonstrates the lowest overall score (2,96%), while the Cell to Cell Distributed switched Capacitor method (Index 2.1.C) offers the best (5.28%).
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pinto, C.F.A. Sizing and Energy Management of Distributed Hybrid Energy Storage System for Electric Vehicle. Ph.D. Thesis, Department of Electrical and Computer Engineering, University of Porto, Porto, Portugal, May 2018. [Google Scholar]
- Chen, Y.; Ghosh, M.; Liu, Y.; Zhao, L. Media Coverage of Climate Change and Sustainable Product Consumption Evidence from the Hybrid Vehicle Market. J. Mark. Res. 2019, 56, 995–1011. [Google Scholar] [CrossRef]
- Pinto, C.F.A.; Barreiras, J.V.; Castro, R.; Araújo, R.E.; Schaltz, E. Study on the combined influence of battery models and sizing strategy for hybrid and battery-based electric vehicles. Energy Int. J. 2017, 137, 272–284. [Google Scholar] [CrossRef]
- Hannan, M.A.; Hoque, M.D.M.; Yusof, Y.; Ker, A.P.J. State-of-the-Art and Energy Management System of Lithium-Ion Batteries in Electric Vehicle Applications: Issues and Recommendations. IEEE Access Spec. Sect. Adv. Energy Storage Technol. Appl. 2018, 6, 19362–19378. [Google Scholar] [CrossRef]
- Wardayanti, A.; Zakaria, R.; Sutopo, W.; Louhenapessy, B.B. Supplier Model of the Lithium-ion Battery using Fuzzy AHP and Analysis of BOCR. Int. J. Sustain. Transp. Technol. 2018, 1, 1–8. [Google Scholar] [CrossRef][Green Version]
- Lingyun, Z.; Ming, C. A SWOT and AHP Methodology for the Formulation of Development Strategies for China’s Waste EV Battery Recycling Industry. In Cascade Use Technologies; Springer Viewer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Pinto, C.; Castro, R.; Barreiras, J.V.; Araújo, R.E.; Howey, D.A. Smart Balancing Control of a Hybrid Energy Storage System based on a Cell-to-Cell Shared Energy Transfer Configuration. In Proceedings of the Vehicle Power and Propulsion (VPPC), IEEE Conference, Chicago, IL, USA, 27–30 August 2018. [Google Scholar] [CrossRef]
- Feng, F.; Hu, X.; Liu, J.; Lin, X.; Liu, B. A review of equalization strategies for series battery packs: Variables, objectives, and algorithms. Renew. Sustain. Energy Rev. 2019, 116, 109464. [Google Scholar] [CrossRef]
- Cui, X.; Shen, W.; Zhang, Y.; Hu, C.; Zheng, J. Novel active LiFePO4 battery balancing method based on chargeable and dischargeable capacity. Comput. Chem. Eng. 2017, 97, 27–35. [Google Scholar] [CrossRef]
- Jossen, A. Fundamentals of battery dynamics. J. Power Sources 2006, 154, 530–538. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; White, R. Quantifying cell-to-cell variations in lithium-ion batteries. Int. J. Electrochem. 2012, 2012, 395838. [Google Scholar] [CrossRef]
- Shin, D.; Poncino, M.; Macii, E.; Chang, N. A statistical model of cell-to-cell variation in li-ion batteries for system-level design. In Low Power Electronics and Design (ISLPED), Proceedings of the IEEE International Symposium, Beijing, China, 4–6 September 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 94–99. [Google Scholar] [CrossRef]
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.C.; Besenhard, J.O.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Sources 2005, 147, 269–281. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef]
- Barreras, J.V. Practical Methods in Li-ion Batteries for Simplified Modeling, Battery Electric Vehicle Design, Battery Management System Testing and Balancing System Control. Ph.D. Thesis, Faculty of Engineering and Science, Aalborg University, Aalborg, Denmark, 2017. [Google Scholar] [CrossRef]
- Barreras, J.V.; Pinto, C.; Castro, R.; Schaltz, E.; Andreasen, S.J.; Araujo, R.E. Multi-objective control of balancing systems for li-ion battery packs: A paradigm shift? In Proceedings of the 2014 IEEE the Vehicle Power and Propulsion Conference (VPPC), Coimbra, Portugal, 27–30 October 2014; pp. 1–7. [Google Scholar] [CrossRef]
- Gallardo-Lozano, J.; Romero-Cadaval, E.; Milanes-Montero, I.M.; Guerrero-Martinez, M. Battery equalization active methods. J. Power Sources 2014, 246, 934–949. [Google Scholar] [CrossRef]
- Daowd, M.; Omar, N.; Van Den Bossche, P.; Mierlo, J.V. Passive and active battery balancing comparison based on matlab simulation. In Proceedings of the 2011 IEEE the Vehicle Power and Propulsion Conference (VPPC), Chicago, IL, USA, 6–9 September 2011; pp. 1–7. [Google Scholar] [CrossRef]
- Cao, J.; Schofield, N.; Emadi, A. Battery balancing methods: A comprehensive review. In Proceedings of the 2011 IEEE the Vehicle Power and Propulsion Conference (VPPC), Harbin, China, 3–5 September 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Ahmad, A.B.; Ooi, C.A.; Ishak, D.; Teh, J. Cell Balancing Topologies in Battery Energy Storage Systems: A Review. In 10th International Conference on Robotics, Vision, Signal Processing and Power Applications. Lecture Notes in Electrical Engineering; Zawawi, M., Teoh, S., Abdullah, N., Mohd Sazali, M., Eds.; Springer: Singapore, 2019; Volume 547, Available online: https://link.springer.com/book/10.1007/978-981-13-6447-1#editorsandaffiliations (accessed on 1 March 2022).
- Pinto, C.; Barreras, J.V.; Schaltz, E.; Araújo, R.E. Evaluation of Advanced Control for Li-ion Battery Balancing Systems Using Convex Optimization. IEEE Trans. Sustain. Energy 2016, 7, 1703–1717. [Google Scholar] [CrossRef]
- Wu, T.; Ji, F.; Liao, L.; Chang, C. Voltage-SOC balancing control scheme for series-connected lithium-ion battery packs. J. Energy Storage 2019, 25, 100895. [Google Scholar] [CrossRef]
- Koseoglou, M.; Tsioumas, E.; Jabbour, N.; Mademlis, C. Highly Effective Cell Equalization in a Lithium-Ion Battery Management System. IEEE Trans. Power Electron. 2019, 35, 2088–2099. [Google Scholar] [CrossRef]
- Santos, S.R.; Fracarolli, J.P.V.; Narita, A.Y.M.; Aranha, C.M.S.; Marques, F.L.R.; Sansão, J.C.; Hamacek, P.V.B. Dissipative lithium-ion cell balancing by recharge control and detection of outliers for energy optimization and heat reduction. In Proceedings of the 44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018. [Google Scholar] [CrossRef]
- Oening, A.P.; Marcilio, D.C.; Andrade, J.D.; Impinnisi, P.R. Analytic Hierarchy Process Algorithm Applied to Battery Energy Storage System Selection for Grid Applications. Braz. Arch. Biol. Technol. 2021, 64. Available online: https://www.scielo.br/j/babt/a/xBsRJ4dsShDQzmDc83V5JNH/?lang=en (accessed on 1 March 2022). [CrossRef]
- Hu, G.; Huang, P.; Bai, Z.; Wang, Q.; Qi, K. Comprehensively analysis the failure evolution and safety evaluation of automotive lithium-ion battery. eTransportation 2021, 10, 100140. [Google Scholar] [CrossRef]
- Panah, P.G.; Bornapour, M.; Hemmati, R.; Guerrero, J.M. Charging station Stochastic Programming for Hydrogen/Battery Electric Buses using Multi-Criteria Crow Search Algorithm. Renew. Sustain. Energy Rev. 2021, 144, 111046. [Google Scholar] [CrossRef]
- Zhang, S.; Peng, N.; Zhang, X. A variable multi-time-scale based dual estimation framework for state-of-energy and maximum available energy of lithium-ion battery. Int. J. Energy Res. 2021, 46, 2876–2892. [Google Scholar] [CrossRef]
- Xu, J.; Mei, X.; Wang, J. A High Power Low-Cost Balancing System for Battery Strings. Energy Procedia 2019, 158, 2948–2953. [Google Scholar] [CrossRef]
- Michael; Sujatmiko, R.P.; Abuzairi, T.; Rizkinia, M.; Kurniawan, T.A. Design of Overcharging Protection and Passive Balancing Circuits using Dioda for Lithium-Ion Battery Management System. In Proceedings of the 2019 16th International Conference on Quality in Research (QIR): International Symposium on Electrical and Computer Engineering, Padang, Indonesia, 22–24 July 2019. [Google Scholar] [CrossRef]
- Dias, B.M.d.A.; da Silva, C.T.; Araújo, R.E.; Castro, R.d.; Pellini, E.L.; Pinto, C.; Laganá, A.A.M. An Analytic Hierarchy Process for Selecting Battery Equalization Methods. Data Arch. 2022, 1, 1–15. [Google Scholar]
- Saaty, T. A scaling method for priorities in hierarchical structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Kim, C.; Langari, R. Adaptive Analytic Hierarchy Process-Based Decision Making to Enhance Vehicle Autonomy. IEEE Trans. Veh. Technol. 2012, 61, 3321–3332. [Google Scholar] [CrossRef]
- Dziadak, B.; Michalski, A. Evaluation of the Hardware for a Mobile Measurement Station. IEEE Trans. Ind. Electron. 2011, 58, 2627–2635. [Google Scholar] [CrossRef]
- Santos, P.H.D.; Neves, S.M.; Sant’Anna, D.O.; Oliveira, C.H.; Carvalho, H.D. The analytic hierarchy process supporting decision making for sustainable development: An overview of applications. J. Clean. Prod. 2019, 212, 119–138. [Google Scholar] [CrossRef]
- Saaty, T. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 2–26. [Google Scholar] [CrossRef]
- Wang, L.; Sharkh, S.; Chipperfield, A.; Cruden, A. Dispatch of Vehicle-to-Grid Battery Storage Using an Analytic Hierarchy Process. IEEE Trans. Veh. Technol. 2017, 66, 2952–2965. [Google Scholar] [CrossRef]
- Saaty, T.L. Fundamentals of Decision Making and Priority Theory with the Analytic Hierarchy Process; Analytic Hierarchy Process Series; RWS Publications: Pittsburgh, PA, USA, 2000; Volume 6, p. 478, ISBN 1888603151, 9781888603156. [Google Scholar]
- Groselj, P.; Stirn, L.Z. Acceptable consistency of aggregated comparison matrices in analytic hierarchy process. Eur. J. Oper. Res. 2012, 223, 417–420. [Google Scholar] [CrossRef]
- Pedrycz, W.; Song, M. Analytic Hierarchy Process (AHP) in Group Decision Making and its Optimization with an Allocation of Information Granularity. IEEE Trans. Fuzzy Syst. 2011, 19, 527–539. [Google Scholar] [CrossRef]

| Intensity of Importance | Definition | Explanation |
|---|---|---|
| 1 | Equal importance | Two criteria contribute equally to the objective |
| 3 | Weak importance of one over another | Experience and judgment slightly favor one criterion over another |
| 5 | Essential or strong importance | Experience and judgment strongly favor one criterion over another |
| 7 | Demonstrated importance | A criterion is strongly favored, and its dominance is demonstrated in practice |
| 9 | Absolute importance | The evidence favoring one criterion over another is of the highest possible order of affirmation |
| 2, 4, 6, 8 | Intermediate values between the two adjacent judgments | When compromise is needed |
| Reciprocals of above nonzero | If criteria i has one of the above nonzero numbers assigned to it when compared with criteria j, then j has the reciprocal value when compared with i | |
| Rational | Ratios arising from the scale | If consistency were to be forced by obtaining n numerical values to span the matrix |
| Criteria | Energy Efficiency | Equalization Speed | Implementation Simplicity | Hardware Size | Total Price | Eigenvector (λ) | Weight Vector (W) |
|---|---|---|---|---|---|---|---|
| 1 | |||||||
| CI | n = total criteria | R1 = Table 3 | CR | ||||
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| RI | 0 | 0 | 0.52 | 0.89 | 1.11 | 1.25 | 1.5 | 1.40 | 1.45 | 1.49 |
| Pairwise Comparison | Result | Conclusion and Meaning |
|---|---|---|
| Implementation vs. PCB Size | −1.2 | Implementation is 1.2 times more important than PCB Size |
| Implementation vs. Price | 2.5 | Price is 2.5 times more important than Implementation |
| Energy Efficiency vs. Implementation | −3 | Energy Efficiency is 3 times more important than Implementation |
| Energy Efficiency vs. PCB Size | −1.8 | Energy Efficiency is 1.8 times more important than PCB Size |
| Energy Efficiency vs. Price | 1.7 | Price is 1.7 times more important than Energy Efficiency |
| Energy Efficiency vs. Equalization Speed | −1.5 | Efficiency is 1.5 times more important than Equalization Speed |
| PCB Size vs. Price | 2.2 | Price is 2.2 times more important than PCB Size |
| Equalization Speed vs. Implementation | −1.8 | Speed is 1.8 times more important than Implementation |
| Equalization Speed vs. PCB Size | −1.8 | Equalization Speed is 1.8 times more important than PCB Size |
| Equalization Speed vs. Price | 2.1 | Price is 2.1 more important than Equalization Speed |
| Criteria | Eigenvector (λ) | Weight Vector (W) | |||||
|---|---|---|---|---|---|---|---|
| 1 | 1.5 | 3 | 1.8 | 0.6 | 1.36 | 26% | |
| 0.7 | 1 | 1.8 | 1.8 | 0.5 | 1.00 | 19% | |
| 0.3 | 0.6 | 1 | 5.0 | 0.4 | 0.57 | 11% | |
| 0.6 | 0.6 | 1.2 | 1 | 0.8 | 0.79 | 15% | |
| 1.7 | 2.1 | 2.5 | 1.2 | 1 | 1.60 | 30% | |
| Criteria vector [Cj] | 4.26 | 5.71 | 9.50 | 6.63 | 3.30 | 5.34 | 100% |
| λ-max | 5.15 | ||||||
| MATRIX SIZE (n) | 5 | CI | 3.89% | ||||
| Random Index (RI) | 1.11 | CR | 3.51% |
| Index—Type | Method | |||
|---|---|---|---|---|
| 1.1 A—Cell Bypass | Cell Bypass | 4.6 | 6.1 | 3 |
| 1.2 B—Cell to Heat | Shunt Resistor | 2.3 | 3.5 | 2.7 |
| 1.2 C—Cell to Heat | Shunt Transistor | 4.7 | 5 | 3.2 |
| 2.1 A—Cell to Cell Shared | Single Switched Capacitor | 6 | 5.5 | 5.5 |
| 2.1 B—Cell to Cell Shared | Single Switched Inductor | 5.7 | 5.1 | 3.7 |
| 2.1 C—Cell to Cell Distributed | Switched Capacitor | 5.7 | 4.9 | 3.9 |
| 2.1 D—Cell to Cell Distributed | Double-tiered Switching Capacitor | 6.1 | 4.6 | 5 |
| 2.1 E—Cell to Cell Distributed | Cûk Converter | 6 | 5.8 | 5.3 |
| 2.1 F—Cell to Cell Distributed | PWM Controlled Converter | 6.3 | 5.8 | 5.3 |
| 2.1 G—Cell to Cell Distributed | Quasi-Resonant Converter | 6.3 | 6.3 | 6 |
| 2.2 A—Cell to Pack | Shunt Inductor | 5.4 | 5.3 | 4.4 |
| 2.2 B—Cell to Pack | Boost Shunting | 5.8 | 5.8 | 4.8 |
| 2.2 C—Cell to Pack | Multiple Transformers | 6.9 | 6.8 | 6.8 |
| 2.2 D—Cell to Pack | Multi-secondary Windings Transformer | 5.3 | 5.3 | 5.7 |
| 2.2 E—Cell to Pack | Switched Transformer | 5.7 | 5 | 4.8 |
| 2.3 A—Pack to Cell | Voltage Multiplier | 5 | 6 | 5.8 |
| 2.3 B—Pack to Cell | Multiple Transformers | 6.4 | 5.4 | 5.1 |
| 2.3 C—Pack to Cell | Multi-secondary Windings Transformer | 5.8 | 5.7 | 4.5 |
| 2.3 D—Pack to Cell | Switched Transformer | 6.8 | 5.9 | 6.1 |
| 2.4 A—Cell to Pack to Cell | PWM Controlled Converter | 5.7 | 5.7 | 6.2 |
| 2.4 B—Cell to Pack to Cell | Full-bridge Converter | 6.7 | 6.2 | 4.7 |
| 2.4 C—Cell to Pack to Cell | Bidirectional Multiple Transformers | 6.8 | 5.6 | 5.6 |
| 2.4 D—Cell to Pack to Cell | Bidirectional multi-secondary Transformer | 5.7 | 5.9 | 5.1 |
| 2.4 E—Cell to Pack to Cell | Bidirectional Switched Windings Transformer | 5.8 | 5.8 | 5 |
| PCB Size (Scale) | Price | Implement. & Ctrl. (Scale) | Hours |
|---|---|---|---|
| Small (1) | $1 | Easy (1) | 168 h |
| Medium (3) | $5 | Medium (5) | 504 h |
| Big (6) | $15 | Hard (9) | 1008 h |
| Very Big (9) | $30 | Work Hour Price | $150 |
| Components | Price |
|---|---|
| Switches | $2 |
| Resistors | $6 |
| Transistors | $3 |
| Capacitor | $5 |
| Filters Capacitor | $1 |
| Inductors | $4 |
| Diode | $1 |
| MOSFET | $4 |
| Multi Secondary Winding Transformer | $1000 |
| Winding Transformer | $10 |
| Bi-Directional Transformers | $30 |
| Bi-Directional Multi Secondary Winding Transformer | $1100 |
| Index | Engineering Work Hour | Design Costs | PCB Price | Main Elements Required to Balance n Cell | Components Price | Total Price | ||
|---|---|---|---|---|---|---|---|---|
| 1.1 A | 336 | $5040.00 | 3 | $5.00 | [2n] switches | $400.00 | $50,805.00 | 1.0 |
| 1.2 B | 302.4 | $45,360.00 | 1 | $1.00 | n resistors, n transistors | $900.00 | $46,261.00 | 1.0 |
| 1.2 C | 358.4 | $53,760.00 | 1 | $1.00 | n transistors | $300.00 | $54,061.00 | 1.0 |
| 2.1 A | 616 | $92,400.00 | 1 | $1.00 | [2n] switches, 1 capacitor | $205.00 | $92,606.00 | 5.9 |
| 2.1 B | 414.4 | $62,160.00 | 3 | $5.00 | [2n] switches, n filters capacitor, 1 inductor | $504.00 | $62,669.00 | 2.1 |
| 2.1 C | 436.8 | $65,520.00 | 1 | $1.00 | n switches, n capacitors | $700.00 | $66,221.00 | 2.6 |
| 2.1 D | 560 | $84,000.00 | 3 | $5.00 | [(n/2) + n] capacitors, 2n switches | $1150.00 | $85,155.00 | 5.0 |
| 2.1 E | 593.6 | $89,040.00 | 3 | $5.00 | [n] inductors, [2n] switches, [n − 1] capacitors | $1295.00 | $90,340.00 | 5.6 |
| 2.1 F | 593.6 | $89,040.00 | 3 | $5.00 | [(2n) − 2] transistors, n inductors | $994.00 | $90,039.00 | 5.6 |
| 2.1 G | 672 | $100,800.00 | 6 | $15.00 | [(2n) − 2] transistors, [(2n) − 4] inductors, [n − 2] capacitors, | $1868.00 | $102,683.00 | 7.2 |
| 2.2 A | 492.8 | $73,920.00 | 1 | $1.00 | [2n +2] switches, 1 inductor, 1 diode | $409.00 | $74,330.00 | 3.6 |
| 2.2 B | 537.6 | $80,640.00 | 3 | $5.00 | [n + 1] switches, [n + 1] diodes, [n + 1] inductors, 1 capacitor | $914.00 | $81,559.00 | 4.5 |
| 2.2 C | 761.6 | $114,240.00 | 9 | $30.00 | [n + 1] MOSFETs, n diodes, 2n inductors, n winding transformers | $2304.00 | $116,574.00 | 9.0 |
| 2.2 D | 638.4 | $95,760.00 | 6 | $15.00 | 1 multi secondary winding transformer, [n + 1] inductors, [n + 1] MOSFETs | $1808.00 | $97,583.00 | 6.6 |
| 2.2 E | 537.6 | $80,640.00 | 3 | $5.00 | 2n switches, [2n + 1] diodes, 1 transformer | $611.00 | $81,256.00 | 4.5 |
| 2.3 A | 649.6 | $97,440.00 | 1 | $1.00 | n capacitors, 2n diodes, 1 transistor | $703.00 | $98,144.00 | 6.6 |
| 2.3 B | 571.2 | $85,680.00 | 9 | $30.00 | 1 MOSFET, n diodes, n windingtransformers | $1104.00 | $86,814.00 | 5.2 |
| 2.3 C | 504 | $75,600.00 | 6 | $15.00 | 1 multi secondary windingtransformer, n inductor, 1 MOSFET | $1404.00 | $77,019.00 | 3.9 |
| 2.3 D | 683.2 | $102,480.00 | 3 | $5.00 | 1 MOSFET, n diodes, 1 windingtransformer | $114.00 | $102,599.00 | 7.2 |
| 2.4 A | 694.4 | $104,160.00 | 3 | $5.00 | n inductors, 2n MOSFET, 1 capacitor | $1205.00 | $105,370.00 | 7.6 |
| 2.4 B | 526.4 | $78,960.00 | 3 | $5.00 | 4n transistors | $1200.00 | $80,165.00 | 4.3 |
| 2.4 C | 627.2 | $94,080.00 | 9 | $30.00 | 2n MOSFETs, n bi-dir transformer | $3800.00 | $97,910.00 | 6.6 |
| 2.4 D | 571.2 | $85,680.00 | 6 | $15.00 | 1 bi-dir multi secondary winding transformer, [n + 1] MOSFETs | $1504.00 | $87,199.00 | 5.2 |
| 2.4 E | 560 | $84,000.00 | 3 | $5.00 | 1 bi-dir transformer, [2n + 1] switches | $432.00 | $84,437.00 | 4.9 |
| Alternative/Criteria | Decision Vector (δ) | ||||||
|---|---|---|---|---|---|---|---|
| Index | Weight Vector (W) | 26% | 19% | 11% | 15% | 30% | |
| 1.1 A | Cell Bypass | 3.35% | 4.59% | 6.49% | 3.13% | 13.58% | 6.96% |
| 1.2 B | Shunt Resistor | 1.67% | 2.63% | 7.21% | 9.38% | 13.58% | 7.17% |
| 1.2 C | Shunt Transistor | 3.42% | 3.76% | 6.08% | 9.38% | 13.58% | 7.71% |
| 2.1 A | Single Switched Capacitor | 4.36% | 4.14% | 3.54% | 9.38% | 2.29% | 4.35% |
| 2.1 B | Single Switched Inductor | 4.15% | 3.83% | 5.26% | 3.13% | 6.47% | 4.75% |
| 2.1 C | Switched Capacitor | 4.15% | 3.68% | 4.99% | 9.38% | 5.32% | 5.28% |
| 2.1 D | Double-tiered Switching Capacitor | 4.44% | 3.46% | 3.89% | 3.13% | 2.73% | 3.49% |
| 2.1 E | Cûk Converter | 4.36% | 4.36% | 3.67% | 3.13% | 2.41% | 3.52% |
| 2.1 F | PWM Controlled Converter | 4.58% | 4.36% | 3.67% | 3.13% | 2.42% | 3.58% |
| 2.1 G | Quasi-Resonant Converter | 4.58% | 4.74% | 3.24% | 1.56% | 1.88% | 3.21% |
| 2.2 A | Shunt Inductor | 3.93% | 3.98% | 4.42% | 9.38% | 3.78% | 4.75% |
| 2.2 B | Boost Shunting | 4.22% | 4.36% | 4.05% | 3.13% | 3.01% | 3.70% |
| 2.2 C | Multiple Transformers | 5.02% | 5.11% | 2.86% | 1.04% | 1.51% | 3.16% |
| 2.2 D | Multi-secondary Windings Transformer | 3.85% | 3.98% | 3.41% | 1.56% | 2.07% | 2.96% |
| 2.2 E | Switched Transformer | 4.15% | 3.76% | 4.05% | 3.13% | 3.03% | 3.58% |
| 2.3 A | Voltage Multiplier | 3.64% | 4.51% | 3.36% | 9.38% | 2.05% | 4.14% |
| 2.3 B | Multiple Transformers | 4.65% | 4.06% | 3.82% | 1.04% | 2.62% | 3.31% |
| 2.3 C | Multi-secondary Windings Transformer | 4.22% | 4.29% | 4.32% | 1.56% | 3.45% | 3.62% |
| 2.3 D | Switched Transformer | 4.95% | 4.44% | 3.19% | 3.13% | 1.88% | 3.47% |
| 2.4 A | PWM Controlled Converter | 4.15% | 4.29% | 3.14% | 3.13% | 1.80% | 3.21% |
| 2.4 B | Full-bridge Converter | 4.87% | 4.66% | 4.14% | 3.13% | 3.13% | 3.97% |
| 2.4 C | Bidirectional Multiple Transformers | 4.95% | 4.21% | 3.48% | 1.04% | 2.05% | 3.20% |
| 2.4 D | Bidirectional multi-secondary Transformer | 4.15% | 4.44% | 3.82% | 1.56% | 2.59% | 3.32% |
| 2.4 E | Bidirectional Switched Windings Transformer | 4.22% | 4.36% | 3.89% | 3.13% | 2.78% | 3.62% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Alcântara Dias, B.M.; da Silva, C.T.; Araújo, R.E.; de Castro, R.; Pellini, E.L.; Pinto, C.; Laganá, A.A.M. An Analytic Hierarchy Process for Selecting Battery Equalization Methods. Energies 2022, 15, 2439. https://doi.org/10.3390/en15072439
de Alcântara Dias BM, da Silva CT, Araújo RE, de Castro R, Pellini EL, Pinto C, Laganá AAM. An Analytic Hierarchy Process for Selecting Battery Equalization Methods. Energies. 2022; 15(7):2439. https://doi.org/10.3390/en15072439
Chicago/Turabian Stylede Alcântara Dias, Bruno Martin, Cynthia Thamires da Silva, Rui Esteves Araújo, Ricardo de Castro, Eduardo Lorenzetti Pellini, Cláudio Pinto, and Armando Antônio Maria Laganá. 2022. "An Analytic Hierarchy Process for Selecting Battery Equalization Methods" Energies 15, no. 7: 2439. https://doi.org/10.3390/en15072439
APA Stylede Alcântara Dias, B. M., da Silva, C. T., Araújo, R. E., de Castro, R., Pellini, E. L., Pinto, C., & Laganá, A. A. M. (2022). An Analytic Hierarchy Process for Selecting Battery Equalization Methods. Energies, 15(7), 2439. https://doi.org/10.3390/en15072439










