Distribution Locational Marginal Price Based Transactive Energy Management in Distribution Systems with Smart Prosumers—A Multi-Agent Approach
Abstract
:1. Introduction
Novelty and Contribution
- Enhanced Multi-Agent-Based TE trading architecture with a high level of integration of the energy market to energy scheduling.
- A customized RBB strategy for trading agents such as consumers, distributed generators (DGs), and energy storage systems TE scheduling with congestion management and loss reduction;
- DLMP-based energy market with three cost components that encourage a fair process and loss and congestion reduction in distributed systems;
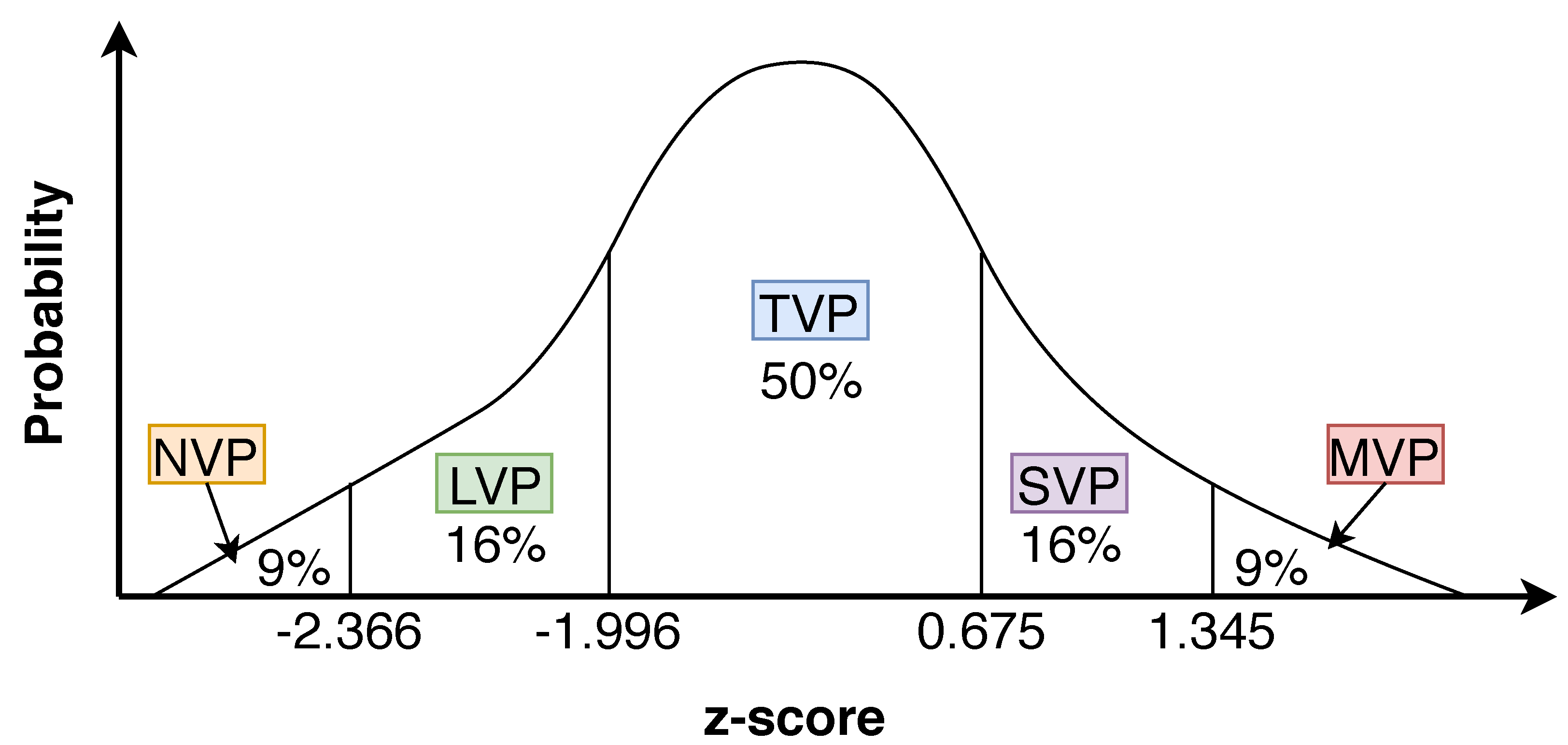
- A novel TE profit (earning) management, called MVP-based earning distribution, which includes the share of the TE stakeholders.
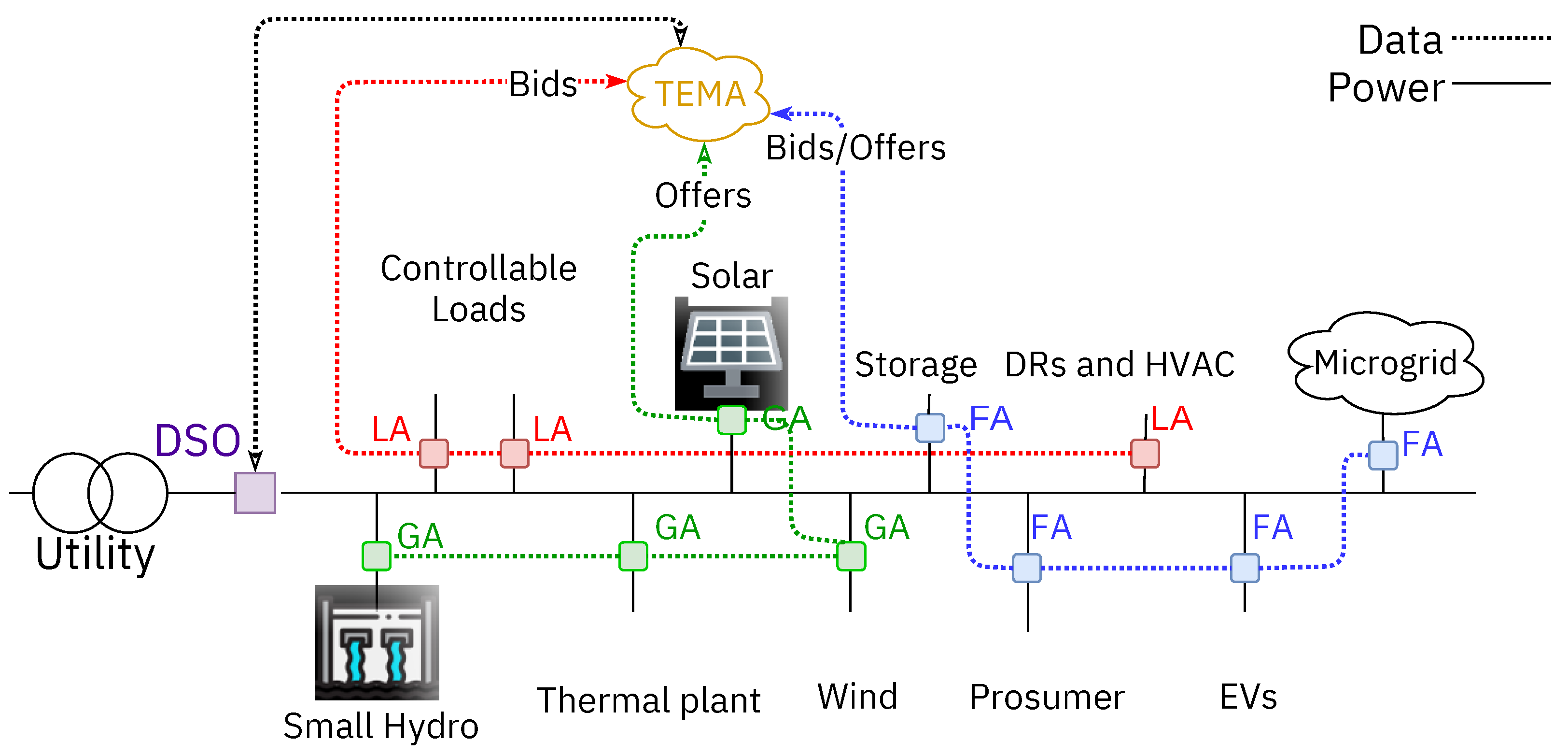
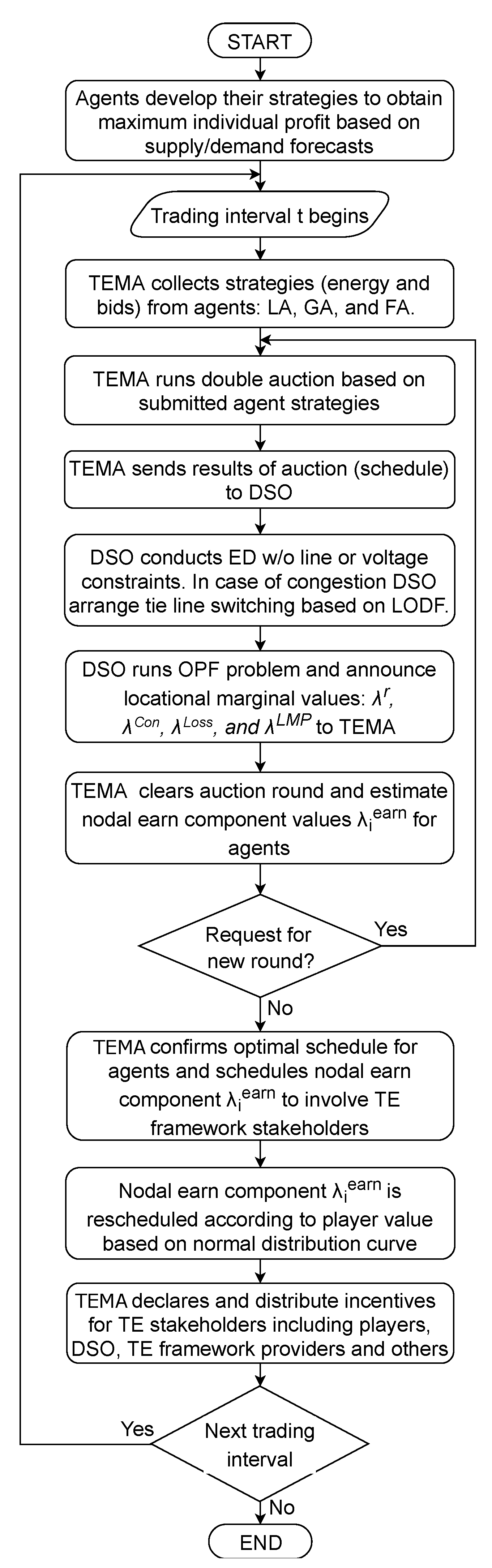
2. MAS Architecture of the DTEMS
2.1. LA—Load Agent
2.2. GA—Generator Agent
2.3. FA—Flexible Agent
2.4. RBB—Risk-Based Bidding
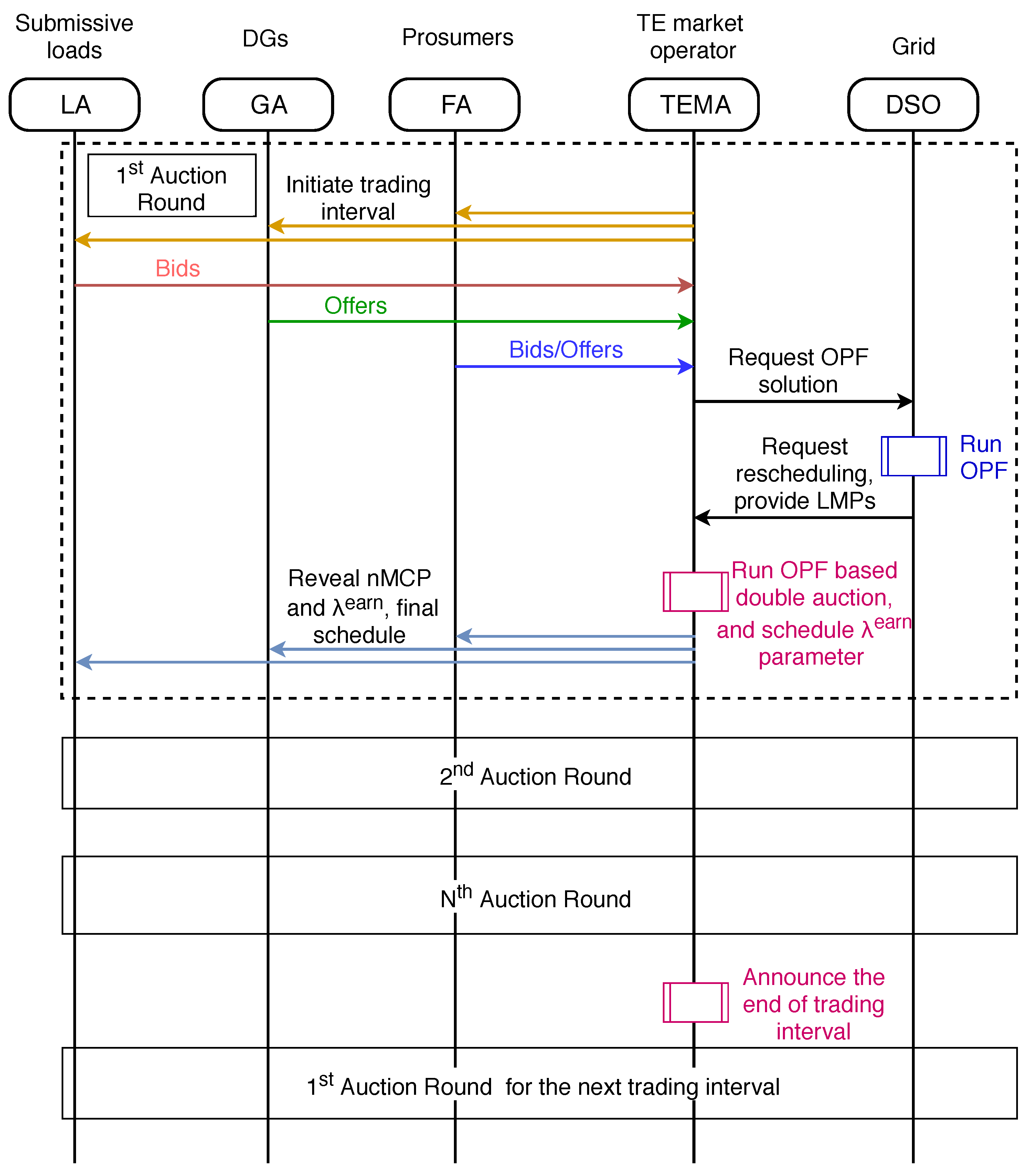
3. Proposed TE Model
3.1. Problem Formulation
3.2. TE Scheduling
3.3. DLMP-Based Market Mechanism
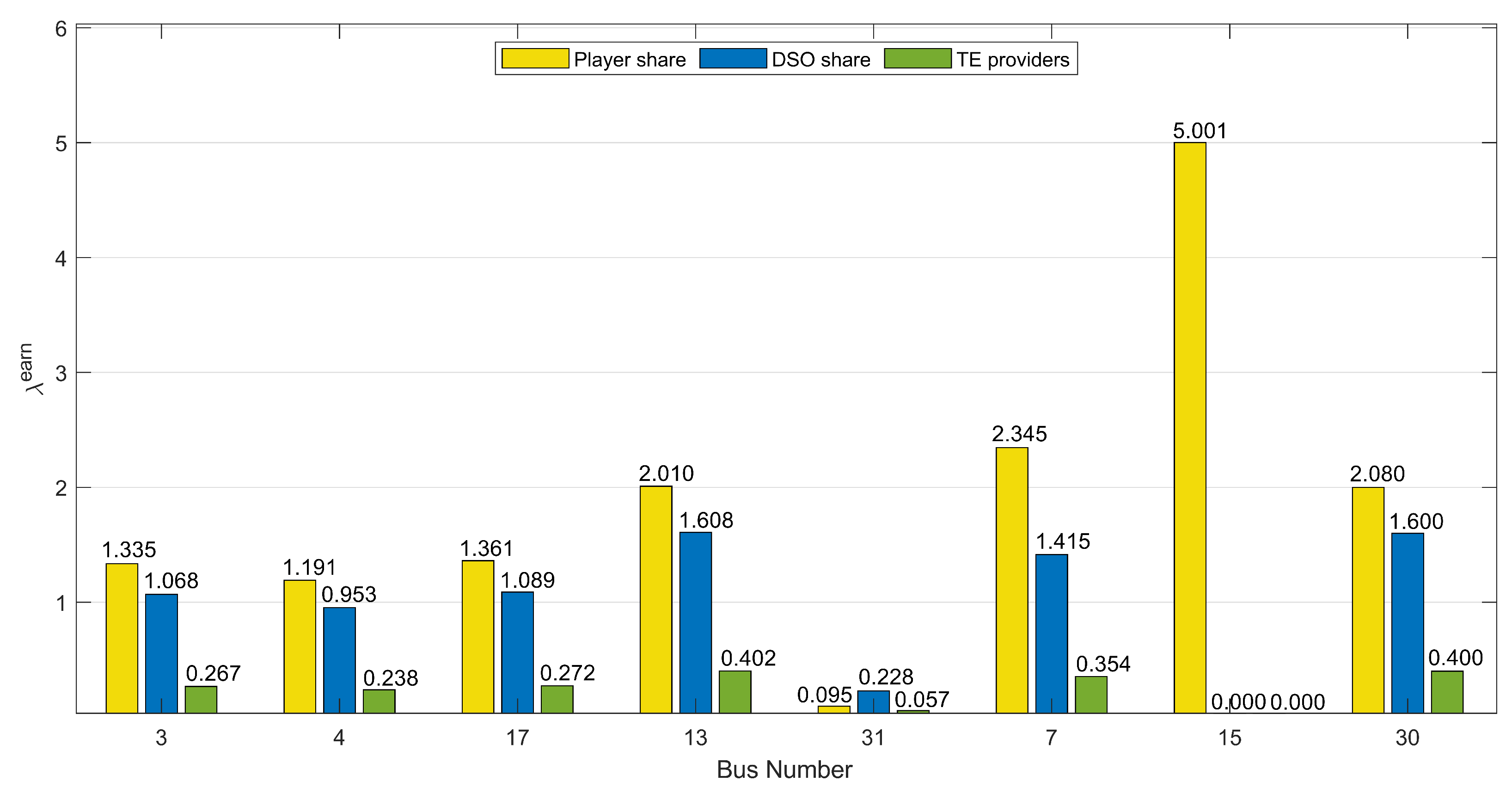
3.4. Nodal Earning Component
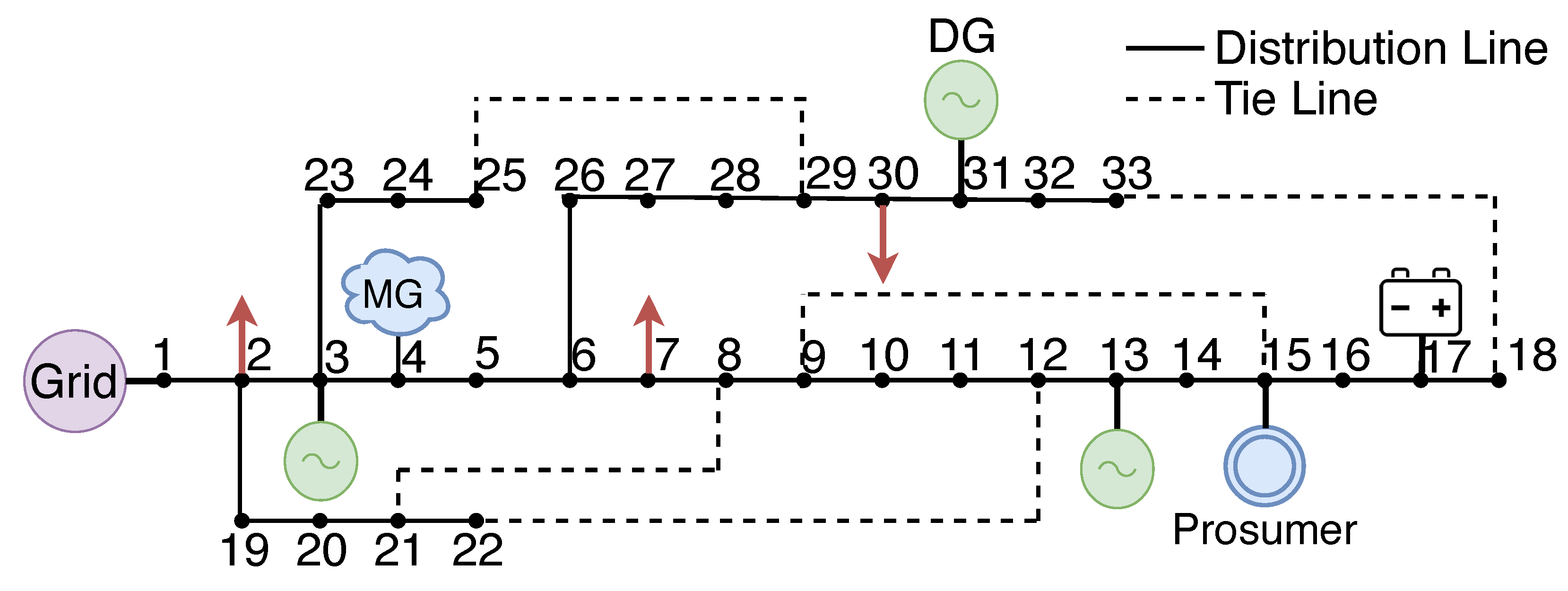
4. Case Study
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DER | Distributed energy resource |
| DESS | Distributed energy storage system |
| DG | Distributed generator |
| DLMP | Distribution locational marginal price |
| DR | Demand response |
| DSO | Distribution system operator |
| DTEMS | DLMP based management system |
| EV | Electric vehicle |
| FA | Flexible agent |
| GA | Generator agent |
| HEMS | Home energy management system |
| LA | Load agent |
| LVP | Least valuable player |
| MAS | Multi-agent system |
| MCP | Market clearing price |
| MVP | Most valuable player |
| NVP | Non-valuable player |
| OPF | Optimal power flow |
| PTDF | Power transfer distribution factor |
| RBB | Risk-based bidding |
| SVP | Second valuable player |
| TE | Transactive energy |
| TEMA | TE market agent |
| TVP | Third valuable player |
Nomenclature
| Requested energy capacity of aggregator (kWh) | |
| Power Transfer Distribution Factor of branch l | |
| Price of energy in the node (¢/kWh) | |
| Line sensitivity factor | |
| Locational Marginal Price at bus i (¢/kWh) | |
| Nodal loss component at bus i (¢/kWh) | |
| Uniform price at each bus k (¢/kWh) | |
| Bid submitted by the load i in market interval t | |
| R | Exchange rates of other uniform pricing rules |
| Requested energy injection from node i to relieve congestion | |
| Nodal earning component at bus i | |
| z | Normally distributed random variable |
| Congestion component of LMP/price MG i pay to responsive | |
| load to clear congestion (¢/kWh) | |
| Constraint cost a.k.a shadow price (¢/kW) | |
| Loss factor at bus k | |
| Line flow in branch l |
References
- Zia, M.F.; Benbouzid, M.; Elbouchikhi, E.; Muyeen, S.M.; Techato, K.; Guerrero, J.M. Microgrid Transactive Energy: Review, Architectures, Distributed Ledger Technologies, and Market Analysis. IEEE Access 2020, 8, 19410–19432. [Google Scholar] [CrossRef]
- Azizi, A.; Aminifar, F.; Moeini-Aghtaie, M.; Alizadeh, A. Transactive Energy Market Mechanism With Loss Implication. IEEE Trans. Smart Grid 2021, 12, 1215–1223. [Google Scholar] [CrossRef]
- Qiu, J.; Zhao, J. Optimal Scheduling for Prosumers in Coupled Transactive Power and Gas Systems. IEEE Trans. Power Syst. 2018, 33, 1970–1980. [Google Scholar] [CrossRef]
- Nematkhah, F.; Bahrami, S.; Aminifar, F.; Catalão, J.P.S. Exploiting the Potentials of HVAC Systems in Transactive Energy Markets. IEEE Trans. Smart Grid 2021, 12, 4039–4048. [Google Scholar] [CrossRef]
- Renani, Y.K.; Ehsan, M. Optimal Transactive Market Operations with Distribution System Operators. IEEE Trans. Smart Grid 2017, 9, 6692–6701. [Google Scholar] [CrossRef]
- Qui, J.; Meng, K. Optimal scheduling of distributed energy resources as a virtual power plant in a transactive energy framework. IET Gener. Transm. Distrib. 2017, 11, 3417–3427. [Google Scholar] [CrossRef]
- Hahn, A.; Singh, R. Smart Contract-based Campus Demonstration of Decentralized Transactive Energy Auctions. In Proceedings of the IEEE Power Energy Society Innovative Smart Grid Technologies Conference, Washington, DC, USA, 23–26 April 2017. [Google Scholar] [CrossRef]
- Amanbek, Y.; Tabarak, Y. Decentralized Transactive Energy Management System for Distribution Systems with Prosumer Microgrids. In Proceedings of the 2018 19th International Carpathian Control Conference (ICCC), Szilvasvarad, Hungary, 28–31 May 2018. [Google Scholar]
- Divshali, P.; Choi, B. Multi-agent transactive energy management system considering high levels of renewable energy source and electric vehicles. IET Gener. Transm. Distrib. 2017, 11, 3713–3721. [Google Scholar] [CrossRef] [Green Version]
- Akter, M.; Mahmud, M. Comparative analysis of energy trading priorities based on open transactive energy markets in residential microgrids. In Proceedings of the 2017 Australasian Universities Power Engineering Conference (AUPEC), Melbourne, VIC, Australia, 19–22 November 2017. [Google Scholar] [CrossRef]
- Gao, Y.; Zhou, X.; Ren, J.; Wang, X.; Li, D. Double Layer Dynamic Game Bidding Mechanism Based on Multi-Agent Technology for Virtual Power Plant and Internal Distributed Energy Resource. Energies 2018, 11, 3072. [Google Scholar] [CrossRef] [Green Version]
- Liu, N.; Wang, J.; Wang, L. Hybrid Energy Sharing for Multiple Microgrids in an Integrated Heat-Electricity Energy System. IEEE Trans. Sustain. Energy 2019, 10, 1139–1151. [Google Scholar] [CrossRef]
- Zhao, T.; Ding, Z. Distributed Finite-Time Optimal Resource Management for Microgrids Based on Multi-Agent Framework. IEEE Trans. Ind. Electron. 2018, 65, 6571–6580. [Google Scholar] [CrossRef] [Green Version]
- Zarabie, A.K.; Das, S.; Faqiry, M.N. Fairness-Regularized DLMP-Based Bilevel Transactive Energy Mechanism in Distribution Systems. IEEE Trans. Smart Grid 2019, 10, 6029–6040. [Google Scholar] [CrossRef] [Green Version]
- Janko, S.A.; Johnson, N.G. Scalable multi-agent microgrid negotiations for a transactive energy market. Appl. Energy 2018, 229, 715–727. [Google Scholar] [CrossRef]
- Prinsloo, G.; Dobson, R.; Mammoli, A. Synthesis of an intelligent rural village microgrid control strategy based on smartgrid multi-agent modelling and transactive energy management principles. Energy 2018, 147, 263–278. [Google Scholar] [CrossRef]
- Ye, Y.; Tang, Y.; Wang, H.; Zhang, X.P.; Strbac, G. A Scalable Privacy-Preserving Multi-Agent Deep Reinforcement Learning Approach for Large-Scale Peer-to-Peer Transactive Energy Trading. IEEE Trans. Smart Grid 2021, 12, 5185–5200. [Google Scholar] [CrossRef]
- Pan, Z.; Yu, T.; Li, J.; Wu, Y.; Chen, J.; Lu, J.; Zhang, X. Multi-Agent Learning-Based Nearly Non-Iterative Stochastic Dynamic Transactive Energy Control of Networked Microgrids. IEEE Trans. Smart Grid 2021, 13, 688–701. [Google Scholar] [CrossRef]
- Rajaei, A.; Fattaheian-Dehkordi, S.; Fotuhi-Firuzabad, M.; Lehtonen, M. Transactive energy management framework for active distribution systems. In Proceedings of the 2021 International Conference on Smart Energy Systems and Technologies (SEST), Vaasa, Finland, 6–8 September 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Pinto, T.; Faia, R.; Ghazvini, M.A.F.; Soares, J.; Corchado, J.M.; Vale, Z. Decision support for small players negotiations under a transactive energy framework. IEEE Trans. Power Syst. 2018, 34, 4015–4023. [Google Scholar] [CrossRef]
- Gomes, L.; Vale, Z.A.; Corchado, J.M. Multi-agent microgrid management system for single-board computers: A case study on peer-to-peer energy trading. IEEE Access 2020, 8, 64169–64183. [Google Scholar] [CrossRef]
- Huang, Q.; McDermott, T.E.; Tang, Y.; Makhmalbaf, A.; Hammerstrom, D.J.; Fisher, A.R.; Marinovici, L.D.; Hardy, T. Simulation-based valuation of transactive energy systems. IEEE Trans. Power Syst. 2018, 34, 4138–4147. [Google Scholar] [CrossRef]
- Li, J.; Zhang, C.; Xu, Z.; Wang, J.; Zhao, J.; Zhang, Y.J.A. Distributed transactive energy trading framework in distribution networks. IEEE Trans. Power Syst. 2018, 33, 7215–7227. [Google Scholar] [CrossRef]
- Daneshvar, M.; Mohammadi-Ivatloo, B.; Asadi, S.; Abapour, M.; Anvari-Moghaddam, A. A transactive energy management framework for regional network of microgrids. In Proceedings of the 2019 International Conference on Smart Energy Systems and Technologies, Porto, Portugal, 9–11 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Kim, B.; Bae, S.; Kim, H. Optimal energy scheduling and transaction mechanism for multiple microgrids. Energies 2017, 10, 566. [Google Scholar] [CrossRef] [Green Version]
- Mehdinejad, M.; Shayanfar, H.; Mohammadi-Ivatloo, B. Peer-to-peer decentralized energy trading framework for retailers and prosumers. Appl. Energy 2022, 308, 118310. [Google Scholar] [CrossRef]
- Farid, A.M. Multi-agent system design principles for resilient operation of future power systems. In Proceedings of the IEEE International Workshop on Intelligent Energy Systems, San Diego, CA, USA, 8 October 2014; pp. 18–25. [Google Scholar] [CrossRef]
- Han, J.; Choi, C.; Park, W.; Lee, I.; Kim, S. Smart home energy management system including renewable energy based on ZigBee and PLC. IEEE Trans. Consum. Electron. 2014, 60, 198–202. [Google Scholar] [CrossRef]
- Rassaei, F.; Soh, W.; Chua, K. Demand Response for Residential Electric Vehicles With Random Usage Patterns in Smart Grids. IEEE Trans. Sustain. Energy 2015, 6, 1367–1376. [Google Scholar] [CrossRef]
- Hu, J.; Yang, G.; Bindner, H.W.; Xue, Y. Application of Network-Constrained Transactive Control to Electric Vehicle Charging for Secure Grid Operation. IEEE Trans. Sustain. Energy 2017, 8, 505–515. [Google Scholar] [CrossRef] [Green Version]
- Zhakiyeva, S.; Gabbassov, M.; Akhmetbekov, Y.; Akybayeva, G.; Zhakiyev, N. The Development of a Risk Assessment Modeling for the Power System of Kazakhstan. In Proceedings of the 2021 IEEE International Conference on Smart Information Systems and Technologies (SIST), Nur-Sultan, Kazakhstan, 28–30 April 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Ali Naseri Javareshk, S.M.; Kouche Biyouki, S.A.; Darban, S.H. Optimal Bidding Strategy in Double-Sided Auctions of the Competitive Power Market Using Agent-Based Algorithm. In Proceedings of the 27th Iranian Conference on Electrical Engineering, Yazd, Iran, 30 April–2 May 2019; pp. 798–803. [Google Scholar] [CrossRef]

| Load | Bid in First Round | Risk | Eagerness Factor | Priority Rise |
|---|---|---|---|---|
| C1 | High | Low | High | Impossible |
| C2 | Medium | Medium | depends on load | Possible |
| C3 | Low | High | depends on load | Possible |
| Bus | Type | Block 1 kW ‖ ¢/kWh | Block 2 kW ‖ ¢/kWh | Block 3 kW ‖ ¢/kWh |
|---|---|---|---|---|
| 1 | GSP | inf ‖ 5.0 | - | - |
| 3 | Solar | 96 ‖ 3.0 | - | - |
| 4 | EV | 12 ‖ 2.0 | 24 ‖ 4.2 | 24 ‖ 8.0 |
| 17 | Battery | 12 ‖ 2.0 | 24 ‖ 4.4 | 24 ‖ 9.0 |
| 13 | Wind | 96 ‖ 2.0 | - | - |
| 31 | Controlable | 50 ‖ 2.0 | 50 ‖ 6.0 | 50 ‖ 8.0 |
| Bus | Type | Block 1 kW ‖ ¢/kWh | Block 2 kW ‖ ¢/kWh | Block 3 kW ‖ ¢/kWh |
|---|---|---|---|---|
| 7 | HVAC | 40 ‖ 10.0 | 30 ‖ 7.0 | 30 ‖ 6.0 |
| 15 | EV | 20 ‖ 10.0 | 20 ‖ 5.0 | 20 ‖ 2.0 |
| 30 | Industry | 100 ‖ 10.0 | 50 ‖ 6.0 | 50 ‖ 5.0 |
| 2 | GBP | inf ‖ 3.0 | - | - |
| Bus | Pg (kW) | (¢/kWh) | Revenue (¢) | Cost (¢) | Earning (¢) | (¢/kWh) |
|---|---|---|---|---|---|---|
| 1 | 2760.7 | 5.000 | 13,803.5 | 13,803.6 | 0.0 | 0.000 |
| 3 | 96.5 | 5.671 | 547.2 | 289.5 | 257.7 | 2.671 |
| 4 | 36.0 | 5.715 | 205.7 | 120.0 | 85.7 | 2.382 |
| 17 | 36.0 | 6.056 | 218.0 | 120.0 | 98.0 | 2.722 |
| 13 | 96.5 | 6.019 | 580.9 | 193.0 | 387.9 | 4.019 |
| 31 | 83.9 | 6.000 | 503.4 | 471.5 | 31.9 | 0.381 |
| 7 | −100.0 | 5.884 | −588.4 | −999.8 | 411.4 | −4.114 |
| 15 | −20.0 | 5.000 | −100.0 | −200.0 | 100.0 | −5.001 |
| 30 | −100.0 | 6.000 | −600.0 | −1000.0 | 400.0 | −4.000 |
| 2 | 0.0 | 5.017 | 0.0 | 0.0 | 0.0 | 0.000 |
| Bus | (¢/kWh) | (¢/kWh) | ||||
|---|---|---|---|---|---|---|
| 1 | 5.000 | 0.000 | 0.000 | 5.000 | 5.000 | 0.000 |
| 3 | 3.000 | 0.343 | 0.059 | 3.402 | 5.671 | 2.671 |
| 4 | 3.333 | 0.383 | 0.093 | 3.810 | 5.715 | 2.382 |
| 17 | 3.333 | 0.412 | 0.291 | 4.037 | 6.056 | 2.722 |
| 13 | 2.000 | 0.245 | 0.163 | 2.408 | 6.019 | 4.019 |
| 31 | 5.619 | 1.943 | -0.819 | 6.743 | 6.000 | 0.381 |
| 7 | 9.998 | 1.186 | 0.582 | 11.766 | 5.884 | −4.114 |
| 15 | 10.001 | −0.001 | 0.001 | 10.001 | 5.000 | −5.001 |
| 30 | 10.000 | 0.790 | 1.210 | 12.000 | 6.000 | −4.000 |
| 2 | 3.000 | 0.000 | 0.010 | 3.010 | 5.017 | 0.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amanbek, Y.; Kalakova, A.; Zhakiyeva, S.; Kayisli, K.; Zhakiyev, N.; Friedrich, D. Distribution Locational Marginal Price Based Transactive Energy Management in Distribution Systems with Smart Prosumers—A Multi-Agent Approach. Energies 2022, 15, 2404. https://doi.org/10.3390/en15072404
Amanbek Y, Kalakova A, Zhakiyeva S, Kayisli K, Zhakiyev N, Friedrich D. Distribution Locational Marginal Price Based Transactive Energy Management in Distribution Systems with Smart Prosumers—A Multi-Agent Approach. Energies. 2022; 15(7):2404. https://doi.org/10.3390/en15072404
Chicago/Turabian StyleAmanbek, Yerasyl, Aidana Kalakova, Svetlana Zhakiyeva, Korhan Kayisli, Nurkhat Zhakiyev, and Daniel Friedrich. 2022. "Distribution Locational Marginal Price Based Transactive Energy Management in Distribution Systems with Smart Prosumers—A Multi-Agent Approach" Energies 15, no. 7: 2404. https://doi.org/10.3390/en15072404
APA StyleAmanbek, Y., Kalakova, A., Zhakiyeva, S., Kayisli, K., Zhakiyev, N., & Friedrich, D. (2022). Distribution Locational Marginal Price Based Transactive Energy Management in Distribution Systems with Smart Prosumers—A Multi-Agent Approach. Energies, 15(7), 2404. https://doi.org/10.3390/en15072404








