Correlations for Convective Laminar Heat Transfer of Carreau Fluid in Straight Tube Flow
Abstract
:1. Introduction
2. Formulation
2.1. Flow
2.2. Temperature
2.3. Nusselt Number
2.4. Evaluation of the Core Flow Rate
2.5. Evaluation of the Nusselt Number
2.6. Numerical Integration
- (1)
- Further divide a subdomain with the largest predicted error.
- (2)
- Apply a cubature rule to the new subdomain.
- (3)
- Update the integral in the subdomains and obtain the global integral.
- (4)
- Check the error by
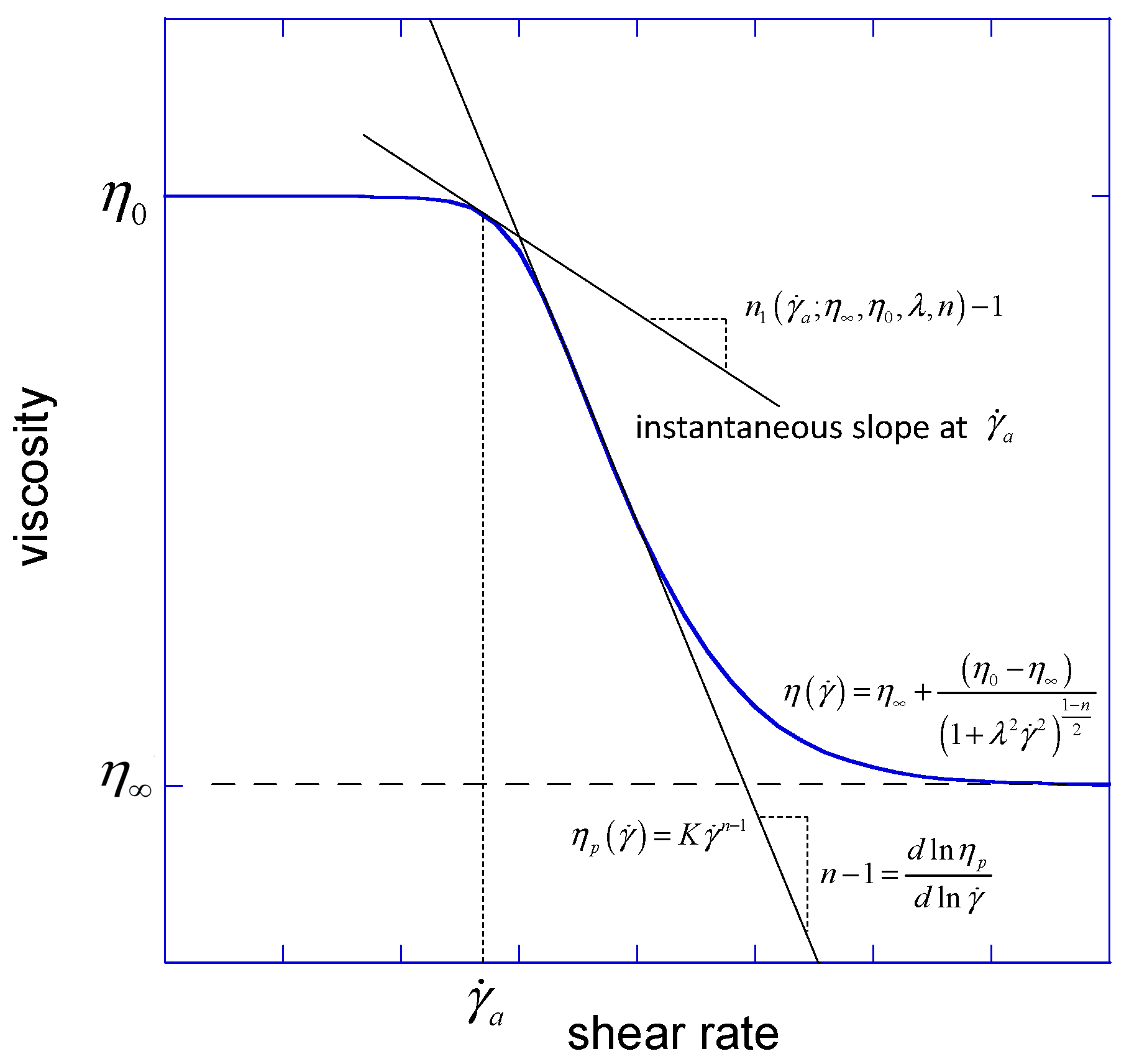
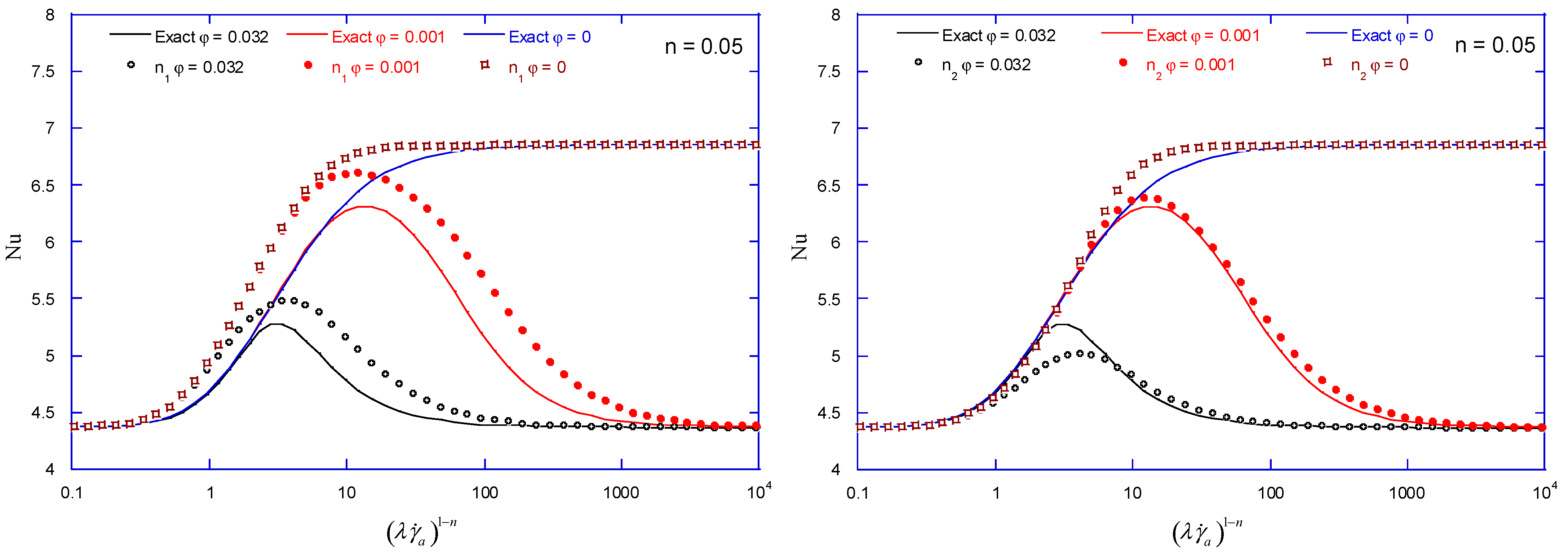
2.7. Expressions for Correlations
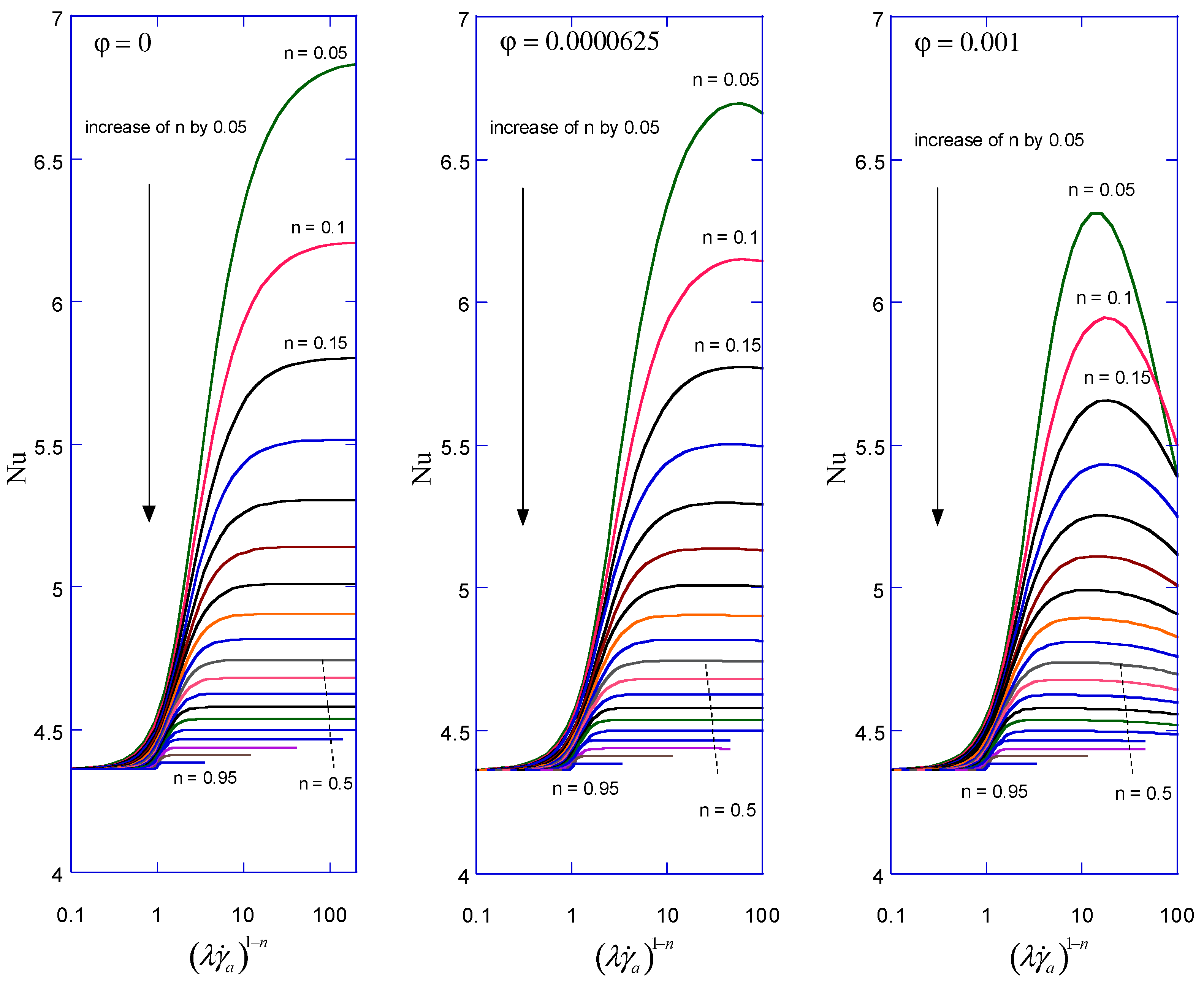
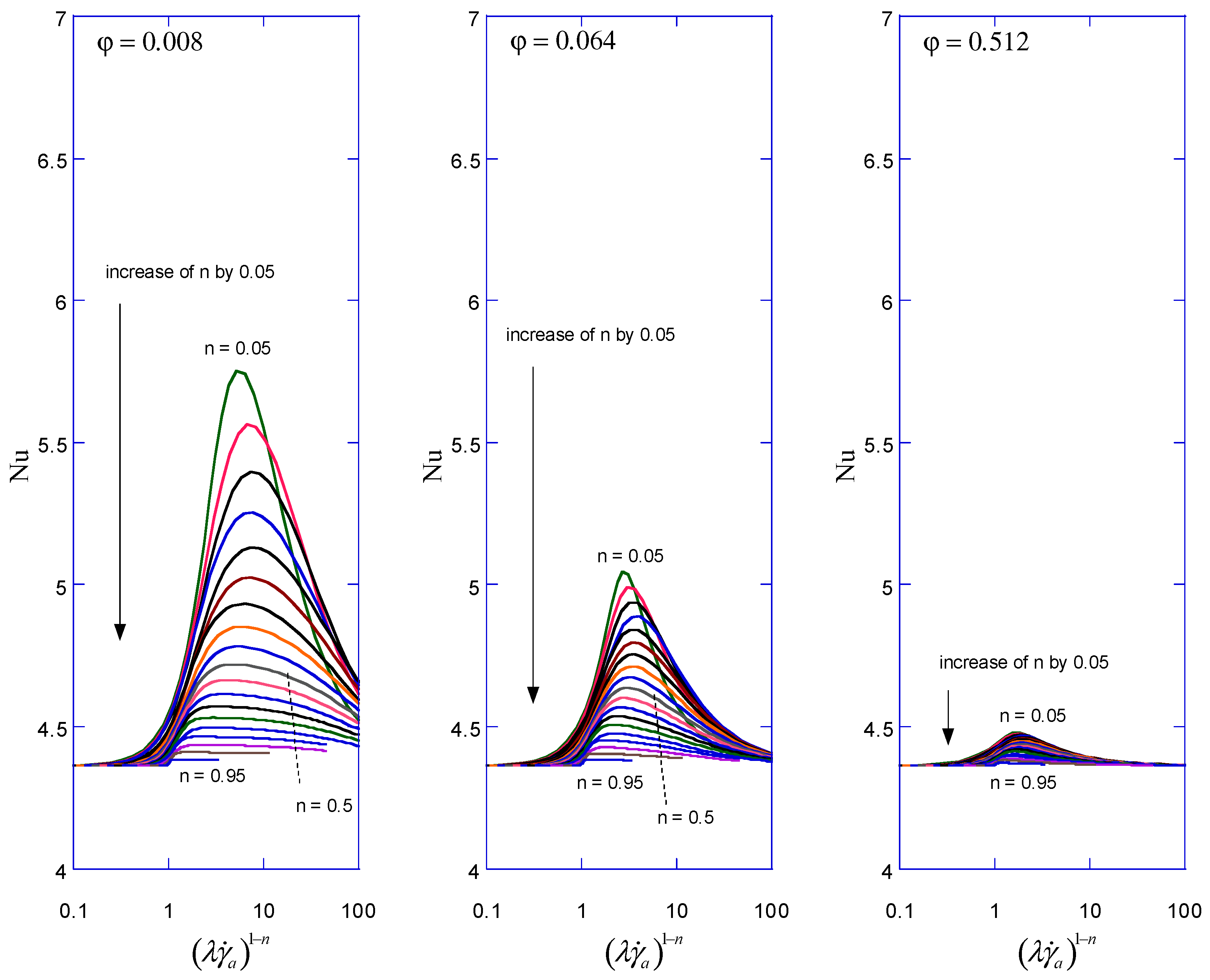
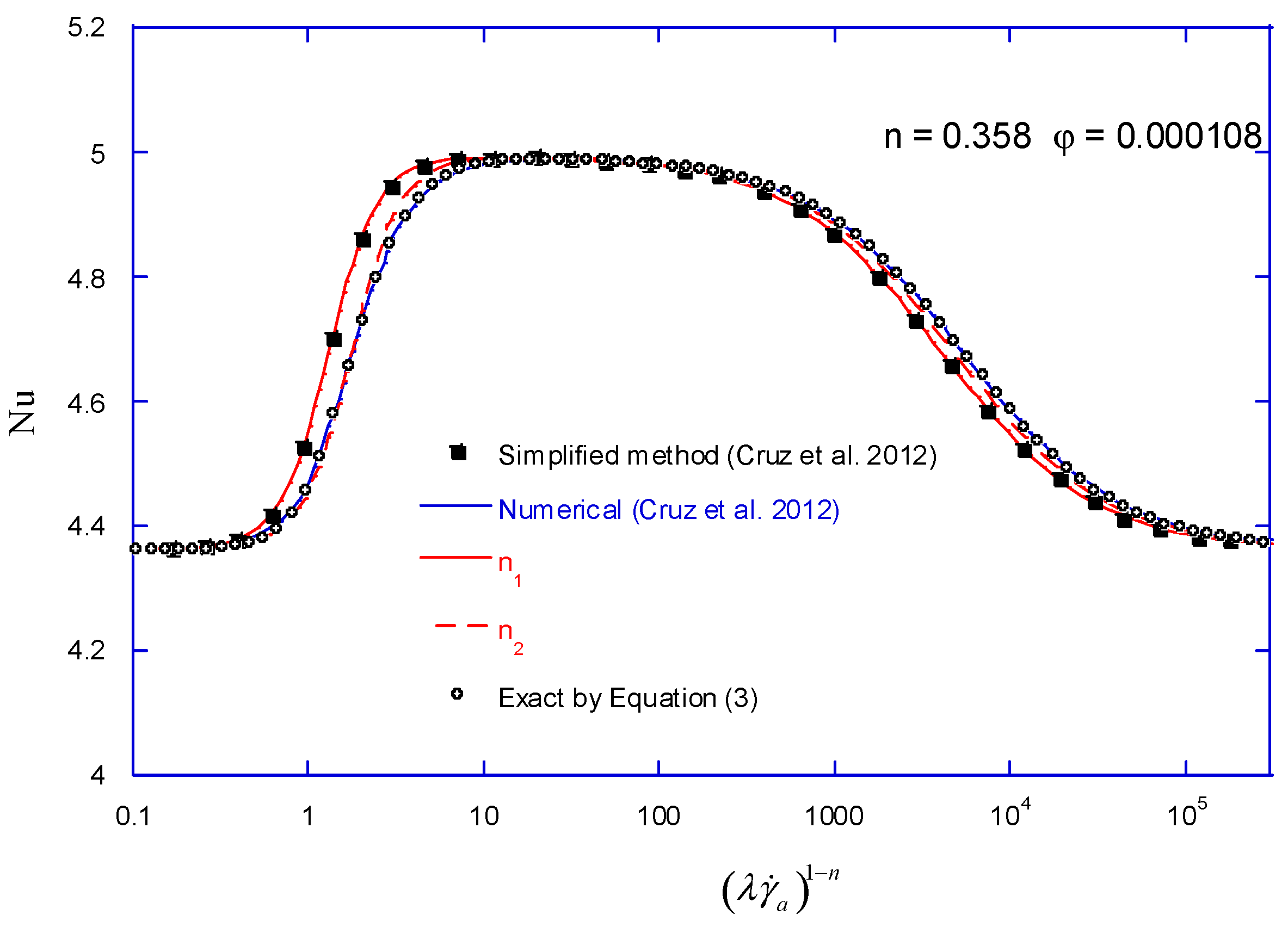
3. Results
3.1. Evaluation of Nusselt Number
3.2. Correlations
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| heat capacity | |
| c(n) | function for apparent index modification |
| d | function for apparent index modification |
| h | heat transfer coefficient |
| h | function for apparent index modification |
| p-th evaluation of the integral by the quadratue | |
| k | thermal conductivity |
| K | consistency of the power law model |
| n | index of the viscosity model (a constant of Carreau model) |
| apparent power law index | |
| modified apparent power law index | |
| Nu | Nusselt number |
| Nusselt number for the Newtonian model | |
| Nusselt number for the power law model | |
| core flow rate | |
| core flow rate for Newtonian model | |
| core flow rate for power law model | |
| core flow rate for Carreau model | |
| uniform wall heat flux | |
| Q | flow rate |
| R | radius |
| r | radial position |
| S | sum of least squares |
| T | temperature |
| mean temperature | |
| surface temperature | |
| u | velocity in the x-direction |
| mean velocity | |
| quadratue for the p-th evaluation at | |
| x | coordinate variable in the flow direction |
| Greek | |
| shear (strain) rate | |
| wall shear rate | |
| apparent wall shear rate | |
| zero-shear viscosity (a constant of Carreau model) | |
| infinite shear rate viscosity (a constant of Carreau model) | |
| φ | ratio of to |
| time constant (a constant of Carreau model) | |
| density | |
| τ | shear stress |
| wall shear stress | |
| subscript | |
| a | apparent |
| C | Carreau |
| i | index for discretized value of n |
| k | index for discretized value of φ |
| m | mean |
| N | Newtonian |
| p | power law |
| w | wall |
References
- Skelland, A.H.P. Non-Newtonian Flow and Heat Transfer; Wiley: New York, NY, USA, 1966. [Google Scholar]
- Patel, S.A.; Chhabra, R.P.; Irvine, T.F., Jr.; Capobianchi, M. Convection heat transfer in non-Newtonian fluids. In CRC Handbook of Thermal Engineering, 2nd ed.; Chhabra, R.P., Ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Skelland, A.H.P. Asymptotic rates of heat or mass transfer in non-Newtonian laminar flow. Ind. Eng. Chem. Res. 1967, 6, 148–151. [Google Scholar] [CrossRef]
- Capobianchi, M.; Irvine, T.F. Predictions of pressure drop and heat transfer in concentric annular ducts with modified power law fluids. Heat Mass Transf. 1992, 27, 209–215. [Google Scholar] [CrossRef]
- Cruz, D.A.; Coelho, P.M.; Alves, M.A. A Simplified Method for Calculating Heat Transfer Coefficients and Friction Factors in Laminar Pipe Flow of Non-Newtonian Fluids. J. Heat Transf. 2012, 134, 091703. [Google Scholar] [CrossRef]
- Saikia, A.; Dalal, A.; Pati, S. Thermo-hydraulic transport characteristics of non-Newtonian fluid flows through corrugated channels. Int. J. Therm. Sci. 2018, 129, 201–208. [Google Scholar]
- Bharti, R.P.; Chhabra, R.P.; Eswaran, V. Steady forced convection heat transfer from a heated circular cylinder to power-law fluids. Int. J. Heat Mass Transf. 2007, 50, 977–990. [Google Scholar] [CrossRef]
- Izadi, R.; Merdasi, A.; Moosavi, A. Heat transfer of power-law fluids under electrowetting actuation in structured microchannels. Int. Commun. Heat Mass Transf. 2022, 130, 105803. [Google Scholar] [CrossRef]
- Alves, M.A.; Baptista, A.; Coelho, P.M. Simplified method for estimating heat transfer coefficients: Constant wall temperature case. Heat Mass Transf. 2015, 51, 1041–1047. [Google Scholar] [CrossRef]
- Kim, S.K. Forced convection heat transfer for the fully-developed laminar flow of the Cross fluid between parallel plates. J. Non-Newton Fluid Mech. 2020, 276, 104226. [Google Scholar] [CrossRef]
- Capobianchi, M.; Wagner, D. Heat transfer in laminar flows of extended modified power law fluids in rectangular ducts. Int. J. Heat Mass Transf. 2010, 53, 558–563. [Google Scholar] [CrossRef]
- Mendes, M.; Alves, M.A.; Coelho, P. Estimating Heat Transfer Coefficients and Friction Factors in Non-Newtonian Flows between Parallel Plates. Heat Transf. Eng. 2019, 40, 549–558. [Google Scholar] [CrossRef]
- Yasuda, K.; Armstrong, R.C.; Cohen, R.E. Investigation of the analogies between viscometric and linear viscoelastic properties of concentrated polystyrene solutions. J. Rheol. 1980, 24, 359–360. [Google Scholar]
- Cross, M.M. Rheology of non-Newtonian fluids—A new flow equation for pseudo-plastic systems. J. Colloid Sci. 1965, 20, 417–437. [Google Scholar] [CrossRef]
- Carreau, P.J. Rheological equations from molecular network theories. J. Rheol. 1972, 16, 99–127. [Google Scholar] [CrossRef]
- Dealy, J.M.; Read, D.J.; Larson, R.G. Structure and Rheology of Molten Polymers, 2nd ed.; Carl Hanser Verlag: München, Germany, 2018. [Google Scholar]
- Kim, S.K. Collective viscosity model for shear thinning polymeric materials. Rheol. Acta 2020, 59, 63–72. [Google Scholar] [CrossRef]
- Cameron, J.R. Rheological Modeling and Scale-Up of a Delayed-Crosslinked Gel in Nonhomogeneous Flow. SPE Prod. Oper. 1993, 8, 23–29. [Google Scholar] [CrossRef]
- Chhabra, R.P.; Richardson, J.F. Non-Newtonian Flow in the Process Industries; Butterworth-Heinemann: Oxford, UK, 1999. [Google Scholar]
- Haldenwang, R.; Sutherland, A.P.N.; Fester, V.G.; Holm, R.; Chhabra, R.P. Sludge pipe flow pressure drop prediction using composite power-law friction factor–Reynolds number correlations based on different non-Newtonian Reynolds numbers. Water SA 2012, 38, 615–622. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.K. Flow-rate based method for velocity of fully developed laminar flow in tubes. J. Rheol. 2018, 62, 1397–1407. [Google Scholar] [CrossRef]
- Kim, S.K. Darcy friction factor and Nusselt number in laminar tube flow of Carreau fluid. Rheol. Acta 2022, 61, 243–255. [Google Scholar] [CrossRef]
- Coelho, P.M.; Pinho, F.T. A generalized Brinkman number for non-Newtonian duct flows. J. Non-Newton. Fluid Mech. 2009, 156, 202–206. [Google Scholar] [CrossRef]
- Sochi, T. Analytical solutions for the flow of Carreau and Cross fluids in circular tubes and thin slits. Rheol. Acta 2015, 54, 745–756. [Google Scholar] [CrossRef] [Green Version]
- Hahn, T. Cuba—A library for multidimensional numerical integration. Comput. Phys. Commun. 2007, 176, 11–12. [Google Scholar] [CrossRef] [Green Version]
- Genz, A.C.; Malik, A.A. An adaptive algorithm for numeric integration over an N-dimensional rectangular region. J. Comput. Appl. Math. 1980, 6, 295–302. [Google Scholar] [CrossRef] [Green Version]




| Apparent Index Method (Cruz et al. 2012) | Modified Apparent Index Method | |
|---|---|---|
| apparent index | ||
| Nusselt number |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.K. Correlations for Convective Laminar Heat Transfer of Carreau Fluid in Straight Tube Flow. Energies 2022, 15, 2368. https://doi.org/10.3390/en15072368
Kim SK. Correlations for Convective Laminar Heat Transfer of Carreau Fluid in Straight Tube Flow. Energies. 2022; 15(7):2368. https://doi.org/10.3390/en15072368
Chicago/Turabian StyleKim, Sun Kyoung. 2022. "Correlations for Convective Laminar Heat Transfer of Carreau Fluid in Straight Tube Flow" Energies 15, no. 7: 2368. https://doi.org/10.3390/en15072368
APA StyleKim, S. K. (2022). Correlations for Convective Laminar Heat Transfer of Carreau Fluid in Straight Tube Flow. Energies, 15(7), 2368. https://doi.org/10.3390/en15072368






