Modelling of Boil-Off and Sloshing Relevant to Future Liquid Hydrogen Carriers
Abstract
:1. Introduction
2. Thermodynamic Model
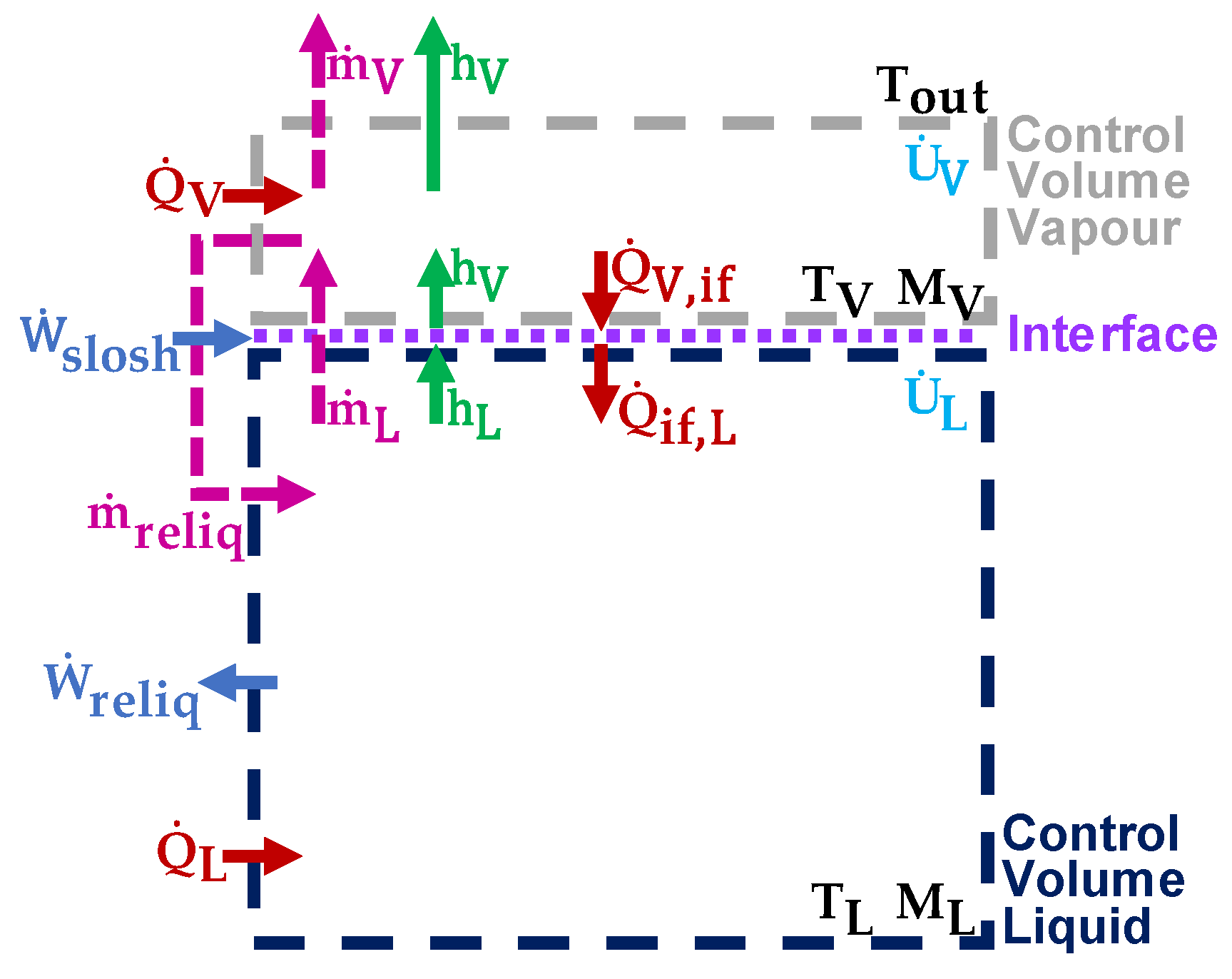
2.1. Generalised Thermodynamic Model
2.2. Thermodynamic Model for an Unsealed, Laden Cryogenic Tank
2.3. Addition of a Reliquefaction Unit
3. Ship Model
3.1. Ship Sizing
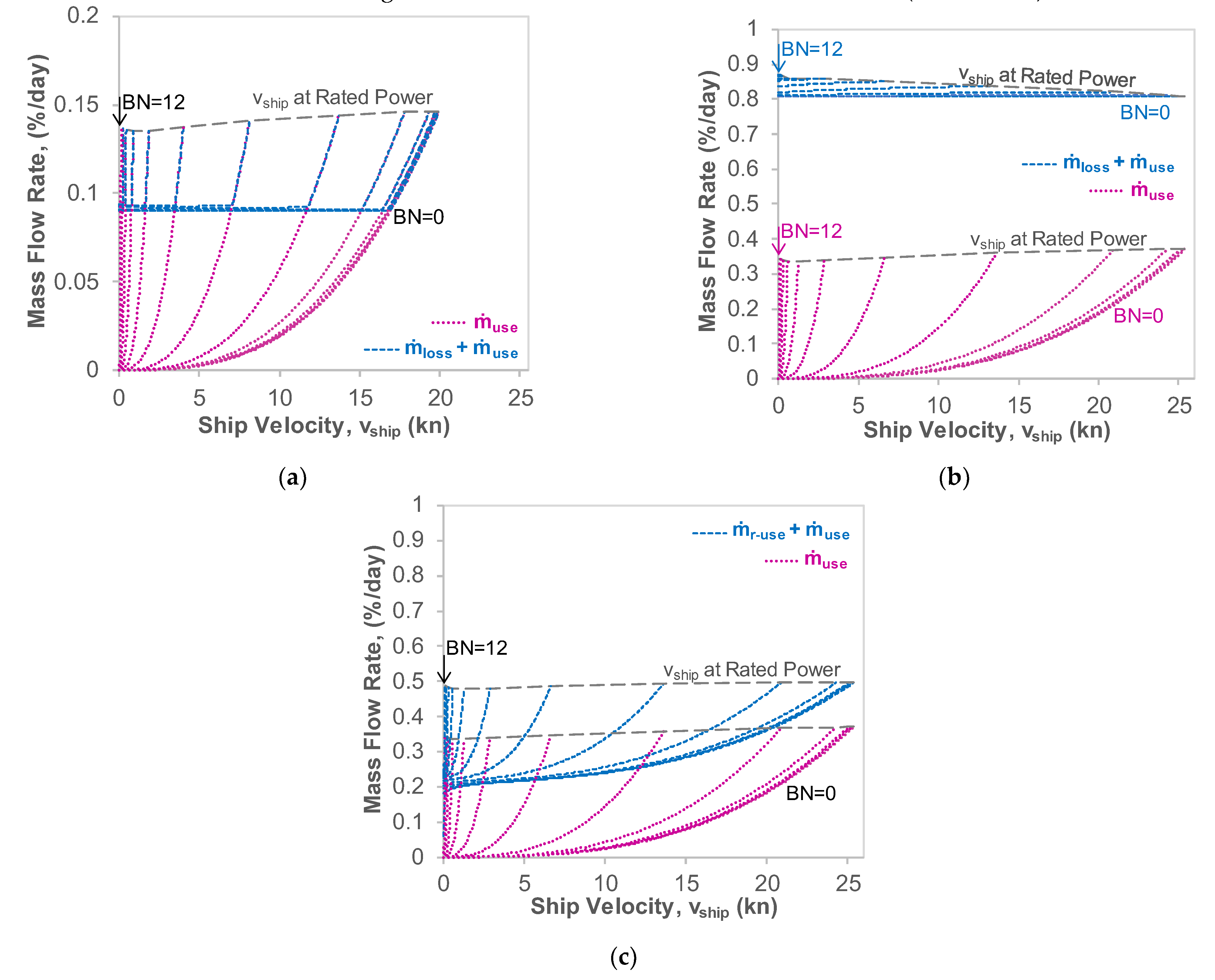
3.2. Power Consumption and Fuel Utilisation
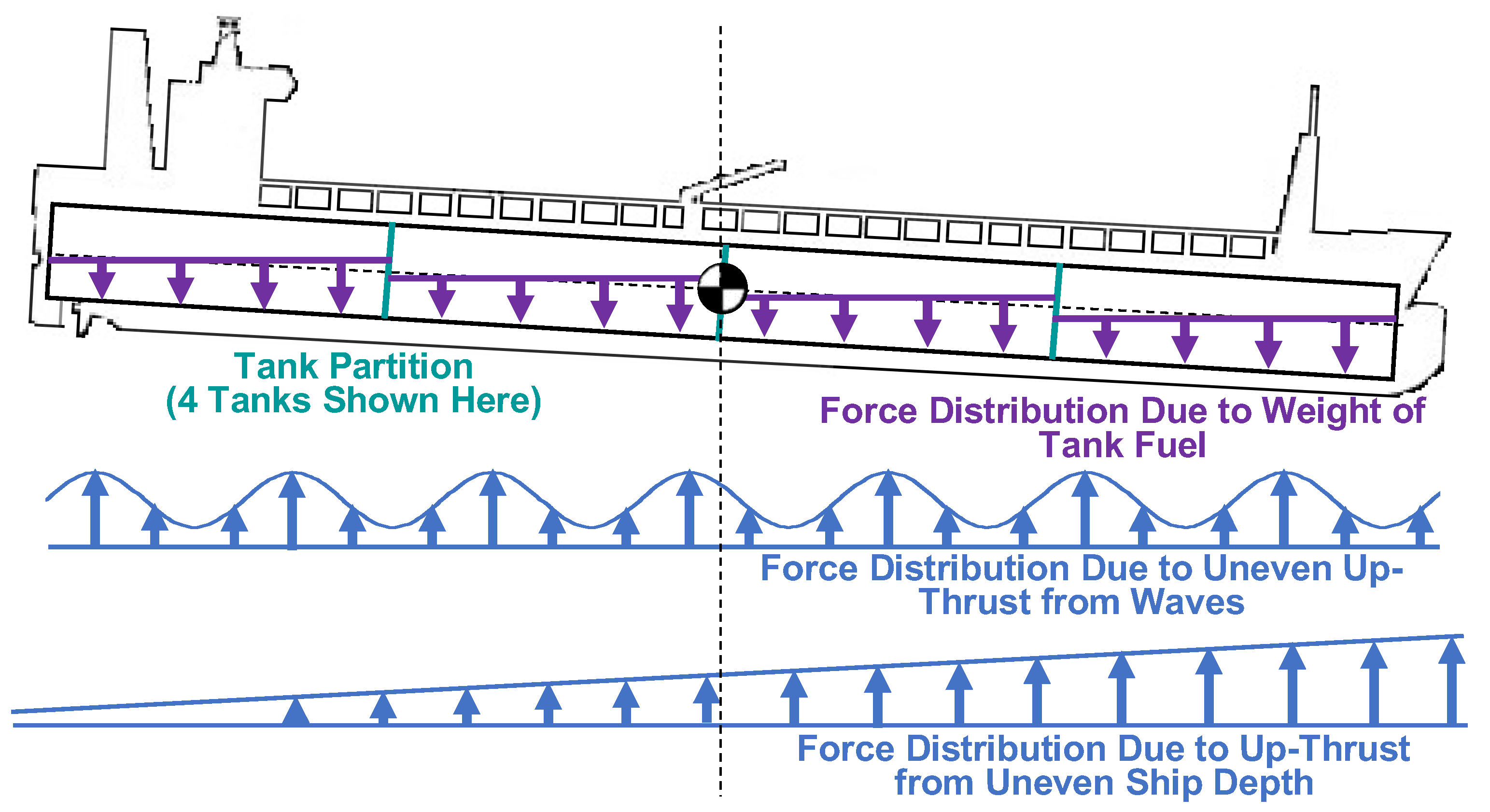
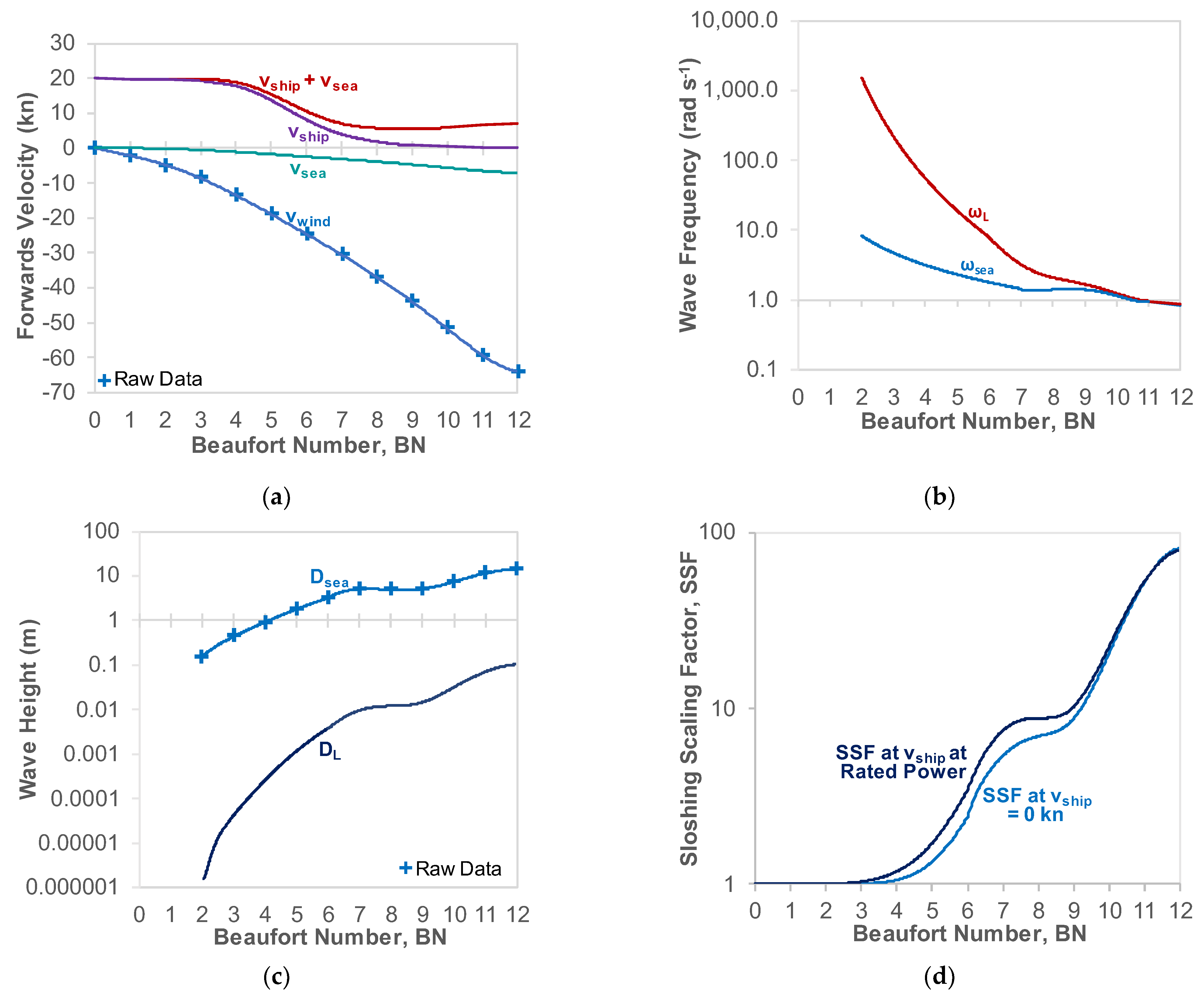
3.3. Sloshing
4. Investigated Fuel Carriers and Design Alterations
4.1. Conventional Liquefied Natural Gas Carrier
| Input | Unit | Quantity |
|---|---|---|
| Ship Velocity | kn | 16.7 |
| Beaufort Number | - | 2 |
| Fuel Utilisation Rate for Propulsion (Best Fit) | kg s−1, %/day | 0.757, 0.0905 |
| Power Consumption (Best Fit) | kW | 14,600 |
| Input | Unit | Quantity | Source |
|---|---|---|---|
| Internal Pressure of Tank | bar | 1.01325 | [28] |
| Average External Pressure | bar | 1.01325 | [67] |
| Average External Sea Temperature | K | 288 | [66] |
| Heat Transfer Rate to Liquid | kW | 386 | [28] |
| Temperature of Liquid | K | 110 | [28] |
| Specific Enthalpy of Vapour Relative to Specific Internal Energy of Liquid * | kJ kg−1 | 685.8 | [44] |
| Total Boil-Off Rate | kg s−1 %/day | 0.757 0.0905 | [28] |
| Surface Area of Tank in Contact with Vapour (Calculated from The Tank Dimensions) | m2 | 8610 | [63] |
| Surface Area of Tank in Contact with Liquid (Calculated from The Tank Dimensions) | m2 | 23,660 | [63] |
| Surface Area of Liquid-Vapour Interface (Calculated from The Tank Dimensions) | m2 | 8296 | [63] |
4.2. Conceptual Liquid Hydrogen Carrier
4.3. Addition of a Reliquefaction Unit
4.4. Use of Electric Propulsion
5. Model Application
5.1. Boil-Off Properties of Combustion Ship Models
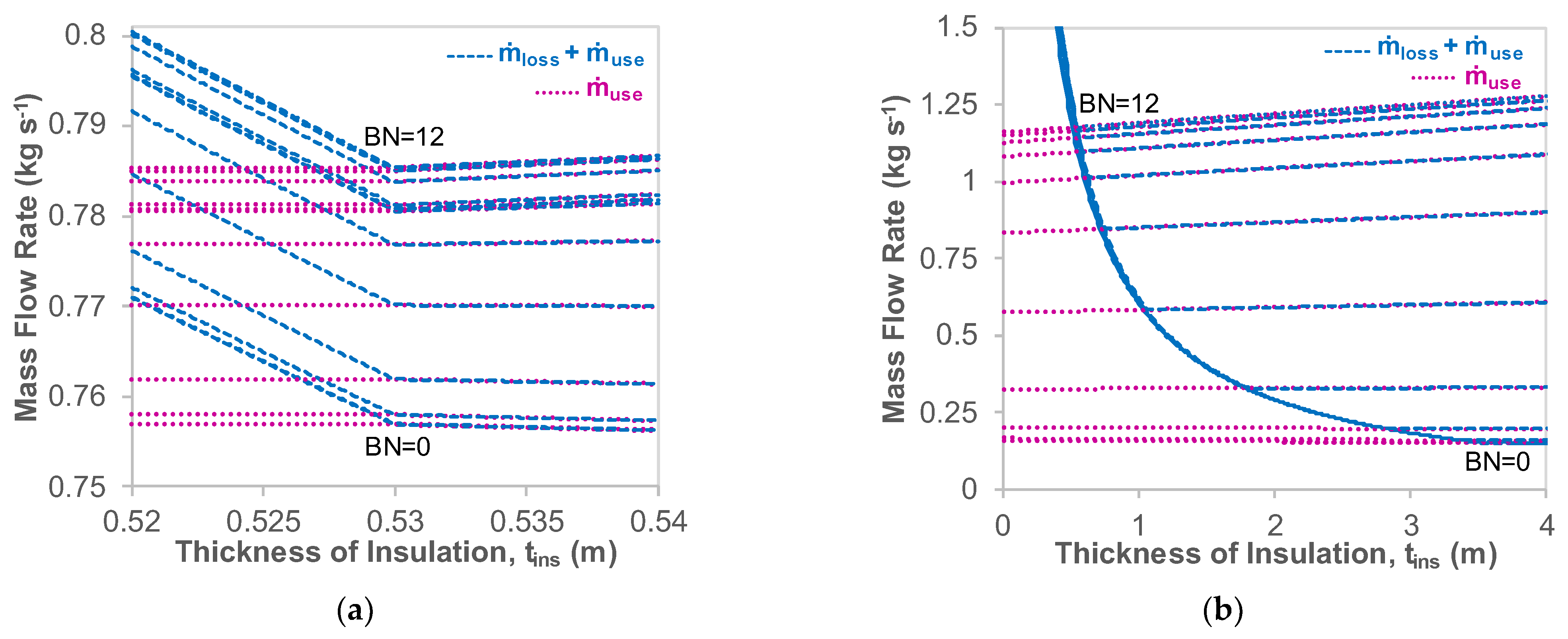
5.2. Effect of Insulation Thickness
5.3. Effect of Electrification
5.4. Additional Fuel Tank Design Variations
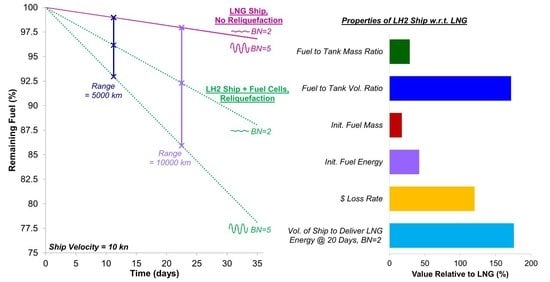
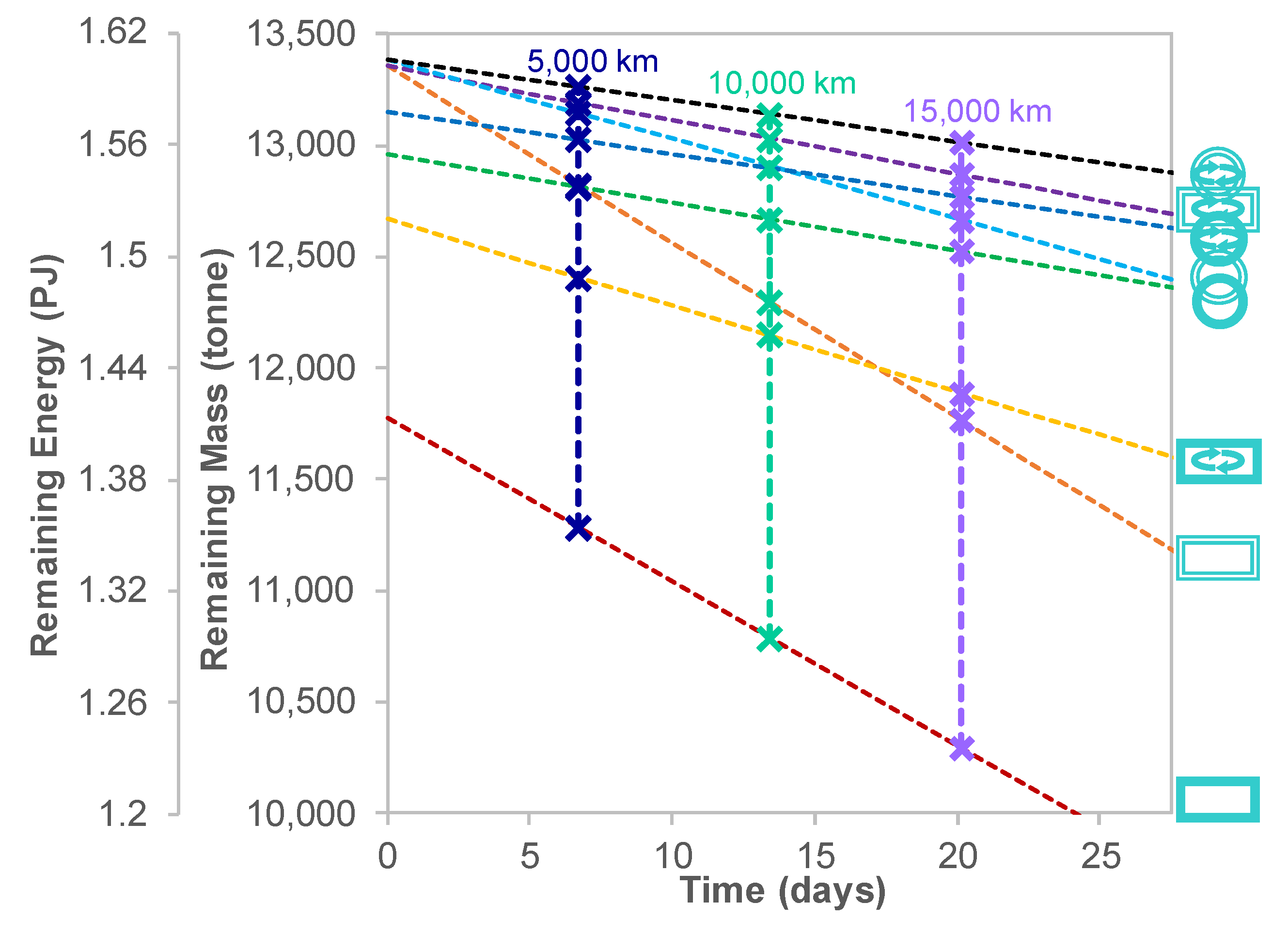
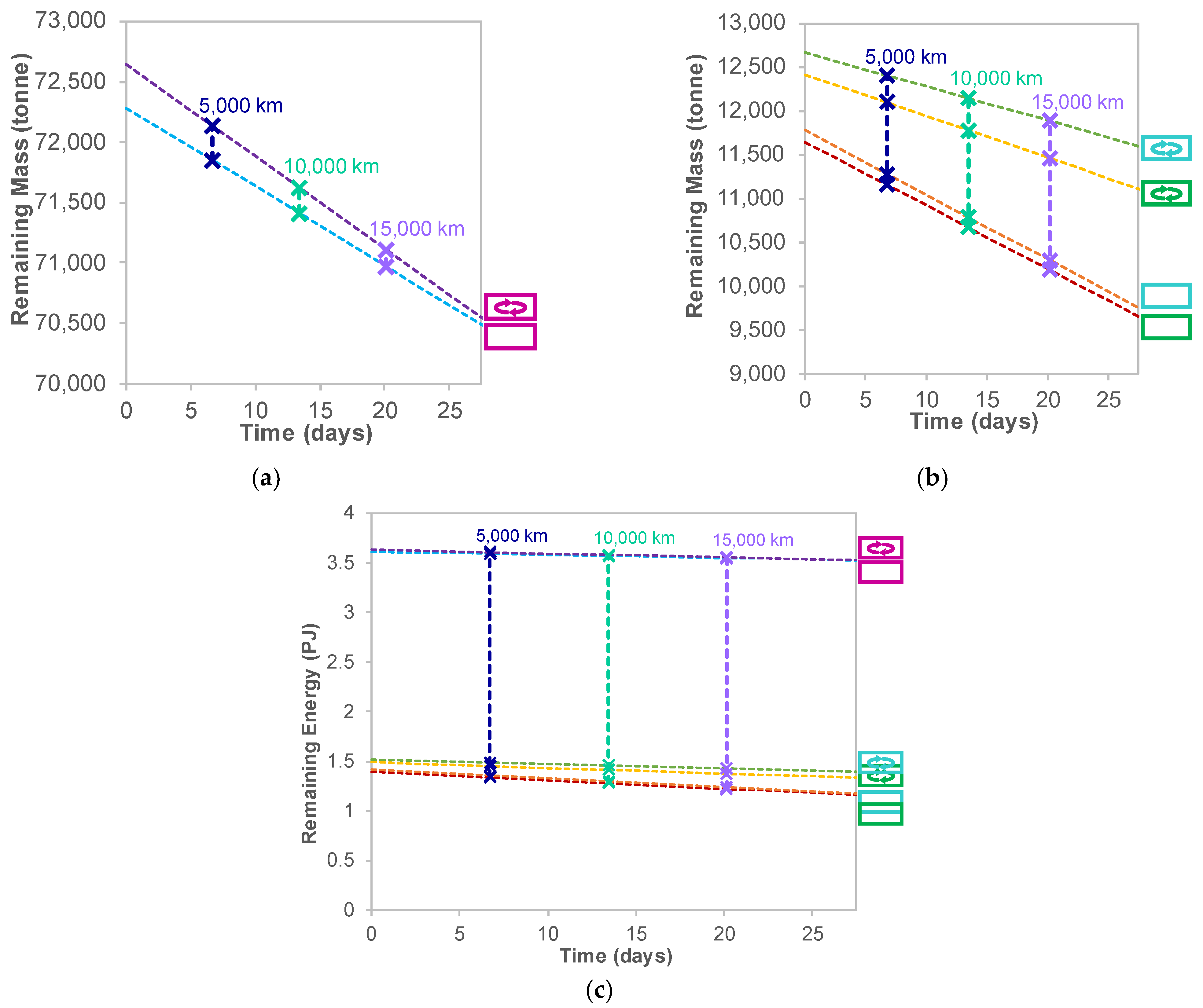
5.5. Sizing Considerations for Targeting a Specific Delivered Energy
6. Conclusions and Recommendations for Future Work
- (1)
- An LH2 carrier with the same fuel tank volume and insulation thickness as an LNG carrier can contain 16.8% of the fuel mass and 40.2% of the fuel energy. The unforced BOR of the LH2 carrier is 8.94 times higher than that of an LNG ship.
- (2)
- The heat transfer and boil-off effects of sloshing on an LH2 carrier are more significant than those on an LNG carrier. In particular, the rate of BOR increase with BN on board the LH2 ship is twice as large relative to an LNG carrier.
- (3)
- Adding a reliquefaction unit to the vessel reduces the fuel depletion rate by at least 38.7%. However, this reduction is highly dependent on the weather and ship velocity, so reliquefaction introduces a significantly higher sensitivity of the fuel depletion rate and delivered fuel to the operating conditions.
- (4)
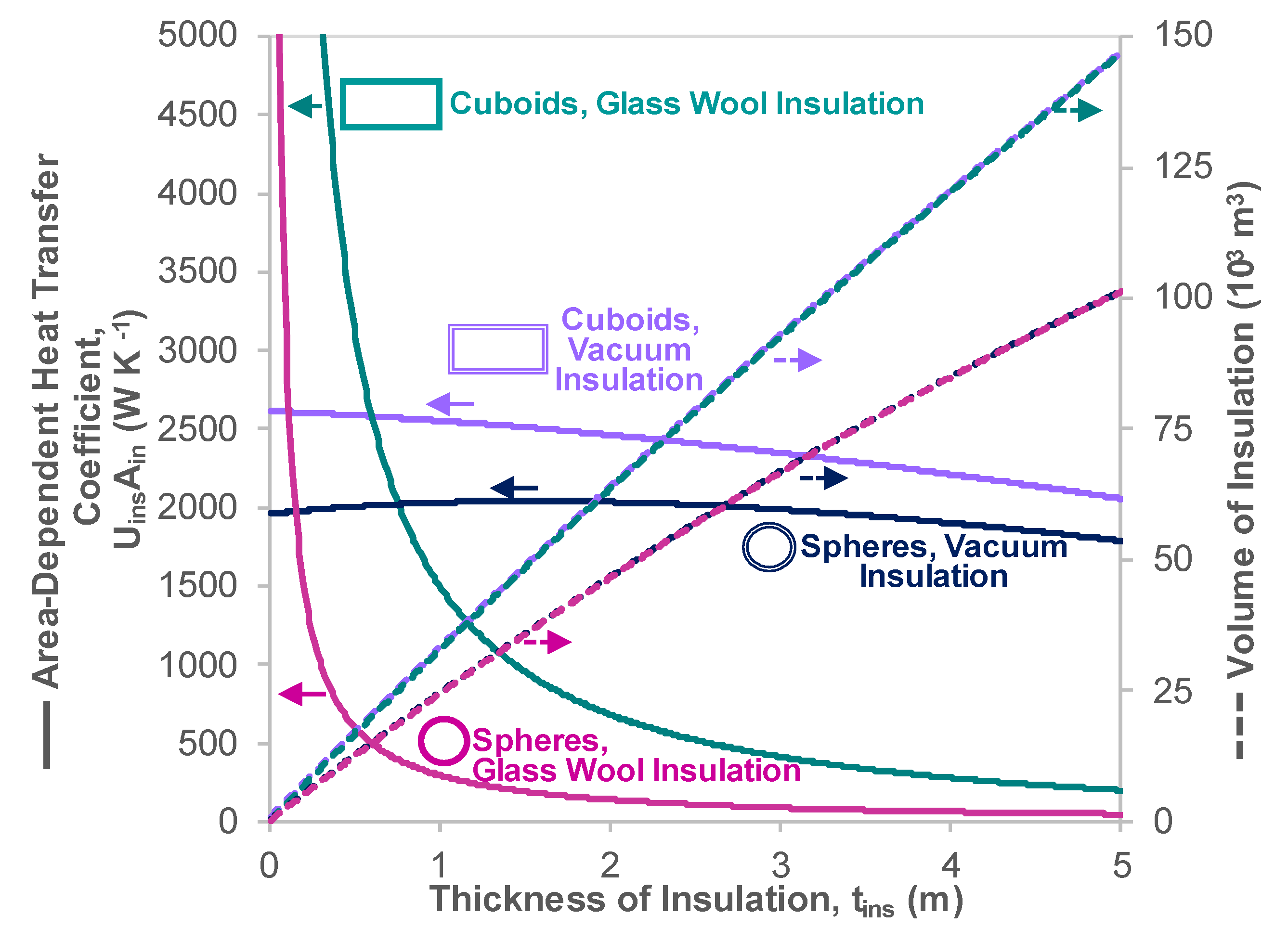
- A parametric analysis illustrated that 1.04 to 6.62 times the insulation thickness of glass wool is required to allow the LH2 carrier to have BOR properties equivalent to the LNG ship, primarily due to the lower LH2 temperature.
- (5)
- An LH2 carrier powered by fuel cells and electric motors delivers at least 1.1% more cargo fuel than one with internal combustion engines due to the lower volume of the electric propulsion system and the higher efficiency of fuel cell and electric motor propulsion.
- (6)
- An LH2 carrier operating with fuel cells and reliquefaction must be at least 1.73 times larger by volume than the LNG carrier to deliver the same energy.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Additional Data Tables
| Value Name | Unit | Quantity |
|---|---|---|
| Density of Sea Water | kg m−3 | 1026 |
| Dynamic Viscosity | Pa-s | 0.00117 |
| Velocity (kn) | Propulsive Power (kW) | Fuel Utilisation Rate (ton/day) |
|---|---|---|
| 10 | 3442 | 29 |
| 11 | 4537 | 34 |
| 12 | 5837 | 40 |
| 13 | 7334 | 47 |
| 14 | 9033 | 55 |
| 15 | 10,936 | 63 |
| 16 | 13,037 | 73 |
| 17 | 15,340 | 83 |
| 18 | 17,878 | 95 |
| 19 | 20,746 | 108 |
| 19.5 | 22,361 | 115 |
| Input | Unit | Quantity | Source |
|---|---|---|---|
| Volumetric Power Density of Heat Exchangers in Reliquefaction Unit * | W m−3 | 75,700 | [75] |
| Estimated Percentage Volume of Aluminium in Reliquefaction Unit Heat Exchangers * | % | 4 | [75] |
| Density of Aluminium | kg m−3 | 2700 | [76] |
| Gravimetric Power Density | W kg−1 | 1020 | [77] |
| Volumetric Power Density | MW m−3 | 1.74 | [77] |
Appendix B. Variation of Boil-Off with Fuel Tank Number and Shape
Appendix B.1. Effect of Fuel Tank Number with Cuboidal Tanks
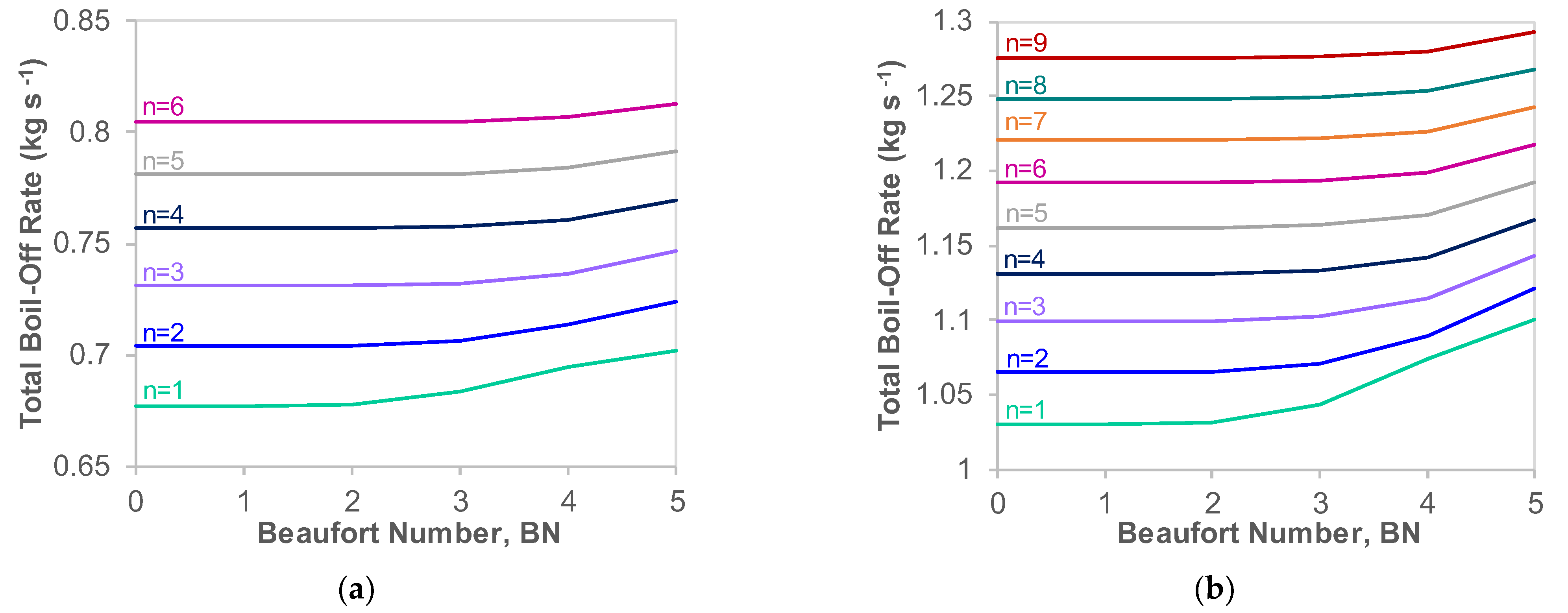
Appendix B.2. Conversion to Spherical Tanks
Appendix C. Heat Transfer Properties of Vacuum Insulated Tanks
| Input | Unit | Quantity | Source |
|---|---|---|---|
| Failure Stress of Aluminium | MPa | 438 | [81] |
| Acceptable Ratio of Maximum Tensile Stress to Failure Stress (mid-range value) | - | 1.7 | [79] |
| Emissivity of Aluminium | - | 0.1 | [67] |
| Input | Unit | Tank Shape | Insulation Type | Quantity | Source |
|---|---|---|---|---|---|
| Heat Transfer Coefficient, | W m−2 K−1 | Cuboid | Glass Wool | 0.092 | Section 4.1 |
| Cuboid | Vacuum Casing | 0.080 | This Section | ||
| Sphere | Glass Wool | 0.023 | Appendix B.2 | ||
| Sphere | Vacuum Casing | 0.083 | This Section | ||
| Surface Area for Heat Ingress Across Tank Wall, | m2 | Cuboid | Any | 32,200 | Section 4.1 |
| Sphere | Any | 24,300 | This Section | ||
| Area Dependent Heat Transfer Coefficient | W K−1 | Cuboid | Glass Wool | 2960 | Above Rows |
| Vacuum Casing | 2590 | Above Rows | |||
| Sphere | Glass Wool | 570 | Above Rows | ||
| Vacuum Casing | 2010 | Above Rows | |||
| Volume of Tank Material | m3 | Cuboid | Any | 17,600 | Table 1 |
| Sphere | Any | 13,200 | Appendix B.2 |
Appendix D. Comparison of Additional Designs
| Ship Variable | Identifier Type | Categories | Identifier | Demonstration |
|---|---|---|---|---|
| Fuel and Propulsion Type | Colour | Methane Internal Combustion Engine | Pink | |
| Hydrogen Internal Combustion Engine | Green | |||
| Hydrogen Electric | Light Blue | |||
| Tank Shape | Icon Shape | Cuboid | Rectangle |  |
| Sphere | Circle |  | ||
| Insulation Type | Outline Type | Glass Wool | Single Line |  |
| Vacuum Insulation | Double Line |  | ||
| Presence of Reliquefaction | Presence of Reliquefaction Symbol | Reliquefaction Present | Symbol Present |  |
| Reliquefaction Absent | Symbol Absent |
| (a) | |||||
|---|---|---|---|---|---|
| Fuel and Propulsion Type | Ship Type | Thickness of Insulation (m) | Initial Mass of Fuel (103 ton) | Mass of Tank (103 ton) | Other Masses (103 ton) |
| Methane Internal Combustion Engine |  | 0.53 | 72.29 | 0.85 | 23.62 |
 | 0.01 | 71.67 | 1.46 | 23.62 | |
 | 0.07 | 73.05 | 0.09 | 23.62 | |
 | 0.01 | 72.60 | 0.53 | 23.62 | |
 | 0.31 | 72.64 | 0.49 | 23.62 | |
 | 0.01 | 71.67 | 1.46 | 23.62 | |
 | 0.07 | 73.05 | 0.09 | 23.62 | |
 | 0.01 | 72.60 | 0.53 | 23.62 | |
| Hydrogen Internal Combustion Engine |  | 0.72 | 11.65 | 1.14 | 23.87 |
 | 0.01 | 13.24 | 1.60 | 23.87 | |
 | 0.26 | 12.85 | 0.31 | 23.87 | |
 | 0.01 | 13.27 | 0.53 | 23.87 | |
 | 0.38 | 12.42 | 0.61 | 23.87 | |
 | 0.01 | 13.24 | 1.60 | 23.87 | |
 | 0.17 | 13.00 | 0.21 | 23.87 | |
 | 0.01 | 13.27 | 0.53 | 23.87 | |
| Hydrogen Fuel Cell |  | 0.71 | 11.78 | 1.13 | 23.18 |
 | 0.01 | 13.35 | 1.62 | 23.18 | |
 | 0.26 | 12.96 | 0.32 | 23.18 | |
 | 0.01 | 13.39 | 0.54 | 23.18 | |
 | 0.32 | 12.67 | 0.52 | 23.18 | |
 | 0.01 | 13.35 | 1.62 | 23.18 | |
 | 0.15 | 13.15 | 0.18 | 23.18 | |
 | 0.01 | 13.39 | 0.54 | 23.18 | |
| (b) | |||||
| Fuel and Propulsion Type | Ship Type | Volume of Tank (103 m3) | Other Volumes (103 m3) | Fuel Depletion Rate (%/day) | Revenue Loss Rate (103 $/day) |
| Methane Internal Combustion Engine |  | 17.62 | 171.97 | 0.0905 | 21.6 |
 | 0.84 | 190.24 | 0.1043 | 24.7 | |
 | 1.78 | 171.97 | 0.0895 | 21.6 | |
 | 0.44 | 171.97 | 0.0901 | 21.6 | |
 | 10.20 | 178.54 | 0.1048 | 25.1 | |
 | 0.84 | 190.24 | 0.0944 | 22.3 | |
 | 1.78 | 171.97 | 0.0895 | 21.6 | |
 | 0.44 | 171.97 | 0.0901 | 21.6 | |
| Hydrogen Internal Combustion Engine |  | 23.79 | 171.97 | 0.6224 | 57.7 |
 | 0.90 | 171.97 | 0.5945 | 62.6 | |
 | 6.55 | 171.97 | 0.1681 | 17.2 | |
 | 0.44 | 171.97 | 0.2686 | 28.4 | |
 | 12.70 | 171.97 | 0.3816 | 37.7 | |
 | 0.90 | 171.97 | 0.2463 | 25.9 | |
 | 4.30 | 171.97 | 0.1702 | 17.6 | |
 | 0.44 | 171.97 | 0.1758 | 18.6 | |
| Hydrogen Fuel Cell |  | 23.57 | 170.31 | 0.6258 | 58.6 |
 | 0.91 | 170.31 | 0.5907 | 62.8 | |
 | 6.59 | 170.31 | 0.1676 | 17.3 | |
 | 0.44 | 170.31 | 0.2678 | 28.5 | |
 | 10.76 | 170.31 | 0.3061 | 30.9 | |
 | 0.91 | 170.31 | 0.1800 | 19.1 | |
 | 3.82 | 170.31 | 0.1440 | 15.1 | |
 | 0.44 | 170.31 | 0.1377 | 14.7 | |
References
- Raj, R.; Ghandehariun, S.; Kumar, A.; Geng, J.; Linwei, M. A techno-economic study of shipping LNG to the Asia-Pacific from Western Canada by LNG carrier. J. Nat. Gas Sci. Eng. 2016, 34, 979–992. [Google Scholar] [CrossRef]
- The Hydrogen Council Hydrogen Decarbonization Pathways. Available online: https://hydrogencouncil.com/wp-content/uploads/2021/01/Hydrogen-Council-Report_Decarbonization-Pathways_Executive-Summary.pdf (accessed on 6 February 2022).
- Fernández, I.A.; Gómez, M.R.; Gómez, J.R.; López-González, L.M. H2 production by the steam reforming of excess boil off gas on LNG vessels. Energy Convers. Manag. 2017, 134, 301–313. [Google Scholar] [CrossRef]
- Krikkis, R.N. A thermodynamic and heat transfer model for LNG ageing during ship transportation. Towards an efficient boil-off gas management. Cryogenics 2018, 92, 76–83. [Google Scholar] [CrossRef]
- Ekanem Attah, E.; Bucknall, R. An analysis of the energy efficiency of LNG ships powering options using the EEDI. Ocean Eng. 2015, 110, 62–74. [Google Scholar] [CrossRef]
- Qu, Y.; Noba, I.; Xu, X.; Privat, R.; Jaubert, J.N. A thermal and thermodynamic code for the computation of Boil-Off Gas–Industrial applications of LNG carrier. Cryogenics 2019, 99, 105–113. [Google Scholar] [CrossRef]
- Schönsteiner, K.; Massier, T.; Hamacher, T. Sustainable transport by use of alternative marine and aviation fuels—A well-to-tank analysis to assess interactions with Singapore’s energy system. Renew. Sustain. Energy Rev. 2016, 65, 853–871. [Google Scholar] [CrossRef]
- Banaszkiewicz, T.; Chorowski, M.; Gizicki, W.; Jedrusyna, A.; Kielar, J.; Malecha, Z.; Piotrowska, A.; Polinski, J.; Rogala, Z.; Sierpowski, K.; et al. Liquefied Natural Gas in Mobile Applications—Opportunities and Challenges. Energies 2020, 13, 5673. [Google Scholar] [CrossRef]
- McFarlan, A. Techno-economic assessment of pathways for liquefied natural gas (LNG) to replace diesel in Canadian remote northern communities. Sustain. Energy Technol. Assess. 2020, 42, 100821. [Google Scholar] [CrossRef]
- Awoyomi, A.; Patchigolla, K.; Anthony, E.J. Process and Economic Evaluation of an Onboard Capture System for LNG-Fueled CO2 Carriers. Ind. Eng. Chem. Res. 2020, 59, 6951–6960. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2007: The Physical Science Basis. In Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; Volume 59, p. 996. [Google Scholar]
- Wijayanta, A.T.; Oda, T.; Purnomo, C.W.; Kashiwagi, T.; Aziz, M. Liquid hydrogen, methylcyclohexane, and ammonia as potential hydrogen storage: Comparison review. Int. J. Hydrog. Energy 2019, 44, 15026–15044. [Google Scholar] [CrossRef]
- Hansson, J.; Månsson, S.; Brynolf, S.; Grahn, M. Alternative marine fuels: Prospects based on multi-criteria decision analysis involving Swedish stakeholders. Biomass Bioenergy 2019, 126, 159–173. [Google Scholar] [CrossRef]
- Al-Breiki, M.; Bicer, Y. Investigating the technical feasibility of various energy carriers for alternative and sustainable overseas energy transport scenarios. Energy Convers. Manag. 2020, 209, 112652. [Google Scholar] [CrossRef]
- Güler, E.; Ergin, S. An investigation on the solvent based carbon capture and storage system by process modeling and comparisons with another carbon control methods for different ships. Int. J. Greenh. Gas Control 2021, 110, 103438. [Google Scholar] [CrossRef]
- A Seamless Hydrogen Supply Chain. Available online: https://media.nature.com/original/magazine-assets/d42473-020-00544-8/d42473-020-00544-8.pdf (accessed on 6 February 2022).
- Kawasaki Develops Cargo Containment System for Large Liquefied Hydrogen Carrier with World’s Highest Carrying Capacity—AiP Obtained from ClassNK. Available online: https://global.kawasaki.com/en/corp/newsroom/news/detail/?f=20210506_9983 (accessed on 6 February 2022).
- Kamiya, S.; Nishimura, M.; Harada, E. Study on introduction of CO2 free energy to Japan with liquid hydrogen. Phys. Procedia 2015, 67, 11–19. [Google Scholar] [CrossRef] [Green Version]
- Ahn, J.; You, H.; Ryu, J.; Chang, D. Strategy for selecting an optimal propulsion system of a liquefied hydrogen tanker. Int. J. Hydrog. Energy 2017, 42, 5366–5380. [Google Scholar] [CrossRef]
- Alkhaledi, A.N.F.N.R.; Sampath, S.; Pilidis, P. A hydrogen fuelled LH2 tanker ship design. Ships Offshore Struct. 2021, 1–10. [Google Scholar] [CrossRef]
- Korberg, A.D.; Brynolf, S.; Grahn, M.; Skov, I.R. Techno-economic assessment of advanced fuels and propulsion systems in future fossil-free ships. Renew. Sustain. Energy Rev. 2021, 142, 110861. [Google Scholar] [CrossRef]
- Leo, T.J.; Durango, J.A.; Navarro, E. Exergy analysis of PEM fuel cells for marine applications. Energy 2010, 35, 1164–1171. [Google Scholar] [CrossRef]
- Klebanoff, L.E.; Pratt, J.W.; LaFleur, C.B. Comparison of the safety-related physical and combustion properties of liquid hydrogen and liquid natural gas in the context of the SF-BREEZE high-speed fuel-cell ferry. Int. J. Hydrog. Energy 2017, 42, 757–774. [Google Scholar] [CrossRef] [Green Version]
- Marandi, S.; Mohammadkhani, F.; Yari, M. An efficient auxiliary power generation system for exploiting hydrogen boil-off gas (BOG) cold exergy based on PEM fuel cell and two-stage ORC: Thermodynamic and exergoeconomic viewpoints. Energy Convers. Manag. 2019, 195, 502–518. [Google Scholar] [CrossRef]
- Liu, Z.; Li, C. Influence of slosh baffles on thermodynamic performance in liquid hydrogen tank. J. Hazard. Mater. 2018, 346, 253–262. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.H.; Cha, S.J.; Kim, J.D.; Kim, J.H.; Kim, S.K.; Lee, J.M. Practical prediction of the boil-off rate of independent-type storage tanks. J. Mar. Sci. Eng. 2021, 9, 36. [Google Scholar] [CrossRef]
- Hydrogen as Marine Fuel. Available online: https://absinfo.eagle.org/acton/attachment/16130/f-bd25832f-8a70-4cc9-b75f-3aadf5d5f259/1/-/-/-/-/hydrogen-as-marine-fuel-whitepaper-21111.pdf (accessed on 6 February 2022).
- Available online: https://www.tradewindsnews.com/gas/maran-gas-maritime-extends-lng-orderbook-with-dsme-option-duo/2-1-1164038 (accessed on 6 February 2022).
- Petitpas, G. Boil-Off Losses along LH2 Pathway; LLNL-TR-750685936219; U.S. Department of Energy: Washington, DC, USA, 2018. [CrossRef]
- Maekawa, K.; Takeda, M.; Hamaura, T.; Suzuki, K.; Miyake, Y.; Matsuno, Y.; Fujikawa, S.; Kumakura, H. First experiment on liquid hydrogen transportation by ship inside Osaka bay. IOP Conf. Ser. Mater. Sci. Eng. 2017, 278, 012066. [Google Scholar] [CrossRef]
- Maekawa, K.; Takeda, M.; Miyake, Y.; Kumakura, H. Sloshing measurements inside a liquid hydrogen tank with external-heating-type MGB2 level sensors during marine transportation by the training ship Fukae-Maru. Sensors 2018, 18, 3694. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wei, G.; Zhang, J. Numerical study of the filling process of a liquid hydrogen storage tank under different sloshing conditions. Processes 2020, 8, 1020. [Google Scholar] [CrossRef]
- Behruzi, P.; Gaulke, D.; Haake, D.; Brosset, L. Modeling of impact waves in LNG ship tanks. Int. J. Offshore Polar Eng. 2017, 27, 18–26. [Google Scholar] [CrossRef]
- Grotle, E.L.; Aesoy, V. Numerical simulations of sloshing and the thermodynamic response due to mixing. Energies 2017, 10, 1338. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.; Ju, Y. Numerical study of the boil-off gas (BOG) generation characteristics in a type C independent liquefied natural gas (LNG) tank under sloshing excitation. Energy 2021, 223, 120001. [Google Scholar] [CrossRef]
- Yu, P.; Yin, Y.-C.; Wei, Z.-J.; Yue, Q.-J. A prototype test of dynamic boil-off gas in liquefied natural gas tank containers. Appl. Therm. Eng. 2020, 180, 115817. [Google Scholar] [CrossRef]
- Mir, H.; Ratlamwala, T.A.H.; Hussain, G.; Alkahtani, M.; Abidi, M.H. Impact of sloshing on fossil fuel loss during transport. Energies 2020, 13, 2625. [Google Scholar] [CrossRef]
- Ludwig, C.; Dreyer, M.E.; Hopfinger, E.J. Pressure variations in a cryogenic liquid storage tank subjected to periodic excitations. Int. J. Heat Mass Transf. 2013, 66, 223–234. [Google Scholar] [CrossRef]
- Igbadumhe, J.F.; Fürth, M. Hydrodynamic analysis techniques for coupled seakeeping-sloshing in zero speed vessels: A review. J. Offshore Mech. Arct. Eng. 2020, 143, 1–37. [Google Scholar] [CrossRef]
- Faltinsen, O.M. Hydrodynamics of marine and offshore structures. J. Hydrodyn. 2015, 26, 835–847. [Google Scholar] [CrossRef]
- Jeong, S.; Jeong, D.; Park, J.; Kim, S.; Kim, B. A voyage optimization model of LNG carriers considering boil-off gas. In Proceedings of the OCEANS 2019 MTS/IEEE SEATTLE, Seattle, WA, USA, 27–31 October 2019. [Google Scholar] [CrossRef]
- Mitra, S.; Wang, C.Z.; Reddy, J.N.; Khoo, B.C. A 3D fully coupled analysis of nonlinear sloshing and ship motion. Ocean Eng. 2012, 39, 1–13. [Google Scholar] [CrossRef]
- Al Ghafri, S.Z.S.; Swanger, A.; Jusko, V.; Siahvashi, A.; Perez, F.; Johns, M.L.; May, E.F. Modelling of Liquid Hydrogen Boil-Off. Energies 2022, 15, 1149. [Google Scholar] [CrossRef]
- Goodwin, D.G.; Speth, R.L.; Moffat, H.K.; Weber, B.W. Cantera: An Object-Oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes; European Organization for Nuclear Research: Genève, Switzerland, 2021. [Google Scholar] [CrossRef]
- Kim, S.; Hwang, H.; Kim, Y.; Park, S.; Nam, K.; Park, J.; Lee, I. Operational Optimization of Onboard Reliquefaction System for Liquefied Natural Gas Carriers. Ind. Eng. Chem. Res. 2020, 59, 10976–10986. [Google Scholar] [CrossRef]
- Son, H.; Kim, J. Automated process design and integration of precooling for energy-efficient BOG (boil-off gas) liquefaction processes. Appl. Therm. Eng. 2020, 181, 116014. [Google Scholar] [CrossRef]
- Son, H.; Kim, J. Energy-efficient process design and optimization of dual-expansion systems for BOG (Boil-off gas) Re-liquefaction process in LNG-fueled ship. Energy 2020, 203, 117823. [Google Scholar] [CrossRef]
- Wang, Z.; Han, F.; Ji, Y.; Li, W. Case Studies in Thermal Engineering Analysis on feasibility of a novel cryogenic heat exchange network with liquid nitrogen regeneration process for onboard liquefied natural gas reliquefaction. Case Stud. Therm. Eng. 2020, 22, 100760. [Google Scholar] [CrossRef]
- Molland, A.; Turnock, S.; Hudson, D. Ship Resistance and Propulsion: Practical Estimation of Propulsive Power; Cambridge University Press: Cambridge, UK, 2011; ISBN 0521760526; 9780521760522. [Google Scholar]
- Chi, Y.; Fuxin, H.; Francis, N. Practical evaluation of the drag of a ship for design and optimization. J. Hydrodyn. 2013, 25, 645–654. [Google Scholar] [CrossRef]
- Moser, C.S.; Wier, T.P.; Grant, J.F.; First, M.R.; Tamburri, M.N.; Ruiz, G.M.; Miller, A.W.; Drake, L.A. Quantifying the total wetted surface area of the world fleet: A first step in determining the potential extent of ships’ biofouling. Biol. Invasions 2016, 18, 265–277. [Google Scholar] [CrossRef]
- Solomon, D.G.; Greco, A.; Masselli, C.; Gundabattini, E.; Rassiah, R.S. A Review on Methods to Reduce Weight and to Increase Efficiency of Electric Motors Using Lightweight Materials, Novel Manufacturing Processes, Magnetic Materials and Cooling Methods. Ann. Chim.-Sci. Des Matériaux 2020, 44, 1–14. [Google Scholar] [CrossRef]
- Aliasand, A.E.; Josh, F.T. Selection of Motor foran Electric Vehicle: A Review. Mater. Today Proc. 2020, 24, 1804–1815. [Google Scholar] [CrossRef]
- Wang, G.; Yu, Y.; Liu, H.; Gong, C.; Wen, S.; Wang, X.; Tu, Z. Progress on design and development of polymer electrolyte membrane fuel cell systems for vehicle applications: A review. Fuel Process. Technol. 2018, 179, 203–228. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, G.; Zhang, X.; Sun, C.; Jiao, K.; Wang, Y. Thermal management of polymer electrolyte membrane fuel cells: A review of cooling methods, material properties, and durability. Appl. Energy 2021, 286, 116496. [Google Scholar] [CrossRef]
- Kifune, H.; Zadhe, M. Efficiency Estimation of Synchronous Generators for Marine Applications and Verification with Shop Trial Data and Real Ship Operation Data. IEEE Trans. J. 2020, 8, 195541–195550. [Google Scholar] [CrossRef]
- Lee, H.; Shao, Y.; Lee, S.; Roh, G.; Chun, K.; Kang, H. Analysis and assessment of partial re-liquefaction system for liquefied hydrogen tankers using liquefied natural gas (LNG)and H2 hybrid propulsion. Int. J. Hydrog. Energy 2019, 44, 15056–15071. [Google Scholar] [CrossRef]
- Beaufort Scale. Available online: https://www.britannica.com/science/Beaufort-scale (accessed on 6 February 2022).
- Xue, H.; Chai, T. Path Optimization along Buoys Based on the Shortest Path Tree with Uncertain Atmospheric and Oceanographic Data. Comput. Intell. Neurosci. 2021, 2021, 1–7. [Google Scholar] [CrossRef]
- Le Gouriérès, D. Chapter I-The Wind. In Wind Power Plants; Le Gouriérès, D.B.T.-W.P.P., Ed.; Pergamon: Oxford, UK, 1982; pp. 1–29. ISBN 978-0-08-029966-2. [Google Scholar]
- Lin, C.S.; Van Dresar, N.T.; Hasan, M.M. Pressure control analysis of cryogenic storage systems. J. Propuls. Power 2004, 20, 480–485. [Google Scholar] [CrossRef] [Green Version]
- Tonnage Shipping. Available online: https://www.britannica.com/technology/gross-tonnage (accessed on 6 February 2022).
- Maran Gas Amphipolis. Available online: https://www.vesselfinder.com/vessels/MARAN-GAS-AMPHIPOLIS-IMO-9701217-MMSI-241414000 (accessed on 6 February 2022).
- Acoustic and Thermal Insulating Materials. In Building Decorative Materials; Li, Y.; Ren, S.; Zhou, Y.; Liu, H. (Eds.) Woodhead Publishing: Cambridge, UK, 2011; pp. 359–374. [Google Scholar] [CrossRef]
- MAN Diesel & Turbo Marine Engine Programme. Available online: https://www.man-es.com/docs/default-source/marine/marine-engine-programme-20205656db69fafa42b991f030191bb3bbb4.pdf?sfvrsn=9cac9964_42 (accessed on 6 February 2022).
- World of Change: Global Temperatures-NASA. Available online: https://earthobservatory.nasa.gov/world-of-change/decadaltemp.php (accessed on 6 February 2022).
- Perry, R.H.; Green, D.W.; Maloney, J.O. Perry’s Chemical Engineers’ Handbook; McGraw-Hill: New York, NY, USA, 1984; ISBN 0070494797. [Google Scholar]
- Klell, M. Storage of Hydrogen in the Pure Form. In Handbook of Hydrogen Storage: New Materials for Future Energy Storage; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010; pp. 1–37. [Google Scholar] [CrossRef]
- Bong, U.; Im, C.; Yoon, J.; An, S.; Jung, S. Investigation on Key Parameters of NI HTS Field Coils for High Power Density Synchronous Motors. IEEE Trans. Appl. Supercond. 2021, 31, 1–5. [Google Scholar] [CrossRef]
- Wang, Y.; Ruiz Diaz, D.F.; Chen, K.S.; Wang, Z.; Adroher, X.C. Materials, technological status, and fundamentals of PEM fuel cells—A review. Mater. Today 2019, 32, 178–203. [Google Scholar] [CrossRef]
- El-Gohary, M.M. The future of natural gas as a fuel in marine gas turbine for LNG carriers. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2012, 226, 371–377. [Google Scholar] [CrossRef]
- Lasserre, F.; Pelletier, S. Polar super seaways? Maritime transport in the Arctic: An analysis of shipowners’ intentions. J. Transp. Geogr. 2011, 19, 1465–1473. [Google Scholar] [CrossRef]
- Natural Gas Prices in 2021. Available online: https://www.switch-plan.co.uk/compare-energy-prices/gas/natural-gas/ (accessed on 6 February 2022).
- Brown, T. The Cost of Hydrogen: Platts Launches Hydrogen Price Assessment. Available online: https://www.ammoniaenergy.org/articles/the-cost-of-hydrogen-platts-launches-hydrogen-price-assessment/ (accessed on 6 February 2022).
- Chang, H.M.; Chung, M.J.; Kim, M.J.; Park, S.B. Thermodynamic design of methane liquefaction system based on reversed-Brayton cycle. Cryogenics 2009, 49, 226–234. [Google Scholar] [CrossRef]
- Chauhan, K.P.S. Influence of Heat Treatment on the Mechanical Properties of Aluminium Alloys (6xxx Series): A Literature Review. Int. J. Eng. Res. 2017, V6, 386–389. [Google Scholar] [CrossRef]
- Ghassemi, M. High power density technologies for large generators and motors for marine applications with focus on electrical insulation challenges. High Volt. 2020, 5, 7–14. [Google Scholar] [CrossRef]
- Xue, M.A.; Jiang, Z.; Hu, Y.A.; Yuan, X. Numerical study of porous material layer effects on mitigating sloshing in a membrane LNG tank. Ocean Eng. 2020, 218, 108240. [Google Scholar] [CrossRef]
- Mital, S.K.; Gyekenyesi, J.Z.; Arnold, S.M.; Sullivan, R.M.; Manderscheid, J.M.; Murthy, P.L.N. Review of Current State of the Art and Key Design Issues with Potential Solutions for Liquid Hydrogen Cryogenic Storage Tank Structures for Aircraft Applications. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20060056194.pdf (accessed on 6 February 2022).
- Siegel, R.; Howell, J.R. Thermal Radiation Heat Transfer; McGraw-Hill: New York, NY, USA, 1971; Volume III. [Google Scholar]
- Chen, Y.; Clausen, A.H.; Hopperstad, O.S.; Langseth, M. Stress-strain behaviour of aluminium alloys at a wide range of strain rates. Int. J. Solids Struct. 2009, 46, 3825–3835. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Jang, C.; Song, T.H. Combined heat transfer in multi-layered radiation shields for vacuum insulation panels: Theoretical/numerical analyses and experiment. Appl. Energy 2012, 94, 295–302. [Google Scholar] [CrossRef]

| Input | Unit | Quantity | Source |
|---|---|---|---|
| Number of Tanks | - | 4 | [28] |
| Deadweight | ton | 95,190 | [63] |
| Density of Glass Wool | kg m−3 | 48 | [64] |
| Fraction of Fuel Vapour | % | 2 | [28] |
| Fuel Capacity | m3 | 173,600 | [28] |
| Gross Tonnage | ton | 113,000 | [63] |
| Rated Power | MW | 23.4 | [28] |
| Ship Beam | m | 46 | [63] |
| Ship Length | m | 295 | [63] |
| Thickness of Glass Wool | m | 0.53 | [28] |
| Reliquefaction Unit Present | True/False | False | [28] |
| Input | Unit | Quantity |
|---|---|---|
| Rated Power | MW | 21.84 |
| Mass | ton | 665 |
| Estimated Volume | m3 | 1568 |
| Input | Unit | Quantity | |||
|---|---|---|---|---|---|
| Natural Gas | Source | Hydrogen | Source | ||
| Temperature of Liquid | K | 110 | [28] | 20.15 | [14] |
| Density of Liquid | kg m−3 | 425 | [28] | 70.95 | [44] |
| Temperature of Vapour (Evaluated) | K | 119.5 | - | 24.3 | - |
| Density of Vapour | kg m−3 | 1.684 | [44] | 1.071 | [44] |
| Lower Calorific Heating Value | MJ kg−1 | 50.01 | [67] | 120 | [68] |
| Specific Enthalpy of Vapour Relative to Specific Internal Energy of Liquid * | kJ kg−1 | 685.8 | [44] | 698.1 | [44] |
| Input | Unit | Quantity |
|---|---|---|
| Boil-Off Rate of Liquefied Natural Gas Ship | %/day | 0.1204 |
| Boil-Off Rate of Liquid Hydrogen Ship | %/day | 1.063 |
| Temperature of Liquid Natural Gas | K | 111 |
| External Temperature | K | 298 |
| Input | Unit | Quantity | Source |
|---|---|---|---|
| Electricity Requirement Per Unit of Reliquefied Natural Gas Mass Flow Rate, (Approximately Mid-Range) | kWh/kg | 1.25 | [45,46,47,48] |
| Electricity Requirement Per Unit of Reliquefied Hydrogen Mass Flow Rate, | kWh/kg | 3.30 | [57] |
| Specific Enthalpy of Vapour Relative to Liquid for Natural Gas * | kJ kg−1 | 533.1 | [44] |
| Specific Enthalpy of Vapour Relative to Liquid for Hydrogen * | kJ kg−1 | 494.2 | [44] |
| Efficiency of Generator (Independent of Engine, Approximately Mid-Range) | % | 92.5 | [56] |
| Input | Unit | Quantity | Source |
|---|---|---|---|
| Overall Electric Engine Efficiency (Mid-Range, Conservative Estimate to Upper Bound) | % | 92.5, 90 to 95 | [52,53] |
| Gravimetric Power Density of Electric Engine | W kg−1 | 5200 | [69] |
| Density of Iron | kg m−3 | 7880 | [69] |
| Proton Exchange Membrane Fuel Cell Efficiency (Mid-Range, Conservative Estimate to Upper Bound) | % | 57, 54 to 60 | [54,55] |
| Gravimetric Power Density of Proton Exchange Membrane Fuel Cell | W kg−1 | 1980 | [70] |
| Volumetric Power Density of Proton Exchange Membrane Fuel Cell | W m−3 | 3,120,000 | [70] |
| Quantity | Liquefied Natural Gas | Liquid Hydrogen |
|---|---|---|
| Mass of Fuel (ton) | 72,000 | 12,100 |
| Mass of Ballast Water (ton) | 23,200 | |
| Mass of Tank (ton) | 846 | |
| Mass of Engines (ton) | 713 | |
| Volume of Fuel (m3) | 174,000 | |
| Volume of Ballast Water (m3) | 22,600 | |
| Ship Variable | Identifier Type | Categories | Identifier | Demonstration |
|---|---|---|---|---|
| Fuel and Propulsion Type | Colour | Methane Internal Combustion Engine | Pink | |
| Hydrogen Internal Combustion Engine | Green | |||
| Hydrogen Electric | Light Blue | |||
| Presence of Reliquefaction | Presence of Reliquefaction Symbol | Reliquefaction Present | Symbol Present |  |
| Reliquefaction Absent | Symbol Absent |
| (a) | ||||||
|---|---|---|---|---|---|---|
| Fuel and Propulsion Type | Ship Type | Thickness of Insulation (m) | Initial Mass of Fuel (103 ton) | Mass of Tank (103 ton) | Other Masses (103 ton) | |
| Methane Internal Combustion Engine |  | 0.53 | 72.29 | 0.85 | 23.62 | |
 | 0.31 | 72.64 | 0.49 | 23.62 | ||
| Hydrogen Internal Combustion Engine |  | 0.72 | 11.65 | 1.14 | 23.87 | |
 | 0.38 | 12.42 | 0.61 | 23.87 | ||
| Hydrogen Fuel Cell |  | 0.71 | 11.78 | 1.13 | 23.18 | |
 | 0.32 | 12.67 | 0.52 | 23.18 | ||
| (b) | ||||||
| Fuel and Propulsion Type | Ship Type | Initial Volume of Fuel (103 m3) | Volume of Tank (103 m3) | Other Volumes (103 m3) | Fuel Depletion Rate (%/day) | Revenue Loss Rate (103 $/day) |
| Methane Internal Combustion Engine |  | 173.63 | 17.62 | 171.97 | 0.0905 | 21.6 |
 | 174.48 | 10.20 | 178.54 | 0.1048 | 25.1 | |
| Hydrogen Internal Combustion Engine |  | 167.46 | 23.79 | 171.97 | 0.6224 | 57.7 |
 | 178.55 | 12.70 | 171.97 | 0.3816 | 37.7 | |
| Hydrogen Fuel Cell |  | 169.35 | 23.57 | 170.31 | 0.6258 | 58.6 |
 | 182.15 | 10.76 | 170.31 | 0.3061 | 30.9 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smith, J.R.; Gkantonas, S.; Mastorakos, E. Modelling of Boil-Off and Sloshing Relevant to Future Liquid Hydrogen Carriers. Energies 2022, 15, 2046. https://doi.org/10.3390/en15062046
Smith JR, Gkantonas S, Mastorakos E. Modelling of Boil-Off and Sloshing Relevant to Future Liquid Hydrogen Carriers. Energies. 2022; 15(6):2046. https://doi.org/10.3390/en15062046
Chicago/Turabian StyleSmith, Jessie R., Savvas Gkantonas, and Epaminondas Mastorakos. 2022. "Modelling of Boil-Off and Sloshing Relevant to Future Liquid Hydrogen Carriers" Energies 15, no. 6: 2046. https://doi.org/10.3390/en15062046
APA StyleSmith, J. R., Gkantonas, S., & Mastorakos, E. (2022). Modelling of Boil-Off and Sloshing Relevant to Future Liquid Hydrogen Carriers. Energies, 15(6), 2046. https://doi.org/10.3390/en15062046