Orderly Charging Strategy Based on Optimal Time of Use Price Demand Response of Electric Vehicles in Distribution Network
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Literature Review
1.3. Paper Contributions and Organizations
- The fuzzy clustering algorithm introduces a novel method for dividing load time scientifically;
- We propose an orderly charging strategy for EVs based on OTOUP demand response, which has been shown to be effective in improving power grid stability and lowering charging costs for users;
- We propose an adaptive genetic algorithm to solve the EV charging scheduling that considers the benefits of power grids and consumers;
- The sensitivity analysis of an EV’s response to the charging effect is extended, discovering a high level of responsiveness results in an overresponse problem.
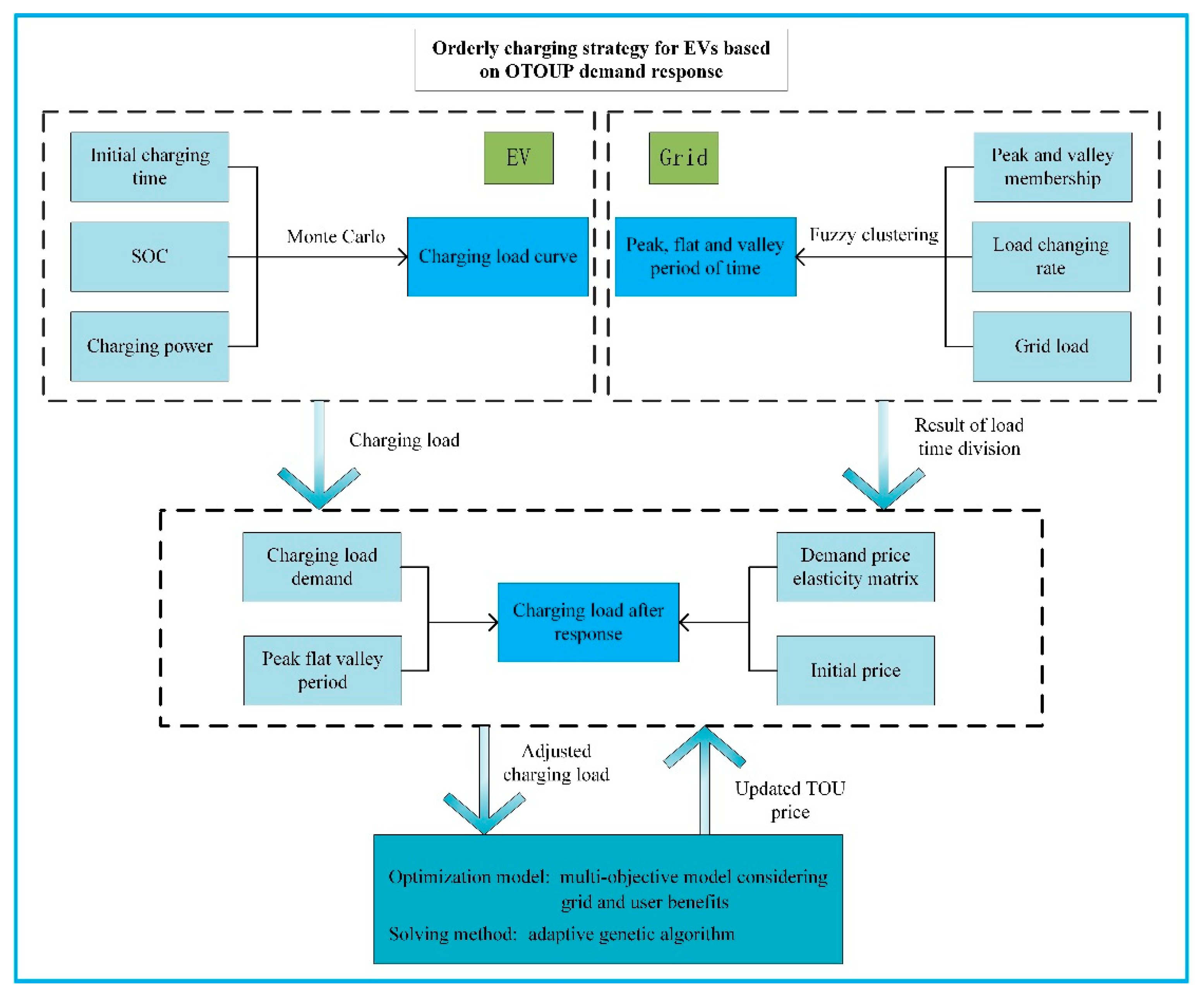
2. Framework for Developing Orderly Charging Strategy for EVs Based on OTOUP Demand Response
3. EV Charging Model Based on Demand Response
3.1. EV Charging Load Prediction
3.2. Load Time Division Based on Fuzzy Clustering
3.3. Modeling Demand Response Based on TOU Price
4. Formulation of Charging Optimization Strategy for EVs
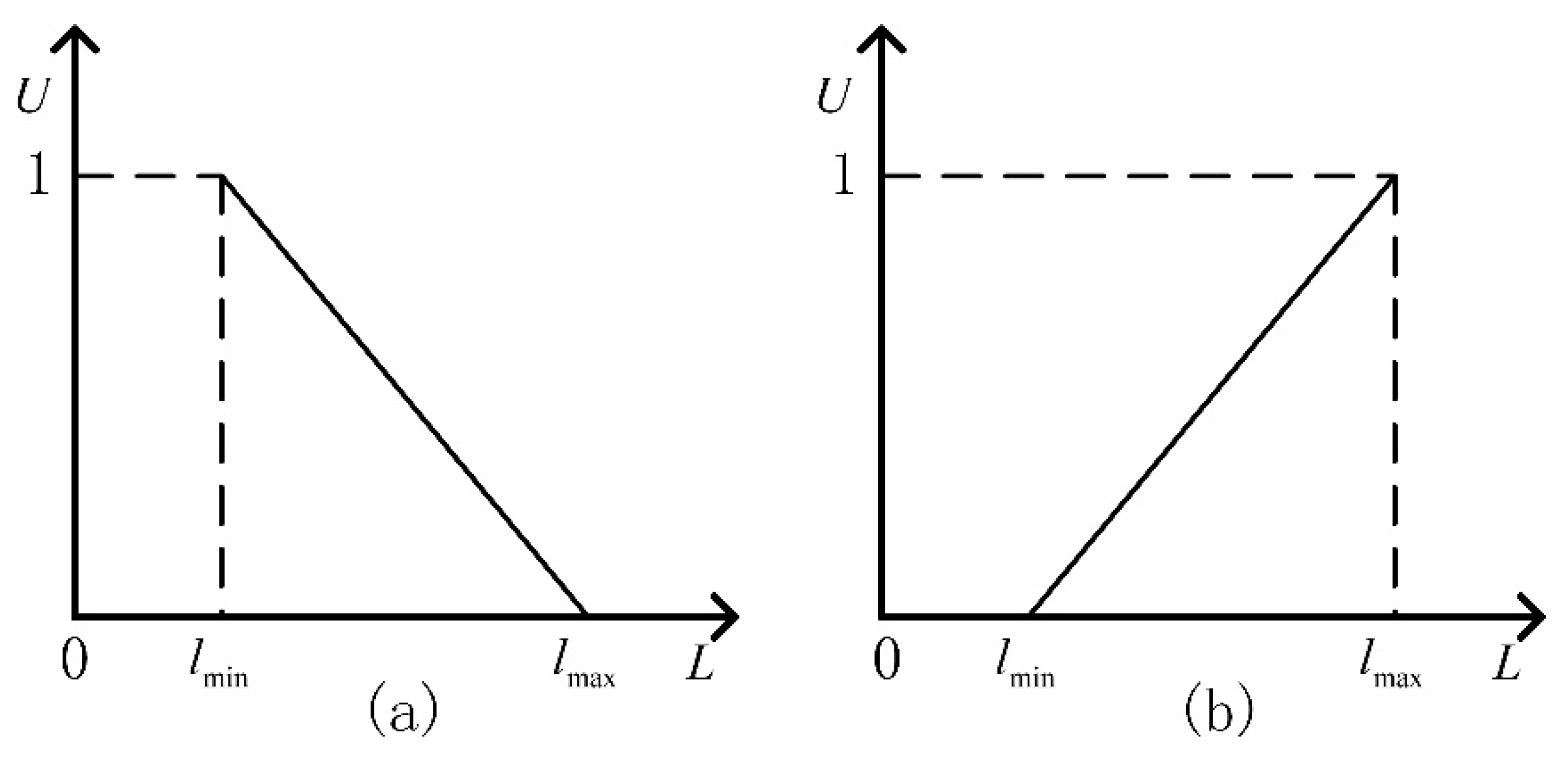
4.1. Objective Functions
4.2. Constraint Condition
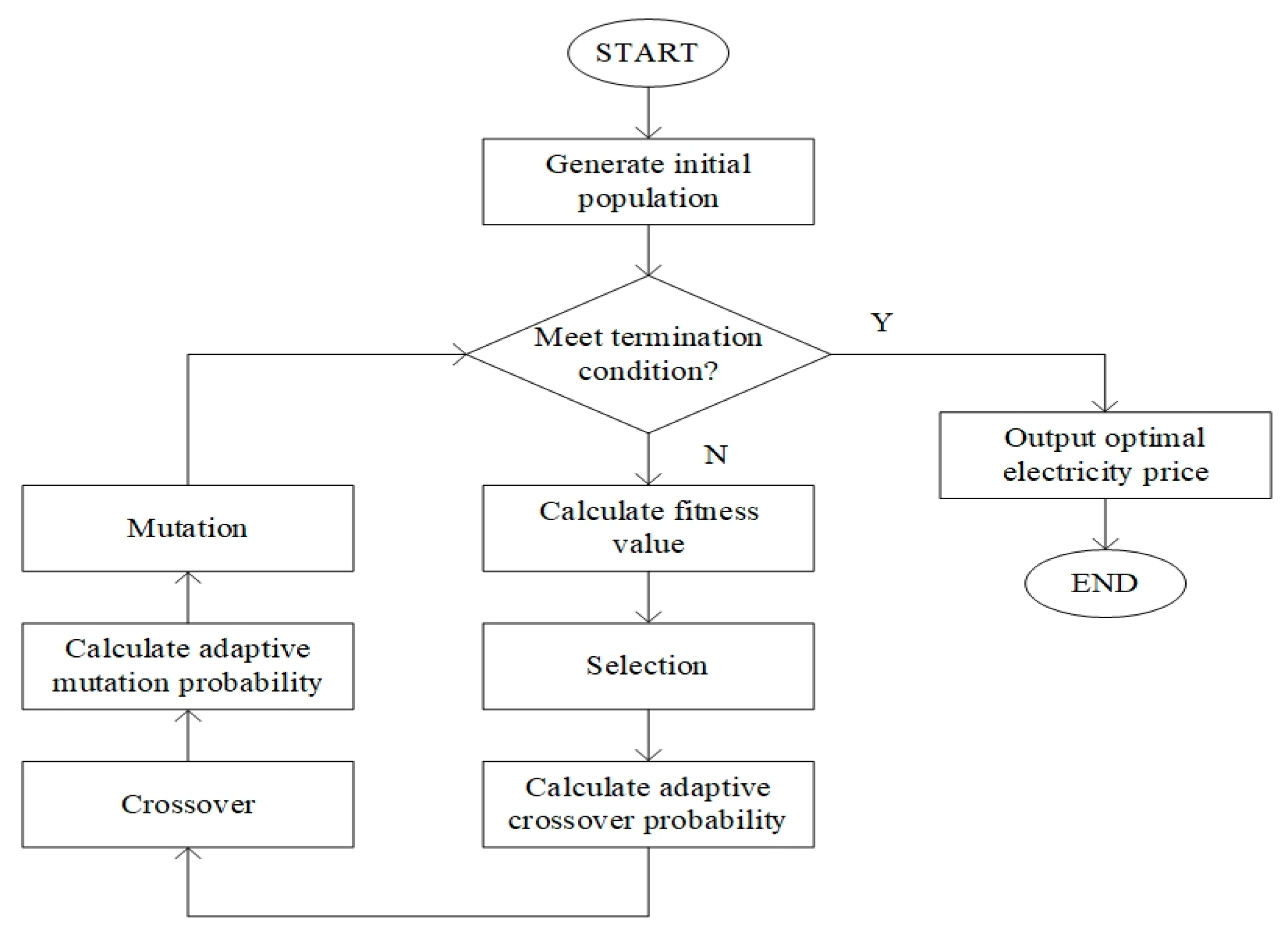
4.3. Solving Algorithm
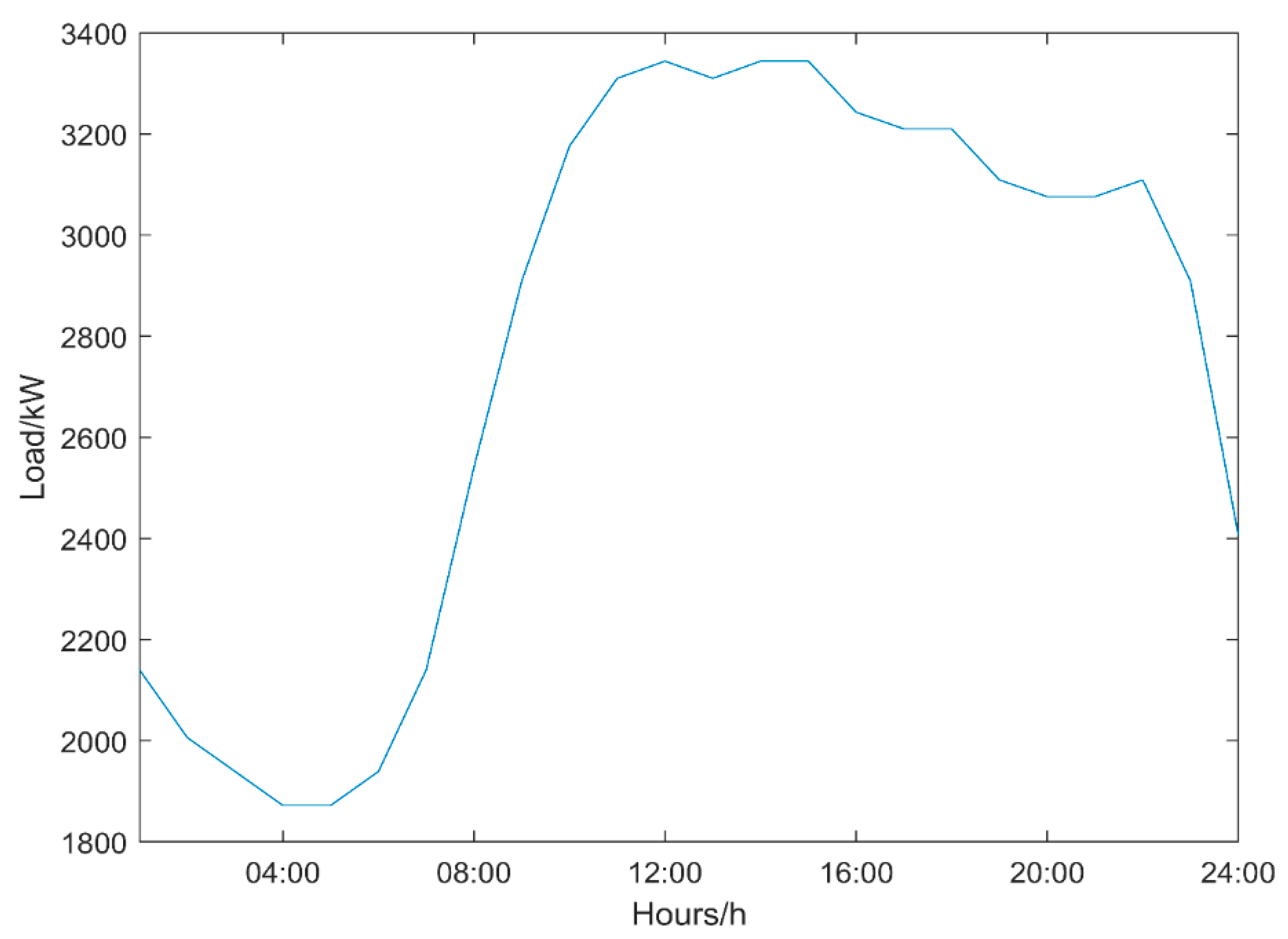
5. Results and Analysis
5.1. Parameter Setting
5.2. Analysis
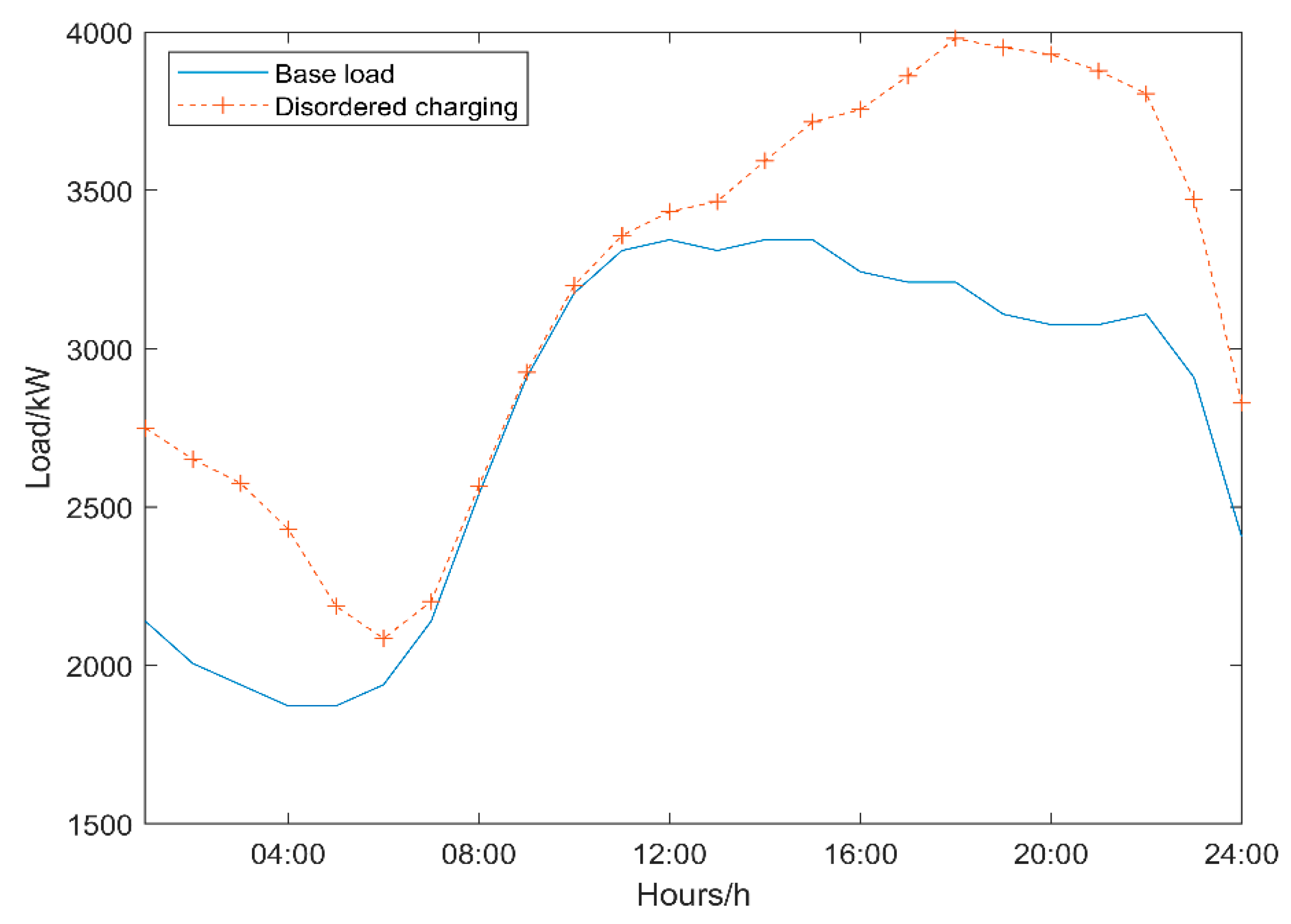
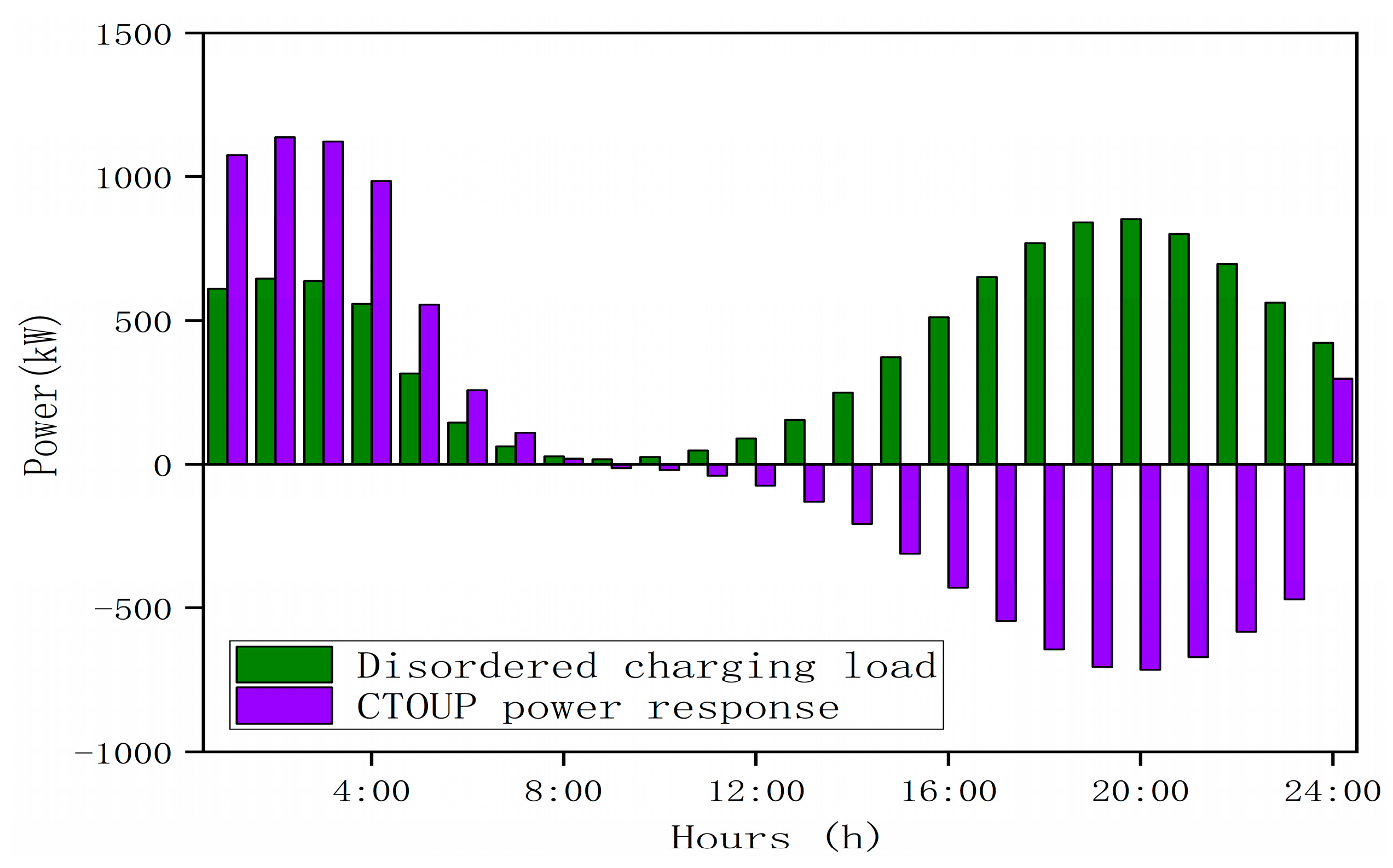
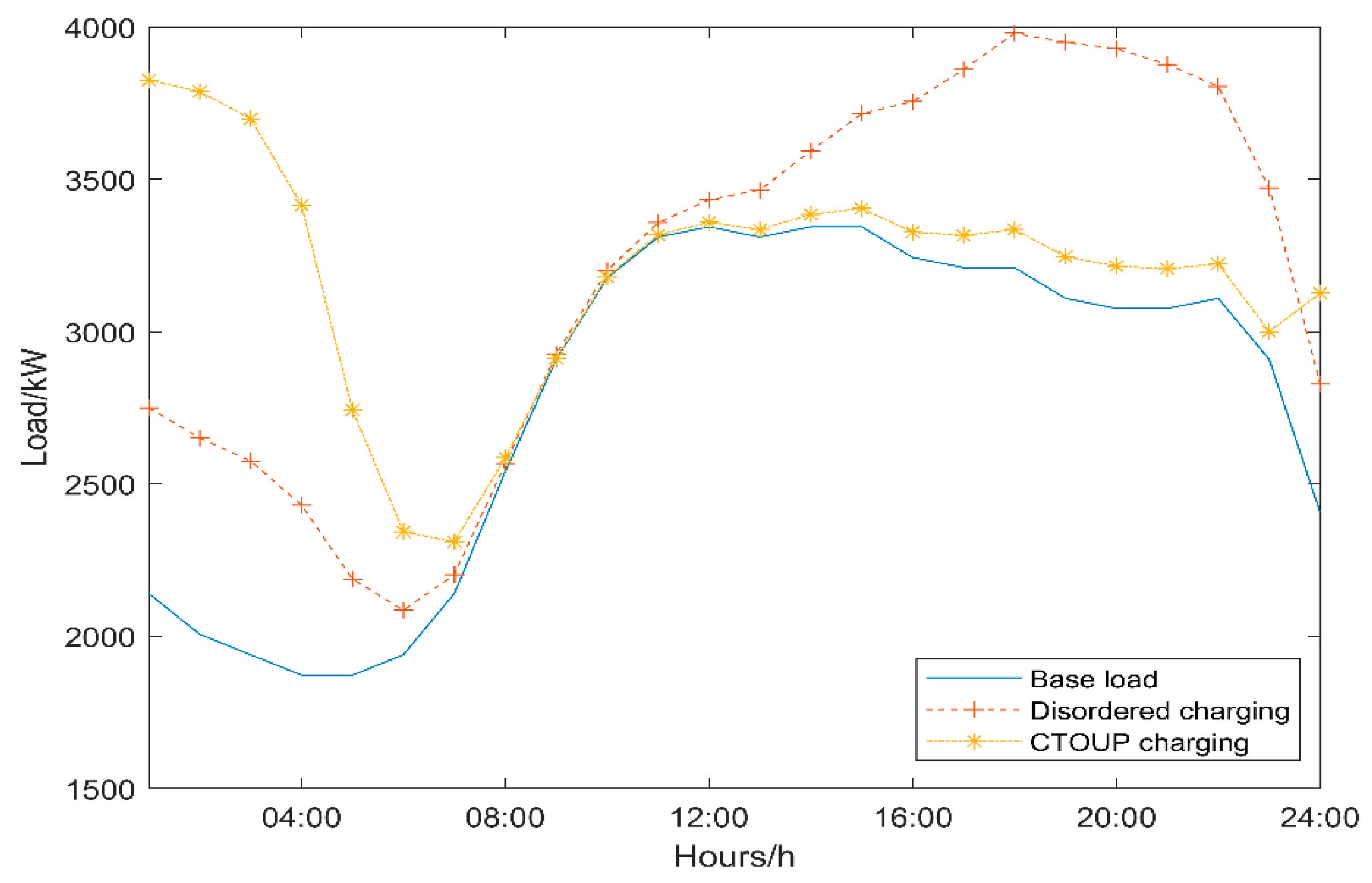
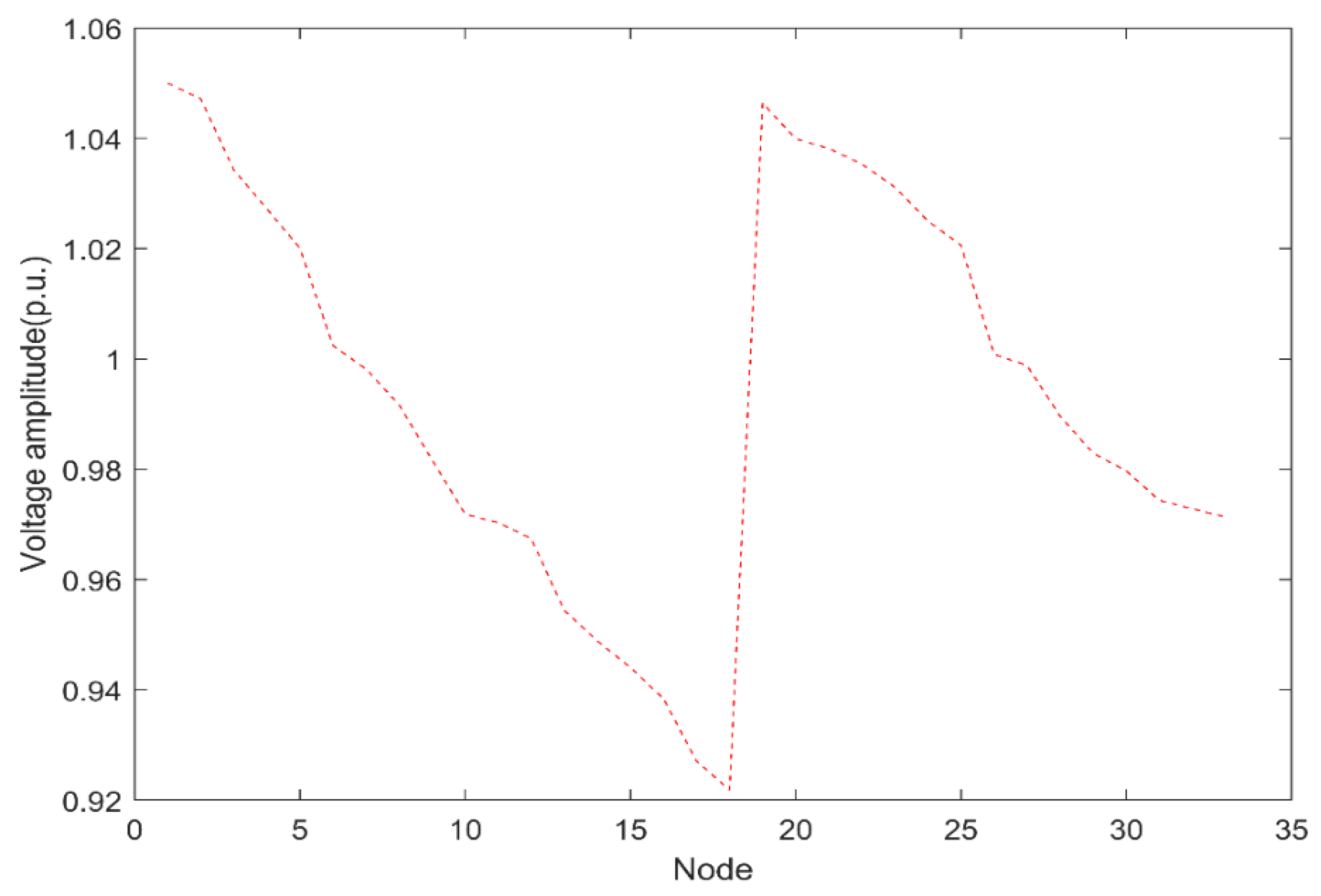
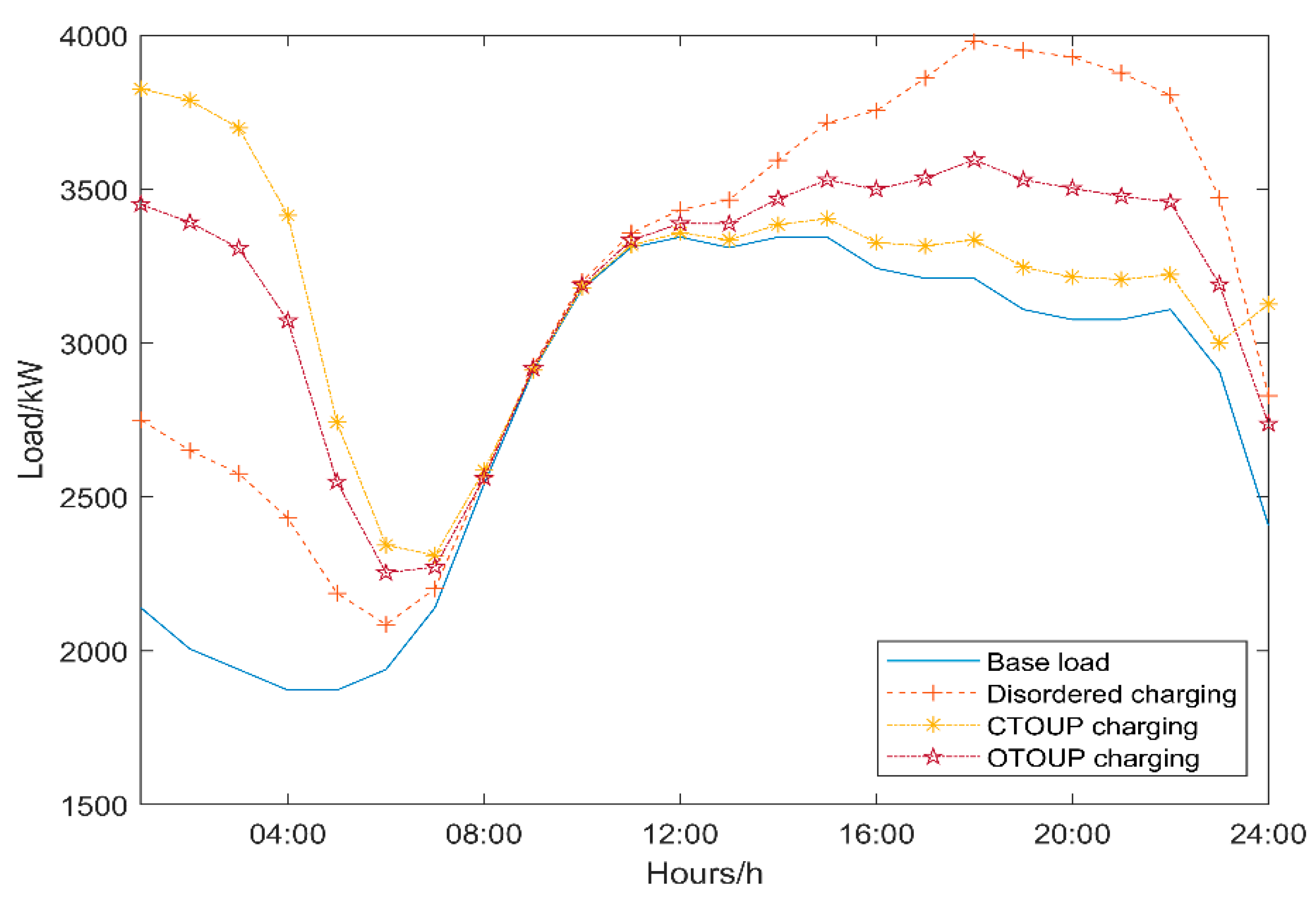
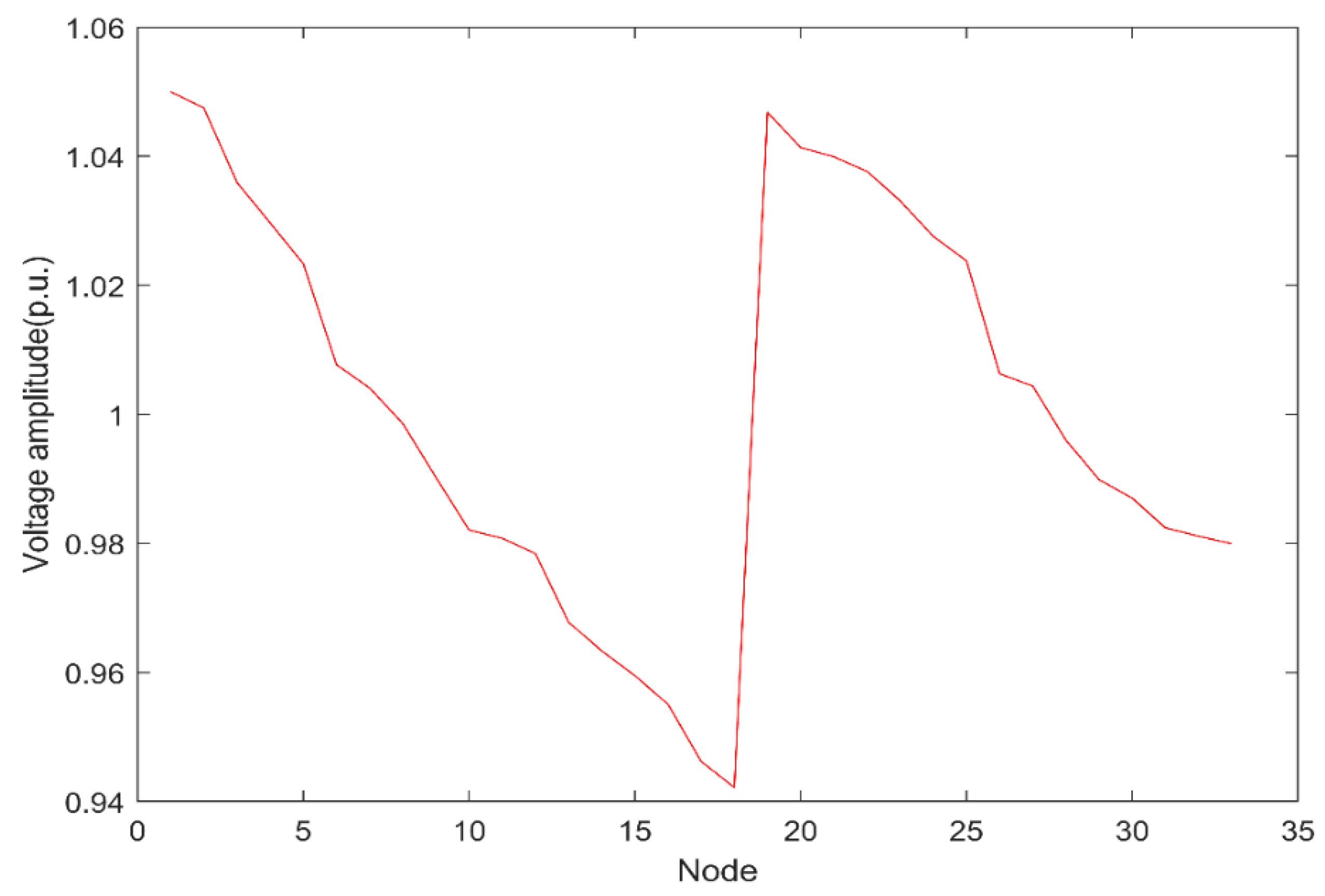
5.2.1. Results of Optimal Electricity Price Charging for EVs
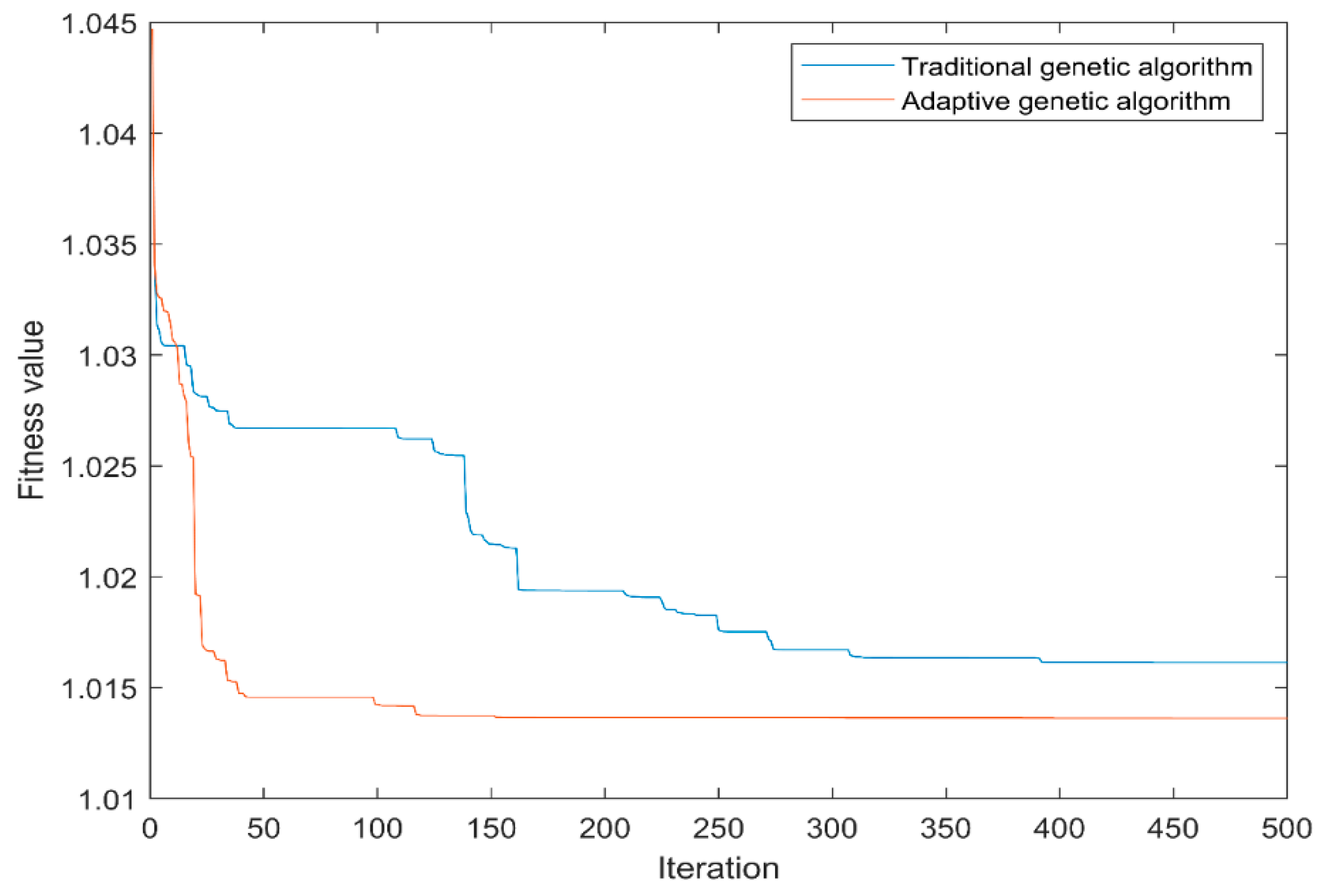
5.2.2. Comparison of Algorithms
5.2.3. The Effect of EVs’ Varying Responsiveness on Charging Strategy
6. Conclusions and Future Work
6.1. Conclusions
6.2. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| EV | electric vehicle |
| TOU | time-of-use |
| OTOUP | optimal time-of-use pricing |
| CTOUP | common time-of-use pricing |
| SOC | state of charge |
| LCR | load change rate |
| CE | clustering effectiveness |
| Indices and sets | |
| index of EV | |
| index of classification | |
| index of clustering object characteristic indicator | |
| index of time period | |
| set of load periods | |
| set of peak period | |
| set of valley period | |
| Parameters | |
| mean and standard deviation of initial charging time | |
| minimum and maximum values of initial state of charge | |
| battery capacity | |
| charging power | |
| charging efficiency | |
| number of EVs | |
| charging state of the i-th EV | |
| charging load of EV in the t-th period | |
| number of load periods | |
| load in the t-th period | |
| minimum and maximum load | |
| rate of change of load in the t-th period | |
| value of the k-th index of the t-th cluster object | |
| value of the k-th index of the t-th cluster object after standardiza-tion | |
| average value of the k-th index | |
| standard deviation of the k-th index | |
| value of the k-th index of the t-th cluster object after normalization | |
| similarity between the t-th clustering object and the s-th clustering object | |
| transitive closure of similar matrix R | |
| confidence level, between 0 and 1 | |
| intercept matrix at confidence level λ | |
| values of elements in the intercept matrix at confidence level λ | |
| number of classifications | |
| number of individuals in class j | |
| clustering center of class j | |
| clustering center of the total sample | |
| g-th sample in class j | |
| clustering effectiveness under r classification number | |
| value of F distribution with degree of freedom (r−1,T−r) under significance level a | |
| self-elastic coefficient | |
| cross elastic coefficient | |
| charge quantity before response in time period t | |
| electricity price before response in time period t | |
| electricity price before response in time period s | |
| highest node voltage | |
| lowest node voltage | |
| weight coefficients of and respectively | |
| weight coefficients of and respectively | |
| disorderly charging price in period t | |
| minimum value of TOU price in t period | |
| maximum value of TOU price in t period | |
| adjustment coefficient | |
| cross coefficient | |
| mutation coefficient | |
| Variables | |
| initial state of charge of the battery | |
| of the battery at the end of EV charging | |
| charge quantity after response in time period t | |
| electricity price after response in time period t | |
| charge change in time period t | |
| price change in time period t | |
| electricity price after response in time period s | |
| price change in time period s | |
| average load of the whole day | |
| load fluctuation standard deviation | |
| load peak–valley difference | |
| sum of voltage deviation | |
| EV charging cost | |
| charging price in time period t | |
| comprehensive objective function value on the power grid side | |
| comprehensive objective function value of power grid side and user side | |
| electricity price in t period after optimization | |
| smaller fitness value of the two crossover individuals | |
| fitness value of the mutated individual | |
| minimum value of population fitness | |
| mean values of population fitness | |
| crossover rate | |
| mutation rate | |
| Operators | |
| synthesis operation of matrix | |
| norm calculation | |
References
- Cui, Q.; Bai, X.; Zhu, S.; Huang, B. Cost-benefit calculation and analysis of V2G system. In Proceedings of the 2016 China International Conference on Electricity Distribution, Xi’an, China, 10–13 August 2016. [Google Scholar]
- Zhang, Z.; Chen, Z.; Xing, Q.; Ji, Z.; Zhang, T. Evaluation of the multi-dimensional growth potential of China’s public charging facilities for electric vehicles through 2030. Util. Policy 2022, 75, 101344. [Google Scholar] [CrossRef]
- Tao, Y.; Huang, M.; Chen, Y.; Yang, L. Orderly charging strategy of battery electric vehicle driven by real-world driving data. Energy 2020, 193, 116806. [Google Scholar] [CrossRef]
- Ren, H.; Zhang, A.; Li, W. Study on Optimal V2G Pricing Strategy under Multi-Aggregator Competition Based on Game Theory. In Proceedings of the 2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019. [Google Scholar]
- Zhong, J.; Xiong, X. An Orderly EV Charging Scheduling Method Based on Deep Learning in Cloud-Edge Collaborative Environment. Adv. Civ. Eng. 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Qian, K.; Zhou, C.; Allan, M.; Yuan, Y. Modeling of load demand due to EV battery charging in distribution systems. IEEE Trans. Power Syst. 2010, 26, 802–810. [Google Scholar] [CrossRef]
- Karmaker, A.K.; Roy, S.; Ahmed, M.R. Analysis of the impact of electric vehicle charging station on power quality issues. In Proceedings of the 2019 International Conference on Electrical, Computer and Communication Engineering (ECCE), Cox’sBazar, Bangladesh, 7–9 February 2019; pp. 1–6. [Google Scholar]
- Crozier, C.; Morstyn, T.; McCulloch, M. The opportunity for smart charging to mitigate the impact of electric vehicles on transmission and distribution systems. Appl. Energy 2020, 268, 114973. [Google Scholar] [CrossRef]
- Jin, Y.; Agyeman, K.A.; Han, S. Grid impact analysis of electric vehicles charging with different load profiles. In Proceedings of the 2019 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Seogwipo, Korea, 8–10 May 2019; pp. 1–5. [Google Scholar]
- Liu, L.; Niu, M.; Li, B.; Zhang, Y.; Zou, M.; Liu, D.; Liu, M. Aggregation Optimization Method of Virtual Energy Storage for Electric Vehicles Considering User Elasticity. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Chongqing, China, 20–22 November 2020. [Google Scholar]
- Dong, X.; Mu, Y.; Xu, X.; Jia, H.; Wu, J.; Yu, X.; Qi, Y. A charging pricing strategy of electric vehicle fast charging stations for the voltage control of electricity distribution networks. Appl. Energy 2018, 225, 857–868. [Google Scholar] [CrossRef]
- Kasani, V.S.; Tiwari, D.; Khalghani, M.R.; Solanki, S.K.; Solanki, J. Optimal Coordinated Charging and Routing Scheme of Electric Vehicles in Distribution Grids: Real Grid Cases. Sust. Cities Soc. 2021, 73, 103081. [Google Scholar] [CrossRef]
- Qu, D.; Liu, Q.; Fan, J.; Yang, J.; Yao, L. Analysis on Peak Clipping Effect of Distribution Network Based on Incentive Demand Response Participated by Electric Vehicles. In Proceedings of the 2020 IEEE Sustainable Power and Energy Conference (iSPEC), Chengdu, China, 23–25 November 2020. [Google Scholar]
- Hou, H.; Wang, Y.; Xie, C.; Xiong, B.; Zhang, Q.; Huang, L. A dispatching strategy for electric vehicle aggregator combined price and incentive demand response. IET Energy Syst. Integr. 2021, 3, 508–519. [Google Scholar] [CrossRef]
- Vuelvas, J.; Ruiz, F.; Gruosso, G. A time-of-use pricing strategy for managing electric vehicle clusters. Sustain. Energy Grids Netw. 2021, 25, 100411. [Google Scholar] [CrossRef]
- Lu, Z.; Qi, J.; Zhang, J.; He, L.; Zhao, H. Modelling dynamic demand response for plug-in hybrid electric vehicles based on real-time charging pricing. IET Gener. Transm. Distrib. 2017, 11, 228–235. [Google Scholar] [CrossRef]
- Tan, J.; Wang, B.; Li, Y. Application of system dynamics on comprehensive benefits valuation of demand response. Autom. Electr. Power Syst. 2014, 38, 128–134. [Google Scholar]
- Azimi, Z.; Hooshmand, R.A.; Soleymani, S. Energy management considering simultaneous presence of demand responses and electric vehicles in smart industrial grids. Sustain. Energy Technol. Assess. 2021, 45, 101127. [Google Scholar] [CrossRef]
- Gong, L.; Cao, W.; Liu, K.; Yu, Y.; Zhao, J. Demand responsive charging strategy of electric vehicles to mitigate the volatility of renewable energy sources. Renew. Energy 2020, 156, 665–676. [Google Scholar] [CrossRef]
- Liao, Y.; Chen, L.; Chen, X. An efficient time-of-use pricing model for a retail electricity market based on pareto improvement. In Proceedings of the 2011 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 25–28 March 2011. [Google Scholar]
- Zheng, Y.; Luo, J.; Yang, X.; Yang, Y. Intelligent regulation on demand response for electric vehicle charging: A dynamic game method. IEEE Access 2020, 8, 66105–66115. [Google Scholar] [CrossRef]
- Lei, H.; Yan, J.; Sang, Z.; Wu, L.; Du, Z.; Yang, D.; Wang, S. A Coordinated Charging Strategy for Electric Vehicles Based on Valley Load Tracking. J. Physics Conf. Ser. 2019, 1314, 012075. [Google Scholar] [CrossRef]
- Wang, H.J.; Wang, B.; Fang, C.; Li, W.; Huang, H.W. Charging load forecasting of electric vehicle based on charging frequency. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Chengdu, China, 7–9 December 2018. [Google Scholar]
- Lin, H.; Shen, X. The Predicting of Charging Load for Pure Electric Buses. In Proceedings of the 8th International Conference on Management and Computer Science (ICMCS 2018), Shenyang, China, 10–12 August 2018. [Google Scholar]
- Zheng, Y.; Shao, Z.; Zhang, Y.; Jian, L. A systematic methodology for mid-and-long term electric vehicle charging load forecasting: The case study of Shenzhen, China. Sust. Cities Soc. 2020, 56, 102084. [Google Scholar] [CrossRef]
- Datchanamoorthy, S.; Kumar, S.; Ozturk, Y.; Lee, G. Optimal time-of-use pricing for residential load control. In Proceedings of the 2011 IEEE International Conference on Smart Grid Communications (SmartGridComm), Brussels, Belgium, 17–20 October 2011. [Google Scholar]
- Ji, Y. Research on Power Forecasting and Optimal Placement for Distributed Photovoltaic. Master’s Thesis, Taiyuan University of Technology, Taiyuan, China, 8 June 2017. [Google Scholar]
- Subcommittee, P.M. IEEE reliability test system. IEEE Trans. Power App. Syst. 1979, 98, 2047–2054. [Google Scholar] [CrossRef]
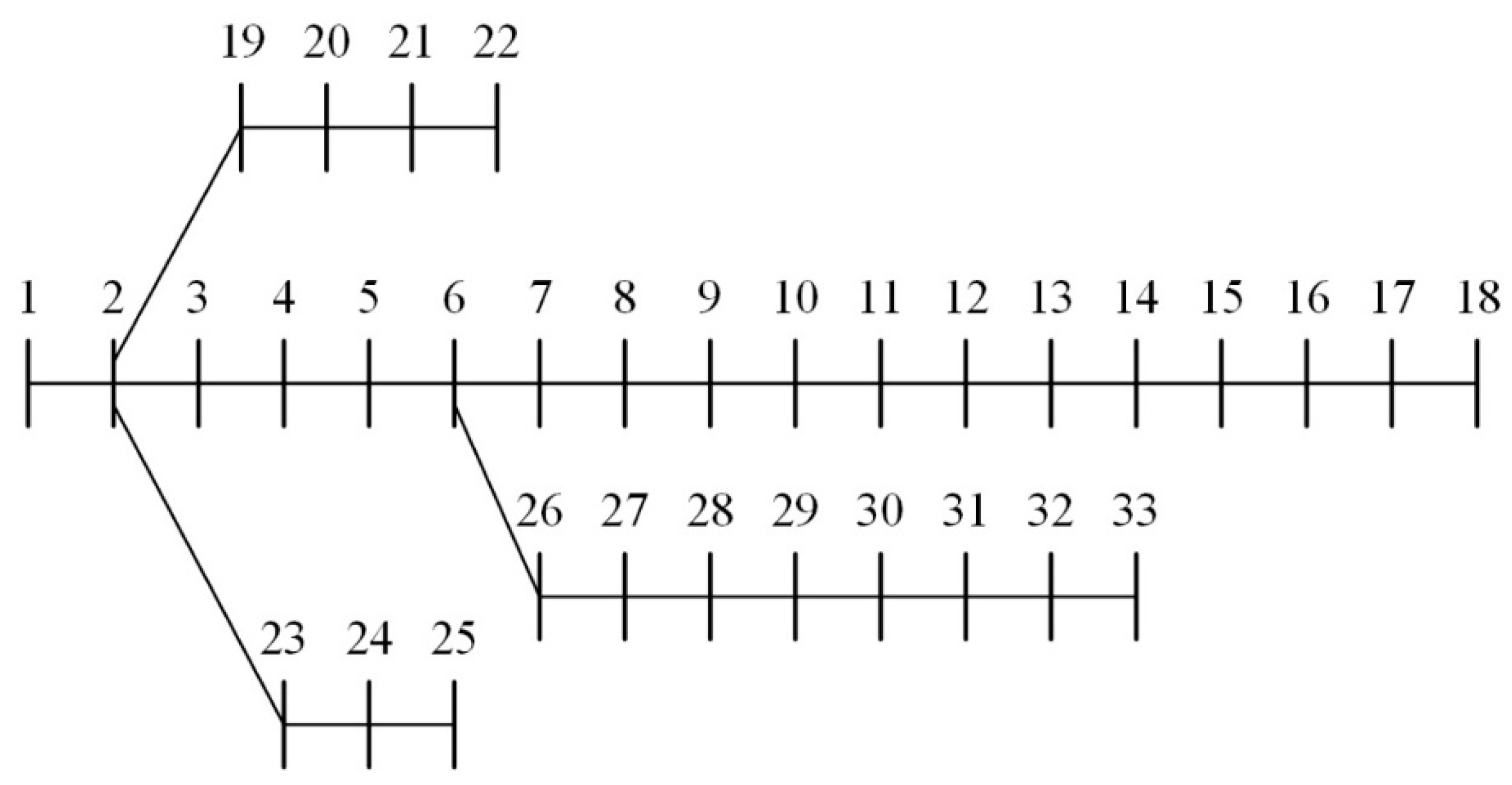



| No. | From | To | Impedance (Ω) | Voltage (p.u.) |
|---|---|---|---|---|
| 1 | 1 | 2 | 0.0922 + j0.047 | 1.05 |
| 2 | 2 | 3 | 0.3660 + j0.1864 | 1 |
| 3 | 3 | 4 | 0.3660 + j0.1864 | 1 |
| 4 | 4 | 5 | 0.3811 + j0.1941 | 1 |
| 5 | 5 | 6 | 0.8190 + j0.7070 | 1 |
| 6 | 6 | 7 | 0.1872 + j0.6188 | 1 |
| 7 | 7 | 8 | 0.7114 + j0.2351 | 1 |
| 8 | 8 | 9 | 1.0300 + j0.7400 | 1 |
| 9 | 9 | 10 | 1.0440 + j0.7400 | 1 |
| 10 | 10 | 11 | 0.1966 + j0.0650 | 1 |
| 11 | 11 | 12 | 0.3744 + j0.1238 | 1 |
| 12 | 12 | 13 | 1.4680 + j1.1550 | 1 |
| 13 | 13 | 14 | 0.5416 + j0.7129 | 1 |
| 14 | 14 | 15 | 0.5910 + j0.5260 | 1 |
| 15 | 15 | 16 | 0.7463 + j0.5450 | 1 |
| 16 | 16 | 17 | 1.2890 + j1.7210 | 1 |
| 17 | 17 | 18 | 0.3720 + j0.5740 | 1 |
| 18 | 2 | 19 | 0.1640 + j0.1565 | 1 |
| 19 | 19 | 20 | 1.5042 + j1.3554 | 1 |
| 20 | 20 | 21 | 0.4095 + j0.4784 | 1 |
| 21 | 21 | 22 | 0.7089 + j0.9373 | 1 |
| 22 | 3 | 23 | 0.4512 + j0.3083 | 1 |
| 23 | 23 | 24 | 0.8980 + j0.7091 | 1 |
| 24 | 24 | 25 | 0.8960 + j0.7011 | 1 |
| 25 | 6 | 26 | 0.2030 + j0.1034 | 1 |
| 26 | 26 | 27 | 0.2842 + j0.1447 | 1 |
| 27 | 27 | 28 | 1.0590 + j0.9337 | 1 |
| 28 | 28 | 29 | 0.8042 + j0.7006 | 1 |
| 29 | 29 | 30 | 0.5075 + j0.2585 | 1 |
| 30 | 30 | 31 | 0.9744 + j0.9630 | 1 |
| 31 | 31 | 32 | 0.3105 + j0.3619 | 1 |
| 32 | 32 | 33 | 0.3410 + j0.5362 | 1 |
| Sort (r) | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| F-statistics | 43.7878 | 72.8242 | 67.1936 | 67.3222 | 54.7459 |
| Fa (a = 0.2) | 1.75 | 1.74 | 1.7 | 1.66 | 1.64 |
| 24.0216 | 40.853 | 38.5256 | 39.5555 | 32.3816 |
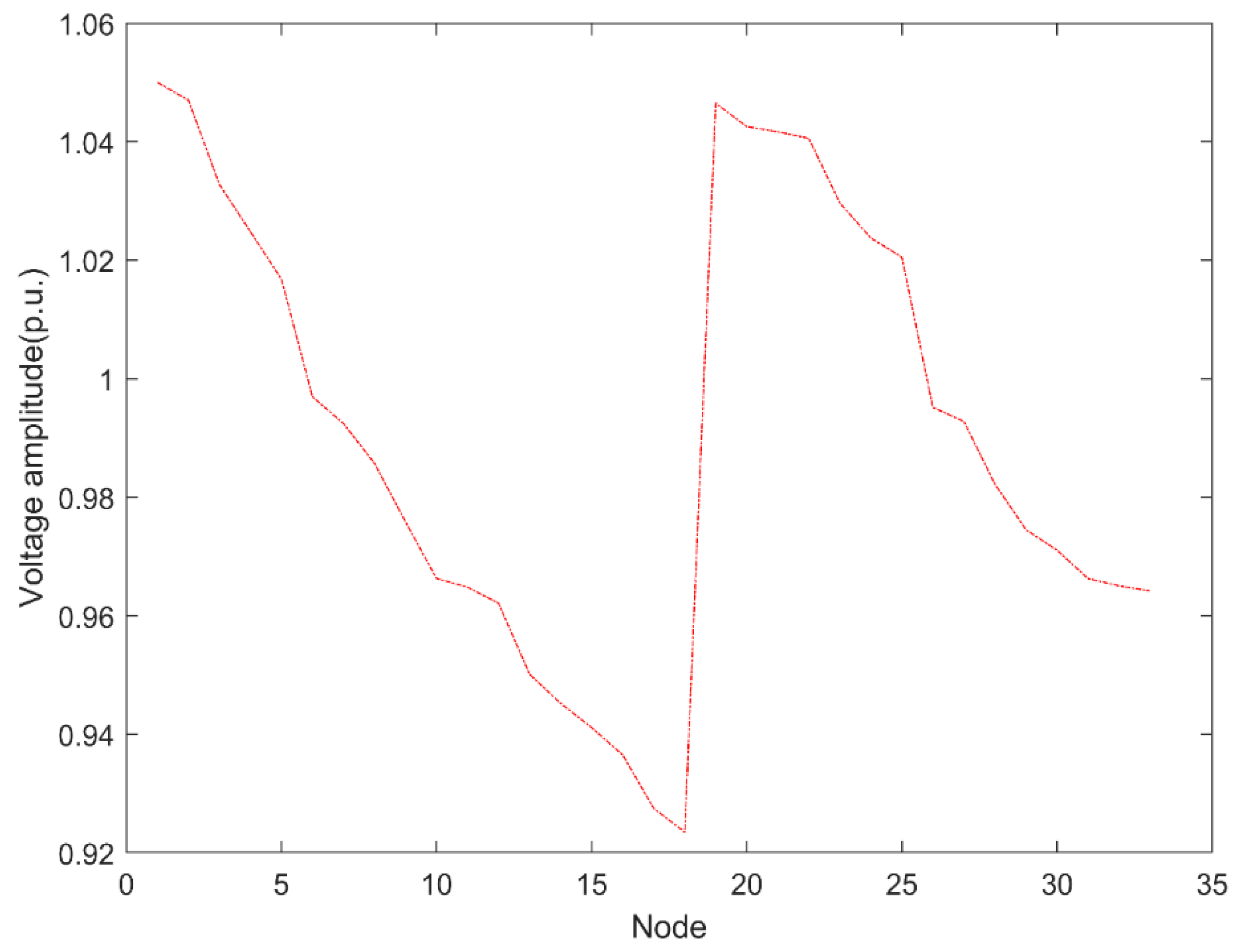
| Standard Deviation (kW) | Peak Valley Difference (kW) | Minimum Voltage (p.u.) | Voltage Deviation (p.u.) | |
|---|---|---|---|---|
| Base load | 553.72 | 1472 | 0.9767 | 1.4466 |
| Scenario 1 | 621.83 | 1895 | 0.9235 | 2.1269 |
| Scenario 2 | 379.44 | 1516 | 0.9219 | 1.9187 |
| Scenario 3 | 407.16 | 1342 | 0.9422 | 1.9128 |
| Charging Cost (CNY) | Peak Electricity Price (CNY/kWh) | Flat Electricity Price (CNY/kWh) | Valley Electricity Price (CNY/kWh) | |
| Base load | - | - | - | - |
| Scenario 1 | 6036 | 0.6 | 0.6 | 0.6 |
| Scenario 2 | 5404.7 | 1.05 | 0.75 | 0.45 |
| Scenario 3 | 5334.6 | 0.9416 | 0.8303 | 0.3 |
| Responsivity | Peak (CNY/kWh) | Flat (CNY/kWh) | Valley (CNY/kWh) | Cost (CNY) |
|---|---|---|---|---|
| 30% | 0.9426 | 0.8177 | 0.3 | 6208.4 |
| 40% | 0.9437 | 0.8027 | 0.3 | 5773.4 |
| 50% | 0.9483 | 0.7421 | 0.3 | 5341.4 |
| 60% | 0.9522 | 0.6826 | 0.3 | 4908.6 |
| 70% | 0.9537 | 0.6701 | 0.3 | 4469.9 |
| 80% | 0.9580 | 0.6122 | 0.3 | 4027.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goh, H.H.; Zong, L.; Zhang, D.; Dai, W.; Lim, C.S.; Kurniawan, T.A.; Goh, K.C. Orderly Charging Strategy Based on Optimal Time of Use Price Demand Response of Electric Vehicles in Distribution Network. Energies 2022, 15, 1869. https://doi.org/10.3390/en15051869
Goh HH, Zong L, Zhang D, Dai W, Lim CS, Kurniawan TA, Goh KC. Orderly Charging Strategy Based on Optimal Time of Use Price Demand Response of Electric Vehicles in Distribution Network. Energies. 2022; 15(5):1869. https://doi.org/10.3390/en15051869
Chicago/Turabian StyleGoh, Hui Hwang, Lian Zong, Dongdong Zhang, Wei Dai, Chee Shen Lim, Tonni Agustiono Kurniawan, and Kai Chen Goh. 2022. "Orderly Charging Strategy Based on Optimal Time of Use Price Demand Response of Electric Vehicles in Distribution Network" Energies 15, no. 5: 1869. https://doi.org/10.3390/en15051869
APA StyleGoh, H. H., Zong, L., Zhang, D., Dai, W., Lim, C. S., Kurniawan, T. A., & Goh, K. C. (2022). Orderly Charging Strategy Based on Optimal Time of Use Price Demand Response of Electric Vehicles in Distribution Network. Energies, 15(5), 1869. https://doi.org/10.3390/en15051869








