An Online Data-Driven LPV Modeling Method for Turbo-Shaft Engines
Abstract
:1. Introduction
2. LPV Model for Turbo-Shaft Engine
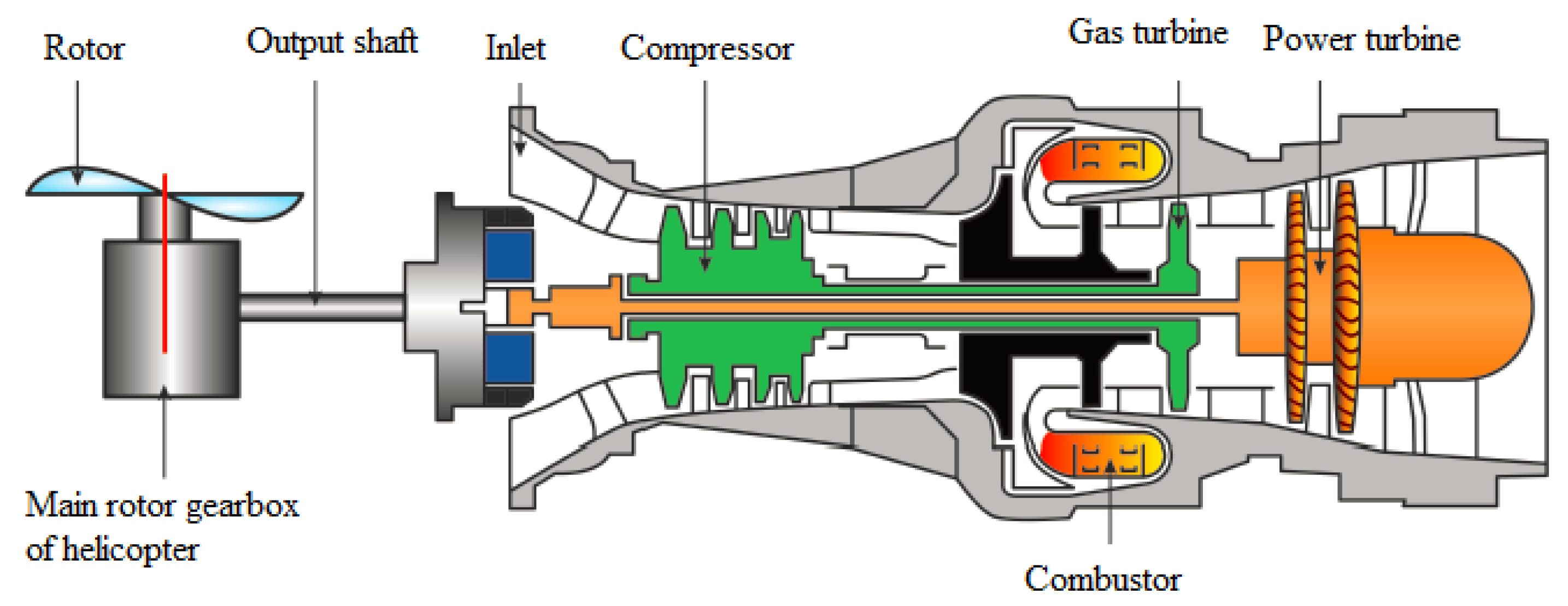
2.1. Brief Introduction of Turbo-Shaft Engine
2.2. LPV Model Description
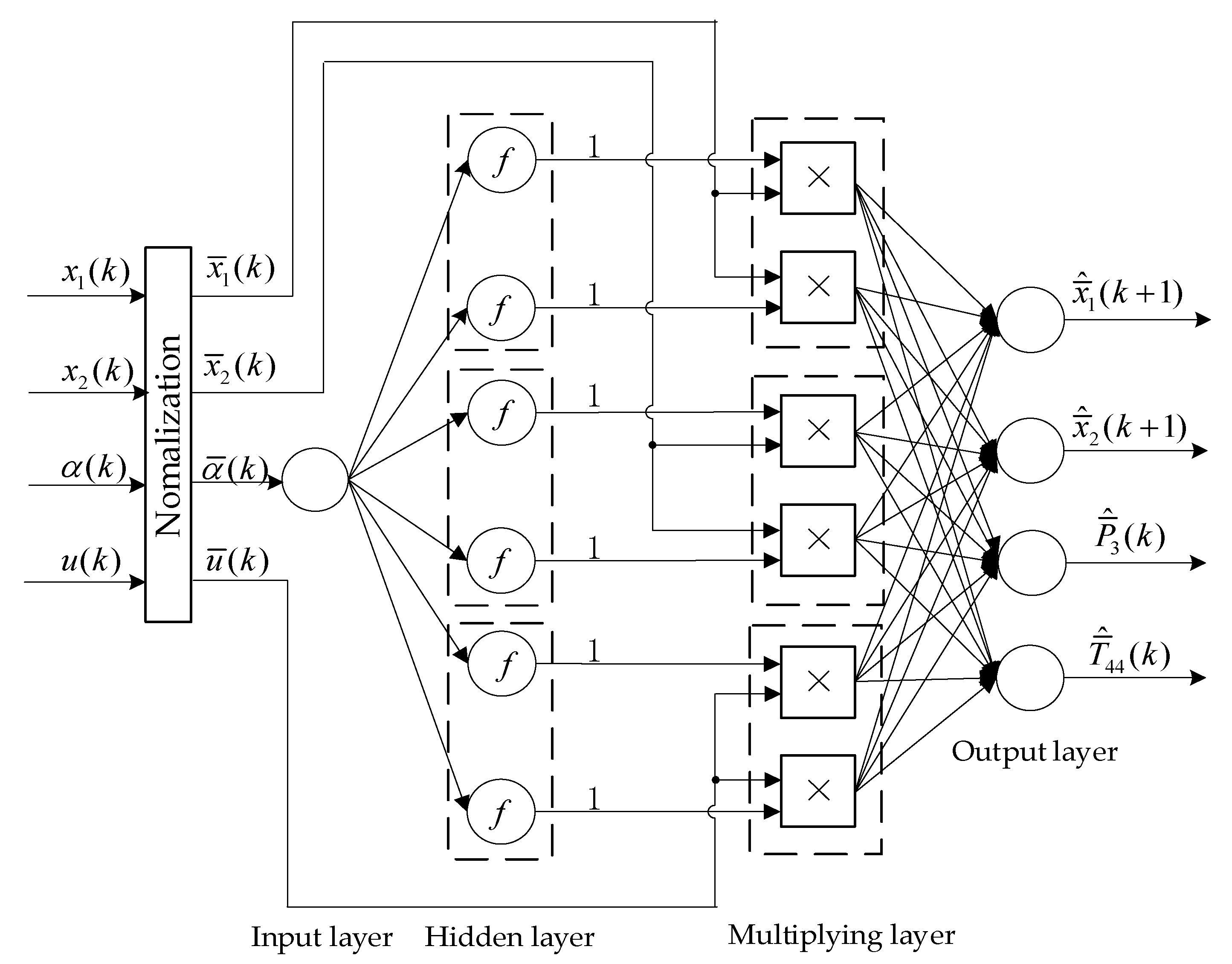
3. Special Structure of MLOS-ELM for DD-LPV Modeling
4. Online Updating Algorithm of MLOS-ELM
- Step 1. Randomly generate the hidden layer parameters W and b, set and ;
- Step 2. Update the output weight : If k = 1, Equation (14) is used. Otherwise, Equation (16) or Equation (17) is used;
- Step 3. Calculate the LPV system matrices , , , according to Equation (9);
- Step 4. Set k = k + 1, go back to Step 2.
5. Simulation and Discussions
5.1. Approximation Ability Verification of the MLOS-ELM
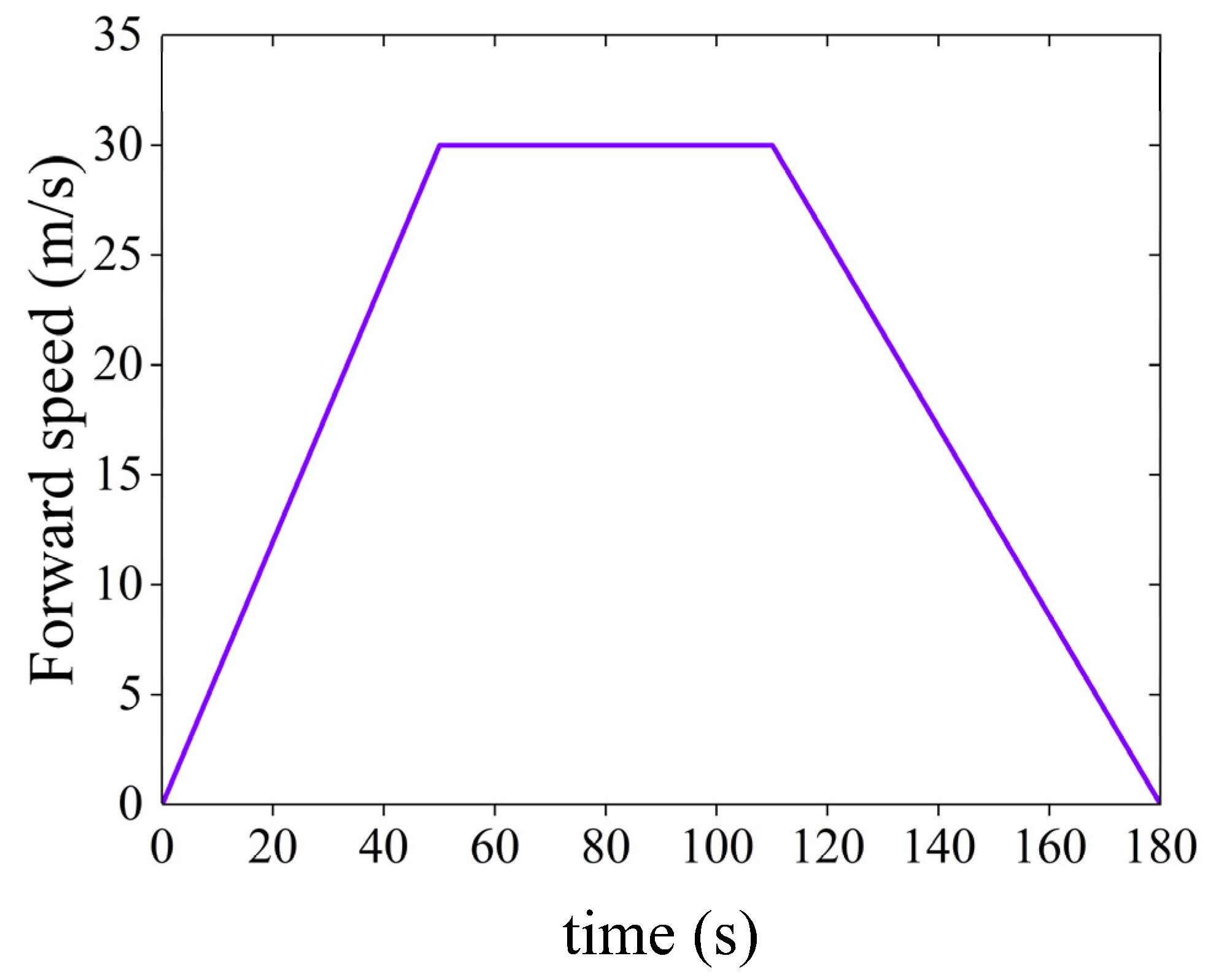
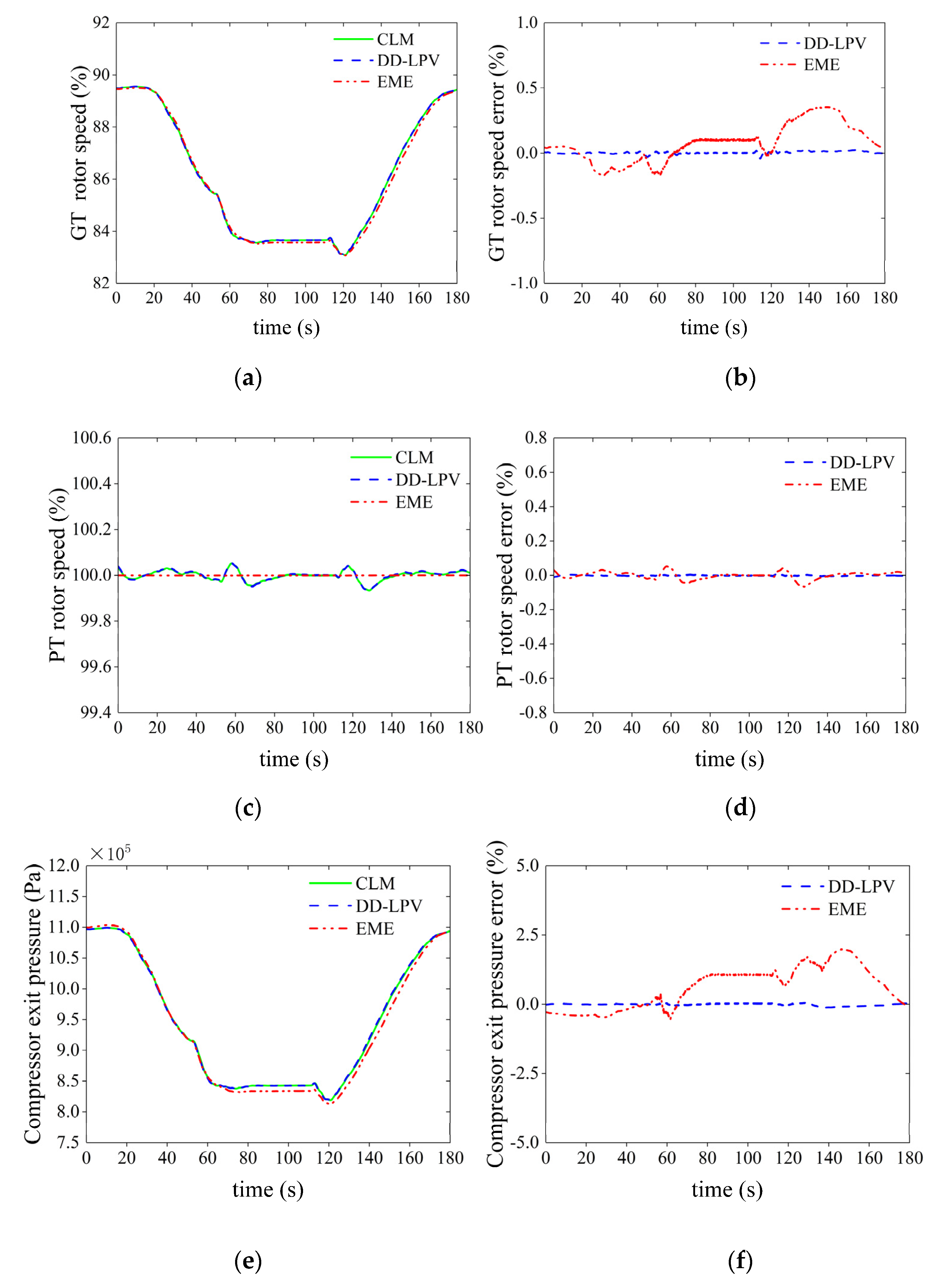
5.2. Prediction Ability Validation of the Online DD-LPV Model in Flight Envelope
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lacerda, M.J.; Palhares, R.M. On discrete-time LPV control using delayed Lyapunov functions. Asian J. Control 2021, 23, 2359–2369. [Google Scholar]
- Lao-atiman, W.; Olaru, S.; Diop, S.; Skogestad, S.; Arpornwichanop, A.; Cheacharoen, R.; Kheawhom, S. Linear parameter-varying model for a refuellable zinc–air battery. R. Soc. Open Sci. 2020, 7, 201107. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Jiang, C.C.; Tang, X.M.; She, M.H. Interpolation Model Predictive Control of Nonlinear Systems Described by Quasi-LPV Model. Autom. Control Comput. Sci. 2018, 52, 354–364. [Google Scholar] [CrossRef]
- Liu, X.; Han, G.; Yang, X. Robust Global Identification of LPV Errors-in-Variables Systems with Incomplete Observations. IEEE Trans. Syst. Man Cybern. Syst. 2021, 1–9. [Google Scholar] [CrossRef]
- Yue, X.; Su, B. Predictive Functional Control of Nonlinear Systems Based on Multiple LPV Models. In Proceedings of the 2019 Chinese Automation Congress, Hangzhou, China, 1 November 2019. [Google Scholar]
- Atam, E. Advanced Air Path Control in Diesel Engines Accounting for Variable Operational Conditions. IEEE Access 2018, 6, 42165–42176. [Google Scholar] [CrossRef]
- Samadzadeh, S.; Mazinan, A.H. LMI-based LPV control strategy considering UAV systems. Spat. Inf. Res. 2019, 27, 425–431. [Google Scholar] [CrossRef]
- Hang, P.; Chen, X. Path tracking control of 4-wheel-steering autonomous ground vehicles based on linear parameter-varying system with experimental verification. Proc. Inst. Mech. Engineers. Part I J. Syst. Control. Eng. 2021, 235, 411–423. [Google Scholar] [CrossRef]
- Alcalá, E.; Puig, V.; Quevedo, J.; Rosolia, U. Autonomous racing using Linear Parameter Varying-Model Predictive Control (LPV-MPC). Control Eng. Pract. 2020, 95, 104270. [Google Scholar] [CrossRef]
- Lim, J.; Kirchen, P.; Nagamune, R. LPV Controller Design for Diesel Engine SCR Aftertreatment Systems Based on Quasi-LPV Models. IEEE Control Syst. Lett. 2020, 5, 1807–1812. [Google Scholar] [CrossRef]
- Gidon, D.; Abbas, H.S.; Bonzanini, A.D.; Graves, D.B.; Velni, J.M.; Mesbah, A. Data-driven LPV model predictive control of a cold atmospheric plasma jet for biomaterials processing. Control Eng. Pract. 2021, 109, 104725. [Google Scholar] [CrossRef]
- López-Estrada, F.R.; Rotondo, D.; Valencia-Palomo, G. A review of convex approaches for control, observation and safety of linear parameter varying and Takagi-Sugeno systems. Processes 2019, 7, 814. [Google Scholar] [CrossRef] [Green Version]
- Hoffmann, C.; Werner, H. A survey of linear parameter-varying control applications validated by experiments or high-fidelity simulations. IEEE Trans. Control Syst. Technol. 2014, 23, 416–433. [Google Scholar] [CrossRef]
- Sun, T.; Sun, X.M.; Sun, A. Optimal Output Tracking of Aircraft Engine Systems: A Data-driven Adaptive Performance Seeking Control. IEEE Trans. Circuits Syst. II Express Briefs 2021. [Google Scholar] [CrossRef]
- Pang, S.W.; Li, Q.H.; Zhang, H.B. A new online modelling method for aircraft engine state space model. Chin. J. Aeronaut 2020, 33, 1756–1773. [Google Scholar] [CrossRef]
- Cox, P.B.; Tóth, R. Linear parameter-varying subspace identification: A unified framework. Automatica 2021, 123, 109296. [Google Scholar] [CrossRef]
- Guangdeng, Z.; Yang, D.; Lam, J.; Song, X. Fault-tolerant control of switched LPV systems: A bumpless transfer approach. IEEE/ASME Trans. Mechatron. 2021. [Google Scholar] [CrossRef]
- Salt Ducajú, J.M.; Salt Llobregat, J.J.; Cuenca, Á.; Tomizuka, M. Autonomous ground vehicle lane-keeping LPV model-based control: Dual-rate state estimation and comparison of different real-time control strategies. Sensors 2021, 21, 1531. [Google Scholar] [CrossRef]
- Rotondo, D.; Nejjari, F.; Puig, V. Quasi-LPV modeling, identification and control of a twin rotor MIMO system. Control Eng. Pract. 2013, 21, 829–846. [Google Scholar] [CrossRef]
- Ferranti, F.; Rolai, Y. Modeling of linear parameter-varying systems using interpolation of root macromodels and scaling coefficients. Mech. Syst. Signal Process. 2015, 60, 836–852. [Google Scholar] [CrossRef]
- Ferranti, F.; Rolain, Y. A local approach for the modeling of linear parameter-varying systems based on transfer function interpolation with scaling coefficients. In Proceedings of the Instrumentation & Measurement Technology Conference, Pisa, Italy, 11–14 May 2015; IEEE: Manhattan, NY, USA, 2015; pp. 606–611. [Google Scholar]
- Marcos, A.; Balas, G.J. Development of Linear-Parameter-Varying Models for Aircraft. J. Guid. Control Dyn. 2004, 27, 218–228. [Google Scholar] [CrossRef] [Green Version]
- De Caigny, J.; Camino, J.F.; Swevers, J. Interpolating model identification for SISO linear parameter-varying systems. Mech. Syst. Signal Process. 2009, 23, 2395–2417. [Google Scholar] [CrossRef]
- Chen, Q.J.; Huang, J.Q.; Pan, M.X.; Lu, F. A Novel Real-Time Mechanism Modeling Approach for Turbofan Engine. Energies 2019, 12, 3791. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.B. Design of Linear Parameter Varying Controllers for Turbo-Fan Engines; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2018. (In Chinese) [Google Scholar]
- Liu, J.F.; Ma, Y.J.; Zhu, L.H.; Zhao, H.; Liu, H.P.; Yu, D.R. Improved. Gain Scheduling Control and Its Application to Aero-Engine LPV Synthesis. Energies 2020, 3, 5976. [Google Scholar] [CrossRef]
- Sun, H.B.; Pan, M.X.; Huang, J.Q. Switching control for turbofan engine based on Double-Layer LPV Model. J. Propuls. Technol. 2018, 39, 2828–2838. [Google Scholar]
- Lv, C.K.; Chang, J.T.; Yu, D.R. Feedback Linearized Sliding Mode Control of Turbofan Engine Based on Multiple Input Multiple Output Equilibrium Manifold Expansion Model. J. Propuls. Technol. 2021, 42, 1681–1689. [Google Scholar]
- Liu, Z.H.; Zheng, Q.G.; Liu, M.L.; Hu, C.P.; Zhang, H.B. Research on the Improved Method of Full-Enveloped Acceleration Control Plan for Turbofan Engine. J. Propuls. Technol. 2022, 43, 346–353. [Google Scholar] [CrossRef]
- Xia, C.J.; Wang, D. Improved correction methods of aircraft engine fan speed based on similarity theory. J. Aerosp. Power 2016, 31, 941–947. [Google Scholar]
- Iannelli, A.; Fasel, U.; Smith, R.S. The balanced mode decomposition algorithm for data-driven LPV low-order models of aeroservoelastic systems. Aerosp. Sci. Technol. 2021, 115, 106821. [Google Scholar] [CrossRef]
- Rödönyi, G.; Tóth, R.; Pup, D.; Kisari, Á.; Vígh, Z.; Kőrös, P.; Bokor, J. Data-driven linear parameter-varying modelling of the steering dynamics of an autonomous car. IFAC-PapersOnLine 2021, 54, 20–26. [Google Scholar] [CrossRef]
- Chen, Y.; Andrey, B. Data-Driven Linear Parameter-Varying Modeling and Control of Flexible Loads for Grid Services. In Proceedings of the 2020 American Control Conference, Denver, CO, USA, 1–3 July 2020. [Google Scholar]
- Yu, M.; Yang, X.; Liu, X. LPV system identification with multiple-model approach based on shifted asymmetric laplace distribution. Int. J. Syst. Sci. 2021, 52, 1452–1465. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, L.; Luo, C. Model reference adaptive control for aero-engine based on system equilibrium manifold expansion model. Int. J. Control 2021. [Google Scholar] [CrossRef]
- Lv, C.; Wang, Z.; Dai, L.; Liu, H.; Chang, J.; Yu, D. Control-Oriented Modeling for Nonlinear MIMO Turbofan Engine Based on Equilibrium Manifold Expansion Model. Energies 2021, 14, 6277. [Google Scholar] [CrossRef]
- Zhu, L.; Liu, J.; Ma, Y.; Zhou, W.; Yu, D. A Corrected Equilibrium Manifold Expansion Model for gas Turbine System Simulation and Control. Energies 2020, 13, 4904. [Google Scholar] [CrossRef]
- Tóth, R.; Laurain, V.; Zheng, W.X.; Poolla, K. Model structure learning: A support vector machine approach for LPV linear-regression models. In Proceedings of the IEEE Conference on Decision and Control, Orlando, FL, USA, 12–15 December 2011; pp. 3192–3197. [Google Scholar]
- Feng, K.; Lu, J.G.; Chen, J.S. Identification and model predictive control of LPV models based on LS-SVM for MIMO system. CIESC J. 2015, 66, 197–205. [Google Scholar]
- Cavanini, L.; Ferracuti, F.; Longhi, S.; Monteriù, A. LS-SVM for LPV-ARX Identification: Efficient Online Update by Low-Rank Matrix Approximation. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020. [Google Scholar]
- Fényes, D.; Németh, B.; Gáspár, P. A Novel Data-Driven Modeling and Control Design Method for Autonomous Vehicles. Enegies 2021, 14, 517. [Google Scholar] [CrossRef]
- Gu, N.N.; Wang, X.; Lin, F.Q. Design of Disturbance Extended State Observer (D-ESO)-Based Constrained Full-State Model Predictive Controller for the Integrated Turbo-Shaft Engine/Rotor System. Energies 2019, 12, 4496. [Google Scholar] [CrossRef] [Green Version]
- Ballin, M.G. A High-Fidelity Real-Time Simulation of a Small Turboshaft Engine; National Aeronautics and Space Administration, Ames Research Center: Mountain View, CA, USA, 1988. [Google Scholar]
- Zheng, Q.; Xu, Z.; Zhang, H.; Zhu, Z. A turboshaft engine NMPC scheme for helicopter autorotation recovery maneuver. Aerosp. Sci. Technol. 2018, 76, 421–432. [Google Scholar] [CrossRef]
- Zhang, M.; Lin, Z.; Huang, H.; Zhang, T. Design and verification of model predictive control for micro-turboshaft engine. Adv. Mech. Eng. 2019, 11, 1687814019890198. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, Q.; Zhang, H.; Chen, H. Study on inversion control for integrated helicopter/engine system with variable rotor speed based on state variable model. Int. J. Turbo Jet-Engines 2020, 000010151520200018. [Google Scholar] [CrossRef]
- Lin, Z.X. Design and Verification of a Micro Turboshaft Engine Control System; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2019. [Google Scholar]
- Gu, N.; Wang, X. Model predictive controller design based on the linear parameter varying model method for a class of turboshaft engines. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018; p. 4620. [Google Scholar]
- Liang, N.; Huang, G.; Saratchandran, P.; Sundararajan, N. A Fast and Accurate Online Sequential Learning Algorithm for Feedforward Networks. IEEE Trans. Neural Netw. 2006, 17, 1411–1423. [Google Scholar] [CrossRef]
- Yan, C.K.; Zhou, X.; Zhang, H.B. Design and simulation of a control scheme for turbo-shaft engine in helicopter autorotation training process. J. Aerosp. Power 2014, 29, 1744–1751. [Google Scholar]
- Jianguo, S.; Vasilyev, V.; Ilyasov, B. Advanced Multivariable Control System of Aeroengines; Beijing University of Aeronautics and Astronautics: Beijing, China, 2005. [Google Scholar]

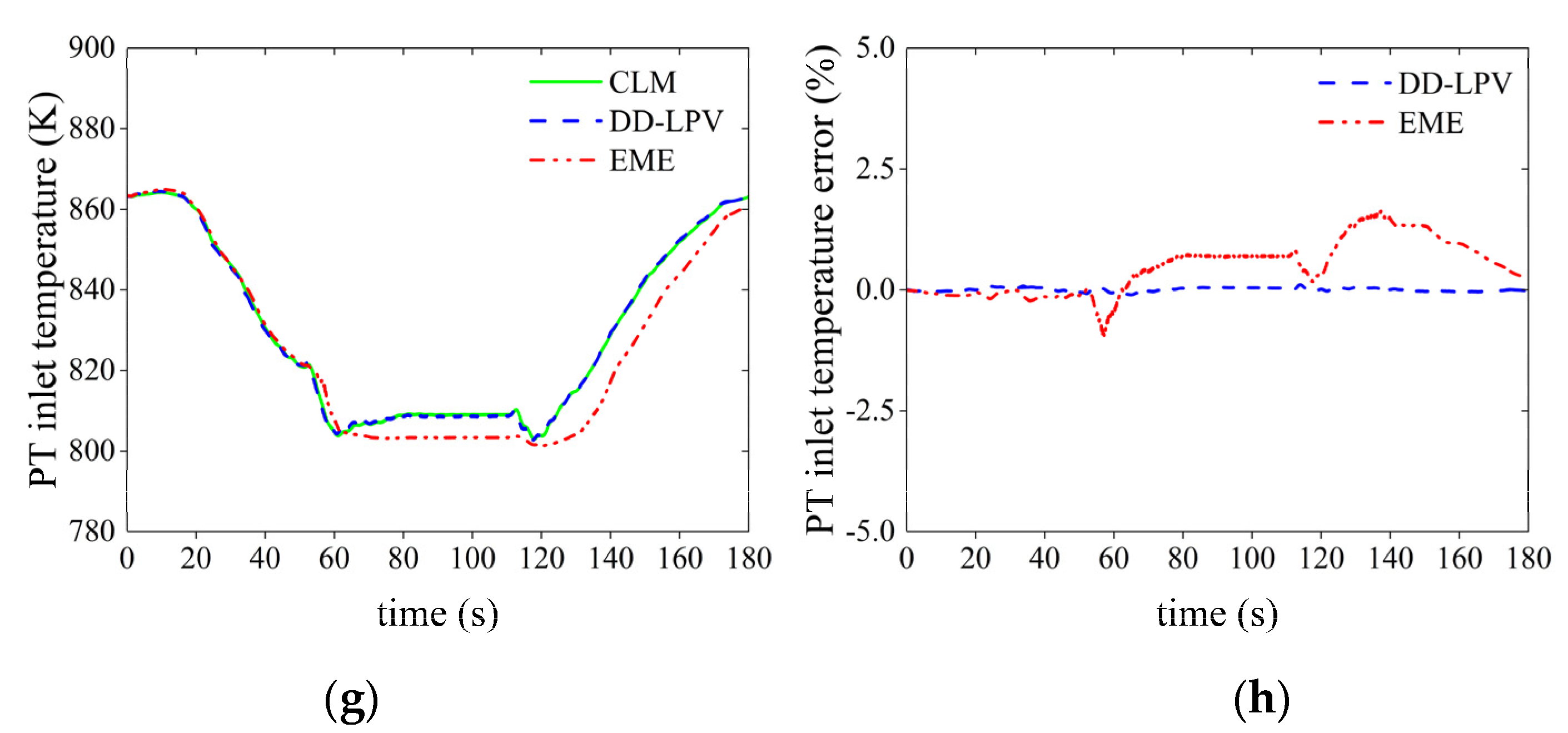


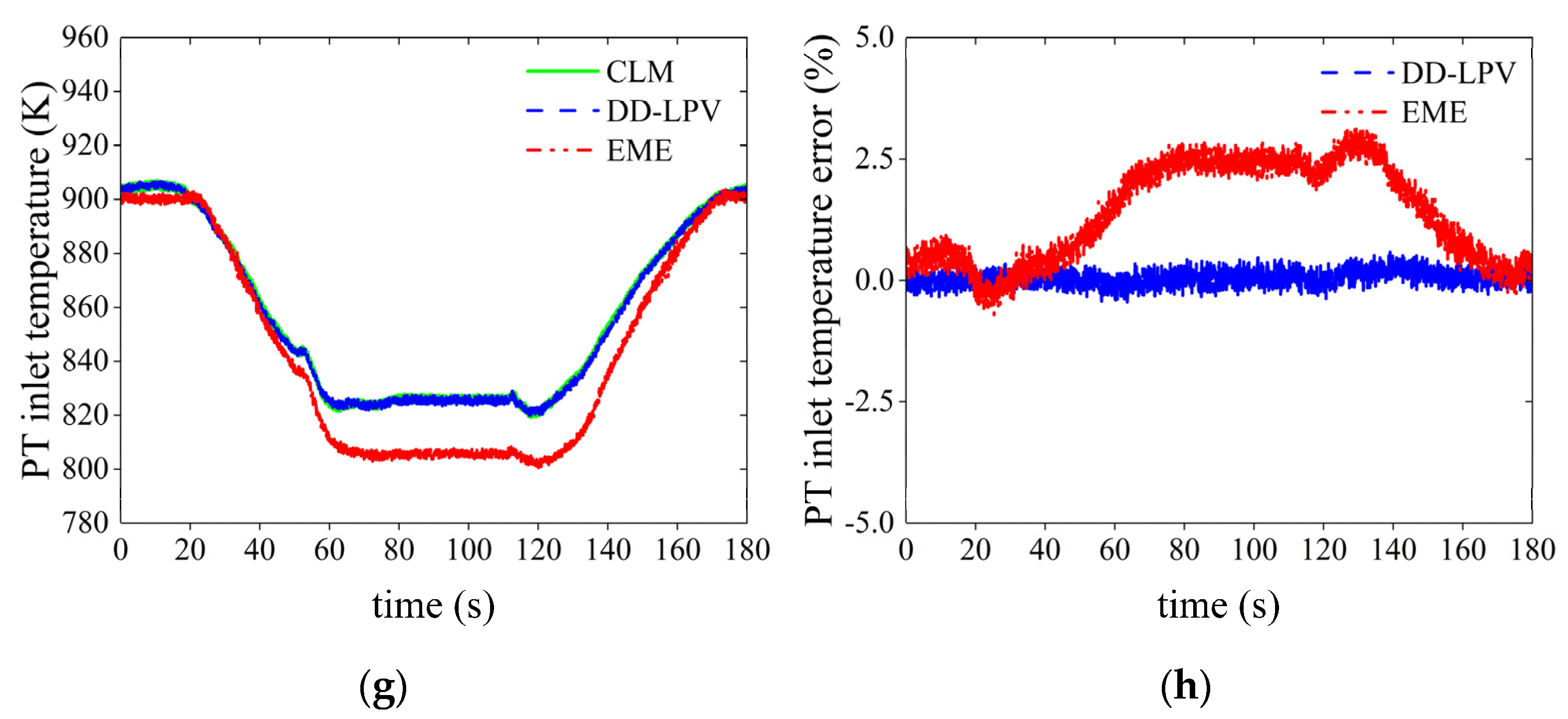
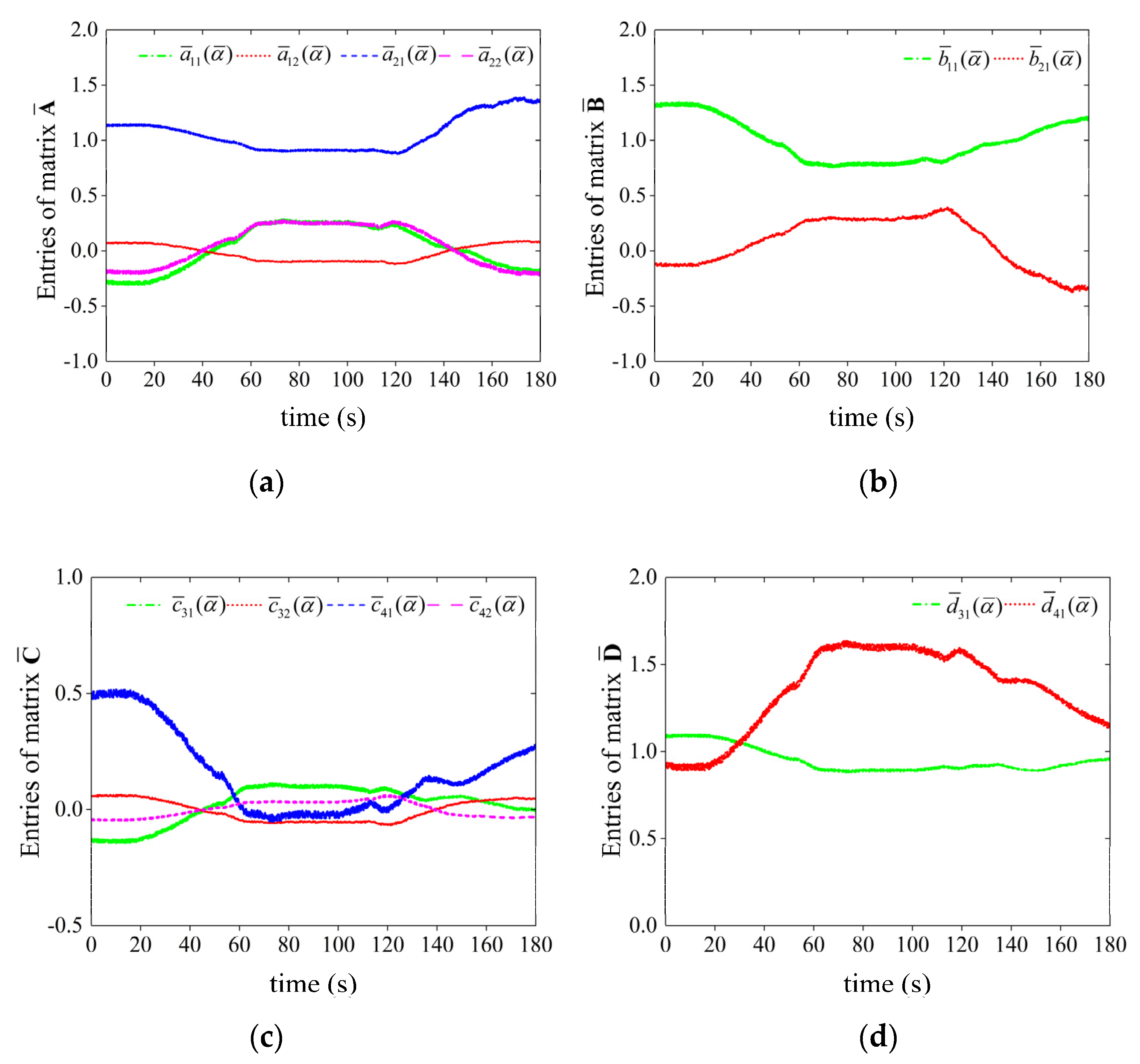
| Altitude | Measurement Noise | Error Type | Prediction Error of DD-LPV Model (%) | Prediction Error of EME Model (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ng | np | P3 | T44 | ng | np | P3 | T44 | |||
| 0 m | no | Average error | 0.0115 | 0.0016 | 0.0415 | 0.0471 | 0.1703 | 0.0222 | 0.6233 | 0.7414 |
| Maximum error | 0.0509 | 0.0092 | 0.1442 | 0.2306 | 0.4203 | 0.0801 | 2.5217 | 1.8090 | ||
| Standard deviation | 0.0105 | 0.0016 | 0.0360 | 0.0355 | 0.1139 | 0.0195 | 0.6301 | 0.3995 | ||
| yes | Average error | 0.1202 | 0.1125 | 0.2320 | 0.1895 | 0.1974 | 0.1034 | 0.6494 | 0.7525 | |
| Maximum error | 0.4447 | 0.3760 | 0.9075 | 0.8425 | 0.6847 | 0.2763 | 2.7619 | 2.1970 | ||
| Standard deviation | 0.0847 | 0.0751 | 0.1787 | 0.1512 | 0.1392 | 0.0622 | 0.6236 | 0.4280 | ||
| 1000 m | no | Average error | 0.0071 | 0.0011 | 0.0316 | 0.0287 | 0.1298 | 0.0157 | 0.7899 | 0.5714 |
| Maximum error | 0.0422 | 0.0066 | 0.1210 | 0.1110 | 0.3540 | 0.0664 | 1.9774 | 1.6577 | ||
| Standard deviation | 0.0069 | 0.0011 | 0.0282 | 0.0247 | 0.0970 | 0.0145 | 0.5461 | 0.4464 | ||
| yes | Average error | 0.1152 | 0.1115 | 0.2240 | 0.1655 | 0.1692 | 0.1016 | 0.8017 | 0.5943 | |
| Maximum error | 0.3945 | 0.3721 | 1.0303 | 0.6901 | 0.6595 | 0.2549 | 2.3002 | 1.9504 | ||
| Standard deviation | 0.0806 | 0.0733 | 0.1786 | 0.1254 | 0.1270 | 0.0593 | 0.5608 | 0.4489 | ||
| 2000 m | no | Average error | 0.0085 | 0.0012 | 0.0172 | 0.0165 | 0.1367 | 0.0150 | 0.9661 | 1.0330 |
| Maximum error | 0.0398 | 0.0065 | 0.0624 | 0.1024 | 0.3419 | 0.0542 | 2.1097 | 2.2256 | ||
| Standard deviation | 0.0079 | 0.0011 | 0.0140 | 0.0185 | 0.0848 | 0.0155 | 0.5126 | 0.6554 | ||
| yes | Average error | 0.1122 | 0.1114 | 0.1976 | 0.1512 | 0.1682 | 0.1018 | 0.9677 | 1.0394 | |
| Maximum error | 0.3900 | 0.3825 | 0.9232 | 0.7013 | 0.6564 | 0.2521 | 2.4632 | 2.5868 | ||
| Standard deviation | 0.0765 | 0.0723 | 0.1573 | 0.1123 | 0.1225 | 0.0601 | 0.5234 | 0.6617 | ||
| 3000 m | no | Average error | 0.0060 | 0.0015 | 0.0230 | 0.0215 | 0.1258 | 0.0154 | 1.0008 | 1.4259 |
| Maximum error | 0.0385 | 0.0086 | 0.0850 | 0.1108 | 0.3158 | 0.0554 | 2.2672 | 2.8193 | ||
| Standard deviation | 0.0058 | 0.0014 | 0.0219 | 0.0156 | 0.1028 | 0.0142 | 0.4752 | 0.9727 | ||
| yes | Average error | 0.1092 | 0.1072 | 0.1727 | 0.1430 | 0.1679 | 0.1027 | 1.0016 | 1.4306 | |
| Maximum error | 0.3454 | 0.3489 | 0.8034 | 0.5814 | 0.5835 | 0.2473 | 2.6232 | 3.1719 | ||
| Standard deviation | 0.0720 | 0.0717 | 0.1304 | 0.1036 | 0.1236 | 0.0588 | 0.4954 | 0.9749 | ||
| 4000 m | no | Average error | 0.0086 | 0.0025 | 0.0896 | 0.0307 | 0.2134 | 0.0205 | 1.1080 | 1.4431 |
| Maximum error | 0.0376 | 0.0141 | 0.5005 | 0.1255 | 0.5116 | 0.0837 | 2.6658 | 2.4238 | ||
| Standard deviation | 0.0087 | 0.0022 | 0.1255 | 0.0311 | 0.1563 | 0.0209 | 1.0029 | 0.6846 | ||
| yes | Average error | 0.1040 | 0.1077 | 0.2251 | 0.1278 | 0.2387 | 0.1018 | 1.1380 | 1.4401 | |
| Maximum error | 0.3071 | 0.3531 | 0.9292 | 0.5040 | 0.8281 | 0.2616 | 3.0371 | 2.7334 | ||
| Standard deviation | 0.0643 | 0.0710 | 0.1762 | 0.0908 | 0.1754 | 0.0611 | 0.9832 | 0.7082 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, Z.; Pang, S.; Zhou, W.; Li, Y.; Li, Q. An Online Data-Driven LPV Modeling Method for Turbo-Shaft Engines. Energies 2022, 15, 1255. https://doi.org/10.3390/en15041255
Gu Z, Pang S, Zhou W, Li Y, Li Q. An Online Data-Driven LPV Modeling Method for Turbo-Shaft Engines. Energies. 2022; 15(4):1255. https://doi.org/10.3390/en15041255
Chicago/Turabian StyleGu, Ziyu, Shuwei Pang, Wenxiang Zhou, Yuchen Li, and Qiuhong Li. 2022. "An Online Data-Driven LPV Modeling Method for Turbo-Shaft Engines" Energies 15, no. 4: 1255. https://doi.org/10.3390/en15041255
APA StyleGu, Z., Pang, S., Zhou, W., Li, Y., & Li, Q. (2022). An Online Data-Driven LPV Modeling Method for Turbo-Shaft Engines. Energies, 15(4), 1255. https://doi.org/10.3390/en15041255






