Abstract
Understanding subsurface hydrocarbon migration is a crucial task for petroleum geoscientists. Hydrocarbons are released from deeply buried and heated source rocks, such as shales with a high organic content. They then migrate upwards through the overlying lithologies. Some hydrocarbon becomes trapped in suitable geological structures that, over a geological timescale, produce viable hydrocarbon reservoirs. This work investigates how intelligent agent models can mimic these complex natural subsurface processes and account for geological uncertainty. Physics-based approaches are commonly used in petroleum system modelling and flow simulation software to identify migration pathways from source rocks to traps. However, the problem with these simulations is that they are computationally demanding, making them infeasible for extensive uncertainty quantification. In this work, we present a novel dynamic screening tool for secondary hydrocarbon migration that relies on agent-based modelling. It is fast and is therefore suitable for uncertainty quantification, before using petroleum system modelling software for a more accurate evaluation of migration scenarios. We first illustrate how interacting but independent agents can mimic the movement of hydrocarbon molecules using a few simple rules by focusing on the main drivers of migration: buoyancy and capillary forces. Then, using a synthetic case study, we validate the usefulness of the agent modelling approach to quantify the impact of geological parameter uncertainty (e.g., fault transmissibility, source rock location, expulsion rate) on potential hydrocarbon accumulations and migrations pathways, an essential task to enable quick de-risking of a likely prospect.
1. Introduction
With the help of petroleum system modelling, geoscientists integrate information about hydrocarbon transport processes (generation, expulsion, migration, and accumulation) with the essential geological elements of a petroleum system (source rock, reservoir, seal, and overburden) into one model to investigate the processes operating in a petroleum system [1,2,3]. This can be useful in mature basins to reconstruct a reservoir filling history or to support future development decisions, and in frontier basins to understand the risks associated with exploration drilling [4,5,6]. However, the source of constraining data for important input parameters for petroleum system modelling is limited to wells and seismic sections that only sparsely cover the basin of interest [7,8]. Additionally, wells usually target potential reservoir sections, leaving a lot of room for interpretation of the nature and location of hydrocarbon generation and migration pathways. This uncertainty leads to significantly different modelling outcomes [9]. This inherent lack of information is also indicated by an average success rate of exploration wells of around 30% [10]. It illustrates a strong need for more comprehensive approaches to uncertainty quantification (UQ) and risk analysis. Numerous models and their simulations would be required to provide sufficient coverage of potential geological scenarios. This need collides with an underlying problem of conventional petroleum system modelling being very time consuming, because they are designed to represent the multiple physio–chemical–thermal processes that are considered essential to understand petroleum generation, primary and secondary migration, and accumulation [5,11]. Routinely, stochastic methods, such as Monte Carlo simulations, would be used in UQ studies [12,13,14,15,16]. However, they entail several-week-long simulations, rendering these impractical for conventional petroleum system modelling [11,17]. This leads to either manual calibration approaches of petroleum system models [18,19,20] or an uncertainty analysis performed separately on individual parameters. The latter replaces assessment of the combined impact of a set of uncertain parameters and is undesirable [21]. There has been some work on global sensitivity methods, but this has only focused on a subset of responses and aspects of basin development [22,23]. There are also hydrogeological studies [24] performing sensitivity analysis on basin-wide problems. However, the investigations are quite different from those appropriate for petroleum system modelling.
There are three principal approaches for modelling secondary hydrocarbon migration: the Darcy approach, the invasion percolation approach, and the flow path method [25,26,27,28]. The Darcy approach is based on Darcy’s law for flow in porous media [29], where hydrocarbon migration is driven by three physical forces: buoyancy, fluid pressure, and capillary pressure. Hydrocarbon migration is calculated by numerically solving partial differential equations in every cell of the simulation model, making this approach very time consuming [30,31]. If the model’s resolution is lowered to shorten simulation time by upscaling the initial grid, the result is an exaggerated loss of hydrocarbon volumes. This effect is due to the overestimation of average hydrocarbon saturation in low permeability zones during vertical hydrocarbon movement [32]. The invasion percolation approach for simulating the migration of hydrocarbons was first introduced by Carruthers and Ringrose [33] and by Carruthers [34]. It is based on the idea that below a critical flux threshold, fluid movement occurs in isolated and self-organised stringers [35,36]. In this scenario, immiscible movement of hydrocarbons over geological time scales is restricted to the migration along isolated pathways with the accumulations forming within trapping structures [37,38,39]. Invasion percolation simulations run in a fraction of the time required for the Darcy approach, allowing for a higher model resolution [40]. However, this speeding up comes at the price of a cruder approximation, especially for the timing of migration [41]. The flow path method also runs quickly as it abstracts the secondary hydrocarbon migration to a purely geometric problem. The only driving force is buoyancy, with migration occurring mainly along the top of carrier beds. One of the downsides of this method is that migration happens in nonspecific time; therefore, geological times and chemical or physical interactions during migration cannot be considered.
The aim of this work is to introduce the agent-based Go with the Flow tool that allows for the rapid approximation of secondary hydrocarbon migration and accumulation processes. The tool’s rapid calculation speed makes it suitable for risk management and thorough uncertainty analysis across different geological scenarios. It allows the identification of geological parameters that have the most significant impact on hydrocarbon migration and permits allocating an appropriate amount of time and resources towards reducing uncertainty around these high impact factors. Agent-based modelling (ABM) describes a class of algorithms aiming to model complex behaviours through the simultaneous simulation of multiple agents [42]. An agent is an active entity acting autonomously by following a set of rules. The collective behaviour of agents interacting with each other, and their surrounding environment allows this approach to recreate complex systems, such as the subsurface migration of hydrocarbons [43,44]. To model fluid flow, every agent represents a volume of fluid. This discrete representation should not be thought of as a precise volume of moving fluid but more as an abstract indicator of the local behaviour of the fluid. The simulation is performed discretely over calculation steps. The agents move from cell to cell at every calculation step with a certain probability, relative to predefined rules. What differentiates the approach developed in this work from the other hydrocarbon migration modelling approaches lies within the setup of the ABM. Simple rules govern the agents’ behaviour. The simplicity of the rules makes it easy to integrate additional rules that increase physical realism as required. Additionally, every agent only solves the rules locally, which minimises the impact on simulation time when adding more rules. Moreover, the number of grid cells of the model has minimal impact on the computing time, allowing for high-speed simulations, even in three-dimensional cases. ABM applications have to be built at the right level of description [42,45]. For secondary hydrocarbon migration, the fluid flow must be studied at a large scale with agents following the main subsurface physical forces (buoyancy, fluid pressure, and capillary pressure). The objective is to complement the existing petroleum system modelling toolkit with a fast and data-driven approach that approximates hydrocarbon migration and accumulations.
The paper’s structure is as follows: In the methods section, we first give an overview about the developed Go with the Flow tool and then introduce how Go with the Flow could fit in a typical uncertainty analysis workflow with the associated modelling and postprocessing techniques. In the results section, we first validate the workings of the agent-based modelling approach on a set of simple geological scenarios and then apply it within a complete uncertainty assessment analysis on a synthetic case study. The paper ends with a discussion of the results, the needed improvements for ABM in subsurface fluid migration, a conclusion, and future outlooks.
2. Methods and Materials
2.1. Go with the Flow—An Agent-Based Library for Modelling Secondary Hydrocarbon Migration
Go with the Flow is an agent-based modelling library for flow modelling in a 3D environment. It was designed as a fast proxy for flow modelling capable of simulating the subsurface movement and accumulation of hydrocarbons. It is not intended to compute the volume of trapped hydrocarbons precisely, but rather it is intended to evaluate and highlight the potential traps and pathways quickly and comprehensively.
The ABMs’ environment is a 3D model of the subsurface. The environment is populated with flow properties, such as barriers, baffles, and pathways. The environment can either be a seismic cube tied with flow properties or a static 3D model populated with flow properties. The agents in the simulation mimic hydrocarbon molecules. Each agent is modelled as a voxel moving in the subsurface. The movement of agents is modelled during a defined number of timeframes or turns. Every agent behaves autonomously in the environment following common physics-driven rules. To model hydrocarbon flow, it is essential to understand the processes of generation, migration, and trapping of hydrocarbons and the main drivers of hydrocarbon molecules in the subsurface.
Hydrocarbons are expelled from source rocks, rich in organic content. Under the correct pressure, temperature, and time conditions, source rocks expel hydrocarbons as their organic content matures. The area where this happens is typically referred to as the kitchen [46]. In the model, the kitchen is defined as the location from which agents are initiated. The location of the kitchen is usually at the bottom of the model. Still, the user can define it precisely according to their knowledge of proven or potential source rocks. The hydrocarbon generation is controlled by two parameters in the simulation: the expulsion rate and the expulsion period. The ABM controls the expulsion rate with the number of agents that are initiated from the kitchen area at every turn. The number of turns modelled represents the expulsion period.
Hydrocarbons migrate from the kitchen area, generally upwards, following two main drivers—buoyancy and capillary pressure—interacting with the different lithologies they pass through [47,48,49,50,51]; the fluid pressure is neglected in the current implementation. Hydrocarbons can be moved by buoyancy forces, which result from the difference of densities of the hydrocarbon phases and the adjacent water phases. The resultant movement is ideally directed vertically upwards. Each agent can move one space to an adjacent cell at each turn. According to buoyancy forces inducing this movement, agents can move upwards, diagonally, and sideways, but cannot move down during the simulation, capturing the architecture of most petroleum systems. Additionally, a move preference matrix is included in the decision process for selecting the cell in which to move. This induces a preference for vertical rather than sideways movement. The capillary pressure is the main force resisting the hydrocarbon movement. The magnitude of the resistance depends on the radius of the pore throat of the rock, the hydrocarbon–water interfacial tension, and wettability. These parameters are mainly related to the pore size of the rock in clastic rock settings. Therefore, the environment is populated with flow facies: barriers where agents cannot move to, baffles that allow a restricted movement, and pathways where agents can move freely. Values are set to the environment reflecting the flow properties: the pathways are set with a higher value than baffles, and barriers are set to zero. Only one agent can exist in a cell and agents cannot be merged or split in the current framework. Thus, possible movements are to the adjacent cells that are neither a barrier to flow nor already occupied by an agent. To decide how to move from this set of possibilities, the agent combines the values from its surrounding environment and its move preference matrix. The agent then moves to the highest value. Additionally, a stochastic move matrix is associated with each agent to introduce a stochastic element to the movement of the agents. According to a predefined factor, a movement is randomly sampled from the stochastic move matrix (default setting: 10% of turns). Figure 1 illustrates the movement of two agents in a 2D environment (Figure 1a) and the decision-making process to select the next move (Figure 1b).


Figure 1.
(a) Migration of two agents moving in a 2D environment; (b) decision-making process for selecting the next move of agent A.
Hydrocarbons get trapped and accumulate if a sealing structure restricts or stops the flow. The three main hydrocarbon trap types are anticlinal, stratigraphic, and faulted [52]. In the simulation, the effect of different traps on migration can be accounted for by populating the environment adequately and respecting geological features, such as structures, facies distributions, and fault core and damage zones. If an agent does not move for five consecutive turns, it is considered trapped and will have a fixed position until the end of the simulation. Fixating trapped agents saves computing time. Agents do not move when all their neighbouring cells are filled. There can be two types of obstacles preventing the movement of an agent: (1) permanent boundaries, such as barriers or trapped agents; (2) agents filling neighbouring cells, while still free to move. The movement of agents is carried out one at a time at every iteration in a shuffled order. Neighbouring free agents might move at any turn. So, waiting for five turns before fixing the position of an agent allows avoidance of fixing agents that still might move in the next iteration. Finally, when agents do not get trapped and reach the top of the environment, they are considered as having escaped, and can be assimilated to exposed and degraded hydrocarbon totals. A summary of the algorithms workings is also given in Appendix A in the form of a flow chart.
The library was first developed for an online data and geoscience contest and was selected as the winning solution [53]. The Go with the Flow contest, organised by Xeek, took place in July 2020. The aim was to provide a dynamic, fast, and 3D simulation model for secondary hydrocarbon migration. The main judging criteria were as follows: (i) similarity of accumulations with blind test volumes; (ii) tracking of the agent movements to analyse how agents move through the environment, e.g., how agents react to tilt or breaks of units in the environment; (iii) speed of the simulation. The submissions were assessed by a panel of geoscientists and data scientists. The library and results presented here were developed in the programming language Python.
2.2. Integration of Go with the Flow for Uncertainty Quantification
2.2.1. Monte Carlo Simulation for Modelling Secondary Hydrocarbon Migration
The speed achieved by Go with the Flow allows for proper uncertainty quantification using Monte Carlo simulations. Monte Carlo simulation is a well-established method across finance, engineering, and sciences [54]. A random value from a probability distribution of every uncertain variable is sampled to generate hundreds of potential model outcomes. This allows evaluation of the probability of different outcomes occurring, as well as explaining the impact of uncertainty around the unknown variables has on the result. For hydrocarbon migration modelling, a typical workflow involves three steps of modelling (Figure 2), as follows: creation of a structural model; populating the model with flow properties; modelling of hydrocarbon migration. Every step of this workflow involves uncertain parameters. Each parameter is associated with a probability distribution that describes the full extent of possible models. In the Monte Carlo simulation framework, hundreds of runs are computed. At each run, a value is sampled from the probability distribution of each parameter. Once all the runs are completed, a sensitivity analysis is performed to understand and quantify the diversity of possible outcomes and the relative importance of the uncertain parameters.

Figure 2.
Setup of the simulation workflow for geomodels in Python: a structural model is first built with GemPy [55,56]. The model is then populated with different facies types with the help of PyKrige [57,58], and afterwards, hydrocarbon simulation is performed with Go with the Flow.
2.2.2. Implementation of Geomodel Designer and Hydrocarbon Migration Simulator within Python
To create a working Monte Carlo simulator that tests out different geological scenarios, the generation of geomodels and simulation of hydrocarbon migration need to be fully integrated and automated. The Python programming language offers several libraries for this purpose. GemPy [55,56] is an open-source 3D geological modelling tool that enables probabilistic modelling. This fits the first modelling step required here—the creation of structural models. The structural models are created from co-kriging interpolation methods, requiring only surface contact points (the boundary between two layers) and orientation measurements. Potential uncertainties in structural modelling include the presence of faults, the offset on the faults, the degree of folding, and the thickness of lithological layers. Models are modified by shifting or adding contact points to accommodate uncertainty. Then, flow properties can be populated within the cells of each lithological layer of the structural model using PyKrige [57,58]. PyKrige is also an open source Python library that implements 3D ordinary and universal kriging. Kriging is a method commonly used in geostatistics for spatial interpolation [59]. It is used to populate each lithological unit with different facies types, where shale, siltstone, and sandstone translate to barriers, baffles, or pathways for agent migration. Uncertainties in property modelling can include the proportion of each facies and the level and distribution of heterogeneities within each lithological layer. These uncertainties can be considered by changing the proportion of facies or the direction and the ranges of the variogram input used for kriging. Fault zones are populated separately to better account for across and along fault flow. Across fault flow potential is calculated using the shale gouge ratio (SGR) in each unit. Based on the reviewed literature, an SGR greater than 0.5 is likely to exclude across-fault flow within a lithological unit [60,61]. According to Barton et al. [62], faults that encounter a high ratio of shear to normal stress are most likely to be critically stressed and exhibit a damage zone around the fault with many open fractures and dilatational features, enhancing horizontal and vertical flow along the fault. Uncertainties relative to along- and across-fault flow can be investigated by varying the parameter associated with the faults’ stress state in the Monte Carlo simulations. Finally, Go with the Flow complements this Python toolkit to simulate secondary migration of hydrocarbons. Uncertainty also exists in the modelling of migration in the form of the kitchen location and the quantity of hydrocarbons expelled. Altogether, these modelling tools allow us to generate, simulate, and evaluate hundreds of different geological models and their impact on hydrocarbon migration and accumulation.
2.2.3. Postprocessing and Evaluation Methods
A set of metrics, evaluation methods, and spatial visualisation tools has been developed to analyse the outcome from the Monte Carlo simulation and quantify the impact of geological uncertainties on hydrocarbon accumulations and on migration pathways. The metrics and visualisations highlight the impact of static rock properties on hydrocarbon molecules’ dynamic migration and accumulation behaviour and can support further decision making.
- (1)
- Detection of the accumulations
When hundreds of simulations are needed, manual picking of accumulations in each simulation is out of the question. The use of density-based clustering algorithms, such as HDBSCAN, can automatically identify accumulations and neglect agents dispersed in the environment. HDBSCAN stands for hierarchical density-based spatial clustering of applications with noise, and it belongs to the class of unsupervised machine learning algorithms [63,64]. It is a nonparametric, density-based clustering approach that is indifferent to the shape of an underlying cluster. Data points that are densely spaced get assigned to a cluster and data points in sparsely populated areas are categorised as noise. After running a hydrocarbon migration simulation, applying HDBSCAN to the final position of each agent in the environment allows automatic differentiation between densely populated areas (accumulations) and areas with no or sparse population (dispersed agents) (Figure 3). The benefit of using HDBSCAN is that it only has a few parameters that significantly impact the clustering results. Therefore, it does not require tuning the parameters for every hydrocarbon migration simulation. The main parameter to select is min_cluster_size. It should be set to the minimum acceptable size of an accumulation.
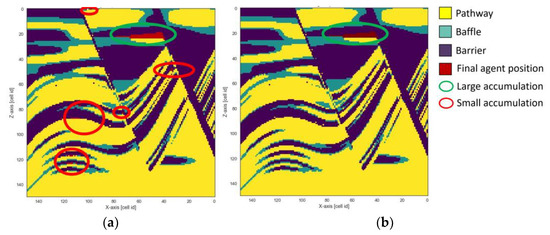
Figure 3.
(a) Final unprocessed agent position (red) after simulation. Significant accumulations as well as minor accumulations are present. (b) Final post-processed agent position after simulation. HDBSCAN detected significant accumulations and discarded minor accumulations and dispersed agents.
- (2)
- Metrics and methods of evaluation
Reducing each simulation to a comparable numeric metric is necessary for a quantitative comparison of individual simulation runs. We propose to compute six different metrics to capture the specificity of the different hydrocarbon migration outputs. The ratio of trapped agents, the average travel time of the agents, the number of accumulations, the ratio of agents in the accumulations, the largest accumulation, in terms of number of agents, and the ratio of the largest accumulations. The ratios mentioned here are ratios over the total number of agents generated. These indicators directly translate into essential concepts for assessing hydrocarbon migration and accumulation. For instance, the number of accumulations is a good indicator of degree of compartmentalisation, and the average travel time of agents is a good indicator of how heterogeneous the lithology is. Longer travel times equate to a more sinuous pathway, often correlated with a heterogeneous environment. Finally, for each accumulation, an approximation of stock tank oil initially in place (STOIIP) could be derived from the number of agents in the accumulation, as follows:
To better understand the relationship between the uncertain parameters of the Monte Carlo simulations and output metrics, we recommend using the Spearman correlation matrix. The Spearman’s rank correlation coefficient is a nonparametric measure for the correlation between two data sets [65], as follows:
where cov() is the covariance of the ranked input data sets , , and , and are the standard deviations of the ranked input data sets. The absolute correlation is computed in this study because the focus is not on negative or positive correlations but instead on its value, ranging from 0 to 1. The visualisation of all pairs of input geological uncertainty and output simulation metrics in a matrix allows quick assessment and ranking correlations. This then helps to distinguish the geological uncertainties that have a high impact on the simulation outputs from those with a negligible impact. Thus, it helps to identify the uncertainties that should be considered for additional investigation when further de-risking a hydrocarbon prospect.
Once these main uncertain parameters are identified, we recommend projecting the simulation results onto a 2D space through a dimensional parameter space reduction. T-distributed stochastic neighbour embedding, or t-SNE, is an unsupervised, non-linear dimension reduction technique, where higher dimensional data are projected into a lower dimensional space [66]. This makes this technique suitable for assessing the impact of multiple parameters in geological datasets [67,68] and provides a comprehensive view on the relationships between all the individual simulations and the chosen metrics. However, the ability to better interpret the data in lower dimensions comes at the cost of accuracy loss. However, it is important to recognise that apparent point separation in a lower dimension is not representative of the true separation in the full dimension case: only probabilities are retained.
- (3)
- Spatial visualisation of 3D simulation results
Go with the Flow offers several 3D visualisation possibilities for a deeper understanding of the simulation outputs. An initial visualisation style focuses on the accumulations and their sealing structures by plotting the final position of all the agents and the flow barriers in low opacity (Figure 4a). A second 3D visualisation focuses on the migration pathways captured by counting the number of agents that pass through each cell of the geological environment and scaling it between 0 and 1 (Figure 4b).
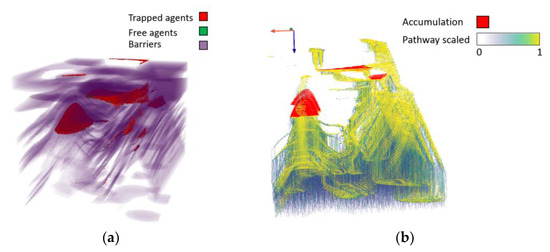
Figure 4.
Spatial visualisation of exemplary 3D simulation results. (a) Agents’ final positions and flow barriers; (b) pathways (scaled between 0 and 1) of the agents where high values are associated with more agents passing in the cell and vice versa. Accumulations are highlighted in red.
An important question in uncertainty analysis is identifying the areas where uncertainty is the largest and can be reduced by collecting more data. Calculating, for example, the entropy for different properties gives an idea about the critical areas for migration pathways and accumulations. Entropy is a measure of missing information or disorder that exists in a system [69]. It is defined by the following:
where H is the systems entropy and pi is the probability of an event to occur. It allows quantifying the level of surprise by the occurrence of an event (i.e., the probability of an event). Events that rarely occur carry a high load of information and events that occur more often carry a low information content. In the context of this work, entropy is treated as a measure for the uncertainty that exists around the discrete property value of each cell in the model [70]. To identify locations of highest uncertainty across all Monte Carlo realisations, the entropy for each cell across all model realisations is calculated and visualised.
This is performed for facies, accumulations, and migration pathways. This can help identify critical areas for migration and, therefore, areas worth focusing on.
3. Results
3.1. Validation of Go with the Flow on Simple Geological Scenarios
Before applying the Monte Carlo simulation workflow presented above, Go with the Flow is tested on three different geological scenarios. This experiment aims to validate the implementation of ABM for secondary hydrocarbon migration independently from the other steps of the workflow. The behaviour of the agents is studied regarding their interaction with the environment. The analysis is performed in a 2D environment instead of 3D to ease the visualisation and provide a complete understanding of the movement of the agents. In these examples, the focus is on the reservoir and trapping components of the petroleum system. The precise location of the kitchen is not modelled but assumed to be underneath the entire model. The agents are initiated from the bottom of the environment. For each scenario, 100 turns are simulated, and 50 agents are initiated at each turn.
The first scenario is a trapping anticline with barriers to flow completely sealing the structure (Figure 5a). The first observation is that the structure is sealing, since no agents move above the thick barrier layer. At the bottom of the environment, many agents get trapped in a thin barrier layer. The agents can be visualised moving toward the trapping structures moving up–dip, following the carrier beds. The second scenario is also an anticlinal structure, but now, it leaks on the left side of the anticline (Figure 5b). Thus, if a part of the agents remained trapped in the barrier layers of the anticline, another part manages to escape from the folded structure. The fraction of escaped agents move, and eventually get trapped higher up in the stratigraphy. The third scenario is modelling a fault block structure (Figure 5c). The fault, located at the top right of the environment, is modelled as entirely impermeable for flow. Thus, the intersections between barrier layers and the fault form traps where most agents simulated get trapped. In all three scenarios, the agents do move upward following the lithology, even in very narrow pathways.
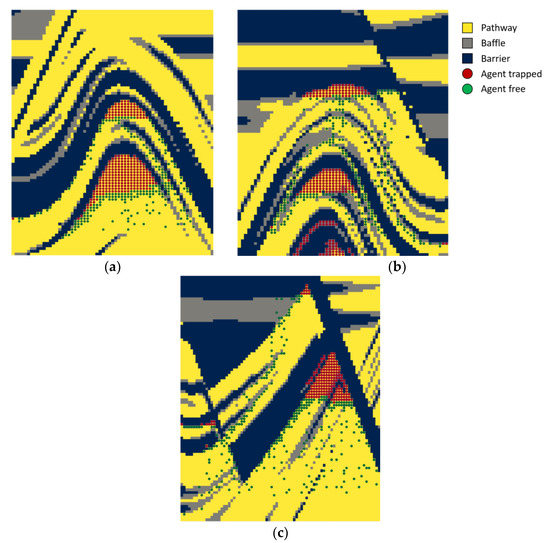
Figure 5.
(a) Anticline scenario with barrier layer completely sealing the structure; (b) anticline scenario leaking on the right side of the structure; (c) fault block scenario with an impermeable fault on the top left side of the environment. For each scenario, the agents are initialised from the bottom layer of the environment.
In conventional approaches, a lot of thinking is carried out regarding conceptual geological understanding. Geologists will typically consider several plausible scenarios and try to assess the likelihood of each. This tool complements this approach, allowing quick quantification of the outcome of conceptual models. Indeed, in computing, for instance, the proportion of agents trapped in each location gives a first idea of the relative importance of each trap. Moreover, in more complex geological settings with multiple possible traps, and particularly in 3D environments, it is not easy to identify and quantify the different potential traps. This is where this method proves to be relevant. The agents behaved as expected in the geological settings: being trapped in sealing structures and migrating along leaking pathways. The results allowed us to qualitatively validate the flow simulation on relatively simple scenarios. It will now be applied to a more complex case study in a Monte Carlo workflow to demonstrate the practical usefulness of the tool for uncertainty quantification.
3.2. Uncertainty Quantification of a Synthetic Case Study
3.2.1. Modelling Objective and Case Study Description
The Monte Carlo simulation workflow described in Section 2.2. is now applied to a synthetic case study. The objective of the case study is to analyse a potential hydrocarbon prospect consisting of an anticlinal trapping structure and a tilted fault block trap (Figure 6). The three main objectives are as follows: (i) to identify the probability of success of finding an economic hydrocarbon accumulation (>300 mmbbl in this case study); (ii) to determine whether the anticline or the tilted fault block structure is preferred; (iii) to determine which geological uncertainties have the most significant impact on hydrocarbon migration pathways and accumulation size.
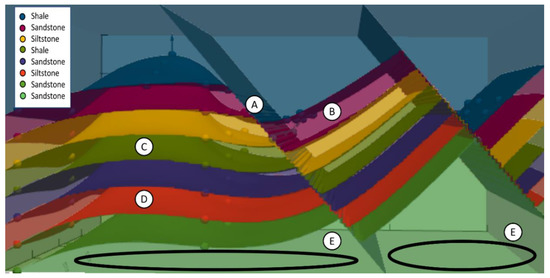
Figure 6.
Base case study model obtained using GemPy [55,56]. The uncertainties related to the case study are located from A to E and described in Table 1.
The area of interest is covered by a model measuring 2000 m × 2000 m × 1000 m in width, length, and height, respectively, and has a resolution of 150 × 150 × 150 cells, leading to a total of 3,375,000 cells (Figure 6). The model consists of multiple units dominated by shales, siltstones, or sandstones. Each unit is populated with the different facies types with the help of universal kriging [59], where shale, siltstone, and sandstone translate to barriers, baffles, or pathways for agent migration. In the left part of the model, the sedimentary succession experienced deformation that led to an anticlinal structure, exhibiting hydrocarbon trapping potential. In the right part of the model, two normal faults are present, forming tilted fault blocks that could also act as suitable hydrocarbon traps. Both strike perpendicular to the section shown in Figure 6 and the right fault dips at 50°.
Several geological uncertainties are associated with this model (Table 1) and are investigated with the Monte Carlo approach. The left fault has a degree of uncertainty regarding its dip, offset, rotation of the adjacent fault block, and stress state. For simplicity, the right fault is modelled as completely sealing for fluid flow across the fault and is not critically stressed. The composition of one of the siltstone-dominated layers and of one of the shale-dominated layers is uncertain. The anisotropy direction of the variogram used to model each of those layers is uncertain. Uncertainty also exists regarding the exact kitchen location and the expulsion quantity of hydrocarbons. The kitchen is assumed to be either under the entire system, only to the left, or only to the right of fault A. The range of uncertainty of each of these parameters is described in Table 1.

Table 1.
Uncertain parameters related to either the structural modelling, the property modelling, or the initiation of an agent (related to the source rock), as seen in Figure 6. To each uncertain parameter, a range of uncertainty is associated (+/− 2σ, if applicable).
3.2.2. Sensitivity Analyses—Identification of Main Migration Drivers and Geological Uncertainties; Evaluation of the Monte Carlo Simulations
The Monte Carlo simulation was iterated 500 times, where, for each iteration, a model was built and simulated by randomly sampling from the uncertain geological parameters listed in Table 1. On a standard workstation, the Monte Carlo simulation took three days to run. It is noteworthy that modifying the code for parallel execution can significantly reduce the computing time.
- (1)
- Accumulation size
The STOIIP Equation (1) is used to determine the accumulation sizes based on the number of agents in the most significant accumulation of each simulation (Figure 7). Here, the assumption is made that each cell (and agent) has a gross rock volume of 1185 m3, a porosity of 15%, a residual water saturation of 20%, and an oil formation volume factor Bo of 1.3. The probability of discovering a fault block accumulation greater than or equal to the economic threshold is 28.0% (red line). The probability of finding an accumulation greater than 1000 mmbbl is 4.2% (green line). The probability of discovering anticline accumulation greater than or equal to the economic threshold is 26.8%. The probability of finding an accumulation greater than 1000 mmbbl is 1.6%.
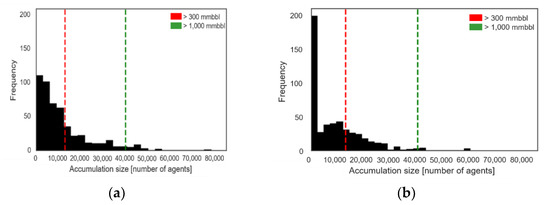
Figure 7.
Accumulation size distribution of the most significant accumulation in the fault block trap (a) and anticlinal trapping structure (b). The red vertical line shows the limit for accumulations of economic value (300 mmbbl); the green line shows the limit for accumulation greater than 1000 mmbbl.
- (2)
- Spearman correlation matrix
The Spearman correlation reveals that many of the geological uncertainties, such as fault dip, fault stress state, and silt facies proportion, have a low correlation with all evaluation metrics (Figure 8). Therefore, they have a negligible impact on the modelled petroleum system. On the other hand, shale facies proportion, kitchen location, and fault block tilt show a significantly higher correlation with the evaluation metrics; therefore, these seem relevant for the modelled formation of hydrocarbon accumulations.
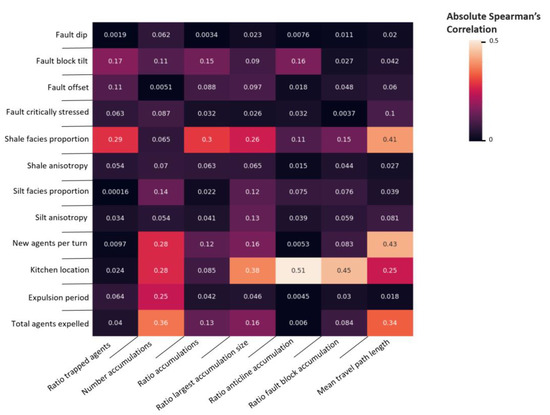
Figure 8.
Spearman correlation matrix showing the correlation of the geological uncertainties with the evaluation metrics.
- (3)
- t-SNE visualisation
With the help of the t-SNE dimension reduction technique, we now try identifying the combinations of geological input parameters that have the most impact on the evaluation metrics. The Spearman correlation matrix already highlighted that shale facies proportion, kitchen location, fault block tilt, and the total number of agents expelled on their own have a high correlation with the evaluation metrics. Therefore, the impact of the combination of these parameters will be further investigated here. It should be mentioned beforehand that, in Figure 9 and Figure 10, each point represents a single model from the Monte Carlo simulation and is placed in the graph regarding its shale facies proportion, kitchen location, fault block tilt, and the total number of agents. All the t-SNE plots presented here use a perplexity value of 30. Still, any perplexity values in the range (5–50), suggested by Van der Maaten and Hinton [66], would lead to very similar observations.
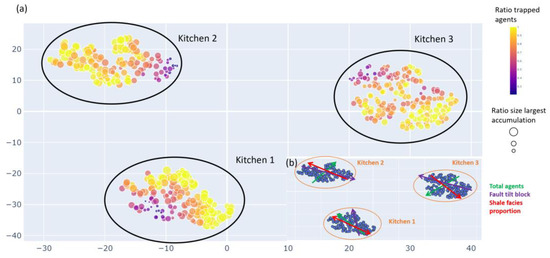
Figure 9.
t-SNE visualisation showing the most impactful geological uncertainties and their correlation with simulation evaluation metrics. Each point represents an individual model from the Monte Carlo simulation. (a) The points are colour coded with the evaluation metric ratio of trapped agents and sized by the size of the most significant accumulation. (b) Display of the trends of the original geological parameters with colour coded arrows.
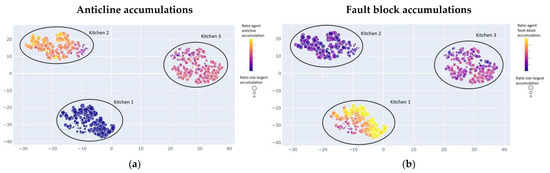
Figure 10.
t-SNE visualisation showing the most impactful geological uncertainties and their correlation with simulation evaluation metrics, colour coded by ratio of agents in anticlinal accumulations (a) and fault block accumulations (b) and sized by the size of the largest accumulation.
Figure 9 illustrates the impact the geological parameters have on the evaluation metrics ratio of trapped agents and ratio of largest accumulation size. The figure shows three isolated point clouds equivalent to the different kitchen locations. Kitchen location 1 corresponds to the case scenario of agents expelled underneath the fault block; kitchen location 2 corresponds to agents expelled underneath the anticline; kitchen location 3 corresponds to agents expelled underneath the entire model. In each cluster of points, the models with a high ratio of trapped agent (colour coded) and the largest accumulation size (point size) are closer together. The t-SNE spatially preserves the trends of the original geological input parameters. For each parameter, these spatial trends are highlighted by colour-coded arrows in Figure 9b (same data as Figure 9a but without colour or size modifications to the points). Figure 9a,b, together, show that for kitchen location 2 and kitchen location 3, the shale facies proportion (red arrow) strongly impacts the evaluation metrics ratio of trapped agents and the ratio of the largest accumulation size. However, it can also be seen that the shale facies proportion plays a subordinate role for the evaluation metrics for models with kitchen location 1 (agents expelled underneath the fault block). Here, the tilt of the fault block has the most considerable impact on the ratio of trapped agents and the ratio of the largest accumulation size.
Figure 10 is a replication of Figure 9, but it is colour coded by the ratio of trapped agents in the anticline (Figure 10a) and the ratio of agents trapped in the fault block (Figure 10b). It highlights the immense impact the kitchen location has on the probability of having large accumulations (>1000 mmbbl) in either the fault block or the anticline. If the kitchen location is below the anticline (kitchen 2 in Figure 10a,b), the largest accumulations can be expected in the anticline. Likewise, if the kitchen location is below the fault block (kitchen 1), the largest accumulations can be expected in the fault block. It also becomes clear that if the source rock is located underneath the fault block, there is no chance for an accumulation to form within the anticline (Figure 10a). This is also reflected in the large accumulations (>1000 mmbbl) that can be found. If the kitchen is located underneath the anticline (kitchen 2), agents can always migrate into the fault block, preventing large accumulations from forming (Cambridge, MA, USA, Appendix B, Figure A2, Figure A3 and Figure A4). This is probably closely related to the tilt of the fault bock and the sealing or along damage zone flow properties of the left fault.
- (4)
- Entropy visualisation
Calculating the entropy for different properties in every cell for all simulations gives an idea about the critical areas for migration pathways and where uncertainty reduction would add the most value. In Figure 11, 2D sections of the entropy distribution of the different facies types (a), the migration pathways (b), and the accumulation positions (c) are displayed. As highlighted in the red polygon in Figure 11a, the facies distribution has a high entropy in this area, translating to a high degree of uncertainty. Looking at Figure 11b,c, one can see a low entropy in these areas. The reason is that there are rarely any accumulations throughout all simulations forming in this area. Therefore, further efforts to reduce entropy and uncertainty in these areas do not add value. The areas enclosed by the red circles in Figure 11a also indicate a high entropy. This is related to the geological uncertainty of the proportion of shale in this layer. The high pathway entropy also reflects this in the same area highlighted (red circles) in Figure 11c. Reducing the uncertainty of the proportion of shale in this layer would reduce the uncertainty around the hydrocarbon migration pathways in this area. Lastly, one can also see that there is a high entropy around the two regions marked for accumulation positions (Figure 11b) and the lower section of Figure 11c for pathway entropy (red polygon). The high entropies and uncertainties are associated with the location of the source rock.

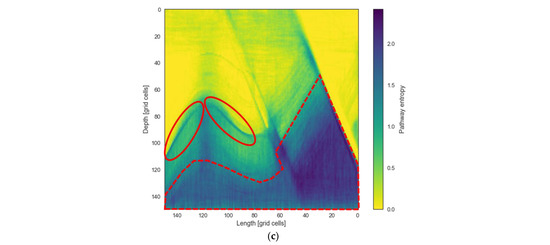
Figure 11.
Two-dimensional slices through the model of the entropy distribution of all simulation runs for facies (a), accumulation location (b), and migration pathways (c).
- (5)
- Case study evaluation
The geological uncertainties with the most significant impact on fault block accumulations are the shale proportion in layer C, the tilt of the fault block, and the source rock location. Based on the available information, the evaluation of the results and derived metrics from the Monte Carlo simulation indicate a 28.0% chance of success in finding an economically feasible hydrocarbon accumulation in the tilted fault block trap. There is also a 26.8% chance of finding an economically feasible hydrocarbon accumulation in the anticlinal trapping structure. The geological uncertainties with the most significant impact on anticlinal accumulations are the shale proportion in layer C and the source rock location. If the source rock is located underneath the tilted fault block, there is little chance of a hydrocarbon accumulation to form in the anticline. However, the benefit from this is that there is a higher chance of finding large accumulations in the fault block. The quantitative findings from the Monte Carlo simulation suggest that investing further time and resources into reducing the uncertainty around the source rock location has the highest value attached.
4. Discussion and Future Perspectives
The agent-based modelling tool presented here offers the possibility of rapidly assessing and visualising uncertainties around secondary hydrocarbon migration pathways and accumulations. We reiterate that the tool’s purpose is not to make precise predictions about fluid movements or accumulation. The aim is to rapidly screen numerous scenarios to better understand the range of possible simulation outcomes and identify the geological parameters that have the most significant impact on these outcomes. More accurate, time-consuming, physics-based simulation can then be utilised after this initial screening process.
The results suggest that the Go with the Flow tool’s agents are suited to mimicking the behaviour of hydrocarbon molecules. Further benchmarking studies need to be conducted to strengthen these findings. In the synthetic case study, we demonstrated how incorporating the Go with the Flow tool into a Monte Carlo simulation framework allows identification of the main drivers for hydrocarbon migration. The impact of the uncertainties and the effect of reducing these could also be assessed. These findings allow channelling resources towards reducing the uncertainties around crucial features instead of following a trial-and-error approach.
It is noteworthy that a single grid cell is always entirely occupied by a single agent with the tool’s current setup. This means that a grid cell is either 100% saturated with hydrocarbons or brine. This also means that changing the resolution of the grid will have a significant impact on the accuracy of evaluation results. Currently, it is also not possible for the agents to distinguish between oil and gas molecules. Accuracy is, however, not what is deemed most important for this tool. The idea is not to replace existing petroleum system modelling tools but to slot in before the complex and time-consuming simulations are performed. This pre-screening allows the users to fully leverage expensive simulation time by focusing only on those scenarios that matter most. The tool can also be used to compare and rank the outcomes of different scenarios. Scenarios that produce accumulations in areas with proven accumulations could receive a higher ranking than scenarios that do not reflect the data. It is also possible to frame the questions in the form of an inverse problem, and answer it with this tool, as follows: Which parameter conditions would lead to the oil accumulations currently present in the known reservoirs in an area? Which migration pathways were most used? This can then be used to verify or discard existing theories on the workings of the petroleum system and help identify new prospects situated within a similar setting.
Another benefit of this tool is the flexibility of application and adaptivity of the code. It is possible to test out different geological conceptual scenarios or different uncertain geological parameters and evaluate their impact on hydrocarbon pathways and accumulation locations. Conceptual thinking about a problem can, therefore, be transformed into a quantitative, measurable response. Instead of applying it to a generated geomodel, one could also use the tool on a seismic cube to quickly screen potential areas for hydrocarbon accumulations. This has been carried out in a separate informal study, where it was proven that the simulated location of hydrocarbon accumulations was similar to the location of already proven hydrocarbon accumulations [71].
The adaptivity of the code emerges from the concept of agent-based modelling itself. Every agent follows a predefined set of simple rules that guides its movement through the subsurface. Adding or removing additional rules or modifying the environment in a way that influences an agent’s behaviour can quickly be carried out. Setting up these rules does not require formulating intricate mathematical equations [44]. This makes understanding these models more intuitive than other simulation algorithms and allows for accessible communication of the functioning of this tool to stakeholders without domain expertise. Introducing new rules to achieve more realistic simulations without compromising on runtime is the scope of future work. For example, incorporating more realistic capillary pressures to better simulate the leakage rate of trapping structures [72] or having preferential migration along concentrated pathways of hydrocarbon molecules. If information about the fluid properties such as density is available, one could also use this information to control the magnitude of movement for different agents at each iteration [47]. Additionally, integrating hydrocarbon composition, thermal maturity, and degradation as it moves through the subsurface would be valuable in improving realism.
In addition to the application in hydrocarbon migration and accumulation analysis, this tool also has great potential for the risk assessment of carbon capture and storage (CCS) sites. Different geological scenarios can be simulated to understand their impact on the migration and distribution of CO2 in the subsurface.
5. Conclusions
We introduced the Go with the Flow tool in this work—an agent-based model for simulating secondary hydrocarbon migration. The initial results suggest that the agent movement is a good approximation for hydrocarbon migration in the subsurface. It allows quick quantitative estimates of conceptual geological scenarios. The tool can be integrated in Monte Carlo workflows to swiftly screen a number of geological scenarios to understand the range of possible simulation outcomes better, and to identify the geological factors that are the most impactful. After this first screening procedure, more precise, time-consuming, physics-based simulations might be used. This permits expensive simulation time to be spent where it is most helpful.
Author Contributions
Conceptualization, B.S., Q.C., N.S., J.N., D.A. and V.D.; methodology, B.S. and Q.C.; software, B.S. and Q.C.; validation, B.S. and Q.C.; formal analysis, B.S. and Q.C.; investigation, B.S. and Q.C.; data curation, B.S. and Q.C.; writing—original draft preparation, B.S. and Q.C.; writing—review and editing, N.S., J.N., D.A. and V.D.; visualization, B.S. and Q.C.; supervision, V.D.; project administration, B.S. and Q.C.; All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the James Watt Scholarship (B.S. 100%, Q.C. 50%) and the NERC National Productivity Investment Fund (NPIF) grant, ref. no. NE/R01051X/1 (Q.C. 50%). The APC was funded by Studio X LLC (50%) and the James Watt Scholarship of B.S. (50%).
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Acknowledgments
We would like to thank the NERC National Productivity Investment Fund (NPIF) grant, ref. no. NE/R01051X/1, and Heriot Watt University, via its James Watt Scholarship scheme, for funding Quentin Corlay’s PhD studies in equal parts; additionally, we would like to thank Heriot Watt University for sponsoring 100% of Bastian Steffens’ PhD studies via its James Watt Scholarship scheme. We would also like to thank the Natural Environmental Research Council (NERC) Centre for Doctoral Training (CDT) in Oil and Gas of which both PhD studies are part. We would also like to acknowledge Shell and Studio X for setting up the Go with the Flow geo-data science challenge and their support for publishing this work. Finally, we would like to thank Helen Lewis, Thomas Wagner, Dave McCarthy, and the anonymous reviewers for their comments and suggestions that improved this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Figure A1.
Flow chart showcasing the workings of the Go with the Flow algorithm. The iterators i, j, k are responsible for the generation of new agents, the movement of active agents and the number of iterations to run, respectively.
Appendix B
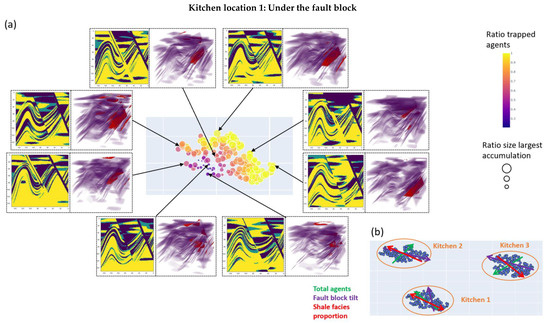
Figure A2.
(a) t-SNE analysis of kitchen scenario 1 showing the most impactful geological uncertainties and their correlation with simulation evaluation metrics. Each point represents an individual model from the Monte Carlo simulation. The points are colour coded with the evaluation metric ratio of trapped agents and sized by the size of the most significant accumulation. One observation is that all the accumulations remain in the fault block area. Exemplary 2D slices of the environment and 3D plots showing the accumulation positions at the end of the simulation (red) and the barriers (purple) are also shown (b) Display of the trends of the original geological parameters with colour coded arrows.
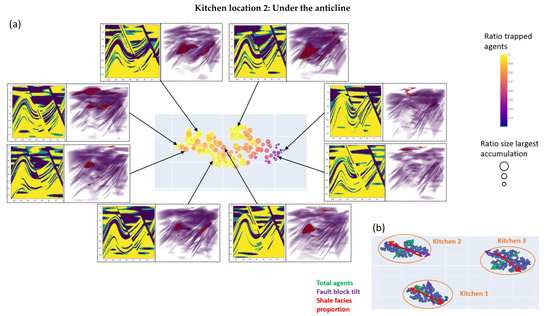
Figure A3.
(a) t-SNE analysis of kitchen scenario 2 showing the most impactful geological uncertainties and their correlation with simulation evaluation metrics. Each point represents an individual model from the Monte Carlo simulation. The points are colour coded with the evaluation metric ratio of trapped agents and sized by the size of the most significant accumulation. One observation is that accumulations are mainly located in the anticline but a significant part (~25%) is also located in the fault block. Exemplary 2D slices of the environment and 3D plots showing the accumulation positions at the end of the simulation (red) and the barriers (purple) are also shown (b) Display of the trends of the original geological parameters with colour coded arrows.
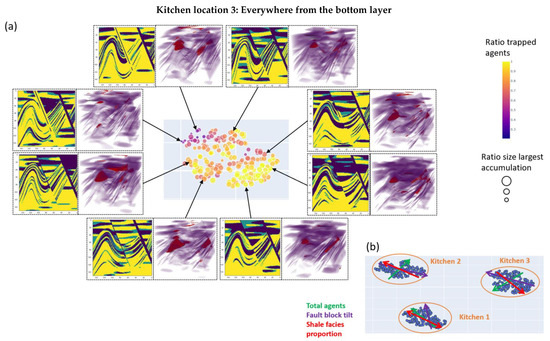
Figure A4.
(a) t-SNE analysis of kitchen scenario 3 showing the most impactful geological uncertainties and their correlation with simulation evaluation metrics. Each point represents an individual model from the Monte Carlo simulation. The points are colour coded with the evaluation metric ratio of trapped agents and sized by the size of the most significant accumulation. One observation is that accumulations are located in the fault block and the anticline. Exemplary 2D slices of the environment and 3D plots showing the accumulation positions at the end of the simulation (red) and the barriers (purple) are also shown (b) Display of the trends of the original geological parameters with colour coded arrows.
References
- Rodriguez, J.F.; Littke, R. Petroleum generation and accumulation in the Golfo San Jorge Basin, Argentina: A basin modeling study. Mar. Pet. Geol. 2001, 18, 995–1028. [Google Scholar] [CrossRef]
- Al-Hajeri, M.M.; Al Saeed, M.; Derks, J.; Fuchs, T.; Hantschel, T.; Kauerauf, A.; Neumaier, M.; Schenk, O.; Swientek, O.; Tessen, N.; et al. Basin and petroleum system modeling. Oilfield Rev. 2009, 21, 14–29. [Google Scholar]
- Magoon, L.B.; Dow, W.G. The petroleum system: From source to trap. AAPG Mem. 1994, 60, 93–120. [Google Scholar]
- Baur, F.; Wielens, H.; Littke, R. Basin and Petroleum Systems Modeling at the Jeanne d’Arc and Carson Basin offshore Newfoundland, Canada. Recorder 2009, 34, 28–36. [Google Scholar]
- Peters, K.E.; Curry, D.J.; Kacewicz, M. An overview of basin and petroleum system modeling: Definitions and concepts. In Basin Modeling: New Horizons in Research and Applications: AAPG Hedberg Series; American Association of Petroleum Geologists: Tulsa, OK, USA, 2012; Volume 4, pp. 1–16. [Google Scholar] [CrossRef]
- Welte, D. Petroleum systems modeling: A guidance tool for the upstream petroleum industry. Energy Explor. Exploit. 2002, 20, 401–405. [Google Scholar] [CrossRef]
- Sylta, Ø. Analysing exploration uncertainties by tight integration of seismic and hydrocarbon migration modelling. Pet. Geosci. 2008, 14, 281–289. [Google Scholar] [CrossRef]
- Tømmerås, A.; Sylta, Ø.; Daszinnies, M.C.; Mencaroni, D. Prewell and postwell predictions of oil and gas columns using an iterative Monte Carlo technique with three-dimensional petroleum systems modeling. AAPG Bull. 2018, 102, 709–728. [Google Scholar] [CrossRef]
- Tong, Y. Basin and Petroleum System Modeling with Uncertainty Quantification: A Case Study on the Piceance Basin, Colorado; Stanford University: Stanford, CA, USA, 2016. [Google Scholar]
- The Impact of DHIs on Exploration Performance, Westwood Global Energy Group. Available online: https://www.westwoodenergy.com/reports/global-ea/the-impact-of-dhis-on-exploration-performance (accessed on 24 June 2021).
- Peters, K.E.; Walters, C.C.; Mankiewicz, P.J. Evaluation of kinetic uncertainty in numerical models of petroleum generation. AAPG Bull. 2006, 90, 387–403. [Google Scholar] [CrossRef]
- Chang, H.; Liao, Q.; Zhang, D. Benchmark problems for subsurface flow uncertainty quantification. J. Hydrol. 2015, 531, 168–186. [Google Scholar] [CrossRef]
- Riva, M.; Guadagnini, A.; De Gaspari, F.; Alcolea, A. Exact sensitivity matrix and influence of the number of pilot points in the geostatistical inversion of moment equations of groundwater flow. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Rogers, D.W.O. Fifty years of Monte Carlo simulations for medical physics. Phys. Med. Biol. 2006, 51, R287. [Google Scholar] [CrossRef] [PubMed]
- Ojeda, P.; Garcia, M.; Londono, A.; Chen, N.Y. Monte Carlo Simulations of Proteins in Cages: Influence of Confinement on the Stability of Intermediate States. Biophys. J. 2009, 96, 1076–1082. [Google Scholar] [CrossRef] [PubMed]
- Tartakovsky, D.M. Assessment and management of risk in subsurface hydrology: A review and perspective. Adv. Water Resour. 2013, 51, 247–260. [Google Scholar] [CrossRef]
- Wendebourg, J.; Trabelsi, K. How wrong can it be? Understanding uncertainty in petroleum systems modelling. In Petroleum Geology Conference Series; Geological Society: London, UK, 2005; Volume 6, pp. 1289–1299. [Google Scholar]
- Kuhn, P.P.; di Primio, R.; Hill, R.; Lawrence, J.R.; Horsfield, B. Three-dimensional modeling study of the low-permeability petroleum system of the Bakken Formation. AAPG Bull. 2012, 96, 1867–1897. [Google Scholar] [CrossRef]
- Schenk, O.; Peters, K.; Burnham, A. Evaluation of alternatives to Easy% Ro for calibration of basin and petroleum system models. In Proceedings of the 79th EAGE Conference and Exhibition 2017, Paris, France, 12–15 June 2017; pp. 1–5. [Google Scholar]
- Paton, D.A.; Di Primio, R.; Kuhlmann, G.; Van Der Spuy, D.; Horsfield, B. Insights into the petroleum system evolution of the southern Orange Basin, South Africa. S. Afr. J. Geol. 2007, 110, 261–274. [Google Scholar] [CrossRef]
- Ducros, M.; Nader, F.H. Map-based uncertainty analysis for exploration using basin modeling and machine learning techniques applied to the Levant Basin petroleum systems, Eastern Mediterranean. Mar. Pet. Geol. 2020, 120, 104560. [Google Scholar] [CrossRef]
- Formaggia, L.; Guadagnini, A.; Imperiali, I.; Lever, V.; Porta, G.; Riva, M.; Scotti, A.; Tamellini, L. Global sensitivity analysis through polynomial chaos expansion of a basin-scale geochemical compaction model. Comput. Geosci. 2013, 17, 25–42. [Google Scholar] [CrossRef]
- Ruffo, P.; Porta, G.M.; Colombo, I.; Scotti, A.; Guadagnini, A. Global sensitivity analysis of geochemical compaction in a sedimentary Basin. In Proceedings of the First EAGE Basin & Petroleum Systems Modeling Workshop, Dubai, United Arab Emirates, 19–22 October 2014; Volume 1, pp. 1–5. [Google Scholar]
- Wainwright, H.M.; Finsterle, S.; Jung, Y.; Zhou, Q.; Birkholzer, J.T. Making sense of global sensitivity analyses. Comput. Geosci. 2014, 65, 84–94. [Google Scholar] [CrossRef]
- Pegaz-Fiornet, S.; Carpentier, B.; Michel, A.; Wolf, S. Comparison between the Different Approaches of Secondary and Tertiary Hydrocarbon Migration Modeling in Basin Simulators. In Basin Modeling: New Horizons in Research and Applications, AAPG Hedberg Series; American Association of Petroleum Geologists: Tulsa, OK, USA, 2012. [Google Scholar] [CrossRef]
- Hantschel, T.; Kauerauf, A.I.; Wygrala, B. Finite element analysis and ray tracing modeling of petroleum migration. Mar. Pet. Geol. 2000, 17, 815–820. [Google Scholar] [CrossRef]
- Baur, F.; di Primio, R.; Lampe, C.; Littke, R. Mass balance calculations for different models of hydrocarbon migration in the Jeanne d’Arc basin, offshore Newfoundland. J. Pet. Geol. 2011, 34, 181–198. [Google Scholar] [CrossRef]
- Baur, F.; Katz, B. Some practical guidance for petroleum migration modeling. Mar. Pet. Geol. 2018, 93, 409–421. [Google Scholar] [CrossRef]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon; Victor Dalmont: Paris, France, 1856; 647p. [Google Scholar]
- Schneider, F. Modeling multiphase flow of petroleum at the sedimentary basin scale. J. Geochem. Explor. 2003, 78, 693–696. [Google Scholar] [CrossRef]
- Wolf, S.; Faille, I.; Pegaz-Fiornet, S.; Willien, F.; Carpentier, B. A new innovating scheme to model hydrocarbon migration at basin scale: A pressure-saturation splitting. In Basin Modeling: New Horizons in Research and Applications: AAPG Hedberg Series; American Association of Petroleum Geologists: Tulsa, OK, USA, 2012; Volume 4, pp. 197–205. [Google Scholar] [CrossRef]
- Sylta, Ø. A probabilistic approach to improved geological knowledge and reduced exploration risks using hydrocarbon migration modelling. Pet. Geosci. 2004, 10, 187–198. [Google Scholar] [CrossRef]
- Carruthers, D.J. Transport Modelling of Secondary Oil Migration Using Gradient-Driven Invasion Percolation Techniques. Ph.D. Thesis, Heriot-Watt University, Edinburgh, UK, 1998. [Google Scholar]
- Carruthers, D.J. Modeling of Secondary Petroleum Migration Using Invasion Percolation Techniques. Multidimens. Basin Modeling 2003, 7, 21–37. [Google Scholar]
- de Gennes, P.G.; Brochard-Wyart, F.; Quéré, D. Capillarity: Deformable Interfaces BT—Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. In Capillarity Wetting Phenom; Springer: New York, NY, USA, 2004; Volume 336. [Google Scholar]
- Glass, R.J.; Yarrington, L. Mechanistic modeling of fingering, nonmonotonicity, fragmentation, and pulsation within gravity/buoyant destabilized two-phase/unsaturated flow. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Cavanagh, A.; Rostron, B. High-resolution simulations of migration pathways and the related potential well risk at the IEAGHG Weyburn-Midale CO2 storage project. Int. J. Greenh. Gas Control. 2013, 16, S15–S24. [Google Scholar] [CrossRef]
- Sylta, Ø. Hydrocarbon Migration Modeling and Exploration Risk. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2004; 200p. [Google Scholar]
- Vasseur, G.; Luo, X.; Yan, J.; Loggia, D.; Toussaint, R.; Schmittbuhl, J. Flow regime associated with vertical secondary migration. Mar. Pet. Geol. 2013, 45, 150–158. [Google Scholar] [CrossRef][Green Version]
- Cavanagh, A.; Ringrose, P. Simulation of CO2 distribution at the In Salah storage site using high-resolution field-scale models. Energy Procedia 2011, 4, 3730–3737. [Google Scholar] [CrossRef]
- Hantschel, T.; Kauerauf, A.I. Fundamentals of Basin and Petroleum Systems Modelling; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. USA 2002, 99, 7280–7287. [Google Scholar] [CrossRef]
- Macal, C.M.; North, M.J. Tutorial on agent-based modelling and simulation. J. Simul. 2010, 4, 151–162. [Google Scholar] [CrossRef]
- Wilensky, U.; Rand, W. An Introduction to Agent-Based Modeling: Modeling Natural, Social, and Engineered Complex Systems with NetLogo; Massachusetts Institute of Technology, MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Tranouez, P.; Bertelle, C.; Olivier, D. Changing the level of description of a fluid flow in an agent-based simulation. In Proceedings of the ESS 2001, the 13th European Simulation Symposium, Marseille, France, 18–20 October 2001. [Google Scholar]
- Hunt, J.M. Petroleum Geochemistry and Geology; W.H. Freeman and Company: San Francisco, CA, USA, 1979; p. 390. [Google Scholar]
- Schowalter, T.T. Mechanics of secondary hydrocarbon migration and entrapment. AAPG Bull. 1979, 63, 723–760. [Google Scholar] [CrossRef]
- Berg, R.R. Capillary pressures in stratigraphic traps. AAPG Bull. 1975, 59, 939–956. [Google Scholar]
- Hubbert, M.K. Entrapment of petroleum under hydrodynamic conditions. AAPG Bull. 1953, 37, 1954–2026. [Google Scholar]
- Thomas, M.M.; Clouse, J.A. Scaled physical model of secondary oil migration. AAPG Bull. 1995, 79, 19–28. [Google Scholar]
- Brooks, R.H.; Corey, A.T. Properties of porous media affecting fluid flow. J. Irrig. Drain. Div. 1966, 92, 61–88. [Google Scholar] [CrossRef]
- Downey, M.W. Evaluating seals for hydrocarbon accumulations. Am. Assoc. Pet. Geol. Bull. 1984, 68, 1752–1763. [Google Scholar] [CrossRef]
- Xeek. Available online: https://xeek.ai/challenges/go-with-the-flow/overview (accessed on 22 June 2021).
- Metropolis, N.; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef]
- GemPy. Available online: https://www.gempy.org/ (accessed on 22 June 2021).
- Varga, M.D.L.; Schaaf, A.; Wellmann, F. GemPy 1.0: Open-source stochastic geological modeling and inversion. Geosci. Model Dev. 2019, 12, 1–32. [Google Scholar] [CrossRef]
- PyKrige. Available online: https://github.com/GeoStat-Framework/PyKrige (accessed on 22 June 2021).
- Murphy, B.S. PyKrige: Development of a Kriging Toolkit for Python. In Proceedings of the American Geophysical Union, Fall Meeting 2014, San Francisco, CA, USA, 15–19 December 2014. H51K-0753. [Google Scholar]
- Matheron, G. Le Krigeage Universel; École Nationale Supérieure des Mines de Paris: Paris, France, 1969; Volume 1. [Google Scholar]
- Yielding, G.; Freeman, B.; Needham, D.T. Quantitative fault seal prediction. AAPG Bull. 1997, 81, 897–917. [Google Scholar] [CrossRef]
- Harris, D.; Yielding, G.; Levine, P.; Maxwell, G.; Rose, P.T.; Nell, P. Using Shale Gouge Ratio (SGR) to model faults as transmissibility barriers in reservoirs: An example from the Strathspey Field, North Sea. Pet. Geosci. 2002, 8, 167–176. [Google Scholar] [CrossRef]
- Barton, C.A.; Zoback, M.D.; Moos, D. Fluid flow along potentially active faults in crystalline rock. Geology 1995, 23, 683–686. [Google Scholar] [CrossRef]
- Campello, R.J.; Moulavi, D.; Sander, J. Density-Based Clustering Based on Hierarchical Density Estimates; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7819 LNAI, pp. 160–172. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Astels, S. Hdbscan: Hierarchical density based clustering. J. Open Source Softw. 2017, 2, 205. [Google Scholar] [CrossRef]
- Spearman, C. “General Intelligence”, Objectively Determined and Measured. Am. J. Psychol. 1904, 15, 59–73. [Google Scholar] [CrossRef]
- Van Der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Balamurali, M.; Silversides, K.L.; Melkumyan, A. A comparison of t-SNE, SOM and SPADE for identifying material type domains in geological data. Comput. Geosci. 2019, 5, 78–89. [Google Scholar] [CrossRef]
- Balamurali, M.; Melkumyan, A. t-SNE based visualisation and clustering of geological domain. In Proceedings of the International Conference on Neural Information Processing, Kyoto, Japan, 16–21 October 2016; pp. 565–572. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Wellmann, J.F.; Regenauer-Lieb, K. Uncertainties have a meaning: Information entropy as a quality measure for 3-D geological models. Tectonophysics 2012, 526, 526–529. [Google Scholar] [CrossRef]
- Griffith, D. (Shell, Cypress, Texas, USA). Personal Communication, Material was internal non published 3d seismic. 30 September 2020.
- Bjørkum, P.A.; Walderhaug, O.; Nadeau, P.H. Physical constraints on hydrocarbon leakage and trapping revisited. Pet. Geosci. 1998, 4, 237–239. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).