Abstract
Evaporators used in organic Rankine cycles (ORC) are designed using existing flow boiling correlations that are mainly based on HVAC&R data. However, the ORC evaporators employed in the industry typically have larger diameters and operational conditions at higher reduced pressures compared to the HVAC&R applications. The present study presents the results of flow boiling heat transfer experiments in operational conditions that are representative for an industrial waste heat recovery low-temperature ORC’s evaporator tube, by being performed at high reduced pressures and in a large-diameter horizontal tube with R245fa as working fluid. The measurements are performed within a range of mass flux, saturation temperature and heat flux at 83–283 kg/m2s, 85–120 °C (8.9–19.2 bar) and 17–29 kW/m2, respectively. Test section is a round and plain horizontal carbon steel tube with 21 mm I.D., 2.5 m length. 513 local two-phase heat transfer coefficients are recorded. The experimental results are compared with each other to reveal heat transfer coefficient trends with respect to varying experimental conditions. Four distinctive heat transfer zones are observed, namely, the nucleate boiling dominant (NBD) zone, weakening nucleate boiling dominance (WNBD) zone, flow boiling zone (FBZ) and the dry-out zone (DOZ). Heat transfer coefficient vs vapor quality trends partly resembled CO2 flow boiling results reported in the literature. Two flow boiling correlations moderately predicted the data.
1. Introduction
The organic Rankine cycles (ORC) are used to produce electricity from heat energy. Typical heat sources for ORCs include geothermal energy, solar heat and industrial waste heat. The operational ORCs have a broad range of thermal capacities, from kWs to MWs. As working fluid inside the closed loop of the thermal system, organic fluids (hydrocarbons, ammonia etc.) are used. Such type of fluids is common in HVAC&R applications, where their low boiling points are utilized to evaporate at much lower temperatures in comparison to water, while ensuring high thermodynamic efficiency. This makes ORCs suitable for utilizing low-grade heat sources (such as industrial waste heat) for generating electricity.
The research carried out on ORCs can be distinguished in three different paths: thermodynamic (or thermo-economic) cycle analysis, methods and models for optimum selection of the suitable working fluids and analysis of the ORC system components. Research on cycle analysis seeks modeling and discovering optimum working conditions and cycle architectures [1,2,3]. The optimum selection of the working fluid is related to the suitability of the thermo-physical and chemical properties of a fluid in accordance with a given application case, where Bao and Zhao provided an extensive review [4]. While ORC expanders are the most often researched ORC components, the research on evaporators [5,6,7] and condensers [8,9,10] that are specifically addressing ORC applications and heat exchanger design considerations is scarce [11]. It is reported in literature that the heat exchangers (evaporator and condenser) may constitute up to the half of the investment cost (costs of the heat exchangers, pump, fan, working fluid and the expander) of an ORC system [2]. Moreover, various analytical models in the literature show that even a minimal error margin on the sizing can be leading to significant operational, material, component selection and maintenance cost increase [3,12,13,14]. Thus, a more accurate sizing of ORC evaporators can lead to more efficient and cheaper systems.
A literature survey of experimental flow boiling heat transfer is carried out for studies utilizing horizontal and plain test sections with internal diameters equal to or larger than 6 mm. Moreover, the flow boiling data of mixtures refrigerants are excluded from the count. Furthermore, only the studies published after 1990 are taken into consideration due to the availability of data, reliability of data due to accuracy related to recent advanced measurement techniques, the more recent phase-outs and regulations (Montreal Protocol signed in 1987) in refrigerants that are rendering the older data in refrigerants less relevant to the present study. Moreover, a large amount of data dating back to 1940’s in printed form, in classified form from the military-backed research in the US and USSR and data obtained through personal communication between the scientists were rigorously collected and correlated by researchers such as Chen [15], Shah [16], Gungor-Winterton [17] and Kandlikar [18]. By taking these points in consideration, 1990 is chosen as an approximate date of milestone for research on flow boiling in tubes and the studies performed after that date are considered as more reasonable to investigate further A comprehensive table is made (see Table A1) indicating study details about the used working fluid, flow geometry, test section size, heating method, number of data points, experimental ranges, and a brief list of findings.
A data point distribution (16931 experimental heat transfer coefficients) from the studies listed in the Table A1 is made with respect to the employed working fluids, tube diameters and reduced pressure values, as can be seen the Figure 1a–c, respectively. Moreover, a heat map plot of the saturation temperatures against the reduced pressure is made in the Figure 2. It can be observed from the Figure 1a that most of the flow boiling data exist for conventional refrigerants, by R134a being the most investigated one. It is followed by R22 and CO2. The Figure 1c shows that the 75% of the tested tube diameters are under 12 mm, which is a common dimension in the refrigeration tubes. Data points obtained for tube diameters that are larger than 16 mm constitute less than 2% of the entire database. The only large diameter tube data is of Aprea et al. [19] where a tube of 20 mm is used for R22 flow boiling. They have found that the Kandlikar [18] correlation predicts the data the best. Moreover, it is stated by Cooper [20] that different fluids demonstrate similar thermodynamic behaviors at the same reduced property. That’s why it is necessary to look in the data point distribution from the aspect of the reduced pressure. The Figure 1b shows that more than 95% of the data is located between pr between 0 and 0.3, while the present study investigates pr between 0.24 and 0.52. The data points available in this range belong to either CO2 or other conventional refrigeration fluids that are tested for heat pump conditions. The problem here is that CO2 has a significantly lower saturation temperature and a higher saturation pressure compared to R245fa, leading to different two-phase heat transfer mechanisms. A similar situation is valid for the conventional refrigerants that are tested at between 20 and 40 °C for generally heat pump application ranges, rendering the existing data less relevant to relatively higher saturation temperatures (and relatively lower saturation pressures) encountered in the low-temperature ORC evaporators. Moreover, the Figure 2 shows the heat map of the data points in the literature from the aspect of the saturation temperatures and the reduced pressure. It can be clearly seen that the present study’s range (85–120 °C with pr between 0.24 and 0.52) lacks flow boiling data. The only overlapping high temperature refrigerant flow boiling data found in the literature is of Niederkruger et al. [21], where R22 is tested at up to 98 °C, corresponding to a reduced pressure of up to 0.77. Yet, the tube diameter is smaller (14 mm), and the corresponding saturation pressure is double the saturation pressures encountered in the present study.
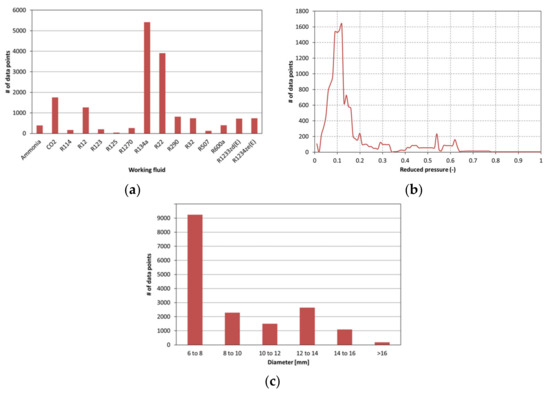
Figure 1.
Distribution of the experimental flow boiling data for horizontal plain tubes having inner diameter larger than 6 mm from the literature between 1990–2021, (a) per working fluid, (b) per reduced pressure and (c) per inner tube diameter.
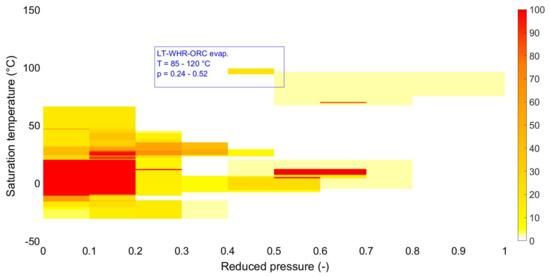
Figure 2.
The experimental flow boiling data for horizontal plain tubes having an inner diameter higher than 6 mm from the literature between 1990–2021 plotted as the saturation temperature vs. reduced pressure, where the right bar is the point intensity indicator.
Majority of the in-tube flow boiling data represent HVAC&R applications, where the tube diameters, reduced pressures and operational conditions are different than in the ORCs, where tubes with larger diameters, higher reduced pressures and different working fluids are employed. Therefore, the mainly HVAC&R data-based models that are employed to design ORC evaporators might contain inherent errors due to extrapolation of less representative boiling data.
For this reason, flow boiling heat transfer experiments are performed in a setting and operational conditions that are representative for a low-temperature waste heat recovery organic Rankine cycle (ORC) evaporator tube, by being at high reduced pressures and in a large-diameter horizontal tube with R245fa as working fluid, since the R245fa is a common working fluid in the industrial applications of low-temperature waste heat recovery ORCs. The measurements are performed within a range of saturation temperature, mass flux and heat flux, 85–120 °C (8.9–19.2 bar), 83–283 kg/m2s and 17–29 kW/m2, respectively. Test section is a round and plain horizontal carbon steel tube with 21 mm I.D., 2.5 m length and heated by heating wires. 513 local two-phase heat transfer coefficients are recorded. The experimental results are compared with each other to reveal heat transfer coefficient trends with respect to varying experimental conditions. The lack of experimental data at relatively higher saturation temperatures (between 85 °C and 120 °C) and higher reduced properties (between 0.24 and 0.52) for fluorocarbons need to be filled in order to reveal the underlying heat transfer mechanisms during flow boiling of R245fa in horizontal large diameter tubes, operating at higher reduced properties and saturation temperatures. Such data can be used to make new heat transfer correlations or extend existing databases. Eventually, this is valuable information to improve the design accuracy of such evaporators.
2. Experimental Setup and Data Reduction
The experimental setup can be seen in the Figure 3. This setup is built to accommodate flow boiling experiments for performing two-phase heat transfer measurements of organic fluids that are used in low-temperature ORCs. The setup consists of two loops: ORC medium loop and cooling loop. In the ORC medium loop the working fluid flows, whereas the cooling loop utilizes a water/glycol solution as heat transfer medium. In the ORC medium loop R245fa is used as working fluid. The working fluid is preheated to a predetermined experimental condition at the preheater. Then the working fluid flows to the test section where the resistive heating is applied to cause evaporation. The evaporated fluid then travels through the electronic expansion valve to be expanded and the saturation pressure is reduced. The expansion valve is also used to further adjust the test section pressure. The expanded fluid undergoes condensation in the condenser. The condensed fluid fills the refrigerant reservoir. A subcooler makes sure that the working fluid is subcooled at the exit of the liquid receiver, in order to avoid cavitation in the pump. At the end of the cycle, the subcooled working fluid is pumped towards the preheater, from where the cycle begins all over again. In the cooling loop, the water/glycol solution is cooled via an outside chiller, is pumped in parallel to the coolant side of the subcooler and the condenser. After the heat transfer to the ORC working fluid at the subcooler and the condenser, the heated water travels back to the chiller to become cooled down. The setup is monitored and controlled via data acquisition equipment connected to a PC. The controls and monitoring are carried out with a user interface made in NI LabView 2017 software.
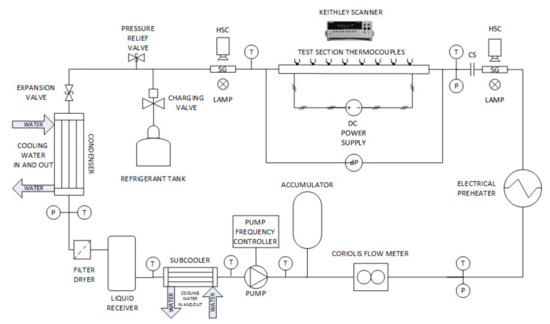
Figure 3.
Experimental test rig.
A resistive heating wire (a.k.a. heat tracing) was wound around the test section tube to apply the heat via current coming from a power supply. The total heat that can be applied through the heating cables is 4875 W. The applied power on the test section can be controlled from the power supply itself. Special attention is given in the placement of the heating cables in order to make them not touch each other, as recommended by the manufacturer. In order to ensure the safe separation, lines of fire insulation strings are wound around the empty areas between the heating cables. To ensure that structure, the entire test section is carefully taped with two layers of Kapton tape. The outer Kapton tape also mitigates the heat loss and forms a protective layer between the heating cables and the glass wool insulation, which has 32 mm thickness and mounted on top of the entire structure.
The used thermocouples are of type T (copper-constantan) which can perform measurements within −200 to 350 °C. They are calibrated by using a Triple point of Water Cell (TWC) device as reference. This device can create triple point conditions for water. Since the temperature is known very precisely at the triple point of water (±0.0005 °C), very precise calibrations can be performed for the thermocouples. There are 57 thermocouples attached onto the test section as shown in the Figure 4 and their uncertainties range from ±0.07 K to ±0.11 K, which gives an average uncertainty of ±0.84 K. Moreover, a PT100 4-wire resistive temperature measurement is carried out for determining the inlet bulk temperature of the working fluid, which has an accuracy of ±0.03 K.
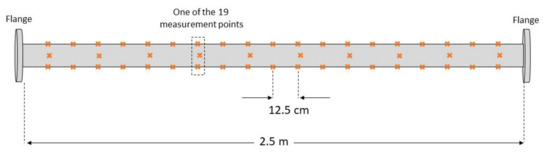
Figure 4.
Side view of the thermocouple placements.
The carbon steel test tube is of type ASTM A179 (mild steel), which has a thermal conductivity of 47.5 W/mK within the entire tube temperature range of this present study (±0.35 W/mK). Although, carbon steel tubes are almost never studied in the flow boiling literature, this type of tube is very commonly used in industrial condensers, boilers and evaporators. Hence, when the operational conditions of the present study are also taken into consideration, the tests are representative to low-temperature ORC evaporators for industrial waste heat recovery.
A glass tube and a high-speed camera are used for flow visualization at the tube outlet. The flow regimes at the tube outlet are identified solely visually for each experimental case. These are not used for deducing a flow map due to the low and dispersed amount of outlet conditions. The flow visualizations are used as reference to interpret and postulate assumptions about the in-tube boiling heat transfer thermohydraulic mechanisms inside the tube.
Moreover, the calculation made by using Müller-Steinhagen and Heck [22] correlation (recommended by Thome and many other researchers for organic fluid flow boiling) for the entire dataset predicted a two-phase pressure drop of 102–636 Pa. These correspond to a Tsat glide of 0.002–0.01 K glide, respectively, rendering the pressure drop negligible.
2.1. Data Reduction
The vapor quality at the location z along the test section is calculated as:
where the applied power on the test section is:
The heat flux is expressed as:
The mass flux is expressed as:
The experimental two-phase heat transfer is calculated as:
where is the averaged circumferential inner wall temperature calculated as:
where the side wall temperature measurement is taken twice for more correct weighted average value. The inner tube wall temperature is calculated through conduction through the tube wall from the measured outer wall temperature as:
where is the volumetric heat flux and is the heating power per unit of heat generation via electrical heating that is expressed as:
The heat losses are determined experimentally. During the real experiments the temperature of the outer tube surface is observed to be changing roughly between 80 °C and 160 °C, where a very large portion of the data correspond to tube outer temperatures of 110–130 °C. To experimentally determine the heat loss five separate measurements are performed at the test section without flow. Power is supplied to heating cables and the tube surface temperature is measured. When the tube surface temperature is stable at the desired temperature the outer surface temperature of the insulation on the test section is measured. Then the power supplied to the heating cables is increased to until the tube reaches the predetermined higher surface temperature level. With steps of 20 K, five measurements are performed, and a graph is created with the simultaneous tube surface temperatures and the insulation surface temperatures. This procedure is employed since the circumference of the test section has a complicated structure with materials and mediums having hard-to-model geometries and thermal conductivities (wound heating cables, Kapton tape, small air gap of approximately 1 cm between the insulation inner surface and the Kapton tape layer). Thus, the outer surface of the insulation is taken as the heat emitting surface towards the ambient air. The following formula is employed to calculate the heat lost to the ambient air:
where v0 is the surface efficiency of the outer surface of the insulation, which is taken as 1 due to its smooth surface characteristic. The outer diameter of the insulated test section is 10 cm, where the Ao,ins is calculated for the 2.5 m length as 0.1 m2. The average natural convection coefficient is calculated with the following formula given by Churchill and Chu [23]:
By means of combining these equations it was observed that the heat loss is less than 1%, and thus, it is taken as negligible in the calculations.
2.2. Uncertainties on Calculated Parameters
A sum of squares method is used to combine measurement errors of different physical quantities. If y is a quantity which is determined from the variables X1, X2, …, Xn: q = y(X1, X2, …, Xn), the uncertainty is calculated as:
In the rest of this section, the uncertainties on pressure, fluid properties, mass flux, heat flux, volumetric heat flux, inner wall temperature, heat transfer coefficient and vapor quality are reported. The uncertainties are given in the Table 1.

Table 1.
Uncertainties of the relevant experimental parameters.
3. Results
The measured local single-phase heat transfer coefficients of R245fa are compared with the predictions given by the Gnielinski correlation [24] which is the most widely used correlation for single-phase forced convection heat transfer prediction. The properties of R245fa are calculated with bulk temperature measurement at the test section inlet. CoolProp v6.4.0 [25] is used to calculate the thermodynamic properties. Single-phase experiments are performed for pin 8.81–13.02 bar with heat flux ranging from 11 to 17 kW/m2. The 93.75% of the data falls in ±10% error band. Similar values have been reported for various refrigerants and tube diameters by other similar studies [26,27,28].
For deducing local two-phase heat transfer coefficients of R245fa for the tube inner top, side and bottom wall temperature values are recorded for 27 experimental conditions. With respect to the observed wall temperature value trends, thermohydraulic assumptions about the inner tube boiling dynamics are made. In order to form the reference basis of the discussions about the experimental findings, four distinctive heat transfer mechanism zones are defined: the nucleate boiling dominant (NBD) zone, the weak nucleate boiling dominant (WNBD) zone, the flow boiling zone (FBZ) and the dry-out zone (DOZ). The link between the measured wall temperatures and the heat transfer mechanism zones are given in the Figure 5. Moreover, an in-tube illustration of the interpreted boiling phenomena and the representative flow visualizations are provided for a complementary flow regime-based interpretation in the Figure 6. Furthermore, five different flow regimes were subjectively identified through visual observation from the flow visualizations at the tube outlet, namely, plug, slug, wavy, stratified-wavy and dry-out. This can be seen from the Figure 6 as well.
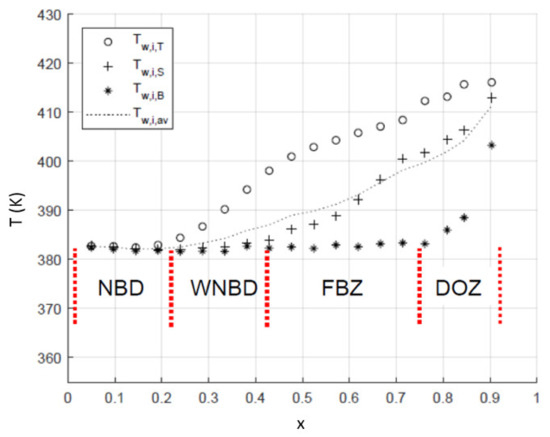
Figure 5.
Inner wall temperatures and the division of the observed heat transfer mechanisms.
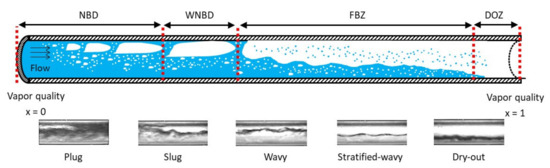
Figure 6.
Illustration of the heat transfer zones during evaporation and the representative flow visualizations from the tube outlet.
Furthermore, two-phase heat transfer coefficient trends are obtained from the wall temperature measurements for 27 different experimental conditions spanning within the vapor quality range from 0 to 1. The highest reached vapor quality is not 1 in most of the experimental runs, due to the limited capacity of the resistive heating that is applied on the test section. The higher attained vapor qualities correspond to experimental runs with lower mass fluxes, higher saturation temperatures (lower latent heat of evaporation) and higher heat fluxes. The observed heat transfer coefficient trends can be interpreted from the following aspects:
- A nucleate boiling dominance that is associated with a plateau of high heat transfer coefficient values at the low vapor quality region,
- A transition region implying a decline of the nucleate boiling that is associated with the decreasing heat transfer coefficients at the mid-range vapor quality region,
- A subsequent secondary plateau of values implying the emergence of the convective boiling with the increasing vapor quality,
- A final steep decrease in values implying a dry-out,
- The effect of carbon steel surface roughness, especially where the nucleate boiling is active,
- The large diameter of the used tube,
- The relatively high saturation temperature in combination with the thermo-physical characteristics of R245fa as shown in Table 2 for the experimental conditions.
 Table 2. Properties of R245fa at the present study’s experimental conditions.
Table 2. Properties of R245fa at the present study’s experimental conditions.
In the following sections, the effects of mass flux, saturation temperature and heat flux on the experimental heat transfer coefficient are shown. Three separate discussion sections representing each changing variable are provided, in which one parameter is being varied whereas the other two are held constant. The same analysis is also carried out for other values of the two constant parameters. In total, nine comparison cases are presented.
3.1. Influence of Mass Flux
The effects of changing mass flux on two-phase heat transfer coefficient trends are observed for three mass flux values, at constant saturation temperature and heat flux. Furthermore, the heat transfer coefficient trends are also observed under another saturation temperature and heat flux conditions, in order to observe different trends with respect to changing mass flux. The three mass flux values are approximately 105 kg/m2s, 190 kg/m2s and 285 kg/m2s. These three mass flux values are employed three cases where the constant values are = 29 kW/m2 and Tsat = 101 °C (see Figure 7a), = 29 kW/m2 and Tsat = 115 °C (see Figure 7b), and = 23k W/m2 and Tsat = 101 °C (see Figure 7c). In the discussion of this section, the three mass fluxes are referred to as low-, medium- and high-G, whereas the two different saturation temperatures are called low- and high-T, whereas the two heat flux values are called low- and high-.
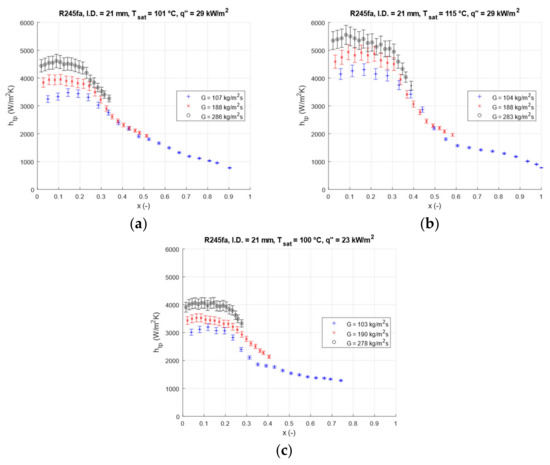
Figure 7.
Local experimental two-phase heat transfer coefficients at changing mass flux, at (a) fixed low-T and high- case (ReL = 13,618–36,399), (b) fixed high-T and high- case (ReL = 16,401–48,839) and (c) fixed low-T and low- case (ReL = 13,109–35,381).
It can be observed from the Figure 7a–c that higher mass flux leads to higher heat transfer coefficients. The values have a very short initial rise presumably due to the minimal subcooled effect at the very inlet, then a plateau and start to drop significantly after x = 0.2 approximately. These changes of slope are interpreted as transitions in the dominance of nucleate or convective boiling mechanisms.
Due to the higher heat transfer contribution of nucleate boiling at high saturation temperatures and heat flux, the heat transfer curves after the departure from the nucleate boiling dominant zone converge more in the high-T and high- condition as shown in the Figure 7b and the least in the low-T and low- condition as shown in the Figure 7c, whereas the low-T and high- case as shown in the Figure 7a shows an intermediate convergence. High saturation temperature and heat flux values make the heat transfer coefficients after the NBD zone less dependent on mass flux. The influence of varying the mass flux becomes more visible at lower saturation temperature and heat flux.
The NBD zone starts to lose dominance and the convective boiling phenomenon becomes more effective. The curve starts to break down approximately at Co = 0.7. As the NBD zone does not end abruptly, the effect of the convective boiling becomes more observable as the Co value becomes less than approximately 0.7, where the distance between the three lines becomes less. This transition value is observed to be slightly higher than what is suggested as 0.65. This shift can be linked to the extended nucleate boiling dominant region due to the surface characteristics of the carbon steel tube, which has more roughness (i.e., nucleation sites compared to tubes that were tested by Kandlikar [18], such as copper and stainless steel. This is in line with the findings of Kandlikar [18,29] where the contributions of nucleate boiling and convective mechanisms are explained for water.
Nucleate boiling is the dominant mechanism in the low vapor quality region [29,30,31]. The dominance of the nucleate boiling is enhanced with more nucleation sites on the heat transfer surface, which is the case of the surface roughness of the used carbon steel tube and the large test section diameter [32,33]. The trends that can be seen from the Figure 7a–c are in line with the findings of da Silva Lima et al. [27], where the increasing mass flux leads to a relatively slight increase in the heat transfer coefficient in the nucleate boiling region as well. On the other hand, the ratio of the nucleate and convective boiling contributions in the heat transfer coefficient value in different heat transfer zones can provide other perspectives. Zürcher et al. [34] stated that the increasing mass flux decreases the nucleate boiling contribution. This is in line with the trends in the Figure 7a–c when the ratio of the nucleate boiling to convective boiling decreases as the mass flux decreases. Moreover, the experimental results of Greco and Vanoli [35] show higher heat transfer coefficients at the NBD zone and a decrease in the FBZ, whereas the increasing mass flux led to higher heat transfer coefficients. Similar findings were reported in the studies of Choi et al. [36], Wongsa-gnam et al. [37] and Kuo and Wang [38]. Furthermore, the similar trend of the convergence of the heat transfer coefficients is mentioned by Greco and Vanoli [35], where the influence of mass flux becomes significantly less in the boiling region between x = 0.50 and 0.83. This corresponds with the plateau and the convergence of the three curves at the middle-range quality region of the present study. It is known that the mass flux mainly influences the convective boiling. However, even in NBD the convection still plays a role, hence, the slightly increased heat transfer coefficient with the increasing mass flux [39].
3.2. Influence of Saturation Temperature
The influence of changing saturation temperature on the two-phase heat transfer coefficient trends is investigated for three saturation temperature values, namely, 85 °C, 100 °C and 120 °C, at a fixed mass flux and heat flux. Furthermore, the heat transfer coefficient trends are also observed under another mass flux and heat flux condition, in order to observe the difference trends with respect to other operational conditions. The three mass flux values are varied for three cases where the constant values are = 29 kW/m2 and G = 189 kg/m2s, = 29 kW/m2 and G = 83 kg/m2s, and = 23 kW/m2 and G = 189 kg/m2s. In the discussion of this section, the three saturation temperatures are referred to as low-, medium- and high-T, whereas the two different mass fluxes are now called low- and high-G, whereas the two heat flux values are called low- and high-. The combinations of the conditions are used to describe the heat transfer coefficient plots. Figure 8, Figure 9and Figure 10a–c show the trends of the heat transfer coefficients for varying Tsat at constant G and values.

Figure 8.
Local experimental two-phase heat transfer coefficients at changing saturation temperature, at (a) fixed high-G and high- case (ReL = 20,045–31,007), (b) fixed low-G and high- case (ReL = 8802–13,616) and (c) fixed high-G and low- case (ReL = 20,151–31,171).
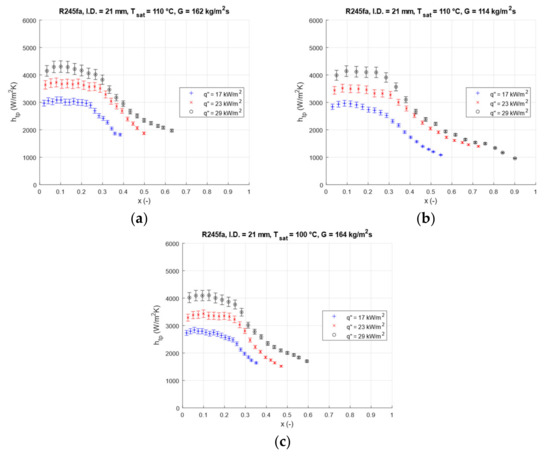
Figure 9.
Local experimental two-phase heat transfer coefficients at changing heat flux, at (a) fixed high-T and high-G case (ReL = 23,301), (b) at fixed high-T and low-G case (ReL = 16,397) and (c) at fixed low-T and high-G case (ReL = 20,872).
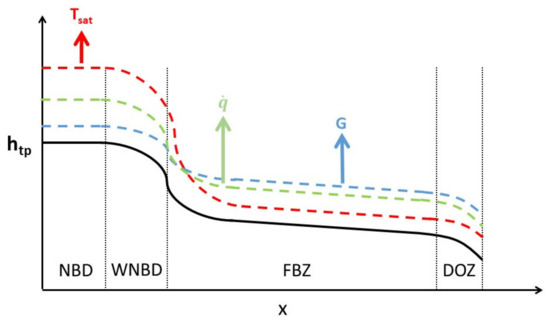
Figure 10.
Representation of the effects of the varying experimental conditions on the heat transfer coefficients for the full vapor quality range.
It can be observed that in all the figures the higher the saturation temperature, the higher the average heat transfer coefficient. The high values at the low vapor quality region start to break down from the plateau approximately between x = 0.2 and x = 0.3. This corresponds to a change in the heat transfer mechanism. The contribution of the nucleate boiling heat transfer is higher at Tsat = 120 °C, where the increase between the Tsat = 120 °C and Tsat = 100 °C is more significant than of Tsat = 100 °C and Tsat = 85 °C. In the experimental data reaching beyond a certain value of vapor quality, namely low-G and medium-G curves, the negative slope decreases after a vapor quality of approximately between 0.2 and 0.6. This corresponds to the WNBD zone and FBZ. It is noticeable that the nucleate boiling heat transfer starts to decline earlier when the saturation temperature is reduced. The WNBD zone is longer when operating at lower mass flux, when Figure 8b is compared to Figure 8a,c. However, in the high-T curve of the low-G/high- case (Figure 8b), the length of the WNBD zone remains unchanged, implying the dominance of the nucleate boiling at high saturation temperature. The curves mostly converge in the plateau zone of the FBZ, as can be observed in the Figure 8b, where the increased saturation temperature causes marginal increase in the heat transfer coefficient. This corresponds to the late FBZ (pre-DOZ), where the contribution of the nucleate boiling becomes almost extinct due to the limited amount of nucleation sites.
At high saturation temperatures (as employed in the present study), the contribution of nucleate boiling is significant in the low vapor quality regions, leading to high heat transfer coefficients [26,40]. Choi et al. [36] observed that increasing saturation temperature leads to higher heat transfer coefficients at constant vapor quality. They observed a strong dependence of heat transfer coefficients on evaporation temperature at low quality region for pure refrigerants.
From the aspect of the thermo-physical properties of the working fluid, the higher the saturation temperature is, the smaller the latent heat of evaporation becomes, leading to an increase in the Boiling number Bo, which is the main indicator of the nucleate boiling contribution. Moreover, at high saturation temperatures lower wall superheat is required to form a stable bubble at the inner tube surface [41]. In addition to that, as can be seen from the Table 2 the ρL /ρV ratio of R245fa drops approximately from 23 to 8, when the saturation temperature is varied from 85 °C to 120 °C. This leads to an increase in the Convection number Co with a factor of 1.7. However, the increasing convective contribution in the parts where the nucleate boiling loses significance, a plateau-like yet declining trend in the Figure 8b occurs. The amount of nucleation sites at the periphery is sufficient to overcome the convective heat transfer mechanism even in the FBZ, presumably a result of using a large diameter tube. Yun et al. [42] observed the same phenomenon, by addressing to the more frequent occurrence of dry-out patches at the tube’s inner periphery.
Greco [40] showed that the heat transfer coefficients increase with the reduced pressure for the entire vapor quality range. At higher mass fluxes, the heat transfer coefficients increase with the reduced pressure at low vapor quality regions, whereas they coefficients tend to merge at higher vapor quality regions. The same trend can be observed in the low-G/high- case shown in the Figure 8b, although the saturation temperature’s influence to increase the heat transfer coefficient in the FBZ is not as apparent. The reduced pressures investigated in Greco’s [40] work are lower than in the present work (0.24–0.52), which is an indicator of a flow boiling phenomenon significantly more dominated by the nucleate boiling mechanism, rendering the convection effects less in combination with the low mass flux in the case of Figure 8b. The convection effects are lower due to the vapor density increase at higher saturation temperatures, reducing the vapor velocity. Moreover, the conductivity of the liquid film decreases with the increasing saturation temperature, hence, reducing the convective contribution to the flow boiling heat transfer. The findings of Yun et al. [42] show that at high qualities the heat transfer coefficients decrease rapidly due to an easy formation of dry-out patches. Thus, the thinner liquid film occurring by the increasing vapor quality and the presence of relatively low mass flux in the low-G/high- case shown in the Figure 8b agrees with the findings of Yun et al. [42]. Padovan et al. [43] observed a significant increase of heat transfer coefficient due to nucleate boiling in response to increased saturation temperature too. The comparison of Figure 8a and Figure 10c the influence of heat flux on this phenomenon. The promoting effect of saturation temperature is more observable at higher heat flux. The same relationship was also observed by Yang et al. [44]. As can be seen from the R245fa properties given at the Table 2, an increasing saturation temperature results in an increase of the vapor density, which results in a lower flow velocity, and a decrease of liquid film conductivity. This results in lower conduction and convection through the liquid film and accordingly less contribution of the convective boiling at high saturation temperatures [26].
3.3. Influence of Heat Flux
The effects of changing heat flux on two-phase heat transfer coefficient trends are observed for three heat flux values, namely, 17 kW/m2, 23 kW/m2 and 29 kW/m2, at fixed mass flux and saturation temperature. Furthermore, the trends are also observed under different mass flux and saturation temperature values, in order to assess the difference trends with respect to other operational conditions. The three heat flux values are varied for three cases where the constant values are = 162 kW/m2 and Tsat = 110 °C, = 114 kW/m2 and Tsat = 110 °C, and = 162 kW/m2 and Tsat = 100 °C. In the discussion of this section, the three heat flux values are referred to as low-, medium- and high-, whereas the two different mass fluxes are now called low- and high-G, whereas the two saturation temperature values are called low- and high-T. The trends of the heat transfer coefficients for varying at constant G and Tsat values are shown in Figure 9a–c.
Like the previous discussions, the higher the heat flux, the higher the average heat transfer coefficient becomes, as well as the values also start to break down after a certain vapor quality. The nucleate boiling heat transfer mechanism contributes distinctively more to the heat transfer coefficient at high-. When the ratio of heat transfer increase against the increasing is considered in the NBD, WNBD and FBZ regions, the heat flux increase causes a more significant increase in the steps between the 17 kW/m2 and 23 kW/m2, compared to 23 kW/m2 and 29 kW/m2. It is noticeable that the nucleate transfer starts to decline earlier when the heat flux is reduced. The WNBD zone is shortest when the heat flux is low. This becomes more pronounced when the mass flux is high, and the saturation temperature is low. This observation agrees with the reasoning from the previous sections. Combinations of low heat flux, low saturation temperature and high mass flux lead to less significant nucleate boiling mechanism compared to the convective boiling mechanism.
Heat flux enhances the nucleate boiling contribution in the nucleate boiling region, while the heat flux’s effect on the total heat transfer coefficient is more dominant than the effect of saturated temperature, as also observed in [44,45,46]. Although, Choi et al. [36] observed that in the low-quality region, the influence of heat flux on heat transfer coefficient was strong, however, the influence was reduced for high heat flux above a certain magnitude in the high quality. In all the figures, especially in the Figure 9b this trend can be clearly seen in the present results as well. Furthermore, when the Figure 10a–c and Figure 11a–c compared, the increasing heat flux’s effect on the total heat transfer coefficient is less than the saturation temperature. The curves mostly converge in the plateau zone of the convective boiling, as can be observed in the Figure 9b, where the heat transfer coefficient is not dependent on the heat flux. This is in parallel with the findings of the experimental results of Greco [40] indicating that the saturation pressure, and therefore the reduced pressure, has a stronger effect on increasing the total heat transfer coefficients. Moreover, although there is a slight increase in the heat flux contribution to the heat transfer coefficient when the mass flux is reduced, it is not a strong dependence as stated by Balachander and Raja [47]. However, this is not surprising since they used very low mass flow rates (about 5 to 40 times smaller than the present study), where almost no convective effect was present, rendering the heat transfer coefficient strongly dependent on the heat flux.
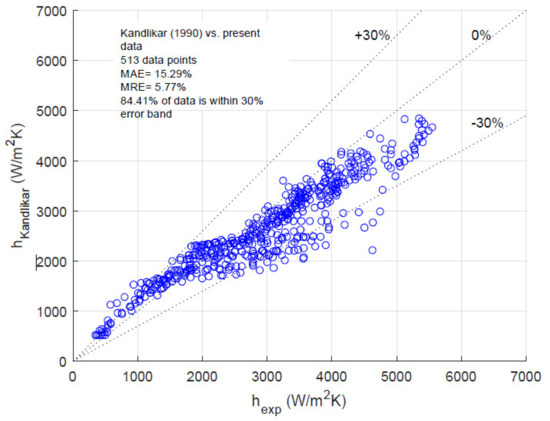
Figure 11.
Kandlikar correlation [18].
4. Synthesis and Discussion
The NBD zone is characterized by the high heat transfer coefficients and their low dependency on vapor quality, since the wall temperatures are constant. The WNBD zone is characterized by the decline of the heat transfer coefficients with the increasing vapor quality, where a cyclic dry-out and rewetting of the tube wall occurs at the top and the side of the tube. The FBZ is where the convective boiling becomes more significant, with a limited nucleate boiling contribution, where the liquid phase is mainly present only at the lower half of the horizontal tube cross section. This is identified as specific for flow boiling at high reduced properties, where very rapid changes in thermo-physical properties happen close to the critical temperature. As the wall superheat increases, the vapor density increases too, whereas on the contrary the vapor viscosity decreases as well. These two facts combined result in a significant increase in the vapor Reynolds number (up to triple fold at high wall superheats), leading to an increased forced convection heat transfer through vapor at the top wall of the tube, or at the liquid periphery of a vapor plug. The bottom half of the tube still accommodates the stratified liquid, where the nucleate boiling still takes place. With the increasing vapor quality, the weakened nucleate boiling contribution at the entire tube perimeter and the increased vapor forced convection heat transfer at the upper half of the tube flattens the heat transfer coefficient trend, or even reaches to a plateau in some of the cases. This is followed by the DOZ at high vapor qualities that are attained in some of the experimental runs, which is characterized by the additional decrease in the heat transfer coefficient slope, whereas the wall temperature at the bottom of the tube starts to increase rapidly.
When the effects of the changing mass flux, saturation temperature and the heat flux on the heat transfer coefficients are considered, it can be observed that the saturation temperature has the largest influence on the heat transfer coefficient in the NBD zone, where the effect on the FBZ is significantly less. A similar trend can be observed with the increasing heat flux as well, however with less increasing effect on NBD heat transfer coefficient values but more at post NBD-zones. The mass flux has less influence on the zones where nucleate boiling plays a significant role, but more influence is observed in the FBZ, where the relative dominance of the nucleate boiling becomes less. An illustration of the effect of the increasing mass flux, saturation temperature and the heat flux on the heat transfer coefficients with respect to the increasing vapor quality is provided in the Figure 10.
Moreover, the decreasing trend can be explained by the stratification effect caused by the large tube diameter, where the thinning liquid film at the wetted perimeter of the tube disappears at the top part and the consecutively the side wall, leading to a decrease of the number of active nucleation sites [26,48,49]. The decrease also corresponds to the bubble frequency reduction with the increasing vapor quality, as the bubbles tend to coalesce to form bigger bubbles [26]. According to Thome [50] the nucleate boiling dominated zone is harder to predict since it is significantly affected by the micro-roughness of the tube interior. Thus, the carbon steel tube is expected to demonstrate different surface characteristics compared to more conventional refrigeration tubing such as copper, stainless steel or brass.
Charnay [26] reported similarities between the R245fa and CO2 flow boiling heat transfer coefficient trends when operating at high saturation temperatures. In the experimental flow boiling study of Yoon et al. [39], where a tube with an internal diameter of 7.53 mm is used at heat fluxes varying from 12 to 20 kW/m2 and mass fluxes varying from 200 to 500 kg/m2s, the trend of initially increasing, then reaching to a local maximum or plateau, then a rapid decrease in CO2 heat transfer coefficients is observed. In the present study, a similar trend is observed in almost all cases. Moreover, the Mastrullo et al. [51] study reported very similar heat transfer coefficient trends especially for CO2 at lower mass fluxes (200 kg/m2s), within a pr range (0.32–0.5) very similar to of the present study (0.24–0.52). Lee et al. [52] observed the same trend for CO2 as well, although they employed much higher mass fluxes in their experimental study (200–1200 kg/m2s). Yun et al. [42] covered a similar operational range with the present study (G = 170–320 kg/m2s and = 10–20 kW/m2), where the similar heat transfer coefficient trends of CO2 can be observed in all their data. In accordance with these findings Oh et al. [53] observed the same trends for CO2. In another experimental study having operational ranges and tube diameters in the same order of magnitude with all the mentioned studies, Mastrullo et al. [54] reported CO2 heat transfer coefficient trends such as the present study. Moreover, the observed secondary plateau or partial flattening (WNBD to FBZ transition) resembles the mid-range vapor quality heat transfer coefficients of CO2 in studies where even higher reduced properties have been tested [39,42]. It is also important to notice that CO2 has higher heat transfer coefficients due to higher attained Reynolds numbers and thermal conductivity at the same reduced pressure with R245fa.
The main explanation of the trend similarity between R245fa operating at high temperature and CO2 is the thermodynamic phenomenon rooting from the high reduced properties. The biggest reason why these trends are not observed in the other refrigerant flow boiling data is due to the lower reduced properties, where the viscosity and surface tension ratio between the vapor and the liquid phase are very different. Since the viscosity and the surface tension of the R245fa at relatively high reduced properties such as 0.24–0.52 are much lower than the refrigerant reduced properties at typical refrigeration ranges (corresponding to −20–40 °C mostly), the thinning liquid film at the top of the horizontal tube becomes prone to break down more easily. After a certain vapor quality, CO2 starts to undergo partial dry-out. This leads to a more rapid increase of the top wall temperature, leading to even more reduced liquid viscosity at the tube’s upper surface. This type of boiling would not be the case at lower saturation temperatures, where the liquid viscosity is higher and a more annular or continuously re-wetted tube periphery can be attained, which would lead to a linear increase in the heat transfer coefficient. This difference between high and low reduced pressure measurements are also reported by [42,51,53,55]. However, the main difference compared to the findings of CO2 boiling studies is that the liquid presence is higher at the lower half of the tube, but due to the stratification effect of the large horizontal tube diameter, instead of rapidly disappearing thin film at the upper wall due to near-critical temperatures as commonly observed in studies investigating the boiling of CO2.
Finally, the data is compared to two well-known flow boiling correlations, namely the Kandlikar [18] and the Shah [16] correlations, with a MAE of 15.29% and 33.86%, respectively (the correlations’ own uncertainty is not considered). The comparisons can be seen in Figure 11 and Figure 12. In both predictions, the NBD-zone is underpredicted, whereas the rest of the heat transfer mechanism zones is overpredicted. Both were able to follow the heat transfer coefficient trends as can be seen from their low MRE. The MAE and MRE are calculated as:
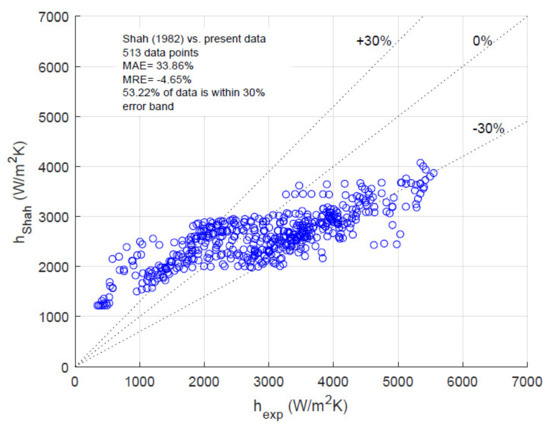
Figure 12.
Shah correlation [16].
Both correlations use an enhancement-factor approach, where a two-phase term is multiplied by the predicted single-phase heat transfer coefficient. In addition, they were made through collection of a very large flow boiling data, where refrigerant boiling data is almost entirely based on refrigeration and heat pump evaporator conditions. Thus, these predictions with similar trends to the present data, but heat transfer coefficient values at different orders of magnitude show that high reduced pressures, large diameter tubes trigger a different heat transfer mechanism than what is seen in evaporators in typical HVAC&R applications.
To conclude, these observed trends for a fluorocarbon refrigerant such as R245fa in a large diameter tube and at high reduced pressure are novel and haven’t been published yet in the flow boiling literature.
5. Conclusions
A literature survey is made for experimental flow boiling studies dating from 1990 to 2021, having horizontal round tube test sections with an I.D. higher than 6 mm, that are using non-mixture refrigerants as working fluid and of which heat transfer coefficient data was available. It was observed that no flow boiling heat transfer data combining high saturation temperature, large tube diameters and R245fa as working fluid exists. It is considered that such data can be useful for improving evaporator design of low-temperature heat recovery ORCs. Therefore, flow boiling heat transfer coefficient measurements are performed within a varying range saturation temperature, mass flux and heat flux, 85–120 °C (8.9–19.2 bar, corresponding to a reduced pressure of 0.24–0.52), 83–285 kg/m2s and 17.5–29.2 kW/m2, respectively. 513 data points for local flow boiling heat transfer coefficients for 27 different experiments are collected. The test section is a round and plain horizontal carbon steel tube with 21 mm I.D. and 2.5 m length and heated by resistive heating wires wound around the test section. The local two-phase heat transfer coefficients are recorded.
The most distinctive trend to be seen in all results is the high heat transfer coefficient at low quality regions and a gradual decline of the heat transfer coefficient after a certain vapor quality value, followed by a less steep decline or a plateau at medium and high vapor qualities, whereas a secondary decline implying the dry-out in several cases. These are interpreted as four distinctive heat transfer mechanism zones, namely, the nucleate boiling dominant (NBD) zone, the weak nucleate boiling dominant (WNBD) zone, the flow boiling zone (FBZ) and the dry-out zone (DOZ).
It was observed that the increase in the saturation temperature leads to the highest increase in the heat transfer coefficients. This is especially the case for the NBD. This implies that the saturation temperature is the largest contributor of the nucleate boiling heat transfer within the flow. The contribution of the saturation temperature is less pronounced at higher vapor qualities due to the declining nucleate boiling contribution (WNBD, FBZ and DOZ). Moreover, the heat flux is also a large contributor to the nucleate boiling mechanism. Higher heat fluxes lead to higher NBD heat transfer coefficients. The mass flux influences the NBD heat transfer coefficients marginally, but the post-NBD mechanisms become more observably influenced. This is since the mass flux is the main contributing parameter to the convective boiling, which is more pronounced at higher vapor qualities, in other words, in the WNBD, FBZ and DOZ regions.
It was observed that the evaporation inside a large diameter tube at high reduced pressures lead to different heat transfer coefficient trends compared to the other refrigerant flow boiling experiment data in the literature. The thin film at the upper inner wall of the tube breaks down and causing a stratification, resulting in an ever-decreasing amount of nucleation sites at the inner tube periphery. This was only observed for CO2 flow boiling studies until now. This is found to be reasonable since only CO2 was studied in the flow boiling literature for high reduced pressures and high reduced pressures. Finally, the Kandlikar’s correlation [18] and the Shah correlation [16] predicted the data with a MAE of 15.29% and 33.86%. The NBD zone is underpredicted, whereas the zones with less nucleate boiling are overpredicted by both correlations.
Author Contributions
Conceptualization, A.K.; methodology, A.K., S.L. and M.D.P.; validation, A.K.; resources, M.D.P.; data curation, A.K.; writing—original draft preparation, A.K.; writing—review and editing, A.K., S.L. and M.D.P.; visualization, A.K.; supervision, M.D.P. and S.L.; project administration, M.D.P.; funding acquisition, M.D.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Ghent University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
Authors declare no conflict of interest.
Nomenclature
| A | Area (m2) |
| Co | Convection number (-) |
| D | Diameter (mm) |
| G | Mass flux (kg/m2s) |
| L | Length (m) |
| Mass flow rate (kg/s) | |
| NuD | Nusselt number based on equivalent diameter (-) |
| P | Pressure (bar) |
| Pr | Prandtl number (-) |
| RaD | Rayleigh number based on equivalent diameter (-) |
| Heat flux (kW/m2) | |
| Volumetric heat flux (kW/m3) | |
| Heating power (W) | |
| T | Temperature (°C) |
| v0 | Surface efficiency (-) |
| x | Vapor quality (-) |
| X | Variable (-) |
| Xtt | Lockhart-Martinelli parameter (-) |
| y | Quantity (-) |
| z | A point’s distance to the tube inlet (m) |
| Subscripts | |
| amb | Ambient |
| av | Average |
| b | Bulk |
| bottom, B | Bottom section |
| el | Electrical |
| H | Enthalpy |
| i | Counter |
| in | Inner |
| ins | Insulation |
| L | Liquid |
| loss | Heat loss |
| LV | Liquid to vapor |
| n | n-th variable |
| o | Outer |
| r | Reduced |
| s | Surface |
| sat | Saturation |
| side, S | Side section |
| top, T | Top section |
| tp | Two-phase |
| ts | Test section |
| tube, | Tube |
| V | Vapor |
| w | Wall |
| z | Location |
| Greek | |
| µL | Liquid viscosity (Pa.s) |
| ρL | Liquid density (kg/m3) |
| ρV | Vapor density (kg/m3) |
| λL | Liquid thermal conductivity (W/m.K) |
| Abbreviations | |
| CS | Capacitive sensor |
| DOZ | Dry-Out Zone |
| FBZ | Flow Boiling Zone |
| HSC | High-speed camera |
| I.D. | Inner diameter |
| LT | Low temperature |
| MAE | Mean absolute error |
| MRE | Mean relative error |
| NBD | Nucleate Boiling Dominant |
| WNBD | Weak Nucleate Boiling Dominance |
| ORC | Organic Rankine cycle |
| WHR | Waste heat recovery |
Appendix A

Table A1.
List of experimental flow boiling studies performed between 1990–2021 with non-mixture refrigerants (except water) with horizontal test tubes having an internal diameter larger than 6 mm.
Table A1.
List of experimental flow boiling studies performed between 1990–2021 with non-mixture refrigerants (except water) with horizontal test tubes having an internal diameter larger than 6 mm.
| Author(s) | Working Fluid and Test Section Details | |
|---|---|---|
| Kundu et al. [56] | R134a Circular, smooth, copper tube Resistive Heating D = 7 mm | Tsat= 5–9 °C pr = 0.08–0.14 G = 100–400 = 2–10 x = 0.1–0.9 |
| Shao et al. [57] | R134a Circular, smooth tube Resistive Heating D = 10 mm | Tsat = 25 °C pr = 0.16 G = 250–400 = 0–10 x = 0–0.8 |
| Greco and Vanoli [41] | R22, R134a Circular, smooth, stainless steel tube Joule Heating D = 6 mm | Tsat = −4–29 °C pr = 0.07–0.17 G = 365 = 18.3–20.4 x = 0–1 |
| Yu et al. [33] | R22, R134a, R123, R114, R12 Circular, smooth and rough, copper tube Secondary heating fluid D = 7.9 and 8.4 mm L = 6 m | Tsat = 19–99 °C pr = 0.06–0.18 G = 100–361 = 2–111 x = 0–1 |
| Grauso et al. [58] | CO2 Circular, smooth and copper tube Resistive heating D = 6 mm L = 0.78 m | Tsat = 8–12 °C pr = 0.57–0.63 G = 150–500 = 5–20 x = 0–1 |
| Park and Hrnjak [59] | R22, CO2 Circular, smooth and copper tube Secondary heating fluid D = 6.1 mm L = 0.15 m | Tsat = −30–−15 °C pr = 0.03–0.32 G = 100–400 = 5–15 x = 0.1–0.8 |
| Yu et al. [60] | R134a Circular, smooth and copper tube Joule heating D = 10.7 mm L = 1.5 m | Tsat = 6 °C pr = 0.09 G = 163–408 = 2.2–56 x = 0–0.6 |
| Del Col [61] | R22, R125, R134a Circular, smooth and copper tube Secondary heating fluid D = 8 mm L = 1 m | Tsat = 24–45 °C pr = 0.19–0.41 G = 200–600 = 9–52 x = 0.07–0.91 |
| Greco [40] | R22, R134a Circular, smooth and copper tube Joule heating D = 6 mm L = 6 m | Tsat = −22–50 °C pr = 0.06–0.33 G = 200–1100 = 3.5–47 x = 0–1 |
| Choi et al. [36] | R22, R134a, R32 Circular, smooth and copper tube Joule heating D = 7.75 mm L = 5.9 m | Tsat = −9–9 °C pr = 0.05–0.19 G = 240–850 = 4.2–28.6 x = 0–1 |
| Shin et al. [62] | R22, R32, R134a, R290, R600a Circular, smooth and stainless steel Joule heating D = 7.7 mm L = 5.9 m | Tsat = 12 °C pr = 0.11–0.20 G = 265–742 = 10–30 x = 0.05–0.7 |
| Eckels and Pate [63] | R12, R134a Circular, smooth and copper tube Secondary heating fluid D = 8 mm L = 3.67 m | Tsat = 5–15 °C pr = 0.09–0.12 G = 125–400 = 7–15 x = 0.05–0.88 |
| Wongsa-ngam et al. [37] | R134a Circular, microfin and smooth and copper tube Secondary heating fluid D = 8.1 mm L = 2.5 m | Tsat = 10–20 °C pr = 0.10–0.13 G = 400–800 = 10 x = 0.1–0.9 |
| Sripattrapan et al. [64] | R134a Circular, smooth and copper tube Secondary heating fluid D = 7.1 mm L = 2.5 m | Tsat = 18 °C pr = 0.12 G = 376–1061 = 10–30 x = 0.12–0.55 |
| Chengjun et al. [65] | R12, R22, R134a Circular, smooth and copper tube Secondary heating fluid D = 6 mm L = 6 m | Tsat = 5 °C pr = 0.09–0.12 G = 50–300 = 10–30 x = 0–1 |
| Niederkruger et al. [21] | R12 Circular, smooth and nickel tube Resistive heating D = 14 mm L = 0.2 m | Tsat = 16–98 °C pr = 0.12–0.77 G = 9.5–100 = 10–30 x = 0.1–0.8 |
| Balachander and Raja [47] | R134a Circular, smooth and copper tube Secondary heating fluid D = 7.49 mm L = 1 m | Tsat = −10–0 °C pr = 0.05–0.07 G = 57–102 = 2–18 x = 0–1 |
| Lim and Kim [66] | R134a, R123 Circular, smooth and stainless steel tube Joule heating D = 10 mm L = 2 m | Tsat = 21 °C pr = 0.15–0.16 G = 150–600 = 5–50 x = 0–1 |
| Kabelac and De Buhr [67] | Ammonia Circular, smooth and low fin and aluminum tube Secondary heating fluid D = 10 mm L = 0.45 m | Tsat = −40–4 °C pr = 0.01–0.10 G = 50–150 = 17–75x = 0–1 |
| Akhavan-Behabadi et al. [68] | R134a Circular, smooth and tape insert and copper tube Resistive heating D = 7.5 mm L = 0.126 m | Tsat = −19–3 °C pr = 0.03–0.06 G = 54–136 = 1.8–0.53 x = 0.2–1 |
| Mastrullo et al. [55] | CO2 Circular, smooth and stainless steel tube Joule heating D = 10 mm L = 0.12 m | Tsat = −7.5–6 °C pr = 0.38–0.55 G = 200–349 = 10–20.6 x = 0.02–0.98 |
| Mastrullo et al. [69] | CO2, R134a Circular, smooth and stainless steel tube Joule heating D = 6 mm L = 1.2 m | Tsat = −9–20 °C pr = 0.05–0.14 G = 197–472 = 8.5–20.1 x = 0.05–0.95 |
| Wattelet et al. [70] | R134a, R22 Circular, smooth and copper tube Joule heating D = 7.04 mm L = 2.43 m | Tsat = −15–5 °C pr = 0.04–0.09 G = 25–100 = 2–10 x = 0.1–0.9 |
| Panek et al. [71] | R134a, R12 Circular, smooth and copper tube Joule heating D = 10.92 mm L = 2.43 m | Tsat = −15–5 °C pr = 0.06–0.12 G = 200–500 = 5–30 x = 0.1–0.9 |
| Yun et al. [42] | CO2, R134a Circular, smooth and stainless steel tube Joule heating D = 6 mm L = 1.4 m | Tsat = 5–10 °C pr = 0.09–0.61 G = 170–320 = 10–20 x = 0.1–0.85 |
| da Silva Lima et al. [27] | R134a Circular, smooth and copper tube Secondary heating fluid D = 13.84 mm L = 3.1 m | Tsat = 5–20 °C pr = 0.08–0.14 G = 300–500 = 7.5–17.5 x = 0.01–0.99 |
| Spindler and Müller-Steinhagen [72] | R134a Circular, microfin and copper tube Resistive heating D = 8.95 mm L = 1 m | Tsat = −20–10 °C pr = 0.03–0.10 G = 25–150 = 1–15 x = 0.1–0.7 |
| Kedzierski and Kaul [73] | R134a, R12 Circular, smooth and quartz tube Joule heating D = 9 mm | Tsat = 18 °C pr = 0.13 = 15–30 x = 0–1 |
| Torikoshi and Ebisu [74] | R134a, R12 Circular, smooth tube D = 8.7 mm L = 3.2 m | Tsat = 5–15 °C pr = 0.09–0.12 G = 45–200 x = 0.2–1 |
| Kattan et al. [75] | R134a Circular, smooth and copper tube D = 12 mm L = 3.2 m | Tsat = −2–10 pr = 0.07–0.10 G = 100–300 x = 0.18–0.9 |
| Kanizawa et al. [76] | R134a Circular, smooth and twisted tape and copper tube Res. heating D = 12.7 and 15.9 mm L = 2 m | Tsat = 5–15 °C pr = 0.09–0.12 G = 75–200 = 5–10 x = 0.05–0.95 |
| Seo and Kim [77] | R22 Circular, smooth and microfin tube Resistive heating D = 7 and 9.52 mm L = 3 m | Tsat = −15–5 °C pr = 0.06–0.12 G = 70–211 = 5–15 x = 0.2–0.85 |
| Wang et al. [78] | R22 Circular, smooth tube Secondary heating fluid D = 6.54 mm L = 1.3 m | Tsat = 2–7 °C pr = 0.11–0.12 G = 50–700 = 2.5–20x = 0–1 |
| Oh et al. [53] | CO2, R22, R134a Circular, smooth and stainless steel tube Resistive heating D = 7.75 mm L = 5 m | Tsat = −5–5 °C pr = 0.41–0.54 G = 200–500 = 10–40 x = 0–1 |
| Saiz-Jabardo and Bandarra-Filho [79] | R134a, R22 Circular, smooth and copper tube Resistive heating D = 12.7 mm L = 2 m | Tsat = 8–15 °C pr = 0.10–0.16 G = 50–500 = 5–20 x = 0.05–0.9 |
| Kuo and Wang [38] | R22 Circular, smooth and microfin Secondary heating fluid D = 9.52 mm L = 1.3 m | Tsat = 6–10 °C pr = 0.12–0.14 G = 100–300 = 6–14 x = 0.1–0.8 |
| Greco and Vanoli [35] | R22 Circular, smooth and stainless steel tube Joule heating D = 6 mm L = 6 m | Tsat = −15.5–20 °C pr = 0.06–0.18 G = 233–303 = 10.5–17 x = 0–1 |
| Murata and Hashizume [80] | R123 Circular, smooth and spirally grooved tubes D = 10.3 mm | Tsat = 47–118 °C pr = 0.05–1 G = 100–300 x = 0–1 |
| Bandarra-Filho and Saiz-Jabardo [79] | R134a Circular, smooth and grooved Copper tubes Resistive heating D = 7, 7.93 and 9.52 mm L = 1.5 m | Tsat = 5 °C pr = 0.08 G = 70–1100 x = 0.05–0.95 |
| Padovan et al. [43] | R134a Circular, microfin and copper tubes Secondary heating fluid D = 7.69 mm L = 1.4 m | Tsat = 30–42 °C pr = 0.19–0.27 G = 80–600 = 14–83.5x = 0.1–0.99 |
| Yoon et al. [39] | CO2 Circular, smooth and stainless steel tube Joule heating D = 7.53 mm L = 5 m | Tsat = −4–20 °C pr = 0.42–0.77 G = 200–530 = 12–20 x = 0–1 |
| Schlager et al. [81] | R22 Circular, microfin and stainless steel tube Heating fluid D = 11.7 mm L = 3.67 m | Tsat = 0–5 °C pr = 0.10–0.12 G = 75–400 x = 0.15–0.85 |
| Schael and Kind [82] | CO2 Circular, smooth and microfin and copper tube Resistive heating D = 14 mm L = 0.2 m | Tsat = 5 °C pr = 0.54 G = 75–500 = 1–70x = 0.1–0.9 |
| Hihara and Dang [83] | CO2 Circular, smooth tube D = 6 mm | Tsat = 5–15 °C pr = 0.54–0.69 G = 360–1440 = 4.5–36 x = 0.1–0.9 |
| Takamatsu et al. [84] | R134a, R22, R114, R12 Circular, smooth and copper tube Secondary heating fluid D = 7.9 mm L = 6 m | Tsat = 11–42.5 °C pr = 0.13–0.23 G = 100–350 = 1.9–85.9 x = 0–0.95 |
| Colombo et al. [85] | R134a Circular, smooth and microfin and copper tube Secondary heating fluid D = 8.92 mm | Tsat = 5 °C pr = 0.09 G = 100–340 = 6–15 x = 0.25–1 |
| Lee et al. [86] | R290, R600a, R1270, R22 Circular, smooth and copper tube Secondary heating fluid D = 9.52 and 12.7 mm L = 5.8 m | Tsat = −10–10 °C pr = 0.03–0.25 G = 50–200 = 4–26 x = 0.1–1 |
| Wellsandt and Vamling [87] | R134a Circular, microfin and copper tube Secondary heating fluid D = 9.1 mm L = 4 m | Tsat = −1–10 °C pr = 0.07–0.10 G = 162–366 = 0.1–38 x = 0.08–1 |
| Aprea et al. [19] | R22 Circular, smooth and copper tube Secondary heating fluid D = 20 mm | Tsat = −10–−5 °C pr = 0.07–0.08 G = 30–140 = 1.9–9.1 x = 0.15–1 |
| Lillo et al. [88] | R290 Circular, smooth and stainless steel tube Joule heating D = 6 mm L = 0.193 mm | Tsat = 25–35 °C pr = 0.29–0.33 G = 150–500 = 2.5–40 x = 0–1 |
| Kim et al. [89] | CO2 Circular, smooth and copper tube Secondary heating fluid D = 11.2 mm L = 0.15 m | Tsat = −30–−15 °C pr = 0.18–0.29 G = 40–200 = 2–10x = 0.1–0.8 |
| Chamra et al. [90] | R22 Circular, smooth and microfin and copper tube D = 14.88 mm L = 2.44 m | Tsat = 2.2 °C pr = 0.11 G = 45–181 = 8–15 x = 0.22–1 |
| Hambraeus [91] | R134a Circular, smooth and copper tube Resistive heating D = 12 mm L = 10 m | Tsat = −5–20 °C pr = 0.06–0.14 G = 60–300 = 2–10 x = 0–1 |
| Lillo et al. [54] | R1233zd(E) Circular, smooth and stainless steel tube Joule heating D = 6 mm L = 0.193 mm | Tsat = 24.2–65.2 °C pr = 0.036–0.125 G = 147–300 = 2.4–40.9 x = 0.008–0.977 |
| Yang et al. [92] | R600a Circular, smooth and stainless steel tube Resistive heating D = 6 mm L = 0.2 m | Tsat = 8–32 °C pr = 0.06–0.11 G = 67–194 = 10.6–75.0 x = 0–1 |
| Qiu et al. [93] | R600a, R1234ze(E) Circular, smooth and copper tube Resistive heating D = 8 mm L = 2.4 m | Tsat = 20 °C pr = 0.09–0.11 G = 200–400 = 5–10 x = 0.1–0.9 |
| Yang et al. [44] | R1234ze(E) Circular, smooth and stainless steel tube Resistive heating D = 6 mm L = 0.2 m | Tsat = 8–32 °C pr = 0.06–0.11 G = 130–258 = 10.6–74.8 x = 0–1 |
References
- Chen, H.; Goswami, D.Y.; Stefanakos, E.K. A review of thermodynamic cycles and working fluids for the conversion of low-grade heat. Renew. Sustain. Energy Rev. 2010, 14, 3059–3067. [Google Scholar] [CrossRef]
- Lecompte, S.; Lemmens, S.; Huisseune, H.; Broek, M.V.D.; De Paepe, M. Multi-Objective Thermo-Economic Optimization Strategy for ORCs Applied to Subcritical and Transcritical Cycles for Waste Heat Recovery. Energies 2015, 8, 2714–2741. [Google Scholar] [CrossRef]
- Quoilin, S.; Broek, M.V.D.; Declaye, S.; Dewallef, P.; Lemort, V. Techno-economic survey of Organic Rankine Cycle (ORC) systems. Renew. Sustain. Energy Rev. 2013, 22, 168–186. [Google Scholar] [CrossRef]
- Bao, J.; Zhao, L. A review of working fluid and expander selections for organic Rankine cycle. Renew. Sustain. Energy Rev. 2013, 24, 325–342. [Google Scholar] [CrossRef]
- Kaya, A.; Lazova, M.; de Paepe, M. Design and Rating of an Evaporator for Waste Heat Recovery Organic Rankine Cycle Using Ses36. In Proceedings of the 3rd International Seminar on ORC Power Systems, Brussels, Belgium, 12–14 October 2015; pp. 1–10. [Google Scholar]
- Walraven, D.; Laenen, B.; D’Haeseleer, W. Optimum configuration of shell-and-tube heat exchangers for the use in low-temperature organic Rankine cycles. Energy Convers. Manag. 2014, 83, 177–187. [Google Scholar] [CrossRef]
- Walraven, D.; Laenen, B.; D’Haeseleer, W. Comparison of shell-and-tube with plate heat exchangers for the use in low-temperature organic Rankine cycles. Energy Convers. Manag. 2014, 87, 227–237. [Google Scholar] [CrossRef]
- Capata, R.; Zangrillo, E. Preliminary Design of Compact Condenser in an Organic Rankine Cycle System for the Low Grade Waste Heat Recovery. Energies 2014, 7, 8008–8035. [Google Scholar] [CrossRef]
- Erhart, T.G.; Eicker, U.; Infield, D. Influence of Condenser Conditions on Organic Rankine Cycle Load Characteristics. J. Eng. Gas Turbines Power 2013, 135, 042301. [Google Scholar] [CrossRef]
- Kaya, A.; Lazova, M.; Bağcı, Ö.; Lecompte, S.; Ameel, B.; De Paepe, M. Design Sensitivity Analysis of a Plate-Finned Air-Cooled Condenser for Low-Temperature Organic Rankine Cycles. Heat Transf. Eng. 2016, 38, 1018–1033. [Google Scholar] [CrossRef]
- Xu, J.; Luo, X.; Chen, Y.; Mo, S. Multi-criteria Design Optimization and Screening of Heat Exchangers for a Subcritical ORC. Energy Procedia 2015, 75, 1639–1645. [Google Scholar] [CrossRef][Green Version]
- Lecompte, S.; Huisseune, H.; Broek, M.V.D.; De Schampheleire, S.; De Paepe, M. Part load based thermo-economic optimization of the Organic Rankine Cycle (ORC) applied to a combined heat and power (CHP) system. Appl. Energy 2013, 111, 871–881. [Google Scholar] [CrossRef]
- Imran, M.; Usman, M.; Park, B.-S.; Kim, H.-J.; Lee, D.-H. Multi-objective optimization of evaporator of organic Rankine cycle (ORC) for low temperature geothermal heat source. Appl. Therm. Eng. 2015, 80, 1–9. [Google Scholar] [CrossRef]
- Fischer, J. Comparison of trilateral cycles and organic Rankine cycles. Energy 2011, 36, 6208–6219. [Google Scholar] [CrossRef]
- Chen, J. A Correlation for Boiling Heat Transfer to Saturated Fluids in Convective Flow. Ind. Eng. Chem. Process Des. Dev. 1962, 5, 322–329. [Google Scholar] [CrossRef]
- Shah, M.M. Chart Correlation for Saturated Boiling Heat Transfer: Equations and Further Study. ASHRAE Trans. 1982, 88, 185–196. [Google Scholar]
- Gungor, K.E.; Winterton, R.H.S. A general correlation for flow boiling in tubes and annuli. Int. J. Heat Mass Transf. 1986, 29, 351–358. [Google Scholar] [CrossRef]
- Kandlikar, S.G. A General Correlation for Saturated Two-Phase Flow Boiling Heat Transfer Inside Horizontal and Vertical Tubes. J. Heat Transf. 1990, 112, 219–228. [Google Scholar] [CrossRef]
- Aprea, C.; Rossi, F.; Greco, A. Experimental evaluation of R22 and R407C evaporative heat transfer coefficients in a vapour compression plant. Int. J. Refrig. 2000, 23, 366–377. [Google Scholar] [CrossRef]
- Cooper, M. Heat flow rates in saturated nucleate pool boiling-A wide-ranging examination using reduced properties. In Advances in Heat Transfer; Hartnett, J.P., Irvine, T.F., Eds.; Elsevier: Amsterdam, The Netherlands, 1984; Volume 16, pp. 157–239. [Google Scholar] [CrossRef]
- Niederkrüger, M.; Steiner, D.; Schlünder, E.-U. Horizontal flow boiling experiments of saturated pure components and mixtures of R846-R12 at high pressures. Int. J. Refrig. 1992, 15, 48–58. [Google Scholar] [CrossRef]
- Müller-Steinhagen, H.; Heck, K. A simple friction pressure drop correlation for two-phase flow in pipes. Chem. Eng. Process. Process Intensif. 1986, 20, 297–308. [Google Scholar] [CrossRef]
- Churchill, S.W.; Chu, H.H. Correlating equations for laminar and turbulent free convection from a horizontal cylinder. Int. J. Heat Mass Transf. 1975, 18, 1049–1053. [Google Scholar] [CrossRef]
- Gnielinski, V. New equation for heat and mass transfer in turbulent pipe and channel flow. Int. Chem. Eng. 1976, 16, 359–368. [Google Scholar]
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and Pseudo-pure Fluid Thermophysical Property Evaluation and the Open-Source Thermophysical Property Library CoolProp. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef] [PubMed]
- Charnay, R.; Revellin, R.; Bonjour, J. Flow boiling heat transfer in minichannels at high saturation temperatures: Part I – Experimental investigation and analysis of the heat transfer mechanisms. Int. J. Heat Mass Transf. 2015, 87, 636–652. [Google Scholar] [CrossRef]
- da Silva Lima, R.J.; Quibén, J.M.; Thome, J.R. Flow boiling in horizontal smooth tubes: New heat transfer results for R-134a at three saturation temperatures. Appl. Therm. Eng. 2009, 29, 1289–1298. [Google Scholar] [CrossRef]
- Quibén, J.M.; Cheng, L.; Lima, R.J.D.S.; Thome, J.R. Flow boiling in horizontal flattened tubes: Part II—Flow boiling heat transfer results and model. Int. J. Heat Mass Transf. 2009, 52, 3645–3653. [Google Scholar] [CrossRef]
- Kandlikar, S.G. Heat Transfer Characteristics in Partial Boiling, Fully Developed Boiling, and Significant Void Flow Regions of Subcooled Flow Boiling. J. Heat Transf. 1998, 120, 395–401. [Google Scholar] [CrossRef]
- Cheng, L.; Mewes, D. Advances in Multiphase Flow and Heat Transfer; Bentham Science Publishers: Sharjah, United Arab Emirates, 2012; Volume 2, p. 314. [Google Scholar]
- Fang, X.; Zhou, Z.; Wang, H. Heat transfer correlation for saturated flow boiling of water. Appl. Therm. Eng. 2015, 76, 147–156. [Google Scholar] [CrossRef]
- Copetti, J.B.; Macagnan, M.H.; Zinani, F.; Kunsler, N.L. Flow boiling heat transfer and pressure drop of R-134a in a mini tube: An experimental investigation. Exp. Therm. Fluid Sci. 2011, 35, 636–644. [Google Scholar] [CrossRef]
- Yu, J.; Momoki, S.; Koyama, S. Experimental study of surface effect on flow boiling heat transfer in horizontal smooth tubes. Int. J. Heat Mass Transf. 1999, 42, 1909–1918. [Google Scholar] [CrossRef]
- Zürcher, O.; Favrat, D.; Thome, J. Development of a diabatic two-phase flow pattern map for horizontal flow boiling. Int. J. Heat Mass Transf. 2002, 45, 291–301. [Google Scholar] [CrossRef]
- Greco, A.; Vanoli, G.P. Evaporation of refrigerants in a smooth horizontal tube: Prediction of R22 and R507 heat transfer coefficients and pressure drop. Appl. Therm. Eng. 2004, 24, 2189–2206. [Google Scholar] [CrossRef]
- Choi, T.; Kim, Y.; Kim, M.; Ro, S. Evaporation heat transfer of R-32, R-134a, R-32/134a, and R-32/125/134a inside a horizontal smooth tube. Int. J. Heat Mass Transf. 2000, 43, 3651–3660. [Google Scholar] [CrossRef]
- Wongsa-ngam, J.; Nualboonrueng, T.; Wongwises, S. Performance of smooth and micro-fin tubes in high mass flux region of R-134a during evaporation. Heat Mass Transf. 2004, 40, 425–435. [Google Scholar] [CrossRef]
- Kuo, C.; Wang, C. In-tube evaporation of HCFC-22 in a 9.52 mm micro-fin/smooth tube. Int. J. Heat Mass Transf. 1996, 39, 2559–2569. [Google Scholar] [CrossRef]
- Yoon, S.H.; Cho, E.S.; Hwang, Y.W.; Kim, M.S.; Min, K.; Kim, Y. Characteristics of evaporative heat transfer and pressure drop of carbon dioxide and correlation development. Int. J. Refrig. 2004, 27, 111–119. [Google Scholar] [CrossRef]
- Greco, A. Convective boiling of pure and mixed refrigerants: An experimental study of the major parameters affecting heat transfer. Int. J. Heat Mass Transf. 2008, 51, 896–909. [Google Scholar] [CrossRef]
- Greco, A.; Vanoli, G.P. Flow-boiling of R22, R134a, R507, R404A and R410A inside a smooth horizontal tube. Int. J. Refrig. 2005, 28, 872–880. [Google Scholar] [CrossRef]
- Yun, R.; Kim, Y.; Kim, M.S.; Choi, Y. Boiling heat transfer and dryout phenomenon of CO2 in a horizontal smooth tube. Int. J. Heat Mass Transf. 2003, 46, 2353–2361. [Google Scholar] [CrossRef]
- Padovan, A.; Del Col, D.; Rossetto, L. Experimental study on flow boiling of R134a and R410A in a horizontal microfin tube at high saturation temperatures. Appl. Therm. Eng. 2011, 31, 3814–3826. [Google Scholar] [CrossRef]
- Yang, Z.-Q.; Chen, G.-F.; Yao, Y.; Song, Q.-L.; Shen, J.; Gong, M.-Q. Experimental study on flow boiling heat transfer and pressure drop in a horizontal tube for R1234ze(E) versus R600a. Int. J. Refrig. 2018, 85, 334–352. [Google Scholar] [CrossRef]
- Hardik, B.; Prabhu, S. Boiling pressure drop and local heat transfer distribution of water in horizontal straight tubes at low pressure. Int. J. Therm. Sci. 2016, 110, 65–82. [Google Scholar] [CrossRef]
- Hsieh, Y.; Lie, Y.; Lin, T. Saturated flow boiling heat transfer of refrigerant R-410A in a horizontal annular finned duct. Int. J. Heat Mass Transf. 2007, 50, 1442–1454. [Google Scholar] [CrossRef]
- Balachander, P.; Raja, B. Investigation on the boiling heat transfer characteristics of R404A and R134a under stratified flow condition. Heat Mass Transf. 2014, 51, 825–835. [Google Scholar] [CrossRef]
- Kasza, K.E.; Didascalou, T.; Wambsganss, M.W. Microscale flow visualization of nucleate boiling in small channels: Mechanisms influencing heat transfer. In Compact Heat Exchangers for the Process Industries; University of Kentucky: Lexington, KY, USA, 1997. [Google Scholar]
- Kattan, N.; Thome, J.R.; Favrat, D. Flow Boiling in Horizontal Tubes: Part 1—Development of a Diabatic Two-Phase Flow Pattern Map. J. Heat Transf. 1998, 120, 140–147. [Google Scholar] [CrossRef]
- Thome, J.R. Update on advances in flow pattern based two-phase heat transfer models. Exp. Therm. Fluid Sci. 2005, 29, 341–349. [Google Scholar] [CrossRef]
- Mastrullo, R.; Mauro, A.; Thome, J.; Toto, D.; Vanoli, G.P. Flow pattern maps for convective boiling of CO2 and R410A in a horizontal smooth tube: Experiments and new correlations analyzing the effect of the reduced pressure. Int. J. Heat Mass Transf. 2012, 55, 1519–1528. [Google Scholar] [CrossRef]
- Lee, S.-J.; Choi, J.-Y.; Lee, J.-H.; Kwon, Y.-C. Experimental Study on Characteristics of Evaporation Heat Transfer of CO2 in a Smooth Tube. J. Energy Eng. 2007, 16, 181–186. [Google Scholar]
- Oh, H.-K.; Ku, H.-G.; Roh, G.-S.; Son, C.-H.; Park, S.-J. Flow boiling heat transfer characteristics of carbon dioxide in a horizontal tube. Appl. Therm. Eng. 2008, 28, 1022–1030. [Google Scholar] [CrossRef]
- Lillo, G.; Mastrullo, R.; Mauro, A.; Viscito, L. Flow boiling of R1233zd(E) in a horizontal tube: Experiments, assessment and correlation for asymmetric annular flow. Int. J. Heat Mass Transf. 2019, 129, 547–561. [Google Scholar] [CrossRef]
- Mastrullo, R.; Mauro, A.W.; Rosato, A.; Vanoli, G.P. Carbon dioxide local heat transfer coefficients during flow boiling in a horizontal circular smooth tube. Int. J. Heat Mass Transf. 2009, 52, 4184–4194. [Google Scholar] [CrossRef]
- Kundu, A.; Kumar, R.; Gupta, A. Comparative experimental study on flow boiling heat transfer characteristics of pure and mixed refrigerants. Int. J. Refrig. 2014, 45, 136–147. [Google Scholar] [CrossRef]
- Shao, J.; Li, X.; Guo, Z.; Ma, T.; Liu, R.; Tian, X. Flow pattern, pressure drop and heat transfer coefficient during two-phase flow boiling of R134a in pump-assisted separate heat pipe. Exp. Therm. Fluid Sci. 2017, 85, 240–247. [Google Scholar] [CrossRef]
- Grauso, S.; Mastrullo, R.; Mauro, A.; Vanoli, G.P. Flow boiling of R410A and CO2 from low to medium reduced pressures in macro channels: Experiments and assessment of prediction methods. Int. J. Heat Mass Transf. 2013, 56, 107–118. [Google Scholar] [CrossRef]
- Park, C.; Hrnjak, P. CO2 and R410A flow boiling heat transfer, pressure drop, and flow pattern at low temperatures in a horizontal smooth tube. Int. J. Refrig. 2007, 30, 166–178. [Google Scholar] [CrossRef]
- Yu, M.-H.; Lin, T.-K.; Tseng, C.-C. Heat transfer and flow pattern during two-phase flow boiling of R-134a in horizontal smooth and microfin tubes. Int. J. Refrig. 2002, 25, 789–798. [Google Scholar] [CrossRef]
- Del Col, D. Flow boiling of halogenated refrigerants at high saturation temperature in a horizontal smooth tube. Exp. Therm. Fluid Sci. 2010, 34, 234–245. [Google Scholar] [CrossRef]
- Shin, J.Y.; Kim, M.S.; Ro, S.T. Experimental study on forced convective boiling heat transfer of pure refrigerants and refrigerant mixtures in a horizontal tube. Int. J. Refrig. 1997, 20, 267–275. [Google Scholar] [CrossRef]
- Eckels, S.; Pate, M. An experimental comparison of evaporation and condensation heat transfer coefficients for HFC-134a and CFC. Int. J. Refrig. 1991, 14, 70–77. [Google Scholar] [CrossRef]
- Sripattrapan, W.; Wongchang, T.; Wongwises, S. Heat transfer and two-phase flow characteristics of refrigerants flowing under varied heat flux in a double-pipe evaporator. Heat Mass Transf. 2004, 40, 653–664. [Google Scholar] [CrossRef]
- Chengjun, G.; Weicheng, W.; Lining, Z. Influence of tube’s diameter on boiling heat transfer performance in small diameter tubes. J. Therm. Sci. 1998, 7, 49–53. [Google Scholar]
- Lim, T.W.; Kim, J.H. An experimental investigation of heat transfer in forced convective boiling of R134a, R123 and R134a/R123 in a horizontal tube. KSME Int. J. 2004, 18, 513–525. [Google Scholar] [CrossRef]
- Kabelac, S.; de Buhr, H.-J. Flow boiling of ammonia in a plain and a low finned horizontal tube. Int. J. Refrig. 2001, 24, 41–50. [Google Scholar] [CrossRef]
- Akhavan-Behabadi, M.; Kumar, R.; Jamali, M. Investigation on heat transfer and pressure drop during swirl flow boiling of R-134a in a horizontal tube. Int. J. Heat Mass Transf. 2009, 52, 1918–1927. [Google Scholar] [CrossRef]
- Mastrullo, N.; Mauro, A.; Rosato, A.; Vanoli, G. Comparison of R744 and R134a heat transfer coefficients during flow boiling in a horizontal circular smooth tube. Renew. Energy Power Qual. J. 2009, 1, 577–581. [Google Scholar] [CrossRef]
- Wattelet, J.P.; Chato, J.C.; Christoffersen, B.R.; Gaibel, J.A. Heat Transfer Flow Regimes of Refrigerants in a Horizon-tal-Tube Evaporator. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 1994. [Google Scholar]
- Panek, J.S.; Chato, J.C.; Jabardo, J.M.S.; de Souza, A.L.; Wattelet, J.P. Evaporation Heat Transfer and Pressure Drop in Ozone-Safe Refrigerants and Refrigerant-Oil Mixtures; Air Conditioning and Refrigeration Center, College of Engineering, University of Illinois at Urbana-Champaign: Champaign, IL, USA, 1992; Volume 61801. [Google Scholar]
- Spindler, K.; Müller-Steinhagen, H. Flow boiling heat transfer of R134a and R404A in a microfin tube at low mass fluxes and low heat fluxes. Heat Mass Transf. 2007, 45, 967–977. [Google Scholar] [CrossRef]
- Kedzierski, M.A.; Kaul, M.P. Horizontal nucleate flow boiling heat transfer coefficient measurements and visual obser-vations for R12, R134a and R134a/ester lubricant mixtures. In The 6th International Symposium on Transport Phenomena in Thermal Engineering, Seoul, Korea, 9–13 May 1993; Begell House: Danbury, CT, USA, 1993; pp. 111–116. [Google Scholar]
- Torikoshi, K.; Ebisu, T. Heat transfer and pressure drop characteristics of R-134a, R-32, and a mixture of R-32/R-134a inside a horizontal tube. ASHRAE Trans. 1999, 2, 90–96. [Google Scholar]
- Kattan, N.; Favrat, D.; Thome, J.R. Two-Phase Flow Patterns during Evaporation of the New Refrigerants in Horizontal Tubes. In Proceedings of the European Two-Phase Flow Group Meeting, Hannover, Germany, 7–10 June 1993; p. H2. [Google Scholar]
- Kanizawa, F.T.; Mogaji, T.S.; Ribatski, G. Evaluation of the heat transfer enhancement and pressure drop penalty during flow boiling inside tubes containing twisted tape insert. Appl. Therm. Eng. 2014, 70, 328–340. [Google Scholar] [CrossRef]
- Seo, K.; Kim, Y. Evaporation heat transfer and pressure drop of R-22 in 7 and 9.52 mm smooth/micro-fin tubes. Int. J. Heat Mass Transf. 2000, 43, 2869–2882. [Google Scholar] [CrossRef]
- Wang, C.C.; Lin, S.P.; Yu, J.G.; Lu, C. An experimental study of convective boiling of refrigerants R-22 and R-410A. Atlanta, GA: American Society of Heating. Refrig. Air-Cond. Eng. 1998, 104, 1144. [Google Scholar]
- Jabardo, J.M.S.; Filho, E.P.B. Convective boiling of halocarbon refrigerants flowing in a horizontal copper tube – an experimental study. Exp. Therm. Fluid Sci. 2000, 23, 93–104. [Google Scholar] [CrossRef]
- Murata, K.; Hashizume, K. Forced Convective Boiling of Nonazeotropic Refrigerant Mixtures Inside Tubes. J. Heat Transf. 1993, 115, 680–689. [Google Scholar] [CrossRef]
- Schlager, L.M.; Pate, M.B.; Bergles, A.E. Evaporation and Condensation Heat Transfer and Pressure Drop in Horizontal, 12. 7-mm Microfin Tubes with Refrigerant J. Heat Transf. 1990, 112, 1041–1047. [Google Scholar] [CrossRef]
- Schael, A.-E.; Kind, M. Flow pattern and heat transfer characteristics during flow boiling of CO2 in a horizontal micro fin tube and comparison with smooth tube data. Int. J. Refrig. 2005, 28, 1186–1195. [Google Scholar] [CrossRef]
- Hihara, E.; Dang, C. Boiling Heat Transfer of Carbon Dioxide in Horizontal Tubes. In Proceedings of the ASME/JSME 2007 Thermal Engineering Heat Transfer Summer Conference, Vancouver, BC, Canada, 8–12 July 2007; ASME International: New York, NY, USA, 2007; Volume 3, pp. 843–849. [Google Scholar]
- Takamatsu, H.; Momoki, S.; Fujii, T. A correlation for forced convective boiling heat transfer of pure refrigerants in a horizontal smooth tube. Int. J. Heat Mass Transf. 1993, 36, 3351–3360. [Google Scholar] [CrossRef]
- Colombo, L.; Lucchini, A.; Muzzio, A. Flow patterns, heat transfer and pressure drop for evaporation and condensation of R134A in microfin tubes. Int. J. Refrig. 2012, 35, 2150–2165. [Google Scholar] [CrossRef]
- Lee, H.; Yoon, J.; Kim, J.; Bansal, P. Evaporating heat transfer and pressure drop of hydrocarbon refrigerants in 9.52 and 12.70mm smooth tube. Int. J. Heat Mass Transf. 2005, 48, 2351–2359. [Google Scholar] [CrossRef]
- Wellsandt, S.; Vamling, L. Evaporation of R134a in a horizontal herringbone microfin tube: Heat transfer and pressure drop. Int. J. Refrig. 2005, 28, 889–900. [Google Scholar] [CrossRef]
- Lillo, G.; Mastrullo, R.; Mauro, A.; Viscito, L. Flow boiling heat transfer, dry-out vapor quality and pressure drop of propane (R290): Experiments and assessment of predictive methods. Int. J. Heat Mass Transf. 2018, 126, 1236–1252. [Google Scholar] [CrossRef]
- Kim, S.; Pehlivanoglu, N.; Hrnjak, P.G. R744 Flow Boiling Heat Transfer with and Without Oil at Low Temperatures in 11.2 mm Horizontal Smooth Tube. In Proceedings of the International Refrigeration and Air Conditioning Conference at Purdue, West Lafayette, IN, USA, 12–15 July 2010; p. 1132. [Google Scholar]
- Chamra, L.; Webb, R.; Randlett, M. Advanced micro-fin tubes for evaporation. Int. J. Heat Mass Transf. 1996, 39, 1827–1838. [Google Scholar] [CrossRef]
- Hambraeus, K. Heat transfer coefficient during two-phase flow boiling of HFC-134a. Int. J. Refrig. 1991, 14, 357–362. [Google Scholar] [CrossRef]
- Yang, Z.; Gong, M.; Chen, G.; Zou, X.; Shen, J. Two-phase flow patterns, heat transfer and pressure drop characteristics of R600a during flow boiling inside a horizontal tube. Appl. Therm. Eng. 2017, 120, 654–671. [Google Scholar] [CrossRef]
- Qiu, J.; Zhang, H.; Yu, X.; Qi, Y.; Lou, J.; Wang, X. Experimental investigation of flow boiling heat transfer and pressure drops characteristic of R1234ze(E), R600a, and a mixture of R1234ze(E)/R32 in a horizontal smooth tube. Adv. Mech. Eng. 2015, 7, 168781401560631. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).