Probabilistic Optimization Techniques in Smart Power System
Abstract
1. Introduction
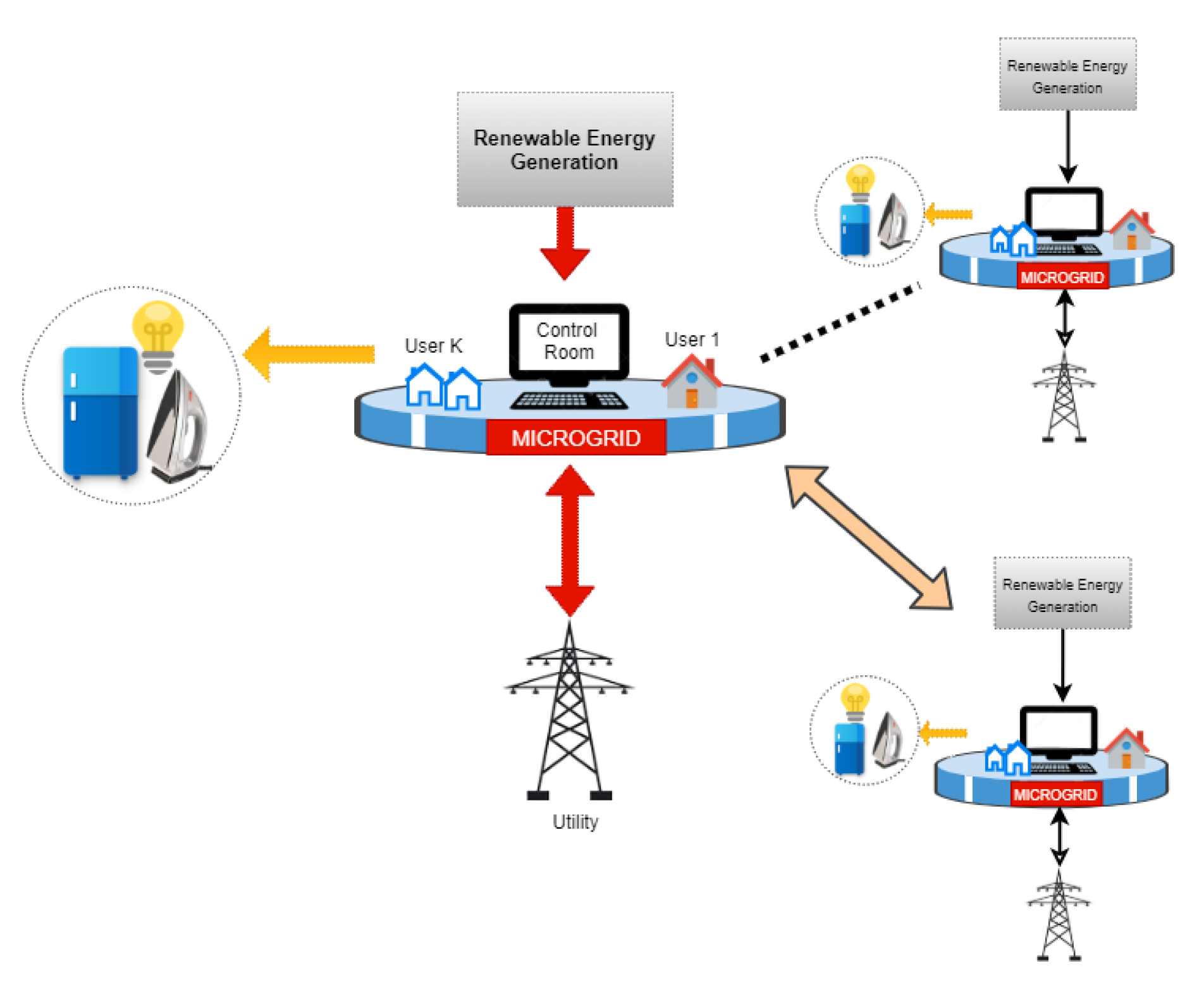
1.1. Smart Power System
1.2. Related Work and Contributions
- It gives a complete review of stochastic, robust, distributionally robust, and chance restricted optimization in the domain of smart power systems in a single survey study.
- An overview of numerous probabilistic optimization strategies, including their taxonomy, application examples, and solution algorithms is included in this survey study.
- Probabilistic mathematical models for various scenarios that can be used as a reference models in the field of smart power system have been developed.
1.3. Organization of the Paper
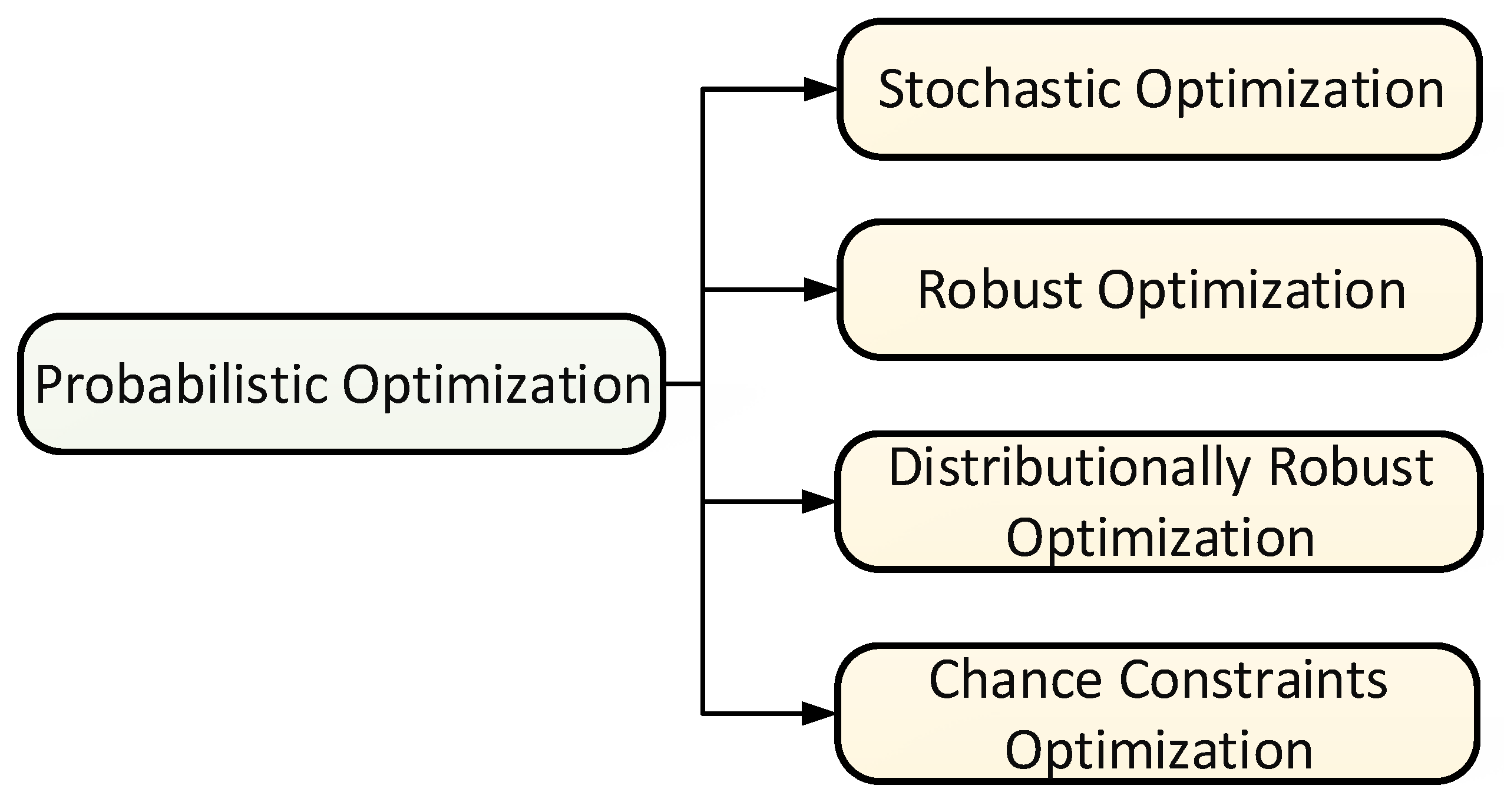
2. Probabilistic Optimization
2.1. Stochastic Optimization
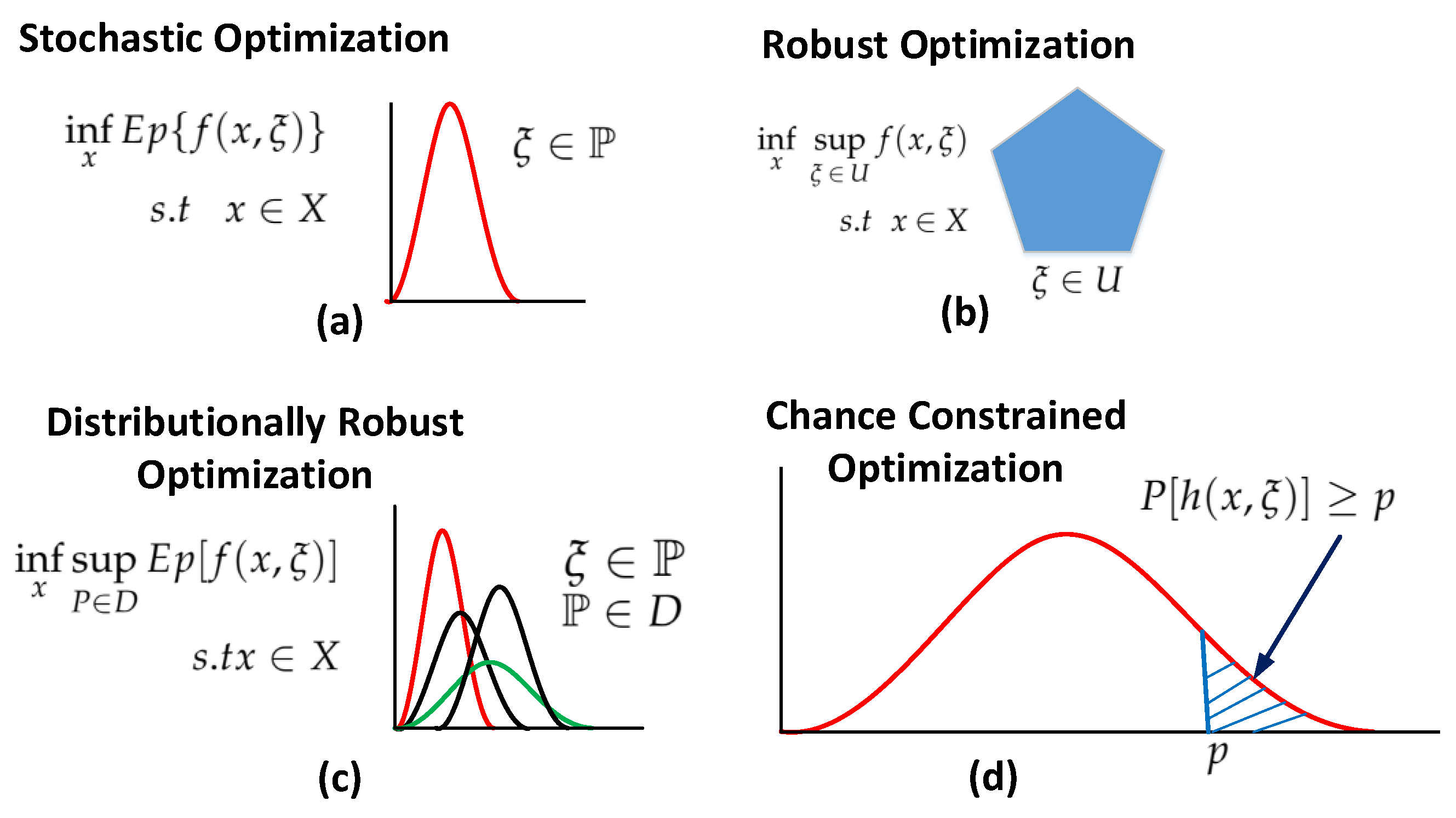
2.1.1. Architecture of Stochastic Optimization
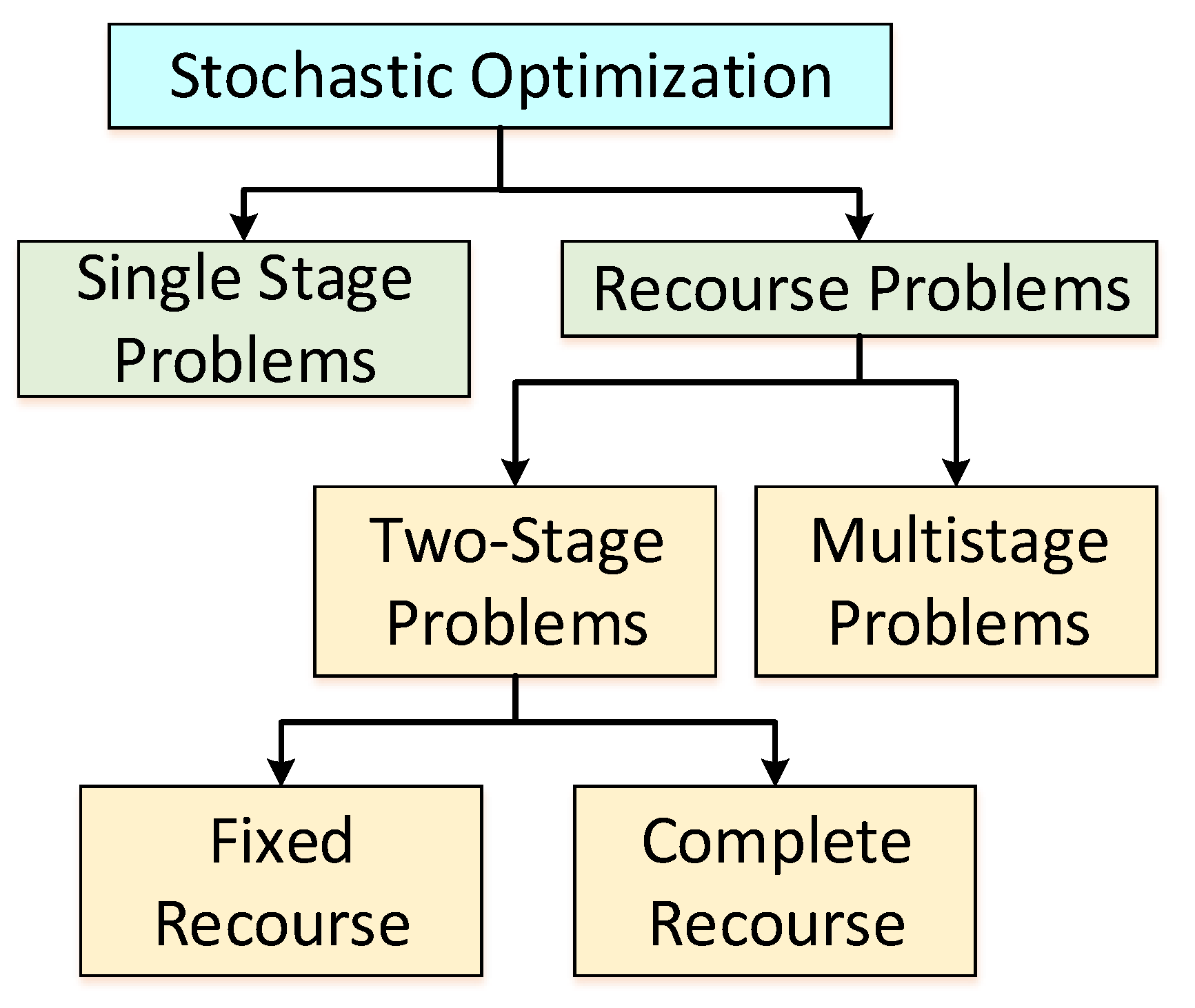
2.1.2. Taxonomy of Stochastic Optimization
2.2. Robust Optimization
2.2.1. Architecture of Robust Optimization
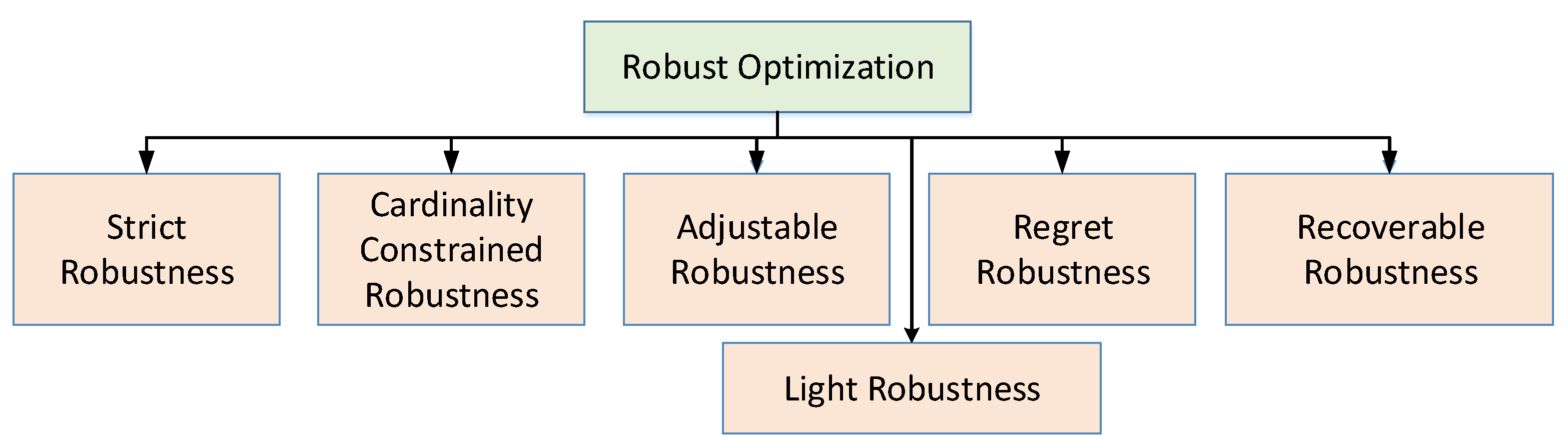
2.2.2. Taxonomy of Robust Optimization
- Strict robustness: This optimization type is sometimes known as classic robust optimization, min–max optimization, absolute deviation, one-stage robustness, or simply robust optimization. It is treated, as the fundamental starting point in the area of robustness. A solution x is called strictly robust if it is feasible for all possible scenarios of uncertainty set U [40].
- Cardinality constrained Robustness: In cardinality constrained robustness, reduction in uncertainty’s space can relax strictness in robust optimization. Analyzing the worst-case scenario in robust optimization, it is improbable that all the uncertainty set parameters will change simultaneously. Hence, it restricts uncertainty space by varying some parameters while considering fixed values for the remaining [41].
- Adjustable robustness: In adjustable robustness, the uncertainty space of strict robustness gets relaxed by dividing uncertainty space into groups of variables such as here and now and wait-and-see. Variables from the here and now group must be evaluated before the scenario is determined where variables from the wait-and-see group can be determined once the scenario is known [42].
- Light robustness:In light robustness, relaxing the constraints in terms of quality can reduce the strictness of the robust optimization, rather than reducing the space of uncertainty. Light robustness develops a trade-off between quality and robustness of the solution [43].
- Regret robustness: In regret robustness, the objective function relaxes the problem. Rather than to minimize the worst case performance of the solution, regret robustness reduces the difference of objective function having the best solution and the objective function that would have been possible in a scenario [44].
- Recoverable robustness: Concept of recovery algorithm gets exploited in recoverable robustness and family of recovery algorithms which is represented by B. It provides the solution in two stages, such as adjustable robustness. A solution x is called recovery robust with respect to recovery algorithm A if for any probable situation an algorithm exist such that when A is applied to the solution x and the scenario makes a solution [45].
2.3. Distributionally Robust Optimization
2.3.1. Architecture of Distributionally Robust Optimization
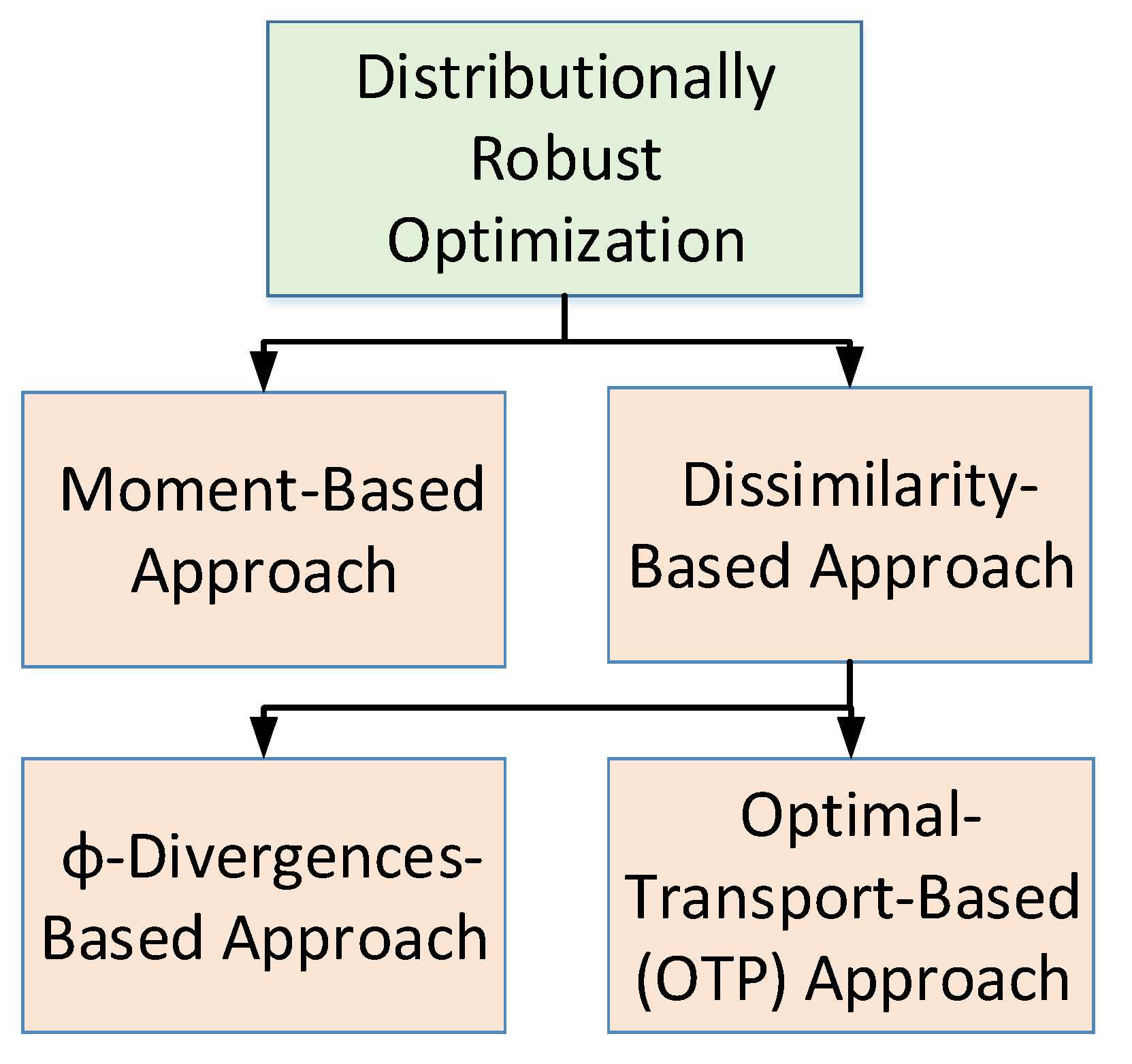
2.3.2. Taxonomy of Distributionally Robust Optimization
- (1)
- (2)
- Dissimilarity-based approach: The ambiguity set in this case is the set of all probability distributions whose dissimilarity to a nominal distribution is lower than or equal to a given value. In this category, the choice of the dissimilarity function leads to couple of different variants which are as follows [47].
- (a)
- (b)
2.4. Chance Constrained Optimization
2.4.1. Architecture of Chance Constrained Optimization
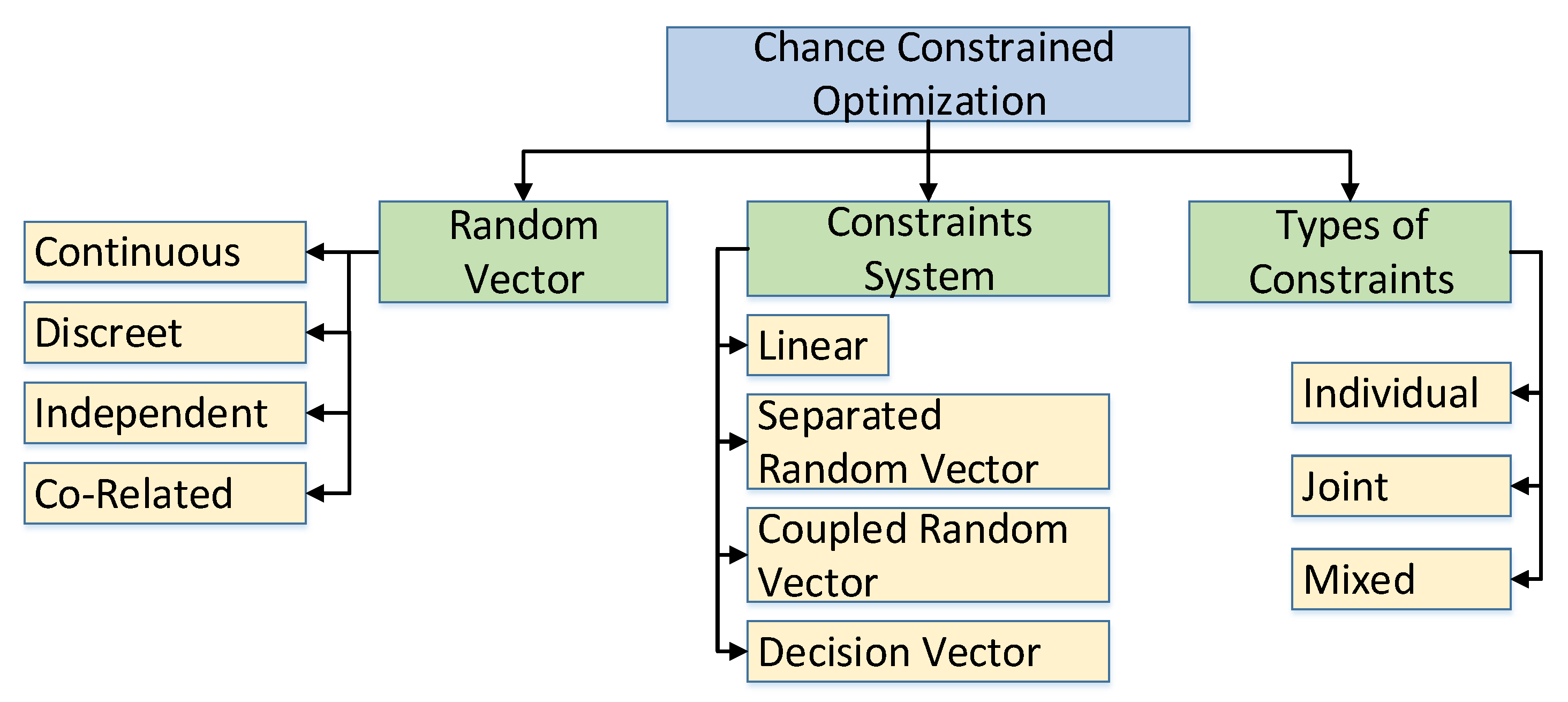
2.4.2. Taxonomy of Chance Constrained Optimization
3. Applications, Objectives and Solution Algorithms of Probabilistic Optimization
3.1. Applications, Objectives and Solution Algorithms of Stochastic Optimization
3.2. Applications, Objectives and Solution Algorithms of Robust Optimization
3.2.1. Smart Grid Energy Management
3.2.2. Microgrid Energy Management
3.2.3. Unit Commitment
3.2.4. Demand Side Management
3.2.5. Smart Home
3.2.6. Plugin Electric Vehicles
3.3. Applications, Objectives and Solution Algorithms of Distributionally Robust Optimization
3.4. Applications, Objectives and Solution Algorithms of Chance Constrained Optimization
3.4.1. Microgrid Energy Management
3.4.2. Distributed Energy Management
3.4.3. Demand Side Management
3.4.4. Smart Distribution Network
3.4.5. Home Energy Management
3.4.6. Unit Commitment
3.4.7. Economic Dispatch
4. Mathematical Models for Various Scenarios
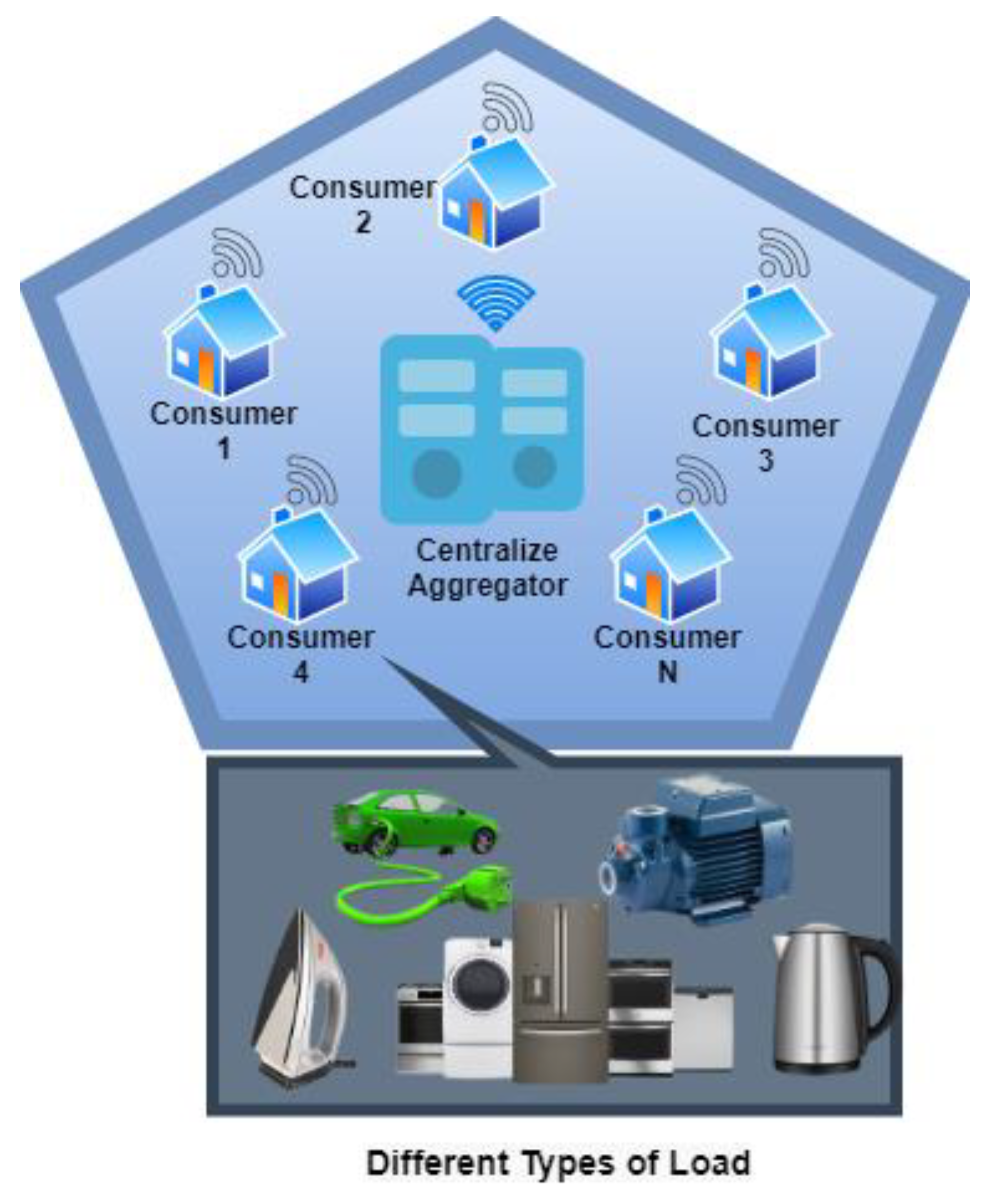
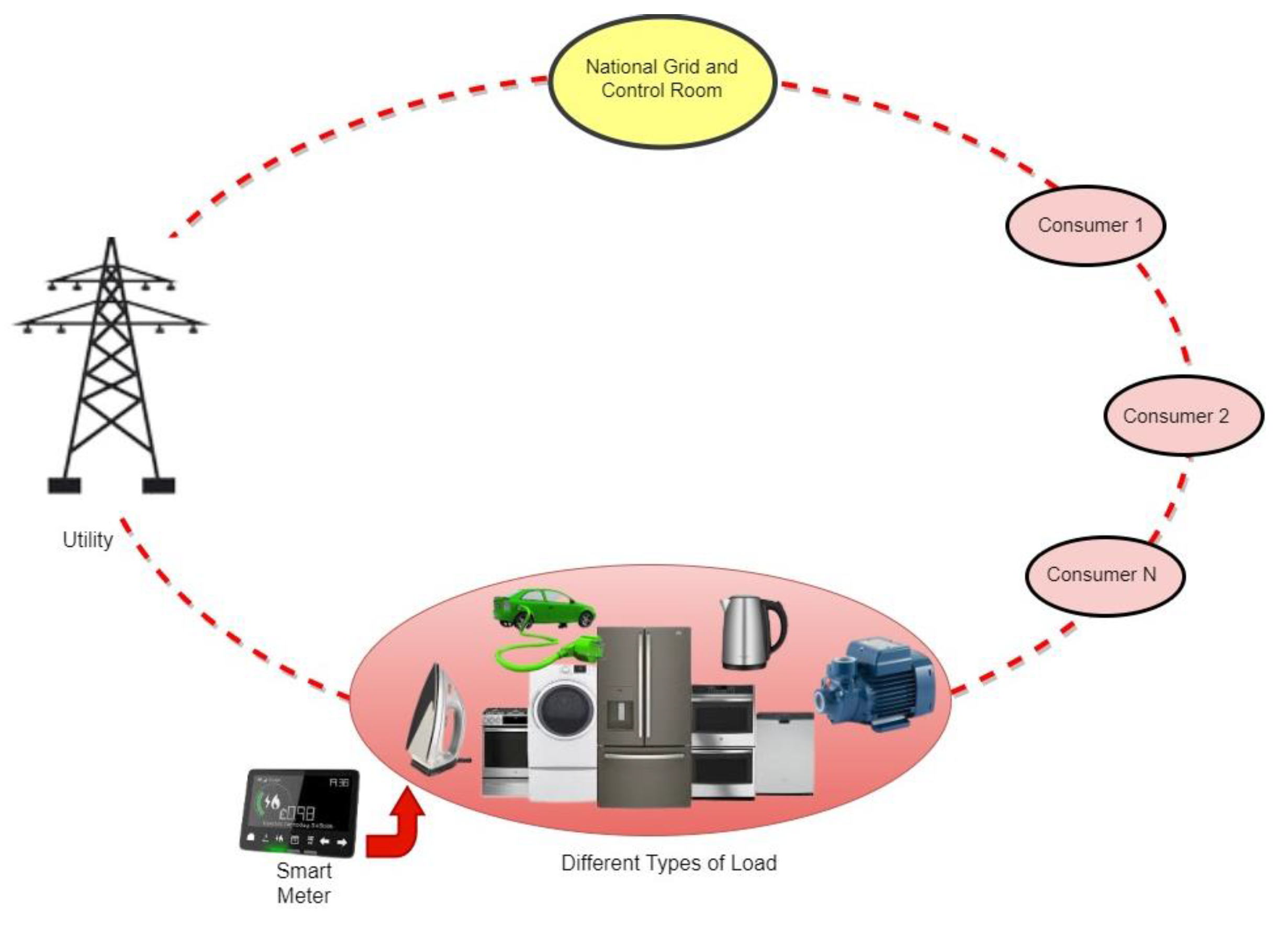
4.1. Scenario 1: Energy Management
- Total number of consumers N in residential compound
- Set of appliances A for each consumers
- Each appliances has a time dependent power profile
- Each appliances operating time
- Scheduled starting time
- Human interaction factor for a certain time
- Price tariff
- Load shedding factor
- To switched on a set of appliances
- Each consumer electricity consumption cost
4.1.1. Stochastic Optimization Model
4.1.2. Robust Optimization Model
4.1.3. Distributionally Robust Optimization Model
4.1.4. Chance Constrained Optimization Model
4.2. Scenario 2: GHG Emission Control Microgrid
4.2.1. Stochastic Optimization Model
4.2.2. Robust Optimization Model
4.2.3. Distributionally Robust Model
4.2.4. Chance Constrained Optimization Model
4.3. Scenario 3: Energy Trading Model for Microgrid System
4.3.1. Stochastic Optimization Model
4.3.2. Robust Optimization Model
4.3.3. Distributionally Robust Optimization
4.3.4. Chance Constrained Optimization Model
4.4. Scenario 4: Joint Energy Management and Trading for Microgrid System
4.4.1. Stochastic Optimization Model
4.4.2. Robust Optimization Model
4.4.3. Distributionally Robust Optimization
4.4.4. Chance Constrained Optimization Model
5. Challenges and Future Research Directions
5.1. Microgrid Energy Management
5.2. Demand Side Management
5.3. Integration of Distribution Energy Resources
5.4. Smart Home
5.5. Unit Commitment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MEM | Micro-grid Energy Management |
| HEM | Home Energy Management |
| DER | Distributed Energy Management |
| SDN | Smart Distribution Network |
| DSM | Demand Side Management |
| PEV | Plugin Electric Vehicles |
| ED | Economic Dispatch |
| UC | Unit Commitment |
| STG | Smart Thermal Grid |
| MEO | Micro-grid Economic Operation |
| RDG | Reconfiguration of Distribution Grid |
| OPF | Optimal Power Flow |
| ERD | Energy and Reserve Dispatch |
| ESS | Energy Storage System |
| SPDA | Scenario Partition and Decomposition Algorithm |
| CCDCGP | Chance Constrained dependent chance goal programming |
| FMEA | Failure-Mode-and Effect analysis |
| IPEA | Inter-generation Projection Evolutionary Algorithm |
| IGDT | Information Gap Decision Theory |
| MPC | Model Predictive Control |
| FPIM | Fuzzy Prediction Interval Model |
| SPD | Scenario Partition and Decomposition |
| BMLM | Big-M Linearization Method |
| LOP | Lyapunov Optimization Method |
| CCG | Column-and-Constraint Generation |
| AM | Analytic Method |
| LDR | Linear Decision Rule |
| MH | Math-Heuristic |
| BD | Benders Decomposition |
| TOA | Taguchis Orthogonal Array |
| DD | Dual Decomposition |
| BB | Branch-and-Bound |
| LM | Lagrangian Multiplier |
| QP | Quadratic Programming |
| MCS | Monte Carlo Simulation |
| IM | Iterative Method |
| SAA | Sample Average Approximation |
| SBM | Scenario Based Method |
| IPM | Interior Point Methods |
| DE | Differential Evolution |
| HABC | Hybrid Artificial Bee Colony |
| POC | Pareto-optimal cuts |
| DD | Dual Decomposition |
| SA | Sensitivity Analysis |
| SVM | Support Vector Machine |
| LR | Linear Regression |
| MDP | Markov Decision Process |
| SO | Stochastic Optimization |
| RO | Robust Optimization |
| CCO | Chance Constrained Optimization |
| DRO | Distributional Robust Optimization |
| SA | Solution Algorithms |
| OF | Objective Function |
| FRD | Future Research Directions |
| GEM | Grid Energy Management |
| TPEM | Two-Point Estimate Method |
| OPGF | Optimal Power Gas Flow |
| SGTD | Smart Grid Tariff Design |
| HE | Heuristic |
| CC | Chance Constrained |
| AR | Architecture |
| TN | Taxonomy |
References
- Martins, F.; Felgueiras, C.; Smitkova, M.; Caetano, N. Analysis of fossil fuel energy consumption and environmental impacts in European countries. Energies 2019, 12, 964. [Google Scholar] [CrossRef]
- Kabalci, E.; Kabalci, Y. Introduction to Smart Grid Architecture. In Smart Grids and Their Communication Systems; Springer: Berlin/Heidelberg, Germany, 2019; pp. 3–45. [Google Scholar]
- Ahmed, S.; Gondal, T.M.; Adil, M.; Malik, S.A.; Qureshi, R. A survey on communication technologies in smart grid. In Proceedings of the 2019 IEEE PES GTD Grand International Conference and Exposition Asia (GTD Asia), Bangkok, Thailand, 19–23 March 2019; pp. 7–12. [Google Scholar]
- Bruno, S.; Lamonaca, S.; La Scala, M.; Rotondo, G.; Stecchi, U. Load control through smart-metering on distribution networks. In Proceedings of the 2009 IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–8. [Google Scholar]
- Momoh, J.A. Smart grid design for efficient and flexible power networks operation and control. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009; pp. 1–8. [Google Scholar]
- Khan, N.; Riaz, M. Reliable and Secure Advanced Metering Infrastructure for Smart Grid Network. In Proceedings of the 2018 International Conference on Computing, Electronic and Electrical Engineering (ICE Cube), Quetta, Pakistan, 12–13 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Nafi, N.S.; Ahmed, K.; Gregory, M.A.; Datta, M. A survey of smart grid architectures, applications, benefits and standardization. J. Netw. Comput. Appl. 2016, 76, 23–36. [Google Scholar] [CrossRef]
- Ahmad, S.; Ahmad, A.; Naeem, M.; Ejaz, W.; Kim, H.S. A compendium of performance metrics, pricing schemes, optimization objectives, and solution methodologies of demand side management for the smart grid. Energies 2018, 11, 2801. [Google Scholar] [CrossRef]
- Malik, S.A.; Gondal, T.M.; Ahmad, S.; Adil, M.; Qureshi, R. Towards optimization approaches in smart grid a review. In Proceedings of the 2019 2nd International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 30–31 January 2019; pp. 1–5. [Google Scholar]
- Hussain, I.; Samara, G.; Ullah, I.; Khan, N. Encryption for End-User Privacy: A Cyber-Secure Smart Energy Management System. In Proceedings of the 2021 22nd International Arab Conference on Information Technology (ACIT), Muscat, Oman, 21–23 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Shakeel, S.R.; Takala, J.; Shakeel, W. Renewable energy sources in power generation in Pakistan. Renew. Sustain. Energy Rev. 2016, 64, 421–434. [Google Scholar] [CrossRef]
- Mosaad, M.I.; Abu-Siada, A.; Ismaiel, M.M.; Albalawi, H.; Fahmy, A. Enhancing the Fault Ride-through Capability of a DFIG-WECS Using a High-Temperature Superconducting Coil. Energies 2021, 14, 6319. [Google Scholar] [CrossRef]
- Tawfiq, A.A.E.; El-Raouf, M.O.A.; Mosaad, M.I.; Gawad, A.F.A.; Farahat, M.A.E. Optimal Reliability Study of Grid-Connected PV Systems Using Evolutionary Computing Techniques. IEEE Access 2021, 9, 42125–42139. [Google Scholar] [CrossRef]
- Hlalele, T.; Du, S. Analysis of power transmission line uncertainties: Status review. J. Elect. Electron. Syst. 2016, 5, 1–5. [Google Scholar] [CrossRef]
- Delle Femine, A.; Gallo, D.; Landi, C.; Lo Schiavo, A.; Luiso, M. Low power contactless voltage sensor for low voltage power systems. Sensors 2019, 19, 3513. [Google Scholar] [CrossRef]
- Alonso, M.; Amaris, H.; Alcala, D.; Florez R, D.M. Smart sensors for smart grid reliability. Sensors 2020, 20, 2187. [Google Scholar] [CrossRef]
- Rojas-Delgado, B.; Alonso, M.; Amaris, H.; de Santiago, J. Wave power output smoothing through the use of a high-speed kinetic buffer. Energies 2019, 12, 2196. [Google Scholar] [CrossRef]
- Vazquez, R.; Amaris, H.; Alonso, M.; Lopez, G.; Moreno, J.I.; Olmeda, D.; Coca, J. Assessment of an adaptive load forecasting methodology in a smart grid demonstration project. Energies 2017, 10, 190. [Google Scholar] [CrossRef]
- Ng, C.H.; Logenthiran, T.; Woo, W.L. Intelligent distributed smart grid network-Reconfiguration. In Proceedings of the 2015 IEEE Innovative Smart Grid Technologies-Asia ISGT ASIA, Bangkok, Thailand, 3–6 November 2015; pp. 1–6. [Google Scholar]
- Hussain, I.; Ullah, M.; Ullah, I.; Bibi, A.; Naeem, M.; Singh, M.; Singh, D. Optimizing Energy Consumption in the Home Energy Management System via a Bio-Inspired Dragonfly Algorithm and the Genetic Algorithm. Electronics 2020, 9, 406. [Google Scholar] [CrossRef]
- Mora-Flórez, J.J.; Herrera-Orozco, R.A.; Bedoya-Cadena, A.F. Fault location considering load uncertainty and distributed generation in power distribution systems. IET Gener. Transm. Distrib. 2015, 9, 287–295. [Google Scholar] [CrossRef]
- Miceli, R. Energy management and smart grids. Energies 2013, 6, 2262–2290. [Google Scholar] [CrossRef]
- Hasan, Z.; El-Hawary, M. Load reduction probabilistic model for smart grid network economic dispatch problem. In Proceedings of the 2017 IEEE Electrical Power and Energy Conference (EPEC), Saskatoon, SK, Canada, 22–25 October 2017; pp. 1–7. [Google Scholar]
- Bakirtzis, E.A.; Simoglou, C.K.; Biskas, P.N.; Bakirtzis, A.G. Storage management by rolling stochastic unit commitment for high renewable energy penetration. Electr. Power Syst. Res. 2018, 158, 240–249. [Google Scholar] [CrossRef]
- Li, C.; Grossmann, I.E. A Review of Stochastic Programming Methods for Optimization of Process Systems under Uncertainty. Front. Chem. Eng. 2020, 2, 34. [Google Scholar] [CrossRef]
- Birge, J.R. State-of-the-art-survey Stochastic programming: Computation and applications. INFORMS J. Comput. 1997, 9, 111–133. [Google Scholar] [CrossRef]
- Reddy, S.S.; Sandeep, V.; Jung, C.M. Review of stochastic optimization methods for smart grid. Front. Energy 2017, 11, 197–209. [Google Scholar] [CrossRef]
- Bertsimas, D.; Brown, D.B.; Caramanis, C. Theory and applications of robust optimization. SIAM Rev. 2011, 53, 464–501. [Google Scholar] [CrossRef]
- Beyer, H.G.; Sendhoff, B. Robust optimization—A comprehensive survey. Comput. Methods Appl. Mech. Eng. 2007, 196, 3190–3218. [Google Scholar] [CrossRef]
- Rahimian, H.; Mehrotra, S. Distributionally robust optimization: A review. arXiv 2019, arXiv:1908.05659. [Google Scholar]
- Küçükyavuz, S.; Jiang, R. Chance-Constrained Optimization: A Review of Mixed-Integer Conic Formulations and Applications. arXiv 2021, arXiv:2101.08746. [Google Scholar]
- Rao, S.S. Engineering Optimization: Theory and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Birge, J.R.; Louveaux, F. Introduction to Stochastic Programming; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Hedman, K.; Korad, A.; Zhang, M.; Dominguez-Garcia, A.; Jiang, X. The Application of Robust Optimization in Power Systems; Final Report to the Power Systems Engineering Research Center; PSERC Publication: Chandigarh, India, 2014; pp. 6–14. [Google Scholar]
- Hannah, L.A. Stochastic optimization. Int. Encycl. Soc. Behav. Sci. 2015, 2, 473–481. [Google Scholar]
- Goh, J.; Sim, M. Distributionally robust optimization and its tractable approximations. Oper. Res. 2010, 58, 902–917. [Google Scholar] [CrossRef]
- Shang, C.; You, F. Distributionally robust optimization for planning and scheduling under uncertainty. Comput. Chem. Eng. 2018, 110, 53–68. [Google Scholar] [CrossRef]
- Ahmed, H. Formulation of Two-Stage Stochastic Programming with Fixed Recourse. Br. Int. Exact Sci. (BIoEx) J. 2019, 1, 18–21. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Nemirovski, A. Robust optimization–methodology and applications. Math. Program. 2002, 92, 453–480. [Google Scholar] [CrossRef]
- Ben-Tal, A.; El Ghaoui, L.; Nemirovski, A. Robust Optimization; Princeton University Press: Princeton, NJ, USA, 2009; Volume 28. [Google Scholar]
- Bertsimas, D.; Sim, M. The price of robustness. Oper. Res. 2004, 52, 35–53. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Goryashko, A.; Guslitzer, E.; Nemirovski, A. Adjustable robust solutions of uncertain linear programs. Math. Program. 2004, 99, 351–376. [Google Scholar] [CrossRef]
- Schöbel, A. Generalized light robustness and the trade-off between robustness and nominal quality. Math. Methods Oper. Res. 2014, 80, 161–191. [Google Scholar] [CrossRef]
- Kouvelis, P.; Yu, G. Robust Discrete Optimization and Its Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 14. [Google Scholar]
- Carrizosa, E.; Goerigk, M.; Schöbel, A. A biobjective approach to recoverable robustness based on location planning. Eur. J. Oper. Res. 2017, 261, 421–435. [Google Scholar] [CrossRef][Green Version]
- Xiong, P.; Jirutitijaroen, P.; Singh, C. A distributionally robust optimization model for unit commitment considering uncertain wind power generation. IEEE Trans. Power Syst. 2017, 32, 39–49. [Google Scholar] [CrossRef]
- Esteban-Pérez, A.; Morales, J.M. Partition-based Distributionally Robust Optimization via Optimal Transport with Order Cone Constraints. arXiv 2019, arXiv:1903.01769. [Google Scholar] [CrossRef]
- Xin, L.; Goldberg, D.A. Time (in) consistency of multistage distributionally robust inventory models with moment constraints. Eur. J. Oper. Res. 2021, 289, 1127–1141. [Google Scholar] [CrossRef]
- Liu, Q.; Wu, J.; Xiao, X.; Zhang, L. A note on distributionally robust optimization under moment uncertainty. J. Numer. Math. 2018, 26, 141–150. [Google Scholar] [CrossRef]
- Esfahani, P.M.; Kuhn, D. Data-driven distributionally robust optimization using the Wasserstein metric: Performance guarantees and tractable reformulations. Math. Program. 2018, 171, 115–166. [Google Scholar] [CrossRef]
- Shafieezadeh-Abadeh, S.; Kuhn, D.; Esfahani, P.M. Regularization via Mass Transportation. J. Mach. Learn. Res. 2019, 20, 1–68. [Google Scholar]
- Namkoong, H.; Duchi, J.C. Stochastic Gradient Methods for Distributionally Robust Optimization with f-divergences. NIPS 2016, 29, 2208–2216. [Google Scholar]
- Bayraksan, G.; Love, D.K. Data-driven stochastic programming using phi-divergences. In The Operations Research Revolution; INFORMS: Oslo, Norway, 2015; pp. 1–19. [Google Scholar] [CrossRef]
- Duchi, J.C.; Glynn, P.W.; Namkoong, H. Statistics of robust optimization: A generalized empirical likelihood approach. Math. Oper. Res. 2021, 46, 835–1234. [Google Scholar] [CrossRef]
- Xie, W. On distributionally robust chance constrained programs with Wasserstein distance. Math. Program. 2021, 186, 115–155. [Google Scholar] [CrossRef]
- Van Ackooij, W.; Zorgati, R.; Henrion, R.; Möller, A. Chance constrained programming and its applications to energy management. In Stochastic Optimization-Seeing the Optimal for the Uncertain; IntechOpen: London, UK, 28 February 2011. [Google Scholar]
- Gassmann, H.I.; Schweitzer, E. A comprehensive input format for stochastic linear programs. Ann. Oper. Res. 2001, 104, 89–125. [Google Scholar] [CrossRef]
- Liu, J.; Rizzoni, G.; Yurkovich, B. Stochastic energy management for microgrids with constraints under uncertainty. In Proceedings of the 2016 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 27–29 June 2016; pp. 1–6. [Google Scholar]
- Wu, X.; Hu, X.; Yin, X.; Moura, S.J. Stochastic optimal energy management of smart home with PEV energy storage. IEEE Trans. Smart Grid 2016, 9, 2065–2075. [Google Scholar] [CrossRef]
- Rostampour, V.; Keviczky, T. Energy management for building climate comfort in uncertain smart thermal grids with aquifer thermal energy storage. IFAC-PapersOnLine 2017, 50, 13156–13163. [Google Scholar] [CrossRef]
- Nikmehr, N.; Najafi-Ravadanegh, S. Probabilistic optimal power dispatch in multi-microgrids using heuristic algorithms. In Proceedings of the 2014 Smart Grid Conference (SGC), Tehran, Iran, 9–10 December 2014; pp. 1–6. [Google Scholar]
- Kopsidas, K.; Kapetanaki, A.; Levi, V. Optimal demand response scheduling with real-time thermal ratings of overhead lines for improved network reliability. IEEE Trans. Smart Grid 2016, 8, 2813–2825. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, L.; Fu, Y. Real-time price-based demand response management for residential appliances via stochastic optimization and robust optimization. IEEE Trans. Smart Grid 2012, 3, 1822–1831. [Google Scholar] [CrossRef]
- Nikmehr, N.; Ravadanegh, S.N. Optimal power dispatch of multi-microgrids at future smart distribution grids. IEEE Trans. Smart Grid 2015, 6, 1648–1657. [Google Scholar] [CrossRef]
- Trpovski, A.; Melo, D.F.R.; Hamacher, T.; Massier, T. Stochastic optimization for distribution grid reconfiguration with high photovoltaic penetration. In Proceedings of the 2017 IEEE International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 14–17 August 2017; pp. 67–73. [Google Scholar]
- Wang, Q.; Wang, J.; Guan, Y. Stochastic unit commitment with uncertain demand response. IEEE Trans. Power Syst. 2012, 28, 562–563. [Google Scholar] [CrossRef]
- Blanco, I.; Morales, J.M. An efficient robust solution to the two-stage stochastic unit commitment problem. IEEE Trans. Power Syst. 2017, 32, 4477–4488. [Google Scholar] [CrossRef]
- Dehghanian, P.; Kezunovic, M. Probabilistic decision making for the bulk power system optimal topology control. IEEE Trans. Smart Grid 2016, 7, 2071–2081. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, Z.; Gu, W.; Li, M.; Deng, Z. Robust real-time distributed optimal control based energy management in a smart grid. IEEE Trans. Smart Grid 2015, 8, 1568–1579. [Google Scholar] [CrossRef]
- Giraldo, J.S.; Castrillon, J.A.; López, J.C.; Rider, M.J.; Castro, C.A. Microgrids energy management using robust convex programming. IEEE Trans. Smart Grid 2018, 10, 4520–4530. [Google Scholar] [CrossRef]
- Hu, W.; Wang, P.; Gooi, H.B. Toward optimal energy management of microgrids via robust two-stage optimization. IEEE Trans. Smart Grid 2016, 9, 1161–1174. [Google Scholar] [CrossRef]
- Guo, Y.; Zhao, C. Islanding-aware robust energy management for microgrids. IEEE Trans. Smart Grid 2016, 9, 1301–1309. [Google Scholar] [CrossRef]
- Rezaei, N.; Ahmadi, A.; Khazali, A.H.; Guerrero, J.M. Energy and frequency hierarchical management system using information gap decision theory for islanded microgrids. IEEE Trans. Ind. Electron. 2018, 65, 7921–7932. [Google Scholar] [CrossRef]
- Ullah, H.; Khan, M.; Hussain, I.; Ullah, I.; Uthansakul, P.; Khan, N. An Optimal Energy Management System for University Campus Using the Hybrid Firefly Lion Algorithm (FLA). Energies 2021, 14, 6028. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, B.; Wang, J.; Kim, J.; Begovic, M.M. Robust optimization based optimal DG placement in microgrids. IEEE Trans. Smart Grid 2014, 5, 2173–2182. [Google Scholar] [CrossRef]
- Xiang, Y.; Liu, J.; Liu, Y. Robust energy management of microgrid with uncertain renewable generation and load. IEEE Trans. Smart Grid 2015, 7, 1034–1043. [Google Scholar] [CrossRef]
- Zhang, Y.; Gatsis, N.; Giannakis, G.B. Robust energy management for microgrids with high-penetration renewables. IEEE Trans. Sustain. Energy 2013, 4, 944–953. [Google Scholar] [CrossRef]
- Ye, H.; Li, Z. Robust security-constrained unit commitment and dispatch with recourse cost requirement. IEEE Trans. Power Syst. 2015, 31, 3527–3536. [Google Scholar] [CrossRef]
- Ullah, I.; Hussain, I.; Uthansakul, P.; Riaz, M.; Khan, M.N.; Lloret, J. Exploiting multi-verse optimization and sine-cosine algorithms for energy management in smart cities. Appl. Sci. 2020, 10, 2095. [Google Scholar] [CrossRef]
- Ullah, I.; Hussain, I.; Singh, M. Exploiting Grasshopper and Cuckoo Search Bio-Inspired Optimization Algorithms for Industrial Energy Management System: Smart Industries. Electronics 2020, 9, 105. [Google Scholar] [CrossRef]
- Gögler, P.; Dorfner, M.; Hamacher, T. Hybrid Robust/Stochastic Unit Commitment With Iterative Partitions of the Continuous Uncertainty Set. Front. Energy Res. 2018, 6, 71. [Google Scholar] [CrossRef]
- Zhao, C.; Guan, Y. Unified stochastic and robust unit commitment. IEEE Trans. Power Syst. 2013, 28, 3353–3361. [Google Scholar] [CrossRef]
- Wang, C.; Liu, F.; Wang, J.; Qiu, F.; Wei, W.; Mei, S.; Lei, S. Robust risk-constrained unit commitment with large-scale wind generation: An adjustable uncertainty set approach. IEEE Trans. Power Syst. 2016, 32, 723–733. [Google Scholar] [CrossRef]
- Velloso, A.; Street, A.; Pozo, D.; Arroyo, J.M.; Cobos, N.G. Two-Stage Robust Unit Commitment for Co-Optimized Electricity Markets: An Adaptive Data-Driven Approach for Scenario-Based Uncertainty Sets. IEEE Trans. Sustain. Energy 2019, 11, 958–969. [Google Scholar] [CrossRef]
- Li, Z.; Shahidehpour, M.; Wu, W.; Zeng, B.; Zhang, B.; Zheng, W. Decentralized multiarea robust generation unit and tie-line scheduling under wind power uncertainty. IEEE Trans. Sustain. Energy 2015, 6, 1377–1388. [Google Scholar] [CrossRef]
- Zhou, H.; Li, Z.; Zheng, J.; Wu, Q.; Zhang, H. Robust Scheduling of Integrated Electricity and Heating System Hedging Heating Network Uncertainties. IEEE Trans. Smart Grid 2019, 11, 1543–1555. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, J.; Watson, J.P.; Guan, Y. Multi-stage robust unit commitment considering wind and demand response uncertainties. IEEE Trans. Power Syst. 2013, 28, 2708–2717. [Google Scholar] [CrossRef]
- Zazo, J.; Zazo, S.; Macua, S.V. Robust worst-case analysis of demand-side management in smart grids. IEEE Trans. Smart Grid 2016, 8, 662–673. [Google Scholar] [CrossRef]
- Du, Y.F.; Jiang, L.; Li, Y.; Wu, Q. A robust optimization approach for demand side scheduling considering uncertainty of manually operated appliances. IEEE Trans. Smart Grid 2016, 9, 743–755. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, Y.; Wu, J.; Wang, J.; Zhang, Y.; Wang, D. Robust-index method for household load scheduling considering uncertainties of customer behavior. IEEE Trans. Smart Grid 2015, 6, 1806–1818. [Google Scholar] [CrossRef]
- Melhem, F.Y.; Grunder, O.; Hammoudan, Z.; Moubayed, N. Energy management in electrical smart grid environment using robust optimization algorithm. IEEE Trans. Ind. Appl. 2018, 54, 2714–2726. [Google Scholar] [CrossRef]
- Bai, X.; Qiao, W. Robust optimization for bidirectional dispatch coordination of large-scale V2G. IEEE Trans. Smart Grid 2015, 6, 1944–1954. [Google Scholar] [CrossRef]
- Xiao, J.; Xie, J.; Chen, X.; Yu, K.; Chen, Z.; Li, Z. Energy cost reduction robust optimization for meeting scheduling in smart commercial buildings. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017; pp. 1–5. [Google Scholar]
- Hajebrahimi, A.; Kamwa, I.; Delage, E.; Abdelaziz, M. Adaptive Distributionally Robust Optimization for Electricity and Electrified Transportation Planning. IEEE Trans. Smart Grid 2020, 11, 4278–4289. [Google Scholar] [CrossRef]
- Lorca, A.; Sun, X.A. Multistage robust unit commitment with dynamic uncertainty sets and energy storage. IEEE Trans. Power Syst. 2016, 32, 1678–1688. [Google Scholar] [CrossRef]
- Gupta, A.; Anderson, C.L. Statistical bus ranking for flexible robust unit commitment. IEEE Trans. Power Syst. 2018, 34, 236–245. [Google Scholar] [CrossRef]
- Bertsimas, D.; Litvinov, E.; Sun, X.A.; Zhao, J.; Zheng, T. Adaptive robust optimization for the security constrained unit commitment problem. IEEE Trans. Power Syst. 2012, 28, 52–63. [Google Scholar] [CrossRef]
- Mahboubi-Moghaddam, E.; Nayeripour, M.; Aghaei, J.; Khodaei, A.; Waffenschmidt, E. Interactive robust model for energy service providers integrating demand response programs in wholesale markets. IEEE Trans. Smart Grid 2016, 9, 2681–2690. [Google Scholar] [CrossRef]
- Jiang, R.; Wang, J.; Guan, Y. Robust unit commitment with wind power and pumped storage hydro. IEEE Trans. Power Syst. 2011, 27, 800–810. [Google Scholar] [CrossRef]
- Morales-Espana, G.; Lorca, Á.; de Weerdt, M.M. Robust unit commitment with dispatchable wind power. Electr. Power Syst. Res. 2018, 155, 58–66. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, F.; Wei, W.; Mei, S.; Chang, N. Robust unit commitment for large-scale wind generation and run-off-river hydropower. CSEE J. Power Energy Syst. 2016, 2, 66–75. [Google Scholar] [CrossRef]
- Cho, Y.; Ishizaki, T.; Ramdani, N.; Imura, J.i. Box-based Temporal Decomposition of Multi-period Economic Dispatch for Two-stage Robust Unit Commitment. IEEE Trans. Power Syst. 2019, 34, 3109–3118. [Google Scholar] [CrossRef]
- Jiang, R.; Wang, J.; Zhang, M.; Guan, Y. Two-stage minimax regret robust unit commitment. IEEE Trans. Power Syst. 2013, 28, 2271–2282. [Google Scholar] [CrossRef]
- Lee, C.; Liu, C.; Mehrotra, S.; Shahidehpour, M. Modeling transmission line constraints in two-stage robust unit commitment problem. IEEE Trans. Power Syst. 2013, 29, 1221–1231. [Google Scholar] [CrossRef]
- Carroll, P. Exploring Smart Grid Time-of-Use Tariffs using a Robust Optimisation Framework. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–6. [Google Scholar]
- Shi, Z.; Liang, H.; Huang, S.; Dinavahi, V. Distributionally robust chance-constrained energy management for islanded microgrids. IEEE Trans. Smart Grid 2018, 10, 2234–2244. [Google Scholar] [CrossRef]
- Sasaki, Y.; Yorino, N.; Zoka, Y.; Wahyudi, F.I. Robust stochastic dynamic load dispatch against uncertainties. IEEE Trans. Smart Grid 2017, 9, 5535–5542. [Google Scholar] [CrossRef]
- Prabakaran, S.; Ramar, R.; Hussain, I.; Kavin, B.P.; Alshamrani, S.S.; AlGhamdi, A.S.; Alshehri, A. Predicting Attack Pattern via Machine Learning by Exploiting Stateful Firewall as Virtual Network Function in an SDN Network. Sensors 2022, 22, 709. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, Q.; Sun, H.; Li, Z.; Wu, W.; Li, Z. A distributionally robust optimization model for unit commitment based on Kullback–Leibler divergence. IEEE Trans. Power Syst. 2018, 33, 5147–5160. [Google Scholar] [CrossRef]
- Zhao, C.; Jiang, R. Distributionally robust contingency-constrained unit commitment. IEEE Trans. Power Syst. 2017, 33, 94–102. [Google Scholar] [CrossRef]
- Valencia, F.; Collado, J.; Sáez, D.; Marín, L.G. Robust energy management system for a microgrid based on a fuzzy prediction interval model. IEEE Trans. Smart Grid 2015, 7, 1486–1494. [Google Scholar] [CrossRef]
- Wei, W.; Liu, F.; Mei, S. Distributionally robust co-optimization of energy and reserve dispatch. IEEE Trans. Sustain. Energy 2015, 7, 289–300. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, Z.; Munsing, E.; Moura, S.J.; Song, Y. Data-driven chance-constrained regulation capacity offering for distributed energy resources. IEEE Trans. Smart Grid 2018, 10, 2713–2725. [Google Scholar] [CrossRef]
- Jabr, R.A. Distributionally robust CVaR constraints for power flow optimization. IEEE Trans. Power Syst. 2020, 35, 3764–3773. [Google Scholar] [CrossRef]
- Liu, J.; Chen, H.; Zhang, W.; Yurkovich, B.; Rizzoni, G. Energy management problems under uncertainties for grid-connected microgrids: A chance constrained programming approach. IEEE Trans. Smart Grid 2016, 8, 2585–2596. [Google Scholar] [CrossRef]
- Zachar, M.; Daoutidis, P. Microgrid/macrogrid energy exchange: A novel market structure and stochastic scheduling. IEEE Trans. Smart Grid 2016, 8, 178–189. [Google Scholar] [CrossRef]
- Cao, X.; Wang, J.; Zeng, B. Networked Microgrids Planning Through Chance Constrained Stochastic Conic Programming. IEEE Trans. Smart Grid 2019, 10, 6619–6628. [Google Scholar] [CrossRef]
- Yang, Z.; Wu, R.; Yang, J.; Long, K.; You, P. Economical operation of microgrid with various devices via distributed optimization. IEEE Trans. Smart Grid 2015, 7, 857–867. [Google Scholar] [CrossRef]
- Akhavan-Hejazi, H.; Mohsenian-Rad, H. Energy storage planning in active distribution grids: A chance-constrained optimization with non-parametric probability functions. IEEE Trans. Smart Grid 2016, 9, 1972–1985. [Google Scholar]
- Cai, Y.; Huang, G.; Yang, Z.; Lin, Q.; Tan, Q. Community-scale renewable energy systems planning under uncertainty. An interval chance-constrained programming approach. Renew. Sustain. Energy Rev. 2009, 13, 721–735. [Google Scholar] [CrossRef]
- Ayyagari, K.S.; Gatsis, N.; Taha, A.F. Chance constrained optimization of distributed energy resources via affine policies. In Proceedings of the 2017 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Montreal, QC, Canada, 14–16 November 2017; pp. 1050–1054. [Google Scholar]
- Hussain, I.; Khan, F.; Ahmad, I.; Khan, S.; Saeed, M. Power loss reduction via distributed generation system injected in a radial feeder. Mehran Univ. Res. J. Eng. Technol. 2021, 40, 160–168. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, Q.; Wang, J.; Guan, Y. Expected value and chance constrained stochastic unit commitment ensuring wind power utilization. IEEE Trans. Power Syst. 2014, 29, 2696–2705. [Google Scholar] [CrossRef]
- Cao, X.; Wang, J.; Zeng, B. Distributed Generation Planning Guidance Through Feasibility and Profit Analysis. IEEE Trans. Smart Grid 2018, 9, 5473–5475. [Google Scholar] [CrossRef]
- Dorini, G.; Pinson, P.; Madsen, H. Chance-constrained optimization of demand response to price signals. IEEE Trans. Smart Grid 2013, 4, 2072–2080. [Google Scholar] [CrossRef]
- Niu, W.; Li, Y. Uncertain optimization decision of interruptible load in demand response program. In Proceedings of the 2014 IEEE Innovative Smart Grid Technologies-Asia (ISGT ASIA), Kuala Lumpur, Malaysia, 20–23 May 2014; pp. 675–679. [Google Scholar]
- Baker, K.; Bernstein, A. Joint Chance Constraints in AC Optimal Power Flow: Improving Bounds through Learning. IEEE Trans. Smart Grid 2019, 10, 6376–6385. [Google Scholar] [CrossRef]
- Arasteh, H.; Vahidinasab, V.; Sepasian, M.S.; Aghaei, J. Stochastic System of Systems Architecture for Adaptive Expansion of Smart Distribution Grids. IEEE Trans. Ind. Inform. 2018, 15, 377–389. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, L.; Guo, W.; Kang, Q.; Wu, Q. Chance constrained optimization in a home energy management system. IEEE Trans. Smart Grid 2016, 9, 252–260. [Google Scholar] [CrossRef]
- Wang, Q.; Guan, Y.; Wang, J. A chance-constrained two-stage stochastic program for unit commitment with uncertain wind power output. IEEE Trans. Power Syst. 2011, 27, 206–215. [Google Scholar] [CrossRef]
- Li, B.; Vrakopoulou, M.; Mathieu, J.L. Chance constrained reserve scheduling using uncertain controllable loads Part II: Analytical reformulation. IEEE Trans. Smart Grid 2017, 10, 1618–1625. [Google Scholar] [CrossRef]
- Vrakopoulou, M.; Li, B.; Mathieu, J.L. Chance constrained reserve scheduling using uncertain controllable loads Part I: Formulation and scenario-based analysis. IEEE Trans. Smart Grid 2017, 10, 1608–1617. [Google Scholar] [CrossRef]
- Peralta, J.; Pérez-Ruiz, J.; De la Torre, S. Unit commitment with load uncertainty by joint chance-constrained programming. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013; pp. 1–6. [Google Scholar]
- Zhang, Y.; Wang, J.; Zeng, B.; Hu, Z. Chance-constrained two-stage unit commitment under uncertain load and wind power output using bilinear benders decomposition. IEEE Trans. Power Syst. 2017, 32, 3637–3647. [Google Scholar] [CrossRef]
- Sundar, K.; Nagarajan, H.; Roald, L.; Misra, S.; Bent, R.; Bienstock, D. Chance-Constrained Unit Commitment with N-1 Security and Wind Uncertainty. IEEE Trans. Control. Netw. Syst. 2019, 6, 1062–1074. [Google Scholar] [CrossRef]
- Li, Z.; Jin, T.; Zhao, S.; Liu, J. Power system day-ahead unit commitment based on chance-constrained dependent chance goal programming. Energies 2018, 11, 1718. [Google Scholar] [CrossRef]
- Chen, D.; Hou, S.; Gong, N.; Zhang, W.; Li, H. A Chance-Constrained Two-Stage Stochastic UC Considering Uncertain Renewable Energy Output Furthermore, Demand Response. In Proceedings of the 2018 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Singapore, 22–25 May 2018; pp. 419–424. [Google Scholar]
- Wang, Z.; Shen, C.; Liu, F.; Wu, X.; Liu, C.C.; Gao, F. Chance-constrained economic dispatch with non-Gaussian correlated wind power uncertainty. IEEE Trans. Power Syst. 2017, 32, 4880–4893. [Google Scholar] [CrossRef]
- Hassan, A.; Mieth, R.; Chertkov, M.; Deka, D.; Dvorkin, Y. Optimal load ensemble control in chance-constrained optimal power flow. IEEE Trans. Smart Grid 2018, 10, 5186–5195. [Google Scholar] [CrossRef]
- Li, B.; Wang, X.; Shahidehpour, M.; Jiang, C.; Li, Z. DER Aggregators Data-Driven Bidding Strategy Using the Information Gap Decision Theory in a Non-Cooperative Electricity Market. IEEE Trans. Smart Grid 2019, 10, 6756–6767. [Google Scholar] [CrossRef]
- Li, R.; Wu, Q.; Oren, S.S. Distribution locational marginal pricing for optimal electric vehicle charging management. IEEE Trans. Power Syst. 2013, 29, 203–211. [Google Scholar] [CrossRef]
- Zare, M.; Niknam, T.; Azizipanah-Abarghooee, R.; Ostadi, A. New stochastic bi-objective optimal cost and chance of operation management approach for smart microgrid. IEEE Trans. Ind. Inform. 2016, 12, 2031–2040. [Google Scholar] [CrossRef]
- Daneshvar, M.; Ivatloo, B.M.; Abapour, M.; Asadi, S.; Khanjani, R. Distributionally Robust Chance Constrained Transactive Energy Framework for Coupled Electrical and Gas Microgrids. IEEE Trans. Ind. Electron. 2020, 68, 347–357. [Google Scholar] [CrossRef]
- Pozo, D.; Contreras, J. A chance-constrained unit commitment with an nK security criterion and significant wind generation. IEEE Trans. Power Syst. 2012, 28, 2842–2851. [Google Scholar] [CrossRef]
- Wang, B.; Dehghanian, P.; Zhao, D. Chance-constrained energy management system for power grids with high proliferation of renewables and electric vehicles. IEEE Trans. Smart Grid 2019, 11, 2324–2336. [Google Scholar] [CrossRef]
- Tang, K.; Dong, S.; Ma, X.; Lv, L.; Song, Y. Chance-Constrained Optimal Power Flow of Integrated Transmission and Distribution Networks with Limited Information Interaction. IEEE Trans. Smart Grid 2020, 12, 821–833. [Google Scholar] [CrossRef]
- Yang, L.; Xu, Y.; Gu, W.; Sun, H. Distributionally Robust Chance-constrained Optimal Power-Gas Flow under Bidirectional Interactions Considering Uncertain Wind Power. IEEE Trans. Smart Grid 2020, 12, 1722–1735. [Google Scholar] [CrossRef]
- Soltani, N.Y.; Nasiri, A. Chance-constrained Optimization of Energy Storage Capacity for Microgrids. IEEE Trans. Smart Grid 2020, 11, 2760–2770. [Google Scholar] [CrossRef]
- Guo, Z.; Pinson, P.; Chen, S.; Yang, Q.; Yang, Z. Chance-Constrained Peer-to-Peer Joint Energy and Reserve Market Considering Renewable Generation Uncertainty. IEEE Trans. Smart Grid 2020, 12, 798–809. [Google Scholar] [CrossRef]
- Ahmad, S.; Naeem, M.; Ahmad, A. Low complexity approach for energy management in residential buildings. Int. Trans. Electr. Energy Syst. 2019, 29, e2680. [Google Scholar] [CrossRef]
- Ahmad, S.; Naeem, M.; Ahmad, A. Unified optimization model for energy management in sustainable smart power systems. Int. Trans. Electr. Energy Syst. 2020, 30, 1–19. [Google Scholar] [CrossRef]
- Ahmad, S.; Alhaisoni, M.M.; Naeem, M.; Ahmad, A.; Altaf, M. Joint energy management and energy trading in residential microgrid system. IEEE Access 2020, 8, 123334–123346. [Google Scholar] [CrossRef]
- Zaman, S.; Khan, L.U.; Hussain, I.; Mihet-Popa, L. Fast Computation of Highly Oscillatory ODE Problems: Applications in High-Frequency Communication Circuits. Symmetry 2022, 14, 115. [Google Scholar] [CrossRef]
- Zaman, S.; Hussain, I.; Singh, D. Fast Computation of Integrals with Fourier-Type Oscillator Involving Stationary Point. Mathematics 2019, 7, 1160. [Google Scholar] [CrossRef]
| Ref. | SO | RO | DRO | CC | AR | TN | OF | SA | Smart Power System |
|---|---|---|---|---|---|---|---|---|---|
| [25] | ✔ | ✔ | ✔ | ||||||
| [26] | ✔ | ✔ | ✔ | ||||||
| [27] | ✔ | ✔ | ✔ | ✔ | ✔ | ||||
| [28] | ✔ | ✔ | |||||||
| [29] | ✔ | ✔ | ✔ | ||||||
| [30] | ✔ | ✔ | |||||||
| [31] | ✔ | ✔ | ✔ | ||||||
| Our Review Paper | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ |
| References | Applications | LP | NLP | MILP | MISOCP | MIQP |
|---|---|---|---|---|---|---|
| [59] | HEM | × | ||||
| [61] | MEM | × | ||||
| [68] | OPF | × | ||||
| [62,63] | DRM | × | ||||
| [23,64] | ED | × | ||||
| [24,66] | UC | × | × | |||
| [60] | STG | × | ||||
| [65] | RDG | × |
| Ref. | Applications | LP | NLP | MIP | MILP | MINLP | MIBLP | MISOCP | MIQP | QP |
|---|---|---|---|---|---|---|---|---|---|---|
| [69] | SGEM | × | ||||||||
| [70,71,72,73,75] | MEM | × | × | × | ||||||
| [90,91] | HEM | × | ||||||||
| [88,89,93] | DSM | × | × | × | ||||||
| [92,94] | PEV | × | × | |||||||
| [67,78,83,84,85,87,95,96,97,98,99,100,101,102,103,104] | UC | × | × | × | × | × | × | |||
| [105] | SGTD | × |
| Ref. | Objectives | CCG | AM | LDR | IPEA and MH | HE | BD | TOA | DD and IGDT | MPC and FPIM | BB | LM | QP | MCS | LOM and BMLM | IM |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [92,106,107] | Minimize Generation Cost | × | × | |||||||||||||
| [89,91] | Minimize Electricity Cost | × | × | |||||||||||||
| [76] | Minimize Social Benefits Cost | × | × | |||||||||||||
| [73,77] | Minimize Microgrid Net Cost | × | × | |||||||||||||
| [90] | Minimize Comfort Violation | × | ||||||||||||||
| [72,78,85,111] | Minimize Operation Cost | × | × | × | ||||||||||||
| [67,71,75,81,82,83,84,86,98,110] | Minimize Overall Cost | × | × | × | × | × | × | × | ||||||||
| [93] | Minimize Electricity Payment | × | × | |||||||||||||
| [69,87] | Maximize Social Welfare | × | × | |||||||||||||
| [75] | Maximize Profits | × |
| Ref. | Applications | LP | NLP | MIP | MILP | MINLP | MIBLP | MISOCP | SOCP | MIQP |
|---|---|---|---|---|---|---|---|---|---|---|
| [115,116,117,118,142,143] | MEM | × | × | × | × | × | ||||
| [129] | HEM | × | ||||||||
| [119,120,121,123,124] | DEM | × | × | × | ||||||
| [127,128] | SDN | × | × | |||||||
| [125,126] | DSM | × | ||||||||
| [141] | PEV | × | ||||||||
| [138] | ED | × | ||||||||
| [130,131,133,134,135,136,137,144] | UC | × | × | × | × | × | × | |||
| [145] | GEM | × | ||||||||
| [146] | OPF | × | ||||||||
| [147] | OPGF | × |
| Ref. | Objectives | SAA | AM | SBM | IPM | HE | BD and DE | HABC | POC | DD | SA | SVM | LR and IM | MDP | MCS | MDP | ADMM |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [106,130] | Minimize Generation Cost | × | × | ||||||||||||||
| [133] | Constraints Satisfaction | × | |||||||||||||||
| [131,132] | Minimize Reserve Cost | × | × | ||||||||||||||
| [125] | Minimize Signal Price | × | |||||||||||||||
| [142] | Minimize Electricity Cost | × | |||||||||||||||
| [115,118,134,135] | Minimize Operating Cost | × | × | × | |||||||||||||
| [116,117,119,120,123,127,136,144,148] | Minimize Overall Cost | × | × | × | × | × | × | ||||||||||
| [121] | Minimize Thermal line losses | × | |||||||||||||||
| [128] | Minimize planning cost | × | |||||||||||||||
| [139] | Minimize Active Power Losses | × | × | ||||||||||||||
| [140] | Maximize payoff | × | |||||||||||||||
| [145] | Minimize Dispatch cost | × | |||||||||||||||
| [149] | Minimize Social cost | × |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riaz, M.; Ahmad, S.; Hussain, I.; Naeem, M.; Mihet-Popa, L. Probabilistic Optimization Techniques in Smart Power System. Energies 2022, 15, 825. https://doi.org/10.3390/en15030825
Riaz M, Ahmad S, Hussain I, Naeem M, Mihet-Popa L. Probabilistic Optimization Techniques in Smart Power System. Energies. 2022; 15(3):825. https://doi.org/10.3390/en15030825
Chicago/Turabian StyleRiaz, Muhammad, Sadiq Ahmad, Irshad Hussain, Muhammad Naeem, and Lucian Mihet-Popa. 2022. "Probabilistic Optimization Techniques in Smart Power System" Energies 15, no. 3: 825. https://doi.org/10.3390/en15030825
APA StyleRiaz, M., Ahmad, S., Hussain, I., Naeem, M., & Mihet-Popa, L. (2022). Probabilistic Optimization Techniques in Smart Power System. Energies, 15(3), 825. https://doi.org/10.3390/en15030825








