An Engine Fault Detection Method Based on the Deep Echo State Network and Improved Multi-Verse Optimizer
Abstract
:1. Introduction
- (1)
- A sparse input weight matrix is designed for the ESN. Optimized by fixed convolution kernels and the autoencoder (AE), a deep ESN is proposed.
- (2)
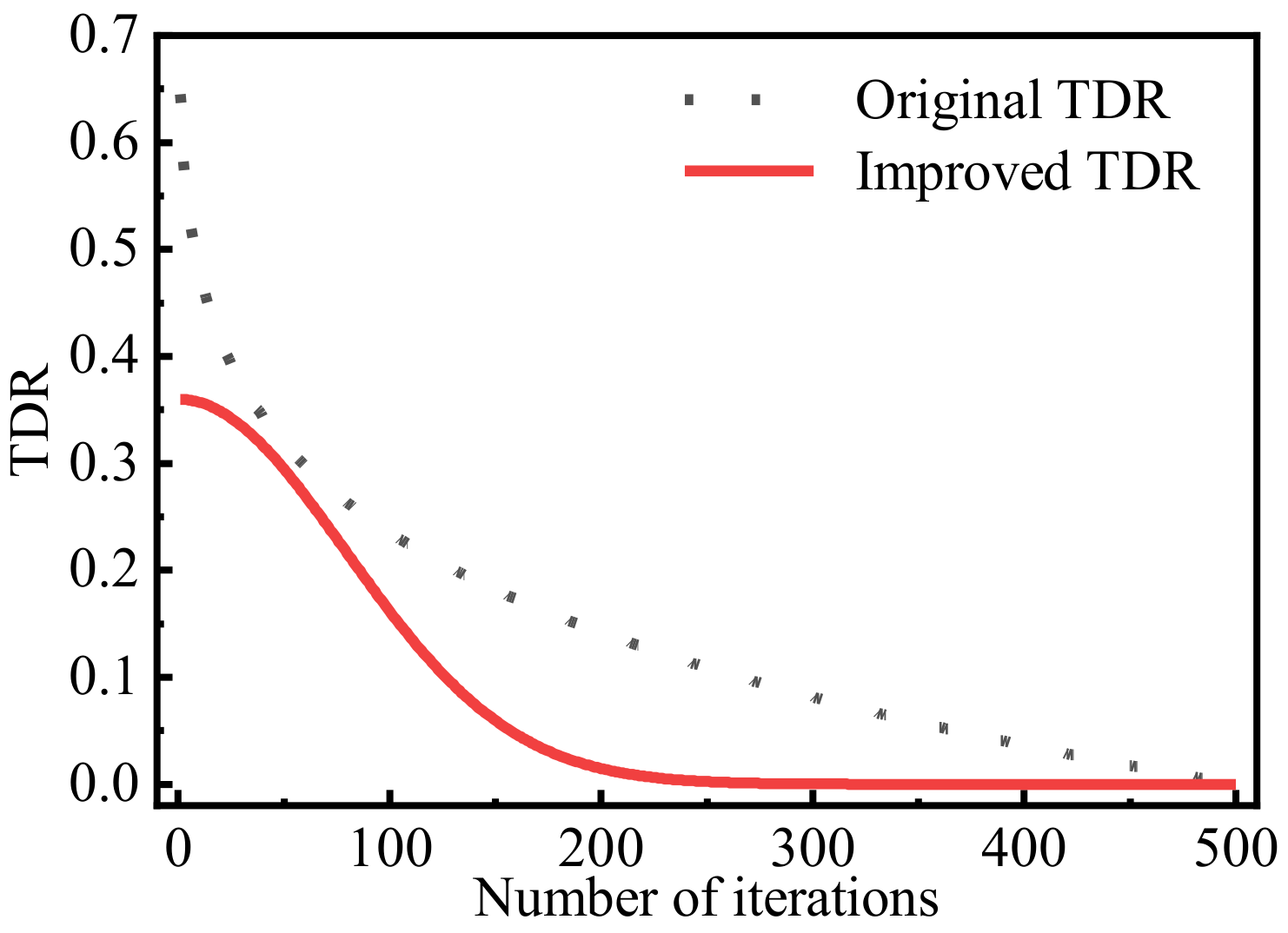
- A novel traveling distance rate (TDR) and universe collapse mechanism are proposed for the MVO to improve the local search and speed it up.
- (3)
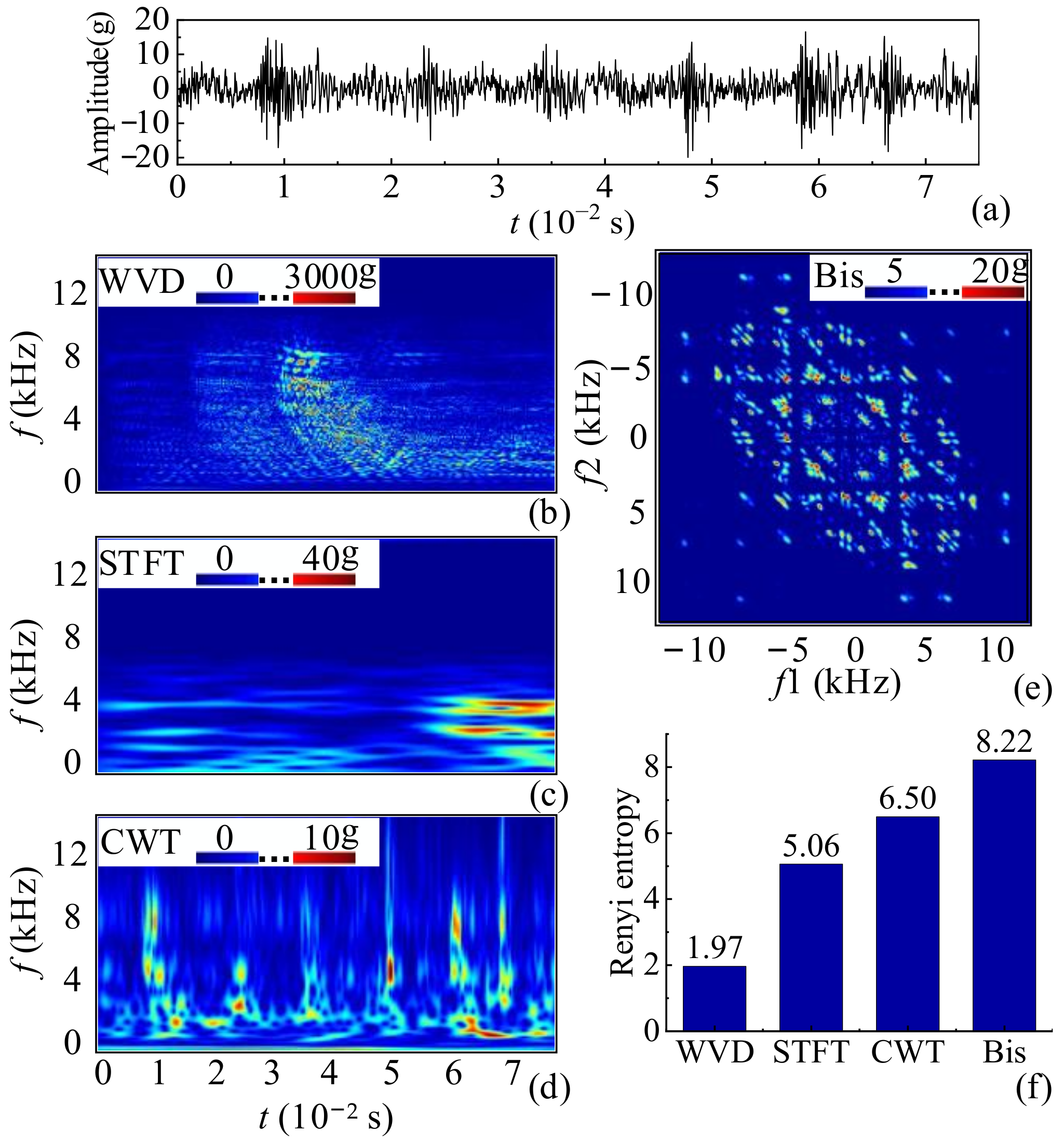
- The bispectrum is employed to transform the one-dimensional time-dependent vibration signal into a two-dimensional matrix with more impact features. An engine fault end-to-end detection model is then built based on the deep ESN, the improved MVO, and the bispectrum.
2. Fundamental Theories
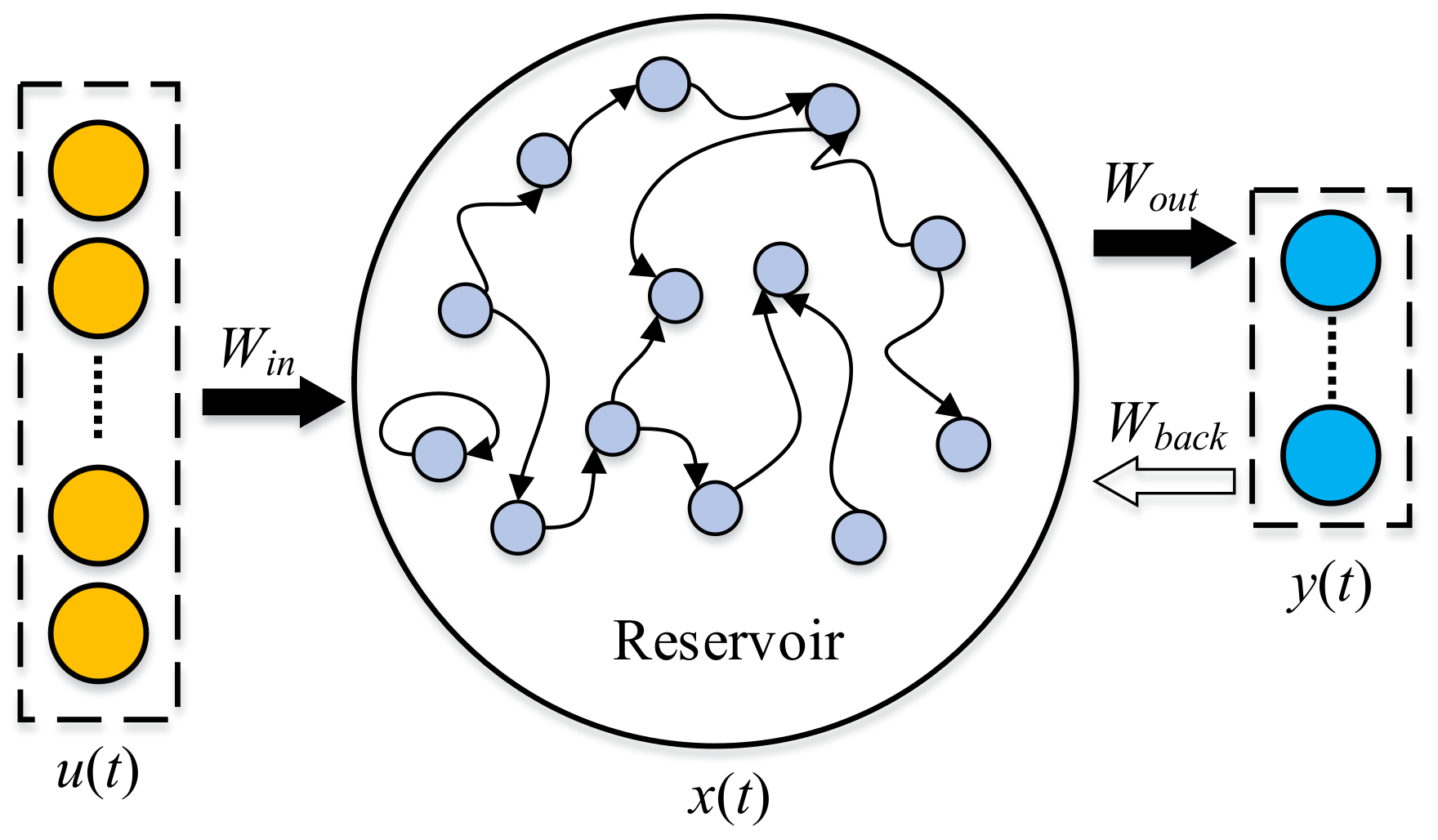
2.1. Echo State Networks
2.2. Multi-Verse Optimizer
3. Deep ESN and Improved MVO
3.1. Deep ESN
3.1.1. Fixed Convolution Kernel
3.1.2. Autoencoder (AE)
3.1.3. Sparse Input Matrix of the ESN
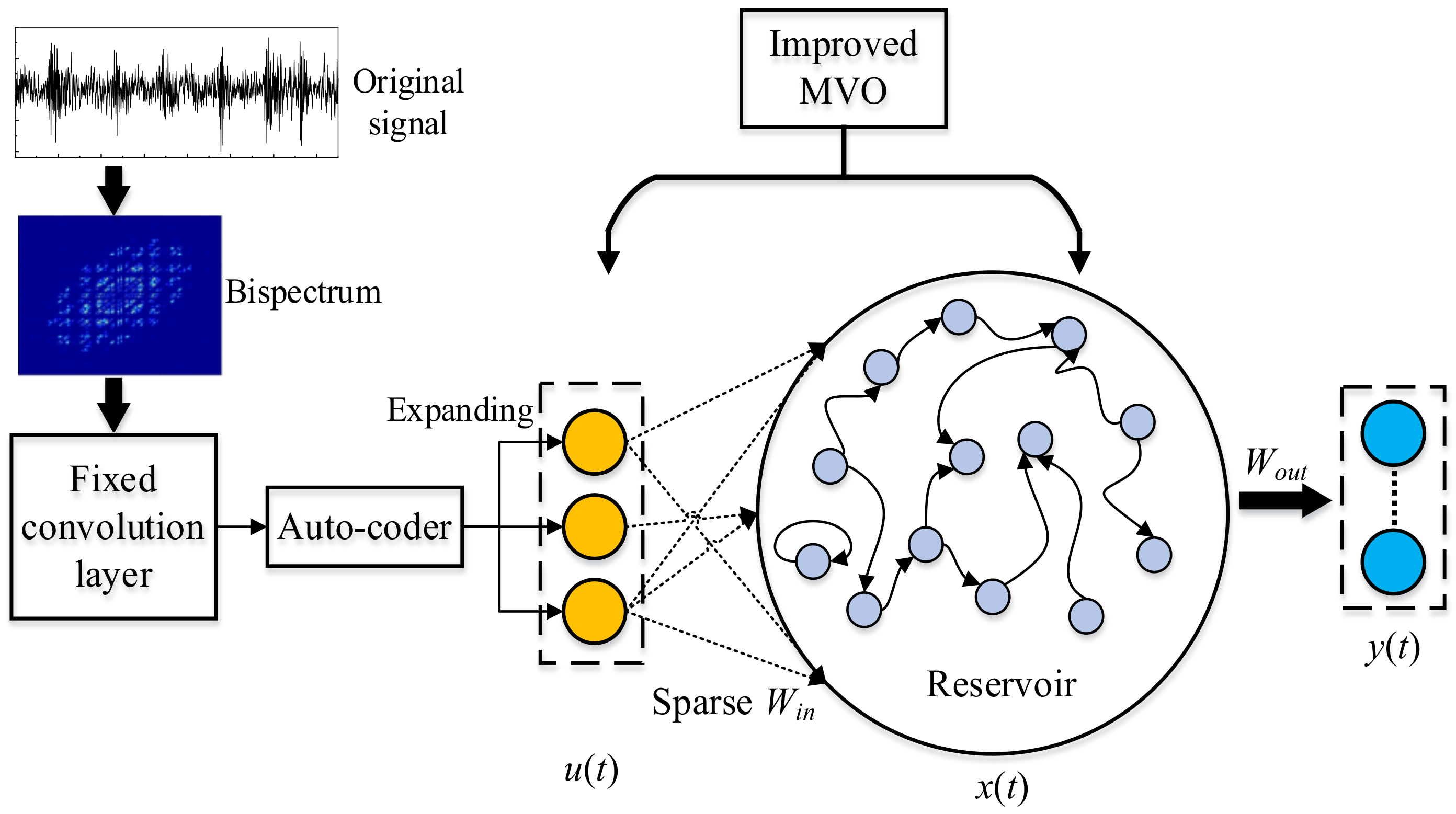
3.1.4. Deep ESN Model
- ①
- Design fixed convolutional layers based on the Prewitt filter, the Sobel filter, and the Gaussian lowpass filter.
- ②
- Process the input data by the designed convolutional and pooling layers.
- ③
- Train the AE by processed data to obtain the encoder matrix .
- ④
- Compress features of the processed data further with Equation (12).
- ⑤
- Build an ESN model with the sparse input matrix based on Equation (16).
- ⑥
- Copy the data twice to obtain three time-steps to activate the internal state of the ESN based on Equation (17).
- ⑦
- Train the ESN based on Equation (6).
- ⑧
- Predict the output labels based on ②, ④, ⑥, and the trained model.
3.2. Optimization of MVO
4. Experiment
5. Results and Analysis
5.1. Data Pre-Processing Method
5.2. Dataset
5.3. Results and Comparisons
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hirose, K.; Matsumura, T. A comparison between emission intensity and emission cap regulations. Energy Policy 2020, 137, 111115. [Google Scholar] [CrossRef]
- Resitoglu, I.A.; Altinisik, K.; Keskin, A. The pollutant emissions from diesel-engine vehicles and exhaust aftertreatment systems. Clean Technol. Environ. Policy 2015, 17, 15–27. [Google Scholar] [CrossRef] [Green Version]
- Nahim, H.M.; Younes, R.; Shraim, H.; Quladsine, M. Oriented review to potential simulator for faults modeling in diesel engine. J. Mar. Sci. Technol. 2016, 21, 533–551. [Google Scholar] [CrossRef]
- Tahan, M.; Tsoutsanis, E.; Muhammad, M.; Karim, K.Z.A. Performance-based health monitoring, diagnostics and prognostics for condition-based maintenance of gas turbines: A review. Appl. Energy 2017, 198, 122–144. [Google Scholar] [CrossRef] [Green Version]
- Vijay, G.S.; Pai, S.P.; Sriam, N.S.; Rao, R.B.K.N. Radial basis function neural network based comparison of dimensionality reduction techniques for effective bearing diagnostics. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2013, 227, 640–653. [Google Scholar]
- Barszcz, T.; Jablonski, A. A novel method for the optimal band selection for vibration signal demodulation and comparison with the Kurtogram. Mech. Syst. Signal Process 2011, 25, 431–451. [Google Scholar] [CrossRef]
- Benkedjouh, T.; Medjaher, K.; Zerhouni, N.; Rechak, S. Remaining useful life estimation based on nonlinear feature reduction and support vector regression. Eng. Appl. Artif. Intell. 2013, 26, 1751–1760. [Google Scholar] [CrossRef]
- Jablonski, A.; Dworakowski, Z.; Dziedziech, K.; Chaari, F. Vibration-based diagnostics of epicyclic gearboxes-From classical to soft-computing methods. Meas. J. Int. Meas. Confed. 2019, 147. [Google Scholar] [CrossRef]
- Zeng, R.L.; Zhang, L.L.; Mei, J.M.; Shen, H.; Zhao, H.M. Fault detection in an engine by fusing information from multivibration sensors. Int. J. Distrib. Sens. Netw. 2017, 13, 1–9. [Google Scholar] [CrossRef]
- Wang, H.D.; Deng, S.E.; Yang, J.X.; Liao, H.; Li, W.B. Parameter-adaptive VMD method based on BAS optimization algorithm for incipient bearing fault diagnosis. Math. Probl. Eng. 2020, 2020, 5659618. [Google Scholar] [CrossRef] [Green Version]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- LeCun, Y.; Bengio, Y. Convolutional networks for images, speech, and time series. In The Handbook of Brain Theory and Neural Networks; MIT Press: Cambrige, MA, USA, 1998. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comp. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.F.; Jia, X.S.; Bai, H.J.; Wang, G.L.; Liu, G.Z.; Guo, C.M. A new fault diagnosis method using deep belief network and compressive sensing. J. Vibroeng. 2020, 22, 83–97. [Google Scholar]
- Jiang, H.K.; Shao, H.D.; Chen, X.X.; Huang, J.Y. A feature fusion deep belief network method for intelligent fault diagnosis of rotating machinery. J. Intell. Fuzzy Syst. 2018, 34, 3513–3521. [Google Scholar] [CrossRef]
- Azamfar, M.; Singh, J.; Bravo-Imaz, I.; Lee, J. Multisensor data fusion for gearbox fault diagnosis using 2-D convolutional neural network and motor current signature analysis. Mech. Syst. Signal Process 2020, 144, 106861. [Google Scholar] [CrossRef]
- Hasan, M.J.; Sohaib, M.; Kim, J.M. A multitask-aided transfer learning-based diagnostic framework for bearings under inconsistent working conditions. Sensors 2020, 20, 7205. [Google Scholar] [CrossRef]
- Alrifaey, M.; Lim, W.H.; Ang, C.K. A novel deep learning framework based rnn-sae for fault detection of electrical gas generator. IEEE Access 2020, 9, 21433–21442. [Google Scholar] [CrossRef]
- Yu, J.; Gao, L.L.; Yu, G.B.; Liu, K.; Guo, Z.Y. Fault identification of planetary gears based on the SDAE and GRUNN. J. Vib. Shock 2021, 40, 156–163. [Google Scholar]
- Xie, J.Q.; You, W.; Shen, C.Q.; Zhu, Z.K. Bearing fault diagnosis based on improved convolution deep belief network. J. Electron. Meas. Instrum. 2020, 34, 36–43. [Google Scholar]
- Liang, K.W.; Qin, N.; Huang, D.Q.; Fu, Y.Z. Convolutional recurrent neural network for fault diagnosis of high-speed train bogie. Complexity 2018, 5, 4501952. [Google Scholar] [CrossRef] [Green Version]
- Zhang., X.C.; Cong, Y.W.; Yuan, Z.; Zhang, T.; Bai, X.T. Early fault detection method of rolling bearing based on MCNN and GRU network with an attention mechanism. Shock Vib. 2021, 3, 6660243. [Google Scholar] [CrossRef]
- Jaeger, H.; Haas, H. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science 2004, 304, 78–80. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Long, J.Y.; Sun, Z.Z.; Li, C.; Hong, Y.; Bai, Y.; Zhang, S.H. A novel sparse echo autoencoder network for data-driven fault diagnosis of delta 3-D printers. IEEE Trans. Instrum. Meas. 2020, 69, 683–692. [Google Scholar] [CrossRef]
- Wootton, A.J.; Taylor, S.L.; Day, C.R.; Haycock, P.W. Optimizing echo state networks for static pattern recognition. Cognitive Comput. 2017, 9, 391–399. [Google Scholar] [CrossRef]
- Ozturk, M.C.; Xu, D.M.; Principe, J.C. Analysis and design of echo state networks. Neural Comp. 2007, 19, 111–138. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.H.; Sun, Z.Z.; Wang, M.; Long, J.Y.; Bai, Y.; Li, C. Deep fuzzy echo state networks for machinery fault diagnosis. IEEE Trans. Fuzzy Syst. 2020, 28, 1205–1218. [Google Scholar] [CrossRef]
- Sun, X.C.; Li, T.; Li, Q.; Huang, Y.; Li, Y.Q. Deep belief echo-state network and its application to time series prediction. Knowl. Based Syst. 2017, 130, 17–29. [Google Scholar] [CrossRef]
- Ma, Q.L.; Chen, E.H.; Lin, Z.X.; Yan, J.Y.; Yu, Z.W.; Wing, W.Y.N. Convolutional multitimescale echo state network. IEEE Trans. Cybern. 2021, 51, 1613–1625. [Google Scholar] [CrossRef] [PubMed]
- Chouikhi, N.; Ammar, B.; Rokbani, N.; Alimi, A.M. PSO-based analysis of echo state network parameters for time series forecasting. Appl. Soft Comput. J. 2017, 55, 211–225. [Google Scholar] [CrossRef]
- Liu, J.X.; Sun, T.N.; Luo, Y.L.; Yang, S.; Cao, Y.; Zhai, J. Echo state network optimization using binary grey wolf algorithm. Neurocomputing 2020, 385, 310–318. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Faris, H.; Aljarah, I.; Mirjalili, S. Training feedforward neural networks using multi-verse optimizer for binary classification problems. Appl. Intell. 2016, 45, 322–332. [Google Scholar] [CrossRef]
- Yang, X.H.; Chen, W.K.; Li, A.Y.; Yang, C.S. A hybrid machine-learning method for oil-immersed power transformer fault diagnosis. IEEJ Trans. Electr. Electron. Eng. 2020, 15, 501–507. [Google Scholar] [CrossRef]
- Jaeger, H.; Lukosevicius, M.; Popovici, D.; Siewert, U. Optimization and applications of echo state networks with leaky-integrator neurons. Neural Netw. 2007, 20, 335–352. [Google Scholar] [CrossRef]
- Verstraeten, D.; Schrauwen, B.; D’Haene, M.; Stroobandt, D. An experimental unification of reservoir computing methods. Neural Netw. 2007, 20, 391–403. [Google Scholar] [CrossRef]
- Cohen, L. Generalized phase-space distribution functions. J. Math. Phys. 1966, 7, 781–786. [Google Scholar] [CrossRef]
- Bi, X.Y.; Cao, S.Q.; Zhang, D.M. Diesel engine valve clearance fault diagnosis based on improved variational mode decomposition and bispectrum. Energies 2019, 12, 661. [Google Scholar] [CrossRef] [Green Version]
- Baraniuk, R.G.; Flandrin, P.; Janssen, A.J.E.; Michel, J.J. Measuring time-frequency information content using the Renyi entropies. IEEE Trans. Inf. Theory 2001, 47, 1391–1409. [Google Scholar] [CrossRef] [Green Version]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lile, France, 6–11 July 2015; Volume 37, pp. 449–456. [Google Scholar]




| Function | Dim | Bounds | fmin | |
|---|---|---|---|---|
| Original MVO | Improved MVO | |||
| 10 | [−100,100] | 2.78 × 10−3 | 9.66 × 10−15 | |
| 10 | [−10,10] | 2.78 × 10−2 | 2.42 × 10−8 | |
| 10 | [−100,100] | 7.26 × 10−3 | 2.09 × 10−14 | |
| 10 | [−100,100] | 2.88 × 10−2 | 5.48 × 10−8 | |
| 10 | [−30,30] | 1.25 × 102 | 1.06 × 102 | |
| 10 | [−100,100] | 1.86 × 10−3 | 9.93 × 10−15 | |
| 10 | [−1.28,1.28] | 7.58 × 10−4 | 1.72 × 10−3 | |
| 10 | [−500,500] | −3.11 × 103 | −3.36 × 103 | |
| 10 | [−5.12,5.12] | 13.04 | 9.95 | |
| 10 | [−32,32] | 0.18 | 3.92 × 10−8 | |
| 10 | [−600,600] | 0.32 | 9.31 × 10−2 | |
| 10 | [−50,50] | 3.12 × 10−2 | 5.37 × 10−5 | |
| 10 | [−50,50] | 2.50 × 10−4 | 1.27 × 10−16 | |
| Items | Parameters |
|---|---|
| Number of Cylinders | 6 |
| Arrangement | Inline |
| Displacement | 7.14 L |
| Air inlet model | Turbocharged and intercooled |
| Firing order | 1-5-3-6-2-4 |
| Rated power | 220 kW@2300 r/min |
| Maximum torque | 1250 N•m@1200–1600 r/min |
| Fault Type | Adjusting Parameters | |
|---|---|---|
| Abnormal injection quantity | 75% | |
| Advance injection timing | −2 °CA | |
| Delayed injection timing | +2 °CA | |
| Low rail pressure | −200 bar | |
| High rail pressure | +200 bar | |
| Small Valve clearance | Intake | −0.05 mm |
| Outtake | −0.05 mm | |
| Big Valve clearance | Intake | +0.05 mm |
| Outtake | +0.05 mm | |
| Fault Types | Number of Samples | |||||||
|---|---|---|---|---|---|---|---|---|
| Speed | 1300 r/min | 1600 r/min | 2000 r/min | Total | ||||
| Load | 100% | 50% | 100% | 50% | 100% | 50% | ||
| Normal working condition | 90 | 150 | 150 | 150 | 120 | 150 | 810 | |
| Abnormal fuel delivery | 90 | 150 | 150 | 150 | 120 | 150 | 810 | |
| High rail pressure | 90 | 150 | 150 | 150 | 120 | 150 | 810 | |
| Low rail pressure | 90 | 150 | 150 | 150 | 120 | 150 | 810 | |
| Big valve clearance | 90 | 150 | 150 | 150 | 120 | 150 | 810 | |
| Small valve clearance | 90 | 150 | 150 | 150 | 120 | 150 | 810 | |
| Delayed injection timing | 90 | 150 | 150 | 150 | 120 | 150 | 810 | |
| Advanced injection timing | 90 | 150 | 150 | 150 | 120 | 150 | 810 | |
| Total | 720 | 1200 | 1200 | 1200 | 960 | 1200 | 6480 | |
| Model | Improved MVO | Deep ESN | ||||||
|---|---|---|---|---|---|---|---|---|
| Deep ESN | Original ESN | DBN | LSTM | GRU | CNN | CNN-BN | ||
| Recognition rate | 93.10% | 23.01% | 12.50% | 65.28% | 78.56% | 12.50% | 86.90% | 90.65% |
| Case | 1 | 2 | 3 | 4 | 5 | 6 |
| Recognition Rate | 93.10% | 93.70% | 92.92% | 93.89% | 93.24% | 92.78% |
| Case | 7 | 8 | 9 | 10 | Average | |
| Recognition Rate | 92.87% | 93.06% | 93.10% | 93.38% | 93.20% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Bi, F.; Zhang, L.; Yang, X.; Zhang, G. An Engine Fault Detection Method Based on the Deep Echo State Network and Improved Multi-Verse Optimizer. Energies 2022, 15, 1205. https://doi.org/10.3390/en15031205
Li X, Bi F, Zhang L, Yang X, Zhang G. An Engine Fault Detection Method Based on the Deep Echo State Network and Improved Multi-Verse Optimizer. Energies. 2022; 15(3):1205. https://doi.org/10.3390/en15031205
Chicago/Turabian StyleLi, Xin, Fengrong Bi, Lipeng Zhang, Xiao Yang, and Guichang Zhang. 2022. "An Engine Fault Detection Method Based on the Deep Echo State Network and Improved Multi-Verse Optimizer" Energies 15, no. 3: 1205. https://doi.org/10.3390/en15031205
APA StyleLi, X., Bi, F., Zhang, L., Yang, X., & Zhang, G. (2022). An Engine Fault Detection Method Based on the Deep Echo State Network and Improved Multi-Verse Optimizer. Energies, 15(3), 1205. https://doi.org/10.3390/en15031205







