Subsalt Rotliegend Sediments—A New Challenge for Geothermal Systems in Poland
Abstract
1. Introduction
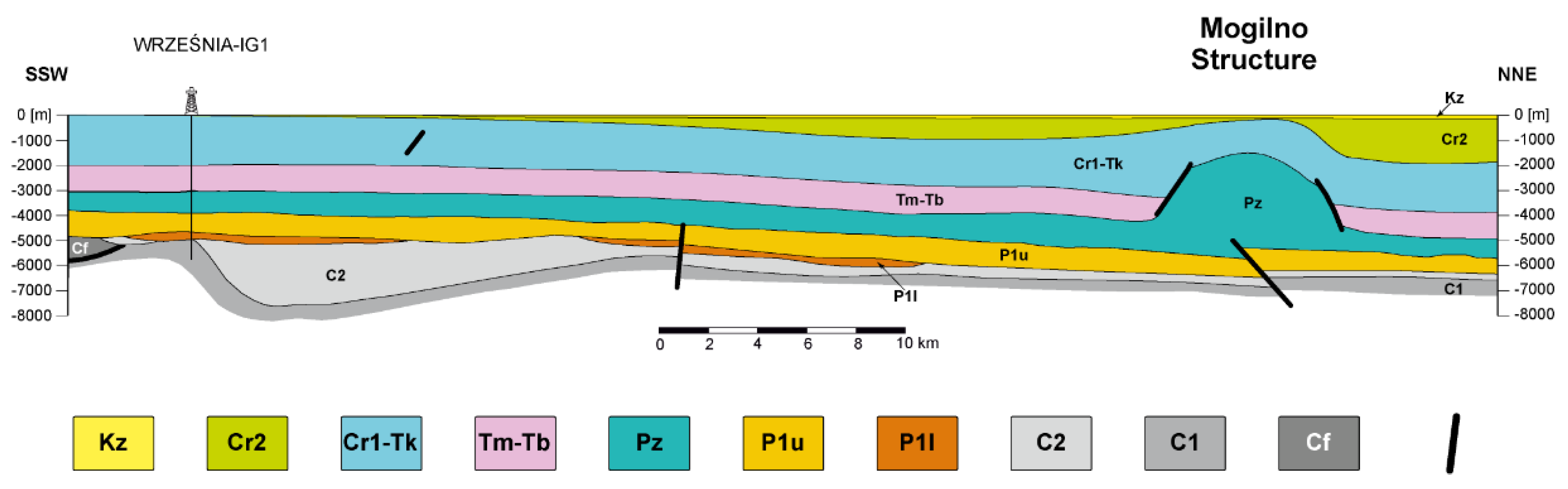
2. Geological Setting
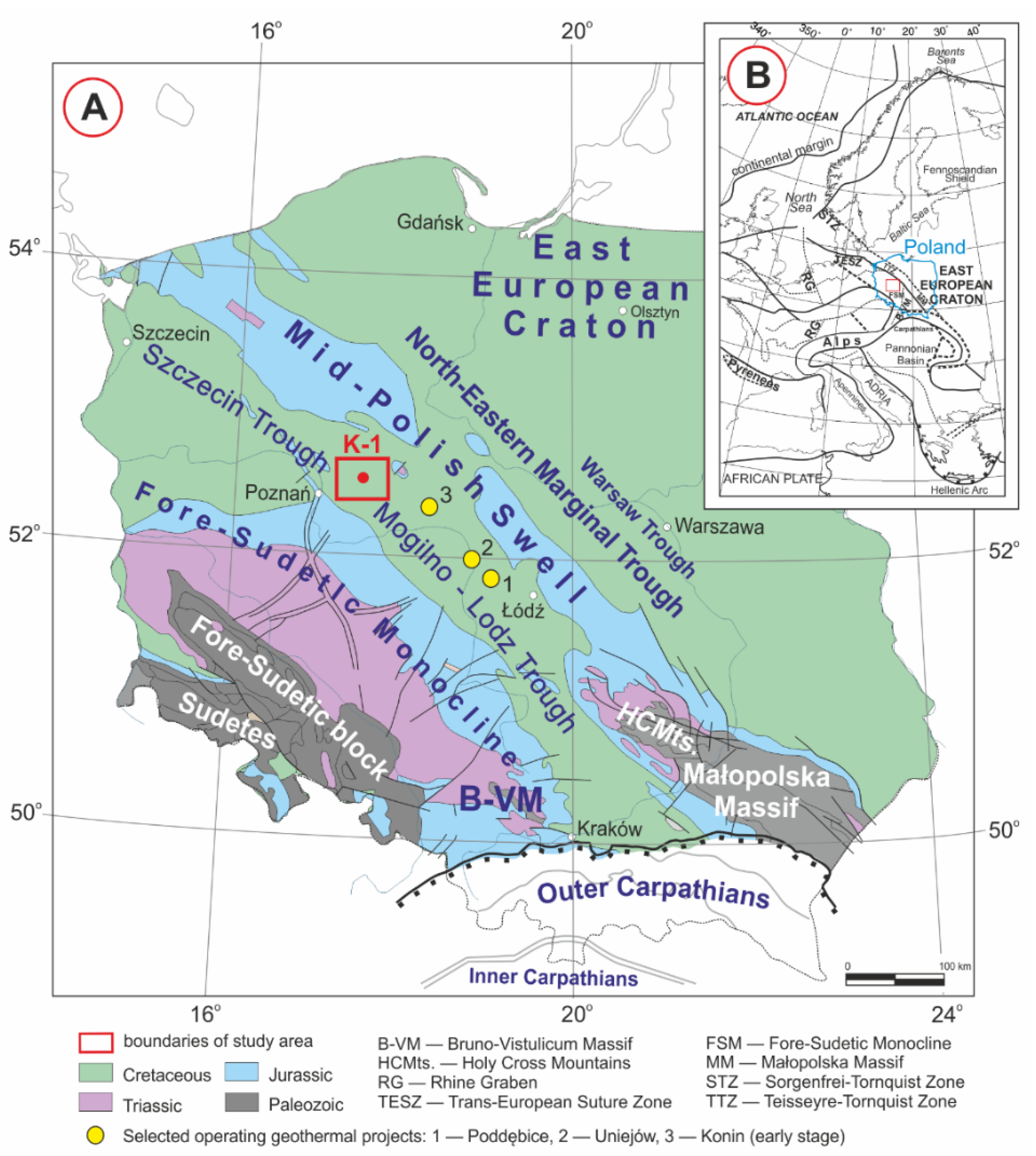
3. Geothermal Setting
- -
- Resistance to water saturation, especially resistivity to swelling, generally going along with the low clay content.
- -
- Susceptibility to massive fracturing.
- -
- Lack or very weak inflow of groundwater into EGS system.
- -
- Maximum allowable reservoir temperature drawdown during the operation—10%.
- -
- Low flow losses in the EGS system—below 10% of injection flow.
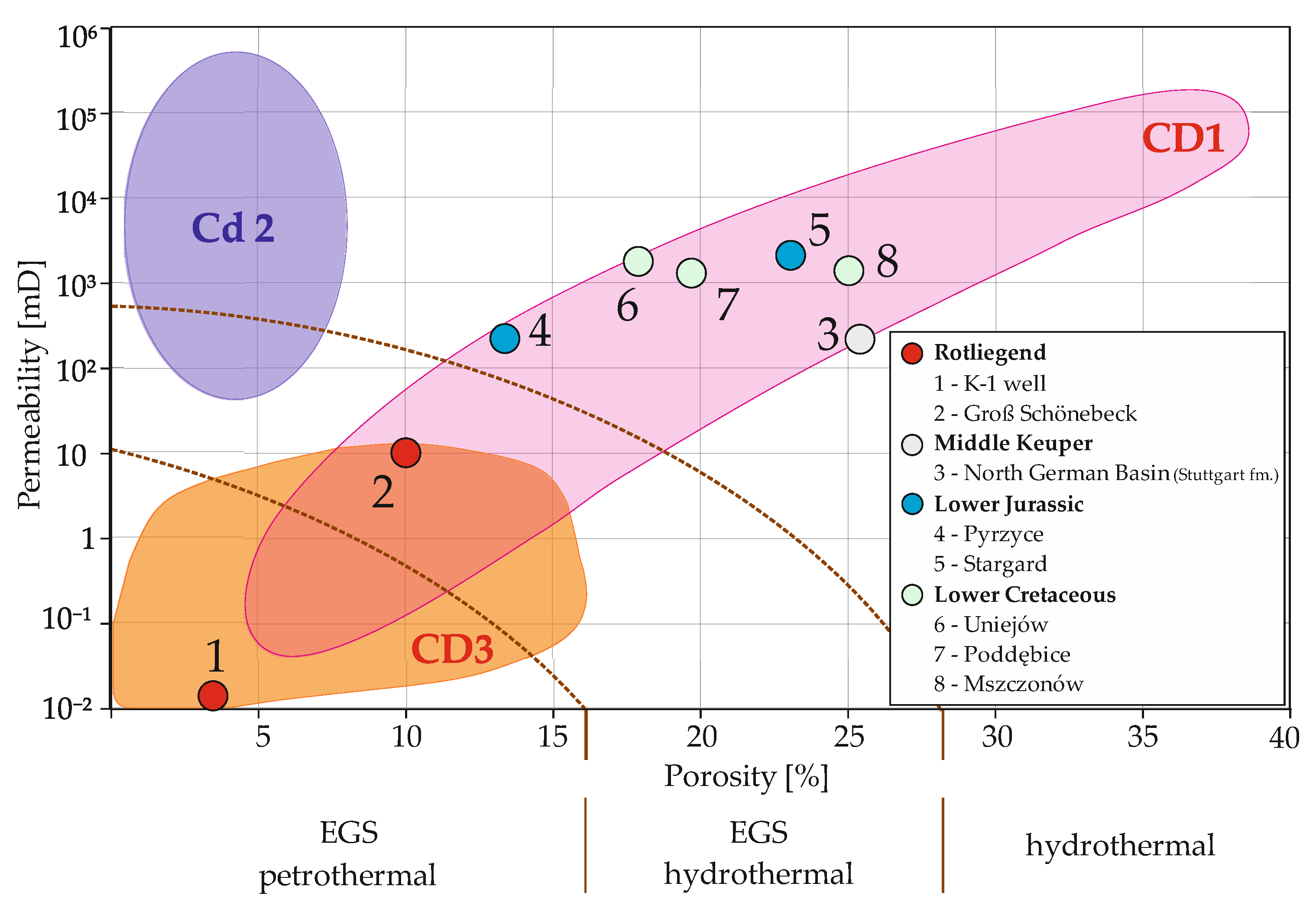
4. Materials and Methods
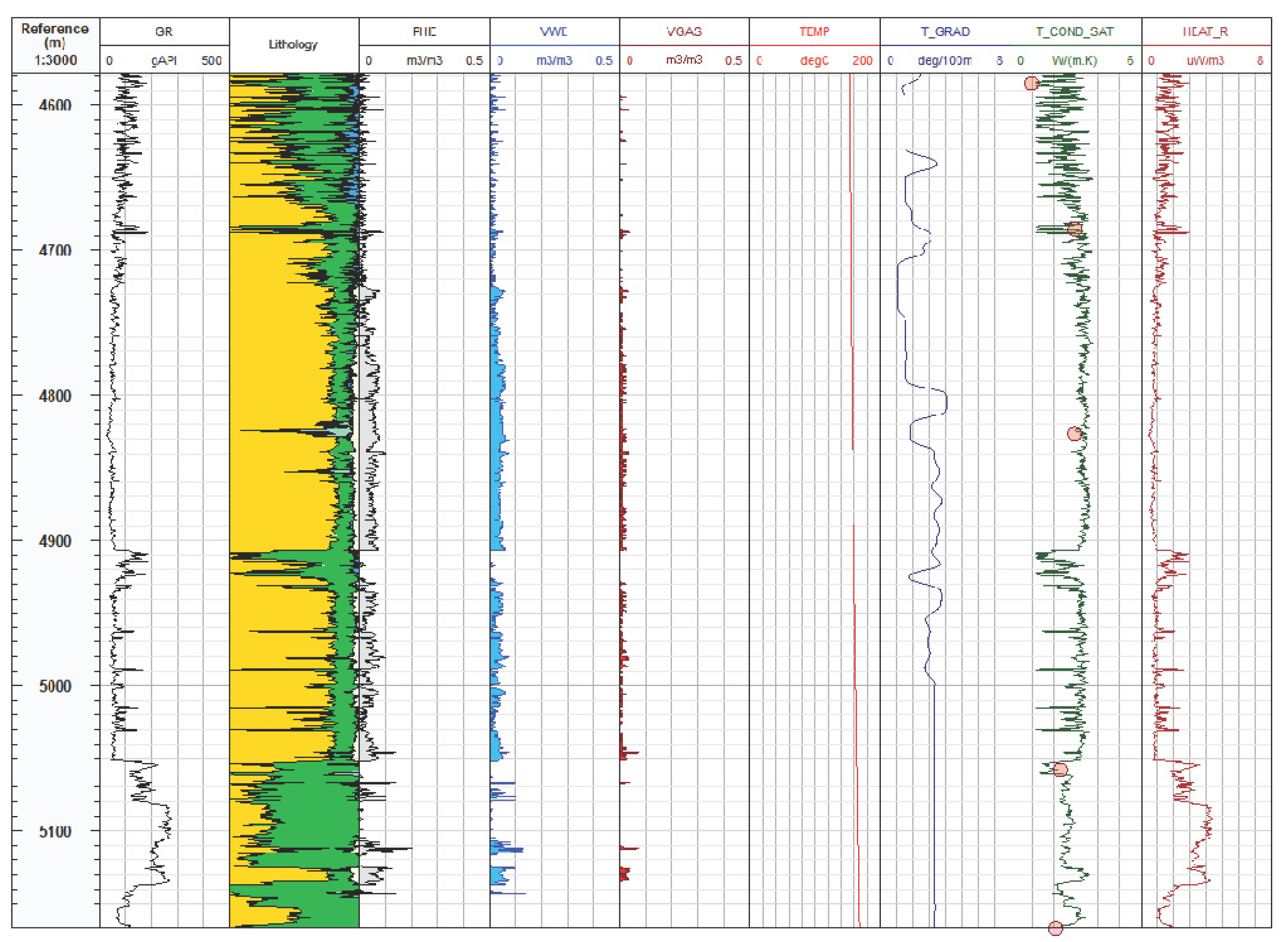
4.1. Sample Based Interpretations
4.2. Log-Based Interpretations
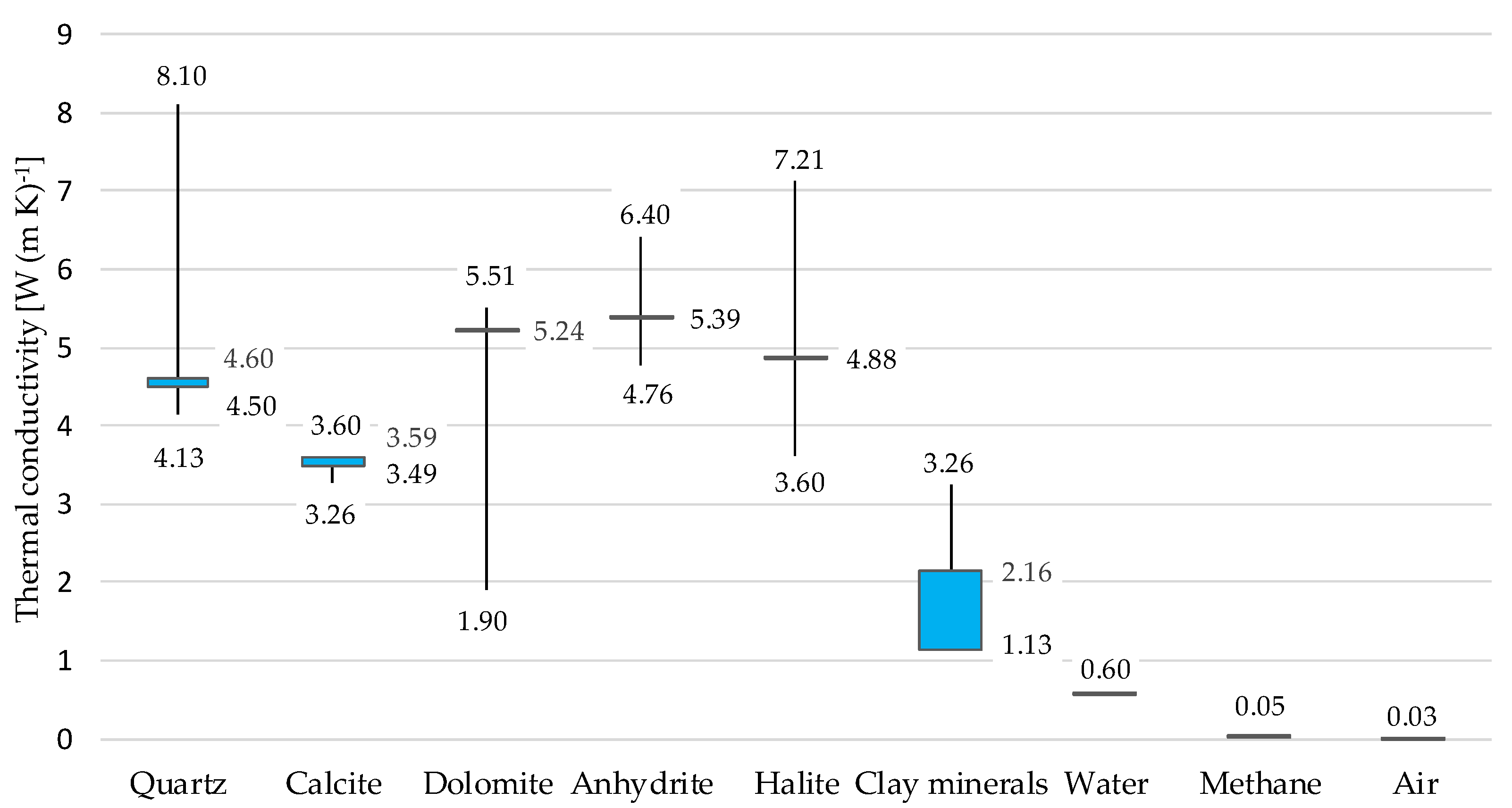
- Q—heat flow (W m−2);
- k—thermal conductivity (W (m K)−1);
- ∇T—thermal gradient (°C m−1).
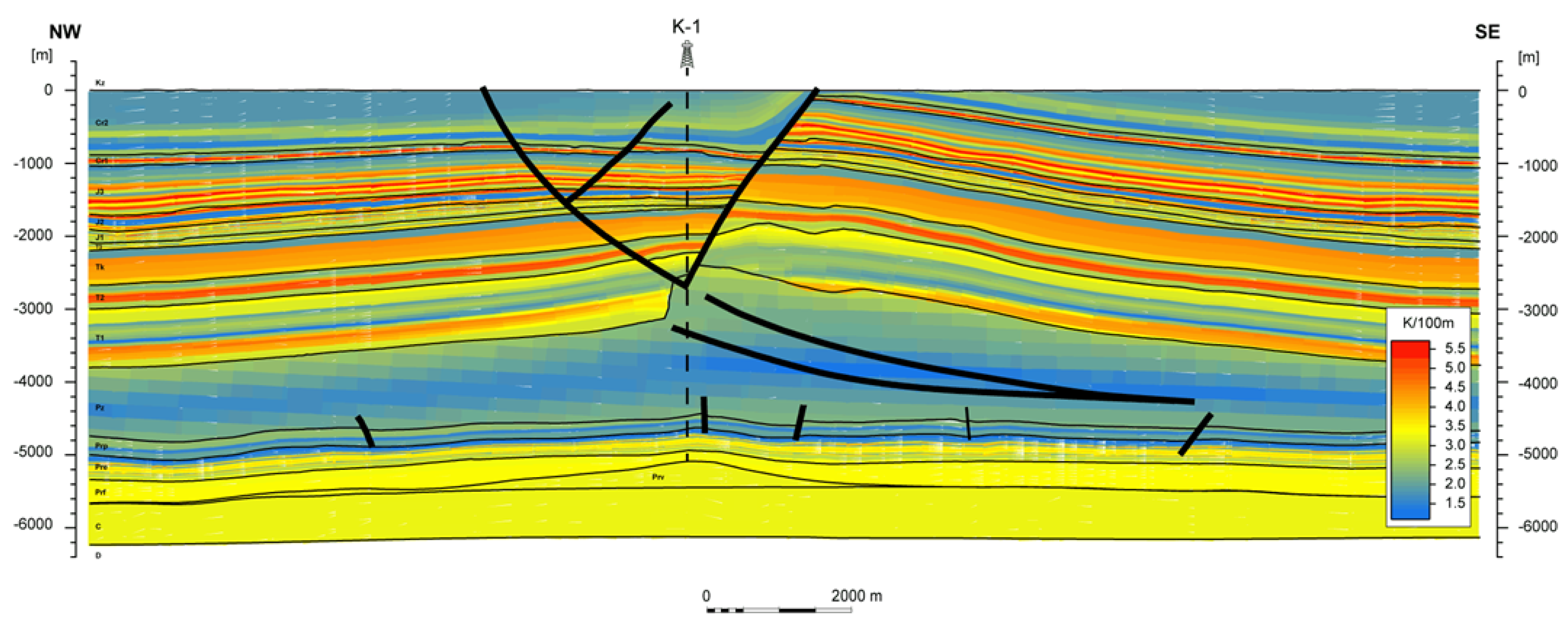
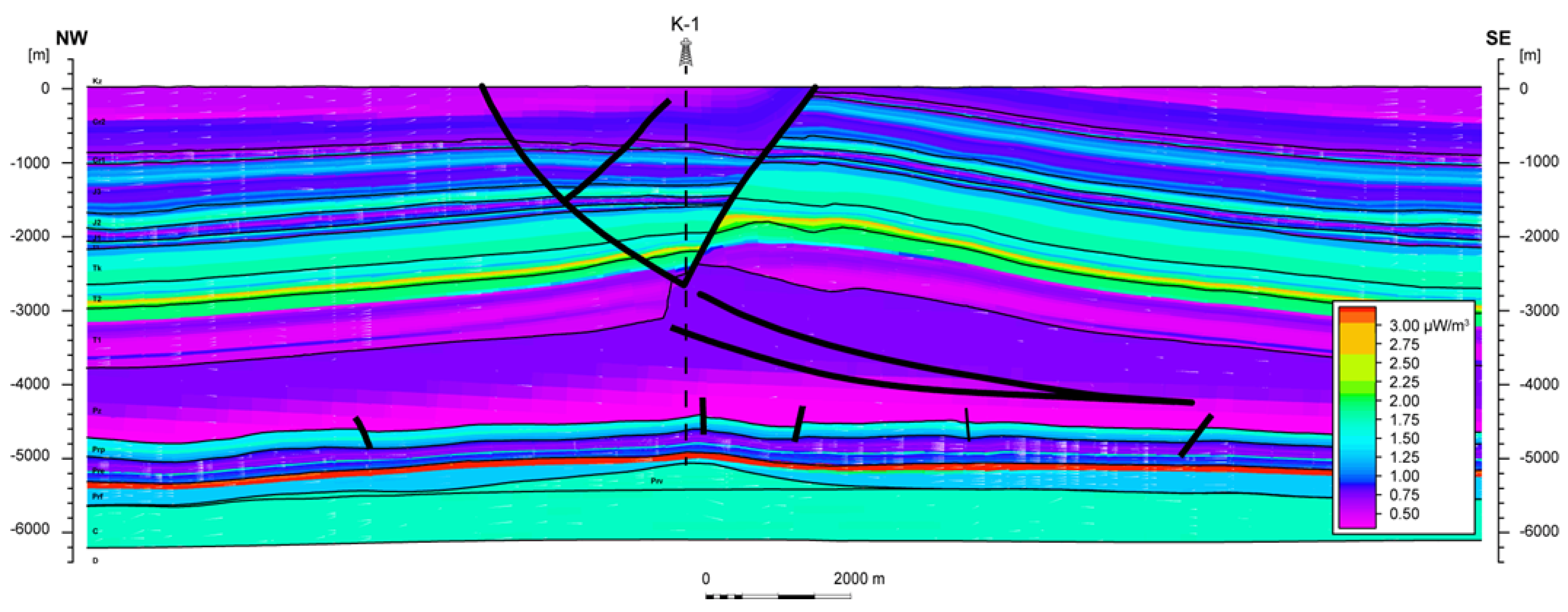
- A—radiogenic heat (µW m−3);
- GR—natural gamma ray (API).
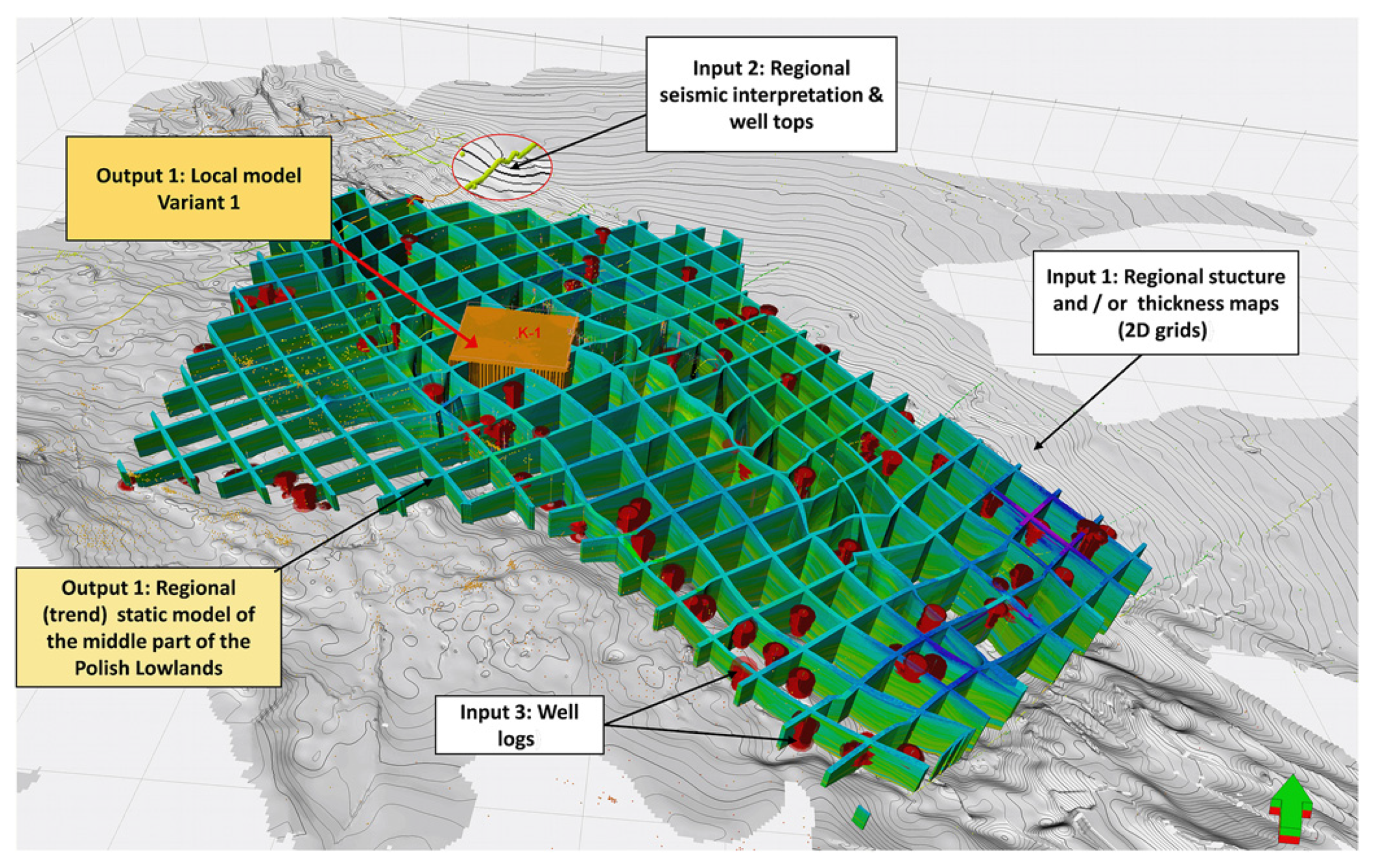
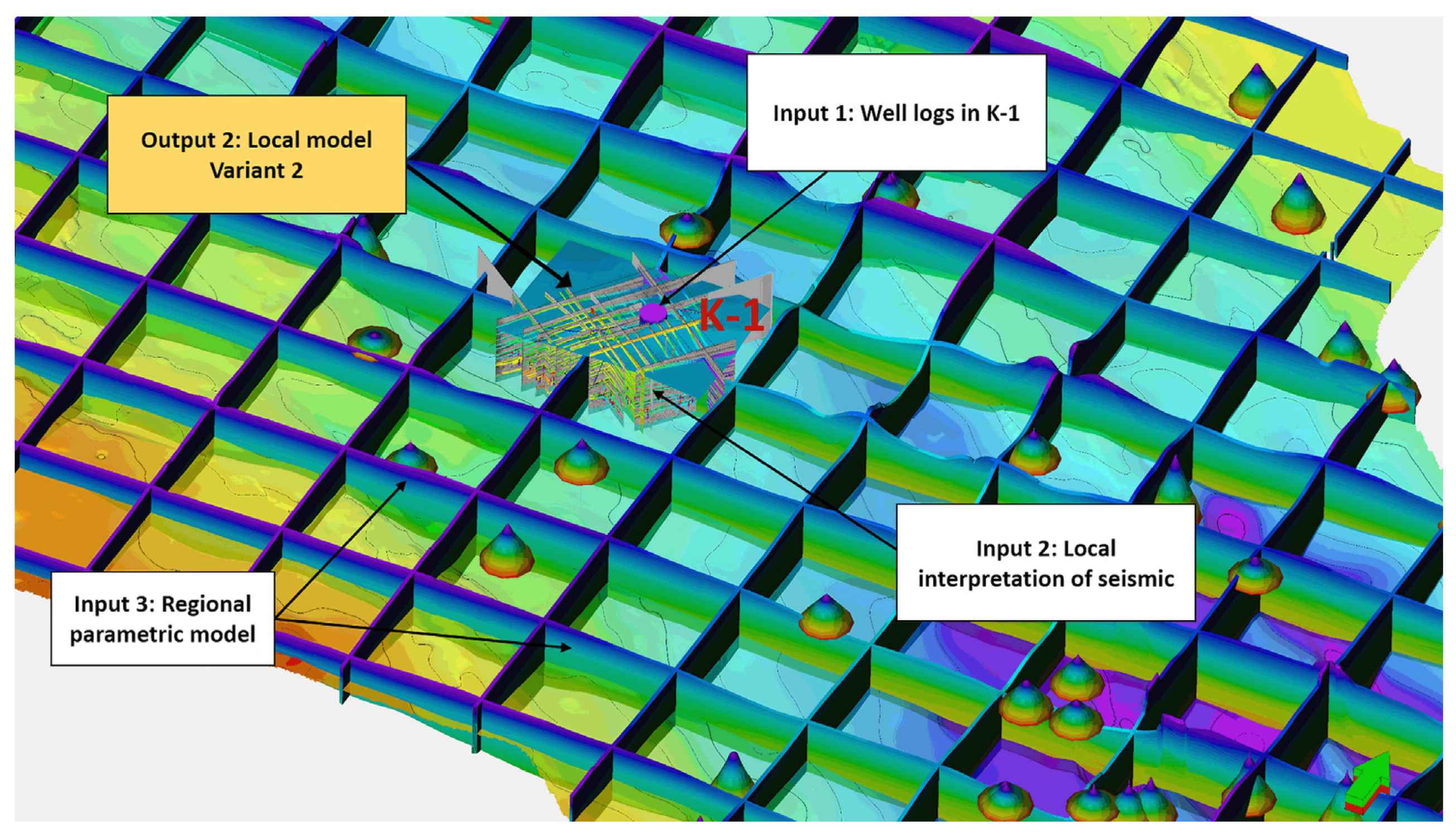
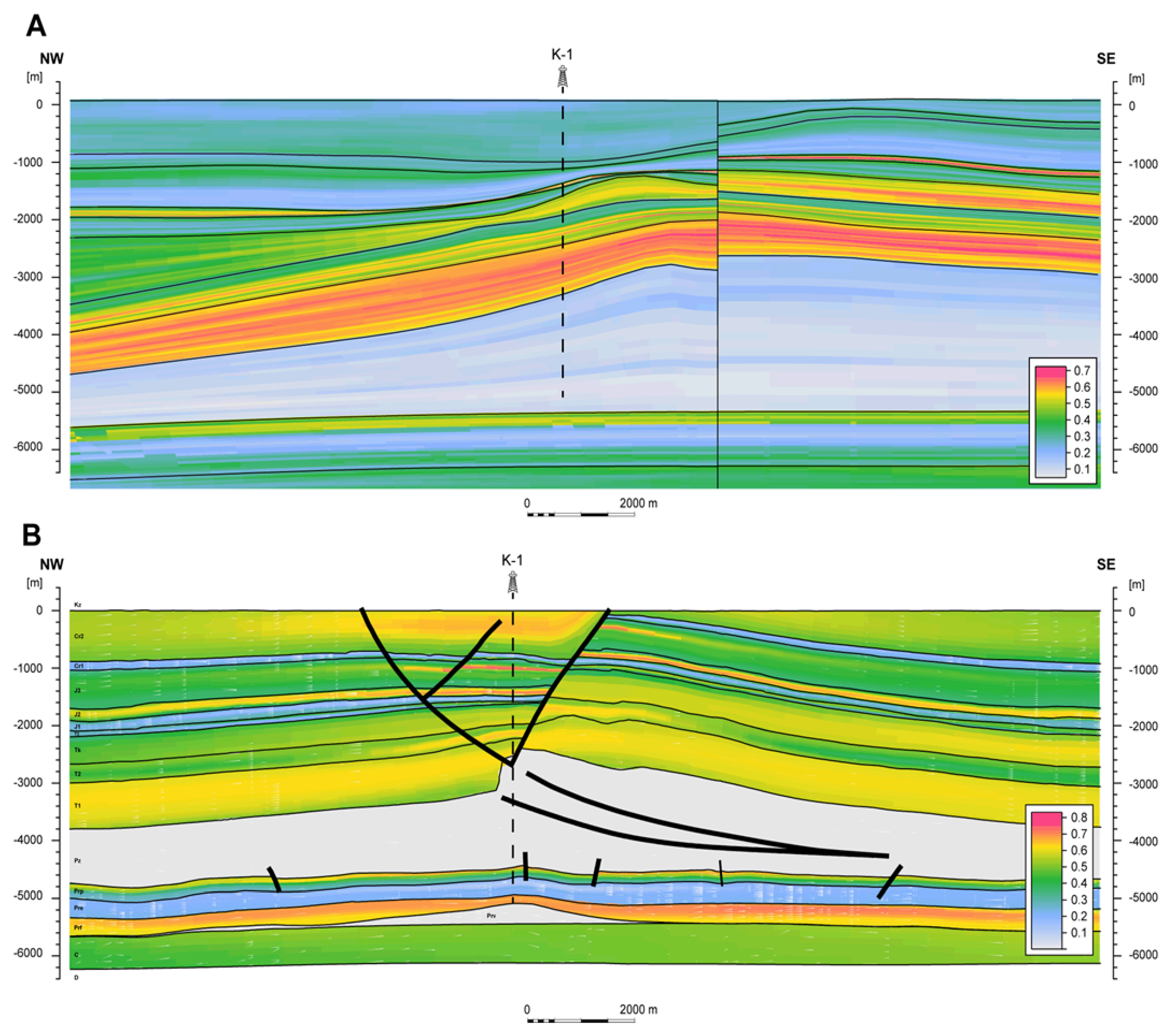
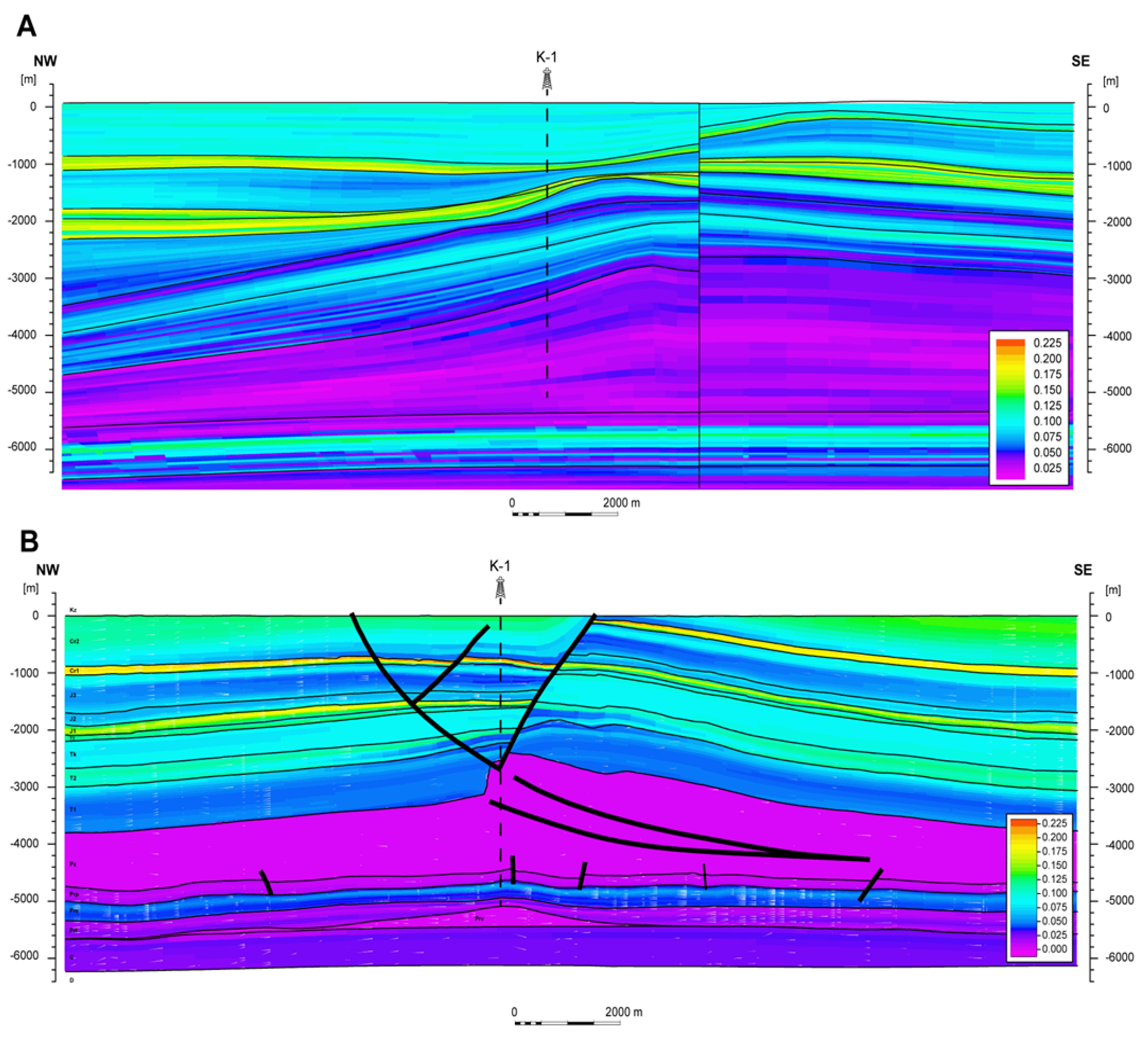
5. Spatial Interpretation
6. Methodology of the Preliminary EGS Potential Assessment
- -
- Massachusetts Institute of Technology (MIT) Interdisciplinary Panel [69];
- -
- Canadian Geothermal Code for Public Reporting, by the CGC Committee [139];
- -
- A Protocol for Estimating and Mapping Global EGS Potential [135];
- -
- New Geothermal Terms and Definitions—the Geothermal Energy Association [140];
- -
- Resource Assessment Protocol for GEO-ELEC [141];
- -
- United Nations Framework Classification for Fossil Energy and Mineral Reserves and Resources 2009 (UNFC-2009) [142].
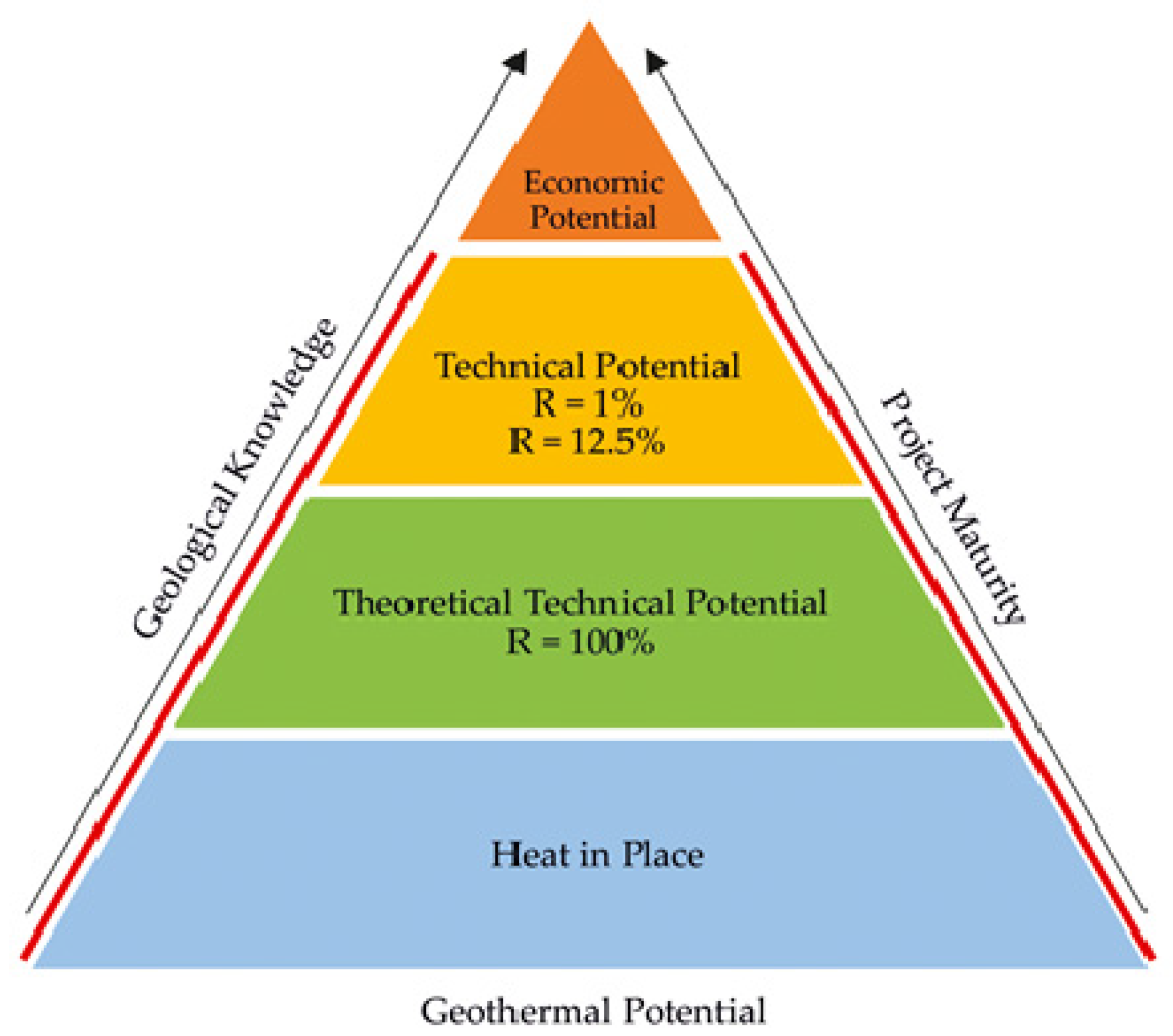
6.1. Theoretical Potential of EGS
- HIP—heat in place (PJ);
- V—reservoir volume (m3);
- ρrock—rock density (kg m−3);
- crock—specific heat of reservoir rock (J (kg·K)−1);
- Tprod—reservoir temperature at the midpoint (°C);
- T0—annual mean ambient air temperature (°C), T0 = 8 °C, according to the Institute of Meteorology and Water Management (IMGW) [143].
- TC—theoretical capacity (PJ);
- HIPe—effective heat in place (J);
- ηth—cycle thermal efficiency for power conversion (–).
- HIPe—effective heat in place (PJ);
- V—reservoir volume (m3);
- ρrock—rock density (kg m−3);
- crock—specific heat of reservoir rock (J (kg·K)−1);
- Tprod—reservoir temperature at the midpoint (°C);
- Tr—the cut-off production temperature for the electricity, equal to the temperature to which the crust can theoretically be reduced through the utilization of geothermal heat (assumed Tr = 88 °C);
- (10−15)—conversion factor from J to PJ.
- ηth—cycle thermal efficiency for power conversion (–);
- Tprod—reservoir temperature at the midpoint (°C).
6.2. Technical Potential of EGS
- TP—technical potential (MWe km−2);
- TC—theoretical capacity (PJ km−2);
- R—recovery factor (0–1);
- 1.057—conversion factor from PJ to MW, considering 30-year life span.
7. Results and Discussion
Preliminary Results of EGS Geothermal Potential Assessment
- -
- TPtheory—the maximum possible (theoretical) technical potential (R = 1.00);
- -
- TPreal—realistic underground technical potential according to typical predictive reservoir engineering approaches and empirical practice expressing mean value of recovery factor (R = 0.125);
- -
- TPlow—conservative approach on calculation of the technical potential, based on Beardsmore et al. [135] (R = 0.01).
- -
- The influence of radiogenic heat on the thermal regeneration of the rock mass was not considered (radiogenic heat is important for the formation of thermal conditions of the rock mass only in the geological time scale);
- -
- A homogeneous permeability of the fractured zone was assumed (the model was divided into fractures and a rock matrix, but the average value of permeability for the entire structure subjected to hydraulic fracturing was assumed, e.g., a single porosity model instead of dual porosity).
8. Summary and Conclusions
- -
- Regional scale 3D models can be used as a more precise tool for geothermal exploration than commonly applied solutions based on simple cartographic techniques;
- -
- Presented here, subsalt thermal anomaly has not been precisely mapped in the regional approach (SMV1), because the distribution of temperature, typical for the entire basin, does not precisely reflect vertical anomalies within the vicinity of salt structures;
- -
- Despite their imperfectness, regional models are indispensable for the creation of local scale models, because they allow external control of the parametric modeling process;
- -
- All data used in this research have been collected during oil and gas exploration operations. All techniques and routines of data processing and analysis as well as applied software were adopted from the petroleum industry. Thus, the petroleum industry can be an important source of data and analytical tools for investigation of the Earth’s thermal field and utilization of geothermal energy;
- -
- Salt structures are potential objectives for geothermal exploration. The positive thermal anomalies at the top and above salt structures are a result of high thermal conductivity of salt. They may be emphasized by contact with low-conductive rocks, e.g., claystones;
- -
- The changes of the thermal gradient are proportional to the salt thickness; the shape of the salt intrusion is also important;
- -
- In Poland over ~100 salt structures have been mapped, a number of them may meet the criteria of being interesting objectives for geothermal exploration mentioned in Table 2;
- -
- Further research of the Paleozoic formations is necessary for better understanding of high temperature resources and to indicate new opportunities for geothermal development in regions outside the areas of proven geothermal potential hosted in Mesozoic formations of the Polish Lowlands;
- -
- Regional- to local-scale 3D models are very valuable for planning a deep geothermal installation. Because of the heterogeneity of the subsurface, basin geometry (especially around salt structures) and thermal properties, temperatures may deviate from the average geothermal gradient trend;
- -
- The proposed methodology appears to be justified when a new well data set is used to verify 3D geological models in the salt structure zones. In particular, the discussed methods and models can be used to refine existing geothermal potential maps or to calibrate 3D parametric models used to assess both conventional and unconventional (EGS) geothermal potential;
- -
- The general applicability of the proposed methodology makes it of interest for a broad range of applications in geothermal utilization as well as for CCS issues.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Górecki, W.; Hajto, M.; Papiernik, B.; Szczepański, A.; Kuźniak, T.; Kozdra, T.; Soboń, J.; Szewczyk, J.; Strzetelski, W.; Haładus, A.; et al. (Eds.) Atlas of Geothermal Resources of Mesozoic Formations in the Polish Lowlands; AGH University of Science and Technology in Krakow: Krakow, Poland; Ministry of Environment: Warsaw, Poland; NFEP&WM: Warsaw, Poland, 2006; p. 484. ISBN 978-83-88927-13-3. Available online: https://kse.agh.edu.pl/uploaded/AGH-Atlas_Geotermalny_Mezozoiku-2006.pdf (accessed on 14 August 2021).
- Górecki, W.; Hajto, M.; Papiernik, B.; Szczepański, A.; Kuźniak, T.; Kozdra, T.; Soboń, J.; Szewczyk, J.; Strzetelski, W.; Haładus, A.; et al. (Eds.) Atlas of Geothermal Resources of Paleozoic Formations in the Polish Lowlands; AGH University of Science and Technology in Krakow: Krakow, Poland; Ministry of Environment: Warsaw, Poland; NFEP&WM: Warsaw, Poland, 2006; p. 240. ISBN 978-83-88927-14-0. Available online: https://kse.agh.edu.pl/uploaded/AGH-Atlas_Geotermalny_Paleozoiku-2006.pdf (accessed on 14 August 2021).
- Zakrevsky, K.E. Geological 3D Modelling; EAGE Publications: Houten, The Netherlands, 2011; pp. 1–261. [Google Scholar]
- Papiernik, B.; Michna, M. Methodology and results of digital mapping and 3D modelling of the Lower Palaeozoic strata on the East European Craton, Poland. Ann. Soc. Geol. Pol. 2019, 89, 405–427. [Google Scholar] [CrossRef]
- Wójcicki, A.; Sowiżdżał, A.; Bujakowski, W. (Eds.) Evaluation of Potential, Thermal Balance and Prospective Geological Structures for Needs of Unconventional Geothermal Systems (Hot Dry Rocks) in Poland; Ministry of the Environment: Warsaw, Poland, 2013; pp. 1–246. (In Polish)
- Karnkowski, P.H. Tectonic subdivision of Poland: Polish Lowlands. Prz. Geol. 2008, 56, 895–903. (In Polish) [Google Scholar]
- Żelaźniewicz, A.; Aleksandrowski, P.; Buła, Z.; Karnkowski, P.H.; Konon, A.; Oszczypko, N.; Ślączka, A.; Żaba, J.; Żytko, K. Regionalizacja Tektoniczna Polski; Komitet Nauk Geologicznych PAN: Warsaw, Poland, 2011. (In Polish) [Google Scholar]
- Pożaryski, W. The Middle European Caledonides—Wrenching orogen composed of terranes. Prz. Geol. 1990, 38, 1–9. (In Polish) [Google Scholar]
- Guterch, A.; Wybraniec, S.; Grad, M.; Chadwick, R.A.; Krawczyk, C.M.; Ziegler, P.A.; Thybo, H.; de Vos, W. Crustal structure and structural framework. In Petroleum Geological Atlas of the Southern Permian Basin Area; Doornenbal, J.C., Stevenson, A.G., Eds.; EAGE Publications: Houten, The Netherlands, 2010; pp. 11–23. [Google Scholar]
- Ziegler, P.A. Geological Atlas of Western and Central Europe, 2nd ed.; Shell Internationale Petroleum Maatschappij: London, UK; Geological Society Publishing House: Bath, UK, 1990; pp. 1–239. [Google Scholar]
- Pharaoh, T.C.; Dusar, M.; Geluk, M.C.; Kockel, F.; Krawczyk, C.M.; Krzywiec, P.; Scheck-Wenderoth, M.; Thybo, H.; Vejbak, O.V.; Van Wees, J.D. Tectonic Evolution. In Petroleum Geological Atlas of the Southern Permian Basin Area; Doornenbal, J.C., Stevenson, A.G., Eds.; EAGE Publications: Houten, The Netherlands, 2010; pp. 25–57. [Google Scholar]
- Krzywiec, P. Triassic-Jurassic evolution of the Pomeranian segment of the Mid-Polish Trough-basement tectonics and sedimentary patterns. Geol. Q. 2006, 50, 139–150. [Google Scholar]
- Krzywiec, P. Structural inversion of the Pomeranian and Kuiavian segments of the Mid-Polish Polish Trough-lateral variations in timing and structural style. Geol. Q. 2006, 50, 151–168. [Google Scholar]
- Jarosiński, M.; Poprawa, P.; Ziegler, P.A. Dynamic evolution of the Polish Platform. Geol. Q. 2009, 53, 3–26. [Google Scholar]
- Mazur, S.; Malinowski, M.; Maystrenko, Y.; Gągała, Ł. Pre-existing lithospheric weak zone and its impact on continental rifting—The Mid-Polish Trough, Central European Basin System. Glob. Planet. Chang. 2021, 198, 103417. [Google Scholar] [CrossRef]
- Mikołajczak, M.; Mazur, S.; Gągała, Ł. Depth-to-basement for the East European Craton and Teisseyre-Tornquist Zone in Poland based on potential field data. Int. J. Earth 2019, 108, 547–567. [Google Scholar] [CrossRef]
- Kiersnowski, H.; Paul, J.; Peryt, T.M.; Smith, D.B. Facies, Paleogeography and Sedimentary History of the Southern Permian Basin in Europe. In The Permian of Northern Pangea; Scholle, P.A., Peryt, T.M., Ulmer-Scholle, D.S., Eds.; Springer: Berlin, Germany, 1995; pp. 119–136. [Google Scholar]
- Stephenson, R.A.; Narkiewicz, M.; Dadlez, R.; van Wees, J.D.; Andriessen, P.A.M. Tectonic subsidence modelling of the Polish Basin in the light of new data on crustal structure and magnitude of inversion. Sediment. Geol. 2003, 159, 59–70. [Google Scholar] [CrossRef]
- Dadlez, R.; Narkiewicz, M.; Stephenson, R.A.; Visser, M.T.M.; van Wees, J.D. Tectonic evolution of the Mid-Polish Trough: Modelling implications and significance for central European geology. Tectonophysics 1995, 252, 179–195. [Google Scholar] [CrossRef]
- Leszczyński, K. Lithofacies evolution of the late Cretaceous basin in the Polish Lowlands. Biul. Państwowego Inst. Geol. 2010, 443, 33–54. (In Polish) [Google Scholar]
- Narkiewicz, M.; Dadlez, R. Geological regional subdivision of Poland: General guidelines and proposed schemes of sub-Cenozoic and sub-Permian units. Prz. Geol. 2008, 56, 391. (In Polish) [Google Scholar]
- Krzywiec, P. Triassic evolution of the Kłodawa salt structure: Basement-controlled salt tectonics within the Mid-Polish trough (central Poland). Geol. Q. 2004, 48, 123–134. [Google Scholar]
- Krzywiec, P. Mesozoic and Cenozoic Evolution of Salt Structures within the Polish Basin—An overview. In Salt Tectonics, Sediments and Prospectivity; Special Publications; Alsop, G.I., Archer, S.G., Hartley, A.J., Grant, N.T., Hodgkinson, R., Eds.; Geological Society: London, UK, 2012; Volume 363, pp. 381–394. [Google Scholar]
- Pożaryski, W. The Early Alpine Laramide Epoch in the Platform Development East of the Fore Sudetic and Silesian-Cracovian Monoclines: Geology of Poland; Wydawnictwa Geologiczne: Warszawa, Poland, 1977; pp. 351–416.
- Marek, S.; Pajchlowa, M. (Eds.) Permian and Mesozoic in Poland; Prace Państwowego Instytutu Geologicznego: Warsaw, Poland, 1997; Volume 153, pp. 1–452.
- Dadlez, R.; Marek, S.; Pokorski, J. Atlas Paleogeograficzny Epikontynentalnego Permu i Mezozoiku w Polsce, 1:2,500,000; Państwowy Instytut Geologiczny: Warsaw, Poland, 1998; pp. 1–7. (In Polish)
- Peryt, T.M.; Geluk, M.C.; Mathiesen, A.; Paul, J.; Smith, K. Zechstein. Peri-Tethyan Rift/Wrench Basins and Passive Margins. In Petroleum Geological Atlas of the Southern Permian Basin Area; Doornenbal, J.C., Stevenson, A.G., Eds.; EAGE Publications: Houten, The Netherlands, 2010; pp. 123–147. [Google Scholar]
- Doornenbal, J.C.; Abbink, O.A.; Duin, E.J.T.; Dusar, M.; Hoth, P.; Jasionowski, M.; Lott, G.K.; Mathiesen, A.; Papiernik, B.; Peryt, T.M.; et al. Introduction, Stratigraphic Framework and Mapping. In Petroleum Geological Atlas of the Southern Permian Basin Area; Doornenbal, J.C., Stevenson, A.G., Eds.; EAGE Publications: Houten, The Netherlands, 2010; pp. 1–9. [Google Scholar]
- Pokorski, J. Formal lithostratigraphic subdivision proposed for the Rotliegendes of the Polish Lowlands. Kwart. Geol. 1981, 25, 41–58, (In Polish with English summary). [Google Scholar]
- Pokorski, J. Rotliegendes lithostratigraphy in north-western Poland. Bull. Pol. Acad. Sc. 2008, 36, 99–108. [Google Scholar]
- Karnkowski, P.H. Rotliegend lithostratigraphy in the central part of the Polish Permian Basin. Geol. Q. 1994, 38, 27–42. [Google Scholar]
- Karnkowski, P.H. Origin and evolution of the Polish Rotliegend Basin. PGI Spec. Pap. 1999, 3, 1–93. [Google Scholar]
- Kiersnowski, H. Depositional development of the Polish Upper Rotliegend Basin and evolution of its sediment source areas. Geol. Q. 1997, 4, 433–456. [Google Scholar]
- Kiersnowski, H. Depositional Architecture of the Rotliegend Basin in Poland, in Sedimentary Basins. Analysis of the Polish Lowlands; Narkiewicz, M., Ed.; Prace Państwowego Instytutu Geologicznego: Warsaw, Poland, 1998; Volume 165, pp. 113–128.
- Kiersnowski, H.; Buniak, A. Evolution of the Rotliegend Basin of northwestern Poland. Geol. Q. 2006, 50, 119–137. [Google Scholar]
- Gast, R.E.; Dusar, M.; Breitkreuz, C.; Gaupp, R.; Schneider, J.W.; Stemmerik, L.; Geluk, M.C.; Geisler, M.; Kiersnowski, H.; Glennie, K.W.; et al. Petroleum Geological Atlas of the Southern Permian Basin Area; Doornenbal, J.C., Stevenson, A.G., Eds.; EAGE Publications: Houten, The Netherlands, 2010; pp. 101–122. [Google Scholar]
- Papiernik, B.; Górecki, W.; Pasternacki, A. Preliminary results of 3D modeling of petrophysical parameters for tight gas prospecting in the Polish Rotliegend Basin. Prz. Geol. 2010, 58, 352–364. (In Polish) [Google Scholar]
- Kiersnowski, H.; Buniak, A. Sand sheets interaction with aeolian dune, alluvial and marginal playa beds in Late Permian Upper Rotliegend setting (western part of the Poznań Basin, Poland). Geol. Q. 2016, 60, 771–800. [Google Scholar] [CrossRef][Green Version]
- Wagner, R.; Leszczyński, K.; Pokorski, J.; Gumulak, K. Palaeotectonic cross-sections through the Mid-Polish Trough. Geol. Q. 2002, 46, 293–306. [Google Scholar]
- Czapowski, G. Geologia permskich struktur i złóż solnych w Polsce—Aktualny stan wiedzy i perspektywy zagospodarowania. Prz. Geol. 2006, 54, 301–302. (In Polish) [Google Scholar]
- Wagner, R. Stratigraphy and Development of the Zechstein Basin in the Polish Lowlands; Prace Państwowego Instytutu Geologicznego: Warsaw, Poland, 1994; Volume 146, pp. 1–71.
- Dadlez, R.; Marek, S.; Pokorski, J. Geological Map of Poland without Cainozoic Deposits; Polish Geological Institute: Warsaw, Poland, 2000.
- Berthelsen, A. Mobile Europe. In A Continent Revealed—The European Geotravers; Blundell, D., Freeman, R., Mueller, S., Eds.; Cambridge University Press: Cambridge, UK, 1992; pp. 11–32. [Google Scholar]
- Bachmann, G.H.; Kozur, H. The Germanic Triassic: Correlations with the international chronostratigraphic scale, numerical ages and Milankovitch cyclicity. Hallesches Jahrb. Geowiss. 2004, B26, 17–62. [Google Scholar]
- Pieńkowski, G. Facies criteria for delimitating the Zechstein/Buntsandstein and the Permian/Triassic boundary in Poland. Zent. Für Geol. Paläontol. 1991, 4, 893–912. [Google Scholar]
- Szyperko-Teller, A.; Moryc, W. Evolution of the Buntsandstein sedimentary basin in Poland. Kwart. Geol. 1988, 32, 53–72. (In Polish) [Google Scholar]
- Bachmann, G.H.; Geluk, M.C.; Warrington, G.; Becker-Roma, A.; Beutler, G.; Hagdorn, H.; Hounslow, M.W.; Nitsch, E.; Röhling, H.-G.; Simon, T.; et al. Petroleum Geological Atlas of the Southern Permian Basin Area; Doornenbal, J.C., Stevenson, A.G., Eds.; EAGE Publications: Houten, The Netherlands, 2010; pp. 149–173. [Google Scholar]
- Marek, S.; Pajchlowa, M. Epikontynentalny Perm i Mezozoik w Polsce; Prace PIG: Warsaw, Poland, 1997; p. 153. (In Polish)
- Pieńkowski, G. The epicontinental Lower Jurassic of Poland; Polish Geological Institute Special Papers; Polish Geological Institute: Warsaw, Poland, 2004; Volume 12, pp. 1–154. [Google Scholar]
- Dadlez, R. Epikontynentalne Baseny Sedymentacyjne w Polsce, od Dewonu po Kredę—Zależności Rozwoju od Budowy Skorupy Krystalicznej; Prace Państwowego Instytutu Geologicznego: Warsaw, Poland, 1998; Volume 165, pp. 17–30. (In Polish)
- Feldman-Olszewska, A. Jura Dolna. Miąższość. In Atlas Paleogeograficzny Epikontynentalnego Permu i Mezozoiku w Polsce, 1:2,500,000; Dadlez, R., Marek, S., Pokorski, J., Eds.; Wydaw. Kartograficzne Polskiej Agencji Ekologicznej: Warsaw, Poland, 1998; p. 36. [Google Scholar]
- Dayczak-Calikowska, K.; Moryc, W. Evolution of sedimentary basin and paleotectonics of the Middle Jurassic in Poland. Geol. Q. 1988, 31, 117–136. [Google Scholar]
- Niemczycka, T.; Brochwicz-Lewiński, W. Evolution of the Upper Jurassic sedimentary basin in the Polish Lowland. Kwart. Geol. 1988, 32, 137–155. (In Polish) [Google Scholar]
- Dembowska, J. Systematization of lithostratigraphy of the Upper Jurassic in northern and central Poland. Kwart. Geol. 1979, 23, 617–630. (In Polish) [Google Scholar]
- Lott, G.K.; Wong, T.E.; Dusar, M.; Andsbjerg, J.; Mönnig, E.; Feldman-Olszewska, A.; Verreussel, R.M.C.H. Jurassic. In Petroleum Geological Atlas of the Southern Permian Basin Area; Doornenbal, J.C., Stevenson, A.G., Eds.; EAGE Publications: Houten, The Netherlands, 2010; pp. 175–193. [Google Scholar]
- Leszczyński, K. The Lower Cretaceous depositional architecture and sedimentary cyclicity in the Mid-Polish Trough. Geol. Q. 1997, 41, 509–520. [Google Scholar]
- Leszczyński, K. The Upper Cretaceous carbonate-dominated sequence of the Polish Lowlands. Geol. Q. 1997, 41, 521–532. [Google Scholar]
- Sokołowski, J. Warunki występowania wód geotermalnych w Polsce i program ich wykorzystania na Podhalu. Tech. Poszuk. Geol. Geosynoptyka I Geoterm. 1988, 1–2, 31–46. (In Polish) [Google Scholar]
- Adamczyk, A.F.; Szczepański, A.; Szklarczyk, T. Atlas Wód Geotermalnych Niżu Polskiego; Objaśnienia tekstowe; Górecki, W., Ed.; Wyd. AGH: Krakow, Poland; ISE AGH: Krakow, Poland; Okręgowe Przedsiębiorstwo Geodezyjno-Kartograficzne: Krakow, Poland, 1990; p. 368. (In Polish) [Google Scholar]
- Górecki, W.; Kuźniak, T.; Łapinkiewicz, A.; Maćkowski, T.; Strzetelski, W.; Szklarczyk, T.; Reicher, B. (Eds.) Atlas Zasobów Energii Geotermalnej na Niżu Polskim; ZSE AGH: Krakow, Poland; Towarzystwo Geosynoptyków GEOS: Krakow, Poland, 1995; p. 37. (In Polish) [Google Scholar]
- Hajto, M.; Górecki, W. Energy potential of thermal waters in the Polish Lowland. Biul. Państwowego Inst. Geol. 2010, 439, 81–86. Available online: https://geojournals.pgi.gov.pl/bp/article/view/28856/20528 (accessed on 22 January 2021). (In Polish).
- Hajto, M.; Górecki, W. The most prospective areas of use of thermal waters for heating purposes in the Polish Lowlands. Biul. Państwowego Inst. Geol. 2010, 441, 27–31. Available online: https://geojournals.pgi.gov.pl/bp/article/view/28871/20544 (accessed on 22 January 2021).
- Sowiżdżał, A.; Papiernik, B.; Machowski, G.; Hajto, M. Characterization of petrophysical parameters of the Lower Triassic deposits in prospective location for Enhanced Geothermal System (central Poland). Geol. Q. 2013, 57, 729–744. [Google Scholar] [CrossRef][Green Version]
- Kępińska, B.; Barbacki, A.P.; Bielec, B.; Bujakowski, W.; Dendys, M.; Hołojuch, G.; Galos, K.; Kasztelewicz, A.; Kęsek, W.; Lankof, L.; et al. (Eds.) Geothermal Energy—A Basis for Low-Emission Space Heating Improving Living Conditions and Sustainable Development—Preliminary Studies for Selected Areas in Poland Study Visits. Report. 2017. Available online: http://www.eeagrants.agh.edu.pl/wp-content/uploads/2017/12/EEA-SVReport_GeoHeatPol-2017.pdf (accessed on 14 February 2021).
- Hałaj, E.; Kępińska, B. Conjunctive uses of the geothermal water resources from Lower Cretaceous formations in the Mogilno–Łódź Trough, Poland. Sustain. Water Resour. Manag. 2019, 5, 1479–1494. [Google Scholar] [CrossRef]
- Sowiżdżał, A.; Hajto, M.; Hałaj, E. Thermal waters of central Poland: A case study from Mogilno–Łódź Trough, Poland. Environ. Earth Sci. 2020, 79, 1–11. [Google Scholar] [CrossRef]
- Papiernik, B.; Doligez, B.; Klimkowski, Ł. Structural and parametric models of the Załęcze and Żuchlów gas field region, Fore-Sudetic Monocline, Poland—An example of a general static modeling workflow in mature petroleum areas for CCS, EGR or EOR purposes. Oil Gas Sci. Technol. Rev. D’ifp Energ. Nouv. 2015, 70, 635–654. [Google Scholar] [CrossRef]
- Moeck, I.S.; Beardsmore, G.A. New ‘Geothermal Play Type’ Catalog: Streamlining Exploration Decision Making. In Proceedings of the 39th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 24 February 2014; pp. 1–8. [Google Scholar]
- Tester, J.W.; Anderson, B.J.; Batchelor, A.S.; Blackwell, D.D.; Dipippo, R.; Drake, E.M.; Garnish, J.; Livesay, B.; Moore, M.C.; Nichols, K.; et al. The Future of Geothermal Energy Impact of Enhanced Geothermal Systems (EGS) on the United States in the 21st Century. An Assessment by an MIT-Led Interdisciplinary Panel. 2006. Available online: https://energy.mit.edu/wp-content/uploads/2006/11/MITEI-The-Future-of-Geothermal-Energy.pdf (accessed on 22 January 2021).
- Moeck, I.S. Catalog of geothermal play types based on geologic controls. Renew. Sustain. Energy Rev. 2014, 37, 867–882. [Google Scholar] [CrossRef]
- Szewczyk, J.; Hajto, M. Heat Flow Versus Subsurface Temperatures in the Polish Lowlands. In Atlas of Geothermal Resources of Mesozoic Formations in the Polish Lowlands; Górecki, W., Hajto, M., Papiernik, B., Szczepański, A., Kuźniak, T., Kozdra, T., Soboń, J., Szewczyk, J., Strzetelski, W., Haładus, A., et al., Eds.; Ministry of Environment: Krakow, Poland; AGH University of Science and Technology: Krakow, Poland, 2006; pp. 143–151. [Google Scholar]
- Szewczyk, J.; Gientka, D. Terrestrial heat flow density in Poland—A new approach. Geol. Q. 2009, 53, 125–140. [Google Scholar]
- Nawrocki, J.; Becker, A. (Eds.) Geological Atlas of Poland; Państwowy Instytut Geologiczny—PIB: Warszawa, Poland, 2017; p. 170. [Google Scholar]
- Majorowicz, J.; Wybraniec, S. New terrestrial heat flow map of Europe after regional paleoclimatic correction application. Int. J. Earth Sci. 2011, 100, 881–887. [Google Scholar] [CrossRef]
- Majorowicz, J.; Polkowski, M.; Grad, M. Thermal properties of the crust and the lithosphere- asthenosphere boundary in the area of Poland from the heat flow variability and seismic data. Int. J. Earth Sci. 2019, 108, 649–672. [Google Scholar] [CrossRef]
- Majorowicz, J.; Grad, M.; Polkowski, M. Terrestrial heat flow versus crustal thickness and topography—European continental study. Int. J. Ter. Heat Flow Appl. Geotherm. 2019, 2, 17–21. [Google Scholar] [CrossRef]
- Plewa, S. Rozkład Parametrów Geotermalnych na Obszarze Polski; Wydaw. Centrum Podst. Prob. Gosp. Surowcami Mineralnymi i Energią PAN: Krakow, Poland, 1994; ISBN 83-86286-15-6. (In Polish) [Google Scholar]
- Szewczyk, J.; Szczepański, A.; Haładus, A.; Kania, J.; Wagner, R.; Pokorski, J.; Hajto, M. Distribution of the Main Geothermal Parameters Referred to the Geological Setting in the Polish Lowlands. In Atlas of Geothermal Resources of Mesozoic Formations in the Polish Lowlands; Górecki, W., Hajto, M., Papiernik, B., Szczepański, A., Kuźniak, T., Kozdra, T., Soboń, J., Szewczyk, J., Strzetelski, W., Haładus, A., et al., Eds.; Ministry of Environment: Krakow, Poland; AGH University of Science and Technology: Krakow, Poland, 2006; pp. 198–255. [Google Scholar]
- Majorowicz, J.; Šafanda, J. Lithosphere thickness from new heat-flow data of the Odra Variscan area, S-W Poland. Pure Appl. Geophys. 2018, 175, 4343–4354. [Google Scholar] [CrossRef]
- Hałaj, E. Characteristics and sustainable utilization prospects of geothermal waters of the Liassic formations in the Mogilno–Łódź Trough, Poland. Sustain. Water Resour. Manag. 2018, 5, 1537–1553. [Google Scholar] [CrossRef]
- Weber, J.; Born, H.; Pester, S.; Moeck, I. Geothermal Energy Use in Germany, Country Update 2015–2019. In Proceedings of the World Geothermal Congress, Melbourne, Australia, 19–25 April 2015; p. 15. [Google Scholar]
- Blöcher, G.; Reinsch, T.; Henninges, J.; Milsch, H.; Regenspurg, S.; Kummerow, J.; Francke, H.; Kranz, S.; Saadat, A.; Zimmermann, G.; et al. Hydraulic history and current state of the deep geothermal reservoir Groß Schönebeck. Geothermics 2016, 63, 27–43. [Google Scholar] [CrossRef]
- Zimmermann, G.; Tischner, T.; Legarth, B.; Huenges, E. Pressure-Dependent Production Efficiency of an Enhanced Geothermal System (EGS): Stimulation Results and Implications for Hydraulic Fracture Treatments. In Rock Physics and Natural Hazards; Pageoph Topical Volumes; Vinciguerra, S., Bernabé, Y., Eds.; Birkhäuser: Basel, Switzerland, 2009; pp. 1089–1106. [Google Scholar] [CrossRef]
- Franz, M.; Barth, G.; Zimmermann, J.; Budach, I.; Nowak, K.; Wolfgramm, M. Geothermal Resources of the North German Basin: Exploration Strategy, Development Examples and Remaining Opportunities in Mesozoic Hydrothermal Reservoirs; Special Publications; Geological Society: London, UK, 2018; Volume 469, pp. 193–222. [Google Scholar] [CrossRef]
- Jupe, A.J.; Bruel, D.; Hicks, T.; Hopkirk, R.; Kappelmeyer, O.; Kohl, T.; Kolditz, O.; Rodrigues, N.; Smolka, K.; Willis-Richards, J.; et al. Modelling of European prototype HDR reservoir. Geothermics 1995, 24, 403–419. [Google Scholar] [CrossRef]
- Huenges, E.; Holl, H.; Bruhn, D.; Brand, W.; Saadat, A.; Moeck, I.; Zimmermann, G. Current State of the EGS Project Groß Schönebeck—Drilling into the Deep Sedimentary Geothermal Reservoir. In Proceedings of the European Geothermal Congress, Unterhaching, Germany, 30 May–1 June 2007; pp. 1–4. [Google Scholar]
- Sausse, J.; Dezayes, C.; Genter, A. From Geological Interpretation and 3D Modelling to the Characterization of the Deep Seated EGS Reservoir of Soultz (France). In Proceedings of the European Geothermal Congress, Unterhaching, Germany, 30 May–1 June 2007; Available online: https://pangea.stanford.edu/ERE/pdf/IGAstandard/EGC/2007/059.pdf (accessed on 22 January 2021).
- Brown, D.W.; Duchane, D.; Heiken, G.; Hriscu, V.T. Mining the Earth’s Heat: Hot Dry Rock Geothermal Energy; Springer Science & Business Media: Berlin, Germany, 2012; p. 657. [Google Scholar]
- Lu, S.M. A global review of enhanced geothermal system (EGS). Renew. Sustain. Energy Rev. 2018, 81, 2902–2921. [Google Scholar] [CrossRef]
- Potter, R.; Robinson, E.; Smith, M. Method of Extracting Heat from Dry Geothermal Reservoirs. US Patent No. 3,786,858, 27 March 1972. [Google Scholar]
- Williams, C.F.; Reed, M.J.; Mariner, R.H. A Review of Methods Applied by the U.S. Geological Survey in the Assessment of Identified Geothermal Resources; USGS Open File Report; US Department of Interior, US Geological Survey: Washington, DC, USA, 2008; Volume 1296, pp. 1–27.
- Bujakowski, W.; Barbacki, A.; Miecznik, M.; Pajak, L.; Skrzypczak, R.; Sowizdzał, A. Modelling geothermal and operating parameters of EGS installations in the lower triassic sedimentary formations of the central Poland area. Renew. Energy 2015, 80, 441–453. [Google Scholar] [CrossRef]
- Pazdro, Z.; Kozerski, B. Hydrogeologia Ogólna; Wydawnictwa Geologiczne: Warsaw, Poland, 1990. (In Polish)
- Chadwick, A.; Arts, R.; Bernstone, C.; May, F.; Thibeau, S.; Zweigel, P. Best Practice for the Storage of CO2 in Saline Aquifers—Observations and Guidelines from the SACS and CO2STORE Projects; British Geological Survey Occasional Publication, 14; British Geological Survey: Nottingham, UK, 2008; p. 267. [Google Scholar]
- Barbier, E. Geothermal energy technology and current status: An overview. Renew. Sustain. Energy Rev. 2002, 6, 3–65. [Google Scholar] [CrossRef]
- Garnish, J.D.; Batchelor, A.S.; Ledingham, P. Hot Dry Rock: Fringe Technology or Key Component? In Proceedings of the International Conference on Industrial Uses of Geothermal Energy, Reykjavik, Iceland, 2–4 September 1992; pp. 1–8. [Google Scholar]
- Rybach, L. The Future of Geothermal Energy and its Challenges. In Proceedings of the World Geothermal Congress 2010, Bali, Indonesia, 25–29 April 2010; pp. 1–4. Available online: https://www.geothermal-energy.org/pdf/IGAstandard/WGC/2010/3109.pdf (accessed on 14 August 2021).
- Jung, R. EGS–Goodbye or Back to the Future, Effective and Sustainable Hydraulic Fracturing; Jeffrey, R., Ed.; InTech: London, UK, 2013; ISBN 978-953-51-1137-5. Available online: https://www.intechopen.com/books/effective-and-sustainable-hydraulic-fracturing/egs-goodbye-or-back-to-the-future-95 (accessed on 14 August 2021). [CrossRef]
- Breede, K.; Dzebisashvili, K.; Liu, X.; Falcone, G. A systematic review of enhanced (or engineered) geothermal systems: Past, present and future. Geotherm. Energy 2013, 1–27. [Google Scholar] [CrossRef]
- McDermott, C.I.; Randriamanjatosoa, A.R.L.; Tenzer, H.; Kolditz, O. Simulation of heat extraction from crystalline rocks: The influence of oupled processes on differential reservoir cooling. Geothermics 2006, 35, 321–344. [Google Scholar] [CrossRef]
- Butler, S.J.; Sanyal, S.K.; Robertson-Tait, A. A Numerical Simulation study of the Performance of Enhanced Geothermal Systems. In Proceedings of the 29th Annual Workshop on Reservoir Engineering, Stanford, CA, USA, 26–28 January 2004. [Google Scholar]
- Brigaud, F.; Chapman, D.S.; le Douaran, S. Estimating thermal conductivity in sedimentary basins using lithologic data and geophysical well logs. AAPG Bull. 1990, 74, 1459–1477. [Google Scholar]
- Demongodin, L.; Pinoteau, B.; Vasseur, G.; Gable, R. Thermal conductivity and well logs: A case study in the Paris Basin. Geophys. J. Int. 1991, 105, 675–691. [Google Scholar] [CrossRef]
- Midttømme, K.; Roaldset, E.; Aagaard, P. Thermal Conductivity of Argillaceous Sediments. In Modern Geophysics in Engineering Geology; McCann, D.M., Eddleston, M., Fenning, P.J., Reeves, G.M., Eds.; Geological Society of London: London, UK, 1997; Volume 12, pp. 355–363. [Google Scholar] [CrossRef]
- Hartmann, A.; Rath, V.; Clauser, C. Thermal conductivity from core and well log data. Int. J. Rock Mech. Min. Sci. 2005, 42, 1042–1055. [Google Scholar] [CrossRef]
- Gąsior, I.; Przelaskowska, A. Estimating thermal conductivity from core and well log data. Acta Geophys. 2014, 62, 785–801. [Google Scholar] [CrossRef]
- Hajto, M.; Przelaskowska, A.; Machowski, G.; Drabik, K.; Ząbek, G. Indirect methods for validating shallow geothermal potential using advanced laboratory measurements from a regional to local scale—A Case study from Poland. Energies 2020, 13, 5515. [Google Scholar] [CrossRef]
- Woodside, W.; Messmer, J.H. Thermal conductivity of porous media. II. Consolidated rocks. J. Appl. Geophys. 1961, 32, 1699–1706. [Google Scholar] [CrossRef]
- Sass, J.H.; Lachenbruch, A.H.; Munroe, R.J. Thermal conductivity of rocks from measurements on fragments and its application to heat-flow determinations. J. Geophys. Res. 1971, 76, 3391–3401. [Google Scholar] [CrossRef]
- Brigaud, F.; Vasseur, G. Mineralogy, porosity and fluid control on thermal conductivity of sedimentary rocks. Int. J. Rock Mech. Min. Sci. 1989, 27, A77. [Google Scholar] [CrossRef]
- Tatar, A.; Mohammadi, S.; Soleymanzadeh, A.; Kord, S. Predictive mixing law models of rock thermal conductivity: Applicability analysis. J. Pet. Sci. Eng. 2020, 197, 107965. [Google Scholar] [CrossRef]
- Lichtenecker, K. Die Herleitung des logarithmischen Mischungsgesetzes aus allgemeinen Prinzipien der stationären Strömung. Phys. Z. 1931, 23, 255–260. [Google Scholar]
- Horai, K.-I.; Simmons, G. Thermal conductivity of rock-forming minerals. Earth Planet. Sci. Lett. 1969, 6, 359–368. [Google Scholar] [CrossRef]
- Horai, K.-I. Thermal conductivity of rock-forming minerals. Geophys. Res. Lett. 1971, 76, 1278–1308. [Google Scholar] [CrossRef]
- Čermák, V.; Rybach, L. Thermal Conductivity and Specific Heat of Minerals and Rocks. In Geophysics—Physical Properties of Rocks; Landolt-Börnstein-Group V Geophysics 1A (Subvolume A); Angenheister, G., Ed.; Springer-Verlag: New York, NY, USA, 1982; pp. 305–403. [Google Scholar]
- Plewa, S. Regionalny Obraz Parametrów Geotermicznych Obszaru Polski; Prace Geofizyczne i Geologiczne: Warsaw, Poland; Wyd. Geofizyka i Geologia Naftowa: Warsaw, Poland, 1966; pp. 1–88. (In Polish) [Google Scholar]
- Pasquale, V.; Verdoya, M.; Chiozzi, P. Geothermics, Heat Flow in the Lithosphere; Springer: Berlin, Germany, 2017; pp. 1–138. [Google Scholar]
- Robertson, E.C. Thermal Properties of Rocks; Open-File Report; United States Department of the Interior, Geological Survey: Washington, DC, USA, 1988; Volume 88–441, pp. 1–106.
- Kudrewicz, R. A 3D model of the thermal field within the Polish Carpathians and the Carpathian Foredeep (S Poland). Geol. Q. 2021, 65, 1–26. [Google Scholar] [CrossRef]
- Fourier, J. Theorie Analytique de la Chaleur; Firmin Didot et Fils: Paris, France, 1822. [Google Scholar]
- Fourier, J. Remarques generales sur les temperatures du globe terrestre et des espaces planetaires. Ann. Chim. Phys. 1824, 27, 136–167. [Google Scholar]
- Bücker, C.; Rybach, L. A simple method to determine heat production from gamma-ray logs. Mar. Pet. Geol. 1996, 13, 373–375. [Google Scholar] [CrossRef]
- Wygrala, B. Unconventional oil and gas—Efficient petrel/petromod workflows for exploration risk and resource assessments. Prz. Geol. 2014, 62, 825–841. (In Polish) [Google Scholar]
- Wachowicz-Pyzik, A.; Pająk, L.; Papiernik, B.; Michna, M. The application of numerical modeling to geothermal investments. Comput. Assist. Methods Eng. Sci. 2015, 22, 385–396. [Google Scholar]
- Dommisse, R.; Janson, X.; Male, F.; Price, B.; Payne, S.; Lewis, A. An Integrated, Multiscale Geomodel of the Northern Delaware Basin. In SPE/AAPG/SEG Unconventional Resources Technology Conference; OnePetro: Richardson, TX, USA, 2019. [Google Scholar] [CrossRef]
- Ringrose, P.; Bentley, M. Reservoir Model Design; Springer Science+Business Media: Berlin, Germany, 2015; pp. 1–260. [Google Scholar]
- Sowiżdżał, A.; Papiernik, B.; Machowski, G. The role of structural and parametric modelling in the process of selecting Enhanced Geothermal System location in sedimentary rocks. Prz. Geol. 2014, 62, 303–307. [Google Scholar]
- Souche, L.; Lepage, F.; Iskenova, G. Volume Based Modeling—Automated Construction of Complex Structural Models. In Proceedings of the 75th EAGE Conference Exhib. Inc. SPE Eur., London, UK, 10–13 June 2013; pp. 10–13. [Google Scholar] [CrossRef]
- Wang, B.; Bauer, S. Converting heterogeneous complex geological models to consistent finite element models: Methods, development, and application to deep geothermal reservoir operation. Environ. Earth Sci. 2016, 75, 1349. [Google Scholar] [CrossRef]
- Papiernik, B.; Zając, J.; Michna, M.; Ząbek, G.; Machowski, G.; Kosakowski, P.; Poprawa, P.; Górecki, W. Application of Multiscale Spatial Modeling for Unconventional Hydrocarbon Assessment in the Central Part of Lublin Basin. In Proceedings of the X International GEOPETROL Conference, Oil and Gas Institute—National Research Institute, Research Papers, Zakopane, Poland, 19–22 September 2016; Volume 209, pp. 93–96. (In Polish). [Google Scholar]
- Trumpy, E.; Botteghi, S.; Caiozzi, F.; Donato, A.; Gola, G.; Montanari, D.; Pluymaekers, M.P.D.; Santilano, A.; van Wees, J.D.; Manzella, A. Geothermal potential assessment for a low carbon strategy: A new systematic approach applied in southern Italy. Energy 2016, 103, 167–181. [Google Scholar] [CrossRef]
- Van Wees, J.D.; Boxem, T.; Angelino, L.; Dumas, P. A Prospective Study on the Geothermal Potential in the EU. GEOELEC Report, Deliverable No. 2.5, 1–96. 2013. Available online: http://www.geoelec.eu/wp-content/uploads/2011/09/D-2.5-GEOELEC-prospective-study.pdf (accessed on 22 January 2021).
- Blackwell, D.D.; Negraru, P.T.; Richard, M.C. Assessment of the enhanced geothermal system. Resource base of the United States. Nat. Resour. Res. 2006, 15, 283e308. [Google Scholar] [CrossRef]
- Van Wees, J.D.; Kramers, L.; Kronimus, A.; Pluymaekers, M.P.D.; Mijnlieff, H.F.; Vis, G.-J. ThermoGISTM V1.0, Part II: Methodology. 2010. Available online: https://www.thermogis.nl/downloads/ThermoGISmanual_partII.pdf (accessed on 22 January 2021).
- Beardsmore, G.; Rybach, L.; Blackwell, D.D.; Baron, C.A. Protocol for estimating the global potential for EGS. Geotherm. Resour. Counc. Trans. 2010, 34, 301–312. [Google Scholar]
- Limberger, J.; Calcagno, P.; Manzella, A.; Trumpy, E.; Boxem, T.; Pluymaekers, M.P.D.; van Wees, J.-D. Assessing the prospective resource base for enhanced geothermal systems in Europe. Geoth. Energ. Sci. 2014, 2, 55–71. [Google Scholar] [CrossRef]
- Chamorro, C.R.; García-Cuesta, J.L.; Mondéjar, M.E.; Linares, M.M. An estimation of the enhanced geothermal systems potential for the Iberian Peninsula. Renew. Energy 2014, 66, 1–14. [Google Scholar] [CrossRef]
- Feng, Y.; Chen, X.; Xu, F.X. Current status and potentials of enhanced geothermal system in China: A review. Renew. Sustain. Energy Rev. 2014, 33, 214–223. [Google Scholar] [CrossRef]
- Deibert, L.; Hjartarson, A.; McDonald, I.; McIlveen, J.; Thompson, A.; Toohey, B.; Yang, D. The Canadian Geothermal Code for Public Reporting. Reporting of Exploration results, Geothermal Resources and Geothermal Reserves. Canadian Geothermal Energy Association. 2010. Available online: https://www.cangea.ca/uploads/3/0/9/7/30973335/canadiangeothermalcodeforpublicreporting.pdf (accessed on 28 February 2021).
- GEA 2010. New Geothermal Terms and Definitions. A Guide to Reporting Resource Development Progress and Results to the Geothermal Energy Association. 2010. Available online: https://nanopdf.com/download/new-geothermal-terms-and-definitions_pdf (accessed on 28 February 2021).
- Van Wees, J.D.; Boxem, T.; Calcagno, P.; Lacasse, L.; Manzella, A. A Resource Assessment Protocol for GEO-ELEC. A Living Document Produced by the GEO-ELEC Project, 1–18. 2011. Available online: http://www.geoelec.eu/wp-content/uploads/2012/04/GEOELEC_RESOURCE-ASSESMENTPROTOCOL_v-16-dec-2011.pdf (accessed on 22 January 2021).
- UNECE. Specifications for the Application of the United Nations Framework Classification for Fossil Energy and Mineral Reserves and Resources 2009 (UNFC-2009) to Geothermal Energy Resources. 2016. Available online: https://unece.org/DAM/energy/se/pdfs/UNFC/UNFC_GEOTH/UNFC.Geothermal.Specs.pdf (accessed on 22 January 2021).
- IMGW. Climate Map for the Reference Period 1981–2010 in Poland. 2021. Available online: https://klimat.imgw.pl/pl/climate-maps/#Mean_Temperature/Yearly/1981-2010/1/Summer (accessed on 28 February 2021).
- Burzewski, W.; Górecki, W.; Maćkowski, T.; Papiernik, B.; Reicher, B. Zasoby prognostyczne—Nieodkryty potencjał gazu ziemnego w polskim basenie czerwonego spągowca. Geologia 2009, 35, 123–128. [Google Scholar]
- Botor, D.; Papiernik, B.; Maćkowski, T.; Reicher, B.; Kosakowski, P.; Machowski, G.; Górecki, W. Gas generation in Carboniferous source rocks of the Variscan Foreland Basin: Implications for a charge history of Rotliegend deposits with natural gases. Ann. Soc. Geol. Pol. 2013, 83, 353–383. [Google Scholar]
- Fromme, K.; Michalzik, D.; Wirth, W. Das geothermische Potenzial von Salzstrukturen in Norddeutschland. Z. Dt. Ges. Geowiss. 2010, 161, 323–333. [Google Scholar]
- Yu, Z.; Lerche, I.; Lowrie, A. Thermal impact of salt: Simulation of thermal anomalies in the Gulf of Mexico. Pure Appl. Geophys. 1992, 138, 181–192. [Google Scholar] [CrossRef]
- Selig, F.; Wallick, G.C. Temperature distribution in salt domes and surrounding sediments. Geophysics 1966, 31, 346–361. [Google Scholar] [CrossRef]
- Fuchs, S.; Förster, A. Rock thermal conductivity of Mesozoic geothermal aquifers in the northeast German basin. Chem. Erde Geochem. 2010, 70, 13–22. [Google Scholar] [CrossRef]
- Daniilidis, A.; Herber, R. Salt intrusions providing a new geothermal exploration target for higher energy recovery at shallower depths. Energy 2017, 118, 658–670. [Google Scholar] [CrossRef]
- Majorowicz, J.; Grad, M. Differences between recent Heat Flow Maps of Poland and deep thermo-seismic and tectonic age constraints. Int. J. Ter. Heat Flow Appl. Geotherm. 2020, 3, 11–19. [Google Scholar] [CrossRef]
- Kaltschmitt, M.; Huenges, E.; Wolff, H. (Eds.) Energie aus Erdwärme—Geologie, Technik und Energiewirtschaft; Deutscher Verlag für Grundstoffindustrie: Stuttgart, Gemany, 1999; pp. 1–265. [Google Scholar]
- Cui, G.; Ning, F.; Dou, B.; Li, T.; Zhou, Q. Particle migration and formation damage during geothermal exploitation from weakly consolidated sandstone reservoirs via water and CO2 recycling. Energy 2022, 240, 122507. [Google Scholar] [CrossRef]
- Cui, G.; Wang, W.; Dou, B.; Liu, Y.; Tian, H.; Zheng, J.; Liu, Y. Geothermal energy exploitation and power generation via a single vertical well combined with hydraulic fracturing. J. Energy Eng. 2022, 148, 04021058. [Google Scholar] [CrossRef]
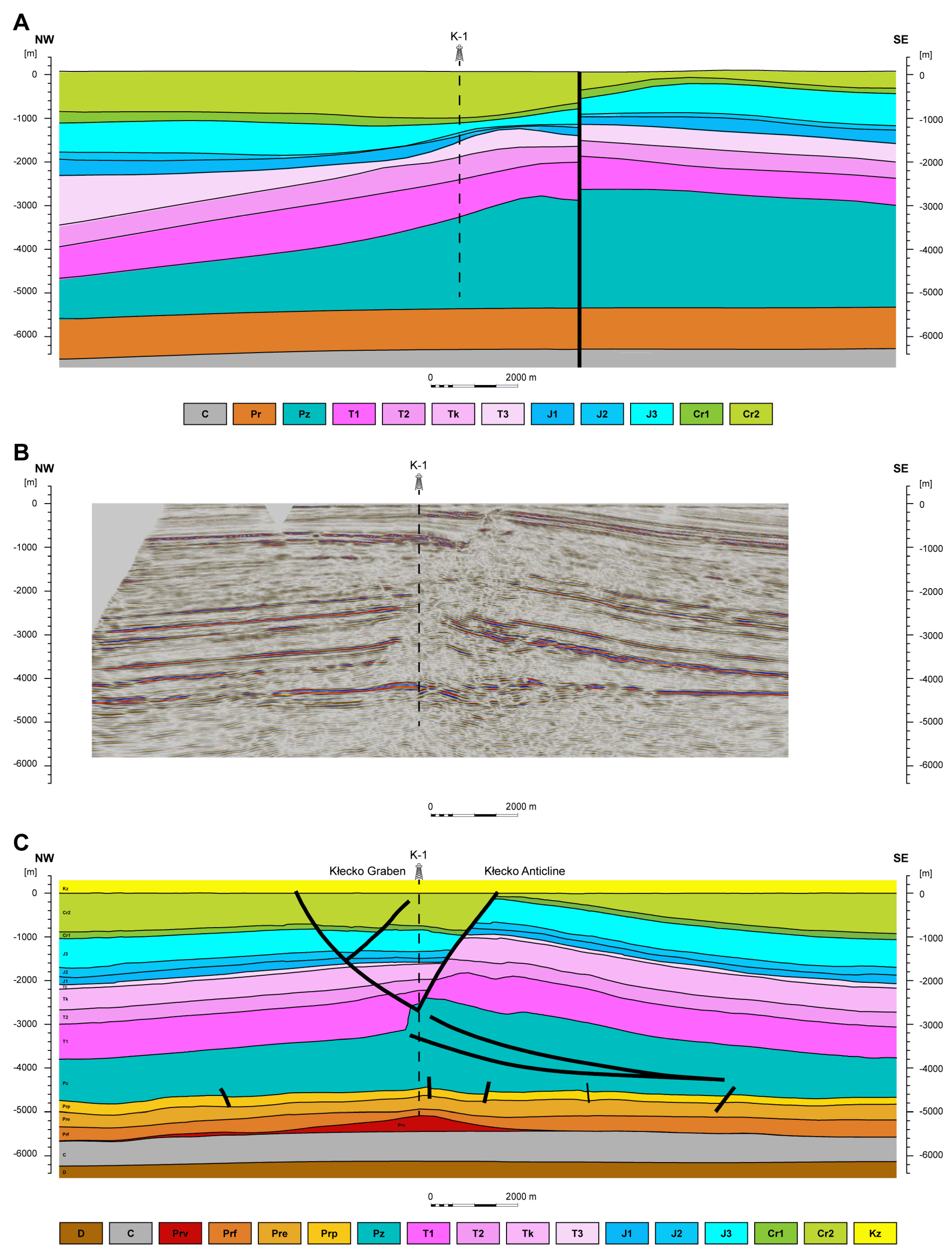
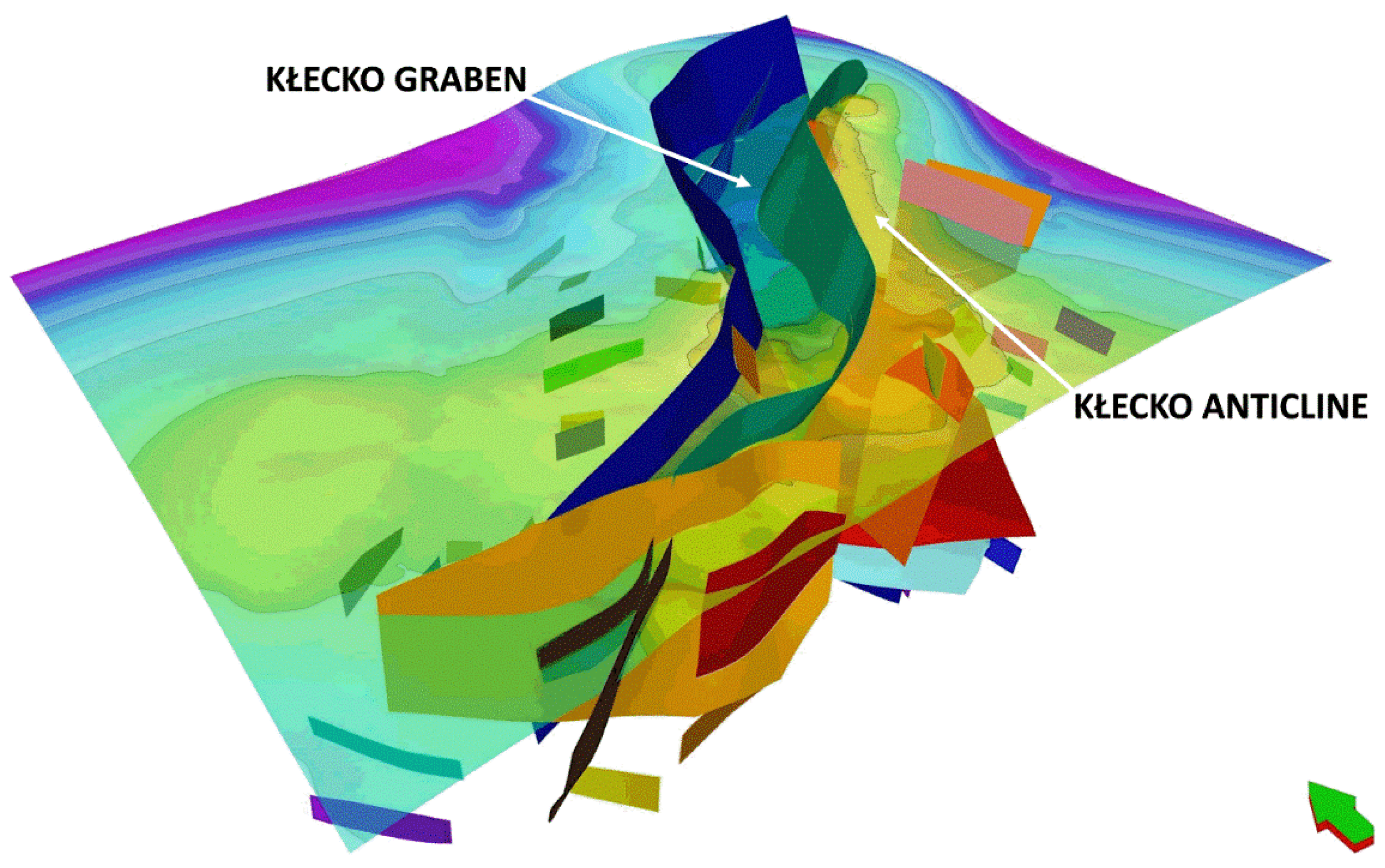
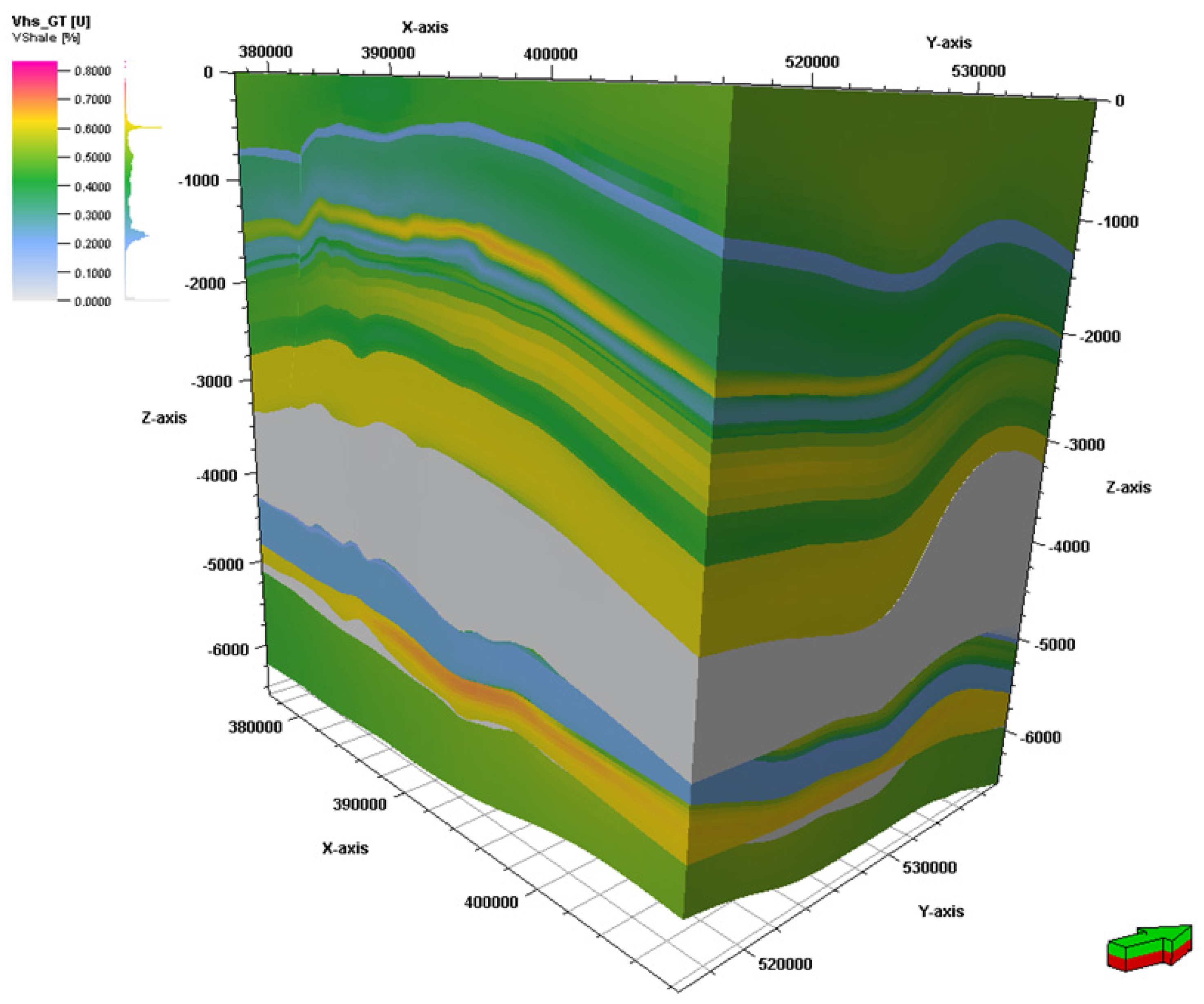
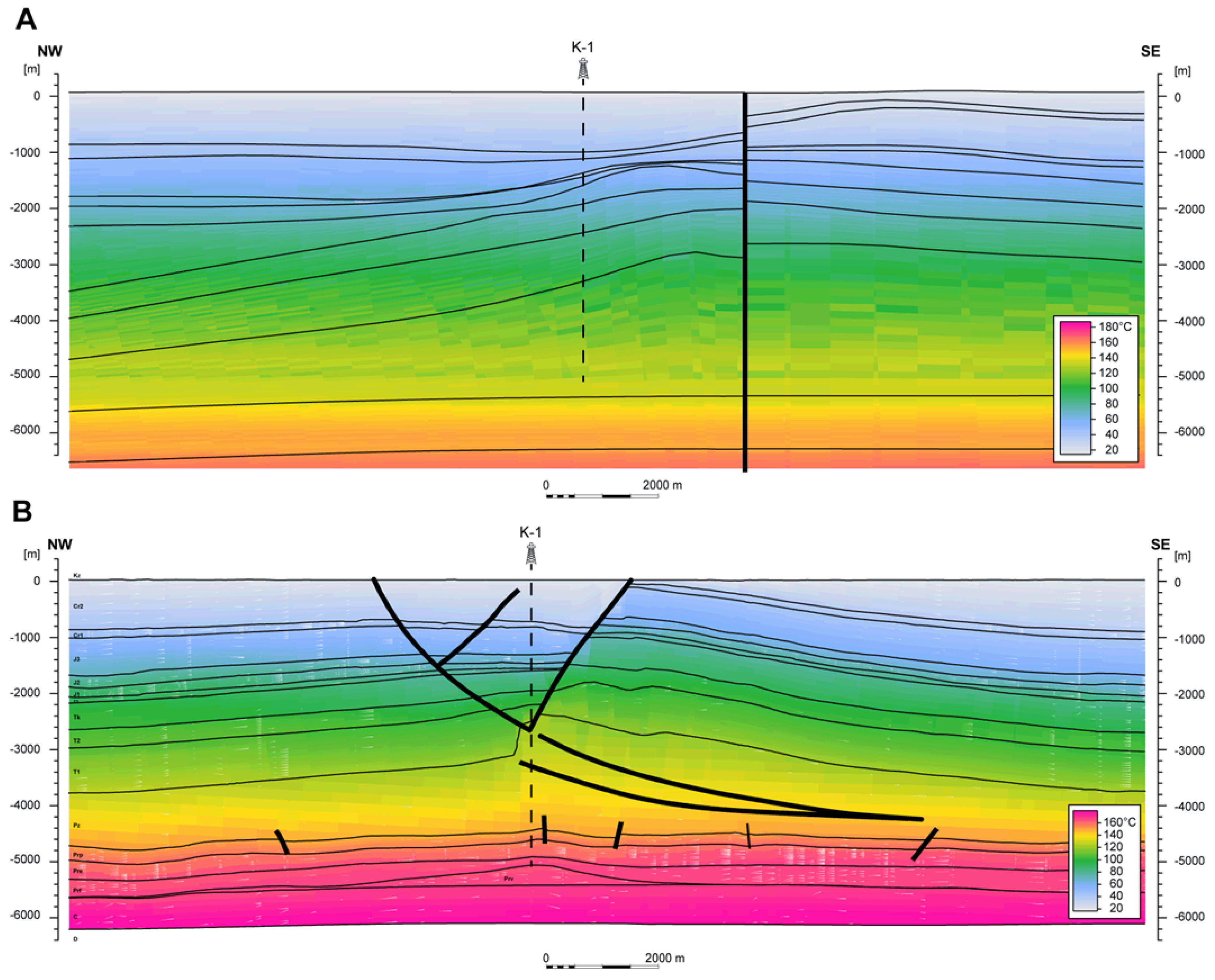
| Location (City) | Aquifer | Well-Head Temperature | Admissible Water Productivity | Water Mineralization | Installed Geothermal Capacity | Total Installed Capacity (Geothermal Plus Peak Load) | Annual Heat Production |
|---|---|---|---|---|---|---|---|
| °C | m3 h−1 | g dm−3 | MWt | MWt | TJ a−1 | ||
| Poddębice | Lower Cretaceous | 71 | 252 | 0.4 | 10.0 | 10.0 | 63 |
| Uniejów | 68 | 120 | 6-8 | 3.4 | 7.4 | 9 |
| Parameter | Minimum Value | Data Source |
|---|---|---|
| Major Criteria | ||
| Reservoir depth | 5–6 km | [90,91] |
| 4–6 km | [5] | |
| Reservoir thickness | ≥200 m | [5] |
| ≥300 m | [92] | |
| Reservoir rock temperature | 90 °C (minimum temperature for electric power production) | [91] |
| >100 °C (enough for heat production for GEODH or moderate for binary cycle electricity production) | [69,86] | |
| >150 °C (effective electricity production) | [69,85] | |
| Initial permeability | The lower the better (<3 mD) | [93] |
| Effective porosity of the rock mass | The lower the better (<3%) | [5] |
| Caprock thickness | >20 m | according to CCS requirements [94] |
| Minor criteria | ||
| Thermo-physical parameters of the reservoir rocks | High thermal conductivity and high specific heat of reservoir rock | [69,85,86] |
| Circulation flow rate | 30 l s−1 (ca. 108 m3 h−1) | [85] |
| 50–75 kg s−1 (ca. 180–270 m3 h−1) | [95] | |
| 50–100 kg s−1 (ca. 180–360 m3 h−1) | [96,97] | |
| 50–100 l s−1 (ca. 180–360 m3 h−1) | [98,99] | |
| Rock volume accessed | >2·108 m3 = 0.2 km3 | [100,101] |
| Effective heat transfer area | >2·106 m2 | [95] |
| Sample Code | Rock Sample Lithology | Sample Depth m b.g.l. | Measurement Temperature °C | Thermal Conductivity W (m K)−1 |
|---|---|---|---|---|
| S1 | mudstone | 4585.15 | 152 | 1.125 |
| S2 | sandstone | 4687.12 | 154 | 2.906 |
| S3 | sandstone | 4832.60 | 157 | 2.821 |
| S4 | mudstone | 5061.38 | 164 | 2.379 |
| S5 | volcanites | 5180.35 | 168 | 2.134 |
| Model | Permeability PERM | Porosity PHI | Shale Volume VSH | Bulk Density RHOB | Temperature °C |
|---|---|---|---|---|---|
| SMV1 | 98 | 107 | 84 | 37 | 55 |
| SMV2 | 99 | 108 | 85 | 38 | 56 |
| Parameter | Model | Playa | Eolian | Fluvial |
|---|---|---|---|---|
| PHI (%) | SMV1 | 1.10–12.45 (3.04) | 1.27–15.76 (8.78) | 0.97–11.06 (5.89) |
| SMV2 | 0.43–3.19 (1.19) | 0.00–8.85 (4.90) | 0.26–3.70 (1.76) | |
| Vsh (%) | SMV1 | 15.53–60.84 (47.40) | 13.17–59.52 (21.56) | 17.05–50.96 (32.57) |
| SMV2 | 0.21–66.87 (32.44) | 9.58–66.69 (22.49) | 35.45–72.84 (60.97) | |
| RHOB (g cm−3) | SMV1 | 2.44–2.77 (2.66) | 2.41–2.75 (2.53) | 2.50–2.74 (2.63) |
| SMV2 | 2.58–2.77 (2.69) | 2.50–2.69 (2.58) | 2.26–2.86 (2.58) | |
| Temp (°C) | SMV1 | 136.34–162.44 (151.29) | 134.83–163.37 (150.93) | 140.11–169.48 (155.04) |
| SMV2 | 135.39–161.59 (152.31) | 150.75–170.07 (160.84) | 160.62–172.83 (166.34) | |
| Thermal gradient (°C 100 m−1) | SMV1 | |||
| SMV2 | 1.56–2.43 (2.08) | 1.10–4.17 (2.83) | 3.21–3.42 (3.37) | |
| Radiogenic heat (µW m−3) | SMV1 | |||
| SMV2 | 0.32–1.65 (1.27) | 0.64–1.90 (0.89) | 1.25–3.24 (1.85) |
| Complex | Model | Th | V | ρrock | crock | Tprod | ηth | HIP | HIPe | TC | TPth | TPreal | TPlow |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m | ×108 m3 | g cm−3 | J (kg·K)−1 | °C | 10−2 | PJ | PJ | PJ | MWe | kWe | kWe | ||
| Playa | SMV1 | 176.85 | 2.00 | 2.66 | 890 | 151 | 11.07 | 67.84 | 29.97 | 3.32 | 3.51 | 438.18 | 35.05 |
| SMV2 | 232.10 | 2.00 | 2.69 | 890 | 152 | 11.12 | 69.10 | 30.79 | 3.42 | 3.62 | 452.42 | 36.19 | |
| Eolian | SMV1 | 372.12 | 4.21 | 2.53 | 980 | 151 | 11.05 | 149.13 | 65.66 | 7.25 | 7.67 | 958.51 | 76.68 |
| SMV2 | 334.25 | 2.88 | 2.58 | 980 | 161 | 11.56 | 111.30 | 53.04 | 6.13 | 6.48 | 810.44 | 64.84 | |
| Fluvial | SMV1 | 206.83 | 2.34 | 2.63 | 900 | 155 | 11.30 | 82.84 | 37.12 | 4.18 | 4.42 | 552.30 | 44.18 |
| SMV2 | 326.31 | 2.81 | 2.58 | 900 | 166 | 11.85 | 103.38 | 51.15 | 6.06 | 6.41 | 800.80 | 64.06 |
| Complex | Model | sHIP | sHIPe | sTC | sTPth | sTPreal | sTPlow |
|---|---|---|---|---|---|---|---|
| PJ km−3 | PJ km−3 | PJ km−3 | MWe km−3 | kWe km−3 | kWe km−3 | ||
| Playa | SMV1 | 339.20 | 149.85 | 16.60 | 17.55 | 2190.90 | 175.25 |
| SMV2 | 345.50 | 153.95 | 17.10 | 18.10 | 2262.10 | 180.95 | |
| Eolian | SMV1 | 354.23 | 155.96 | 17.22 | 18.22 | 2276.75 | 182.14 |
| SMV2 | 386.46 | 184.17 | 21.28 | 22.50 | 2814.03 | 225.14 | |
| Fluvial | SMV1 | 354.02 | 158.63 | 17.86 | 18.89 | 2360.26 | 188.80 |
| SMV2 | 367.90 | 182.03 | 21.57 | 22.81 | 2849.82 | 227.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kudrewicz, R.; Papiernik, B.; Hajto, M.; Machowski, G. Subsalt Rotliegend Sediments—A New Challenge for Geothermal Systems in Poland. Energies 2022, 15, 1166. https://doi.org/10.3390/en15031166
Kudrewicz R, Papiernik B, Hajto M, Machowski G. Subsalt Rotliegend Sediments—A New Challenge for Geothermal Systems in Poland. Energies. 2022; 15(3):1166. https://doi.org/10.3390/en15031166
Chicago/Turabian StyleKudrewicz, Rafał, Bartosz Papiernik, Marek Hajto, and Grzegorz Machowski. 2022. "Subsalt Rotliegend Sediments—A New Challenge for Geothermal Systems in Poland" Energies 15, no. 3: 1166. https://doi.org/10.3390/en15031166
APA StyleKudrewicz, R., Papiernik, B., Hajto, M., & Machowski, G. (2022). Subsalt Rotliegend Sediments—A New Challenge for Geothermal Systems in Poland. Energies, 15(3), 1166. https://doi.org/10.3390/en15031166







