Fatigue Strength Analysis of a Prototype Francis Turbine in a Multilevel Lifetime Assessment Procedure Part I: Background, Theory and Assessment Procedure Development

Abstract

Electricity generation is becoming increasingly flexible in Europe these days. Due to the integration of new renewable energy sources like wind and photovoltaic, other conventional resources, such as hydropower, operate within a brought range around their best efficiency point, thus leading to higher dynamical loads at the water-bearing parts, especially at the runner and the guide vanes (background). By scrutinizing the literature of the past years, one could summarize the outcome in that way, that research projects focused either on model measurements with higher visual accessibility or, less often, on prototype measurements in existing power plants. Today prototype measurements are performed, if possible, to eliminate scaling effects. Moreover, increasing computing power allows prototype simulations to be carried out within a reasonable time. At the acknowledged research projects, prototype and model measurements and numerical simulations have been performed to identify the main gaps in Francis turbines’ lifetime assessment (methods). One special outcome of these investigations was the impracticality of numerical simulations and calculation time, respectively, of start and stop events. Therefore, a prototype measurement with focus at this operating point should be performed to provide more data and an insight into the unit’s behavior. The future goal is a comprehensive machine unit lifetime assessment of the water-bearing parts in a Francis turbine machine set (results). This complex task needs several steps, beginning from measurements through simulations towards data processing. A particular challenge is posed, when the assessment methods are applied to old machines.

1. Introduction

In the latest report of Working Group 1, the Intergovernmental Panel on Climate Change (IPCC) acknowledged the need for a temperature limit of 1.5${}^{\circ }$ for future global warming. Accordingly, worldwide measures must be taken to achieve these climate targets by 2050. The individual national states are requested to implement these targets at the national level.

There is a consensus among European nations that all member states set corresponding programs to achieve these global climate targets. The leading western industrialized countries have already ensured the revival of renewable energy sources by creating related environmental laws. In particular, wind energy, photovoltaics, and biomass have been promoted to the extent possible by the relevant legislation. Either feed-in tariffs or investment subsidies are used. Through these tools, corresponding generation capacities have been built up within Europe over the last two decades. Figure 1 shows Austria’s annual growth rate in installed wind and solar power during the previous 20 years.

The subsidies for renewable energy sources and primary feed-in regulations lead the electrical grid to new challenges. The volatile production of electrical energy has to be supplemented by other energy sources or stored on a large basis. Hydroelectric power plays an essential role in this process due to its rapid load change capabilities. The use of this energy source to stabilize the electrical grid within Europe has been progressively expanded in recent years.

The successive phase-out of primary energy sources, like coal, oil, or nuclear power, creates additional hurdles within the electrical grid. Especially, the enormous output of those power plants, with their synchronous generators, was the backbone of grid stability in the past decades when feed-in from wind energy or PV was not possible. The gradual shutdown of thermal or nuclear power plants and the increasing demand for electricity due to the electrification of new sectors (industry, transport) pose significant difficulties. The missing grid load has to be compensated for and expanded by renewable energy sources. Different national activity programs are used for this purpose. The additional expansion of wind energy on a large scale or photovoltaics will drastically increase the fluctuation range and, consequently, the grid’s need for primary control power. Figure 2 highlights this hypothesis by showing an example from Germany where the change in renewable energy production for several sources increases the activity of grid-stabilizing measures to compensate for the overproduction for the same period at past different years.

Figure 2 serves also as a global, representative example for restructuring the electrical distribution system in the future. See also Kyushu (Japan) for a similar case, where increasing renewable energy source production leads to higher pumped-storage activity (see Figure 4.16 on p.104 in [4]). The necessity of converting to a renewable energy system is evident only the desired expansion of hydropower shows a particular discrepancy worldwide. Although the demand for this energy source to cover basic supply and primary control power will increase, the social acceptance for the construction of new plants seems to be declining.

However, in Europe, legal framework conditions, such as the European Water Framework Directive, can delay these expansion plans and make them more expensive. It requires an improvement in water quality during the development of a hydropower plant. In the future, retrofit projects will also be subject to those directives, and it will, therefore, be challenging to implement the required and ecologically necessary expansion plans.

Another point of discussion in expanding new hydropower plants is the age structure of existing plants. In most European countries, the hydropower fleet is already aging and needs to be refurbished anyway. That issues new technical requests of the operation and retrofitting of old plants. The first step in this process is to determine the technical condition of all plant components, calculate the residual lifetime, and conduct a reasonable techno-economic analysis. Retrofit potentials are then ranked and financed according to their return on investment period.

Considering the recent changes in the energy system and forecasting for the future, it becomes evident that grid regulation will become more critical due to the increasing volatility. Accordingly, energy system analyses of the future have to consider the lifetime of energy sources. Until now, one had the impression that the only link between the grid operator and the power plant operator was the individual profit maximization.

Such complex systems have the objective of determining an overall optimum (lifetime and profit) instead of finding singular optima, like profit maximization. For this purpose, additional information, like the remaining lifetime or the availability of the energy source, must be transferred to the energy vector side.

Figure 3 shows the newly installed hydropower digital twin to ensure data exchange at the energy source/energy vector interface. For the first time, we get the opportunity to exchange data among the system boundaries to pursue the energy transition towards zero emissions in 2050 holistically. With the information of the lifetime prediction of the energy resource (see the red branch-Lifetime assessment-on the right side of Figure 3) on the energy system level, we can include the availability of the same in the long-term energy analyses and thus develop better forecasting models. This enables better scientific support for the societal transformation of energy production that will impact our future daily lives. The following points need to be considered:

• Change in the energy mix
• Changes in the operation of hydropower plants due to the new realities
• Changes in the development and expansion of digitalisation

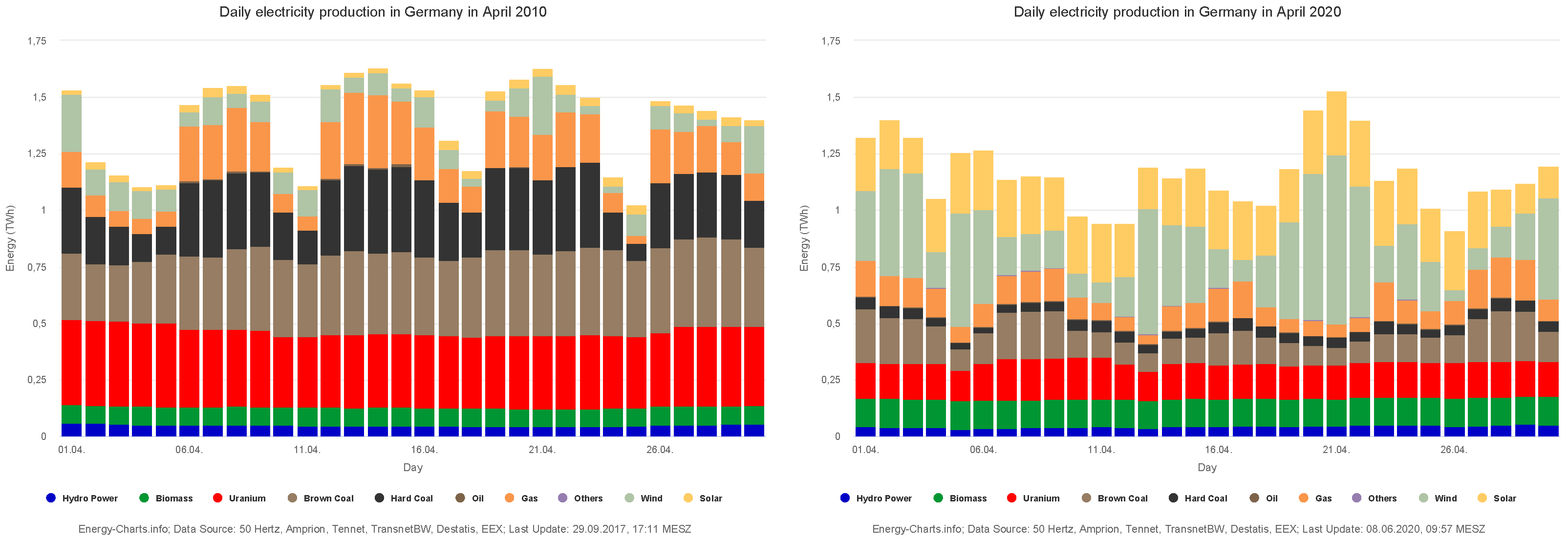
1.1. Change in the Energy Mix

Today, some regions in Europe are already faced with over-capacities in electricity production at certain times since wind or photovoltaic and any other installation of renewable energy sources is coupled either to storage possibilities [5] or increasing electric grid development or both (see [6,7,8,9,10,11,12]). These two options are under discussion, but whereas storage technologies at different power and capacity levels are researched into or developed, the extension of the electric grid at high and ultra-high voltage levels is made more problematic by the resistance of the people concerned. Although the need for further grid development was emphasized in several of the studies, only a few projects were realized. Concerning storage technologies, diversification is one of the major tasks. Looking at power and capacity levels from high to low, one can find well-known technologies, such as pumped storage or compressed air, on the upper end, and batteries and supercapacitors on the lower end. In between, there are also flywheels and other technologies. An overview of current storage technologies can be found in [13]. One of the future challenges will be developing appropriate storage technologies for all grid-level voltages with a useful capacity. If this is solved, the future for new technologies and energy systems will become tangible. Special road maps for single-storage technologies (for example [14] or [15]) are available as are ideas for energy systems in terms of smart grids [16].

Another future energy system could be the installation of a web-of-cells (WoC) concept [17] where single cells are defined and connected with each other. The advantage of such a concept is a lower power shifting at the high and highest voltage grid level and to overcome a backup structure of the electrical grid, where a few big storage plants serve as backbone for all. In the WoC concept, each single cell should assume its frequency control and power balancing on its own. The foundation for such an innovative system is the availability of large centralized storage plants as a backup and further storage technologies at all cell levels, which could be small home batteries, at the distribution grid level, or swarm batteries–utility-scale batteries–at the medium-voltage level. All storage technologies combined with a further development of decentralized structures and digitalization will be needed to install such a future WoC concept. Part of the future digitalization [18] is also the whole area of blockchain and cryptocurrencies, such as Bitcoin or Ethereum, which will boost the energy market in another way [19].

Although these future visions will need some time horizon, the increasing demand for ancillary services to stabilize the electrical grid is already reality today. Transmission system operators (TSO), such as TenneT, spent approximately 1 billion Euros for grid stabilization and re-dispatch measures in 2017 (see [20]), which is an increase of 50% compared with 2016. Facts like these show that grid expansion is urgently needed, but lags far behind forecasts and is far from being realized. As a result, hydraulic machines are subject to extremely high loads, since they have been mostly used for electric grid support. In the past, high-head hydropower plant machine sets (Pelton or Francis turbines with attached storage pumps or pump–turbines) were primarily used for this task, as they are more flexible in operation than Kaplan turbines. Nevertheless, investigations have been made in the recent past to modernize and upgrade existing low-head hydropower plants as a contribution to regulate the power market. Successful examples show that this is possible, but the reduction of machine lifetimes is obvious. Concentrating on high-head hydropower plants, different publications [21,22,23] described, already, the higher dynamic load on the installed machine sets. To understand where these dynamic loads result from, it is important to look at all operational points of the machine set. As a result, the question about off-design operation, and thus the resulting impact, becomes a major task for all hydraulic turbines participating in frequency control and power balancing.

1.2. Changes in the Operation of Hydropower Plants Due to the New Realities

Due to the changes in the energy market over the last two decades, the requirements for hydropower plants have also changed to some extent. In order to remain competitive in the liberalised electricity market, some hydropower plant operators began to place their plants at the disposal of the grid operator to provide ancillary services. Especially the quick response time to grid volatility plays an essential role, and this favours hydropower. Further investigations will consider two different modes of operation, namely (I) base load electricity production and (II) grid control operation.

1.2.1. Base Load Electricity Production

Base load electricity production is characterised by the fact that the so-called partial load range is only passed through and most of the operating time occurs around the optimum or design point. The machine is not used according to grid requirements, but purely to produce electricity. This mode of operation was dominant for a long time, as hydropower was the largest source of energy in Austria. Therefore, it was not necessary to react that quickly to grid volatility, and respectively, this was achieved by selected regulating power plants. Their machines were designed for this mode of operation from the very beginning.

1.2.2. Grid Control Operation

The increased use of new renewable energy sources shifted the operation of hydropower plants towards grid control. Volatile feed-in made it necessary to provide corresponding control power (frequency containment reserve (FCR), automatic frequency restoration reserves (aFRR) and manual frequency restoration reserves (mFRR)) as shown in Figure 4.

Figure 4 shows the control energy types concerning their activation periods. Primary control must be activated within the shortest possible time and guarantee the entire power supply or consumption within a time frame of 30 s. Secondary control follows on from primary control and must assure full power supply or consumption in a time frame between 30 s and 5 min. After 5 min, the minute reserve is activated, which has up to 15 min to provide full power supply or consumption. After 60 min, the balancing group manager regulates the electrical grid.

Based on

Table 1. The following table shows the different types of balancing energy and their characteristics.

Type of Control Energy	FCR	aFRR	mFRR
Provided by	ENTSO-E	TSO	TSO
activation	frequency-controlled; independent measurement/intervention on site by FCR provider	by control area responsible TSO-automatically replaces FCR	by control area responsible TSO-manual request by TSO
full power	within 30 s	within 5 min	within 15 min
period to be covered after an incident	0–15 min	from 30 s to 15 min	from 15 min to 60 min
remuneration	demand rate	demand and energy rate	demand and energy rate
minimum bid size	From +/− 1 MW (symmetrical)	5 MW positive or negative	5 MW positive or negative
daily products	positive and negative: 6 time slices over 4 h	positive and negative: 6 time slices over 4 h	positive and negative: 6 time slices over 4 h

, the following aspects arise concerning mechanical equipment and the operation of hydropower plants:

• Taking positive and negative balancing power into account, pumped storage plants equipped with two machine-setup units or ternary units are preferable. Only those units can deliver the needed services.
• In terms of mFRR, hydropower plants are one possible resource among others. Start-up of the machine within 5 min and supply of full power by 15 min is achievable for all machine units regardless of age and condition. Even the auxiliary units do not have to be ready for operation and start from a standstill. First, the oil–hydraulic unit must be activated to provide the oil pressure for the auxiliary systems. After that, the turbine shut-off valve is opened, which takes a considerable amount of time to start a hydraulic machine. Only then can the guide vane or the nozzle needle be adjusted and the runner set in rotation. The acceleration of the runner to synchronous speed takes place very quickly. Standard start-up times for Francis turbines require 4–5 min. Pelton turbines can start even faster.
• If pumped storage units are used for secondary control (aFRR), specific prerequisites are already necessary. For example, it is no longer possible to start the machine unit from a standstill in 30 s. Here, at least the turbine shut-off device must already be open and the oil–hydraulic unit pressurized. Only the guide apparatus or the nozzle needle have to be adjusted to synchronize the machine unit with the grid during this period. Power consumption or supply within 5 min is no longer a significant challenge after that. If the start-up time of 30 s is still not achievable under these circumstances, the unit could also remain in standby mode. However, this causes more wear and tear. For aFRR, both types, pump turbines and ternary machine sets, can be used.
• In primary control (FCR), only ternary pumped storage units can be used due to positive and negative power requirements. Conventional pump turbines take too long to switch from the turbine to pump mode. Switchover times of 5–6 min are not uncommon. To react to grid frequency at the crucial period, even the ternary machine sets have to run synchronized on the grid and only shift the load. For the changeover from supply to consumption mode, the machine set must be equipped additionally with a hydraulic shortcut circuit, as otherwise, the changeover time would take too long. Since the machine set must already be running to react in the required time, the pure demand rate is probably not economically sufficient.

These circumstances shift the operation of hydraulic machine units towards more partial load operation, and faster load step changes. Results of these load shifts are higher mechanical stresses and reduced lifetime, which are the main topics of this publication.

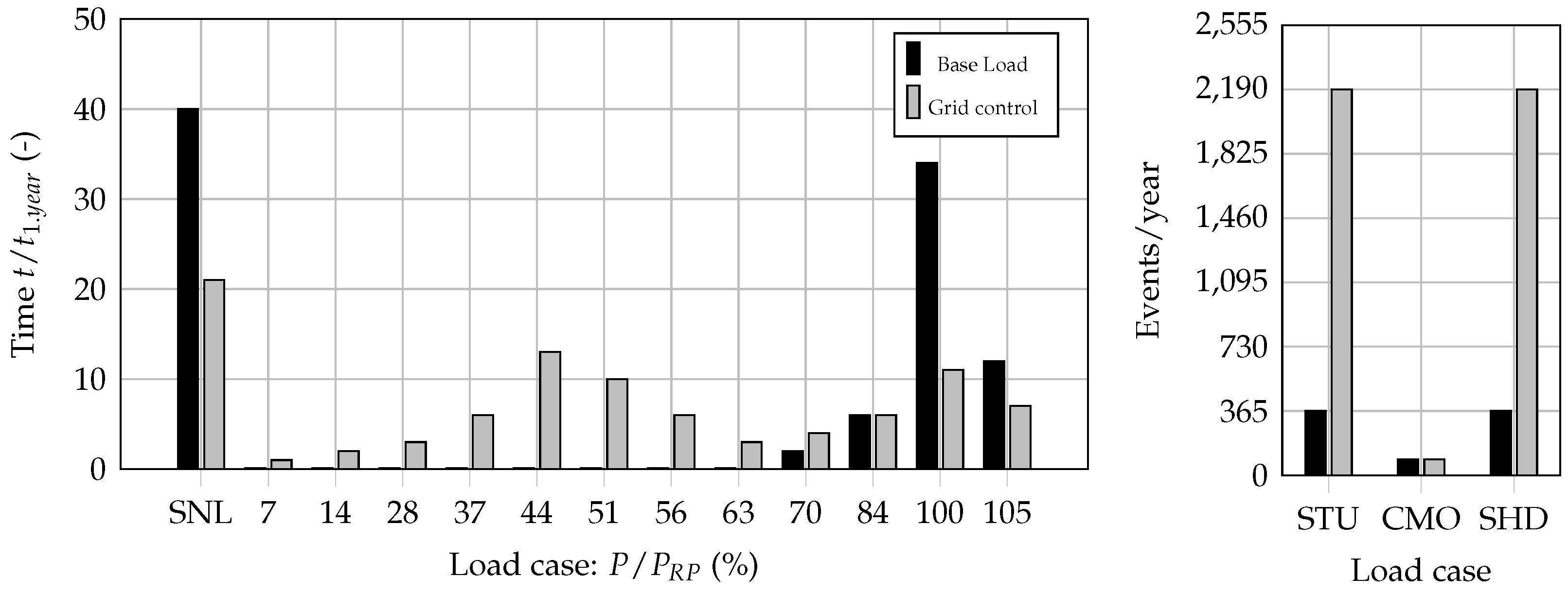
1.2.3. Comparison between Base Load Production and Grid Control Operation

The operating period of a machine set at different load steps is the best way to illustrate the operating mode difference. Here, the base load electricity production is reflected with an intensified mode of operation around the design point. The partial load regions are only passed through, and lingering at these load levels is not envisaged. In grid-support mode, the machine set is operated within all load ranges, depending on the needed power at the regulatory market. This means that the mechanically unfavourable partial load regions are also approached more often, and generally, a quicker load change is executed.

Figure 5 shows the different operating times of one typical machine set in one year (basic data have been provided by the operator and standardized for one year of operation). It becomes apparent that the hydraulic machine set is increasingly operated in the partial load range (25–60% of the design point) for grid service operation. In other words, volatile fluctuations in the grid are compensated by a variable, additive share from hydropower. Looking at the decades of operation in base load mode, it is noticeable that the machine set is driven directly into the design point range from the start and remains there. Most of the time, the machine is operated at full power output to generate the electricity market’s corresponding income.

Since hydropower plants are not only operated in synchronised mode but also have to be started and shut down, the following pattern occurs for these transient operating phases in combination with the two previously mentioned scenarios:

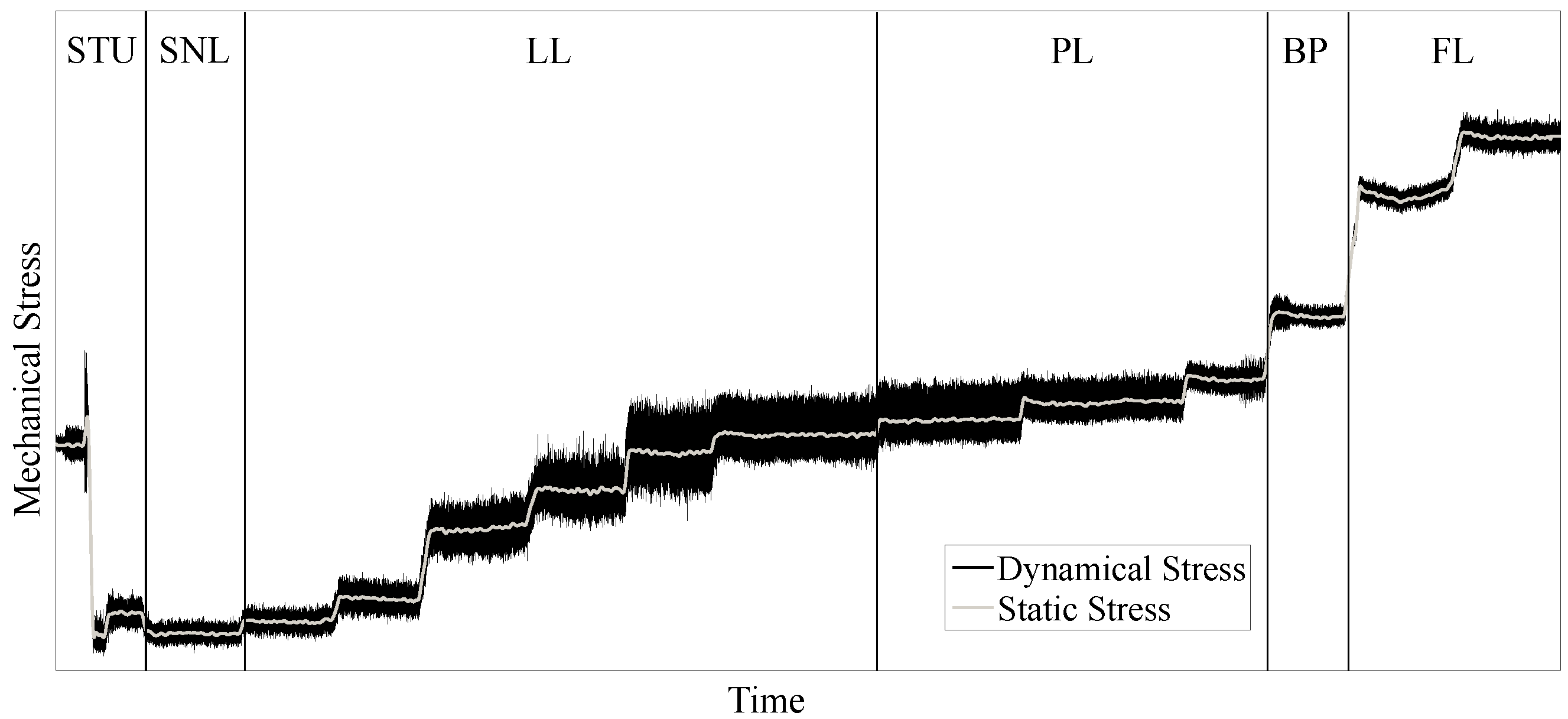
• In base-load electricity production, the machine runs predominantly at its optimum. Therefore, the number of starts and stops of the machine set per day is also lower. In Figure 5, the number of starts and stops per day was set to one, which means that the machine set is started up once a day and remains at the optimum operating point. If the power demand from the grid is deficient, the machine set is left in a synchronized state (SNL) and rotates in “idle mode” in order to be quickly brought back to the optimum and to be able to deliver power when needed.
• In contrast, the machine unit in grid-control mode (aFRR, mFRR) is started and stopped up to six times a day. This is also caused by the purchase of balancing energy on the electricity market in quarter-hour cycles. The machine unit is increasingly operated in the hydraulically unfavorable partial load range, and it is also started and stopped more often than conventionally planned. This results in the high number of start-ups (STU) and shut-downs (SHD) in Figure 5.
• Since the frequency containment reserve (FCR) is primarily intended to mitigate short-term load changes, the entire capacity range has to be provided within a maximum of 30 s and remain continuously available for at least 15 min. This operation means synchronized machine unit and load shifting either from speed-no-load (SNL) point to full load or part load to full load. Additionally, change over from supply to consumption mode is part of this operational field. Start and stops of the machine are less important than faster load shifts and part load operation.
• On the one hand, condenser-mode operation (CMO) only affects machines equipped for such operation, and on the other hand, it is only required for reactive power compensation in the grid. The new renewable energy sources are indeed steadily reducing the reactive power in the grid. However, there are still enough large synchronous generators of the grid’s primary energy suppliers to compensate for this. Hydropower generators can take over this task to some extent. The number of condenser mode operations (CMO) was set at the same low level for the remaining considerations.

These changes in the operation of hydraulic machines form the basis of many investigations regarding the components’ lifetime. The latest scientific results in this context are already being implemented in the design of turbines in new plants. However, the far more critical issue is the assessment of old runners and machines, especially when these plants have been converted from base load generation to grid stabilization.

1.3. Changes in the Development and Expansion of Digitalisation

Energy suppliers are facing significant challenges due to the social changes in the electricity market. Digitalisation is playing an increasingly important role in this context, such as boosting efficiency in all areas of the company, energy production, maintaining grid stability, billing customers for consumption, or the remote control of hydropower plants. In electricity production, the trend towards a comprehensive rollout of sensors and cameras in the power plants is particularly noticeable, enabling remote control and predictive maintenance. Besides, operating procedures, drawings and work processes are increasingly being digitalised. Examples of this are digital documentation and the introduction of workforce management systems. Similar developments can be seen in the area of electrical grids. The expansion of the grids towards a smart grid allows optimized control of the grids and predictive maintenance.

In the future, the possibilities of networking, combined with a comprehensive rollout of sensors in hydropower plants, will lead to a profound change in energy generation. This influences the control and maintenance of the generation plants. The plant sensors provide data to control energy generation intelligently or trigger demand-based maintenance and servicing at an early stage (see also [25]). Today, sensors and other measuring equipment already transmit data on the condition of plant components. However, fully automated control of the assets would require a comprehensive database and the interconnection of different data sources. Both prerequisites have not always been achieved so far.

1.3.1. Data Collection

To couple the energy system with the operation of a hydropower plant (see Figure 3), a data exchange must take place concerning the lifetime and consequently the boundary conditions on the side of the electrical grid. At the interface of this data exchange, harmonization problems arise due to the different time scales. While the demand for electrical energy from different sectors (industry, private consumption, commerce, tourism,...) is determined on a coarse scale of hours, days, or even weeks, the operation and load shifting take place over intervals of seconds. The hydropower system essentially fulfills two tasks: meeting the electrical demand of different sectors and, secondly, regulating the electrical grid (see Section 1.2.2). These tasks, therefore, require a much tighter time scale (seconds, milliseconds).

Closing this gap at the interface requires a multi-level approach. The starting point is the turbine hill chart. This map reflects the possible operational limits of the hydraulic machine. On the one hand, the minimum and maximum net head limit the operating range. The flow through the turbine is restricted at the lower end by the cavitation limit and at the upper end by the maximum discharge capacity of the machine. Many operators restrict the operation below the cavitation limit by only passing through this area at machine start-up. Permanent operational use of this deep, partial-load area is suspended for mechanical reasons. Recently, however, the requirements of the load dispatcher (TSO, DSO) for grid regulation can lead to an opening of this operating range. It seems clear that this unfavorable operation reduces the component lifetime. The scientific challenge is to permanently determine the remaining service life of hydraulic machines as a function of the current machine operation. Digitalisation can help in this case to provide the needed data, data handling and data visualisation. Critical points are the amount of data due to higher sampling rates at the machine level and harmonization issues in terms of low data amount at the system level side. Providing the remaining lifetime continually needs a permanent correlation between operating hours, machine load and component damage.

1.3.2. Real-Time Lifetime Prediction

All the influences described above change the boundary conditions for the safe operation of a hydropower plant. With increasing digitalisation, there is a new possibility to assess the continuous ageing process of a hydraulic component. Ultimately, methods that are already common in other technical areas are finding their way into this area of technology. It is just much more challenging to implement mass production methods on prototypes. However, this is becoming necessary because hydropower requirements are changing so rapidly that one can no longer continue without newer assessment methods and sophisticated health management. Ultimately, the development is moving towards real-time methods to determine the condition of a component at any moment, taking into account as many factors as possible. Real-time methods are the only way to develop forward-looking maintenance strategies and make the best possible use of the component’s utilisation reserve.

This publication is the beginning of a series of different publications. It deals with the essential prerequisites for developing a P.C. to determine the lifetime of hydraulic components.

State of the art, as a starting point and a necessary step to establish such a system, is the content of this paper. Conventional numerical methods are listed and briefly described to provide the background for further development. New computational methods and applications are required to accomplish the task of a real-time assessment. The complexity of the topic demands additional publications to present the whole scope. Thus, Part II of the publication series deals with the numerical approaches and procedures, Part III with the prototype measurements for validation purposes of the system, and Part IV with the comparison of the results from Parts II and III and the uncertainty considerations of the complete procedure.

This paper presents at Section 1 the basic idea, the procedure, the necessary tools and upcoming research tasks. Section 2 deals with the state-of-the-art in lifetime prediction, Section 3 with the new multilevel approach, Section 4 with the expected results of this novel approach and Section 5 discusses future scientific investigations needed for the subsequent publications.

2. Background and Theory

2.1. Stress–Time Correlation at the Runner

In the light of expected higher load changes for Francis and pump–turbines, investigations started some time ago by using different methods. Some major results could be briefly summarized on a time line over which [26] showed, already, the first investigations on the dynamic behavior of Francis turbines in 2005 and published some dynamic stress calculations in 2007 [27]. In 2012, the publication [28] showed a failure investigation of a pump–turbine runner to understand the possible damage mechanism at this hydraulic part. Questions of appropriate numerical assessment for the pressure field simulation were answered by [29] in his PhD thesis. Since then, computational power is available to simulate the entire machine set from spiral case to the draft tube and to extend the models into the direction of coupled investigation–flow field and subsequent mechanical stress simulation. To get an idea about the needed simulation tools, the impact on the runner itself must be determined and was published by [30] based on prototype measurements. Overlapping projects led to further ideas on the methods required for the calculation of the mechanical impact on Francis runners and were published in [31,32] focusing on fluid–structure interaction (FSI) as a basic element in this field of coupled numerical investigation. One of the latest articles in this field was published by another group who investigated model and prototype runners in the same manner. The background and results in [33] are quite comparable to the findings mentioned by other research groups.

The present paper’s goal is less to provide yet another paper on dynamic load and impact to Francis runners but rather a description of the measurement techniques and hardware required for the raw data acquisition, simulation approaches and subsequent post-processing, component analysis and lifetime prediction or health management.

The complexity of this task becomes obvious when looking at the stress-versus-time correlation (see Figure 6) of a Francis runner at all load steps. Stress was taken from a strain gauge measurement mounted at the trailing edge close to the crown at the suction side of the blade. The observation starts from the machine set start-up (STU), until synchronization, followed by the speed–no-load (SNL) area. Next in line is the low-load (LL) area attached to the part-load (PL) region heading up at the best-point (BP) area. Afterwards, the machine set operates at full-load (FL) conditions.

The transition between the single operational regions could be defined like following: between STU and SNL, there is the unique point of grid synchronization, between SNL and LL the first increase in power output of the machine, between LL and PL the approximately 50% power limit of full machine load, between PL and BP the disappearance of the dynamical stress and between BP and FL the increase in the reappearing dynamical stress. As one can imagine, some of the limits are fixed and easy to find, whereas others are gradual ones. Such an operational behavior is only to be attributed to the measurement procedure, whereas in reality, some load points are only passed through, and others are used regularly. The change in the past decade was to extend the operational region into the direction of part-load or even low load operation where higher loads occur and result in higher dynamical stresses. Especially for economic considerations, plant owners would like to eliminate any machine set’s power restrictions to participate in the entire power regulation market. New machine sets today can ensure such zero limitations, but older power plants have never been designed for such an operation extension. If these hydropower plants are used for power balancing and frequency control, their suitability has to be checked on a case-by-case basis. Precise strain gauge measurements have been used at the runner or neighboring parts to predict the hydraulic parts’ lifetime. As known, strain gauge measurements are very useful but not suited for permanent installation. In this context, helpful measurement techniques play a vital role. Correct correlations and interpretations can only be performed if the underlying flow and fatigue phenomena are understood correctly. The most feasible procedures and sensors are used.

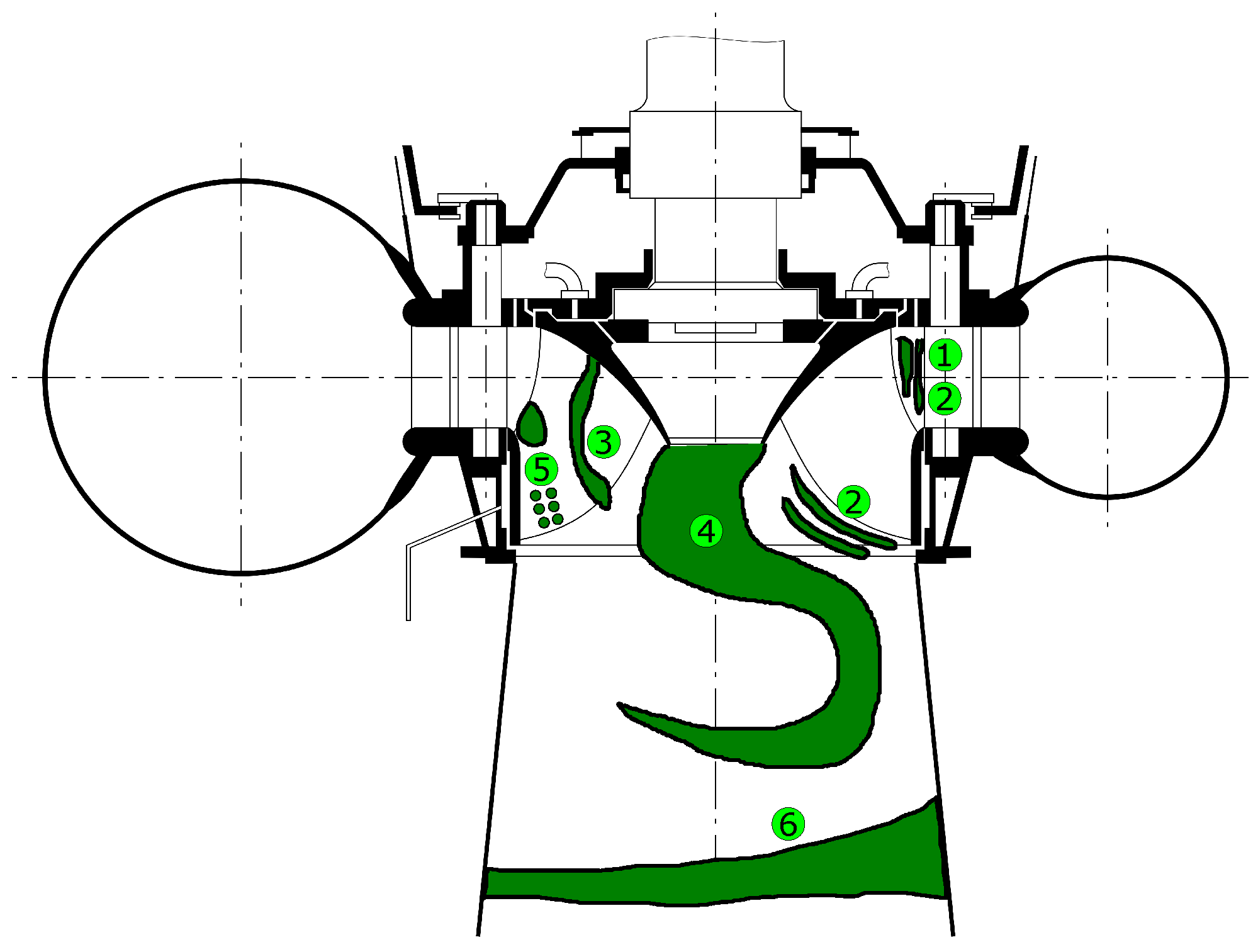
2.2. Flow Phenomena

To visualize the above-mentioned flow patterns according to their position within the turbine system, one can use Figure 7 by using the following nomenclature: ➀ rotor–stator interaction (RSI), ➁ vortex Shedding (VOS), ➂ inter-blade cavitation vortex (ICV), ➃ draft-tube-vortex (DTV), ➄ stochastic-pressure pulsations, cavitation (SPP) and ➅ free-surface oscillation (FSO).

Looking at the position and possible phenomena, it becomes obvious that the interaction between stationary and rotating parts of a Francis turbine operated in off-design regions is a complex matter. The flow entrance into the machine set system starts in stationary mode at the spiral case, followed by the stay and guide vanes before switching over to the rotating domain of the runner and leaving towards the draft tube, which is, again, a stationary domain. Although energy conversion by hydraulic turbines is a field that dates back more than hundred years, the complexity of flow determination has risen due to this new requirement. Therefore, both research options have been exploited to gain a better understanding of the machine set behavior. On the one hand, measurements and visualization techniques have been employed on model test rigs with the advantage of visual accessibility for validation and, on the other hand, prototype measurements have been used to investigate the impact on the structure without scaling effects. All insights gained are necessary to get an overall impression about the mechanical effects and lifetime reduction.

As all these phenomena are not likely to coincide in time and position, performing a correlation between the operating range according to Figure 6 and the flow pattern generated in this region appears to make sense. Adding the class of deterministic or stochastic load to the structure extends the classification significantly. This distinction is vital for any subsequent signal interpretation in the frequency domain. Taking these three assessment criteria into account, one can aggregate them, as shown in

Table 2. Flow phenomena correlated to the operational region and resulting structure load (Phenomena in brackets could appear but not necessarily).

Operational Region	Deterministic	Stochastic
start-up (STU)	RSI, VOS	SPP, VOS
speed–no-load (SNL)	RSI, VOS	SPP, VOS
low-load (LL)	RSI, (VOS, DTV)	ICV, SPP, VOS
part-load (PL)	RSI, DTV	(ICV, SPP), VOS
best point (BP)	RSI
full-load (FL)	RSI, DTV
condenser mode (CMO)	FSO	(DTV)

.

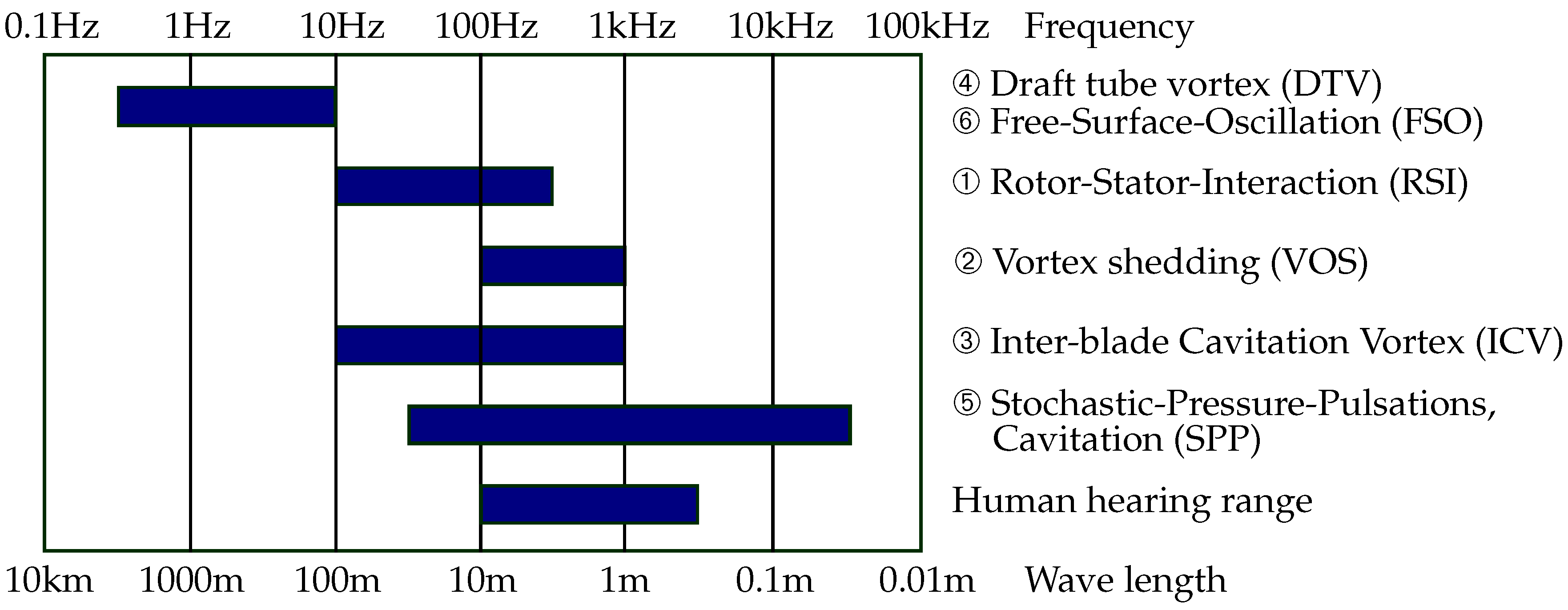
2.3. Frequencies of Flow Phenomena

Figure 7 and Table 2 show the relationship between flow phenomena, load step and structural loading quite clearly. To perform a lifetime analysis of a component, it is necessary to know the frequency of the occurring dynamic stress amplitudes. A rough estimation of the frequency ranges associated with the flow phenomena presented earlier shows Figure 8. The diversity of the different flow phenomena can be recognized by the bandwidth of the wavelength or the corresponding frequency spectra.

The change of flow phenomena at the crossover between the operating regions is not a strict one but of a flowing nature. Moreover, it is also essential to know whether the unit will be started or stopped due to possible hysteresis effects.

Explaining the theoretical background, possible flow phenomena and correlations between each other, resulting in machine behavior, raises the question of measurement techniques and methods of collecting sufficient data for a profound lifetime investigation of the hydraulic parts involved. One possible approach is using strain gauges directly applied at the inlet or trailing edge of the runner to measure the resulting strains from the combination of deterministic and stochastic loads. The results obtained and transferred to the frequency domain are shown in Figure 9.

Figure 9 shows the comparison of two frequency spectrum waterfall plots (normalized frequency spectrum versus normalized power) for strain gauge applications at the same runner location with different specific speeds $n_q=n·\frac{\sqrt{Q_{RP}}}{H_{RP}^{3/4}}$ of the runner. The runner on the left-hand side has a specific speed of $n_q=25.4$ min${}^{-1}$ and the one on the right hand side has $n_q=62.2$ min${}^{-1}$. The most obvious difference is the frequency peak of the normalized gate-passing frequency $f_{GP,norm}$, which is $f_{GP,norm}=20(f_{GP}/f_0)$ for the left runner and $f_{GP,norm}=24(f_{GP}/f_0)$ for the right runner. However, this signal’s amplitude is much more pronounced on the left runner, while on the right, it is only slightly visible at the optimum load point [31]. This is probably because the rotor–stator interaction with an $n_q$ of $25.4$ min${}^{-1}$ is much stronger than that of a runner with $n_q=62.2$ min${}^{-1}$. Ref. [36] came to the same findings. The vaneless space has a significant influence, here. However, it has to be mentioned that the strain gauges, having been mounted on the impeller exit side, and can, therefore, only weakly resolve the leading edge phenomenon, as it is very far away from the trailing edge.

Concerning the draft tube vortex, the situation is different: this phenomenon appears at both runners identically. At part load, around 30–50% of the rated point, the according amplitudes are visible. Additionally, regions with several undefined frequencies and amplitudes are for both runners in common. They belong to the stochastic phenomena at low load ranges.

However, Figure 9 illustrates that an assessment of the lifetime of a hydraulic component, which is affected by a wide range of flow phenomena, is only possible through strain gauge measurements. Correlation with other sensors can eliminate the need for a strain gauge measurement, though this requires an initial strain gauge measurement to calibrate the transfer function.

2.4. Damage Regions

If we correlate now Table 2 with Figure 9, it becomes evident that the most damaging flow phenomenon for these two impellers is the draft tube vortex. The significant stress amplitudes at part load make the remaining phenomena look insignificant, at least in terms of the dynamic stress signal. This draft tube vortex originates at the runner hub and continues into the draft tube. There, it forms pressure fluctuations that in turn affect the building. The turbine runner also sees part of this as a dynamic load.

In the speed–no-load and low-load ranges, cavitation is added as a damage mechanism. This is, however, in the very high range in terms of frequency. Although this results in a large number of weak pressure peaks, they, in turn, damage the runner in terms of stress. Cavitation erosion is undoubtedly the more dominant factor.

Refs. [37,38] give a comprehensive review on transient and fatigue damage mechanisms in Francis turbines. Within the scope of the two research projects GSG LowLoad and MDREST, the same results were compiled and investigated by means of numerical as well as measurement techniques. In the process, the damage-relevant flow phenomena were investigated individually and then superimposed.

All operating ranges must be examined and included in the assessment to guarantee a holistic approach in the lifetime assessment of a hydraulic component. Unique phenomena, as well as their occurring frequency and amplitude, were previously presented. To date, only the most significant damage mechanisms have been assessed individually according to state-of-the-art procedures. Comprehensive assessment methods are lacking due to their complexity and calculation time. Suppose a real-time lifetime analysis is desired in the future to make this information available to the energy system. In that case, a comprehensive determination of all simultaneously occurring damage mechanisms must occur. Due to the different time scales between machine monitoring and the energy system, a self-learning function accessible to both sides is needed at the interface.

The next chapter presents the primary methods available today as state-of-the-art.

3. State-of-the-Art in Lifetime Assessment

Based on the findings at the introduction, background and theory, one can determine the state-of-the-art methods as shown in Figure 16 (green marked objects). The subsequent sections give a brief overview about the needed steps for conventional dimensioning, as suppliers also use it in a turbine’s design. Basically steady/unsteady CFD simulations, determination of mechanical stresses in the runner by FE analysis and conventional damage hypotheses are used at this stage. Transient simulations and subsequent stress computation, respective to lifetime prediction, are not state-of-the-art at a standard design process in the industry (see Figure 16-red marked objects). Therefore, the following text passages describe only methods needed for the standard design process.

3.1. Numerical Tools and Measurement Techniques

This chapter describes the data acquisition methods used, namely CFD, FE, and measurement methods.

3.1.1. Steady/Unsteady CFD Simulations

Applying the findings of the introduction and the theory from Section 2 to different load steps, it becomes evident that today’s standard methods will not suffice.

State-of-the-art in CFD is limited to steady (RANS) or unsteady (URANS) simulations. Here, the boundary conditions are constant at each load step of the calculation but represent realistic discharge and pressure levels. The corresponding turbulence model’s choice (two-equation models, k-$\omega$-SST or SAS) depends on the flow phenomena to be exposed. All information regarding typical CFD belongings (for example: meshing, interfaces, Y+, wall treatment, mesh independence study, turbulence model, boundary conditions,...) have been published in [31].

As a result of the calculation, unsteady pressure fields are obtained, which can be:

(1)

Time-averaged for the static FE analysis; however, in this case, only load steps with constant speed (synchronisation speed) can be calculated (see Section 3.1.3).

(2)

Fourier transformed and split-up in amplitude and phase parts, to be used for subsequent HRA investigations (see Section 3.3.2).

(3)

used directly as a time signal for a transient FEM (see Section 4.2.2).

3.1.2. Fluid–Structure Interaction (FSI)

Fluid–structure interaction simulations are characterized by the coupling of computational fluid dynamics (CFD) and computational structure mechanics (CSM). Since the meshes of those two Systems usually do not match (see also [39]), an interpolation method is needed to exchange data (for example pressure or temperature). Two of the most common methods, which are also implemented in ANSYS Mechanical, are further described.

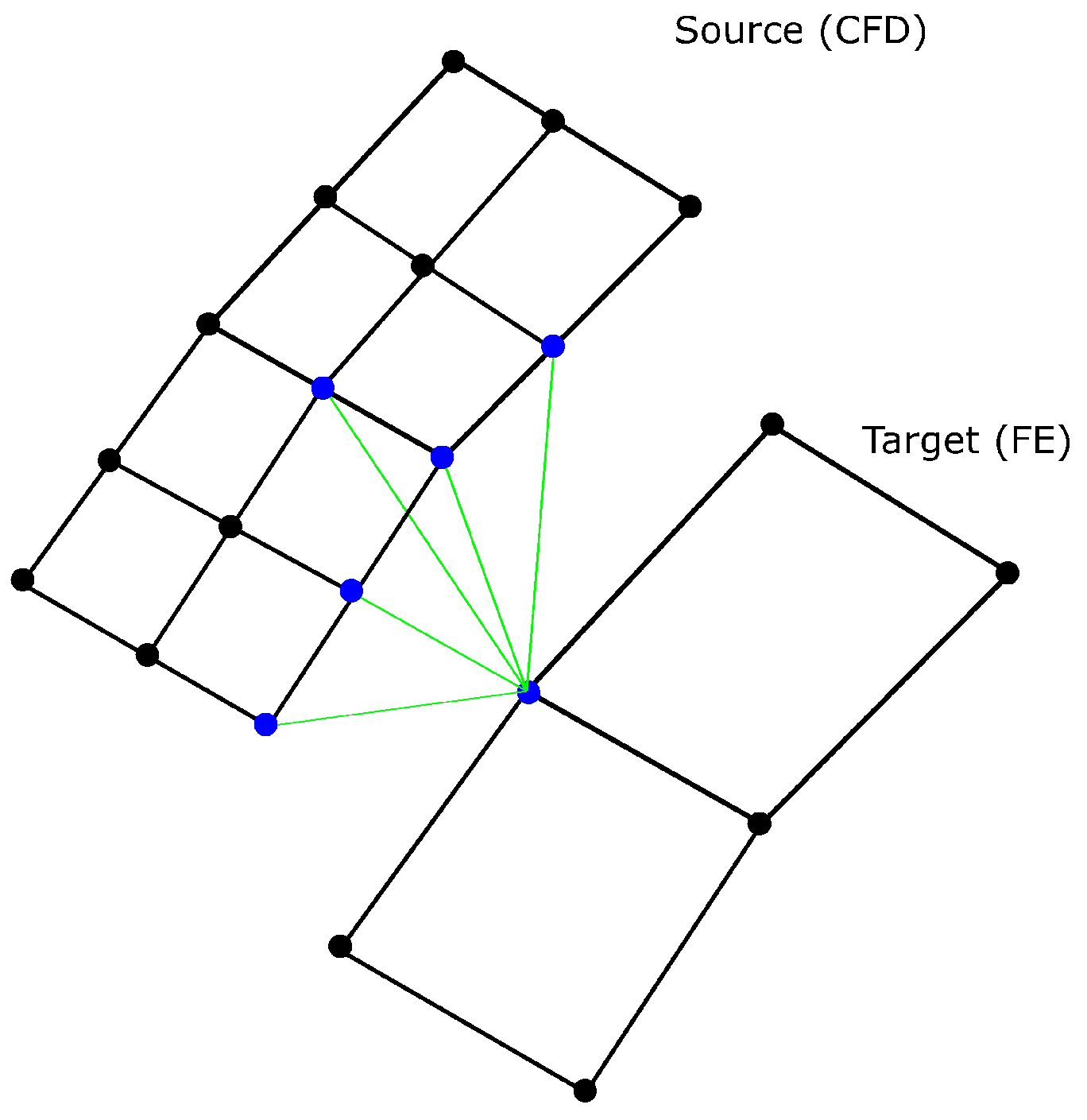
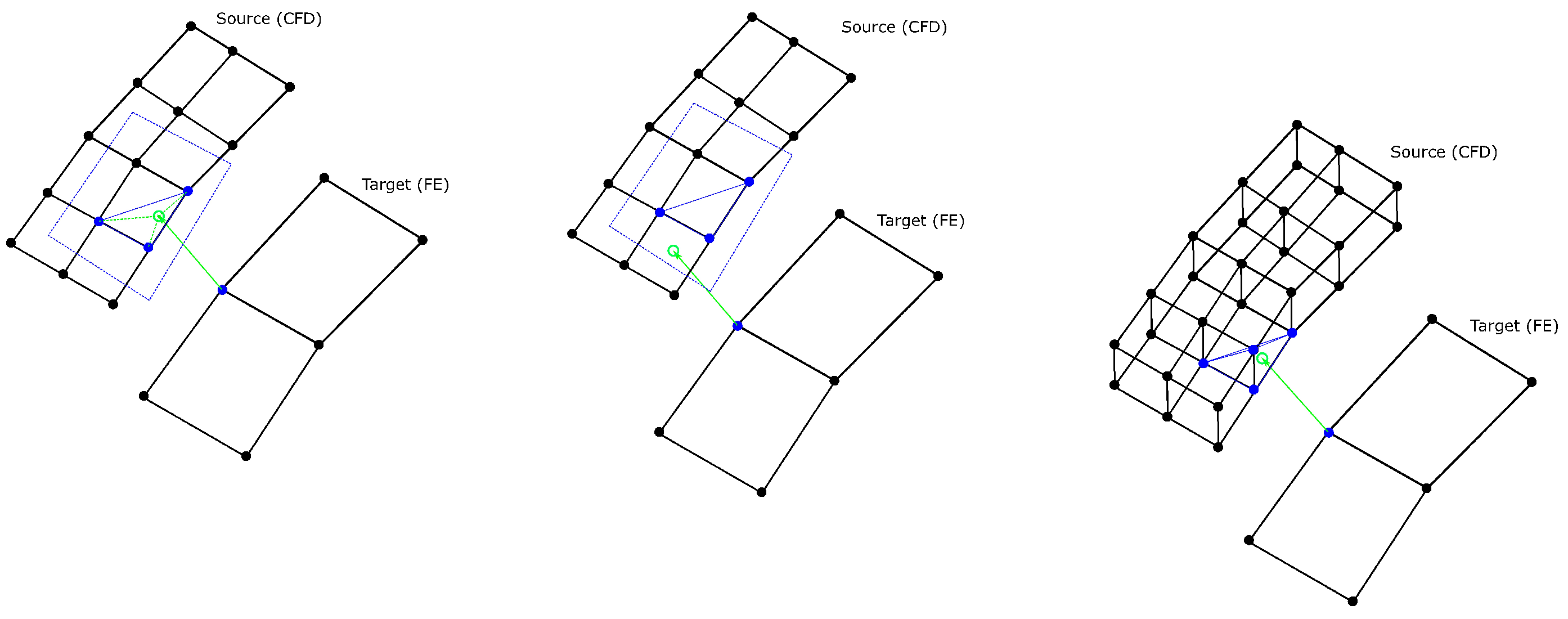
• Next-Neighbor Interpolation (Distance-Based Average)
  This interpolation calculates the distance from one target-node to a specified number of source-nodes (five nodes in Figure 10). Those Distances are used to calculate weightings. Finally, the values of the source-nodes are proportionally added up for the value of the target-node. If only one source-node is used, then the so-called nearest-neighbor Interpolation is obtained.
• Triangulation
  The algorithm creates temporary elements with source-nodes in which the target-node is projected. Those elements are of two types:
  • Surface: the target-node is projected onto a plane of a triangle (three source-points used)
  • Volumetric: the target-node is projected into a tetrahedron (four source-points used)
  For the creation of the elements, the nearest source-nodes are preferred. If the projected target-point is located outside of the created element (Figure 11), the next nodes are considered. The number of considered nodes is limited by a certain number (default is 20). In case that every projection is located outside the elements, the distance-based average method is used instead.

3.1.3. Static FEM Simulations

The time-averaged unsteady pressure field, pressure distribution at the runner side chambers and additional initial forces are used to calculate the runner’s mean stresses ${\sigma }_m$. These loads are essential for the general layout of the runner during the design process. Mean stresses always have to be below the design rules, and since this has been a common rule for decades, no further description is necessary. Nevertheless, for the subsequent fatigue analysis, it is crucial to start at this point.

For base-load operation (see Figure 5), this method has been used for decades, now, and has worked flawlessly. As there are no unsteady flow phenomena to observe, the used way to determine the mechanical stresses and hot spots is valid. To speed up the design process and minimize computational time, symmetry relations at the numerical model are used and allowed. The obtained failure is acceptable and covered by risk supplement.

3.1.4. Modal Analysis (Natural Frequencies)

To obtain a dynamic analysis of a structure the knowledge of the natural frequencies and mode shapes is of major importance. Therefore a modal analysis of the entire runner has to be performed. It is common sense that the dynamic structure could be described by the following equation:

$$\left[M_S\right]\left\{\ddot{u}\right\}+\left[C_S\right]\left\{\dot{u}\right\}+\left[K_S\right]\left\{u\right\}=\left\{F_S\right\}$$

(1)

where $\left[M_S\right]$ is the structural mass matrix, $\left[C_S\right]$ the structural damping matrix, $\left[K_S\right]$ the structural stiffness matrix, $\left\{F_S\right\}$ the applied load vector and $\left\{u\right\}$ the nodal displacement vector. As the runner operates in water, a coupled structure–water model has to be investigated. For further mathematical description see [40]. The solution of the finite element modal analysis from the runner–water coupled model gives, as a result, the natural frequencies and the modal shapes of the structure. For further literature of this topic see also [41,42]. Modes from rotational symmetric parts can be categorized by their number of nodal-diameters (ND) and nodal-circles (NC). In vibration theory nodes are points that are standing still while the part is oscillating. Therefore nodal-diameters are radial running lines that are not moving if the part oscillates with the appropriate frequency (see Figure 12 in the middle). Analogous to that, nodal circles perform a circular, closed line, which stands still if the part is oscillating (see Figure 12 right). A mode with nodal diameters shares its Eigenfrequency with a nearly equal mode. Therefore they are called doublet modes. The only difference between these two modes is a phase shift about the rotational axis.

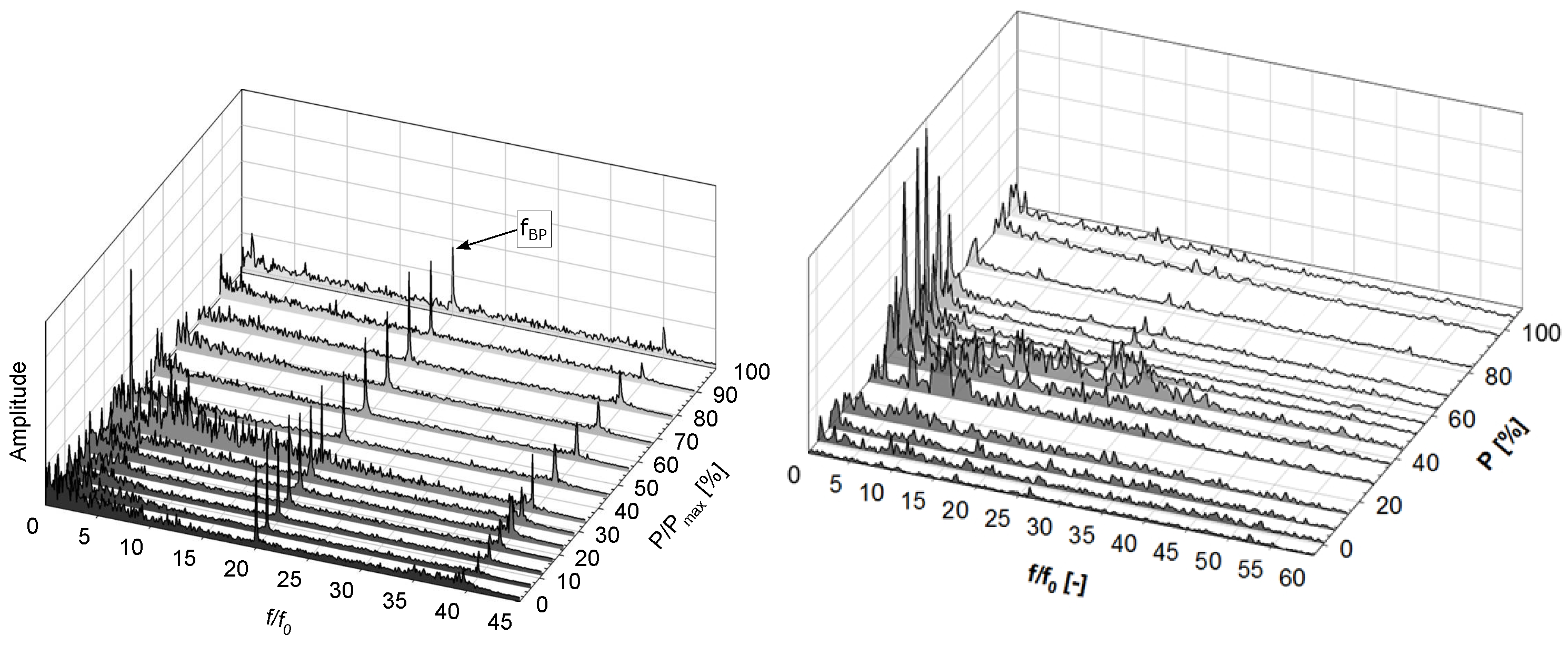
3.1.5. Harmonic Response Analysis

The HRA method was developed to determine the structural response to harmonic excitation. A precise excitation frequency is decomposed into its amplitude plus phase parts and applied to the structure as a boundary condition. Cyclic stresses of the component are the response, which can be decomposed into static mean stress and a dynamic fraction. The dynamic stress fraction then serves as the input parameter for the subsequent fatigue calculation.

One of the most important harmonic excitation in this case is the RSI between GV and RN. The application of the theory and procedure for an operational point of the investigated runner within the PSP-LowLoad project has been published at [32]. Similar results were obtained by [29,36,42].

The calculated stresses, according to this method, show a relatively good agreement with the measured mechanical stresses in the PSP-LowLoad project. However, for this validation process, the added mass effect, the pressure distribution at the runner-side chamber of the turbine and the damping of the water had to be included in the numerical consideration.

3.1.6. Measurement Techniques

Two main factors are important in determining the remaining lifetime of a hydraulic component. Firstly, the dynamic load at the respective load step and secondly, the operating period at this load step. The actual damage can only be determined using strain gauges. However, they are not suitable for permanent measurement because they cannot withstand the flow in the long term. They are indispensable as a “calibration measurement”. The operating period can be determined via machine diagnostic sensors and correlated with the “calibration measurement” to support the service life determination metrologically. Operation management values support the validation of the numerical model.

3.2. Damage Hypotheses

The actual lifetime calculation is made up of two multiplicands. To determine (1) the damage factor, i.e., how harmful the operating point is due to the flow phenomena that occur and (2) the operating time. Combinations can occur where the load point is very destructive to the turbine, but since it is never used or only passed through, it is hardly included in the turbine’s lifetime. This is mainly the case when the turbine is operated at optimum, as the damaging load points are usually only passed through when the turbines are run up to optimum. However, if the machine is used in grid-stabilisation mode, then the partial load points are also used for a correspondingly long time (see Figure 5). As a result, the damaging phenomena become more significant. In this case, the influence of damage must be taken into account.

3.2.1. Palmgren–Miner on Fatigue Calculation before Crack

According to Palmgren [44] and Miner [45], the linear damage accumulation hypothesis is the method with the greatest significance for determining component fatigue in the case of complex vibration loading with variable amplitudes. For this purpose, the occurring vibration cycles $n_i$ with amplitude ${\sigma }_{a_i}$ are compared with the number of fracture vibrations $N_i$ from the material S-N-Curve. The required load spectrum is determined from the time signal using a counting method such as the rainflow cycle count [46,47]. Figure 13 shows the procedure as well as different modifications of the Miner original method [48,49].

The vibration loading causes many partial damages $\mathsf{\Delta }{D}_i$ of the material, which accumulate in the course of their action until a critical damage value is reached, where sequence and interaction effects are not taken into account. The damage measure D is therefore defined as the sum of the damage contributions $\mathsf{\Delta }{D}_i$.

$$\mathsf{\Delta }{D}_i=\frac{n_i}{N_i}$$

(2)

$$D=\sum _i^n\mathsf{\Delta }{D}_i=\sum \frac{n_i}{N_i}$$

(3)

In addition to these values, the mean stress or the stress ratio R also significantly influences the damage. This relationship can be shown in the so-called Haigh diagram in Figure 14 based on the mean stress sensitivity M. It is constructed from many S-N-curves for different mean stresses and provides the tolerable load cycles $N_i$ for each combination of ${\sigma }_a$ and ${\sigma }_m$. Detailed elaborations are given in [48,49] and similar literature.

$$R=\frac{{\sigma }_m+{\sigma }_a}{{\sigma }_m-{\sigma }_a}$$

(4)

3.2.2. Fracture Mechanics of Crack Propagation

The topic of fracture mechanics for assessing the remaining lifetime of hydraulic components should only be mentioned here for the sake of completeness. It is not the aim of this publication series to research fracture mechanics and develop the method to this extent. For the time being, only the elastic range of the material is considered in terms of fatigue strength utilizing the S–N curve. The fracture mechanics approach must be chosen if there is already an initial crack in the component, and one wants to determine the remaining operating time. In this case, one has to deal with the stress intensity factor $\mathsf{\Delta }K$, the stress cycle range $\mathsf{\Delta }\sigma$, the crack length a and the stress intensity correction factor for a given geometry $Y\left(a\right)$. More and precise information relating to the fracture mechanic background and application to turbines can be obtained from [50,51,52,53,54,55,56,57,58].

3.3. Lifetime Prediction

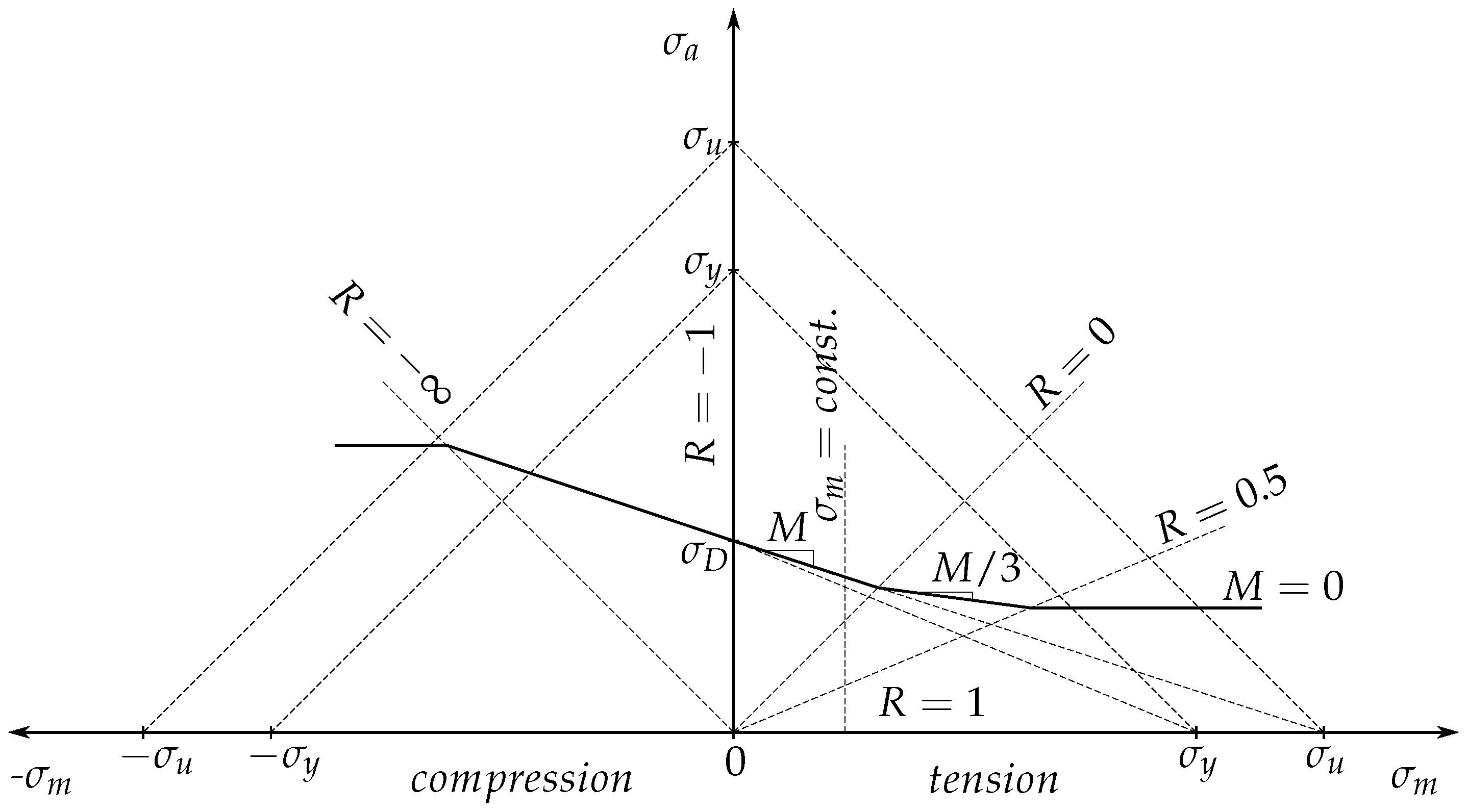
3.3.1. Stress Concentration Factor (k-Factor Concept) and Lifetime Assessment

The results of both the static mean stress evaluation and the HRA form the basis for the subsequent lifetime analysis. To determine the lifetime of the component, it is necessary to resolve the maximum stress intensity points (hotspots). Since the measurements only provide strains at the locations where the strain gauges were applied, an extrapolation must be made to those locations of the runner where the maximum stresses are expected. This is done by utilizing so-called stress concentration factors k. The concept of stress concentration factor assessment has been used in other areas of mechanical engineering for decades. At the design point of a turbine, and thus the more or less static load, this method yields relatively accurate values. However, the major problem arises when one tries to apply this stress concentration factor method to the partial load steps. Here one can see that the dynamic stresses have a more significant impact and, besides, the hotspot shifts over the structure at the different operating steps. Although the HRA calculates the amplitude and phase of the exciting frequency and introduces those as input parameters into the structure analysis, this solution’s significance is only limited to the frequency under investigation. However, since the RSI is decisive in the partial load range, as other flow phenomena have a much more significant influence on the dynamic stresses, these influences must be investigated separately. This results in the problem that the stress concentration factors k for both the mean stress and the HRA are not meaningful. As a minimum, the calculation of the stress concentration factors k under unsteady conditions should be investigated.

Ref. [59] has shown the influence of steady versus unsteady simulations on the stress concentration factor k for the investigated runner. He used a mix of numerical simulations validated with measurements to investigate the local stresses at the occurring hotspots.

The entire stress concentration factor concept is only useful for calculating the maximum stresses under static load. Beyond that, local stresses should always be used. Lifetime assessment for this procedure concentrates on fatigue strength which should be below the nominal design stress.

3.3.2. HRA, Damage Factors and Lifetime Assessment

If we consider the lifetime calculation based on HRA, we need fatigue strength concepts such as the linear damage accumulation hypothesis according to Palmgren–Miner. This is the only way to integrate the cyclic loads of the exciting frequency into lifetime determination. The dynamic stresses are used to obtain the damage factors according to Section 3.2.1. Together with Figure 5, the lifetime for the component can then be calculated, taking into account the precise, exciting frequency. However, the results are only valid for this one, investigated frequency. If another flow phenomenon triggers significantly higher dynamic loads but has a different frequency or even a frequency band, this can only be investigated with separate calculations. Then one can decide which of the flow phenomena has the more significant damage influence on the component. Suppose the exciting frequencies of the negative flow phenomena are known. In that case, one can determine the respective damage factor in each load step utilizing a separate HRA and then combine them to total damage. It can be seen immediately that this procedure soon becomes quite complex with several damage factors and frequencies.

3.4. Summary

For the state-of-the-art procedure, the following statements can be summarized:

(1)

The state-of-the-art procedure is a fast method to determine the required data considering lower computer capacity.

(2)

Although this state-of-the-art method is not sufficient, it cannot be omitted because the mean stress ${\sigma }_m$ and stress amplitude ${\sigma }_a$ are needed for fatigue strength determinations.

(3)

The HRA can close the gap between static and dynamic approach but only for one precise frequency. One special flow phenomena with one particular frequency can be observed. For this excitation frequency the remaining lifetime can be calculated. HRA is in the middle between static investigation and totally unsteady/transient simulations. The advantage is the lower simulation time and faster approach.

(4)

Since this method can only represent load shifts with a synchronized machine, the simulation of transient operating conditions (STU, CMO, LR) are not possible.

(5)

In this case, the permanent machine diagnosis is seen more as a monitoring tool and less suitable for determining the lifetime.

Table 3. Summary lifetime assessment.

Method	Mean Stress	RSI	VOS	ICV	DTV	SPP	FSO
k-factor concept (Section 3.3.1)	yes	no	no	no	no	no	no
HRA (Section 3.3.2)	yes	yes	yes	no	yes	no	no
transient assessment (Section 4.2.3)	yes	yes	yes	yes	yes	yes	yes

summarizes in a comprehensive way the state-of-the-art procedures.

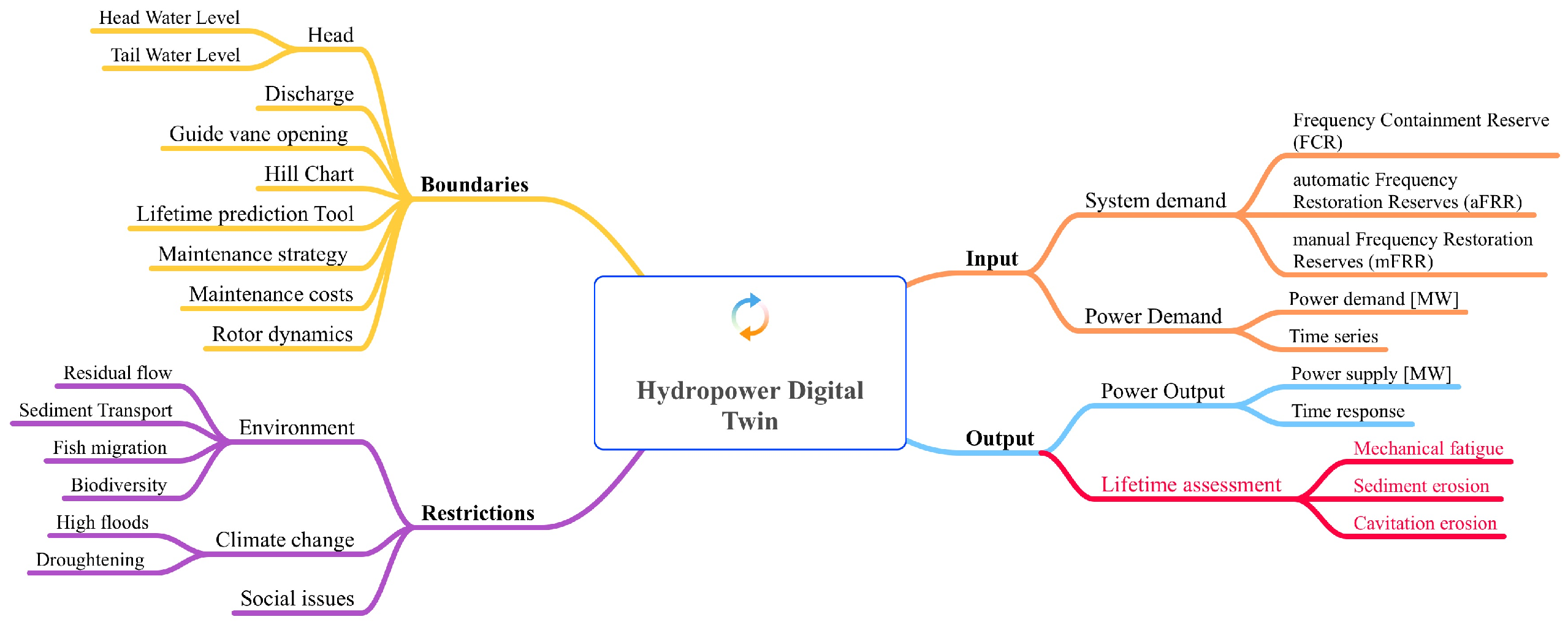
4. Multilevel Approach

Suppose the energy system is to be coupled with the operation of a hydropower plant (see Figure 3). In that case, data exchange about the lifetime and thus the boundary conditions on the part of the electrical grid must take place at the interface. The starting point of a multi-level approach is the turbine’s hill chart. This characteristic diagram reflects the hydraulic machine’s power output, performance, and possible operating limits. Further information can be added by additional levels, thus giving the system expandability. All other classes have to depend on the main hill chart. The recent publication shows a method for the fatigue assessment of a runner to create the first significant level of lifetime prediction. Figure 15 shows a multi-level approach for this relationship.

Pairing the hill chart with the lifetime function by a new assessment tool should consider specific boundary conditions:

(1)

Due to the increased part-load operation of the machine set, a static stress analysis is no longer permissible.

(2)

In the method development, it is necessary to distinguish whether one is still in the elastic stress range or already in the plastic one. Assuming that at least one crack is already present, fracture mechanics methods have to be applied. Otherwise, the fatigue analysis can suffice.

(3)

All load steps must be included in consideration of the damage—the more refined the gradation, the more accurate the method.

(4)

Attention must be paid to the validation of the numerically calculated results. Numerical methods contain many sources of error that must be handled with care.

(5)

The lifetime calculation is based on real measurements, on the one hand, and certain assumptions on the other hand. The result of such a lifetime assessment should therefore be seen as an indicator and critically reviewed.

(6)

When developing such an assessment tool, a mix of real prototype measurements and numerical calculations will be the most cost-effective option. Most of the time, the stress hotspot is unknown in the prototype measurement or a sensor application is not possible there. Only the combination brings this option of component assessment.

The following illustration describes an evaluation tool that considers the mentioned boundary conditions for the elastic range. If a crack has already appeared, it is not possible to continue with this procedure.

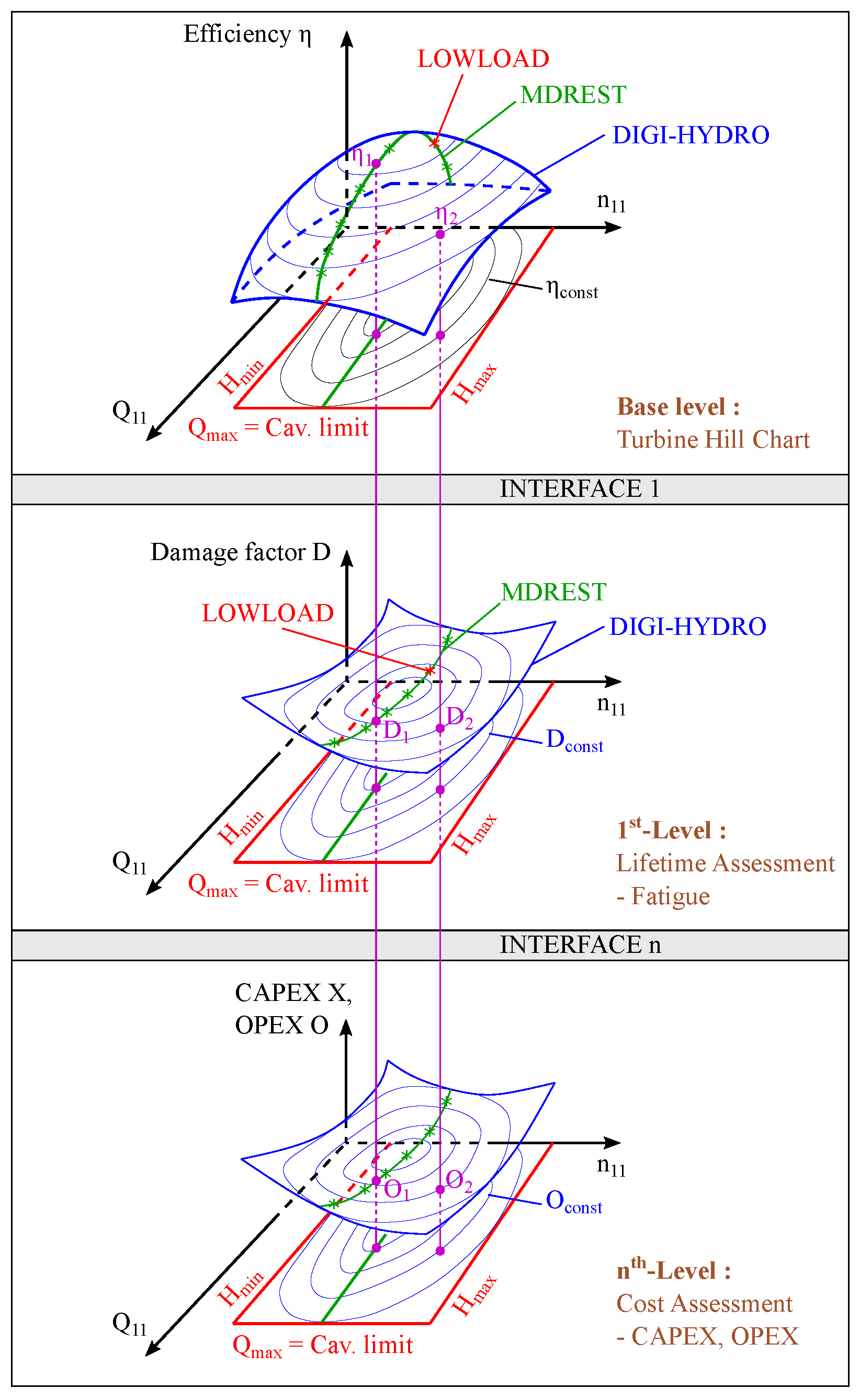
4.1. General Overview

To interpret the measured stresses (see Figure 6) at the runner correctly, information of the derived frequency spectrum are beneficial. Figure 9 gives an impression about the underlying excitations of the structure. From the literature [26,27,29,33,56] we know several flow phenomena and their structural impact at different operation points. Table 2 should give a brief classification of them correlated to the operational region and deterministic or stochastic appearance. Different mathematical or numerical approaches are necessary to correlate the appearing flow phenomena with their impact on runner fatigue. Up-to-date calculation methods include mostly deterministic loads. A way to deal with the measured data and calculate the deterministic parts of runner excitation is the measurement data decomposition like shown for example at [30]. In case of super-positioned stochastic excitations, a more sophisticated method has been developed. Figure 16 shows the different pathways for different approaches. Green marks today’s state-of-the-art procedure, which is also implemented in the industry, whereas red shows the way beyond the state-of-the-art investigations performed by the authors.

Figure 16. Assessment method.

Figure 16. Assessment method.

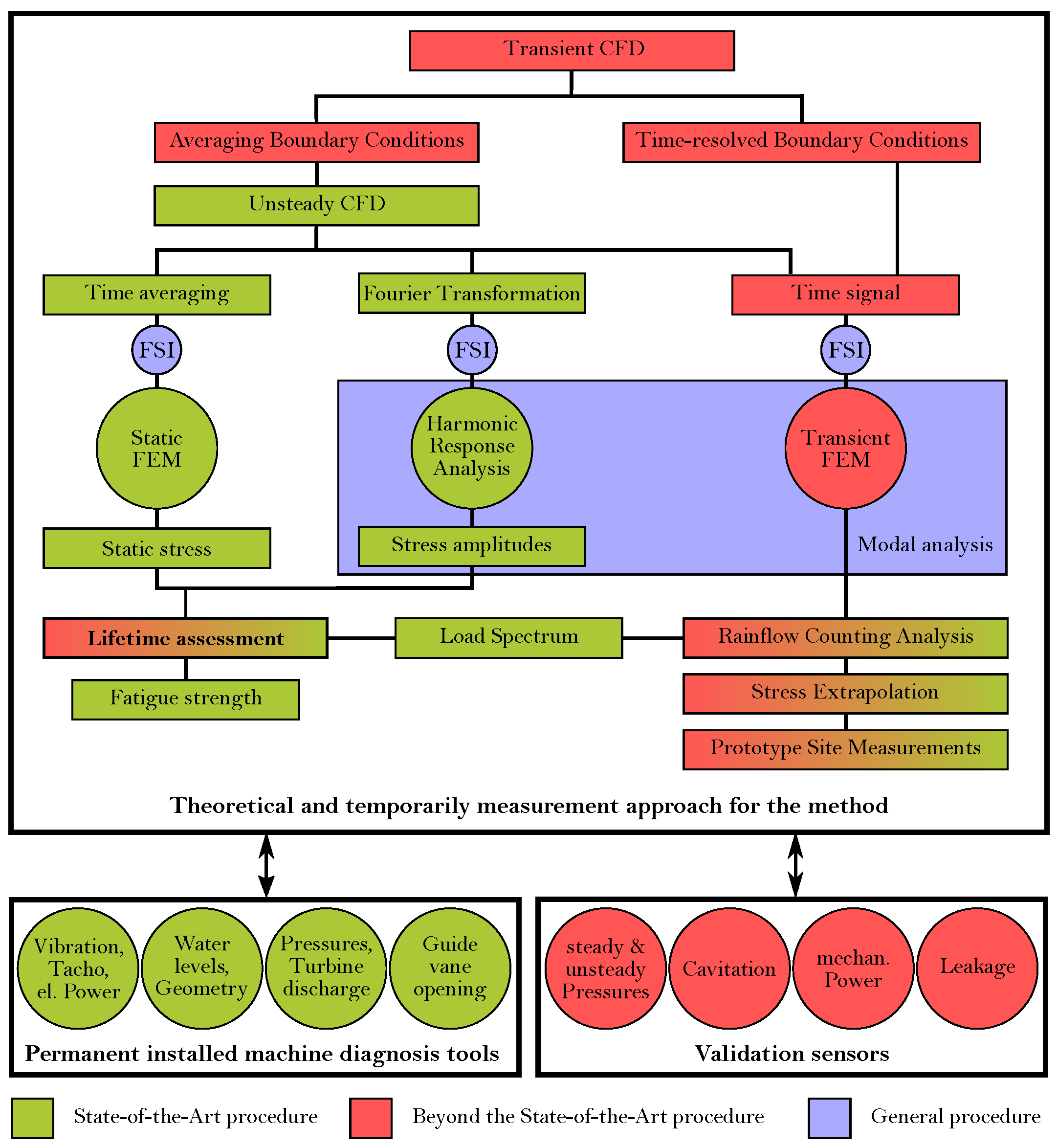
4.2. Beyond the State-of-the-Art Investigations—The Transient Assessment Model

Based on the well-investigated introduction and the subsequent findings, one can realize that a static analysis and the rotor–stator interaction’s consideration is too little to determine the component’s lifetime. At the GSG-PSP LowLoad project (see acknowledgment) the loads in the deep partial-load range were investigated, focusing on the calculation method in the unsteady CFD domain and the transient FE. However, the machine is synchronized, and there are only load changes within SNL and overload. The evaluation shows that the transient machine operation produces even more severe damage to the runner. These operation ranges were investigated in the MDREST project (see acknowledgment). Here, the standard method was extended to include transient CFD to be able to consider variable boundary conditions, such as the guide vane adjustment or increasing speed during the machine’s start-up.

4.2.1. Transient CFD Simulations

If transient operating conditions are to be included in the calculation, the state-of-the-art simulation must be expanded. As one can recognize in Section 3.3.2, the methodology of a singular assessment of flow phenomena is not sufficient. Since many of the flow phenomena mentioned in Section 2.2 can be found over the entire application range, a tool is needed that covers all exciting and natural frequencies. However, this means that the CFD simulation must be extended in the direction of transient changes in the calculation area. For example, during the machine’s start-up, the speed and guide vane adjustment are kept variable. This, in turn, means that the calculation area must be re-meshed during the simulation. The simulation must not be interrupted within the process. Since these transient conditions require a change of the underlying mesh, it is advisable to think also about the varying boundary conditions at the in- and outlet. Here, for example, the headwater distribution system’s fluctuations result in additional varying BC of the calculation model.

Taking these changing boundary conditions into account, two options are possible: (a) the averaging of these BC and application to the steady/unsteady simulation described previously and (b) to use the time-resolved BC for the simulation of transient machine operation. Option (a) leads directly to the already mentioned unsteady simulations resulting in a time signal for the load shifting with the synchronized machine. Option (b) delivers the time signal for the previously mentioned transient load steps. Both options (a) and (b) together cover the entire machine behavior and result in the computational domain’s pressure fields for each iteration. As we need several runner revolutions to resolve the physics, the amount of generated data is enormous.

Nevertheless, using measurements at selected monitoring points to calibrate the numerical solutions, the simulations can deliver a sophisticated pressure-time signal equivalent to the measurements. This procedure’s advantage is then pressure-time information at the entire calculation model and not only at selected points, serving as a base for any subsequent structural analysis.

4.2.2. Transient FE Simulations

Based on the pressure fields obtained by transient CFD calculations, the runner’s mechanical stresses are determined in this step. Pressure field by pressure field is uploaded as an input file and solved in terms of the structure’s mechanical stresses. This procedure transforms the pressure–time signal into a stress–time signal equivalent to that of the measurement.

The further processing of this stress–time signal is conducted at two selected points. Firstly, at the strain gauge positions of the measurement to enable validation of the stresses, and secondly, at the hotspot of the corresponding load step. The respective stress-time functions are time-averaged to determine the mean stress ${\sigma }_m$ and the dynamic stress amplitude ${\sigma }_a$. Afterwards, a rainflow cycle count algorithm (RFC) is applied to group the dynamic amplitudes ${\sigma }_a$ accordingly. A handicap is the relative short simulation time in relation to the measurement time. This drawback was taken into account using the statistical methods of [47]. For more information and application see [60].

4.2.3. Damage Factors and Lifetime Prediction

The last step in developing the method deals with lifetime prediction. As already presented earlier for the state-of-the-art, this calculation is based on the damage accumulation hypothesis presented in Section 3.2.1. The difference between the state-of-the-art and the transient method is that not only one single, exciting frequency is investigated, but all frequencies of the underlying flow phenomena are included. Therefore, the numerical method is equivalent to the measurement. Accordingly, the evaluation of the calculated results is done in the same way. The benefit is now the suspension in stress evaluation to the position of the strain gauges. Lifetime prediction is evaluated at the hotspots of the structure.

An essential point of the procedure is the validation of the system. Here, corresponding error estimation and propagation has to be carried out. This is discussed in Part IV of the publication series and is based on evaluating the available validation and machine diagnostic sensors. For more information regarding validation sensors, see Section 4.2.4; regarding prototype measurement, see Section 3.1.6 and error estimation, see PART IV.

4.2.4. Validation Measurements

As part of the method development for predicting the lifetime of hydraulic components in hydropower plants, prototype measurements were chosen. Plant operators made their specific plants available for these measurements. This option was chosen to prevent scaling effects from model size to actual size. The numerical calculations were also based on prototype dimensions. The power plant selection was according to the specific speed of the turbines installed. The planning of the measurements took several months, the local execution 2–3 days. An exemplary list of the installed sensors in one of the measured power plants, grouped according to operating variables, machine diagnostic sensors, temporary strain gauge sensors and validation sensors, is presented in Part III of the publication series.

For this form of transient investigation, it is essential to perform an exact validation. It makes sense to attach as many sensors as possible to the machine, namely sensors that allow a time-resolved measurement of the parameter. Dynamic measurement variables at selected monitor points are an immense advantage. These include flush-mounted pressure sensors or appropriately positioned acceleration sensors. Especially the first ones allow a comparison of the numerical flow calculation with absolute values. The validation of the mechanical stresses proved helpful to measure pressure profiles, and leakage water flows in the turbine’s runner-side chamber.

Another essential objective of validation sensors signifies measuring points at the inlet and outlet of the machine. These include existing ring lines after the inlet’s shut-off valve and a pressure measurement at the draft tube outlet. Hence, the boundary conditions of the CFD can be adapted to natural conditions. An increasing number of validation sensors installed as part of a prototype measurement results in more validation options for the individual process steps. Part III of these publications shows a list of installed sensors including validation ones.

5. Results

This chapter applies the presented procedure to a unique hydropower plant. Figure 17 shows the cross-section of the powerhouse (left) and the Francis turbine under investigation (right). More detailed information on the powerhouse (flow rate, head, machine set description) can be found in Part II of the publication series. The condensed presentation conveys the application of the actual test case.

The primary question is to determine the lifetime of a Francis turbine under different load assumptions, as shown in Figure 5. The new method incorporates aspects of turbine measurement and numerical calculation methods. This combination is chosen for two reasons: (1) the determination of the location with the maximum stresses at the runner is not possible by a pure plant measurement, and (2) the numerical calculation of the runner hotspot is much cheaper than expensive plant measurements. The optimal, most cost-effective option is to use the plant measurements to validate the computed values. Only where the limits of numerics were exceeded, a hybrid approach was proposed for evaluation. Especially STU, CMO, LR are operating modes that require a too-complex simulation and many resources. Some of these have already been carried out within the research group.

Supposing that operating points in the low load region (LL) are more damaging than those in the optimal operating area (BP), it can be expected that the lifetime of the runner will be reduced. The locations with the maximum stresses (hotspots of the runner) are used as a basis for further considerations. As derived in Part II, there are two hotspots for the runner under analysis, specifically one on the pressure side (HS1) and one on the suction side (HS2) of the runner blade. These computed values are calibrated with the measured values of the nearest strain gauges and the damage factors (according to Equation (3)) per operating point are determined. The corrected damage factors for HS1${}_{\gamma }$ and HS2${}_{\gamma }$ are significantly higher than the values for HS1 and HS2. Almost all operating points are thus classified as far more critical for both hotspots.

With the damage factors at the hotspots derived at Part II and the known load spectrum from Figure 5, the lifetime of the Francis runner can be qualitatively estimated. For this purpose, the damage factors determined are multiplied by the operating time for the respective operating point.

Table 4. Numerically estimated runner lifetime at different positions for scenarios base load and grid control.

Position	Base Load	Grid Stabilization
	[Years]	[Years]
computed HS1	13,517	363
validated HS1${}_{\gamma }$	$\mathbf{219}$	83
computed HS2	22,676	47
validated HS2${}_{\gamma }$	761	$\mathbf{22}$

summarizes the analyzed lifetime of the two load scenarios, base load and grid control, as discussed in Section 1.2.3.

Considering the pure computed results at the hotspots HS1 and HS2, the critical one for both scenarios is HS1. However, it should be mentioned that this results in unrealistic high lifetime values, especially for the base load case. The validated simulation results utilizing the strain gauge measurements show different values. In the case of base load operation, HS1 would collapse first, but when the system changes to grid control, HS2 pivots to be the point with the lowest expected lifetime. Furthermore, the enormous validation influence becomes apparent. The correction results in a theoretical lifetime reduction for pure base load operation by approximately 61.7 $(=$$13517/219)$ and for pure grid control by a factor of 16.5 $(=$$363/22)$. Furthermore, the change of the operating regime from base load to grid control means a reduction of the lifetime by a factor of 10 $(=$$219/22)$. Comparing these values with those of the measurement from PART III, it can be seen that they are of approximately the same order of magnitude, at least for the case of grid stabilization.

Table 4 shows how important it is to validate the computed values properly. The calibration of the simulation results using measured data gives a more natural dimension of the runner’s lifetime. This calibration was carried out utilizing unidirectional strain gauges in the range of one-dimensional stress gradients on the turbine runner. A more detailed description of the method is given in Part IV.

However, since strain gauges do not withstand the flow permanently, they can only be used for load-increasing tests. These tests then serve as a valid basis for the FE calculation. In the course of these load-increasing tests, as shown in Figure 7 in Part II and at Figure 18 (right side below), other machine diagnostic parameters are also obtained. The motivation for this is the subsequent correlation of the individual measured variables with each other in order to identify those sensor signals that exhibit synchronous behavior and can thus also represent the flow conditions in the turbine.

Figure 18 shows a data correlation of selected sensor signals obtained during the prototype measurement. Red boxes show a positive Pearson correlation, i.e., both signals show the same tendency, while dark blue boxes show a reciprocal tendency of the signals. The advantage is the possibility to determine which signals interpret the machine behavior in the same way and could be replaced vice versa.

By verifying the numerical simulations with prototype measurements, the potential of the extended measurement techniques for maintenance strategies was recognized. The acquired time series have a time axis resolution that allows a detailed analysis of the harmful mechanisms. However, this high time-axis resolution of the data requires more memory and a faster and more efficient data handling and analysis method. Conventional, human interpretation of the data has to be replaced by integrated machine learning algorithms, which allow a large amount of data to be processed automatically and linked to other parameters beyond the plant itself. The upcoming digitization is rewriting the future of hydropower. Optimized machine operations and better maintenance strategies will follow.

6. Conclusions/Outlook

The future goal is an in situ data acquisition tool as a basis for an internet of things (IoT), also known as the industrial internet approach. Therefore, it is of great importance to study the possible techniques and their outcome. A key role will be the amount of data gained through the applied sensors and their fast processing in the direction of key performance indicators (KPI) for a sophisticated maintenance strategy. These kinds of prototype investigations are different from model measurements on a laboratory test rig because there are no visual inspection possibilities during run-time. Machine access for sensor application might be limited. Numerical simulations can help overcome some limits of prototype measurements, and the most powerful method is a combination of both: simulation and measurements. The paper series provides a list of technologies and a related method of lifetime evaluation. As the entire topic would not fit into one paper, a splitting and division of contents were made. The following structure and content were decided:

(1)

Part I—model development and general overview

(2)

Part II—application and numerical lifetime calculation

(3)

Part III—measurements and lifetime investigation

(4)

Part IV–failure investigation, uncertainties, validation of lifetime calculation