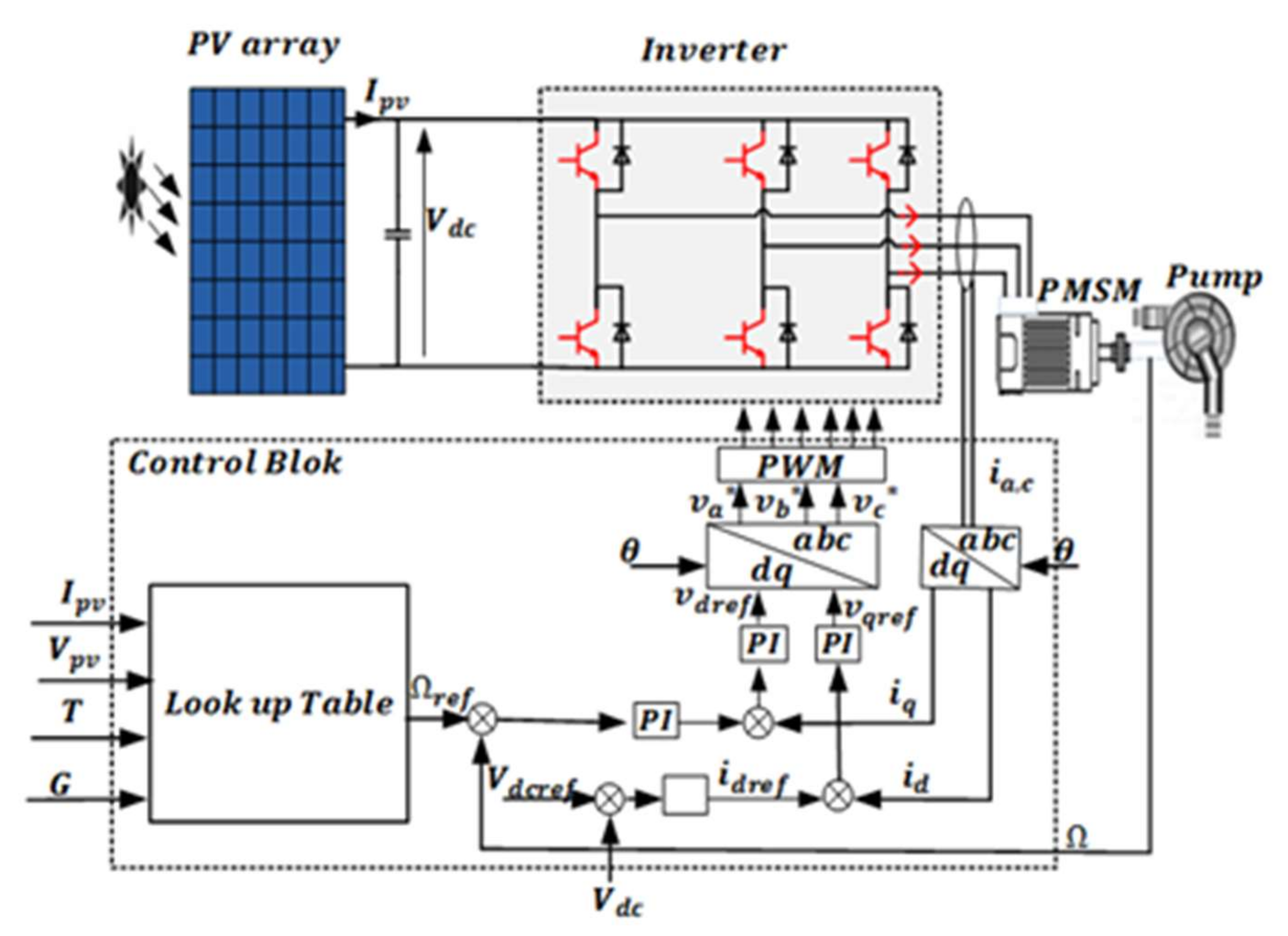
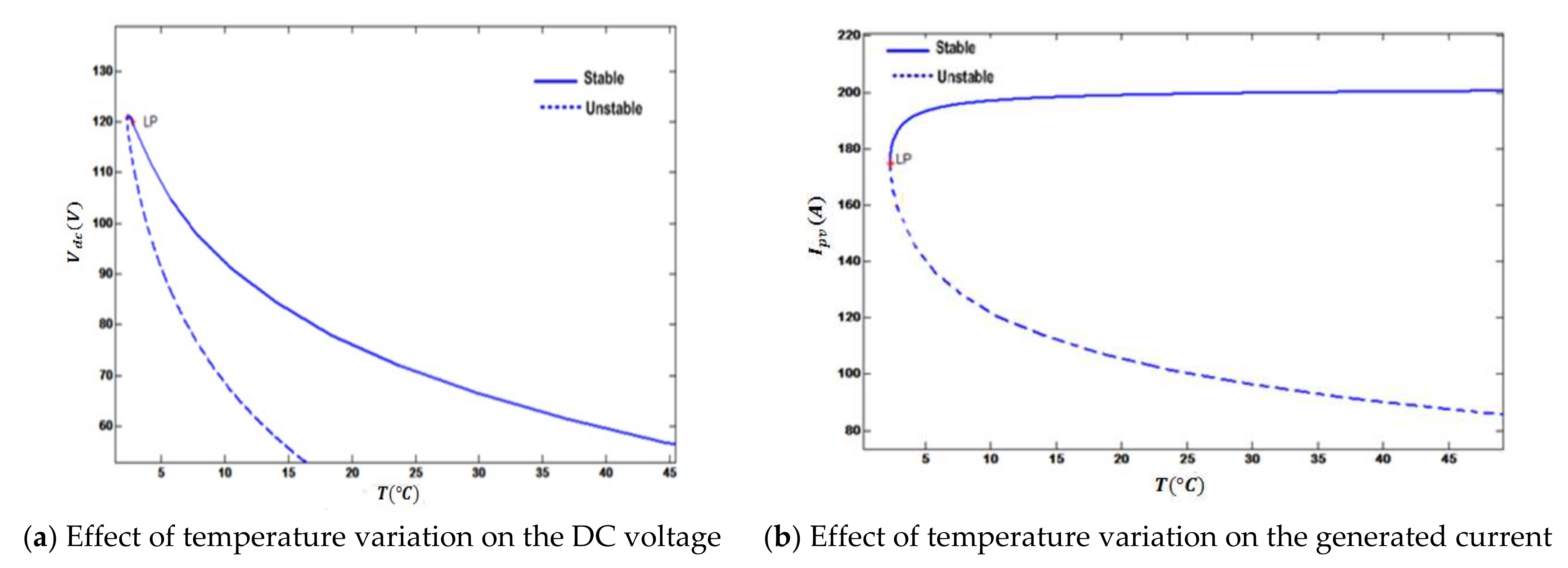
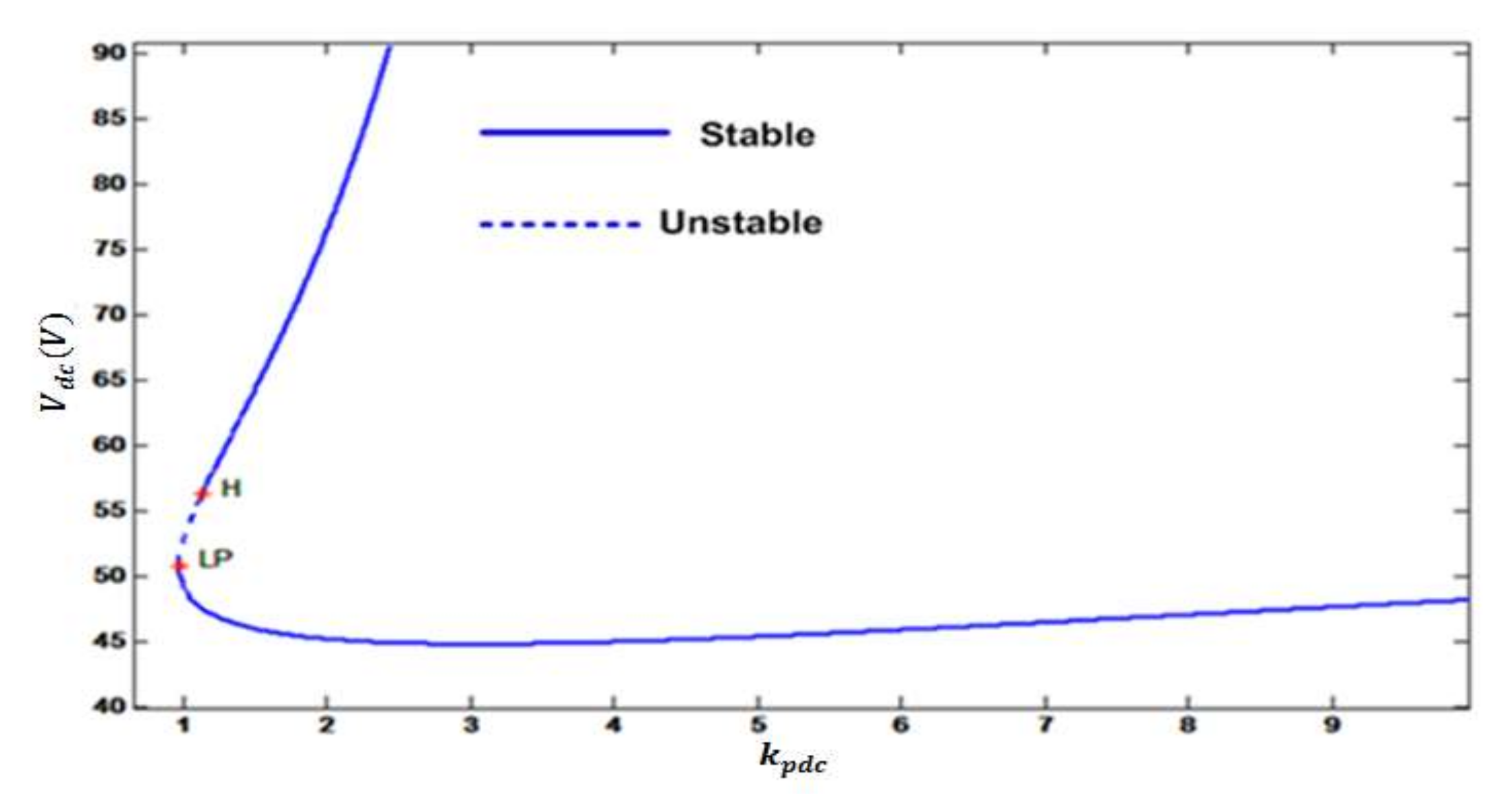
1. Introduction
Photovoltaic (PV) power systems are one of the most economical sources for water pumping in rural areas. The importance of PV power systems is due to their affordability, reliability, and maintenance. However, photovoltaic systems’ complexity comes from photovoltaic modules and switching-mode converters possess nonlinearity and time-variant characteristics. Generally, a PV generation system consists of a photovoltaic array, maximum power point tracking (MPPT) controller, DC/AC converter, and the associated controllers. Hence, the entire model is a nonlinear multivariate system, and its performance depends on weather conditions.
PV generators could be coupled directly to the pumping systems, standalone, or connected to the battery. The latter is an optimal choice from the stability point of view as it provides a fixed amount of power. Meanwhile, the stored energy would be available at nighttime. However, although researchers have been working to tackle such a problem, energy storage is an expensive option. In contrast, a direct connection to the pumping system is preferable since it saves some money. However, delivered power is subject to fluctuation and loss due to the susceptibility of PV energy.
MPPT is a common problem in PV energy systems to increase power extraction efficiency. It is crucial for any PV generator system, such as a PV pumping system, to minimize losses and to improve the entire system performance [
1,
2,
3,
4]. Even though MPPT is an efficient technique to harvest energy, the stability of the electromechanical part of the pumping system will be affected by power operating points. The electromechanical part is composed of an electric motor and pump. For each of them, the meaning of stability must be well defined. For the latter, usually, water pressure and flow rate should be within a certain limit. In contrast, the stability of the former is based on current, voltage, and motor angular speed. Consequently, the stability of the coupled system, motor and pump, should be consistent with PV operating points. For instance, the paper [
5] developed a PV drip irrigation system that has many orifices fed by a pump controlled by a motor to keep pressure and flow at some values. Therefore, motor angular speed should be governed by choosing desired voltage operating point. On the other hand, the optimal voltage that runs the system at MPP might affect pump stability in terms of pressure and flow. Thus, possible improvement of system performance could be achieved if the system is studied from a wide-angle and considers the said points. To understand all components’ effects on the system stability, the authors calibrated the motor voltage and the pump pressure in a standalone PV drip irrigation system. They analyzed the system performance under different environmental conditions. The results showed that the stability of the hydraulic system is affected by fluctuation of PV generator environmental parameters, irradiance and temperature. Many studies have been performed in the literature based on tracking MPP through power electronics converters, DC/DC or DC/AC, such that the global system is stable at some operating points [
6,
7,
8]. However, the tradeoff between MPP and stability should be optimized.
The relationship between MPP and stability under the effect of different parameters should be well understood. Analytically, it is not simple to find such a relationship, as there is no easy analytical solution for such a complicated system. Therefore, studying system behavior under varying parameters, bifurcation, is of interest for many researchers as different system characteristics can be presented. For instance, the papers [
9,
10,
11] investigated how parameter variation can affect stability, and they design controllers accordingly. Moreover, in complicated power conversion systems, they are usually connected to multi-input energy sources, and they can work in a different mode with different structures. Consequently, the dynamics of the overall system are complicated, and the effect of changing parameters might be investigated to determine stable operating points for each structure and operation mode [
12,
13,
14].
In pumping systems, we need to evaluate the behavior of the overall system under varying parameters, temperature and irradiance, to find optimal operating points that jointly achieve MPP and optimized stability. Therefore, we proposed a new control strategy based on stability-constraint power maximization problem. The proposed optimization problem is formulated as a minimization cost function of photocurrent. Precisely, the cost function is the product of output power, between critical points, by the real part of dominant eigen values of the entire system at each instant of photocurrent. This cost function must be continuous in photocurrent to ensure the existence of local minima. The photocurrent that achieves local minima of such a function is the optimal operating point that ensures MPP and reasonable stability simultaneously. Our contribution can be summarized in the following steps:
We investigate the parameter dynamics of the global system.
We introduced a power bifurcation diagram based on the PV output current and voltage plane analysis.
By a novel proposed algorithm, we determine the system optimal operating points that jointly achieve MPP and stability.
This paper starts with the subsystem models to formulate the global system model with the problem formulation in
Section 1. We identify and discuss parametric singularities in parameter planes of the PV output current and voltage in
Section 2. In
Section 3 we present the set of operating points on power bifurcation diagrams.
Section 4 proposes an algorithm to search for operating points that achieve optimal tradeoff between MPP and stability. Finally, we conclude this paper by comparing our proposed method and P&O algorithm results in
Section 5.
3. The Proposed Algorithm
The main goal is to select operating points that achieve an optimal tradeoff between delivering the maximum power and stability. If the objective controller is only extracting maximum power, then operating points that achieve this goal might be on the boundary of system stability, leading to impaired reliability. In contrast, strong stable points may compromise the amount of delivered power. Therefore, we propose a new methodology to select operating points midway between the points that maximize output power and achieve strong stability. Let’s define three types of operating points:
The maximum power operating point (MPP) at which the maximum power is delivered by the PV system, regardless of stability.
The operating point (OP) is placed equidistant from the closest critical points, regardless of the power level.
The optimal operating point (MPOP) is placed midway between the MPP and OP points to ensure both stability and delivering sufficient power.
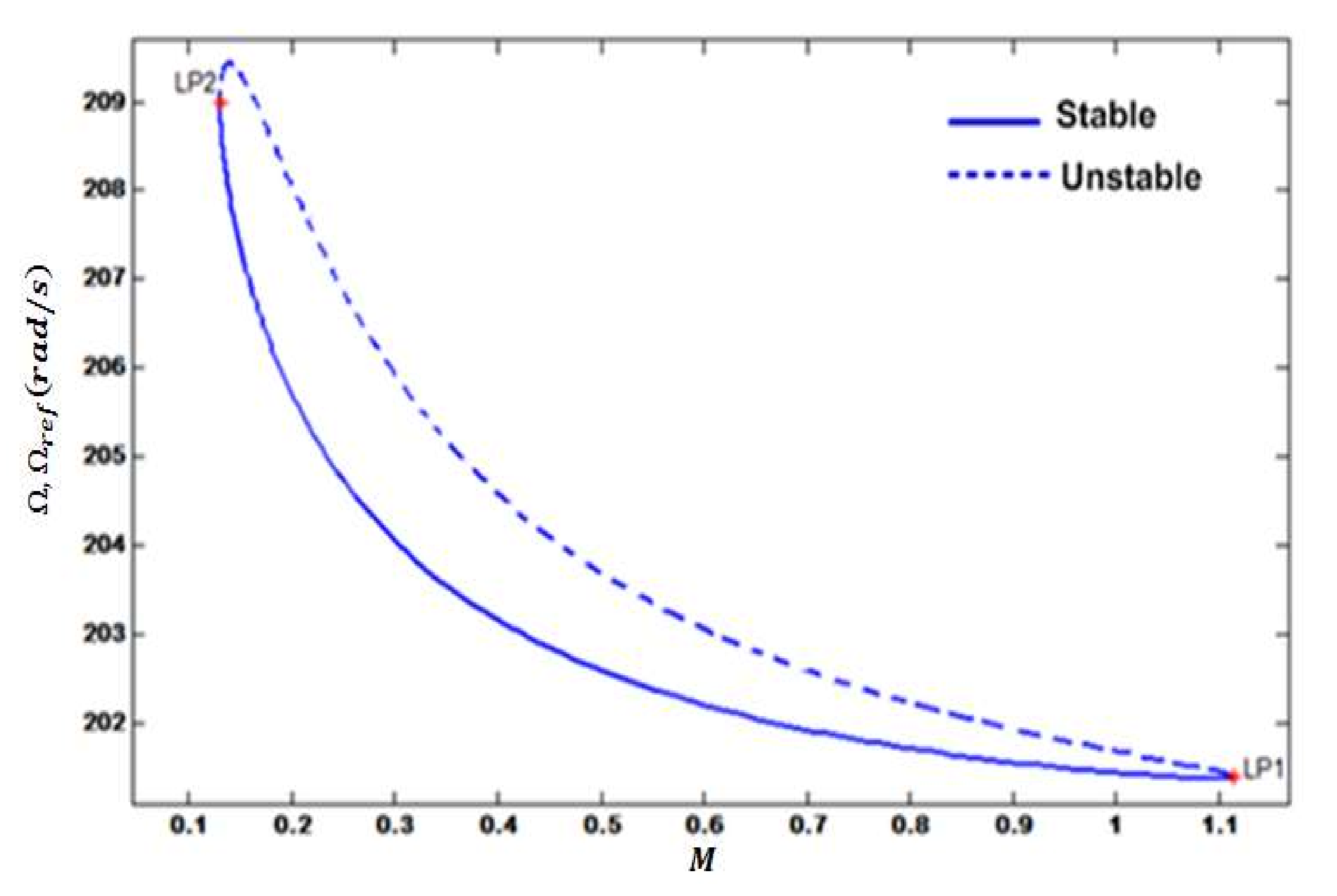
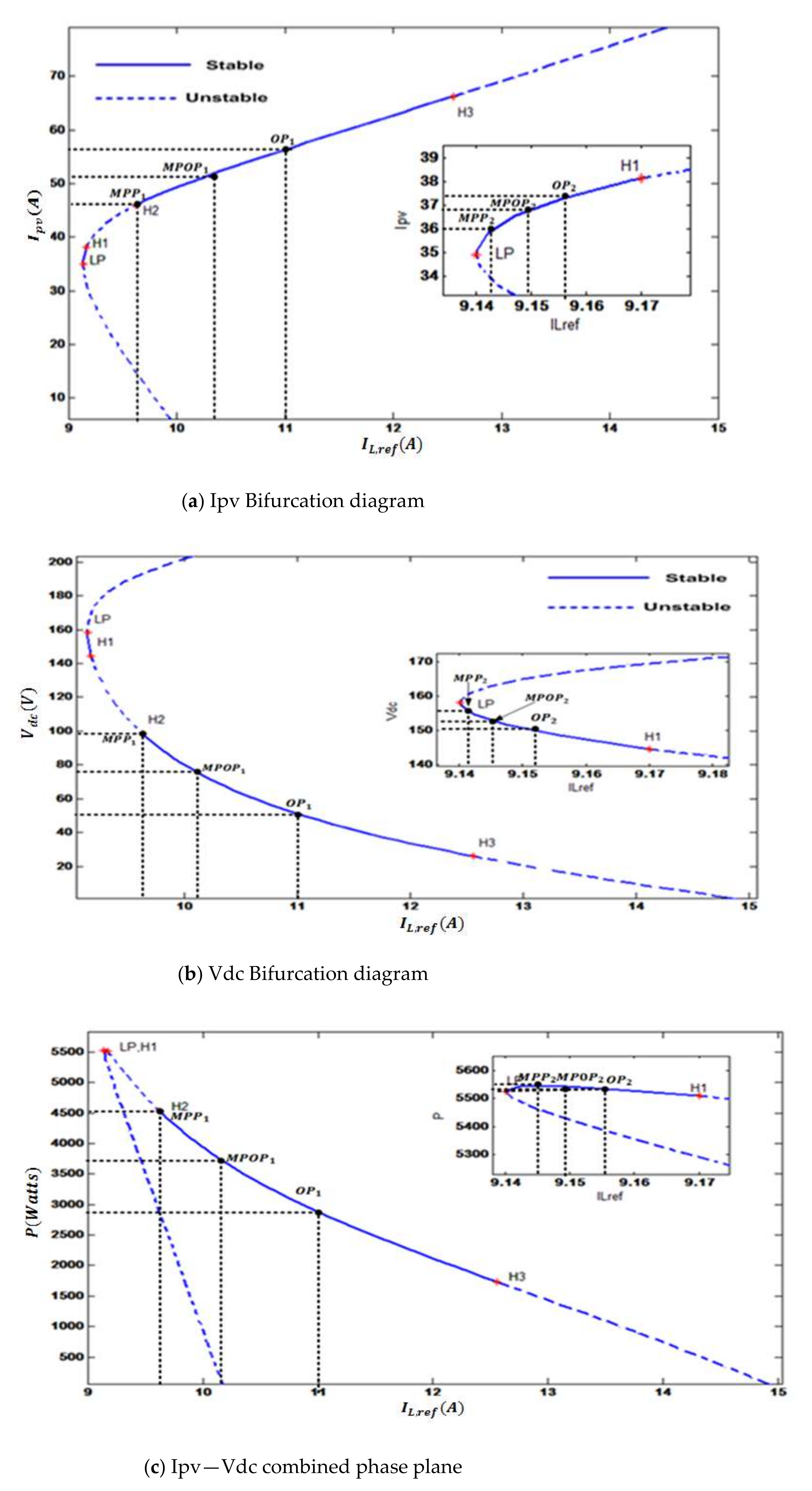
A stability assessment of the entire system needs eigenvalues estimation, which is often computationally expensive for multiple parameters. Therefore, few effective parameters are selected to investigate the parametric singularities and to inspect the anomalous behaviors. We mainly studied the photocurrent on stability and produced power as it is the control parameter that was considered in this work. In other words, we varied output current and observed the change in the output voltage, as shown in
Figure 7 To elaborate, assume
Figure 7b, at temperature T = 25° and irradiance G = 200 watt/m
2, we have one saddle-node, LP, and three critical Hopf points, H1, H2 and H3, with an associated dominant pair of complex conjugate eigenvalues. To find the optimal operating point, MPOP, we must find OP and MPP first, then MPOP will be placed midway between them to ensure that the system works far enough from critical points and outputs a fair amount of power. The figure shows two stable regions bounded by pairs of critical points (LP, H1) and (H2, H3). Possibly, MPOP could be in either region. Therefore, two points of OP (OP1, OP2) and two MPP (MPP1,MPP2) points should be determined for region1 and region2, respectively. OP points in both regions are placed far enough from critical points, namely, midway of each pair of critical points, so that the system won’t be subject to a harmful response. Consequently, MPOP in each region (MPOP1, MPOP2) were chosen to be midway between the pairs of (OP1, MPP1) and (OP2, MPP2), respectively, as shown in
Figure 7b.
We claim that this methodology of selecting MPOP results in optimal trade-off between stability and maximum power delivery. To validate our claim, MPOP can be estimated speculatively as local minima of the cost function. Such a function is the product of all instant amount of power between critical points by the real part of the dominant eigenvalue of states 2 and 4, iq and id, respectively, in Equation (24), which are denoted as
. In other words, the cost function for each stable region is computed by varying photocurrent. At each instant photocurrent, we found corresponding power, the dominant eigenvalues
, and the product of power by the real part of dominant eigenvalues
. This cost function must be continuous in photocurrent to ensure the existence of local minima. In our system, cost function in the first region, J
1, was computed by taking the instant output power between critical points H2 and H3 and multiplying it by the corresponding real part of
. Samwise, in the second region, instant output power between critical points H1 and LP were multiplied by the real part of dominant eigenvalue
to form cost function, J
2. The general form of this minimization cost function is as follows:
Such that
where
is the photocurrent at time k,
is the corresponding output power at a given photocurrent,
and
are lower and upper bounds, respectively, of photocurrent at both critical points.
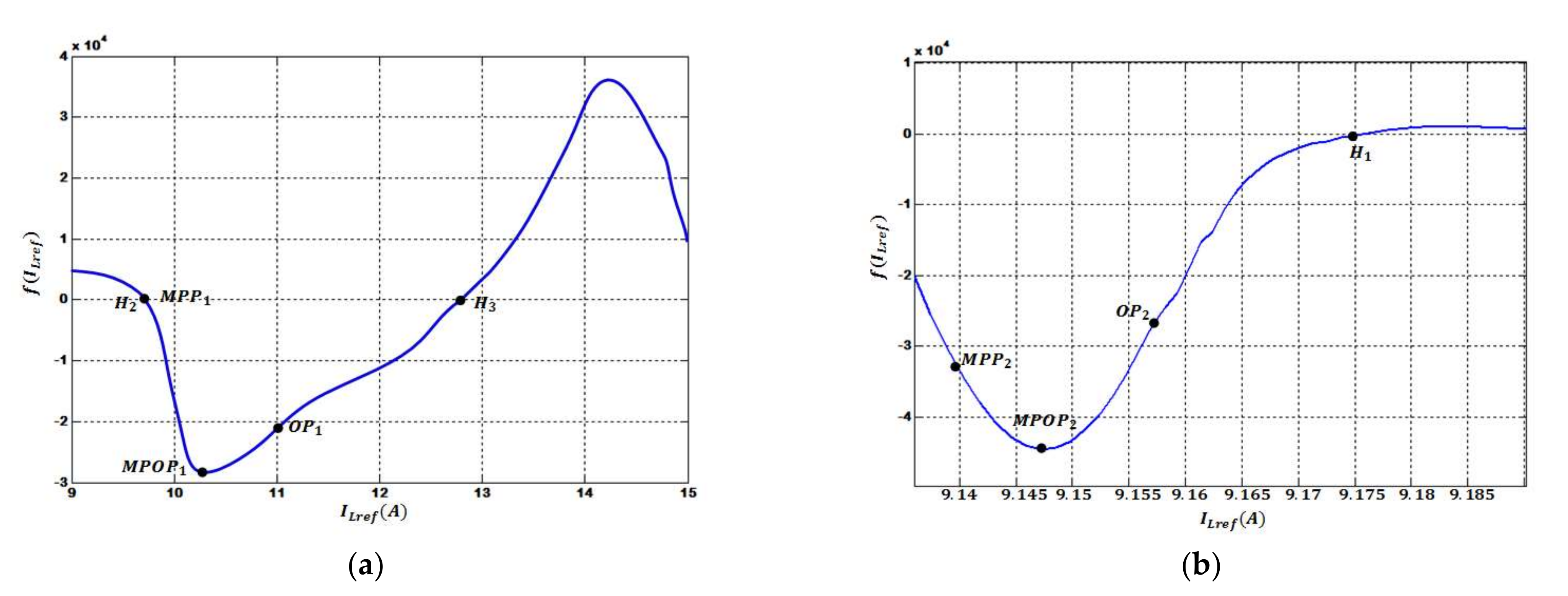
Figure 8 represents both cost functions (f(
IL1), f(
IL2)) for region1 and region2, respectively. MPOP1 and MPOP2 label local minima for both functions at
IL1 = 10:4 A and
IL2 = 9:15 A, respectively, which can be easily verified from
Figure 9c.
The result that we concluded is based on a specific amount of temperature and irradiance, T = 25° and G 200 watt/m
2. However, those parameters are varying over time, and they could be any different combination. Consequently, stable regions and corresponding cost functions were subject to change, resulting in varying local minima and, hence, different MPOP placement. Therefore, we repeated the procedure of selecting MPOP under temperature and irradiance variations, and the results are shown in
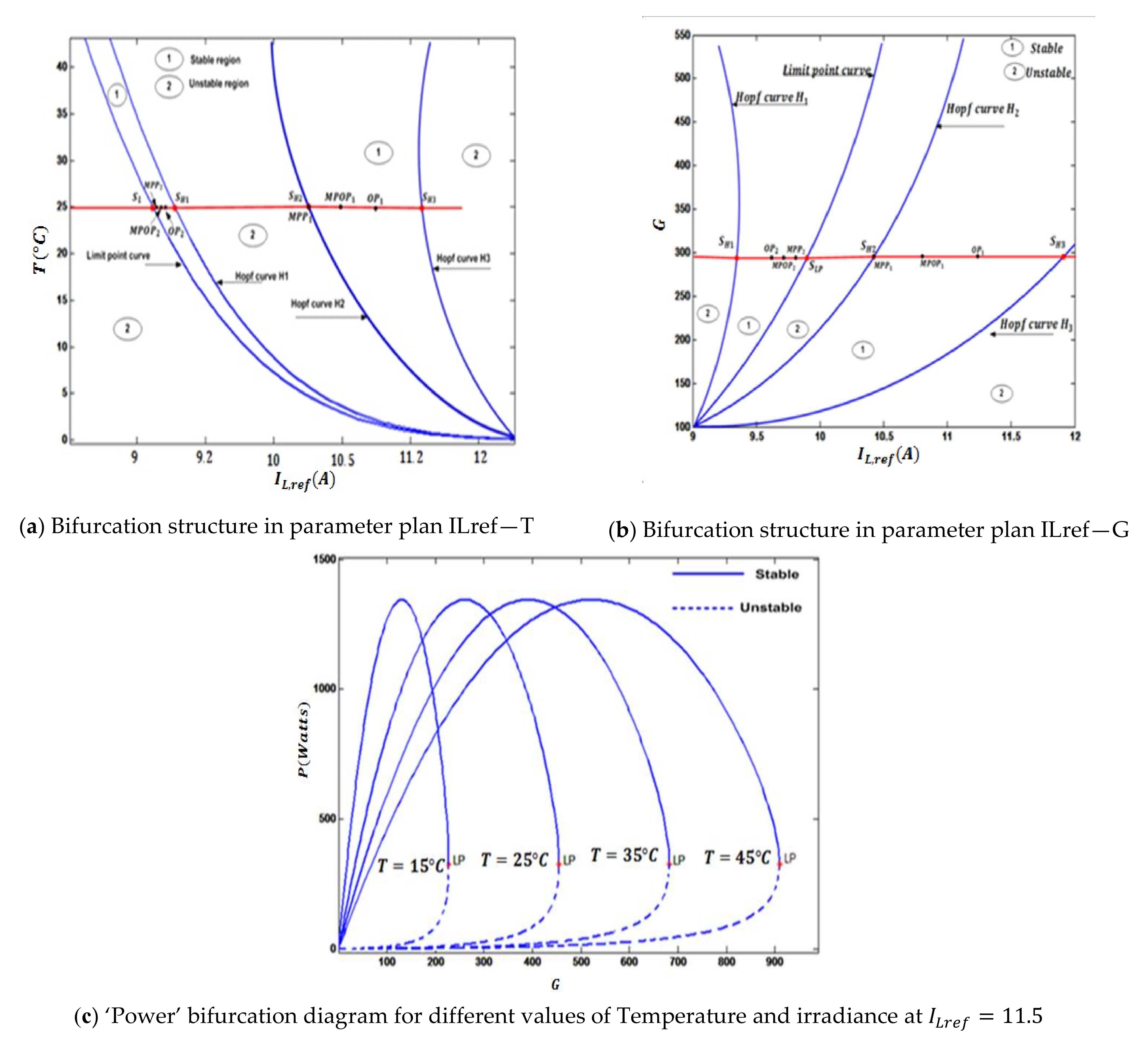
Figure 9.
Figure 9a, and
Figure 9b show curves split regions into stable, labeled with the number 1, and unstable, labeled with the number 2. Finding MPOP was achieved using the same explained technique at each instant amount of temperature and irradiance in stable regions. For example, to help find MPOP at T = 25° and G = 300 watt/m
2, red lines were drawn horizontally. Their intersections with curves determine corresponding critical points and associated eigenvalues that contribute to cost function implementation. Temperature degrees and the strength of irradiance directly affected operation regions. Increasing those parameters results in critical points spacing and distinguishable regions that help to decide MPOP positioning. For instance, at each instant of temperature and irradiance, the system displayed more than one stable region, resulting in multiple MPOP placements in each region. Only one of them should be nominated to be the optimal operating point. In our proposed method, the one associated with a widen stable region, with enough distance between two critical points, was selected for safety assurance.
At a specific photocurrent, the right combination of temperature and irradiance led to analogous output power. In
Figure 9c, photocurrent was fixed at 11.5 amperes, and the output power was a function of temperatures and irradiance. At low degrees of temperature, maximum power could be reached with a minimal amount of irradiance. On the other hand, with increased temperature, a higher amount of irradiance was required to achieve the same amount of output power, which is reasonable by the principle of PV power generation. Unfortunately, such parameters are uncontrollable, and the right choice of MPOP requires knowing the effect of parameters variation on the complete range of photocurrent. In other words,
Figure 9c should be recreated for each instance of current and I
Lref; MPOP was determined based on the actual reading of irradiance, temperature, and the optimal current that balanced between MPP and reliable stability. In real-time, MPOP should be determined at any combination of PV parameters. Therefore, a dataset might be collected experimentally, and then an online solution can be found using machine learning tools.
To recap, our proposed methodology of finding MPOP passes through the following steps:
Step 1: Define the basic design parameters,
, see
Table 1.
Step 2: Using the PV pumping system model (24), compute the equilibrium points and their eigenvalues.
Step 3: based on step 2, find phase planes, and identify stable regions for IPV and Vdc according to ILref variation.
Step 4: from IPV and Vdc phase planes, draw the output power phase plane.
Step 5: Define the MPP and the OP points on the power bifurcation diagram and derive the MPOP. The corresponding DC voltage value is chosen from
ILref–
Vdc Phase plane as in
Figure 8.
Step 6: For DC voltage regulation, the corresponding proportional gain can be defined from the
phase plane as in
Figure 5.
4. Validation and Results
To validate our proposed algorithm, we compare our proposed algorithm against Perturb and Observe algorithm, P&O, in terms of stability and extracted power. Use of this algorithm is a common technique to track maximum power point in the PV system. P&O only extracts MPP by adjusting the output voltage at the DC/DC converter regardless of the other system components. Although P&O is an efficient algorithm for power extraction, it does not consider system stability. The simulation results show that our proposed algorithm offers a good alternative that balances power extraction and system stability.
We set up MATLAB/Simulink with shown parameters in
Table 1 [
17]. We assumed a fixed amount of temperature, T = 25°, as the change in temperature was slow compared to the change in the light intensity, which might fluctuate rapidly. Therefore, simulation started with initial illumination, G = 30 watt/m
2, and changed to 500, 100, and 800 watt/m
2 at the 1st, 3rd and 6th second, respectively. According to these values, motor velocity should be set at 150, 50 and 180 rad/s to track maximum power point. Performance of tracking control was evaluated under three different operating points, OP, MPP, and MPOP, in each stable region. With the current considered scenario, we found two stable regions, see
Figure 7c, where we needed to evaluate our system performance with proposed operating points in both regions.
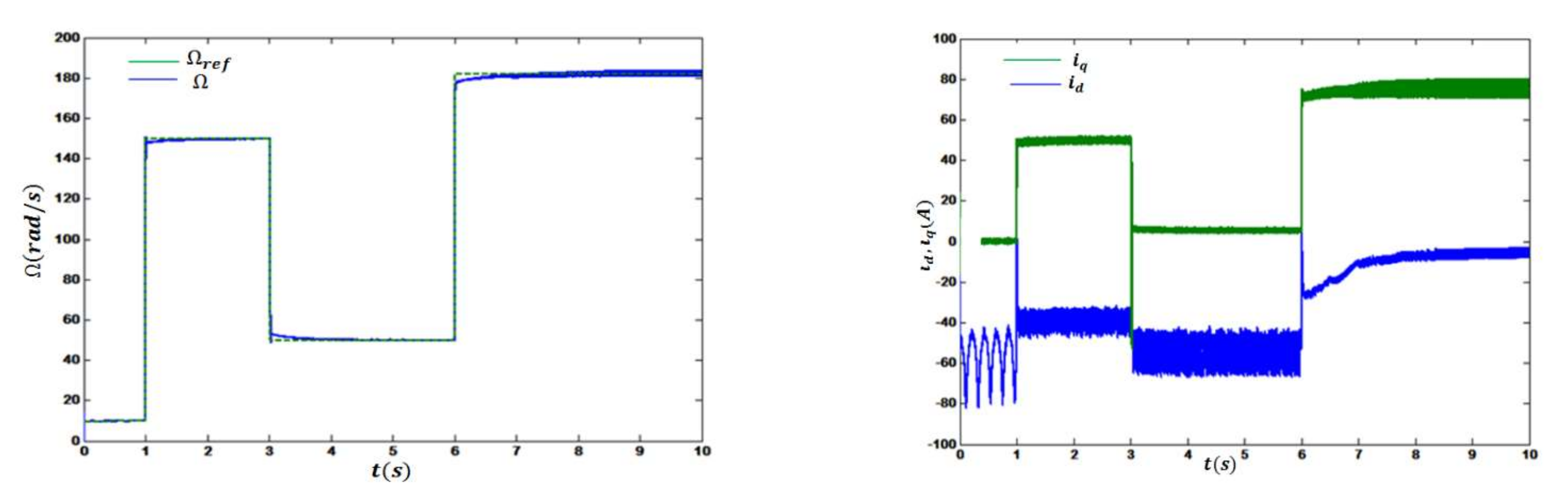
4.1. Evaluation of Operating Points in Stable Region #1
This region was sandwiched between two critical points. The operating points could be controlled with an
IL current in the range of 9.6 and 12.7 A. Particularly, the maximum change of
IL current in this region was 3.1 A, which is a fair amount that ensures optimal operating point placement based on the cost function explained earlier. Starting from
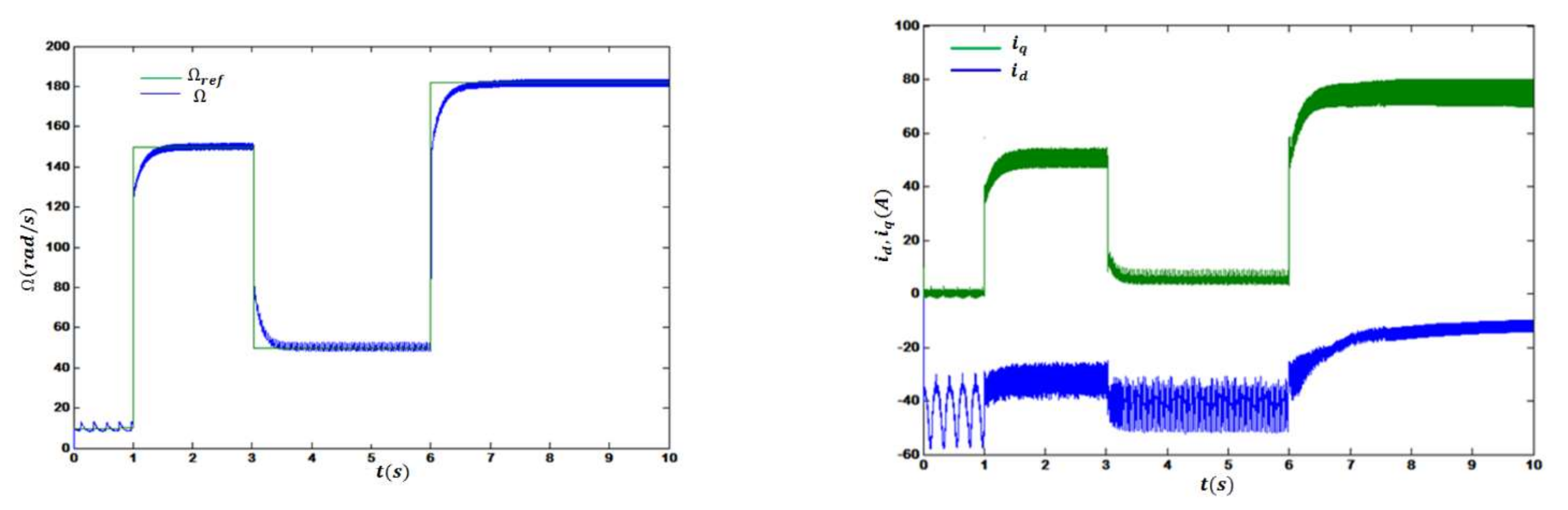
Figure 10 the PV PMSM system operates at the point OP1. The transitions of the motor speed and stator currents are shown in this figure. At the third second, the iq current of the PMSM was negative when the speed changed from 150–50 rad/s because PMSM operates in generator mode. Moreover, the stator currents were reduced because of vector control with the q-axis reference current,
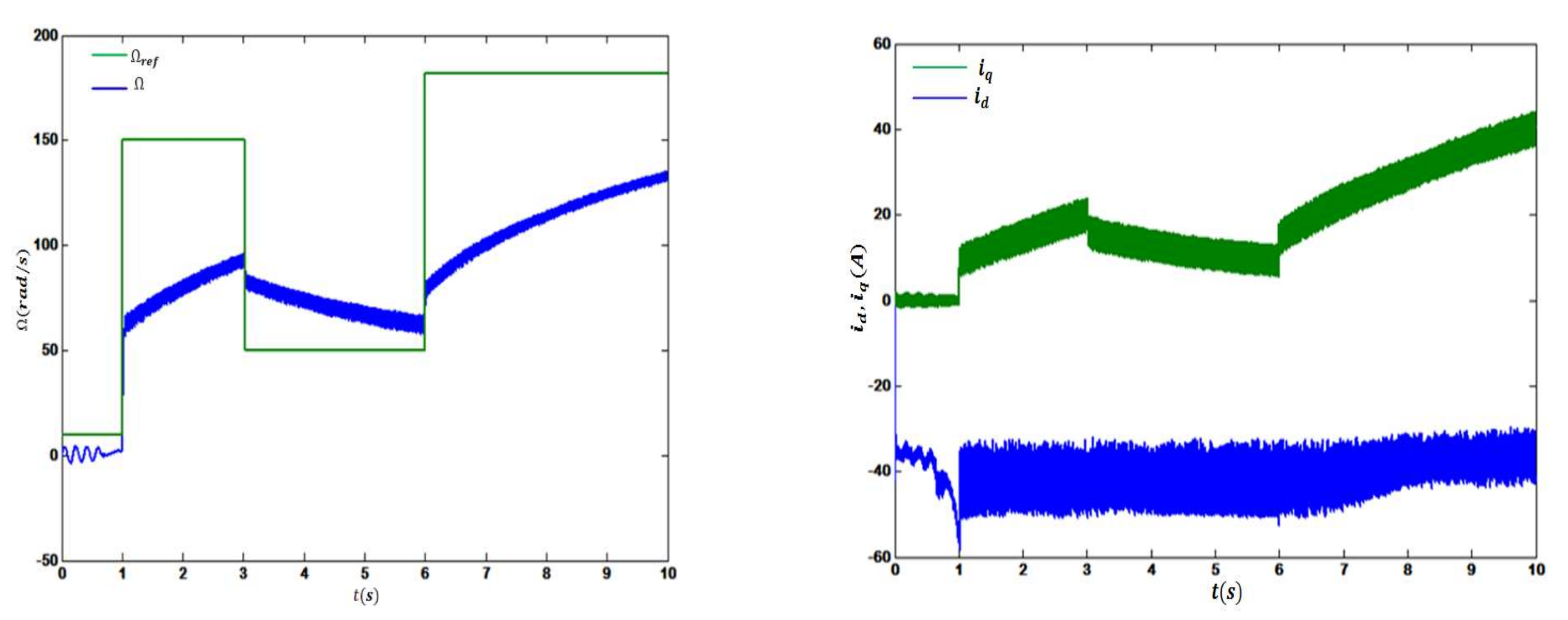
Iq. The figure shows that dynamics with OP1 were acceptable in terms of oscillation because of its distance from critical points. However, results showed a loss of some amount of delivered power.
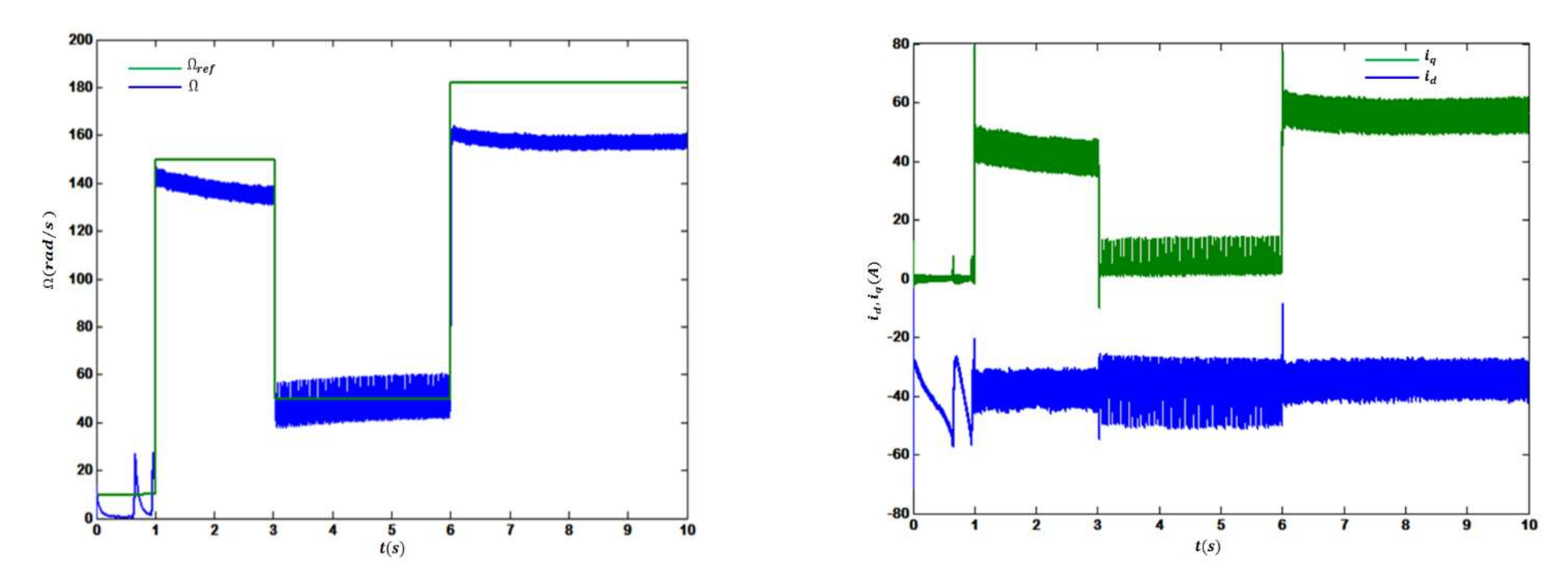
Figure 11 explains that, by changing the operation point to MPOP1, the system’s performance could be ameliorated. System dynamics associated with the operating point MPOP1 were optimal in terms of stability and maximum delivered power, reducing oscillation, and better reference tracking. The effect of the operating point location was obvious on the stator current, where little variation in rotor speed showed a significant impact on it. In contrast, dynamics with MPP1 resulted in a tolerant amount of delivered power, although oscillation increased due to the location of the point MPP1, see
Figure 12. Comparing part b of
Figure 10,
Figure 11 and
Figure 12 tells us that closeness of operating point from critical points resulted in distortional current.
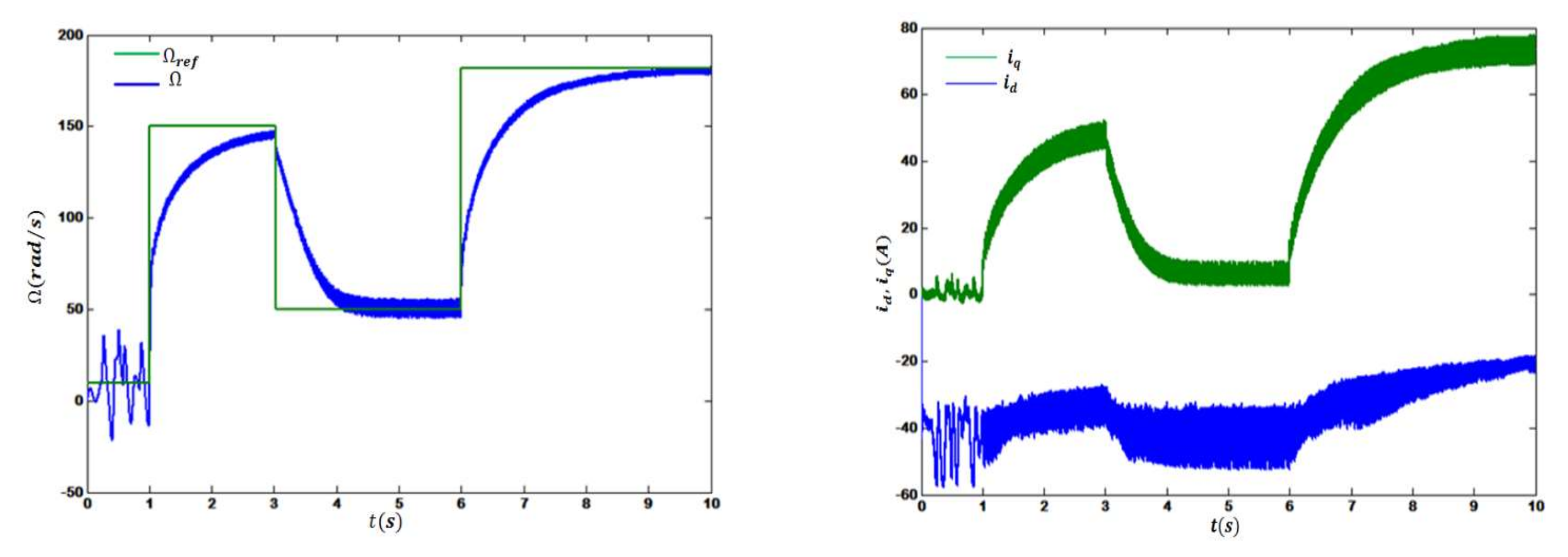
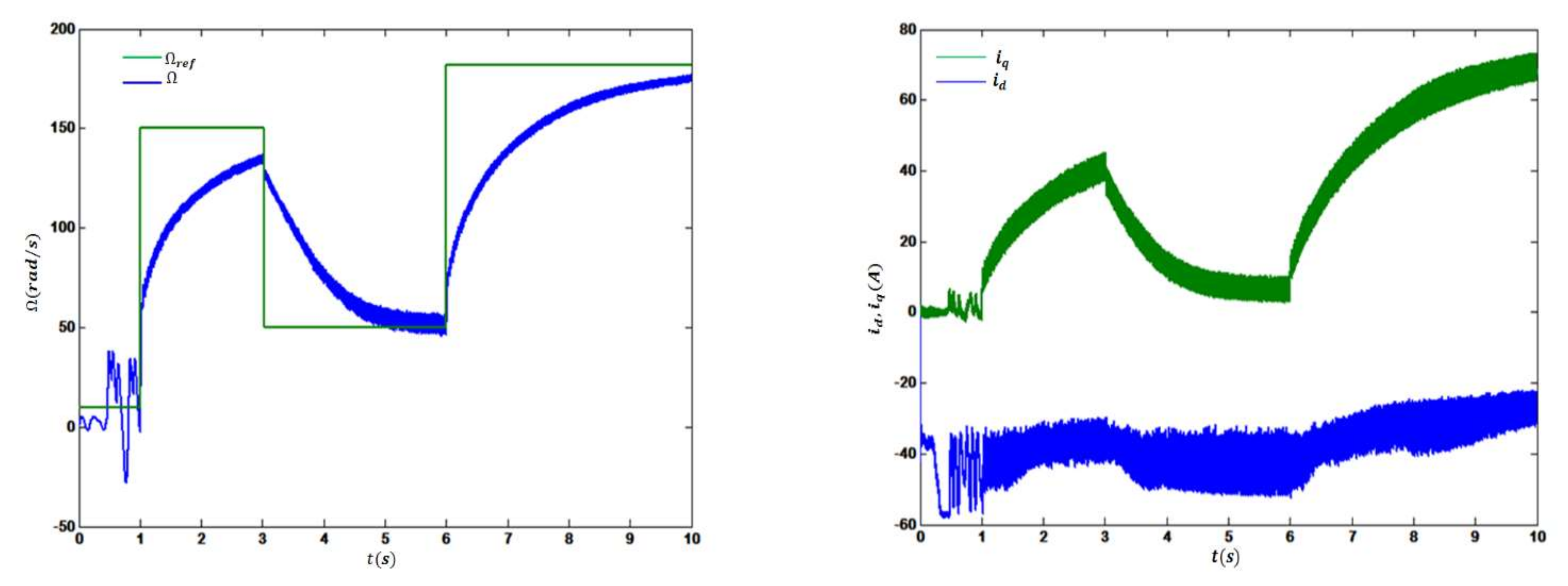
4.2. Evaluation of Operating Points in Stable Region #2
In this narrow region, the transient system from stable to unstable state was susceptible to change in
IL current. In other words, little change in
IL, at a scale of milliampere, or even slight perturbation in initial conditions, might lead to destabilized system dynamics. Therefore, work in this region is risky and may result in unpleasant performance. As shown in
Figure 13 and
Figure 14, both operating points, OP2 and MPOP2, showed a similar effect on reference tracking control and the consequent stator current. However, due to its location midway between two critical points, OP2 was located at the furthest possible distance from those points. Consequently, running the system at this operating point improved tracking control slightly, although general performance was imperfect compared to running the system at OP1 in region1. In contrast, MPOP2 was placed midway between MPP2, which is close to the critical point, and OP2, causing MPOP2 to be pushed up toward the stability boundary. Therefore, it is not surprising to have found a worse control performance than when the system runs at OP2. The worst-case scenario is when MPP2 is chosen to be operating point wherein the quality of reference tracking is inferior, resulting in wasting delivered power and undesirable system vibration, as shown in
Figure 15. In all cases, the points OP2, MPOP2, and MPP2 were located in distances of milliampere from each other. Such an arrangement causes the validation of our proposed algorithm to be difficult in this region. Hence, no optimal tradeoff solution could be found.
In conclusion, if we possess a system with multiple stable regions, and to get the best of our proposed algorithm, the region that guarantees placement of MPOP at enough distance from critical points is selected where the sensitivity of stability to the current variation in this region is minimal.
4.3. Comparison between Conventional MPPT and Proposed Algorithm
In this subsection, we need to study the system behavior when tracking maximum power with two different approaches, 1—using conventional P&O algorithm to track MPPT regardless of stability, 2—using our proposed algorithm that balances stability and maximization of delivered power. Initially, simulation starts with assumed light intensity G = 530 watt/m
2 and changes to G = 550 watt/m
2 and G = 510 watt/m
2 at the third and 6th second with corresponding generator speeds that achieve maximum power extraction, 100, 110, and 90 rad/s, respectively.
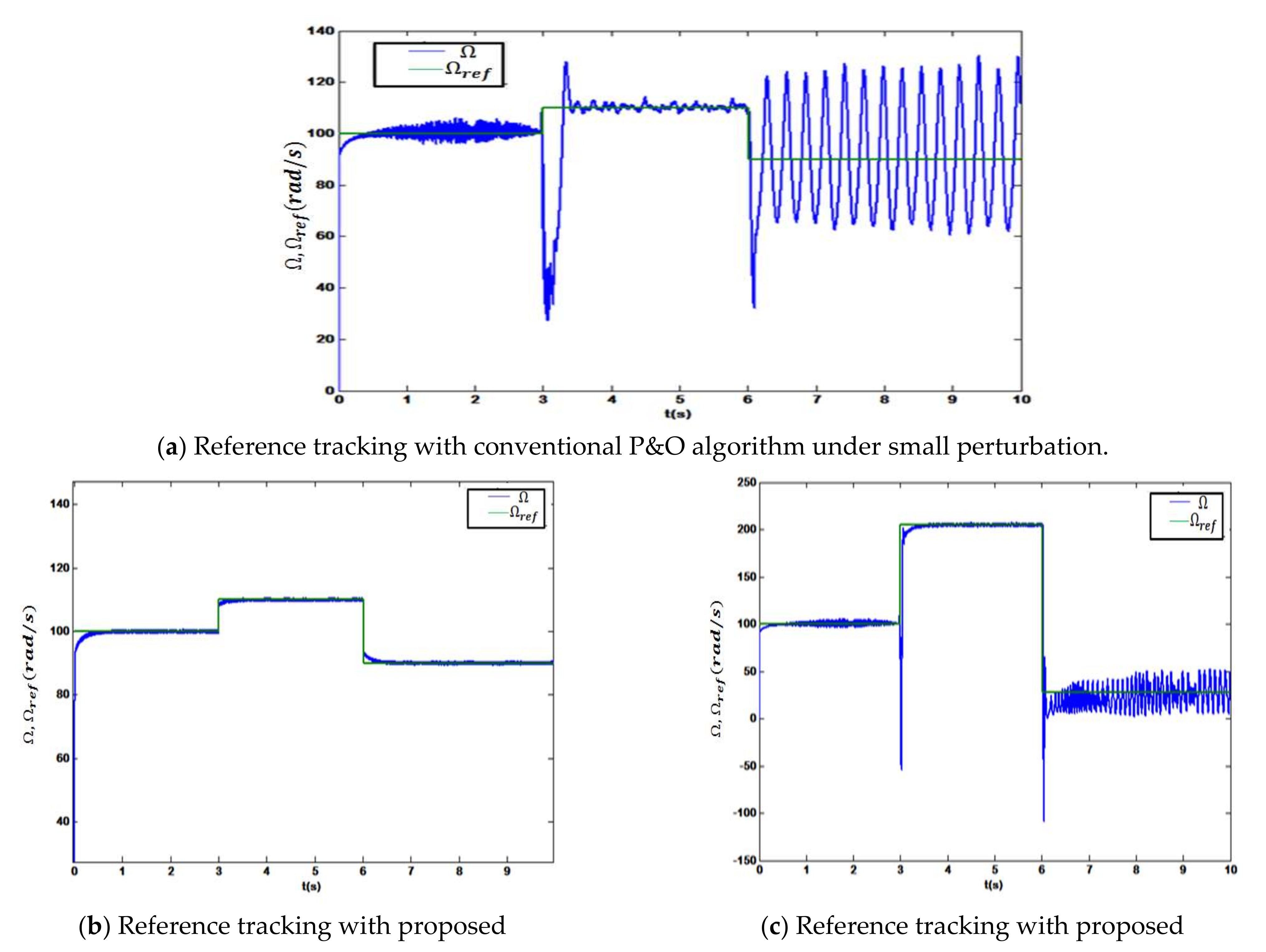
Figure 16a shows generator velocity tracking with the conventional MPPT algorithm, wherein the operating point chosen by this algorithm, MPP1, is close to the critical point. Therefore, the system starts tracking velocity at 100 rad/s, initially, with rapid swinging around the reference signal. The first perturbation occurred at the 3rd s when the reference speed changed from 100 up to 110 rad/s. Even though the change in generator speed was slight, 10 rad/s, it caused a big undershoot, and the system took about 0.5 s to catch up with the reference speed. Tracking became worse when the second perturbation occurs at the 6th second. Reference speed changed from 110 down to 90 rad/s, which was a bigger change than the first perturbation. In this case, the system become closer to the critical point associated with pure complex conjugate eigenvalues. Therefore, the system started oscillating between those values; any further change in the same direction might have led to unstable operation.
In contrast, with our proposed algorithm, the operating point, MPOP1, was far enough from the critical point. When a minor disturbance occurred, it was rejected faster with desirable transience, as shown in
Figure 16b. To investigate the impact of significant disturbance on the system behavior, we repeated simulation with G = 530, 830, and watt/m
2 with the corresponding generator speeds 100, 200, and 25 rad/s, respectively, as shown in
Figure 16c. The first change occurred at the 3rd second with the difference of 100 rad/s about the initial speed. In this case, the control system can still mitigate the effect of this big jump. The figure showed perfect tracking of the generator speed, which means that the system was delivering maximum power steadily. Generator speed fell from 200 down to 25 rad/s at the 6th second, with 175 rad/s about the previous speed. Indeed, this was a huge difference, and may have drug operating points away from equilibrium points and, hence, avoided linear control functionality. However, the proposed algorithm ensures that the huge perturbation effect will be mitigated due to a good selection of operating points, as shown in the same figure.