Impact of Dynamic Electricity Tariff and Home PV System Incentives on Electric Vehicle Charging Behavior: Study on Potential Grid Implications and Economic Effects for Households
Abstract
:1. Introduction
1.1. Background and Scope
1.2. Structure
2. Innovation Compared to Previous Research
2.1. Literature Review
2.2. Innovation and Development in This Research
- The interdependency of mobility parameters such as commuting distance, travel behavior, and probability of vehicle usage for each day have been considered in the charging profile simulation using weighted distributions from the standard dataset package of the survey “Mobilität in Deutschland 2017” [22]. This allows a much more precise charging demand prediction than most previous studies.
- The division into spatial and socioeconomic mobility groups and the assignment of probability distributions of the mentioned parameters to these groups allow an exact spatial selection to specific households so that calculations for real low-voltage networks can be performed.
- The consideration of temperature and seasonal interdependencies and a consistent database for weather-dependent devices PV, household, and EVs inside the optimization framework allow a precise prediction of expected grid load.
- The complex optimization framework combined with the comprehensive databases for weather data, PV generation, EV charging profiles, household load, and future electricity prices enable a detailed understanding of implications on charging behavior and grid load.
- Future electricity price estimations from energy system optimization depict the potential user benefits for different charging strategies.
3. Materials and Methods
3.1. Charging Strategies
3.2. Charging Profile Generation
3.2.1. Driving and Charging Profiles
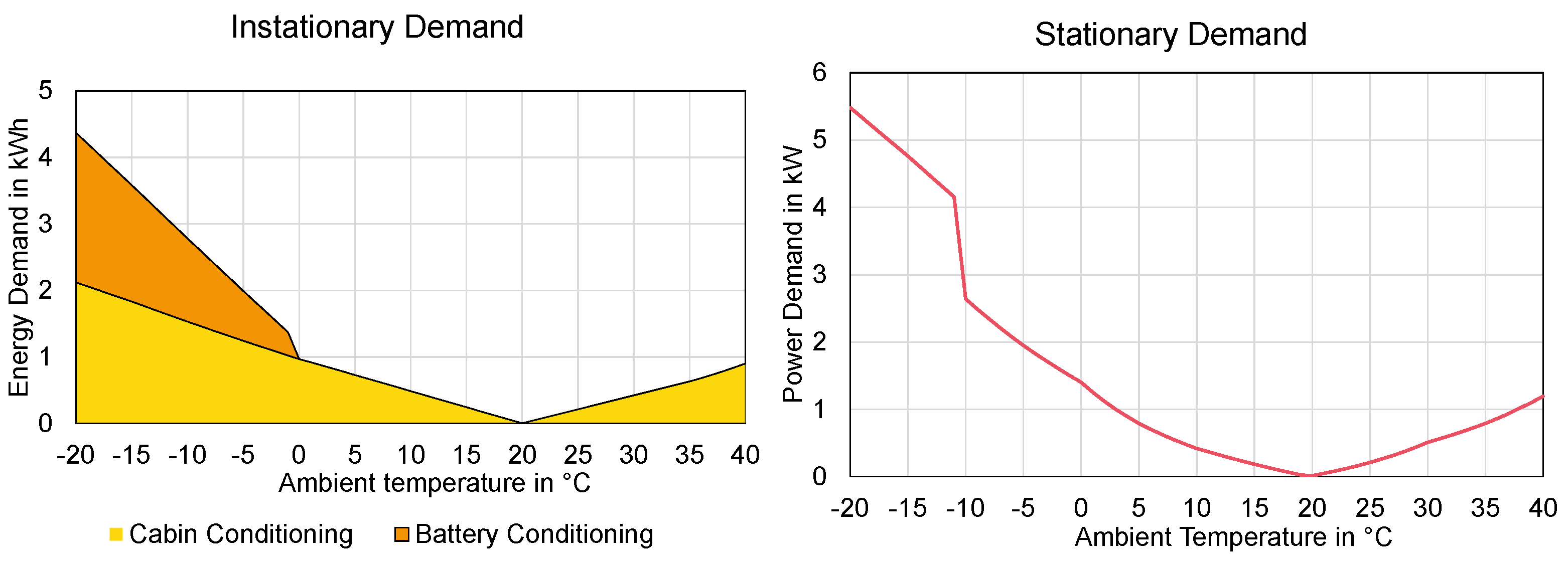
3.2.2. Impact of Temperature
3.3. Input Data
3.3.1. Electric Vehicle
3.3.2. Photovoltaic
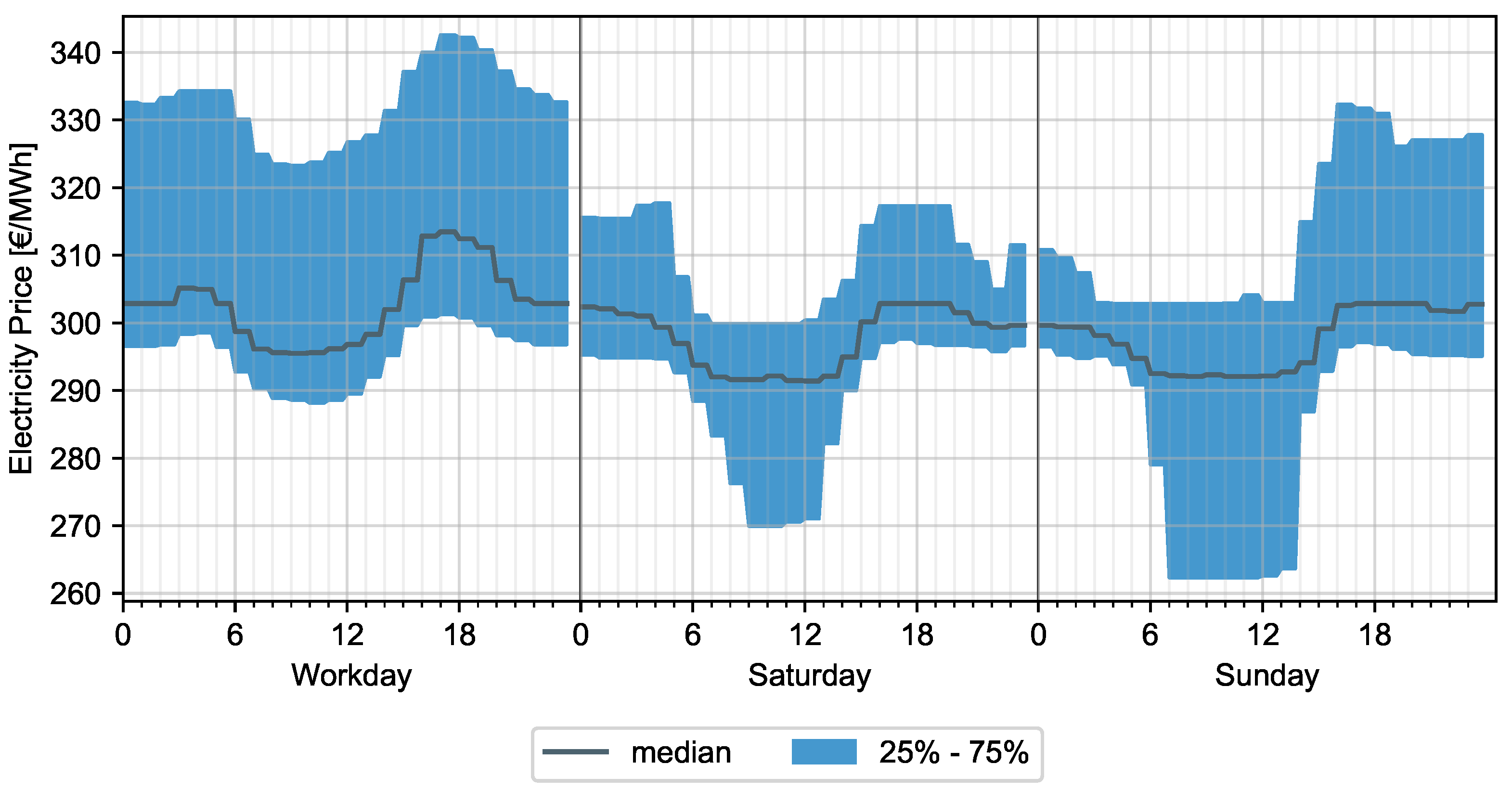
3.3.3. Dynamic Electricity Price
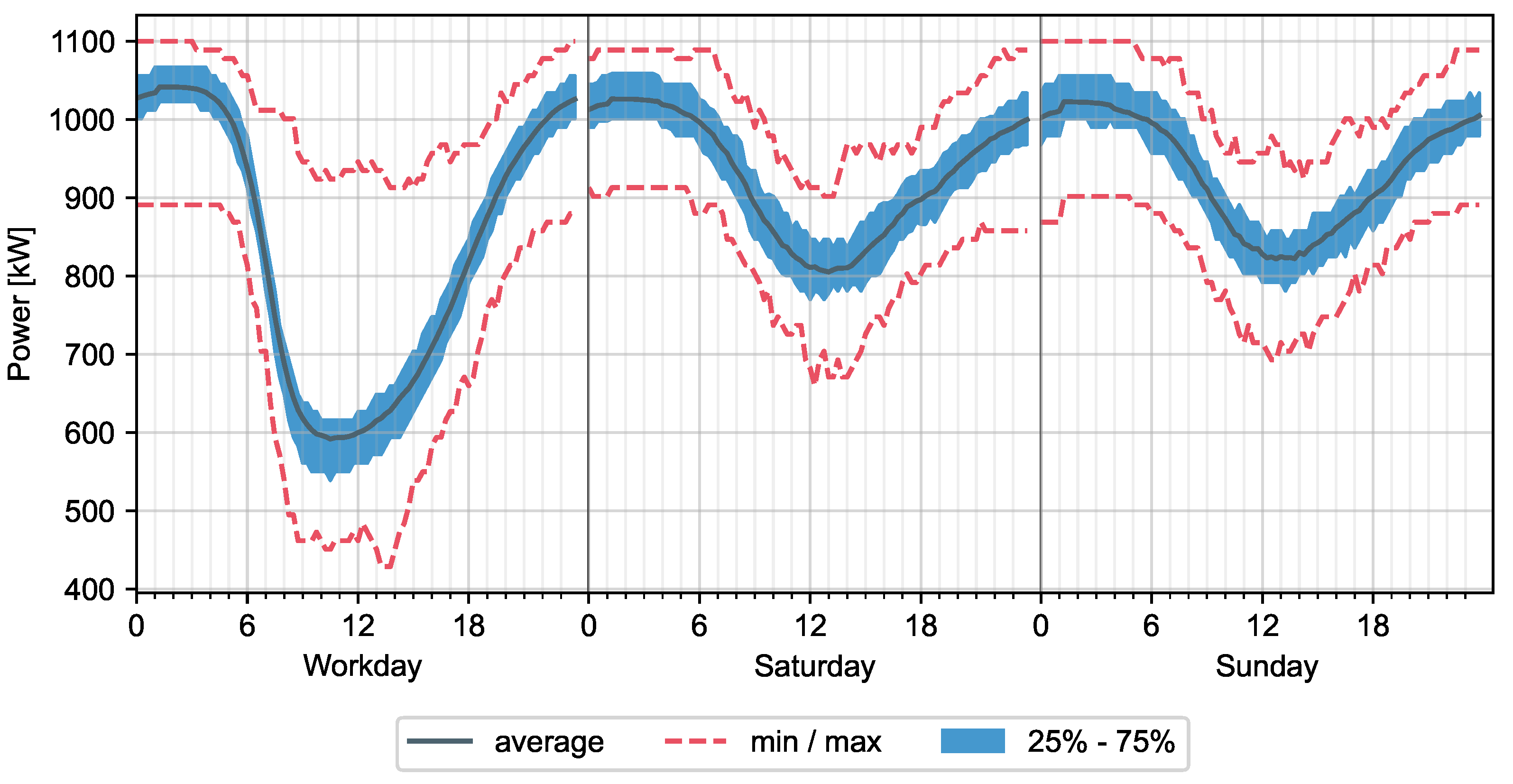
3.3.4. Household Load
3.4. Optimization Model
4. Results
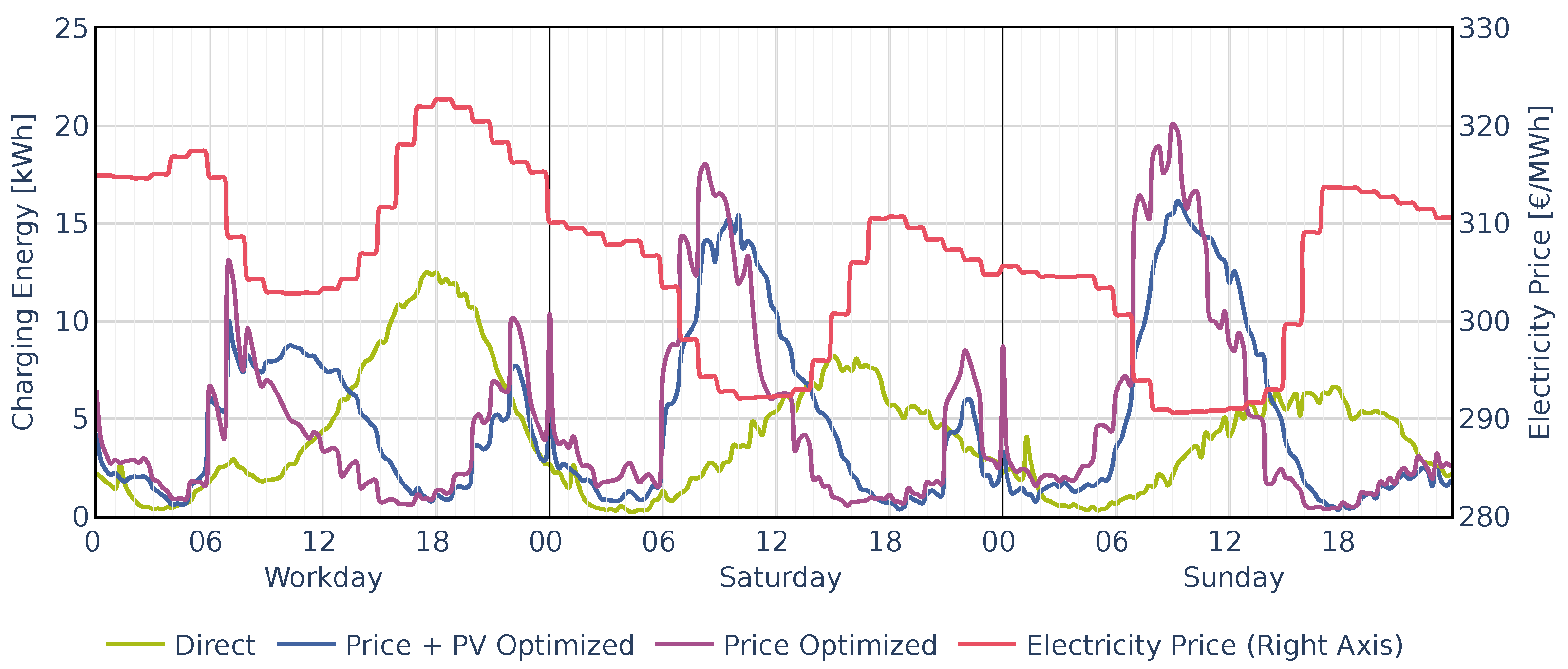
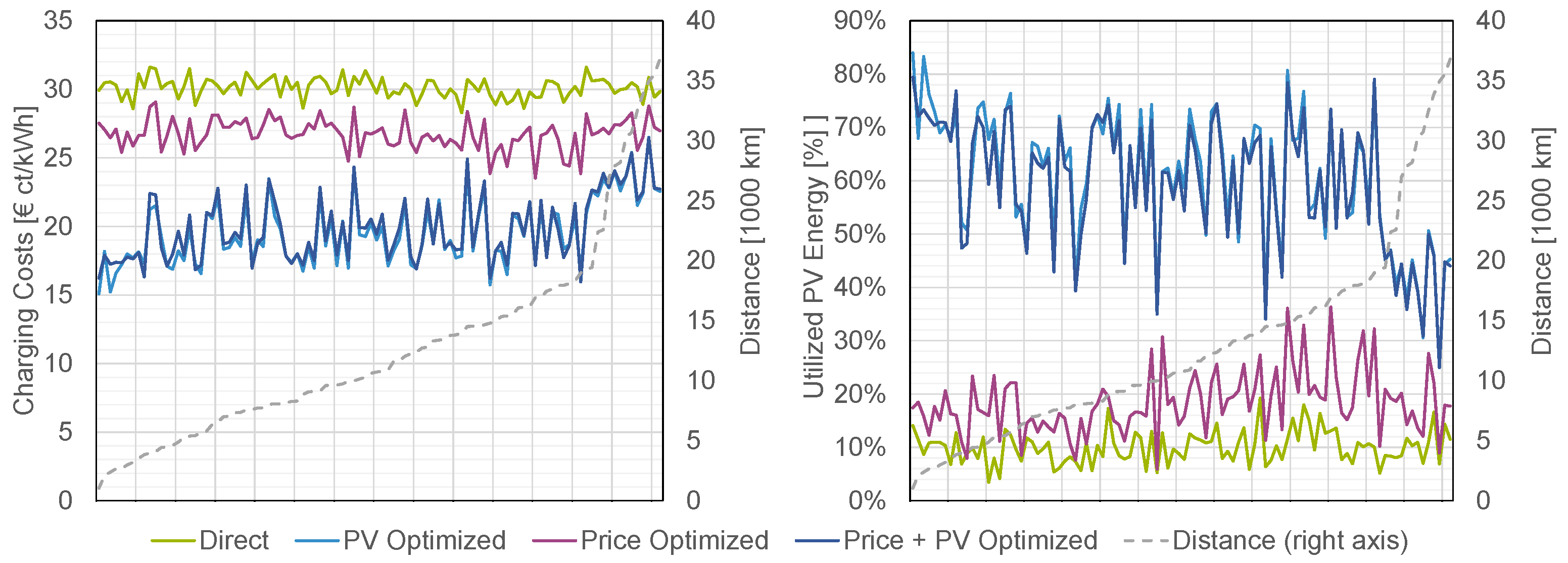
4.1. Effects of Optimized Charging Configurations on Load Shifting
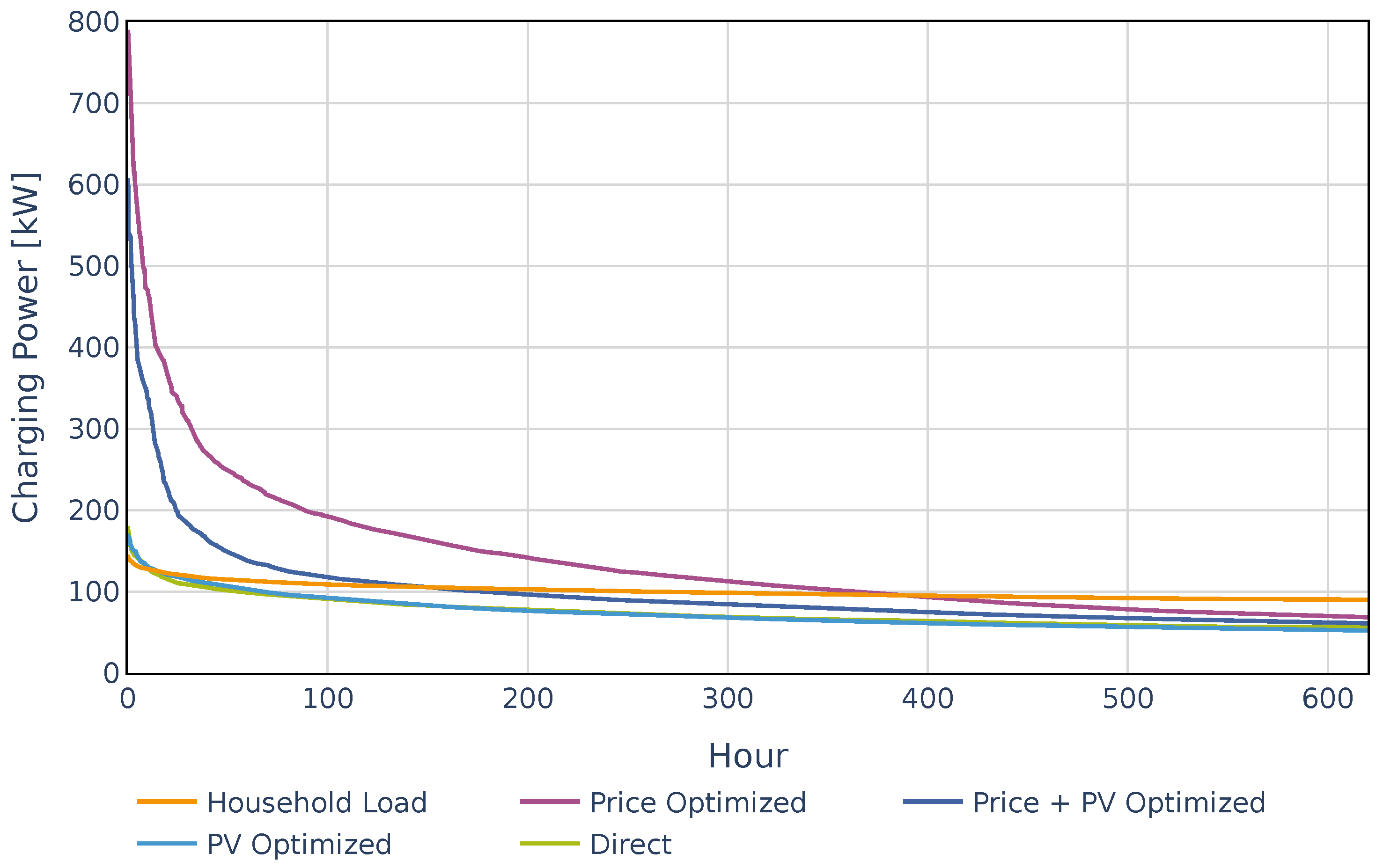
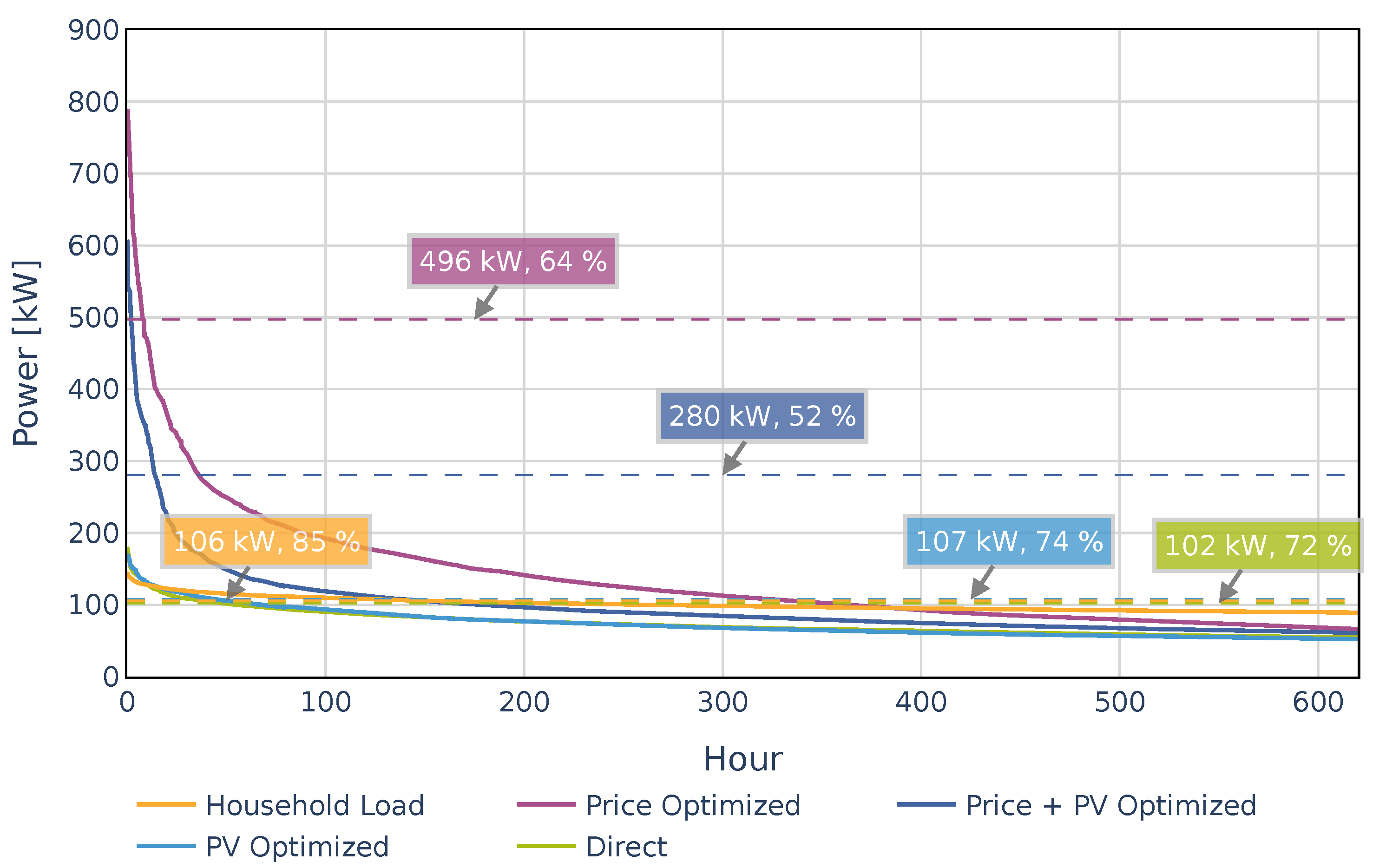
4.2. Occurrence and Extent of Charging Peaks
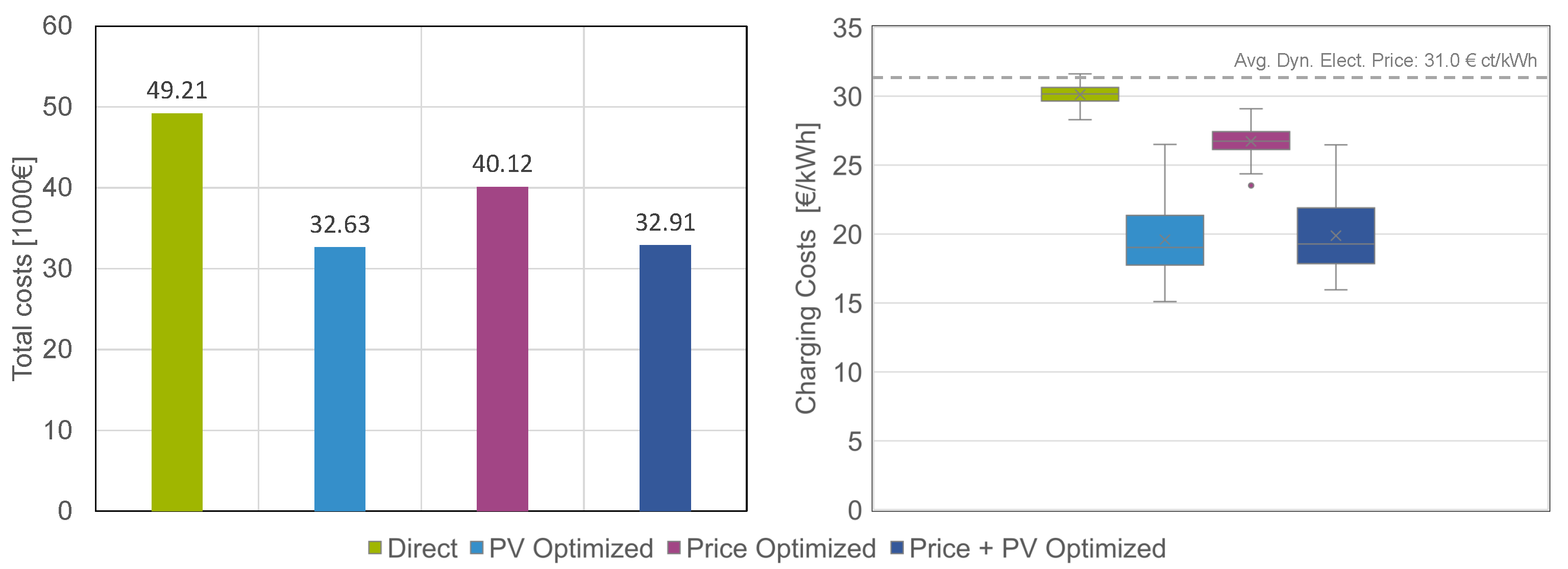
4.3. Economical Aspects on Households
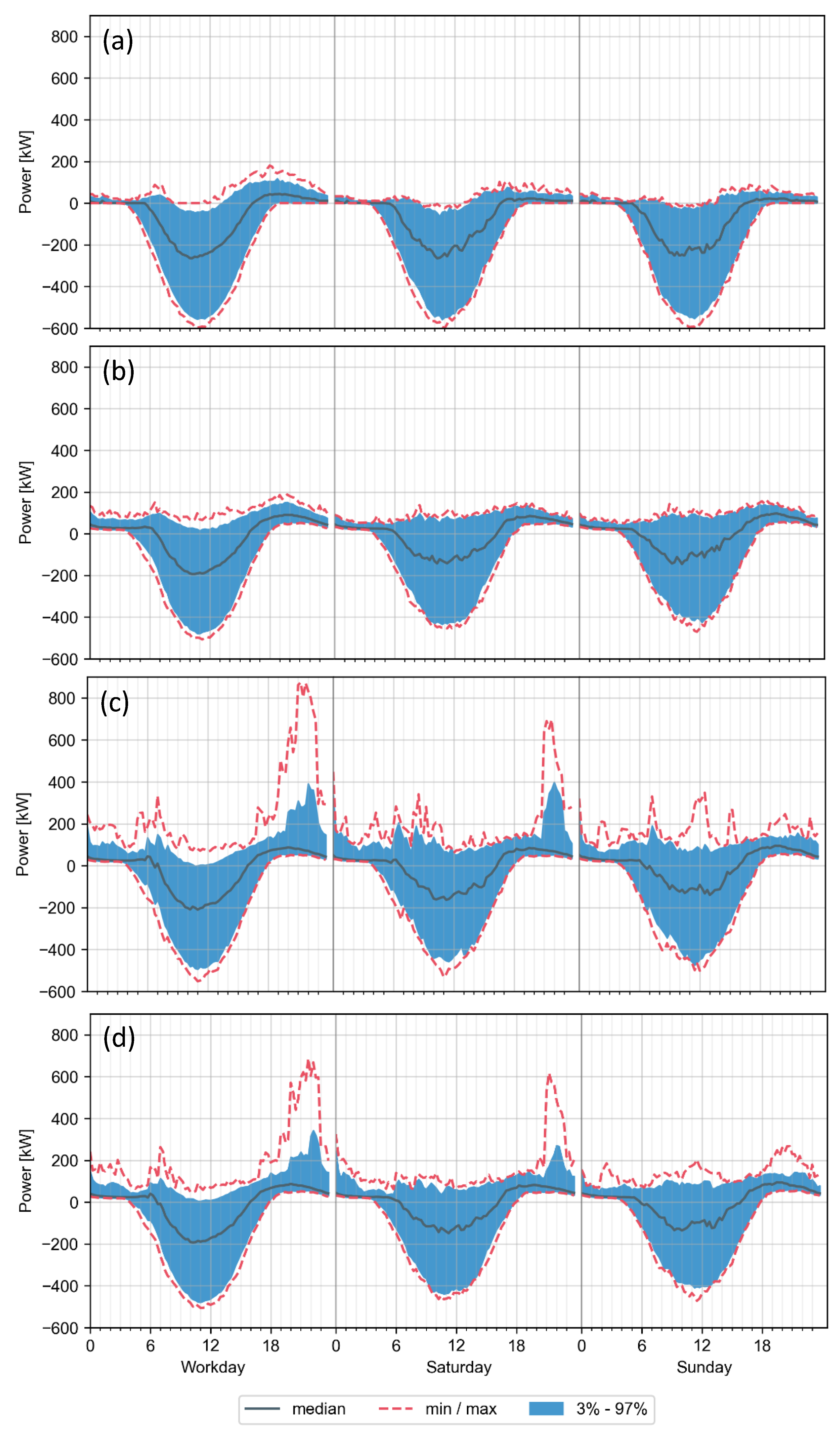
4.4. Effect on Grid Load Considering Aggregated Configuration with Household Load
5. Sensitivity Analysis
5.1. Number of Households and EVs
5.2. Yearly Driven Distance
5.3. Electricity Price Volatility
6. Discussion and Outlook
- Home battery storage systems could reduce the grid load significantly further. This should be taken into account in future investigations.
- Further aspects of grid load should be addressed, especially voltage issues, that can be approached by the spread of maximum positive and negative load inside a grid area.
- However, in terms of system convenience, further feedback effects with the energy system and eventually with the transmission grid must be considered.
- An option to meet this demand would be direct central control of decentralized flexibility by an aggregator marketer. This could address both the challenges regarding market integration and congestion management.
- To address these questions of system design, further calculations with central control should be compared to the results in this study. Furthermore, in this context, the load and flexible operation of heat pumps should be considered.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BTOEIt | Bundestarifordnung Elektrizität |
| CMS | charging management system |
| DSO | distribution system operator |
| EEA | European Environment Agency |
| EnWG | Energiewirtschaftsgesetz |
| ESS | energy storage system |
| EV | electric vehicle |
| GHG | greenhouse gas emissions |
| HEMS | home energy management system |
| LCoE | levelized cost of electricity |
| PV | photovoltaic |
| RL | reinforcement learning |
| SoC | state of charge |
References
- EEA Greenhouse Gases—Data viewer—European Environment Agency. 2021. Available online: https://www.eea.europa.eu/data-and-maps/data/data-viewers/greenhouse-gases-viewer (accessed on 21 January 2022).
- IEA, International Energy Agency. Global EV Outlook 2021: Accelerating Ambitions Despite the Pandemic; IEA: Paris; France, 2021. [Google Scholar] [CrossRef]
- Koalitionsvertrag 2021–2025 zwischen der Sozialdemokratischen Partei Deutschlands (SPD), BÜNDNIS 90 / DIE GRÜNEN und den Freien Demokraten (FDP). 2021. Available online: https://www.tagesschau.de/koalitionsvertrag-147.pdf (accessed on 26 November 2021).
- § 14a EnWG—Einzelnorm: Steuerbare Verbrauchseinrichtungen in Niederspannung; Verordnungsermächtigung: Gesetz über die Elektrizitäts- und Gasversorgung. 2021. Available online: https://dejure.org/gesetze/EnWG/14a.html (accessed on 29 November 2021).
- Buzer.de. § 7 BTOElt Wärmepumpen und Andere Unterbrechbare Verbrauchseinrichtungen Bundestarifordnung Elektrizität. 2021. Available online: https://www.buzer.de/gesetz/395/a4751.htm (accessed on 18 January 2022).
- Fachrizal, R.; Shepero, M.; Meer, D.v.; Munkhammar, J.; Widén, J. Smart charging of electric vehicles considering photovoltaic power production and electricity consumption: A review. eTransportation 2020, 4, 100056. [Google Scholar] [CrossRef]
- Assad, M.; Ramon, Z.; Tek, L.T. Integration of electric vehicles in the distribution network: A review of PV based electric vehicle modelling. Energies 2020, 13, 4541. [Google Scholar] [CrossRef]
- Habib, S.; Khan, M.M.; Abbas, F.; Numan, M.; Ali, Y.; Tang, H.; Yan, X. A framework for stochastic estimation of electric vehicle charging behavior for risk assessment of distribution networks. Front. Energy 2020, 14, 298–317. [Google Scholar] [CrossRef]
- Blasius, E.; Wang, Z. Effects of charging battery electric vehicles on local grid regarding standardized load profile in administration sector. Appl. Energy 2018, 224, 330–339. [Google Scholar] [CrossRef]
- Franco, F.L.; Ricco, M.; Mandrioli, R.; Grandi, G. Electric vehicle aggregate power flow prediction and smart charging system for distributed renewable energy self-consumption optimization. Energies 2020, 13, 5003. [Google Scholar] [CrossRef]
- Morsy, N.; Sayed, M.S.; Abdelfatah, A.; Csaba, F. Smart Charging of Electric Vehicles According to Electricity Price; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Spencer, S.I.; Fu, Z.; Apostolaki-Iosifidou, E.; Lipman, T.E. Evaluating smart charging strategies using real-world data from optimized plugin electric vehicles. Transp. Res. Part Transp. Environ. 2021, 100, 103023. [Google Scholar] [CrossRef]
- Müller, M.; Samweber, F.; Leidl, P. Impact of different charging strategies for electric vehicles on their grid integration. In Netzintegration der Elektromobilität 2017; Liebl, J., Ed.; Springer: Wiesbaden, Germany, 2017; pp. 41–55. [Google Scholar] [CrossRef]
- Ninkovic, T.; Calasan, M.; Mujovic, S. Coordination of Electric Vehicles Charging in the Distribution System; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Ioakimidis, C.S.; Dimitrios, T.; Pawel, R.; Konstantinos, N.G. Peak shaving and valley filling of power consumption profile in non-residential buildings using an electric vehicle parking lot. Energy 2018, 148, 148–158. [Google Scholar] [CrossRef]
- Tuchnitz, F.; Ebell, N.; Schlund, J.; Pruckner, M. Development and Evaluation of a Smart Charging Strategy for an Electric Vehicle Fleet Based on Reinforcement Learning. Appl. Energy 2021, 285, 116382. [Google Scholar] [CrossRef]
- Konstantinidis, G.; Kanellos, F.D.; Kalaitzakis, K. A Simple Multi-Parameter Method for Efficient Charging Scheduling of Electric Vehicles. Appl. Syst. Innov. 2021, 4, 58. [Google Scholar] [CrossRef]
- Yao, L.; Damiran, Z.; Lim, W.H. Optimal Charging and Discharging Scheduling for Electric Vehicles in a Parking Station with Photovoltaic System and Energy Storage System. Energies 2017, 10, 550. [Google Scholar] [CrossRef]
- Li, D.; Zouma, A.; Liao, J.; Yang, H. An energy management strategy with renewable energy and energy storage system for a large electric vehicle charging station. eTransportation 2020, 6, 100076. [Google Scholar] [CrossRef]
- Schroeder, B. dena-NETZFLEXSTUDIE: Optimierter Einsatz von Speichern für Netz- und Marktanwendungen in der Stromversorgung. 2017. Available online: https://www.dena.de/fileadmin/dena/Dokumente/Pdf/9191_dena_Netzflexstudie.pdf (accessed on 20 October 2021).
- Carli, R.; Dotoli, M. A Distributed Control Algorithm for Optimal Charging of Electric Vehicle Fleets with Congestion Management. IFAC-PapersOnLine 2018, 51, 373–378. [Google Scholar] [CrossRef]
- Infas Institut für Sozialwissenschaft. Mobilität in Deutschland. 2017. Available online: http://www.mobilitaet-in-deutschland.de (accessed on 20 October 2021).
- Automatische Zählstellen auf Autobahnen und Bundesstraßen. 2019. Available online: https://www.bast.de/BASt_2017/DE/Verkehrstechnik/Fachthemen/v2-verkehrszaehlung/zaehl_node.html (accessed on 26 November 2021).
- Gauglitz, P.; Ulffers, J.; Thomsen, G.; Frischmuth, F.; Geiger, D.; Scheidler, A. Modeling Spatial Charging Demands Related to Electric Vehicles for Power Grid Planning Applications. Energies 2020, 9. [Google Scholar] [CrossRef]
- Fraunhofer-Institut für Energiewirtschaft und Energiesystemtechnik. Ladeinfrastruktur 2.0. Available online: https://www.iee.fraunhofer.de/de/projekte/suche/laufende/ladeinfrastruktur2-0.html (accessed on 4 December 2021).
- Trost, T.; Sterner, M.; Bruckner, T. Impact of electric vehicles and synthetic gaseous fuels on final energy consumption and carbon dioxide emissions in Germany based on long-term vehicle fleet modelling. Energy 2017, 141, 1215–1225. [Google Scholar] [CrossRef]
- Böttger, D.; Dreher, A.; Ganal, I.; Gauglitz, P.; Geiger, D.; Gerlach, A.; Gerhardt, N.; Harms, Y.; Härtel, P.; Jentsch, M.; et al. SYSTEMKONTEXT: Modellbildung für nationale Energieversorgungsstrukturen im Europäischen Kontext unter Besonderer Berücksichtigung der Zulässigkeit von Vereinfachungen und Aggregationen. Available online: https://www.enargus.de/pub/bscw.cgi/?op=enargus.eps2&q=Fraunhofer-Institut%20f%C3%BCr%20Energiewirtschaft%20und%20Energiesystemtechnik%20(IEE)&v=10&p=2&s=8&id=600797 (accessed on 20 October 2021).
- von Appen, J. Sizing and Operation of Residential Photovoltaic Systems in Combination with Battery Storage Systems and Heat Pumps. Ph.D. Thesis, University of Kassel, Kassel, Germany, 2018. [Google Scholar] [CrossRef]
- Böttger, D.; Härtel, P. On Wholesale Electricity Prices and Market Values in a Carbon-Neutral Energy System. Energy Econ. 2022, 106, 105709. [Google Scholar] [CrossRef]
- Tjaden, T.; Bergner, J.; Weniger, J.; Quaschning, V. Repräsentative elektrische Lastprofile für Wohngebäude in Deutschland auf 1-sekündiger Datenbasis. Hochschule für Technik und Wirtschaft (HTW) Berlin. 2015. Available online: https://solar.htw-berlin.de/elektrische-lastprofile-fuer-wohngebaeude/ (accessed on 12 November 2021).
- BDEW Bundesverband der Energie- und Wasserwirtschaft e.V. Standardlastprofile Strom. Available online: https://www.bdew.de/energie/standardlastprofile-strom/ (accessed on 19 October 2021).
- Bynum, M.L.; Hackebeil, G.A.; Hart, W.E.; Laird, C.D.; Nicholson, B.L.; Siirola, J.D.; Watson, J.P.; Woodruff, D.L. Pyomo—Optimization Modeling in Python; Springer Nature: Berlin/Heidelberg, Germany, 2021; Volume 67. [Google Scholar]
- Härtel, P.; Korpås, M. Demystifying market clearing and price setting effects in low-carbon energy systems. Energy Econ. 2021, 93, 105051. [Google Scholar] [CrossRef]
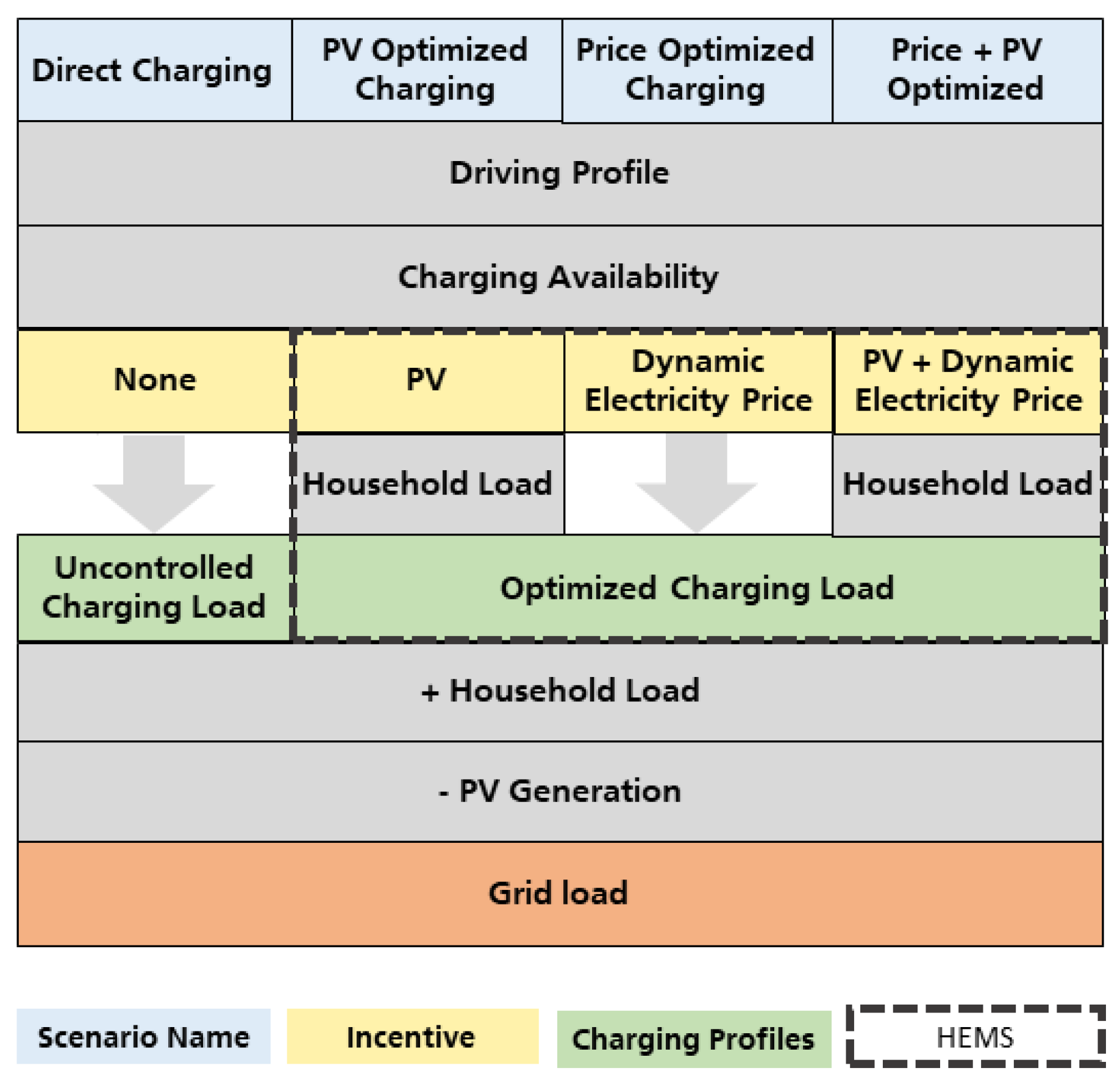




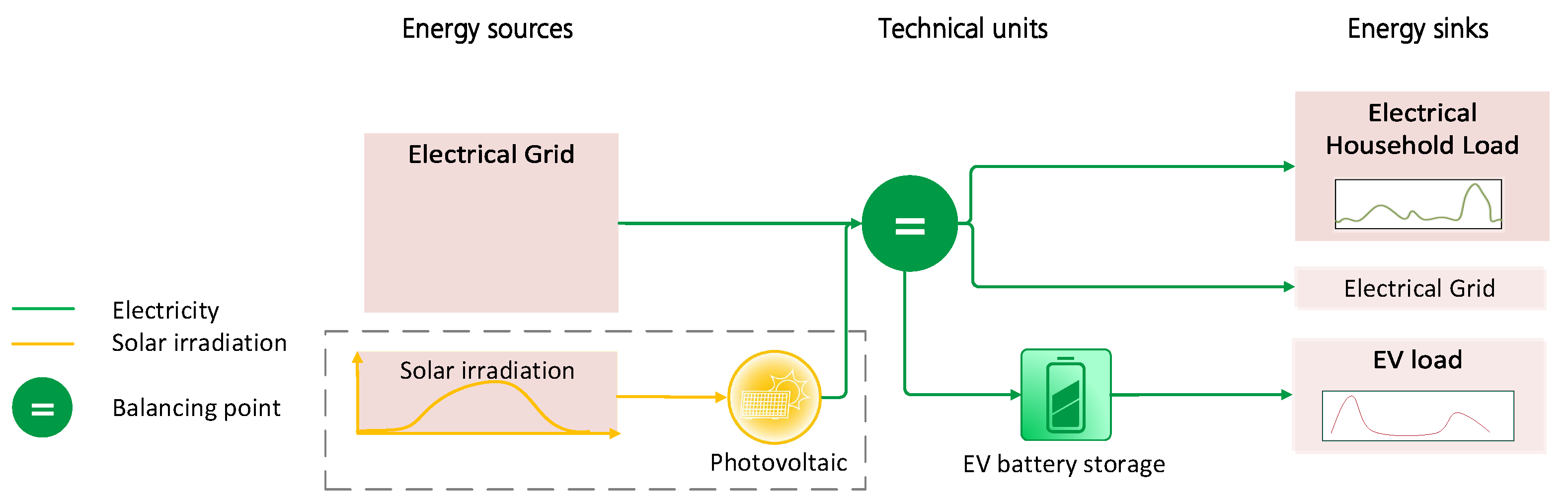








| Charging Strategy | Incentive | Description | |
|---|---|---|---|
| Uncontrolled | “Direct Charging” | None | Users charge their car directly to the maximum capacity as soon as they arrive back home. |
| Controlled | ”PV Optimized Charging” | PV generation | Users with a home PV system shift the charging process to maximize self-sufficiency while considering home demand. |
| ”Price Optimized Charging” | Electricity costs | Users directly receive the signal of the wholesale electricity prices and adapt the charging configuration to minimize electricity costs for charging. | |
| ”Combined Price + PV Optimized Charging” | PV generation & Electricity costs | Users receive price signal of the wholesale electricity prices and adapt the charging configuration to minimize total household electricity costs. | |
| Spatial Type | |
|---|---|
| Urban | Rural |
| Metropolis | Central city |
| Bigger city | Urban area |
| Suburbia | Village area |
| Village area | |
| Household | |
| Net Income | Type |
| EUR < 2000 | Single |
| EUR 2000–4000 | Multi-person without children |
| EUR >4000 € | Multi-person with children |
| Type | Capacity [kWh] | Consumption [kWh/km] | Qty. |
|---|---|---|---|
| BEV small | 35.00 | 0.16 | 28 |
| BEV small (second car) | 25.00 | 0.16 | 11 |
| BEV medium | 60.00 | 0.20 | 28 |
| BEV medium (second car) | 50.00 | 0.20 | 1 |
| BEV big | 80.00 | 0.25 | 9 |
| BEV light utility vehicle | 45.00 | 0.28 | 4 |
| PHEV small | 8.80 | 0.16 | 1 |
| PHEV small (second car) | 8.80 | 0.16 | 1 |
| PHEV medium | 11.50 | 0.20 | 12 |
| PHEV medium (second car) | 11.50 | 0.20 | 5 |
| Total Quantity | 100 | ||
| Charging Configuration | Reference at = 1 | Volatility at = 2 | Volatility at = 4 | ||
|---|---|---|---|---|---|
| Total costs [EUR 1000], Avg. Charging costs [EUR ct/kWh] | Total costs [EUR 1000], Avg. Charging costs [EUR ct/kWh] | +/− [%] | Total costs [EUR 1000], Avg. Charging costs [EUR ct/kWh] | +/− [%] | |
| Direct | 49.21, 30.11 | 50.92, 31.19 | +3.37%, +3.44% | 54.21, 33.23 | +9.22%, +9.37% |
| PV Optimized | 32.63, 19.59 | 32.97, 19.91 | +1.02%, +1.66% | 33.11, 20.01 | +1.44%, +2.08% |
| Price Optimized | 40,12, 26.72 | 40.00, 26.68 | −0.30%, −0.18% | 37.08, 24.37 | −8.20%, −9.66% |
| Price + PV Optimized | 32.91, 19.88 | 32.76, 19.80 | −0.45%, −0.40% | 32.90, 19.89 | −0.02%, +0.03% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
von Bonin, M.; Dörre, E.; Al-Khzouz, H.; Braun, M.; Zhou, X. Impact of Dynamic Electricity Tariff and Home PV System Incentives on Electric Vehicle Charging Behavior: Study on Potential Grid Implications and Economic Effects for Households. Energies 2022, 15, 1079. https://doi.org/10.3390/en15031079
von Bonin M, Dörre E, Al-Khzouz H, Braun M, Zhou X. Impact of Dynamic Electricity Tariff and Home PV System Incentives on Electric Vehicle Charging Behavior: Study on Potential Grid Implications and Economic Effects for Households. Energies. 2022; 15(3):1079. https://doi.org/10.3390/en15031079
Chicago/Turabian Stylevon Bonin, Michael, Elias Dörre, Hadi Al-Khzouz, Martin Braun, and Xian Zhou. 2022. "Impact of Dynamic Electricity Tariff and Home PV System Incentives on Electric Vehicle Charging Behavior: Study on Potential Grid Implications and Economic Effects for Households" Energies 15, no. 3: 1079. https://doi.org/10.3390/en15031079
APA Stylevon Bonin, M., Dörre, E., Al-Khzouz, H., Braun, M., & Zhou, X. (2022). Impact of Dynamic Electricity Tariff and Home PV System Incentives on Electric Vehicle Charging Behavior: Study on Potential Grid Implications and Economic Effects for Households. Energies, 15(3), 1079. https://doi.org/10.3390/en15031079






