Investigation of Multiple Degradation Mechanisms of a Proton Exchange Membrane Fuel Cell under Dynamic Operation
Abstract
1. Introduction
2. PEM Fuel Cell Model
2.1. Modelling of the Gas Diffusion Layer
2.2. Modelling of Membrane Water Transport
2.3. Modelling of Voltage Degradation
2.3.1. The Basic Voltage Model
2.3.2. Introduction of the Degradation Parameters
2.4. Energy Conservation of the PEMFC Stack
3. PEMFC Durability Test
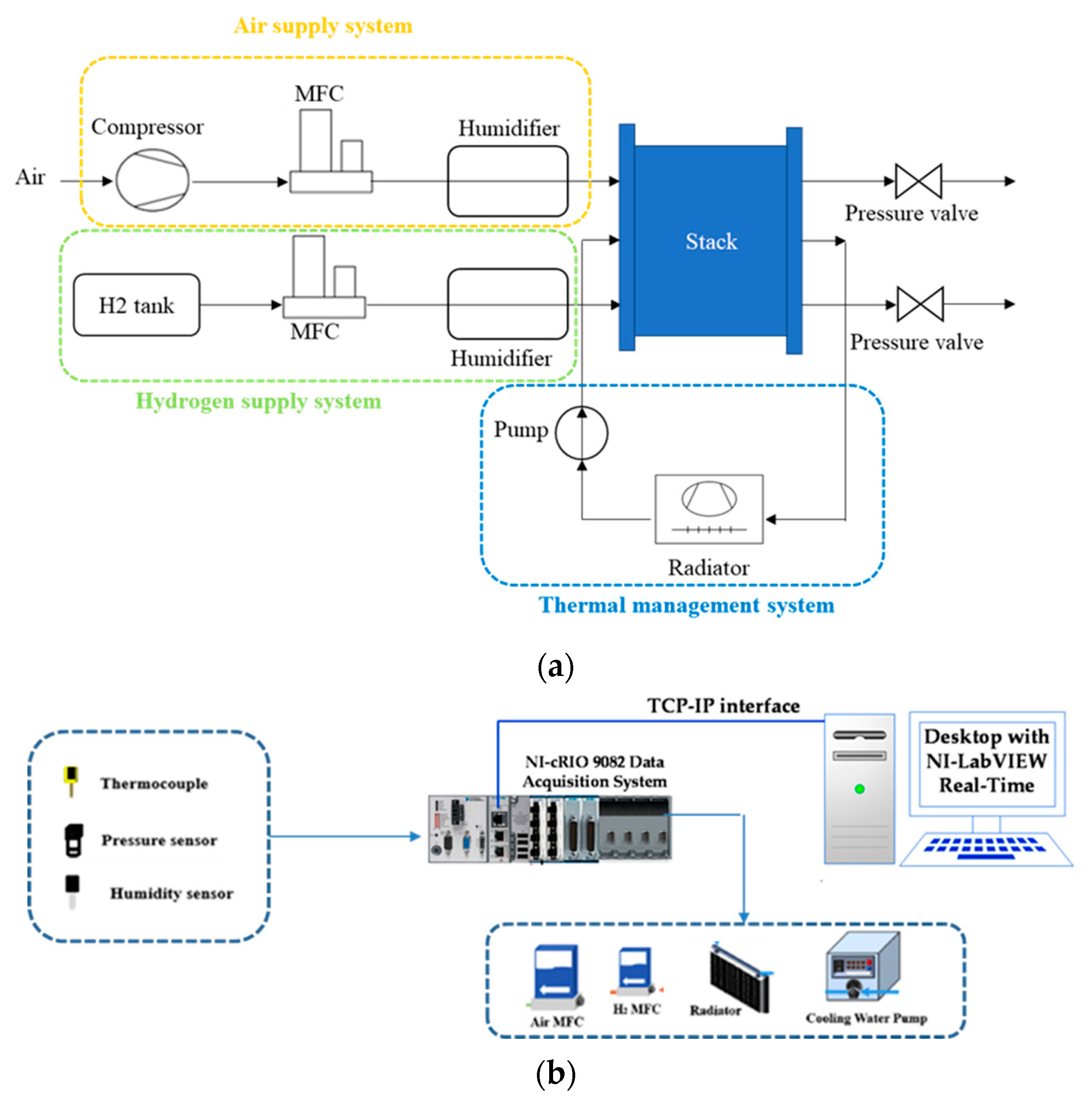
3.1. Test Bench
3.2. Durability Test
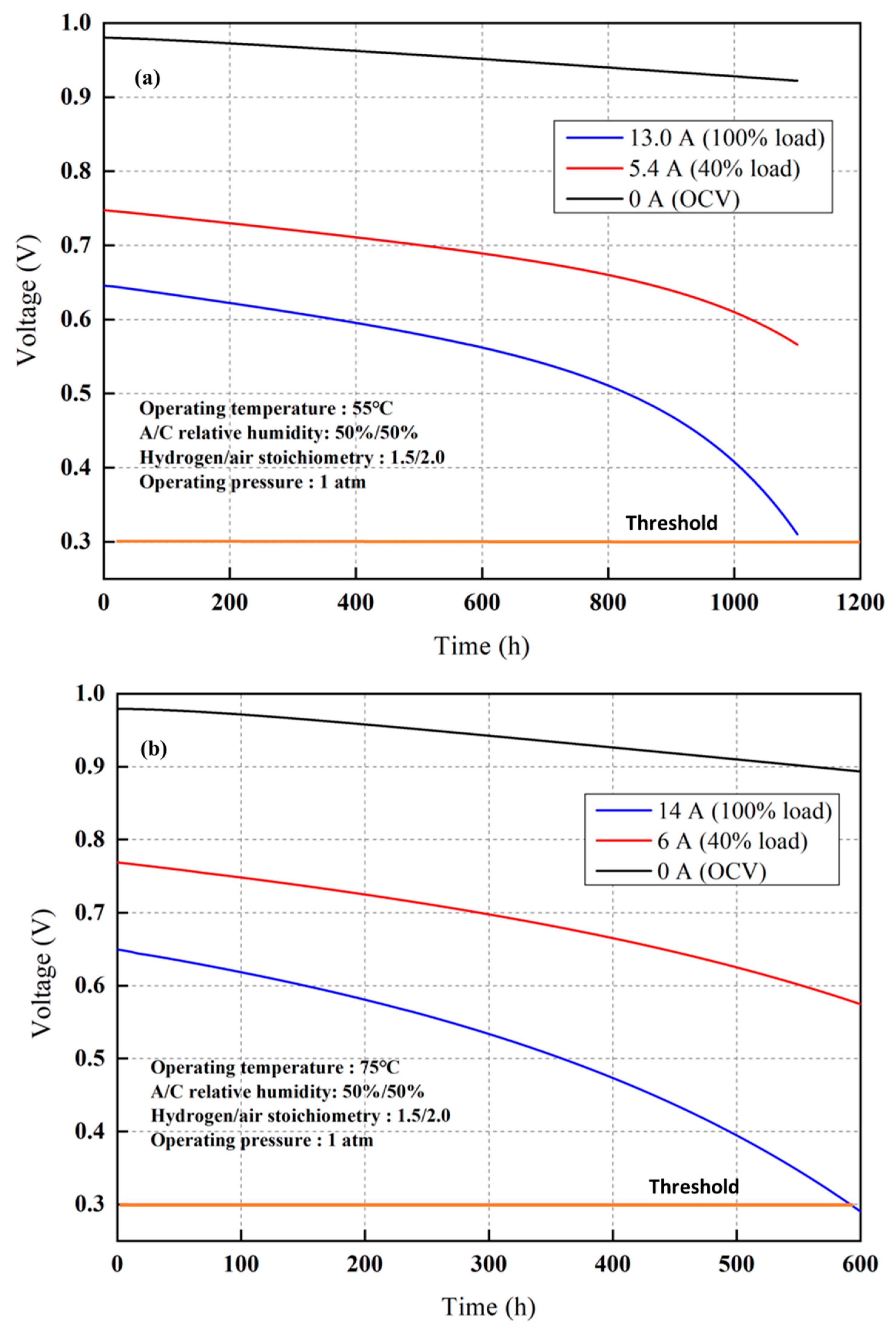
4. Results and Discussion
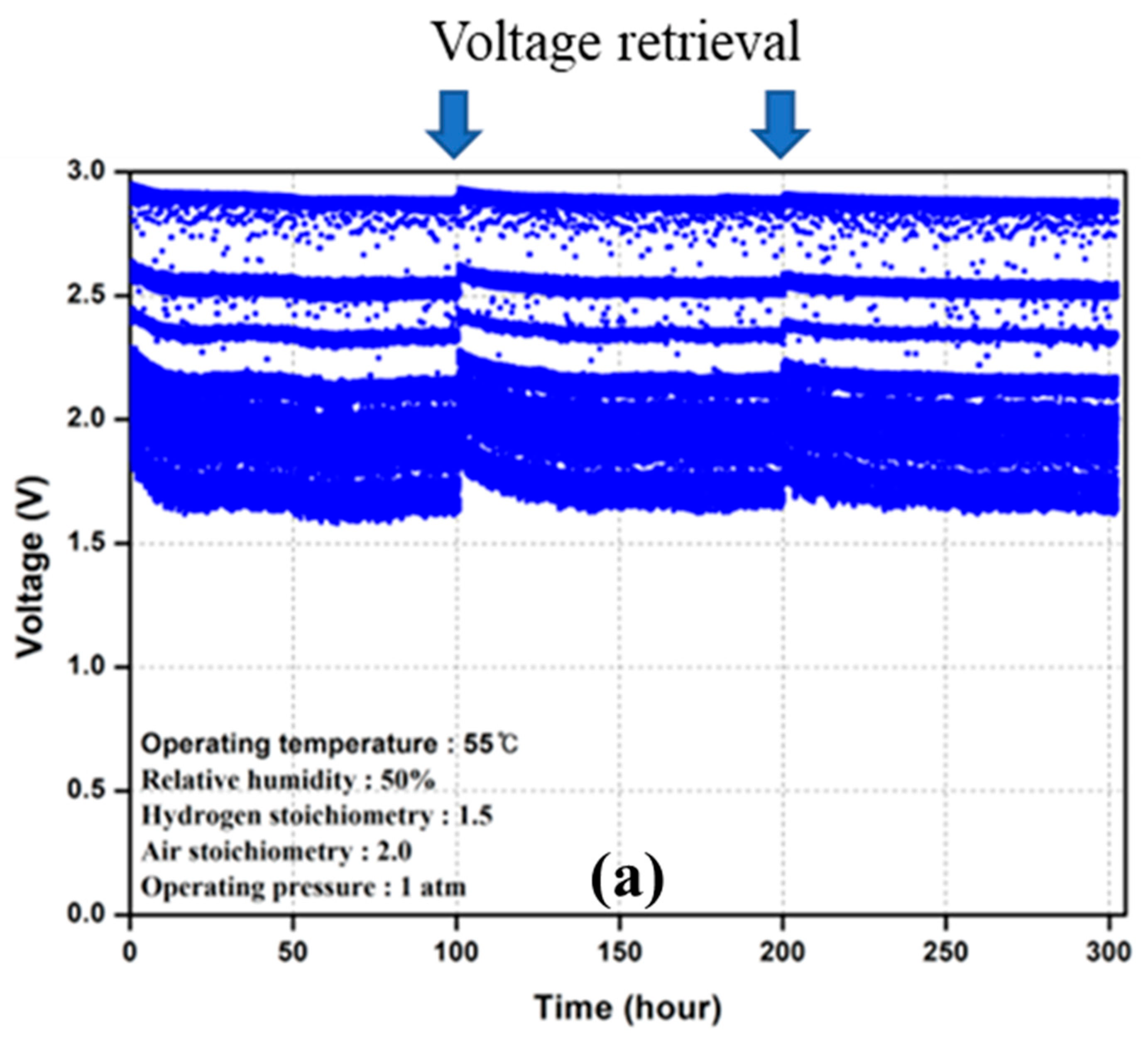
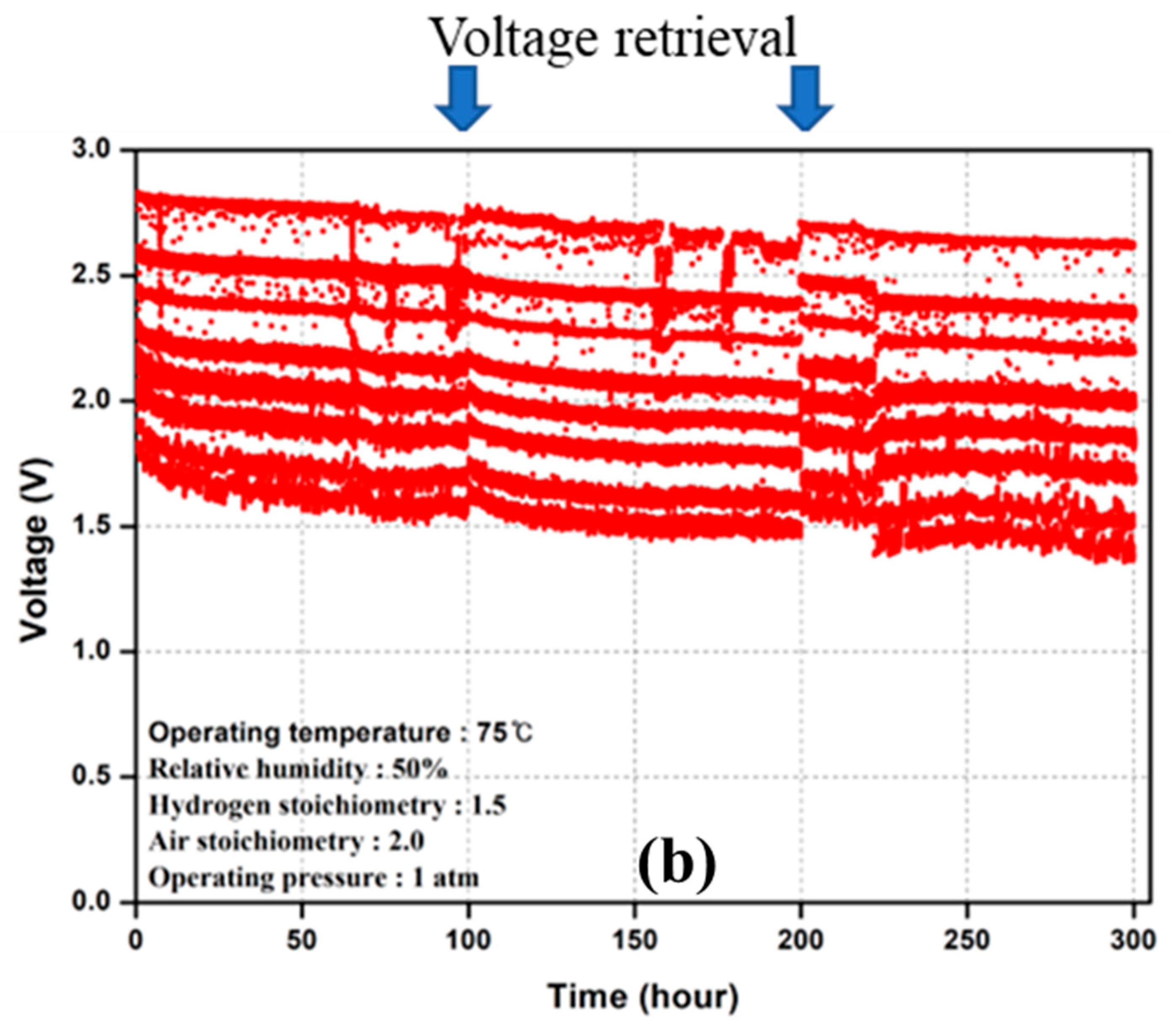
4.1. PEMFC Degradation Behavior
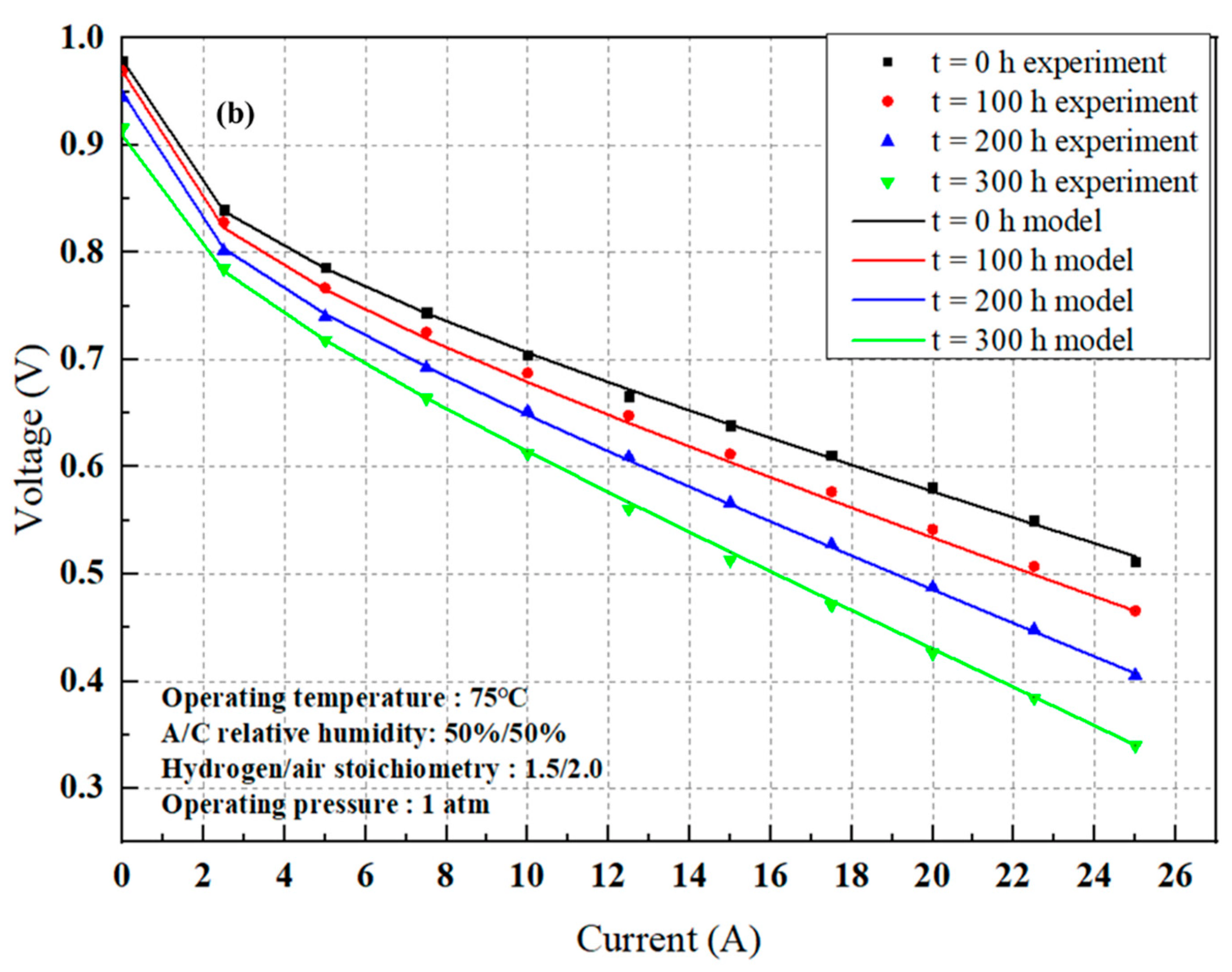
4.2. Modeling Results
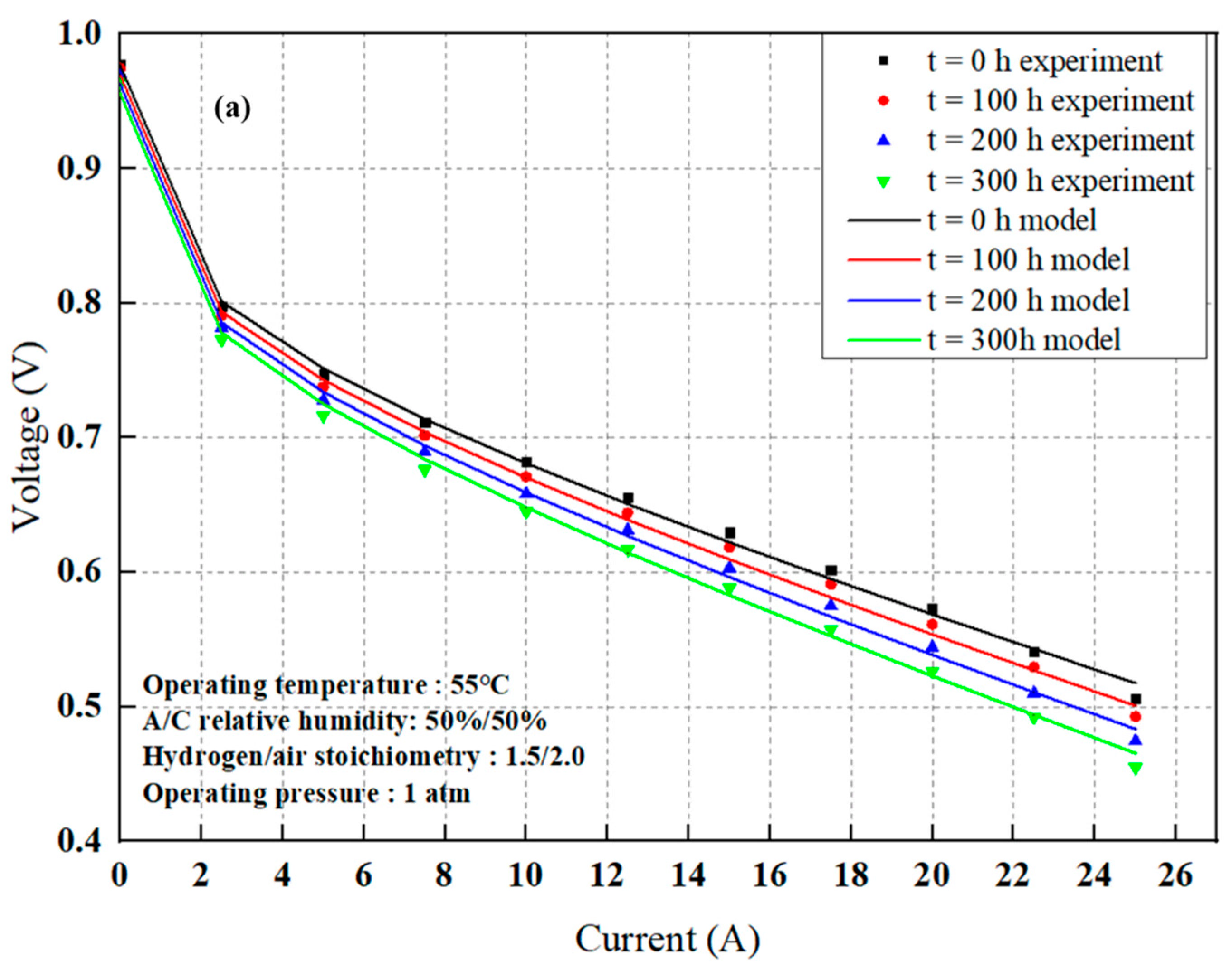
4.2.1. Model Parameter Estimate
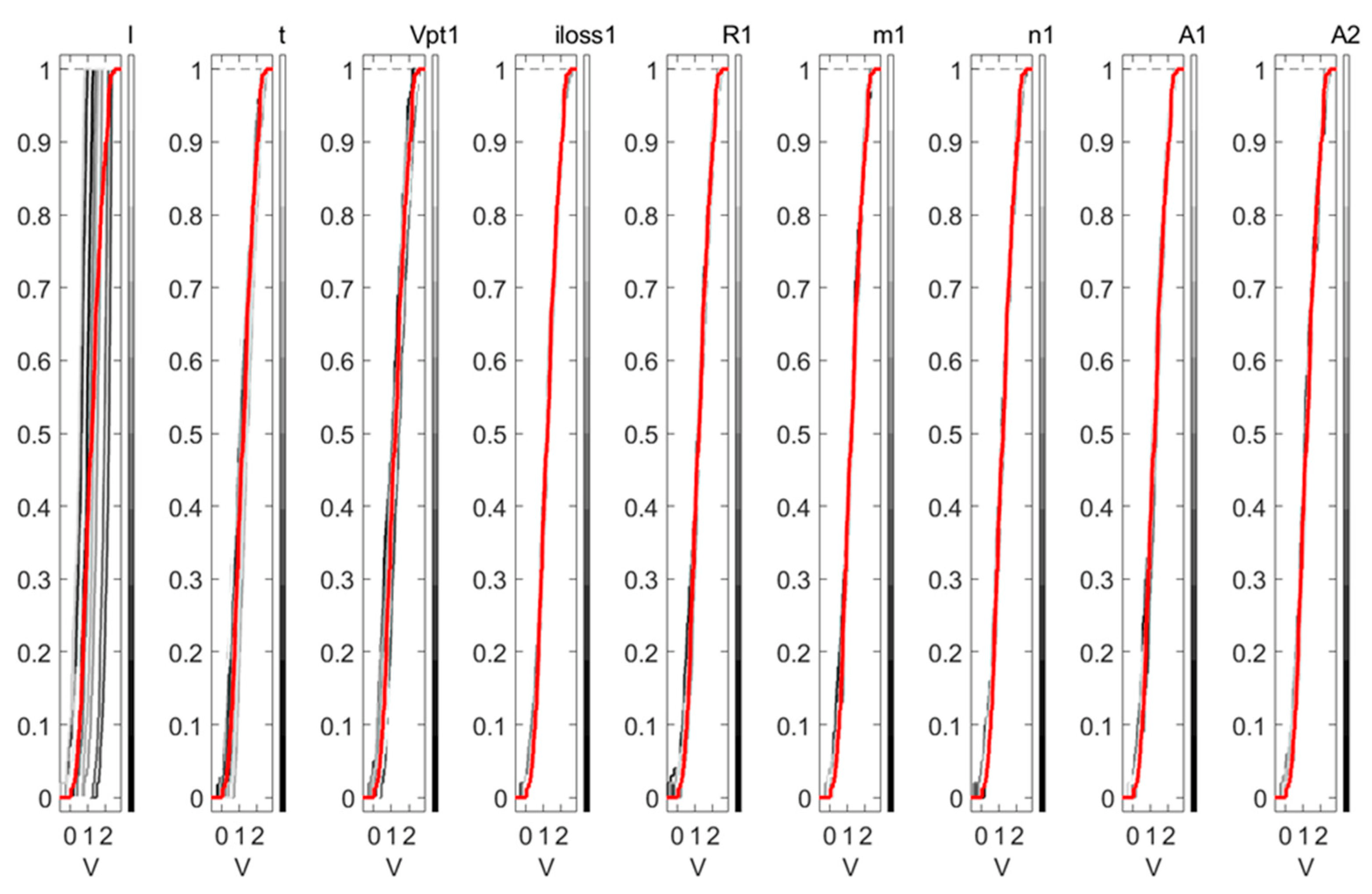
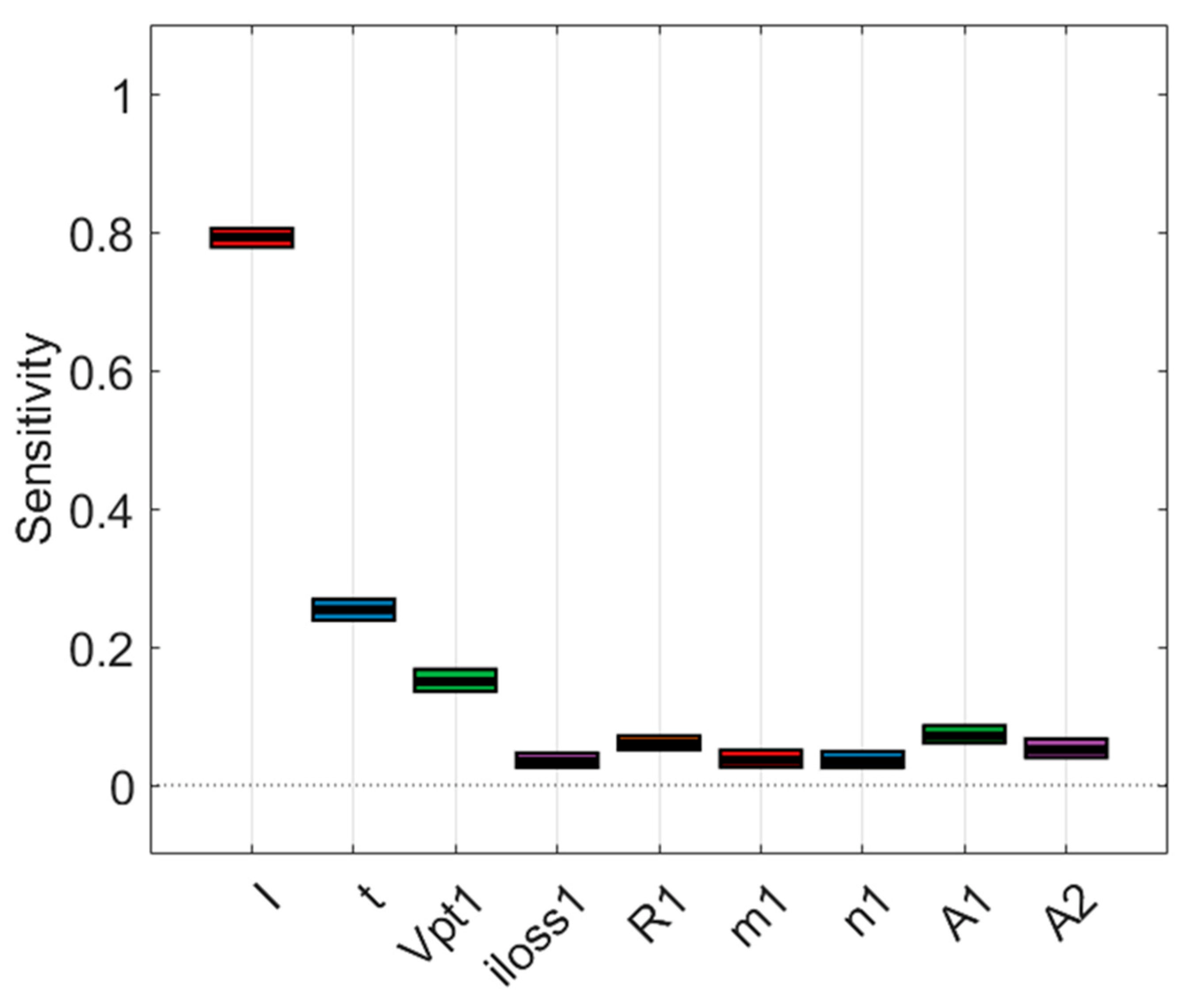
4.2.2. Sensitivity Analysis
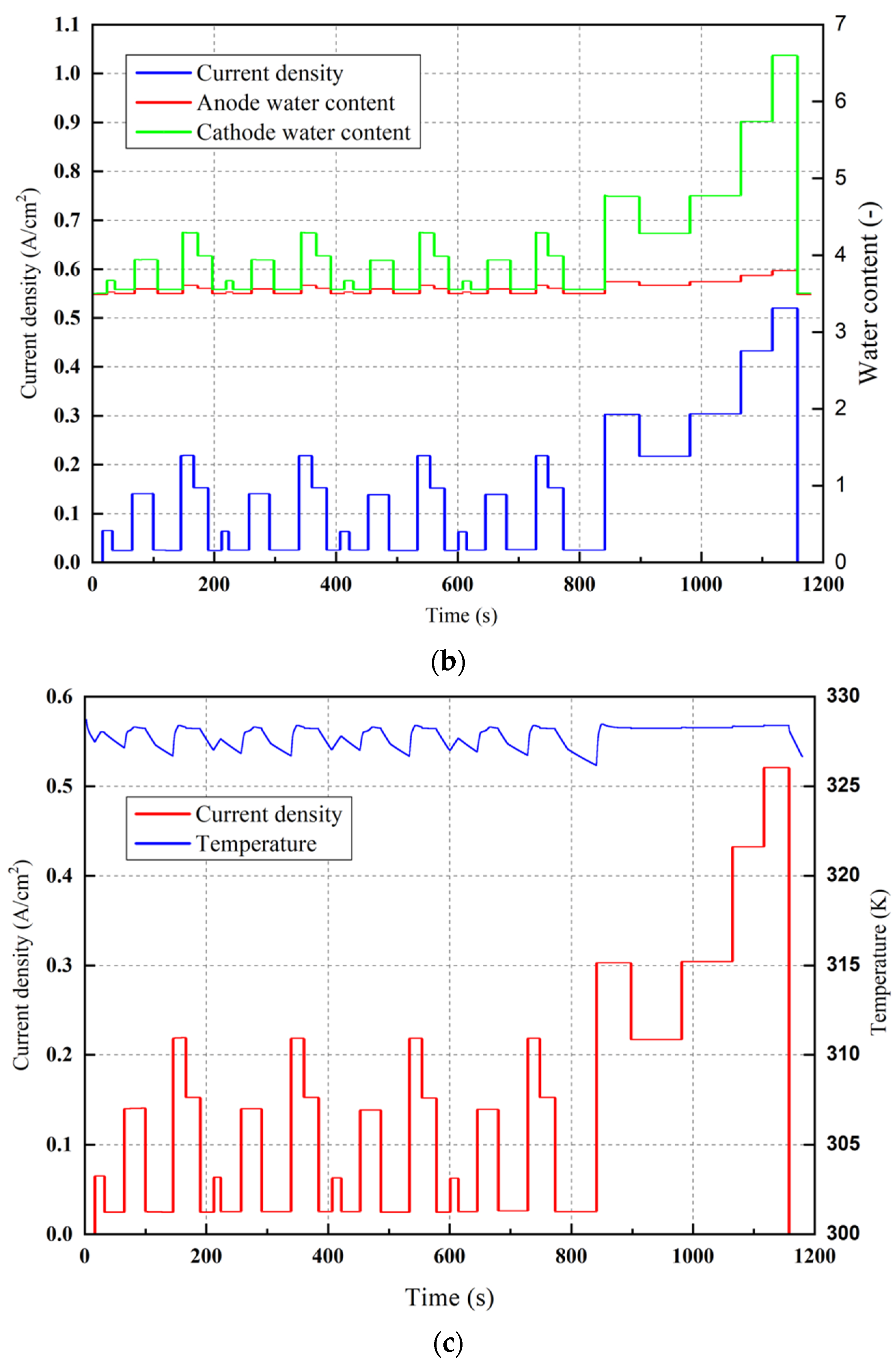
4.2.3. Transient Responses of a Modular Stack Model
4.2.4. Voltage Degradation and PEMFC Lifetime Prediction
4.3. Potential Use of the Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | area [m2] |
| a | Water activity [-] |
| A1 | Active surface area aging parameter [cm2] |
| A2 | Active surface area aging parameter [h−1] |
| Ao | Active surface area at t = 0 [cm2] |
| Ba | Anode concentration loss parameter [V] |
| Bc | Cathode concentration loss parameter [V] |
| c | Concentration [mol.cm−3] |
| cp | Specific heat [J.kg−1.K−1] |
| cw | the water concentration, in mol/cm3 |
| Dij | Diffusion coefficient of species i and j [cm2.s−1] |
| Dλ | Water diffusivity [cm2.s−1] |
| Erev | Reversible open-circuit voltage [V] |
| F | Faraday constant [96485 C.mol−1] |
| h | Heat transfer coefficient [W.m−2.K−1] |
| I | Current [A] |
| i | Current density [A.cm−2] |
| iL,a | Limiting current density at the anode [A.cm−2] |
| iL,c | Limiting current density at the cathode [A/cm−2] |
| iloss,1 | Aging parameter of iloss [h−1] |
| iloss,o | Initial parameter of iloss [A.cm−2] |
| iloss | Internal current density [A.cm−2] |
| io,a | Exchange current density at the anode [A.cm−2] |
| io,c | Exchange current density at the cathode [A.cm−2] |
| J | Diffusion flux [mol.m−2.s−1] |
| Jw,d | Electro-osmotic drag [mol.s−1.cm−2] |
| Jw,diff | Back diffusion drag [mol.s−1.cm−2] |
| L | membrane thickness (cm) |
| m | Empirical parameter in concentration loss equation [V] |
| m | Mass flow rate [kg.s−1] |
| m1 | Aging parameter of m [h−1] |
| Mm | Membrane dry equivalent weight [kg.mol−1] |
| mo | Initial parameter of m [V] |
| n | Empirical parameter in concentration loss equation [cm2.A−1] |
| n1 | Aging parameter of n [h−1] |
| nd | Electro-osmotic drag coefficient [-] |
| no | Initial parameter of n [cm2/A] |
| p | Pressure [pa] |
| PH2 | the partial pressure of H2 [atm] |
| PO2 | the partial pressure of O2 [atm] |
| Qdry | Membrane dry density [kg.cm−3] |
| R | Idea gas constant [8.314 J.mol−1.K−1] |
| R | Ohmic resistance [ohm.cm2] |
| R1 | Aging parameter of R [h−1] |
| Rcr | Contact resistance [ohm.cm2] |
| Rele | Electronic resistance [ohm.cm2] |
| RH | Relative humidity [%] |
| Rmemb | Membrane resistance [ohm.cm2] |
| Ro | Initial parameter of R [ohm.cm2] |
| s | Stoichiometry [-] |
| T | Temperature [K] |
| tA | Anode electrode thickness |
| Tc,in | Coolant temperature outlet [K] |
| Tc,o | Coolant temperature outlet [K] |
| tC | Cathode electrode thickness |
| Tg,in | Gas temperature inlet [K] |
| Tg,o | Gas temperature outlet [K] |
| VPtO,1 | Aging parameter of VPtO [h−1] |
| VPtO,o | Initial parameter of VPtO [V] |
| VPtO | Platinum oxide overvoltage [V] |
| x | Mole fraction [0~1] |
| αa | Charge transfer coefficient at the anode |
| αc | Charge transfer coefficient at the cathode |
| λ | Water content [-] |
References
- Nguyen, H.L.; Han, J.; Nguyen, X.L.; Yu, S.; Goo, Y.M.; Le, D.D. Review of the Durability of Polymer Electrolyte Membrane Fuel Cell in Long-Term Operation: Main Influencing Parameters and Testing Protocols. Energies 2021, 14, 4048. [Google Scholar] [CrossRef]
- Borup, R.; Meyers, J.; Pivovar, B.; Kim, Y.S.; Mukundan, R.; Garland, N.; Myers, D.; Wilson, M.; Garzon, F.; Wood, D.; et al. Scientific Aspects of Polymer Electrolyte Fuel Cell Durability and Degradation. Chem. Rev. 2007, 107, 3904–3951. [Google Scholar] [CrossRef]
- Yuan, X.Z.; Li, H.; Zhang, S.; Martin, J.; Wang, H. A Review of Polymer Electrolyte Membrane Fuel Cell Durability Test Protocols. J. Power Sources 2011, 196, 9107–9116. [Google Scholar] [CrossRef]
- Mayur, M.; Strahl, S.; Husar, A.; Bessler, W.G. A Multi-Timescale Modeling Methodology for PEMFC Performance and Durability in a Virtual Fuel Cell Car. Int. J. Hydrogen Energy 2015, 40, 16466–16476. [Google Scholar] [CrossRef]
- Han, J.; Han, J.; Yu, S. Investigation of FCVs Durability under Driving Cycles Using a Model-Based Approach. J. Energy Storage 2020, 27, 101169. [Google Scholar] [CrossRef]
- Ehlinger, V.M.; Kusoglu, A.; Weber, A.Z. Modeling Coupled Durability and Performance in Polymer-Electrolyte Fuel Cells: Membrane Effects. J. Electrochem. Soc. 2019, 166, F3255–F3267. [Google Scholar] [CrossRef]
- Zheng, W.; Xu, L.; Hu, Z.; Ding, Y.; Li, J.; Ouyang, M. Dynamic Modeling of Chemical Membrane Degradation in Polymer Electrolyte Fuel Cells: Effect of Pinhole Formation. J. Power Sources 2021, 487, 229367. [Google Scholar] [CrossRef]
- Zheng, W.; Xu, L.; Hu, Z.; Zhao, Y.; Li, J.; Ouyang, M. Dynamic Modeling of Pt Degradation and Mitigation Strategies in Polymer Electrolyte Membrane Fuel Cells. eTransportation 2022, 12, 100171. [Google Scholar] [CrossRef]
- Kregar, A.; Gatalo, M.; Maselj, N.; Hodnik, N.; Katrašnik, T. Temperature Dependent Model of Carbon Supported Platinum Fuel Cell Catalyst Degradation. J. Power Sources 2021, 514, 230542. [Google Scholar] [CrossRef]
- Jouin, M.; Gouriveau, R.; Hissel, D.; Péra, M.C.; Zerhouni, N. Degradations Analysis and Aging Modeling for Health Assessment and Prognostics of PEMFC. Reliab. Eng. Syst. Saf. 2016, 148, 78–95. [Google Scholar] [CrossRef]
- Zhou, D.; Wu, Y.; Gao, F.; Breaz, E.; Ravey, A.; Miraoui, A. Degradation Prediction of PEM Fuel Cell Stack Based on Multiphysical Aging Model with Particle Filter Approach. IEEE Trans. Ind. Appl. 2017, 53, 4041–4052. [Google Scholar] [CrossRef]
- Bressel, M.; Hilairet, M.; Hissel, D.; Ould Bouamama, B. Extended Kalman Filter for Prognostic of Proton Exchange Membrane Fuel Cell. Appl. Energy 2016, 164, 220–227. [Google Scholar] [CrossRef]
- Liu, H.; Chen, J.; Zhu, C.; Su, H.; Hou, M. Prognostics of Proton Exchange Membrane Fuel Cells Using A Model-Based Method. FAC-Pap. 2017, 50, 4757–4762. [Google Scholar] [CrossRef]
- Song, K.; Wang, Y.; Hu, X.; Cao, J. Online Prediction of Vehicular Fuel Cell Residual Lifetime Based on Adaptive Extended Kalman Filter. Energies 2020, 13, 6244. [Google Scholar] [CrossRef]
- Zhang, D.; Baraldi, P.; Cadet, C.; Yousfi-Steiner, N.; Bérenguer, C.; Zio, E. An Ensemble of Models for Integrating Dependent Sources of Information for the Prognosis of the Remaining Useful Life of Proton Exchange Membrane Fuel Cells. Mech. Syst. Signal Process 2019, 124, 479–501. [Google Scholar] [CrossRef]
- Mao, L.; Jackson, L.; Jackson, T. Investigation of Polymer Electrolyte Membrane Fuel Cell Internal Behaviour during Long Term Operation and Its Use in Prognostics. J. Power Sources 2017, 362, 39–49. [Google Scholar] [CrossRef]
- Han, J.; Han, J.; Yu, S. Experimental Analysis of Performance Degradation of 3-Cell PEMFC Stack under Dynamic Load Cycle. Int. J. Hydrogen Energy 2020, 45, 13045–13054. [Google Scholar] [CrossRef]
- Sharaf, O.Z.; Orhan, M.F. An Overview of Fuel Cell Technology: Fundamentals and Applications. Renew. Sustain. Energy Rev. 2014, 32, 810–853. [Google Scholar] [CrossRef]
- Barbir, F. PEM Fuel Cells: Theory and Practice; Elsevier Academic Press: Burlington, NJ, USA, 2005. [Google Scholar]
- Kim, J.; Lee, S.; Srinivasan, S.; Chamberlin, C.E. Modeling of Proton Exchange Membrane Fuel Cell Performance with an Empirical Equation. J. Electrochem. Soc. 1995, 142, 2670–2674. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, Y.; Song, C.; Zhang, J.; Wang, H. PEM Fuel Cell Open Circuit Voltage (OCV) in the Temperature Range of 23 °C to 120 °C. J. Power Sources 2006, 163, 532–537. [Google Scholar] [CrossRef]
- Ahmadi, V. Modeling of Proton Exchange Membrane Fuel Cell Performance Degradation and Operation Life. Master’s Thesis, University of Victoria, Victoria, BC, Canada, 2021. [Google Scholar]
- Huang, L.; Zhang, X.; Jiang, Y.; Huang, P.; Lin, L. Modeling-Based Analytics of Degradation Behavior for Fuel Cell Stack under Actual Dynamic Ambient Temperature. Energy Convers. Manag. 2022, 269, 116100. [Google Scholar] [CrossRef]
- Abderezzak, B. Introduction to Transfer Phenomena in PEM Fuel Cell; Elsevier Ltd.: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Lee, H.; Han, C.; Park, T. Experimental Investigation of Charge Transfer Coefficient and Exchange Current Density in Standard Fuel Cell Model for Polymer Electrolyte Membrane Fuel Cells. Korean J. Chem. Eng. 2020, 37, 577–582. [Google Scholar] [CrossRef]
- Jao, T.C.; Jung, G.B.; Kuo, S.C.; Tzeng, W.J.; Su, A. Degradation Mechanism Study of PTFE/Nafion Membrane in MEA Utilizing an Accelerated Degradation Technique. Int. J. Hydrogen Energy 2012, 37, 13623–13630. [Google Scholar] [CrossRef]
- Mukundan, R.; Baker, A.M.; Kusoglu, A.; Beattie, P.; Knights, S.; Weber, A.Z.; Borup, R.L. Membrane Accelerated Stress Test Development for Polymer Electrolyte Fuel Cell Durability Validated Using Field and Drive Cycle Testing. J. Electrochem. Soc. 2018, 165, F3085–F3093. [Google Scholar] [CrossRef]
- Han, J.; Han, J.; Ji, H.; Yu, S. “Model-Based” Design of Thermal Management System of a Fuel Cell “Air-Independent” Propulsion System for Underwater Shipboard. Int. J. Hydrogen Energy 2020, 45, 32449–32463. [Google Scholar] [CrossRef]
- Noacco, V.; Sarrazin, F.; Pianosi, F.; Wagener, T. Matlab/R Workflows to Assess Critical Choices in Global Sensitivity Analysis Using the SAFE Toolbox. MethodsX 2019, 6, 2258–2280. [Google Scholar] [CrossRef]
- Pianosi, F.; Wagener, T. A Simple and Efficient Method for Global Sensitivity Analysis Based Oncumulative Distribution Functions. Environ. Model. Softw. 2015, 67, 1–11. [Google Scholar] [CrossRef]
- Pianosi, F.; Wagener, T. Distribution-Based Sensitivity Analysis from a Generic Input-Output Sample. Environ. Model. Softw. 2018, 108, 197–207. [Google Scholar] [CrossRef]
- FCTESTNET Test Module PEFC SC 5-6, Version 30 04, JRC Scientific and Technical Reports; Publications Office of the European Union: Luxembourg, 2010.






| Parameters | Value |
|---|---|
| Active area of the fuel cell | 25 cm2 |
| Number of cells | 3 |
| Membrane (Nafion 211) thickness | 23 μm |
| Catalyst layer thickness | 42 μm |
| Gas diffusion thickness | 320 μm |
| Durability test 1 (T = 55 °C) | VPtO,o (V) | αa | αa | Iloss,o (A/cm2) | io,a (A/cm2) |
| 0.2582 | 0.5 | 0.5 | 0.0027 | 0.0083 | |
| io,c (A/cm2) | Ro (ohm/cm2) | mo | no | ||
| 0.0083 | 0.2067 | 0.0082 | 0.1065 | ||
| Durability test 2 (T = 75 °C) | VPtO,o (V) | αa | αa | Iloss,o (A/cm2) | io,a (A/cm2) |
| 0.1972 | 0.5 | 0.5 | 0.0080 | 0.0095 | |
| io,c (A/cm2) | Ro (ohm/cm2) | mo | no | ||
| 0.0091 | 0.1659 | 0.3872 | 0.1872 |
| Durability test 1 (T = 55 °C) | VPtO,1 (1/h) | iloss,1 (1/h) | A1 (cm2) | A2 (1/h) |
| 6.75 × 10−5 | 2.11 × 10−6 | 0.0360 | 0.0019 | |
| R1 (1/h) | m1 (1/h) | n1 (1/h) | ||
| 4.29 × 10−4 | 0.0055 | 0 | ||
| Durability test 2 (T = 75 °C) | VPtO,1 (1/h) | iloss,1 (1/h) | A1 (cm2) | A2 (1/h) |
| 1.33 × 10−4 | 1.32 × 10−3 | 0.1172 | 1.87 × 10−4 | |
| R1 (1/h) | m1 (1/h) | n1 (1/h) | ||
| 5.97 × 10−5 | 0.0033 | 6.54 × 10−5 |
| SSE | R-Square | RMSE | |
|---|---|---|---|
| Durability test 1 | 0.0015 | 0.9981 | 0.0062 |
| Durability test 2 | 0.0006 | 0.9994 | 0.0041 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, H.L.; Han, J.; Vu, H.N.; Yu, S. Investigation of Multiple Degradation Mechanisms of a Proton Exchange Membrane Fuel Cell under Dynamic Operation. Energies 2022, 15, 9574. https://doi.org/10.3390/en15249574
Nguyen HL, Han J, Vu HN, Yu S. Investigation of Multiple Degradation Mechanisms of a Proton Exchange Membrane Fuel Cell under Dynamic Operation. Energies. 2022; 15(24):9574. https://doi.org/10.3390/en15249574
Chicago/Turabian StyleNguyen, Huu Linh, Jaesu Han, Hoang Nghia Vu, and Sangseok Yu. 2022. "Investigation of Multiple Degradation Mechanisms of a Proton Exchange Membrane Fuel Cell under Dynamic Operation" Energies 15, no. 24: 9574. https://doi.org/10.3390/en15249574
APA StyleNguyen, H. L., Han, J., Vu, H. N., & Yu, S. (2022). Investigation of Multiple Degradation Mechanisms of a Proton Exchange Membrane Fuel Cell under Dynamic Operation. Energies, 15(24), 9574. https://doi.org/10.3390/en15249574






